2007-2016年安徽省高中数学竞赛初赛试题及答案详解

合集下载

2016年安徽数学竞赛试题(初赛)

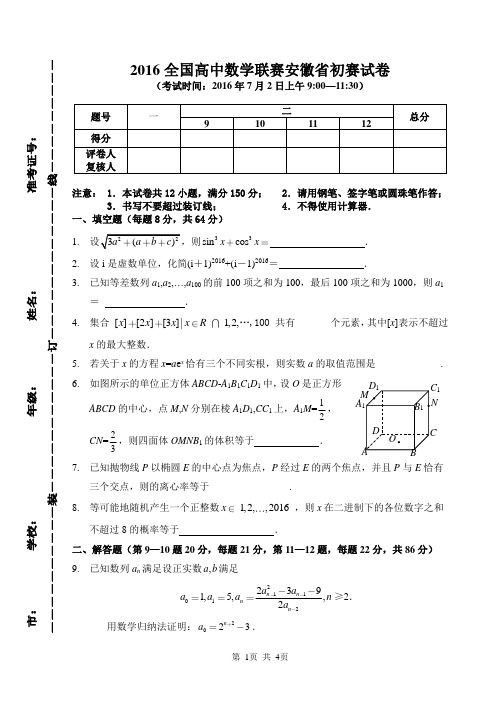
2016全国高中数学联赛安徽省初赛试卷（考试时间：2016年7月2日上午9:00—11:30）注意： 1．本试卷共12小题，满分150分； 2．请用钢笔、签字笔或圆珠笔作答；3．书写不要超过装订线； 4．不得使用计算器．一、填空题（每题8分，共64分）1. 22()a b c ，则33sin cos x x ．2. 设i 是虚数单位，化简(i ＋1)2016+(i －1)2016＝．3. 已知等差数列a 1,a 2,…,a 100的前100项之和为100，最后100项之和为1000，则a 1＝．4. 集合[][2][3]|1,2,x x x x R …,100共有_______个元素，其中[x ]表示不超过x 的最大整数．5. 若关于x 的方程x =a e x 恰有三个不同实根，则实数a 的取值范围是_____________.6. 如图所示的单位正方体ABCD -A 1B 1C 1D 1中，设O 是正方形ABCD 的中心，点M ,N 分别在棱A 1D 1,CC 1上，A 1M =12，CN =23，则四面体OMNB 1的体积等于．7. 已知抛物线P 以椭圆E 的中心点为焦点，P 经过E 的两个焦点，并且P 与E 恰有三个交点，则的离心率等于________________.8. 等可能地随机产生一个正整数1,2,,2016x ，则x 在二进制下的各位数字之和不超过8的概率等于．二、解答题（第9—10题20分，每题21分，第11—12题，每题22分，共86分）9. 已知数列a n 满足设正实数b a ,满足2110122391,5,,2n n n n a a a a a n a ≥2．用数学归纳法证明：2023n a ．A 110.ΔABC的内切圆与三边相切于点D,E,F．证明：ΔABC与ΔDEF相似当且仅当ΔABC是正三角形．11.证明：对任意实数a,b,c都有2222ab b a ac c≥22()a b c.并求等号成立的充分必要条件.12.求满足1≤m n－n m≤mn的所有正整数对(m,n)．。

2016年全国高中数学联赛试题及答案

下面验证符合条件．
事实上，当中有某条直线斜率不存在时，则可设，就是前面所讨论的的情况，这时有若的斜率都存在，不妨设
注意这里（否则将与的渐近线平行，从而与只有一个交点）．
联立与的方程知，即
这是一个二次方程式，其判别式为．故与有两个不同的交点．同样，与也有两个不同的交点由弦长公式知，
又所以，即平分
四、（50分）设是任意一个11元实数集合．令集合求的元素个数的最小值．
解：先证明考虑到将中的所有元素均变为原来的相反数时，集合不变，故不妨设中正数个数不少于负数个数．下面分类讨论：
情况一：中没有负数．
设是中的全部元素，这里于是
上式从小到大共有个数，它们均是的元素，这表明
另解：首先注意到，若为正整数，则对任意整数，若，则这是因为，当时，，这里是一个整数，故
因此，当整数满足时，
容易验证，当正整数满足时，只有当时，等式才成立．而，故当时，满足正整数的个数为
二、解答题：（共3小题，共56分）
9.（16分）已知是各项均为正数的等比数列，且是方程
2016
一试
一、选择题：（每小题8分，共64分）
1.等比数列的各项均为正数，且则的值为．
答案：6．
解：由于且故
另解：设等比数列的公比为，则又因
而，从而
2.设，则平面点集的面积为．
答案：7．
解：点集如图中阴影部分所示，其面积为
3.已知复数满足（表示的共轭复数），则的所有可能值的积为．
用代替，同理可得于是
综上所述，为符合条件的值．
加试
一、（40分）非负实数和实数满足：

全国高中数学联赛安徽省预赛试题及参考答案

全国高中数学联赛安徽省预赛试题一、填空题（每小题8分，共64分）1．以X 表示集合X 的元素个数. 若有限集合C B A ,,满足20=B A ，30=C B ，40=A C ，则C B A 的最大可能值为 . 2．设a 是正实数. 若R ∈++++-=x a ax x a ax x x f ，222252106)(的最小值为10，则=a .3．已知实系数多项式d cx bx ax x x f ++++=234)(满足2)1(=f ，4)2(=f ，6)3(=f ，则)4()0(f f +的所有可能值集合为 . 4．设展开式2011)15(10≥+++=+n x a x a a x n n n ， .若),,,max(102011n a a a a =，则=n .5．在如图所示的长方体EFGH ABCD -中，设P是矩形EFGH 的中心，线段AP 交平面BDE于点Q . 若3=AB ，2=AD ，1=AE ，则=PQ .6．平面上一个半径r 的动圆沿边长a 的正三角形的外侧滚动，其扫过区域的面积为 .7．设直角坐标平面上的点),(y x 与复数i y x +一一对应. 若点B A ,分别对应复数1,-z z （R ∉z ），则直线AB 与x 轴的交点对应复数（用z 表示）. 8．设n 是大于4的偶数. 随机选取正n 边形的4个顶点构造四边形，得到矩形的概率为 .二、解答题（第9—10题每题22分，第11—12题每题21分，共86分） 9．已知数列}{n a 满足121==a a ，4121-++-=n n a a a （3≥n ），求n a 的通项公式.10．已知正整数n a a a ,,,21 都是合数，并且两两互素，求证：2111121<+++n a a a . 11．设c bx ax x f ++=3)(（c b a ,,是实数），当10≤≤x 时，1)(0≤≤x f . 求b 的第5题第6题最大可能值.12．设点)0,2()0,1()0,1(C B A ，，-，D 在双曲线122=-y x 的左支上，A D ≠，直线CD 交双曲线122=-y x 的右支于点E . 求证：直线AD 与BE 的交点P 在直线21=x 上.解答1. 10.2. 2.3. {32}.4. 2413.5.417. 6. 2π46r ar +. 7. zz zz ++1. 8.)3)(1(3--n n .9．1221144n n n n a a aa a ---++=-=-1211112222n n n n n a a a a ----⎛⎫⇒-=-==⎪⎝⎭11212122----=⇒==+=⇒n n n n n n n a n a a .10．设k a 的最小素因子k p ，因为k a 不是素数，所以2k k p a ≥. 于是211222211114(21)114(21)1111242nnk k k k n k nk a p k k n ====≤≤+-≤+--=-<∑∑∑∑11．由(0)(1)f c f a b cf c ⎧=⎪⎪=++⎨⎪=+⎪⎩可知2(1)1)(0)b f f =--≤)()(3233x x x f -=满足题设，b 的最大可能值为233.12．设),(),(),(2211y x P y x E y x D ，，，直线CD 的方程)2(-=x k y ，则222(2)1x k x --=，所以221212122241451()114k k x x x x x x k k -++==-=-++--，， ① 1212(1)(1)11y yx y x x x +==-+-，所以21212121121221212121212211112322341111y y x x x x x x x x x x x y y x x x x x x x x --++-+-+--===-------+-+。

2007安徽省高中数学竞赛初赛试题

2007年安徽省高中数学竞赛初赛试题一选择题1.如果集合.A B 同时满足{}1.2.3.4AB ={}1A B =,{}{}1,1A B ≠≠就称有序集对(),A B 为“好集对”。

这里的有序集对(),A B 意指当A B ≠，()(),,A B B A 和是不同的集对，那么“好集对”一共有（）个。

64862AB C D２.设函数()()lg 101xf x -=+,()()122x x f f --=方程的解为( )()()()()2222.log lg21.lg log 101.lg lg21.log log 101A B C D --++3.设100101102499500A =是一个1203位的正整数,由从100到500的全体三位数按顺序排列而成那么A 除以126的余数是( )783660A B C D4.在直角ABC 中, 90C ∠=,CD 为斜边上的高,D为垂足. ,,1AD a BD b CD a b ===-=.设数列{}k u 的通项为()1221,1,2,3,,kk k k k k u a a b a b b k --=-+-+-=则( )2008200720062008200720062008200720082007 2007200820082007.. .. u u u u u u u u u u A B C D =+=-==5.在正整数构成的数列1.3.5.7……删去所有和55互质的项之后,把余下的各项按从小到大的顺序排成一个新的数列{}n a ,易见123451,3,7,9,13a a a a a =====那么2007____________a =192759.. 55 .. A B C D 2831 95976.设A B ==1+cos871-cos87则():A B =. .A B C D二.填空题7.边长均为整数且成等差数列,周长为60的钝角三角形一共有______________种. 8.设2007n ≥,且n为使得nn a =取实数值的最小正整数,则对应此n 的n a 为( ).9.若正整数n 恰好有4个正约数,则称n 为奇异数,例如6,8,10都是奇异数.那么在27,42,69,111,125,137,343,899,3599,7999这10个数中奇异数有_____________________个. 10.平行六面体1111ABCD A B C D -中,顶点A 出发的三条棱1,,AB AD AA 的长度分别为2,3,4,且两两夹角都为60那么这个平行六面体的四条对角线1111,,,AC BD DB CA 的长度(按顺序)分别为___________________11.函数()(),f x g x 的迭代的函数定义为()()()()()()()12,,f x f x f x ff x ==()()()()()()()()()()()()()()()()()1121,,,n n n n f x f f x g x g x g x g g x g x g g x --====其中n =2,3,4…设()()23,32f x x g x x =-=+,则方程组()()()()()()()()()()()()969696f x g y f y g z f z g x ⎧=⎪⎪=⎨⎪=⎪⎩的解为_________________12.设平行四边形ABCD中，4,2,AB AD BD ===则平行四边形ABCD 绕直线AC 旋转所得的旋转体的体积为_______________三解答题13.已知椭圆22412:3y x +=Γ和点(),0,Q q 直线,l Q A B Γ过且与交于两点(可以重合). 1)若AOB ∠为钝角或平角(O 为原点),4,q =试确定l 的斜率的取值范围.2)设A 关于长轴的对称点为1A ,,4,F q =为椭圆的右焦点试判断1,A F B 和三点是否共线,并说明理由.3)问题2)中,若14,,,q A F B ≠那么三点能否共线?请说明理由.14.数列{}n x 由下式确定:112,1,2,3,,121nn n x x n x x +===+,试求[]20072007l g l g .x k x =整数部分(注[]a 表示不大于a 的最大整数,即a 的整数部分.)15.设给定的锐角ABC 的三边长,,,,,a b c x y z 正实数满足,ayz bzx cxyp x y z++=其中p 为给定的正实数,试求()()()222s b c a x c a b y a b c z =+-++-++-的最大值,并求出当s 取此最大值时, ,,x y z 的取值.解答一、选择题1.C.2.A.3.C.4.A.5.B6.D.1.逐个元素考虑归属的选择. 元素1必须同时属于A 和B .元素2必须至少属于A 、B 中之一个，但不能同时属于A 和B ，有2种选择：属于A 但不属于B ，属于B 但不属于A .同理，元素3和4也有2种选择.但元素2，3，4不能同时不属于A ，也不能同时不属于B .所以4个元素满足条件的选择共有62222=-⨯⨯种.换句话说，“好集对”一共有6个. 答：C.2.令)110lg(+=-x y ，则0>y ，且y x10110=+-，11010-=-y x ，)110lg(-=-y x ，)110lg(--=y x .从而)110lg()(1--=-x x f .令t x=2，则题设方程为 )()(1t ft f -=-，即 )110lg()110lg(--=+t t ，故 0)]110)(110lg[(=-+t t ，1)110)(110(=-+t t ，2102=t， 2lg 2=t ，解得 2lg 212==t x. 从而 1)2(l g l o g )2lg 21(log 22-==x . 答：A. 3. 注意 972126⨯⨯=,2,7和9两两互质. 因为 0≡A （mod2）, ）（）（）（）（）（005994201101001+++++++++++++++≡ A500102101100++++≡ 2401500100÷⨯+≡）（6120300≡≡（mod9）, 所以 6≡A （mod18）. （1）又因为1103-≡，nn )1(103-≡（mod7）, 所以ii i A 3410)500(⨯-=∑=i i i ）（1)500(4000-⨯-≡∑= 100)101102()495496()497498()499500(+-++-+-+-≡ 6300≡=（mod7）.(2)由（1），（2）两式以及7和18互质，知6≡A （mod126）. 答：C.另解：632126⨯=，99999963，1109999996-=，）（）（11011066--n ，,3,2,1=n .所以499500104974981010310410101102101006118811941200+⨯++⨯+⨯+⨯= A+-⨯++-⨯+-⨯+-⨯=）（）（）（）（1104974981101031041101011021101006118811941200）（499500497498103104101102100+++++2200499500101102100999999÷⨯+++=）（B 60060200100999999++=B 60060300999999+=B 60360999999+=C ，其中B ，C 为整数.从而6036063+=D A 663+=E ，其中D ，E 为整数.所以A 除以63的余数为6.因为A 是偶数，所以A 除以126的余数也为6. 答：C.4.易见BD AD CD ⋅=2，即ab b a =-2）（，又已知1=-b a ，故1=ab ，1)1(=-a a ，012=--a a ；1)1(=+b b ，012=++b b .显然k u 是首项为ka ，公比为abq -=的等比数列的前1+k 项和.故 ba b a q q a u k k k k k +--=--=+++111)(1)1(， 3,2,1=k . 从而ba b a b a b a u u k k k k k k +--++--=++++++22111)()(])()([11212++++----++=k k k k b b a a ba )]1()()1([111+---++=++b b a a b a k k ])([12121b b a a b a k k ⋅--⋅+=++ 233])([1+++=--+=k k k u b a ba ， 3,2,1=k . 故答案为A.（易知其余答案均不成立）另解：易见BD AD CD ⋅=2，即ab b a =-2）（，又已知1=-b a ，故1=ab ，51414)((222=⨯+=+-=+ab b a b a ），5=+b a .解得215+=a ， 215-=b . 显然k u 是首项为ka ，公比为abq -=的等比数列的前1+k 项和，故 ba b a q q a u k k k k k +--=--=+++111)(1)1(])251()251[(5111++--+=k k ，,3,2,1=k .于是数列{}k u 就是斐波那契数列1，2，3，5，8，13，21，…，它满足递推关系 ,12k k k u u u +=++ ,3,2,1=k . 所以答案为A.5.{}n a 可看成是在正整数数列1，2，3，4，5，6，7，…中删去所有能被2，5或11整除的项之后，把余下的各项按从小至大顺序排成的数列.由三阶容斥原理，1，2，3，4，…，m 中不能被2，5或11整除的项的个数为⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1101022551152m m m m m m m m x m ，其中⎣⎦a 不表示不大于a 的最大整数，即a 的整数部分.估值：设11010225511522007m m m m m m m m x m -+++---≈=)1111)(511)(211(---⨯=m 11105421⨯⨯⨯=m m 114=，故 55194112007≈⨯≈m . 又因为⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1105519105519225519555519115519555192551955195519x=5519-2759-1103-501+100+250+551-50=2007，并且5519不是2，5，11的倍数，从而知55192007=a . 答：B.又解：{}n a 可看成是在正整数数列1，2，3，4，5，6，7，…中删去所有能被2，5 或11整除的项之后，把余下的各项按从小至大顺序排成的数列.因为2，5，11是质数，它们的最小公倍数为110.易见，-54，-53，…，0，1，2，3，…，55中不能被2，5，11整除的数为，，；，，，17139731±±±±±±，；2119±±；，，292723±±±，，，；，，474341393731±±±±±±535149±±±，；,共40个.（或由欧拉公式，1，2，3，…，110中不能被2，5，11整除的数的个数，等于1，2，3，…，110中与110互质的数的个数，等于401111511211110110=-⨯-⨯-⨯=∅）（）（）（）（.）显然1，2，3，…中每连续110个整数，不能被2，5，11整除的数都有40个.所以，1，2，3，…，550050110=⨯中，不能被2，5，11整除的数有20005040=⨯个.大于5500中的数不能被2，5，11整除的，是5500+1，5500+3，5500+7，5500+9，5500+13，5500+17，5500+19，….所以5519是第2007个不能被2，5，11整除的数，亦即所求的55192007=a . 答：B .6.显然 287cos 127cos 123cos 12++++++=A5.43cos 5.5cos 5.3cos 5.1cos ++++=；287cos 127cos 123cos 12-++-+-=B5.43sin 5.5sin 5.3sin 5.1sin ++++=. 注意到)1sin()1sin(1sin cos 2--+=θθθ， )1cos()1cos(1sin sin 2+--=θθθ, 所以+-+-+-=⨯)5.4sin 5.6(sin )5.2sin 5.4(sin )5.0sin 5.2(sin 21sin 2A)5.42sin 5.44(sin -+ 22sin 5.22cos 25.0sin 5.44sin =-=，+-+-+-=⨯)5.6cos 5.4(cos )5.4cos 5.2(cos )5.2cos 5.0(cos 21sin 2B)5.44cos 5.42(cos -+ 22sin 5.22sin 25.44cos 5.0cos =-=.故5.22cot )22sin 5.22sin 2(:)22sin 5.22cos 2()21sin 2(:)21sin 2(:==⨯⨯=B A B A12+=. 答：D.另解：2A 00005.43cos 5.5cos 5.3cos 5.1cos +++++= ，2B 5.43sin 5.5sin 5.3sin 5.1sin ++++=，++++=+)5.3sin 5.3(cos )5.1sin 5.1(cos 22i i B iA )5.43sin 5.43(cos i ++∑=++=21)2sin 2(cos )5.1sin 5.1(cos k k i i)2sin 2(cos 1)2sin 2(cos 1)5.1sin 5.1(cos 22i i i +-+-+= )2sin 2(cos 1)44sin 44(cos 1)5.1sin 5.1(cosi i i +-+-+=1cos 1sin 21sin 222cos 22sin 222sin 2)5.1sin 5.1(cos 22i i i --+=)1sin 1)(cos 1sin 2()22sin 22)(cos 22sin 2)(5.1sin 5.1(cos i i i i i +-+-+==)5.22sin 5.22(cos 1sin 22sini +.因为2A 和2B 是实数，所以 1sin 5.22cos 22sin 2=A ，1sin 5.22sin 22sin 2=B , 122222222145sin 45cos 15.22cos 5.22sin 25.22cos 25.22sin 5.22cos 2:2:2+=+=+=+====B A B A .答：D.二、填空题（满分54分，每小题9分）7.解：设△ABC 三边长c b a ,,为整数，c b a c b a c b a ,,,,60≥≥=++成等差数列，A ∠为钝角，则必有c a b +=2，222a c b <+.易解得 b b b c a b c b a 32)(60=+=++=++=，40,20=+=c a b ；222c a b -<))((c a c a -+=，即c a c a -<-<10),(40202.因此a a c a c a <=-++<25,2)()(50，即26≥a .另外，29,30,260,≤<=+>++=>+a a a a a c b a a c b .易检验),,(c b a)11,20,29(),12,20,28(),13,20,27(),14,20,26(=都是钝角三角形. 答：4.8.注意到22-=x ，22+=y 满足4)22()22(22=++-=+y x ，0,>y x ，故可令θcos 2=x ，θsin 2=y ，0＜θ＜2π.从而22c o s 42-=θ，-2cos 422-=θ，-θπθ2cos 43cos 1cos 2222==-=，故83πθ=，83cos )83sin 83(cosπππn i a n n =+=+ 83sin πn i . n a 取实数，当且仅当083sin=πn ，当且仅当k n 8=，∈k Z.满足此条件且2007≥n 的最小正整数n 为2008，此时1753cos 820083cos 2008-====ππx a a n .答：-1.9.易见奇异数有两类：第一类是质数的立方3p （p 是质数）；第二类是两个不同质数的乘积21p p （21,p p 为不同的质数）.由定义可得3327=是奇异数（第一类）； 73242⨯⨯=不是奇异数； 23369⨯=是奇异数（第二类）；373111⨯=是奇异数（第二类）；35125=是奇异数（第一类）； 137是质数，不是奇异数；37343=是奇异数（第一类）；221301900899-=-=）（130+=2931130⨯=-）（是奇异数（第二类）；）（16016013600359922+=-=-=5961160⨯=-）（是奇异数（第二类）；42119)12020)(120(120180007999233⨯=++-=-=-=是奇异数（第二类）. 答：8.10. 解：将向量1AA ，，分别记为，，.2==a3==b，4==c ，且易见c b a AC ++=1， c b a C A ++-=1， c b a BD +-=1， c b a DB -+=1.)(2)(2222⋅+⋅+⋅+++=++=022260cos )(2ca bc ab c b a +++++=ca bc ab c b a +++++=222244332432222⨯+⨯+⨯+++==55，故551=AC . 类似地，可算得，191=BD ，151=DB ，271=CA =33.答：55，19，15，33.11.令t x =-3，易见3+=t x ，323)3(232)(+=-+=-=t t x x f ，)32(2)()2(+=t x f 3-32)(,,32)(2+=+=t x f t n n ；令s y =+1，易见1-=s y ，2)1(323)(+-=+=s y y g 13-=s ，,132)13(3)(2)2(-=+-=s s y g ，13)()(-=s y g n n ， ,3,2,1=n .因此，题设方程组可化为⎪⎩⎪⎨⎧-+=+--+=+--+=+-)3.(1)1(33)3(2)2(,1)1(33)3(2)1(,1)1(33)3(2696969x z z y y x （1）-（2），（2）-（3），（3）-（1）得⎪⎩⎪⎨⎧-=--=--=-)6).((3)(2)5(),(3)(2)4(),(3)(2696969y x x z x z z y z y y x所以)()23()()23()(2339629696y x x z z y y x -=-=-=-⇒00=-⇒=-z y y x z y x ==⇒.代入（1）得1)1(33)3(269-+=+-x x ，1)1(7293)3(512-+=+-x x ，7287291533512+=-x x ， 2261217=-x , 32331=-x , 31323-=x . 所以原方程组的解为31323-===z y x . 答：31323-===z y x . 12.以l T V -表示平面图形T 绕直线l 所得旋转体体积.记直线AC 为l ，作l DN BM ⊥,，交l 于F E ,，分别交CD ，AB 于N M ,.过O 作l PQ ⊥，分别交CD AB ,于Q P ,.由于O 是BD 的中点，所以Q P ,分别是DM BN ,的中点.由对称性，易见所求旋转体体积为)(2l NPQ D l AD N l ABCD V V V V --∆-+==平行四边形平行四边形.由于2324===AD BD AB ，，，易见3090=∠=∠DBA ADB ，，73422=+=+=DO AD AO ，72=AC .显然CAB DCA DAC ∠=∠>∠，FN DF >.且21727322==⨯==∆AO DO AD AO S DF ADO ，74716712422==-=-=DF AD AF .从而由圆锥体积公式得 ππππ749167716747123312==⨯⨯=⨯⨯⨯==-∆-∆AF DF V V l ADF l ADN . 又71074147472=-=-=-=AF AC CF ，7==AO CO ，QO DF CO CF ::=，215171021727=÷⨯=⨯=CF DF CO QO .从而由圆锥体积公式得COQO CF DF V V V V l CQO l CDF l FOQD l NPQD ⨯⨯-⨯⨯=-==-∆-∆--223131ππ梯形平行四边形ππππ71225657122534310007)2574940(7)72521710712(3=-⨯=-=⨯-⨯=.从而 17573021225105772)12256574916(72)7122565774916(2πππππ=⨯=+=+=V . 答：所求体积为1757302π：13.解：I ）可设l ：4+=my x ，与Γ联立得03624)43(22=+++my y m . 这是y 的一元二次方程，由判别式0≥∆解得42≥m .记）（11,y x A ，）（22,y x B ，则4324221+-=+m m y y ，4336221+=m y y . 由题设条件，02121<+=⋅y y x x ，即0)4)(4(2121<+++y y my my ，得 016)(4)1(21212<++++y y m y y m ，即016432444336)1(222<++-⋅++⋅+m mm m m ，即 0)43(424)1(9222<++-+m m m .得02532<+-m ， 3252>m ， 253)1(2<m ，5353<<-m . 故l 的斜率的取值范围为)53,53(-. 因为F (1,0),所以）（111,1y x FA --=，）（22,1y x FB -=，从而 12211221)3()3())(1()1(y my y my y x y x +++=---- 04324343362)(32222121=+-⋅++⋅=++=m mm m y y y my . ∴1与共线，即1A与F 、B 三点共线. III ）假设4≠q ，过)0,(q Q 的直线与Γ交于A 、B ，且A 关于长轴的对称点为1A ，如果1A 、F 、B 三点共线.我们另取点)0,4(P .设直线AP 与Γ交于1B ，那么如II ）的证明，1A 、F 、B 三点必共线.故B 与1B 重合，从而直线AB 和1AB 重合，就是AQ 与AP 重合.所以P 与Q 重合，4=q ，与假设矛盾.这就是说，4≠q 时，三点1A 、F 、B 不能共线.14.解：n n n n n x x x x x 1212121+=+=+， 22211441nn n x x x ++=+，)1(4112221+=-+n nn x x x ， 3,2,1=n . 故 ∑∑==++=-20061220061221)1(4)11(n n n n n x x x ，亦即 80244112006122122007∑=+=-n n x x x ，由11=x 得80254120061222007∑=+=n n x x . （*）由于112121<+=+n n n x x x ，,,3,2,1 =n 且显然0>n x ，故{}n x 是递减数列，且 31122112=+=x x x ，11319231122223=+=+=x x x ，故∑∑==++=2006322200612)31(1n n n nx x15120041219911)113(911200632<⨯++=++<∑=n ，由（*）式得 8629802515141802522007=+⨯<<x，,802518629122007<<x 80251lg lg 86291lg 22007<<x ， 8025lg lg 28629lg 2007-<<-x ，3lg 242007-<<-x ，23lg 22007-<<-x ，∴⎣⎦2lg 2007-==x k .15.证明：因为△ABC 是锐角三角形，其三边c b a ,,满足0,,>c b a ，以及 222222222,,,,,c b a b a c a c b c b a b a c b c b >+>+>+>+>+>+. 因此，由平均不等式可知222222222222)()()(z c b a y b a c x a c b -++-++-+)()(21)()(21)()(21222222222222222222222222xy y x z c b a z x x z y b a c y z z y x a c b +-+++-+++-+≤ 222222222222zy x c y x z b x z y a ++=)(2)(2222abz cay bcx z cxy y bzx x ayz ++-++=，从而22222222222)(])[(])[(])[(P zcxy y bzx x ayz z c b a y b a c x a c b =++≤-++-++-+，亦即2)(P S c b a ≤++，cb a P S ++≤2.上式取等式当且仅当222z y x ==，亦即===z y x cb a P++.因此所求的S 的最大值为cb a P ++2，当S 取最大值时，===z y x c b a P ++.（第13题答图）（第10题答图）（第12题答图）yyA A 1B 1C 1D 1B CDABCDQ M O F E。

2007年安徽省高中数学联赛初赛试卷及答案

能同时不属于 B.所以 4 个元素满足条件的选择共有 2 2 2 2 6 种.换句话说，“好集对”一共有 6 个. 答：
C.
2.令 y lg(10x 1) ，则 y 0 ，且10x 1 10 y ，10x 10 y 1， x lg(10 y 1) ，
x lg(10 y 1) . 从而 f 1 (x) lg(10 x 1) . 令 2 x t ，则题设方程为 f (t) f 1 (t) ，即
8.设 n≥2007,且 n 为使得 an = ( 2 2 i 2 2 )n 取实数值的最小正整数,则对应此 n 的
an =____________.
9.若正整数 n 恰好有 4 个正约数,则称 n 为奇异数,例如 6,8,10 都是奇异数.那么,在 27,42,69,111,125,137,343,899,3599,7999 这 10 个正整数中,奇异数有__________. 10.平行六面体 ABCD-- A1B1C1D1 中,顶点 A 出发的三条棱 AA 1 ,AB,AD 的长度分别为 2,3,4,且
1)若∠AOB 为钝角或平角(O 为原点).q=4.试确定 l 的斜率的取值范围.
2)设 A 关于长轴的对称点为 A1 ,F 为椭圆的右焦点,q=4,试判断 A1 与 F,B 三点是否共线,并说明理由.
3)问题 2)中,q≠4,那么 A1 ,F,B 三点还能否共线?请说明理由.
14.数列{
xn
}由下式确定:
所以 A 100 101200 101102 101194 103104 101188 497498 106 499500
100 （101200 1） 101102 （101194 1） 103104 （101188 1） 497498 （106 1）

2021年安徽省高中数学竞赛初赛试题及答案详解

安徽省高中数学竞赛初赛试题一.选取题1.如果集合.A B 同步满足{}1.2.3.4AB ={}1A B =,{}{}1,1A B ≠≠就称有序集对(),A B 为“好集对”。

这里有序集对(),A B 意指当A B ≠，()(),,A B B A 和是不同集对，那么“好集对”一共有（）个。

64862A B C D２.设函数()()lg 101x f x -=+,()()122x x f f --=方程的解为( )()()()()2222.log lg21.lg log 101.lg lg21.log log 101A B C D --++3.设100101102499500A =是一种1203位正整数,由从100到500全体三位数按顺序排列而成那么A 除以126余数是( )4.在直角ABC 中，90C ∠=,CD 为斜边上高,D 为垂足. ,,1AD a BD b CD a b ===-=.设数列{}k u 通项为()1221,1,2,3,,kkk k k k u a ab a b b k --=-+-+-=则( )2008200720062008200720062008200720082007 2007200820082007.. .. u u u u u u u u u u A B C D =+=-==5.在正整数构成数列1.3.5.7……删去所有和55互质项之后,把余下各项按从小到大顺序排成一种新数列{}n a ,易见123451,3,7,9,13a a a a a =====那么2007____________a =192759.. 55 .. A B C D 2831 95976.设A B ==1+cos871-cos87则():A B =...A B C D 227.边长均为整数且成等差数列,周长为60钝角三角形一共有______________种. 8.设2007n ≥,且n为使得nn a =取实数值最小正整数,则相应此n na 783660A B C D为9.若正整数n 正好有4个正约数,则称n 为奇异数,例如6,8,10都是奇异数.那么在27,42,69,111,125,137,343,899,3599,7999这10个数中奇异数有_____________________个. 10.平行六面体1111ABCD A B C D -中,顶点A 出发三条棱1,,AB AD AA 长度分别为2,3,4,且两两夹角都为60那么这个平行六面体四条对角线1111,,,AC BD DB CA 长度(按顺序)分别为___________________11.函数()(),f x g x 迭代函数定义为()()()()()()()12,,fx f x f x f f x ==()()()()()()()()()()()()()()()()()1121,,,n n n n f x f f x g x g x g x g g x g x g g x --====其中n =2,3,4…设()()23,32f x x g x x =-=+,则方程组()()()()()()()()()()()()969696f x g y f y g z f z g x ⎧=⎪⎪=⎨⎪=⎪⎩解为_________________12.设平行四边形ABCD中，4,2,AB AD BD ===则平行四边形ABCD 绕直线AC 旋转所得旋转体体积为_______________三．解答题13.已知椭圆22412:3y x +=Γ和点(),0,Q q 直线,l Q A B Γ过且与交于两点(可以重叠).1)若AOB ∠为钝角或平角(O 为原点)，4,q =试拟定l 斜率取值范畴.2)设A 关于长轴对称点为1A ,,4,F q =为椭圆的右焦点试判断1,A F B 和三点与否共线,并阐明理由.3)问题2)中,若14,,,q A F B ≠那么三点能否共线?请阐明理由. 14.数列{}n x 由下式拟定：112,1,2,3,,121nn n x x n x x +===+,试求[]20072007lg lg .x k x =整数部分(注[]a 表达不不不大于a 最大整数,即a 整数某些.)15. 设给定锐角ABC 三边长,,,,,a b c x y z 正实数满足,ayz bzx cxyp x y z++=其中p 为给定正实数,试求()()()222s b c a x c a b y a b c z =+-++-++-最大值,并求出当s 取此最大值时，,,x y z 取值.安徽省高中数学竞赛初赛答案一、选取题1.C.2.A.3.C.4.A.5.B6.D. 第1题解答过程逐个元素考虑归属选取. 元素1必要同步属于A 和B .元素2必要至少属于A 、B 中之一种，但不能同步属于A 和B ，有2种选取：属于A 但不属于B ，属于B 但不属于A . 同理，元素3和4也有2种选取.但元素2，3，4不能同步不属于A ，也不能同步不属于B .因此4个元素满足条件选取共有62222=-⨯⨯种.换句话说，“好集对”一共有6个. 答：C.第2题解答过程令)110lg(+=-xy ，则0>y ，且y x 10110=+-，11010-=-y x ，)110lg(-=-y x ，)110lg(--=y x .从而)110lg()(1--=-x x f . 令t x =2，则题设方程为)()(1t ft f -=-，即)110lg()110lg(--=+t t ，故 0)]110)(110lg[(=-+t t ，1)110)(110(=-+t t ，2102=t ， 2lg 2=t ，解得 2lg 212==t x . 从而 1)2(lg log )2lg 21(log 22-==x . 答：A.第3解答过程注意 972126⨯⨯=,2,7和9两两互质. 由于 0≡A （mod2）,）（）（）（）（）（005994201101001+++++++++++++++≡ A 500102101100++++≡ 2401500100÷⨯+≡）（6120300≡≡（mod9）, 因此6≡A （mod18）. （1）又由于1103-≡，nn)1(103-≡（mod7）,因此ii i A 3400010)500(⨯-=∑=ii i ）（1)500(4000-⨯-≡∑=100)101102()495496()497498()499500(+-++-+-+-≡ 6300≡=（mod7）.(2)，（1），（2）两式以及7和18互质，知6≡A （mod126）. 答：C.另解：632126⨯=，99999963，1109999996-=，）（）（11011066--n ， ,3,2,1=n 因此499500104974981010310410101102101006118811941200+⨯++⨯+⨯+⨯= A+-⨯++-⨯+-⨯+-⨯=）（）（）（）（1104974981101031041101011021101006118811941200 ）（499500497498103104101102100+++++ 2200499500101102100999999÷⨯+++=）（B 60060200100999999++=B60060300999999+=B 60360999999+=C ，其中B ，C 为整数.从而6036063+=D A 663+=E ，其中D ，E 为整数.因此A 除以63余数为6.由于A 是偶数，因此A 除以126余数也为6. 答：C. 第4解答过程易见BD AD CD ⋅=2，即ab b a =-2）（，又已知1=-b a ，故1=ab ，1)1(=-a a ，012=--a a ；1)1(=+b b ，012=++b b .显然k u 是首项为k a ，公比为a bq -=等比数列前1+k 项和.故ba b a q q a u k k k k k +--=--=+++111)(1)1(， 3,2,1=k .即 b a b a b a b a u u k k k k k k +--++--=++++++22111)()(])()([11212++++----++=k k k k b b a a ba)]1()()1([111+---++=++b b a a b a k k ])([12121b b a a b a k k ⋅--⋅+=++ 233])([1+++=--+=k k k u b a b a ， 3,2,1=k .故答案为A.（易知别的答案均不成立）另解：易见BD AD CD ⋅=2，即ab b a =-2）（，又已知1=-b a ，故1=ab ，51414)((222=⨯+=+-=+ab b a b a ），5=+b a .解得215+=a ， 215-=b . 显然k u 是首项为ka ，公比为abq -=等比数列前1+k 项和，故 ba b a q q a u k k k k k +--=--=+++111)(1)1(])251()251[(5111++--+=k k ，,3,2,1=k . 于是数列{}k u 就是斐波那契数列1，2，3，5，8，13，21，…，它满足递推关系 ,12k k k u u u +=++ ,3,2,1=k . 因此答案为A. 第5题解答过程{}n a 可当作是在正整数数列1，2，3，4，5，6，7，…中删去所有能被2，5或11整除项之后，把余下各项按从小至大顺序排成数列.由三阶容斥原理，1，2，3，4，…，m 中不能被2，5或11整除项个数为⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1101022551152m m m m m m m m x m ，其中⎣⎦a 不表达不不不大于a 最大整数，即a 整数某些. 估值：设11010225511522007m m m m m m m m x m -+++---≈=)1111)(511)(211(---⨯=m 11105421⨯⨯⨯=m m 114=，故 55194112007≈⨯≈m . 又因⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1105519105519225519555519115519555192551955195519x=5519-2759-1103-501+100+250+551-50=，并且5519不是2，5，11倍数，从而知55192007=a . 答：B.又解：{}n a 可当作是在正整数数列1，2，3，4，5，6，7，…中删去所有能被2，5 或11整除项之后，把余下各项按从小至大顺序排成数列.由于2，5，11是质数，它们最小公倍数为110.易见，-54，-53，…，0，1，2，3，…，55中不能被2，5，11整除数为，，；，，，17139731±±±±±±，；2119±± ；，，292723±±±，，，；，，474341393731±±±±±±535149±±±，；,共40个.（或由欧拉公式，1，2，3，…，110中不能被2，5，11整除数个数，等于1，2，3，…，110中与110互质数个数，等于401111511211110110=-⨯-⨯-⨯=∅）（）（）（）（.）显然1，2，3，…中每持续110个整数，不能被2，5，11整除数均有40个.因此，1，2，3，…，550050110=⨯中，不能被2，5，11整除数有20005040=⨯个.不不大于5500中数不能被2，5，11整除，是5500+1，5500+3，5500+7，5500+9，5500+13，5500+17，5500+19，….因此5519是第个不能被2，5，11整除数，亦即所求55192007=a . 答：B . 第6题解答过程显然 287cos 127cos 123cos 12++++++=A5.43cos 5.5cos 5.3cos 5.1cos ++++=；287cos 127cos 123cos 12-++-+-=B5.43sin 5.5sin 5.3sin 5.1sin ++++=. 注意到)1sin()1sin(1sin cos 2 --+=θθθ， )1cos()1cos(1sin sin 2 +--=θθθ,因此+-+-+-=⨯)5.4sin 5.6(sin )5.2sin 5.4(sin )5.0sin 5.2(sin 21sin 2A)5.42sin 5.44(sin -+ 22sin 5.22cos 25.0sin 5.44sin =-=，+-+-+-=⨯)5.6cos 5.4(cos )5.4cos 5.2(cos )5.2cos 5.0(cos 21sin 2B )5.44cos 5.42(cos -+ 22sin 5.22sin 25.44cos 5.0cos =-=.故5.22cot )22sin 5.22sin 2(:)22sin 5.22cos 2()21sin 2(:)21sin 2(:==⨯⨯=B A B A12+=. 答：D.另解：2A 00005.43cos 5.5cos 5.3cos 5.1cos +++++= ，2B 5.43sin 5.5sin 5.3sin 5.1sin ++++=，++++=+)5.3sin 5.3(cos )5.1sin 5.1(cos 22i i B iA )5.43sin 5.43(cos i ++∑=++=21)2sin 2(cos )5.1sin 5.1(cos k k i i)2sin 2(cos 1)2sin 2(cos 1)5.1sin 5.1(cos 22i i i +-+-+= )2sin 2(cos 1)44sin 44(cos 1)5.1sin 5.1(cosi i i +-+-+=1cos 1sin 21sin 222cos 22sin 222sin 2)5.1sin 5.1(cos 22i i i --+= )1sin 1)(cos 1sin 2()22sin 22)(cos 22sin 2)(5.1sin 5.1(cosi i i i i +-+-+==)5.22sin 5.22(cos 1sin 22sini +. 由于2A 和2B是实数，因此 1sin 5.22cos 22sin 2=A ，1sin 5.22sin 22sin 2=B , 122222222145sin 45cos 15.22cos 5.22sin 25.22cos 25.22sin 5.22cos 2:2:2+=+=+=+====BAB A . 答：D. 第7解答过程解：设△ABC 三边长c b a ,,为整数，c b a c b a c b a ,,,,60≥≥=++成等差数列，A ∠为钝角，则必有c a b +=2，222a cb <+.易解得 b b b c a b c b a 32)(60=+=++=++=，40,20=+=c a b ；222c a b -<))((c a c a -+=，即c a c a -<-<10),(40202.因而a a c a c a <=-++<25,2)()(50，即26≥a .此外，29,30,260,≤<=+>++=>+a a a a a c b a a c b .易检查),,(c b a)11,20,29(),12,20,28(),13,20,27(),14,20,26(=都是钝角三角形. 答：4.第8题解答过程注意到22-=x ，22+=y 满足4)22()22(22=++-=+y x ，0,>y x ，故可令θcos 2=x ，θsin 2=y ，0＜θ＜2π.从而22cos 42-=θ，-2cos 422-=θ，-θπθ2cos 43cos 1cos 2222==-=，故83πθ=，83cos )83sin 83(cosπππn i a n n =+=+ 83sin πn i . n a 取实数，当且仅当083sin=πn ，当且仅当k n 8=，∈k Z.满足此条件且2007≥n 最小正整数n 为2008，此时1753cos 820083cos2008-====ππx a a n . 答：-1. 第9题解答过程易见奇异数有两类：第一类是质数立方3p （p 是质数）；第二类是两个不同质数乘积21p p （21,p p 为不同质数）.由定义可得3327=是奇异数（第一类）； 73242⨯⨯=不是奇异数；23369⨯=是奇异数（第二类）； 373111⨯=是奇异数（第二类）； 35125=是奇异数（第一类）；137是质数，不是奇异数；37343=是奇异数（第一类）；221301900899-=-=）（130+=2931130⨯=-）（是奇异数（第二类）；）（16016013600359922+=-=-=5961160⨯=-）（是奇异数（第二类）； 42119)12020)(120(120180007999233⨯=++-=-=-=是奇异数（第二类）.答：8. 第10解答过程解：将向量1AA ，，分别记为a ，b ，c . 2==a 3==b 4==c ，且易见c b a AC ++=1， c b a C A ++-=1， c b a BD +-=1， c b a DB -+=1.)(2)(2222⋅+⋅+⋅+++=++=22260cos )(2ca bc ab c b a +++++=ca bc ab c b a +++++=222244332432222⨯+⨯+⨯+++==55，故551=AC . 类似地，可算得，191=BD ，151=DB ，271=CA =33.答：55，19，15，33. 第11题解答过程令tx =-3，易见3+=t x ，323)3(232)(+=-+=-=t t x x f ，)32(2)()2(+=t x f 3-32)(,,32)(2+=+=t x f t n n ；令s y =+1，易见1-=s y ，2)1(323)(+-=+=s y y g 13-=s ，,132)13(3)(2)2(-=+-=s s y g ，13)()(-=s y g n n ， ,3,2,1=n .因而，题设方程组可化为⎪⎩⎪⎨⎧-+=+--+=+--+=+-)3.(1)1(33)3(2)2(,1)1(33)3(2)1(,1)1(33)3(2696969x z z y y x （1）-（2），（2）-（3），（3）-（1）得⎪⎩⎪⎨⎧-=--=--=-)6).((3)(2)5(),(3)(2)4(),(3)(2696969y x x z x z z y z y y x因此)()23()()23()(2339629696y x x z z y y x -=-=-=-⇒00=-⇒=-z y y x z y x ==⇒.代入（1）得1)1(33)3(269-+=+-x x ，1)1(7293)3(512-+=+-x x ，7287291533512+=-x x ， 2261217=-x ， 32331=-x ， 31323-=x . 因此原方程组解为31323-===z y x . 答：31323-===z y x . 第12题解答过程.以l T V -表达平面图形T 绕直线l 所得旋转体体积.记直线AC 为l ，作l DN BM ⊥,，交l 于F E ,，分别交CD ，AB 于N M ,.过O 作l PQ ⊥，分别交CD AB ,于Q P ,.由于O 是BD 中点，因此Q P ,分别是DM BN ,中点.由对称性，易见所求旋转体体积为)(2l NPQD l ADN l ABCD V V V V --∆-+==平行四边形平行四边形.由于2324===AD BD AB ，，，易见3090=∠=∠DBA ADB ，，73422=+=+=DO AD AO ，72=AC .显然CAB DCA DAC ∠=∠>∠，FNDF >.且21727322==⨯==∆AO DO AD AO S DF ADO ，74716712422==-=-=DF AD AF .从而由圆锥体积公式得 ππππ749167716747123312==⨯⨯=⨯⨯⨯==-∆-∆AF DF V V l ADF l ADN . 又71074147472=-=-=-=AF AC CF ，7==AO CO ，QO DF CO CF ::=， 215171021727=÷⨯=⨯=CF DF CO QO .从而由圆锥体积公式得COQO CF DF V V V V l CQO l CDF l FOQD l NPQD ⨯⨯-⨯⨯=-==-∆-∆--223131ππ梯形平行四边形ππππ71225657122534310007)2574940(7)72521710712(3=-⨯=-=⨯-⨯=.从而17573021225105772)12256574916(72)7122565774916(2πππππ=⨯=+=+=V . 答：所求体积为1757302π：第13题解答过程解：I ）可设l ：4+=my x ，与Γ联立得03624)43(22=+++my y m . 这是y 一元二次方程，由鉴别式0≥∆解得42≥m .记）（11,y x A ，）（22,y x B ，则4324221+-=+m m y y ，4336221+=m y y . 由题设条件，02121<+=⋅y y x x ，即0)4)(4(2121<+++y y my my ，得 016)(4)1(21212<++++y y m y y m ，即016432444336)1(222<++-⋅++⋅+m mm m m ，即 0)43(424)1(9222<++-+m m m .得02532<+-m ， 3252>m ， 253)1(2<m ，5353<<-m . 故l 斜率取值范畴为)53,53(-. 由于F (1,0),因此）（111,1y x --=，）（22,1y x -=，从而 12211221)3()3())(1()1(y my y my y x y x +++=---- 04324343362)(32222121=+-⋅++⋅=++=m mm m y y y my . ∴1FA 与共线，即1A 与F 、B 三点共线.III ）假设4≠q ，过)0,(q Q 直线与Γ交于A 、B ，且A 关于长轴对称点为1A ，如果1A 、F 、B 三点共线.咱们另取点)0,4(P .设直线AP 与Γ交于1B ，那么如II ）证明，1A 、F 、B 三点必共线.故B 与1B 重叠，从而直线AB 和1AB 重叠，就是AQ 与AP 重叠.因此P 与Q 重叠，4=q ，与假设矛盾.这就是说，4≠q 时，三点1A 、F 、B 不能共线. 第14题解答过程 14.解：n n n n n x x x x x 1212121+=+=+， 22211441nn n x x x ++=+，)1(4112221+=-+n nn x x x ， 3,2,1=n . 故∑∑==++=-20061220061221)1(4)11(n n n nn x x x，亦即80244112006122122007∑=+=-n n x x x ，由11=x 得80254120061222007∑=+=n n x x . （*）由于112121<+=+n n n x x x ，,,3,2,1 =n 且显然0>n x ，故{}n x 是递减数列，且 31122112=+=x x x ，11319231122223=+=+=x x x ，故∑∑==++=2006322200612)31(1n n n nx x15120041219911)113(911200632<⨯++=++<∑=n ，由（*）式得 8629802515141802522007=+⨯<<x，,802518629122007<<x 80251lglg 86291lg 22007<<x ， 8025lg lg 28629lg 2007-<<-x ，3lg 242007-<<-x ，23lg 22007-<<-x ，∴⎣⎦2lg 2007-==x k .第15题解答过程证明：由于△ABC 是锐角三角形，其三边c b a ,,满足0,,>c b a ，以及222222222,,,,,c b a b a c a c b c b a b a c b c b >+>+>+>+>+>+. 因而，由平均不等式可知222222222222)()()(z c b a y b a c x a c b -++-++-+)()(21)()(21)()(21222222222222222222222222xy y x z c b a z x x z y b a c y z z y x a c b +-+++-+++-+≤ 222222222222zy x c y x z b x z y a ++=)(2)(2222abz cay bcx z cxy y bzx x ayz ++-++=，从而22222222222)(])[(])[(])[(P zcxy y bzx x ayz z c b a y b a c x a c b =++≤-++-++-+，亦即2)(P S c b a ≤++，cb a P S ++≤2.上式取等式当且仅当222z y x ==，亦即===z y x cb a P++.因而所求S 最大值为c b a P ++2，当S 取最大值时，===z y x cb a P++.（第13题答图）（第10题答图）（第12题答图）yy AA 1B 1C 1D 1B CDABCD Q M P N O F E安徽高中数学竞赛初赛试题一、选取题1.若函数()y f x =图象绕原点顺时针旋转2π后，与函数()y g x =图象重叠，则（）（A ）()()1g x f x -=- （B ）()()1g x f x -= （C ）()()1g x f x -=--（D ）()()1g x f x -=-2.平面中，到两条相交直线距离之和为1点轨迹为（）（A ）椭圆（B ）双曲线一某些（C ）抛物线一某些（D ）矩形3.下列4个数中与cos1cos2cos2008+++最接近是（）（A ）- （B ）-1（C ）1（D ）4.四周体6个二面角中至多也许有（）个钝角。

2016年全国高中数学联赛安徽省初赛试题解答及评分参考

2016年全国高中数学联赛安徽省初赛试题解答及评分参考一、填空题，每题8分 1.设1sin cos 2+=x x ，则33sin cos +=x x 解答：由1sin cos 2+=x x ，可得112sin cos 4+=x x ，故3sin cos 8=-x x ，从而33sin cos +=x x 221311(sin cos )(sin cos sin cos )(1)2816+-+=+=x x x x x x2.设i 为虚数单位，化简20162016(1)(1)++-=i i解答：由2(1)2+=i i ，可得20161008(1)2+=i ，同理可得20161008(1)2-=i 故201620161009(1)(1)2++-=i i3.已知等差数列121000,,a a a 的前100项之和为100，最后100项之和为1000，则1=a解答：设等差数列的公差为d ，则有11004950100+=a d ，1100949501000+=a d 解得10.505=a4. 集合[][][]{}{}231,2,,100++∈x x x x R 共有个元素，其中[]x 表示不超过x 的最大整数。

解答：设[][][]()23=++f x x x x 则有(1)()6+=+f x f x ，当01≤<x 时，()f x 的所有可能值为0,1,2,3.由此()f x 得值域{}6,61,62,63=+++∈S k k k k k Z ,[][][]{}{}231,2,,100417167++∈=⨯-=x x x x R 个元素。

5.若关于x 的方程2=x x ae 有三个不同的实根，则实数a 的取值范围是解答：设2()-=xf x x e，则2'()(2)-=-xf x x x e当0≤x 时，2()-=xf x x e单调递减，当02≤≤x 时，2()-=x f x x e 单调递增，当2≥x 时，2()-=x f x x e 单调递减，(0)0=f ，2(2)4-=f e ，当→+∞x 时()0→f x 因此，2()-==xf x x e a 有三个不同的实根当且仅当204-<<a e6.在如图所示的单位正方体1111-ABCD A B C D 中，设O 为正方体的中心，点,M N 分别在棱111,A D CC 上，112,23==A M CN ,则四面体1OMNB 的体积等于解答：以A 为原点，1,,AB AD AA 为,,x y z 轴建立空间直角坐标系，则有11112(,,0),(0,,1),(1,1,),(1,0,1)2223O M N B 由此四面体1OMNB 的体积1111672=⨯⨯=V OB ON OM 7.已知抛物线P 以椭圆E 的中心为焦点，P 经过E 的两个焦点，并且P 与E 恰有三个交点，则E 得离心率等于解答：不妨设椭圆E 的方程为22221(0)+=>>x y a b a b ，P 经过E 的两个焦点，222=+x cy c 222=+a b c ，P 与E 恰有三个交点，所以2=c b ，则E得离心率等于5==c e a 8. 等可能地随机产生一个正整数{}1,2,,2016∈x ，则x 在二进制下的各位数字之和不超过8的概率等于解答：设{}1,2,,2016∈x 的二进制表示是109102()x x x x 即102==∑i i i x x 其中{}0,1∈i x我们考查满足108=>∑ii x的x 的个数。

2016年全国高中数学联赛试题及答案详解(B卷)

2016年全国高中数学联赛（B 卷）一试一、选择题：（每小题8分，共64分）1.等比数列{}n a 的各项均为正数，且213263236,a a a a a ++=则24a a +的值为． 2.设{}|12A a a =−≤≤，则平面点集(){},|,,0B x y x y A x y =∈+≥的面积为． 3.已知复数z 满足22z z z z +=≠（z 表示z 的共轭复数），则z 的所有可能值的积为． 4.已知()(),f x g x 均为定义在R 上的函数，()f x 的图像关于直线1x =对称，()g x 的图像关于点()1,2−中心对称，且()()391x f x g x x +=++，则()()22f g 的值为． 5.将红、黄、蓝3个球随机放入5个不同的盒子,,,,A B C D E 中，恰有两个球放在同一盒子的概率为．6.在平面直角坐标系xOy 中，圆221:0C x y a +−=关于直线l 对称的圆为222:2230,C x y x ay ++−+=则直线l 的方程为．7.已知正四棱锥V -ABCD 的高等于AB 长度的一半，M 是侧棱VB 的中点，N 是侧棱VD 上点，满足2DN VN =，则异面直线,AM BN 所成角的余弦值为．8.设正整数n 满足2016n ≤，且324612n n n n+++= ．这样的n 的个数为．这里{}[]x x x =−，其中[]x 表示不超过x 的最大整数．二、解答题：（共3小题，共56分）9.（16分）已知{}n a 是各项均为正数的等比数列，且5051,a a 是方程()2100lg lg 100x x = 的两个不同的解，求12100a a a 的值．10.（20分）在ABC 中，已知23.AB AC BA BC CA CB ⋅+⋅=⋅（1）将,,BC CA AB 的长分别记为,,a b c ，证明：22223a b c +=；（2）求cos C 的最小值．11.（20分）在平面直角坐标系xOy 中，双曲线C 的方程为221x y −=．求符合以下要求的所有大于1的实数a ：过点(),0a 任意作两条互相垂直的直线1l 与2l ，若1l 与双曲线C 交于,P Q 两点，2l 与C 交于,R S 两点，则总有PQ RS =成立．加试一、（40分）非负实数122016,,,x x x 和实数122016,,,y y y 满足：（1）221,1,2,,2016k k x y k +== ；（2）122016y y y +++ 是奇数．求122016x x x +++ 的最小值．二、（40分）设,n k 是正整数，且n 是奇数．已知2n 的不超过k 的正约数的个数为奇数，证明：2n 有一个约数d ，满足2.k d k <≤三、（50分）如图所示，ABCD 是平行四边形，G 是ABD 的重心，点,P Q 在直线BD 上，使得,.GP PC GQ QC ⊥⊥证明：AG 平分.PAQ ∠四、（50分）设A 是任意一个11元实数集合．令集合{}|,,.B uv u v A u v =∈≠求B 的元素个数的最小值．QG P DCBA2016年全国高中数学联赛（B 卷）试题及答案一试一、选择题：（每小题8分，共64分）1.等比数列{}n a 的各项均为正数，且213263236,a a a a a ++=则24a a +的值为．答案：6．解：由于()2222132632424243622,a a a a a a a a a a a =++=++=+且240,a a +>故24 6.a a += 另解：设等比数列的公比为q ，则52611.a a a q a q +=+又因 ()()()()()22252132631111122223331111112436222,a a a a a a a q a q a q a q a q a q a qa q a q a q aa =++=⋅+⋅+=+⋅⋅+=+=+而240a a +>，从而24 6.a a +=2.设{}|12A a a =−≤≤，则平面点集(){},|,,0B x y x y A x y =∈+≥的面积为．答案：7．解：点集B 如图中阴影部分所示，其面积为 133227.2MRS MNPQ S S −=×−××=正方形3.已知复数z 满足22z z z z +=≠（z 表示z 的共轭复数），则z 的所有可能值的积为．答案：3．解：设()i ,.z a b a b R =+∈由22z z z +=知， 222i 22i i,a b ab a b a b −+++=−比较虚、实部得220,230.a b a ab b −+=+=又由z z ≠知0b ≠，从而有230,a +=即32a =−，进而b 于是，满足条件的复数z的积为33 3.22 −+−−=   4.已知()(),f x g x 均为定义在R 上的函数，()f x 的图像关于直线1x =对称，()g x的图像关于点()1,2−中心对称，且()()391x f x g x x +=++，则()()22f g 的值为．答案：2016. 解：由条件知()()002,f g += ①()()22818190.f g +++ ②由()(),f x g x 图像的对称性，可得()()()()02,024,f f g g =+=−结合①知， ()()()()22400 2.f g f g −−=+= ③由②、③解得()()248,242,f g ==从而()()2248422016.f g =×=另解：因为()()391x f x g x x +=++， ① 所以()()2290.f g += ②因为()f x 的图像关于直线1x =对称，所以 ()()2.f x f x =− ③又因为()g x 的图像关于点()1,2−中心对称，所以函数()()12h x g x =++是奇函数，()()h x h x −=−，()()1212g x g x −++=−++ ，从而 ()()2 4.g x g x =−−− ④ 将③、④代入①，再移项，得 ()()3229 5.x f x g x x −−−=++ ⑤ 在⑤式中令0x =，得()()22 6.f g −= ⑥由②、⑥解得()()248,246.f g ==于是()()222016.f g =5.将红、黄、蓝3个球随机放入5个不同的盒子,,,,A B C D E 中，恰有两个球放在同一盒子的概率为．解：样本空间中有35125=个元素．而满足恰有两个球放在同一盒子的元素个数为223560.C P ×=过所求的概率为6012.12525p ==6.在平面直角坐标系xOy 中，圆221:0C x y a +−=关于直线l 对称的圆为222:2230,C x y x ay ++−+=则直线l 的方程为．答案：2450.x y −+=解：12,C C 的标准方程分别为()()2222212:1,:1 2.C x y C x y a a +=++−=−由于两圆关于直线l 对称，所以它们的半径相等．因此220,a a =−>解得 2.a =故12,C C 的圆心分别是()()120,0,1,2.O O −直线l 就是线段12O O 的垂直平分线，它通过12O O 的中点1,12M−，由此可得直线l 的方程是2450.x y −+=7.已知正四棱锥V -ABCD 的高等于AB 长度的一半，M 是侧棱VB 的中点，N 是侧棱VD 上点，满足2DN VN =，则异面直线,AM BN 所成角的余弦值为．解：如图，以底面ABCD 的中心O 为坐标原点，,,AB BC OV 的方向为,,x y z 轴的正向，建立空间直角坐标系．不妨设2,AB =此时高1,VO =从而()()()()1,1,0,1,1,0,1,1,0,0,0,1.A B D V −−−−由条件知111112,,,,,222333M N−−，因此311442,,,,,.222333AM BN ==−设异面直线,AM BN 所成的角为θ，则cos AM BN AM BNθ⋅==⋅xA8.设正整数n 满足2016n ≤，且324612n n n n+++= ．这样的n 的个数为．这里{}[]x x x =−，其中[]x 表示不超过x 的最大整数．解：由于对任意整数n ，有135113,2461224612n n n n +++≤+++=等号成立的充分必要条件是()1mod12n ≡−，结合12016n ≤≤知，满足条件的所有正整数为()1211,2,,168,n k k =−= 共有168个．另解：首先注意到，若m 为正整数，则对任意整数,x y ，若()mod x y m ≡，则.x y m m = 这是因为，当()mod x y m ≡时，x y mt =+，这里t 是一个整数，故.x x x y mt y mt y y y y y t t m m m m m m m m m m ++=−=−=+−+=−= 因此，当整数12,n n 满足()12mod12n n ≡时，11112222.2461224612n n n n n n n n+++=+++容易验证，当正整数满足112n ≤≤时，只有当11n =时，等式324612n n n n+++=才成立．而201612168=×，故当12016n ≤≤时，满足324612n n n n+++= 正整数n 的个数为168.二、解答题：（共3小题，共56分）9.（16分）已知{}n a 是各项均为正数的等比数列，且5051,a a 是方程 ()2100lg lg 100x x = 的两个不同的解，求12100a a a 的值．解对50,51k =，有()2100lg lg 1002lg ,k k k a a a ==+即()2100lg lg 20.k k a a −−=因此，5051lg ,lg a a 是一元二次方程210020t t −−=的两个不同实根，从而 ()505150511lg lg lg ,100a a a a =+=即1100505110.a a =由等比数列的性质知，()5015010012100505110a a a a a===10.（20分）在ABC 中，已知23.AB AC BA BC CA CB ⋅+⋅=⋅（1）将,,BC CA AB 的长分别记为,,a b c ，证明：22223a b c +=；（2）求cos C 的最小值．解（1）由数量积的定义及余弦定理知，222cos .2b c a AB ACcb A +−⋅== 同理得，222222,.22a cb a bc BA BC CA CB +−+−⋅=⋅= 故已知条件化为 ()()22222222223,b c a a c b a b c +−++−=+− 即22223.a b c +=（2）由余弦定理及基本不等式，得 ()2222222123cos 2236a b a b a b c C ab ab a b b a +−++−===+≥等号成立当且仅当::a b c =因此cos C11.（20分）在平面直角坐标系xOy 中，双曲线C 的方程为221x y −=．求符合以下要求的所有大于1的实数a ：过点(),0a 任意作两条互相垂直的直线1l 与2l ，若1l 与双曲线C 交于,P Q 两点，2l 与C 交于,R S 两点，则总有PQ RS =成立．解过点(),0a 作两条互相垂直的直线1:l x a =与2:0.l y =易知，1l 与C交于点((00,,P a Q a （注意这里1a >），2l 与C 交于点()()001,0,1,0,R S −由条件知00002P Q R S ==，解得a = 这意味着符合条件的a下面验证a =符合条件．事实上，当12,l l 中有某条直线斜率不存在时，则可设12:,:0l x a l y ==，就是前面所讨论的12,l l 的情况，这时有.PQ RS =若12,l l 的斜率都存在，不妨设((()121:,:0,l y k x l y x k k==−≠注意这里1k ≠±（否则1l 将与C 的渐近线平行，从而1l 与C 只有一个交点）．联立1l 与C的方程知，(22210,x kx −−−=即()22221210,k xx k −−−−=这是一个二次方程式，其判别式为2440k ∆=+>．故1l 与C 有两个不同的交点,P Q ．同样，2l 与C 也有两个不同的交点,.R S 由弦长公式知，2212.1k PQ k +=⋅−用1k −代替k ，同理可得()()22221122.11k k RS k k −−+−+=⋅=−−−于是.PQ RS = 综上所述，a =为符合条件的值．加试一、（40分）非负实数122016,,,x x x 和实数122016,,,y y y 满足：（1）221,1,2,,2016k k x y k +== ；（2）122016y y y +++ 是奇数．求122016x x x +++ 的最小值．解：由已知条件（1）可得：1,1,1,2,,2016,k k x y k ≤≤= 于是（注意0i x ≥）()2016201620162016201622211111120162016.k kkk k k k k k k x xy y y =====≥=−=−≥−∑∑∑∑∑ ①不妨设112016,,0,,,0,02016,m m y y y y m +>≤≤≤ 则201611,2016.mkk k k m ym y m ==+≤−≤−∑∑若11m k k y m =>−∑，并且201612015,k k m y m =+−>−∑令 2016111,2015,mk k k k m y m a y m b ==+=−+−=−+∑∑则0,1,a b <<于是()201620161111201522016,m kkk k k k m y yy m a m b m a b ===+=+=−+−−+=−+−∑∑∑由条件（2）知，20161k k y =∑是奇数，所以a b −是奇数，这与0,1a b <<矛盾．因此必有11m k k y m =≤−∑，或者201612015,k k m y m =+−≤−∑则201620161112015.m kk k k k k m yy y ===+=−≤∑∑∑于是结合①得201611.k k x =≥∑又当122015201612201520160,1,1,0x x x x y y y y ========== 时满足题设条件，且使得不等式等号成立，所以122016x x x +++ 的最小值为1．二、（40分）设,n k 是正整数，且n 是奇数．已知2n 的不超过k 的正约数的个数为奇数，证明：2n 有一个约数d ，满足2.k d k <≤证明：记{}||2,0,A d d n d k d =<≤是奇数，{}||2,0,B d d n d k d =<≤是偶数，则,2A B n =∅ 的不超过k 的正约数的集合是.A B若结论不成立，我们证明.A B =对d A ∈，因为d 是奇数，故2|2d n ，又22d k ≤，而2n 没有在区间(],2k k 中的约数，故2d k ≤，即2d B ∈，故.A B ≤反过来，对d B ∈，设2d d ′=，则|d n ′，d ′是奇数，又2kd k ′≤<，故,d A ′∈从而.B A ≤ 所以.A B =故2n 的不超过k 的正约数的个数为偶数，与已知矛盾．从而结论成立．三、（50分）如图所示，ABCD 是平行四边形，G 是ABD 的重心，点,P Q 在直线BD 上，使得,.GP PC GQ QC ⊥⊥证明：AG 平分.PAQ ∠解：连接AC ，与BD 交于点.M 由平行四边形的性质，点M 是,AC BD 的中点．因此，点G 在线段AC 上．由于90GPC GQC ∠=∠= ，所以,,,P G Q C 四点共圆，并且其外接圆是以GC 为直径的圆．由相交弦定理知QG P DCBA.PM MQ GM MC ⋅=⋅ ①取GC 的中点.O 注意到::2:1:3,AG GM MC =故有1,2OCGC AG == 因此,G O 关于点M 对称．于是.GM MC AM MO ⋅=⋅ ②结合①、②，有PM MQ AM MO ⋅=⋅，因此,,,A P O Q 四点共圆．又1,2OP OQ GC ==所以PAO QAO ∠=∠，即AG 平分.PAQ ∠ 四、（50分）设A 是任意一个11元实数集合．令集合{}|,,.B uv u v A u v =∈≠求B 的元素个数的最小值．解：先证明17.B ≥考虑到将A 中的所有元素均变为原来的相反数时，集合B 不变，故不妨设A 中正数个数不少于负数个数．下面分类讨论：情况一：A 中没有负数．设1211a a a <<< 是A 中的全部元素，这里120,0,a a ≥>于是 1223242113111011,a a a a a a a a a a a a <<<<<<<上式从小到大共有19818++=个数，它们均是B 的元素，这表明18.B ≥情况二：A 中至少有一个负数．设12,,,k b b b 是A 中的全部非负元素，12,,,l c c c 是A 中的全部负元素．不妨设 110,l k c c b b <<<≤<<其中,k l 为正整数，11k l +=，而k l ≥，故 6.k ≥于是有 111212,k k l k c b c b c b c b c b >>>>>> 它们是B 中的110k l +−=个元素，且非正数；又有 23242526364656,b b b b b b b b b b b b b b <<<<<< 它们是B 中的7个元素，且为正数．故10717.B ≥+=由此可知，17.B ≥ 另一方面，令{}2340,1,2,2,2,2,A =±±±±±则{}236780,1,2,2,2,,2,2,2B =−±±±±±− 是个17元集合．综上所述，B 的元素个数的最小值为17.。

2007-2016年安徽省高中数学竞赛初赛试题及标准答案详解

2007年安徽省高中数学竞赛初赛试题一.选择题1.如果集合.A B 同时满足{}1.2.3.4A B ={}1A B =,{}{}1,1A B ≠≠就称有序集对(),A B 为“好集对”。

这里的有序集对(),A B 意指当A B ≠，()(),,A B B A 和是不同的集对，那么“好集对”一共有（ )个。

64862A B C D2.设函数()()lg 101x f x -=+，()()122x x f f --=方程的解为（ ) ()()()()2222.log lg21.lg log 101.lg lg21.log log 101A B C D --++3.设100101102499500A =是一个1203位的正整数,由从１０0到500的全体三位数按顺序排列而成那么Ａ除以126的余数是( ）4.在直角ABC 中, 90C ∠=,CD 为斜边上的高,D为垂足. ,,1AD a BD b CD a b ===-=.设数列{}k u 的通项为()1221,1,2,3,,k k k k k k u a a b a b b k --=-+-+-=则（ )2008200720062008200720062008200720082007 2007200820082007.. .. u u u u u u u u u u A B C D =+=-==5．在正整数构成的数列1.3.５.7……删去所有和55互质的项之后,把余下的各项按从小到大的顺序排成一个新的数列{}n a ，易见123451,3,7,9,13a a a a a =====那么2007____________a =192759.. 55 .. A B C D 2831 95976.设A B ==1+cos871-cos87 则():A B =.. .A B C D 22７.边长均为整数且成等差数列，周长为60的钝角三角形一共有＿＿＿___＿＿＿_____种.8.设2007n ≥,且n为使得nn a +=取实数值的最小正整数，则对应此n 的n a 为 783660A B C D9.若正整数n 恰好有4个正约数,则称n 为奇异数,例如6,8,1０都是奇异数．那么在2７,42,６9，１1１,1２５,13７，３4３,８９９,３５9９,７999这10个数中奇异数有_______＿______＿______个.10．平行六面体1111ABCD A B C D -中，顶点A 出发的三条棱1,,AB AD AA 的长度分别为2,3,4,且两两夹角都为60那么这个平行六面体的四条对角线1111,,,AC BD DB CA 的长度(按顺序）分别为__＿＿___＿______＿____11.函数()(),f x g x 的迭代的函数定义为()()()()()()()12,,f x f x f x f f x == ()()()()()()()()()()()()()()()()()1121,,,n n n n f x f f x g x g x g x g g x g x g g x --====其中n ＝2，3,4… 设()()23,32f x x g x x =-=+,则方程组()()()()()()()()()()()()969696f x g y f y g z f z g x ⎧=⎪⎪=⎨⎪=⎪⎩的解为＿____＿_＿_＿＿___＿_＿１2.设平行四边形ABCD 中,4,2,AB AD BD ===则平行四边形ABCD 绕直线AC 旋转所得的旋转体的体积为________＿_____＿三．解答题1３.已知椭圆22412:3y x +=Γ和点(),0,Q q 直线,l Q A B Γ过且与交于两点(可以重合). 1）若AOB ∠为钝角或平角（O 为原点), 4,q =试确定l 的斜率的取值范围.2)设A 关于长轴的对称点为1A ,,4,F q =为椭圆的右焦点试判断1,A F B 和三点是否共线,并说明理由.3)问题２)中,若14,,,q A F B ≠那么三点能否共线?请说明理由.1４．数列{}n x 由下式确定: 112,1,2,3,,121n n n x x n x x +===+,试求[]20072007lg lg .x k x =整数部分(注[]a 表示不大于a 的最大整数,即a 的整数部分.)15. 设给定的锐角ABC 的三边长,,,,,a b c x y z 正实数满足,ayz bzx cxy p x y z ++=其中p 为给定的正实数，试求()()()222s b c a x c a b y a b c z =+-++-++-的最大值,并求出当。

安徽省高中数学竞赛初赛试题及答案详解

2007年安徽省高中数学竞赛初赛试题一.选择题1.如果集合.A B 同时满足{}1.2.3.4A B =U {}1A B =I ,{}{}1,1A B ≠≠就称有序集对(),A B 为“好集对”。

这里的有序集对(),A B 意指当A B ≠，()(),,A B B A 和是不同的集对，那么“好集对”一共有（）个。

２.设函数()()lg 101x f x -=+,()()122x x f f --=方程的解为()()()()()2222.log lg21.lg log 101.lg lg21.log log 101A B C D --++ 3.设100101102499500A =L 是一个1203位的正整数,由从100到500的全体三位数按顺序排列而成那么A 除以126的余数是()4.在直角ABC V 中,90C ∠=o ,CD 为斜边上的高,D 为垂足.,,1AD a BD b CD a b ===-=.设数列{}k u 的通项为()1221,1,2,3,,kk k k k k u a a b a b b k --=-+-+-=L L 则()5.……删去所有和55互质的项之后,把余下的各项按从小到大的顺序排成一个新的数列{}n a ,易见123451,3,7,9,13a a a a a =====L 那么2007____________a =192759.. 55 .. A B C D 2831 95976.设A B ==L L 则():A B =7.边长均为整数且成等差数列,周长为60的钝角三角形一共有______________种. 8.设2007n ≥,且n为使得nn a =取实数值的最小正整数,则对应此n 的n a 为9.若正整数n 恰好有4个正约数,则称n 为奇异数,例如6,8,10都是奇异数.那么在27,42,69,111,125,137,343,899,3599,7999这10个数中奇异数有_____________________个. 10.平行六面体1111ABCD A B C D -中,顶点A 出发的三条棱1,,AB AD AA 的长度分别为2,3,4,且两两夹角都为60o 那么这个平行六面体的四条对角线1111,,,AC BD DB CA 的长度(按顺序)分别为___________________11.函数()(),f x g x 的迭代的函数定义为()()()()()()()12,,f x f x f x f f x ==L()()()()()()()()()()()()()()()()()1121,,,n n n n f x f f x g x g x g x g g x g x g g x --====L 其中n =2,3,4…设()()23,32f x x g x x =-=+,则方程组()()()()()()()()()()()()969696f x g y f y g z f z g x ⎧=⎪⎪=⎨⎪=⎪⎩的解为_________________12.设平行四边形ABCD中，4,2,AB AD BD ===则平行四边形ABCD 绕直线AC 旋转所得的旋转体的体积为_______________三．解答题13.已知椭圆22412:3y x +=Γ和点(),0,Q q 直线,l Q A B Γ过且与交于两点(可以重合). 1)若AOB ∠为钝角或平角(O 为原点),4,q =试确定l 的斜率的取值范围.2)设A 关于长轴的对称点为1A ,,4,F q =为椭圆的右焦点试判断1,A F B 和三点是否共线,并说明理由.3)问题2)中,若14,,,q A F B ≠那么三点能否共线请说明理由. 14.数列{}n x 由下式确定:112,1,2,3,,121nn n x x n x x +===+L ,试求[]20072007lg lg .x k x =整数部分(注[]a 表示不大于a 的最大整数,即a 的整数部分.)15.设给定的锐角ABC V 的三边长,,,,,a b c x y z 正实数满足,ayz bzx cxyp x y z++=其中p 为给定的正实数,试求()()()222s b c a x c a b y a b c z =+-++-++-的最大值,并求出当s 取此最大值时,,,x y z 的取值.2007年安徽省高中数学竞赛初赛答案一、选择题A.3.C.4.A.第1题解答过程逐个元素考虑归属的选择. 元素1必须同时属于A 和B .元素2必须至少属于A 、B 中之一个，但不能同时属于A 和B ，有2种选择：属于A 但不属于B ，属于B 但不属于A .同理，元素3和4也有2种选择.但元素2，3，4不能同时不属于A ，也不能同时不属于B .所以4个元素满足条件的选择共有62222=-⨯⨯种.换句话说，“好集对”一共有6个.答：C.第2题解答过程令)110lg(+=-x y ，则0>y ，且y x 10110=+-，11010-=-y x ，)110lg(-=-y x ，)110lg(--=y x .从而)110lg()(1--=-x x f.令t x =2，则题设方程为)()(1t ft f -=-，即)110lg()110lg(--=+t t ，故0)]110)(110lg[(=-+t t ，1)110)(110(=-+t t ，2102=t ，2lg 2=t ，解得2lg 212==t x .从而1)2(lg log )2lg 21(log 22-==x .答：A. 第3解答过程注意972126⨯⨯=,2,7和9两两互质.因为0≡A （mod2）, 500102101100++++≡Λ2401500100÷⨯+≡）（6120300≡≡（mod9）, 所以6≡A （mod18）.（1）又因为1103-≡，nn)1(103-≡（mod7）,所以ii i A 3400010)500(⨯-=∑=ii i ）（1)500(4000-⨯-≡∑=100)101102()495496()497498()499500(+-++-+-+-≡Λ6300≡=（mod7）.(2)，（1），（2）两式以及7和18互质，知6≡A （mod126）.答：C.另解：632126⨯=，99999963，1109999996-=，）（）（11011066--n ，Λ,3,2,1=n 所以499500104974981010310410101102101006118811941200+⨯++⨯+⨯+⨯=ΛA60060300999999+=B 60360999999+=C ，其中B ，C 为整数.从而6036063+=D A 663+=E ，其中D ，E 为整数.所以A 除以63的余数为6.因为A 是偶数，所以A 除以126的余数也为6.答：C. 第4解答过程易见BD AD CD ⋅=2，即ab b a =-2）（，又已知1=-b a ，故1=ab ，1)1(=-a a ，012=--a a ；1)1(=+b b ，012=++b b .显然k u 是首项为k a ，公比为abq -=的等比数列的前1+k 项和.故ba b a q q a u k k k k k +--=--=+++111)(1)1(，Λ3,2,1=k .即b a b a b a b a u u k k k k k k +--++--=++++++22111)()(])()([11212++++----++=k k k k b b a a ba233])([1+++=--+=k k k u b a ba ，Λ3,2,1=k . 故答案为A.（易知其余答案均不成立）另解：易见BD AD CD ⋅=2，即ab b a =-2）（，又已知1=-b a ，故1=ab ，51414)((222=⨯+=+-=+ab b a b a ），5=+b a .解得215+=a ，215-=b .显然k u 是首项为k a ，公比为abq -=的等比数列的前1+k 项和，故b a b a q q a u k k k k k +--=--=+++111)(1)1(])251()251[(5111++--+=k k ，Λ,3,2,1=k .于是数列{}k u 就是斐波那契数列1，2，3，5，8，13，21，…，它满足递推关系,12k k k u u u +=++Λ,3,2,1=k .所以答案为A. 第5题解答过程{}n a 可看成是在正整数数列1，2，3，4，5，6，7，…中删去所有能被2，5或11整除的项之后，把余下的各项按从小至大顺序排成的数列.由三阶容斥原理，1，2，3，4，…，m 中不能被2，5或11整除的项的个数为⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1101022551152m m m m m m m m x m ，其中⎣⎦a 不表示不大于a 的最大整数，即a 的整数部分.估值：设11010225511522007m m m m m m m m x m -+++---≈=)1111)(511)(211(---⨯=m 11105421⨯⨯⨯=m m 114=，故55194112007≈⨯≈m . 又因⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1105519105519225519555519115519555192551955195519x=5519-2759-1103-501+100+250+551-50=2007，并且5519不是2，5，11的倍数，从而知55192007=a .答：B.又解：{}n a 可看成是在正整数数列1，2，3，4，5，6，7，…中删去所有能被2，5或11整除的项之后，把余下的各项按从小至大顺序排成的数列.因为2，5，11是质数，它们的最小公倍数为110.易见，-54，-53，…，0，1，2，3，…，55中不能被2，5，11整除的数为，，；，，，17139731±±±±±±，；2119±±；，，292723±±±，，，；，，474341393731±±±±±±535149±±±，；,共40个.（或由欧拉公式，1，2，3，…，110中不能被2，5，11整除的数的个数，等于1，2，3，…，110中与110互质的数的个数，等于401111511211110110=-⨯-⨯-⨯=∅）（）（）（）（.）显然1，2，3，…中每连续110个整数，不能被2，5，11整除的数都有40个.所以，1，2，3，…，550050110=⨯中，不能被2，5，11整除的数有20005040=⨯个.大于5500中的数不能被2，5，11整除的，是5500+1，5500+3，5500+7，5500+9，5500+13，5500+17，5500+19，….所以5519是第2007个不能被2，5，11整除的数，亦即所求的55192007=a .答：B. 第6题解答过程显然287cos 127cos 123cos 12οοοΛ++++++=AοοοοΛ5.43cos 5.5cos 5.3cos 5.1cos ++++=； οοοοΛ5.43sin 5.5sin 5.3sin 5.1sin ++++=.注意到)1sin()1sin(1sin cos 2οοο--+=θθθ，)1cos()1cos(1sin sin 2οοο+--=θθθ,所以)5.42sin 5.44(sin οο-+οοοο22sin 5.22cos 25.0sin 5.44sin =-=， )5.44cos 5.42(cos οο-+οοοο22sin 5.22sin 25.44cos 5.0cos =-=.故οοοοοοο5.22cot )22sin 5.22sin 2(:)22sin 5.22cos 2()21sin 2(:)21sin 2(:==⨯⨯=B A B A12+=.答：D.另解：2A 00005.43cos 5.5cos 5.3cos 5.1cos +++++=Λ，2B οοοοΛ5.43sin 5.5sin 5.3sin 5.1sin ++++=，=)5.22sin 5.22(cos 1sin 22sin οοοοi +. 因为2A 和2B是实数，所以οοο1sin 5.22cos 22sin 2=A ，οοο1sin 5.22sin 22sin 2=B , 122222222145sin 45cos 15.22cos 5.22sin 25.22cos 25.22sin 5.22cos 2:2:2+=+=+=+====οοοοοοοB A B A . 答：D.第7解答过程解：设△ABC 三边长c b a ,,为整数，c b a c b a c b a ,,,,60≥≥=++成等差数列，A ∠为钝角，则必有c a b +=2，222a c b <+.易解得b b b c a b c b a 32)(60=+=++=++=，40,20=+=c a b ；222c a b -<))((c a c a -+=，即c a c a -<-<10),(40202.因此a a c a c a <=-++<25,2)()(50，即26≥a .另外，29,30,260,≤<=+>++=>+a a a a a c b a a c b .易检验),,(c b a)11,20,29(),12,20,28(),13,20,27(),14,20,26(=都是钝角三角形.答：4.第8题解答过程注意到22-=x ，22+=y 满足4)22()22(22=++-=+y x ，0,>y x ，故可令θcos 2=x ，θsin 2=y ，0＜θ＜2π.从而22cos 42-=θ，-2cos 422-=θ，-θπθ2cos 43cos 1cos 2222==-=，故83πθ=，83cos )83sin 83(cos πππn i a n n =+=+ 83sinπn i .n a 取实数，当且仅当083sin =πn ，当且仅当k n 8=，∈k Z.满足此条件且2007≥n 的最小正整数n 为2008，此时1753cos 820083cos 2008-====ππx a a n .答：-1.第9题解答过程易见奇异数有两类：第一类是质数的立方3p （p 是质数）；第二类是两个不同质数的乘积21p p （21,p p 为不同的质数）.由定义可得3327=是奇异数（第一类）；73242⨯⨯=不是奇异数；23369⨯=是奇异数（第二类）； 373111⨯=是奇异数（第二类）；35125=是奇异数（第一类）；137是质数，不是奇异数；37343=是奇异数（第一类）；221301900899-=-=）（130+=2931130⨯=-）（是奇异数（第二类）；）（16016013600359922+=-=-=5961160⨯=-）（是奇异数（第二类）； 42119)12020)(120(120180007999233⨯=++-=-=-=是奇异数（第二类）.答：8. 第10解答过程解：将向量1AA ，，分别记为，，.2==a 3==b 4==c ，且易见AC ++=1，A ++-=1，BD +-=1，DB -+=1.所以)(2)(2222⋅+⋅+⋅+++=++=244332432222⨯+⨯+⨯+++==55，故551=AC .类似地，可算得，191=BD ，151=DB ，271=CA =33. 答：55，19，15，33. 第11题解答过程令t x =-3，易见3+=t x ，323)3(232)(+=-+=-=t t x x f ，)32(2)()2(+=t x f 3-32)(,,32)(2+=+=t x f t n n Λ；令s y =+1，易见1-=s y ，2)1(323)(+-=+=s y y g 13-=s ，Λ,132)13(3)(2)2(-=+-=s s y g ，13)()(-=s y g n n ，Λ,3,2,1=n .因此，题设方程组可化为（1）-（2），（2）-（3），（3）-（1）得所以)()23()()23()(2339629696y x x z z y y x -=-=-=-⇒00=-⇒=-z y y x z y x ==⇒.代入（1）得1)1(33)3(269-+=+-x x ，1)1(7293)3(512-+=+-x x ，7287291533512+=-x x ，2261217=-x ,32331=-x ,31323-=x . 所以原方程组的解为31323-===z y x .答：31323-===z y x .第12题解答过程.以l T V -表示平面图形T 绕直线l 所得旋转体体积.记直线AC 为l ，作l DN BM ⊥,，交l 于F E ,，分别交CD ，AB 于N M ,.过O 作l PQ ⊥，分别交CD AB ,于Q P ,.由于O 是BD 的中点，所以Q P ,分别是DM BN ,的中点.由对称性，易见所求旋转体体积为)(2l NPQD l ADN l ABCD V V V V --∆-+==平行四边形平行四边形.由于2324===AD BD AB ，，，易见οο3090=∠=∠DBA ADB ，，73422=+=+=DO AD AO ，72=AC .显然CAB DCA DAC ∠=∠>∠，FN DF >.且21727322==⨯==∆AO DO AD AO S DF ADO ，74716712422==-=-=DF AD AF .从而由圆锥体积公式得ππππ749167716747123312==⨯⨯=⨯⨯⨯==-∆-∆AF DF V V l ADF l ADN .又71074147472=-=-=-=AF AC CF ，7==AO CO ，QO DF CO CF ::=，215171021727=÷⨯=⨯=CF DF CO QO .从而由圆锥体积公式得 ππππ71225657122534310007)2574940(7)72521710712(3=-⨯=-=⨯-⨯=.从而17573021225105772)12256574916(72)7122565774916(2πππππ=⨯=+=+=V . 答：所求体积为1757302π：第13题解答过程解：I ）可设l ：4+=my x ，与Γ联立得03624)43(22=+++my y m .这是 y 的一元二次方程，由判别式0≥∆解得42≥m .记）（11,y x A ，）（22,y x B ，则4324221+-=+m m y y ，4336221+=m y y . 由题设条件，02121<+=⋅y y x x ，即0)4)(4(2121<+++y y my my ，得016)(4)1(21212<++++y y m y y m ，即016432444336)1(222<++-⋅++⋅+m mm m m ，即0)43(424)1(9222<++-+m m m .得02532<+-m ，3252>m ，253)1(2<m ，5353<<-m . 故l 的斜率的取值范围为)53,53(-. 因为F (1,0),所以）（111,1y x --=，）（22,1y x -=，从而 04324343362)(32222121=+-⋅++⋅=++=m mm m y y y my .∴1FA 与FB 共线，即1A 与F 、B 三点共线.III ）假设4≠q ，过)0,(q Q 的直线与Γ交于A 、B ，且A 关于长轴的对称点为1A ，如果1A 、F 、B 三点共线.我们另取点)0,4(P .设直线AP 与Γ交于1B ，那么如II ）的证明，1A 、F 、B 三点必共线.故B 与1B 重合，从而直线AB 和1AB 重合，就是AQ 与AP 重合.所以P 与Q 重合，4=q ，与假设矛盾.这就是说，4≠q 时，三点1A 、F 、B 不能共线. 第14题解答过程 14.解：n n n n n x x x x x 1212121+=+=+，22211441nn n x x x ++=+，)1(4112221+=-+n nn x x x ，Λ3,2,1=n . 故∑∑==++=-20061220061221)1(4)11(n n n nn x x x，亦即80244112006122122007∑=+=-n n x x x ，由11=x 得80254120061222007∑=+=n n x x .（*）由于112121<+=+n n n x x x ，,,3,2,1Λ=n 且显然0>n x ，故{}n x 是递减数列，且 31122112=+=x x x ，11319231122223=+=+=x x x ，故∑∑==++=2006322200612)31(1n n n nx x 15120041219911)113(911200632<⨯++=++<∑=n ，由（*）式得8629802515141802522007=+⨯<<x ，,802518629122007<<x 80251lglg 86291lg 22007<<x ， 8025lg lg 28629lg 2007-<<-x ，3lg 242007-<<-x ，23lg 22007-<<-x ，∴⎣⎦2lg 2007-==x k .第15题解答过程证明：因为△ABC 是锐角三角形，其三边c b a ,,满足0,,>c b a ，以及222222222,,,,,c b a b a c a c b c b a b a c b c b >+>+>+>+>+>+.因此，由平均不等式可知)()(21)()(21)()(21222222222222222222222222xy y x z c b a z x x z y b a c y z z y x a c b +-+++-+++-+≤222222222222zy x c y x z b x z y a ++=)(2)(2222abz cay bcx z cxy y bzx x ayz ++-++=，从而22222222222)(])[(])[(])[(P zcxy y bzx x ayz z c b a y b a c x a c b =++≤-++-++-+，亦即2)(P S c b a ≤++，cb a P S ++≤2.上式取等式当且仅当222z y x ==，亦即===z y x cb a P++.因此所求的S 的最大值为c b a P ++2，当S 取最大值时，===z y x cb a P++.（第13题答图）（第10题答图）（第12题答图）2008年安徽高中数学竞赛初赛试题一、选择题1.若函数()y f x =的图象绕原点顺时针旋转2π后，与函数()y g x =的图象重合，则（）（A ）()()1g x f x -=- （B ）()()1g x f x -= （C ）()()1g x f x -=--（D ）()()1g x f x -=-2.平面中，到两条相交直线的距离之和为1的点的轨迹为（）（A ）椭圆（B ）双曲线的一部分（C ）抛物线的一部分（D ）矩形 3.下列4个数中与cos1cos2cos2008+++o o o L 最接近的是（）（A ）-2008 （B ）-1 （C ）1 （D ）2008 4.四面体的6个二面角中至多可能有（）个钝角。

2016年全国高中数学联赛试题及答案详解(A卷)

知 MK BC ，从而 MKH 为二面角 M BC A 的平面角．
因 MH AH 1 ，结合 HK 与 AB 平行知， HK HC 3 ，即 HK 3 ，
2
AB AC 4
4
这样 tan MKH MH 2 ．故二面角 M BC A 的大小为 arctan 2 ．

，
n 2,3, ．这里 x 表示不小于实数 x 的最小整数．证明：对 n 3, 4, , p 1 均有 n | pan1 1 ．
2016 年全国高中数学联合竞赛一试（A 卷）
参考答案及评分标准
说明：
1. 评阅试卷时，请依据本评分标准. 填空题只设 8 分和 0 分两档；其他各题的
a2015

a2 2016
a2016 a12 的最大值．
二、（本题满分 40 分）如图所示，在△ABC 中，X、Y 是直线 BC 上两点（X、B、C、Y 顺次排列），使得 BX AC CY AB ．设△ACX、△ABY 的外心分别为 O1,O2 ，直线 O1O2 分别与 AB、AC 交于点 U、V．证明：△AUV 是等腰三角形．
1. 设实数 a 满足 a < 9a3 −11a < a ，则 a 的取值范围是
．
答案：
a
∈

−
2
3
3
,
−
10 3

．
解：由 a < a 可得 a < 0 ，原不等式可变形为
1 > 9a3 −11a > a = −1，
a
a
即 −1 <
9a2
−11 < 1，所以 a2
∈

2016年高中数学联赛试题答案

2 2
2
2
3. 正实数 u , v, w 均不等于 1，若 log u vw log v w 5 ， log v u log w v 3 ，则． log w u 的值为 4 答案：． 5 解：令 log u v a, log v w b ，则 1 1 log v u , log w v ， log u vw log u v log u v log v w a ab ， a b 1 1 5 条件化为 a ab b 5, 3 ，由此可得 ab ．因此 a b 4 1 4 log w u log w v log v u ． ab 5 4. 袋子 A 中装有 2 张 10 元纸币和 3 张 1 元纸币，袋子 B 中装有 4 张 5 元纸币和 3 张 1 元纸币．现随机从两个袋子中各取出两张纸币，则 A 中剩下的纸币面值
M 为 AP 的中点．若 AB 1, AC 2, AP 2 ，则二面角 M BC A 的大小为． 2 答案： arctan ． 3 解：由 ABC 90 知， AC 为底面圆的直径．设底面中心为 O ，则 PO 平面 ABC ．易知 1 AO AC 1 ，进而 PO AP 2 AO 2 1 ． 2 设 H 为 M 在底面上的射影，则 H 为 AO 的中点．在底面中作 HK BC 于点 K ，则由三垂线定理知 MK BC ，从而 MKH 为二面角 M BC A 的平面角． 3 1 HK HC 3 因 MH AH ，结合 HK 与 AB 平行知，，即 HK ， 4 2 AB AC 4 MH 2 2 这样 tan MKH ．故二面角 M BC A 的大小为 arctan ． 3 HK 3 kx kx 6. 设函数 f ( x) sin 4 cos 4 ，其中 k 是一个正整数．若对任意实数 a ， 10 10 均有 f ( x) a x a 1 f ( x) x R ，则 k 的最小值为．

全国高中数学联赛安徽赛区试卷含解析

全国高中数学联赛安徽初赛试卷一、选择题（本题满分36分，每小题6分）1．正数列满足()231221,10,103n n n t a a a a a n --===≥，则100lg ()a =A 、98B 、99C 、100D 、1012．已知lg x 的小数部分为a ，则21lg x 的小数部分为 A 、2a -的小数部分 B 、12a -的小数部分 C 、22a -的小数部分 D 、以上都不正确3．过原点O 引抛物线224y x ax a =++的切线，当a 变化时，两个切点分别在抛物线（）上A 、2213,22y x y x ==B 、2235,22y x y x == C 、22,3y x y x == D 、223,5y x y x == 4．已知△ABC 为等腰直角三角形，∠C = 90°，D 、E 为AB 边上的两个点，且点D 在AE 之间，∠DCE = 45°，则以AD 、DE 、ED 为边长构成的三角形的最大角是A 、锐角B 、钝角C 、直角D 、不能确定5．将正整数从1开始不间断的写成一行，第2006个数码是（旁注：这是希望杯的培训题）A 、0B 、5C 、7D 、以上都不正确6．已知圆锥的顶点V 和底面圆心O 的连线垂直于底面（旁注，这句话实际上是废话），一个过VO 中点M 的平面与圆O 相切，与圆锥的交线是一个椭圆，若圆O 半径为1，则椭圆的短轴的长为A、 BCD 、以上结果都不对二、（每小题9分，共54分）7．设等差数列的首项和公差均为正整数，项数为不小于3的素数，且各项之和为2006，则这样的数列共有_____个．8．已知实数x 、y 满足()()()()55111511541545x x y y ⎧-+-=⎪⎨-+-=-⎪⎩，则x y +=_____．（旁注：联赛原题） 9．正八边形所有对角线在其内部交点的个数为_____．10．若x 、y 为实数，且223x xy y ++=，则22x xy y -+的最大值和最小值分别为_____．11．一个正方体的8个顶点可以组成_____个非等边三角形．12．若关于x的方程2kx +恰有一个实根，则k 的取值范围是_____．三、论述题（本题满分60分，每小题20分）13．设有2006个互不相同的复数，其中任何两个数的积（包括自乘）是这2006个数之一，求这2006个数的和．14．求3221123nnk k k n n n k k k C n k C n kC ==-+∑∑的值．15．已知数列{}()0n a n ≥满足00a =，对于所有n N +∈，有115n n a a +=+，求n a 的通项公式．全国高中数学联赛安徽初赛参考答案1B2C3B5A6B7(15)8(15)9(65)10(6和2)11(48)12()14(0)15() )2,3[]3,2(⋃--2]2)56()56([nn n a --+=。