哈工大信号与系统实验电气学院
哈工大随机信号实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y实验报告课程名称:随机信号分析院系:电信学院班级: 1205201 姓名:学号:指导教师:郑薇实验时间: 2014年 11月哈尔滨工业大学实验一 各种分布随机数的产生一、 实验目的在很多系统仿真的过程中,需要产生不同分布的随机变量。
利用计算机可以很方便地产生不同分布的随机变量,各种分布的随机变量的基础是均匀分布的随机变量。
有了均匀分布的随机变量,就可以用函数变换等方法得到其他分布的随机变量。
二、 实验内容产生均匀分布的随机数、高斯分布的随机数和其它分布的随机数。
三、 实验原理1. 均匀分布随机数的产生原理产生伪随机数的一种实用方法是同余法,它利用同余运算递推产生伪随机数序列。
最简单的方法是加同余法)(m od 1M c y y n n +=+My x n n 11++=为了保证产生的伪随机数能在[0,1]内均匀分布,需要M 为正整数,此外常数c 和初值y0亦为正整数。
加同余法虽然简单,但产生的伪随机数效果不好。
另一种同余法为乘同余法,它需要两次乘法才能产生一个[0,1]上均匀分布的随机数)(m od 1M ay y nn =+M y x n n 11++=式中,a 为正整数。
用加法和乘法完成递推运算的称为混合同余法,即)(m od 1M c ay y n n +=+My x n n 11++=用混合同余法产生的伪随机数具有较好的特性,一些程序库中都有成熟的程序供选择。
常用的计算语言如Basic 、C 和Matlab 都有产生均匀分布随机数的函数可以调用,只是用各种编程语言对应的函数产生的均匀分布随机数的范围不同,有的函数可能还需要提供种子或初始化。
Matlab 提供的函数rand()可以产生一个在[0,1]区间分布的随机数,rand(2,4)则可以产生一个在[0,1]区间分布的随机数矩阵,矩阵为2行4列。
哈工大电气学院仪器科学与技术

哈工大电气学院仪器科学与技术自动化测试与控制系简介哈尔滨工业大学自动化测试与控制系仪器科学与技术学科创建于1955年,在苏联专家的帮助下,以前苏联人才培养模式培养出国内第一批精密仪器专业研生和本科生,这批学生均成为我国该学科领域的学术带头人和技术带头人。
该学科现为国家重点一级学科, 1998年成为全国首批按一级学科培养和授予博士学位的学科点,同年被批准建立仪器科学与技术博士后流动站。
本学科在2001-2003年间全国一级学科整体水平评估中,全国排名第二, 2004-2006年间全国一级学科整体水平评估中,全国排名第三。
本学科具有较高的学术声誉和影响力。
本学科始终瞄准国际高科技前沿和国家重大需求,针对航天和国防尖端技术的前沿科学问题和关键技术问题,开展科学研究与工程关键技术研究,形成了以航天、航空、尖端与先进装备制造、微电子与信息装备制造为背景,以精密/超精密测量技术与仪器、自动化综合测试与控制技术、光电信息技术与系统为主要特色的科学研究方向,取得了以国家技术发明奖一等奖为标志的一批重大科研成果。
近三年累计科研经费超过2.6亿元。
此外,还申请国际发明专利和中国发明专利150余项,已获授权70余项;近年来完成国防航天重点预研和工程项目与国家自然科学基金项目近百项。
本学科由四个研究所、五个研究室及一个基础课教研室组成。
现有教授32人,副教授36人,其中博士生导师28硕士生导师53人。
本学科不仅在科学研究与工程关键技术研究上取得了较突出的成果,还在研究生培养方面取得了突出的成绩,共有4人获得全国百名优秀博士学位论文奖,2人获得全国百名优秀博士学位论文提名奖。
硕士研究生就业去向:国内各科研院所、国企、外企、各大公司、技术开发类企业,以及国家机关等单位,或去国内外高校攻读博士学位。
电气工程及自动化学院已走过17年的风雨路程,作为哈工大的重要组成部分,在教学与科研工作上始终处于校内的前列,并取得了令人瞩目的成绩。
哈工大数字逻辑电路与系统实验报告

哈工大数字逻辑电路与系统实验报告引言本实验旨在通过对数字逻辑电路与系统的学习与实践,加深对数字逻辑电路原理和应用的理解,掌握数字逻辑电路实验的设计与调试方法。
本报告将详细介绍实验步骤、实验结果以及实验心得体会。
实验目的1.掌握基本的数字逻辑电路设计方法;2.熟悉数字逻辑电路的布线和调试方法;3.学会使用EDA软件进行数字逻辑电路的仿真和验证。
实验器材•FPGA开发板•EDA软件实验过程实验一:逻辑门的基本控制本实验采用FPGA开发板进行实验,以下是逻辑门的基本控制步骤:1.打开EDA软件,新建工程;2.选择FPGA开发板型号,并进行相应配置;3.在原理图设计界面上,依次放置与门、或门、非门和异或门,并连接输入输出引脚;4.面向测试向量实现逻辑门的控制和数据输入;5.运行仿真并进行调试。
实验二:数字逻辑电路实现本实验以4位全加器为例,进行数字逻辑电路的实现,以下是实验步骤:1.打开EDA软件,新建工程;2.选择FPGA开发板型号,并进行相应配置;3.在原理图设计界面上,放置输入引脚、逻辑门和输出引脚,并进行连接;4.根据全加器的真值表,设置输入信号,实现加法运算;5.运行仿真并进行调试。
实验三:数字逻辑电路的串联与并联本实验旨在通过对数字逻辑电路的串联与并联实现,加深对逻辑门的理解与应用。
以下是实验步骤:1.打开EDA软件,新建工程;2.选择FPGA开发板型号,并进行相应配置;3.在原理图设计界面上,放置多个逻辑门,并设置输入输出引脚;4.进行逻辑门的串联与并联连接;5.根据逻辑门的真值表,设置输入信号,进行运算;6.运行仿真并进行调试。
实验结果经过实验测试,实验结果如下:1.实验一:逻辑门的基本控制–与门的功能得到实现;–或门的功能得到实现;–非门的功能得到实现;–异或门的功能得到实现。
2.实验二:数字逻辑电路实现–4位全加器的功能得到实现;–正确进行了加法运算。
3.实验三:数字逻辑电路的串联与并联–逻辑门的串联与并联功能得到实现;–通过逻辑门的串联与并联,实现了复杂的逻辑运算。
(精编)哈工大通信原理实验报告

(精编)哈工大通信原理实验报告H a r b i n I n s t i t u t e o f T e c h n o l o g y通信原理实验报告课程名称:通信原理院系:电子与信息工程学院班级:姓名:学号:指导教师:倪洁实验时间:2015年12月哈尔滨工业大学实验二帧同步信号提取实验一、实验目的1.了解帧同步的提取过程。
2.了解同步保护原理。
3.掌握假同步,漏同步,捕捉动态和维持态的概念。
二、实验原理时分复用通信系统,为了正确的传输信息,必须在信息码流中插入一定数量的帧同步码,帧同步码应具有良好的识别特性。
本实验系统帧长为24比特,划分三个时隙,每个时隙长度8比特,在每帧的第一时隙的第2至第8码元插入七位巴克码作为同步吗。
第9至24比特传输两路数据脉冲。
帧结构为:X11100101010101011001100,首位为无定义位。
本实验模块由信号源,巴克码识别器和帧同步保护电路三部分构成,信号源提供时钟脉冲和数字基带脉冲,巴克码识别器包裹移位寄存器、相加器和判决器。
其余部分完成同步保护功能。
三、实验内容1.观察帧同步码无错误时帧同步器的维持状态。
2.观察帧同步码有一位错误时帧同步器的维持态和捕捉态3.观察帧同步器假同步现象和同步保护器。
四、实验步骤1.开关K301接2.3脚。
K302接1.2脚。
2.接通电源,按下按键K1,K2,K300,使电路工作。
3.观察同步器的同步状态将信号源中的SW001,SW002,SW003设置为11110010,10101010,11001100(其中第2-8位为帧同步码),SW301设置为1110,示波器1通道接TP303,2通道接TP302,TP304,TP305,TP306,观察上述信号波形,使帧同步码(SW001的2-8位)措一位,重新做上述观察,此时除了TP303外,个点波形不变,说明同步状态仍在维持。
4.观察同步器的失步状态。
关闭电源,断开K302,在开电源(三个发光二极管全亮)。
哈尔滨工业大学电子与信息工程学院2012学年秋学期研究生助教岗聘任公示名单
12B905015
B
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
谷献模
10B907009
A
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
陈蒙
11S005042
C
13
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
陈美航
11S005098
C
通信电子线路
赵雅琴、陈浩、侯成宇
60/24
张亚非
11S005013
C
通信电子线路
吴群、孟繁义、秦月梅
40/6
李宛露
11S005005
C
24
通信电子线路实验
赵雅琴
24
吴龙文
12S105034
C
25
电磁兼容原理与技术
张狂
32
周长飞
12S105024
D
26
交换技术
王学东、叶亮
28
李斌
11S105012
D
27
光纤通信
张文彬、吴玮
30
邱昕
11B905021
C
12B905010
B
卫星定位导航原理与应用
孟维晓、迟永钢
36/4
邹德岳
11B905006
A
6
通信原理I
于启月、赵洪林
60/12
郑艺
11S005069
C
7
通信原理II
苏雁泳、刘春刚
60/12
杨堃
11S105013
C
通信原理I
于启月、赵洪林
60/12
赵莹
11S105041
C
信号与系统3.5

2F(2ω)
缩
π
τ
ω
−τ O
τ t
τ
τ
ω
f(2t) 缩 1 缩 展
τ /2
O
4π
1 F(ω / 2) 2
展
4π
−τ / 4 O τ / 4 t
−
τ
τ
ω
11
时域中的压缩(扩展)等于频域中的扩展(压缩) 时域中的压缩(扩展)等于频域中的扩展(压缩)
哈尔滨工业大学(威海)信息与电气工程学院 通信工程系 哈尔滨工业大学(威海)
解
Qe
−at
2a ↔ 2 a + ω2
a=1
1 −t 1 ∴ e ↔ 2 1+ ω2
1 1 − −ω −ω ∴ 2 ↔ 2π e = πe t +1 2
9
哈尔滨工业大学(威海)信息与电气工程学院 通信工程系 哈尔滨工业大学(威海)
信号与系统
4. 尺度变换性
时间波形的扩展和压缩, 时间波形的扩展和压缩,将影响频谱的波形 a为实常数
信号与系统
信号与系统 例 尺度变换变换后语音信号的变化
f(t)
0.5 0.4 0.3 0.2 0.1 0 -0.1 -0.2 -0.3 -0.4 -0.5 0
f(2t)
f(t/2)
f (t)
f (1.5t)
f (0.5t)
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
一段语音信号( 对了 对了” 一段语音信号(“对了”) 。抽样频率 =22050Hz
1 ω f (t) ↔ F(ω) 则 f (at) ↔ F( ) a a
哈工大电路实验答案【电工学实验】
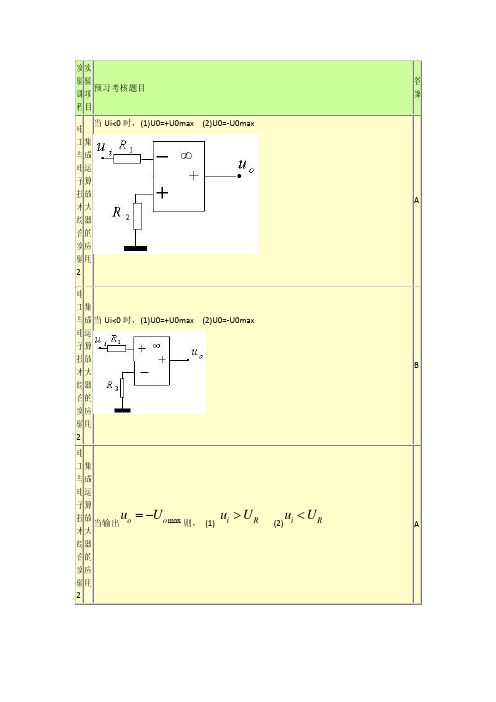
集成运算放大器的应用当Ui<0时,(1)U0=+U0max (2)U0=-U0maxA集成运算放大器的应用当Ui<0时,(1)U0=+U0max (2)U0=-U0maxB集成运算放大器的应用电路如图,改变Ui可使U0发生变化,当U0由正电压跃变为负电压时的Ui值和U0由负电压跃变为正电压时的Ui值:B集成运算放大器的应用电路如图:A大器的应用集成运算放大器的应用电路如图:A集成运算放大器的应用电路如图:B集成运算放大器的应用电路如图:B集成运算放大器的应用电路如图.当和相位相同时,则A )(1ωjU∙)(2ωjU∙组合逻辑电路及其应用当ui=A,则1) u0=A,2)B组合逻辑电路及其应用当ui=A,则1) u0=A,2)B组合逻辑电路及其应用当ui=A,则1) u0=A,2)BAuo=Auo=Auo=其应用组合逻辑电路及其应用当ui=A,则1) u0=A,2)B组合逻辑电路及其应用当ui=A,则1) u0=A,2)AAuo=Auo=触发器及时序逻辑电路电路如图,已知A=1,JK触发器的功能是A序逻辑电路触发器及时序逻辑电路当M=1时为几进制A与电子技直流直流电路下图的开路电压UOC的测定方法中,哪个是正确的。
A直流电路下图中电源的等效内阻RO的测定方法中,哪个是正确的。
A交流电路如图,当输入的交流信号U1的幅值一定时,输入信号的频率越高,输出电压的幅值A交流电路如图,当输入的交流信号Ui的幅值一定时,输入信号的频率越高,则输出电压的幅值B交流电路当电源电压一定,电路发生谐振时,则电路中的电流IA路交流电路在电感元件电路中,在相位上A集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放C 大器的应用集成运算放B 大器的应用集成运算放B 大器的应用集成运算放C 大器的应用集成运算放C 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放A 大器的应用集成运算放B 大器的应用触发器及时序逻辑电路电路如图,已知A=1,JK触发器的功能是A触发器及时序逻辑电路当74LS161的输出状态为1111时,再来一个计数脉冲,则下一个状态为B触发器及时序逻辑电路当M=1时为几进制A电路网络的频率特性一阶RC低通滤波器实验电路图是:A电路网络的频率特性一阶RC高通滤波器实验电路图是:B的频率特性电路网A 络的频率特性。
哈工大电气培养方案【精选】

电气工程及其自动化专业本科生培养方案一、培养目标本专业培养具备电气工程领域相关的基础理论、专业技术和实践能力,具有宽广的自然科学基础和良好的人文素养,富于创新精神,能在电机与电器、电力系统、工业自动化以及电气装备制造等领域从事科学研究、工程设计、系统运行、试验分析、管理等工作的宽口径、复合型高级工程技术人才,以及具有国际竞争力的高水平研究型精英人才或工程领军人才。
二、培养要求本专业学生主要学习电路、电磁场、电子技术基础、计算机技术、信号分析与处理、通信与网络技术、电机学、自动控制理论和电力电子技术等方面基础理论和专业知识,接受电工、电子、信息、控制及计算机技术方面的基本训练,掌握解决电气工程领域中的装备设计与制造、系统分析与运行及控制的基本能力。
毕业生应当具备以下几方面的知识和能力:1.掌握较扎实的高等数学和大学物理等自然科学基础知识,具有较好的人文社会科学和管理科学基础,具有一定的外语国际交流和运用能力;2.系统地掌握电气工程学科的基础理论和基本知识,主要包括电工理论、电子技术、信息处理、控制理论、计算机软硬件基本原理与应用等;3.掌握电气工程相关的系统分析方法、设计方法和实验技术;4.具有本专业领域内至少一个专业方向(电机、电力系统、工业自动化和电器)的专业知识和技能,了解本专业学科前沿的发展趋势;5.具有较强的适应能力,具备一定的科学研究、技术开发和组织管理能力;6.具有较好的工程实践动手能力和计算机应用能力,能综合运用所学知识分析和解决本领域工程问题;7.掌握其他的一些技能,如信息技术获取,组织管理,团队合作,持续的知识学习等。
三、主干学科电气工程。
四、专业主干课程C语言程序设计、机械学基础、电路、模拟电子技术基础、数字电子技术基础、电磁场、电机学、自动控制理论、嵌入式系统原理及应用、仿真技术与应用、电力电子技术、信号与系统、工业通信与网络技术。
五、修业年限、授予学位及毕业学分要求修业年限:四年。
哈工大电气学院课程设计

哈工大电气学院课程设计一、课程目标知识目标:1. 学生能够掌握电路分析的基本原理,理解并运用复数表达法进行交流电路的计算。
2. 学生能够运用基本电路定理,如欧姆定律、基尔霍夫定律,分析简单的电气网络。
3. 学生能够识别并描述常见电子元件的工作原理和特性。
技能目标:1. 学生能够设计简单的电路图,并进行模拟计算,验证电路性能。
2. 学生通过实验和模拟软件操作,培养动手能力和实际问题解决能力。
3. 学生能够运用电气工程相关软件进行基础电路设计与仿真。
情感态度价值观目标:1. 学生培养对电气工程学科的兴趣,增强探究精神和创新意识。
2. 学生通过团队合作完成项目任务,培养沟通能力和团队协作精神。
3. 学生能够在电路设计和分析中,认识到科技对社会发展的贡献,增强社会责任感和职业道德。
本课程针对哈工大电气学院高年级学生设计,课程性质以实践与应用为主,结合理论教学。
学生具备一定的物理和数学基础,对电气工程有初步了解。
教学要求强调理论与实践相结合,注重培养学生的实际操作能力、创新思维和解决复杂工程问题的能力。
通过具体学习成果的达成,为学生未来从事电气工程领域工作打下坚实基础。
二、教学内容1. 电路分析基本原理:复数表达法,相量图绘制,交流电路的阻抗与导纳分析。
- 教材章节:第三章“交流电路的分析方法”2. 基本电路定理:欧姆定律,基尔霍夫定律,节点分析,回路分析。
- 教材章节:第四章“电路定理及其应用”3. 电子元件特性:电阻、电容、电感元件的伏安特性,频率响应特性。
- 教材章节:第二章“电路元件及其特性”4. 电路设计与仿真:利用Multisim、LTSpice等软件进行电路设计、模拟与验证。
- 教材章节:第六章“电路仿真技术”5. 实践项目:设计并搭建简单的放大电路,测试其性能参数。
- 教材章节:第五章“电子电路设计与实践”教学内容安排与进度:第一周:电路分析基本原理,复数表达法的应用。
第二周:基本电路定理学习,进行相关习题练习。
信号与系统_2015_40学时_第3章_习题课

HIT_Prof. Liu X.S.
哈尔滨工业大学电气工程系专业技术基础课
第3章 连续时间信号与系统的频域分析 (习题课)
第 1页
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
本章学习重点
1. 了解函数正交的条件及完备正交函数集的概念。 2. 能用傅里叶级数的定义式、基本性质求解周期信
j 5t
, A为常数。求其傅里叶
解: 根据常用函数——单位直流信号的傅里叶变换, 可知,
1 2πδ(ω)
根据傅里叶变换的线性性,有
A 2πAδ(ω)
根据傅里叶变换的频移特性,有
e A 2πAδ(ω 5)
j 5t
即
F (ω) 2πAδ(ω 5)
第 页
电气工程系平台课 《信号处理技术》
0 0 0 0
0
0
根据对称性,有 2πG (ω) 2ω Sa(ω t )
2 ω0 0 0
第13页
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
ω0 根据线性性质,即有 G2ω (ω) Sa(ω0t ) π 2 ω0 ω0 所以 F (ω) G2ω (ω) 的原函数是 f (t ) Sa(ω0t ) π π 1 1 1 (4) F (ω) 2 ( jω α ) jω α jω α
温馨提示:傅里叶变换频移性质
HITPEED
sin t 。求其傅里叶变换 F (ω) 。 例4 已知函数 f (t ) t
解: 根据常用函数——门信号的傅里叶变换,可知,
2
哈工大-自适应信号处理_LMS自适应滤波器实验报告

.Harbin Institute of Technology自适应平衡器计算机实验课程名称:自适应信号处理院系:电子与信息工程学院姓名:学号:授课教师:**哈尔滨工业大学一、实验目的:1. 深入掌握自适应平衡器的理论基础和以及它的可能用途。
2. 理解最小均方自适应算法的适用条件,以及最小均方自适应算法的理论推导。
3. 改变特征值扩散度)(R χ与步长参数μ,观察实验结果,深入理解理解这些参数对实验结果的重要性。
4. 探究在线性色散信道中使用最小均方自适应算法引起的失真问题。
二、实验内容:在此次实验中我们研究LMS 算法自适应均衡引起未知失真的线性色散信道问题。
假设数据是实数,图2.1表示用来进行该项研究的系统框图。
自适应均衡器用来纠正存在白噪声的信道的畸变。
通过随机数发生器1产生用来探测信道的测试信号n x ;通过随机数发生器2来产生干扰信道输出的白噪声源()v n 。
这两个发生器是相互独立的。
经过适当延迟,随机数发生器1页提供用作训练序列的自适应均衡器的期望相应。
加到信道输入的随机序列{}n x 由伯努利序列组成,其中1n x =±,随机变量n x 具有零均值和单位方差。
信道的单位脉冲响应应用升余弦表示为20.5[1cos((2))]1,2,30n n n h Wπ⎧+-=⎪=⎨⎪⎩,其他 (2-1)等价地,参数W 控制均衡器抽头输入的相关矩阵的特征值分布()χR ,并且特征值分布随着W 的增大而扩大。
随机数发生器2产生的序列是零均值,方差20.001v σ=。
随机噪声发生器(1)信道随机噪声发生器(2)延迟∑自适应横向滤波器∑nx nv +-ne图2.1 自适应均衡实验框图这里均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于2n =时对称,均衡器的最优抽头权值on w 在5n =时对称。
因此信道的输入n x 被延时了=∆2+5=7个样值,以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时Δ,LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
哈工大电路实验1实验报告

竭诚为您提供优质文档/双击可除哈工大电路实验1实验报告篇一:哈工大数字电路实验报告实验二数字逻辑电路与系统上机实验讲义实验二时序逻辑电路的设计与仿真课程名称:院系:班级:姓名:学号:教师:哈尔滨工业大学20XX年12月实验二时序逻辑电路的设计与仿真3.1实验要求本实验练习在maxplusII环境下时序逻辑电路的设计与仿真,共包括6个子实验,要求如下:3.2同步计数器实验3.2.1实验目的1.练习使用计数器设计简单的时序电路2.熟悉用mAxpLusII仿真时序电路的方法3.2.2实验预习要求1.预习教材《6-3计数器》2.了解本次实验的目的、电路设计要求3.2.3实验原理计数器是最基本、最常用的时序逻辑电路之一,有很多品种。
按计数后的输出数码来分,有二进制及bcD码等区别;按计数操作是否有公共外时钟控制来分,可分为异步及同步两类;此外,还有计数器的初始状态可否预置,计数长度(模)可否改变,以及可否双向等区别。
本实验用集成同步4位二进制加法计数器74Ls161设计n分频电路,使输出信号cpo的频率为输入时钟信号cp频率的1/n,其中n=(学号后两位mod3.2.4实验步骤1.打开mAxpLusII,新建一个原理图文件,命名为exp3_2.gdf。
2.按照实验要求设计电路,将电路原理图填入下表。
3.新建一个波形仿真文件,命名为exp3_2.scf,加入时钟输入信号cp及输出信号cpo,并点击mAxpLusII左侧工具条上的时钟按钮,将cp的波形设置为周期性方波。
4.运行仿真器得到输出信号cpo的波形,将完整的仿真波形图(包括全部输入输出信号)附于下表。
3.3时序电路分析实验3.3.1实验目的练习用mAxpLusII进行时序逻辑电路的分析。
3.3.2实验预习要求1.预习教材《6-3-1异步二进制计数器》2.了解本次实验的目的、电路分析要求3.3.3实验原理分析如下时序电路的功能,并判断给出的波形图是否正确。
哈工大威海信系统实验报告

《信号与系统》实验报告姓名:学号:同组人:无指导教师:成绩:实验一典型连续时间信号描述及运算实验报告要求:(1)仿照单边指数信号的示例程序,按要求完成三种典型连续信号,即:正弦信号、衰减正弦信号、钟型信号的波形绘制。
(要求:要附上程序代码,以下均如此,不再说明)(2)根据《信号与系统》教材第一章的习题1.1(1,3,5,8)函数形式绘制波形。
(3)完成三种奇异信号,即:符号函数、阶跃信号、单位冲激信号的波形绘制。
(4)完成实验一中信号的运算:三、6 实验内容中的(1)(2)(3)(4)。
(5)求解信号的直流/交流分量,按第四部分的要求完成。
正文:(1)<1>正弦信号:代码:>> t=-250:1:250;>> f1=150*sin(2*pi*t/100);>> f2=150*sin(2*pi*t/200);>> f3=150*sin(2*pi*t/200+pi/5);>> plot(t,f1,'-',t,f2,'--',t,f3,'-.')<2>衰减正弦信号<3>代码:>> t=-250:1:250;>> f1=400*exp(-1.*t.*t./10000);>> f1=400*exp(-1.*t.*t./22500);>> f1=400*exp(-1.*t.*t./62500);>> plot(t,f1,'-',t,f2,'--',t,f3,'-.') (2)习题1,3,5,8<1>代码:t=0:1:10;f=t;plot(t,f)<3>代码:t=1:1:10;f=t;plot(t,f)<5>代码:t=0:1:10;f=2-exp(-1.*t.);plot(t,f)<8>代码:t=1:0.1:2;f=exp(-1.*t.)*cos(10*pi*t);plot(t,f)(3)三种奇异函数<1>符号函数代码: t=-5:0.05:5;f=sign(t);plot(t,f)<2>阶跃信号代码:>> t=-5:0.1:5;>> f=u(t);>> plot(t,f)<3>单位冲激信号代码:function chongji(t1,t2,t0)dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt]) title('单位冲激信号δ(t) ')(4)实验三1234<1>syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); subplot(1,2,1);ezplot(f1);y1=subs(f1,t,-t);f3=f1+y1;subplot(1,2,2);ezplot(f3);function f=u(t) f=(t>0);<2>4、function f=u(t)f=(t>0)syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); subplot(1,3,1);ezplot(f1);f2=sym('sin(2*pi*t)');subplot(1,3,2);ezplot(f2);f6=f1.*f2;subplot(1,3,3);ezplot(f6);5、function f=u(t)f=(t>0)syms tf1=sym('(-t+4)*(u(t)-u(t-4))'); f2=sym('sin(2*pi*t)');subplot(1,3,1);ezplot(f2);f6=f1.*f2;y6=subs(f6,t,t-2);subplot(1,3,2);ezplot(y6);f7=y6+f2;subplot(1,3,3);ezplot(f7);四、t=0:0.1:500;f=100.*abs(sin(2.*pi.*t./50)); plot(t,f,t,fD,t,fA)调用子程序:function fD=fDC(f)fD=mean(f);function fA=fAC(f,fD)fA=f-fD;(5)求解信号的交直流分量代码:function fD=fDC(f)fD=mean(f);function fA=fAC(f,fD)fA=f-fD;t=0:0.1:500;f(t)=100|sin(2*PI*t/50)|;plot(t,fD,t,fA)实验二线性系统时域分析实验报告要求:(1)求解下面两个信号的卷积积分。
哈工大各院系部分科研方向简介201复件-山东工商联

哈尔滨工业大学(威海)各院系部分科研方向简介⏹材料科学与工程学院特种焊接与表面工程主要研究方向:1.水下焊接设备及工艺2.核电焊接装备与技术3.新材料及异种材料连接4.空间焊接技术先进热成形技术与装备主要研究方向:1.高强钢板(22MnB5)热冲压工艺以及热冲压模具设计关键技术研究2.热冲压过程的有限元软件模拟及研究预测冷却规律和组织转变规律3.热成形设备的设计与研发粉末冶金与特种材料成形主要研究方向:1.有色金属特种塑性成形2.新能源材料及系统3.粉末冶金塑性加工理论4.特种成形技术及装备5.难变形材料精密塑性成形新技术及装备先进再制造技术与装备主要研究方向:1.激光熔覆及激光表面改性2.电弧熔敷表面抗高温烧蚀材料3.等离子喷焊与感应加热熔覆表面耐磨材料内高压成形技术与装备主要研究方向:1.管材液压成形2.板材液压成形3.液压成形装备4.管材性能测试装备复合材料与结构主要研究方向:1.不连续增强金属基复合材料制备工艺问题研究2.碳纤维增强树脂基复合材料制备工艺研究3.复合材料界面及结构的多层次模拟与设计研究4.复合材料回收与应用技术研究特种陶瓷与碳材料主要开展新型特种陶瓷和碳材料的设计、合成,以及在航天防热、透波与隐身、电子封装热电管理、口腔修复、新能源和海水淡化等工程上的应用研究。
1. 新型陶瓷与碳材料设计、合成、表征、强韧化2. 有机硅硼高分子、复合材料、陶瓷化制品3. 玻璃与微晶玻璃的析晶控制与强韧化4. 准一维纳米陶瓷材料与半导体器件5. 纳米碳纤维及复合膜电极6. 天然石墨深加工技术:石墨烯、隐身材料、电极材料、复合材料材料模拟与计算主要研究方向:1.低模量高强度钛合金设计2.羟基磷灰石与钛作用机理的模拟3.Mg基储氢材料设计4.稀磁半导体材料设计电子封装材料与技术主要研究方向:1.电子封装与组装技术2.微纳系统封装制造3.传感器与微纳器件4.高性能电子封装材料5.微组装焊点的可靠性6.互连界面的组织演变7.无铅钎料合金基础研究⏹信息与电气工程技术学院控制科学与工程主要研究方向:1.超声信号检测及处理:三维B超,彩色超声成像设备2.工业控制机器人:机器人控制、小型自动化生产线的工业控制机器人3.仿真与试验系统:转台等军用仿真用非标设备及军/民用仿真控制系统测控技术及仪器主要研究方向:1.海洋光电检测技术:近程海面激光成像技术,大视场、高帧频激光三维水下成像技术,激光海洋探测研究及仪器开发2.无线传感器网络及网络化测试技术:复杂环境下无线传感器网络构建机理,无线传感器网络节点定位技术3.自动测试理论、技术及系统:测试与故障诊断,故障预测与健康管理、信号处理方法电气工程主要研究方向:1.新能源发电及控制技术:太阳能、风能等新能源发电及控制技术2.舰船综合电力推进:舰船电力推进、舰船综合电力系统仿真;舰船大功率变频器应用技术等3.智能变电站监控:智能变电站检测、保护、无功补偿。
哈工大通信原理实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y通信原理实验报告课程名称:通信原理院系:电子与信息工程学院班级:姓名:学号:指导教师:倪洁实验时间: 2015年 12月哈尔滨工业大学实验二帧同步信号提取实验一、实验目的1.了解帧同步的提取过程。
2.了解同步保护原理。
3.掌握假同步,漏同步,捕捉动态和维持态的概念。
二、实验原理时分复用通信系统,为了正确的传输信息,必须在信息码流中插入一定数量的帧同步码,帧同步码应具有良好的识别特性。
本实验系统帧长为24比特,划分三个时隙,每个时隙长度8比特,在每帧的第一时隙的第2至第8码元插入七位巴克码作为同步吗。
第9至24比特传输两路数据脉冲。
帧结构为:X11100101010101011001100,首位为无定义位。
本实验模块由信号源,巴克码识别器和帧同步保护电路三部分构成,信号源提供时钟脉冲和数字基带脉冲,巴克码识别器包裹移位寄存器、相加器和判决器。
其余部分完成同步保护功能。
三、实验内容1.观察帧同步码无错误时帧同步器的维持状态。
2.观察帧同步码有一位错误时帧同步器的维持态和捕捉态3.观察帧同步器假同步现象和同步保护器。
四、实验步骤1.开关K301接2.3脚。
K302接1.2脚。
2.接通电源,按下按键K1,K2,K300,使电路工作。
3.观察同步器的同步状态将信号源中的SW001,SW002,SW003设置为11110010,10101010,11001100(其中第2-8位为帧同步码),SW301设置为1110,示波器1通道接TP303,2通道接TP302,TP304, TP305,TP306,观察上述信号波形,使帧同步码(SW001的2-8位)措一位,重新做上述观察,此时除了TP303外,个点波形不变,说明同步状态仍在维持。
4.观察同步器的失步状态。
关闭电源,断开K302,在开电源(三个发光二极管全亮)。
哈工大-自适应信号处理_LMS自适应滤波器实验报告材料

实用Harbin Institute of Technology自适应平衡器计算机实验课程名称:自适应信号处理院系:电子与信息工程学院姓名:学号:授课教师:邹斌哈尔滨工业大学一、实验目的:1. 深入掌握自适应平衡器的理论基础和以及它的可能用途。
2. 理解最小均方自适应算法的适用条件,以及最小均方自适应算法的理论推导。
3. 改变特征值扩散度)(R χ与步长参数μ,观察实验结果,深入理解理解这些参数对实验结果的重要性。
4. 探究在线性色散信道中使用最小均方自适应算法引起的失真问题。
二、实验内容:在此次实验中我们研究LMS 算法自适应均衡引起未知失真的线性色散信道问题。
假设数据是实数,图2.1表示用来进行该项研究的系统框图。
自适应均衡器用来纠正存在白噪声的信道的畸变。
通过随机数发生器1产生用来探测信道的测试信号n x ;通过随机数发生器2来产生干扰信道输出的白噪声源()v n 。
这两个发生器是相互独立的。
经过适当延迟,随机数发生器1页提供用作训练序列的自适应均衡器的期望相应。
加到信道输入的随机序列{}n x 由伯努利序列组成,其中1n x =±,随机变量n x 具有零均值和单位方差。
信道的单位脉冲响应应用升余弦表示为20.5[1cos((2))]1,2,30n n n h Wπ⎧+-=⎪=⎨⎪⎩,其他 (2-1)等价地,参数W 控制均衡器抽头输入的相关矩阵的特征值分布()χR ,并且特征值分布随着W 的增大而扩大。
随机数发生器2产生的序列是零均值,方差20.001v σ=。
随机噪声发生器(1)信道随机噪声发生器(2)延迟∑自适应横向滤波器∑nx nv +-ne图2.1 自适应均衡实验框图这里均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于2n =时对称,均衡器的最优抽头权值on w 在5n =时对称。
因此信道的输入n x 被延时了=∆2+5=7个样值,以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时Δ,LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
哈工大数字逻辑电路与系统实验报告

哈工大数字逻辑电路与系统实验报告Harbin Institute of Technology Harbin Institute of Technology数字逻辑电路与系统课程名称, 数字逻辑电路与系统院系, 电子与信息工程学院班级,哈尔滨工业大学2014年11月实验一组合逻辑电路的设计与仿真 2.1 实验要求本实验练习在 Maxplus II 环境下组合逻辑电路的设计与仿真,共包括5 个子实验,要求如下:节序实验内容要求2.2 三人表决电路实验必做2.3 译码器实验必做2.4 数据选择器实验必做2.5 ‘101’序列检测电路实验必做2.6 ‘1’的个数计算电路实验选做2.2 三人表决电路实验2.2.1 实验目的1. 熟悉MAXPLUS II 原理图设计、波形仿真流程2. 练习用门电路实现给定的组合逻辑函数2.2.2 实验预习要求1. 预习教材《第四章组合逻辑电路》2. 了解本次实验的目的、电路设计要求2.2.3 实验原理设计三人表决电路,其原理为:三个人对某个提案进行表决,当多数人同意时,则提案通过,否则提案不通过。
输入:A、B、C,为’1’时表示同意,为’0’时表示不同意;输出:F,为’0’时表示提案通过,为’1’时表示提案不通过;电路的真值表如下:要求使用基本的与门、或门、非门在MAXPLUS II 环境下完成电路的设计与波形仿真。
2.2.4 实验步骤1. 打开MAXPLUS II, 新建一个原理图文件,命名为EXP2_2.gdf。
2. 按照实验要求设计电路,将电路原理图填入下表。
三人表决电路原理图3. 新建一个波形仿真文件,命名为EXP2_2.scf,加入所有输入输出信号,并绘制输入信号A、B、C 的波形(真值表中的每种输入情况均需出现)。
4. 运行仿真器得到输出信号F 的波形,将完整的仿真波形图(包括全部输入输出信号)附于下表。
三人表决电路仿真波形图2.3 译码器实验2.3.1 实验目的熟悉用译码器设计组合逻辑电路,并练习将多个低位数译码器扩展为一个高位数译码器。
哈工大电路自主设计实验

哈工大电路自主设计实验(总10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--姓名 班级 学号 实验日期 节次 教师签字 成绩影响RLC 带阻滤波器性能参数的因素的研究与验证1.实验目的(1)学习带阻滤波器的设计方法 (2)测量RLC 带阻滤波器幅频特性曲线(3)研究电阻、电容和品质因素Q 对滤波器性能的影响 (4)加深对滤波器滤波概念的理解 2.总体设计方案或技术路线(1)理论推导,了解滤波器的主要性能参数及与滤波器性能有关的因素 (2)设计RLC 带阻滤波器电路图 (3)研究电阻R 对于滤波器参数的影响 (4)研究电容C 对于滤波器参数的影响 (5)研究电感L 对于滤波器参数的影响(6)合理设计实验测量,结合电容C 和电感L 对滤波器参数的影响 (7)将实际测量结果与理论推导作对比,并分析实验结果3.实验电路图R1V-V+4.仪器设备名称、型号函数信号发生器 1台FLUKE190-104数字便携式示波表 1台十进制电阻箱 1只十进制电容箱 1只十进制电感箱 1只5.理论分析或仿真分析结果带阻滤波器是指能通过大多数频率分量、但将某些范围的频率分量衰减到极低水平的滤波器,与带通滤波器的概念相对。
理想带阻滤波器在阻带内的增益为零。
带阻滤波器的中心频率f o,品质因素Q和抑制带宽BW之间的关系为仿真结果:R=2000Ω C= L=R=500Ω C= L=R=2000Ω C= L=R=2000Ω C= L=R=2000Ω C= L=改变R时对比图改变C时对比图改变L时对比图6.详细实验步骤及实验结果数据记录(包括各仪器、仪表量程及内阻的记录)(1)电阻R对于滤波器参数的影响任务1:电路如图所示,其中信号源输出Us=5V,电容C=,电感L=,根据R= 2000f/kHzfc1=fo=4fc2=57 U/VR= 1500f/kHz1fc1=fo=4fc2=57 U/VR=50f/kHz3fc1= fo= fc2= 47U/V5根据所测数据在下图画出三条对应的幅频特性曲线,并根据图中实验结果进行分析分析结果:由图看出,当R变化,L C不变时,中心频率不变,但是阻带宽度随着R变大而变大。
哈工大电气学院仪器科学与技术

哈工大电气学院仪器科学与技术自动化测试与控制系简介哈尔滨工业大学自动化测试与控制系仪器科学与技术学科创建于1955年,在苏联专家的帮助下,以前苏联人才培养模式培养出国内第一批精密仪器专业研生和本科生,这批学生均成为我国该学科领域的学术带头人和技术带头人。
该学科现为国家重点一级学科, 1998年成为全国首批按一级学科培养和授予博士学位的学科点,同年被批准建立仪器科学与技术博士后流动站。
本学科在2001-2003年间全国一级学科整体水平评估中,全国排名第二, 2004-2006年间全国一级学科整体水平评估中,全国排名第三。
本学科具有较高的学术声誉和影响力。
本学科始终瞄准国际高科技前沿和国家重大需求,针对航天和国防尖端技术的前沿科学问题和关键技术问题,开展科学研究与工程关键技术研究,形成了以航天、航空、尖端与先进装备制造、微电子与信息装备制造为背景,以精密/超精密测量技术与仪器、自动化综合测试与控制技术、光电信息技术与系统为主要特色的科学研究方向,取得了以国家技术发明奖一等奖为标志的一批重大科研成果。
近三年累计科研经费超过2.6亿元。
此外,还申请国际发明专利和中国发明专利150余项,已获授权70余项;近年来完成国防航天重点预研和工程项目与国家自然科学基金项目近百项。
本学科由四个研究所、五个研究室及一个基础课教研室组成。
现有教授32人,副教授36人,其中博士生导师28硕士生导师53人。
本学科不仅在科学研究与工程关键技术研究上取得了较突出的成果,还在研究生培养方面取得了突出的成绩,共有4人获得全国百名优秀博士学位论文奖,2人获得全国百名优秀博士学位论文提名奖。
硕士研究生就业去向:国内各科研院所、国企、外企、各大公司、技术开发类企业,以及国家机关等单位,或去国内外高校攻读博士学位。
电气工程及自动化学院已走过17年的风雨路程,作为哈工大的重要组成部分,在教学与科研工作上始终处于校内的前列,并取得了令人瞩目的成绩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 常用连续时间信号的实现1 实验目的 (1) 了解连续时间信号的特点; (2) 掌握连续时间信号表示的方法; (3) 熟悉MATLAB 基本绘图命令的应用。
2 实验原理 (1) 信号的定义:信号是带有信息的随时间变化的物理量或物理现象。
(2) 信号的描述:时域法和频域法。
(3) 信号的分类:信号的分类方法很多,可以从不同角度对信号进行分类。
在信号与系统分析中,根据信号与自变量的特性,信号可分为确定信号与随机信号,周期信号与非周期信号,连续时间信号与离散时间信号,能量信号与功率信号,时限与频限信号,物理可实现信号。
3 涉及的MATLAB 函数 (1) 正弦信号; (2) 指数信号; (3) 单位冲激信号; (4) 单位阶跃信号; (5) 抽样信号。
4 实验内容与方法参考给出的程序并观察产生的信号,并通过改变相关参数(例如频率,周期,幅值,相位,显示时间段等),进一步熟悉这些工程实际与理论研究中常用信号的特征。
5 实验要求 (1) 在MATLAB 中输入程序,验证实验结果,并将实验结果存入指定存储区。
(2) 要求通过对验证性实验的练习,自行编制完整的程序,实现以下几种信号的模拟,并得出实验结果。
(1)()(),010f t t t ε==取~ (2)()(),010f t t t t ε==取~(3)2()5e 5e ,010ttf t t --=-=取~ (4)()cos100cos 2000,=00.2f t t t t =+取~(5)0.5()4ecos ,=010t f t t t π-=取~(3)在实验报告中写出完整的自编程序,并给出实验结果。
6 实验结果(1)()(),010f t t t ε==取~t=-1:0.01:10;程序和输出如下y=heaviside(t); plot(t,y);axis([-1,10,-0.1,1.2])-11234567891000.20.40.60.81(3)2()5e 5e,010ttf t t --=-=取~程序和输出如下A=5;a=-1;b=-2; t=0:0.001:10;ft=A*exp(a*t)-A*exp(b*t); plot(t,ft)0123456789100.20.40.60.811.21.4(4)()cos100cos 2000,=00.2f t t t t =+取~程序和输出如下A=100;B=2000; t=0:0.001:0.2;ft=cos(A*t)+cos(B*t); plot(t,ft)00.020.040.060.080.10.120.140.160.180.2-2-1.5-1-0.500.511.52实验二常用LTI系统的频域分析1.实验目的(1)掌握连续时间信号傅里叶变换和傅里叶反变换的实现方法以及傅里叶变换的特性实现方法;(2)了解傅立叶变换的特点及其应用;(3)掌握MATLAB相关函数的调用格式及作用;(4)掌握傅里叶变化的数值计算方法以及绘制信号频谱图的方法;(5)能够应用MATLAB对系统进行频域分析。
2.实验原理(1)傅里叶级数的三角函数形式(2)傅立叶级数的指数形式(3)非周期信号的傅里叶变换3.涉及的MATLAB函数(1)fourier函数;(2)ifourier函数;(3)quad8函数;(4)quad1函数;(5)freds函数;4.实验内容与方法周期信号的傅里叶级数MATLAB实现;利用MATLAB画出下图所示的周期三角波信号的频谱。
5. 实验要求(1)在MATLAB中输入程序,验证实验结果,并将实验结果存入指定存储区。
(2)在实验报告中写出完整的自编程序,并给出实验结果。
6. 实验结果 实验程序如下%三角波脉冲信号的傅里叶级数实现 N=10;n1=-N:-1;c1=-4*j*sin(n1*pi/2)/pi^2./n1.^2; c0=0;n2=1:N;c2=-4*j*sin(n2*pi/2)/pi^2./n2.^2; cn=[c1 c0 c2];n=-N:N;subplot 211;stem(n,abs(cn));ylabel('Cn 的幅度'); subplot 212;stem(n,angle(cn));ylabel('Cn 的相位'); xlabel('\omega/\omega_0')输出频谱如下-10-8-6-4-224681000.10.20.30.40.5C n 的幅度-10-8-6-4-20246810-2-1012C n 的相位ω/ω0实验三 连续LTI 系统的复频域分析1. 实验目的(1)掌握连续时间信号拉普拉斯变换和拉普拉斯反变换的实现方法以及拉普拉斯变换的特性实现方法; (2)了解拉普拉斯变换的特点及其应用;(3)掌握MATLAB 相关函数的调用格式及作用; (4)能够应用MATLAB 对系统进行复频域分析。
2. 实验原理(1)拉普拉斯变换(2)拉普拉斯的收敛域(3)拉普拉斯反变换计算方法 (4)微分方程的拉普拉斯变换解法 (5)系统函数H (s ) 3. 涉及的MATLAB 函数 (1)residue 函数 (2)laplace 函数 (3)i laplace 函数 (4)ezplot 函数 (5)roots 函数 4. 实验内容与方法已知连续时间信号()sin()()f t t t ε=,求出该信号的拉普拉斯变换,并用MATLAB 绘制拉普拉斯变换的曲面图。
5. 实验要求(1)在MATLAB 中输入程序,验证实验结果,并将实验结果存入指定存储区。
(2)在实验报告中写出完整的自编程序,并给出实验结果。
6. 实验结果 程序如下%绘制单边正弦信号拉普拉斯变换曲面图程序 clf;a=-0.5:0.08:0.5; b=-1.99:0.08:1.99; [a,b]=meshgrid(a,b); d=ones(size(a)); c=a+i*b;c=c.*c; c=c+d; c=1./c; c=abs(c); mesh(a,b,c); surf(a,b,c);axis([-0.5,0.5,-2,2,0,15]);title('单边正弦信号拉普拉斯变换曲面图'); colormap(hsv);输出结果如下-0.50.5-2-112051015单边正弦信号拉普拉斯变换曲面图实验四离散时间信号的卷积和1 实验目的(1)熟悉离散时间信号卷积的定义和表示以及卷积的结果;(2)掌握利用计算机进行离散时间信号卷积运算的原理和方法;(3)熟悉离散时间信号的相关计算方法;(4)熟悉离散时间信号卷积运算函数dconv的应用。
2 实验原理(1)卷积的定义;(2)卷积计算的几何解法;(3)卷积积分的应用。
3 涉及的MATLAB函数(1)dconv函数;(2)conv函数。
4实验内容与方法(1)用MATLAB计算两个离散序列的卷积和,并绘制它们的时域波形;(2)用MATLAB图解法计算两个离散序列的卷积和。
5 实验要求(1)在MATLAB中输入程序,验证实验结果,并将实验结果存入指定存储区域。
(2)要求通过对验证性实验的练习,自行编制完整的程序,实现以下几种情况的模拟,并得出实验结果。
已知序列1为, 05[]0,n nh n≤≤⎧=⎨⎩其他,序列2为1, 05[]0,nf n≤≤⎧=⎨⎩其他,分别计算和绘出下列信号的图形:①1[][][]y n f n h n=*;②2[][][5]y n f n h n=*+(3)在实验报告中写出完整的自编程序,并给出实验结果。
6. 实验结果程序和输出如下1.计算法①f1 = [0 1 2 3 4 5];k1= [0 1 2 3 4 5];f2 = [1 1 1 1 1 1];k2= [0 1 2 3 4 5];f = conv(f1,f2)k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2;k=k0:k0+k3subplot 221stem(k1,f1)title('f1(k)')xlabel('k')ylabel('f1(k)')subplot 222stem(k2,f2)title('f2(k)')xlabel('k')ylabel('f2(k)')subplot 223stem(k,f)title('f(k)=f1(k)*f2(k)')xlabel('k')ylabel('f(k)')h=get(gca,'position');h(3)=2.3*h(3);set(gca,'position',h)f =0 1 3 6 10 15 15 14 12 9 5 k =0 1 2 3 4 5 6 7 8 9 100246246f1(k)kf 1(k )02460.51f2(k)kf 2(k )01234567891051015f(k)=f1(k)*f2(k)kf (k )②f1 = [0 1 2 3 4 5]; k1= [-5 -4 -3 -2 -1 0]; f2 = [1 1 1 1 1 1]; k2= [0 1 2 3 4 5]; f = conv(f1,f2) k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2; k=k0:k0+k3 subplot 221 stem(k1,f1) title('f1(k)') xlabel('k') ylabel('f1(k)') subplot 222 stem(k2,f2) title('f2(k)') xlabel('k') ylabel('f2(k)') subplot 223 stem(k,f)title('f(k)=f1(k)*f2(k)') xlabel('k') ylabel('f(k)')h=get(gca,'position'); h(3)=2.3*h(3);set(gca,'position',h) f =0 1 3 6 10 15 15 14 12 9 5 k =-5 -4 -3 -2 -1 0 1 2 3 4 5-6-4-200246f1(k)kf 1(k )02460.51f2(k)kf 2(k )-5-4-3-2-1012345051015f(k)=f1(k)*f2(k)kf (k )2.图解法 ①n=[-10:10];x=[0 0 0 0 0 0 0 0 0 0 0 1 2 3 4 5 0 0 0 0 0] h=[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0] subplot 321;stem(n,x,' *k'); subplot 322;stem(n,h,'k'); n1=fliplr(-n);h1=fliplr(h);subplot 323;stem(n,x,' *k');hold on;stem(n1,h1,'k'); h2=[0,h1];h2(length(h2)) = [];n2 = n1;subplot 324;stem(n,x,' *k');hold on;stem(n2,h2,'k'); h3=[0,h2];h3(length(h3)) = [];n3 = n2;subplot 325;stem(n,x,' *k');hold on;stem(n3,h3,'k');n4=-n;nmin=min(n1)-max(n4);nmax=max(n1)-min(n4);n=nmin:nmax;y=conv(x,h)subplot 326;stem(n,y,'.k');-10-55100246-10-551000.51-10-55100246-10-55100246-10-55100246-20-101020051015②n=[-10:10];x=[0 0 0 0 0 0 1 2 3 4 5 0 0 0 0 0 0 0 0 0 0] h=[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0] subplot 321;stem(n,x,' *k'); subplot 322;stem(n,h,'k'); n1=fliplr(-n);h1=fliplr(h);subplot 323;stem(n,x,' *k');hold on;stem(n1,h1,'k'); h2=[0,h1];h2(length(h2)) = [];n2 = n1;subplot 324;stem(n,x,' *k');hold on;stem(n2,h2,'k'); h3=[0,h2];h3(length(h3)) = [];n3 = n2;subplot 325;stem(n,x,' *k');hold on;stem(n3,h3,'k');n4=-n;nmin=min(n1)-max(n4);nmax=max(n1)-min(n4);n=nmin:nmax; y=conv(x,h)subplot 326;stem(n,y,'.k');-10-55100246-10-551000.51-10-55100246-10-55100246-10-55100246-20-101020051015实验五 常用LTI 系统的频域分析1. 实验目的(1) 熟悉离散LTI 系统在典型激励信号下的响应及其特征; (2) 掌握用卷积法计算离散时间系统的零状态响应; (3) 掌握MATLAB 相关函数的调用格式及其作用; (4) 通过该实验,掌握应用MATLAB 对系统进行频域分析基本方法。
