非周期信号的频谱分析
实验四非周期信号频域分析

实验四 非周期信号频域分析1 实验目的(1) 掌握傅里叶变换的分析方法及其物理意义。
(2) 掌握各种典型的连续时间非周期信号的频谱特征以及傅里叶变换的主要性质。
(3) 学习掌握利用MA TLAB 语言编写计算CTFT 的仿真程序,并能利用这些程序对一些典型信号进行频谱分析,验证CTFT 的若干重要性质。
2 实验原理及方法2.1连续时间信号傅里叶变换——CTFT傅里叶变换在信号分析中具有非常重要的意义,它主要是用来进行信号的频谱分析的。
傅里叶变换和其逆变换定义如下:⎰∞∞--=dt e t x j X t j ωω)()( 4-1 ⎰∞∞-=ωωπωd e j X t x t j )(21)( 4-2连续时间傅里叶变换主要用来描述连续时间非周期信号的频谱。
任意非周期信号,如果满足狄里克利条件,它可以被看作是由无穷多个不同频率(这些频率都是非常的接近)的周期复指数信号e j ωt 的线性组合构成的,每个频率所对应的周期复指数信号e j ωt 称为频率分量,其相对幅度为对应频率的|X(j ω)|之值,其相位为对应频率的X(j ω)的相位。
X(j ω)通常为关于ω的复函数,可以按照复数的极坐标表示方法表示为:X(j ω)=| X(j ω)|e j ∠ X(j ω)其中,| X(j ω)|称为x(t)的幅度谱, ∠X(j ω)称为x(t)的相位谱。
给定一个连续时间非周期信号x(t),它的频谱是连续且非周期的。
对于连续时间周期信号,也可以用傅里叶变换来表示其频谱,其特点是,连续时间周期信号的傅里叶变换是由冲激序列构成的,是离散的——这是连续时间周期信号的傅里叶变换的基本特征。
2.2 用MA TLAB 实现CTFT 及其逆变换2.2.1 用MATLAB 实现CTFT 的计算MA TLAB 进行傅里叶变换有两种方法,一种利用符号运算的方法计算,另一种是数值计算,本实验采用数值计算的方法。
严格来说,用数值计算的方法计算连续时间信号的傅里叶变换需要有个限定条件,即信号是时限信号,也就是当时间|t|大于某个给定时间时其值衰减为零或接近于零,这个条件与前面提到的为什么不能用无限多个谐波分量来合成周期信号的道理是一样的。
03第1章_瞬变非周期信号与连续频谱

其中: j ( f ) X( f ) X( f )e
X ( f ) Re2 [ X ( f )] Im2 [ X ( f )] 幅值谱 ( amplitude spectrum )
Im[ X ( f )] ( f ) arctg 相位谱 Re[ X ( f )] ( phase spectrum )
T
T
n
x(t )
2 2 2 0
n 0 (n 1) 0 0
Cn
t
T
2 d 0 T
非周期信号的频谱分析
2, Fourier 变换
Fourier 变换的推导 ( 1 ) 由以上思路推导公式
x(t ) lim xT (t )
( x(t )e j 2ft dt)e j 2ft df
令为 X( f )
非周期信号的频谱分析
非周期信号是时间上不会重复出现的信号,一般 为时域有限信号,具有收敛可积条件,其能量为 有限值。这种信号的频域分析手段是傅立叶变换 (Fourier transform)。 傅立叶变换的定义
非周期信号的频谱分析
对比:方波谱
非周期信号的频谱分析
例:矩形脉冲信号(rectangular pulse signal) G(t ) (窗函数(window function))
E, t T / 2 G(t ) 0, t T / 2
矩形脉冲信号的 Fourier 变换为
a
m 1
k
m m
x (t ) am X m ( f )
m 1
k
非正弦周期信号的频谱

频谱分析在通信、电力、自动控制等领域 都有广泛的应用,其分析结果可以为相关 领域的发展提供支持和指导。
02
非正弦周期信号的基本概念
非正弦周期信号的定义
01
非正弦周期信号是指在一个周期 内,信号的波形不是正弦波形的 周期信号。
02
与正弦周期信号相比,非正弦周 期信号的波形更加复杂,包含多 种频率成分。
05
非正弦周期信号频谱分析的应 用
在通信领域的应用
调制与解调
在通信系统中,非正弦周期信号 常被用作调制信号,通过频谱分 析可以了解信号的频率成分,进
而实现信号的调制与解调。
信道特性分析
通过分析信道对非正弦周期信号的 频谱影响,可以评估信道的传输特 性,为信道均衡和信号恢复提供依 据。
干扰识别与抑制
高精度算法
02
发展更高精度的频谱分析算法,以应对复杂和微弱信号的挑战,
提高分析的灵敏度和分辨率。
多域联合分析
03
结合时域、频域和其他变换域的分析方法,提供更全面、深入
的信号特征提取和理解。
对未来技术的展望
实时分析技术
开发能够实时处理和分析非正弦周期信号的技术,以满足实时监 测和控制的需求。
自适应分析技术
频谱的奇对称性
如果非正弦周期信号的波形具有奇对称性(即波形关于原 点对称),则其频谱具有奇对称性。在这种情况下,正负 频率分量的幅度相等,相位相同。
频谱的非对称性
对于不具有偶对称性或奇对称性的非正弦周期信号,其频 谱可能呈现出非对称性。这意味着正负频率分量的幅度和 相位关系可能不遵循简单的对称规律。
在通信系统中,干扰信号往往具有 特定的频谱特征。通过频谱分析, 可以识别干扰信号并采取相应的抑 制措施。
2.5信号的频域分析(非周期信号)2.6傅立叶变换的性质

能 量 谱
由此最后得
E = ∫ x2 (t )dt =
−∞ ∞
1 ∞ 2 X(ω) dω 2π ∫−∞
(16)
式(15)亦称巴塞伐尔方程或 能量等式。它表示,一个非周 期信号x(t)在时域中的能量可由 它在频域中连续频谱的能量来 表示。 式(15)亦可写成
E= 1 ∞ 2 X(ω) dω 2π ∫−∞ 1 ∞ 2 = ∫ X(ω) dω = ∫ S(ω)dω
证明: 由欧拉公式
X (ω) = ∫ x(t)e
−∞
∞ −∞
∞
− jωt
dt
∞ −∞
X (ω) = ∫ x(t) cosωtdt − j∫ x(t) sin ωtdt
= Re X (ω) + j Im X (ω)
若x(t)为实函数
Re X (ω) = Re X (−ω) Im X (ω) = − Im X (−ω)
x(t) = Arect
(t − t0 )
T
图2.30 具有时移t0的矩形脉冲
X( f ) = AT sin c(πfT) sin c(πfT) > 0 − 2πt0 f , ϕ( f ) = − 2πt0 f ±π , sin c(πfT) < 0
测试技术
2.6傅里叶变换的性质 2.6傅里叶变换的性质
∫
∞
−∞
x(t) dt < ∞
但上述条件并非必要条件 必要条件。因为当引入广义函数概 必要条件 念之后,许多原本不满足绝对可积条件的函数也能进行傅 里叶变换。 若将上述变换公式中的角频率ω用频率f来替代,则由 于ω=2πf,式(5)和(6)分别变为
X( f ) = ∫ x(t)e− j 2πft dt
离散非周期信号频域分析

离散⾮周期信号频域分析离散信号频域分析、快速傅⾥叶变换与采样定理⼀、离散信号频域分析(⼀)周期离散⽅波信号频域分析与周期模拟信号⼀样,周期离散信号同样可以展开成傅⾥叶级数形式,并得到离散傅⾥叶级数(DFS)上式可以看成周期离散信号x(n)的离散傅⾥叶级数展开。
上式是DFS的反变换,记作IDFS并且称错误!未找到引⽤源。
与错误!未找到引⽤源。
构成⼀对离散傅⾥叶级数变换对。
(以上两式中错误!未找到引⽤源。
)在MTALAB中,DFS通过建⽴周期延拓函数语句实现:function Xk=DFS(n,x,N)if N>length(x)n=0:N-1;x=[x zeros(1,N-length(x))];endk=0:N-1;WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=x*WNnk;end建⽴⼀个离散⾮周期⽅波信号错误!未找到引⽤源。
通过周期延拓后所得的周期序列利⽤DFS计算实现代码如下:clear all;close all;clc;n=0:3;x=ones(1,4);X=fft(x,1024);Xk1=DFS(n,x,4);Xk2=DFS(n,x,8);figure(1);plot((-1023:2048)/2048*8,[abs(X) abs(X) abs(X)],'--');hold on;stem(-4:7,[abs(Xk1) abs(Xk1) abs(Xk1)],'LineWidth',2);grid;figure(2);plot((-1023:2048)/2048*16,[abs(X) abs(X) abs(X)],'--');hold on;stem(-8:15,[abs(Xk2) abs(Xk2) abs(Xk2)],'LineWidth',2);grid;set(gcf,'color','w');运⾏后得到的是分别以4和8为周期延拓后的错误!未找到引⽤源。
非周期信号的频谱分析第三节连续时间Fourier变换的课件.ppt

F( j)
πF (0)
()
若信号不存在直流分量即F(0)=0
则t
f
( )d
F
1
j
F( j)
18
例3 试利用积分特性求图示信号f(t)的频谱函数。
f(t) 1
y(t)=p(t0.5) 1
t
0
1
t
0
1
解: f (t) = t p(t 0.5)dt = t y(t)dt
由于 p(t 0.5) F Y ( j) = Sa (0.5)e j0.5
F F1 ( j)
1 Sa (0.5)e j0.5 j
利用修正的微分特性,可得
F( j) = π( f () f ()) () F1 ( j) j
= 3π () 1 Sa (0.5)ej0.5 j
与例4结果 一致! 24
23
10. 频域微分积分特性
若f (t) F( j)
则( jt)n f (t) F (n) ( j)
由上式利用时域微分特性,得
2
F[ f '(t)] = (j)F(j) = A 2jsin( )
2
因此有
F( j) = 2A sin( ) = ASa( )
2
2
21
20
例6 试利用微分特性求图示信号f(t)的频谱函数。
f(t) 2 1
f '(t) 1
t
0
1
t
0
1
解: f '(t) = p(t 0.5) F Sa(0.5)e j0.5
f1(t) d n f (t
f )
2 (t) F F ( j)
1
2π n
[F1( j) F( j)
非周期信号(方波,锯齿波,三角波)的合成分解以及频谱分析的MATLAB实现

1.2 主要功能
1.数值分析 2.数值和符号计算 3.工程与科学绘图 4.控制系统的设计与仿真 5.数字图像处理 6.数字信号处理 7.通讯系统设计与仿真 8.财务与金融工程
2
连续周期信号的傅立叶级数分析及其 MATLAB 实现
2 连续周期信号的傅立叶级数
频域分析法即傅里叶分析法,它是变换域分析法的基石。其中,傅里叶级数 是变换域分析法的理论基础,傅里叶变换作为频域分析法的重要数学工具,具有 明确的物理意义,在不同的领域得到广泛的应用。
2.1 连续时间周期信号的分解
以高等数学的知识,任何周期为 T 的周期函数,在满足狄里赫利条件时,则 该周期信号可以展开成傅里叶级数。傅里叶级数有三角形式和指数形式两种。
(3-2)
2
2
3
MATLAB 实现程序:
n=7;
6
连续周期信号的傅立叶级数分析及其 MATLAB 实现
T0=2;A=2; T1=2; tn_i=1; for tn=0:0.01:T1*T0
y_t(tn_i)=A* rem (tn,T0)/T0; t_t(tn_i)=tn; tn_i=tn_i+1; end; t=0:0.01:T1*T0; x=A/2; pi=3.1415926; w0=2*pi/T0; for i=1:n fw(i)=i*w0; a(i)=-A/(pi*i); y(i,:)=a(i)*sin(fw(i)*t); x=x+y(i,:); end; subplot(1,3,1); plot(t_t,[y_t;x]); title('锯齿波、锯齿波合成图') subplot(1,3,2); plot(t,[x; y]); title('0-n 次谐波及合成图') subplot(1,3,3); stem(fw,a); title('锯齿波频谱图') 生成图形:
§3-3 非周期信号的频谱分析
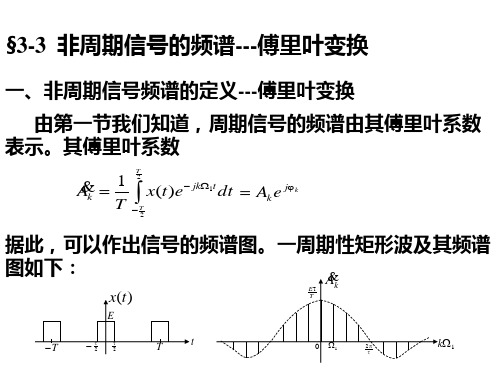
x(t)
E
T
2
2
T
t
x(t)
E
T
2
2
T
t
x(t)
E
2
2
t
TA k E
0 1
2
k1
TA k E
0 1
2
k1
TA k E
0
2
对应的傅里叶级数展开式
x(t)
Ak e jk1t
k
TAk e jk1t
我们将X(jΩ)表示非周期信号的频谱,即是傅里叶正变 换
X ( j) x(t)e jt dt
式
x(t)
1
X ( j)e jt d
2
即是傅里叶反变换。上两式称作傅里叶变换对,常表示为
x(t) FT X ( j) ℱ x(t)
x(t) ℱ -1 X ( j)
k
1 T
1 2
TAk e jk1t
k
2 T
当T→∞的时候,
lim x(t)
T
1 2
TAk e
k
jk1t
2 T
lim
T
1 2
TAk e
k
jk1t
1
1
X ( j)e jt d
2
T
E
T
2
2
T
t
0 1
2
k1
x(t)
E
T
2
2
非周期信号的频谱

(2) 若f(t)为t的奇函数,即f(-t)=-f(t),则f(t)的频 谱函数F(jω)为ω的虚函数,且为ω的奇函数。
与周期信号类似,也可将非周期信号的傅里叶变
换表示式改写成三角函数的形式,即
.
6
f(t)21
F(j)ejtd
21
F(j)ej[t()]d
2 1 F (j)co ts [()d ]
2
0
2
t
实偶
4
2
0
2
4
实偶
图 3.4-1 门函数及其频谱
一般而言,信号的频谱函数需要用幅度谱 F( j)和相位
谱 ( )两个图形才能将它完全表示出来。但如果频谱
函数是实函数或虚函数,那么只用一条曲线即可。
F(j) 为负代表相位为 ,
0
.
F(为j正) 代表相位为 。
11
由图可见,第一个零值的角频率为 2 (频率 1 )。
为了描述非周期信号的频谱特性,引入频谱密度的 概念。
令
F(j)T l i m 1F /n TT l i m FnT
称 F(j)为频谱密.度函数。
2
如何求频谱密度函数? F(j)T l i m 1F /n TT l i m FnT
由式
f(t) Fnejnt
n
,Fn
1 T
T
2 T
2
f(t)ej ntd t可得
可知
'(t)ejtd tdejt j
dt t 0
即 ℱ 'tj
同理可得 ℱ [(n)(t). ](j)n
23
例3.4-6 求单位直流信号的频谱
f(t)1 - t
显然,该信号不满足绝对可积条件,但其傅里叶变换
连续非周期信号频谱分析及Matlab实现

连续⾮周期信号频谱分析及Matlab实现《信号与系统A(1)》课程⾃学报告实施报告题⽬:连续⾮周期信号频谱分析及Matlab实现学号:姓名:任课教师:联系⽅式:第⼀部分. 理论⾃学内容阐述(⼀)系统物理可实现性、佩利-维纳准则通过之前的学习我们知道,理想低通滤波器在物理上是不可能实现的,但是我们却可以做出传输特性接近理想特性的⽹络。
如下图是⼀个低通滤波器,其中 R =√RC图1-1 ⼀个低通滤波⽹络则其⽹络传递函数为:(式1-1)引⼊符号ωc =1√LC,则(式1-1)改为:其中)(1t v CRL )(2t v --++()()()R L LC C RL C R V V H ωωωωωωωωj 11 j 11j j 11j j j 212+-=+++==()()()ω?ωωωωωωωωωωωj 222e j 3j 33j 11j H H c c cc c c =+ + -=2+222=()()????--=???+ -=2c c 2c 22c 1arctan 11j ωωωωω?ωωωωωH求出其冲激响应为:h (t )=2ωc √3eωc 2sin (√3ωct )画出波形图及频谱图如下:图1-2 h(t)的波形图幅度特性相位特性图1-3 幅度特性和相位特性可以看出这些曲线与理想低通滤波器有相似之处,但是同时也有不同之处。
这个电路的幅度特性不可能出现零值,冲激响应的起始时刻在t=0处。
那么究竟什么样的系统数学模型可以在物理上实现呢?就时间域特性⽽⾔,⼀个物理可实现⽹络的冲激响应h(t)在t<0时必须为0。
那么由于理想低通滤波器不是⼀个因果系统,所以它是不可能在物理上实现的。
从频域特性来看,|H(jw)|要满⾜平⽅可积条件。
佩利和维纳证明了对于幅度函数|H(jw)|物理可实现的必要条件是这就是佩利—维纳准则。
佩利—维纳准则只从幅度特性上提出要求,⽽在相位特性⽅⾯却没有给出约束,因此该准则只是系统物理可实现的必要条件,⽽不是充分条件。
非周期信号的频谱

F(j)称为 f(t) 的傅里叶变换或频谱密度函数,简称频谱;
f(t) 称为F(j) 的傅里叶反变换或原函数。
也可简记为: F ( j )
f (t)
f (t)
1 F ( j)
或者: f (t ) F ( j )
频谱密度函数
F ( j ) 一般为复函数,可写为
F ( j) F ( j) ej () F ( ) e j ()
0,
2
A e j tdt
2
A e j t 2
j
2A sin 2
A Sa( )
2
2
t
2
t
2
8.矩形脉冲信号的频谱
f (t ) A
2π
F( j)
A
t 2 0 2
0 2π 4π
Ag (t)
A
Sa( )
2
傅里叶变换对 F ( j ) f ( t ) e j t d t
T
Fn
2Fn 1
Fn f1
T
2 T
f ( t ) e j n 1t d t
2
其中, Fn 或 Fn 表示单位频带上的频谱值,即频谱密度。
1
f1
对上式取极限 T ,各变量将相应改为 T
虽然 记作
Fn 0
F ( j)
,但
T
F
n 趋于一有限函数
1
2
T
d
n 1 n
F ( j )
et t 0
f (t) e t t 0
为 0的实数
F ( j) 0 eate jtdt eate jtdt j
2
0
2 a2
F (j) 2 2 a2
非周期信号的频谱分析

X
4.傅里叶变换对
F(
j )
f
(t)ej t
dt
F
f
(t)
正变换
f
(t)
1
2
F
j
e j
t
d
F
1 F
j
反变换
简写
f t F j
记做:
F f (t) F( j) F 1 F( j) f (t)
二、傅里叶反变换的物理意义——信号分解
f (t) 1 F j e j t d F j d e j t
π
2
O
π2
O π 2
注意:只有α>0时傅里叶变换才存在, α<0时f(t)不
满足绝对可积条件
8.升余弦脉冲信号(自学)
f
t
E 2
1
cos
π
t
0 t
f t
E
E
2
F j f t ejt d t
O
2
E 2
1
cos π t
e jt
dt
t
2
E
ejt d t E
2
(t)
Sa 2
(
w 2
)
1 f2τ△ (t)
注意对比两 者不同
F j
-τ 0 τ
t
2π O 2π 4π
X
第
五.非周期信号频谱的特点
34 页
1.连续性
特例:直流和阶跃信号的频谱含冲激。
2.收敛性
第 13 页
4)与周期信号傅立叶级数展开的收敛条件比较
f (t) d t (有限值或收敛)
T
傅里叶变换存在的条件与傅立叶级数展开的收敛条 件一样。 信号绝对可积; 任何有限区间里,只有有限个最大值和最小值; 任何有限区间里,有有限个不连续点,且不连续点有值。
第五章 非周期信号频域分析

2
5.1 连续非周期信号的频谱
注意到
T0
lim fT0 (t ) f (t )
相应地,T (t ) 的Fourier级数将等于f(t)的Fourier级数。 f0
(a)
(b) 图5-1 非周期信号的周期化
3
5.1 连续非周期信号的频谱
为了避免 T0 时,式(5.2)中的Cn趋于零,将(5.1)和(5.2)等 价地定义为
1
2 2
相位频谱为 () arctan
(5 21)
20
5.2 常见连续信号的频域分析
5 单边指数信号 f (t ) e
t
u(t ), 0
单边指数信号的幅度频谱和相位频谱见图5-8。
图5-8 单边指数信号的幅度频谱和相位频谱
21
(5 13)
15
5.2 常见连续信号的频域分析
2 单位冲激信号 利用冲激信号的取样特性,可得
F[ (t )] f (t )e
jt
dt (t )e jt dt 1 (5 14)
单位冲激信号及其频谱函数见图5-5所示。
图5-5 单位冲激信号及其频谱函数
Dn jn0t fT0 (t ) e n=- T0 Dn
T0 / 2 T0 / 2
(5.3) (5.4)
fT0 (t )e jn0t dt
下面说明如何由周期矩形脉冲的频谱得出非周期矩形脉冲 信号的频谱。由4-1节知,周期为T0、宽度为 的周期矩形脉 冲的Fourier系数为
52常见连续信号的频域分析单位冲激信号利用冲激信号的取样特性可得图55单位冲激信号及其频谱函数171752常见连续信号的频域分析由单位冲激信号是偶函数得直流信号ft1利用单位冲激信号的频谱和fourier反变换公式可得图56直流信号及其频谱函数18因此单位阶跃信号的频谱函数为52常见连续信号的频域分析单位阶跃信号ut单位阶跃信号也不满足dirichlet条件但其fourier变换存在
§3.3 非周期信号的频谱---傅立叶变换

信号与系统
2. 周期信号的平均功率和功率谱 T
周期信号的平均功率为 P 1 2 f (t) 2 dt
T T
T2
T
根据傅立叶级数展开有 P
1 T
2 T
f 2 (t)dt
1 T
2 T
f
(t) Fne jnt0 dt
n
2
2
T
n
F n
1 T
2 T
f (t)e-jn0tdt
F nF n
根据前面的傅立叶系数公式知道:
an 是 n 的偶函数, bn 是 n 的奇函数。
An 是 n 的偶函数, n 是 n 的奇函数。
信号与系统
周期信号 f (t) ,周期为T
,角频率
0
2f
0
2
T
该信号可以展开为下式复指数形式的傅立叶级数。
f (t) Fne jnt0
n
T
其中
1
Fn T
2
f (t)e -jnt0 dt,
dt
2(w
w
)0
信号与系统
(6)常数函数(直流信号) f (t) = A
直流信号不满足绝对可积条件,可采用取极限的方法导出其傅立叶变换
。当矩形脉冲宽度 τ →∞ 时,矩形脉冲便趋于直流信号,因此直流信号的
傅立叶变换为矩形脉冲信号在 τ→∞ 时的傅立叶变换。
而矩形脉冲的傅立叶变换为
sin( )
F () A
变换的物理含义。对信号进行傅立叶变换和对信号进行频谱分
析具有同样含义,所谓求信号的频谱和求信号的傅立叶变换是
一回事。
信号与系统
非周期信号的频谱
F ( ) 一般为复函数,可以写为 F () F()e j() F () ~ 曲线称为非周期信号的幅度频谱
非周期信号的频谱分析

lim T
1 T
f (t)e jt dt
2
傅里叶变换:
F
(
j)
lim
T
TCn
f (t)e jt dt
物理意义: F(j)是单位频率所具有的信号频谱,
称之为非周期信号的频谱密度函数,简称频谱函数。
4
二、周期和非周期信号频谱函数的区别
(1)周期信号的频谱为离散频谱, 非周期信号的频谱为连续频谱。
狄里赫莱条件是充分不必要条件
8
例 试求图示非周期矩形脉冲信号的频谱函数。
解: 非周期矩形脉冲信号f(t)的时域表示式为
f
(t
)
A, 0,
| t | t / 2 | t | t / 2
由傅里叶正变换定义式,可得
F ( j)
f (t)e jt dt
t
2t
A e jt dt
2
At Sa(t )
2π
T , 记 n0 = , 0 = 2p/T = d,
f
(t)
1 2π
F ( j)e jt d
物理意义:非周期信号可以分解为无数个频率为, 复振幅为[F(j)/2p]d 的虚指数信号ej t的线性组合。
6
傅立叶正变换: 傅立叶反变换:
符号表示ห้องสมุดไป่ตู้ 或
F( j) f (t)e jt dt
f
(t)
16
一、常见非周期信号的频谱
4. 直流信号 f (t)
直流信号及其频谱
1
F ( j)
(2π)
0
t
0
对照冲激、直流时频曲线可看出:
时域持续越宽的信号,其频域的频谱越窄;
时域持续越窄的信号,其频域的频谱越宽。
信号分析基础(非周期信号频域分析)

频谱函数(相当于原来的Cn)为:
x (t ) 1 X ( ) e j t d 2 x ( t ) e j t dt X ( )
非周期信号的频谱 5.傅立叶变换的主要性质
(1).奇偶虚实性
X( jf) x(t)ej2ftdt
x(t)cos 2 f tdt j x(t)sin 2 f tdt
R e X( jf) jI mX( jf)
a.若x(t)是实函数,则X(jƒ)是复函数; b.若x(t)为实偶函数,则ImX(jƒ)=0,而X(jƒ)是实偶函数,即 X(jƒ)= ReX(jƒ); c.若x(t)为实奇函数,则ReX(jƒ)=0,而X(jƒ)是虚奇函数,即 X(jƒ)=-j ImX(jƒ); d.若x(t)为虚偶函数,则ImX(jƒ)=0,而X(jƒ)是虚偶函数; e.若x(t)为虚奇函数,则ReX(jƒ)=0,而X(jƒ)是实奇函数。
1 j n t 0 C x ( t ) e dt n T 2
频谱图: Cn
2 π 2 π
T 2 T 2
0
N为偶数
N为奇数
n
2 7π
-7ω 0
2 5π
-5ω 0
2 3π
2 3π
2 5π
2 7π
-3ω 0
-ω 0
0ω
0
3ω 0
5ω 0
7ω 0
ω
非周期信号的频谱
矩形脉冲函数的频谱
S (t)
单 位 面 积 = 1
lim S t) ( t) (
典型非周期信号的频谱

at
(t 0)
e
at
1 u (t ) a j
1 a Fe ( j ) 2 j 2 2 2 a j a a A( ) jB ( )
A( ) lim A( ) 0
a 0
( 0)
( 0)
ห้องสมุดไป่ตู้
A( ) lim A( )
) 单个矩形脉冲的变换
n1 E 1 Sa( ) ( n1 ) 2 n
E f (t ) T1
n1 jt Sa( 2 )e n
F ( j ) 2 Fn ( n1 )
n
2 2 1 8 秒 T 1 s 1 令: T1 0.25 4 20
B( ) lim B( )
1
§3.9 周期信号的傅立叶变换
• 一般周期信号的傅立叶变换 • 傅立叶级数FS与其单脉冲的傅立叶 变换FT的关系 • 正余弦信号的傅立叶变换FT • 复指数信号的傅立叶变换 • 周期单位冲激序列的FS和 FT • 周期矩形脉冲的FS和FT • 周期矩形脉冲与单矩形脉冲的关系
d (t )
1 f1 (t ) 2
[ e
j ( t )
d ] f 2 ( )d
(t ) f 2 ( )d f 2 (t )
f1 (t ), f 2 (t ) 在积分意义上相等。
傅立叶变换的唯一性表明了信 号及其频谱的唯一对应关系。
a0
( j )
2
2
.... 0
1 f (t ) 2
非周期信号的频谱分析傅里叶变换.

X( )
1
a j
a2
a
2
j a2 2
Re( )
lim
a0
a2
a
2
0
( 0)
Re( )
lim
a0
a2
a
2
( = 0)
lim
a0
Re( )d lim
a0
d( / a) 1 ( / a)2
lim arctan
a0
a
14
Im( )
lim
a0
a2
ቤተ መጻሕፍቲ ባይዱ
2
1
Re() = δ()
Im() = –1/
X() = Re() + jIm()
= δ() – j1/
= δ() +1/ e j – /2
阶跃信号的频谱在存在一个冲激,因为含有直流分量, 此外,它不是纯直流信号,在t = 0处有跳变,所以频谱 中还出现其它高频分量。
15
2.3.3 傅里叶变换的性质 1、奇偶性
若x(t)为实函数,则有幅频|X()|为偶函数,相频()
零。 由于频谱幅度趋于0,因此仍采用原来的幅度频谱的
概念将产生困难。事实上,由于频谱已转变为连续谱, 因此说明频谱上某一点频率上的幅度有多少是不行的。
研究频谱密度的变化,即单位频带上频谱幅度的大小,
以X(n1) /1来表示,也是的函数,且与原来幅度谱具
有相似的图形。
T1 ,1 0,X(n1) 0,但X(n1) /1却相对 稳定,将趋于稳定的极限值,这个 的函数称为频谱密
T1增大频谱的谱线变密,谱线变短。
1
x(t) E
0
T1
t
x(t)
瞬变非周期信号的频谱分析

瞬变非周期信号的频谱分析1.傅立叶变换当周期信号的周期趋于无穷大时,该信号就成为非周期信号了。
周期信号频谱谱线的频率间隔为△ω=ω0=2π/T ,由于T为无穷大时,其频率间隔Δω为无穷小,所以非周期信号的频谱是连续的。
非周期信号的幅值谱表示单位频宽上的幅值,精确地讲X(F)是频谱密度函数。
2.傅立叶变换的主要性质奇偶虚实性:x(t)为实偶函数,X(f)是实偶函数x(t)为实奇函数,X(f)是虚奇函数线性叠加性:假如f1(t)←→F1(jω),f2(t)←→F2(jω)则对于任何常数a1、a2有:a1f1(t)+a2f2(t)←→a1f1(jω)+a2f2(jω)对称性:时间尺度转变特性:时间尺度压缩,频谱的频带加宽,幅值降低;时间尺度扩大,频谱变窄,幅值增高。
时移和频移特性:时域的延时对应频谱在频域内的相位滞后。
卷积特性:该部分内容请同学自己阅读教材。
微分和积分特性:知道震惊系统的位移、速度、或加速度中任一个参数,应用微分、积分特性就可以获得其他参数的频谱。
3.几种典型信号的频谱矩形窗函数的频谱:时域有限区间内有值的信号,频谱可延长至无限频率。
在时域中若截取信号的一段记录长度,则相当于原信号和矩形窗函数之乘积,因而所得到的频谱将是原信号频域函数和sinc函数的卷积,它将是连续的、频率无限延长的频谱。
单位脉冲函数及其频谱:在极短时间内激发一个矩形脉冲(三角、钟形、双边指数),其面积为1。
当激发时间趋于0时,矩形脉冲的极限就称为单位脉冲函数。
单位脉冲函数的筛选性质:具有采样性质。
单位脉冲函数与其他函数的卷积:就是简洁地将x(t)在发生脉冲函数的坐标位置上(以此为坐标原点)重新构图。
δ(t)的频谱:具有无限宽广的频谱,在全部的频段上都是等强度,是抱负的白噪声。
周期性单位脉冲序列的频谱:若时域中脉冲间隔为T,则频域中也为脉冲间隔,间隔为1/T;时域中脉冲幅值为1,频域中幅值为1/T。
时域只要是周期性的,频谱就是离散的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非周期信号的频谱分析一、 实验目的1) 掌握用MATLAB 编程,分析门信号的频谱; 2) 掌握用MATLAB 编程,分析冲击信号的频谱; 3) 掌握用MATLAB 编程,分析直流信号的频谱; 4) 掌握用MATLAB 编程,分析阶跃信号的频谱; 5) 掌握用MATLAB 编程,分析单边信号的频谱; 二、 实验原理 常见的非周期信号有: 1、 门信号门信号的傅里叶变换对为:12sin()22()()202t g t F j Sa t ττωτωτωττω⎧<⎪⎪⎛⎫=⇔==⎨⎪⎝⎭⎪>⎪⎩它的幅度频谱和相位频谱分别为()2F j Sa ωτωτ⎛⎫= ⎪⎝⎭ 0sin()02()sin()02ωτϕωωτπ⎧>⎪⎪=⎨⎪<⎪⎩ 2、 冲激信号冲激信号的傅里叶变换对为()1t δ⇔3、 直流信号直流信号的傅里叶变换为12()πδω⇔4、 阶跃信号阶跃信号的傅里叶变换为111()sgn()()22u t t j πδωω=+⇔+ 5、 单边指数信号单边指数信号的傅里叶变换对为01()0ate tf t j t αω-⎧≥=⇔⎨+<⎩ 幅度频谱和相位频谱分别为()F j ω=()arctan()a ωϕω=-三、涉及的MATLAB函数1、fourier函数2、ifourier函数四、实验内容与方法1、验证性试验1)门信号的傅里叶变换MATLAB程序:Clear all;syms t wut=sym('heaviside(t+0.5)-heaviside(t-0.5)');subplot(2,1,1);ezplot(ut)hold onaxis([-1 1 0 1.1]);plot([-0.5 -0.5],[0,1]);plot([0.5 0.5],[0,1]);Fw=fourier(ut,t,w);FFP=abs(Fw);subplot(2,1,2);ezplot(FFP,[-10*pi 10*pi]);axis([-10*pi 10*pi 0 1.1]);程序运行结果图2)冲激信号的傅里叶变换MATLAB程序:clear allsyms t wut1=sym('heaviside(t+0.5)-heaviside(t-0.5)');subplot(2,1,1);ezplot(ut1);title('脉宽为1的矩形脉冲信号')xlabel('t')hold onaxis([-1 1 0 1.1]);plot([-0.5 -0.5],[0 1]);plot([0.5 0.5],[0 1]);Fw=fourier(ut1,t,w);FFw=abs(Fw);subplot(2,1,2);ezplot(FFw,[-10*pi 10*pi]);axis([-10*pi 10*pi 0 1.1]);title('脉宽为1的矩形脉冲信号的幅度频谱')hold onpauseut2=10*sym('heaviside(t+0.05)-heaviside(t-0.05)'); subplot(2,1,1);ezplot(ut2);title('脉宽为1、0.1矩形脉冲信号')xlabel('t')hold onaxis([-1 1 0 11]);plot([-0.05 -0.05],[0 10]);plot([0.05 0.05],[0 10]);Fw2=fourier(ut2,t,w);FFw2=abs(Fw2);subplot(2,1,2);ezplot(FFw2,[-10*pi 10*pi]);axis([-10*pi 10*pi 0 1.1]);title('脉宽为1、0.1的矩形脉冲信号的幅度频谱')hold onpauseut3=100*sym('heaviside(t+0.005)-heaviside(t-0.005)'); subplot(2,1,1);ezplot(ut3);title('脉宽为1、0.1和0.01矩形脉冲信号')xlabel('t')hold onaxis([-1 1 0 110]);plot([-0.005 -0.005],[0 100]);plot([0.005 0.005],[0 100]);Fw3=fourier(ut3,t,w);FFw3=abs(Fw3);subplot(2,1,2);ezplot(FFw3,[-10*pi 10*pi]);axis([-10*pi 10*pi 0 1.1]);title('脉宽为1、0.1和0.01的矩形脉冲信号的幅度频谱') hold onpause程序运行结果图3)直流信号的傅里叶变换MATLAB程序:clear all;display('Please input the value of a')a=input('a=');syms tf=exp(-a*abs(t));subplot(1,2,1)ezplot(f);axis([-2*pi 2*pi 0 1]);ylabel('时域波形');F=fourier(f);subplot(1,2,2)ezplot(abs(F));axis([-3 3 0 2/a])程序运行结果图a=0.1时:a=0.01时:a=0.001时:a=0.0001时:4)阶跃信号的傅里叶变换MATLAB程序:clear allsyms w;xw=1/(j*w);ezplot(abs(imag(xw)));axis([-3 3 -1.5*pi 1.5*pi]);hold ony=0:0.01:pi;plot(0,y);hold ony=-pi:pi;plot(0,y);hold ontitle('阶跃信号频谱');xlabel('\omega');axis([-pi pi -6 6]);x=-pi:0.001:pi;plot(x,0)hold ony=-6:0.01:6;plot(0,y);hold on程序运行结果图5)单边指数信号的傅里叶变换MATLAB程序:clear allsyms t v w phase im ref=exp(-2*t)*sym('heaviside(t)'); Fw=fourier(f);subplot(3,1,1);ezplot(f);axis([-1 2.5 0 1.1]);xlabel('时域波形');subplot(3,1,2)ezplot(abs(Fw));xlabel('幅度频谱');im=imag(Fw);re=real(Fw);phase=atan(im/re);subplot(3,1,3);ezplot(phase);xlabel('相位频谱');程序运行结果图2、 程序设计实验确定下列信号的傅里叶变换的数学表达式1)2()()1t f t e U t -=+的傅里叶变换1()2()2F j j ωπδωω=++ MATLAB 程序:clear allsyms t v w phase im ref=exp(-2*t)*sym('heaviside(t)')+1; Fw=fourier(f); Fw=simple(Fw); subplot(3,1,1); ezplot(f);axis([-1 2.5 0 1.1]); xlabel('时域波形'); subplot(3,1,2) ezplot(abs(Fw)); im=imag(Fw); re=real(Fw); xlabel('幅度频谱'); phase=atan(im/re); subplot(3,1,3); ezplot(phase); xlabel('相位频谱');程序运行结果图2)2()(1)()t f t e U t G t -=-+的傅里叶变换12sin ()1j e F j j ωωωωω--=++MATLAB 程序:clear allsyms t v w phase im ref=exp(-1*t)*sym('heaviside(t-1)')+heaviside(t+1)-heavis ide(t-1);Fw=fourier(f); Fw=simple(Fw); subplot(3,1,1); ezplot(f);axis([-2.5 2.5 0 1.1]); xlabel('时域波形'); subplot(3,1,2) ezplot(abs(Fw)); im=imag(Fw); re=real(Fw); xlabel('幅度频谱'); phase=atan(im/re); subplot(3,1,3); ezplot(phase); xlabel('相位频谱');程序运行结果图3)()2()(4)f t U t t δ=+-的傅里叶变换41()2(())j j F j e e j ωωωπδωω--=++MATLAB 程序:clear allsyms t v w phase im ref=2*sym('heaviside(t-1)')+dirac(t-4); Fw=fourier(f); Fw=simple(Fw); subplot(3,1,1); ezplot(f)axis([-1 6 0 1.5]); xlabel('时域波形'); subplot(3,1,2) ezplot(abs(Fw)); im=imag(Fw); re=real(Fw); xlabel('幅度频谱'); phase=atan(im/re); subplot(3,1,3); ezplot(phase); xlabel('相位频谱');程序运行结果图。
