专题13 合成路线的精准设计(解析版)

合集下载

有机合成路线设计总结

② 武慈反应
R-X + R-X Na R-R 其中：R/ 最好为伯烷基
X 为Cl、Br、I
③ 铜锂试剂反应
R-X Li R-Li CuI R2CuLi R/X R-R/
其中：R/ 最好为伯烷基； R 一般无限制 X 为Cl、Br、I
④ 傅-克反应
烷基化：
R
+ R-X AlCl3
（或烯、醇）
R ≥3 时重排产物为主
OH
α -氰醇
α -羟基酸
应用范围：醛、甲基脂肪酮、C8以下环酮
2. 增加二个碳原子的反应
R MgX + CH2 CH2 O
R CH2CH2 H3O+ RCH2CH2OH OMgX
3. 增加多个碳原子的反应
① R-C CH NaNH2 R-C CNa R/X R-C C-R/
其中：R/ 为伯卤代烃 X 为Cl、Br、I
R-X
OO
CH3-C-CH-C-OC2H5 R
① 浓OH-, △ ② H+
① 稀OH② H+, △
=
O R-CH2C-OH
酸式分解
=
O CH3-C-CH2-R 酮式分解
CH2(COOC2H5)2 C2H5ONa
-+
CH(COOC2H5)2 Na
R-X
R-CH(COOC2H5)2
①
-
OH /
H2O
② H+ ，△
R C OCH3 H OCH3
缩醛酮：对还原剂氧化剂、碱、格氏试剂稳定; 但对酸不稳定;
4 羧基的保护
R-COOH
5 氨基的保护
CH3OH / H+ H2O / H+或OH-

专题13 名著阅读-备战2024-2025学年八年级语文上学期期中真题分类汇编(北京专用)(教师版)

专题13名著阅读（解析版）【1-2023-2024学年北京市海淀区清华附属中学八年级上学期期中语文试题】名著阅读古语云：“开卷有益。

”有的书洋溢着对自然生命的尊重，有的书闪耀着革命理想的光芒……请从《昆虫记》《红星照耀中国》中任选一本，结合具体内容，谈谈这本书带给你的启迪。

（100字左右）【答案】示例一：《昆虫记》中松毛虫的团结精神是人类不可多得的财富。

它们即使走错巢，也会很安静地和平相处，团结吐丝织巢。

松毛虫队列无论怎样都会照着领头的松毛虫的路线和方式走，领头松毛虫产生的方式是随机的、暂时的。

它们会在出走的路上吐丝线留作回家的路标，也让大团队的各分子按既定路线行走，行动一致。

昆虫尚如此，人类也唯有团结一心才能取得集体的成功。

示例二：《红星照耀中国》中朱德在蔡锷将军的影响下，虽有了军事救国的思想，而且转战南北，功名赫赫，但究竟怎样救国，仍没有明确的答案。

他在不断地学习和思索中寻找共产党，为此不远万里到了法国，又到德国柏林，见到了周恩来，终于加入中国共产党。

革命的成功是艰辛的，有志之士孜孜以求，以坚定的革命信念为救国救民探寻光明之路，也告诉我们要始终坚定信念，不怕困难才能拨云见日、取得成功。

【解析】本题考查名著阅读。

开放类试题，结合相关名著的内容和主旨拟写即可。

如《昆虫记》启示人们要尊重自然，实现人与自然的和谐共处，《红星照耀中国》启示人们要学习革命者坚韧苦干的革命精神等等。

示例一：《昆虫记》中法布尔在自然中观察蝉的生活，不是把它放在木匣中或浸在酒精中。

他发现蝉在地下“潜伏”四年才能钻出地面，却只能在阳光下生存五个多星期。

他关注蝉的生命过程。

在生活中，我们应该尊重每一个生命。

示例二：《红星照耀中国》中的“红小鬼”们，他们自愿加入革命，对红军忠贞不二。

虽然他们年龄很小，但大多数人参加过长征和战争，他们胜任号手、通讯员、勤务员、侦察员等多种工作，我们要学习他们身上坚忍苦干的革命精神。

【2-2023-2024学年北京市海淀区中国人民大学附属中学八年级上学期期中语文试题】名著阅读（5分）17. 为了促进同学们阅读名著《红星照耀中国》，班级开展了以“讲好红星故事，传承红星精神”为主题的读书交流活动。

专题13 开放性试题(解析版)-2021年高考历史三轮冲刺复习热点专题优选优练

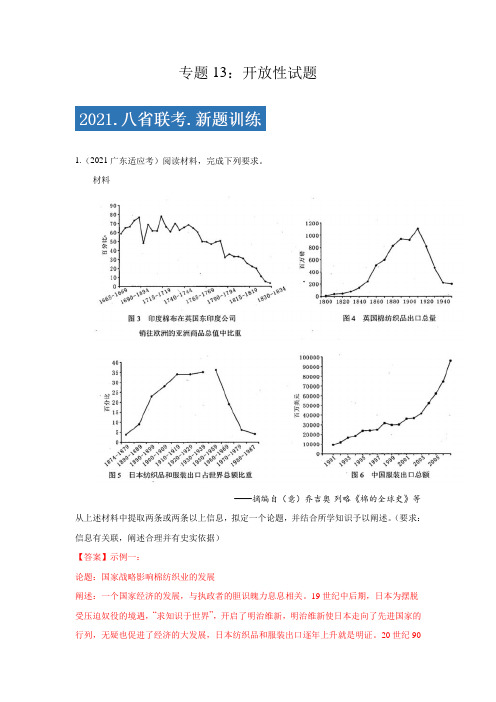
专题13：开放性试题1.（2021广东适应考）阅读材料，完成下列要求。

材料——摘编自（意）乔吉奥·列略《棉的全球史》等从上述材料中提取两条或两条以上信息，拟定一个论题，并结合所学知识予以阐述。

（要求：信息有关联，阐述合理并有史实依据）【答案】示例一：论题：国家战略影响棉纺织业的发展阐述：一个国家经济的发展，与执政者的胆识魄力息息相关。

19世纪中后期，日本为摆脱受压迫奴役的境遇，“求知识于世界”，开启了明治维新，明治维新使日本走向了先进国家的行列，无疑也促进了经济的大发展，日本纺织品和服装出口逐年上升就是明证。

20世纪90年代，中国确立了建立市场经济体制的战略目标，2001年加入世界贸易组织，迎合世界潮流，积极参与国际竞争，焕发了经济发展的潜力，中国服装出口与日俱增就是就是铁证。

可见，高瞻远瞩的战略是一个国家发展的定海神针。

示例二：论题：民族独立是国家经济发展的前提保障阐述：一个国家一个民族要想屹立于世界民族之林，必须发展经济，而经济发展需要有一个强大的国家做后盾。

近代史上，印度一度沦为英国的殖民地，经济发展受东印度公司的掣肘，发展艰难；中国沦为西方列强的半殖民地，经济上成为列强的附庸，受资本主义世界市场的操控，艰难发展。

但新中国成立后，特别是改革开放后，民族独立为经济发展保驾护航，中国经济建设的成就零世界瞩目，1991年以来中国服装出口与日俱增就是就是明证。

总之，经济要发展，民族独立是必不可少的保障。

【详解】示例一：根据材料中图5、图6两条信息，拟定一个论题——国家战略影响棉纺织业的发展。

从日本进行明治维新和中国确立市场经济体制战略的角度进行阐述。

示例二：根据材料中图4、图6两条信息，拟定一个论题——民族独立是国家经济发展的前提保障。

从近代印度和现代中国两个角度进行阐述。

还可以从材料中提取其他两条或两条以上信息，拟定一个具体论题，结合相关史实阐述即可。

此题为开放试题，言之有理即可。

2.（2021湖北适应考）（电报与近代中国）小楚同学在校园文化节中承担“电报与近代中国”展板的设计任务，通过搜集整理。

高考化学专题复习合成路线的精准设计

人教版化学选修五专题复习13 合成路线的精准设计1. 官能团的引入引入官能团有关反应羟基(—OH) 烯烃与水加成、醛(酮)加氢、卤代烃水解、酯的水解卤素原子(—X) 烃与X 2取代、不饱和烃与HX 或X 2加成、醇与HX 取代碳碳双键某些醇或卤代烃的消去、炔烃不完全加氢醛基(—CHO) 某些醇(含有—CH 2OH)的氧化、烯烃的氧化羧基(—COOH)醛的氧化、酯的酸性水解、羧酸盐的酸化、苯的同系物(侧链上与苯环相连的碳原子上有氢原子)被强氧化剂氧化酯基(—COO —)酯化反应2. 熟记常见的合成路线掌握常见的合成方法，作为合成路线的元件。

然后进行合理组装改造就可得到复杂的合成路线。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． (1)一元物质(单官能团)的转化模块：R —CH===CH 2――→加成HX 卤代烃――――――→取代(水解)一元醇――→氧化一元醛――→氧化一元羧酸――→酯化酯(2)一元醇、卤代烃合成二元物质(醇、卤代烃、醛、酸等)的合成路线。

例如：(3)一元醇、卤代烃合成聚烯烃、聚卤烯烃。

例如：CH 3CH 2OH ――→消去CH 2=CH 2――→加成HX CH 2X —CH 2X ――→消去HC ≡CH ――→加成HX CH 2=CHX ――→加聚[—CH 2—CH |X]— nCH 2=CH 2――→加聚[—CH 2—CH 2]— n(4)芳香化合物合成路线。

例如：CH 3―――取代CH 2Cl ―――→取代CH 2OH ――→氧化CHO ――氧化COOH ―――→取代芳香酯3. 有机合成中常见官能团的保护(1)酚羟基的保护：因为酚羟基易被氧化，所以在氧化其他基团前可以先使其与NaOH 反应，把—OH 变成—ONa ，将其保护起来，待氧化后再酸化将其转变为—OH 。

(2)碳碳双键的保护：碳碳双键也容易被氧化，在氧化其他基团前可以利用其与HCl 等的加成反应将其保护起来，待氧化后再利用消去反应转变为碳碳双键。

2022年上海中考化学一模分类汇编专题13 基础实验(解析版)

专题15 基础实验1．（2022·上海金山·一模）实验中出现异常情况的原因分析，错误的是A．浑浊的液体过滤后仍然浑浊：液面低于滤纸边缘B．点燃氢气时发生爆炸：点燃前没有检验纯度C．粗盐提纯的产率偏低：溶解粗盐的水量可能过少D．用启普发生器制取CO2，关闭活塞后固液无法分离：稀盐酸可能已反应完【答案】A【解析】A、液面低于滤纸边缘是正确操作，不是滤液浑浊的原因，错误；B、氢气具有可燃性，不纯的氢气点燃可能发生爆炸，正确；C、溶解粗盐的水量可能过少，导致部分食盐没有溶解，造成损失，正确；D、用启普发生器制取CO2，关闭活塞后固液无法分离：稀盐酸可能已反应完，正确。

故选A。

2．（2022·上海金山·一模）下列实验对水的主要作用解释错误的是A．隔绝白磷与氧气接触，并提供热量B．集气瓶中的水可以观察气体收集的情况C．冷却溅落的熔化物，吸收热量D．吸收放出的热量【答案】D【解析】A、探究燃烧条件的实验中，水的主要作用是隔绝白磷与氧气接触，并提供热量，正确；B、排水法收集气体时集气瓶中的水可以观察气体收集的情况，正确；C、铁丝燃烧放出大量的热，生成黑色固体，水可以冷却溅落的熔化物，吸收热量，正确；D、硫和氧气生成有毒气体二氧化硫，水可以吸收二氧化硫减少污染，错误。

故选D。

3．（2022·上海金山·一模）为了帮助同学们更好地理解空气中氧气含量测定的实验原理，老师利用传感器技术实时测定了实验装置（如图 1 所示）内的气体压强、温度和氧气浓度，它们随时间的变化曲线如图2 所示。

说法错误的是A．图1 中接通电源使用电烙铁发热，引燃红磷，使实验结果更精确B．图2 中X 曲线表示的是氧气浓度变化，Y 曲线表示的是温度变化C．图2 中BC 段变化的原因是由于温度升高所增加的气压大于氧气消耗所减小的气压D．图2 中当反应时间为t1时才打开活塞K，看到烧杯中的水进入集气瓶【答案】B【解析】A. 接通电源使用电烙铁发热，引燃物质红磷，防止了燃烧匙伸入集气瓶中时导致的部分气体受热膨胀逸出，实验结果更准确，故选项说法正确；B. 红磷燃烧放出热量，温度升高，冷却后温度降低，X曲线表示的是温度；红磷燃烧消耗氧气，氧气浓度减小，Y曲线表示氧气浓度，故选项说法错误；C.结合图可知，图2中BC段气压变化的原因是温度升高所增加的气压大于氧气消耗所减小的气压，故选项说法正确；D.从图2中看出t1时才打开活塞K，压强突然增大，说明烧杯中的水进入集气瓶，故选项说法正确。

有机合成推断及合成路线设计---2023年高考化学一轮复习(新高考)

M
M＋_2_8__
(关系式中 M 代表第一种有机物的相对分子质量)
4.根据反应条件推断反应类型热点强化18 3.常见反应条件与反应类型的关系。 5.根据官能团的衍变推断反应类型
6.根据题目提供的信息推断常见的有机新信息总结如下： (1)苯环侧链引入羧基
如短碳链。Leabharlann (R代表烃基)被酸性KMnO4溶液氧化生成
HI ―――→
(3)醛基：在氧化其他基团前可以用乙醇(或乙二醇)加成保护。
①
―C―2―H―5O―H→
HCl
―H―＋―/―H―2O→
②
―H―O――—―C―H―2―C―H―2—――O―H→
H＋
―H―＋―/―H―2O→
(4)氨基：在氧化其他基团前可以用醋酸酐将氨基转化为酰胺，然后再水解转化为氨基。
――C――H―3―C―O――2―O→
。
答案 ―K―M――n―O―4―/―H→＋
―浓――浓硫――硝酸――酸，――△→
―――C―l―2 → 催化剂
――――C―2H――5―O―H――→ 浓H2SO4，△
2.苯乙酸乙酯是一种常见的合成香料。请设计合理方案，以苯甲醛和乙醇为主要原
料(无机试剂任选)，合成苯乙酸乙酯(
)。
已知：①R—Br＋NaCN―→R—CN＋NaBr；
――――H―2―O――→ H＋或OH－
(5)醇羟基、羧基可以成酯保护。
提升关键能力
一、根据已知信息设计合成路线
1.合成路线流程图示例如下： CH3CH2OH―浓1―7―硫0――℃酸→H2C==CH2―B―r→2
请设计合理方案，以甲苯为主要原料，其他物质可根据需要自主选择，合成局部麻
醉剂氯普鲁卡因盐酸盐的中间体

目标性复习在高三复习课中的应用——合成路线的设计

二、课程标准
能利用不同类型有机化合物之间的转化关系设计合理路线合成简单有机物．
三、学情分析
高考试卷中有机部分考点的考查比较稳定，其中同分异构体的书写与有机合成部分一直是难点部分，学生得分率较低，更有些同学浏览题目后，觉得没有思路变放弃合成题的书写，本节课就是专题介绍有机合成书写方法，帮助学生找到解题突破点和方法，克服畏难情绪．
年份
类型一—
—
备注
２０ｌ１２０１２２０１３２０１４２０１５２０１６２０１７
通过考试要求的梳理，使学生从大的方向明确这部
分知识在高考中的要求；然后通过分析近几年高考中信
息使用的情况，知道从哪里找突破点，使学生明确解答此
浓ＨＮＯ
———
———－——
——————
———————
———
浓ＨＳＯ、△
Ｃ００Ｈ
／／／／
ｌｌ
Ｉ
＼／／
１
ＮＯ２
根据已有知识并结合相关信息，写出以
ｃＨ３
ｃＨ２ｃＨＯ
ｃＨｃ０ＯＨ
ｌ／为原料制备
的合成路
收稿日期：２０１８—０ｌ一２０作者简介：姜雪（１９８１．５一），女，江苏省南京人，中学一级教师，从事化学教学研究
／＝＝＼
已知：① 苯胺（
一ＮＨ：）易被氧化；②

专题13电路、电流、电压、电阻(原卷版+解析)(第2期)

②保持M位置不变，把RX接入电路，如图乙所示。闭合开关，此时电流表的示数为0.20A。请在虚线框内画出图乙的电路图___________，并求出此时RX的电阻为___________Ω；
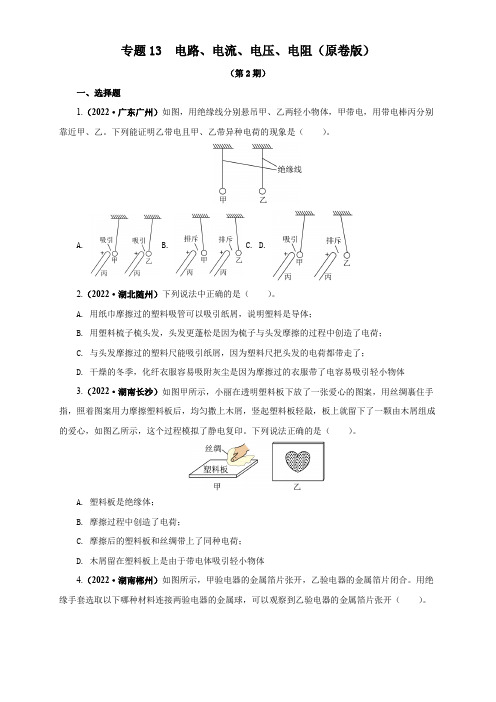
③小明实验时电源的实际电压比3V略低，则他测算出的电阻值___________（偏大/偏小/不变）；
④为了消除因电源电压降低对电阻测量结果的影响，小明用原实验电路，改变测量方法就可以消除影响。其做法是：
A. 干木条B. 橡胶棒C. 玻璃棒D. 石墨棒
5.（2022·湖南常德）用塑料梳子梳头发时，头发容易被梳子“粘”起。下列现象中“粘”的原因与其相同的是（）。
A. 两个铅柱底面削平挤压后能“粘” 一起；
B. 干燥的天气里，化纤布料的衣服容易“粘”在身上；
C. 用湿手拿冰冻的东西，手被粘住了；
D. 用硬纸片盖住装满水的玻璃杯并倒置，纸片“粘”在杯口
（1）如果不能估计电流大小，他应把导线a接到电流表标有___________（选填“-”、“0.6”或“3”）的接线柱上，通过开关来试触并观察；
（2）闭合开关后，他观察到小灯泡正常发光，而电流表指针偏转角度很小，对于该现象，下列分析合理的是___________。
A．可能某处导线断了 B．可能电流表烧坏
C．电流表的量程过大 D．电源的电压过低
（3）某次测量中，小郑不小心将电流表的正、负接线柱接反了，造成表的指针反向偏转，为弄清原因，他查看了说明书，表头结构示意图如图乙，他作出如下分析：当反接时，电流方向改变，磁场对通电线圈的作用力方向改变，带动指针反偏，你认为小郑的上述分析_______（选填“有”或“没有”）道理。
专题13 电路、电流、电压、电阻（原卷版）
（第2期）
一、选择题
1.（2022·广东广州）如图，用绝缘线分别悬吊甲、乙两轻小物体，甲带电，用带电棒丙分别靠近甲、乙。下列能证明乙带电且甲、乙带异种电荷的现象是（）。

专题13 探究两个互成角度的力的合成规律(解析版)

2023届高三物理一轮复习重点热点难点专题特训专题13 探究两个互成角度的力的合成规律【特训典例】1．两位同学一起做“研究共点力的合成”实验。

（1）实验采用的主要科学方法是( )A．理想实验法B．等效替代法C．控制变量法D．模拟研究法（2）他们的实验操作的部分步骤如下，老师指出①、②步骤中各有一处存在遗漏。

①一位同学直接取用图（a）的两个弹簧测力计分别钩住绳套，平行于图板互成角度地拉伸橡皮筋使结点至P点（示意图如（b）），另一同学记录下P点位置、两测力计对应拉力F1、F2的大小和方向。

②再用一只弹簧测力计，通过一个细绳套拉伸橡皮筋使其伸长相同长度，记录测力计的示数F′和细绳的方向，并按同一标度作出F′的图示。

请说明①步骤中遗漏的内容_________；②步骤中遗漏的内容_____。

（3）两同学怀疑实验中的橡皮筋会因多次拉伸而弹性发生变化，于是设计如下实验来探究：将钉有白纸的图板竖直固定，橡皮筋上端固定于O点，一个细绳套上挂一重物，用与白纸平行的水平力拉另一细绳套，缓慢移动结点，在白纸上记录下结点的轨迹，如图（c）中“轨迹1”所示。

把橡皮筋多次拉伸后，重复实验，在同一张纸上记录下结点的轨迹2，如图（d）所示。

过O点作一条直线与轨迹交于a、b两点，则两次实验中橡皮筋分别被拉到a、b时，橡皮筋拉力的方向_____（选填“相同”或“不同”），由此推断拉力的大小Fa____Fb（选填“>”、“<”或“=”）。

【答案】 B 弹簧测力计使用前应水平调零应把橡皮筋的结点拉到同一位置相同 =【详解】（1）[1]研究共点力的合成是保证两个力拉橡皮筋的效果和一个力拉橡皮筋的效果相同，故采用了等效替代法，故选B ；（2）[2]两只弹簧测力计使用前指针没有指到零刻度先，则步骤①中遗漏的内容为弹簧测力计使用前应水平调零；[3]为了保证两次拉动橡皮筋的效果相同，则②步骤中遗漏的内容应把橡皮筋的结点拉到同一位置；（3）[4]过O 点作一条直线与轨迹交于a 、b 两点，橡皮筋的拉力沿橡皮筋收缩的方向，则两次实验中橡皮筋的拉力方向相同；[5]由于缓慢地移动P ，结点始终处于平衡，而所受重力不变，而橡皮筋的拉力方向不变，由力的三角形规律可得F a 、F b 的大小关系为a b F F2．某实验小组用如图1所示装置进行验证力的平行四边形定则的实验，其中A 为固定橡皮筋的图钉，O 为橡皮筋与细绳的结点，OB 和OC 为细绳。

2024届高三化学第一轮复习：有机合成路线的设计与实施课件

CH2COOH CH2OH
CH2COOCH2CH3 CH2OOCCH3
乙酸 C2H4O2 乙醇
推断：A、B、C、D、E、F的结构简式?
乙烯
【同步练习】[练习4] 已知：注意读懂题干信息
加成
分析下图变化，写出A、B、C、D、E、F的结构简式?
加聚反应
O CH3 C
--
--
=
加成 OH
消去
酯化
CH3
【同步练习】已知：①CH3CH2Br＋NaCN 醇 CH3CH2CN＋NaBr 取代反应
练习6
②CH3CH2CN H2O，H＋ CH3CH2COOH 水解反应
③CH3CH2COOH Br2，P CH3CHBrCOOH取代反应
有下列有机物之间的相互转化： CH3-CH CH3 Br
-
CH3-CH CH3 COOH
【典例】卡托普利为血管紧张素抑制剂，其合成线路几各步反应的转化率如下：
则该合成路线的总产率是
A． 58.5%
B．93.0%
A
C．76% D．68.4%
【课堂练习3】以下已甲苯为原料合成苯甲酸苯甲酯的两种路线，哪种方案更科学？
路线1：步骤多，反应条件复杂，成本高，且使用较多的Cl2，不利于环境保护路线2：步骤少，反应条件简单，成本低，且使用Cl2较少
分析:
CH2OH CH2OH
CH2Br CH2Br
CH2＝CH2
合成路线:
CH2＝CH2
Br2
CH2Br CH2Br
NaOH/H2O CH2OH CH2OH
H2SO4
△
2.苯甲酸苯甲酯
是一种有水果香气的析法设计它的合成路线。
分析:

高中化学专题13 元素及其化合物知识的综合应用-2021年高考真题和模拟题化学分项汇编(解析版)

专题13 元素及其化合物知识的综合利用1．（2021·全国高考甲卷真题）碘(紫黑色固体，微溶于水)及其化合物广泛用于医药、染料等方面。

回答下列问题：(1)2I 的一种制备方法如下图所示：①加入Fe 粉进行转化反应的离子方程式为_______，生成的沉淀与硝酸反应，生成_______后可循环使用。

②通入2Cl 的过程中，若氧化产物只有一种，反应的化学方程式为_______；若反应物用量比()()22n Cl /n FeI =1.5时，氧化产物为_______；当()()22n Cl /n FeI >1.5，单质碘的收率会降低，原因是_______。

(2)以3NaIO 为原料制备2I 的方法是：先向3NaIO 溶液中加入计量的3NaHSO ，生成碘化物；再向混合溶液中加入3NaIO 溶液，反应得到2I ，上述制备2I 的总反应的离子方程式为_______。

(3)KI 溶液和4CuSO 溶液混合可生成CuI 沉淀和2I ，若生成21mol I ，消耗的KI 至少为_______mol 。

2I 在KI 溶液中可发生反应--23I +I I 。

实验室中使用过量的KI 与4CuSO 溶液反应后，过滤，滤液经水蒸气蒸馏可制得高纯碘。

反应中加入过量KI 的原因是_______。

【答案】2AgI+Fe=2Ag+ Fe 2++2I - AgNO 3 FeI 2+Cl 2= I 2+FeCl 2 I 2、FeCl 3 I 2被过量的2Cl 进一步氧化 --2-+332422IO +5HSO =I +5SO +3H +H O 4 防止单质碘析出【解析】(1) ①由流程图可知悬浊液中含AgI ，AgI 可与Fe 反应生成FeI 2和Ag ，FeI 2易溶于水，在离子方程式中能拆，故加入Fe 粉进行转化反应的离子方程式为2AgI+Fe=2Ag+ Fe 2++2I -，生成的银能与硝酸反应生成硝酸银参与循环中，故答案为：2AgI+Fe=2Ag+ Fe 2++2I -；AgNO 3；②通入2Cl 的过程中，因I -还原性强于Fe 2+，2Cl 先氧化还原性强的I -，若氧化产物只有一种，则该氧化产物只能是I 2，故反应的化学方程式为FeI 2+Cl 2= I 2+FeCl 2，若反应物用量比()()22n Cl /n FeI =1.5时即2Cl 过量，先氧化完全部I -再氧化Fe 2+，恰好将全部I -和Fe 2+氧化，故氧化产物为I 2、FeCl 3，当()()22n Cl /n FeI >1.5即2Cl 过量特别多，多余的氯气会与生成的单质碘以及水继续发生氧化还原反应，单质碘的收率会降低，故答案为：FeI 2+Cl 2= I 2+FeCl 2；I 2、FeCl 3；I 2被过量的2Cl 进一步氧化；(2)先向3NaIO 溶液中加入计量的3NaHSO ，生成碘化物即含I -的物质；再向混合溶液中（含I -）加入3NaIO 溶液，反应得到2I ，上述制备2I 的两个反应中I -为中间产物，总反应为-3IO 与-3HSO 发生氧化还原反应，生成2-4SO 和2I ，根据得失电子守恒、电荷守恒]及元素守恒配平离子方程式即可得：--2-+332422IO +5HSO =I +5SO +3H +H O ，故答案为：--2-+332422IO +5HSO =I +5SO +3H +H O ； (3) KI 溶液和4CuSO 溶液混合可生成CuI 沉淀和2I ，化学方程式为4KI+2CuSO 4=2CuI ↓ +I 2+2K 2SO 4，若生成21mol I ，则消耗的KI 至少为4mol ；反应中加入过量KI ，I -浓度增大，可逆反应--23I +I I 平衡右移，增大2I 溶解度，防止2I 升华，有利于蒸馏时防止单质碘析出，故答案为：4；防止单质碘析出。

高中化学有机合成路线的设计

1:利用逆推法设计乙二酸二乙酯的合成路线
设计背景
乙二酸二乙酯为无色油状液体，有芳香气味。主要用作溶剂、染料中间体及油漆、药物的合成。
提示：①充分利用已学有机化合物的化学性质 ②原料分子尽量是常见烃类物质
O
C
C
O CH2CH3
O
O CH2CH3
2：书107第 3，4题
【实战演练4】尝试设计
设计方案由氯乙烷合成乙二醇，并写出每步反应的化学方程式．

2CH 3 CH 2 COCHO O 2 催化剂 2CH 3 CH 2 COCOOH

CH 2 CH 2 CH CH 2 H 2 O 催化剂 CH 3 CH 2 CH(OH)CH 3

CH 3 CH 2 COCOOH CH 3 CH 2 CH (OH )CH 3 浓硫酸
光
CHCl2 NaOH
H2O
CHO
O C O CH2
氧化剂
O C OH
概括整合
有机合成路线的设计

1.有机合成路线的设计方法一般有：正推法、逆推法和两头凑法 2.学习一种典型的设计方法---逆推合成法 3、选择有机合成路线的原则：原料易得、过程简单、成本低、副产品少、尽量是绿色合成。
【实战演练3】尝试设计
碳骨架特征及官能团的种类和位置
由目标化合物分子逆推原料分子并设计合成路线
碳骨架的构建官能团的引入或转化
（符合化学原理、操作安全可靠）
原子经济性原子经济性 1
步骤尽量简单
优选合成路线
符合绿色合成思想 9 原料绿色化
9 1
试剂和催化剂无公害性
案例:利用逆推法设计苯甲酸苯甲酯的合成路线

有机合成路线设计

有机合成路线设计【考试要求】1、掌握烃（烷烃、烯烃、炔烃和芳香烃）及其衍生物（卤代烃、醇、酚、醛、羧酸、酯）的组成、结构特点和主要性质。

2、能利用不同类型有机化合物之间的转化关系设计合理路线合成简单有机化合物。

【命题趋势】根据已经学过的有机反应以及题目给出的信息进行有机化合物的合成路线设计。

【要点梳理】1．有机合成的原则：（1）起始原料要廉价易得，低毒性、低污染。

（2）应尽量选择步骤最少的合成路线。

（3）原子经济性高，具有较高产率。

（4）有机合成反应要操作简单、条件温和、能耗低、易于实现。

2．表达方式：合成路线图 3．有机合成方法：多以逆推为主，其思维途径是（1）首先确定要合成的有机物属于何种类型，以及题中所给的条件与所要合成的有机物之间的关系。

（2）以题中要求最终物质为起点，考虑这一有机物如何从另一有机物甲经过一步反应制得。

若甲不是所给已知原料，需再进一步考虑甲又是如何从另一有机物乙经一步反应制得，过程中需要利用给定（或隐藏）信息，一直推导到题目给定得原料为终点。

（3）在合成某产物时，可能会产生多种不同方法和途径，应当在兼顾原料省、产率高的前提下选择最合理、最简单的方法和途径。

4．有机合成中官能团引入与转化的常见方法A B C 反应物反应条件反应物反应条件 ……D基引入双键例1．化合物H是合成药物盐酸沙格雷酯的重要中间体，其合成路线如下：已知：。

化合物是合成抗癌药物美发伦的中间体，请写出以和为原料制备该化合物的合成路线流程图(无机试剂任用)。

合成路线流程图示例如下：【答案】：1．敌草胺是一种除草剂。

它的合成路线如下：已知：，写出以苯酚和乙醇为原料制备的合成路线流程图（无机试剂任用）。

合成路线流程图例如下：2．常见氨基酸中唯一不属于α－氨基酸的是脯氨酸。

它的合成路线如下：HOOCCH 2CH 2CHCOOH NH 2C 2H 5OOCCH 2CH 2CHCOOHNH 2N H COOH N HCOOH·C 6(OH)Cl 5乙醇、浓硫酸KBH 4、H 2O脯氨酸25 ℃A BCD五氯酚分离氨水①N HCOOH ②③④C分离已知：R －NO 2Fe 、HClR －NH 2，写出以甲苯和乙醇为原料制备CH 3NCH 2CH 3CH 2CH 3的合成路线流程图（无机试剂任选）。

三年高考(2023-2023)地理真题分项版解析-专题13以中国区域为背景综合题(解析版)-图文

三年（2023-2023）高考地理试题分项版专题13以中国区域为背景综合题【2023年高考题】（2023·新课标Ⅰ卷）37．阅读图文资料，完成下列要求。

（22分）（1）河流排水受阻常形成堰塞湖，乌裕尔河排水受阻却形成沼泽湿地。

据此推测扎龙湿地的地貌、气候特点。

（6分）（2）分析从乌裕尔河成为内流河至扎龙湿地面积稳定，乌裕尔河流域降水量、蒸发量数量关系的变化。

（6分）（3）指出未来扎龙湿地水中含盐量的变化，并说明原因。

（6分）（4）有人建议，通过工程措施恢复乌裕尔河为外流河。

你是否同意，并说明理由。

（4分）【答案】（1）地势平坦、开阔。

气候较为干旱（蒸发能力强）。

（2）降水量基本不变化，蒸发量逐渐增大，二者数量关系由降水量大于蒸发量最终变为降水量等于蒸发量。

（3）变化：水中含盐量逐渐增加。

原因：河水不断为湿地带来盐分（矿物质）；随着湿地水分蒸发，盐分（矿物质）富集（最终饱和）。

（4）同意，可防止盐分（矿物质）富集；减少泥沙淤积；扩大鱼类种群规模；减轻水体富营养化。

不同意，应减少对自然的干扰；保持湿地水量稳定；保护生物多样性；维护食物链完整（保护丹顶鹤）；防止湿地环境变化。

【解析】精准分析：（3）湿地水分因无法外流，水中溶解的盐分会在湿地中积累，使盐度增大，有点类似于水流只进不出的湖泊最终会成为咸水湖的原理。

或者盐沼的形成。

盐分的大小与含盐量、水量有关，湿地中盐分增加，一是无法排出，没有向外的水流通道；二是河流不断地带来溶解盐分，不断地在湿地积累。

水量变小，盐度相对增加，造成水量减少的原因有：一是降水量大于蒸发量；二是人类用水，使注入湿地的河水减少；三是河流泥沙淤积，湿地水浅，单位面积湿地的含盐量增大。

（4）该题为开放性试题，正反观点都行，言之有理即可。

赞同通过工程措施恢复乌裕尔河为外流河，河道得到恢复，水量增大，盐分不易累积，可以防止盐分富集；乌裕尔河带来的泥沙会随嫩江向下游输送，就会减少泥沙在本区的淤积；由于乌裕尔河水量集中，并与嫩江相连通，会扩大鱼群规模，由于自净能力增强，会减轻水体富营养化。

2021届全国新高考化学精品备考有机合成路线的设计

写出用 2-苯基乙醇为原料(其他无机试剂任选)制备化合物 D 的合成路线_____________________________________。
[解析] 已知物 2-苯基乙醇的结构为
，目标产
物 D 的结构为
，由已知物到目标产物的碳原子数相同，
碳骨架结构相同，因此设计合成路线只是将官能团进行改变，
③通过加成或氧化反应等消除醛基；
④通过水解反应消除酯基、肽键、卤素原子。
(2)官能团的改变
①利用官能团的衍生关系进行衍变，如
R—CH2OH
O2 H2
R—CHO―O―2→R—COOH；
②通过某种化学途径使一个官能团变为两个，如
CH3CH2OH―—消―H去2→OCH2=== CH2―＋加―C成→l2 Cl—CH2—CH2Cl―水―解→HO—CH2—CH2—OH；
碳碳双键
氧化
化为—NH2
用氯化氢先与烯烃加成转易与卤素单质加成，易
化为氯代物，最后用被氧气、臭氧、双氧水、
NaOH 醇溶液通过消去反酸性高锰酸钾溶液氧化
应，重新转化为碳碳双键
被保护的官被保护的官
能团
能团性质
保护方法
醛基保护一般是把醛基制成缩醛，最后再将缩醛水解得到醛基 (常用乙二醇)
醛基
提素能•好题
1．(2019·上海高考)白藜芦醇是一种抗肿瘤的药物，合成它的一种路线如图：
根据已有知识并结合相关信息，写出以 HO—CH2—CH2—CH2—CH2—OH 和 CH3OH 为原料制备 CH3OOCCH2CH2CH2CH2COOCH3 的合成路线流程图(无机试剂任用)。(已知 RCNH―＋―/H→2ORCOOH)合成路线流程图如下：(甲
参考题目中制备化合物 E 的合成路线和③的反应可设计出制

部编数学九年级上册专题13点和圆、直线和圆的位置关系(解析版)(重点突围)含答案

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！专题13 点和圆、直线和圆的位置关系考点一判断点与圆的位置关系考点二直线与圆的位置关系考点三已知直线与圆的位置关系求半径的求值考点四切线的性质定理考点五切线的性质和判定的综合应用考点六应用切线长定理求解考点七应用切线长定理证明考点一判断点与圆的位置关系例题：（2022·浙江宁波·九年级期末）已知⊙O 的半径为5，点P 到圆心O 的距离为d ，若点P 在圆内，则d 的取值范围为（）A ．5d £B ．5d =C ．5d >D ．05d £<【答案】D【解析】【分析】根据点与圆的位置关系判断得出即可．【详解】解：∵点P 在圆内，且⊙O 的半径为5，∴0≤d ＜5，故选：D ．【点睛】此题主要考查了点与圆的位置关系．解题的关键在于熟练掌握点与圆的位置关系有3种：⊙O 的半径为r ，点P 到圆心的距离OP =d ，则有：①点P 在圆外⇔d ＞r ，②点P 在圆上⇔d =r ，③点P 在圆内⇔d ＜r ．【变式训练】1．（2022·广东广州·一模）A ，B 两个点的坐标分别为（3，4），（﹣5，1），以原点O 为圆心，5为半径作⊙O ，则下列说法正确的是（）A ．点A ，点B 都在⊙O 上B ．点A 在⊙O 上，点B 在⊙O 外C ．点A 在⊙O 内，点B 在⊙O 上D ．点A ，点B 都在⊙O 外【答案】B【解析】【分析】根据勾股定理，可得OA、OB的长，根据点与圆心的距离d，则d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．【详解】解：∵OA＝5，OB5，∴点A在⊙O上，点B在⊙O外．故选：B．【点睛】本题主要考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r 时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．2．（2021·全国·九年级期中）已知⊙O的半径为6cm，当线段OA＝8cm时，点A和⊙O的位置关系是_________．【答案】点A在⊙O外【解析】【分析】根据点与圆的位置关系进行判断．【详解】解：∵⊙O的半径为6cm，OA＝8cm，∴OA＞⊙O的半径，∴点A在⊙O外．故答案为点A在⊙O外．【点睛】本题考查了点与圆的位置关系：设⊙O的半径为r，点P到圆心的距离OP=d，则点P在圆外⇔d＞r；点P在圆上⇔d=r；点P在圆内⇔d＜r．考点二直线与圆的位置关系例题：（2022·四川成都·二模）⊙O 的直径为8，圆心O 到直线a 的距离为4，则直线a 与⊙O 的位置关系是（）A ．相离B ．相切C ．相交D ．不能确定【答案】B【解析】【分析】直接根据直线与圆的位置关系进行解答即可．【详解】解：∵⊙O 的直径是8，∴⊙O 的半径是4，又∵圆心O 到直线a 的距离是4，∴直线a 与⊙O 相切．故选：B ．【点睛】本题考查的是直线与圆的位置关系，设⊙O 的半径为r ，圆心O 到直线l 的距离为d ，当d <r 时，直线与圆O 相交；当d =r 时，直线与圆O 相切；当d >r 时，直线与圆O 相离．【变式训练】1．（2022·河北承德·九年级期末）在ABC V 中，5AB AC ==，8BC =，以A 为圆心2.5为半径作圆．下列结论中正确的是（）A ．直线BC 与圆O 相切B ．直线BC 与O e 相离 C ．点B 在圆内D ．点C 在圆上【答案】B【解析】【分析】过A 点作AH ⊥BC 于H ，如图，利用等腰三角形的性质得到BH =CH =12BC =4，则利用勾股定理可计算出AH =3，然后根据直线与圆的位置关系的判定方法对A 选项和B 选项进行判断；根据点与圆的位置关系对C 选项和D 选项进行判断．【详解】解：过A 点作AH ⊥BC 于H ，如图，∵AB =AC ，∴BH =CH =12BC =4，在Rt △ABH 中，3AH ===，∵AH ⊥BC ，AH =3＞2.5，∴直线BC 与⊙A 相离，所以A 选项不符合题意，B 选项符合题意．∵AB =5＞2.5，∴B 点在⊙A 外，所以C 选项不符合题意；∵AC =5＞2.5，∴C 点在⊙A 外，所以D 选项不符合题意；故选：B ．【点睛】本题考查了直线与圆的位置关系：设⊙O 的半径为r ，圆心O 到直线l 的距离为d ，若直线l 和⊙O 相交⇔d ＜r ；直线l 和⊙O 相切⇔d ＝r ；直线l 和⊙O 相离⇔d ＞r ．也考查了点与圆的位置关系和等腰三角形的性质．2．（2020·全国·九年级期中）已知O e 的直径为6cm ，点O 到直线a 的距离为4cm ，则O e 与直线a 的位置关系是____________．【答案】相离【解析】【分析】先求出O e 的半径，再比较点O 到直线a 的距离d 与圆半径r 大小，根据当d >r ，则直线与圆相离，当d =r ，则直线与圆相切，当d <r ，则直线与圆相交，所此即可求解．【详解】解：∵O e 的直径为6cm ，∴O e 的半径为3cm ，∵4cm >3cm ，e与直线a的位置关系是相离．∴O故答案为：相离【点睛】本题考查直线与圆满的位置关系，熟练掌握“设点O到直线a的距离d，圆半径r，当d>r，则直线与圆相离，当d=r，则直线与圆相切，当d<r，则直线与圆相交”是解题的关键．考点三已知直线与圆的位置关系求半径的求值例题：（2022·浙江宁波·九年级期末）已知圆与直线有两个公共点，且圆心到直线的距离为4，则该圆的半径可能为（）A．2B．3C．4D．5【答案】D【解析】【分析】根据直线和圆相交，则圆心到直线的距离小于圆的半径，即可得到问题答案．【详解】解：∵圆与直线有两个公共点，且圆心到直线的距离为4，∴该圆的半径＞4，故选：D．【点睛】本题考查了直线和圆的位置关系，熟悉直线和圆的位置关系，圆心到直线的距离与半径的关系是解题的关键．【变式训练】1．（2022·江苏南通·一模）如图，点D是等腰直角△ABC斜边AB上一点，点E是BC上一点，AB＝2，DA＝DE，则AD的取值范围是____．【答案】21AD££【解析】【分析】以D为圆心，AD的长为半径画圆，分BC与圆相交和相切时分情况讨论，即可求出．【详解】以D为圆心，AD的长为半径画圆①如图，当圆与BC相切时，DE⊥BC时，∵△ABC是等腰直角三角形，∴∠ABC＝45°，∴BD DE，∵AB＝2，DA＝DE，+AD＝2，∴AD＝﹣2；AB＝1，②如图，当圆与BC相交时，若交点为B或C，则AD＝12∴AD的取值范围是2≤AD≤1．故答案为：21AD££．【点睛】本题考查了圆的作法，圆与直线的位置关系，圆的相关性质，分情况讨论并画出图形是解题的关键．2．（2021·河北·金华中学九年级阶段练习）在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，若以点C为圆心，r为半径的圆与边AB所在直线相离，则r的取值范围为_____；若⊙C与AB边只有一个有公共点，则r的取值范围为_____．【答案】 0<r<245r=245【解析】【分析】根据d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内，可得答案；根据圆心到直线的距离等于半径时直线与圆只有一个公共点．【详解】解：如图，作CH⊥AB于H．在Rt△ABC中，∵∠ACB=90°，AC=6，BC=8，∴AB=，∵S△ABC=12•AC•BC=12•AB•CH，∴CH=245，∵以点C为圆心，r为半径的圆与边AB所在直线相离，∴0<r<245；∵以点C为圆心，r为半径的圆与边AB所在直线只有一个公共点，∴r=245．故答案为：0<r<245；r=245．【点睛】本题考查了点与圆的位置关系，d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．考点四切线的性质定理例题：（2022·江苏泰州·中考真题）如图，PA与⊙O相切于点A，PO与⊙O相交于点B，点C在¼AmB上，且与点A，B不重合，若∠P=26°，则∠C的度数为_________°．【答案】32【解析】【分析】连接OA，根据切线的性质和直角三角形的性质求出∠O=64°．再根据圆周角的定理，求解即可．【详解】解：连接OA，∵PA与⊙O相切于点A，∴∠PAO=90°，∴∠O=90°-∠P，∵∠P=26°，∴∠O=64°，∠O=32°．∴∠C=12故答案为：32．【点睛】此题考查了切线的性质以及圆周角定理，解题的关键是正确利用切线的定理，作出辅助线，求出∠O的度数．【变式训练】1．（2022·山东德州·九年级期末）如图，PA、PB分别与⊙O相切于A、B，C为⊙O上一点，∠ACB=126°，则∠P的度数为________．【答案】72°##72度【解析】【分析】利用圆内接四边形的性质求出∠ADB=54°，再根据圆周角定理得到∠AOB=108°，接着利用切线的性质得到∠OAP=∠OBP=90°，然后根据四边形的内角和计算∠P的度数．【详解】解：如图所示，连接OA，OB，在优弧AB上取点D，连接AD，BD，∵∠ACB+∠ADB=180°，∴∠ADB=180°-126°=54°，∴∠AOB=2∠ADB=108°，∵PA、PB分别与⊙O相切于A、B，∴OA⊥PA，OB⊥PB，∴∠OAP=∠OBP=90°，∴∠P=180°-∠AOB=180°-108°=72°．故答案为：72°．【点睛】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．2．（2022·湖北鄂州·中考真题）工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A、B、E三个接触点，该球的大小就符合要求．图（2）是过球心及A、B、E三点的截面示意图，已知⊙O的直径就是铁球的直径，AB 是⊙O 的弦，CD 切⊙O 于点E ，AC ⊥CD 、BD ⊥CD ，若CD =16cm ，AC =BD =4cm ，则这种铁球的直径为（）A ．10cmB ．15cmC ．20cmD ．24cm【答案】C【解析】【分析】连接OA ，OE ，设OE 与AB 交于点P ，根据AC BD =，AC CD ^，BD CD ^得四边形ABDC 是矩形，根据CD 与O e 切于点E ，OE 为O e 的半径得OE CD ^，OE AB ^，即PA PB =，PE AC =，根据边之间的关系得8PA cm =，4AC BD PE cm ===，在Rt OAP △，由勾股定理得，222+=PA OP OA ，进行计算可得10OA =，即可得这种铁球的直径．【详解】解：如图所示，连接OA ，OE ，设OE 与AB 交于点P ，∵AC BD =，AC CD ^，BD CD ^，∴四边形ABDC 是矩形，∵CD 与O e 切于点E ，OE 为O e 的半径，∴OE CD ^，OE AB ^，∴PA PB =，PE AC =，∵AB =CD =16cm ，∴8PA cm =，∵4AC BD PE cm ===，在Rt OAP △，由勾股定理得，222+=PA OP OA 2228+(4)=OA OA -解得，10OA =，则这种铁球的直径＝221020OA cm =´=，故选C ．【点睛】本题考查了切线的性质，垂径定理，勾股定理，解题的关键是掌握这些知识点．考点五切线的性质和判定的综合应用例题：（2022·辽宁盘锦·模拟预测）如图，△ABC 内接于⊙O ，∠ABC ＝45°，连接AO 并延长交⊙O 于点D ，连接BD ，过点C 作CE ∥AD 与BA 的延长线交于点E ．(1)求证：CE 与⊙O 相切；(2)若AD ＝4，∠D ＝60°，求线段AB ，BC 的长．【答案】(1)见解析(2)线段AB 的长为BC 【解析】【分析】（1）连接OC ，根据圆周角定理得∠AOC ＝90°，再根据AD ∥EC ，可得∠OCE ＝90°，从而证明结论；（2）过点A 作AF ⊥EC 交EC 于F ，由AD 是圆O 的直径，得∠ABD ＝90°，结合AD ＝4，60D Ð°＝可得到AB ==45ABC Ð°＝，知△ABF 是等腰直角三角形，进而求出AF BF AB====CF，即可求解．(1)证明：连接OC，如图：∵∠ABC＝45°，∴∠AOC＝90°．∵AD∥EC，∴∠AOC+∠OCE＝180°，∴∠OCE＝90°，∴OC⊥CE，∵OC为半径，∴CE是⊙O的切线；(2)解：过点A作AF⊥BC于F，如图．∵AD是圆O的直径，∴∠ABD＝90°，∵AD＝4，∠D＝60°，∴∠BAD＝30°，∴122BD AD==，∴AB==∵∠ABC＝45°，∴△ABF是等腰直角三角形，∴AF BF====∵△AOC是等腰直角三角形，OA＝OC＝2，∴AC=∴CF===∴BC BF CF=+=答：线段AB的长为BC．【点睛】本题主要考查了圆周角定理，切线的判定与性质，等腰直角三角形的判定和性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．【变式训练】1．（2022·山东威海·九年级期末）如图，AB是⊙O的直径，弦CD⊥AB于点E，且DC＝AD．过点A作⊙O 的切线，过点C作DA的平行线，两直线交于点F，FC的延长线交AB的延长线于点G．(1)求证：FG与⊙O相切；(2)连接EF，若AF＝2，求EF的长．【答案】(1)见解析(2)EF=【解析】【分析】（1）连接OC，AC．先证明△ACD为等边三角形．可得∠ACO=∠OAC=30°．再由FG∥DA，可得∠ACF=∠DAC=60°．从而得到∠OCF=90°．即可求证；（2）根据AD∥FG，可得∠AGF=∠DAE=30°．再根据直角三角形的性质可得FG=2AF=4，AG==△ADE≌△GCE．可得AE=GE(1)证明：连接OC，AC．∵AB是⊙O的直径，CD⊥AB，∴CE=DE，AD=AC．∵DC=AD，∴DC=AD=AC．∴△ACD为等边三角形．∴∠D=∠DCA=∠DAC=60°．∴∠AOC=30°，∵OA=OC，∴∠ACO=∠OAC=30°．∵FG∥DA，∴∠ACF=∠DAC=60°．∴∠OCF=90°．∴OC⊥FG．∵OC为半径，∴FG与⊙O相切．(2)解∶∵AD∥FG，∴∠AGF=∠DAE=30°．∵AF为⊙O的切线，∴∠FAG=90°，∴FG=2AF=4，∴AG =在△ADE 和△GCE 中，∵∠AGF =∠DAE =30°．∠CEG =∠AED ，DE =CE ，∴△ADE ≌△GCE ．∴AE=GE∴EF ==【点睛】本题主要考查了垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理，熟练掌握垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质是解题的关键．2．（2022·广西·中考真题）如图，在ABC V 中，AB AC =，以AC 为直径作O e 交BC 于点D ，过点D 作DE AB ^，垂足为E ，延长BA 交O e 于点F ．(1)求证：DE 是O e 的切线(2)若2,103AE AF DE ==，求O e 的半径．【答案】(1)见解析(2)13【解析】【分析】（1）连接OD ，只要证明OD ⊥DE 即可；（2）连接CF ，证OD 是△ABC 的中位线，得CF =2DE ，再证DE 是△FBC 的中位线，得CF =2DE ,设AE =2x ，DE =3k ，则CF =6k ，BE =EF =AE +AF =2k +10，AC =BA =EF +AE =4k +10，然后在Rt △ACF 中，由勾股定理，得 (4k +10)2=102+(6k )2，解得：k =4，从而求得AC =4k +10=4×4+10=26，即可求得O e 的半径OA 长，即可求解．(1)证明：连接OD；∵OD=OC，∴∠C=∠ODC，∵AB=AC，∴∠B=∠C，∴∠B=∠ODC，∴OD∥AB，∴∠ODE=∠DEB；∵DE⊥AB，∴∠DEB=90°，∴∠ODE=90°，即DE⊥OD，∴DE是⊙O的切线．(2)解：连接CF，由（1）知OD⊥DE，∵DE⊥AB，∴OD∥AB，∵OA=OC，∴BD =CD ，即OD 是△ABC 的中位线，∵AC 是O e 的直径，∴∠CFA =90°，∵DE ⊥AB ，∴∠BED =90°，∴∠CFA =∠BED =90°，∴DE ∥CF ，∴BE =EF ，即DE 是△FBC 的中位线，∴CF =2DE ,∵23AE DE =，∴设AE =2x ，DE =3k ，CF =6k ，∵AF =10，∴BE =EF =AE +AF =2k +10，∴AC =BA =EF +AE =4k +10，在Rt △ACF 中，由勾股定理，得AC 2=AF 2+CF 2，即(4k +10)2=102+(6k )2，解得：k =4，∴AC =4k +10=4×4+10=26，∴OA =13,即O e 的半径为13．【点睛】本题考查圆周角定理，切线的判定与性质，勾股定理，三角形中位线的判定与性质，证OD 是△ABC 的中位线， DE 是△FBC 的中位线是解题的关键．考点六应用切线长定理求解例题：（2022·湖北·武汉一初慧泉中学九年级阶段练习）如图，在四边形ABCD 中，,,AD BC AB BC O ^P e 是四边形ABCD 的内切圆，,CD BC 分别切O e 于F ，E 两点，若3,6AD BC ==，则EF 的长是（）A B C D 【答案】A【解析】【分析】作DG ⊥BC 于点G ，连接OC 、OE ，根据切线长定理可得CE =CF ，OC 平分∠ECF ，DF =DH ，所以OC 垂直平分EF ，令OC 、EF 相交于点M ，则EM =FM ，设圆半径为R ，则DG =2R ，CG =3，CD =6-R +3-R ，根据勾股定理可求出R ，再利用1122OEC S OE CE OC EM =×=×V 求出EM 即可求得EF ．【详解】连接OC ，与EF 相交于点M ，作DG ⊥BC 于点G ，连接OE ，设AD 与圆的切点为H ，如图，∵,,AD BC AB BC DG BC ^^∥，∴四边形ABGD 是矩形，∴BG =AD =3，CG =BC -BG =6-3=3，∵点E 、F 、H 是切点，∴DF =DH ，CF =CE ，OC 平分∠ECF ，∴△ECF 是等腰三角形，OC 是EF 的垂直平分线，∴EM =FM ，设圆O 半径为R ，则BE =R ，DG =2R ，，∴CE =CF =6-R ，DF =DH =3-R ，∵222DG CG CD +=，∴()()()22223[36]R R R +=-+-解得：R=2，∴CE=6-2=4，∴OC∵1122OECS OE CE OC EM=×=×V，∴OE CEEMOC×==∴22EF EM==故选A．【点睛】本题考查了切线长定理，充分利用切线长定理求解相关线段长度是解题关键．【变式训练】1．（2022·辽宁·黑山县教师进修学校二模）如图所示，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD＝OB，连接AD．∠DAC＝78°，那么∠AOD等于_____度．【答案】64【解析】【分析】由已知条件推导出∠CAO=∠OAB=∠BAD，∠ABD=90°，由此根据∠DAC=78°，能求出∠AOD的大小．【详解】解：∵AB、AC为⊙O的切线，B和C是切点，BD=OB，AB\垂直平分OD,∠CAO=∠OABAO AD\=\∠OAB=∠BAD，∴∠CAO=∠OAB=∠BAD，∠ABD=90°，∵∠DAC=78°，∴∠BAO =13∠DAC =26°，∴∠AOD =90°-26°=64°．故答案为：64．【点睛】本题考查角的大小的求法，解题时要认真审题，注意切线性质的灵活运用是解题的关键．2．（2022·天津河东·二模）已知AB 是O e 直径，PC ，PB 分别切O e 于点C ，B ．(1)如图①，若58A Ð=°，求P Ð的度数；(2)如图②，延长OB 到点D ，使BD OB =，连接PD ，若81DPC Ð=°，求D Ð的度数．【答案】(1)64°(2)63°【解析】【分析】（1）连接OC ，根据切线的性质得到∠PCO =∠PBO =90°，根据等腰三角形的性质得到∠A =∠ACO =58°，根据三角形外角的性质和四边形的内角和定理即可得到结论；（2）连接OP ，根据切线的性质得到∠CPO =∠BPO ，∠PBO =90°，证明PB 是OD 的垂直平分线，可得∠OPB =∠DPB =∠CPO ，进而可以解决问题．(1)解∶如图，连接OC ，∵PC ，PB 分别切OO 于点C ，B ，AB 是直径，∴∠PCO =∠PBO =90°，∵OC =OA ，∴∠A =∠ACO =58°，∴∠BOC =∠A +∠ACO =116°，∴∠P =360°-90°-90°-116°=64°；(2)解：如图，连接OP ，∵PC ，PB 分别切OO 于点C ，B ，AB 是直径，∴∠CPO =∠BPO ，∠PBO =90°，∵BD =OB ，∴PB 是OD 的垂直平分线，∴PO =PD ，∴∠OPB =∠DPB ，∴∠OPB =∠DPB =∠CPO ，∵∠DPC =81°，∴∠OPB =∠DPB =∠CPO =27°，∴∠D =90°-27°=63°．【点睛】本题考查了切线的性质，等腰三角形的性质，正确地作出辅助线是解题的关键．考点七应用切线长定理证明例题：（2022·北京·首都师范大学附属中学九年级阶段练习）如图，Rt ABC V 中，90ABC Ð=°，O 为BC 上一点，以O 为圆心，OB 长为半径的圆恰好与AC 相切于点D ，交BC 于点E ，连接DO ，并延长交于O e 点F ．(1)求证：BAO F Ð=Ð；(2)若3AD =，2CD =，求O e 的半径及EF 的长．【答案】(1)见解析(2)O e 的半径为1.5，EF =【解析】【分析】（1）连接DE ，根据切线长定理可得∠BAO =∠DAO ，∠PDC =90°，从而得到∠BAO =12∠BAD ，从而得到∠BAO =12()1902C COD °-Ð=Ð=∠F ，即可求证；（2）根据切线长定理可得AB =AD =3，再由勾股定理可得BC =4，设O e 的半径为x ，则OD =x ，OC =4-x ，在Rt COD V 中，由勾股定理可得O e 的半径为1.5，由（1）可得1tan tan 2F BAO =Ð=，在Rt DEF △中，由勾股定理，即可求解．(1)证明：如图，连接DE ，∵90ABC Ð=°，∴AB 与O e 相切，∵AD 与O e 相切，∴∠BAO =∠DAO ，∠PDC =90°，∴∠BAO =12∠BAD ，∵∠BAD =90°-∠C ，∠C =90°-∠COD ，∴∠BAO =12()1902C COD °-Ð=Ð=∠F ；(2)解：∵AB 与O e 相切，AD 与O e 相切，∴AB =AD =3，∵CD =2，∴AC =5，∴BC =4，设O e 的半径为x ，则OD =x ，OC =4-x ，在Rt COD V 中，由勾股定理得：222OD CD OC +=，∴()222x 24x +=-，解得：x =1.5，∴O e 的半径为1.5，即OB =1.5，∵DF 为直径，DF =3，∴∠DEF =90°，∵BAO F Ð=Ð，∴ 1.51tan tan 32OB F BAO AB =Ð===，∴EF =2DE ，在Rt DEF △中，由勾股定理得：222DF DE EF =+，∴222132EF EF æö=+ç÷èø，解得：EF =EF =（舍去）．【点睛】本题主要考查了切线长定理，圆周角定理，勾股定理，熟练掌握切线长定理，圆周角定理是解题的关键．【变式训练】（2022·广东·模拟预测）如图，AB 是⊙O 直径，BC ⊥AB 于点B ，点C 是射线BC 上任意一点，过点C 作CD 切⊙O 于点D ，连接AD ．(1)求证：BC＝CD；(2)若∠C＝60°，BC＝3，求AD的长．【答案】(1)见解析【解析】【分析】（1）根据切线长定理证明即可；△是等边三角形，根据直径所对的圆周角是直角，含30度角的直角三角形的（2）根据已知条件可得BCD性质，勾股定理求解即可．(1)证明：∵AB是⊙O直径，BC⊥AB于点B，\CB是Oe的切线，e的切线，Q CD是O\=CD CB(2)OD OC，DB，连接,Q ,CD CB 是O e 的切线，DCB Ð60=°， BC ＝3，DBC \△是等边三角形，60DBC \Ð=°，3BC DB ==AB BC^Q 30ABD \Ð=°Q AB 是直径\ 90ADB Ð=°12AD AB \=DB \=\AD DB ==【点睛】本题考查了切线长定理，切线的性质，直径所对的圆周角是直角，含30度角的直角三角形的性质，等边三角形的性质与判定，勾股定理，掌握圆的切线的性质是解题的关键．一、选择题1．（2022·黑龙江哈尔滨·三模）如图，PA 、PC 是⊙O 的两条切线，点A 、C 为切点，点B 为⊙O 上任意一点，连接AB 、BC ，若∠B =52°，则ÐP 的度数为（）．A ．68°B ．104°C ．70°D ．76°【答案】D 【解析】【分析】利用同弧所对的圆周角等于所对圆心角的一半求出∠AOC的度数，再根据切线的性质以及四边形的内角和即可求出∠P的度数．【详解】解：连接OA、OC，如图：∵∠B=52°，∴∠AOC=2∠B=104°，∵PA、PB是⊙O的切线，∴OA⊥AP，OC⊥CP，∴∠OAP=∠OCP=90°，∴∠P =360°-（∠OAP+∠OCP+∠AOC）=76°，故选：D．【点睛】此题考查了切线的性质，圆周角定理以及四边形的内角和，熟练掌握切线的性质是解本题的关键．2．（2021·辽宁抚顺·九年级阶段练习）矩形ABCD中，AB＝8，BC＝4，点P在边AB上，且AP＝3，如果⊙P是以点P为圆心，PD为半径的圆，那么下列判断正确的是（）A．点B、C均在⊙P内B．点B在⊙P上、点C在⊙P内C．点B、C均在⊙P外D．点B在⊙P上、点C在⊙P外【答案】D【解析】【分析】如图所示，连接DP，CP，先求出BP的长，然后利用勾股定理求出PD的长，再比较PC与PD的大小，PB与PD的大小即可得到答案．【详解】解：如图所示，连接DP，CP，∵四边形ABCD是矩形，∴∠A=∠B=90°，∵AP=3，AB=8，∴BP=AB-AP=5，∵5PD==，∴PB=PD，∴PC PB PD>=，∴点C在圆P外，点B在圆P上，故选D．【点睛】本题主要考查了点与圆的位置关系，勾股定理，矩形的性质，熟知用点到圆心的距离与半径的关系去判断点与圆的位置关系是解题的关键．3．（2022·重庆八中二模）如图，OA是⊙О的一条半径，点P是OA延长线上一点，过点P作⊙O的切线PB，点B为切点．若PA=1，PB=2，则半径OA的长为（）A．43B．32C．85D．3【答案】B 【解析】【分析】由题意得， PBO V 是直角三角形，设OA =x ，则OB =x ，在Rt PBO V 中，1PO x =+，根据勾股定理得，2222(1)x x +=+，解得32x =，即可得．【详解】解：由题意得，1PA =，2PB =，90PBO Ð=°，∴PBO V 是直角三角形，设OA =x ，则OB =x ，在Rt PBO V 中，1PO x =+，根据勾股定理得，2222(1)x x +=+22421x x x +=++解得32x =，则半径OA 的长为32，故选B ．【点睛】本题考查了圆，勾股定理，解题的关键是掌握这些知识点．4．（2022·重庆·三模）如图，PA 、PB 是⊙O 的切线，A 、B 是切点，点C 在⊙O 上，且∠ACB =63°，则∠APB 等于（）A ．62°B ．54°C ．53°D ．63°【答案】B【解析】【分析】先由圆周角定理求出∠AOB =126°，根据切线的性质得到∠OBP =∠OAP =90°，再利用四边形内角和定理求解即可．【详解】解：∵∠ACB=63°，∴∠AOB=2∠ACB=126°，∵PA、PB都是圆O的切线，∴∠OBP=∠OAP=90°，∴∠APB=360°-∠AOB-∠OBP-∠OAP=54°，故选：B．【点睛】本题主要考查了圆周角定理，切线的性质，四边形内角和定理，熟知切线的性质与圆周角定理是解题的关键．5．（2022·重庆·模拟预测）如图，PM、PN是⊙O的切线，B、C是切点，A、D是⊙O上的点，若∠P＝44°，∠D＝98°，则∠MBA的度数为（）A．38°B．28°C．30°D．40°【答案】C【解析】【分析】根据切线的性质得到PB＝PC，根据等腰三角形的性质得到∠PBC＝∠PCB＝12´（180°﹣44°）＝68°，根据圆内接四边形的性质得到∠ABC＝180°﹣∠D＝82°，于是得到结论．【详解】解：∵PM，PN是⊙O的切线，∴PB＝PC，∵∠P＝44°，∴∠PBC＝∠PCB＝12´（180°﹣44°）＝68°，∵∠D＝98°，∴∠ABC＝180°﹣∠D＝82°，∴∠MBA＝180°﹣∠PBC﹣∠ABC＝30°，故选：C．【点睛】本题主要考查了切线的性质、切线长定理、等腰三角形的性质以及圆内接四边形的性质，熟练掌握切线长定理是解题的关键．二、填空题6．（2022·湖南怀化·中考真题）如图，AB与⊙O相切于点C，AO=3，⊙O的半径为2，则AC的长为_____．【解析】【分析】根据切线的性质得到∠OCA=90°，再利用勾股定理求解即可．【详解】解：连接OC，∵AB与⊙O相切于点C，∴OC⊥AB，即∠OCA=90°，在Rt△OCA中，AO=3 ，OC=2，∴AC=【点睛】本题考查了切线的性质，勾股定理，熟练掌握切线的性质是解题关键．切线的性质：圆的切线垂直于经过切点的半径．7．（2021·江苏泰州·九年级期中）已知⊙O与点P在同一平面内，若⊙O的半径为6，线段OP的长为4，则点P与⊙O的位置关系是_________．【答案】点P在⊙O内【解析】【分析】比较⊙O的半径为r与点P到圆心的距离的大小，进而判断点与圆的位置关系．【详解】解：∵⊙O的半径为6，线段OP的长为4，∴⊙O的半径＞线段OP的长，∴点P在⊙O内，故答案为：点P在⊙O内．【点睛】本题考查的是点与圆的位置关系有3种．设⊙O的半径为r，点P到圆心的距离OP＝d，则有：①点P在圆外⇔d＞r；②点P在圆上⇔d＝r；③点P在圆内⇔d＜r．8．（2022·浙江·九年级专题练习）如图，切线PA、PB分别与⊙O相切于点A、B，切线EF与⊙O相切于点C，且分别交PA、PB于点E、F，若△PEF的周长为6，则线段PA的长为_____．【答案】3【解析】【分析】通过切线长定理将相等的线段进行转换，得出三角形PEF的周长等于PA+PB=6，又因为PA=PB，所以可求出PA 的长．【详解】解：∵EA ，EC 都是圆O 的切线，∴EC ＝EA ，同理FC ＝FB ，PA ＝PB ，∴△PEF 的周长＝PF +PE +EF ＝PF +PE +EA +FB ＝PA +PB ＝2PA ＝6，∴PA ＝3；故答案为：3．【点睛】本题考查的是切线长定理，解此题的关键是得出△PEF 的周长=PA +PB ．9．（2022·江苏·星海实验中学二模）如图，在矩形ABCD 中，4AB =，3AD =，M ，N 分别是BC ，DC 边上的点，若O e 经过点A ，且与BC ，DC 分别相切于点M ，N ，则O e 的半径为______．【答案】7-7-【解析】【分析】连接OM ，ON ，OA ，延长NO 交AB 于点E ，设O e 的半径为r ，根据切线的性质可得OM ⊥BC ，ON ⊥CD ，可得四边形BMOE 、四边形OMCN 都为矩形，从而得到BE =OM =r ，OE =BM ，CM =ON =r ，进而得到OE =BM =BC -MC =3-r ，AE =AB -BE =4-r ，再由勾股定理，即可求解．【详解】解：如图，连接OM ，ON ，OA ，延长NO 交AB 于点E ，设O e 的半径为r ，∵O e 与BC ，DC 分别相切于点M ，N ，∴OM ⊥BC ，ON ⊥CD ，在矩形ABCD 中，AB ∥CD ，∠B =∠C =90°，∴NE ⊥AB ，∴∠AEN =∠BEN =90°，∴四边形BMOE 、四边形OMCN 都为矩形，∴BE =OM =r ，OE =BM ，CM =ON =r ，∴OE =BM =BC -MC =3-r ，AE =AB -BE =4-r ，在Rt △AOE 中，（3-r ）2+（4-r ）2=r 2，解得： 1277r r =-=+（舍去），∴O e 的半径为7-故答案为：7-【点睛】本题主要考查了切线的性质，矩形的判定和性质，勾股定理，熟练掌握切线的性质，矩形的判定和性质，勾股定理是解题的关键．10．（2022·浙江金华·中考真题）如图，木工用角尺的短边紧靠⊙O 于点A ，长边与⊙O 相切于点B ，角尺的直角顶点为C ，已知6cm,8cm AC CB ==，则⊙O 的半径为_____cm ．【答案】253##183【解析】【分析】设圆的半径为rcm ，连接OB 、OA ，过点A 作AD ⊥OB ，垂足为D ，利用勾股定理，在Rt △AOD 中，得到r 2＝（r −6）2＋82，求出r 即可．【详解】解：连接OB 、OA ，过点A 作AD ⊥OB ，垂足为D ，如图所示：∵CB 与O e 相切于点B ，∴OB CB ^，∴90CBD BDA ACB Ð=Ð=Ð=°，∴四边形ACBD 为矩形，∴8AD CB ==，6BD AC ==，设圆的半径为rcm ，在Rt △AOD 中，根据勾股定理可得：222OA OD AD =+，即r 2＝（r −6）2＋82，解得：253r =，即O e 的半径为253cm ．故答案为：253．【点睛】本题主要考查了切线的性质，矩形的判定和性质，勾股定理，作出辅助线，构造直角三角形，利用勾股定理列出关于半径r 的方程，是解题的关键．三、解答题11．（2021·全国·九年级课时练习）已知A 为O e 上的一点，O e 的半径为1，O e 所在的平面上另有一点P ．（1）如果PA =P 与O e 有怎样的位置关系？（2）如果PA =P 与O e 有怎样的位置关系？【答案】（1）点P 在O e 外；（2）点P 可能在O e 外，也可能在O e 内，还可能在O e 上，实际上，点P 位于以A 【解析】【分析】（1）点P 和圆的位置关系有：①在圆外，②在圆上，③在圆内，再逐个判断即可；（2）点P 和圆的位置关系有①在圆外，②在圆上，③在圆内，再逐个判断即可．【详解】解：（1）PA =Q ，O e 的直径为2\点P 的位置只有一种情况在圆外，即点P 与O e 的位置关系是点在圆外．（2）PA =Q O e 的直径为2\点P 的位置有三种情况：①在圆外，②在圆上，③在圆内．即点P 可能在O e 外，也可能在O e 内，还可能在O e 上，实际上，点P 位于以A 圆上．【点睛】本题考查了圆的认识的应用，解题的关键是做注意多种情况的考虑，注意：点和圆有三种位置关系：点在圆外，点在圆上，点在圆内．12．（2022·辽宁葫芦岛·三模）如图，正方形ABCD 的边长AD 为O e 的直径，E 是AB 上一点（不与A ，B 重合），将正方形的一个角沿EC 折叠，使得点B 恰好与圆上的点F 重合．(1)判断直线CF 与O e 的位置关系？并说明理由；(2)若O e 的半径为1，求AE 的长？【答案】(1)见解析(2)43【解析】【分析】（1）如图所示，连接OF ，OC ，只需要证明△OCF ≌△OCD 得到∠OFC =∠ODC =90°，即可得到结论；（2）先证明O 、E 、F 三点共线，设AE =x ，则BE =AB -AE =2-x ，OE =OF +EF =3-x ，在Rt △AEO 中，由勾股定理得到222AE OA OE +=，则()22213x x +=-，据此求解即可．(1)解：直线CF 与圆O 相切，理由如下：如图所示，连接OF ，OC ，由折叠的性质可知，CF =BC ，∵四边形ABCD 是正方形，∴CD =BC ，∠ODC =90°，∴CF =CD =BC ，∵AD 是圆O 的直径，F 在圆O 上，∴OF =OD ，又∵OC =OC ，∴△OCF ≌△OCD （SSS ），∴∠OFC =∠ODC =90°，∴直线CF 与圆O 相切；(2)解：∵AD 是圆O 的直径，圆O 的半径为1，四边形ABCD 是正方形，。

87.专题十三第5练有机合成综合-2021高考化学选择题常考易错100练(解析版)

专题十三有机化学基础第5练有机合成综合1．某栏目报道一超市在售的鸡蛋为“橡皮弹”，煮熟后蛋黄韧性胜过乒乓球，但经检测为真鸡蛋。

专家介绍，该是由于鸡饲料里添加了棉籽饼，从而使鸡蛋里含有过多的棉酚所致。

已知棉酚的结构简式如图所示，下列说法正确的是A．棉酚的一氯代物有3种B．棉酚能与溴水发生加成反应C．1mol棉酚最多与10mol H2反应D．1mol棉酚最多与6 molNaOH反应【答案】D【解析】A．分子中氢原子种类超过3种，则一氯代物超过3种，故A错误；B．不含碳碳双键，与溴水不发生加成反应，故B错误；C．能与氢气发生加成反应的为醛基、苯环，由结构可知，含4个苯环结构2个-CHO，则能与12molH2加成，故C错误；D．含6个酚-OH，与6molNaOH反应，故D正确。

2．左氧氟沙星是一种广谱抗菌药物，其结构简式如图，则对左氧氟沙星说法正确的是A．分子式为C18H18FN3O4B．1 mol左氧氟沙星和足量Na反应生成11.2LH2C．左氧氟沙星含有3种含氧官能团D．该有机物能使KMnO4溶液、溴水褪色，原理相同【答案】C【解析】A．由结构简式可知分子式为C18H20FN3O4，故A错误；B．气体存在的条件未知，不能确定体积大小，故B错误；C．含有官能团为羧基、羰基、醚键，故C正确；D．含有碳碳双键，可与溴水发生加成反应，与酸性高锰酸钾发生氧化反应，故D错误。

3．劣质洗发水中含有超标致癌物二噁烷()。

关于该化合物的说法正确的是A ．1mol 二噁烷完全燃烧消耗5molO 2B ．与互为同系物C ．核磁共振氢谱有4组峰D ．分子中所有原子均处于同一平面【答案】A 【解析】A.二噁烷的分子式为C 4H 8O 2，完全燃烧后生成二氧化碳和水，1mol 二噁烷完全燃烧消耗5molO 2，故A 正确；B. 二噁烷中含有2个氧原子，与组成上并非只相差n 个CH 2原子团，所以两者不是同系物，故B 错误；C. 根据二噁烷的结构简式可知，其分子中只有一种化学环境的氢原子，故核磁共振氢谱只有1组峰，C 错误；D. 分子中碳原子都是sp 3杂化，所以所有原子不可能处于同一平面，故D 错误。