运筹学第三章
运筹学PPT——第三章

第三章整数规划Integer Programming§1问题的提出[eg.1]用集装箱托运货物问:甲乙货物托运多少箱,使总利润最大?货物m3/箱百斤/箱百元/箱甲5220乙4510限制2413分析:设x1为甲货物托运箱数,x2为乙货物托运箱数。
则max z= 20x1+10x25x1+4x2≤242x1+5x2≤13x 1,x2≥0x 1,x2取整数图解法:x 1x 24321012 4.8①2.6②(4,1)∴x 1*= 4 x 2*= 1 z I *= 90一般,整数规划的最优解不会优于相应线性规划的最优解。
对于max 问题,z I * ≤z l *对于min 问题,z I *≥ z l *数学模型:取整数j j nj iijij nj jj x nj x m i b xa x c z ,,10,,1max 11 =≥=≤=∑∑==§2 分枝定界法用单纯形法,去掉整数约束IP LP xl*判别是否整数解x I *= xl*Yes去掉非整数域No多个LP……§3 0-1规划(xi= 0或1的规划)[eg.2]选择投资场所A i 投资Bi元,总投资≤B,收益Ci元.问:如何选择Ai ,使收益最大?A6A7A4A5A3A2A1最多选2个最少选1个最少选1个分析:引入xi= 1 A i选中0 Ai落选max z= C1x1+C2x2+… +C7x7x 1+x2+x3≤2x 4+x5≥1x 6+x7≥1B 1x1+B2x2+… +B7x7≤Bx i = 0或1南区西区东区[eg.3]求解如下0-1规划max z= 3x1-2x2+5x3x1+2x2-x3≤2 ①x 1+4x2+x3≤4 ②x 1+x2≤3 ③4x2+x3≤6 ④x 1,x2,x3= 0或1解:(1)观察一个可行解x1= 1 x2= x3= 0此时,z= 3(2)增加一个过滤条件3x1-2x2+5x3≥3 *(3)列表计算x x x *可行?z0015√51003110√3123①②③④0000×-1115010-2×01131×110180211√81101×111626×∴ 最优解:x 1*= 1 x 2*= 0 x 3*= 1 此时,z *= 8第四章。
运筹学-3运输问题

产大于销 销大于供
当产销平衡时,其模型如下:
当产大于销时,其模型是:
mn
min Z
cij xij
i1 j1
xij ai xij bj
xij
0
( ai bj)
当销大于产时,其模型是:
min Z
cij xij
xij ai xij bj
可行解的方法
Review
二、表上作业法的步骤
Step1.找出初始基本可行解(在m*n产销平衡 表上寻找初始调运方案,一般m+n-1个数字 格),用最小元素法、西北角法、伏格尔法;
Step2.求出各非基变量的检验数,判别是否达 到最优解。如果是停止计算,否则转入下一步, 用闭回路或位势法计算;
Step3.改进当前的基本可行解(确定换入、 换出变量),用闭合回路法调整; Step4.重复2. 3,直到找到最优解为止。
(3)运输问题的解
定义1. 闭回路
x x x x x x 闭回路是能折成 i1 j1, i1 j2 , i2 j2 , i2 j3 ,..., isjs , isj1
形式的变量组集合。其中 i1 , i2 , …, is 互不相同,j1 , j2 , …, js 互不相 同。每个变量称为闭回路的顶点,连接闭回路相邻两顶点的直线段叫做闭
统计学院
运筹学-第三章 运输问题
张红历
本章内容
1.运输问题及其数学模型 2.表上作业法 3.运输问题的进一步讨论
4.应用问题举例
第一节 运输问题及其数学模型
一、运输问题的提出
例:某运输问题的资料如下:
单位 销地 运价
产地
A1 A2 A3
销量
运筹学第三章 运输问题

销地 产地 A1
A2
B1
B2
B3
B4
产量
6
5 3
3 1
4
4
2
A3
销量 2
4 7
1 3
4
4 6
3
7 5
3
5
6
8
4 3 13
σ11=-3, σ12=-2,σ23=-4, σ31=-1,σ33=1, σ34=-1
销地 产地 A1
A2
B1
B2
B3
B4
产量
6
5 0
3 4
4
4
2
A3
销量 2
4 7
4
4 6
3
4 3
5
3
4
3
4 7
1
5
4 6
A3 销量 2
7
0
4
6
3
5
3
4
8
3 13
x11检验数为 6-4+8-6+4-4=4
销地 产地 A1
A2
B1
B2
B3
B4
产量
6 4 2 4
5
3
4
3
4 7
1
5
4 6
A3 销量 2
7
0
4
6
3
5
3
4
8
3 13
x12检验数为 5-4+8-6=3
销地 产地 A1
A2
B1
B2
B3
B4
产量
2、位势法 当运输问题变量的格数较多时,用闭 回路法计算检验数比较麻烦,而位势法比 较简便。 对于运输问题 minf=CX AX=b X≥0 设B为其一个可行基,则xij的检验数为 σ ij=CBB-1Pij-Cij
运筹学第三章TP

收点 B1 发点 A1 6 A2 42 A3 7 收量 2
kj 2
B2 B3 B4 发量 hi
5 33 4 4 11 4 7 5 6 11 6 58 32 4 3 4 13 1 21
Operations Research
收 点 B1 B2 B3 B4 发 量 hi 发点 A 1 6 5 3 3 4 4 11 A 2 4 2 4 7 5 6 11 A 3 7 63 5 8 3 2 收 量 2 4 3 4 13
收 点 B1 B2 B3 B4 发 量 发点
A1 6 2 5
34
4
A2 4
4
75
6
A3 7
6
58
3
收 量 2 4 3 4 13
Operations Research
(2)向a1,b1较大方向移动一格(或向 右,或向下)此时向右移动一格(A1,B2) B2需要4吨,而A1只有2吨,A1已发完,划 去A1行,并把b2改成(4-2)=2。
A 2 42 41 7 53 6
A 3 7 63 5 8 3 收 量 2 4 3 4 13
kj
Operations Research
西北角法得到初始方案:x11=2,x12=2, x22=2,x23=3,x24=1,x34=3,总运费 =6*2+5*2+4*2+7*3+5*1+8*3=80(元)
最小元素法得到初始方案:x13=3,x14=1, x21=2,x22=4,x34=3,总运费 =3*3+4*1+4*2+4*4+8*3=61(元)
Operations Research
运输问题的图表形式
Ai Bj
运筹学 第三章 运输问题

这样可以保证填过数或零的格为m+n-1个,即保证基变量的个数为 m+n-1个。
2021/3/14
14
2.Vogel法
Vogel法的思想是:一地的产品如果不能按照最小运
费就近供应,就考虑次小运费,这就有差额,差额越大, 说明不能按最小运费调运时,运费增加得越多。因而差 额越大处,就应当采用最小运费调运。
同理可以求得 v4=10,u2= -1,等等见上表。
检验数的求法,即用公式 ijciju,i vj
如 1 1 c 1 1 u 1 v 1 3 0 2 1 。
2021/3/14
23
位势法计算检验数:
检验数: ijcijCBB1Pij
cijYiP jcij(u1,..u.m , ,v1,.v.n.)Pij
3
B4
ui
3 10
0
-1 8
-1
35
-5
10
B1
3
31
7
2
B2
11 9
64
9
B3
4(+1) 3 1 (-1) 2
10
3
B4
ui
3(-1) 10
0
+1 8
-1
35
-5
10
2021/3/14
26
调整运量后的新方案:
销地
产地
B1
A1
A2
3
A3
B2
B3
5
6
销量
3
6
5
B4
产量
2
7
1
4
3
9
运筹学——第3章_线性规划问题的计算机求解
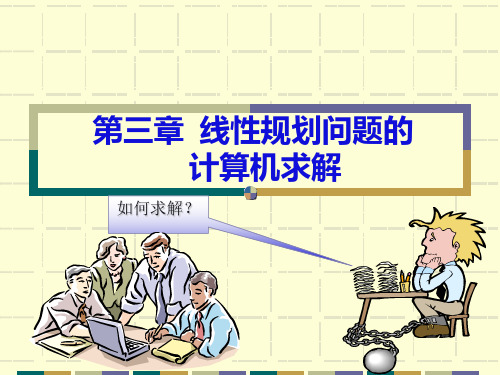
变量 下限 当前值 上限
x1
0
50
100
x2
50
100 无上限
从上面可知目标函数中X1的系数的上限为100,故C1
允许增加量为: 上限-现在值=100-50=50;
而X2的下限为50,故C2的允许减少量为: 现在值-下限=100-50=50。
定义Ci 的允许增加(减少)百分比为:Ci 的增加量 (减少量)除以Ci 的允许增加量(允许减少量)的值。
在上题中C1 的允许增加百分比与C2 的允许减 少百分比之和为92%不超过100%,所以当每件产 品Ⅰ利润从50元增加到74元,每件产品Ⅱ利润从 100元减少到78元时,此线性规划最优解仍然为Ⅰ 产品生产50件, Ⅱ产品生产250件(即x1= 50, x2=250),此时有最大利润为:
74× 50+78× 250=3700+19500=23200(元)。
为50元,即增加了一个台时数就可使总利润增加50元;
原料A还有50千克没有使用,原料A的对偶价格当然为零,
即增加1千克A原料不会使总利润有所增加;原料B全部使
用完,原料B的对偶价格为50元,即增加一千克原料B就
可使总利润增加50元。
在目标函数系数范围一栏中,所谓的当前值是指在目标函数 中决策变量的当前系数值。如x1的系数值为50,x2的系数值为100。 所谓的上限与下限值是指目标函数的决策变量的系数(其它决策 变量的系数固定在当前值)在此范围内变化时,其线性规划的最 优解不变。例如当c1= 80时,因为0≤80≤100,在x1的系数变化范 围内,所以其最优解不变(此时要固定c2=100),也即当x1=50, x2=250时,有最大利润。当然由于产品Ⅰ的单位利润由50变为80 了,其最大利润也增加了(最优值变了),
运筹学-第三章-整数规划

于是,对原问题增加两个新约束条件,将原问题分为两个 子问题,即有
max z 40x1 90x2
max z 40x1 90x2
9x1 7x2 56
s.t
7 x1
20 x2
70
x1 4
x1, x2 0
(LP1)
9x1 7x2 56
和
s.t
7
x1
20
x2
70
(LP2)
x1 5
表 3.1
货物 体积(米 3/箱) 重量(百公斤/箱) 利润(百元/箱)
甲
5
2
20
乙
4
5
10
托运限制 24 米 3
13 百公斤
解: 设x1,x2 分别为甲、乙两种货物的托运箱数,则数 学模型可以表示为:
max z 20x1 10x2
5x1 4x2 24 2x1 5x2 13 x1, x2 0, x1, x2整数
其中,目标函数表示追求最大的卫星实验价值;第1,2个约
束条件表示体积和重量的限制;第3-5个约束条件表示特定的卫
星装载要求,该问题的决策变量是0-1整数变量。
3.2.3隐枚举法 从上面两个例子可以看出,此类型问题是整数规划中的特
殊情形,其中决策变量 xi 的取值只能为0或1,此时变量 xi 称 为0-1变量,这类问题被称为0-1整数规划。对于 xi 的取值的 0-1约束,可以转化成下述整数约束条件:xi 1, xi 0, xi Z
目前对于整数规划问题的求解主要有两种方法:分支 定解法和割平面法。本章仅介绍分枝定界法,该方法在上 世纪60年代由Land Doig和Dakin等人提出,其具有灵活 且便于计算机求解的优点,所以现在已成为解决整数规划 问题的重要方法。下面通过例子说明分支定界方法的算法 思想和步骤。
运筹学 第三章 运输问题

mn
Min Z = cij xij i1 j1 m xij =ai (i=1, ..., m)产量约束 i 1 n xij =bj(j=1, ..., n)销量约束 j1
xij ≥ 0(i=1, ..., m;j=1, ..., n)
15
2. 伏格尔法(Vogel)
例5
销地 产地
A1
B1 3
②
B2
B3
11
3
⑤
B4
ai
10 7 0 0 0 0
1
A2
①
9
2③ 8 4 1 1 1 1
A3
7
4
⑥
10
③
5 9 12 - -
bj
3
6
5
6 20
2513
2 - 13
2 - 12
2-1-
Z=2×3 +1×1+6×4+5×3+3×8+3×5=85 16
0
2.决策变量xij的系数列向量为:
1
i位 置
aij
1
m
j位 置
3. 线性无关的行数为m+n-1.
0
5
四、闭回路
1. 概念
例3
销地 产地
A1
A2
A3 bj
B1
B2
B3
B4
ai
3
11 ④
3 ③
10 7
1 ③
9
2
①
84
7
4
⑥
10 ③
59
3
6
5
6 20
1) 数字格 2) 空格
《运筹学》第三章 运输问题

二、表上作业法
计算步骤:
(1) 找出初始调运方案。即在(m×n)产销平衡表 上给出m+n-1个数字格。(最小元素法、西北角法 或伏格尔法) 确定m+n-1个基变量 (2) 求检验数。(闭回路法或位势法) 判别是 否达到最优解。如已是最优解,则停止计算,否 则转到下一步。 空格 (3)对方案进行改善,找出新的调运方案。 (表上闭回路法调整) (4) 重复(2)、(3),直到求得最优调运方案。
B1 A1 A2 A3 销量 3 1
B2 2
B3 4
B4 3
产量 7 4
3
6 6
1
3 5 6
9
B1 A1 A2 A3 销量 3 1
B2 2
B3 4
B4 3
产量 7 4 9
3
6 6
1
-1
3
5
6
B1 A1 A2 A3 销量 3 1 3
B2 2 1 6 6
B3 4 1
B4 3 -1 3
产量 7 4 9
(ui+vj)
- B2 9 8 4 B3 3 2 -2 B4 10 9 5
A3 -3
σij
B1 = A1 A2 A3 1 0 10 B2 2 1 0 B3 B4 0 0 0 -1 12 0
表中还有负数,说明 还未得到最优解,应 继续调整。 用位势法与用闭回路法 算出的检验数? 相同
3、解的改进
——闭合回路调整法(原理同单纯形法一样) 上例: min( σ ij 0 ) pq
m
n
系数列向量的结构: A ij ( 0, 0, 0 ,, 0, 0 ) 1, 0 1,
第 i个
第 ( m j )个
运筹学第三章 运输问题

8
1.运输问题模型及有关概念
表4-3 运输问题数据表
销地
产地
A1 A2
┇
Am
销量
B1 B2 … Bn
c11
c12 … c1n
c21
c22 … c2n
┇ ┇ ┇┇
cm1
cm2 … cmn
b1
b2 … bn
产量
a1 a2
┇
am
设 xij 为从产地 Ai 运往销地 Bj 的运
式(4-8)中的变量称为这个闭回路的顶点。
22
1.运输问题模型及有关概念
例如,x13, x16, x36, x34, x24, x23 ; x23, x53, x55, x45, x41, x21 ; x11, x14, x34, x31等都是闭回路。
若把闭回路的各变量格看作节点, 在表中可以画出如下形式的闭回路:
得到下列运输量表:
4
1.运输问题模型及有关概念
Min Z s.t.
= 6x11+4x12+6x13+6x21+5x22+5x23 x11+ x12 + x13 = 200
x21 + x22+ x23 = 300
x11 + x21 = 150
x12 + x22 = 150
x13 + x23 = 200
2.每列只有两个 1,其余为 0,分别 表示只有一个产地和一个销地被使用。
7
1.运输问题模型及有关概念
一般运输问题的线性规划模型及求解思路
一般运输问题的提法:
假设 A1, A2,…,Am 表示某物资的m个 产地;B1,B2,…,Bn 表示某物资的n个销地; ai表示产地 Ai 的产量;bj 表示销地 Bj 的 销量;cij 表示把物资从产地 Ai 运往销地 Bj 的单位运价(表4-3)。如果 a1 + a2 + … + am = b1 + b2 + … + bn
运筹学(第三章)课件

i =1
例1:
某市有三个造纸厂A1,A2和A3,其纸的产量分别为 8,5和9个单位。由各造纸厂到各用户的单位运价 如表所示,请确定总运费最少的调运方案。
销地 产地 A1
A2
A3 销量
B1 3 11 6
4
B2 12 2 7
3
B3 3 5 1
5
B4
产量
4 8
9 5
5 9
6
运筹学(第三章)
销地 产地 A1
A2
A3 销量
B1 4
8
2
8
8
B2
12
8
10
6
5
14
B3
4
3
4
11
8
12
B4
产量
11
16 ②
9
10 ④
6
14
22 ⑥
14
48
①
③
⑤
⑥
8×4+8×12 +6×10+4×3+8×11+14×6= 372(元)
运筹学(第三章)
最小元素法——每次找最小元素
销地 产地 A1
A2
A3 销量
B1 4
2
8
8
8
B2 12
价为 cij (i = 1,2,..., m; n = 1,2,..., n) ,又假设产销是平衡的,即:
m
n
ai = b j ,问应如何安排运输可使总运费最小?
i =1
j =1
运筹学(第三章)
二、运输问题的数学模型
假定 xij 表示由 Ai 到 B j 的运输量,则平衡条件下的运输问题可写出
用表上作业法求解运输问题
(教育学)运筹学第3章

03
约束条件可以是等式或 不等式,限制了决策变 量的取值范围。
04
决策变量是问题中需要 优化的未知数。
非线性规划的求解方法
01
02
03
04
非线性规划的求解方法可以分 为直接法和迭代法两大类。
直接法是通过直接搜索和计算 来寻找最优解的方法,如梯度
法、牛顿法等。
迭代法是通过不断迭代和逼近 最优解的方法,如序列二次规
整数规划的数学模型
决策变量
整数规划的决策变量是整数,通常表示为$x_1, x_2, ldots, x_n$。
约束条件
整数规划的约束条件可以是等式或不等式,如$a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或$a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
将大规模问题分解为若干 个小规模问题,分别求解 后再综合,适用于多目标、 多约束问题。
04 整数规划
整数规划的基本概念
整数规划问题
优化目标
整数规划是一类特殊的线性规划问题, 其中一部分或全部决策变量被限制为 整数。
整数规划的目标是最小化或最大化一 个线性目标函数,如成本、收益等。
约束条件
整数规划问题通常具有线性约束条件, 以确保决策变量的取值满足一定的限 制。
划、信赖域方法等。
求解非线性规划问题时,选择 合适的求解方法非常重要,需 要根据问题的性质和规模进行
选择划是一种通过将问题分解为相互重叠的子问题,并存储子问题的解决方案, 以便在需要时重复使用它们的方法。
它是一种优化技术,用于解决多阶段决策问题,其中每个阶段的决策都会影响未来 的决策。
运筹学 第三章 运输问题

1)闭环回路法: 在给出的初始调运方案表上,从每一空格 出发找一条闭环回路,它是以某空格为起点 ,用水平或垂直线向前划,每碰到一数字格 转90°后(回路的转角点必须是一个基变量 ) ,继续前进,直到回到起始空格为止。 从每一空格出发一定存在且只有唯一的闭 环回路。 从空格开始加减闭环各个顶点的运输单价 ,可得每个空格对应的检验数。
《运筹学》
第三章 运输问题
Slide 16
销地
B1
产地
A1
A2
3
A3
销量 3
B2 B3
4 1 6
65
B4 产量
37
4
39
6
销地
产地
B1 B2 B3 B4
A1
3 11 3 10
A2
19 2 8
A3
7 4 10 5
空格 (11) (12) (22) (24) (31) (33)
闭环回路 (11)-(21)-(23)-(13)-(11) (12)-(32)-(34)-(14)-(12) (22)-(32)-(34)-(14)-(13) -(23)-(22) (24)-(14)-(13)-(23)-(24) (31)-(34)-(14)-(13)-(23) -(21)-(31) (33)-(34)-(14)-(13)-(33)
基变量:
X13 U1+V3=C13=3
X14 U1+V4=C14=10
X21 U2+V1=C21=1
1
3 10 U1=0
2
U2=-1
X23 U2+V3=C23=2
4
运筹学第三章
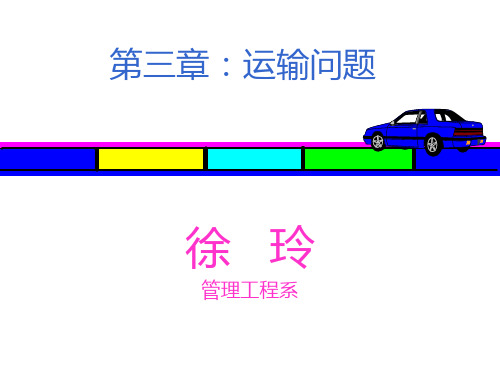
B2
B3
10 2
B4
6
产量
4
11
要保证产销平衡,则
x11 x11 1 x13 x13 1 x23 x23 x x21 1 211 称为闭回路 z z0 4 4 3 2 1,11 1
A 1 A2 A3
销量
B1
4
8
2
8
8
B4 产量 4 6 11 1 6 2 12 3 9 10 1 10 14 5 8 6 22 11 14 12 14 48
几点说明:P88
当检验数为负的变量超过两个,选择最 小者对应的变量换入; 在最优解的表中,若有检验数=0,则该 运输问题有无穷多最优解; 迭代过程中,若某一格填数时需同时划 去一行和一列,此时出现退化。为保证 m+n-1个非空格,需在上述的行或列中 填入数字0(它的位置是在对应这时同时 划去的那行或那列的所有空格处中对应 单位运价最小的任一空格)。
B2
B3 10 2
12 12 11 6 5 2 22 10 3 4 11 6 5 1
检验数表
A 1 A2 A3
销量
B1
1 4 2
8
10
8
8
B4 产量 4 6 11 1 6 2 12 3 -1 9 1 0 1 10 14 5 12 11 8 6 2 2 14 12 14 48
ei 1 0 0
3.2运输问题的解法:表上作业法
Байду номын сангаас
表上作业法是单纯形法在求解运输问题 的一种简便方法。 单纯形法与表上作业法的关系:
(1)找出初始基可行解 表上给出m+n-1个数字格
《运筹学》第三章运输问题

Vogel近似法
考虑运输成本差异, 进行逼近最优解。
运输问题的扩展和变体
1
生产产能约束
考虑生产能力限制,同时优化货物的运输方案。
2
供需不平衡
存在供需不平衡时如何有效分配货物,避免浪费和延误。
3
多目标运输问题
同时考虑多个目标,如最小化成本和最大化利润。
运输问题的应用实例和案例分析
物流领域的应用
通过运输问题的优化,提升物流效率,降低成本。
运输问题的基本模型
运输方案的表示
常用的表示方法包括运输矩阵和网络图。
目标函数和约束条件
目标函数通常是最小化运输成本,约束条件包 括供需平衡和容量限制。
运输问题的解决方法
最小成本法
逐步分配货物,直至 达到最小总成本。
北北角法
按照最小单位运输成 本进行分配,直至l's Approximation Method)法为基础, 逐步分配货物。
《运筹学》第三章运输问 题
运输问题是运筹学中重要的问题之一,涉及到各种场景下的货物运输优化。 本章将介绍运输问题的定义、基本模型、解决方法,以及其在物流和生产调 度中的应用实例。
运输问题的概念和应用领域
• 运输问题是一种优化问题,旨在找到使运输成本最小的货物运输方案。 • 运输问题广泛应用于物流管理、供应链优化以及交通规划等领域。
生产调度中的应用
合理安排生产计划,提高生产线的利用率。
总结和展望
运输问题是优化领域的重要研究方向,未来随着物流技术的发展将有更多的应用场景和解决方法出现。
运筹学第3章

§3.2 表上作业法
运输表上任何有序的至少四个以上 不同格被称为圈, 如果它们满足:
任何两个接续格在同一行或同一列; 在同一行或同一列不存在三个或三个 以上的接续格; 最后一个格应和第一个格在同一行或 同一列。
§3.3 特殊情况的处理
例3·:某农场有四种土壤,面积分别为 6 500亩、1000亩、600亩和500亩,准备将不 同的三个小麦品种播在这四种土壤上。根据 市场需求和本场的具体情况,确定这三个品 种的播种面积分别为400亩、1000亩和1200 亩,又根据过去的生产规律和未来气候的变 化以及生产物资供应的保证情况,用多元回 归方程预测得不同品种的小麦播在不同土壤 上的亩产量(公斤)如后表所示,问怎样安 排播种才能使小麦的总产量最高?
x21 x22 x23 27
s.t.
xij 0, (i 1, 2; j 1, 2,3)
例3·:一般运输问题 2 一般的运输问题可以描述为: 有 m 个供应点, n 个需求点, 第 i 个供应点的 供应量 ai ,第 j 个需求点的需求量 bj , 从 i 到 j的运费为 cij, 求费用最小的运输方 案。
6
35 10
5
0 2
工厂2 25
10
12
7
vj
8
仓库一
5
仓库三
仓库二
ui
工厂1 工厂2
7
15 10
17 +
- 174 0 6
6 12
18 35 - 10+ 27
5
5 7
0 2
25 8
运筹学第三章

3.2.3
销地
产地 A1
解的最优性检验
4 2
+1
第三章 运输问题
B1
+1
B2 12
10
10 -1 6
B3 4
B4
-1
产量 11 9 6
+1
16
A2
A3 销量
8 -1
8
8 14 5
-1
2 +1
12
3
10
22 48
11
8
14
x11 +1
-1 x21
14
x13 -1 x23 +1
11 4 2 3 4 1
第三章 运输问题
设xij为产地i运往销地j的运量
B1 A1 A2
销量
B2 7 3 10
B3 4 2 5
5 7 20
产量 15 20 35 35
B1 A1 A2 x11 x21
B2 x12 x22
B3 x13 x23
min Z 5 x11 7 x12 4 x13 7 x21 3x22 2 x23 x11 x12 x13 15 x x x 20 23 21 22 x11 x21 20 s.t. x12 x22 10 x13 x23 5 xij 0
第三章 运输问题
4. 运输问题的解直接用单纯形法
min Z cij xij
i 1 j 1
m
n
求解,需要增加 m +n 个人工变 量,使变量总数达到(mn +m +n)
n (i 1,2,, m) xij ai j 1 m ( j 1,2,, n) xij b j i 1 xij 0, (i 1,2,, m; j 1,2,, n)
运筹学第三章课后习题答案PPT课件

16
表3-29
销地 B1
B2
B3
B4
产量
产地
A1
3
7
6
4
5
A2
2
4
3
2
2
A3
4
3
8
5
6
销量
3
3
2
2
解:(2)表3-29用三种方法计算,用位势法检验。因 为总产量=13,总销量=10,所以该题的总产量>总销 量,所以该题是产销不平衡的问题,故假设一销地B5 ①用最小元素法计算如下表所示
3.1 与一般线性规划的数学模型相比,运输问题的数 学模型具有什么特征?
答: 与一般线性规划的数学模型相比,运输问题的数 学模型具有如下特征:1.运输问题不象一般线性规划问 题那样,线性规划问题有可能有无穷多最优解,运输问 题只有有限个最优。2.运输问题约束条件系数矩阵的元 素等于0或1;且每一列有两个非零元素。3.运输问题的 解的个数不可能大于(m+n-1)个。 3.2 运输问题的基可行解应满足什么条件?试判断形表 3-26和表3-27中给出的调运方案是否作为表上作业法迭 代时的基可行解?为什么?
17
①最小元素法求解:
销地 B1
B2
4
排运输。这就是最小元素法和沃格尔法质量不同的原因。
3.7 表3-28和表3-29分别给出了各产地和各销地的产量 和销量,以及各产地至各销地的单位运价,试用表上作业 法求最优解。
表3-28
销地 B1
B2
B3
B4
产量
产地
A1
4
1
4
6
8
A2
1
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 2 2 1 6 3
v4 11 6 3 3 v5 17 v6 2
5
一、一般提法:
设有网络D=(V, A, C),其中C={cij}, cij为弧(vi,vj) 上的容量,现在D上要通过一个流f={fij}, fij为弧 (vi,vj)上的流量。 问题:如何安排fij,可使网络D上的总流量V最大?
二、最大流问题的模型
Vs
8 3
Vt
17 2
5
v3
v5
2. 增广链 f为一可行流,u为vs至vt的链,令u+={正向弧}, u-={反向弧}。若u+中弧皆非饱,且u-中弧皆非零,则称 u为关于f的一条增广链。
10
5
v2
3 4 1
5 0 2 1 6 3
v4
11 6 3 3
Vs
8 3
Vt
17 2
5
v3
v5
2. 增广链 f为一可行流,u为vs至vt的链,令u+={正向弧}, u-={反向弧}。若u+中弧皆非饱,且u-中弧皆非零,则称 u为关于f的一条增广链。
2 1 5
7 v3
[4,v2/ v4]
[8,v5]
5 3
v6
5 7
[13,v6]
v7
1
v5[7,v3]
最短路模型的应用——设备更新问题(P120 例 5.3)
第 i年 1 2 价格ai 11 11 3 4 5 12 12 13 使用寿命 0~1 1~2 2~3 3~4 4~5 费用bj 5 6 8 11 18
第三章 图与网络分析
第三章 图与网络分析
3.1 图的基本概念 3.2 最小支撑树问题 3.3 最短路径问题 3.4 网络最大流问题
天津大学管理与经济学部
第三章 图与网络分析
图论起源——哥尼斯堡七桥问题
A C B D C B A D
问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点?
例: G2为G1的支撑子图
v5
v5 v1 v4
v1
v4
v2
G1
v3
v2
G2
v3
天津大学管理与经济学部
第三章 图与网络分析
6、赋权图(网络) 图的每条边都有一个表示一定实际含义的 权数,称为赋权图。记作D=(V,A,C)。
例: 5
v1
3 7.5 5.5 4 2
第三章 图与网络分析
4、连通图
任何两点之间至少存在一条链的图称为连通图, 否则称为不连通图。 例: G1为不连通图, G2为连通图
G1
天津大学管理与经济学部
G2
第三章 图与网络分析
5、支撑子图 图G=(V,E)和G'=(V ' ,E '),若V =V ' 且 E ' E ,则称G' 为G的支撑子图。
3.3 最短路问题
问题:求网络中起点到其它点之间的一条路 v2
2 3 1 2 1
6
v5
2
v8
6 10 3
3
v1
v3 v4
6
4
v9 v7
4
10
v6
2
算法:Dijkstra(狄克斯拉)标号法
基本思想:从起点vs开始,逐步给每个结点vj标号[dj, vi],其中dj为起点vs到vj的最短距离,vi为该最短路线 上的前一节点。
v2
2 [5, v2]
[0, v1]
v1
4
v5
v6
1
2.5 2 4 [9, v7]
[4, v1]
v4
3
[7, v4/ v6] 2
v7
v9 [8.5, v6]
v8
[课堂练习] 无向图情形
求网络中v1至v7的最短路。
v2 2 v1 3 v4 5 2 1 5 7 v3 3 v5 5 v6 1 5 7 v7
v1
3 4 2
v5
v3 3.5 v4
解: 该问题实为求图 的支撑树问题, 共需铺4条路。
v1 v2 v5 v3
v4
v1
三、最小支撑树问题
v2
问题:求网络的支撑树,使其权和最小。 算法(避圈法):把所有的边按权从小到 大排列,依次将边添入图中,若出现圈, 则删去其中最大边,直至填满n-1条边为止 (n为结点数) 。 [例] 求上例中的最小支撑树 v1 解: 5 5.5
v4 v3
第三章 图与网络分析
3、链与路、圈与回路 无向图: 链 有向图: 路
v5 v1 v4 v1
点边交错的序列 圈 起点=终点的链 起点=终点的路
点弧交错的序列 回路
v5 v4
v2
v3
v2
v3
天津大学管理与经济学部
3
v1
1
v3
6
4
v9 v7
4
v4
[1, v1]
10
v6
2
(4) 重复(3),直至终点vn标上号[dn, vi],则dn即为v1→ vn的最短距离,反向追踪可求出最短路。
(1) 给起点v1标号[0, v1] 步骤: (2) 把顶点集V分成
VA:已标号点集 VB:未标号点集
(3) 考虑所有这样的边[vi , vj],其中vi∈VA, vj∈VB,挑选 其中与起点v1距离最短(min{di+cij})的vj,对vj进行标号
例 若V1={vs,v1},则 截集为:{(vs,v2), (v1,v2), (v1,v3), (v1,v4)}; 截量为: C(V1,V2) =8+4+5+3=20
v5
6
2
v8
6 10 3
3
v1
1
v3
2
4
v9 v7
4
v4
[1, v1]
10
v6
2
[5, v3] 6
[0, v1]
v2 v3
2
1 2 [3, v1]
[6, v2]
v5
6
2
v8
6 10 3
3
v1
1
3
4
v9 v7
4
v4
[1, v1]
10
v6
2
[5, v3] [0, v1] 6
[6, v2] 1
v2 v3
10
5
v2
3 4 1
5 0 2 1 6 3
v4
11 6 3 3
Vs
8 3
Vt
17 2
5
v3
v5
2. 增广链 f为一可行流,u为vs至vt的链,令u+={正向弧}, u-={反向弧}。若u+中弧皆非饱,且u-中弧皆非零,则称 u为关于f的一条增广链。
10
5
v2
3 4 1
5 0 2 1 6 3
v4
11 6 3 3
天津大学管理与经济学部
第三章 图与网络分析
1857年英国的哈密尔顿 环球旅行问题
天津大学管理与经济学部
第三章 图与网络分析
3.1 图的基本概念
1. 图 由点和边组成,记作G=(V,E),其中 V=(v1,v2,……,vn)为结点的集 合,E=(e1,e2,……,em) 为边的集 合。 点表示研究对象 边表示研究对象之间的特定关系
二、图的支撑树
若一个图 G =(V , E)的支撑子图 T=(V , E’ ) 构成树,则称 T 为 G的支撑树,又称生成树、部分树。
例
(G1)
(G2)
(G)
(G3)
(G4)
图的支撑树的应用举例 5 [例] 某地新建5处居民点,拟修 道路连接5处,经勘测其道路可铺 v2 7.5 成如图所示。为使5处居民点都有 5.5 道路相连,问至少要铺几条路?
10 5 Vs v2 3 4 1 3 v3 5 5 2 2 1 6 3 3 3 v5 17 v4 116 Vt 2
max v=v(f)
8
0 f ij c ij
s.t.
容量约束
f
ij j j
v( f ) i s f ji v( f ) i t 0 i s, t
v2
v5
v3
天津大学管理与经济学部
3.5
v4
3.2 最小支撑树问题
一、树的概念与性质 树 无圈连通图
例 判断下面图形哪个是树:
(A) 树的性质: 1、树中任两点中有且仅有一条链;
(B)
(C)
2、树任删去一边则不连通,故树是使图保持连通且具有最少边数的一种图形。 3、边数 = 顶点数 – 1。
(1) 给起点v1标号[0, v1] 步骤: (2) 把顶点集V分成
VA:已标号点集 VB:未标号点集
(3) 考虑所有这样的边[vi , vj],其中vi∈VA, vj∈VB,挑选 其中与起点v1距离最短(min{di+cij})的vj,对vj进行标号
[0, v1] 6
v2
2 3 2
1
v5
2
v8
6 10 3
平衡约束
注:满足约束条件的流f称为可行流
三、基本概念与定理
饱和弧 fij=cij
1. 弧按流量分为
非饱和弧 fij<cij 零流弧 fij=0
10
5
v2
3 4 1
5 2 2 1
非零流弧 fij≠0
v4
11 3 3 6
v1
8 3
v6
2 17
5
v3
6 3
v5
2. 增广链 f为一可行流,u为vs至vt的链,令u+={正向弧}, u-={反向弧}。若u+中弧皆非饱,且u-中弧皆非零,则称 u为关于f的一条增广链。
