IIR切比雪夫低通数字滤波器
切比雪夫低通滤波器设计

摘要随着信息和数字时代的到来,数字信号处理已成为当今一门极其重要的学科和技术领域。
在现代通信系统中,由于信号中经常混有各种复杂成分,因此很多信号的处理都是基于滤波器而进行的。
所以,数字滤波器在数字信号处理中起着举足轻重的作用。
而数字滤波器的设计都要以模拟滤波器为基础的,这是因为模拟滤波器的理论和设计方方法都已发展的相当成熟,且有典型的模拟滤波器供我们选择。
,如巴特沃思滤波器、切比雪夫滤波器等。
本次课程设计将运用MATLAB设计一个基于切比雪夫低通滤波器,并出所设计滤波器的幅度及幅度衰减特性。
关键词:模拟低通滤波切比雪夫1课题描述数字滤波器是数字信号处理的重要工具之一,它通过数值运算处理改变输入信号所含频率成分的相对比例或者滤出某些频率成分的数字器件或程序,而数字滤波器处理精度高、体积小、稳定、重量轻、灵活、不存在阻抗匹配问题,可以实现模拟滤波器无法实现的特殊功能。
故本课题使用MATLAB 信号处理箱和运用切比雪夫法设计数字低通滤波器。
2设计原理切比雪夫滤波器介绍在巴特沃兹滤波器中,幅度响应在通带和阻带内都是单调的。
因此,若滤波器的技术要求是用最大通带和阻带的逼近误差来给出的话,那么,在靠近通带低频端和阻带截止频率以上的部分都会超出技术指标。
一种比较有效的途径是使逼近误差均匀地分布于通带或阻带内,或同时在通带和阻带内都均匀分布,这样往往可以降低所要求的滤波器阶次。
通过选择一种具有等波纹特性而不是单调特性的逼近方法可以实现这一点。
切比雪夫型滤波器就具有这种性质:其频率响应的幅度既可以在通带中是等波纹的,而在阻带中是单调的(称为I 型切比雪夫滤波器),也可以在通带中是单调的,而在阻带中是等波纹的(称为II 型切比雪夫滤波器)。
I 型切比雪夫滤波器的幅度平方函数是2|)(|Ωj H C =)/(1122c N C ΩΩ+ε 式中为N 阶切比雪夫多项式,定义为)cos cos()(1x N x C N -=从定义切比雪夫多项式可以直接得出由)(x C N 和)(1x C N -求)(1x C N +的递推公式。
用双线性变换法设计原型低通为切比雪夫I型的数字IIR低通滤波器

数字信号处理专业课程设计任务书说明:本表由指导教师填写,由教研室主任审核后下达给选题学生,装订在设计(论文)首页1 需求分析:滤波器从广义上来说对特定的频点或频点以外的频率进行有效滤波的电路,这种电路保留输入信号中的有用信息,滤除不需要的信息,从而达到信号的检测、提取、识别等不同的目的。
如果处理的信号是时域离散信号,那么相应的处理系统就称为数字滤波器,由于在实际工作中被处理的信号都是幅度量化的数字信号,因此,数字滤波器实际上是用有限精度的算法实现一个线性时不变的时域离散系统。
目前,数字滤波器的应用越来越广泛,它已深入到很多领域,如图象处理、医学生物信息处理、地质信号处理和模式识别处理等。
数字滤波器的种类很多,分类方法也不同,可以从功能上分类,也可以从实现方法上及设计方法上来分类等等。
滤波器在功能上总的可分为四类,即低通(LP)、高通(HP)、带通(BP)、带阻(BS)滤波器等,从实现方法上,由有限长冲激响应的数字滤波器被称为FIR滤波器,具有无限长冲激响应的数字滤波器称作IIR滤波器。
切比雪夫滤波器的幅度特性具有等纹波特性。
他有两种类型,一种是通带内为等纹波的,在阻带内是单调的成为切比雪夫Ι型滤波器;一种是通带内单调,阻带内等纹波的,称为切比雪夫ΙΙ型。
本实验采用切比雪夫Ι型滤波器。
利用双线性变换法将模拟传输信号Ha(s)变换为数字传输函数G(z),从而是z域的数字传输函数保留s域的模拟传输函数的基本性质。
设计成的IIR数字低通滤波器能够去掉信号中不必要的高频成分,降低采样频率,避免频率混淆,去掉高频干扰。
我和班长柴彬通力合作,我两合作将一些基本参数搞定后,我负责低通滤波器输入输出信号图形的实现,他负责信号幅频特性以及相频特性图形的实现。
成效显著。
2 概要设计:滤波器的设计流程图如图1所示图1 滤波器设计流程方框图包括在此说明每个部分的算法设计说明(可以是描述算法的流程图);每个程序中使用的存储结构设计说明(如果题目已经指定了数据存储的,按照指定的设计,并且写出该存储结构的定义)。
切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比
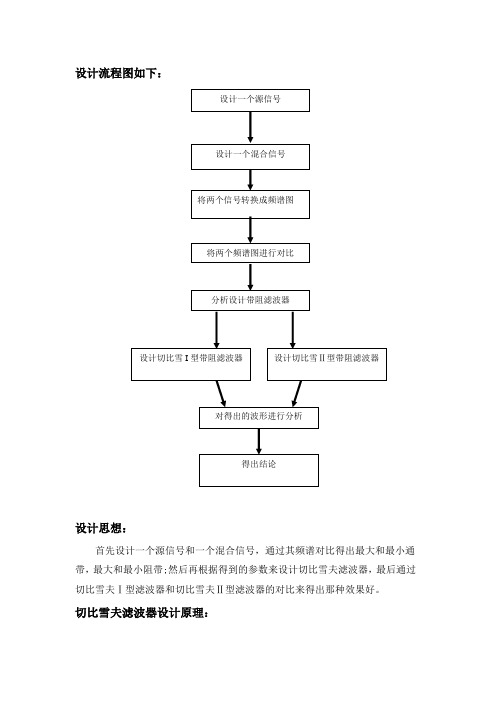
设计流程图如下:设计思想:首先设计一个源信号和一个混合信号,通过其频谱对比得出最大和最小通带,最大和最小阻带;然后再根据得到的参数来设计切比雪夫滤波器,最后通过切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比来得出那种效果好。
切比雪夫滤波器设计原理:切比雪夫滤波器的振幅具有等波纹特性,它有两种形式:1)振幅特性在通带内是等波纹的、在阻带内是单调的切比雪夫I 型滤波器;2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫II型滤波器,采用何种形式的切比雪夫滤波器取决于实际用途.切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内,或者均匀分布在整个阻带内,或者均匀分布在两者之内,这样就可以使滤波器阶数大大降低。
切比雪夫I型滤波器平方幅度响应函数表示为:2)(ΩjG=[1+2εC2N(Ω)]2/1-其中ε<1(正数),它与通带波纹有关,ε越大,波纹也越大;CN(Ω) 是切比雪夫多项式,它被定义为:CN (Ω)=cos(Narccos(Ω)),Ω≤1, CN(Ω)=cosh(Narcosh(Ω)),Ω>1. 而切比雪夫II型滤波器平方幅度响应函数表示为:)(ΩjG2={1+2ε{ C2N(Ω)/[2N(Ω/cΩ)]2}}1-其中ε<1(正数),表示波纹变化情况;cΩ为截止频率;N为滤波器的阶次,也是CN (NΩΩ/)的阶次。
源信号编码及其图形:t=-1:0.01:1y=(cos(2*pi*10*t)+cos(2*pi*40*t)); N=length(y);fx=fft(y);df=100/N;n=0:N/2;f=n*df;subplot(2,1,1);plot(f,abs(fx(n+1))*2/N); grid;title('源波形频谱')图(一)混合信号编码及其图形:t=-1:0.01:1;X=(cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*40*t));N=length(X);fx=fft(X);df=100/N;n=0:N/2;f=n*df;subplot(2,1,2);plot(f,abs(fx(n+1))*2/N); grid;title('混合波形频谱')图(二)从图(一)和图(二)对比可以得出:为了能达到和满足我们的要求,我们取以下的参数,最大通带wp2:0.5,最小通带wp1:0.05,最大阻带w s2:0.3,最小阻带ws1:0.1。
巴特沃斯Ⅱ型低通滤波器和切比雪夫Ⅱ型低通滤波器IIR低通数字滤波器设计

巴特沃斯Ⅱ型低通滤波器和切比雪夫Ⅱ型低通滤波器I I R低通数字滤波器设计(总24页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--南华大学课程设计报告课程名称:数字通信课程设计设计名称: IIR低通数字滤波器设计姓名: XXXX学号: xxxx班级:xxxx指导教师:XXXX起止日期:南华大学电气工程学院制课程设计任务书学生班级: xxxx 学生姓名: phatonic 学号: XXXXXXXX 设计名称:IIR低通数字滤波器设计起止日期:指导教师: XX课程设计学生日志课程设计考勤表课程设计评语表IIR低通数字滤波器设一、设计目的和意义目的:1.深入理解数字信号处理基础知识的理解;2.加深对MATLAB基础知识的理解;3.掌握低通数字滤波器的设计方法;4.了解冲激响应不变法的基本原理和特点;5.了解双线性变换法的基本原理和特点;意义:通过课程设计设计可以加深我们对课本基础知识的理解,对已经学习的知识进行实践训练,起到了理论联系实践的作用。
在设计过程中,一定会遇到很多的困难和问题,在解决问题的过程中,不仅锻炼了我解决实际问题的能力,而且也培养了我设计的综合能力。
总之,理论联系实践,对我来说是非常的重要。
IIR低通数字滤波器设计是滤波器设计中很经典的问题,而滤波器设计则是是《数字信号处理》的核心内容。
所以,IIR低通数字滤波器设计是数字信号处理的经典内容。
二、设计原理1.数字滤波器原理与模拟滤波器类似,数字滤波器按频率特性划分为低通、高通、带通、带阻、全通等类型。
由于频率响应的周期性,频率变量以数字频率w来表示(w=ΩT=Ω/fs, Ω为模拟角频率,T为抽样时间间隔,fs为抽样频率),所以数字滤波器设计中必须给出抽样频率。
一般情况下,数字滤波器是一个线性移不变离散时间系统,利用有限精度算法来实现。
具体的实现方法有很多,不过主流的方法是:先设计出对应的模拟滤波器,再将模拟滤波器数字化为数字滤波器。
IIR数字滤波器切比雪夫设计法的Matlab实现

切 比雪夫 I 型低 通模 拟 滤波器 的幅频 特性 为 :
1
。 ) 蒜 GQ1 ( 2
( )+B( ) I 1 2 z1+… + ( +1 )一 A1 ( )+A( ) +… +A( +1 z肘 2 )一 2 F 数 字滤 波器 的 Malb实现 m t a
Ab tac : IR iia l r i o e f t e mo t mp ra a s f d gtl sg a r c s i . Uii g Che y h v s r t I d gtl f t s n o h s i o tntme n o iia i n l p o e sng i e sn b s e ag rt m e lz s t e d sg fIR iia le a e n Ma lb.Th i l t n r s l s o h tb a so h loi h r aie h e in o I d gt lf trb s d o ta i e smu a i e ut h wst a y me n ft e o sg a r c si g tob x i t b t e IR iia le y be d sg e fe tv l n i y. in lp o e sn o lo n Ma l h I d gtlf t rma e in d efc iey a d smpl a i
rsos) epne 两种 滤 波器 ¨ 。Maa J tb已成 为 数 字 滤波 器 l 设 计 的基础 软件 。它可 以快速 有效 地 实现 滤波器 的 设计、 分析仿 真 和最 优化 。
1 I I R数字 滤波 器 的设计 原理
1+ l
_ , l
切 比雪夫 I型 幅度 特性 在 通 带 内是 单 调 的 , I 在 阻带 内是 等波 纹 的。这 种滤波 器在 |平 面上 既有极 s 点 , 有零 点 。 因此 通 带 中 的群延 迟 特 征 比切 比雪 又 夫 I 型滤 波器 好 , 位 响应更 线性 。 相 ( )模 拟低 通滤 波器 转换 为数 字低通 滤 波器 3 模 拟滤 波器 离散 化 的基本方 法有 脉 冲响应 不变 法 和 双线性 变换 法 。其变 换后 的系 统 函数 为 :
切比雪夫II型带通滤波器要点

NANHUA University课程设计(论文)题目用切比雪夫Ⅱ型IIR设计带通(数字频带变换)滤波器学院名称电气工程学院指导教师陈忠泽班级电子091 学号*********** 学生姓名潘星2012年 12 月2.对课程设计成果的要求〔包括图表(或实物)等硬件要求〕:滤波器的初始设计通过手工计算完成;在计算机辅助计算基础上分析滤波器结构对其性能指标的影响(至少选择两种以上合适的滤波器结构进行分析);在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响;以上各项要有理论分析和推导、原程序以及表示计算结果的图表;课程设计结束时提交设计说明书。
3.主要参考文献:[1]高息全丁美玉.《数字信号处理》[M].西安:西安电子科技大学出版社,2008.8[2]陈怀琛.《数字信号处理教程——MATLAB释义与实现》[M].北京:电子工业出版社,2004.12[3]张德丰.《详解MATLAB数字信号处理》[M].北京:电子工业出版社,2010.6[4]飞思科技产品研发中心.《MATLAB7辅助信号处理技术与应用》[M].北京:电子工业出版社,2005.34.课程设计工作进度计划:序号起迄日期工作内容接到题目,搜集资料1 2012.12.26-2013.12.31整理资料,构思设计方案2 2012.12.31-2013.1.3手工计算进行滤波器的初步设计3 2013.1.3-2013.1.5完善初步设计,学习Matlab软件操作4 2013.1.5-2013.1.7通过Matlab软件分析设计内容,逐步落实课题目标5 2013.1.8-2013.1.9上交课程设计,并做细节修改并完成设计6 2013.1.10-2013.1.13主指导教师日期:年月日一 手工计算完成切比雪夫2型IIR 带通滤波器初始设计1.设计要求滤波器的设计指标要求为⑴阻带下截止频率rad d i πω2.05.0e 501s ⋅⋅= ⑵通带下截止频率rad d i πω3.05.0e 501p ⋅⋅=⑶通带上截止频率,rad d i πω7.05.0e 502p ⋅⋅= ⑷阻带上截止频率 rad d i πω8.05.0e 502s ⋅⋅=⑸通带最大衰减错误!未找到引用源。
IIR滤波器和FIR滤波器的区别与联系

IIR滤波器和FIR滤波器的区别与联系1.两种滤波器都是数字滤波器。
根据冲激响应的不同,将数字滤波器分为有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。
对于FIR滤波器,冲激响应在有限时间内衰减为零,其输出仅取决于当前和过去的输入信号值。
对于IIR滤波器,冲激响应理论上应会无限持续,其输出不仅取决于当前和过去的输入信号值,也取决于过去的信号输出值。
2.FIR:有限脉冲响应滤波器。
有限说明其脉冲响应是有限的。
与IIR相比,它具有线性相位、容易设计的优点。
这也就说明,IIR滤波器具有相位不线性,不容易设计的缺点。
而另一方面,IIR却拥有FIR所不具有的缺点,那就是设计同样参数的滤波器,FIR比IIR需要更多的参数。
这也就说明,要增加DSP 的计算量。
DSP需要更多的计算时间,对DSP的实时性有影响。
以下都是低通滤波器的设计。
FIR的设计:FIR滤波器的设计比较简单,就是要设计一个数字滤波器去逼近一个理想的低通滤波器。
通常这个理想的低通滤波器在频域上是一个矩形窗。
根据傅里叶变换我们可以知道,此函数在时域上是一个采样函数。
通常此函数的表达式为:sa(n)=sin(n∩)/n∏,但是这个采样序列是无限的,计算机是无法对它进行计算的。
故我们需要对此采样函数进行截断处理。
也就是加一个窗函数。
就是传说中的加窗。
也就是把这个时域采样序列去乘一个窗函数,就把这个无限的时域采样序列截成了有限个序列值。
但是加窗后对此采样序列的频域也产生了影响:此时的频域便不在是一个理想的矩形窗,而是成了一个有过渡带,阻带有波动的低通滤波器。
通常根据所加的窗函数的不同,对采样信号加窗后,在频域所得的低通滤波器的阻带衰减也不同。
通常我们就是根据此阻带衰减去选择一个合适的窗函数。
如矩形窗、汉宁窗、汉明窗、BLACKMAN窗、凯撒窗等。
选择一个具体的窗函数之后,根据所设计滤波器的参数来计算所需的阶数、此窗函数的表达式。
然后用这个窗函数去和采样序列相乘,就可以得到实际滤波器的脉冲响应。
数字信号处理-切比雪夫Ⅰ型带阻IIR数字滤波器的设计

1ω=0.2551、2ω0.5060、3ω=0.6991、 4ω= 0.8909课程设计任务书题 目 切比雪夫Ⅰ型带阻IIR 数字滤波器的设计学生姓名学号专业班级设 计 内 容 与 要 求一、设计内容设计切比雪夫Ⅰ带阻滤波器,四个参数1ω~4ω通过MATLAB 的rand 函 数随机在0~1间产生,且满足1ω˂2ω˂3ω˂4ω。
(1)通带下截止频率 pl ω=1ω*π rad (2)阻带下截止频率 sl ω=2ω*π rad(3)阻带上截止频率 su ω=3ω*π rad (4)通带上截止频率 pu ω=4ω*π rad (5)通带最大衰减 p ∂=1db(6)阻带最大衰减 s ∂=60db二、设计要求(1)滤波器的初始设计通过手工完成(2)在计算机辅助计算的基础上分析滤波器结构对其性能指标的影响(至少 选择两种以上合适的滤波器结构进行分析)(3)在计算机辅助计算的基础上分析滤波器参数的字长对其性能指标的影响 (4)以上各项要有理论分析和推导,源程序以及表示计算结果的图表1.手工计算完成初始设计过程1.1 整体设计思路(1) (2)(3)(6) (5)(4) 图 1-1-1 整体设计流程图1.2 计算过程(1)通过MATLAB 的rand 函数随机在0~1间产生,且满足1ω˂2ω˂3ω˂4ω。
程序与运行结果如下: >> rand(1,4)ans =0.2551 0.5060 0.6991 0.8909 所以有:① 通同带下截止频率 pl ω=0.5*π rad ② 阻同带下截止频率 sl ω=0.85*π rad ③ 阻同带上截止频率 su ω=0.65*π rad ④ 通同带上截止频率 pu ω=0.35*π rad数字带阻指标模拟带阻指标数字带阻滤波器 模拟低通指标切比雪夫设计模拟低通滤波器数字低通滤波器⑤ 通带最大衰减 p ∂=1db⑥ 阻带最大衰减 s ∂=60db(2)数字带阻指标转化为模拟带阻指标 转化公式:令T=2s ,预畸变校正得到模拟边界频率:pl Ω=0.4236 rad/s pu Ω=5.7780 rad/s p ∂=1dbsl Ω=1.0190 rad/s su Ω=1.9558 rad/s s ∂=80db而 pl Ω*pu Ω=2.4476 sl Ω*su Ω=1.9930 不满足 2pl pu sl su o ΩΩ=ΩΩ=Ω 修正 pl pu sl suΩΩΩ=Ω=1.2515 rad/s所以,转化后的模拟带阻的各项指标为:pl Ω=0.4236 rad/s pu Ω=5.7780 rad/s p ∂=1dbsl Ω=1.2515 rad/s su Ω=1.9558 rad/s s ∂=60db(3)将模拟带阻指标转化为模拟低通指标 带阻→低通的映射为: 220wsB λλΩ=-Ω-Ω其中Bw 为阻带宽度,w B =su Ω-sl Ω=0.25*π, 取低通原型通带边界频率p λ=1且λ=p λ时的映射为Ω=-pl Ω 带入上式得到:s λ=7.6026 p ∂=1db⎪⎭⎫⎝⎛=Ω2tan 2ωTs ∂=80db(4)设计切比雪夫模拟低通滤波器 求滤波器阶数N 和参数ε 0.1101pαε=- 11arch k arch sN λ-=其中,0.1110.1101k 101s pαα--=-=1965 取符合条件的N 的最小整数,取N=7;ε=0.0.3493 求归一化极点Pk()()2121sincos 22k k k p ch jch NNππξξ--=-+其中,11arsh N ξε==0.375 求出的四个归一化极点分别为: -0.1395 + 0.9834 j -0.3369 + 0.4073 j-0.3369 - 0.4073 j -0.1395 - 0.9834 j 求归一化系统函数()a p G ()()111*2Na p N i i G p p ε-==-∏带入后得到 ()4320.24570.9528 1.45390.74260.2756a p G p p p p =++++ 由于所求的是切比雪夫滤波器,故p c Ω=Ω。
切比雪夫I型IIR低通数字滤波器设计

数字信号处理课程设计设计题目切比雪夫I型IIR低通数字滤波器设计题目编号 0201学院名称电气学院指导教师陈忠泽班级电子11级02班学号 20114470203 学生姓名设计说明说每位同学抽签得到一个四位数,由该四位数索引下表确定待设计数字滤波器的类型及其设计方法,然后用指定的设计方法完成滤波器设计。
要求: 滤波器的设计指标:低通:⑴通带截止频率rad i d pc πω20)ln(=,⑵过渡带宽度rad i d tz πω100)(log 10≤∆, ⑶滚降dB roll 60=α;高通:⑴阻带截止频率rad i d sc πω20)ln(=,⑵通带截止频率rad i i d d pc πω⎪⎭⎫ ⎝⎛+=100)(log 20)ln(10,⑶通带最大衰减dB p 1=α,⑷阻带最小衰减dB s 60=α; 带通:⑴阻带下截止频率rad i d sl πω20)ln(=,⑵通带下截止频率rad i i d d pl πω⎪⎭⎫ ⎝⎛+=100)(log 20)ln(10, ⑶通带上截止频率rad i i d d pu πω⎪⎭⎫ ⎝⎛--=100)(log 20)ln(110, ⑷阻带上截止频率rad i d su πω⎪⎭⎫ ⎝⎛-=20)ln(1,⑸通带最大衰减dB p 1=α, ⑹阻带最小衰减dB s 60=α;带阻:⑴通带下截止频率rad i d pl πω20)ln(=, ⑵阻带下截止频率rad i i d d sl πω⎪⎭⎫ ⎝⎛+=100)(log 20)ln(10, ⑶阻带上截止频率rad i i d d su πω⎪⎭⎫ ⎝⎛--=100)(log 20)ln(110, ⑷通带上截止频率rad i d pu πω⎪⎭⎫ ⎝⎛-=20)ln(1, ⑸通带最大衰减dB p 1=α, ⑹阻带最小衰减dB s 60=α;等波纹滤波器:⑴通带波纹05.0≤p r , ⑵阻带波纹05.0≤s r ,⑶过渡带宽度rad i d tz πω100)(log 10≤∆,⑷滚降dB roll 60=α 陷波器: ⑴陷波中心频率rad i d no πω20)ln(=, ⑵陷波频率分量最小衰减dB no 60=α, ⑶−3 dB 处的频带宽度rad i d no πω100)(log 10≤∆ 其中,d i —抽签得到那个四位数。
用双线性变换法设计切比雪夫II型的数字IIR带通滤波器

用双线性变换法设计切比雪夫II型的数字IIR带通滤波器用双线性变换法设计切比雪夫II 型的数字IIR 带通滤波器用双线性变换法设计原型低通为切比雪夫II 型的数字IIR 带通滤波器,要求通带边界频率为400Hz ,500Hz ,阻带边界频率分别为350Hz ,550Hz ,通带最大衰减1dB ,阻带最小衰减40dB ,抽样频率为2000Hz ,用MATLAB 画出幅频特性,画出并分析滤波器传输函数的零极点;信号)2sin()2sin()()()(2121t f t f t x t x t x ππ+=+=经过该滤波器,其中=1f 450Hz ,=2f 600Hz ,滤波器的输出)(t y 是什么?用Matlab 验证你的结论并给出)(),(),(),(21t y t x t x t x 的图形。
Matlab 详细设计:% Design of a Cheb II Bandpass Digital Filter by using bilinear method clc; clear all ;Rp = 1; % bandpass attenuation in dB Rs = 40; % bandstop attenuation in dB OmegaS1_1=350; OmegaS1_2=550; OmegaP1_1=400; OmegaP1_2=500;Fp=2000; % samling frequency Wp1=2*pi*OmegaP1_1/Fp; Wp2=2*pi*OmegaP1_2/Fp; Ws1=2*pi*OmegaS1_1/Fp; Ws2=2*pi*OmegaS1_2/Fp;OmegaP1=2*Fp*tan(Wp1/2); % nonlinearlization OmegaP2=2*Fp*tan(Wp2/2); % nonlinearlization OmegaS1=2*Fp*tan(Ws1/2); % nonlinearlization OmegaS2=2*Fp*tan(Ws2/2); % nonlinearlizationOmegaP0=sqrt(OmegaP1*OmegaP2);% equivalent mid frequency Bw=OmegaP2-OmegaP1; % bandwith Eta_P0=OmegaP0/Bw; % Normalization Eta_P1=OmegaP1/Bw; % Normalization Eta_P2=OmegaP2/Bw; % Normalization Eta_S1=OmegaS1/Bw; % Normalization Eta_S2=OmegaS2/Bw; % NormalizationLemta_P_EquivalentLowPass=Eta_P2/(Eta_P2^2-Eta_P0^2); % change to theequivalent Lowpass patameterLemta_S1_EquivalentLowPass=-Eta_S1/(Eta_S1^2-Eta_P0^2); % change to the equivalent Lowpass patameterLemta_S2_EquivalentLowPass=Eta_S2/(Eta_S2^2-Eta_P0^2); % change to the equivalent Lowpass patameterLemta_S_EquivalentLowPass=min(Lemta_S1_EquivalentLowPass,Lemta_S2_Equ ivalentLowPass); % get the smallest% Estimate the Filter Order[N, Wn]=cheb2ord(Lemta_P_EquivalentLowPass, Lemta_S_EquivalentLowPass, Rp, Rs,'s');% Design the Filter[num1,den1]=cheby2(N,Rs,Wn,'s');[num2,den2]=lp2bp(num1,den1,OmegaP0,Bw);[num,den]=bilinear(num2,den2,Fp);% Compute the gain responsew = 0:pi/255:pi;h = freqz(num,den,w);g = 20*log10(abs(h));% Plot the gain responsefigure;plot(w/pi,g);gridaxis([0 1 -60 5]);xlabel('\omega /\pi'); ylabel('Gain in dB');title('Gain Response of a Cheb II Bandpass Filter');%Plot the poles and zeros[z,p,k]=tf2zp(num,den);figure;zplane(z,p); %»æÖÆ´«Ê亯ÊýÁ㼫µãtitle('´«Ê亯ÊýµÄÁ㼫µã')f1=450;f2=600;t=0:0.0001:1x1=sin(2*pi*f1*t);x2=sin(2*pi*f2*t);x=x1+x2;figure;subplot(2,2,1)%»æÖÆx1µÄ²¨ÐÎplot(x1);grid on;axis([0,50*pi,-3,3]);xlabel('t');ylabel('x1(t)');title('x1µÄ²¨ÐÎ');subplot(2,2,2)%»æÖÆx1µÄ²¨ÐÎplot(x2);grid on;axis([0,50*pi,-3,3]);xlabel('t');ylabel('x2(t)');title('x2µÄ²¨ÐÎ');subplot(2,2,3)%»æÖÆÊäÈëxµÄ²¨ÐÎplot(x);grid on;axis([0,50*pi,-3,3]);xlabel('t');ylabel('x(t)');title('ÊäÈëÐźÅxµÄ²¨ÐÎ')%X=fft(x);y=filter(num,den,x);%Êý×ÖÂ˲¨Æ÷Êä³ösubplot(2,2,4);%»æÖÆÊä³öyµÄ²¨ÐÎplot(real(y));grid on;axis([0,50*pi,-3,3]);xlabel('t');ylabel('y');title('Â˲¨Æ÷Êä³öyµÄ²¨ÐÎ');测试结果:图三实验程序截图运行结果如下:00.10.20.30.40.50.60.70.80.91-60-50-40-30-20-10ω /πG a i n i n d BGain Response of a Cheb II Bandpass Filter-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81Real PartI m a g i n a r y P a r t传输函数的零极点50100150-202tx 1(t )x1的波形50100150-202tx 2(t )x2的波形50100150-202t x (t )输入信号x 的波形050100150-202ty滤波器输出y 的波形。
IIR数字滤波器设计及应用要点

IIR数字滤波器设计及应用要点
数字滤波器设计及应用的要点如下:
1.滤波器类型选择:根据需要的滤波特性(例如低通、高通、带通、
带阻等),选择适当的滤波器类型,如巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
2.滤波器参数确定:确定滤波器的参数,包括通带和阻带的边界频率、通带最大衰减、阻带最小衰减等。
这些参数的选择决定了滤波器的性能。
3.滤波器设计方法选择:根据具体的需求和要求,选择合适的滤波器
设计方法。
常用的设计方法包括窗函数法、频率抽取法、脉冲响应法等。
4.滤波器结构实现:根据设计方法和参数,确定滤波器的结构实现方式。
常见的结构包括直接形式结构、级联结构、并行结构等。
5.滤波器性能评估:设计好的滤波器需要评估其性能,包括频率响应、相位响应、群延迟、滤波特性等。
可以使用频域分析、时域分析等方法进
行评估。
6.滤波器应用:将设计好的滤波器应用到实际问题中。
常见的应用包
括信号去噪、信号增强、频谱分析、通信系统等。
在实际应用中,还需注意滤波器设计与系统需求的匹配,选择适当的
采样率、位宽和滤波器阶数,以满足实际系统的要求。
同时,对于滤波器
的实时性要求较高的应用,还需要考虑滤波器的计算复杂度和实时性能。
IIR数字滤波器设计和应用

IIR 数字滤波器设计和应用一、实验目的1、熟悉IIR 数字滤波器的设计方法。
2、掌握模拟滤波器的matlab 实现。
3、熟悉用脉冲响应不变法设计IIR 数字滤波器的原理与方法。
4、熟悉用双线性变换法设计IIR 数字滤波器的原理与方法。
5、掌握数字滤波器的计算机仿真方法。
6、通过观察对实际心电图信号的滤波作用, 获得数字滤波的感性知识。
二、实验内容和要求1、用Matlab 语言分别设计巴特奥斯低通滤波器和切比雪夫低通滤波器,其技术指标为:通带截止频率)5(2KHz p ⋅=Ωπ,通带最大衰减dB P 3=α;阻带起始频率)10(2KHz s ⋅=Ωπ,阻带最小衰减dB s 30=α;要求:求出他们的零点、极点、阶数、增益等,并画出图形作比较。
(1)巴特奥斯低通滤波器:%Design a Butterworth Analog bandpass filter %Desired performents of the filterwp=5000*2*pi;ws=10000*2*pi;Rp=3;Rs=30;%compute oder and cutoff frequency [N,Wn]=buttord(wp,ws,Rp,Rs,'s');NFc=Wn/(2*pi)%Compute the filter[b,a]=butter(N,Wn,'s');%Outputw=linspace(1,3000,1000)*2*pi;H=freqs(b,a,w);magH=abs(H);phaH=unwrap(angle(H));plot(w/(2*pi),20*log10(magH));xlabel('Frequency(Hz)');ylabel('Magnidute(dB)');title('Butterworth Analog bandpass filter') grid on运算结果:N =5Fc = 5.0124e+003(2)切比雪夫低通滤波器:%Chebyshev ¢ñlowpass filter%Desired performentswp=5000*2*pi;ws=10000*2*pi;Rp=3;Rs=30;%Compute Order Nebs=sqrt(10^(Rp/10)-1);A=10^(Rs/20);Wc=wpWr=ws/wp;g=sqrt(A*A-1)/ebs;N1=log10(g+sqrt(g*g-1))/log10(Wr+sqrt(Wr*Wr-1));N=ceil(N1)运算结果:Wc = 3.1416e+004N = 42、切比雪夫低通滤波器,其技术指标为:通带截止频率MHz f p 3=,通带最大衰减dB P 1.0=α;阻带起始频率MHz f s 12=,阻带最小衰减dB s 60=α;要求:求出他们的零点、极点、阶数、增益等,并画出图形作比较。
基于IIR模拟低通数字低通滤波器的设计基于FIR汉宁窗升余弦滤波器的设计

课程设计题目基于IIR模拟低通数字低通滤波器的设计基于FIR汉宁窗升余弦滤波器的设计学生姓名于倩学号所在院(系)物理学系专业班级电子信息科学与技术081班指导教师蒋媛完成地点实验楼506教室2011 年 10 月 19 日基于IIR模拟低通数字低通滤波器的设计基于FIR升余弦滤波器的设计作者:于倩关键词:MATLAB,低通滤波器陕西理工学院(物电学院)电子信息科学与技术专业2008级陕西汉中723000指导教师:蒋媛[摘要]本设计中都是设计的低通滤波器,在软件上的仿真,利用个人设定的滤波器的参数,进行低通滤波器的设计。
通过在MATLAB软件中的仿真,可以看出利用不同的设计方法设计低通滤波器,产生的效果有很大的差别。
[关键词]MATLAB,低通滤波器Abstract: This design is the design of low-pass filter, software simulation, using one set of filter parameters, were low-pass filter design. Through the MATLAB software in the simulation, we can see the use of differentdesign approaches in the design of low-pass filter, the effect is very different。
Key words:MATLAB, low-pass filter一. 设计目的和要求1. 设计环境软件: MATLAB7.0软件。
硬件:笔记本电脑,安装MATLAB软件2.设计要求设计一个低通滤波器,滤波器的各项基本参数可以自己设定,分别刊滤波器的各项性能图像可以清楚的看出低通滤波器由于设计方法的不同的区别。
在这个设计中,我们会利用三种方法设计低通滤波器,对他们进行对比,之后可以分析出哪一种的结果是最好的,最理想的。
iir二阶滤波器参数

iir二阶滤波器参数IIR二阶滤波器参数的设计与应用引言:IIR滤波器是一种常见的数字滤波器,由于其具有稳定性好、设计灵活等优点,在信号处理领域得到了广泛应用。
本文将着重介绍IIR二阶滤波器的参数设计及其在实际应用中的一些特点和注意事项。
一、IIR二阶滤波器的基本结构IIR滤波器是指其系统函数(传递函数)的分母和分子都是多项式,且分母多项式的次数不小于分子多项式的次数。
而二阶IIR滤波器是指系统函数的分母和分子都是二次多项式。
二阶IIR滤波器的传递函数一般表示为H(z) = (b0 + b1z^(-1) + b2z^(-2)) / (1 + a1z^(-1) + a2z^(-2)),其中b0、b1、b2为前向系数,a1、a2为反馈系数。
这些系数的选择将直接影响滤波器的性能。
二、IIR二阶滤波器参数设计1. 频率响应要求:在设计滤波器时,首先需要明确所需的频率响应特性。
常见的频率响应要求有低通、高通、带通、带阻等。
根据不同的需求,可以选择不同的滤波器类型和参数。
2. 范围和阶数选择:根据所需的频率响应和性能要求,确定滤波器的阶数。
一般情况下,二阶滤波器已经能够满足大部分应用的要求。
3. 频率转换:将所需的频率响应特性转化为模拟滤波器的频率响应。
常用的方法有频率归一化和频率预畸。
这一步骤可以帮助确定滤波器的截止频率和通带增益。
4. 频率变换:将模拟滤波器的频率响应转化为数字滤波器的频率响应。
常用的方法有双线性变换、脉冲响应不变法等。
这一步骤可以帮助确定滤波器的数字化参数。
5. 系数计算:根据频率变换得到的数字滤波器的参数,通过一定的计算方法得到前向系数b0、b1、b2和反馈系数a1、a2的具体数值。
常用的计算方法有巴特沃斯、切比雪夫、椭圆等。
三、IIR二阶滤波器的应用特点1. 实时处理:IIR滤波器具有实时性好的特点,适用于需要对实时信号进行滤波处理的应用场景。
例如音频处理、图像处理等。
2. 相位响应:相比于FIR滤波器,IIR滤波器的相位响应更加复杂。
基于切比雪夫I型低通滤波器设计IIR数字带通滤波器

基于切比雪夫I型低通滤波器设计IIR数字带通滤波器陈绍荣;刘郁林;王开;徐舜【摘要】首先,介绍归一化切比雪夫多项式、归一化切比雪夫I型模拟低通滤波器极点分布的特点、设计切比雪夫I型模拟低通滤波器的步骤;其次,介绍模拟带通滤波器到模拟低通滤波器的频率变换公式及利用模拟低通滤波器设计模拟带通滤波器的步骤;最后,介绍利用双线性变换法设计IIR数字带通滤波器的步骤,并给出了基于切比雪夫I型低通滤波器来设计IIR数字带通滤波器的实例.【期刊名称】《通信技术》【年(卷),期】2019(052)001【总页数】10页(P1-10)【关键词】切比雪夫I型低通滤波器;频率变换;双线性变换法;IIR数字带通滤波器【作者】陈绍荣;刘郁林;王开;徐舜【作者单位】陆军工程大学通信士官学校,重庆 400035;重庆市经信委,重庆400015;陆军工程大学通信士官学校,重庆 400035;陆军工程大学通信士官学校,重庆 400035【正文语种】中文【中图分类】TN7130 引言在国内外《数字信号处理》著作[1-3]中,均介绍了IIR数字低通滤波器的设计方法。
关于IIR数字高通、带通及带阻滤波器的设计,一般有两种方法:一是先在s域上设计相应的模拟高通、带通及带阻滤波器,再通过双线性变换完成IIR数字高通、数字带通及数字带阻滤波器的设计;二是先在s域上设计相应的模拟低通滤波器,再将模拟低通滤波器变换成IIR数字低通滤波器,最后将IIR数字低通滤波器在相应的变换函数下变换成IIR数字高通、数字带通及数字带阻滤波器,那么研究相应的变换函数就成为关键问题。
由于模拟低通、高通、带通和带阻滤波器设计已经有了一套相当成熟的方法,它不但有一套完整的设计公式,而且还有较完整的图表供查询。
充分利用这些已有的资源,将会给IIR数字滤波器设计带来很大的方便。
基于这一事实,通常采用第一种方法设计IIR数字高通、数字带通及数字带阻滤波器。
而所列著作[1-3]中,个别之处的推理过略,不便于理解。
切比雪夫低通滤波器

课程设计课程名称:数字信号处理题目编号: 0202题目名称:切比雪夫Ⅱ型IIR低通滤波器专业名称:电子信息工程班级:电子1204班学号: 20124470411学生姓名:刘春阳任课教师:黄国玉2015年09月30日数字信号处理课程设计课程设计任务书目录1. 数字滤波器的设计任务及要求(编号202) (2)2. 数字滤波器的设计及仿真 (3)2.1数字滤波器(编号202)的设计 (3)2.2数字滤波器(编号202)的性能分析 (6)3. 数字滤波器的实现结构对其性能影响的分析 (7)3.1数字滤波器的实现结构一(直接型)及其幅频响应 (8)3.2数字滤波器的实现结构二(级联型)及其幅频响应 (10)3.3 数字滤波器的实现结构对其性能影响的小结 (10)4. 数字滤波器的参数字长对其性能影响的分析 (11)4.1数字滤波器的实现结构一(直接型)参数字长及幅频响应特性变化 (12)4.2数字滤波器的实现结构二(级联型)参数字长及幅频响应特性变化 (14)4.3 数字滤波器的参数字长对其性能影响的小结 (16)5. 结论及体会 (16)5.1 滤波器设计、分析结论 (16)5.2 我的体会 (16)5.3 展望 (17)1.数字滤波器的设计任务及要求(0202)每位同学抽签得到一个四位数,由该四位数索引下表一确定待设计数字滤波器的类型及其设计方法, 然后用指定的设计方法完成滤波器设计。
要求:(1)滤波器设计指标:通带截止频 pc ln ()32d rad i πω=, 过渡带宽度10tz()160log drad i πω∆≤,滚降roll 60dB α=;其中, id —抽签得到那个四位数(题目编号) (2)滤波器的初始设计通过手工计算完成;(3)在计算机辅助计算基础上分析滤波器结构对其性能指标的影响(至少选择两种 以上合适的滤波器结构进行分析);(4)在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响; (5) 以上各项要有理论分析和推导、原程序以及表示计算结果的图表; (6)课程设计结束时提交设计说明书。
脉冲响应不变法方案切比雪夫II型IIR数字低通滤波器

课程设计课程设计名称:基于脉冲响应不变法设计切比雪夫II型IIR数字低通滤波器专业班级:电子信息工程学生姓名:学号:指导教师:课程设计时间:2018年6月数字信号处理专业课程设计任务书,,=0.001果性能。
说明:本表由指导教师填写,由教研室主任审核后下达给选题学生,装订在设计<论文)首页1 需求分析切比雪夫数字(Chbyshev>滤波器的振幅特性具有等波纹特性,低通滤波器振幅特性在通带内是单调的、在阻带内是等波纹的。
阻带内具有等波纹的欺负特性,而在通带内是单调的、平滑的,阶数越高,频率特性曲线越接近矩形,传输函数既有极点又有零点。
本设计要求切比雪夫II 型的数字滤波器所需的四个参数分别是归一化的通带截止频率=0.25,阻带截止频率=0.4,通带误差容限=0.01,通带误差容限=0.001;由此得到对应的模拟原型低通滤波器的各个主要参数为Wp=0.25*pi/Ts 。
Ws=0.4*pi/Ts 。
Rp=20*log10(1/0.99>。
Rs=20*log10(1/0.001>。
2 概要设计本设计采用经典设计法设计IIR 数字低通滤波器,就是先根据技术指标设计出来相应的模拟滤波器,然后把设计好的模拟滤波器通过脉冲响应不变法转换成IIR 数字滤波器,它能很好地重现的原型模拟滤波器频率特性。
基本实现流程如下图所示图2.1Chebyshev-II 型IIR 数字低通滤波器设计流程图3 运行环境操作系统:Windows 7软件:MATLAB4 开发工具和编程语言MATLAB和MATLAB编程语言5详细设计数字滤波器采用经典低通滤波器作为连续域上的设计模型,通过频域变换得到IIR数字滤波器,最后还要进行离散化处理。
用MATLAB提供的低通模拟滤波器原型函数cheb2ap频域变换函数包括lp2lp;离散化处理函数impinvar。
(1>确定数字低通滤波器的技术指标:通带截止频率、阻带截止频率、通带最小衰减和阻带最小衰减。
切比雪夫II型带通滤波器要点

NANHUA University课程设计(论文)题目用切比雪夫Ⅱ型IIR设计带通(数字频带变换)滤波器学院名称电气工程学院指导教师陈忠泽班级电子091 学号*********** 学生姓名潘星2012年 12 月2.对课程设计成果的要求〔包括图表(或实物)等硬件要求〕:滤波器的初始设计通过手工计算完成;在计算机辅助计算基础上分析滤波器结构对其性能指标的影响(至少选择两种以上合适的滤波器结构进行分析);在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响;以上各项要有理论分析和推导、原程序以及表示计算结果的图表;课程设计结束时提交设计说明书。
3.主要参考文献:[1]高息全丁美玉.《数字信号处理》[M].西安:西安电子科技大学出版社,2008.8[2]陈怀琛.《数字信号处理教程——MATLAB释义与实现》[M].北京:电子工业出版社,2004.12[3]张德丰.《详解MATLAB数字信号处理》[M].北京:电子工业出版社,2010.6[4]飞思科技产品研发中心.《MATLAB7辅助信号处理技术与应用》[M].北京:电子工业出版社,2005.34.课程设计工作进度计划:序号起迄日期工作内容接到题目,搜集资料1 2012.12.26-2013.12.31整理资料,构思设计方案2 2012.12.31-2013.1.3手工计算进行滤波器的初步设计3 2013.1.3-2013.1.5完善初步设计,学习Matlab软件操作4 2013.1.5-2013.1.7通过Matlab软件分析设计内容,逐步落实课题目标5 2013.1.8-2013.1.9上交课程设计,并做细节修改并完成设计6 2013.1.10-2013.1.13主指导教师日期:年月日一 手工计算完成切比雪夫2型IIR 带通滤波器初始设计1.设计要求滤波器的设计指标要求为⑴阻带下截止频率rad d i πω2.05.0e 501s ⋅⋅= ⑵通带下截止频率rad d i πω3.05.0e 501p ⋅⋅=⑶通带上截止频率,rad d i πω7.05.0e 502p ⋅⋅= ⑷阻带上截止频率 rad d i πω8.05.0e 502s ⋅⋅=⑸通带最大衰减错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理课程设计报告课题名称:系别:学号:姓名:班级:指导教师:目录摘要2第1章任务书41.1题目41.2目的41.3容及要求41.4论文格式4第2章数字滤波器的设计52.1数字滤波器的概念52.2数字滤波器的分类52.3数字滤波器的设计要求72.4IIR数字滤波器的设计82.4.1IIR数字滤波器的设计步骤82.4.2双线性变换法设计IIR数字滤波器9第3章切比雪夫低通数字滤波器的MATLAB设计133.1设计步骤133.2MATLAB程序13总结15参考文献16摘要1在现代通信系统中,由于信号中经常混有各种复杂成分,所以很多信号分析都是基于滤波器而进行的,而数字滤波器是通过数值运算实现滤波,具有处理精度高、稳定、灵活、不存在阻抗匹配问题,可以实现模拟滤波器无法实现的特殊滤波功能。
数字滤波器根据其冲激响应函数的时域特性,可分为两种,即无限长冲激响应(IIR)数字滤波器和有限长冲激响应(FIR)数字滤波器。
实现IIR滤波器的阶次较低,所用的存储单元较少,效率高,精度高,而且能够保留一些模拟滤波器的优良特性,因此使用很广。
Matlab软件以矩阵运算为基础,把计算、可视化及程序设计有机融合到交互式工作环境中,并且为数字滤波的研究和使用提供了一个直观、高效、便捷的利器。
尤其是Matlab中的信号处理工具箱使各个领域的研究人员可以直观方便地进行科学研究和工程使用。
本文首先介绍了数字滤波器的概念,分类以及设计要求。
接着利用MATLAB函数语言编程,用信号处理图形界面FDATool来设计滤波器以及Sptool界面设计的方法,并用FDATool 模拟IIR数字滤波器处理信号。
重点设计Chebyshev I型和Chebyshev II型数字低通滤波器,并介绍最优化设计。
关键字:IIR;滤波器;FDATool;Sptool;SimulinkABSTRACTIn modern communication systems, Because often mixed with various signal complex components, So many signal analysis is based on filters, and the digital filter is realized through numerical computation, digital filters filter with high precision, stability and flexibility, don't exist, can realize the impedance matching simulating the special filter cannot achieve fi lter function. Digital filter according to its impulse response function and characteristics of the time can be divided into two kinds, namely the infinite impulse response (IIR) digital filter and finite impulse response (FIR digital filters). The order of realizing IIR filter is used, low and high efficiency less storage unit, high precision, and can keep some simulation characteristics of filter, so it is widely used. Matlab software based on matrix computation, the calculation, visualization and program design of organic integration to interactive environment for digital filter, and the research and application of provides an intuitive, efficient and convenient tool. Especially in the Matlab signal processing to all areas of research toolbox personnel can easily for scientific research and engineering application. This paper introduces the concept of digital filter, classification and design requirements. Then using MATLAB language programming, with functions of signal processing FDATool graphical interface design of interface design and Sptool filter, and FDATool analog signal processing IIR digital filter. Key design Chebyshev type I and II digital Chebyshev lowpass filter, and introduces optimization design.Keywords:IIR;Filter;FDATool;Sptool;Simulink第1章任务书1.1题目设计原型为切比雪夫型的数字IIR低通滤波器。
1.2目的1)学会MATLAB的使用,掌握MATLAB的程序设计方法。
2)掌握数字信号处理的基本概念、基本理论和基本方法。
3)掌握MATLAB设计IIR数字滤波器的方法。
4)学会用MATLAB对信号进行分析和处理。
1.3容及要求1)设计原型为切比雪夫型的数字IIR低通滤波器(本文用双线性变换法,原型为切比雪夫I型)。
2)低通数字滤波器的技术指标:通带截止频率,通带衰减,阻带截止频率,阻带衰减。
3)求出所设计滤波器的Z变换。
4)用MATLAB画出幅频特性图。
1.4论文格式1)任务书及摘要。
2)目录,中间打点号。
3)章节,如:第1章,每一章都要另起一页,居中;二级目录要打头写,如:1.1;每个图都要有图标和名称,如:图1-1 ++++++。
4)课程设计总结,主要包括课程设计意义、感受、遇到的问题及解决办法。
参考文献,格式如:[1] 阎石.数字电子技术基础.:高等教育,1998.第2章 数字滤波器的设计2.1 数字滤波器的概念滤波器是指用来对输入信号进行滤波的硬件和软件。
数字滤波器是对数字信号实现滤波的线性时不变系统。
数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化过程中,使信号按预定的形式变化。
数字滤波实质上是一种运算过程,实现对信号的运算处理。
数字滤波器和模拟滤波器相比,因为信号的形式和实现滤波的方法不同,数字滤波器具有比模拟滤波器精度高、稳定、体积小、重量轻、灵活、不要求阻抗匹配等优点。
输入数字信号(数字序列)通过特定的运算转变为输出的数字序列,因此,数字滤波器本质上是一个完成特定运算的数字计算过程,也可以理解为是一台计算机。
描述离散系统输出和输入关系的卷积和差分方程只是给数字信号滤波器提供运算规则,使其按照这个规则完成对输入数据的处理。
时域离散系统的频域特性:)()()(ωωωj j j e H e X e Y =其中)(ωj e Y 、)(ωj e X 分别是数字滤波器的输出序列和输入序列的频域特性(或称为频谱特性), )(ωj e H 是数字滤波器的单位取样响应的频谱,又称为数字滤波器的频域响应。
输入序列的频谱)(ωj e X 经过滤波后)()(ωωj j e H e X ,因此,只要按照输入信号频谱的特点和处理信号的目的, 适当选择)(ωj e H ,使得滤波后的)()(ωωj j e H e X 满足设计的要求,这就是数字滤波器的滤波原理。
2.2 数字滤波器的分类按照不同的分类方法,数字滤波器有许多种类,但总起来可以分成两大类:经典滤波器和现代滤波器。
经典滤波器的特点是其输入信号中有用的频率成分和希望滤除的频率成分占有不同的频带,通过一个合适的选频滤波器滤除干扰,得到纯净信号,达到滤波的目的。
但是,如果信号和干扰的频谱相互重叠,则经典滤波器不能有效地滤除干扰,最大限度地恢复信号,这时就需要现代滤波器,例如维纳滤波器、卡尔曼滤波器、自适应滤波器等最佳滤波器。
现代滤波器是根据随机信号的一些统计特性,在某种最佳准则下,最大限度地抑制干扰,同时最大限度地回复信号,从而达到最佳滤波的目的。
经典数字滤波器从滤波特性上分类,可以分为:低通滤波器、高通滤波器、带通滤波器、带阻滤波器。
图2.2.1各种理想滤波器的幅频特性数字滤波器根据其冲激响应函数的时域特性,可分为两种,即无限长冲激响应(IIR)数字滤波器和有限长冲激响应(FIR)数字滤波器。
IIR数字滤波器的特征是,具有无限持续时间冲激响应,需要用递归模型来实现。
其差分方程为:∑∑==-+-=NiNiiiinybinxany01)()()((式2-2-1)系统函数为:kNkiMrrrZaZbzH-==-∑∑+=11)((式2-2-2)设计IIR滤波器的任务就是寻求一个物理上可实现的系统函数H(z),使其频图 2.3.1低通滤波器的技术要求率响应H(z)满足所希望得到的频域指标,即符合给定的通带截止频率、阻带截止频率、通带衰减系数和阻带衰减系数。
2.3 数字滤波器的设计要求滤波器的指标常常在频域给出。
数字滤波器的频响特性函数)(jw e H 一般为复函数,所以通常表示为:)()(|)()(w j jw e z jw e e H z H e H jw Φ=== (式2-3-1)其中,)(jw e H 称为幅频特性函数,Φ(w)称为相频特性函数。
幅频特性表示信号通过该滤波器后各频率成分的衰减情况,而相频特性反映各频率通过滤波器后在时间上的延时情况。
一般IIR 数字滤波器,通常只用幅频响应函数)(jw e H 来描述设计指标,相频特性一般不作要求。
IIR 滤波器指标参数如下图所示。
图中,p ω和p ω分别为通带边界频率和阻带边界频率;δ1和δ2分别为通带波纹和阻带波纹;允许的衰减一般用dB 数表示,通带所允许的最大衰减(dB )和阻带允许的最小衰减(dB )分别为p α和s α表示:111111lg 2011lg 20δδδδα-+=+--=p (式2-3-2) 2lg 20δα-=s(式2-3-3) 一般要求:当pωω≤≤0时,p jw eH α≤-)(lg 20; 当πωω≤≤时,)(lg 20jw e H s -≤α。
