高中数学必修一集合复习课课件
合集下载
高中数学必修一必修1全章节ppt课件幻灯片
22
(2)方程x2+2x+1=0的解集中有两个元素. (3)组成单词china的字母组成一个集合.
【解题探究】 1.集合中的元素有哪些特性？ 2.集合中的元素能重复吗？
探究提示： 1.集合中的元素有三个特性，即确定性、互异性和无序性. 2.构成集合的元素必须是不相同的，即集合元素具有互异性， 相同的元素只能算作一个. 【解析】1.①不正确.因为成绩较好没有明确的标准． ②正确．中国海洋大学2013级大一新生是确定的，明确的． ③正确．因为参加2012年伦敦奥运会的所有国家是确定的， 明确的． ④不正确．因为高科技产品的标准不确定． 答案：②③
(3)无序性：集合与其中元素的排列顺序无关，如由元素a，b， c与由元素b，a，c组成的集合是相等的集合．这个性质通常 用来判断两个集合的关系．
3.元素和集合之间的关系 (1)根据集合中元素的确定性可知，对任何元素a和集合A，在 a∈A和a∉A两种情况中有且只有一种成立. (2)符号“∈”和“∉”只是表示元素与集合之间的关系. 4.对一些常用的数集及其记法要关注的两点
第一章 集合与函数概念 1.1 集合
1.1.1 集合的含义与表示 第1课时 集合的含义
一、元素与集合 1.定义： (1)元素：一般地，把所研究的_对__象_统称为元素，常用小写的 拉丁字母a,b,c，…表示. (2)集合：一些元素组成的总体，简称为_集_，常用大写拉丁字 母A,B,C，…表示. 2.集合相等：指构成两个集合的元素是_一__样_的. 3.集合中元素的特性：_确__定__性_、_互_异__性__和_无__序__性__.
类型 一 集合的判定
【典型例题】
1.下列说法中正确的序号是
.
①高一(四)班学习成绩较好的同学组成一个集合；
(2)方程x2+2x+1=0的解集中有两个元素. (3)组成单词china的字母组成一个集合.
【解题探究】 1.集合中的元素有哪些特性？ 2.集合中的元素能重复吗？
探究提示： 1.集合中的元素有三个特性，即确定性、互异性和无序性. 2.构成集合的元素必须是不相同的，即集合元素具有互异性， 相同的元素只能算作一个. 【解析】1.①不正确.因为成绩较好没有明确的标准． ②正确．中国海洋大学2013级大一新生是确定的，明确的． ③正确．因为参加2012年伦敦奥运会的所有国家是确定的， 明确的． ④不正确．因为高科技产品的标准不确定． 答案：②③
(3)无序性：集合与其中元素的排列顺序无关，如由元素a，b， c与由元素b，a，c组成的集合是相等的集合．这个性质通常 用来判断两个集合的关系．
3.元素和集合之间的关系 (1)根据集合中元素的确定性可知，对任何元素a和集合A，在 a∈A和a∉A两种情况中有且只有一种成立. (2)符号“∈”和“∉”只是表示元素与集合之间的关系. 4.对一些常用的数集及其记法要关注的两点
第一章 集合与函数概念 1.1 集合
1.1.1 集合的含义与表示 第1课时 集合的含义
一、元素与集合 1.定义： (1)元素：一般地，把所研究的_对__象_统称为元素，常用小写的 拉丁字母a,b,c，…表示. (2)集合：一些元素组成的总体，简称为_集_，常用大写拉丁字 母A,B,C，…表示. 2.集合相等：指构成两个集合的元素是_一__样_的. 3.集合中元素的特性：_确__定__性_、_互_异__性__和_无__序__性__.
类型 一 集合的判定
【典型例题】
1.下列说法中正确的序号是
.
①高一(四)班学习成绩较好的同学组成一个集合；
课件集合的基本运算_人教版高中数学必修一PPT课件_优秀版
(3)(∁SA)∪(∁SB)；
6
解析：
• 【解析】(1)由并集的概念可知A∪B＝{1,2,3,4,5,6}；
•
(2)借助数轴(如图)
•
•
∴M∪N＝{x|x＜－5或x＞－3}．
• 【答案】(1){1,2,3,4,5,6} (2)A
7
方法归纳：
• 并集的运算技巧： • (1)若集合中元素个数有限，则直接根据并集的定义求解，但要注意集合中元素的
互异性． • (2)若集合中元素个数无限，可借助数轴，利用数轴分析法求解，但是要注意含“＝”
用实心点表示，不含“＝”用空心点表示．
8
探究一 并集的运算
9
解析：
10
探究二 交集的运算
• 【例】(1)已知集合A＝{x|(x－1)(x＋2)＝0}，B＝{x|(x＋2)(x－3)＝0}，则A∩B＝________.
•
(2)已知集合A＝{x|x≥5}，集合B＝{x|x≤m}，且A∩B＝{x|5≤x≤6}，则实数m＝
________.
•
11
解析：
• 【解析】(1)A＝{x|x＝1或x＝－2}，B＝{x|x＝－2或x＝3}，
•
∴A∩B＝{－2}．
•
(2)结合数轴：
•
•
由图可知m＝6.
• 【答案】(1){－2} (2)6
是否存在？若存在，求出x；
∴(∁RA)∩B＝{x|2＜x＜3或7≤x＜10}．
由此可得：(1)(∁SA)∩(∁SB)＝{x|1<x<2}∪{7}．(2)∁S(A∪B)＝{x|1<x<2}∪{7}；
(3)(∁SA)∪(∁SB)＝{x|1<x<3}∪{x|5≤x≤7}＝{x|1＜x＜3，或5≤x≤7}；
人教版高中数学必修一一集合PPT课件
集合相等：只要构成这两个集合的元素 是一样的，则这个集合是相等的。
例：{两边相等的三角形}和{等腰三角形}
问题
如果用A表示高一（3）班学生组成的集合，a表示高 一（3）班的一位同学，b表示高一（4）班的一位同 学,那么a、b与集合A分别有什么关系？由此看出元 素与集合之间有什么关系？
元素与集合的关系
为_______；用描述法表示为 .
（2）集合{(x, y) | x y 6, x N, y N}
用列举法表示为
.
复习回顾
1、元素和集合的定义 2、集合的特性 3、元素和集合的关系 4、集合的表示方法
实数有相等关系，大小关系， 类比 实数之间的关系，集合之间是否具备类 似的关系？
新课
常用的数集
数集 自然数集(非负整数集)
正整数集 整数集
有理数集 实数集
符号
N N* 或N+
Z Q R
判断Q与N,N*,Z的关系? 课堂练习P5 第1题
解析:判断一个元素是否在某个集合中,关键在于 弄清这个集合由哪些元素组成的.
集合的表示方法
问题 (1) 如何表示“地球上的四大洋”组成的集合?
(2) 如何表示“方程(x-1)(x+2)=0的所有实数根”组 成的集｛合太? 平洋，大西洋，印度洋，北冰洋｝ ｛1,-2｝
③ A＝{x|x2－3x＋2＝0}， B＝{1，2}.
练习1：观察下列各组集合，并指明两个
集合的关系
① A＝Z ，B＝N；
AB
② A＝{长方形}， B＝{平行四边形方形}；AB
③ A＝{x|x2－3x＋2＝0}， B＝{1，2}.
练习1：观察下列各组集合，并指明两个
集合的关系
高中数学必修一第一章 章末复习课课件
反思与感悟
解析答案
跟踪训练2 某粮店销售大米，若一次购买大米不超过50 kg时，单价 为m元；若一次购买大米超过50 kg时，其超出部分按原价的90%计算， 某人一次购买了x kg大米，其费用为y元，则y与x的函数关系式y＝
mx，0≤x≤50， __0_.9_m__x_＋__5_m_，__x_＞__5_0___. 解析 当0≤x≤50时，y＝mx； 当x＞50时，y＝50m＋(x－50)×90%·m＝0.9mx＋5m.
2.数学四大思想：函数与方程、转化与化归、分类讨论、数形结合思想， 本章用到以下思想方法： (1)函数与方程思想体现在函数解析式部分，将实际问题中的条件转化为 数学模型，再通过研究函数性质解决诸如最大、最优等问题. (2)转化与化归主要体现在集合部分符号语言、文字语言、图形语言的转 化，函数中求定义域大多转化成解不等式，求值域大多可以化归为求二 次函数等基本函数的值域. (3)分类讨论主要体现在集合中对空集和区间端点的讨论，函数中主要是 欲去绝对值而正负不定，含参数的函数式的各种性质的探讨. (4)数形结合主要体现在用数轴求并交补集，借助函数图象研究函数性质.
(5)数学交流体现在使用了大量的文字、符号、图形语言，用以刻画集 合的关系运算及函数表示和性质，往往还需要在三种语言间灵活转换， 有意识地培养灵活选择语言，清晰直观而又严谨地表达自己的想法， 听懂别人的想法，从而进行交流与合作. (6)运用信息技术的技能主要表现在应用网络资源拓展知识，了解数学 史及发展前沿，以及应用计算机强大的计算能力描点作图探究新知等 方面.
所以 Q P.
解析答案
1 234
3.设函数 f(x)＝x22x＋，2x，>2x，≤2， 则 f(－4)＝____1_8___，若 f(x0)＝8，则 x0 ＝__－___6_或___4_____. 解析 f(－4)＝(－4)2＋2＝18，由 f(x0)＝8，得xx020≤ ＋22， ＝8， 或x20x>0＝2，8， 得 x0＝－ 6，或 x0＝4.
人教高中数学必修一A版《充分条件与必要条件》集合与常用逻辑用语教学说课复习课件
课件 课件
课件 课件
课件
课件
1．记集合 A＝{x|p(x)}，B＝{x|q(x)}，若 p 是 q 的充分不必要条件，
则集合 A，B 的关系是什么？若 p 是 q 的必要不充分条件呢？
提示：若 p 是 q 的充分不必要条件，则 A B，若 p 是 q 的必要不充分 条件，则 B A.
栏目导航
2．记集合 M＝{x|p(x)}，N＝{x|q(x)}，若 M⊆N，则 p 是 q 的什么条 课件 课件 课件 课件 课件 课件 课件 课件
(2)若 p⇒q，但 q p，则称 p 是 q 的充分不必要条件．
(3)若 q⇒p，但 p q，则称 p 是 q 的必要不充分条件．
(4)若 p q，且 q p，则称 p 是 q 的既不充分也不必要条件．
栏目导航
思考 2：(1)若 p 是 q 的充要条件，则命题 p 和 q 是两个相互等价的命
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
课件
课件
充要条件的探求与证明
【例 3】 试证：一元二次方程 ax2＋bx＋c＝0 有一正根和一负根的
充要条件是 ac＜0.
[思路点拨] 从“充分性”和“必要性”两个方面来证明．
栏目导航
[证明] ①必要性：因为方程 ax2＋bx＋c＝0 有一正根和一负根，所
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
高中必修一数学第一章集合间的基本关系ppt课件-人教版
高中数学
[导入新知] 子集的概念
任意一个
包含
A⊆B B⊇A
高中数学
⊆ ⊆
高中数学
[化解疑难] 对子集概念的理解
(1)集合 A 是集合 B 的子集的含义是：集合 A 中的 个元素都是集合 B 中的元素，即由 x∈A 能推出 x∈B.例 ⊆{－1,0,1}，则 0∈{0,1},0∈{－1,0,1}．
(2)若两集合相等，则两集合所含元素完全相同，与 列顺序无关.
高中数学
真子集 [提出问题] 给出下列集合： A＝{a，b，c}，B＝{a，b，c，d，e}． 问题1：集合A与集合B有什么关系？ 提示：A⊆B. 问题2：集合B中的元素与集合A有什么关系？ 提示：集合B中的元素a，b，c都在A中，但元素d，e不
高中数学
[导入新知] 集合相等的概念
如果集合 A 是集合 B 的 子集 (A⊆B)，且集合 B A 的 子集 (B⊆A)，此时，集合 A 与集合 B 中的元素 的，因此，集合 A 与集合 B 相等，记作 A＝B .
高中数学
[化解疑难] 对两集合相等的认识
(1)若 A⊆B，又 B⊆A，则 A＝B；反之，如果 A＝ ⊆B，且 B⊆A.这就给出了证明两个集合相等的方法，即 ＝B，只需证 A⊆B 与 B⊆A 同时成立即可．
(2)若 A 不是 B 的子集，则 A 一定不是 B 的真子集
高中数学
空集 [提出问题] 一个月有32天的月份组成集合T. 问题1：含有32天的月份存在吗？ 提示：不存在． 问题2：集合T存在吗？是什么集合？ 提示：存在，是空集．
高中数学
[导入新知]
空集的概念
定义 我们把 不含任何元素 的集合，叫做空
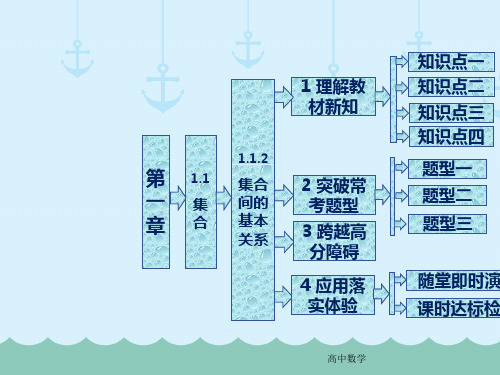
1 理解教 材新知
1.1.2
[导入新知] 子集的概念
任意一个
包含
A⊆B B⊇A
高中数学
⊆ ⊆
高中数学
[化解疑难] 对子集概念的理解
(1)集合 A 是集合 B 的子集的含义是：集合 A 中的 个元素都是集合 B 中的元素，即由 x∈A 能推出 x∈B.例 ⊆{－1,0,1}，则 0∈{0,1},0∈{－1,0,1}．
(2)若两集合相等，则两集合所含元素完全相同，与 列顺序无关.
高中数学
真子集 [提出问题] 给出下列集合： A＝{a，b，c}，B＝{a，b，c，d，e}． 问题1：集合A与集合B有什么关系？ 提示：A⊆B. 问题2：集合B中的元素与集合A有什么关系？ 提示：集合B中的元素a，b，c都在A中，但元素d，e不
高中数学
[导入新知] 集合相等的概念
如果集合 A 是集合 B 的 子集 (A⊆B)，且集合 B A 的 子集 (B⊆A)，此时，集合 A 与集合 B 中的元素 的，因此，集合 A 与集合 B 相等，记作 A＝B .
高中数学
[化解疑难] 对两集合相等的认识
(1)若 A⊆B，又 B⊆A，则 A＝B；反之，如果 A＝ ⊆B，且 B⊆A.这就给出了证明两个集合相等的方法，即 ＝B，只需证 A⊆B 与 B⊆A 同时成立即可．
(2)若 A 不是 B 的子集，则 A 一定不是 B 的真子集
高中数学
空集 [提出问题] 一个月有32天的月份组成集合T. 问题1：含有32天的月份存在吗？ 提示：不存在． 问题2：集合T存在吗？是什么集合？ 提示：存在，是空集．
高中数学
[导入新知]
空集的概念
定义 我们把 不含任何元素 的集合，叫做空
1 理解教 材新知
1.1.2
人教版高中数学必修1《集合的概念》PPT课件
• 题型二 元素与集合的关系 • 【学透用活】
• 元素与集合的关系解读
a∈A与a∉A取决于a是不是集合A中的元素，只 唯一性
有属于和不属于两种关系 符号“∈”“∉”具有方向性，左边是元素， 方向性 右边是集合
[典例 2] (1)满足“a∈A 且 4－a∈A，a∈N 且 4－a∈N ”，有且只有 2
名称 自然数集 正整数集 整数集 有理数集 实数集
记法
N _________
_N_*_或N_＋_
_Z__
_Q__
_R__
• [微思考] N与N*有何区别？
• 提示：N*是所有正整数组成的集合，而N是由0和所有的 正整数组成的集合，所以N比N*多一个元素0.
(二)基本知能小试
1．给出下列关系：①13∈R ；② 5∈Q ；③－3∉Z ；④－ 3∉N ，其中正确的个
数为
()
A．1
B．2
C．3
D．4
解析：13是实数，①正确； 5是无理数，②错误；－3 是整数，③错误；－ 3
是无理数，④正确．故选 B. 答案：B
2．已知集合 M 有两个元素 3 和 a＋1，且 4∈M，则实数 a＝________.
解析：由题意可知 a＋1＝4，即 a＝3. 答案：3
• 知识点三 集合的表示方法
• [方法技巧] • 用列举法表示集合的3个步骤
• (1)求出集合的元素．
• (2)把元素一一列举出来，且相同元素只能列举一次．
• (3)用花括号括起来．
• 提醒：二元方程组的所有实数解组成的集合、函数图象 上的所有点构成的集合都是点的集合，一定要写成实数对 的形式，元素与元素之间用“，”隔开，如{(2,3)，(5，－ 1)}．
人教版(新教材)高中数学第一册(必修1)精品课件：第一章集合与常用逻辑用语章末复习课
【例1】 (1)设集合A＝{1，2，4}，集合B＝{x|x＝a＋b，a∈A，b∈A}，则集合B中元
素的个数是( )
A.4
B.5
C.6
D.7
(2)已知集合A＝{0，1，2}，则集合B＝{x－y|x∈A，y∈A}中元素的个数是( )
A.1
B.3
ቤተ መጻሕፍቲ ባይዱ
C.5
D.9
解析 (1)∵a∈A，b∈A，x＝a＋b，所以x＝2，3，4，5，6，8，∴B中有6个元素， 故选C. (2)当x＝0，y＝0时，x－y＝0；当x＝0，y＝1时，x－y＝－1；当x＝0，y＝2时，x－y ＝－2；当x＝1，y＝0时，x－y＝1；当x＝1，y＝1时，x－y＝0；当x＝1，y＝2时，x －y＝－1；当x＝2，y＝0时，x－y＝2；当x＝2，y＝1时，x－y＝1；当x＝2，y＝2时， x－y＝0.根据集合中元素的互异性知，B中元素有0，－1，－2，1，2，共5个. 答案 (1)C (2)C
【训练4】 (1)若p：x2＋x－6＝0是q：ax＋1＝0的必要不充分条件，则实数a的值为 ________. (2) 若 － a<x< － 1 成 立 的 一 个 充 分 不 必 要 条 件 是 － 2<x< － 1 ， 则 a 的 取 值 范 围 是 ________.
解析 (1)p：x2＋x－6＝0，即x＝2或x＝－3. q：ax＋1＝0，当 a＝0 时，方程无解；当 a≠0 时，x＝－1a. 由题意知p q，q p，故a＝0舍去；
当 a≠0 时，应有－1a＝2 或－1a＝－3，解得 a＝－12或 a＝13. 综上可知，a＝－12或 a＝13. (2)根据充分条件、必要条件与集合间的包含关系，应有{x|－2<x<－1} {x|－a<x< －1}，故有a>2. 答案 (1)－12或13 (2)a>2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
集合结构图 集合
集合含义与表示 集合间关系 集合基本运算
新余四中 曾艳红
一、概念复习
(1), A B
若由任意元素x A,能推出x B,则A B
它分为A B与A=B两种情形
A B :若① A B ② 存在x B且x A, 则A B
A B : A B且B A
同理可知：10 P,8 P;12 P, 2 P.
又P 2, 4,6,8,10,12 P 4,10,12
例3，已知全集U=R,A=x x 1, B x 1 x 2
求：A B, A B, A (CU B), A (CU B)
解：CU B x x 1或x>2 可画数轴如下：
解： A
B
3,
3
A且3
B
32 32
3a 3c
b 0 15 0
解得：3cab8
9
B
x x2 8x 15 0
3,5
又A B 3,5 B A B且3 A又A B 3 A 3 （为什么？）
可用此结论证明两个集合相等。
A B
AB :
A B:
(2), A B x x A或x B
① 其中元素x必为下列三种情形之一 （I),x A但x B (II ), x B但x A
(III ), x A且x B 即任何元素都满足x A或x B
Venn图 AB
1
1 2
x
1
1 2
x
1
A B=x 1 x 2 A B=x x>-1
A (CU B) x x 2 A (CU B) x x 1或x 1
点评 (I),画数轴上方的线时，同一集合画同一高度，
不同的集合画不同的高度。
(II),两个集合的交集是两个集合的线同时对应下数
x2 ax b 0有两相等实根， a2 4b 0又3a b 9 解得：a 6,b 9
a 6,b 9,c 8
练习：1，例3中，已知全集U=R,A=x x 1, B x 1 x 2 求 (CU A) (CU B),CU ( A B)
轴上的数，而两个集合的并只只需一条线对应即可。
(III),要注意检查是否包含端点，对于交集， 端点必须在两个集合才能在交集里，而对于 并集只需在一个集合即可满足要求。
例4，已知A= x x2 ax b 0 ,B= x x2 cx 15 0
又A B=3,5, A B 3,求a,b,c的值。
2,求满足1,3 A 1,3,5的所有集合A
答案：1，（CU A) (CU B) CU ( A B) x x 1
2,A=5或1，5或3，5或1，3，5
探索题：
已知S
x N
x6
, AS,BS
且A B 4,5, (Cs B) A 1, 2
② 符合上述三种情况之一的元素必 在 A B 中，即所有满足条件的 元素都在 A B 中
(3), A B x x A且x B
它包含两层意思
① A B中任何一个元素都是A与B的公共元素
② 集合A,B的所有公共元素都在A B中 A B不是由部分公共元素组成的
Venn图
AB
(4),CU A x | x U且x A
Venn图 U
A
同样要注意每个元素都是有共同特征 和集合包含所有符合共同特征的元素 这两点实质上是描述法表示集合的共 同特点
一、例题讲解
例1，填空
(1),A A=__A__ A =____ A A=_A___ CUU ____ CU _U___ CU (CU A) _A___
U A
(CS A) (CS B) 5
B 3
6
答案：A=1,2,4,5, B 3,4,5
小结
本节课复习了集合的子集，交集，并集 补集的概念
作业
第二教材P14 , 3, 4; P17 , 7，8
A B ____ A ____ A B; 若A B,则A B __A__ A B=__B__
A AB B
BA
例2，已知集合 P 4,6 4, P 8,10 10 P 2,12 12,且P 2, 4, 6,8,10,12,求集合P
解： P 4,6 4 4 P,6 P（为什么？）
集合含义与表示 集合间关系 集合基本运算
新余四中 曾艳红
一、概念复习
(1), A B
若由任意元素x A,能推出x B,则A B
它分为A B与A=B两种情形
A B :若① A B ② 存在x B且x A, 则A B
A B : A B且B A
同理可知：10 P,8 P;12 P, 2 P.
又P 2, 4,6,8,10,12 P 4,10,12
例3，已知全集U=R,A=x x 1, B x 1 x 2
求：A B, A B, A (CU B), A (CU B)
解：CU B x x 1或x>2 可画数轴如下：
解： A
B
3,
3
A且3
B
32 32
3a 3c
b 0 15 0
解得：3cab8
9
B
x x2 8x 15 0
3,5
又A B 3,5 B A B且3 A又A B 3 A 3 （为什么？）
可用此结论证明两个集合相等。
A B
AB :
A B:
(2), A B x x A或x B
① 其中元素x必为下列三种情形之一 （I),x A但x B (II ), x B但x A
(III ), x A且x B 即任何元素都满足x A或x B
Venn图 AB
1
1 2
x
1
1 2
x
1
A B=x 1 x 2 A B=x x>-1
A (CU B) x x 2 A (CU B) x x 1或x 1
点评 (I),画数轴上方的线时，同一集合画同一高度，
不同的集合画不同的高度。
(II),两个集合的交集是两个集合的线同时对应下数
x2 ax b 0有两相等实根， a2 4b 0又3a b 9 解得：a 6,b 9
a 6,b 9,c 8
练习：1，例3中，已知全集U=R,A=x x 1, B x 1 x 2 求 (CU A) (CU B),CU ( A B)
轴上的数，而两个集合的并只只需一条线对应即可。
(III),要注意检查是否包含端点，对于交集， 端点必须在两个集合才能在交集里，而对于 并集只需在一个集合即可满足要求。
例4，已知A= x x2 ax b 0 ,B= x x2 cx 15 0
又A B=3,5, A B 3,求a,b,c的值。
2,求满足1,3 A 1,3,5的所有集合A
答案：1，（CU A) (CU B) CU ( A B) x x 1
2,A=5或1，5或3，5或1，3，5
探索题：
已知S
x N
x6
, AS,BS
且A B 4,5, (Cs B) A 1, 2
② 符合上述三种情况之一的元素必 在 A B 中，即所有满足条件的 元素都在 A B 中
(3), A B x x A且x B
它包含两层意思
① A B中任何一个元素都是A与B的公共元素
② 集合A,B的所有公共元素都在A B中 A B不是由部分公共元素组成的
Venn图
AB
(4),CU A x | x U且x A
Venn图 U
A
同样要注意每个元素都是有共同特征 和集合包含所有符合共同特征的元素 这两点实质上是描述法表示集合的共 同特点
一、例题讲解
例1，填空
(1),A A=__A__ A =____ A A=_A___ CUU ____ CU _U___ CU (CU A) _A___
U A
(CS A) (CS B) 5
B 3
6
答案：A=1,2,4,5, B 3,4,5
小结
本节课复习了集合的子集，交集，并集 补集的概念
作业
第二教材P14 , 3, 4; P17 , 7，8
A B ____ A ____ A B; 若A B,则A B __A__ A B=__B__
A AB B
BA
例2，已知集合 P 4,6 4, P 8,10 10 P 2,12 12,且P 2, 4, 6,8,10,12,求集合P
解： P 4,6 4 4 P,6 P（为什么？）