自动控制原理:方框图的化简..54页PPT
合集下载
自动控制原理方框图

[注意]:
相临的信号相加点位置可以互换;见下例
X1(s)
X2(s)
X3(s)
Y (s)
X1(s)
X3(s)
X 2 (s)
Y (s)
同一信号的分支点位置可以互换:见下例
X1(s)
X (s) G(s) Y (s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下,不能互换。
§2-3 控制系统的结构图与信号流图
一、结构图的组成和绘制
1、结构图的组成 由四种基本图形符号组成
(1)函数方块
R(s) r(t) G(s)
C(s) c(t)
(2)信号线
R(s) r(t)
(3)分支点(引出点)
R(s) r(t)
R(s) r(t) R(s) r(t)
(4)综合点(比较点或相加点)
R(s)
R
R1Cs
2I
2
(s)
UI (cs)(s)
R2
R1
Uc (s)
U c (s)
I1 (s)
Uc (s)
几点说明:
(1)在结构图中,每一个方框中的传递函数都应是考虑了负 载效应后的传递函数。
(2)描述一个系统的结构图不是唯一的,选择不同的中间变 量得到不同的结构图;
(3)结构图中的方框与实际系统的元部件并非一定是一一对 应的;
X1(s) G(s) X2(s) N(s)
Y (s)
N(s) ? Y (s) [X1(s) X 2 (s)]G(s), 又 : Y (s) X (s)1G(s) X 2 (s)N(s), N(s) G(s)
把相加点从环节的输出端移到输入端:
自动控制原理方框图的化简课件

化简过程中的误差分析
误差来源分析
分析化简过程中可能产生的误差来源,如近似处理、线性化等。
误差传递与影响
评估误差对系统性能的影响,了解误差传递的方式和程度。
误差补偿与修正
根据误差分析结果,采取适当的补偿和修正措施,减小误差对系 统性能的影响。
化简后系统的性能分析
稳定性分析
通过化简后系统的传递函数或状态方程,分析系统的 稳定性。
方框图的组成元素
总结词
方框图由输入、输出、转换和反馈四个基本元素组成。
详细描述
方框图由输入、输出、转换和反馈四个基本元素组成。输入是系统接收的信号 或信息,输出是系统输出的信号或信息,转换是系统内部对输入进行处理的过 程,反馈则是系统对输出的反应或调整。
方框图的作用
• 总结词:方框图可以清晰地表示系统的结构、功能和动态特性。
04
方框图化简的注意事项
化简方法的适用性
确定化简方法的适用范围
01
不同的化简方法适用于不同类型和规模的方框图,应先判断所
处理的方框图是否适用。
理解化简方法的原理
02
掌握化简方法的原理和步骤,确保正确应用化简方法。
考虑化简后的系统性能
03
在化简方框图时,应考虑化简对系统性能的影响,如稳定性、
动态响应等。
02
通过化简方框图,可以快速识 别故障传递路径和关键环节, 提高故障诊断的效率和准确性 。
03
化简后的方框图可以作为故障 诊断的参考模型,为故障排除 提供指导和支持。
谢谢观看
• 详细描述:方框图具有多种作用。首先,它可以清晰地表示系统的结构,将复杂的系统分解为若干个简单的组成部分, 便于理解和分析。其次,通过方框图可以明确地表示出系统的功能,即各个组成部分的作用及其相互关系。此外,方框 图还可以表示系统的动态特性,例如信号的传递、处理和反馈过程,有助于揭示系统的动态行为和性能。在自动控制原 理中,方框图是分析和设计控制系统的重要工具之一。通过对方框图的分析,可以了解系统的性能、稳定性、可控性和 可观测性等方面的问题,为控制系统的设计和优化提供依据。
自动控制理论第六讲 方框图

06
总结与展望
本讲内容总结
方框图基本概念
方框图的绘制方法
介绍了方框图的基本元素,包括方块、箭 头、分支点和交汇点等,以及它们在控制 系统中的含义。
详细讲解了如何根据控制系统的结构和功 能,选择合适的方块和连接方式,绘制出 清晰、准确的方框图。
方框图的分析方法
方框图在控制系统中的应用
介绍了方框图的分析步骤和方法,包括前 向通路、反馈通路、开环传递函数和闭环 传递函数的计算等。
梅森公式介绍
01
梅森公式是一种用于求解复杂控制系统方框图传递函
数的数学方法。
梅森公式应用步骤
02 首先找出所有前向通道、回路和不相交回路的传递函
数;然后按照梅森公式计算系统的总传递函数。
梅森公式在化简复杂方框图中的优势
03
能够简化计算过程,避免繁琐的代数运算,提高求解
效率。
实例分析:典型系统方框图化简过程
05
方框图在控制系统分析中的应用
稳定性分析:通过方框图判断系统稳定性
01
稳定性定义
系统受到扰动后,能够自动恢复到平衡状态的能力。
02 03
稳定性判据
通过方框图中各环节传递函数的极点位置,判断系统是否稳定。若极点 全部位于复平面的左半部分,则系统稳定;若有极点位于复平面的右半 部分,则系统不稳定。
结合实际工程问题进行实践
通过实际工程问题,将所学的方框图知识应用到实践中去,提高分析 和解决问题的能力。
拓展相关领域的知识
学习与自动控制理论相关的其他领域知识,如现代控制理论、智能控 制等,以完善自己的知识体系。
THANKS
感谢观看
方框图的作用
方框图是一种用图形符号表示系统各 环节间相互关系的图解表示法,它简 洁明了地表示了系统的结构和功能。
自动控制原理第二章方框

详细描述
在自动控制原理中,串联方框通常表示线性元件或环节,它们的输出是输入的线性变换。因此,当多 个串联方框连接在一起时,可以将它们的输出和输入端连接在一起,简化为一个单一的方框,这个方 框的传递函数是所有串联方框传递函数的乘积。
并联方框的简化
总结词
并联方框的简化是将多个并联的方框简化为单一方框,通过将多个方框的输出端合并为单一输出实现。
输入信号的特性
决定了系统输出信号的变 化规律,是分析系统性能 的重要依据。
常见的输入信号
阶跃信号、正弦信号数
描述系统内部动态特性的数学模型, 表示系统输出与输入之间的函数关系。
传递函数的定义
传递函数的性质
与时间变量无关,只与系统内部参数 有关,决定了系统对输入信号的响应 特性。
方框图的绘制方法
01
02
03
确定系统组成部分
首先需要确定系统的各个 组成部分,并了解它们的 功能和相互关系。
绘制方框图
根据各组成部分之间的关 系,使用方框、箭头和文 字绘制方框图。
标注参数和变量
在方框图中标注各组成部 分的参数和变量,以便于 分析和设计。
02
方框图的组成
输入信号
输入信号
表示系统外部对系统的激 励或作用力,是系统输入 端所接收的信号。
VS
详细描述
在自动控制原理中,反馈环是由一系列的 串联和并联方框组成的闭环系统。为了简 化方框图,可以将反馈环中的某些环节省 略,从而消除反馈环。这种简化方法可以 减少系统的复杂性和计算难度,但需要注 意保留必要的反馈环节以保持系统的稳定 性和性能。
04
方框图的分析
稳定性分析
1
稳定性分析是控制系统的重要特性,它决定了系 统在受到扰动后能否回到平衡状态。
在自动控制原理中,串联方框通常表示线性元件或环节,它们的输出是输入的线性变换。因此,当多 个串联方框连接在一起时,可以将它们的输出和输入端连接在一起,简化为一个单一的方框,这个方 框的传递函数是所有串联方框传递函数的乘积。
并联方框的简化
总结词
并联方框的简化是将多个并联的方框简化为单一方框,通过将多个方框的输出端合并为单一输出实现。
输入信号的特性
决定了系统输出信号的变 化规律,是分析系统性能 的重要依据。
常见的输入信号
阶跃信号、正弦信号数
描述系统内部动态特性的数学模型, 表示系统输出与输入之间的函数关系。
传递函数的定义
传递函数的性质
与时间变量无关,只与系统内部参数 有关,决定了系统对输入信号的响应 特性。
方框图的绘制方法
01
02
03
确定系统组成部分
首先需要确定系统的各个 组成部分,并了解它们的 功能和相互关系。
绘制方框图
根据各组成部分之间的关 系,使用方框、箭头和文 字绘制方框图。
标注参数和变量
在方框图中标注各组成部 分的参数和变量,以便于 分析和设计。
02
方框图的组成
输入信号
输入信号
表示系统外部对系统的激 励或作用力,是系统输入 端所接收的信号。
VS
详细描述
在自动控制原理中,反馈环是由一系列的 串联和并联方框组成的闭环系统。为了简 化方框图,可以将反馈环中的某些环节省 略,从而消除反馈环。这种简化方法可以 减少系统的复杂性和计算难度,但需要注 意保留必要的反馈环节以保持系统的稳定 性和性能。
04
方框图的分析
稳定性分析
1
稳定性分析是控制系统的重要特性,它决定了系 统在受到扰动后能否回到平衡状态。
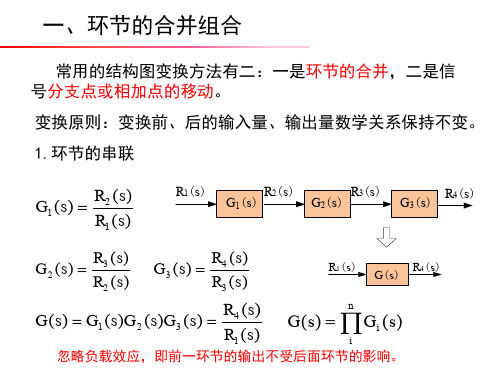
自动控制理论_哈尔滨工业大学_2 第2章线性系统的数学模型_(2.6.1) 方框图的化简PPT
c(t)
G(s) U2(s)
U1(s)
r(t)
1
R1R2C1C2S 2 (R1C1 R1C2 R2C2 )s 1
如果加入隔离放大器忽略负载效应。
G(s) C(s) 1 K 1
R(s) R1C1s 1
R2C2s 1
R1 C1 r1(t) r1(t)
R1
R2
C1 K r(t)
Y X1 X2 X3
G(s) Y
Y
6
2. 分支点的移动和互换 分支点后移:
X1
Y
G(s)
X1
分支点前移:
X1
Y
G(s)
Y
X1 G(s)
Y
X1 1/G(s)
X1
Y
G(s)
G(s)
Y
7
分支点互换
Y
Y
Y
Y
Y
Y
如何进行方框图的化简?
(1) 方框图化简的关键是解除环路与环路的交叉,使之分开 或形成大环套小环的形式。 (2)解除交叉连接的有效方法是移动相加点或分支点。相邻的 分支点(或综合点)可以彼此交换。 (3)分支点与综合点相邻时,它们不能作简单的位置交换。
控制系统方框图变换的原则和化简的方法。
X1 +
Y
X2 +
Y
X1
+ X1
X2
+Y
分支点移动
G1
H2 G2
1 G4
G3 a G4 b
H1
H2
G4
-
+
G1(s) +
G2 (s)
-
G3G4 1 G3G4H3
H1(s)
H3
向同类移动!
+ -
自动控制原理第二章方框图

X 3 (s)
X (s)
G(s)
X (s)
X 2 (s)
X 3 (s)
G(s)
X 2 (s)
故:一般情况下,相加点向相加点移动,分支点向分支点移动
注: (1) 结构图简化的关键是解除环路与环路的交叉,使之分开或 形成大环套小环的形式。 (2)解除交叉连接的有效方法是移动相加点或分支点。 (3)当分支点与综合点相邻时,它们的位置就不能作简单的交 换。
R(s) G1(S)
G2(S) G3(S)
C(s) G4(S)
R(s)
C(s)
G1(S)
G2(S)
G3(S)
G4(S)
U1(s)+
- U3(s)
I2(s) 1 I1(s) -
R1 +
1 U3(s) C1s + -
1
1 U2(s)
R2 I2(s) C2 s
U2(s)
考虑移动某些信号的相加点和分支点
环节的并联:
和
G1 ( s )
X (s)
Gn (s)
Y (s)
G(s)
Y (s) X (s)
n i 1
Gi (s)
反馈联接:
X (s) E(s) G(s) Y (s)
B(s)
H (s)
Y (s) E(s)G(s)
E(s) X (s) H (s)Y (s),
G(s)
Y (s) X (s)
1
G(s) G(s)H (s)
U c (s) I (s)R2
U r (s)
1 I1(s)
U c (s)
R1
I 2 (s)C
I1 (s) R1Cs I 2 (s)
I (s)
控制系统的方框图 ppt课件

E1( s) R( s ) 1 G1( s)G 2( s) H ( s)
R(s) E(s) B(s) H
ppt课件 22
G1G2
C(s)
N(s)
② R(s)=0时(无参数输入)
E(s) B(s)
C(s) G2
G1 H
E ( s) B( s) H ( s )C ( s )
H ( s )G 2( s )[N ( s ) G1( s ) E ( s )] H ( s )G 2( s ) E 2 ( s) N ( s) 1 G1G 2 H ( s )
G(s) X (s) Y(s)
其中G(S)=G1(S)G2(S)
ppt课件 11
2.并联:环节输入信号相同,输出信号相加(减)
G1 X(S) G2
Y(S)
等效:
X (s)
G(s)
Y(s)
其中G(S)=G1(S)G2(S)
ppt课件 12
3. 反馈联接
R(s)
E(s) B(s)
G(s)
C(s)
H(s)
利用叠加原理:(R(s)、N(s)同时作用)
E(s) E1(s) E2(s) 1 G2H R( s) N ( s) 1 G1G2H 1 G1G 2 H
ppt课件 23
1.传递函数
① N(s)=0时(无扰动) 输入R(s),输出C(s)
G1( s)G 2( s) C1( s) R( s ) 1 G1( s)G 2( s) H ( s)
ppt课件
R(s)
C(s)
G1G2
H
20
N(s)
② R(s)=0时(无参数输入)
C 2( s) G 2( s) N ( s) 1 G1( s)G 2( s) H ( s)
R(s) E(s) B(s) H
ppt课件 22
G1G2
C(s)
N(s)
② R(s)=0时(无参数输入)
E(s) B(s)
C(s) G2
G1 H
E ( s) B( s) H ( s )C ( s )
H ( s )G 2( s )[N ( s ) G1( s ) E ( s )] H ( s )G 2( s ) E 2 ( s) N ( s) 1 G1G 2 H ( s )
G(s) X (s) Y(s)
其中G(S)=G1(S)G2(S)
ppt课件 11
2.并联:环节输入信号相同,输出信号相加(减)
G1 X(S) G2
Y(S)
等效:
X (s)
G(s)
Y(s)
其中G(S)=G1(S)G2(S)
ppt课件 12
3. 反馈联接
R(s)
E(s) B(s)
G(s)
C(s)
H(s)
利用叠加原理:(R(s)、N(s)同时作用)
E(s) E1(s) E2(s) 1 G2H R( s) N ( s) 1 G1G2H 1 G1G 2 H
ppt课件 23
1.传递函数
① N(s)=0时(无扰动) 输入R(s),输出C(s)
G1( s)G 2( s) C1( s) R( s ) 1 G1( s)G 2( s) H ( s)
ppt课件
R(s)
C(s)
G1G2
H
20
N(s)
② R(s)=0时(无参数输入)
C 2( s) G 2( s) N ( s) 1 G1( s)G 2( s) H ( s)
第4讲控制系统的方框图及其化简1

ui u o i R
L
ui ( s ) u o ( s ) i(s) R
U i ( s)
一阶RC网络
x
U o ( s) (b)
I(s)
由电容元件特性可得:
uo
idt
c
积 分 定 理
U i (s)
x
- U o ( s)
I(s)
U o ( s)
(d)
L
变 换
相同 的信 号线 连接
U c ( s)
A
1 sC 2
U c ( s)
UC1 (s)
(c)方块图
在RC之间加入输入阻抗很大而输出阻抗很小的隔离放大器
R1
U r ( s)
R2 隔 离 K 放 大 器
( a)
x
1 R1 u r
1 C1 sC 1
xC 2
1 R2 u c
1 sC 2
U c ( s)
图2-22 带隔离放大器的两级RC网络
U r (s) x U C ( s)
1 R1
U r (s) I 1 (s) R1 U C (s)
U C ( s) I ( s) R2
I 1 ( s)
I (s)
R2
U C ( s)
例2
绘制无源网络的方块图
1 I 2 ( s) I 1 (s) R1 Cs
I1 (s)
R1
Cs
I 2 ( s)
G1( s )
G 2( s )
C( s )
-
-
H 1( s )
R( s )
G1( s )
G 2( s )
C( s )
-
1 G1( s )
控制工程基础:2.5 控制系统的方块图及其化简

输出信号C(s)与输入信号R(s)之比。
C(s) G1 (s)G2 (s) G(s) R(s) 1 H (s)G(s) 1 H (s)G(s)
N(s)
+ E(s)
++
C(s)
R(s)
G1(s)
G2 (s)
-
B(s)
H(s)
打开反馈
图2-18 反馈控制系统方块图
推导:因为 C(s) E(s)G(s) [R(s) C(s)H (s)]G(s)
基本步骤 1、消除交叉点 2、由内环-----外环化简
G5 G2G3 G4 串联和并联
G7
G6
R(s)
-
-
G1 H1G2
B
G5
-
C C(s)
H2
1 G5
G6
G5 1 G5 H 2
反馈公式
G1G5
G7
G1G6 1 G1G6 H1G2
1 G5
1 G5 H 2 1 G1H1G2 1 G5 H 2
(3)开环传递函数 Open-loop Transfer Function 假设N(s)=0, 主反馈信号B(s)与误差信号E(s)之比。
B(s) E(s)
G1 (s)G2 (s)H (s)
G(s)H (s)
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0
方块图是一种很有用的图示法。对于复杂的控制系统,方 块图的简化过程仍较复杂,且易出错。Mason提出的信号流 图,既能表示系统的特点,而且还能直接应用梅逊公式方便 的写出系统的传递函数。因此,信号流图在控制工程中也被 广泛地应用。
2.6.1信号流图中的术语
自动控制原理课件ppt

03
非线性控制系统
非线性控制系统的特点
非线性特性
01
非线性控制系统的输出与输入之间存在非线性关系,
如放大器、继电器等。
复杂的动力学行为
02 非线性控制系统具有复杂的动力学行为,如混沌、分
叉、稳定和不稳定等。
参数变化范围广
03
非线性控制系统的参数变化范围很广,如电阻、电容
、电感等。
非线性控制系统的数学模型
线性控制系统的性能指标与评价
性能指标
衡量一个控制系统性能的好坏,需要使用一些性能指标,如响应时间、超调量、稳态误差等。
性能分析
通过分析系统的性能指标,可以评价一个控制系统的优劣。例如,响应时间短、超调量小、稳态误差小的系统性能较 好。
系统优化
根据性能分析的结果,可以对控制系统进行优化设计,提高控制系统的性能指标。例如,可以通过调整 控制器的参数,减小超调量;或者通过改变系统的结构,减小稳态误差。
。
采样控制系统的数学模型
描述函数法
描述函数法是一种分析采样控制系统的常用方法,通过将连续时间 函数离散化,用差分方程来描述系统的动态特性。
z变换法
z变换法是一种将离散时间信号变换为复平面上的函数的方法,可 用于分析采样控制系统的稳定性和性能。
状态空间法
状态空间法是一种基于系统状态变量的方法,可以用于分析复杂的采 样控制系统。
航空航天领域中的应用
总结词
高精度、高可靠性、高安全性
详细描述
自动控制原理在航空航天领域中的应用至关重要。例如 ,在飞机系统中,通过使用自动控制原理,可以实现飞 机的自动驾驶和自动着陆等功能,从而提高飞行的精度 和安全性。在火箭和卫星中,通过使用自动控制原理, 可以实现推进系统的精确控制和姿态调整等功能,从而 保证火箭和卫星能够准确地进行轨道变换和定点着陆。
自动控制原理课件

2 . 并联 : 若各个环节接受同一 输入信号而输出信号又汇合在 一点时,称为并联。 一点时,称为并联。 如图2-34所示。由图可知 所示。 如图 所示
C(s) = C1(s) + C2 (s) +L+ Cn (s) C1(s) = G1(s)R(s) C2 (s) = G2 (s)R(s) 环节的并联 M Cn (s) = Gn (s)R(s) C(s) C1 (s) +C 2(s) +L+ Cn (s) = 总的传递函数为 G(s) = R(s) R(s)
2.4.3 环节间的连接
环节的连接有串联、并联和反馈三种基本形式。 环节的连接有串联、并联和反馈三种基本形式。
1.串联 : 串联
在单向的信号传递中, 若前一个环节的输出就 在单向的信号传递中 , 是后一个环节的输入, 并依次串接如图所示, 是后一个环节的输入 , 并依次串接如图所示 , 这 种联接方式称为串联。 种联接方式称为串联。
3、各环节方框图
RC网络方框图 4、RC网络方框图
例 2 - 6 图中为电 枢电压控制的直流 他励电动机,描述 其运动方程为
dia (t ) ua (t ) = La dt + Raia (t ) + ea (t ) ea (t ) = ceω(t ) MD = cM ia (t ) dω + ML MD = J dt
零初始条件下, 零初始条件下,对式中两边取拉氏变换
Ua (s) = (Ra + La s)I a (s) + Ea (s) Ea (s) = ce (s) MD (s) = cM I a (s) MD (s) = JsΩ(s) + ML (s)
自动控制原理方框图的化简PPT学习教案

G(s)
G(s)
X1(s)
第23页/共54页
6. 相加点变换的其他规则
a.相加点之间相互交换
X1(s)
X (s)
X2(s) X3(s)
X1(s)
X (s) X1(s) X2(s) X3(s)
X (s)
X3(s) X2(s)
b.相加点之合并与拆分
X1(s)
X (s)
X2(s) X3(s)
第2页/共54页
3)分支点
分支点表示同一信号向不同方向的传递,在分支 点引出的信号不仅量纲相同,而且数值也相等.
X1(s) X1(s)
X1(s)
第3页/共54页
2.建立系统方框图的步骤
1)建立系统元件的原始微分方程; 2)分别对上述微分方程在初始条件为零的条
件下进行Laplace变换,并根据各Laplace变换 的因果关系,分别绘出各自的方框图; 3)按照信号在系统中传递、变换的过程,依 次将上述各个传递函数方框图连接起来 (同一变量的信号通路连在一起),系统 的输入量置于左端,输出量置于右端,便 得到系统的传递函数方框图。
Xi (s)
G(s)
Xo (s)
第27页/共54页
例1
R(s)
G1 G2
G3
H4
G4
G5
H2
H1
C(s) G6
R(s)
1
G2
H4
G1
G2 G3
G4 G5
H2
H1
第28页/共54页
C(s) G6
R(s)
R(s)
G1
G2
H4 G2
G3
G4G5
H2
H1
H4
