八年级数学《全等三角形》专题训练 (1)

合集下载

中考数学复习《全等三角形》专题(卷1)

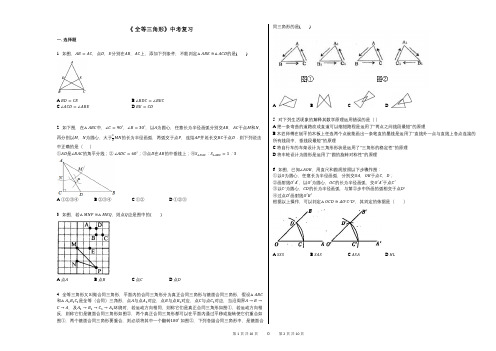
《全等三角形》中考复习一. 选择题1. 如图，AB=AC，点D，E分别在AB，AC上，添加下列条件，不能判定△ABE≅△ACD的是( )A.BD=CEB.∠BDC=∠BECC.∠ACD=∠ABED.BE=CD2. 如下图，在△ABC中，∠C=90∘，∠B=30∘，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M，N 为圆心，大于12MN的长为半径画弧，两弧交于点P ，连结AP 并延长交BC于点D．则下列说法中正确的是（）①AD是∠BAC的角平分线；②∠ADC=60∘；③点D在AB的中垂线上；④S△DAC：S△ABC=1：3.A.①②③④B.②③④C.①②D.①②③3. 如图，若△MNP≅△MEQ，则点Q应是图中的()A.点AB.点BC.点CD.点D4. 全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC 和△A1B1C1是全等（合同）三角形，点A与点A1对应，点B与点B1对应，点C与点C1对应，当沿周界A→B→C→A，及A1→B1→C1→A1环绕时，若运动方向相同，则称它们是真正合同三角形如图①，若运动方向相反，则称它们是镜面合同三角形如图②，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合如图①，两个镜面合同三角形要重合，则必须将其中一个翻转180∘如图②，下列各组合同三角形中，是镜面合同三角形的是( )A. B. C. D.5. 对下列生活现象的解释其数学原理运用错误的是（）A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理6. 如图，已知∠AOB，用直尺和圆规按照以下步骤作图：①以O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；②画射线O′A′，以O′为圆心，OC的长为半径画弧，交O′A′于点C′③以C′为圆心，CD的长为半径画弧，与第②步中所画的弧相交于点D′④过点D′画射线O′B′根据以上操作，可以判定△OCD≅ΔO′C′D′，其判定的依据是（）A.SSSB.SASC.ASAD.HL7. 如图，在扇形OAB中，点C是弧AB上任意一点（不与点A，B重合），CD//OA交OB于点D，点I是△OCD 的内心，连结OI，BI，∠AOB=β，则∠OIB等于()A.180∘−βB.180∘−12β C.90∘+12β D.90∘+β8. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1，2，3，4的四块），你认为将其中的哪一块带去玻璃店，就能配一块与原来一样大小的三角形玻璃.应该带( )A.第1块B.第2块C.第3块D.第4块二. 填空题三角形具有稳定性，所以要使六边形木架不变形，至少要钉上________根木条．如图，在x、y轴上分别截取OA、OB，使OA=OB，再分别以点A、B 为圆心，以大于12AB的长度为半径画弧，两弧交于点C．若C的坐标为(3a,−a+8)，则a=________.如图，在菱形ABCD中，已知AB=4，∠ABC=60∘，∠EAF=60∘，点E在CB的延长线上，点F在DC的延长线上，有下列结论：①BE=CF；②∠EAB=∠CEF；③△ABE∼△EFC；④若∠BAE=15∘，则点F到BC的距离为2√3−2.正确序号________.如图，△ABC中，点A的坐标为(0, 1)，点C的坐标为(4, 3)，如果要使△ABD与△ABC全等，那么点D的坐标是________．三. 解答题如图，小明用五根宽度相同的木条拼成了一个五边形，已知AE//CD，∠A=12∠C，∠B=120∘.(1)∠D+∠E=________度；(2)求∠A的度数；(3)要使这个五边形木架保持现在的稳定状态，小明至少还需钉上________根相同宽度的木条．根据要求完成下列各题．(1)如图1，在∠AOB的内部有一点P．①过点P画直线PC//OA交OB于点C；②过点P画直线PD⊥OA，垂足为D．(2)如图2，AB⊥BF,CD⊥BF,∠1=∠2，试说明∠3=∠E在下面解答中填空．解：∵AB⊥BF,CD⊥BF（已知），∴∠ABF=∠________=90∘（________），∴AB//CD（________）∵∠1=∠2（已知），∴AB//EF（________），∴CD//EF（平行于同一条直线的两条直线互相平行），∴∠3=∠E（________）如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF= BD，连接BF．(1)线段BD与CD有何数量关系，为什么？(2)当△ABC满足什么条件时，四边形AFBD是矩形？请说明理由．(3)当△ABC满足________条件时，四边形AFBD是正方形？（直接写出结论，不用说明理由）一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．（要求，画出示意图，并标出字母，结合图形简要叙述你的方案）参考答案与试题解析一. 选择题1.【答案】D【解析】欲使△ABE≅△ACD，已知AB＝AC，可根据全等三角形判定定理AAS、SAS、ASA添加条件，逐一证明即可．2.【答案】A【解析】①连接NP，MP，根据SSS定理可得△ANP≅△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30∘，根据直角三角形的性质可知∠ADC=60∘；③根据∠1=∠B可知AD=BD，故可得出结论；④先根据直角三角形的性质得出∠2=30∘，CD=12AD，再由三角形的面积公式即可得出结论．3.【答案】D【解析】此题暂无解析4.【答案】B【解析】认真阅读题目，理解真正合同三角形和镜面合同三角形的定义，然后根据各自的定义或特点进行解答．5.【答案】B【解析】根据圆的有关定义、垂线段的性质、三角形的稳定性等知识结合生活中的实例确定正确的选项即可．6.【答案】A【解析】此题暂无解析7.【答案】B 【解析】此题暂无解析8.【答案】B【解析】本题应先假定选择哪块，再对应三角形全等判定的条件进行验证．二. 填空题【答案】3【解析】三角形具有稳定性，所以要使六边形木架不变形需把它分成三角形，即过六边形的一个顶点作对角线，有几条对角线，就至少要钉上几根木条．【答案】2【解析】此题暂无解析【答案】①②【解析】①只要证明△BAE≅△CAF即可判断；②根据等边三角形的性质以及三角形外角的性质即可判断；③根据相似三角形的判定方法即可判断；④求得点F到BC的距离即可判断．【答案】(4, −1)或(−1, 3)或(−1, −1)【解析】因为△ABD与△ABC有一条公共边AB，故本题应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论，计算即可得出答案．三. 解答题【答案】180(2)五边形的内角和为(5−2)×180∘=540∘，由(1)可知，∠D+∠E=180∘，又∠B=120∘，∠A=12∠C.设∠A=x，则∠C=2x，∴∠A+∠B+∠C+∠D+∠E=540∘,即x+120∘+2x+180∘=540∘,解得x=80∘,∴∠A=80∘.2【解析】(1)根据平行线性质，两直线平行同旁内角互补即可得到180∘.先由AE//CD，根据平行线的性质得出∠E+∠D=180∘．再根据∠B=120∘，∠A=12∠C，设∠A=x∘，则∠C=2x∘．利用五边形的内角和为540∘列出方程x+120+2x+180=540，求解即可.根据五边形不具有稳定性，而三角形具有稳定性即可求解．【答案】解：（1）①如图，直线PC即为所求；②如图，直线PD即为所求；（2）解：∵AB⊥BF,CD⊥BF（已知），∴∠ABF=∠CDF=90∘（垂直的定义），∴AB//CD（同位角相等，两直线平行）∵∠1=∠2（已知），∴AB//EF（内错角相等，两直线平行），∴CD//EF（平行于同一条直线的两条直线互相平行），∴∠3=∠E（两直线平行，同位角相等）【解析】此题暂无解析【答案】解：(1)BD=CD．理由如下：依题意得AF // BC，∴∠AFE=∠DCE，∵E是AD的中点，∴AE=DE，在△AEF和△DEC中，{∠AFE=∠DCE，∠AEF=∠DEC，AE=DE，∴△AEF≅△DEC(AAS)，∴AF=CD，∵AF=BD，∴BD=CD；(2)当△ABC满足AB=AC时，四边形AFBD是矩形．理由如下：∵AF // BD，AF=BD，∴四边形AFBD是平行四边形，∵AB=AC，BD=CD，∴∠ADB=90∘，∴四边形AFBD是矩形．AB=AC，∠BAC=90∘【解析】（1）根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90∘，由等腰三角形三线合一的性质可知必须是AB=AC．【答案】解：在河南岸AB的垂线BF上取两点C、E，使CE=BE，再定出BF的垂线CD，使A、E、D在同一条直线上，这时测得CD的长就是AB的长．如图所示：【解析】已知等边及垂直，在直角三角形中，可考虑AAS证明三角形全等，从而推出线段相等．。

【教师卷】洛阳市八年级数学上册第十二章《全等三角形》经典复习题(专题培优)(1)

一、选择题1．如图，在△ABC 中，AB=AC ，AB ＞BC ，点D 在BC 边上，BD=12DC ，∠BED=∠CFD=∠BAC ，若S △ABC =30，则阴影部分的面积为（）A ．5B ．10C ．15D ．20D解析：D【分析】根据△ABE ≌△CAF 得出△ACF 与△ABE 的面积相等，可得S △ABE +S △CDF =S △ACD ，即可得出答案．【详解】∵∠BED=∠CFD=∠BAC ，∠BED=∠BAE+∠ABE ，∠BAC=∠BAE+∠CAF ，∠CFD=∠FCA+∠CAF ，∴∠ABE=∠CAF ，∠BAE=∠FCA ，在△ABE 和△CAF 中，ABE CAF AB AC BAE FCA ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABE ≌△CAF （ASA ），∴S △ABE =S △ACF ， ∴阴影部分的面积为S △ABE +S △CDF =S △ACD ，∵S △ABC =30，BD=12DC ， ∴S △ACD =20，故选：D ．【点睛】本题考查了全等三角形的性质和判定，三角形的面积，三角形的外角性质等知识点，解题的关键是正确寻找全等三角形解决问题．2．如图，,,AB AD CB CD AC BD ==、相交于点O ，则下列说法中正确的个数是（） ①OD OB =；②点O 到CB CD 、的距离相等；③BDA BDC ∠=∠；④BD AC ⊥A ．4B ．3C ．2D ．1B解析：B【分析】先根据全等三角形的判定定理得出△ACD ≌△ACB ，△ABO ≌△ADO ，再根据全等三角形的性质即可得出结论．【详解】解：在△ABC 和△ADC 中，∵AB AD BC CD AC AC ⎧⎪⎨⎪⎩＝＝＝，∴△ABC ≌△ADC （SSS ），∴∠BAC=∠DAC ， ∠DCA=∠BCA∴点O 到CB 、CD 的距离相等．故②正确在△ABO 与△ADO 中AB AD BAC DAC OA OA ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABO ≌△ADO （SAS ），∴BO=DO ，∠BOA=∠DOA∵∠BOA+∠DOA=180°∴∠BOA=∠DOA=90°，即BD AC ⊥故①④正确；∵AD≠CD∴BDA BDC ∠≠∠，故③错误所以，正确的结论是①②④，共3个，故选：B ．【点睛】本题考查了全等三角形的判定和性质，掌握全等三角形的判定方法是解题的关键． 3．如图，ABC 的面积为26cm ，AP 垂直B 的平分线BP 于P ，则PBC 的面积为（）A ．21cmB ．22cmC ．23cmD ．24cm C解析：C【分析】延长AP 交BC 于E ，根据AP 垂直∠B 的平分线BP 于P ，即可求出△ABP ≌△BEP ，又知△APC 和△CPE 等底同高，可以证明两三角形面积相等，即可证明三角形PBC 的面积．【详解】解：延长AP 交BC 于E ，∵AP 垂直∠B 的平分线BP 于P ，∴∠ABP =∠EBP ，∠APB =∠BPE =90∘，在△APB 和△EPB 中∠=∠⎧⎪=⎨⎪∠=∠⎩APB EPB BP BPABP EBP ∴△APB ≌△EPB (ASA )，∴APB EPB S S =△△，AP =PE ，∴△APC 和△CPE 等底同高，∴APC PCE S S =,∴PBC PCE PCE S S S =+△△△=12ABC S=1632⨯= 故选C ．【点睛】本题考查了三角形的面积和全等三角形的性质和判定的应用，关键是求出PBC PCE PCE S S S =+△△△=12ABC S ．4．下列判断正确的个数是（）①三角形的三条高都在三角形的内部，并且相交于一点；②两边及一角对应相等的两个三角形全等；③两角及一边对应相等的两个三角形全等；④到三角形的三边所在的直线距离相等的点有三个；⑤两边及第三边上的高对应相等的两个三角形全等．A ．4B ．3C ．2D ．1D解析：D【分析】根据三角形的高线、角平分线的性质及全等三角形的判定分析各个选项即可．【详解】解：①只有当三角形是锐角三角形时，三条高才在三角形的内部，此选项错误； ②有两边及一角对应相等的两个三角形全等，此选项错误；③有两角和一边对应相等，满足AAS 或ASA ，此选项正确；④在三角形内部到三边距离相等的点是三条内角平分线的交点，交点重合，只有一点；在三角形的外部到三条边所在直线距离相等的点是外角平分线的交点，交点不重合，有三个．则到三角形三边所在直线距离相等的点有4个，此选项错误；⑤两边及第三边上的高对应相等的两个三角形不一定全等，此选项错误．正确的有一个③，故选：D ．【点睛】本题考查了全等三角形的判定方法及三角形的角平分线，垂心等概念，熟练掌握概念和性质是解题的关键．5．已知：如图，BD 为△ABC 的角平分线，且BD=BC ，E 为BD 延长线上的一点，BE=BA ，过E 作EF ⊥AB ，F 为垂足，下列结论：①△ABD ≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF 其中正确的是（）A ．①②③B ．①③④C ．①②④D ．①②③④D解析：D【分析】易证ABD EBC ∆∆≌，可得BCE BDA ∠=∠，AD=EC 可得①②正确；再根据角平分线的性质可求得DAE DCE ∠=∠ ，即③正确，根据③可判断④正确；【详解】∵ BD 为∠ABC 的角平分线，∴ ∠ABD=∠CBD ，∴在△ABD 和△EBD 中，BD=BC ，∠ABD=∠CDB ，BE=BA ，∴△ABD EBC ∆∆≌(SAS)，故①正确；∵ BD 平分∠ABC ，BD=BC ，BE=BA ，∴ ∠BCD=∠BDC=∠BAE=∠BEA ，∵△ABD ≌△EBC ，∴∠BCE=∠BDA ，∴∠BCE+∠BCD=∠BDA+∠BDC=180°，故②正确；∵∠BCE=∠BDA ，∠BCE=∠BCD+∠DCE ，∠BDA=∠DAE+∠BEA ，∠BCD=∠BEA ，∴∠DCE=∠DAE ，∴△ACE 是等腰三角形，∴AE=EC ，∵△ABD ≌△EBC ，∴AD=EC ，∴AD=AE=EC ，故③正确；作EG ⊥BC ，垂足为G ，如图所示：∵ E 是BD 上的点，∴EF=EG ，在△BEG 和△BEF 中BE BE EF EG=⎧⎨=⎩ ∴ △BEG ≌△BEF ，∴BG=BF ，在△CEG 和△AFE 中EF EG AE CE =⎧⎨=⎩∴△CEG ≌△AFE ，∴ AF=CG ，∴BA+BC=BF+FA+BG-CG=BF+BG=2BF ，故④正确；故选：D ．【点睛】本题考查了全等三角形的判定，全等三角形对应边、对应角相等的性质，本题中熟练求证三角形全等和熟练运用全等三角形对应边、对应角相等的性质是解题的关键；6．如图，点D 在线段BC 上，若1802ACE ABC x ∠=︒-∠-︒，且BC DE =，AC DC =，AB EC =，则下列角中，大小为x ︒的角是( )A ．EFC ∠B ．ABC ∠ C ．FDC ∠D ．DFC ∠ C解析：C【分析】先证明()ABC CED SSS ∆≅∆得到B E ∠=∠、FCD FDC ∠=∠，再根据1802ACE ABC x ∠=︒-∠-︒可得2CFE x ∠=︒；然后根据外角的性质可得2EFC FDC FCD FDC ∠=∠+∠=∠即可解答．【详解】解：在ABC ∆和CED ∆中，AC CD AB CE BC ED =⎧⎪=⎨⎪=⎩，()ABC CED SSS ∴∆≅∆，B E ∴∠=∠，FCD FDC ∠=∠1802180ACE ABC x E CFE ∠=︒-∠-︒=︒-∠-∠，2CFE x ∴∠=︒，2EFC FDC FCD FDC ∠=∠+∠=∠=2x ︒，FDC x ∴∠=︒．故答案为C ．【点睛】本题主要考查全等三角形的判定和性质、三角形的外角的性质等知识，弄清题意、理清角之间的关系是解答本题的关键．7．如图所示，已知∠A ＝∠C ，∠AFD ＝∠CEB ，那么给出的条件不能得到ADF CBE △≌△是（）A ．∠B ＝∠DB ．EB=DFC ．AD=BCD ．AE=CF A解析：A【分析】直接利用全等三角形的判定方法进行判断即可；三角形全等的证明方法有：SSS 、SAS 、AAS 、ASA ；【详解】A ∵∠A=∠C ，∠AFD=∠CEB ，∠B=∠D ，三个角相等，不能判定三角形全等，该选项不符合题意；B ∵∠A=∠C ，∠AFD=∠CEB ，EB=DF ，符合AAS 的判定，该选项符合题意；C ∵∠A=∠C ，∠AFD=∠CEB ，AD=BC ，符合AAS 的判定，该选项符合题意；D ∵∠A=∠C ，∠AFD=∠CEB ，AE=CF ，∴AF=CE ，符合ASA 的判定，该选项符合题意；故选：A ．【点睛】本题考查了全等三角形的判定方法，正确掌握判定方法是解题的关键；8．如图，要判定△ABD ≌△ACD ，已知AB ＝AC ，若再增加下列条件中的一个，仍不能说明全等，则这个条件是（）A ．CD ⊥AD ，BD ⊥ADB ．CD ＝BDC ．∠1＝∠2D ．∠CAD ＝∠B AD C解析：C【分析】在△ACD 和△ABD 中，AD=AD ，AB=AC ，由全等三角形判定定理对选项一一分析，排除不符合题意的选项即可．【详解】解：添加A 选项中条件可用HL 判定两个三角形全等，故选项A 不符合题意；添加B 选项中的条件可用SSS 判定两个三角形全等，故选项B 不符合题意；添加C 选项中的条件∠1＝∠2可得∠CDA=∠BDA ，结合已知条件不SS 判定两个三角形全等，故选项C 符合题意；添加D 选项中的条件可用SAS 判定两个三角形全等，故选项D 不符合题意．故选：C ．【点睛】本题考查了全等三角形的判定，判定三角形全等的方法：SSS 、SAS 、ASA 、AAS ，判断直角三角形全等的方法：“HL”．9．如图，AD 是ABC 的中线，E ，F 分别是AD 和AD 延长线上的点，且DE DF =，连结BF ，CE ．下列说法：①CE BF =；②ACE △和CDE △面积相；③//BF CE ；④BDF CDE ≌．其中正确的有（）A ．1个B ．2个C ．3个D ．4个C解析：C【分析】根据“SAS”可证明△CDE ≌△BDF ，则可对④进行判断；利用全等三角形的性质可对①进行判断；由于AE 和DE 不能确定相等，则根据三角形面积公式可对②进行判断；根据全等三角形的性质得到∠ECD=∠FBD ，则利用平行线的判定方法可对③进行判断；【详解】∵ AD 是△ABC 的中线，∴ CD=BD ，∵ DE=DF ，∠CDE=∠BDF ，∴ △CDE ≌△BDF(SAS)，所以④正确；∴ CE=BF ，所以①正确；∵ AE 与DE 不能确定相等，∴ △ACE 和△CDE 面积不一定相等，所以②错误；∵ △CDE ≌△BDF ，∴∠ECD=∠FBD ，∴BF ∥CE ，所以③正确；故选：C ．【点睛】本题考查了全等三角形的判定与性质，三角形的面积，熟练掌握三角形全等的判定方法并准确识图是解题的关键．10．如图，已知，CAB DAE ∠=∠，AC AD =．下列五个选项：①AB AE =，②BC ED =，③C D ∠=∠，④B E ∠=∠，⑤12∠=∠，从中任选一个作为已知条件，其中能使ABC AED ≌△△的条件有（）A ．2个B ．3个C ．4个D ．5个B解析：B添加条件①可以用“SAS”证明，添加条件③可以用“ASA”证明，添加条件④可以用“AAS”证明．【详解】解：①在ABC 和AED 中，AC AD CAB DAE AB AE =⎧⎪∠=∠⎨⎪=⎩，∴()ABC AED SAS ≅△△；②不可以；③在ABC 和AED 中，C D AC ADCAB DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴()ABC AED ASA ≅；④在ABC 和AED 中，B E CAB DAE AC AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()ABC AED AAS ≅；⑤不可以；故选：B ．【点睛】本题考查全等三角形的判定，解题的关键是掌握全等三角形的所有判定定理．二、填空题11．如图，△ABC 中，∠ACB =90°，点D 在边AC 上，DE ⊥AB 于点E ，DC =DE ，∠A =32°，则∠BDC 的度数为________．61°【分析】首先利用直角三角形的性质求得∠ABC 的度数然后利用角平分线的判定方法得到BD 为∠ABC 的平分线再求出∠ABD 的度数根据三角形外角的性质进而求得结论【详解】解：∵∠A=32°∠ACB=9解析：61°【分析】首先利用直角三角形的性质求得∠ABC 的度数，然后利用角平分线的判定方法得到BD 为∠ABC 的平分线，再求出∠ABD 的度数，根据三角形外角的性质进而求得结论．解：∵∠A=32°，∠ACB =90°，∴∠CBA=58°，∵DE ⊥AB ，DC ⊥BC ，DC=DE ，∴BD 为∠ABC 的平分线，∴∠CBD=∠EBD ，∴∠CBD=12∠CBA=12×58°=29°, ∴∠BDC=∠A+∠ABD=32°+29°=61°．故答案为：61°．【点睛】本题考查了角平分线的判定与性质，解题的关键是根据已知条件得到BD 为∠ABC 的平分线，难度不大．12．如图，△ABE ≌△ADC ≌△ABC ，若∠1＝130°，则∠α的度数为________．100°【分析】根据全等三角形对应角相等可得然后根据周角等于求出再根据三角形的内角和定理求出从而得解【详解】解：（对顶角相等）故答案为：【点睛】本题考查了全等三角形对应角相等的性质三角形的内角和定理解析：100°【分析】根据全等三角形对应角相等可得1BAE ∠=∠，ACB E ∠=∠，然后根据周角等于360︒求出2∠，再根据三角形的内角和定理求出2α∠=∠，从而得解．【详解】解：ABE ADC ABC ∆≅∆≅∆，1130BAE ∴∠=∠=︒，ACB E ∠=∠，23601360130130100BAE ∴∠=︒-∠-∠=︒-︒-︒=︒，180DFE E α∴∠=︒-∠-∠，1802AFC ACD ∠=︒-∠-∠，DFE AFC ∠=∠（对顶角相等），1801802E ACD α∴︒-∠-∠=︒-∠-∠，2100α∴∠=∠=︒．故答案为：100︒．【点睛】本题考查了全等三角形对应角相等的性质，三角形的内角和定理，对顶角相等的性质，准确识图，找出对应角是解题的关键．13．如图，两根旗杆间相距22米，某人从点B 沿BA 走向点A ，一段时间后他到达点M ，此时他分别仰望旗杆的顶点C 和D ，两次视线的夹角为90°，且CM DM =．已知旗杆BD 的高为12米，该人的运动速度为2米/秒，则这个人运动到点M 所用时间是________秒．5【分析】根据题意证明利用证明根据全等三角形的性质得到米再利用时间=路程÷速度计算即可【详解】解：∵∴又∵∴∴在和中∴∴米（米）∵该人的运动速度他到达点M 时运动时间为s 故答案为5【点睛】本题考查了全解析：5【分析】根据题意证明C DMB ∠=∠，利用AAS 证明ACM BMD ≌，根据全等三角形的性质得到12BD AM ==米，再利用时间=路程÷速度计算即可．【详解】解：∵90CMD ∠=︒，∴90CMA DMB +=︒∠∠，又∵90CAM ∠=︒，∴90CMA C ︒∠+∠=，∴C DMB ∠=∠，在 Rt ACM △和Rt BMD △中， A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()Rt ACM Rt BMD AAS ≌，∴12BD AM ==米，221210BM =-=（米），∵该人的运动速度2m/s ，他到达点M 时，运动时间为5210=÷s ．故答案为5．【点睛】本题考查了全等三角形的应用；解答本题的关键是利用互余关系找三角形全等的条件，对应角相等，并巧妙地借助两个三角形全等，寻找所求线段与已知线段之间的等量关系．本题的关键是求得Rt ACM Rt BMD ≌．14．如图，在△ABC 中，∠ACB ＝120°，BC ＝4，D 为AB 的中点，DC ⊥BC ，则点A 到直线CD 的距离是_____．4【分析】根据垂直的定义得到∠BCD=延长CD 到H使DH=CD 由线段中点的定义得到AD=BD 根据全等三角形的性质得到AH=BC=4【详解】∵DC ⊥BC ∴∠BCD=∵∠ACB=∴∠ACD=如图延长CD解析：4【分析】根据垂直的定义得到∠BCD=90︒，延长CD 到H 使DH=CD ，由线段中点的定义得到 AD=BD ，根据全等三角形的性质得到 AH=BC=4．【详解】∵ DC ⊥BC ，∴ ∠BCD=90︒，∵ ∠ACB=120︒，∴ ∠ACD=30︒，如图，延长 CD 到 H 使 DH=CD ，∵ D 为 AB 的中点，∴ AD=BD ，在 ΔADH 与 ΔBCD 中，CD DH ADH BDC AD BD =⎧⎪∠=∠⎨⎪=⎩，∴ ΔADH ≅ΔBCD(SAS)，∴ AH=BC=4，∠AHD=∠BCD=90°，∴点A 到CD 的距离为4，故答案为：4．【点睛】本题考察全等三角形的判定与性质，正确作出辅助线是解题的关键．15．如图，AC AE =，AD AB =，90ACB DAB ∠=∠=︒，33BAE ∠=︒，//CB AE ，AC 与DE 相交于点F ．（1）DAC ∠=______．（2）当1AF =时，BC 的长为______．33°2【分析】（1）作DG ⊥AC 的延长线于G 然后根据平行线的性质可以推出结论；（2）证明△ADG ≌△BAC （AAS ）由全等三角形的性质得出DG ＝AC ＝AE ；AG ＝BC 证明△AEF ≌△GDF （AAS 解析：33° 2【分析】（1）作DG ⊥AC 的延长线于G ，然后根据平行线的性质可以推出结论；（2）证明△ADG ≌△BAC （AAS ），由全等三角形的性质得出DG ＝AC ＝AE ；AG ＝BC ，证明△AEF ≌△GDF （AAS ），得出1122AF GF AG BC ===，则可得出答案．【详解】解：（1）∵90ACB ∠=︒，//AE BC ，∴18090CAE ACB ∠=︒-∠=︒．∵90DAB CAE ∠=∠=︒，∴DAC CAB BAE CAB ∠+∠=∠+∠，∴33DAC BAE ∠=∠=︒．故答案为：33．（2）如图，过点D 作DG AC ⊥，交AC 的延长线于点G ，∴90AGD ACB ∠=∠=︒．∵//AE CB ，∴DAG BAE B ∠=∠=∠．在ADG 和BAC 中，,,,AGO BCA DAG B AD BA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ADG BAC ≅△△，∴DG AC AE ==，AG BC =．在AEF 和GDF 中，,,,EFA DFG EAF DGF AE DG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS AEF GDF ≅△△， ∴1122AF GF AG BC ===， ∴22BC AF ==．故答案为：2．【点睛】此题考查了全等三角形的判定与性质，用到的知识点是平行线的性质和全等三角形的判定与性质，解题的关键是熟练掌握全等的三角形的判定与性质．16．如图，在△ABC 中，∠ABC 的平分线与外角∠ACE 的平分线交于点D ，若∠D ＝20°，则∠A ＝_____．40°【分析】利用角平分线的性质可知∠ABC ＝2∠DBC ∠ACE ＝2∠DCE 再根据三角形外角的性质可得出∠D ＝∠DCE ﹣∠DBE ∠A ＝∠ACE ﹣∠ABC 即得出∠A ＝2∠D 即得出答案【详解】∵∠ABC 解析：40°【分析】利用角平分线的性质可知∠ABC ＝2∠DBC ，∠ACE ＝2∠DCE ．再根据三角形外角的性质可得出∠D ＝∠DCE ﹣∠DBE ，∠A ＝∠ACE ﹣∠ABC ．即得出∠A ＝2∠D ，即得出答案．【详解】∵∠ABC 的平分线交∠ACE 的外角平分线∠ACE 的平分线于点D ，∴∠ABC ＝2∠DBC ，∠ACE ＝2∠DCE ，∵∠DCE 是△BCD 的外角，∴∠D ＝∠DCE ﹣∠DBE ，∵∠ACE 是△ABC 的外角，∠A ＝∠ACE ﹣∠ABC ＝2∠DCE ﹣2∠DBE ＝2（∠DCE ﹣∠DBE ），∴∠A ＝2∠D ＝40°．故答案为：40°．【点睛】本题考查角平分线和三角形外角的性质，熟练利用角平分线和三角形外角的性质来判断题中角之间的关系是解答本题的关键．17．已知点(2,1)P m m -，当m =____时，点P 在二、四象限的角平分线上．【分析】根据第二四象限角平分线上点的横坐标与纵坐标互为相反数列方程求解即可【详解】解：∵点P （2mm-1）在二四象限的角平分线上∴2m=-（m-1）解得m=故答案为：【点睛】本题考查了点的坐标熟记第解析：13 【分析】根据第二四象限角平分线上点的横坐标与纵坐标互为相反数列方程求解即可．【详解】解：∵点P （2m ，m-1）在二、四象限的角平分线上，∴2m=-（m-1），解得m=13．故答案为：13．【点睛】本题考查了点的坐标，熟记第二四象限角平分线上点的横坐标与纵坐标互为相反数是解题的关键．18．如图，在ABC 中，AD 平分BAC ∠，P 为线段AD 上的一个动点，PE AD ⊥交直线BC 于点E ．若35B ∠=︒，85ACB ∠=︒，则E ∠的度数为______．25°【分析】利用三角形内角和定理得出∠BAC 的度数进而得出∠ADC 的度数再利用三角形内角和定理和外角性质得出即可【详解】解：∵∠B=35°∠ACB=85°∴∠BAC=60°∵AD 平分∠BAC ∴∠B解析：25°【分析】利用三角形内角和定理得出∠BAC 的度数，进而得出∠ADC 的度数，再利用三角形内角和定理和外角性质得出即可．【详解】解：∵∠B=35°，∠ACB=85°，∴∠BAC=60°，∵AD 平分∠BAC ，∴∠BAD=30°，∴∠ADC=35°+30°=65°，∵∠EPD=90°，∴∠E 的度数为：90°-65°=25°．故答案为：25°．【点睛】此题主要考查了三角形内角和定理以及角平分线的性质和三角形外角的性质，根据已知得出∠BAD 度数是解题关键．19．ABC 中，4AB =，6AC =，则第三边BC 边上的中线m 的取值范围是______．【分析】如图延长AD 至点E 使得DE=AD 可证△ABD ≌△CDE 可得AB=CEAD=DE 在△ACE 中根据三角形三边关系即可求得AE 的取值范围即可解题【详解】解：延长AD 至点E 使得DE=AD ∵点D 是BC解析：15a <<【分析】如图延长AD 至点E ，使得DE=AD ，可证△ABD ≌△CDE ，可得AB=CE ，AD=DE ，在△ACE 中，根据三角形三边关系即可求得AE 的取值范围，即可解题．【详解】解：延长AD 至点E ，使得DE=AD ，∵点D 是BC 的中点，∴BD=CD在△ABD 和△CDE 中，AD DE ADB CDE BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△CDE （SAS ），∴AB=CE ，∵△ACE 中，AC-CE ＜AE ＜AC+CE ，即：AC-AB ＜AE ＜AC+AB ，∴2＜AE ＜10，∴1＜AD ＜5．故答案为：1＜AD ＜5．【点睛】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ABD ≌△CDE 是解题的关键．20．如图，在△ABC 和△DBC 中，∠ACB=∠DBC=90°，E 是BC 的中点，DE ⊥AB ，垂足为F ，AB=DE ．若BD=8cm ，则AC 的长为_________．4cm 【分析】由DE ⊥AB 可得∠BFE=90°由直角三角形两锐角互余可得∠ABC+∠DEB=90°由∠ACB=90°由直角三角形两锐角互余可得∠ABC+∠A=90°根据同角的余角相等可得∠A=∠DE解析：4cm ．【分析】由DE ⊥AB ，可得∠BFE=90°，由直角三角形两锐角互余，可得∠ABC+∠DEB=90°，由∠ACB=90°，由直角三角形两锐角互余，可得∠ABC+∠A=90°，根据同角的余角相等，可得∠A=∠DEB ，然后根据AAS 判断△ABC ≌△EDB ，根据全等三角形的对应边相等即可得到BD=BC ，AC=BE ，由E 是BC 的中点，得到BE=12BC=12BD=4．【详解】解：∵DE ⊥AB ，可得∠BFE=90°，∴∠ABC+∠DEB=90°，∵∠ACB=90°，∴∠ABC+∠A=90°，∴∠A=∠DEB ，在△ABC 和△EDB 中， ACB DBC A DEBAB DE ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△ABC ≌△EDB （AAS ），∴BD=BC ，AC=BE ，∵E 是BC 的中点，BD=8cm ，∴BE=12BC=12BD=4cm ， ∴AC=4cm ．故答案为：4cm ．【点睛】此题考查了全等三角形的判定与性质，普通两个三角形全等共有四个定理，即AAS 、ASA 、SAS 、SSS ，直角三角形可用HL 定理，但AAA 、SSA ，无法证明三角形全等，本题是一道较为简单的题目，找准全等的三角形是解决本题的关键．三、解答题21．已知：MON α∠=，点P 是MON ∠平分线上一点，点A 在射线OM 上，作180APB α∠=︒-，交直线ON 于点B ，作PC ON ⊥于点C ．（1）观察猜想：如图1，当90MON ∠=︒时，PA 和PB 的数量关系是______．（2）探究证明：如图2，当60MON ∠=︒时，（1）中的结论还成立吗?若成立，请写出证明过程；若不成立，请直接写出PA ，PB 之间另外的数量关系．（3）拓展延伸：如图3，当60MON ∠=︒，点B 在射线ON 的反向延长线上时，请直接写出线段OC ，OA 及BC 之间的数量关系：______．解析：（1）PA=PB ；（2）成立证明见解析；（3）OA=BC+OC【分析】（1）作PD ⊥OM 于点D ，根据角平分线的性质得到PC=PD ，证明△APD ≌△BPC ，根据全等三角形的性质定理证明；（2）作PD ⊥OM 于点D ，根据角平分线的性质得到PC=PD ，证明△APD ≌△BPC ，根据全等三角形的性质定理证明；（3）仿照（2）的解法得出△APD ≌△BPC ，从而得出AD=BC ，再根据HL 得出Rt △OPD ≌△RtOPC ，得出OC=OD ，继而得出结论．【详解】（1）作PD ⊥OM 于点D ，∵点P 在∠MON 的角平分线上，且PC ⊥ON 于C ，∴PC=PD ，∵∠MON=90°，∴∠APB=90°，∠CPD=90°，∴∠APD+∠BPD=90°，∠BPC+∠BPD=90°∴∠APD=∠BPC ，∵∠PDA=∠PCB=90°，在△APD 和△BPC 中，APD BPC PD PCADP BCP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△APD ≌△BPC （ASA ），∴AP=BP ．（2）（1）中的结论还成立理由如下：如图2，作PD ⊥OM 于点D ，∵点P 在∠MON 的角平分线上，且PC ⊥ON 于C ，∴PC=PD ，∵∠MON=60°，∴∠APB=120°，在四边形OCPD 中，∠CPD=360°-90°-90°-60°=120°，∴∠APD+∠BPD=120°，∠BPC+∠BPD=120°∴∠APD=∠BPC ，∵∠PDA=∠PCB=90°，在△APD 和△BPC 中，APD BPC PD PCADP BCP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△APD ≌△BPC （ASA ），∴AP=BP ．（3）OA=2BC-OB ．理由如下：如图3，作PD ⊥OM 于点D ，同（2），可证△APD ≌△BPC ，∴AD=BC ，点P 在∠MON 的角平分线上，且PC ⊥ON 于C ，∴PC=PD ，在Rt △OPD 和RtOPC 中，PC PD OP OP =⎧⎨=⎩∴Rt △OPD ≌△RtOPC ，∴OC=OD ，∴OA-AD=OD=OC ，∴OA-BC=OC ，∴OA=BC+OC ．【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理、灵活运用类比思想是解题的关键．22．如图，Rt ABC 与Rt DEF △的顶点A ，F ，C ，D 共线，AB 与EF 交于点G ，BC 与DE 相交于点H ，90B E ∠=∠=︒，AF CD =，AB DE =．（1）求证：Rt ABC Rt DEF ≌；（2）若1GF =，求线段HC 的长．解析：（1）见详解；（2）1【分析】（1）先证明AC=DF ，再根据HL 证明Rt ABC Rt DEF ≌；（2）先证明∠AFG=∠DCH ，从而证明∆AFG ≅∆DCH ，进而即可求解．【详解】（1）∵AF CD =，∴AF+CF=CD+CF ，即AC=DF ，在Rt ABC 与Rt DEF △中，∵AC DF AB DE =⎧⎨=⎩， ∴Rt ABC ≅Rt DEF △（HL ）；（2）∵Rt ABC ≅Rt DEF △，∴∠A=∠D ，∠EFD=∠BCA ，∵∠AFG=180°-∠EFD ，∠DCH=180°-∠BCA ，∴∠AFG=∠DCH ，又∵AF CD =，∴∆AFG ≅∆DCH ，∴HC=GF =1．【点睛】本题主要考查全等三角形的判定和性质，熟练掌握HL 和ASA 证明三角形全等，是解题的关键．23．如图，△ABC 中，AB=AC ，∠BAC=90°，CD 平分∠ACB ，BE ⊥CD ，垂足E 在CD 的延长线上．求证：CD=2BE ．解析：见解析【分析】根据等角的余角相等求出∠ACD=∠ABF ，再利用“角边角”证明△AFB ≌△ADC 可得CD=BF ，利用“角边角”证明△BCE 和△FCE 全等，根据全等三角形对应边相等BE=EF ，整理即可得证．【详解】证明：∵BE ⊥CD ，∠BAC=90°，∴∠ACD+∠F=180°-90°=90°，∠ABF+∠F=180°-90°=90°，∴∠ACD=∠ABF ，在△AFB 和△ADC 中，90ACD ABF AB ACCAD BAF ∠∠⎧⎪⎨⎪∠∠︒⎩＝＝＝＝， ∴△AFB ≌△ADC （ASA ）；∴CD=BF ，∵CD 平分∠ACB ，∴∠BCE=∠FCE ，在△BCE 和△FCE 中，90BCE FCE CE CEBEC FEC ∠∠⎧⎪⎨⎪∠∠︒⎩＝＝＝＝， ∴△BCE ≌△FCE （ASA ），∴BE=EF ，∴BF=2BE∴CD=2BE ．【点睛】本题考查了全等三角形的判定与性质，熟练掌握三角形全等的证明方法并准确识图是解题的关键．24．如图，已知∠AOC 是直角，∠BOC =46°，OE 平分∠BOC ，OD 平分∠AOB ．（1）试求∠DOE 的度数；（2）当∠BOC =α（0°≤α≤90°），请问∠DOE 的大小是否变化？并说明理由．解析：（1）45︒；（2）不会变化，理由见解析．【分析】（1）根据题意可知DOE BOD BOE ∠=∠-∠，12BOD AOB ∠=∠，12BOE BOC ∠=∠．即可推出12DOE AOC ∠=∠，即可求出DOE ∠．（2））根据（1）可知DOE ∠的大小与∠BOC 的大小无关，所以DOE ∠的大小不会变化．【详解】（1）由图可知DOE BOD BOE ∠=∠-∠，∵OE 平分∠BOC ，OD 平分∠AOB ． ∴12BOD AOB ∠=∠，12BOE BOC ∠=∠． ∴1111()2222DOE AOB BOC AOB BOC AOC ∠=∠-∠=∠-∠=∠， ∵∠AOC 是直角，∴90AOC ∠=︒， ∴1452DOE AOC ∠=∠=︒．（2）根据（1）可知DOE ∠的大小与∠BOC 的大小无关， ∴DOE ∠的大小不会变化且大小为12AOC ∠．【点睛】本题考查角的计算，角平分线的性质．利用角平分线的性质找出图形中角的关系是解答本题的关键．25．如图，在△ABD 中，∠ABD ＝90°，AB=BD ，点E 在线段BD 上，延长AB 使BC=BE ，连接AE、CE、CD，点M在线段AE上，点N在线段CD上，BM⊥BN，易证△ABE≌△DBC；仔细观察，请逐一找出图中其他的全等三角形，并说明理由．解析：△ABM≌△DBN，△BME≌△BNC，理由见解析．【分析】观察图形，可找出△ABM≌△DBN，△BME≌△BNC．①由△ABE≌△DBC可得到∠BAE=∠BDC，根据BM⊥BN可得到∠AMB+∠MBE =∠DBN+∠MBE，继而得到∠AMB=∠DBN，AB=BD，可得△ABM≌△DBN；②由△ABM≌△DBN可得BM=BN，根据∠NBE+∠MBE =∠NBE+∠NBC，可得∠MBE =∠NBC，继而可证得△BME≌△BNC．【详解】解：全等三角形：△ABM≌△DBN，△BME≌△BNC，理由如下：由题意知△ABE≌△DBC，∴∠BAE=∠BDC，∵BM⊥BN，∴∠MNB=90 ，∴∠ABM+∠MBE =∠DBN+∠MBE，∴∠ABM=∠DBN，AB=BD，∴△ABM≌△DBN，∴BM=BN,∵∠NBE+∠MBE =∠NBE+∠NBC，∴∠MBE =∠NBC，∵BE=BC，∴△BME≌△BNC．【点睛】本题考察全等三角形的判定与性质，熟知全等三角形的判定与性质是解题关键．26．如图①，∠BAD=90°，AB=AD，过点B作BC⊥AC于点C，过点D作DE⊥CA的延长线点E，由∠1+∠2=∠D+∠2=90°，得∠1=∠D，又∠ACB=∠AED=90°，AB=AD，得△ABC≌△DAE进而得到AC=DE，BC=AE，我们把这个数学模型称为“K字”模型或“一线三等角”模型．请应用上述“一线三等角”模型，解决下列问题：（1）如图②，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接BC、DE，且BC⊥AH于点H，DE与直线AH 交于点G ，求证：点G 是DE 的中点．（2）如图③，在平面直角坐标系中，点A 为平面内任意一点，点B 的坐标为（4，1），若△AOB 是以OB 为斜边的等腰直角三角形，请直接写出点A 的坐标．解析：（1）见解析；（2）A(32，52)或(52，-32)．【分析】（1）过点D 作DM ⊥AM 交AG 于点M ，过点E 作EN ⊥AG 于点N ．根据“K 字模型”即可证明AH=DM 和AH=EN ，即EN=DM ，再根据全等三角形的判定和性质即可证明DG=EG ，即点G 是DE 的中点．（2）分情况讨论①当A 点在OB 的上方时，作AC 垂直于y 轴，BE 垂直于x 轴，CA 和EB 的延长线交于点D ．根据“K 字模型”即可证明AC BD OC AD DE ===，，再利用B 点坐标即可求出A 点坐标．②当A 点在OB 的下方时，作AP 垂直于y 轴，BM 垂直于x 轴，PA 和BM 的延长线交于点Q ．同理即能求出A 点坐标．【详解】（1）如图，过点D 作DM ⊥AM 交AG 于点M ，过点E 作EN ⊥AG 于点N ，则∠DMA=90°，∠ENG=90°．∵∠BHA=90 ，∴∠2+∠B=90°．∵∠BAD=90°，∴∠1+∠2=90°．∴∠B=∠1 ．在△ABH 和△DAM 中1BHA AMD B AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABH ≅△DAM （AAS ），∴AH=DM ．同理 △ACH ≅△EAN （AAS ），∴ AH=EN ．∴EN=DM ．在△DMG 和△ENG 中MGD NGE DMG ENG DM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DMG ≅△ENG （AAS ）．∴DG=EG ．∴点G 是DE 的中点．（2）根据题意可知有两种情况，A 点分别在OB 的上方和下方．①当A 点在OB 的上方时，如图，作AC 垂直于y 轴，BE 垂直于x 轴，CA 和EB 的延长线交于点D ．利用“K 字模型”可知ACO BDA ≅，∴AC BD OC AD DE ===，，设AC x =，则BD x =，∵1DE BD BE x =+=+，∴1OC AD DE x ===+，又∵4CD AD AC =+=，即14x x ++=，解得32x =， ∴32AC =，35122DE =+=．即点A 坐标为(32，52)．②当A 点在OB 的下方时，如图，作AP 垂直于y 轴，BM 垂直于x 轴，PA 和BM 的延长线交于点Q ．根据①同理可得：52AP =，32MQ =．即点A 坐标为(52，32-)．【点睛】本题考查了三角形全等的判定和性质．熟练利用三角形的判定方法是解答本题的关键．27．在ABC 中，AD BC ⊥，CE AB ⊥，垂足分别为D ，E ，AD ，CE 交于点H ，已知3EH EB ==，4AE =，求CH 的长．解析：CH=1【分析】根据AD ⊥BC ，CE ⊥AB ，可得出∠EAH+∠B=90°∠EAH+∠AHE=90°，则∠B=∠AHE ，则可证△AEH ≌△CEB ，从而得出CE=AE ，再根据已知条件得出CH 的长．【详解】解：∵AD ⊥BC ，∴∠EAH+∠B=90°，∵CE ⊥AB ，∴∠EAH+∠AHE=90°，∴∠B=∠AHE ，∵EH=EB ，在△AEH 和△CEB 中，AHE B EH BEAEH BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AEH ≌△CEB （ASA ），∴CE=AE=4，∵EH=EB=3，∴CH=CE-EH=4-3=1．【点睛】本题考查了全等三角形的判定和性质，根据同角的余角相等得出∠B=∠AHE ，是解此题的关键．28．已知：如图，AOB ∠．求作： A O B '''∠，使A O B AOB '''∠=∠．作法：①以点O 为圆心，任意长为半径画弧，分别交OA ,OB 于点C ,D ；②画一条射线O A ''，以点O '为圆心，OC 长为半径画弧，交O A ''于点C '； ③以点C '为圆心，CD 长为半径画弧，与②中所画的弧相交于点D ；④过点D 画射线O B ''，则A O B AOB '''∠=∠；A OB '''∠就是所求作的角．（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；（2）完成下面的证明证明：连接C D ''．由作法可知OC O C ''=,，，∴COD C O D '''≅．（）（填推理依据）．∴A O B AOB '''∠=∠．∴A O B '''∠就是所求作的角．解析：（1）补全图形见解析；（2）OD O D ''=，CD C D ''=，SSS ．【分析】（1）根据题意要求作图即可；（2）根据题意利用SSS 证明COD C O D '''≅即可．【详解】(1)作图：(2)连接C D ''，∵OC O C ''=，OD O D ''= ，CD C D ''=，∴COD C O D '''≅（SSS ），∴A O B AOB '''∠=∠．∴A O B '''∠就是所求作的角故答案为：OD O D ''=，CD C D ''=，SSS ．．【点睛】此题考查作图能力—作一个角等于已知角，全等三角形的判定及性质，根据题意画出图形并确定对应相等的条件证明三角形全等是解题的关键．。

八年级上册数学第十二章全等三角形解答题专题训练 12916含解析.docx

第十二章《全等三角形》解答题专题训练(12)一、解答题1.如图，点、B , F , C , E在一条直线上，FB = CE, AB = DE, AC = DF,求证：AB//DE.2.如图所示，已知ZDCE=90°, ZDAC=90°,BE±AC于B,且DC=EC,请找出与AB+AD相等的线段，并说明理由.3.如图，RtAABC中，AB=AC, ZBAC=90°,直线AE®是经过点AIS的任一直线，BD丄AE于D, CE±AE 于E,若BD>CE,试解答：(1) AD与CE的大小关系如何？请说明理由；(2) 若BD=5,CE=2,求DE 的长.5.如图，CD是ZACB的平分线，EFXCD于H,交AC于F,交BC于G.16.如图，四边形ABCD 中，BA=BC, DA=DC,我们把这种两组邻边分别相等的四边形叫做 "筝形"，其对角线AC 、BD 交于点M,请你猜想关于筝形的对角线的一条性质，并加以证明.猜想：证明：7.如图，在锐角△ABC 中，AB=2cm, AC=3cm.（1）尺规作图：作BC 边的垂直平分线分别交4C, BC 于点D 、E （保留作图痕迹，不要求写作法）；（2）在（1）的条件下，连结BD,求AABD 的周长.&如图，两车从路段AB 的两端同吋出发，沿平行路线以相同的速度行驶，相同吋间后分别到达C 、D 两地，CEXAB, DFXAB, C 、D 两地到路段AB 的距离相等吗？为什么？ £ d f 9.如图所示，△ABC 是等腰直角三角形，ZA = 90° , AB=AC, D 是斜边BC 的中点，E,F 分别是AB 、AC 边上的点，且DE 丄DF,若BE=15, CF=8,求ZX/IEF 的面积.求证：®ZCFG=ZCGF ； ®ACFE = -^BAC + Z4BC). 乙 D B10.如图，要测量河流AB的长，因为无法测河流附近的点4,可以在AB线外任取一点D，在AB的延长线上任取一点E,连结ED和B£＞，并且延长BD到点G,使DG = BD ；延长ED到点F,使= 连结FG ,并延长FG到点H,使点H.D, 4在同一直线上•证明：测量出线段HG的长就是河流AB的长.ZA = 60°, ZC= 40°, DE 垂直平分BC,连接BD.（1）尺规作图：过点D作AB的垂线，垂足为F.（保留作图痕迹，不写作法）（2）求证：点D到B/», BC的距离相等.12.如图，BD，CE是ZkABC的高，S.AE = AD，求证：AB = AC.A13.已知：如图，AE〃BF, ZE=ZF, DE=CF,（1）求证：AC=BD；（2）请你探索线段DE与CF的位置关系，并证明你的结论.'B14.如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形.(D若固定三根木条AB, BC, AD不动，AB = AD = 2cm, BC = 5cm,如图，量得第四根木条CD= 5cm,判断此时与是否相等，并说明理由.(2)若固定二根木条AB，不动，AB = 2cm, BC = 5cm,量得木条CD = 5cnz,ZB = 90，写出木条4D的长度可能取到的一个值(直接写出一个即可).⑶若固定一根木条4B不动，AB = 2cm,量得木条CD = 5c〃.如果木条AD,BC的长度不变，当点£>移到B4的延长线上时，点C也在的延长线上；当点C移到AB的延长线上时，点4，C, D 能构成周长为30c加的三角形，求出木条A£>, BC的长度.15.如图，点O在AABC的内部，且在ZBAC的角平分线上，OM丄AB,垂足为M；ON丄AC,垂足为N,并且OB=OC.求证：AB=AC.16.如图，点E在长方形ABCD的边BC上，AE丄EF,点F在边CD上，已知EC=AB=3cm,BC=5cm.求四边形AEFD的面积.17.已知：如图，CD丄AB 于D, BE±AC 于E, Z1=Z2.求证：OB = OC.18.如图，在口ABDC中，分别取AC、BD的中点E和F,连接BE、CF,过点A作AP〃BC, 交DC的延长线于点P.(1)求证：△ABE9Z\DCF；(2)当ZP满足什么条件时，四边形BECF是菱形？证明你的结论.19. (1)如图1,在四边形ABCD 中，AB = AD, ZB=ZD = 90°, E、F 分别是边BC、CD上的点，且ZEAF=丄ZBAD.求证:EF=BE + FD;2(2) 如图2在四边形ABCD中，AB = AD, ZB+ZD = 180°, E、F分别是边BC、CD ±的点，且ZEAF=fzBAD,⑴中的结论是否仍然成立？不用证明.(3) 如图3在四边形ABCD中，AB = AD, ZB+ZADC= 180°, E、F分别是边BC、CD延长线上的点，且ZEAF=丄ZBAD,⑴中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.B, C, D 在同一条直线上，EAXAD, FDXAD, AE=DF, AB=DC.A图1 图2 图3试说明：ZACE=ZDBF. 20.如图，点A,【答案与解析】一、解答题1. 见详解由EB = CE得到BC = FE,利用SSS证明△ ABC^ADEF,得到ZB=ZE,即可得到AB//DE.解:•: FB = CE ,:.FB+FC^CE+CF,即BC = FE,V AB = DE, AC^DF,A AABC^ADEF,.\ZB=ZE,AB//DE-【点睛】本题考查了全等三角形的判定的应用，注意：全等三角形的判定定理有SAS, ASA, AAS, SSS.2. AC和BE,理由见解析.根据题意通过“角角边”证明厶DAC处CBE,得到AD=BC, AC=BE,贝ljAB+AD=AB+BC=AC=BE.解：与AB+AD相等的线段有AC、BE.理由：V BE±AC,:.ZACE+ZACD=90°,'：ZDAC=90°,.•.ZD+Z4CD=90°,.I ZACE=ZD,在△D4C 与ZiCBE 中，\z.A = ^EBCZD =厶BCEI DC = EC ':.厶DAC竺"BE (AAS),:.AD=BC, AC=BE,:.AB+AD=AB+BC=AC=BE.【点睛】本题考点：全等三角形的判定与性质.3. （1） AD=CE,理由见解析；（2） 3.试题分析：（1）利用角角边证ABD^ACAE；得出BD=AE, AD=CE；（2）证法同上，从而得出BD=DE+CE.试题解析：（8分）（1） AD = CE因为ZBAC = 90°, BD1AE,所以ZABD=ZCAE,又因为AB = AC, ZADB=ZAEC = 90°,根据"AAS"可得Z\ABD竺ACAE,所以AD = CE.（2）因为△ ABD^ACAE,所以BD = AE,所以DE=AE-AD = BD-CE=5 — 2=3.考点：全等三角形的判定.4•证明见解析.先证明AADC竺△AEC,贝IJZACD=ZACE,再由AB〃DC,得至IJZACD=ZBAC,于是ZACB=ZBAC.证明：TAB 〃DC.•.ZACD=ZBACTAE 丄BCAZAEC=90°在RtAACE 和RtAACD 中AC = ACCE = CD:.RtAACE^RtAACD （HL）.・.ZACB=ZACD..•.ZACB=ZBAC,【点睛】本题主要考查了全等三角形的判定与性质以及平行线的性质，熟练掌握全等三角形的判定方法是解决问题的关键.5.见解析（1）根据角平分线的性质以及全等三角形的判定得出ACFH^ACGH,进而得出ZCFG=ZCGF；（2）根据外角的性质以及（1）中结论得出ZBAC+ZABC=ZCFG+ZCGF,即可得出答案. 证明：①TCD是ZACB的平分线，EF±CD于H,:.ZFCH=ZGCH,•.•在ACFH和ACGH 中，Z.FCH =厶GCH CH = CHIzCHF =厶CHG:.ACFH^^CGH(ASA),:.ZCFG=ZCGF；②'：ZE+ZBGE=ZABC,:.Z BAC+ ZABC= Z BAC+ ZE+ZBGE,•: ZCGF=ZBGE,:.Z BAC+ ZABC= ZBAC+ ZE+ZCGF,•: ZBAC+ZE=ZCFG,:.Z BAC+ ZABC= ZCFG+ ZCGF,•: ZCFG=ZCGF,1：.^CFE = -^BAC + Z/1BC).【点睛】考查全等三角形的判定与性质，三角形外角的性质等，掌握全等三角形的判定定理是解题的关键.6.筝形有一条对角线平分一组对角，即BD平分ZABC且BD平分ZADC；证明见解析利用SSS 定理证明厶ABD^ACBD,可得ZABD=ZCBD, ZADB=ZCDB,从而可写出关于筝形的对角线的一条性质，筝形有一条对角线平分一组对角.解：筝形有一条对角线平分一组对角，即BD平分ZABC且BD平分ZADC证明：•.•在AABD和ACBD中BA=BC, DA=DC, BD=BD.•.AABD^ACBD(SSS).•.ZABD=ZCBD, ZADB=ZCDB即BD平分ZABC,且BD平分ZADC.A【点睛】本题考查全等三角形的判定及性质，掌握SSS定理及全等三角形对应角相等是本题的解题关键.7. （1）作图见解析；（2）ABD的周长为5cm.分析：（1）利用基本作图（作已知线段的垂直平分线）作DE垂直平分BC；（2）利用线段垂直平分线的性质得到DB=DC,贝闲用等量代换得到AABD的周长=AB+AC,然后把AB=2cm, AC=3cm代入计算计算.详解：（1）如图，DE为所作；（2） VDE垂直平分BC,.・.DB=DC,.'.△ABD 的周长=AB+BD+AD=AB+CD+AD=AB+AC=2+3=5 （cm）.点睛：本题考查了基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）.8 . CE=DF,理由见解析.根据题意可得ZAEC=ZBFD=90° , AC=BD,再根据平行线的性质可得ZCAE=ZDBF, 然后再利用AAS 判定△ AEC竺△BFD,进而可得CE=DF.解：AC=BD又T AC〃DB.・.ZCAE=ZDBF又TZDFB=ZCEA=90°；在AOBF和Z\CAE中ACEA = ZDFB<ZCAE = ZDBFAC = BDA ADBF^ACAE (AAS)CE=DFAC, D两地到路段AB的距离相等.【点睛】此题主要考查了全等三角形的应用，关键是正确理解题意，找出证明三角形全等的条件.9. 60由"ASA"可证△ AED^ACFD,可得AE = CF = 8,可得AF = BE = 15,即可求解.解：I•在RtAABC中，AB = AC, AD为BC边的中线，.•.ZDAC=ZBAD=ZC=45°, AD丄BC, AD = DC,又TDE丄DF, ADXDC,.•.ZEDA+ZADF=ZCDF+ZFDA=90°,.\ZEDA=ZCDF在Z\AED 与ACFD 中，/EDA = ZCDF<AD = CDZEAD = ZCAAAED^ACFD (ASA)..・.AE = CF = 8,/.AB - AE=AC - CF,.•.AF = BE=15,VZEAF = 90°,1:.S AAEF —— xAExAF = 60.2【点睛】本题考查了全等三角形的判定和性质，等腰直角三角形的性质，求AE=CF是本题的关键.10.见解析.利用全等三角形的判定得出△ BED^AGFD (SAS),结合题意，根据全等三角形的性质得到△ ABD 竺△HGD (ASA),根据利用全等三角形的性质对应边相等，进而得出答案. •.•在ABED 和Z:\GFD 中BD = DG< ZBDE = ZGDF ,DE = FD.'.△BED 竺△GFD(SAS),.•.ZE=ZF, ZEBD=ZFGD,.•.ZABD=ZHGD,在ZkABD 和Z\HGD 中ZABD = ZHGD•: <BD = DG ,ZBDA = ZGDH.-.AABD^AHGD(ASA),根据利用全等三角形的性质对应边相等..\HG=AB.【点睛】本题考查全等三角形的判定(ASA、SAS)与性质，解题的关键是掌握全等三角形的判定(ASA、SAS)与性质.11. (1)如图所示，DF即为所求，见解析；(2)见解析.(1) 直接利用过一点作已知直线的垂线作法得出符合题意的图形；(2) 根据角平分线的性质解答即可.(2) '.•△ABC 中，Z4 = 60°, ZC=40°,ZABC=80°,T DE垂直平分BC,:.BD = DC,.•.ZDBC=ZC= 40°,Z4BD=ZDBC=40°,即BD是ZABC的平分线，"：DF±AB, DE±BC,:.DF=DE,即点D到BA, BC的距离相等.【点睛】此题主要考查了复杂作图，正确利用角平分线的性质解答是解题关键.12. 详见解析直接利用已知得出ZADB=ZAEC,进而利用全等三角形的判定与性质得出答案.BD, CE是AABC 的咼，ZADB = ZAEC = 90°，在AABD和AACE中，= ZA< AD = AEZADB = ZAEC:.ABD^ ACE (ASA).AB=AC.【点睛】本题主要考查了全等三角形的判定与性质，正确掌握全等三角形的判定方法是解题关键.13. (1)见解析⑵见解析试题分析:⑴先根据两直线平行，内错角相等证得ZA=ZB,再根据,A=,B,ZE=ZF,DE=CF可证得△4ED竺ZXBFC,再根据全等三角形的性质可得AD=BC,根据线段和差关系得:AC=BD,⑵因为(1)中厶AED竺“BFC,所以ZEDA=ZFCB,根据内错角相等,两直线平行，可证DE//CF.(1)TAE〃BF, .I ZA=ZB,，ZA=ZB在AADE 和ZkBCF 中，< AE=BF ，ZE=ZFLA A ADE^A BCF, .・.AD=BC,...AD - DC=BC - CD,即：AC=BD .(2)DE/7CF.V AADE^ABCF,.•.ZADE=ZBCF,.・.DE〃CF.14. (1)相等，理由见解析；(2) A/29-5<AD<A/29+5;(3) AD = 13, BC^IO或AD=8, BC=15试题分析：（1）相等.连接AC,根据SSS 证明两个三角形全等即可.（2）由勾股定理求出AC,再根据三角形三边的关系求出AD 的取值范围.（3）分两种情形①当点C 在点D 右侧时，②当点C 在点D 左侧时，分别列出方程组即可解决问题，注意最后理由三角形三边关系定理，检验是否符合题意.试题解析：⑴解：相等.理由如下：连结AC,如图所示：AD^AB,BC = CD,AC^AC.-.AABC = AA£>C:.ZB = ZD(2)解：连结AC,ZB = 90:.AC = 7AB 2+BC 2 = V29.•.A /29-5< AD<>/29 + 5（只要直接写出一个符合要求的值即可，如：1, 2等）⑶设= BC = y,AD = 13,BC = 10. ①当点C 在点D 右侧时，＜ x+2=y+5 2 + y + 5 + x = 30 解得: x = 13 y = io②当点C 在点D 左侧时，＜解得：V 卜=15AD = &BC = 15.【点睛】此题是三角形综合题，主要考查全等三角形的判定和性质、二元一次方程组、三角形三边关系定理等知识，解题的关键是学会分类讨论，考虑问题要全面.15•证明见解析试题分析：利用斜边直角边定理证明ABOM和ACON全等，根据全等三角形对应角相等得到ZMBO=ZNCO,再根据等角对等边的性质即可得到AB=AC；试题解析：证明：•.•点0在ZBAC的角平分线上，0M丄AB, ON±AC.•.OM=ON,又VOB=OC,在RtABOM 与RtACON 中OM = ONOB = OCRtABOM ^RtACON,.•.ZMBO=ZNCO,又VOB=OC,.•.ZOBC=ZOCB,/.ZABC=ZACB,.・.AB=AC.16. ｛解析｝根据ASA可证明A ABE= AECF,利用S HWAEFD=S长方形ABCD-2S AABE即可得答案.•.•ZCEF+ZAEB=90°, ZAEB+ZBAE=90°,.•.ZBAE=ZCEF,又TAB=CE, ZABE=ZECF=90°, .'.AABE^AECF,•'•S H边JKAEFD=S出方）BABCD-2S AABE=3X5-2X——x （5-3 ） x3=9.2【点睛】本题考查全等三角形的判定及长方形、三角形面积公式，利用ASA证明AABE^AECF是解题关键.17. 证明见解析试题分析：又CD丄AB, BE丄AC, Z1=Z2,可得OE=OD, ZBDO=ZCEO=90°,再由Z BOD=ZCOE,可得△ BOD竺△COE,从而0B = OC.试题解析：TCD丄AB, BE丄AC, Z1=Z2, .•.OE=OD, ZBDO=ZCEO=90°,又VZBOD=ZCOE, .'.△BOD 竺△COE, /.OB = OC.考点：1.角平分线的性质；2.三角形全等的判定与性质.18. （1）证明详见解析；（2） ZP=90。

中考数学复习《全等三角形》专题训练-附带参考答案

中考数学复习《全等三角形》专题训练-附带参考答案一、选择题1．下列选项中表示两个全等的图形的是（）A．形状相同的两个图形B．周长相等的两个图形C．面积相等的两个图形D．能够完全重合的两个图形2．如图，点D、E分别在线段AB、AC上，BE、CD相交于点O，AE＝AD，则不一定能使△ABE≌△ACD的条件是（）A．AB＝AC B．∠B＝∠CC．∠AEB＝∠ADC D．CD＝BE3．如图是用直尺和圆规作已知角的平分线的示意图，则说明∠CAD=∠DAB的依据是（）A．SAS B．ASA C．AAS D．SSS4．如图△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为点F，若∠BCE=65°，则∠CAF的度数为（）A．25°B．30°C．35°D．65°5．如图EF=CF，BF=DF则下列结论不一定正确的是（）A．△BEF≌△DCF B．△ABC≌△ADEC．DC=AC D．AB=AD6．如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=3，则PQ的最小值为（）A．2 B．3 C．4 D．57．如图，CD⊥AB，BE⊥AC，垂足分别为点D，点E，BE、CD相交于点O．∠1＝∠2，则图中全等三角形共有（）A．2对B．3对C．4对D．5对8．如图，AD 是△ABC中∠BAC的平分线，DE⊥AB于点E，△ABC的面积为12，DE =2，AB = 7，则 AC 的长是（）A．3 B．4 C．5 D．6二、填空题9．如图，∠ACD＝∠BCE，BC＝EC，要使△ABC≌△DEC，则可以添加的一个条件是．10．如图所示，在△ABC中，∠C=90°，AB=8，AD是△ABC的一条角平分线．若CD=2，则△ABD的面积为．11．如图，在Rt△ABC中，∠BAC＝90°，分别过点B，C作过点A的直线的垂线BD，若BD＝4cm，CE＝3cm则DE= cm．12．如图，把两根钢条AB，CD的中点连在一起做成卡钳，已知AC的长度是6cm，则工件内槽的宽BD是cm．13．如图，△ABC为等腰直角三角形AC=BC，若A(−3，0)，C(0，2)，则点B的坐标为.三、解答题14．如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°（1）求证：△ADE≌△CDE．（2）求∠BDC度数．15．如图，已知，EC＝AC，∠BCE＝∠DCA，∠A＝∠E.（1）求证：BC＝DC；（2）若∠A ＝25°，∠D ＝15°，求∠ACB 的度数.16．如图，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE.（1）求证：△ABD ≌△ACE ；（2）若∠1＝25°，∠2＝30°，求∠3的度数.17．如图，在ABC 中90C ∠=︒，BD 是ABC ∠的平分线，DE AB ⊥于点E ，点F 在BC 上，连接DF ，且AD DF =． (1)求证：CF AE =；(2)若3AE =，BF=4，求AB 的长．18．如图，∠BAD ＝∠CAE ＝90°，AB ＝AD ，AE ＝AC ，AF ⊥CB ，垂足为F ．(1)求证：△ABC ≌△ADE ；(2)求∠FAE 的度数；(3)求证：CD ＝2BF+DE ．1．D2．D3．D4．A5．C6．B7．C8．C9．AC ＝DC （答案不唯一）10．811．712．613．(2，-1)14．（1）证明：∵DE 是线段AC 的垂直平分线 ∴DA=DC ，AE=CE在△ADE 与△CDE 中：DA=DCAE=CEDE=DE∴△ADE ≌△CDE （SSS ）；（2）解：∵△ADE ≌△CDE ．∴∠DCA=∠A=50°∴∠BDC=∠DCA+∠A=100°15．（1）证明：∵∠BCE ＝∠DCA∴∠BCE +∠ACE ＝∠DCA +∠ECA即∠BCA ＝∠DCE .在△BCA 和△DCE 中{∠BCA =∠DCE AC =EC ∠A =∠E∴△BCA ≌△DCE （ASA ）（2）解：∵△BCA ≌△DCE∴∠B ＝∠D ＝15°.∵∠A ＝25°∴∠ACB ＝180°−∠A −∠B ＝140°.16．（1）证明：∵∠BAC ＝∠DAE∴∠BAC ﹣∠DAC ＝∠DAE ﹣∠DAC∴∠1＝∠EAC在△ABD 和△ACE 中{AB =AC ∠1=∠EAC AD =AE∴△ABD ≌△ACE （SAS ）（2）解：∵△ABD ≌△ACE∴∠ABD ＝∠2＝30°∵∠1＝25°∴∠3＝∠1+∠ABD ＝25°+30°＝55°.17．（1）证明：（1）∵90C ∠=︒∴DC BC ⊥又∵BD 是ABC ∠的平分线DE AB ⊥∴DE DC = 90AED ∠=︒在Rt AED △和Rt FCD △中∵AD DFDE DC =⎧⎨=⎩∴()Rt Rt AED FCD HL ≌△△∴CF AE =．（2）解：由（1）可得3CF AE ==∴437BC BF CF =+=+=∵DE AB ⊥∴90DEB ∠=︒∴DEB C ∠=∠∵BD 是ABC ∠的平分线∴ABD CBD ∠=∠在BED 和BCD △中∵DEB C EBD CBD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BED BCD AAS ≌△△ ∴7BE BC ==∴7310AB BE AE =+=+=∴AB 的长为10．18．（1）证明：∵90BAD CAE ∠=∠=︒∴90BAC CAD ∠+∠=︒ 90CAD DAE ∠+∠=︒ ∴BAC DAE ∠=∠在△BAC 和△DAE 中∵AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴()BAC DAE SAS ≌△△；（2）解：∵90CAE ∠=︒，AC=AE∴45E ∠=︒由（1）知BAC DAE ≌△△∴45BCA E ∠=∠=︒∵AF BC ⊥∴90CFA ∠=︒∴45CAF ∠=︒∴4590135FAE FAC CAE ∠=∠+∠=︒+︒=︒；（3）证明：延长BF 到G ，使得FG FB = ∵AF BG ⊥∴90AFG AFB ∠=∠=︒在△AFB 和△AFG 中∴BF GF AFB AFG AF AF =⎧⎪∠=∠⎨⎪=⎩∴()AFB AFG SAS ≌△△∴AB AG = ABF G ∠=∠∵BAC DAE ≌△△∴AB AD = CBA EDA ∠=∠ CB=ED ∴AG AD = ABF CDA ∠=∠∴CGA CDA ∠=∠∵45GCA DCA ∠=∠=︒∴在△CGA 和△CDA 中GCA DCA CGA CDA AG AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CGA CDA AAS ≌△△∴CG CD =∵22CG CB BF FG CB BF DE BF =++=+=+ ∴2CD BF DE =+．。

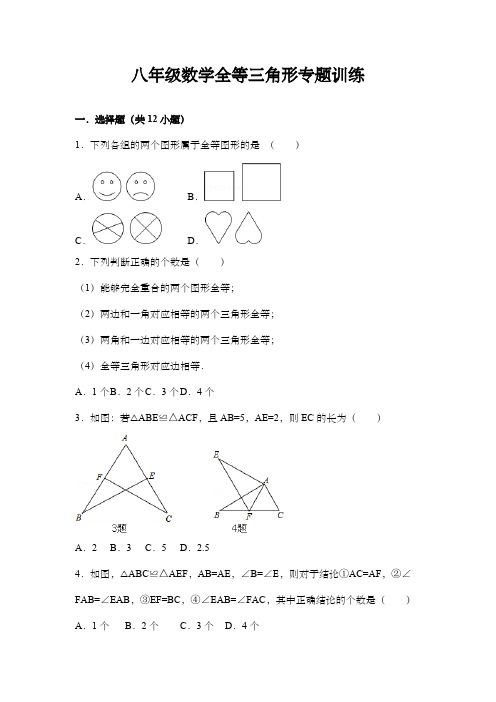
八年级全等三角形专题练习(解析版)

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,：在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为：在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用：如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解：(1)证实：BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下：: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下：由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实：PC=PE；〔2〕求N CPE的度数：〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论：⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案；(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE；⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>：⑶、AP = CE理由是：在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点：三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£＞为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系：②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由；〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析：②成立,理由见解析：〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可：〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解：〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD：②成立,理由如下：如图2：VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD：(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证：△.所为等腰直角三角形：〔2〕假设△ABC的面积为7,求四边形AEDF•的面积：〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析；〔2〕 3.5：〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形；〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可；〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解：〔1〕证实：如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又；Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn；AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又；Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又：Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空：AABC的面积等于—；(2)连接CE,求证：CE是NAC3的平分线；(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—：〔2〕证实见解析：〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得：〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实：〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解：〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为：—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=；(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为：50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm ：(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等？假设存在,请求出v的值：假设不存在,请说明理由.【答案】(1) (12-2/)； (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长：(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得；(3)先分两种情况：当BP=CQ, AB=PC 时,△ABPgZ\PCQ：或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解：(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin：.PC = BC-BP = (n-2i)cm故答案为：(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下：①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item：.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.：在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证：MN = CN — BM ；(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析：(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM： (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实：・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由：•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA：.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现：如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证：△BADgZkCAE；(2)在(1)的条件下,求N8EC的度数：拓广探索：(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析：(2) 70°； (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实：如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,：.Z EAC=A DAB,AE=AD. AC=AB9：.△ BAD^ & CAE (SAS).(2)解：如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解：如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,：AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是；②设NBA尸=a,用.表示NBCF的大小；〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE；②NBCF=.：(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案；②由釉对称性,得：AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解：(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,：.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下：作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证：CF = EG ；〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证：CD = CE+CF；〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解；〔2〕证实见详解：〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论：(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论；(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, ：.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即：ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),：.CF = EG ；(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、：.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即：ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下：过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即：NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。

苏科版八年级数学上册试题第1章全等三角形单元测试卷(含详解)

第1章《全等三角形》单元测试卷一、单选题（本大题共10小题，每小题3分，共30分）1．下列说法正确的是（）A ．两个等边三角形一定全等B ．腰对应相等的两个等腰三角形全等C ．形状相同的两个三角形全等D ．全等三角形的面积一定相等2．已知与全等，A 、B 、C 的对应点分别为D 、E 、F ，且E 点在AE 上，B 、F 、C 、D 四点共线，如图所示若，，则下列叙述何者正确？（）A ．，B ．，C ．，D ．，3．如图，在△ABC 中，AB ＝BC ，点D 为AC 上的点，连接BD ，点E 在△ABC 外，连接AE ，BE ，使得CD ＝BE ，∠ABE ＝∠C ，过点B 作BF ⊥AC 交AC 点F ，若∠BAE ＝21°，∠C ＝28°，则∠FBD ＝（）A ．49°B ．59°C ．41°D ．51°4．如图，有一块边长为4的正方形塑料模板，将一块足够大的直角三角板的直角顶点落在点，两条直角边分别与交于点F ，与延长线交于点E ．则四边形的面积是（）ABC V DEF V ．=40A ∠︒=35CED ∠︒=EF EC =AE FC=EF EC AE FC ≠EF EC ≠=AE FC EF EC ≠AE FC≠ABCD A CD CB AECFA ．4B ．6C ．10D ．165．如图，在的网格中，每一个小正方形的边长都是1，点，，，都在格点上，连接，相交于，那么的大小是（）A ．B ．C ．D ．6．△ABC 中，AB ＝AC ，∠ABC ＝72°，以B 为圆心，以任意长为半径画弧，分别交BA 、BC 于M 、N ，再分别以M 、N为圆心，以大于MN 为半径画弧，两弧交于点P ，射线BP 交AC 于点D ，则图中与BC 相等的线段有（）A ．BD B ．CD C ．BD 和AD D ．CD 和AD7．如图，在Rt △ABC 中，∠C=90°，以顶点A 为圆心，适当长为半径画弧，分别交AB 、AC 于点M 、N ，再分别以点M 、N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，射线AP 交边BC 于点D ．下列说法错误的是（）33⨯A B C D AC BD P APB ∠80︒60︒45︒30︒1212A ．B ．若，则点D 到AB 的距离为2C ．若，则D ．8．如图，长方形中，点为上一点，连接，将长方形沿着直线折叠，点恰好落在的中点上，点为的中点，点为线段上的动点，连接、，若、、，则的最小值是( )A ．B ．C ．D ．9．如图，点在线段上，于，于．，且，，点以的速度沿向终点运动，同时点以的速度从开始，在线段上往返运动（即沿运动），当点到达终点时，，同时停止运动．过，分别作的垂线，垂足为，．设运动时间为，当以，，为顶点的三角形与全等时，的值为（）A ．1或3B ．1或C ．1或或 D ．1或或510．如图，在中，，和的平分线、相交于点，交于点，交于点，若已知周长为，，，则长为（）CAD BAD ∠=∠2CD =30B ∠=CDA CAB ∠=∠2ABD ACDS S =V V ABCD E AD CE ABCD CE D AB F G CF P CE PF PG AE a =ED b =AF c =PF PG +a c b +-2b c +2a b c ++a b+C BD AB BD ⊥B ED BD ⊥D 90ACE ∠=︒5cm AC =6cm CE =P 2cm/s A C E →→E Q 3cm/s E EC E C E C →→→→⋅⋅⋅P P Q P Q BD M N s t P C M QCN △t 115115235115ABC V 60A ∠=︒ABC ∠ACB ∠BD CE O BD AC D CE AB E ABC V 207BC =:4:3AE AD =AEA． B ． C ． D ．4二、填空题（本大题共8小题，每小题4分，共32分）11．如图，已知正方形中阴影部分的面积为3，则正方形的面积为．12．数学课上，老师出示如下题目：“已知：．求作：．”如图是小宇用直尺和圆规的作法，其中的道理是作出△，根据全等三角形的性质，得到．△的依据是．13．如图，已知，，，直线与，分别交于点，，且，，则的度数为．14．如图，在△ABC 中，点D 是AC 的中点，分别以AB ，BC 为直角边向△ABC 外作等腰直角三角形ABM 和等腰直角三角形BCN ，其中∠ABM ＝NBC ＝∠90°，连接MN ，已知MN ＝4，则BD ＝．187247267AOB ∠A O B AOB '''∠=∠ΔC O D COD ''≅'A O B AOB '''∠=∠ΔC O D COD ''≅'AB AD =AC AE =BC DE =BC AD DE F G 65DGB ∠=︒120EAB ∠=︒CAD ∠15．如图，为的平分线，为上一点，且于点，，给出下列结论：①；②；③；④；⑤四边形的面积是面积的2倍，其中结论正确的个数有．16．如图，把两块大小相同的含45°的三角板ACF 和三角板CFB 如图所示摆放，点D 在边AC 上，点E 在边BC 上，且∠CFE ＝13°，∠CFD ＝32°，则∠DEC 的度数为．17．如图，在中，，，，有下列结论：①；②；③连接，；④过点作交于点，连接，则．其中正确的结论有．18．如图，在Rt △ABC 中，∠C ＝90°，两锐角的角平分线交于点P ，点E 、F 分别在边BC 、AC 上，且都不与点C 重合，若∠EPF ＝45°，连接EF ，当AC ＝6，BC ＝8，AB ＝10时，则△CEF的BN MBC ∠P BN PD BC ⊥D 180APC ABC ∠+∠=︒MAP ACB ∠=∠PA PC =2BC AB CD -=BP AC =BAPC PBD △ABC V AD BC ⊥AD BD =BF AC =ADC BDF △≌△BE AC ⊥DE 135AED ∠=︒D DM AB ∥AC M FM BF AM MD =+周长为．三、解答题（本大题共6小题，共58分）19．（8分）如图，，点E 在BC 上，且，．(1) 求证：；(2) 判断AC 和BD的位置关系，并说明理由．BD BC =BE AC =DE AB =ABC EDB V V ≌20．（8分）如图，在五边形中，，．(1) 请你添加一个条件，使得，并说明理由；(2) 在(1)的条件下，若，，求的度数．21．（10分）在复习课上，老师布置了一道思考题：如图所示，点M ，N 分别在等边的边上，且，，交于点Q ．求证：．同学们利用有关知识完成了解答后，老师又提出了下列问题：(1) 若将题中“”与“”的位置交换，得到的是否仍是真命题？请你给出答案并说明理由．ABCDE AB DE =AC AD =ABC DEA △△≌66CAD ∠=︒110B ∠=︒BAE ∠ABC V ,BC CA BM CN =AM BN 60BQM ∠=︒BM CN =60BQM ∠=︒(2) 若将题中的点M ，N 分别移动到的延长线上，是否仍能得到？请你画出图形，给出答案并说明理由．22．（10分）如图1，点P 、Q 分别是边长为4cm 的等边三角形ABC 的边AB 、BC 上的动点，点P 从顶点A ，点Q 从顶点B 同时出发，且它们的速度都为1cm/s ．（1）连接AQ 、CP 交于点M ，则在P ，Q 运动的过程中，证明≌；（2）会发生变化吗？若变化，则说明理由，若不变，则求出它的度数；（3）P 、Q 运动几秒时，是直角三角形？,BC CA 60BQM ∠=︒ABQ ∆CAP ∆CMQ ∠PBQ ∆（4）如图2，若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动，直线AQ 、CP 交点为M ，则变化吗？若变化说明理由，若不变，则求出它的度数。

八年级数学上册第一章《全等三角形》测试卷-苏科版(含答案)

八年级数学上册第一章《全等三角形》测试卷-苏科版（含答案）一．选择题1．如图，△ABC≌△CDA，∠BAC＝∠DCA，则BC的对应边是（）A．CD B．CA C．DA D．AB2．下列图形中与已知图形全等的是（）A．B．C．D．3．如图，△ABC≌△DEF．若BC＝5cm，BF＝7cm，则EC＝（）A．1cm B．2cm C．3cm D．4cm4．如图，△ABC≌△AEF，AB＝AE，∠B＝∠E，则对于结论①AC＝AF，②∠FAB＝∠EAB，③EF＝BC，④∠EAB＝∠FAC，其中正确结论的个数是（）A．1个B．2个C．3个D．4个5．如图所示，AB＝BD，BC＝BE，要使△ABE≌△DBC，需添加条件（）A．∠A＝∠D B．∠C＝∠E C．∠D＝∠E D．∠ABD＝∠CBE 6．如图，∠BAD＝∠BCD＝90°，AB＝CB，可以证明△BAD≌△BCD的理由是（）A．HL B．ASA C．SAS D．AAS7．已知△ABC≌△DEF，BC＝EF＝6cm，△ABC的面积为18平方厘米，则EF边上的高是（）A．6cm B．7cm C．8cm D．9cm8．如图，在3×3正方形网格中，∠1+∠2+∠3+∠4+∠5等于（）A．145°B．180°C．225°D．270°9．如图所示，AD平分∠BAC，AB＝AC，连接BD、CD并延长分别交AC、AB于F、E点，则此图中全等三角形的对数为（）A．2对B．3对C．4对D．5对10．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE，下列说法：①△ABD和△ACD面积相等；②∠BAD＝∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE＝AE．其中正确的是（）A．①②B．③⑤C．①③④D．①④⑤二．填空题11．能够的两个图形叫做全等图形．12．如图，∠B＝∠D＝90°，BC＝DC，∠1＝40°，则∠2＝度．13．如图为4×4的正方形网格，图中的线段均为格点线段（线段的端点为格点），则∠1+∠2+∠3+∠4+∠5的度数为．14．由同一张底片冲洗出来的五寸照片和七寸照片全等图形（填“是”或“不是”）．15．如图，点C在线段BD上，AB⊥BD于B，ED⊥BD于D．∠ACE＝90°，且AC＝5cm，CE＝6cm，点P以2cm/s的速度沿A→C→E向终点E运动，同时点Q以3cm/s的速度从E开始，在线段EC上往返运动（即沿E→C→E→C→…运动），当点P到达终点时，P，Q同时停止运动．过P，Q分别作BD的垂线，垂足为M，N．设运动时间为ts，当以P，C，M为顶点的三角形与△QCN全等时，t的值为．16．如图，在△ABC中，∠A＝90°，DE⊥BC，垂足为E．若AD＝DE且∠C＝50°，则∠ABD＝°．17．△ABC≌△DEF，且△ABC的周长为12，若AC＝3，EF＝4，AB＝．18．如图，CE⊥AB于点E，BD⊥AC于点D，BD、CE交于点O，且AO平分∠BAC，则图中的全等三角形共有对．19．某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是，理由是．20．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB＝10，DO＝4，平移距离为6，则阴影部分面积为．三．解答题21．如图，在△ABC中，AB＞AC，点D在边AB上，且BD＝CA，过点D作DE∥AC，并截取DE＝AB，且点C，E在AB同侧，连接BE．求证：△DEB≌△ABC．22．如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，AB＝DE，BF＝CE，AB ∥DE，求证：△ABC≌△DEF．23．如图，已知△ABC≌△DEF，∠A＝85°，∠B＝60°，AB＝8，EH＝2．（1）求角F的度数与DH的长；（2）求证：AB∥DE．24．如图，已知△EFG≌△NMH，∠F与∠M是对应角．（1）写出相等的线段与角．（2）若EF＝2.1cm，FH＝1.1cm，HM＝3.3cm，求MN和HG的长度．25．我们知道能完全重合的图形叫做全等图形，因此，如果两个四边形能完全重合，那么这两个四边形全等，也就是说，当两个四边形的四个内角、四条边都分别对应相等时，这两个四边形全等．请借助三角形全等的知识，解决有关四边形全等的问题．如图，已知，四边形ABCD和四边形A′B′C′D′中，AB＝A′B′，BC＝B′C′，∠B＝∠B′，∠C＝∠C′，现在只需补充一个条件，就可得四边形ABCD≌四边形A′B′C′D′．下列四个条件：①∠A＝∠A′；②∠D＝∠D′；③AD＝A′D′；④CD＝C′D′（1）其中，符合要求的条件是．（直接写出编号）（2）选择（1）中的一个条件，证明四边形ABCD≌四边形A′B′C′D′．参考答案一．选择题1．解：∵△ABC≌△CDA，∠BAC＝∠DCA，∴∠BAC与∠DCA是对应角，∴BC与DA是对应边（对应角对的边是对应边）．故选：C．2．解：A、圆里面的正方形与已知图形不能重合，错；B、与已知图形能完全重合，正确；C、中间是长方形，与已知图形不重合，错；D、中间是长方形，与已知图形不重合，错．故选：B．3．解：∵BC＝5cm，BF＝7cm，∴CF＝BF﹣BC＝2cm，∵△ABC≌△DEF，∴FE＝BC＝5cm，∴EC＝EF﹣CF＝5cm﹣2cm＝3cm，故选：C．4．解：∵△ABC≌△AEF，∴AC＝AF，故①正确；∠EAF＝∠BAC，∴∠FAC＝∠EAB≠∠FAB，故②错误；EF＝BC，故③正确；∠EAB＝∠FAC，故④正确；综上所述，结论正确的是①③④共3个．故选：C．5．解：∵AB＝BD，BC＝BE，∴要使△ABE≌△DBC，需添加的条件为∠ABE＝∠DBC，又∠ABE﹣∠DBE＝∠DBC﹣∠DBE，即∠ABD＝∠CBE，∴可添加的条件为∠ABE＝∠DBC或∠ABD＝∠CBE．综合各选项，D选项符合．故选：D．6．解：∵∠BAD＝∠BCD＝90°，AB＝CB，DB＝DB，∴△BAD≌△BCD（HL）．故选：A．7．解：设△DEF的面积为s，边EF上的高为h，∵△ABC≌△DEF，BC＝EF＝6cm，△ABC的面积为18平方厘米∴两三角形的面积相等即s＝18又S＝•EF•h＝18，∴h＝6故选：A．8．解：在△ABC和△AEF中，，∴△ABC≌△AEF（SAS），∴∠5＝∠BCA，∴∠1+∠5＝∠1+∠BCA＝90°，在△ABD和△AEH中，，∴△ABD≌△AEH（SAS），∴∠4＝∠BDA，∴∠2+∠4＝∠2+∠BDA＝90°，∵∠3＝45°，∴∠1+∠2+∠3+∠4+∠5＝90°+90°+45°＝225°．故选：C．9．解：图中全等三角形的对数有4对，有△ADB≌△ADC，△ABF≌△ACE，△AED≌△AFD，△EDB≌△FDC，理由是：∵AD平分∠BAC，∴∠BAD＝∠CAD，在△ADB和△ADC中∴△ADB≌△ADC（SAS），∴∠B＝∠C，∠ADB＝∠ADC，∵∠EDB＝∠FDC，∴∠ADB﹣∠EDB＝∠ADC﹣∠FDC，∴∠ADE＝∠ADF，在△AED和△AFD中∴△AED≌△AFD（ASA），∴AE＝AF，在△ABF和△ACE中∴△ABF≌△ACE（SAS），∵AB＝AC，AE＝AF，∴BE＝CF，在△EDB和△FDC中∴△EDB≌△FDC（AAS），故选：C．10．解：∵AD是△ABC的中线，∴BD＝CD，∴△ABD和△ACD面积相等，故①正确；∵AD为△ABC的中线，∴BD＝CD，∠BAD和∠CAD不一定相等，故②错误；在△BDF和△CDE中，，∴△BDF≌△CDE（SAS），故③正确；∴∠F＝∠DEC，∴BF∥CE，故④正确；∵△BDF≌△CDE，∴CE＝BF，故⑤错误，正确的结论为：①③④，故选：C．二．填空题11．解：能够完全重合的两个图形叫做全等图形．故答案为完全重合．12．解：在直角△ABC与直角△ADC中，BC＝DC，AC＝AC ∴△ABC≌△ADC∴∠2＝∠ACB在△ABC中∠ACB＝180°﹣∠B﹣∠1＝50°∴∠2＝50°．13．解：在图中标上字母，如图所示．∵四边形ABCD为4×4的正方形，∴∠3＝45°．∵四边形ANPE为1×1的正方形，∴AE＝AN．∵四边形CDEF和四边形BCMN均为4×3的长方形，∴CE＝CN．在△ACE和△ACN中，，∴△ACE≌△ACN（SSS），∴∠AEC＝∠ANC，∴∠2+∠4+90°＝180°，∴∠2与∠4互余．同理可得：∠1与∠5互余．∴∠1+∠2+∠3+∠4+∠5＝（∠1+∠5）+（∠2+∠4）+∠3＝90°+90°+45°＝225°．故答案为：225°．14．解：由全等形的概念可知：由同一张底片冲洗出来的五寸照片和七寸照片，大小不一样，所以不是全等图形．故答案为：不是．15．解：当点P在AC上，点Q在CE上时，∵以P，C，M为顶点的三角形与△QCN全等，∴PC＝CQ，∴5﹣2t＝6﹣3t，∴t＝1，当点P在AC上，点Q第一次从点C返回时，∵以P，C，M为顶点的三角形与△QCN 全等，∴PC＝CQ，∴5﹣2t＝3t﹣6，∴t＝，当点P在CE上，点Q第一次从E点返回时，∵以P，C，M为顶点的三角形与△QCN 全等，∴PC＝CQ，∴2t﹣5＝18﹣3t，∴t＝，综上所述：t的值为1或或．16．解：∵∠C＝50°，∠A＝90°，∴∠ABC＝40°，∵DE⊥BC，∴∠A＝∠BED＝90°，在Rt△ABD和Rt△EBD中，，∴Rt△ABD≌Rt△EBD（HL），∴∠ABD＝∠DBE，∴∠ABD＝∠ABC＝20°，故答案为：20．17．解：∵△ABC≌△DEF，∴BC＝EF＝4，由题意得，AB+BC+AC＝12，∴AB＝12﹣3﹣4＝5，故答案为：5．18．解：①在△AEO与△ADO中∵CE⊥AB于点E，BD⊥AC于点D，AO平分∠BAC，∴∠AEO＝∠ADO＝90°，∠EAO＝∠DAO∵AO＝AO∴△AEO≌△ADO（AAS）∴AE＝AD，OE＝OD；②在△OBE与△OCD中∵∠OEB＝∠0DC＝90°，∠EOB＝∠DOC，OE＝OD∴△OBE≌△OCD（AAS）∴OB＝OC，BE＝DC，∠B＝∠C；③在△ABO与△ACO中∵AE＝AD∴AB＝AC∵AB＝AC，AO＝AO，BO＝CO∴△ABO≌△ACO（SSS）④在△AEC与△ADB中∵∠AEC＝∠ADB＝90°，AC＝AB，AE＝AD∴△AEC≌△ADB（HL）所以共有四对全等三角形．19．解：第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．最省事的方法是应带③去，理由是：ASA．故答案为：带③去，ASA．20．解：由平移的性质知，BE＝6，DE＝AB＝10，∴OE＝DE﹣DO＝10﹣4＝6，∴S四边形ODFC ＝S梯形ABEO＝（AB+OE）•BE＝（10+6）×6＝48．故答案为48．三．解答题21．证明：∵DE∥AC，∴∠EDB＝∠A．在△DEB与△ABC中，，∴△DEB≌△ABC（SAS）．22．证明：∵BF＝CE，∴BF+FC＝CE+FC，即BC＝EF．∵AB∥DE，∴∠B＝∠E．在△ABC和△DEF中，∴△ABC≌△DEF（SAS）．23．解：（1）∵∠A＝85°，∠B＝60°，∴∠ACB＝180°﹣∠A﹣∠B＝35°，∵△ABC≌△DEF，AB＝8，∴∠F＝∠ACB＝35°，DE＝AB＝8，∵EH＝2，∴DH＝8﹣2＝6；（2）证明：∵△ABC≌△DEF，∴∠DEF＝∠B，∴AB∥DE．24．解：（1）∵△EFG≌△NMH，∠F与∠M是对应角，∴EF＝NM，EG＝NH，FG＝MH，∠F＝∠M，∠E＝∠N，∠EGF＝∠NHM，∴FH＝GM，∠EGM＝∠NHF；（2）∵EF＝NM，EF＝2.1cm，∴MN＝2.1cm；∵FG＝MH，FH+HG＝FG，FH＝1.1cm，HM＝3.3cm，∴HG＝FG﹣FH＝HM﹣FH＝3.3﹣1.1＝2.2cm．25．解：（1）符合要求的条件是①②④，故答案为：①②④；（2）选④，证明：连接AC、A′C′，在△ABC与△A′B′C′中，，∴△ABC≌△A′B′C′（SAS），∴AC＝A′C′，∠ACB＝∠A′C′B′，∵∠BCD＝∠B′C′D′，∴∠BCD﹣∠ACB＝∠B′C′D′﹣∠A′C′B′，∴∠ACD＝∠A′C′D′，在△ACD和△A′C′D中，，∴△ACD≌△A′C′D′（SAS），∴∠D＝∠D，∠DAC＝∠D′A′C′，DA＝D′A′，∴∠BAC+∠DAC＝∠B′A′C′+∠D′A′C′，即∠BAD＝∠B′A′D′，∴四边形ABCD和四边形A′B′C′D′中，AB＝A′B′，BC＝B′C′，AD＝A′D′，DC＝D′C′，∠B＝∠B′，∠BCD＝∠B′C′D′，∠D＝∠D′，∠BAD＝∠B′A′D′，∴四边形ABCD≌四边形A′B′C′D′．。

专题全等三角形压轴题训练(30题)(解析版)

（苏科版）八年级上册数学《第1章全等三角形》专题全等三角形压轴题训练（30题）1．如图，△ABC中，AB＝AC，D为AC边上一点，E为AB延长线上一点，且CD＝BE，DE与BC相交于点F．（1）求证：DF＝EF．（2）过点F作FG⊥DE，交线段CE于点G，若CE⊥AC，CD＝4，S＝5，求EG的长．△EFG【分析】（1）过点D作DH∥AB交BC于点H，根据等腰三角形的性质及平行线的性质得到∠BEF＝∠HDF，∠DHC＝∠DCH，则DH＝CD，结合∠BFE＝∠HFD，即可利用AAS判定△BEF≌△HDF，根据全等三角形的性质即可得解；（2）根据三角形的面积公式求解即可．【解答】（1）过点D作DH∥AB交BC于点H，∵AB＝AC，∴∠ABC＝∠ACB，∵DH∥AB，∴∠DHC＝∠ABC，∴∠DHC＝∠ACB＝∠DCH，∴DH＝CD，∵CD＝BE，∴DH＝BE，∵DH∥AB，∴∠BEF＝∠HDF，在△BEF和△HDF中，∠BFE=∠HFD∠BEF=∠HDFBE=DH，∴△BEF≌△HDF（AAS），∴DF＝EF；（2）连接DG，∵DF＝EF，FG⊥DE，∴S△DFG ＝S△EFG＝5，∴S△DEG＝10，∵CE⊥AC，CD＝4，∴S△DEG =12EG•CD=12EG×4，∴12EG×4＝10，∴EG＝5．【点评】此题考查了全等三角形的判定与性质，利用AAS判定△BEF≌△HDF是解题的关键．2．如图，四边形ABCD中，AB＝BC＝2CD，AB∥CD，∠C＝90°，E是BC的中点，AE与BD相交于点F，连接DE．（1）求证：△ABE≌△BCD；（2）判断线段AE与BD的数量关系及位置关系，并说明理由；【分析】（1）由平行线的性质得出∠ABE+∠C＝180°，得出∠ABE＝90°＝∠C，再证出BE＝CD，由SAS证明△ABE≌△BCD即可；（2）由全等三角形的性质得出AE＝BD，证出∠ABF+∠BAE＝90°，得出∠AFB＝90°，即可得出结论．【解答】（1）证明：∵AB∥CD，∴∠ABE+∠C＝180°，∵∠C＝90°，∴∠ABE＝90°＝∠C，∵E是BC的中点，∴BC＝2BE，∵BC＝2CD，∴BE＝CD，在△ABE和△BCD中，AB=BC∠ABE=∠C BE=CD，∴△ABE≌△BCD（SAS）；（2）解：AE＝BD，AE⊥BD，理由如下：由（1）得：△ABE≌△BCD，∴AE＝BD，∵∠BAE＝∠CBD，∠ABF+∠CBD＝90°，∴∠ABF+∠BAE＝90°，∴∠AFB＝90°，∴AE⊥BD．【点评】本题考查了全等三角形的判定与性质、直角三角形的性质等知识；证明三角形全等是解题的关键．3．如图1，在等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，点P为BC边上的一个动点，连接AP，以AP为直角边，A为直角顶点，在AP右侧作等腰直角三角形PAD，连接CD．（1）当点P在线段BC上时（不与点B重合），求证：△BAP≌△CAD；（2）当点P在线段BC的延长线上时（如图2），试猜想线段BP和CD的数量关系与位置关系分别是什么？请给予证明．【分析】（1）证得∠BAP＝∠CAD，根据SAS可证明△BAP≌△CAD；（2）可得∠BAP＝∠CAD，由SAS可证明△BAP≌△CAD，可得BP＝CD，∠B＝∠ACD，则结论得证．【解答】（1）证明：∵∠BAC＝∠PAD＝90°，∴∠BAC﹣∠PAC＝∠PAD﹣∠PAC，即：∠BAP＝∠CAD，在△BAP和△CAD中AB=AC∠BAP=∠CAD，PA=DA∴△BAP≌△CAD（SAS）；（2）猜想：BP＝CD，BP⊥CD．证明：∵∠BAC＝∠PAD＝90°，∴∠BAC+∠PAC＝∠PAD+∠PAC，即：∠BAP＝∠CAD，在△BAP和△CAD中AB=AC∠BAP=∠CAD，PA=DA∴△BAP≌△CAD（SAS），∴BP＝CD（全等三角形的对应边相等），∠B＝∠ACD（全等三角形的对应角相等），∵∠B+∠ACB＝90°，∴∠ACD+∠ACB＝90°，即：BP⊥CD．【点评】本题考查了全等三角形的判定与性质，等腰直角三角形的性质，根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键．4．（2023春•市南区期末）如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC边上一点，连接BE与AD交于点F，G为△ABC外一点，满足∠ACG＝∠ABE，∠FAG＝∠BAC，连接EG．（1）求证：△ABF≌△ACG；（2）求证：BE＝CG+EG．【分析】（1）根据已知条件可得∠BAD＝∠CAG，然后利用ASA即可证明△ABF≌△ACG；（2）结合（1）的结论，再证明△AEF≌△AEG，即可解决问题．【解答】（1）证明：∵∠BAC＝∠FAG，∴∠BAC﹣∠CAD＝∠FAG﹣∠CAD，∴∠BAD＝∠CAG，在△ABF和△ACG中，∠BAD=∠CAGAB=AC，∠ABF=∠ACG∴△ABF≌△ACG（ASA）；（2）证明：∵△ABF≌△ACG，∴AF＝AG，BF＝CG，∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD，∵∠BAD＝∠CAG，∴∠CAD＝∠CAG，在△AEF和△AEG中，AF=AG∠FAE=∠GAE，AE=AE∴△AEF≌△AEG（SAS）．∴EF＝EG，∴BE＝BF+FE＝CG+EG．【点评】本题考查了全等三角形的判定与性质，解决本题的关键是得到△AEF≌△AEG．5．（2022秋•新宾县期中）如图（1）所示，A，E，F，C在一条直线上，AE＝CF，过E，F分别作DE⊥AC，BF⊥AC，若AB＝CD．（1）求证：EG＝FG．（2）若将△DEC的边EC沿AC方向移动，变为图（2）时，其余条件不变，上述结论是否成立？请说明理由．【分析】（1）先利用HL判定Rt△ABF≌Rt△CDE，得出BF＝DE；再利用AAS判定△BFG≌△DEG，从而得出GE＝GF；（2）结论仍然成立，同理可以证明得到．【解答】解：（1）证明：∵DE⊥AC，BF⊥AC，∴∠DEF＝∠BFE＝90°．∵AE＝CF，AE+EF＝CF+EF．即AF＝CE．在Rt△ABF和Rt△CDE中，AB=CDAF=CE，∴Rt△ABF≌Rt△CDE（HL），∴BF＝DE．在△BFG和△DEG中，∵∠BFG=∠DEG ∠BGF=∠DGE BF=DE，∴△BFG≌△DGE（AAS），∴GE＝GF；（2）结论依然成立．理由：∵DE⊥AC，BF⊥AC，∴∠BFA＝∠DEC＝90°∵AE＝CF∴AE﹣EF＝CF﹣EF，即AF＝CE，在Rt△ABF和Rt△CDE中，AB=CDAF=CE，∴Rt△ABF≌Rt△CDE（HL），∴DE＝BF在△BFG和△DEG中，∵∠BFG=∠DEG ∠BGF=∠DGE BF=DE，∴△BFG≌△DGE（AAS），∴GE＝GF．【点评】本题考查三角形全等的判定与性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．6．（2023春•市南区期末）如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC边上一点，连接BE与AD交于点F，G为△ABC外一点，满足∠ACG＝∠ABE，∠FAG＝∠BAC，连接EG．（1）求证：△ABF≌△ACG；（2）求证：BE＝CG+EG．【分析】（1）根据已知条件可得∠BAD＝∠CAG，然后利用ASA即可证明△ABF≌△ACG；（2）结合（1）的结论，再证明△AEF≌△AEG，即可解决问题．【解答】（1）证明：∵∠BAC＝∠FAG，∴∠BAC﹣∠CAD＝∠FAG﹣∠CAD，∴∠BAD＝∠CAG，在△ABF和△ACG中，∠BAD=∠CAGAB=AC，∠ABF=∠ACG∴△ABF≌△ACG（ASA）；（2）证明：∵△ABF≌△ACG，∴AF＝AG，BF＝CG，∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD，∵∠BAD＝∠CAG，∴∠CAD＝∠CAG，在△AEF和△AEG中，AF=AG∠FAE=∠GAE，AE=AE∴△AEF≌△AEG（SAS）．∴EF＝EG，∴BE＝BF+FE＝CG+EG．【点评】本题考查了全等三角形的判定与性质，解决本题的关键是得到△AEF≌△AEG．7．（2022秋•忠县期末）在△ABC中，点D、E分别在AB、AC边上，设BE与CD相交于点F．（1）如图①，设∠A＝60°，BE、CD分别平分∠ABC、∠ACB，证明：DF＝EF．（2）如图②，设BE⊥AC，CD⊥AB，点G在CD的延长线上，连接AG、AF；若∠G＝∠6，BD＝CD，证明：GD＝DF．【分析】（1）在BC上截取BM＝BD，连接FM，证明△BFD≌△BFM，△ECF≌△MCF，进而可以解决问题；（2）根据已知条件证明△BDF≌△CDA，进而可以解决问题．【解答】证明：（1）如图，在BC上截取BM＝BD，连接FM，∵∠A＝60，∴∠BFC＝90°+60°÷2＝120°，∴∠BFD＝60°，∵BE平分∠ABC，∴∠1＝∠2，在△BFD和△BFM中，BD=BM∠1=∠2，BF=BF∴△BFD≌△BFM（SAS），∴∠BFM＝∠BFD＝60°，DF＝MF，∴∠CFM＝120°﹣60°＝60°，∵∠CFE＝∠BFD＝60°，∴∠CFM＝∠CFE，∵CD平分∠ACB，∴∠3＝∠4，又CF＝CF，在△ECF和△MCF中，∠CFE=∠CFMFC=FC，∠3=∠4∴△ECF≌△MCF（ASA），∴EF＝MF，∴DF＝EF；（2）∵BE⊥AC，CD⊥AB，∴∠BDF＝∠CDA＝90°，∴∠1+∠BFD＝90°，∠3+∠CFE＝90°，∠BFD＝∠CFE，∴∠1＝∠3，∵BD＝CD，在△BDF和△CDA中，∠BDF=∠CDABD=CD，∠1=∠3∴△BDF≌△CDA（ASA），∴DF＝DA，∵∠ADF＝90°，∴∠6＝45°，∵∠G＝∠6，∴∠5＝45°∴∠G＝∠5，∴GD＝DA，∴GD＝DF．【点评】本题属于三角形的综合题，考查了全等三角形的判定与性质，角平分线的性质，解决本题的关键是掌握全等三角形的判定与性质．8．（2023春•宣汉县校级期末）已知：∠ACB＝90°，AC＝BC，AD⊥CM，BE⊥CM，垂足分别为D，E，（1）如图1，把下面的解答过程补充完整，并在括号内注明理由．①线段CD和BE的数量关系是：CD＝BE；②请写出线段AD，BE，DE之间的数量关系并证明．解：①结论：CD＝BE．理由：∵AD⊥CM，BE⊥CM，∴∠ACB＝∠BEC＝∠ADC＝90°，∴∠ACD+∠BCE＝90°，∠BCE+∠CBE＝90°，∴∠ACD＝　在△ACD和△CBE中，（）∴△ACD≌△CBE，（）∴CD＝BE．②结论：AD＝BE+DE．理由：∵△ACD≌△CBE，∴ ∵CE＝CD+DE＝BE+DE，∴AD＝BE+DE．（2）如图2，上述结论②还成立吗？如果不成立，请写出线段AD，BE，DE之间的数量关系．并说明理由．【分析】（1）根据同角的余角相等，全等三角形的判定和性质即可解决问题；（2）结论：DE﹣BE＝AD，只要证明△ACD≌△CBE即可解决问题；【解答】解：（1）∵AD⊥CM，BE⊥CM，∴∠ACB＝∠BEC＝∠ADC＝90°，∴∠ACD+∠BCE＝90°，∠BCE+∠CBE＝90°，∴∠ACD＝∠CBE在△ACD和△CBE中，（∠ADC=∠BEC ∠ACD=∠CBE AC=BC）∴△ACD≌△CBE，（AAS）∴CD＝BE．②结论：AD＝BE+DE．理由：∵△ACD≌△CBE，∴AD＝CE∵CE＝CD+DE＝BE+DE，∴AD＝BE+DE．故答案为：∠CBE，∠ADC=∠BEC∠ACD=∠CBEAC=BC，AAS，AD＝CE．（2）不成立，结论：DE﹣BE＝AD．理由：∵AD⊥CM，BE⊥CM，∴∠ACB＝∠BEC＝∠ADC＝90°，∴∠ACD+∠BCE＝90°，∠BCE+∠CBE＝90°，∴∠ACD＝∠CBE在△ACD和△CBE中，∠ADC=∠BEC∠ACD=∠CBEAC=BC，∴△ACD≌△CBE，（AAS）∴AD＝CE，CD＝BE，∴DE﹣BE＝DE﹣DC＝CE＝AD．【点评】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形的全等条件，灵活运用知识解决问题．9．如图，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E、F分别在BC、CD上，且∠EAF=1 2∠BAD，求证：DF＝EF﹣BE．【分析】由边角边证明△ADF≌△ABH得AF＝AH，∠DAF＝∠BAH，同理可得△HAE≌△FAE，其性质得HE＝EF，最后由线段和差和等式的性质得DF＝EF﹣BE．【解答】证明：在CB的延长线上取BH＝DF，如图所示：∵∠ABE+∠ABH＝180°，∠ABE+∠D＝180°，∴∠ABH＝∠D，在△ADF和△ABH中，AD=AB∠D=∠ABHDF=BH，∴△ADF≌△ABH（SAS），∴AF＝AH，∠DAF＝∠BAH，∴∠BAD＝∠HAF，∵∠EAF=12∠BAD，∴∠EAF＝∠HAE=12∠HAF，在△HAE和△FAE中，AH=AF∠HAE=∠FAEAE=AE，∴△HAE≌△FAE（SAS），∴HE＝EF，又∵HE＝HB+BE，HB＝DF，∴EF＝BE+DF，∴DF＝EF﹣BE．【点评】本题综合考查了全等三角形的判定与性质，角平分线的定义，同角的补角相等，线段的和差和等量代换等知识点，重点掌握全等三角形的判定与性质，难点是构建全等三角形和角平分线．10．在Rt△ABC中，∠ABC＝90°，点D是CB延长线上一点，点E是线段AB上一点，连接DE．AC＝DE，BC＝BE．（1）求证：AB＝BD；（2）BF平分∠ABC交AC于点F，点G是线段FB延长线上一点，连接DG，点H是线段DG上一点，连接AH交BD于点K，连接KG．当KB平分∠AKG时，求证：AK＝DG+KG．【分析】（1）证明Rt△ACB≌Rt△DEB即可解决问题；（2）作BM平分∠ABD交AK于点M，证明△BMK≌△BGK，△ABM≌△DBG，即可解决问题．【解答】证明：（1）在Rt△ACB和Rt△DEB中，AC=DEBC=BE，∴Rt△ACB≌Rt△DEB（HL），∴AB＝BD，（2）如图：作BM平分∠ABD交AK于点M，∵BM平分∠ABD，KB平分∠AKG，∴∠ABM＝∠MBD＝45°，∠AKB＝∠BKG，∵∠ABF＝∠DBG＝45°∴∠MBD＝∠GBD，在△BMK和△BGK中，∠MBD=∠GBDBK=BK，∠AKB=∠BKG∴△BMK≌△BGK（ASA），∴BM＝BG，MK＝KG，在△ABM和△DBG中，AB=BD∠ABM=∠DBG，BM=BG∴△ABM≌△DBG（SAS），∴AM＝DG，∵AK＝AM+MK，∴AK＝DG+KG．【点评】本题考查了全等三角形的判定与性质，解决本题的关键是得到△BMK≌△BGK．11．（2023春•余江区期末）如图，大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处，AC＝BC，DC＝EC，连接AE、BD，点A恰好在线段BD上．（1）找出图中的全等三角形，并说明理由；（2）当AD＝AB＝4cm，则AE的长度为　cm．（3）猜想AE与BD的位置关系，并说明理由．【分析】（1）根据SAS证明△CBD≌△CAE即可；（2）根据全等三角形的性质解答即可；（3）根据全等三角形的性质和垂直的定义解答即可．【解答】解：（1）△CBD≌△CAE，理由如下：∵∠ACB＝∠DCE＝90°，∴∠ACB+∠ACD＝∠DCE+∠ACD，即∠BCD＝∠ACE，在△CBD与△CAE中，BC=AC∠BCD=∠ACE，DC=EC∴△CBD≌△CAE（SAS）；（2）∵△CBD≌△CAE，∴BD＝AE＝AD+AB＝4+4＝8（cm），故答案为：8；（3）AE⊥BD，理由如下：AE与CD相交于点O，在△AOD与△COE中，∵△CBD≌△CAE，∴∠ADO＝∠CEO，∵∠AOD＝∠COE，∴∠OAD＝∠OCE＝90°，∴AE⊥BD．【点评】此题考查全等三角形的判定和性质，关键是根据SAS得出△CBD与△CAE全等解答．12．如图①点A、B、C、D在同一直线上，AB＝CD，作CE⊥AD，BF⊥AD，且AE＝DF．（1）证明：EF平分线段BC；（2）若△BFD沿AD方向平移得到图②时，其他条件不变，（1）中的结论是否仍成立？请说明理由．【分析】（1）由AB＝CD，利用等式的性质得到AC＝BD，再由AE＝DF，利用HL得到直角三角形ACE 与直角三角形DBF全等，利用全等三角形对应边相等得到EC＝BF，再利用AAS得到三角形ECG与三角形FBG全等，利用全等三角形对应边相等得到BG＝CG，即可得证；（2）（1）中的结论成立，理由为：由AC＝DB，利用等式的性质得到AC＝BD，再由AE＝DF，利用HL 得到直角三角形ACE与直角三角形DBF全等，利用全等三角形对应边相等得到EC＝BF，再利用AAS 得到三角形ECG与三角形FBG全等，利用全等三角形对应边相等得到BG＝CG，即可得证．【解答】（1）证明：∵CE⊥AD，BF⊥AD，∴∠ACE＝∠DBF＝90°，∵AB＝CD，∴AB+BC＝BC+CD，即AC＝DB，在Rt△ACE和Rt△DBF中，AE=DFAC=DB，∴Rt△ACE≌Rt△DBF（HL），∴CE＝FB，在△CEG和△BFG中，∠ECG=∠FBG=90°∠EGC=∠BGF，EC=FB∴△CEG≌△BFG（AAS），∴CG＝BG，即EF平分线段BC；（2）（1）中结论成立，理由为：证明：∵CE⊥AD，BF⊥AD，∴∠ACE＝∠DBF＝90°，∵AB＝CD，∴AB﹣BC＝CD﹣BC，即AC＝DB，在Rt△ACE和Rt△DBF中，AE=DFAC=DB，∴Rt△ACE≌Rt△DBF（HL），∴CE＝FB，在△CEG和△BFG中，∠ECG=∠FBG=90°∠EGC=∠BGF，EC=FB∴△CEG≌△BFG（AAS），∴CG＝BG，即EF平分线段BC．【点评】此题考查了全等三角形的判定与性质，以及平移的性质，熟练掌握全等三角形的判定与性质是解本题的关键．13．在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时①请说明△ADC≌△CEB的理由；②请说明DE＝AD+BE的理由；（2）当直线MN绕点C旋转到图2的位置时，DE、AD、BE具有怎样的等量关系？请直接在横线上写出这个等量关系：　．（3）当直线MN绕点C旋转到图3的位置时，DE、AD、BE具有怎样的等量关系？请直接在横线上写出这个等量关系：　．【分析】（1）①由已知推出∠ADC＝∠BEC＝90°，因为∠ACD+∠BCE＝90°，∠DAC+∠ACD＝90°，推出∠DAC＝∠BCE，根据AAS即可得到答案；②由①得到AD＝CE，CD＝BE，即可求出答案；（2）结论：DE＝AD﹣BE．与（1）证法类似可证出∠ACD＝∠EBC，能推出△ADC≌△CEB，得到AD ＝CE，CD＝BE，代入已知即可得到答案．（3）结论：DE＝BE﹣AD．证明方法类似．【解答】解：（1）①证明：如图1中，∵AD⊥DE，BE⊥DE，∴∠ADC＝∠BEC＝90°，∵∠ACB＝90°，∴∠ACD+∠BCE＝90°，∠DAC+∠ACD＝90°，∴∠DAC＝∠BCE，在△ADC和△CEB中，∠CDA=∠BEC∠DAC=∠ECB，AC=BC∴△ADC≌△CEB（AAS）．②证明：由（1）知：△ADC≌△CEB，∴AD＝CE，CD＝BE，∵DC+CE＝DE，∴AD+BE＝DE．（2）结论：DE＝AD﹣BE．理由：如图2中，∵BE⊥EC，AD⊥CE，∴∠ADC＝∠BEC＝90°，∴∠EBC+∠ECB＝90°，∵∠ACB＝90°，∴∠ECB+∠ACE＝90°，∴∠ACD＝∠EBC，在△ADC和△CEB中，∠ACD=∠CBE∠ADC=∠BEC，AC=BC∴△ADC≌△CEB（AAS），∴AD＝CE，CD＝BE，∴DE＝EC﹣CD＝AD﹣BE．（3）结论：DE＝BE﹣AD．理由如下：如图3中，∵∠ACB＝90°，∴∠ACD+∠BCE＝90°∵AD⊥MN，BE⊥MN，∴∠ADC＝∠CED＝90°，∴∠ACD+∠DAC＝90°，∴∠DAC＝∠ECB，在△ACD和△CBE中，∠ADC=∠CEB∠DAC=∠ECB，AC=CB∴△ACD≌△CBE（AAS），∴AD＝CE，CD＝BE，∴DE＝CD﹣CE＝BE﹣AD．故答案为DE＝AD﹣BE，DE＝BE﹣AD．【点评】本题主要考查了邻补角的意义，全等三角形的性质和判定等知识点，能根据已知证出符合全等的条件是解此题的关键，题型较好，综合性比较强．14．已知：在△AOB和△COD中，OA＝OB，OC＝OD．（1）如图①，若∠AOB＝∠COD＝60°．①求证：AC＝BD．②求∠APB的度数．（2）如图②，若∠AOB＝∠COD＝α，∠APD的大小为（直接写出结果，不证明）．【分析】（1）①根据已知先证明∠AOC＝∠BOD，再由SAS证明△AOC≌△BOD，所以AC＝BD．②由△AOC≌△BOD，可得∠OAC＝∠OBD，再结合图形，利用角的和差，可得∠APB＝60°．（2）由（1）小题的证明可知，∠APB＝α，则可得出答案．【解答】（1）①证明：∵∠AOB＝∠COD＝60°，∴∠AOB+∠BOC＝∠COD+∠BOC，∴∠AOC＝∠BOD，在△AOC和△BOD中，AO=BO∠AOC=∠BOD，OC=OD∴△AOC≌△BOD（SAS），∴AC＝BD；②解：∵△AOC≌△BOD，∴∠OAC＝∠OBD，∴∠OAC+∠AOB＝∠OBD+∠APB，∴∠OAC+60°＝∠OBD+∠APB，∴∠APB＝60°；（2）解：由（1）可知：△AOC≌△BOD（SAS），∴∠OAC＝∠OBD，∴∠OAC+∠AOB＝∠OBD+∠APB，∴∠OAC+α＝∠OBD+∠APB，∴∠APB＝α，∴∠APD＝180°﹣α．故答案为：180°﹣α．【点评】本题主要考查了全等三角形的判定和性质，正确运用全等三角形的性质是解题的关键．15．（1）已知，如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE＝BD+CE．（2）如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意钝角，请问结论DE＝BD+CE是否成立？若成立，请你给出证明；若不成立，请说明理由．【分析】（1）根据BD⊥直线m，CE⊥直线m得∠BDA＝∠CEA＝90°，而∠BAC＝90°，根据等角的余角相等得∠CAE＝∠ABD，然后根据“AAS”可判断△ADB≌△CEA，则AE＝BD，AD＝CE，于是DE＝AE+AD＝BD+CE；（2）利用∠BDA＝∠BAC＝α，则∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，得出∠CAE＝∠ABD，进而得出△ADB≌△CEA即可得出答案．【解答】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中∠ABD=∠CAE∠BDA=∠CEA，AB=AC∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）结论DE＝BD+CE仍然成立，理由是：∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中∠ABD=∠CAE∠BDA=∠CEAAB=AC，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．【点评】本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；得出∠CAE＝∠ABD是解题关键．16．已知：如图AC∥BD，AE和BE分别平分∠CAB和∠DBA，CD过点E．求证：（1）AE⊥BE；（2）AB＝AC+BD．【分析】（1）首先证明∠CAB+∠DBA＝180°，再利用角平分线的性质证明∠EAB=12∠CAB，∠EBA=12∠DBA，可得到∠EAB+∠EBA＝90°，进而可证出AE⊥BE；（2）首先在AB上截取AF＝AC，连接EF，证明△CAE≌△FAE，可证出∠CEA＝∠FEA，可得到∠FEB ＝∠DEB，再证明△DEB≌△FEB，可得到BD＝BF，即可证出AB＝AC+BD．【解答】证明：（1）∵AC∥BD，∴∠CAB+∠DBA＝180°又∵AE和BE分别平分∠CAB和∠DBA，∴∠EAB=12∠CAB，∠EBA=12∠DBA，∴∠EAB+∠EBA=12(∠CAB+∠DBA)=90°，∴AE⊥BE（2）在AB上截取AF＝AC，连接EF，在△CAE和△FAE中AC=AF∠CAE=∠FAE AE=AE，∴△CAE≌△FAE，则∠CEA＝∠FEA，又∠CEA+∠BED＝∠FEA+∠FEB＝90°，∴∠FEB＝∠DEB，∵BE平分∠DBA，∴∠DBE＝∠FBE，在△DEB和△FEB中∠DEB=∠FEB EB=EB∠DBE=∠FBE，∴△DEB≌△FEB（ASA），∴BD＝BF，又∵AF＝AC，∴AB＝AF+FB＝AC+BD．【点评】此题主要考查了垂直，角平分线，以及三角形全等的判定和性质，证明三角形全等是证明线段和角相等的重要手段．17．问题情境：如图①，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D．可知：∠BAD＝∠C（不需要证明）；（1）特例探究：如图②，∠MAN＝90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN 上，且AB＝AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；（2）归纳证明：如图③，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB＝AC，∠1＝∠2＝∠BAC．求证：△ABE≌△CAF；（3）拓展应用：如图④，在△ABC中，AB＝AC，AB＞BC．点D在边BC上，CD＝2BD，点E、F在线段AD上，∠1＝∠2＝∠BAC．若△ABC的面积为24，则△ACF与△BDE的面积之和为．（直接写出结果）【分析】（1）证明∠ABD＝∠CAF，利用AAS定理证明；（2）根据三角形的外角的性质证明∠ABE＝∠CAF，∠BAE＝∠FCA，利用ASA定理证明；（3）根据CD＝2BD，求出△ABD的面积，根据全等三角形的性质计算即可．【解答】（1）证明：如图②，∵CF⊥AE，BD⊥AE，∠MAN＝90°，∴∠BDA＝∠AFC＝90°，∴∠ABD+∠BAD＝90°，∠ABD+∠CAF＝90°，∴∠ABD＝∠CAF，在△ABD和△CAF中，∠ADB=∠CFA∠ABD=∠CAF，AB=AC∴△ABD≌△CAF（AAS）；（2）证明：如图③，∵∠1＝∠2＝∠BAC，∠1＝∠BAE+∠ABE，∠BAC＝∠BAE+∠CAF，∠2＝∠FCA+∠CAF，∴∠ABE＝∠CAF，∠BAE＝∠FCA，在△ABE和△CAF中，∠ABE =∠CAF AB =AC ∠BAE =∠ACF，∴△ABE ≌△CAF （ASA ）；（3）解：如图④，∵△ABC 的面积为24，CD ＝2BD ，∴△ABD 的面积是：13×24＝8，由（2）可知，△ABE ≌△CAF ，∴△ACF 与△BDE 的面积之和等于△ABE 与△BDE 的面积之和，即等于△ABD 的面积是8，故答案为：8．【点评】本题考查的是三角形的知识的综合应用，掌握全等三角形的判定定理和性质定理、三角形的面积公式是解题的关键．18．在△ABC 中，AB ＝AC ，D 是直线BC 上一点，以AD 为一条边在AD 的右侧作△ADE ，使AE ＝AD ，∠DAE ＝∠BAC ，连接DE ，CE ．（1）如图，当点D 在BC 延长线上移动时，求证：BD ＝CE ．（2）设∠BAC ＝α，∠DCE ＝β．①当点D 在线段BC 的延长线上移动时，α与β之间有什么数量关系？请说明理由．②当点D 分别在线段BC 上、线段BC 的反向延长线上移动时，α与β之间有什么数量关系？请说明理由.【分析】（1）根据SAS 证△BAD ≌△CAE ，可得结论；（2）①由△BAD ≌△CAE ，推出∠B ＝∠ACE ，根据三角形外角性质求出即可；②α+β＝180°或α＝β，根据三角形外角性质求出即可．【解答】（1）证明：∵∠DAE ＝∠BAC ，∴∠DAE +∠CAD ＝∠BAC +∠CAD ，∴∠BAD＝∠CAE，在△BAD和△CAE中，AB=AC∠BAD=∠CAE，AD=AE∴△BAD≌△CAE（SAS），（2）解：①当点D在线段BC的延长线上移动时，α与β之间的数量关系是α＝β，理由是：由（1）知△BAD≌△CAE，∴∠B＝∠ACE，∵∠ACD＝∠B+∠BAC＝∠ACE+∠DCE，∴∠BAC＝∠DCE，∵∠BAC＝α，∠DCE＝β，∴α＝β；②分三种情况：i）当D在线段BC上时，如图2，α+β＝180°，理由是：同理可证明：△ABD≌△ACE（SAS），∴∠ADB＝∠AEC，∠ABC＝∠ACE，∵∠ADC+∠ADB＝180°，∴∠ADC+∠AEC＝180°，∴∠DAE+∠DCE＝180°，∵∠BAC＝∠DAE＝α，∠DCE＝β，∴α+β＝180°，ii）当点D在线段BC反向延长线上时，如图3，α＝β．如图3，同理可证明：△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵∠ACE＝∠ACD+∠DCE，∠ABD＝∠ACD+∠BAC，∴∠ACD+∠DCE＝∠ACD+∠BAC，∴∠BAC＝∠DCE，∵∠BAC＝α，∠DCE＝β，∴α＝β；ii）当点D在线段BC的延长线上时，如图1，α＝β．综上，当点D在BC上移动时，α＝β或α+β＝180°．【点评】本题是三角形的综合题，考查了全等三角形的性质和判定，三角形的外角性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．19．（2023春•新市区期末）在△ABC中，∠ACB＝90°，AC＝BC，D是直线AB上一点（点D不与点A、B重合），连接DC并延长到E，使得CE＝CD，过点E作EF⊥直线BC，交直线BC于点F．（1）如图1，当点D为线段AB上的任意一点时，用等式表示线段EF、CF、AC的数量关系，并证明；（2）如图2，当点D为线段BA的延长线上一点时，依题意补全图2，猜想线段EF、CF、AC的数量关系是否发生改变，并证明；（3）如图3，当点D在线段AB的延长线上时，直接写出线段EF、CF、AC之间的数量关系．【分析】（1）过D作DH⊥CB于H，由“AAS”可证△FEC≌△HDC，可得CH＝FC，DH＝EF，可得结论；（2）过D作DH⊥CB于H，由“AAS”可证△FEC≌△HDC，可得CH＝FC，DH＝EF，可得结论．（3）过D作DH⊥CB交CB的延长线于H，由“AAS”可证△FEC≌△HDC，可得CH＝FC，DH＝EF，可得结论．【解答】解：（1）结论：AC＝EF+FC．理由如下：过D作DH⊥CB于H，∴∠DHC＝∠DHB＝90°，∵EF⊥CF，∴∠EFC＝∠DHC＝90°，在△FEC和△HDC中，∠EFC=∠DHC=90°∠FCE=∠DCH，EC=DC∴△FEC≌△HDC（AAS），∴CH＝FC，DH＝EF，∵∠ACB＝90°，AC＝BC，∴∠B＝45°，∵∠DHB＝90°，∴∠B＝∠HDB＝45°，∴DH＝HB＝EF，∵BC＝CB+HB，∴AC＝FC+EF；（2）依题意补全图形，结论：AC＝EF﹣CF，理由如下：过D作DH⊥CB交BC的延长线于H，∵EF⊥CF，∴∠EFC＝∠DHC＝90°，在△FEC和△HDC中，∠FCE=∠DCH∠EFC=∠DHC=90°，EC=DC∴△FEC≌△HDC（AAS），∴CH＝FC，DH＝EF，∵∠DHB＝90°，∴∠B＝∠HDB＝45°，∴DH＝HB＝EF，∵BC＝HB﹣CH，∴AC＝EF﹣CF；（3）AC＝CF﹣EF．如图3，过D作DH⊥CB交CB的延长线于H，同理可证△FEC≌△HDC（AAS），∴CH＝FC，DH＝EF，∵∠DHB＝90°，∴∠B＝∠HDB＝45°，∴DH＝HB＝EF，∵BC＝CH﹣BH，∴AC＝CF﹣EF．【点评】本题是三角形综合题，考查了全等三角形的判定和性质，添加恰当辅助线构造全等三角形是本题的关键．20．如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（1）如果AB＝AC，∠BAC＝90°，①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为，线段CF、BD的数量关系为　；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F 不重合），并说明理由．【分析】（1）当点D在BC的延长线上时①的结论仍成立．由正方形ADEF的性质可推出△DAB≌△FAC，所以CF＝BD，∠ACF＝∠ABD．结合∠BAC＝90°，AB＝AC，得到∠BCF＝∠ACB+∠ACF＝90°．即CF⊥BD．（2）当∠ACB＝45°时，过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，可推出∠ACB＝∠AGC，所以AC＝AG，由（1）①可知CF⊥BD．【解答】证明：（1）①正方形ADEF中，AD＝AF，∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，又∵AB＝AC，∴△DAB≌△FAC，∴CF＝BD，∠B＝∠ACF，∴∠ACB+∠ACF＝90°，即CF⊥BD．②当点D在BC的延长线上时①的结论仍成立．由正方形ADEF得AD＝AF，∠DAF＝90度．∵∠BAC＝90°，∴∠DAF＝∠BAC，∴∠DAB＝∠FAC，又∵AB＝AC，∴△DAB≌△FAC，∴CF＝BD，∠ACF＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACF＝45°，∴∠BCF＝∠ACB+∠ACF＝90度．即CF⊥BD．（2）当∠ACB＝45°时，CF⊥BD（如图）．理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC ＝90°﹣45°＝45°，∴∠ACB ＝∠AGC ＝45°，∴AC ＝AG ，∵∠DAG ＝∠FAC （同角的余角相等），AD ＝AF ，∴△GAD ≌△CAF ，∴∠ACF ＝∠AGC ＝45°，∠BCF ＝∠ACB +∠ACF ＝45°+45°＝90°，即CF ⊥BC ．【点评】本题考查三角形全等的判定和直角三角形的判定，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．21．（2022春•沙坪坝区校级期中）如图，在△ABC 中，∠ABC 、∠ACB 的平分线交于点D ，延长BD 交AC 于E ，G 、F 分别在BD 、BC 上，连接DF 、GF ，其中∠A ＝2∠BDF ，GD ＝DE ．（1）当∠A ＝80°时，求∠EDC 的度数；（2）求证：CF ＝FG +CE ．【分析】（1）方法一：先求∠ABC 和∠ACB 的和为100°，再根据角平分线求∠DBC +∠DCB ＝50°，再根据外角即可解决问题；方法二：在BC 上取点M ，使CM ＝CE ，证明△CDE ≌△CDM （SAS ），可得DE ＝DM ，∠DEC ＝∠DMC ，∠EDC ＝∠MDC ，证明∠BDM ＝180°―12∠ABC ﹣∠DMB ＝180°―12∠ABC ﹣∠AEB ＝∠A ＝80°，进而可以解决问题．（2）结合（1）然后证明△DGF≌△DMF（SAS），可得GF＝MF，进而可以解决问题．【解答】（1）解：方法一：∵∠A＝80°，∴∠ABC+∠ACB＝100°，∵BE平分∠ABC、CD平分∠ACB，∴∠DBC+∠DCB＝50°，∴∠EDC＝∠DBC+∠DCB＝50°；方法二：如图，在BC上取点M，使CM＝CE，∵CD平分∠ACB，∴∠ACD＝∠BCD，在△CDE和△CDM中，CE=CM∠ECD=∠MCDCD=CD，∴△CDE≌△CDM（SAS），∴DE＝DM，∠DEC＝∠DMC，∠EDC＝∠MDC，∵GD＝DE，∴GD＝MD，∵∠DEC+∠AEB＝180°，∠DMC+∠DMF＝180°，∴∠AEB＝∠DMF，∵BE平分∠ABC，∴∠ABE＝∠CBE=12∠ABC，∴∠BDM＝180°―12∠ABC﹣∠DMB＝180°―12∠ABC﹣∠AEB＝∠A＝80°，∴∠EDM＝100°，∴∠EDC＝50°；（2）证明：∵∠A＝2∠BDF，∴∠BDM＝2∠BDF，∴∠FDM＝∠BDF，在△DGF和△DMF中，DG=DM∠GDF=∠MDF，DF=DF∴△DGF≌△DMF（SAS），∴GF＝MF，∴CF＝CM+FM＝CE+GF．∴CF＝FG+CE．【点评】本题考查了全等三角形的判定与性质，角平分线的定义，解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF．22．（2022秋•大同月考）已知△ABC和△CDE中，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，AE与BD交于点F．（1）如图1．当α＝90°时．求证：①△ACE≌△BCD；②AE⊥BD；（2）如图2．当α＝60°时，直接写出∠AFB的度数为；（3）如图3，直接写出∠AFD的度数为（用含α的式子表示）．【分析】（1）先根据等角的余角相等得到∠ACE＝∠BCD，再根据等腰直角三角形的性质得AC＝BC，EC＝DC，于是可根据“SAS”判断△ACE≌△BCD，然后根据相似三角形的性质得到∠CAE＝∠CBD，根据三角形的内角和即可得到结论；（2）由已知条件得到∠ACE＝∠BCD，推出△ACE≌△BCD（SAS），根据全等三角形的性质得到∠CAE ＝∠CBD，推出A，B，F，C四点共圆，根据圆周角定理即可得到结论．（3）由已知条件得到∠ACE＝∠BCD，推出△ACE≌△BCD（SAS），根据全等三角形的性质得到∠CAE ＝∠CBD即可得到结论．【解答】证明：（1）∵∠ACB＝∠DCE＝90°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，又∵△ABC和△ECD都是等腰直角三角形∴AC＝BC，EC＝DC，在△ACE和△BCD中，AC=BC∠ACE=∠BCD，CE=CD∴△ACE≌△BCD（SAS），∴∠CAE＝∠CBD，∵∠CAE+∠EAB+∠ABC＝90°，∴∠CBD+∠EAB+∠ABC＝90°，∴∠AFB＝90°，∴AE⊥BD；（2）∵∠ACB＝∠DCE＝60°，∴∠ACB﹣∠ACD＝∠DCE﹣∠ACD，即∠ACE＝∠BCD，在△ACE和△BCD中，AC=BC∠ACE=∠BCD，CE=CD∴△ACE≌△BCD（SAS），∴∠CAE＝∠CBD，∵∠CAE+∠EAB+∠ABC＝120°，∴∠CBD+∠EAB+∠ABC＝120°，∴∠AFB＝∠ACB＝60°；故答案为：60°；（3））∵∠ACB＝∠DCE＝α，∴∠ACB+∠BCE＝∠DCE+∠BCE即∠ACE＝∠BCD，在△ACE和△BCD中，AC=BC∠ACE=∠BCD，CE=CD∴△ACE≌△BCD（SAS），∴∠CAE＝∠CBD，∵∠CAE+∠EAB+∠ABC＝180°﹣α，∴∠CBD+∠EAB+∠ABC＝180°﹣α∴∠AFB＝∠ACB＝α，∴∠AFD＝180°﹣α．故答案为：180°﹣α．【点评】本题考查了全等三角形的判定与性质：判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应角相等，对应边相等．23．将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．（1）求证：AF+EF＝DE；（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．【分析】（1）我们已知了三角形BED和CAB全等，那么DE＝AF+CF，因此只要求出EF＝CF就能得出本题所求的结论，可通过全等三角形来实现，连接BF，那么证明三角形BEF和BCF全等就是解题的关键，这两三角形中已知的条件有BE＝BC，一条公共边，根据斜边直角边定理，这两个直角三角形就全等了，也就得出EF＝CF，也就能证得本题的结论了；（2）解题思路和辅助线的作法与（1）完全一样；（3）结论不成立．结论：AF＝DE+EF．同（1）得CF＝EF，由△ABC≌△DBE，可得AC＝DE，AF＝AC+FC＝DE+EF．【解答】（1）证明：连接BF（如图①），∵△ABC≌△DBE（已知），∴BC＝BE，AC＝DE．∵∠ACB＝∠DEB＝90°，∴∠BCF＝∠BEF＝90°．在Rt△BFC和Rt△BFE中，BF=BFBC=BE∴Rt△BFC≌Rt△BFE（HL）．∴CF＝EF．又∵AF+CF＝AC，∴AF+EF＝DE．（2）解：画出正确图形如图②∴（1）中的结论AF+EF＝DE仍然成立；（3）不成立．结论：AF＝DE+EF．证明：连接BF，∵△ABC≌△DBE，∴BC＝BE，∵∠ACB＝∠DEB＝90°，∴△BCF和△BEF是直角三角形，在Rt△BCF和Rt△BEF中，BC=BEBF=BF，∴△BCF≌△BEF（HL），∴CF＝EF；∵△ABC≌△DBE，∴AC＝DE，∴AF＝AC+FC＝DE+EF．【点评】本题考查了全等三角形的判定和性质，通过构建全等三角形来得出简单的线段相等是解题的关键．24．（2023春•沙坪坝区校级期中）如图，在△ABC和△DCE中，∠ACB＝90°，CA＝CB，∠DCE＝90°，CD＝CE．（1）如图1，当点D在BC上时，CB＝10，AE＝4，则S四边形ABDE＝；（2）如图2，当B、C、E三点共线时，D在AC上，连接BD、AE，F是AD的中点，过点A作AG∥BD，交BF的延长线于点G，求证：AG＝AE且AG⊥AE；（3）如图3，B、C、E三点共线，且∠DBE＝15°，将线段AE绕点A以每秒10°的速度逆时针旋转，同时线段BE绕点E以每秒20°的速度顺时针旋转180°后立即以相同速度回转，设转动时间为t秒，当BE回到出发时的位置时同时停止旋转，则在转动过程中．当BE和AE互相平行或者垂直时，请直接写出此时t的值．【分析】（1）根据S四边形ABDE ＝S△ABC﹣S△DCE，求解即可．（2）如图2中，延长BD交AE于T．证明△BCD≌△ACE（SAS），推出BD＝AE，∠CBD＝∠CAE，推出BD⊥AE，证明△AFG≌△DFB（AAS），推出AG＝BD，可得结论．（3）从开始到结束出现平行，垂直，平行，平行四种情形，分别构建方程求解即可．【解答】（1）解：如图1中，∵CA＝CB＝10，AE＝4，∴CE＝CD＝AC﹣AE＝10﹣4＝6，∴S四边形ABDE ＝S△ABC﹣S△DCE=12×10×10―12×6×6＝32，故答案为：32．（2）证明：如图2中，延长BD 交AE 于T ．∵∠BCD ＝∠ACE ＝90°，BC ＝AC ，DC ＝EC ，∴△BCD ≌△ACE （SAS ），∴BD ＝AE ，∠CBD ＝∠CAE ，∵∠BDC ＝∠ADT ，∴∠BCD ＝∠ATD ＝90°，∴BD ⊥AE ，∵AG ∥BD ，∴∠G ＝∠FBD ，∵AF ＝FD ，∠AFG ＝∠DFB ，∴△AFG ≌△DFB （AAS ），∴AG ＝BD ，∴AG ＝AE ，∵AG ∥BD ，BD ⊥AE ，∴AG ⊥AE ．（3）由题意，第一次平行时，10t ＝75°﹣20t ，解得t =52，第一次垂直时，10t +20t ﹣75°＝90°，解得t =112，第二次平行时，20t ﹣75°+10t ＝180°．解得y =516，第三次平行时，105°﹣（20t ﹣180°）+10t ＝180°，解得t =212，综上所述，满足条件的t 的值为52或112或516或212．【点评】本题属于四边形综合题，考查了全等三角形的判定和性质，平行线的判定和性质，三角形的面。

八年级数学三角形全等(动点问题)(人教版)(专题)(含答案)

（1）线段PC的长可用含t的式子表示为( )
A.6-t B.4-t
C.2t D.t
答案：A
解题思路：
点P速度已知，可判断此题为动点问题，按照动点问题的解决方法解决：
①研究基本图形，标注：
②研究动点运动状态，包括起点，终点，状态转折点，速度，时间范围，
如图：
③表达线段长，建等式．
线段BP为已走路程，故BP=t，PC为未走路程，故PC=6-t．
由题意，点P在运动过程中有2个状态转折点，需分成3种情况：
①点P在BC上，对应的时间范围：0≤t≤4；
②点P在CD上，对应的时间范围：4<t≤7；
③点P在DA上，对应的时间范围：7<t≤11．
可知，当点P在CD上运动时，对应的t的取值范围是4≤t≤7．
故选C．
试题难度：三颗星知识点：略
7.（上接第6题）（2）当点P在DA上运动时，线段DP的长可用含t的式子表示为( )cm．
A.1 B.2
C.4 D.5
答案：C
解题思路：
由题意，△DCP≌△DCE，对应关系明确，
要使△DCP≌△DCE，
则需CP=CE，
即，
解得（符合题意）
故选C．
试题难度：三颗星知识点：略
6.已知：如图，在长方形ABCD中，AB=6cm，AD=8cm，点E为BC上一点，且CE=2cm．动点P从点B出发，以每秒2cm的速度沿BC-CD-DA向终点A运动，连接AP，BP，DE．设点P运动时间为t秒．请回答下列问题：
故选A．
试题难度：三颗星知识点：略
4.（上接第3题）（2）若某一时刻，△DCP的面积为10，则此时t的值为( )
A.5 B.
C. D.1
答案：D

八年级数学全等三角形专项练习题(含答案)

八年级数学全等三角形专项练习题一、单选题1．如图，△ABC ≌△DEF ，点A 与D ，B 与E 分别是对应顶点，且测得BC=5cm ，BF=7cm ，则EC 长为（）A ．1cmB ．2cmC ．3cmD ．4cm 2．已知图中的两个三角形全等，则α∠的度数是（）A ．72°B ．60°C ．58°D ．50° 3．在下列各组条件中，不能说明ABC DEF ∆∆≌的是（）A ．AB=DE ，∠B=∠E ，∠C=∠FB ．AB=DE ，∠A=∠D ，∠B=∠EC ．AC=DF ，BC=EF ，∠A=∠D D ．AB=DE ，BC=EF ，AC=ED 4．如图，在四边形ABCD 中，AB=AD ，CB=CD ，若连接AC 、BD 相交于点O ，则图中全等三角形共有（）A ．1对B ．2对C ．3对D ．4对5．如图，已知12,AC AD ∠=∠=，增加下列条件，不能肯定ABC AED ≌的是（）A ．C D ∠=∠B ．B E ∠=∠C ． AB AE =D ．BC ED = 6．“经过已知角一边上的一点，作一个角等于已知角”的尺规作图过程如下：已知：如图，AOB ∠和OA 上一点C ．求作：一个角等于AOB ∠，使它的顶点为C ，一边为CA ．作法：如图．（1）在OA 上取一点()D OD OC <，以点O 为圆心，OD 长为半径画弧，交OB 于点E ；（2）以点C 为圆心，OD 长为半径画弧，交CA 于点F ，以点F 为圆心，DE 长为半径画弧，两弧交于点G ；（3）作射线CG ．则GCA ∠就是所求作的角．此作图的依据中不含有（）A ．三边分别相等的两个三角形全等B ．全等三角形的对应角相等C ．两直线平行同位角相等D ．两点确定一条直线7．如图，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（）A ．线段CD 的中点B ．OA 与OB 的中垂线的交点C ．OA 与CD 的中垂线的交点 D ．CD 与∠AOB 的平分线的交点 8．如图所示，在ABC ∆中，AD 平分BAC ∠，DE AB ⊥于E ，15ABC S ∆=，3DE =，6AB =，则AC 长是（）A ．4B ．5C ．6D ．79．如图,在Rt △ABC 中,∠C=90°,∠A=30°,BD 是∠ABC 的平分线,AD=20,则BC 的长是( )A ．20B ．C ．30D ．10 10．如图，在△ABC 中，AB=AC ，∠BAC=90°，直角∠EPF 的顶点P 是BC 中点，PE ，PF 分别交AB ，AC 于点E ，F ，给出下列四个结论：①△APE ≌△CPF ；②AE=CF ；③△EAF 是等腰直角三角形；④S △ABC =2S 四边形AEPF ，上述结论正确的有（）A ．1个B ．2个C ．3个D ．4个二、填空题 11．已知△ABC ≌△DEF ，△ABC 的周长为100cm ，DE ＝30cm ，DF ＝25cm ，那么BC ＝_______． 12．如图，要测量河两岸相对两点A 、B 间的距离，先在过点B 的AB 的垂线上取两点C 、D ，使CD=BC ，再在过点D 的垂线上取点E ，使A 、C 、E 三点在一条直线上，可证明△EDC ≌△ABC ，所以测得ED 的长就是A 、B 两点间的距离，这里判定△EDC ≌△ABC 的理由是__．13．如图，△ABC 的三边AB 、BC 、CA 的长分别为30、40、15，点P 是三条角平分线的交点，将△ABC 分成三个三角形，则APB S ∆︰BPC S ∆︰CPA S ∆等于____．14．如图，的正方形ABCD绕点A逆时针方向旋转30°后得到正方形A′B′C′D′，则图中阴影部分面积为_______平方单位．15．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=_________三、解答题16．如图，点E、F在AC上，DF＝BE，AE＝CF，∠AFD＝∠CEB．求证：AD∥CB．17．已知：如图，∠ACB ＝90°，AC ＝BC ，AD ⊥CE ，BE ⊥CE ，垂足分别是点D ，E ．（1）求证：△BEC ≌△CDA ；（2）当AD ＝3，BE ＝1时，求DE 的长．18．嘉淇同学要证AE BF =，她先用下列尺规作图步骤作图：①//,90AD BC BAD ∠=；②以点B 为圆心，BC 长为半径画弧，与射线AD 相交于点E ，连接BE ；③过点C 作CF BE ⊥，垂足为点F ．并写出了如下不完整的已知和求证．（1）在方框中填空，以补全已知和求证；（2）按嘉淇的想法写出证明过程．19．如图，点C为线段AB上一点，△ACM与△CBN都是等边三角形，AN与MB交于P．（1）求证：AN＝BM；（2）连接CP，求证：CP平分∠APB．20．如图，在△ABC中，∠BAC=90°，AB=AC，点D是BC上一动点，连接AD，过点A 作AE⊥AD，并且始终保持AE=AD，连接CE．（1）求证：△ABD≌△ACE；（2）若AF平分∠DAE交BC于F，探究线段BD，DF，FC之间的数量关系，并证明；（3）在（2）的条件下，若BD=3，CF=4，求AD的长．答案1．C2．D3．C4．C5．D6．C7．D8．A9．D10．C11．45cm12．ASA13．6：8：314．6﹣15．135°16.∵A E＝CF∴AE﹣EF＝CF﹣EF，即AF＝CE，又∵∠AFD＝∠CEB，DF＝BE，△ADF≌△CBE（SAS），∴∠A＝∠C∴AD∥CB．17.（1）证明：∵AD⊥CE，BE⊥CE，∴∠ADC＝∠E＝90°，∵∠ACB＝90°，∴∠ACD+∠BCE＝90°，∠∠CBE＝90°，∴∠ACD＝∠CBE，在△ADC和△CEB中，ADC E90 ACD CBE AC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩，∴△ADC≌△CEB（AAS），（2）解：∵△ADC≌△CEB，∴BE＝CD＝1，AD＝EC＝3，∴DE＝CE﹣CD＝3﹣1＝2．18.（1）∵以点B为圆心，BC长为半径画弧∴BC=BE根据已知条件第一句话，得到AE=BF故答案为：BE；BF；（2）证明：∵CF⊥BE，∴∠BFC=90°，又∵AD∥BC，∴∠AEB=∠FBC．∵以点B为圆心，BC长为半径画弧，∴BE=BC，在△ABE与△FCB中，BAE CFB AEB FBC BE CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△FCB ，∴AE=BF19.（1）∵△ACM 与△CBN 都是等边三角形， ∴AC ＝CM ，CN ＝CB ，∠ACM ＝∠BCN ＝60°， ∴∠ACN ＝∠BCM ＝120°，且AC ＝CM ，CN ＝CB ，∴△ACN ≌△MCB （SAS ）， ∴AN ＝BM ；（2）过点C 作CE ⊥AN 于点E ，作CF ⊥BM 于点F ， ∵△ACN ≌△MCB ，∴S △ACN ＝S △MCB ， ∴12×AN ×CE ＝12×BM ×CF ，且AN ＝BM ， ∴CE ＝CF ，且CE ⊥AN ，CF ⊥BM ， ∴CP 平分∠APB ．20.（1）证明：如图，∵AE ⊥AD ，∴∠DAE=∠DAC+∠2=90°，又∵∠BAC=∠DAC+∠1=90°， ∴∠1=∠2，在△ABD 和△ACE 中 12AB AC AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△ACE ．（2）结论：BD 2+FC 2=DF 2．理由如下：连接FE ，∵∠BAC=90°，AB=AC ， ∴∠B=∠3=45°由（1）知△ABD ≌△ACE ∴∠4=∠B=45°，BD=CE ∴∠ECF=∠3+∠4=90°， ∴CE 2+CF 2=EF 2， ∴BD 2+FC 2=EF 2， ∵AF 平分∠DAE ， ∴∠DAF=∠EAF ，在△DAF 和△EAF 中 AF AF DAF EAF AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△DAF ≌△EAF ∴DF=EF∴BD 2+FC 2=DF 2．（3）过点A 作AG ⊥BC 于G ，由（2）知DF 2=BD 2+FC 2=32+42=25 ∴DF=5，∴BC=BD+DF+FC=3+5+4=12， ∵AB=AC ，AG ⊥BC ， ∴BG=AG=12BC=6， ∴DG=BG -BD=6-3=3，∴在Rt △ADG 中，。

八年级全等三角形专题练习(解析版)

八年级全等三角形专题练习（解析版）一、八年级数学轴对称三角形填空题（难）1．如图，在锐角△ABC中，AB=5，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是______．【答案】5【解析】【分析】作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN为所求的最小值，再根据AD是∠BAC的平分线可知MH=MN，再由等腰直角三角形的性质即可得出结论．【详解】如图，作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN 为所求的最小值．∵AD是∠BAC的平分线，∴MH=MN，∴BH是点B到直线AC的最短距离（垂线段最短）．∵AB=5，∠BAC=45°，∴BH==5．∵BM+MN的最小值是BM+MN=BM+MH=BH=5．故答案为5．【点睛】本题考查了轴对称﹣最短路线问题，解答此类问题时要从已知条件结合图形认真思考，通过角平分线性质，垂线段最短，确定线段和的最小值．的边长为8，E是中线AD上一点，以CE为一边在CE下方作2．如图，已知等边ABC等边CEF ∆，连接BF 并延长至点,N M 为BN 上一点，且5CM CN ==，则MN 的长为_________．【答案】6【解析】【分析】作CG ⊥MN 于G ，证△ACE ≌△BCF ，求出∠CBF=∠CAE=30°，则可以得出124CG BC ==，在Rt △CMG 中，由勾股定理求出MG ，即可得到MN 的长．【详解】解：如图示：作CG ⊥MN 于G ，∵△ABC 和△CEF 是等边三角形，∴AC=BC ，CE=CF ，∠ACB=∠ECF=60°，∴∠ACB-∠BCE=∠ECF-∠BCE ，即∠ACE=∠BCF ，在△ACE 与△BCF 中AC BC ACE BCFCE CF =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△BCF （SAS ），又∵AD 是三角形△ABC 的中线∴∠CBF=∠CAE=30°，∴124CG BC ==，在Rt △CMG 中，2222543MG CM CG =-=-，∴MN=2MG=6，故答案为：6．【点睛】本题考查了勾股定理，等边三角形的性质，全等三角形的性质和判定的应用，解此题的关键是推出△ACF ≌△BCF ．3．如图，点P 是AOB 内任意一点，5OP cm =，点P 与点C 关于射线OA 对称，点P 与点D 关于射线OB 对称，连接CD 交OA 于点E ，交OB 于点F ，当PEF 的周长是5cm 时，AOB ∠的度数是______度．【答案】30【解析】【分析】根据轴对称得出OA 为PC 的垂直平分线，OB 是PD 的垂直平分线，根据线段垂直平分线性质得出12COA AOP COP ，12POB DOB POD ，PE=CE ，OP=OC=5cm ，PF=FD ，OP=OD=5cm ，求出△COD 是等边三角形，即可得出答案．【详解】解：如图示：连接OC ，OD ，∵点P 与点C 关于射线OA 对称，点P 与点D 关于射线OB 对称，∴OA 为PC 的垂直平分线，OB 是PD 的垂直平分线， ∵OP=5cm ，∴12COA AOP COP ，12POB DOB POD ，PE=CE ，OP=OC=5cm ，PF=FD ，OP=OD=5cm ，∵△PEF 的周长是5cm ，∴PE+EF+PF=CE+EF+FD=CD=5cm ，∴CD=OD=OD=5cm ，∴△OCD 是等边三角形，∴∠COD=60°， ∴11122230AOB AOP BOP COP DOP COD ，故答案为：30．【点睛】本题考查了线段垂直平分线性质，轴对称性质和等边三角形的性质和判定，能求出△COD 是等边三角形是解此题的关键．4．如图，在△ABC 中，P ，Q 分别是BC ，AC 上的点，PR ⊥AB ，PS ⊥AC ，垂足分别是R ，S ，若AQ PQ =，PR PS =，那么下面四个结论：①AS AR =；②QP //AR ；③△BRP ≌△QSP ；④BRQS ，其中一定正确的是（填写编号）_____________.【答案】①，②【解析】【分析】连接AP ，根据角平分线性质即可推出①，根据勾股定理即可推出AR=AS ，根据等腰三角形性质推出∠QAP=∠QPA ，推出∠QPA=∠BAP ，根据平行线判定推出QP ∥AB 即可；在Rt △BRP 和Rt △QSP 中，只有PR=PS ．无法判断△BRP ≌△QSP 也无法证明BRQS ．【详解】解：连接AP①∵PR ⊥AB ，PS ⊥AC ，PR=PS ，∴点P 在∠BAC 的平分线上，∠ARP=∠ASP=90°，∴∠SAP=∠RAP ，在Rt △ARP 和Rt △ASP 中，由勾股定理得：AR 2=AP 2-PR 2，AS 2=AP 2-PS 2，∵AP=AP ，PR=PS ，∴AR=AS ，∴①正确；②∵AQ=QP ，∴∠QAP=∠QPA ，∵∠QAP=∠BAP ，∴∠QPA=∠BAP ，∴QP ∥AR ，∴②正确；③在Rt △BRP 和Rt △QSP 中，只有PR=PS ，不满足三角形全等的条件，故③④错误；故答案为：①②.【点睛】本题主要考查了角平分线的性质与勾股定理的应用，熟练掌握根据垂直与相等得出点在角平分线上是解题的关键.5．如图，ABC ∆中，AB AC =，点D 是ABC ∆内部一点，DB DC =，点E 是边AB 上一点，若CD 平分ACE ∠，100AEC =∠，则BDC ∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD ，再根据角的和差关系得到∠ECB =∠ACB －2∠ACD ，然后利用外角定理得到∠ABC+∠ECB=100°，代换化简得出∠ACB －∠ACD=50°，即∠DCB=50°，从而求出∠BDC 即可.【详解】∵CD 平分∠ACE ，∴∠ACE=2∠ACD=2∠ECD ，∴∠ECB=∠ACB －∠ACE=∠ACB －2∠ACD ，∵∠AEC=100°，∴∠ABC+∠ECB=100°，∴∠ABC+∠ACB－2∠ACD=100°，∵AB=AC，∴∠ABC=∠ACB,∴2∠ACB－2∠ACD=100°，∴∠ACB－∠ACD=50°，即∠DCB=50°，∵DB=DC，∴∠DBC=∠DCB，∴∠BDC=180°－2∠DCB=180°－2×50°=80°.【点睛】本题考查了角平分线，三角形内角和，外角定理，及等边对等角的性质等知识，熟练掌握基本知识，找出角与角之间的关系是解题的关键.6．如图，△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点，如果点P在线段BC 上以v厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动。

八年级数学全等三角形专题训练

14．如图，已知△ABC≌△ADE，D 是∠BAC 的平分线上一点，且∠ BAC=60°，则∠CAE= ．
15．△ABC 中，∠A：∠C：∠B=4：3：2，且△ABC≌△DEF，则∠ DEF= ． 16．如图，已知△ACE≌△DBF，CF=BF，AE=DF，AD=8，BC=2，则 AC= ． 17．已知△ABC≌△DEF，且△DEF 的周长为 12，若 AB=5，BC=4， AC= ． 18．如图，△ABC≌△ADE，BC 的延长线交 DE 于 F，∠B=30°，∠ AED=110°，∠DAC=10°，则∠DFB 的度数为．
八年级数学全等三角形专题训练
一．选择题（共 12 小题）
1．下列各组的两个图形属于全等图形的是（）
A．
B．Biblioteka C．D．2．下列判断正确的个数是（）
（1）能够完全重合的两个图形全等；
（2）两边和一角对应相等的两个三角形全等；
（3）两角和一边对应相等的两个三角形全等；
（4）全等三角形对应边相等．
A．15° B．20° C．25° D．30° 【考点】全等三角形的性质．【分析】先根据全等三角形对应角相等求出∠B=∠D，∠BAC=∠DAE，所以 ∠BAD=∠CAE，然后求出∠BAD 的度数，再根据△ABG 和△FDG 的内角和都等于 180°，所以∠DFB=∠BAD．【解答】解：∵△ABC≌△ADE， ∴∠B=∠D，∠BAC=∠DAE，又∠BAD=∠BAC﹣∠CAD，∠CAE=∠DAE﹣∠CAD， ∴∠BAD=∠CAE， ∵∠DAC=60°，∠BAE=100°，
A．1 个B．2 个C．3 个D．4 个【考点】全等三角形的性质．【分析】根据全等三角形对应边相等，全等三角形对应角相等结合图象解答即可．【解答】解：∵△ABC≌△AEF， ∴AC=AF，故①正确； ∠EAF=∠BAC，

初二数学全等三角形练习题及答案

初二数学全等三角形练习题及答案一、选择题1. 已知三角形ABC和三角形DEF的对应边长关系为AB=DE，AC=DF，∠B=∠E，则三角形ABC与三角形DEF的关系是（）。

A. 全等B. 相似C. 不全等也不相似D. 不确定2. 在△ABC中，∠A=∠C，AB=BC，则∠B的度数为（）。

A. 60°B. 90°C. 120°D. 不确定3. 已知三角形ABC和三角形CDE的对应边长关系为AB=CD，AC=CE，BC=DE，则三角形ABC与三角形CDE的关系是（）。

A. 全等B. 相似C. 不全等也不相似D. 不确定4. 若两个三角形的对应角相等，且其中一个三角形的一条边与另一个三角形的一条边相等，则这两个三角形一定是（）。

A. 全等B. 相似C. 不全等也不相似D. 不确定5. 在△ABC中，∠B=∠C，AC=BC，则这个三角形是（）。

A. 等腰三角形B. 直角三角形C. 锐角三角形D. 不确定二、填空题1. 若全等三角形ABC和DEF中∠B=∠E=90°，则∠A=______，∠C=______。

2. 在△ABC中，∠A=∠B=60°，则∠C=______。

3. 已知△ABC≌△DEF，若AC=DF=12cm，AC∥DF，BC=9cm，则DE=______。

4. 若三角形ABC与三角形DEF全等，则∠ABC=______°，∠BAC=______°。

5. 在△ABC≌△XYZ中，∠B=47°，∠X=26°，∠Y=______°。

三、解答题1. 已知△ABC≌△DEF，AB=5cm，AC=8cm，BC=7cm，求DE的长度。

解：由全等三角形的定义可知，当两个三角形全等时，它们的对应边长相等。

因此，DE的长度也为7cm。

2. 由题可得，四边形ABCD中，AB=BC=CD，AD⊥BC，∠C=90°。

第12章全等三角形 —几何压轴专题练习(一)八年级数学人教版上册

第12章《全等三角形》——几何压轴专题练习（一）1．如图，△ABC的角平分线AD、BE相交于点P，（1）在图1中，分别画出点P到边AC、BC、BA的垂线段PF、PG、PH，这3条线段相等吗？为什么？（2）在图2中，∠ABC是直角，∠C＝60°，其余条件都不变，请你判断并写出PE与PD 之间的数量关系，并说明理由．2．如图1，图2，在△ABC中，∠ACB＝90°，AC＝BC，AB＝8，点D是AB边的中点，点E 是AB边上一动点（点E不与点A、B重合），连接CE，过点B作BF⊥CE于F，交射线CD 于点G．（1）当点E在点D的左侧运动时，（图1），求证：△ACE≌△CBG；（2）当点E在点D的右侧运动时（图2），（1）中的结论是否成立？请说明理由；（3）当点E运动到何处时，BG＝5，试求出此时AE的长．3．在△ABC中，∠ACB＝2∠B，如图①，当∠C＝90°，AD为∠BAC的角平分线时，在AB上截取AE＝AC，连接DE，易证AB＝AC+CD．（1）如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想：（2）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．4．在△ABC中，AB＝AC，点D是BC上一点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE．（1）如图1，若∠BAC＝90°，①求证；△ABD≌△ACE；②求∠BCE的度数．（2）设∠BAC＝α，∠BCE＝β．如图2，则α，β之间有怎样的数量关系？请直接写出你的结论．5．已知：在△ABC中，AC＝BC，∠ACB＝90°，CD平分∠BCA且CD⊥AB，点E是AB边上一点．（1）求∠CAB和∠CBA的度数；（2）直线BF⊥直线CE于点F，交CD于点G（如图①），求证：AE＝CG；（3）直线AH⊥直线CE，垂足为点H，交CD的延长线于点M（如图②），找出图中与BE 相等的线段，并证明．6．在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，猜想线段DE、AD与BE有怎样的数量关系？请写出这个关系（不用证明）；（2）当直线MN绕点C旋转到图2的位置时，求证：DE＝AD﹣BE；（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．7．如图所示，BD、CE是△ABC的高，点P在BD的延长线上，CA＝BP，点Q在CE上，QC＝AB．（1）探究PA与AQ之间的关系；（2）若把（1）中的△ABC改为钝角三角形，AC＞AB，∠A是钝角，其他条件不变，上述结论是否成立？画出图形并证明你的结论．8．已知点P是Rt△ABC斜边AB上一动点（不与A，B重合），分别过A，B向直线CP作垂线，垂足分别为E，F．（1）如图1，当点P为AB的中点时，连接AF，BE．求证：四边形AEBF是平行四边形；（2）如图2，当点P不是AB的中点，取AB的中点Q，连接EQ，FQ．试判断△QEF的形状，并加以证明．9．问题背景：如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系，小王同学探究此问题的方法是，延长FD到点G．使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；探索延伸：如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD 上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由；实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以70海里/小时的速度前进，舰艇乙沿北偏东50°的方向以90海里/小时的速度，前进2小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．10．在△ABC中，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．（1）①如图（1），当∠B＝60°，∠ACB＝90°，则∠AFC＝；②如图（2），如果∠ACB不是直角，∠B＝60°时，请问在①中所得的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．（2）如图（3），在②的条件下，请猜想EF与DF的数量关系，并证明你的猜想．11．已知∠ABC＝90°，D是直线AB上的点，AD＝BC．（1）如图1，过点A作AF⊥AB，并截取AF＝BD，连接DC，DF，CF，判断△CDF的形状并证明；（2）如图2，E是直线BC上的一点，直线AE，CD相交于点P，且∠APD＝45°，求证：BD＝CE．12．已知∠MAN＝120°，AC平分∠MAN．（1）在图1中，若∠ABC＝∠ADC＝90°，求证：AB+AD＝AC；（2）在图2中，若∠ABC+∠ADC＝180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．13．如图，CD和BE是△ABC的两条高，∠BCD＝45°，BF＝FC，BE与DF、DC分别交于点G、H，∠ACD＝∠CBE．（1）证明：AB＝BC；（2）判断BH与AE之间的数量关系，并证明你的结论；（3）结合已知条件，观察图形，你还能发现什么结论？请写出两个（不与前面结论相同）．14．如图（1），在等边△ABC的顶点B、C处各有一只蜗牛，它们同时出发分别以每分钟1个单位的速度由B向C和由C向A爬行，其中一只蜗牛爬到终点s时，另一只也停止运动，经过t分钟后，它们分别爬行到D，P处，请问：（1）在爬行过程中，BD和AP始终相等吗？为什么？（2）问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化？请证明你的结论．（3）若蜗牛沿着BC和CA的延长线爬行，BD与AP交于点Q，其他条件不变，如图（2）所示，蜗牛爬行过程中的∠DQA大小变化了吗？若无变化，请证明．若有变化，请直接写出∠DQA的度数．15．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°．（1）当点D在AC上时，如图①，线段BD，CE有怎样的数量关系和位置关系？请证明你的猜想；（2）将图①中的△ADE绕点A顺时针旋转α（0°＜α＜90°），如图②，线段BD，CE 有怎样的数量关系和位置关系？请说明理由．。

8年级数学全等三角形经典例题

8年级数学全等三角形经典例题一、全等三角形经典例题1。

例1：如图，在△ABC中，AB = AC，AD是BC边上的中线，求证：△ABD≌△ACD。

解析：1. 在△ABD和△ACD中：- 已知AB = AC（题目中给出的等腰三角形的两腰相等）。

- 因为AD是BC边上的中线，所以BD = CD（中线的定义）。

- AD = AD（公共边）。

2. 根据SSS（边边边）全等判定定理，可得△ABD≌△ACD。

二、全等三角形经典例题2。

例2：已知：如图，AB = AD，∠B = ∠D，∠1=∠2，求证：△ABC≌△ADE。

解析：1. 因为∠1 = ∠2，所以∠1+∠DAC = ∠2+∠DAC，即∠BAC = ∠DAE。

2. 在△ABC和△ADE中：- 已知AB = AD。

- ∠B = ∠D。

- 且∠BAC = ∠DAE（已证）。

3. 根据ASA（角边角）全等判定定理，可得△ABC≌△ADE。

三、全等三角形经典例题3。

例3：如图，在△ABC中，∠C = 90°，AC = BC，AD平分∠CAB交BC于D，DE⊥AB于E，AB = 6cm，求△DEB的周长。

解析：1. 因为AD平分∠CAB，∠C = 90°，DE⊥AB，根据角平分线的性质，可知CD = DE。

2. 在Rt△ACD和Rt△AED中：- AD = AD（公共边）。

- CD = DE（已证角平分线性质）。

- 根据HL（斜边直角边）定理，可得Rt△ACD≌Rt△AED。

- 所以AC = AE。

3. 因为AC = BC，AB = 6cm，设AC = BC=x，根据勾股定理AC^2+BC^2=AB^2，即x^2+x^2=6^2，2x^2=36，x^2=18，x = 3√(2)。

4. 又因为AE = AC = 3\sqrt{2}\)，所以BE=AB - AE = 6 - 3\sqrt{2}\)。

5. 而△DEB的周长为DE+DB+BE，因为CD = DE，BC = BD + CD，所以△DEB的周长为BC+BE = 3\sqrt{2}+6 - 3\sqrt{2}=6cm。

八年级数学全等三角形测试题

八年级数学全等三角形测试题一、选择题（每题3分，共30分）1. 下列说法正确的是（）A. 全等三角形是指形状相同的两个三角形B. 全等三角形的周长和面积分别相等C. 全等三角形是指面积相等的两个三角形D. 所有的等边三角形都是全等三角形解析：选项A：全等三角形不仅形状相同，而且大小也相同，所以A错误。

选项B：全等三角形能够完全重合，所以它们的周长和面积分别相等，B正确。

选项C：面积相等的三角形不一定全等，比如一个底为4，高为3的三角形和一个底为6，高为2的三角形面积相等，但不全等，C错误。

选项D：所有等边三角形形状相同，但大小不一定相同，所以不是所有的等边三角形都是全等三角形，D错误。

2. 如图，已知△ABC≌△DEF，∠A = 50°，∠B = 70°，则∠F的度数为（）A. 50°B. 60°C. 70°D. 80°解析：在△ABC中，根据三角形内角和为180°，可得∠C=180°∠A ∠B = 180° 50°70° = 60°。

因为△ABC≌△DEF，全等三角形对应角相等，所以∠F = ∠C = 60°，答案为B。

3. 如图，在△ABC和△DEC中，已知AB = DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（）A. BC = EC，∠B = ∠EB. BC = EC，AC = DCC. ∠B = ∠E，∠A = ∠DD. BC = DC，∠A = ∠D解析：选项A：AB = DE，BC = EC，∠B = ∠E，根据SAS（边角边）可判定△ABC≌△DEC。

选项B：AB = DE，BC = EC，AC = DC，根据SSS（边边边）可判定△ABC≌△DEC。

选项C：AB = DE，∠B = ∠E，∠A = ∠D，根据AAS（角角边）可判定△ABC≌△DEC。

八年级上册数学全等三角形必考题

八年级上册数学全等三角形必考题全文共5篇示例，供读者参考八年级上册数学全等三角形必考题1《全等三角形的判定》这一课，要求学生会通过观察几何图形识别两个三角形全等，并能通过正确的分类动手探索出两个三角形全等的条件。

具体说：（1）正确识别两个三角形全等——会将两个三角形相等的边和角对应重叠在一起，看是否重合；（2）相信判定两个三角形全等不一定要3条边和3个角都相等，可能一边或一角相等就足够（这个判断不一定要正确，但要有这种想法，探索命题的真假才有可能）；（3）能正确地将三角形的6个元素按条件的个数分成：①一个元素：一个边或一条角对应相等。

②两个元素：两边或一边一角或两角对应相等。

③三个元素：三边或两边和一角或一边和两角或三角对应相等。

或者按：①边（一条边或两条边或三条边分别对应相等）。

②角（一个角或两个角或三个角分别对应相等）。

③边和角[一条边和一个角或一条边和两个角（又分为角边角和角角边两种）或两条边和一个角（又分为边角边和边边角两种）分别对应相等]；（4）能将分好的三大类（12小类）条件用画图的方法进行验证，找出能判定两个三角形全等的三条公理和一条定理；（5）能用这四个判定，直接判定两个三角形是否全等或能补充一个条件使两个三角形全等。

基于知识的完整性和分类的数学思想的渗透，我认为这个教学设计体现了知识与技能目标。

增强学生的观察、猜想和动手操作能力。

八年级上册数学全等三角形必考题2一、制订好复习课的复习目标复习要对以前多节新课中的知识点或数学思想方法进行压缩整理，所以要制订好复习课的复习目标。

首先，选择合适的知识范围非常重要。

其次，应确定对所选知识点中重点的复习深度，过易会让学生索然无味，过难会让学生畏惧前行，失去信心。

我对这节课的难度把握是保全突尖，教学流程本身有梯度，例题与配套变式也有梯度。

不过对于例3“求证两线段相等”这个问题既需要添加辅助线，又要连续两次证全等。

问题的梯度设置过大，许多学生还观察不出。

《易错题》初中八年级数学上册第十二章《全等三角形》经典练习题(专题培优)(1)

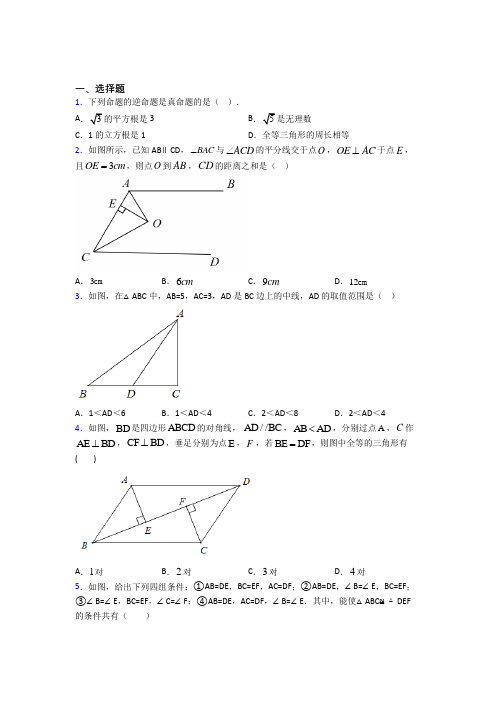
一、选择题1．下列命题的逆命题是真命题的是（）．A ．3的平方根是3B ．5是无理数C ．1的立方根是1D ．全等三角形的周长相等2．如图所示，已知AB ∥CD ，BAC ∠与ACD ∠的平分线交于点O ，OE AC ⊥于点E ，且3OE cm =，则点O 到AB ，CD 的距离之和是（）A ．3cmB ．6cmC ．9cmD ．12cm 3．如图，在△ABC 中，AB=5，AC=3，AD 是BC 边上的中线，AD 的取值范围是（）A ．1＜AD ＜6B ．1＜AD ＜4C ．2＜AD ＜8 D ．2＜AD ＜4 4．如图，BD 是四边形ABCD 的对角线， AD//BC ，AB AD <，分别过点A ，C 作AE BD ⊥，CF BD ⊥，垂足分别为点E ，F ，若BE DF =，则图中全等的三角形有( )A ．1对B ．2对C ．3对D ．4对 5．如图，给出下列四组条件：①AB=DE ，BC=EF ，AC=DF ；②AB=DE ，∠B=∠E ，BC=EF ；③∠B=∠E ，BC=EF ，∠C=∠F ；④AB=DE ，AC=DF ，∠B=∠E ．其中，能使△ABC ≌△DEF 的条件共有（）A ．1组B ．2组C ．3组D ．4组6．已知如图，AC ⊥BC ，DE ⊥AB ，AD 平分∠BAC ，下面结论错误的是（）A ．BD +ED ＝BCB ．DE 平分∠ADBC ．AD 平分∠EDC D ．ED +AC ＞AD 7．如图，∠ACB=90°，AC=BC ，AD ⊥CE ，BE ⊥CE ，垂足分别是点D 、E ，AD=3，BE=1，则DE 的长是（）A ．1.5B ．2C ．22D ．10 8．如图，在ABC 中，90C ∠=︒，AD 是BAC ∠的角平分线，E 是边AB 上一点，若6CD =，则DE 的长可以是（）A ．1B ．3C ．5D ．79．下列命题中，假命题是（）A ．在同一平面内，垂直于同一条直线的两直线平行B ．到线段两端点距离相等的点在这条线段的垂直平分线上C ．一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等D ．一边长相等的两个等腰直角三角形全等10．如图，AB BC ⊥，CD BC ⊥，AC BD =，则能证明ABC DCB ≅的判定法是( )A．SAS B．AAS C．SSS D．HL11．如图，OB平分∠MON，A为OB的中点，AE⊥ON，EA=3，D为OM上的一个动点，C 是DA延长线与BC的交点，BC//OM，则CD的最小值是（）A．6 B．8 C．10 D．12∠=∠，E、D、F分别是AB、BC、AC上的点，且12．如图，在ABC中，B C=，BD CFBE CD=，若104∠=︒，则EDFA∠的度数为（）A．24°B．32°C．38°D．52°13．如图，AD平分∠BAC，AB=AC，连接BD，CD并延长，分别交AC，AB于点F，E，则图中全等三角形共有（）A．2对B．3对C．4对D．5对14．下列命题，真命题是（）A．全等三角形的面积相等B．面积相等的两个三角形全等C．两个角对应相等的两个三角形全等D．两边和其中一边的对角对应相等的两个三角形全等15．如图，已知AE平分∠BAC，BE⊥AE于E，ED∥AC，∠BAE＝34°，那么∠BED＝（）A ．134°B ．124°C ．114°D ．104°二、填空题16．如图，四边形ABCD 中，AC BC =，90ACB ADC ∠=∠=︒，10CD =，则BCD ∆的面积为______．17．如图，D ，E 分别是AB ，AC 上的点，AD=AE ，请添加一个条件，使得ABE ≌ACD ．这个条件可以为_____（只填一个条件即可）．18．如图所示，在ABC 中，D 是BC 的中点，点A 、F 、D 、E 在同一直线上．请添加一个条件，使BDE CDF ≌（不再添其他线段，不再标注或使用其他字母），并给出证明．你添加的条件是______19．如图，已知//AD BC ，点E 为CD 上一点，AE ，BE 分别平分DAB ∠，CBA ∠．若3cm AE =，4cm BE =，则四边形ABCD 的面积是________．20．如图，AB ＝4cm ，AC ＝BD ＝3cm ，∠CAB ＝∠DBA ，点P 在线段AB 上以1cm/s 的速度由点A 向点B 运动，同时，点Q 在线段BD 上由点B 向点D 运动．设运动时间为t （s ），则当△ACP 与△BPQ 全等时，点Q 的运动速度为__cm/s ．21．如图，点D 在BC 上，DE ⊥AB 于点E ，DF ⊥BC 交AC 于点F ，BD ＝CF ，BE ＝CD ．若∠AFD ＝145°，则∠EDF ＝_____．22．如图，∠1＝∠2，要使△ABC ≌△ADC ，还需添加条件：_____．（填写一个你认为正确的即可）23．如图所示，AB AC =，AD AE =，BAC DAE ∠=∠，点D 在线段BE 上．若125∠=︒，230∠=︒，则3∠=______．24．已知△ABC ≌△DEF ，△ABC 的三边分别为3，m ，n ，△DEF 的三边分别为5，p ，q ．若△ABC 的三边均为整数，则m+n+p+q 的最大值为________．25．如图，已知AB AC =，D 为BAC ∠的角平分线上面一点，连接BD ，CD ；如图，已知AB AC =，D 、E 为BAC ∠的角平分线上面两点，连接BD ，CD ，BE ，CE ；如图，已知AB AC =，D 、E 、F 为BAC ∠的角平分线上面三点，连接BD ，CD ，BE ，CE ，BF ，CF ；…，依此规律，第n 个图形中有全等三角形的对数是______．26．如图，在ABC 中，60BAC ∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ，DE AB ⊥交AB 的延长线于点E ，DF AC ⊥于点F ，现有下列结论：①120EDF ∠=︒；②DM 平分EDF ∠；③DE DF AD +=；④2AB AC AE +>；其中正确的有________(请将正确结论的序号填写在横线上)．三、解答题27．（阅读理解）课外兴趣小组活动时，老师提出了如下问题：如图1，ABC 中，若8AB =，6AC =，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE AD =，请根据小明的方法思考：（1）由已知和作图能得到ADC ≌EDB △的理由是______．（2）求得AD 的取值范围是______．（感悟）解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．（问题解决）（3）如图2，在ABC 中，点D 是BC 的中点，点M 在AB 边上，点N 在AC 边上，若DM DN ⊥，求证：BM CN MN +>．28．阅读下面材料：学习了三角形全等的判定方法（即“SAS ”“ASA ”“AAS ”“SSS ”）和直角三角形全等的判定方法（即“HL ”）后，小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．小聪将命题用符号语言表示为在ABC 和DEF 中，AC DF =，BC EF =，B E ∠=∠．小聪的探究方法是对B 分为“直角、钝角、锐角”三种情况进行探究．第一种情况：当B 是直角时，如图1，在ABC 和DEF 中，AC DF =，BC EF =，90B E ∠=∠=︒，根据“HL ”定理，可以知道Rt Rt ABC DEF ≌△△．第二种情况：当B 是锐角时，如图2，90B E ∠=∠<︒，BC EF =．（1）在射线EM 上是否存在点D ，使DF AC =？若存在，请在图中作出这个点，并连接DF ；若不存在，请说明理由；（2）这种情形下，ABC 和DEF 的关系是（选填“全等”“不全等”或“不一定全等”）；第三种情况：当B 是钝角时，如图3，在ABC 和DEF 中，AC DF =，BC EF =，90B E ∠=∠>︒．（3）请判断这种情形下，ABC 和DEF 是否全等，并说明理由．29．求证：全等三角形对应边上的中线相等．（根据图形写出已知，求证并完成证明）30．在数学课本中，有这样一道题：如图1，AB ∥CD ，试用不同的方法证明∠B +∠C ＝∠BEC（1）某同学写出了该命题的逆命题，请你帮他把逆命题的证明过程补充完整．已知：如图1，∠B+∠C＝∠BEC求证：AB∥CD证明：如图2，过点E，作EF∥AB，∴∠B＝∠∵∠B+∠C＝∠BEC，∠BEF+∠FEC＝∠BEC（已知）∴∠B+∠C＝∠BEF+∠FEC（等量代换）∴∠＝∠（等式性质）∴EF∥∵EF∥AB∴AB∥CD（平行于同一条直线的两条直线互相平行）（2）如图3，已知AB∥CD，在∠BCD的平分线上取两个点M、N，使得∠BMN＝∠BNM，求证：∠CBM＝∠ABN．（3）如图4，已知AB∥CD，点E在BC的左侧，∠ABE，∠DCE的平分线相交于点F．请直接写出∠E与∠F之间的等量关系．。

初二数学全等三角形证明题专题训练

初二数学全等三角形证明题专题训练1.如图，,,,A F E B 四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =。

求证：ACF BDE ∆≅∆。

2.如图，在ABC ∆中，BE 是∠ABC 的平分线，AD BE ⊥，垂足为D 。

求证：21C ∠=∠+∠。

3.如图，在ABC ∆中，AB BC =，90ABC ∠=。

F 为AB 延长线上一点，点E 在BC 上，BE BF =，连接,AE EF 和CF 。

求证：AE CF =。

4.如图，AB //CD ，AD //BC ，求证：AB CD =。

5. 如图，,AP CP 分别是ABC ∆外角MAC ∠和NCA ∠的平分线，它们交于点P 。

求证：BP 为MBN ∠的平分线。

6.如图，D 是ABC ∆的边BC 上的点，且CD AB =，ADB BAD ∠=∠，AE 是ABD ∆的中线。

求证：2AC AE =。

7.如图，在ABC ∆中，AB AC >，12∠=∠，P 为AD 上任意一点。

求证：AB AC PB PC ->-。

8.直线CD 经过BCA ∠的顶点C ，CA=CB ．E 、F 分别是直线CD 上两点，且BECCFA α∠=∠=∠．（1）若直线CD 经过BCA ∠的内部，且E 、F 在射线CD 上，请解决下面两个问题： ①如图1，若90,90BCA α∠=∠=，则EF BE AF -（填“>”，“<”或“=”号）；②如图2，若0180BCA <∠<，若使①中的结论仍然成立，则α∠与BCA ∠ 应满足的关系是；（2）如图3，若直线CD 经过BCA ∠的外部，BCA α∠=∠，请探究EF 、与BE 、AF 三条线段的数量关系，并给予证明．9.已知：如图，△ABC 中，∠ABC =45°，CD ⊥AB 于D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，H 是BC 边的中点，连结DH 与BE 相交于点G 。

八年级数学 《全等三角形》专题训练 (1)

中考数学复习《全等三角形》专题(卷1)

【教师卷】洛阳市八年级数学上册第十二章《全等三角形》经典复习题(专题培优)(1)

八年级上册数学第十二章全等三角形解答题 专题训练 12916含解析.docx

中考数学复习《全等三角形》专题训练-附带参考答案

八年级全等三角形专题练习(解析版)

苏科版八年级数学上册试题 第1章 全等三角形 单元测试卷(含详解)

八年级数学上册第一章《全等三角形》测试卷-苏科版(含答案)

专题 全等三角形压轴题训练(30题)(解析版)

八年级数学三角形全等(动点问题)(人教版)(专题)(含答案)

八年级数学全等三角形专项练习题(含答案)

八年级全等三角形专题练习(解析版)

八年级数学全等三角形专题训练

初二数学全等三角形练习题及答案

第12章 全等三角形 —几何压轴专题练习(一)八年级数学人教版上册

8年级数学全等三角形经典例题

八年级数学全等三角形测试题

八年级上册数学全等三角形必考题

《易错题》初中八年级数学上册第十二章《全等三角形》经典练习题(专题培优)(1)

初二数学全等三角形证明题专题训练

八年级数学《全等三角形》专题训练 (1)

八年级上册数学第十二章全等三角形解答题专题训练 12916含解析.docx

苏科版八年级数学上册试题第1章全等三角形单元测试卷(含详解)

专题全等三角形压轴题训练(30题)(解析版)

第12章全等三角形 —几何压轴专题练习(一)八年级数学人教版上册