初三数学《相似三角形》专题复习
初三数学相似知识点

初三数学相似知识点
1. 相似三角形:相似三角形是指具有相同形状但大小不同的三角形。
相似三角形的对
应边长成比例,对应角度相等。
2. 相似比例:相似三角形的边长比值称为相似比例。
如果两个三角形的对应边长分别
为a:b:c和ka:kb:kc,那么它们的相似比例为a:b:c。
3. 相似三角形定理:包括AAA相似定理、AA相似定理和对应角边比相等定理。
其中,AAA相似定理指出如果两个三角形的对应角度相等,那么它们相似;AA相似定理指出如果两个三角形的两个对应角度相等,那么它们相似;对应角边比相等定理指出如果
两个三角形的两个对应角度相等,并且对应边长之比相等,那么它们相似。
4. 相似三角形的性质:相似三角形的相似比例等于对应边长之比;相似三角形的相似
比例等于对应角度的正弦值、余弦值或正切值;相似三角形的高线、中线等与对应边
长成等比例;相似三角形的面积与边长平方成比例。
5. 相似三角形的应用:相似三角形的定理在解决实际问题中有很多应用,如利用相似
三角形进行测量、解决影子问题、求解高度、求解距离等。
6. 图形的相似:除了三角形,其他图形(如矩形、圆、椭圆等)也有相似的概念和相
似关系,可以利用相似关系解决相关问题。
这些内容是初三数学中关于相似的主要知识点,希望对你有帮助!如有其他问题,请
随时提问。
九年级数学相似三角形知识点汇总参考(搜集整理全面细致)

.
( 5)平行线分线段成比例定理 :两条直线被三条平行的直线所截,截得的对应线段成比例
.
( 6)平行线等分线段定理:两条直线被三条平行的直线所截,如果在一条直线上截得的线段相等,那么在
另一条直线上截得的线段也相等 .
这几个定理主要提出由平行线可得到比例式;反之
, 有比例可得到平行线 . 首先要弄清三个基本图形:
九年级数学相似三角形知识点汇总参考
一、比例线段及比例的性质
1.比例线段: ( 1)线段的比:如果选用同一长度单位量得两条线段
a, b 的长度分别是 m, n,那么就说这两条线段的比是
a:b=m:n ,或写成
, 其中 a 叫做比的前项 ;b 叫做比的后项 .
( 2)成比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比
( 3)向量平行的 判定定理: a 是一个非零向量,若存在一个实数 m ,使 b ma ,则向量 b 与非零向量 a 平行 .
( 4)向量平行的性质定理:若向量 b与非零向量 a 平行 ,则存在一个实数 m ,使 b ma .
( 5) A、 B、 C 三点的共线
AB// BC 若存在实数 λ ,使 AB λBC .
3
诠释: ( 1)向量数乘结果是一个与已知向量平行(或共线)的向量; ( 2)实数与向量不能进行加减运算;
( 3) ka 表示向量的数乘运算, 书写时应把实数写在向量前面且省略乘号,
面;
( 4)向量的数乘体现几何图形中的位置关系和数量关系
.
3.实数与向量相乘的运算律
设 m 、 n 为实数,则:
注意不要将表示向量的箭头写在数字上
, 所截得的三角形的
三边与原三角形三边的对应成比例 .
(完整word版)九年级数学相似三角形知识点及习题

相似三角形要点一、本章的两套定理第一套(比例的有关性质): b a n d b m c a n d b n m d c b a =++++++⇒≠+++=== :)0(等比性质 涉及概念:①第四比例项②比例中项③比的前项、后项,比的内项、外项④黄金分割等。
二、有关知识点:1.相似三角形定义: 对应角相等,对应边成比例的三角形,叫做相似三角形。
2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。
3.相似三角形的相似比: 相似三角形的对应边的比叫做相似比。
4.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
5.相似三角形的判定定理:(1)三角形相似的判定方法与全等的判定方法的联系列表如下:类型斜三角形 直角三角形 全等三角形的判定 SASSSS AAS (ASA ) HL 相似三角形的判定 两边对应成比例夹角相等 三边对应成比例 两角对应相等一条直角边与斜边对应成比例 从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理,这就是我们数学中的用类比的方法,在旧知识的基础上找出新知识并从中探究新知识掌握的方法。
6.直角三角形相似:(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
7.相似三角形的性质定理:(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
8.相似三角形的传递性 如果△ABC ∽△A 1B 1C 1,△A 1B 1C 1∽△A 2B 2C 2,那么△ABC ∽A 2B 2C 2三、注意1、相似三角形的基本定理,它是相似三角形的一个判定定理,也是后面学习的相似三角形的判定定理的基础,这个定理确定了相似三角形的两个基本图形“A ”型和“ X ”型。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

专题13 相似三角形一.选择题1.(2022·黑龙江哈尔滨)如图,,,AB CD AC BD ∥相交于点E ,1,2,3AE EC DE ===,则BD 的长为( )A .32B .4C .92D .6【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长,即可求得BD 的长.【详解】∵//AB CD ∴ABE CDE ∽ ∴AE BE EC DE= ∵1,2,3AE EC DE ===,∴32BE =∵BD BE ED =+ ∴92BD = 故选:C .【点睛】本题考查了相似三角形的对应边长成比例,解题的关键在于找到对应边长.2.(2022·广西贺州)如图,在ABC 中,25DE BC DE BC ==∥,,,则:ADE ABC S S 的值是( )A .325B .425C .25D .35【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ,根据相似三角形的面积比等于相似比的平方计算,得到答案.【详解】解:25DE BC DE BC ==∥,,∴ADE ABC ,∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ,故选:B .【点睛】此题考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.3.(2022·广西梧州)如图,以点O 为位似中心,作四边形ABCD 的位似图形''''A B C D ﹐已知'13OA OA =,若四边形ABCD 的面积是2,则四边形''''A B C D 的面积是( )A .4B .6C .16D .18【答案】D 【分析】两图形位似必相似,再由相似的图形面积比等于相似比的平方即可求解.【详解】解:由题意可知,四边形ABCD 与四边形''''A B C D 相似,由两图形相似面积比等于相似比的平方可知:''''22'1139ABCD A B C D S OA S OA ⎛⎫⎛⎫= ⎪= ⎪= ⎪ ⎪⎝⎭⎝⎭,又四边形ABCD 的面积是2,∴四边形''''A B C D 的面积为18,故选:D .【点睛】本题考察相似多边形的性质,属于基础题,熟练掌握相似图形的性质是解决本题的关键.4.(2022·四川雅安)如图,在△ABC 中,D ,E 分别是AB 和AC 上的点,DE ∥BC ,若AD BD =21,那么DE BC =( )A .49B .12C .13D .23【答案】D【分析】先求解2,3AD AB =再证明,ADE ABC ∽可得2.3DE AD BC AB ==【详解】解: AD BD =21,2,3AD AB ∴= DE ∥BC ,,ADE ABC ∴ ∽ 2,3DE AD BC AB ∴== 故选D 【点睛】本题考查的是相似三角形的判定与性质,证明ADE ABC △△∽是解本题的关键.5.(2022·内蒙古包头)如图,在边长为1的小正方形组成的网格中,A ,B ,C ,D 四个点均在格点上,AC 与BD 相交于点E ,连接,AB CD ,则ABE △与CDE △的周长比为( )A .1:4B .4:1C .1:2D .2:1【答案】D 【分析】运用网格图中隐藏的条件证明四边形DCBM 为平行四边形,接着证明ABE CDE ∽,最后利相似三角形周长的比等于相似比即可求出.【详解】如图:由题意可知,3DM =,3BC =, ∴DM BC =,而DM BC ∥,∴四边形DCBM 为平行四边形,∴AB DC ∥,∴BAE DCE ∠=∠,ABE CDE ∠=∠,∴ABE CDE ∽,∴21ABE CDE C AB C CD ===△△.故选:D .【点睛】本题考查了平行四边形的判定与性质、相似三角形的判定与性质及勾股定理,熟练掌握相关知识并正确计算是解题关键.6.(2022·黑龙江绥化)如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得ABE CBP =∠∠,如果2AB =,5BC =,AP x =,PM y =,其中25x < .则下列结论中,正确的个数为( )(1)y 与x 的关系式为4y x x =-;(2)当4AP =时,ABP DPC ∽;(3)当4AP =时,3tan 5EBP ∠=.A .0个B .1个C .2个D .3个【答案】C 【分析】(1)证明ABM APB ∽,得AB AM AP AB=,将2AB =,AP x =,PM y =代入,即可得y 与x 的关系式;(2)利用两组对应边成比例且夹角相等,判定ABP DPC ∽;(3)过点M 作MF BP ⊥垂足为F ,在Rt APB △中,由勾股定理得BP 的长,证明FPM APB ∽,求出MF ,PF ,BF 的长,在Rt BMF △中,求出tan EBP ∠的值即可.【详解】解:(1)∵在矩形ABCD 中,∴AD BC ∥,90A D ∠=∠=︒,5BC AD ==,2AB DC ==,∴APB CBP ∠=∠,∵ABE CBP =∠∠,∴ABE APB ∠=∠,∴ABM APB ∽,∴AB AM AP AB=,∵2AB =,AP x =,PM y =,∴22x y x -=,解得:4y x x=-,故(1)正确;(2)当4AP =时,541DP AD AP =-=-=,∴12DC DP AP AB ==,又∵90A D ∠=∠=︒,∴ABP DPC ∽,故(2)正确;(3)过点M 作MF BP ⊥垂足为F ,∴90A MFP MFB ∠=∠=∠=︒,∵当4AP =时,此时4x =,4413y x x =-=-=,∴3PM =,在Rt APB 中,由勾股定理得:222BP AP AB =+,∴BP ===,∵FPM APB ∠=∠,∴FPM APB ∽,∴MF PF PM AB AP PB ==,∴24MF PF ==∴MF =PF =∴BF BP PF =-=∴3tan 4MF EBP BF ∠===故(3)不正确;故选:C .【点睛】本题主要考查相似三角形的判定和性质,勾股定理的应用,矩形的性质,正确找出相似三角形是解答本题的关键.7.(2022·湖北鄂州)如图,定直线MN ∥PQ ,点B 、C 分别为MN 、PQ 上的动点,且BC =12,BC 在两直线间运动过程中始终有∠BCQ =60°.点A 是MN 上方一定点,点D 是PQ 下方一定点,且AE ∥BC ∥DF ,AE =4,DF =8,ADBC 在平移过程中,AB +CD 的最小值为()A .B .C .D .【答案】C 【分析】如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,可证明四边形CDFH 是平行四边形,得到CH =DF =8,CD =FH ,则BH =4,从而可证四边形ABHE 是平行四边形,得到AB =HE ,即可推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,证明四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,得到EG =BC =12,然后通过勾股定理和解直角三角形求出ET 和TF 的长即可得到答案.【详解】解:如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,∵BC DF FH CD ∥∥,,∴四边形CDFH 是平行四边形,∴CH =DF =8,CD =FH ,∴BH =4,∴BH =AE =4,又∵AE BC ∥,∴四边形ABHE 是平行四边形,∴AB =HE ,∵EH FH EF +≥,∴当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,∵MN PQ BC AE ∥∥,,∴四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,∴EG =BC =12,∴=cos =6=sin GT GE EGT ET GE EGT ⋅⋅∠,∠,同理可求得8GL AL ==,,4KF DK ==,,∴2TL =,∵AL ⊥PQ ,DK ⊥PQ ,∴AL DK ∥,∴△ALO ∽△DKO ,∴2AL AO DK DO==,∴2133AO AD DO AD ====∴24OL OK ===,,∴42TF TL OL OK KF =+++=,∴EF ==故选C .【点睛】本题主要考查了平行四边形的性质与判定,相似三角形的性质与判定,勾股定理,解直角三角形,正确作出辅助线推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF 是解题的关键.8.(2022·广西贵港)如图,在边长为1的菱形ABCD 中,60ABC ∠=︒,动点E 在AB 边上(与点A 、B 均不重合),点F 在对角线AC 上,CE 与BF 相交于点G ,连接,AG DF ,若AF BE =,则下列结论错误的是( )A .DF CE =B .120BGC ∠=︒C .2AF EG EC =⋅D .AG【答案】D【分析】先证明△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,得DF =CE ,判断A 项答案正确,由∠GCB +∠GBC =60゜,得∠BGC =120゜,判断B 项答案正确,证△BEG ∽△CEB 得BE CE GE BE= ,即可判断C 项答案正确,由120BGC ∠=︒,BC =1,得点G 在以线段BC 为弦的弧BC 上,易得当点G 在等边△ABC 的内心处时,AG 取最小值,由勾股定理求得AG D 项错误.【详解】解:∵四边形ABCD 是菱形,60ABC ∠=︒,∴AB =AD =BC =CD ,∠BAC =∠DAC =12∠BAD =12(180)ABC ⨯︒-∠=60ABC ︒=∠,∴△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,∴DF =CE ,故A 项答案正确,∠ABF =∠BCE ,∵∠ABC =∠ABF +∠CBF =60゜,∴∠GCB +∠GBC =60゜,∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜,故B 项答案正确,∵∠ABF =∠BCE ,∠BEG =∠CEB ,∴△BEG ∽△CEB ,∴BE CE GE BE = ,∴2BE GE CE = ,∵AF BE =,∴2AF GE CE = ,故C 项答案正确,∵120BGC ∠=︒,BC =1,点G 在以线段BC 为弦的弧BC 上,∴当点G 在等边△ABC 的内心处时,AG 取最小值,如下图,∵△ABC 是等边三角形,BC =1,∴BF AC ⊥,AF =12AC =12,∠GAF =30゜,∴AG =2GF ,AG 2=GF 2+AF 2,∴2221122AG AG ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭, 解得AG D 项错误,故应选:D【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理,熟练掌握菱形的性质是解题的关键.9.(2022·贵州贵阳)如图,在ABC 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC 与ACB △的周长比是( )A .B .1:2C .1:3D .1:4【答案】B 【分析】先证明△ACD ∽△ABC ,即有12AC AD CD AB AC BC ===,则可得12AC AD CD AB AC BC ++=++,问题得解.【详解】∵∠B =∠ACD ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AD CD AB AC BC ==,∵12AC AB =,∴12AC AD CD AB AC BC ===,∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++,∴△ADC 与△ACB 的周长比1:2,故选:B .【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD ∽△ABC 是解答本题的关键.10.(2022·广西)已知△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,则△ABC 与△A 1B 1C 1的面积比( )A .1 :3B .1:6C .1:9D .3:1【答案】C【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.【详解】∵△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,∴△ABC 与△A 1B 1C 1的面积比为1:9,故选:C .【点睛】本题考查位似图形的性质,熟练掌握位似图形的面积比等于位似比的平方是解题的关键.11.(2022·山东临沂)如图,在ABC 中,∥DE BC ,23AD DB =,若6AC =,则EC =( )A .65B .125C .185D .245【答案】C【分析】由∥DE BC ,23AD DB =,可得2,3AD AE DB EC ==再建立方程即可.【详解】解: ∥DE BC ,23AD DB =,2,3AD AE DB EC ∴== 6AC =,62,3CE CE -∴= 解得:18.5CE =经检验符合题意故选C 【点睛】本题考查的是平行线分线段成比例,证明“23AD AE DB EC ==”是解本题的关键.12.(2022·山东威海)由12个有公共顶点O 的直角三角形拼成如图所示的图形,∠AOB =∠BOC =∠COD =…=∠LOM =30°.若S △AOB =1,则图中与△AOB 位似的三角形的面积为( )A .(43)3B .(43)7C .(43)6D .(34)6【答案】C【分析】根据题意得出A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,确定与△AOB 位似的三角形为△GOH ,利用锐角三角函数找出相应规律得出OG=6x ,再由相似三角形的性质求解即可.【详解】解:∵∠AOB =∠BOC =∠COD =…=∠LOM =30°∴∠AOG =180°,∠BOH =180°,∴A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,∴与△AOB 位似的三角形为△GOH ,设OA =x ,则OB=1cos30OA x ==︒,∴OC=24cos303OB x x ==︒,∴OD=3cos30OC x ==︒,…∴OG=6x ,∴6OG OA =,∴12643GOH AOB S S ⎛⎫== ⎪⎝⎭ ,∵1AOB S = ,∴643GOH S ⎛⎫= ⎪⎝⎭ ,故选:C .【点睛】题目主要考查利用锐角三角函数解三角形,找规律问题,相似三角形的性质等,理解题意,找出相应边的比值规律是解题关键.二.填空题13.(2022·贵州黔东南)如图,折叠边长为4cm 的正方形纸片ABCD ,折痕是DM ,点C 落在点E 处,分别延长ME 、DE 交AB 于点F 、G ,若点M 是BC 边的中点,则FG =______cm.【答案】53【分析】根据折叠的性质可得DE =DC =4,EM =CM =2,连接DF ,设FE =x ,由勾股定理得BF ,DF ,从而求出x 的值,得出FB ,再证明FEG FBM ∆∆ ,利用相似三角形对应边成比例可求出FG .【详解】解:连接,DF 如图,∵四边形ABCD 是正方形,∴4,90.AB BC CD DA A B C CDA ︒====∠=∠=∠=∠=∵点M 为BC 的中点,∴114222BM CM BC ===⨯=由折叠得,2,4,ME CM DE DC ====∠90,DEM C ︒=∠=∴∠90DEF ︒=,90,FEG ∠=︒设,FE x =则有222DF DE EF =+∴2224DF x =+又在Rt FMB ∆中,2,2FM x BM =+=,∵222FM FB BM =+∴FB ==∴4AF AB FB =-=在Rt DAF ∆中,222,DA AF DF +=∴2224(44,x +=+解得,124,83x x ==-(舍去)∴4,3FE =∴410233FM FE ME =+=+=∴83FB ==∵∠90DEM ︒=∴∠90FEG ︒=∴∠,FEG B =∠又∠.GFE MFB =∠∴△FEG FBM∆ ∴,FG FE FM FB=即4310833FG =∴5,3FG =故答案为:53【点睛】本题主要考查了正方形的性质,折叠的性质,勾股定理,相似三角形的判定与性质,正确作出辅助线是解答本题的关键.14.(2022·上海)如图,在△ABC 中,∠A =30°,∠B =90°,D 为AB 中点,E 在线段AC 上,AD DE AB BC=,则AE AC =_____.【答案】12或14【分析】由题意可求出12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,满足112DE BC =,进而可求此时112AE AC =,然后在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,证明△DE1E2是等边三角形,求出E1E2=14AC ,即可得到214AE AC =,问题得解.【详解】解:∵D 为AB中点,∴12AD DE AB BC ==,即12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,此时DE 1∥BC ,112DE BC =,∴112AE AD AC AB ==,在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,∵∠A =30°,∠B =90°,∴∠C =60°,BC =12AC ,∵DE 1∥BC ,∴∠DE1E2=60°,∴△DE1E2是等边三角形,∴DE 1=DE 2=E1E2=12BC ,∴E1E2=14AC ,∵112AE AC =,∴214AE AC =,即214AE AC =,综上,AE AC 的值为:12或14,故答案为:12或14.【点睛】本题考查了三角形中位线的性质,平行线分线段成比例,等边三角形的判定和性质以及含30°角的直角三角形的性质等,根据12DE BC =进行分情况求解是解题的关键.15.(2022·北京)如图,在矩形ABCD 中,若13,5,4AF AB AC FC ===,则AE 的长为_______.【答案】1【分析】根据勾股定理求出BC ,以及平行线分线段成比例进行解答即可.【详解】解:在矩形ABCD 中:AD BC ∥,90ABC ∠=︒,∴14AE AF BC FC ==,4BC =,∴144AE =,∴1AE =,故答案为:1.【点睛】此题考查了勾股定理以及平行线分线段成比例,掌握平行线分线段成比例是解题的关键.16.(2022·江苏常州)如图,在Rt ABC △中,90C ∠=︒,9AC =,12BC =.在Rt DEF 中,90F ∠=︒,3DF =,4EF =.用一条始终绷直的弹性染色线连接CF ,Rt DEF 从起始位置(点D 与点B 重合)平移至终止位置(点E 与点A 重合),且斜边DE 始终在线段AB 上,则Rt ABC △的外部被染色的区域面积是______.【答案】28【分析】过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如图,需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形,所以需要利用勾股定理,相似三角形、平行四边形的判定及性质,求出相应边长,即可求解.【详解】解:过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如下图:90C ∠=︒ ,9AC =,12BC =,15AB ∴==,在Rt DEF 中,90F ∠=︒,3DF =,4EF =.5DE ∴==,15510AE AB DE =-=-= ,//,EF AF EF AF ''= ,∴四边形AEFF '为平行四边形,10AE FF '∴==,11622DEF S DF EF DE GF =⋅=⋅= ,解得:125GF =, //DF AC ,,DFM ACM FDM CAM ∴∠=∠∠=∠,DFM ACM ∴ ∽,13DM DF AM AC ∴==,1115344DM AM AB ∴===,//BC AF ' ,同理可证:ANF DNC ' ∽,13AF AN BC DN '∴==,345344DN AN AB ∴===,451530444MN DN DM ∴=-=-=,Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形,故答案为:28.【点睛】本题考查了直角三角形,相似三角形的判定及性质、勾股定理、平行四边形的判定及性质,解题的关键是把问题转化为求梯形的面积.17.(2022·广西)数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为______米.【答案】12【分析】根据同时、同地物高和影长的比不变,构造相似三角形,然后根据相似三角形的性质解答.【详解】解:设旗杆为AB ,如图所示:根据题意得:ABC DEF ∆∆ ,∴DE EF AB BC= ∵2DE =米, 1.2EF =米,7.2BC =米,∴2 1.2=7.2AB 解得:AB =12米.故答案为:12.【点睛】本题考查了中心投影、相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.18.(2022·广东深圳)已知ABC 是直角三角形,90,3,5,B AB BC AE ∠=︒===连接CE 以CE 为底作直角三角形CDE 且,CD DE =F 是AE 边上的一点,连接BD 和,BF BD 且45,FBD ∠=︒则AF 长为______.【分析】将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,利用SAS 证明EDH CDB ∆≅∆,得5EH CB ==,90HED BCD ∠=∠=︒,从而得出////HE DC AB ,则ABF EHF ∆∆∽,即可解决问题.【详解】解:将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,BDH ∴∆是等腰直角三角形,又EDC ∆ 是等腰直角三角形,HD BD ∴=,EDH CDB ∠=∠,ED CD =,()EDH CDB SAS ∴∆≅∆,5EH CB ∴==,90HED BCD ∠=∠=︒,90EDC ∠=︒ ,90ABC ∠=︒,////HE DC AB ∴,,ABF EHF BAF HEF ∴∠=∠∠=∠,ABF EHF ∴∆∆∽,∴==-AB AF AF EH EF AE AF ,AE =∴35=AF ∴=,【点睛】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,解题的关键是作辅助线构造全等三角形.19.(2022·广西河池)如图,把边长为1:2的矩形ABCD 沿长边BC ,AD 的中点E ,F 对折,得到四边形ABEF ,点G ,H 分别在BE ,EF 上,且BG =EH =25BE =2,AG 与BH 交于点O ,N 为AF 的中点,连接ON ,作OM ⊥ON 交AB 于点M ,连接MN ,则tan ∠AMN =_____.【答案】58##0.625【分析】先判断出四边形ABEF 是正方形,进而判断出△ABG ≌△BEH ,得出∠BAG =∠EBH ,进而求出∠AOB =90°,再判断出△AOB ~△ABG ,求出OA OB ==△OBM ~△OAN ,求出BM =1,即可求出答案.【详解】解:∵点E ,F 分别是BC ,AD 的中点,∴11,22AF AD BE BC ==,∵四边形ABCD 是矩形,∴∠A =90°,AD ∥BC ,AD =BC ,∴12AF BE AD ==,∴四边形ABEF 是矩形,由题意知,AD =2AB ,∴AF =AB ,∴矩形ABEF 是正方形,∴AB =BE ,∠ABE =∠BEF =90°,∵BG =EH ,∴△ABG≌△BEH(SAS),∴∠BAG=∠EBH,∴∠BAG+∠ABO=∠EBH+∠ABO=∠ABG=90°,∴∠AOB=90°,∵BG=EH=25BE=2,∴BE=5,∴AF=5,∴AG==∵∠OAB=∠BAG,∠AOB=∠ABG,∴△AOB∽△ABG,∴OA OB ABAB BG AG==,即52OA OB==∴OA OB==∵OM⊥ON,∴∠MON=90°=∠AOB,∴∠BOM=∠AON,∵∠BAG+∠FAG=90°,∠ABO+∠EBH=90°,∠BAG=∠EBH,∴∠OBM=∠OAN,∴△OBM~△OAN,∴OB BM OA AN=,∵点N是AF的中点,∴1522AN AF==,52BM=,解得:BM=1,∴AM=AB-BM=4,∴552tan48ANAMNAM∠===.故答案为:5 8【点睛】此题主要考查了矩形性质,正方形性质和判定,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,求出BM 是解本题的关键.20.(2022·内蒙古赤峰)如图,为了测量校园内旗杆AB 的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点O 处,然后观测者沿着水平直线BO 后退到点D ,这时恰好能在镜子里看到旗杆顶点A ,此时测得观测者观看镜子的俯角α=60°,观测者眼睛与地面距离CD =1.7m ,BD =11m ,则旗杆AB 的高度约为_________m . 1.7≈)【答案】17【分析】如图容易知道CD ⊥BD ,AB ⊥BD ,即∠CDO =∠ABO =90°.由光的反射原理可知∠COD =∠AOB =60°,这样可以得到△COD ∽△AOB ,然后利用对应边成比例就可以求出AB .【详解】解:由题意知∠COD =∠AOB =60°,∠CDE =∠ABE =90°,∵CD =1.7m ,∴OD =60CD tan =︒≈1(m),∴OB =11-1=10(m),∴△COD ∽△AOB .∴CD OD AB OB =,即1.7110AB =,∴AB =17(m),答:旗杆AB 的高度约为17m .故答案为:17.【点睛】本题考查了解直角三角形的应用,相似三角形的应用,本题只要是把实际问题抽象到相似三角形中,利用相似三角形的性质就可以求出结果.21.(2022·湖北鄂州)如图,在边长为6的等边△ABC 中,D 、E 分别为边BC 、AC 上的点,AD 与BE 相交于点P ,若BD =CE =2,则△ABP 的周长为 _____.【答案】6+【分析】如图所示,过点E 作EF ⊥AB 于F ,先解直角三角形求出AF ,EF ,从而求出BF ,利用勾股定理求出BE 的长,证明△ABD ≌△BCE 得到∠BAD =∠CBE ,AD =BE ,再证明△BDP ∽△ADB ,得到62BP PD==,即可求出BP ,PD ,从而求出AP ,由此即可得到答案.【详解】解:如图所示,过点E 作EF ⊥AB 于F ,∵△ABC 是等边三角形,∴AB =BC ,∠ABD =∠BAC =∠BCE =60°,∵CE =BD =2,AB =AC =6,∴AE =4,∴cos 2sin AF AE EAF EF AE EAF =⋅∠==⋅∠=,,∴BF =4,∴BE =又∵BD =CE ,∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,AD =BE ,又∵∠BDP =∠ADB ,∴△BDP ∽△ADB ,∴BD BP DP AD AB BD==,62BP PD==,∴BP PD =∴AP AD AP =-=,∴△ABP 的周长=6AB BP AP ++=故答案为:6+【点睛】本题主要考查了等边三角形的性质,解直角三角形,勾股定理,相似三角形的性质与判定,全等三角形的性质与判定,正确作出辅助线是解题的关键.22.(2022·山东潍坊)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD 的面积为4,以它的对角线的交点为位似中心,作它的位似图形A B C D '''',若:2:1A B AB ='',则四边形A B C D ''''的外接圆的周长为___________.【答案】【分析】根据正方形ABCD 的面积为4,求出2AB =,根据位似比求出4A B ''=,周长即可得出;【详解】解: 正方形ABCD 的面积为4,∴2AB =,:2:1A B AB ''=,∴4A B ''=,∴A C ''==所求周长=;故答案为:.【点睛】本题考查位似图形,涉及知识点:正方形的面积,正方形的对角线,圆的周长,解题关键求出正方形ABCD 的边长.23.(2022·内蒙古包头)如图,在Rt ABC 中,90ACB ∠=︒,3AC BC ==,D 为AB 边上一点,且BD BC =,连接CD ,以点D 为圆心,DC 的长为半径作弧,交BC 于点E (异于点C ),连接DE ,则BE的长为___________.【答案】3##3-+【分析】过点D 作DF ⊥BC 于点F ,根据题意得出DC DE =,根据等腰三角形性质得出CF EF =,根据90ACB ∠=︒,3AC BC ==,得出AB =CF x =,则3BF x =-,证明DF AC ,得出BF BDCF AD=,列出关于x 的方程,解方程得出x 的值,即可得出3BE =.【详解】解:过点D 作DF ⊥BC 于点F ,如图所示:根据作图可知,DC DE =,∵DF ⊥BC ,∴CF EF =,∵90ACB ∠=︒,3AC BC ==,∴AB ===∵3BD BC ==,∴3AD =,设CF x =,则3BF x =-,∵90ACB ∠=︒,∴AC BC ⊥,∵DF BC ⊥,∴DF AC ,∴BF BDCF AD =,即3x x -=,解得:x =,∴226CE x ===-,∴3363BE CE =-=-+=.故答案为:3.【点睛】本题主要考查了等腰三角形的性质和判定,勾股定理,平行线分线段成比例定理,平行线的判定,作出辅助线,根据题意求出CF 的长,是解题的关键.24.(2022·江苏泰州)如图上,Δ,90,8,6,ABC C AC BC ∠=== 中O 为内心,过点O 的直线分别与AC 、AB 相交于D 、E ,若DE=CD+BE ,则线段CD 的长为__________.【答案】2或12##12或2【分析】分析判断出符合题意的DE 的情况,并求解即可;【详解】解:①如图,作//DE BC ,OF BC OG AB ⊥⊥,,连接OB ,则OD ⊥AC ,∵//DE BC ,∴OBF BOE ∠=∠∵O 为ABC ∆的内心,∴OBF OBE ∠=∠,∴BOE OBE ∠=∠∴BE OE =,同理,CD OD =,∴DE=CD+BE ,10AB ===∵O 为ABC ∆的内心,∴OF OD OG CD ===,∴BF BG AD AG==,∴6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=∴2CD =②如图,作DE AB ⊥,由①知,4BE =,6AE =,∵ACB AED CAB EAD ∠=∠∠=∠,∴ABC ADE ∆∆ ∴AB ADAC AE=∴1061582AB AE AD AC ⋅⨯===∴151822CD AC AD =-=-=∵92DE ===∴19422DE BE CD =+=+=∴12CD =故答案为:2或12.【点睛】本题主要考查三角形内心的性质、勾股定理、三角形的相似,根据题意正确分析出符合题意的情况并应用性质定理进行求解是解题的关键.25.(2022·黑龙江绥化)如图,60AOB ∠=︒,点1P 在射线OA 上,且11OP =,过点1P 作11PK OA ⊥交射线OB 于1K ,在射线OA 上截取12PP ,使1211PPPK =;过点2P 作22P K OA ⊥交射线OB 于2K ,在射线OA 上截取23P P ,使2322P P P K =.按照此规律,线段20232023P K 的长为________.20221【分析】解直角三角形分别求得11PK ,22P K ,33P K ,……,探究出规律,利用规律即可解决问题.【详解】解:11PK OA ⊥ ,11OPK ∴△是直角三角形,在11Rt OPK 中,60AOB ∠=︒,11OP =,12111tan 60PP PK OP ∴==⋅︒=11PK OA ⊥ ,22P K OA ⊥,1122PK P K ∴∥,2211OP K OPK ∴△∽△,222111P K OP PK OP ∴=,=221P K ∴,同理可得:2331P K =+,3441P K =,……,11n n n P K -∴=,2022202320231P K ∴=,20221.【点睛】本题考查了图形的规律,解直角三角形,平行线的判定,相似三角形的判定与性质,解题的关键是学会探究规律的方法.26.(2022·黑龙江)如图,在平面直角坐标系中,点1A ,2A ,3A ,4A ……在x 轴上且11OA =,212OA OA =,322OA OA =,432OA OA =……按此规律,过点1A ,2A ,3A ,4A ……作x轴的垂线分别与直线y =交于点1B ,2B ,3B ,4B ……记11OA B ,22OA B △,33 OA B ,44 OA B ……的面积分别为1S ,2S ,3S ,4S ……,则2022S =______.【答案】2【分析】先求出11A B =,可得11OA B S =112233n n A B A B A B A B ⋯⋯∥∥∥∥,从而得到11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,再利用相似三角形的性质,可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231:2:2:2::2n ,即可求解.【详解】解:当x =1时,y =,∴点(1B ,∴11A B =∴11112OA B S =⨯= ,∵根据题意得:112233n n A B A B A B A B ⋯⋯∥∥∥∥,∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S :……∶n n OA B S = OA 12∶OA 22∶OA 32∶……∶OAn 2,∵11OA =,212OA OA =,322OA OA =,432OA OA =,……,∴22OA =,2342OA ==,3482OA ==,……,12n n OA -=,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231246221:2:2:2::21:2:2:2::2n n --= ,∴11222n n n OA B OA B S S -= ,∴220222202222S ⨯-==故答案为:2【点睛】本题主要考查了图形与坐标的规律题,相似三角形的判定和性质,明确题意,准确得到规律,是解题的关键.27.(2022·广西)如图,在正方形ABCD 中,AB =,对角线,AC BD 相交于点O .点E 是对角线AC 上一点,连接BE ,过点E 作EF BE ⊥,分别交,CD BD 于点F 、G ,连接BF ,交AC 于点H ,将EFH △沿EF 翻折,点H 的对应点H '恰好落在BD 上,得到EFH '△若点F 为CD 的中点,则EGH '△的周长是_________.【答案】5+【分析】过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,得到BP =CQ ,从而证得BPE ≌EQF △,得到BE =EF ,再利用BC =F 为中点,求得BF ==BE EF ===,再求出2EO ==,再利用AB //FC ,求出ABH CFH △∽△21AH CH ==,求得216833AH =⨯=,18833CH =⨯=,从而得到EH =AH -AE =1610233-=,再求得EOB GOE △∽△得到21242OG ===,求得EG OG =1, 过点F 作FM ⊥AC 于点M ,作FN ⊥OD 于点N ,求得FM =2,MH =23,FN =2,证得Rt FH N '△≌Rt FMH 得到23H N MH '==,从而得到ON =2,NG =1,25133GH '=+=,从而得到答案.【详解】解:过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,∵AD //PQ ,∴AP =DQ ,BPQ CQE ∠=∠,∴BP =CQ ,∵45ACD ∠=︒,∴BP =CQ =EQ ,∵EF ⊥BE ,∴90PEB FEQ ∠+∠=︒∵90PBE PEB ∠+∠=︒∴PBE FEQ ∠=∠,在BPE 与EQF △中BPQ FQE PB EQPBE FEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BPE ≌EQF △,∴BE =EF ,又∵BC AB ==F 为中点,∴CF =∴BF ==∴BE EF ===,又∵4BO ==,∴2EO ==,∴AE =AO -EO =4-2=2,∵AB //FC ,∴ABH CFH △∽△,∴AB AH CF CH=,21AH CH ==,∵8AC ==, ∴216833AH =⨯=,18833CH =⨯=,∴EH =AH -AE =1610233-=,∵90BEO FEO ∠+∠=︒,+90BEO EBO ∠∠=︒,∴FEO EBO ∠=∠,又∵90EOB EOG ∠=∠=︒,∴EOB GOE△∽△∴EG OG OE BE OE OB==,21242OG ===,∴EG OG =1,过点F 作FM ⊥AC 于点M ,∴FM=MC 2=,∴MH =CH -MC =82233-=, 作FN ⊥OD 于点N ,2,FN ==,在Rt FH N '△与Rt FMH 中FH FH FN FM'=⎧⎨=⎩∴Rt FH N '△≌Rt FHM∴23H N MH '==,∴ON =2,NG =1,∴25133GH '=+=,∴10533EGH C EH EG GH EH EG GH '''=++=++=△,故答案为:【点睛】本题考查了正方形的性质应用,重点是与三角形相似和三角形全等的结合,熟练掌握做辅助线是解题的关键.28.(2022·辽宁)如图,在正方形ABCD 中,E 为AD 的中点,连接BE 交AC 于点F .若6AB =,则AEF 的面积为___________.【答案】3【分析】由正方形的性质可知1113222AE AD AB BC ====,//AD BC ,则有AEF CBF ∽△△,然后可得12EF AE BF BC ==,进而问题可求解.【详解】解:∵四边形ABCD 是正方形,6AB =,∴6AD BC AB ===,//AD BC ,∴AEF CBF ∽△△,∴EF AE BF BC=,∵E 为AD 的中点,∴1113222AE AD AB BC ====,∴12EF AE BF BC ==,192ABE S AE AB =⋅= ,∴13EF BE =,∴133AEF ABE S S == ;故答案为3.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.29.(2022·贵州贵阳)如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,6cm AC BC ==,90ACB ADB ∠=∠=︒.若2BE AD =,则ABE △的面积是_______2cm ,AEB ∠=_______度.【答案】 36-36- 112.5【分析】通过证明ADE BCE ,利用相似三角形的性质求出23m AE =,263m CE =-,再利用勾股定理求出其长度,即可求三角形ABE 的面积,过点E 作EF ⊥AB ,垂足为F ,证明AEF 是等腰直角三角形,再求出AE CE =,继而证明()Rt BCE Rt BFE HL ≅ ,可知122.52EBF EBC ABC ∠=∠=∠=︒,利用外角的性质即可求解.【详解】90,ACB ADB AED BEC ∠=∠=︒∠=∠ ,ADE BCE ∴ ,AD AE BC BE∴=,6,2BC AC BE AD === ,设,2AD m BE m ==,62m AE m∴=,23m AE ∴=,263m CE ∴=-,在Rt BCE 中,由勾股定理得222BC CE BE +=,22226(6)(2)2m m ∴+-=,解得236m =-或236m =+ 对角线AC ,BD 相交于点E ,236m ∴=-,12AE ∴=-,6CE ∴=,∴(2111263622ABE S AE BC =⋅⋅=⨯-⨯=- ,过点E 作EF ⊥AB ,垂足为F ,90,ACB AC BC ∠=︒= ,45BAC ABC AEF ∴∠=∠=︒=∠,6AE AF AE CE ∴====,BE BE = ,()Rt BCE Rt BFE HL ∴≅ ,122.52EBF EBC ABC ∴∠=∠=∠=︒,112.5AEB ACB EBC ∴∠=∠+∠=︒,故答案为:36-,112.5.【点睛】本题考查了相似三角形的判定和性质,勾股定理,等腰直角三角形的判定和性质,全等三角形的判定和性质及三角形外角的性质,熟练掌握知识点是解题的关键.三.解答题30.(2022·河北)如图,某水渠的横断面是以AB 为直径的半圆O ,其中水面截线MN AB ∥.嘉琪在A 处测得垂直站立于B 处的爸爸头顶C 的仰角为14°,点M 的俯角为7°.已知爸爸的身高为1.7m .(1)求∠C 的大小及AB 的长;(2)请在图中画出线段DH ,用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据:tan 76︒取4 4.1)【答案】(1)=76C ∠︒, 6.8(m)AB =(2)见详解,约6.0米【分析】(1)由水面截线MN AB ∥可得BC AB ⊥,从而可求得76C ∠=︒,利用锐角三角形的正切值即可求解.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,水面截线MN AB ∥,即可得DH 即为所求,由圆周角定理可得14BOM ∠=︒,进而可得ABC OGM ,利用相似三角形的性质可得4OG GM =,利用勾股定理即可求得GM 的值,从而可求解.(1)解:∵水面截线MN AB∥BC AB ∴⊥,90ABC ∴∠=︒,90=76C CAB ∴∠=︒-∠︒,在t R ABC 中,90ABC ∠=︒, 1.7BC =,tan 76 1.7AB AB BC ∴︒==,解得 6.8(m)AB ≈.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,如图所示:水面截线MN AB ∥,OH AB ⊥,DH MN ∴⊥,GM OD =,DH ∴为最大水深,7BAM ∠=︒ ,214BOM BAM ∴∠=∠=︒,90ABC OGM ∠=∠=︒ ,且14BAC ∠=︒,ABC OGM ∴ ,OG MG AB CB ∴=,即6.8 1.7OG MG =,即4OG GM =,在Rt OGM △中,90OGM ∠=︒, 3.42AB OM =≈,222OG GM OM ∴+=,即2224(3.4)GM GM +=(),解得0.8GM ≈,= 6.80.86DH OH OD ∴-=-≈,∴最大水深约为6.0米.【点睛】本题考查了解直角三角形,主要考查了锐角三角函数的正切值、圆周角定理、相似三角形的判定及性质、平行线的性质和勾股定理,熟练掌握解直角三角形的相关知识是解题的关键.31.(2022·吉林)下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC S BC h =⋅ ,12DBC S BC h =⋅△.∴ABC DBC S S = .【探究】(1)如图②,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ',则ABC DBC S h S h ='△△.证明:∵ABC S(2)如图③,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM =△△.证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,∴AE ∥ .∴AEM △∽ .∴AE AM DF DM =.由【探究】(1)可知ABC DBC S S =△△ ,∴ABC DBC S AM S DM =△△.(3)如图④,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBC S S △△的值为 .【答案】(1)证明见解析(2)证明见解析(3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅ ,由此即可得证;(2)过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,先根据平行线的判定可得AE DF ,再根据相似三角形的判定可证AEM DFM ~ ,根据相似三角形的性质可得AE AM DF DM=,然后结合【探究】(1)的结论即可得证;(3)过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,先根据相似三角形的判定证出AME DNE ~ ,再根据相似三角形的性质可得73AM AE DN DE ==,然后根据三角形的面积公式可得12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,由此即可得出答案.(1)证明:12ABC S BC h =⋅ ,12DBC BC h S '=⋅ ,ABC DBC S h S h ∴='.(2)证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,AE DF ∴∥.AEM DFM ~∴ .AE AM DF DM∴=.由【探究】(1)可知ABC DBC S AE S DF= ,ABC DBC S AM S DM ∴= .(3)解:过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,则90AME DNE ∠=∠=︒,AM DN ∴ ,AME DNE ∴~ ,AM AE DN DE∴=, 点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE ∴=-=, 1.5DE =,3.571.53AM DN ∴==,又12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,73ABCDBC S AM S DN =∴= ,故答案为:73.【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.32.(2022·山东青岛)如图,在Rt ABC △中,90,5cm,3cm ACB AB BC ∠=︒==,将ABC 绕点A 按逆时针方向旋转90︒得到ADE ,连接CD .点P 从点B 出发,沿BA 方向匀速运动,速度为1cm/s ;同时,点Q 从点A 出发,沿AD 方向匀速运动,速度为1cm/s .PQ 交AC 于点F ,连接,CP EQ .设运动时间为(s)(05)t t <<.解答下列问题:(1)当EQ AD ⊥时,求t 的值;(2)设四边形PCDQ 的面积为()2cm S ,求S 与t 之间的函数关系式;(3)是否存在某一时刻t ,使PQ CD ∥?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)16s 5(2)213714210S t t =-+(3)存在,65s 29t =【分析】(1)利用AQE AED △∽△得AQ AE AE AD =,即445t =,进而求解;(2)分别过点C ,P 作,CM AD PN BC ⊥⊥,垂足分别为M ,N ,证ABC CAM △∽△得,AB BC AC CA AM CM ==,求得121655AM CM ==,再证BPN BAC △∽△得BP PN BA AC=,得出45PN t =,根据ABC ACD APQ BPC PCDQ S S S S S S ==+-- 四边形即可求出表达式;(3)当PQ CD ∥时AQP ADC ∠=∠,易证APQ MCD △∽△,得出AP AQ MC MD =,则5161355t t -=,进而求出t 值.(1)解:在Rt ABC △中,由勾股定理得,4AC ===∵ABC 绕点A 按逆时针方向旋转90︒得到ADE。
相似三角形中考复习(知识点+题型分类练习)

相似三角形一、知识概述1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
3.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形.4.相似三角形的基本性质①相似三角形的对应边成比例、对应角相等.②相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示:①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例.②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC的相似比,当且仅当它们全等时,才有k=k′=1.③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出.5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。
温馨提示:(1)判定三角形相似的几条思路:①条件中若有平行,可采用判定定理1;②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例;③条件中若有两边对应成比例,可找夹角相等;但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等.④条件中若有等腰关系,可找顶角相等或底角相等,也可找腰和底对应成比例。
(2)在综合题中,注意相似知识的灵活运用,并熟练掌握线段代换、等比代换、等量代换技巧的应用,培养综合运用知识的能力。
(3)运用相似的知识解决一些实际问题,要能够在理解题意的基础上,把它转化为纯数学知识的问题,要注意培养当数学建模的思想。
相似三角形中考考点归纳与典型例题

相似三角形中考考点归纳与典型例题相似三角形是初中数学中常出现的重要概念,它是几何学中研究两个三角形之间形状关系的一个重要内容。
掌握相似三角形的性质和应用是解决几何问题的基础。
相似三角形的重要性质:1. 定义:如果两个三角形的对应角相等,对应边成比例,则它们是相似三角形。
记作ΔABC ~ ΔDEF。
其中A、B、C是ΔABC的顶点,D、E、F是ΔDEF的顶点。
2. 判定定理:(1) AA相似定理:如果两个三角形的两个对应角相等,则它们是相似的。
(2) AAA相似定理:如果两个三角形的三个对应角相等,则它们是相似的。
3. 边比例关系:相似三角形的对应边成比例。
即对于ΔABC ~ΔDEF,有AB/DE = BC/EF = AC/DF。
4. 高比例关系:相似三角形的高线成比例。
即对于ΔABC ~ΔDEF,有h1/h2 = AB/DE = BC/EF = AC/DF。
5. 相似三角形的性质:(1) 对应角相等,即∠A = ∠D,∠B = ∠E,∠C = ∠F。
(2) 对应边成比例,即AB/DE = BC/EF = AC/DF。
(3) 相似三角形的顶角相等,边比例相等,它们的面积比例也相等。
(4) 相似三角形的高线间成比例。
相似三角形的典型例题:例题1:如图,在直角三角形ABC中,∠B = 90°,BM是AC的中线,求比值AB/BC。
解:由与直角三角形的垂直关系可知∠A = ∠CBM,∠C = ∠ABM。
所以∠ABC ~ ∠CBM。
根据相似三角形的性质可得AB/BC = CB/BM = 2/1,即AB/BC = 2。
例题2:如图,上底AE = 4cm,下底BC = 8cm,连结CD,且CD = AE,点F是AE的中点,连接BF,求比值∠AFB/∠ACD。
解:由AE = CD可得∠A = ∠C。
又由BF = FE可得∠B = ∠AFE。
所以∠AFB ~ ∠ACD。
根据相似三角形的性质可得∠AFB/∠ACD = AB/AD= BC/CD = 2。
初三数学相似三角形的性质与判定知识精讲
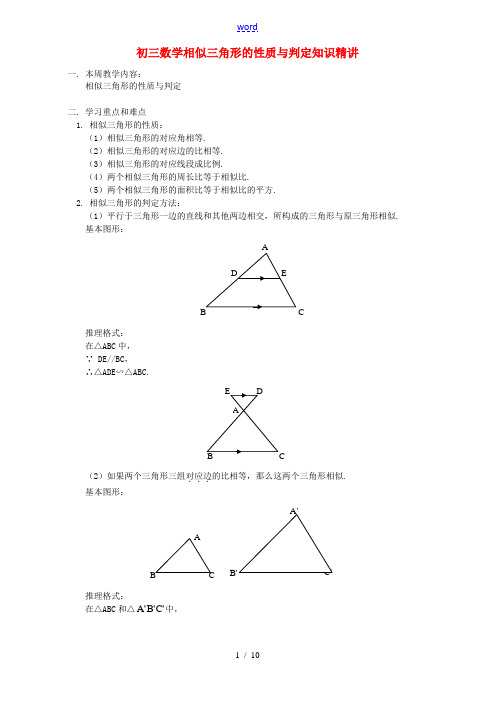
初三数学相似三角形的性质与判定知识精讲一. 本周教学内容:相似三角形的性质与判定二. 学习重点和难点1. 相似三角形的性质:(1)相似三角形的对应角相等.(2)相似三角形的对应边的比相等.(3)相似三角形的对应线段成比例.(4)两个相似三角形的周长比等于相似比.(5)两个相似三角形的面积比等于相似比的平方.2. 相似三角形的判定方法:(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.基本图形:C推理格式:在△ABC中,∵ DE//BC,∴△ADE∽△ABC.(2)如果两个三角形三组对应边...的比相等,那么这两个三角形相似. 基本图形:B推理格式:在△ABC和△'C'B'A中,'A 'C CA 'C 'B BC 'B 'A AB ==, ∴△ABC ∽△'C 'B 'A .(3)如果两个三角形的两组对应边...的比相等,并且相应的夹角相等,那么这两个三角形相似.基本图形:B推理格式:在△ABC 和△'C 'B 'A 中,'C 'A AC 'B 'A AB =,∠A=∠'A ABC ∆∴∽△'C 'B 'A . (4)如果一个三角形的两个角与另一个三角形的两个角对应..相等,那么这两个三角形相似. 基本图形:B推理格式:在△ABC 和△'C 'B 'A 中,∵∠A=∠'A ,∠B=∠'B ,∴△ABC ∽△'C 'B 'A .三. 我们的目标:通过学习进一步理解相似三角形的性质与判定,熟练掌握相似三角形的性质与判定定理的应用.例1. 如图,BC ⊥AF ,FD ⊥AB ,垂足分别为C 、D ,那么图中有_________对相似三角形.FCEA D B分析:观察图形,我们可以发现,图中有4个∆Rt ,它们是ADF R t ABC R t ∆∆,,E DB Rt ∆,CFE Rt ∆.这四个∆Rt 每两个之间都相似,所以一共有6对三角形相似.△ABC ∽△EBD ,△ABC ∽△AFD ,△ABC ∽△EFC△AFD ∽△EBD ,△AFD ∽△EFC ,△BED ∽△FEC答:6对注意:在复杂图形中辨认相似三角形时,要着重抓住图形的特征.如本题重在找相等的角,然后再判定.例2. 如图,∠ADE=∠B ,则)()()()(AC AE ==.B C分析:∵∠ADE=∠B ,∠A=∠A∴△ADE ∽△ABCABAD BC DE AC AE ==∴ 注意:首先要判断△ADE ∽△ABC ,然后正确找出对应边.例3. 如图,已知DE//BC ,DF 与AC 交于G ,则图中的相似三角形有:△__________∽△__________,△__________∽△__________.答案:△ADE △ABC ,△DEG △FCG. 注意:要抓住DE//BC 的条件,利用基本图形进行判定.例4. 如图,AD=DF=FB ,DE//FG//BC ,则=321S :S :S __________.AD EF GB C 1 2 3答案:1:3:5分析:∵DE//FG//BC ,∴△ADE ∽△AFG ∽△ABC又∵AD=DF=FB∴AD :AF :AB=1:2:3.4121S S 2AFG 1=⎪⎭⎫ ⎝⎛=∴∆ 3:1S :S 21=∴9432S S 2ABC AFG =⎪⎭⎫ ⎝⎛=∴∆∆ 53S S 32=∴ 5:3:1S :S :S 321=∴注意:要抓住AD=DF=FB ,DE//FG//BC 的条件,利用基本图形进行判定三角形相似,然后利用性质解题.例5. 如图,△ABC 中,D 为AC 上一点,CD=2DA ,∠BAC=45°,∠BDC=60°,CE ⊥BD 于E ,连结AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形,若有请写出来,并说明理由;若没有请说明理由.(3)求△BEC 与△BEA 的面积比.BEC D A解:(1)DE=DA ,EC=EA=EB.证明: ∵∠DEC=90°,∠BDC=60°,∴∠DCE=30°.DA CD 21DE ==∴,即DE=DA. ∴∠DEA=∠DAE.又∵∠EDC=∠DEA+∠DAE=60°,∴∠DAE=∠DEA=30°.又∵∠BAC=45°,∴∠EAB=∠BAC -∠DAE=15°.又∠DEA=∠EAB+∠EBA ,∴∠EBA=∠DEA -∠EAB=15°.∴∠EBA=∠EAB.∴EA=EB.∵∠DCE=∠DAE=30°,∴EC=EA.∴EC=EA=EB.(2)①△ADE ∽△CEA ,或②△BCD ∽△ACB① 理由:△ADE ,△CEA 均为底角为30°的等腰△,∴△ADE ∽△CEA.② 理由:∵∠CBD=∠CAB=45°,∠CDB=∠ABC=60°,∴△BCD ∽△ACB.(3)过点A 作AF ⊥BD ,交BD 延长线于点F ,则∠AFD=∠CED=90°.又∠ADF=∠CDE ,∴△CED ∽△AFD.2ADAD 2AD CD AF CE ===∴, 2AF CE AF BE 21CE BE 21S S BEA BEC ==⋅⋅=∴∆∆. 即2S S BEA BEC =∆∆.(答题时间:60分钟)一、选一选1. 下列四条线段成比例的是( )A. 2,3,2,3B. 3,2,6,4C. 4,5,6,10D. 12,8,11,162. 用一个3倍放大镜照一个△ABC ,下列说法正确的是( )A. △ABC 放大后,∠A 是原来的3倍B. △ABC 放大后,周长是原来的3倍C. △ABC 放大后,面积是原来的3倍D. 以上答案都不正确3. 若23b a =,则ba b +等于( ) A. 3:2 B. 2:3 C. 2:5 D. 5:24. 下列两个三角形不一定相似的是( )A. 两个等边三角形B. 两个全等三角形C. 两个直角三角形D. 有一个角是120°的两个等腰三角形5. 如图所示,下列各式能使△ACB ∽△DCA 的是( )A. AB AC BDCD = B.CD AC AC CB = C. BC AC AB AD = D. AB AD AD AC =6. 过三角形一边上一点画直线与另一边相交,且截得的三角形与原三角形相似,那么最多可画这样的直线的条数是( )A. 1条B. 2条C. 3条D. 4条7. 如图所示,已知EF//BC ,△AEF 和梯形EBCF 的面积分别为18,80。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B C
初三数学期末复习
相似三角形及应用
一、比例的基本性质,线段的比、成比例线段,黄金分割.
(1)比例的基本性质:b a =d
c ⇔ad=bc (b
d ≠0) 1、甲、乙两地的实际距离20千米,则在比例尺为 1∶1000000 的地图上两地间的距离应为 厘米.
2、若3a =5b ,则a b
= . 3、若线段a 、b 、c 、d 成比例且a =3cm ,b =6cm ,c =5cm ,则d = cm .
二、两个三角形相似的条件.常用基本图形——A 形、X 形……
例1、已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB 、CD 交于O 点,对于各图中的两个的两个三角形而言,下列说法正确的是( )
A.都相似
B.都不相似
C.只有(1)相似
D.只有(2)相似
2、如图, 小正方形的边长均为1, 则下列图中的三角形(阴影部分)与△ABC 相似的是( )
三、相似三角形的概念、性质:相似多边形的对应角相等,对应边成比例,面积比等于对应边
比的平方.
例题1.△ABC 的三条边的长分别为3、4、5,与△ABC 相似的△A′B′C′的最长边为15.
求△ A′B′C′最短边的长.
变化:△ABC 的三条边的长分别为3、4、5,与△ABC 相似的△A′B′C′的一边长为15.
求△ A′B′C′的周长.
4、如图,在梯形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O , 若1AD =,3BC =,则AO CO 的值为
(1) A B C D O 4 3 6 8 (2)
5、如图,□ ABCD 中,E 为DC 边的中点,AE 交BD 于O ,若DO =4cm ,BO = cm .
6、如图所示,在△ABC 中,∠C=90°,AC=3,D 为BC 上一点,过点D 作DE ⊥BC 交AB 于E ,若ED=1,BD=2,则DC 的长为________.
7、如图所示,在△ABC 中,∠C=90°,AC=3,D 为BC 上一点,过点D 作
DE ⊥AB 于E ,若ED=1,BD=2,则DC 的长为________.
8、如图,△ABC 中,DE ∥BC ,DE 分别交边AB 、AC 于D 、E 两点,若AD :AB =1:3,则△ADE
与△ABC 的面积比为 .
9、如图,DE 是△ABC 的中位线,S △ADE =2,则S △ABC =_______.
10、如图所示,已知点E F 、分别是ABC △中AC AB 、边的中点,BE CF 、相交于点G ,
2FG =,则CF =_______.
11、如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B 重合,
折痕为DE ,则S △BCE :S △BDE 等于( )
A . 2:5
B .14:25
C .16:25
D . 4:21
12、如图,△ABC,是一张锐角三角形的硬纸片,AD 是边BC 上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ,使它的一边EF 在BC 上,顶点G 、H 分别在AC ,AB 上,AD 与HG 的交点为M.
(1)、求证:;AM HG AD BC
= (2)、求这个矩形EFGH 的周长.
A D E C B
O A F E C B
日日清
1、若
312=-n n m ,则=n
m . 2、已知三个数1,2,3,请你再添上一个数,使它们能构成一个比例式,则这个数是________. 3、已知,线段AB =15,点C在AB 上,且AC ∶BC =3∶2,则BC = .
4、在同一时刻物高与影长成比例,小华量得综合楼的影长为 6 米,同一时刻她量得身高 1.6米的同学的影长为 0.6 米,则可知综合楼高为 .
5、如图,D 是△ABC 的边AB 上的点,请你添加一个条件,使△ACD 与△ABC 相似.你添加的条件是_____ .
6、在△ABC 中,AB=12,AC=10,BC=9,AD 是BC 边上的高.将△ABC
按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为( )
A .9.5
B .10.5
C .11
D .15.5
7、如图,△ABC 中,∠B=90°,AB=6,BC=8,将△ABC 沿DE 折叠,使点C 落在AB •边上的C′处,并且C′D ∥BC ,则CD 的长是( )
A .40
50
15
25 (9944)
B C D
8、如图,在6×8网格图中,每个小正方形边长均为1,点O 和△ABC 的顶点均在小正方形的顶点.
(1)以O 为位似中心,在网格图中作△A ′B ′C ′和△ABC 位似,且位似比为1︰2;
(2)连接(1)中的AA ′,求四边形AA ′C ′C 的周长.(结果保留根号)
9、为了测量水塘边A 、B 两点之间的距离,在可以看到A 、B 的E 处,取AE 、BE 延长线上的C 、D 两点,使CD ∥AB ,如果测量得CD =5米,AD =15米,ED =3米,你能求出AB
两点之间的距离吗?
第6题 第7题
10、如图5,点P 在平行四边形ABCD 的CD 边上,连结BP 并延长与 AD 的延长线交于点Q .
(1)求证:△DQP ∽△CBP ;
(2)当△DQP ≌△CBP ,且AB=8时,求DP 的长.
11、如图,D 是 △ABC 的边AB 上一点,连结CD .若AD = 2,BD = 4, ∠ACD =∠B 。
求AC 的长.
12、.在△ABC 中,AB=3,AC=4,BC=5,现将它折叠,使B 点与C 点重合,如图,则折痕DE 的长是多少?
图5
P Q D C B
A
B A。
