9.6 热力学第二定律的统计意义 玻尔兹曼熵
第八节热力学第二定律的统计意义和熵的概念

Ω2 = (nV2 /V1 ) N = (V2 ) N
Ω1
n
V1
∴ ∆S = K ln Ω2 = NK ln V2 = υR ln V2
V1
注意:
Ω1
V1
V1
1)熵是状态函数,初末态定,熵定,与过程无关.
2)讨论是针对孤立系统.
若要: ∆S → 0 则 V2 >V1 故方向小→大
4. 开放系统:
熵的改变来自: 熵的产生: dSi 系统内部的不可逆过程引起熵的增加. 熵 流: dSe与外界交换中流入系统的熵(可能有负熵).
S : 熵, (单位 J/K) ; K: 波耳兹曼常数 ; Ω: 微观态数.
2. 熵增: 孤立系统中的一切实际过程都是熵的增加过程.
原理:
d S >0
从状态 1Æ 状态2 熵增为
∆S2 = S2 − S1 = K ln Ω2 − K ln Ω1 = K 若孤立系统进行的是可逆过程,则熵相等.
ln
Ω2 Ω1
dS = dSi + dSe
(三) 熵的宏观表示
熵与过程无关,设计一可逆等温过程, 是气体有状态(T,V1)Æ(T,V2).
可逆等温过程: QT
与(1)式比较: ∆S =
= υRT ln
υRlnV2
V2 V1
V1
∴∆S =QT /T
对无限小过程:(可逆等温)dS = dQ / T
d Q是无限小可逆过程,从外界吸收的热量. T 是系统的温度.
第八节 热力学第二定律的统计意义
和熵的概念
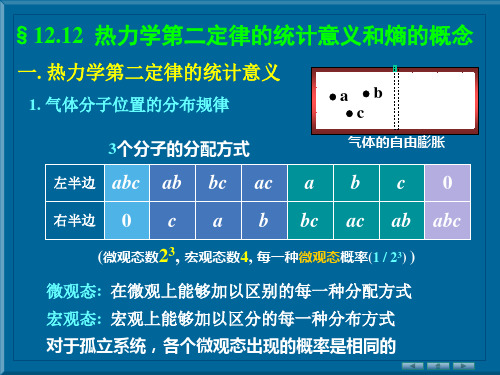
(一) 热二定律的统计意义 (微观态 宏观态)
. VA=VB 任一分子在热运动中出现于A或B的机会相等, 出现 的概率都是1/2. N个分子在A和B中共有2N种分配方式, 而每种分配方式出现的概率都是1/2N .
热力学中的熵与热力学第二定律

热力学中的熵与热力学第二定律熵是热力学中一个非常重要的概念,它与热力学第二定律密切相关。
本文将介绍熵的概念以及它在热力学中的应用,同时探讨熵与热力学第二定律的关系。
一、熵的概念熵是热力学中描述系统无序程度的物理量。
熵的增加代表了系统的无序程度增加。
根据能量守恒定律,一个孤立系统的能量是守恒的,那么系统的状态必然朝着熵增的方向演化。
热力学第二定律正是描述了这一演化趋势,即在孤立系统中,熵总是不减的。
二、熵的公式熵的计算公式为:S = k ln Ω其中,S表示熵,k为玻尔兹曼常数,Ω为系统的微观状态数。
这个公式告诉我们,熵与系统的微观状态数成正比。
微观状态数越多,系统的熵越大,也就代表了系统的无序程度越高。
三、熵的应用熵在热力学中具有广泛的应用。
例如在化学反应中,可以通过计算反应前后的熵变来判断反应的进行方向。
若反应前的熵较大,反应后的熵较小,那么反应是自发进行的。
另外,在热力学研究中,熵也经常用于描述物质的相变过程以及平衡态的性质。
四、熵与热力学第二定律熵与热力学第二定律密不可分。
热力学第二定律规定了自然界中的过程必须遵循的规律,即孤立系统的熵不减。
热力学第二定律的一个重要表述是熵增原理,即孤立系统的熵趋向于最大值。
这意味着熵对自发过程的方向性起着决定性的作用。
通过熵的概念和热力学第二定律,我们可以更好地理解自然界中广泛存在的一些现象。
例如,为什么热量总是从高温物体传递到低温物体?这是因为热传导过程中,系统的熵增加,使得整个系统达到更高的无序状态。
总之,熵是热力学中一个重要的概念,它描述了系统的无序程度。
熵与热力学第二定律密切相关,它帮助我们理解自然界中的各种现象。
更深入地理解熵的概念和研究其应用,对于热力学及相关领域的科学研究具有重要意义。
热力学第二定律的统计解释
负熵 S k ln 1 1 WW
有序度
生命科学: 熵的高低反映生命力的强弱.
信息论: 负熵是信息量多寡的量度.
环境学: 负熵流与环境.
玻尔兹曼墓碑
为了纪念玻尔 兹曼给予熵以统计 解释的卓越贡献 , 他的墓碑上寓意隽 永地刻着 .
S k logW
这表示人们对玻尔 兹曼的深深怀念和 尊敬.
耗散结构
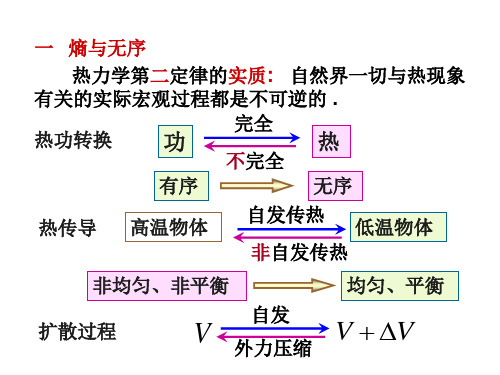
一 熵与无序
热力学第二定律的实质: 自然界一切与热现象
有关的实际宏观过程都是不可逆的 .
完全
热功转换
功
热
不完全
有序
无序
热传导 高温物体
自发传热 低温物体 非自发传热
非均匀、非平衡
均匀、平衡
扩散过程
自发
V 外力压缩 V V
二 无序度和微观状态数
不可逆过程的本质
系统从热力学概率小的状态向热力学概率大的 状态进行的过程 .
1)宇宙真的正在走向死亡吗? 实际宇宙万物,宇宙发展充满了无序到有序的发 展变化 . 2) 生命过程的自组织现象 生物体的生长和物种进化是从无序到有序的发展.
3) 无生命世界的自组织现象 云、雪花、太阳系、化学实验、热对流、激光等.
4)开放系统的熵变
(和外界有能量交换和物质交换的系统叫开放系 统)
开放系统熵的变化 dS dSe dSi
dSe
系统与外界交换能量或物质而引起的熵流
dSi
系统内部不可逆过程所产生的熵增加
孤立系统 dSi 0, dS 0
开放系统 dSi 0, dSe 0
dSi dSe , dS 0
n3 4
W
1 16
1 24
n5 1 粒子均匀分布的概率 W ' 6 3
统计力学中的熵与热力学第二定律

统计力学中的熵与热力学第二定律在热力学中,熵是一个重要的概念,它与物质的无序程度有关。
而统计力学则通过分子运动的统计规律来解释热力学现象。
本文将分享关于统计力学中熵和热力学第二定律的一些基本概念和应用。
一、熵的概念在统计力学中,熵(Entropy)描述了一个物理系统的无序程度。
熵越高,系统越混乱无序;熵越低,系统越有序。
熵的概念最早由热力学第二定律引入,并在统计力学中得到解释。
在经典统计力学中,一个系统的熵可以通过统计物理量的平均数来计算。
对于离散的微观状态,在给定状态下,每个可能的微观排列有相应的概率,而熵就是这些概率的对数的加权平均值。
对于连续的微观状态,在计算熵时需要进行积分运算。
在系统平衡时,其熵取得最大值。
熵在自发过程中不断增加,这是热力学第二定律的具体表现。
二、热力学第二定律热力学第二定律是描述自然界中热现象的规律,它为热力学系统带来了时间箭头。
热力学第二定律有多种表述方式,其中最著名的是卡诺热机效率表述和熵增定律表述。
卡诺热机效率表述指出,在所有工作在相同高温和低温热库之间的热机中,卡诺热机的效率最高。
卡诺热机效率可以表示为等温过程所提供的热量与等温过程所吸收的热量之比,即η=1-Tc/Th,其中η为效率,Tc为低温热库的温度,Th为高温热库的温度。
熵增定律是热力学第二定律的另一种表述方式,它指出孤立系统的熵在自发过程中不会减小,只会增加或保持不变。
对于自发过程,系统始态的熵小于末态的熵。
三、熵与统计力学统计力学的出发点是分子运动的统计规律,它可以通过统计大量微观粒子的行为来预测宏观系统的行为。
在统计力学中,熵可以通过统计微观粒子的分布来计算。
根据玻尔兹曼熵公式S = k lnΩ,其中S为熵,k为玻尔兹曼常数,Ω为微观状态的数目。
这个公式表明,系统的熵与系统的微观状态数目成正比。
统计力学通过概率和微观状态的统计平均来计算熵。
通过计算各个可能微观状态的熵的期望值,我们可以得到系统的平均熵。
热力学第二定律和熵的概念

热力学第二定律和熵的概念热力学是研究能量转换和传递的科学,其第二定律是热力学基础理论之一。
另一重要概念是熵,也是热力学的核心概念之一。
本文将介绍热力学第二定律和熵的概念,以及它们在热力学中的重要性。
一、热力学第二定律的概念热力学第二定律给出了自然界中一种不可逆过程的方向性。
简单来说,热力学第二定律即“自发的过程总是朝着熵增加的方向进行”。
这是一个统计平均性质的表述,具体来说,熵的定义可以理解为系统的无序程度。
二、熵的概念及其特性熵是描述系统无序度的物理量,也是热力学的核心概念之一。
熵的数学定义为S = k ln W,其中k是玻尔兹曼常数,W是系统的微观状态数。
熵具有以下特性:1. 熵与无序度正相关:系统的熵越大,其无序度越高。
例如,一个均匀分布的气体比起聚集在一个小区域的气体熵要更大,因为前者的无序度更高。
2. 熵的增加:热力学第二定律表明,自发的过程使得系统熵增加。
换言之,自然界中的过程总是趋向于无序化,即系统的熵增加。
3. 熵的守恒:在封闭系统中,熵守恒。
即系统熵的变化是由于与外界交换能量而引起的。
三、热力学第二定律和熵的重要性热力学第二定律和熵的概念在热力学中具有重要的意义和应用。
以下是其重要性的几个方面:1. 描述自然界不可逆过程:熵的增加是自发性过程的一个普遍规律,在自然界中广泛存在。
熵的概念使得我们能够描述自然现象和过程中无序度的变化。
2. 热机效率的限制:热力学第二定律揭示了热机的效率上限,即卡诺循环效率。
根据热力学第二定律,任何一个热机的效率都不可能达到100%,存在一定的损耗。
3. 熵增原理在自然界的应用:熵增原理在环境科学、生态学和化学工程等领域都有着广泛应用。
例如,探讨系统的可持续发展、环境污染治理等。
4. 热力学第二定律在工程和技术中的应用:热力学第二定律在能源转换、燃烧动力学、制冷技术等工程和技术领域中有重要应用。
例如,协助设计高效能源系统和提高资源利用率。
总结:热力学第二定律和熵的概念是热力学的核心内容之一。
热力学第二定律的本质和熵的统计意义

微观状态数的总和
例如:有4个不同颜色的小球a,b,c,d分
装在两个盒子中,总的分装方式应该有16种。 因为这是一个组合问题,有如下几种分配
方式,其热力学概率是不等的。
分配方式
分配微观状态数
(4, 0) C44 1 (3,1) C43 4 (2, 2) C42 6 (1,3) C41 4 (0, 4) C40 1
热力学第二定律的本质和熵的统计意义
热力学第二定律的本质
热与功转换的不可逆性 热是分子混乱运动的一种表现,而功是分子 有序运动的结果。 功转变成热是从规则运动转化为不规则运动, 混乱度增加,是自发的过程; 而要将无序运动的热转化为有序运动的功就 不可能自动发生。
热力学第二定律的本质 气体混合过程的不可逆性 将N2和O2放在一盒内隔板的两边,抽去隔板, N2和O2自动混合,直至平衡。 这是混乱度增加的过程,也是熵增加的过程, 是自发的过程,其逆过程决不会自动发生。
热力学第二定律的本质
热传导过程的不可逆性
处于高温时的系统,分布在高能级上的分子 数较中;
而处于低温时的系统,分子较多地集中在低 能级上。
当热从高温物体传入低温物体时,两物体各 能级上分布的分子数都将改变,总的分子分布的 花样数增加,是一个自发过程,而逆过程不可能 自动发生。
热力学第二定律的本质
从以上几个不可逆过程的例子可以看出:
一切不可逆过程都是向混乱度增加的方向进行, 而熵函数可以作为系统混乱度的一种量度,
这就是热力学第二定律所阐明的不可逆过程 的本质。
熵和热力学概率的关系——Boltzmann公式
热力学概率就是实现某种宏观状态的微观状
态数,通常用 表示。
数学概率是热力学概率与总的微观状态数之比。
热力学第二定律和熵增原理

热力学第二定律和熵增原理热力学第二定律是热力学基本原理之一,它与熵增原理密切相关。
本文将探讨热力学第二定律和熵增原理的概念、推导以及应用。
一、热力学第二定律的概念热力学第二定律是指在孤立系统中,热量不会自发地从低温物体传递到高温物体。
换句话说,热力学第二定律描述了一个自然过程的不可逆性,即熵的增加。
二、熵的概念熵是描述系统无序程度的物理量,也可以理解为能量在转化过程中的损失。
熵增原理是基于熵的概念的,它指出自然界中孤立系统的熵总是趋向于增加。
三、熵增原理的推导熵增原理可以通过玻尔兹曼公式进行推导。
根据玻尔兹曼公式,熵的表达式为S=k lnW,其中S为熵,k为玻尔兹曼常数,W为系统的微观状态数。
通过对热力学系统的分析,可以得到熵的变化量为ΔS=kln(W2/W1),其中W2为系统最后的微观状态数,W1为系统初始的微观状态数。
考虑到熵是一个状态函数,可以得到熵的增加量ΔS=kln(W2)-k ln(W1)=k ln(W2/W1),从而推导出了熵增原理。
四、熵增原理的应用熵增原理在热力学中有广泛的应用。
一方面,熵增原理解释了为什么热量不会自发地从低温物体传递到高温物体,因为这样的传递过程会导致系统熵的减小,与熵增原理相矛盾。
另一方面,熵增原理也解释了自然界中一切过程的不可逆性,以及为什么一些反向过程是不可能实现的。
在工程领域,熵增原理也被广泛应用于能源转化和能量利用的评估。
例如,熵增原理可以用于评估热力学循环的效率,比如汽车发动机、蒸汽轮机等。
通过最大化熵增原理,可以提高热力学循环的效率,从而降低能源消耗和环境污染。
此外,熵增原理还被应用于信息理论中的熵和信息量的概念。
信息的不确定程度可以通过熵的概念来描述,而熵增原理则指出信息的增加总是会伴随着熵的增加。
总结:热力学第二定律和熵增原理是热力学中非常重要的概念,它们揭示了自然界中过程的不可逆性以及熵的增加趋势。
熵增原理不仅在热力学领域有着广泛的应用,还在能源转化、信息理论等领域发挥着重要作用。
9.6 热力学第二定律的统计意义 玻尔兹曼熵

二、热力学概率与玻尔兹曼熵 1、热力学概率 B A
不可逆过程的初态和终态存在怎样的差别? 不可逆过程的初态和终态存在怎样的差别? 假设A中装有a 个分子( 假设 中装有 、b、c、d 4个分子(用四种颜色标记)。 个分子 用四种颜色标记) 开始时, 个分子都在 个分子都在A部 抽出隔板后分子将向B部扩 开始时,4个分子都在 部,抽出隔板后分子将向 部扩 散并在整个容器内无规则运动。 散并在整个容器内无规则运动。
意味着此事件观察不到。 意味着此事件观察不到。 实际过程是由概率小的宏观态向概率大的宏观态进行。 实际过程是由概率小的宏观态向概率大的宏观态进行。 热力学概率 宏观态所对应的微观态数, 表示。 宏观态所对应的微观态数,用Ω 表示。
2、玻尔兹曼熵 引入态函数熵
若系统分子数为N,则总微观态数为 若系统分子数为 ,则总微观态数为2N,N个分 个分 子自动退回A室的几率为 室的几率为1/2 子自动退回 室的几率为 N。 1mol气体的分子自由膨胀后,所有分子退回到 气体的分子自由膨胀后, 气体的分子自由膨胀后 所有分子退回到A 室的几率为 23
1/ 2
6.023×10
∆S > 0
分布 详细分布 宏观态) 微观态) (宏观态) (微观态)
A4B0(宏观态) (宏观态) 微观态数 1 A3B1(宏观态) (宏观态) 微观态数4 微观态数
A2B2(宏观态) (宏观态) 微观态数 6
分布 详细分布 宏观态) 微观态) (宏观态) (微观态) A1B3(宏观态) (宏观态) 微观态数 4 A0B4(宏观态) (宏观态) 微观态数 1 从图知,4个粒子的分布情况,总共有 个微观态。 从图知 个粒子的分布情况,总共有16=24个微观态。 个粒子的分布情况 A4B0和A0B4, 微观态各为 ,几率各为 和 微观态各为1,几率各为1/16; A3B1和A1B3, 微观态各为 ,几率各为 微观态各为4,几率各为4/16, 和 , A2B2, 微观态为6,几率最大为6/16。 , 微观态为 ,几率最大为 。
热力学第二定律与熵

热力学第二定律与熵热力学是关于能量转换和物质转移的科学,它研究了能量与物质的性质、转换和传递规律。
热力学第二定律是热力学中最基本的定律之一,是指自然界中存在着一个不可逆的方向,即熵增加的方向。
本文将探讨热力学第二定律与熵的关系以及它们的意义。
1. 热力学第二定律的基本原理热力学第二定律是热力学的基础之一,它包含了两个基本原理:热量不会自发地从低温物体转移到高温物体,以及任何一个系统都不能在不受外界干扰的情况下自发地从无序状态转变为有序状态。
这意味着自然界中存在着一个时间箭头,从低熵(有序)状态向高熵(无序)状态演化。
2. 热力学第二定律的数学表述热力学第二定律可以用数学等式来表述,其中最著名的是克劳修斯不等式和等熵过程的熵增定理。
克劳修斯不等式表示任何一个热力学过程中,系统的熵增加大于等于传递给系统的热量与系统温度之商。
数学表达式为:ΔS≥Q/T其中,ΔS表示系统的熵增,Q表示传递给系统的热量,T表示系统的温度。
等熵过程的熵增定理指出,对于一个封闭系统,其绝热过程中的熵增为零。
这意味着在没有能量交换的情况下,系统的熵保持不变。
3. 熵与系统的无序程度熵是热力学中一个重要的概念,它可以用来描述系统的无序程度。
熵的数值越大,系统的无序程度越高。
熵的改变可以通过热量的传递和温度的变化来实现。
当热量从高温物体传递到低温物体时,系统的熵会增加;而当热量从低温物体传递到高温物体时,系统的熵会减少。
4. 热力学第二定律的应用热力学第二定律在自然界的各个领域都有广泛的应用。
例如,在能源转换中,热力学第二定律告诉我们不能完全将热能转化为有用的机械能,因为在这个过程中总会有一部分热能转化为无用的热量而被散失出去。
这也是为什么制冷机和汽车发动机等热机无法达到100%的效率。
此外,热力学第二定律还与统计力学、信息论和生态学等领域有着密切的联系。
它的应用范围涉及到了从宏观的热力学系统到微观的粒子运动,从有序的晶体结构到无序的分子排列等各个方面。
热力学第二定律的统计意义和熵的概念.
孤立系统中发生的一切实际过程都是从微观态数少的宏观态 向微观态数多的宏观态进行.
3. 分析几个不可逆过程 (1) 气体的自由膨胀 气体可以向真空自由膨胀但却不能自动收缩。因为气体 自由膨胀的初始状态所对应的微观态数最少,最后的均 匀分布状态对应的微观态数最多。如果没有外界影响, 相反的过程,实际上是不可能发生的。 (2) 热传导
(3) 熵是一个宏观量,对大量的分子才有意义。
2. 熵增原理
Ω2 > Ω1 (自动进行)
孤立系统
Ω1
Ω2
S1 k ln 1
S2 k ln 2
从状态(1)变化到状态(2) 的过程中,熵的增量为
2 S2 S1 k ln 0 (等号仅适用于可逆过程) 1
孤立系统的熵永不会减少。这一结论称为熵增原理 说明 熵增原理只能应用于孤立系统,对于开放系统,熵是可以 减少的。 例如某溶液在冷却过程中的结晶的现象。其内的分子从溶 液中无序的运动转变为晶体的有规则排列,熵是减少的。 3. 熵的宏观表示 在无限小的可逆过程中,系统熵的元增量等于其热温比, 即
两物体接触时,能量从高温物体传向低温物体的概率, 要比反向传递的概率大得多!因此,热量会自动地从 高温物体传向低温物体,相反的过程实际上不可能自 动发生。
(3) 功热转换 功转化为热就是有规律的宏观运动转变为分子的无序热
运动,这种转变的概率极大,可以自动发生。相反, 热转化为功的概率极小,因而实际上不可能自动发生。
V
CV
R
V
T1
V1
dV
T V S S0 CV ln R ln T1 V1
190 1
包含微观状态数最多的宏观状态是出现的概率最大的状态
结论 (1) 系统某宏观态出现的 概率与该宏观态对应 的微观态数成正比。
热力学第二定律的统计意义

热力学第二定律的统计意义热力学第二定律是热力学中的一条基本定律,它表明在自然界中存在着一种趋势,即热量自热源向周围环境传递,而不会自动从低温体传向高温体,因此熵(或热力学不可逆性)总是增加的。
然而,这个定律的本质并不明确,这导致了许多学者对它的解释存在争议。
随着物理学的发展,人们发现这个定律与热力学的统计基础有着密切的关系。
首先,我们需要理解热力学中一个基本概念——熵。
熵是一种用来度量系统无序程度的物理量,表示了体系各个微观状态的分布不均匀程度。
通常来说,系统内互相独立的微观变化越多,其熵就越大。
例如,对于一个有序的水晶,在所有原子处于完美排列状态时,其熵最小。
而当温度升高时,原子会破坏这个有序状态,等效于增加了水晶的“混乱程度”,其熵也就增加了。
热力学第二定律实际上是在告诉我们一个事实:任何一个完全隔离的系统,熵不可能永远减少。
也就是说,熵的增加是一个不可逆的过程,这也是热量从高温体传向低温体时熵增加的原因。
概括而言,该定律表明了一个趋势,即系统中的能量将倾向于从高能量的状态向低能量的状态流动,从而使得系统的熵增加。
从统计学的角度来看,热力学第二定律是由这样一个事实推导而来的:在一个大的体系中,微观粒子的随机运动会经常导致某些相对独立事件的不完全或无法恢复性,这些事件包括:1. 分子/原子的碰撞: 分子或原子相互碰撞时,有一部分能量被转移给周围环境中的分子,这会导致大的系统中的能量总体降低;2. 动能的分布: 分子的运动速度分布不服从热力学平衡状态的Maxwell-Boltzmann分布时,也将导致无序增加;3. 热交换: 热量从高温体向低温体传递时,热力学不可逆性也将随之增加。
以上这些现象都会导致系统设在某个起始状态后一段时间后回不到原始状态的情况,这也就是在热力学第二定律中所描述的不可逆性增加。
这个过程是由大量微观粒子的无序运动造成的,也被称为热力学平衡状态的降解。
总体来说,热力学第二定律的统计意义是,它实际上是对许多微观随机过程导致的热力学不可逆性增加的描述。
热力学第二定律的统计意义

热力学第二定律的统计意义
热力学第二定律是热力学中的一个基本定律,它描述了热能的转化过程中存在的不可逆性。
热力学第二定律的统计意义是将宏观不可逆过程与微观粒子运动的随机性联系起来,从而解释热力学第二定律的基本原理。
在热力学中,熵是一个重要的概念,它描述了系统中的混乱程度。
热力学第二定律可以被表述为熵在任何一个孤立系统中总是增加的原则。
这个原则可以通过微观粒子的随机热运动来解释。
在一个系统中,随着时间的推移,分子的位置和速度会随机变化,使得系统的状态逐渐变得更为混乱。
因此,熵增加代表着系统的混乱程度增加,也就是更接近于平均状态。
此外,热力学第二定律还可以通过热力学概率来解释。
热力学概率是指一个系统处于某个状态的概率。
根据热力学第二定律,处于高熵(即更为混乱)状态的概率更大,因为这样的状态更接近于平均状态。
这也反映了分子热运动的随机性,即处于高熵状态的概率更大,因为更多的状态都是高熵状态。
总之,热力学第二定律的统计意义是将宏观的不可逆过程与微观粒子的随机性联系起来,从而解释热力学第二定律的基本原理。
这个原理可以通过系统中的熵增加、分子热运动的随机性以及热力学概率等方面来进行解释。
热力学第二定律的统计意义

与热力学第二定律的统计表述相比较
熵与热力学 几率有关
玻尔兹曼建 立了此关系
越大,微观态 数就越多,系统 就越混乱越无序。
玻尔兹曼公式:S = k ln
(k为玻尔兹曼常数)
熵的微观意义:系统
热力学第二定律的统计意义
从统计观点探讨过程的不可逆性和熵的微观意义, 由此深入认识第二定律的本质。
不可逆过程的统计性质
(以气体自由膨胀为例) 一个被隔板分为A、B相等两部分的容器,装有 4个涂以不同颜色分子。 开始时,4个分子都在A部,抽出隔板后分子将 向B部扩散并在整个容器内无规则运动。 隔板被抽出后,4分子在容器中可能的分布情形 如下图所示:
平衡态相应于一定宏观 条件下 最大的状态。
热力学第二定律的统计表述: 孤立系统内部所发生的过程总是从包含微观态 数少的宏观态向包含微观态数多的宏观态过渡, 从热力学几率小的状态向热力学几率大的状态 过渡。
熵的微观意义和玻尔兹曼公式
宏观热力学指出:孤立系统内部所发生的过 程总是朝着熵增加的方向进行。
在上例中,均匀分布这种宏观态,相应的微 观态最多,热力学几率最大,实际观测到的 可能性或几率最大。对于1023个分子组成的 宏观系统来说,均匀分布这种宏观态的热力 学几率与各种可能的宏观态的热力学几率的 总和相比,此比值几乎或实际上为100%。 因此,实际观测到的总是均匀分布这种宏观 态。即系统最后所达到的平衡态。
对单个分子或少量分子来说,它们扩散到B部 的过程原则上是可逆的。但对大量分子组成的 宏观系统来说,它们向B部自由膨胀的宏观过 程实际上是不可逆的。这就是宏观过程的不可 逆性在微观上的统计解释。
第二定律的统计表述
(依然看前例) 左边一列的各种分布仅指出A、B两边各有几 个分子,代表的是系统可能的宏观态。 中间各列是详细的分布,具体指明了这个或那 个分子各处于A或B哪一边,代表的是系统的 任意一个微观态。 4个分子在容器中的分布对应5种宏观态。 一种宏观态对应若干种微观态。 不同的宏观态对应的微观态数不同。 均匀分布对应的微观态数最多。 全部退回A边仅对应一种微观态。
热学中的熵和热力学第二定律

热学中的熵和热力学第二定律熵是热力学中的一个重要概念,它是描述系统无序度的物理量。
在热学中,熵的概念与热力学第二定律密切相关。
本文将对熵和热力学第二定律进行探讨。
一、熵的基本概念熵是热力学中描述系统无序度的物理量,通常用符号S表示。
熵的增加意味着系统的无序度增加,而熵的减少则意味着系统的有序度增加。
熵的单位是焦耳/开尔文(J/K)。
熵的定义可以通过统计力学的观点来理解。
根据统计力学理论,系统的熵与微观状态数成正比。
微观状态是指系统在给定的宏观条件下所有可能的微观构型。
熵可以用下式表示:S = k ln Ω其中,k是玻尔兹曼常数,Ω是系统的微观构型数。
根据这个定义,我们可以看出,熵是与系统的无序度有直接联系的物理量。
二、熵的特性熵具有以下几个基本特性:1. 熵的增加性:在孤立系统中,熵的增加是不可逆的。
熵增定律指出,在任何一个孤立系统中,熵不会减少,而只会增加或保持不变。
这是因为系统的微观构型数一般会随着时间的推移而增加,从而导致系统的熵增加。
2. 熵的可加性:当系统由多个子系统组成时,系统的总熵等于各个子系统的熵之和。
这个特性可以通过统计力学的方法来证明。
3. 熵与温度的关系:根据统计力学理论,系统的熵与它的温度成正比。
这个关系由热力学第二定律给出。
三、热力学第二定律热力学第二定律描述了能量传递和转换的方向性。
在熵的概念引入之前,人们主要根据经验规律来描述热传递方向和能量的转化方式。
但随着热学的发展,熵的概念被引入热力学,使得热力学的理论更为完善。
热力学第二定律有多种等价的表述方式,其中一种是Clausius表述。
Clausius表述指出,热量不会自发地从低温物体传递到高温物体。
也就是说,热量的传递方向是从高温物体到低温物体。
这个观点可以通过熵的概念来解释。
根据熵的定义,熵的增加意味着系统的无序度增加。
对于一个孤立系统,如果从低温物体向高温物体传递热量,那么低温物体的熵会减少,而高温物体的熵会增加,从而整个系统的熵减少。
热力学第二定律统计意义

热力学第二定律统计意义热力学第二定律是热力学中的重要定律之一,其统计意义可以通过热力学的统计学方法来解释。
热力学第二定律表明,在孤立系统中,不发生外界干扰的情况下,热量不可能从低温物体传递到高温物体。
这个定律的统计学意义是基于热力学理论中的熵的概念。
熵是一个衡量系统无序程度的物理量。
熵越大,系统的无序程度越高。
在孤立系统中,熵的增加是不可避免的,因为它与系统的无序程度有关。
因此,热力学第二定律可以用熵的概念来说明。
在热力学理论中,有一个重要的概念叫做微观状态。
微观状态是指一个系统在某个瞬间的所有粒子的位置、速度和动量等细节参数。
对于一个宏观体系来说,其微观状态的数量非常巨大,因此宏观热力学只考虑了一些平均量,如温度、压力和体积等。
但是,对于一个孤立的宏观体系来说,其微观状态是保持不变的,因此熵也是保持不变的。
但是,如果我们考虑一个孤立的宏观体系与其外界发生相互作用的情况下,就会发现熵的增加是不可避免的。
这是因为,外界的干扰会导致系统微观状态的变化,而微观状态的变化会导致熵的增加。
由于熵的增加代表系统的无序增加,因此热力学第二定律也就表明了系统无序程度的增加是不可避免的。
具体来说,考虑一个受到外界干扰的系统,如果其能量分布保持不变,那么其微观状态数量也是不变的。
这就意味着,任何微观状态的出现的概率都是相等的。
但是,我们可以发现,如果能量分布不均匀,例如在一个被分割成两部分的系统中,把高能量的粒子放在一侧,低能量的粒子放在另一侧,那么高能量与低能量之间就会产生一个能量差,从而导致能量从高温物体流向低温物体,也就是出现了“热流”的现象。
从统计学的角度来看,这种现象是微观状态变化所导致的。
高能量与低能量之间的差异会导致一些微观状态的出现概率比其他微观状态高,因此会引起一部分微观粒子流动的现象,也就是热流现象。
这种现象符合热力学第二定律的要求,也就表明了该定律的统计学意义。
综上所述,热力学第二定律的统计学意义是基于熵的概念,主要是通过微观状态变化引起的无序程度增加来解释的。
大学物理第9章第6节-热力学第二定律的统计意义 玻尔兹曼熵

一. 热力学第二定律的微观意义 热力学系统所经历的过程是大量微观 粒子作无序运动的结果. 与热现象有关的自然过程的方向 (i) 从有序到无序 (ii) 由无序程度小到无序程度大
(1) 单摆的摆动过程: 由有序到无序; (2) 做功转换成内能的过程: 大量分子 作定向运动转化为大量的微观粒子的无规 则热运动; (3) 热传递过程: 由无序程度小到无序 程度大; (4) 气体的绝热自由膨胀过程: 由无序 度小到无序度大.
A2 A1
V2 N N V2 V1 V1A AA
S S 2 S1 k B ln 2 k B ln 1 k B ln 2 1
k B lnV2 V1
NA
N A k B lnV2 V1
R lnV2 V1
复合系统的熵 设两个子系统的热力学概率分别为 1 和 2 , 复合系统的热力学概率为 1 2 . 复合系统的熵
S k B ln k B ln(1 2 ) k B ln 1 k B ln 2 S1 S 2
复合系统的熵等于子系统的熵之和.
熵增加原理: 孤立系统中的自然过程总 是沿着熵增大的方向进行, 平衡态对应于熵 最大的状态.
S 0
热力学第二定律可以用熵增加原理来 描述.
例9.5 用热力学概率方法计算摩尔数 为 的理想气体向真空绝热自由膨胀时的 玻尔兹曼熵增加, 设体积从 V1 膨胀到 V 2 , 且 初、末态为平衡态. 解 气体绝热自由膨胀过程, 系统内能 不变, 温度不变. 绝热自由膨胀: Q 0, A 0
A
B
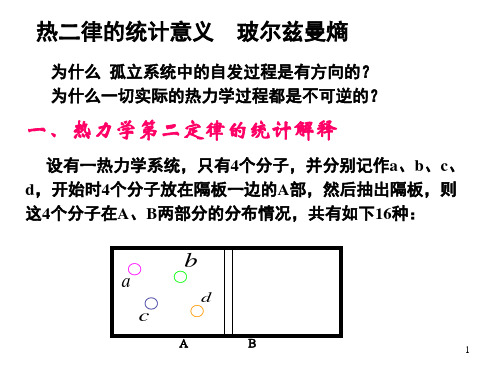
b
a
d
c
微观态: 宏观态中的每一种分子的组合 宏观态只考虑 A 室与 B 室各有几个分
热二律的统计意义 玻尔兹曼熵
p2 (V2 )N
p1 V1
12
而这些分子处于V1和V2的热力学概率 当然正比于它们处V1
和V2的概率p,故有
2 1
p2 p1
V2 V1
N
∴ 初、终两态的玻尔兹曼熵应为
S
S2
S1
k
ln
2
k
ln
1
k
ln
2 1
N
S
k
ln
1、玻尔兹曼熵的建立
“自然界的一切自发过程都是向着微观状态 数大的方向进行的”。
---波尔兹曼----
又,热力学概率大的时候,也是系统内分子运动的无 序度大的时候。因此,上述结论又可表述为:
在一孤立系统内所发生的一切自发过程总是沿着使分 子运动更加无序的方向进行。
例如:摩擦生热:大量分子的有序运动转变为分子的无规则
热二律的统计意义 玻尔兹曼熵
为什么 孤立系统中的自发过程是有方向的? 为什么一切实际的热力学过程都是不可逆的?
一、热力学第二定律的统计解释
设有一热力学系统,只有4个分子,并分别记作a、b、c、 d,开始时4个分子放在隔板一边的A部,然后抽出隔板,则 这4个分子在A、B两部分的分布情况,共有如下16种:
热运动——可行;
热生摩擦:大量分子的无规则热运动,自动地做有序
运动——不可行;
7
实际的热力学过程不可逆性说明过程初态和终态间应 有一种重要性质上的差异,这种性质如果用一物理量来描 述,则该物理量应是状态的函数,并能用这个函数的变化 来说明和判断系统过程的方向。这个态函数就是熵S。
由上面讨论可知,S应与有关。
1877年玻尔兹曼建立起S与的关系为 S=kln
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S 0
A2B2(宏观态) 微观态数 6
分布 详细分布 (宏观态) (微观态) A1B3(宏观态) 微观态数 4 A0B4(宏观态) 微观态数 1 从图知,4个粒子的分布情况,总共有16=24个微观态。 A4B0和A0B4, 微观态各为1,几率各为1/16; A3B1和A1B3, 微观态各为4,几率各为4/16, A2B2, 微观态为6,几率最大为6/16。
若系统分子数为N,则总微观态数为2N,N个分 子自动退回A室的几率为1/2N。 1mol气体的分子自由膨胀后,所有分子退回到A 室的几率为 23
1/ 2
6.02310
意味着此事件观察不到。 实际过程是由概率小的宏观态向概率大的宏观态进行。 热力学概率
宏观态所对应的微观态数,用 表示。
2、玻尔兹曼熵 自然过程是向热力学概率 增大的方向进行。
引入态函数熵
S k ln
熵具有可加性 S S1 S2
玻尔兹曼熵
熵的微观意义是系统内分子热运动无序性的量度
S k ln k ln 1 2 k ln 1 k ln 2
在孤立系统中所进行的自然过程总是沿着熵增大的 方向记性,平衡态对应于熵最大的状态,即熵增加 原理。
9.6 热力学第二定律的统计意义 玻尔兹曼熵
一、热力学第二定律的微观意义
系统的热力学过程就是大量分子无序运动状态的变化
功变热过程、热传递过程、气体自由膨胀过程 大量分子从无序程度较小(或有序)的运动状态 向无序程度大(或无序)的运动状态转化 热力学第二定律的微观意义
一切自然过程总是沿着无序性增大的方向进行。
二、热力学概率与玻尔兹曼熵
的差别? 假设A中装有a、b、c、d 4个分子(用四种颜色标记)。 开始时,4个分子都在A部,抽出隔板后分子将向B部扩 散并在整个容器内无规则运动。
分布 详细分布 (宏观态) (微观态)
A4B0(宏观态) 微观态数 1 A3B1(宏观态) 微观态数4
