B1鲍摩——瓦尔夫模型选址方法
物流节点选址模型与方法

第四章物流节点选址模型与方法第一节物流设施选址问题固定设施选址问题是物流网络中一项十分重要的战略决策。
一、物流设施选址问题类型⏹按备选点的离散程度分连续选址模型(Continuous Location Models)和离散选址模型(Discrete Location Models)两类。
⏹从选址目标来看,物流设施选址有三种基本类型(成本最小化、服务最优化、物流量最大化)和综合型。
二、物流设施选址问题的特点在选址问题的研究中,Daskin总结了五个特点:(一)选址决策是研究不同层次的人类组织的选址问题,从个人、家庭到公司、政府机构甚至是国际机构(二)选址决策是一个战略决策,需要考虑长期的资金利用和经济效益(三)选址决策还涵盖了经济的外延含义,包括污染、交通拥挤和经济潜力等。
(四)由于大多数选址问题是NP-HARD问题,很难求得选址模型的最优解,特别是大型问题。
(五)选址问题都有相应的应用背景,模型的结构(目标函数、变量和约束)由相应的应用背景决定。
第二节物流设施选址的程序和步骤一、物流设施选址约束条件分析(一)需求条件(二)运输条件(三)配送服务的条件(四)用地条件(五)法律法规(六)流通职能条件(七)其他二、搜集整理资料(一)掌握业务量1. 工厂到物流设施之间的运输量2. 向顾客配送的货物数量3.物流设施保管的数量4. 配送路线上的其他业务量(二)掌握费用1. 工厂至物流设施之间的运输费;2.物流设施到顾客之音质配送费;3. 与设施、土地有关的费用及人工费、业务费等。
三、地址筛选四、定量分析五、结果评价六、复查七、确定选址结果八、选址的注意事项(1)选址因素相互矛盾(2)不同因素的相对重要性很难确定和度量(3)判断的标准会随时间变化而变化第三节 整数规划选址方法一、0-1整数规划方法选址问题的提出建设一个新工厂,应合理选择厂址。
假设厂址候选地点有s 个,分别用D 1,D 2…表示;原材料、燃料、零配件的供应地有M 个,分别用A 1、A 2…表示,其供应量分别用P 1、P 2表示;产品销售地有N 个,分别用B 1、B 2表示,其销售量分别用Q 1、Q 2表示,如下图所示。
基于鲍摩_瓦尔夫模型的配送中心选址

基于鲍摩_瓦尔夫模型的配送中心选址
鲍摩_瓦尔夫模型是一种最小配送成本模型,用于确定终端顾客需求点和配送中心的
最佳位置,在传统市场分析中广泛应用。
该模型的基本假设是,顾客需求点的需求量恒定,且距离配送中心越远,配送成本越高。
选择配送中心的最佳位置可能涉及多个因素,例如人口密度、土地成本、运输成本等。
在执行模型分析之前,应先考虑与配送相关的各种因素,以确定权衡决策所需的权重。
首先,要确定可行的候选地点,并确定重点考虑的因素。
然后,收集这些因素的数据,并将其用于计算每个地点的相对宜居指数。
接着,可以利用鲍摩_瓦尔夫模型来计算每个候选地点的最小配送成本。
此时,需要
指定每个需求点的需求量,以及连接每个需求点和候选配送中心的距离。
一旦计算得出最
小配送成本,可以从中选择一个“最优”的配送中心位置。
有许多工具和技术可以帮助执行上述任务,例如GIS(地理信息系统),它可以绘制地图、计算距离和执行统计分析。
除此之外,采用交通状况分析工具可以考虑道路交通流量
和容量等因素,这些因素也可以影响最终的配送成本。
需要注意的是,在执行鲍摩_瓦尔夫模型时,仅考虑了成本因素,而没有考虑其他与
顾客相关的因素,例如品牌声誉和购买体验。
因此,在最终选址方案中,应该综合考虑珂
以平衡各类因素,以取得最优的运营效益。
鲍摩-瓦尔夫(Baumol-Wolfe)模型

鲍摩-瓦尔夫(Baumol-Wolfe )模型简单表述:生产工厂、消费区域既定情况下,在若干被选地址中,找出物流节点的数量和位置,使得通过物流节点所运送的产品固定成本及可变成本在下列约束条件下最低:1) 不能超过每个工厂的供货能力;2) 所有产品的需求必须得到满足;3) 每个物流节点的总进货量等于总出货量。
目标函数:()()()p ij ij j j j j jk jk j j j k f z C X D Y W Z V r Z =+++∑∑∑∑ 约束条件:()ij i j XA =∑满足工厂供货能力要求()jk k j Y B =∑满足顾客需求()ijjk i k X Y =∑∑满足总进货量等于总出货量要求0ij X >0jk Y >式中::(1,2,3,,);i i m =工厂…:(1,2,3,,);j j s =配送中心…:(1,2,3,,);k k n =顾客…:(1,2,,);i A i i m =工厂的供应量…:(1,2,,);k B k k n =顾客的需求量…:;ij C i j 从工厂到配送中心的单位运输成本:;jk D j k 从配送中心到用户的单位运输成本:;j Z j 配送中心的产品通过量:;j V j 配送中心的固定费用():00,1;j j r Z Z =时取否则取:,,,01,,;j j W j p p j W <<配送中心每单位通过量的变动费用在考虑变动费时引进指数满足 条件以便考虑配送中心的规模经济性配送中心的变动费为 :1;p j Z p =如果不考虑规模的经济性,可令:;ij X i j 工厂到配送中心的运量:jk Y j k 配送中心到用户的运量。
节点选址方法汇总分析
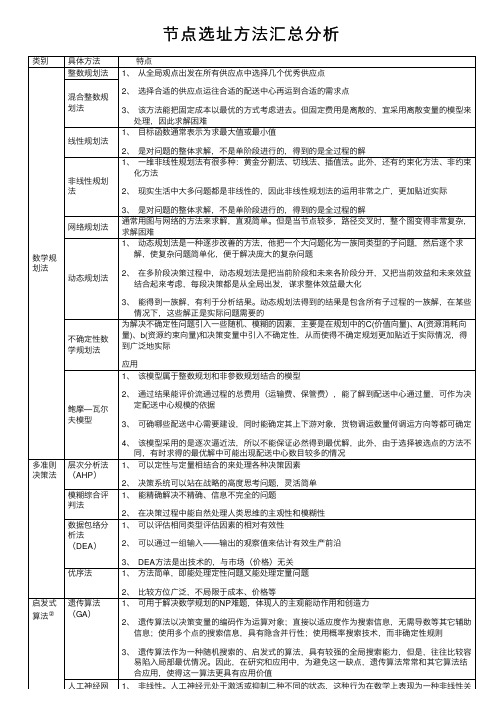
节点选址⽅法汇总分析类别具体⽅法特点数学规划法整数规划法1、从全局观点出发在所有供应点中选择⼏个优秀供应点2、选择合适的供应点运往合适的配送中⼼再运到合适的需求点3、该⽅法能把固定成本以最优的⽅式考虑进去。
但固定费⽤是离散的,宜采⽤离散变量的模型来处理,因此求解困难混合整数规划法线性规划法1、⽬标函数通常表⽰为求最⼤值或最⼩值2、是对问题的整体求解,不是单阶段进⾏的,得到的是全过程的解⾮线性规划法1、⼀维⾮线性规划法有很多种:黄⾦分割法、切线法、插值法。
此外,还有约束化⽅法、⾮约束化⽅法2、现实⽣活中⼤多问题都是⾮线性的,因此⾮线性规划法的运⽤⾮常之⼴,更加贴近实际3、是对问题的整体求解,不是单阶段进⾏的,得到的是全过程的解⽹络规划法通常⽤图与⽹络的⽅法来求解,直观简单。
但是当节点较多,路径交叉时,整个图变得⾮常复杂,求解困难动态规划法1、动态规划法是⼀种逐步改善的⽅法,他把⼀个⼤问题化为⼀族同类型的⼦问题,然后逐个求解,使复杂问题简单化,便于解决庞⼤的复杂问题2、在多阶段决策过程中,动态规划法是把当前阶段和未来各阶段分开,⼜把当前效益和未来效益结合起来考虑,每段决策都是从全局出发,谋求整体效益最⼤化3、能得到⼀族解,有利于分析结果。
动态规划法得到的结果是包含所有⼦过程的⼀族解,在某些情况下,这些解正是实际问题需要的不确定性数学规划法为解决不确定性问题引⼊⼀些随机、模糊的因素,主要是在规划中的C(价值向量)、A(资源消耗向量)、b(资源约束向量)和决策变量中引⼊不确定性,从⽽使得不确定规划更加贴近于实际情况,得到⼴泛地实际应⽤鲍摩—⽡尔夫模型1、该模型属于整数规划和⾮参数规划结合的模型2、通过结果能评价流通过程的总费⽤(运输费、保管费),能了解到配送中⼼通过量,可作为决定配送中⼼规模的依据3、可确哪些配送中⼼需要建设,同时能确定其上下游对象,货物调运数量何调运⽅向等都可确定4、该模型采⽤的是逐次逼近法,所以不能保证必然得到最优解,此外,由于选择被选点的⽅法不同,有时求得的最优解中可能出现配送中⼼数⽬较多的情况多准则决策法层次分析法(AHP)1、可以定性与定量相结合的来处理各种决策因素2、决策系统可以站在战略的⾼度思考问题,灵活简单模糊综合评判法1、能精确解决不精确、信息不完全的问题2、在决策过程中能⾃然处理⼈类思维的主观性和模糊性数据包络分析法(DEA)1、可以评估相同类型评估因素的相对有效性2、可以通过⼀组输⼊——输出的观察值来估计有效⽣产前沿3、 DEA⽅法是出技术的,与市场(价格)⽆关优序法1、⽅法简单,即能处理定性问题⼜能处理定量问题2、⽐较⽅位⼴泛,不局限于成本、价格等启发式算法②遗传算法(GA)1、可⽤于解决数学规划的NP难题,体现⼈的主观能动作⽤和创造⼒2、遗传算法以决策变量的编码作为运算对象;直接以适应度作为搜索信息,⽆需导数等其它辅助信息;使⽤多个点的搜索信息,具有隐含并⾏性;使⽤概率搜索技术,⽽⾮确定性规则3、遗传算法作为⼀种随机搜索的、启发式的算法,具有较强的全局搜索能⼒,但是,往往⽐较容易陷⼊局部最优情况。
离散型配送中心选址鲍姆尔-沃尔夫算法

离散型配送中心选址鲍姆尔-沃尔夫算法1、原理所谓离散型配送中心选址,就是配送中心的地址是不能任意选择的,只能限制在预先给定的几个备选地点。
在很多情况下,配送中心地址选址是有限制的,如在原有的大仓库、大货场等,还有的地点可能在自然条件不允许选用的地方等等。
所以在实际应用中,大部分采用离散型模型,离散型配送中心的选址算法,更具有应用价值。
鲍姆尔-沃尔夫模型是一种简明的配送中心选址模型。
如图1所示的是从几个工厂经过几个仓库向用户输送物资的选址模型,对此问题一般只考虑运费最小的运输规划,而鲍姆尔-沃尔夫选址算法所要考虑的问题是,各个工厂向哪些仓库运输多少物资?各个仓库向哪些用户发送多少物资?然后根据物流量的大小,来决定仓库的容量。
工厂(k) 仓库(i) 用户(j) k=123. . .. . ..m图1 鲍姆尔-沃尔夫选址模型2、操作步骤1.求初始解。
要求最初的工厂到用户(k,j)间的运输费用相对最小,也就是说,要求工厂到仓库间的运输费率和仓库到用户间的发货费率h ij之和为最小,即C ki 0=min(C kj 0+h ij )设所有的(k,j)取最小费率C kj 0,仓库序号是I kj 0。
这个结果决定了所有工厂到用户间的费用。
如果工厂的生产能力和用户的需要量已知。
按希契科克运输问题求解,使费用函数∑C ki 0 x kj 为最小时,{ X ki 0}就为初始解。
2.二次解。
根据初始解,仓库i 的通过量可按下式计算:W i 0=∑{ 所有的k,j 如I kj 0=i } X kj 0用通过量反过来计算仓库的可变费用:{}1)(min --++=θθi n i i ij ki n KJ W v h C C在这个阶段中,对于所有的(k,j )取下式: {}12)(min -++=θθθi i i ij hi hj W v h C CC hj 2的仓库序号设为h hj 2。
再次按希契科克运输问题求解,使费用函数∑C hj 2 x ni 为最小时,就为二次解。
基于鲍莫尔—沃尔夫模型的农产品配送中心选址问题研究

【相关文献】
[1]杨波:《多品种随机数学模型的物流配送中心选址问题》,载于《中国管理科学》2003年第2期。
[2]周爱莲、李旭宏、毛海军:《一类企业物流中心动态选址模型研究》,载于《系统工程学报》2011年第3期。
[3]方磊、何建敏:《综合AHP和目标规划方法的应急系统选址规划模型》,载于《系统工程理论与实践》2003年第12期。
基于鲍莫尔—沃尔夫模型的农产品配送中心选址问题研究
李远远;刘礼帅
【期刊名称】《经济研究参考》
【年(卷),期】2015(000)029
【总页数】3页(P90-92)
【作 者】李远远;刘礼帅
【作者单位】广西社科规划办;桂林电子科技大学
【正文语种】中 文
合理选择配送中心可在满足相应节点需求量的同时有效降低物流成本。本文在分析影响农产品配送中心选址因素的前提下,利用鲍莫尔—沃尔夫选址模型进行选址,并通过实例验证该选址模型的实用性。
(一)自然环境。
农产品物流中心选址受自然环境约束大。一方面,农产品保质期短、易腐易损的特性决定了在选址时要考虑温度、湿度等有关自然条件;另一方面,农产品种类繁多,分布范围广,因此在存储过程中,必须采用先进的技术来保证农产品的鲜活度。
(二)市场特性。
一方面,农业作业对象固定,农产品产能受自然条件约束大;另一方面,大部分农产品是必需品,需求弹性小,因而其供、需弹性小,容易导致价格波动。因此农产品配送中心选址要与农产品的资源分布和农产品的需求分布相适应。
基于鲍摩_瓦尔夫模型的配送中心选址的研究

覆盖、压实,铺设土工膜作面板底模,待管桩达到设计强度的100%时压桩;d)面板采用整体性面板,厚30cm,避免因后期垃圾土的分解腐化导致路基产生过大沉降而降低稳定性;e)根据施工期及使用初期、后期垃圾土沉降等不同工况分别验算面板配筋及混凝土应力;f)为使桩芯混凝土砼和面板砼连接成为整体,桩芯和面板砼必须一起浇注,面板的钢筋和桩芯的钢筋必须要连接;g)面板的砼形成一定强度后,切割伸缩缝,伸缩缝下面填塞浸润沥青的软木条,并在上面填塞胶泥,使面板可自由伸缩。
4结语软弱地基的处理方案,应结合道路等级、交通量及工程所在地的地质条件、材料供应、工期要求和环境保护等因素,按照因地制宜、就地取材、综合治理的原则,在充分论证的基础上综合考虑,选用技术先进,经济合理的方案。
本工程采用PTC管桩加改进型整体桩帽的方案处理深厚软弱垃圾土地基,具有一定的灵活性、创造性。
通过对该工程一段时间的通车运行观察可知,目前的使用状况良好。
参考文献[1]JC888-2001,先张法预应力混凝土薄壁管桩[S].[2]GB13476-1999,先张法预应力混凝土管桩[S].[3]江苏沪宁高速公路扩建工程指挥部,江苏省交通基础技术工程研究中心.软弱土层带帽控沉疏桩复合地基加固工程技术规定[Z].南京:江苏沪宁高速公路扩建工程指挥部,2005.[4]JTGF10-2006,公路路基施工技术规范[S].作者简介:陈小兵(1973-),男(汉族),江苏海安人,硕士,副研究员,主要从事道路、桥梁的教学、设计、科研工作。
收稿日期:2007-04-23!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!胡志华1,孙志强1,郭欢欣2(1.华北水利水电学院机械系,河南郑州450011;2.郑州宇通客车股份有限公司,河南郑州450016)摘要:配送中心的选址决定着具体的配送线路,进而影响到各个配送中心的流通量和运输成本。
基于鲍摩-瓦尔夫模型及 算法在木材仓储中心选址中的应用

基于鲍摩-瓦尔夫模型及算法在木材仓储中心选址中的应用作者:豆佳梅孟利清钱良辉潘祥来源:《物流科技》2014年第06期摘要:木材仓储中心是木材物流系统的重要组成部分,木材仓储中心的选址决定着具体的配送线路,进而影响到各个木材仓储中心的流通量和运输成本。
鲍摩-瓦尔夫模型不仅考虑了运输成本,而且还考虑了可变成本和固定成本,因此将鲍摩-瓦尔夫模型用于解决考虑运输费用和仓储中心经济规模费用的木材仓储中心选址问题,可为木材仓储中心选址问题提供一种方便有效的计算方法。
通过实例计算,得到较好效果。
关键词:木材仓储中心;选址;鲍摩-瓦尔夫模型;应用中图分类号:F253文献标识码:AAbstract: Wood storage center is an important part of logistics system, the location of wood storage center decides specific distribution lines, thereby affects the circulation of every wood storage center and transportation costs. The Baumol-Wolfe model not only considers the transport cost, but also the variable cost and fixed cost. Through Baumol-Wolfe model is used in resolving the localization of wood storage center in terms of transportation cost and its economy scale, which can provide a convenient effective algorithm for the localization of the wood storage center. Through the solution by its algorithm and according to case study.Key words: wood storage center; location selection; Baumol-Wolfe model; application在木材仓储中心的选址规划过程中,如何确保总的木材仓储成本和运输成本最优化,是非常重要的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B1鲍摩——瓦尔夫模型选址方法
瓦尔夫模型,又称鲍摩—瓦尔夫模型(The Baumo-Walpole Model),是一种用于选址决策的数学模型。
该模型适用于研究解决选址问题时的决
策过程,并可作为指导决策者做出最佳选址决策的工具。
瓦尔夫模型的特
点是综合考虑了各个因素对于选址决策的重要性,并进行了权衡。
瓦尔夫模型的基本原则是通过对选址因素进行评估,并为每个因素赋
予适当的权重,然后将各因素的权重和评估值相乘,得到每个选址候选点
的综合评分,最终选择评分最高的候选点作为最佳选址。
瓦尔夫模型的四个主要步骤如下:
1.识别选址因素:选址因素是影响选址决策的各种因素,如用地成本、交通便利性、市场需求、竞争状况等。
在这一步骤中,需要对选址问题进
行全面分析,确定所有与选址相关的因素。
3.赋予权重:为每个选址因素赋予适当的权重,以反映其在选址决策
中的重要性。
权重的确定可以通过专家意见征询、决策者的权衡等方式进行。
一般来说,权重应尽可能客观地反映各因素的重要性。
4.综合评分:将每个选址因素的权重和评估值相乘,得到每个选址候
选点的综合评分。
评分最高的候选点被选择为最佳选址。
在这一步骤中,
可以使用数学模型或电子表格等工具进行计算。
瓦尔夫模型的优点是综合考虑了各种因素的重要性,并能够准确评估
每个选址候选点的优劣。
然而,该模型也存在一些局限性,例如对于一些
主观因素的评估可能存在误差,以及权重的确定可能会受到决策者主观意
愿的影响。
总之,瓦尔夫模型是一种较为科学和系统的选址方法,可以为选址决策者提供决策支持。
但在实际应用中,需要根据具体情况对模型进行适当的改进和调整,以使其更符合实际情况。
