圆和扇形的周长与面积(二)
学而思培优之圆和扇形的周长与面积(二)
3
差不变——化不规则为规则
【例4】(★★★) ( ) 如图,两个正方形摆放在一起,其中大正方形 边长为12,那么阴影部分面积是多少?(圆周率取 3.14) D A E
B
C
F
等积变形——化不可求为可求
【例5】(★★★★) 【例 】( ) 如图,矩形ABCD中,AB= 6厘米,BC= 4厘米,扇形ABE 半径AE =6 厘米,扇形CBF 的半径CB= 4厘米,求阴影部分的面积。(π 取3)
圆和扇形的周长与面积(二)
加油站
圆的周长
弓形: 弓形 弓形一般不要求周长 般不要求周长,主要求面积。 主要求面积。 弓形面积=扇形面积-三角形面积。
C=πd 或 C=2πr
圆的面积
“弯角”:弯角的面积=正方形 弯角 :弯角的面积=正方形-扇形 扇形
S=πr2 扇形的弧长 C=2 r
n 360
“谷子”: “谷子”的面积=弓形面积×2
整体考虑——柳暗花明 【例6】(★★★) (1)如图,求阴影部分的面积。( π取3)
北大附中“资优博雅杯”数学竞赛) (2)如图,阴影正方形的顶点分别是大正方形EFGH各边的中点,分别以 大正方形各边的一半为直径向外做半圆,再分别以阴影正方形的各边 为直径向外作半圆,形成8个“月牙形”。这8个“月牙形”的总面积 为32平方厘米 问大正方形EFGH的面积是多少? 为32平方厘米,问大正方形 A E H C F B G D
从简单情况入手 从特殊到一般 【例7】(★★★★★) 传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有 10平方米。每当太阳西下,钟面就会出现奇妙的阴影(如下图)。那么, 阴影部分的面积是多少平方米? 12 1 11 2 10
9 8 7 6 5 4
第2讲圆、扇形的面积与周长(二)

第2讲圆形、扇形的面积与周长(二)重点摘要本讲主要讲授利用等积变形,重叠等方法求解圆形、扇形的面积与周长。
以及求解圆形、扇形与其他平面图形所组成的平面组合图形的面积。
精讲精练例题1、有七根直径5cm 的塑料管,用一根橡皮筋把它们勒成一捆(如图所示),此时橡皮筋的长度是多少?(π取3.14)练习1、如下图所示,圆的周长为15.7分米,圆的面积是长方形面积的32,问图中阴影部分的周长是多少分米?(π=3.14)例题2、如图,图①和图②是两个相同的正方形,图①中阴影部分是4个圆,图②中阴影部分是9个圆。
那么图中阴影部分的面积大?为什么?练习2、下左图是一个圆环,L 是圆环内最长的线段,下右图是以L 为直径的圆。
问:下左图的圆环与下右图的圆相比,谁的面积大?L L例题3、如下图,等边三角形边长是10厘米,那么阴影部分的周长是厘米?(π取3.14)练习3、如图所示,图中圆的直径AB是4厘米,平行四边形ABCD的面积是7平方厘米,∠ABC=30度,求阴影部分的面积(π取3.14,得数保留两位小数)。
例题4、如图所示,阴影部分的面积是200平方厘米,求两个圆之间的圆环面积。
(π取3.14)练习4、在正方形ABCD中,AC=6厘米。
求阴影部分的面积。
例题5、如图所示,求图中阴影部分的面积(π取3.14)。
练习5、图中阴影部分的面积是多少平方厘米?(π取3.14)例题6、求图中阴影部分的面积(π取3.14)。
练习6、等腰直角三角形的一腰的长是8厘米,以它的两腰为直径分别画了两个半圆,那么阴影部分的面积共有多少平方厘米?(π取3.14)【拓展题】如图正方形边长为1,则阴影部分面积为多少?。
(结果保留π)【课堂练习】1、求图形中阴影部分的面积(π取3.14)。
2、右图是由五个圆所构成的,其中总共有3种不同长度的直径,且有部分的圆彼此相切,如图所示。
若最大圆内白色部分的总面积是20cm2,则其中阴影部分的面积是多少平方厘米?3、三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米.AB长40厘米,BC长多少厘米?(π取3.14)4、下图三个圆的半径都是5厘米,三个圆两两相交于圆心。
五年级奥数圆和扇形的周长与面积二

加油站
C B
答案:1
【例6】(★★★★)(北大附中“资优博雅杯”数学竞赛)(2)如图,阴影正方形的顶点分别是大正方形
各边的中点,分别以大正方形各边的一半为直径向外
各边的中点分别以大正方形各边的一半为直径向外
做半圆,再分别以阴影正方形的各边为直径向外作半
圆,形成个月牙形个月牙形
圆,形成8个“月牙形”。
这8个“月牙形”的总面积
为32平方厘米,问大正方形EFGH的面积是多少?
A
H
D
加加点睛
三个转化:化未知为已知;
化不规则为规则;为不可求为可求
四个基本方法:割补、变换、
差不变、整体、
重点例题:例1,例2,例3,例4,例5。
第二讲圆和扇形的周长与面积学案及详解[六年级秋]
![第二讲圆和扇形的周长与面积学案及详解[六年级秋]](https://img.taocdn.com/s3/m/100c3e80f524ccbff121843f.png)
第二讲图形问题(二)————圆的周长与面积知识导航一、概念。
圆:到定点等于定长的点的集合叫做圆,其中定点叫做圆心,圆心用字母O表示。
圆的半径:从圆心到圆上任意一点之间的线段叫做圆的半径,用字母r表示。
在同一个圆中有无数条半径,所有半径长度都相等。
圆的直径:通过圆心并且两端都在圆上的线段叫做圆的直径,直径用字母d表示。
在同一个圆里有无数条直径,所有直径长度都相等。
圆周率:圆的周长与它的直径的比值叫做圆周率,用字母π表示。
它是一个固定的数,是一个无限不循环小数(即无理数)。
圆的周长:围成圆的曲线的长叫做圆的周长。
圆的面积:圆所占平面的大小叫做圆的面积。
圆是轴对称图形,圆的直径所在的直线就是圆的对称轴,它有无数条对称轴。
二、常用公式。
用字母C、S分别表示圆的周长与面积,计算公式可以表示为:C=πd或C=2πr S=πr²三、解题策略数形结合、代换……精典例题例1:把一个圆切拼成一个宽等于半径的近似长方形后,周长增加12cm,那么这个圆的面积与周长各是多少?(2007年成都七中育才学校东区衔接班招生考试题1)思路点拨想一想:你能画出切拼图吗?并在图上标出切拼图与圆的关系吗?模仿练习把一个圆切拼成一个宽等于半径的近似长方形后,这个长方形的周长是33.12cm,那么这个圆的面积与周长各是多少?例2:在一个面积为20cm²的正方形中画一个最大的圆,这个圆的面积是多少?思路点拨想一想:在一个正方形中画一个最大的圆,这个圆与正方形有什么关系?如果从另一个角度想:要求圆的面积必须知道的最直接的条件是什么?友情提示:所谓的最直接的条件,就是指知道后可以只用一步计算就能回答问题的。
模仿练习在一个正方形中画一个最大的圆,这个最大圆的面积是15.7cm²,那么这个正方形的面积是多少?例3:图中阴影部分的面积是4cm²,环形面积是多少?(2004年成都七中育才东区初中招生考试题)思路点拨想一想:难吧!其实不难,把问题想简单一点儿!什么叫做圆环,圆环的面积怎么计算?想清楚后,你会发现这道题格外的简单!模仿练习如图,阴影部分的面积是60cm²,那么圆环的面积是多少?例4:如图所示,已知正方形的边长是3cm,那么阴影部分的面积是多少?思路点拨想一想,计算阴影部分面积的基本方法是什么?你认为关键是要先求出什么?现在你可以计算了吗?再想一想,还有没有更巧的方法呢?模仿练习已知下图长方形的长宽分别是6cm、4cm,分别以长、宽为半径作了两个直角扇形,计算阴影部分的面积。
圆和扇形的面积计算公式

圆和扇形的面积计算公式在我们的数学世界里,圆和扇形就像是两个独特的小精灵,它们的面积计算公式可是非常有趣且实用的。
记得有一次,我带着侄子去公园玩耍。
那是一个阳光明媚的周末,公园里热闹非凡。
侄子突然指着一个圆形的花坛问我:“姑姑,这个花坛有多大呀?”这一下可把我问住了,不过我灵机一动,心想这不正是给侄子讲解圆面积计算公式的好机会嘛。
咱们先来说说圆的面积计算公式,那就是S = πr²。
其中,S 表示圆的面积,π是一个神奇的常数,约等于 3.14159 ,r 则是圆的半径。
这个公式就像是一把神奇的钥匙,能够帮助我们打开圆面积的神秘大门。
比如说,有一个圆,它的半径是 5 厘米,那么它的面积就是3.14×5×5 = 78.5 平方厘米。
想象一下,这个圆就像是一个大大的披萨,而我们通过这个公式就能算出它可以被切成多少块。
再来说说扇形。
扇形就像是从圆这个大蛋糕上切下来的一块美味。
扇形的面积计算公式是 S = (n/360)×πr² ,这里的 n 表示扇形圆心角的度数。
举个例子,如果有一个扇形,它的半径是8 厘米,圆心角是60 度,那么它的面积就是(60÷360)×3.14×8×8 ≈ 33.5 平方厘米。
就像那次在公园,我给侄子解释完花坛面积的计算方法后,他似懂非懂地点点头。
后来我们走到一个卖风筝的小摊前,有一个风筝的形状就是扇形的。
侄子又好奇地问我:“姑姑,这个风筝的面积能算出来吗?”我笑着告诉他:“能呀,只要知道半径和圆心角的度数,就能算出来啦。
”在日常生活中,圆和扇形的面积计算可太有用啦!比如我们装修房子时,要计算圆形的地毯面积;做蛋糕时,要计算圆形蛋糕模具能装多少面糊;设计扇子时,要知道扇形的面积来确定用料多少。
总之,圆和扇形的面积计算公式虽然看起来有点复杂,但只要我们多练习、多思考,就能像掌握魔法一样,轻松地算出它们的面积,解决生活中的各种小难题。
学而思-----第二讲 圆和扇形的周长与面积

D
E
D
E
A
A
B
C
F
B
C
F
4、旋转法(例 6) 旋转法是本讲的重 点与难点,对于“羊吃草”的问题还是比较 简单的。关键是直线型旋转面积,学员无法 想到
直线旋转后所扫发到 过的面积,其实,由教师讲解后你会发现, 一般情况下直线所扫过一周的面积(有特例 ,如:钝
角三角形的长边绕钝角顶点旋转时)就是一个圆环的面积。所以旋转多少度就再乘以 即可。
够活动的最大范围是 多少?(
)
分析:如图,羊活动的范围是受绳子的牵制的,所以羊活动的最大范围即绳子 AE 所扫过的总面积。(三部分)
(1) 红色部分为按绳长 30 米所能达到的最大范围(绳子不受任何牵制),此图形为半径 30,
圆心角 270 度的扇形。
(2) 黄色部分为按绳长 10 米所能达到的最大范围(绳子受点 D 牵制),所以之后只能按半径
由第三个图可知:所求面积已转化为扇环的面积,圆心角度数为 120 度。所以 阴影=
(
)
S=
E
E
E
C
C
G
C
G
A
B
D
A
F
B
D
A
F
B
D
第二讲 圆和扇形的周长和面积 2.2
五年级秋季班 第二讲 圆和扇形的周长与面积
曹威
拓展练习:“羊吃草 ”问题
草场上有一个长 20 米,宽 10 米的关闭着的羊圈,在羊圈外的一角,用长 30 米的绳子拴着一只羊,问这只羊能
B
C
C
B
O
A
O
A
分析:与丄题同理 A 点移到 O 点,阴影面积变为扇形 OBC 的面积,注意:圆心角 COB=60 度。
六年级数学圆和扇形知识点总结

六年级数学圆和扇形知识点总结一、圆的认识1、圆的定义圆是平面内到一定点的距离等于定长的点的集合。
这个定点称为圆心,定长称为半径。
2、圆的各部分名称(1)圆心:用字母 O 表示,圆心决定圆的位置。
(2)半径:连接圆心和圆上任意一点的线段叫做半径,用字母 r 表示。
半径决定圆的大小。
(3)直径:通过圆心并且两端都在圆上的线段叫做直径,用字母 d 表示。
3、圆的特征(1)在同圆或等圆中,直径是半径的 2 倍,半径是直径的一半,用字母表示为:d = 2r,r = d÷2。
(2)圆是轴对称图形,直径所在的直线是圆的对称轴,圆有无数条对称轴。
二、圆的周长1、圆的周长的定义围成圆的曲线的长度叫做圆的周长。
2、圆的周长计算公式圆的周长 C =πd 或 C =2πr (其中π是圆周率,通常取值 314)3、半圆的周长半圆的周长=圆周长的一半+直径,即 C 半圆=πr + 2r三、圆的面积1、圆的面积的定义圆所占平面的大小叫做圆的面积。
2、圆的面积计算公式圆的面积 S =πr²3、圆环的面积圆环的面积=外圆面积内圆面积,即 S 圆环=π(R² r²)(其中R 为外圆半径,r 为内圆半径)四、扇形1、扇形的定义由圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
2、扇形的面积扇形的面积=圆心角的度数÷360°×圆的面积,即 S 扇形=n÷360×πr² (其中 n 为圆心角的度数)3、扇形的周长扇形的周长=弧长+ 2 条半径,弧长=圆心角的度数÷360°×圆的周长,即 C 扇形=n÷360×2πr + 2r五、圆和扇形的应用1、已知圆的半径或直径,求圆的周长、面积例如:一个圆的半径是 5 厘米,求它的周长和面积。
周长:C =2πr = 2×314×5 = 314(厘米)面积:S =πr² = 314×5²= 785(平方厘米)2、已知圆的周长,求圆的半径或直径例如:一个圆的周长是 2512 分米,求它的半径。
[第4讲]圆和扇形的周长与面积(二)
![[第4讲]圆和扇形的周长与面积(二)](https://img.taocdn.com/s3/m/e2a8d9056c175f0e7cd1373c.png)
(2008 年北大附中“资优博雅杯”数学竞赛) 如下图,在以 AB 为直径的半圆上取一点,分别以 AC 和 BC 为直径在△ABC 外作半圆 AEC 和 BFC。已知 AC 的长度为 4,BC 的长度为 3,AB 的长度为 5。试求阴影部分的面积。
(2008 年北大附中“资优博雅杯”数学竞赛) 如图,阴影正方形的顶点分别是大正方形 EFGH 各边的中点,分别以大正方形各边的一半 为直径向外做半圆, 再分别以阴影正方形的各边为直径向外作半圆, 再分别以阴影正方形的 各边为直径向外作半圆,形成 8 个“月牙形” 。这 8 个“月牙形”的总面积为 32 平方厘米, 问大正方形 EFGH 的面积是多少平方厘米?
1
如图,直角三角形 ABC 中,AB 是圆的直径,且 AB=20,阴影甲的面积比阴影乙的面积大 7,求 BC 长。(π取 3.14)
如图是一个直径为 3cm 的半圆,让这个半圆以 A 点为轴沿逆时针方向旋转 60°,此时 B 点 移动到 B'点,求阴影部分的面积。(图中长度单位为 cm,圆周率按 3 计算)。
弓形: 弓形一般不要求周长,主要求面积。 一般来说,弓形面积=扇形面积-三角形面积。(除了半圆)
“弯角” :弯角的面积=正方形-扇形
“谷子” : “谷子”的面积=弓形面积×2
(第 6 届“迎春杯”决赛试题) 如图中扇形的半径 OA=OB=6 厘米,∠AOB=45°,AC 垂直 OB 于 C,那么图中阴影部分 的面积是 平方厘米。(π≈3.14)
2
1.圆的周长与面积 2.扇形的周长与面积 3.常用的数学思想 常用的思想: 转化思想 等积变形 借来还去 容斥 外围入手
在线测试题
温馨提示:请在线作答,以便及时反馈孩子的薄弱环节。 1.如下图所示,扇形的半径 OA=OB=6 cm ,∠AOB=45°,AC 垂直 OB 于 C,那么途中阴 影部分的面积是( A. 3 ) cm2 ( 取 3) B.4.5 C.6 D. 9
爱提分圆和扇形的周长及面积公式

一:周长与面积公式知识精讲在同一平面内,到定点的距离等于定长的点的集合叫做圆.点O就称为该圆的圆心;圆心与圆周上任意一点的连线(例如线段OA)叫做半径;通过圆心,并且两端都在圆上的线段叫做直径.直径长恰好是半径长的两倍.圆心确定了圆所在的位置,半径长度确定了圆的大小.一个圆只要确定了“圆心”和“半径”,就能完全确定下来.圆周长与直径的比值是一个固定不变的数,我们称之为圆周率,用希腊字母表示.圆周率是一个无限不循环小数,无法写成分数的形式.在实际问题的计算中,常常取近似值.一.圆的周长与面积公式1.直径长度通常用字母d表示,半径长度通常用r表示,圆周长通常用C 表示,圆面积通常用字母S表示.2.圆周长公式:蜜蜂飞行:无论小圆有多少个,大小是否相等,只要所有小圆的直径之和等于大圆的直径,那么它们的周长之和也等于大圆的周长.3.圆面积公式:二.扇形的周长与面积公式扇形是指圆上被两条半径和半径之间的弧所包围的部分.其中,圆的半径也称为扇形的半径,而两条半径所成的夹角称为扇形的圆心角.扇形是圆的一部分.要想知道扇形的弧长与面积,只要知道它是所在圆的几分之几就可以了.它是圆的几分之几,它的弧长就是圆周长的几分之几,它的面积也同样就是圆面积的几分之几.1.扇形弧长公式:2.扇形面积公式:3.温馨提示:扇形的弧长不是它的周长,扇形的周长还必须加上两条半径.三点剖析重难点:扇形周长公式,需要加上两条半径题模精讲题模一圆的周长与面积公式例、已知一个圆的直径为2厘米,那么这个圆的周长为_________厘米,面积为_________平方厘米.答案:;解析:周长为厘米,面积为平方厘米.例、已知一个圆的周长为厘米,那么这个圆的直径为_________厘米.答案:16解析:直径为厘米.例、有一个圆形花坛,直径为20米,一只小蜜蜂沿着花坛外周飞了一圈,请问它飞了多少米如果小蜜蜂沿着图中的虚线,飞一个“8”字,路线构成过花坛圆心的两个小圆,那么这次它飞了多少米(取)答案:(1)米(2)米解析:小圆半径是5米,飞行路线为两个小圆周长,所以是米.无论小圆有多少个,大小是否相等,只要所有小圆的直径之和等于大圆,那么它们的周长之和也等于大圆.例、如图,已知长方形的面积是12,则图中阴影部分的面积是多少(取)答案:解析:长方形可以分成两个面积相等的正方形,面积都是6.方中圆,方和圆的面积比为,可求出小圆的面积是,那么阴影部分的面积是.例、如图,在一块面积为平方厘米的圆形铝板中,裁出了7个同样大小的圆铝板.问:余下的边角料的总面积是多少平方厘米(取)答案:平方厘米解析:,大圆半径是3厘米.小圆半径是1厘米,所以边角料面积为平方厘米.例、已知大圆的直径为10厘米,有四个大小不等的圆,圆心都在大圆的一条直径上,并且它们的直径之和与大圆相等.那么4个小圆的周长之和是________厘米.(取)答案:解析:假设中间4个小圆的直径分别为a、b、c、d,则有,4个小圆的周长之和为厘米.例、如图,直角三角形的面积是40平方厘米,圆的面积是________平方厘米(π取3).答案:240解析:直角三角形的直角边即为圆的半径,所以,,圆的面积是平方厘米.题模二扇形的周长与面积公式例、如图3,圆P的直径OA是圆O的半径,,,则阴影部分的面积是__________.(π取3)答案:75解析:阴影部分的面积等于大圆面积的一半减去小圆的面积,即.例、一个扇形的半径为6平方厘米,圆心角为60°,这个扇形的周长是__________厘米.(取)答案:解析:这个扇形是它所在圆的,所以这个扇形的弧长是cm,扇形的周长是厘米.例、一个扇形的面积为平方厘米,圆心角为45°,这个扇形的周长是_______厘米.(取)解析:这个扇形是它所在圆的,所以这个圆的半径的平方是,所以这个圆的半径是4厘米,所以扇形的半径是4厘米,扇形的周长是厘米.例、在荷兰的小镇卡茨赫弗尔,2013年6月建成了一个由三个半圆组成的城市雕塑,三个半圆的直径分别为,,.这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形(Arbelos),即下图中阴影部分所示的图形.那么,该城市雕塑中的鞋匠刀形的周长为__________(圆周率用π表示)答案:πm解析:鞋匠刀形的周长是由3条半圆形弧线组成,所以周长为m.例、如图,等边三角形ABC的边长是1,依次以A、C、B为圆心,以BA、CD、BE为半径画扇形,那么三个扇形的面积和是多少(结果保留π)答案:解析:各扇形圆心角均为,半径分别为1、2、3,因此三个扇形的面积和是.例、一个半径为3分米的扇形,面积为平方分米,那么它的圆心角是__________,它的弧长又是__________分米.答案:80°,根据题意得,,所以,所以圆心角是度.弧长为.例、如图,边长为3cm与5cm的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是________(结果保留π).答案:解析:连结AC、FB.易知,故,.例、如图,有三个同心半圆,它们的直径分别为2,6,10,用线段分割成9块,如果每块字母代表这一块的面积并且相同的字母代表相同的面积,那么(A+B):C =_______答案:55:48解析:设A的半径为,B的半径为,C的半径为A的面积:B的面积:3B=,.C的面积:5C=,..题模三捆圆的周长和面积已知下图中的每个小圆的半径均为1,这个图形的面积是__________.(取)答案:解析:如图,对图形进行分割后可知这个图形的面积相当于8个边长为2的正方形和一个半径为1的圆的面积的和.面积为.例、如图,有8个半径为1的小圆,用它们圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.那么花瓣图形的周长和面积分别是多少答案:周长,面积解析:如图,做辅助线后可以看出周长为4个的圆弧加上4个半圆弧,所以周长为;而面积为正方形减去4个半圆加上4个圆,即.例、如图,每个圆的面积都为,求该图形的外周长.答案:解析:圆半径为2.图形外周长可以分为三段长为4的线段和三段120°角的圆弧,则外周长为.如图,有七根直径为5厘米的塑料管,用一根橡皮筋把它们扎成一捆,此时橡皮筋的长度是多少厘米答案:解析:如图,作辅助线后可以发现外周长是由6段长度为5的线段和6个60°角的圆弧组成,所以皮筋长度为.随堂练习随练、已知一个圆的直径是12厘米,那么这个圆的面积为__________平方厘米(取)答案:解析:直径为12厘米,那么半径为6厘米,面积是平方厘米.随练、已知一个圆的面积为314平方厘米,那么这个圆的直径为_______厘米(取)答案:20解析:这个圆的半径为平方是,所以这个圆的半径是10厘米,直径是20厘米.随练、半径分别为1、2、3、4厘米的四个圆的周长之和是多少厘米(取)答案:厘米解析:圆的周长公式为,周长之和为厘米.随练、如图,在一块面积为平方厘米的纸板中,裁出了2个同样大小的圆纸板.问:余下的纸板的总面积是多少平方厘米(取)答案:平方厘米解析:大圆的面积是平方厘米,可求出大圆的半径是2厘米,那么小圆的半径是1厘米,面积是平方厘米.阴影部分的面积是平方厘米.随练、已知三个小圆的圆心在大圆同一直径上,周长分别为3、1、2厘米,则大圆周长为多少厘米(π取近似值)答案:6解析:大圆的直径等于三个小圆的直径之和,周长也恰为3个小圆周长之和.随练、如图,边长为3cm与5cm的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是__________(结果保留π).答案:解析:阴影部分面积为梯形ABFE与扇形ABC的面积之和减去三角形FEC的面积,易得为.随练、已知一个扇形的半径是10厘米,圆心角是,那么:(1)这个扇形所在圆的周长是_________厘米,扇形的圆心角占圆周角的_________,它的弧长占圆周长的_________,这个扇形的弧长是_________厘米,周长是_________厘米.(2)这个扇形面积占它所在圆的面积的_________,是_________平方厘米.答案:(1);;;;(2);解析:(1)这个扇形所在圆的周长是厘米,扇形的圆心角占圆周角的,它的弧长占圆周长的,这个扇形的弧长是厘米,周长是.(2)这个扇形面积占它所在圆的面积的,面积是平方厘米.随练、半径为10、20、30的三个扇形如下图放置,是的__________倍.答案:5解析:为,为,所以是的5倍.随练、根据图中所给的数值,求这个图形的面积.(π取近似值)答案:解析:平方厘米.4个直角扇形的面积之和是4,因此整个圆角矩形的面积就是.随练、如图,有七根直径为4厘米的塑料管,用一根橡皮筋把它们扎成一捆,此时橡皮筋的长度是多少厘米(π取近似值)答案:解析:把圆角六边形的周长分为12个部分,由6条直线段和6段圆弧组成.6条直线段中,每段的长度都是5厘米,它们的长度和是厘米6段圆弧中,每段所对应的圆心角都是60°,每段的弧长都是圆周长的,6段圆弧恰好能拼成一个完整的圆周.它们的弧长之和就是圆周长,即厘米.圆角六边形的周长就是这两部分长度之和,即厘米.课后作业作业1、已知圆的直径为20米,那这个圆的周长为多少米(π取近似值)答案:解析:圆周长的计算公式为:C圆=π×D.作业2、把两根横截面半径都是10厘米的钢管用铁丝紧紧捆在一起,如果捆绑处不计,至少要用铁丝____________厘米.答案:解析:厘米.作业3、一辆压路机的前轮是圆柱形,轮宽米,直径是米.前轮转动一周,压路的面积是______平方米.答案:平方米解析:轮子压一周,周长为米,即压在路面上的长是米,压路的面积=长×宽平方米.作业4、已知圆的面积是314平方米,那圆的周长是多少米(π取近似值)答案:解析:由圆的面积可以求出半径的平方,算出半径后可由公式计算圆的周长,为.作业5、已知三个小圆的圆心在大圆同一直径上,周长分别为1、2、3厘米,则大圆周长为多少厘米(π取近似值)答案:6解析:大圆的直径等于三个小圆的直径之和,周长也恰为3个小圆周长之和.作业6、如图,在一块面积为36平方厘米的圆形铝板中,裁出了7个同样大小的圆铝板.问:余下的边角料的总面积是多少平方厘米答案:8平方厘米解析:小圆的半径是整个大圆半径的,因此小圆的面积是大圆面积的,为平方厘米;大圆去掉7个小圆后剩下的面积是平方厘米.作业7、已知一个扇形的圆心角为120°,半径为2,这个扇形的面积是________,周长是________(π取).答案:面积,周长解析:扇形的面积;周长.作业8、如图,求各图中阴影部分的面积.(取)答案:解析:阴影部分面积为半径为4的半圆面积减去对角线为8的等腰直角三角形面积.阴影部分面积为.作业9、已知扇形的半径为3米,面积为米,那扇形的圆心角为多少度(π取近似值)答案:180解析:扇形所在圆的面积≈×32=平方米,由此可知该扇形是它所在圆的.那么圆心角应该是360°的二分之一.作业10、已知一个扇形的半径为5厘米,弧长为厘米,这个扇形的面积是多少答案:解析:因为扇形的弧长为厘米,所以,可得.扇形面积为平方厘米.作业11、根据图中所给的数值,求这个图形的面积.(π取近似值)答案:解析:平方厘米.4个直角扇形的面积之和是,因此整个圆角矩形的面积就是.作业12、如图,三个圆的半径都是4,那整个图形的外周长是多少(π取近似值)答案:解析:整个外周长可以分为3段直线和3段弧形.作业13、如图,有七根直径为10厘米的塑料管,用一根橡皮筋把它们扎成一捆,此时橡皮筋的长度是多少厘米(π取近似值)答案:解析:把圆角六边形的周长分为12个部分,由6条直线段和6段圆弧组成.6条直线段中,每段的长度都是5厘米,它们的长度和是厘米6段圆弧中,每段所对应的圆心角都是60°,每段的弧长都是圆周长的,6段圆弧恰好能拼成一个完整的圆周.它们的弧长之和就是圆周长,即厘米.圆角六边形的周长就是这两部分长度之和,即厘米.。
扇形的周长公式和面积公式是什么

扇形的周长公式和面积公式是什么
扇形也是一种图形,那么扇形的周长公式和面积公式是多少呢?有些同学需要这种问题的解答。
下面是由小编为大家整理的“扇形的周长公式和面积公式是什么”,仅供参考,欢迎大家阅读。
扇形的周长公式和面积公式是什么
1、扇形周长公式为:扇形周长=扇形半径×2+弧长,即C=2r+ (n÷360) πd=2r+(n÷180)πr。
扇形面积公式是S=(lR)/2 或S=(1/2)θR²,R是底圆的半径,l为扇形弧长,θ为圆心角。
2、一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形)。
拓展阅读:如何计算扇形圆心角的度数
计算扇形圆心角的度数的方法:
1、用弧长除以周长,用这个比值乘以圆周角360度;
2、用扇形面积除以圆的面积,用所得比值乘以圆周角360度即可。
扇形是什么图形
一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形)。
《几何原本》中这样定义扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形。
扇形,是圆的一部分,由两个半径和和一段弧围成,在较小的区域被称为小扇形,较大的区域被称为大扇形。
在右图中,θ是扇形的角弧度,r是圆的半径,L是小扇形的弧长。
圆弧为180°的扇形称为半圆。
其他圆弧角的扇形有时给予其特别的名字,其中包括象限角(90°)、六分角(60°)以及八分角(45°),它们分别是整圆的1/4、1/6、1/8。
爱提分圆和扇形的周长及面积公式

一:周长与面积公式知识精讲在同一平面内,到定点的距离等于定长的点的集合叫做圆.点O就称为该圆的圆心;圆心与圆周上任意一点的连线(例如线段OA)叫做半径;通过圆心,并且两端都在圆上的线段叫做直径.直径长恰好是半径长的两倍.圆心确定了圆所在的位置,半径长度确定了圆的大小.一个圆只要确定了“圆心”和“半径”,就能完全确定下来.圆周长与直径的比值是一个固定不变的数,我们称之为圆周率,用希腊字母表示.圆周率是一个无限不循环小数,无法写成分数的形式.在实际问题的计算中,常常取近似值.一.圆的周长与面积公式1.直径长度通常用字母d表示,半径长度通常用r表示,圆周长通常用C 表示,圆面积通常用字母S表示.2.圆周长公式:蜜蜂飞行:无论小圆有多少个,大小是否相等,只要所有小圆的直径之和等于大圆的直径,那么它们的周长之和也等于大圆的周长.3.圆面积公式:?二.扇形的周长与面积公式扇形是指圆上被两条半径和半径之间的弧所包围的部分.其中,圆的半径也称为扇形的半径,而两条半径所成的夹角称为扇形的圆心角.扇形是圆的一部分.要想知道扇形的弧长与面积,只要知道它是所在圆的几分之几就可以了.它是圆的几分之几,它的弧长就是圆周长的几分之几,它的面积也同样就是圆面积的几分之几.1.扇形弧长公式:2.扇形面积公式:3.温馨提示:扇形的弧长不是它的周长,扇形的周长还必须加上两条半径.三点剖析重难点:扇形周长公式,需要加上两条半径题模精讲题模一?圆的周长与面积公式例、已知一个圆的直径为2厘米,那么这个圆的周长为_________厘米,面积为_________平方厘米.答案:;解析:周长为厘米,面积为平方厘米.?例、已知一个圆的周长为厘米,那么这个圆的直径为_________厘米.答案:16解析:直径为厘米.?例、有一个圆形花坛,直径为20米,一只小蜜蜂沿着花坛外周飞了一圈,请问它飞了多少米?如果小蜜蜂沿着图中的虚线,飞一个“8”字,路线构成过花坛圆心的两个小圆,那么这次它飞了多少米?(取)答案:(1)米(2)米解析:小圆半径是5米,飞行路线为两个小圆周长,所以是米.无论小圆有多少个,大小是否相等,只要所有小圆的直径之和等于大圆,那么它们的周长之和也等于大圆.?例、如图,已知长方形的面积是12,则图中阴影部分的面积是多少?(取)答案:解析:长方形可以分成两个面积相等的正方形,面积都是6.方中圆,方和圆的面积比为,可求出小圆的面积是,那么阴影部分的面积是.?例、如图,在一块面积为平方厘米的圆形铝板中,裁出了7个同样大小的圆铝板.问:余下的边角料的总面积是多少平方厘米?(取)答案:平方厘米解析:,大圆半径是3厘米.小圆半径是1厘米,所以边角料面积为平方厘米.?例、已知大圆的直径为10厘米,有四个大小不等的圆,圆心都在大圆的一条直径上,并且它们的直径之和与大圆相等.那么4个小圆的周长之和是________厘米.(取)答案:解析:假设中间4个小圆的直径分别为a、b、c、d,则有,4个小圆的周长之和为厘米.?例、如图,直角三角形的面积是40平方厘米,圆的面积是________平方厘米(π取3).答案:240解析:直角三角形的直角边即为圆的半径,所以,,圆的面积是平方厘米.?题模二?扇形的周长与面积公式例、如图3,圆P的直径OA是圆O的半径,,,则阴影部分的面积是__________.(π取3)答案:75解析:阴影部分的面积等于大圆面积的一半减去小圆的面积,即.?例、一个扇形的半径为6平方厘米,圆心角为60°,这个扇形的周长是__________厘米.(?取)答案:解析:这个扇形是它所在圆的,所以这个扇形的弧长是cm,扇形的周长是厘米.?例、一个扇形的面积为平方厘米,圆心角为45°,这个扇形的周长是_______厘米.(取)答案:解析:这个扇形是它所在圆的,所以这个圆的半径的平方是,所以这个圆的半径是4厘米,所以扇形的半径是4厘米,扇形的周长是厘米.?例、在荷兰的小镇卡茨赫弗尔,2013年6月建成了一个由三个半圆组成的城市雕塑,三个半圆的直径分别为,,.这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形(Arbelos),即下图中阴影部分所示的图形.那么,该城市雕塑中的鞋匠刀形的周长为__________(圆周率用π表示)答案:πm解析:鞋匠刀形的周长是由3条半圆形弧线组成,所以周长为m.?例、如图,等边三角形ABC的边长是1,依次以A、C、B为圆心,以BA、CD、BE 为半径画扇形,那么三个扇形的面积和是多少?(结果保留π)答案:解析:各扇形圆心角均为,半径分别为1、2、3,因此三个扇形的面积和是.?例、一个半径为3分米的扇形,面积为平方分米,那么它的圆心角是__________,它的弧长又是__________分米.答案:80°,解析:根据题意得,,所以,所以圆心角是度.弧长为.?例、如图,边长为3cm与5cm的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是________(结果保留π).答案:解析:?连结AC、FB.易知,故,.?例、如图,有三个同心半圆,它们的直径分别为2,6,10,用线段分割成9块,如果每块字母代表这一块的面积并且相同的字母代表相同的面积,那么(A+B):C =_______答案:55:48解析:设A的半径为,B的半径为,C的半径为A的面积:B的面积:3B=,.C的面积:5C=,..?题模三?捆圆的周长和面积例、已知下图中的每个小圆的半径均为1,这个图形的面积是__________.(取)答案:解析:如图,对图形进行分割后可知这个图形的面积相当于8个边长为2的正方形和一个半径为1的圆的面积的和.面积为.?例、如图,有8个半径为1的小圆,用它们圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.那么花瓣图形的周长和面积分别是多少?答案:周长,面积解析:如图,做辅助线后可以看出周长为4个的圆弧加上4个半圆弧,所以周长为;而面积为正方形减去4个半圆加上4个圆,即.?例、如图,每个圆的面积都为,求该图形的外周长.答案:解析:圆半径为2.图形外周长可以分为三段长为4的线段和三段120°角的圆弧,则外周长为.?例、如图,有七根直径为5厘米的塑料管,用一根橡皮筋把它们扎成一捆,此时橡皮筋的长度是多少厘米?答案:解析:如图,作辅助线后可以发现外周长是由6段长度为5的线段和6个60°角的圆弧组成,所以皮筋长度为.?随堂练习随练、已知一个圆的直径是12厘米,那么这个圆的面积为__________平方厘米?(取)答案:解析:直径为12厘米,那么半径为6厘米,面积是平方厘米.?随练、已知一个圆的面积为314平方厘米,那么这个圆的直径为_______厘米?(取)答案:20解析:这个圆的半径为平方是,所以这个圆的半径是10厘米,直径是20厘米.?随练、半径分别为1、2、3、4厘米的四个圆的周长之和是多少厘米?(取)答案:厘米解析:圆的周长公式为,周长之和为厘米.?随练、如图,在一块面积为平方厘米的纸板中,裁出了2个同样大小的圆纸板.问:余下的纸板的总面积是多少平方厘米?(取)答案:平方厘米解析:大圆的面积是平方厘米,可求出大圆的半径是2厘米,那么小圆的半径是1厘米,面积是平方厘米.阴影部分的面积是平方厘米.?随练、已知三个小圆的圆心在大圆同一直径上,周长分别为3、1、2厘米,则大圆周长为多少厘米?(π取近似值)答案:6解析:大圆的直径等于三个小圆的直径之和,周长也恰为3个小圆周长之和.?随练、如图,边长为3cm与5cm的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是__________(结果保留π).答案:解析:阴影部分面积为梯形ABFE与扇形ABC的面积之和减去三角形FEC的面积,易得为.?随练、已知一个扇形的半径是10厘米,圆心角是,那么:(1)这个扇形所在圆的周长是_________厘米,扇形的圆心角占圆周角的_________,它的弧长占圆周长的_________,这个扇形的弧长是_________厘米,周长是_________厘米.(2)这个扇形面积占它所在圆的面积的_________,是_________平方厘米.答案:(1);;;;(2);解析:(1)这个扇形所在圆的周长是厘米,扇形的圆心角占圆周角的,它的弧长占圆周长的,这个扇形的弧长是厘米,周长是.(2)这个扇形面积占它所在圆的面积的,面积是平方厘米.?随练、半径为10、20、30的三个扇形如下图放置,是的__________倍.答案:5解析:为,为,所以是的5倍.?随练、根据图中所给的数值,求这个图形的面积.(π取近似值)答案:解析:平方厘米.4个直角扇形的面积之和是4,因此整个圆角矩形的面积就是.?随练、如图,有七根直径为4厘米的塑料管,用一根橡皮筋把它们扎成一捆,此时橡皮筋的长度是多少厘米?(π取近似值)答案:解析:把圆角六边形的周长分为12个部分,由6条直线段和6段圆弧组成.6条直线段中,每段的长度都是5厘米,它们的长度和是厘米6段圆弧中,每段所对应的圆心角都是60°,每段的弧长都是圆周长的,6段圆弧恰好能拼成一个完整的圆周.它们的弧长之和就是圆周长,即厘米.圆角六边形的周长就是这两部分长度之和,即厘米.?课后作业作业1、已知圆的直径为20米,那这个圆的周长为多少米?(π取近似值)答案:解析:圆周长的计算公式为:C=π×D.?作业2、把两根横截面半径都是10厘米的钢管用铁丝紧紧捆在一起,如果捆绑处不计,至少要用铁丝____________厘米.答案:解析:厘米.?作业3、一辆压路机的前轮是圆柱形,轮宽米,直径是米.前轮转动一周,压路的面积是______平方米.答案:平方米解析:轮子压一周,周长为米,即压在路面上的长是米,压路的面积=长×宽平方米.?作业4、已知圆的面积是314平方米,那圆的周长是多少米?(π取近似值)答案:解析:由圆的面积可以求出半径的平方,算出半径后可由公式计算圆的周长,为.?作业5、已知三个小圆的圆心在大圆同一直径上,周长分别为1、2、3厘米,则大圆周长为多少厘米?(π取近似值)答案:6解析:大圆的直径等于三个小圆的直径之和,周长也恰为3个小圆周长之和.?作业6、如图,在一块面积为36平方厘米的圆形铝板中,裁出了7个同样大小的圆铝板.问:余下的边角料的总面积是多少平方厘米?答案:8平方厘米解析:小圆的半径是整个大圆半径的,因此小圆的面积是大圆面积的,为平方厘米;大圆去掉7个小圆后剩下的面积是平方厘米.?作业7、已知一个扇形的圆心角为120°,半径为2,这个扇形的面积是________,周长是________(π取).答案:面积,周长解析:扇形的面积;周长.?作业8、如图,求各图中阴影部分的面积.(取)答案:解析:阴影部分面积为半径为4的半圆面积减去对角线为8的等腰直角三角形面积.阴影部分面积为.?作业9、已知扇形的半径为3米,面积为米,那扇形的圆心角为多少度?(π取近似值)答案:180解析:扇形所在圆的面积≈×3=平方米,由此可知该扇形是它所在圆的.那么圆心角应该是360°的二分之一.?作业10、已知一个扇形的半径为5厘米,弧长为厘米,这个扇形的面积是多少?答案:解析:因为扇形的弧长为厘米,所以,可得.扇形面积为平方厘米.作业11、根据图中所给的数值,求这个图形的面积.(π取近似值)答案:解析:平方厘米.4个直角扇形的面积之和是,因此整个圆角矩形的面积就是.?作业12、如图,三个圆的半径都是4,那整个图形的外周长是多少?(π取近似值)答案:解析:整个外周长可以分为3段直线和3段弧形.作业13、如图,有七根直径为10厘米的塑料管,用一根橡皮筋把它们扎成一捆,此时橡皮筋的长度是多少厘米?(π取近似值)答案:解析:把圆角六边形的周长分为12个部分,由6条直线段和6段圆弧组成.6条直线段中,每段的长度都是5厘米,它们的长度和是厘米6段圆弧中,每段所对应的圆心角都是60°,每段的弧长都是圆周长的,6段圆弧恰好能拼成一个完整的圆周.它们的弧长之和就是圆周长,即厘米.圆角六边形的周长就是这两部分长度之和,即厘米.。
圆和扇形的相关知识点总结

圆和扇形的相关知识点总结一、圆的基本概念圆是平面上一组到一点距离相等的所有点的集合。
它由一个中心点和一个半径组成。
圆的半径是从中心点到圆上任意一点的距离。
二、圆的性质 1. 圆的周长:圆的周长是圆上一点到另一点的距离。
圆的周长公式为C = 2πr,其中C表示圆的周长,r表示圆的半径,π是一个常数,约等于3.14159。
2. 圆的面积:圆的面积是圆内部的平面面积。
圆的面积公式为A = πr^2,其中A表示圆的面积,r表示圆的半径。
3. 圆的直径:圆的直径是通过圆心并且两端点都在圆上的线段。
直径是半径的两倍,即d = 2r。
4. 圆的弧长:圆的弧长是圆上一段弧的长度。
弧长的公式为L = 2πr(θ/360°),其中L表示弧长,r表示圆的半径,θ表示弧度的角度。
5. 圆的弧度:圆的弧度是圆上一段弧所对应的圆心角的度量。
弧度和角度之间的转换关系为:1弧度≈ 57.3°。
6. 圆的切线:圆上一点的切线是与圆相切且与半径垂直的直线。
三、扇形的基本概念扇形是由圆心、圆弧和两条半径所围成的图形。
扇形可以看作是一个圆心角所对应的圆弧和两条半径组成的图形。
四、扇形的性质 1. 扇形的圆心角:扇形的圆心角是扇形两条边所夹的角度。
圆心角的度数可以用扇形的圆心角度量来表示。
2. 扇形的弧长:扇形的弧长是扇形圆弧的长度。
弧长的计算公式为L = 2πr(θ/360°),其中L表示弧长,r表示扇形的半径,θ表示圆心角的度数。
3. 扇形的面积:扇形的面积是扇形所覆盖的圆形面积的一部分。
扇形的面积计算公式为A = πr^2(θ/360°),其中A表示扇形的面积,r表示扇形的半径,θ表示圆心角的度数。
五、常见应用场景 1. 扇形在地理上用于表示地球表面上的各种区域,如时区和地域划分。
2. 扇形在建筑设计中用于确定某个区域的角度和面积,如窗户的设计和阳台的布局。
3. 扇形在机械制造中用于设计和制造各种旋转部件,如轮胎和齿轮。
六年级圆、扇形的周长与面积

学员姓名年级:学科教师:辅导科目:授课日期XX年XX月XX日时间 A / B / C / D / E / F 段主题圆、扇形的周长与面积教学内容------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------1扮习目标1 •理解圆周率的意义,推导出圆周长的计算公式,并能正确进行计算;2 •会推导弧长计算公式并能运用弧长公式解决弧长、图形周长问题;3•理解圆的面积计算公式并能正确进行计算,理解扇形的概念,掌握扇形面积与圆面积之间的关系,并正确运用公式进行扇形面积的计算;4•利用扇形面积、圆心角与圆的关系看懂扇形统计图,并能解答相关的问题.说明:C表示圆的周长,d表示直径,r表示半径,S表示圆的面积,二表示圆周率,是个无限不循环小数, 近似等于3.14。
知识抢答圆的面积计算公式:n0圆心角所对的扇形的面积计算公式: S扇形個为弧长所以S扇形360■r21 n 1r r |r )2 180 2(此环节设计时间在10- 15分钟)圆周长计算公式:C=2r= dn o圆心角所对的弧长nl 2 :r 厂360n 一r 180动探索360练习1圆的周长是直径的()5•圆的面积扩大为原来的四倍,则半径( )A 、扩大为4倍;B 、扩大为16倍;C 、不变;D 、 扩大为2倍6.一个扇形的半径扩大2倍,圆心角扩大 3倍,则扇形的面积() A 、扩大5倍 B 、扩大6倍C 、扩大18倍D 、 扩大12倍7.一个扇形的圆心角扩大3倍,弧长扩大 6倍,则扇形的面积()A 、扩大5倍B 、扩大6倍C 、扩大18倍D 、 扩大12倍 &扇形的面积是157平方厘米,它所在的圆面积是1256平方厘米,则扇形的圆心角是 9•已知圆心角为120。
圆和扇形的周长与面积(二)
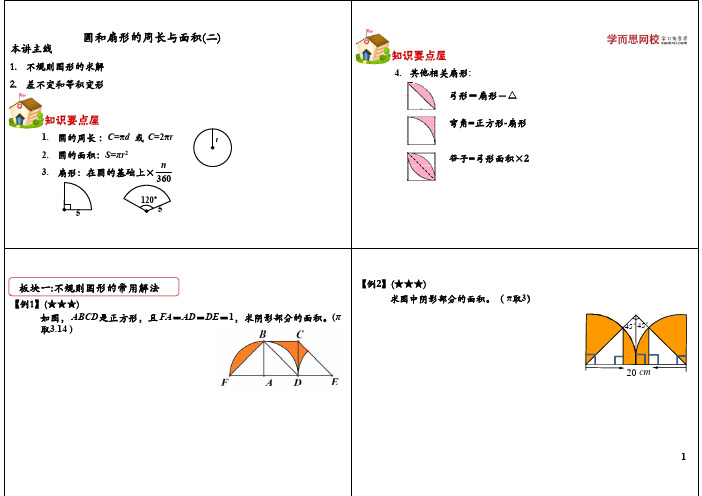
【例2】(★★★)
求图中阴影部分的面积。( π取3)
45° 45°
20 cm
1
板块二:差不变和等积变形
【例3】(★★★☆) 在图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积 差。(圆周率取3 )
A
B
C
3
本讲主线
圆和扇形的周长与面积(二)
4. 其他相关扇形: 弓形=扇形-△ 弯角=正方形-扇形
1. 不规则图形的求解 2 差不变和等积变形 2.
1 圆的周长 :C=πd 或 C=2πr 1. 2. 圆的面积:S=πr2
r 谷子=弓形面积×2
n 3. 扇形:在圆的基础上× 360
120° 5
5
板块一:不规则图形的常用解法
n 360 基本模型:弓形,弯角,谷子 不规则图形:割补、平移、旋转、对称 两个考点: ⑴同加同减差不变 ⑵等积变形 一个模型:两个月亮换个三角 个模型 两个月亮换个三角
公式:圆= 公式 圆 π×r2 扇形=圆×
【今日讲题】 例 超常大挑战 例1~超常大挑战 【讲题心得】 ______________________________________________________________ 【家长评价】 ______________________________________________________________
【例4】(★★★) 如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分 面积是多少?(圆周率取 3.14) D E A
B
C
F
【例5】(★★★★) 如图,矩形ABCD中,AB= 6厘米,BC= 4厘米,扇形ABE 半径AE =6 厘米,扇形CBF 的半径CB= 4厘米圆中的直角三角形:顶点在圆上,并且经过圆心的三角形是直角三 角形. 例如:
五年级奥数思维训练圆与扇形的周长与面积计算

练一练
根据已知信息,将表格填补完整。(单位:厘米,π取3.14)
半径(r) 1 2 3 4
直径(d) 2 4 6 8
周长(C) 2π 4π 6π 8π
面积(S) 1π 4π 9π
25π
通过观察此表,回答:圆的半径扩大n倍,周长和面积分别扩 大几倍?
练一练
根据已知信息,将表格填补完整。(单位:厘米,π取3.14)
直径(d) 2 4 6
周长(C) 2π 4π 6π 8π
面积(S) 1π 4π
25π
通过观察此表,回答:圆的半径扩大n倍,周长和面积分别扩 大几倍?
练一练
根据已知信息,将表格填补完整。(单位:厘米,π取3.14)
半径(r) 1 2 3
直径(d) 2 4 6
周长(C) 2π 4π 6π 8π
面积(S) 1π 4π 9π
练一练
根据已知信息,将表格填补完整。(单位:厘米,π取3.14)
半径(r) 1 2
直径(d) 2 4 6
周长(C) 2π
8π
面积(S) 1π
25π
通过观察此表,回答:圆的半径扩大n倍,周长和面积分别扩 大几倍?
练一练
根据已知信息,将表格填补完整。(单位:厘米,π取3.14)
半径(r) 1 2
直径(d) 2 4 6
ห้องสมุดไป่ตู้
半径(r) 1 2
直径(d) 2
6
周长(C) 2π
8π
面积(S) 25π
通过观察此表,回答:圆的半径扩大n倍,周长和面积分别扩 大几倍?
练一练
根据已知信息,将表格填补完整。(单位:厘米,π取3.14)
半径(r) 1 2
直径(d) 2
六年级圆、扇形的周长与面积

六年级圆、扇形的周长与面积(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1.理解圆周率的意义,推导出圆周长的计算公式,并能正确进行计算;2.会推导弧长计算公式并能运用弧长公式解决弧长、图形周长问题;3.理解圆的面积计算公式并能正确进行计算,理解扇形的概念,掌握扇形面积与圆面积之间的关系,并正确运用公式进行扇形面积的计算;4.利用扇形面积、圆心角与圆的关系看懂扇形统计图,并能解答相关的问题.(此环节设计时间在10-15分钟)说明: C 表示圆的周长,d 表示直径,r 表示半径,S 表示圆的面积,π表示圆周率,是个无限不循环小数,近似等于14.3。
知识抢答圆周长计算公式:d r C ππ==2on 圆心角所对的弧长: r n r n l ππ1802360=⨯=圆的面积计算公式:2S r π=on 圆心角所对的扇形的面积计算公式:2360r nS π=扇形或12S lr =扇形 (因为弧长r n l π180= 所以lr r r n r n S 21180213602=⨯⨯==ππ扇形)练习1.圆的周长是直径的()A、倍;B、倍;C、3倍;D、 倍2.圆的半径扩大为原来的3倍()A、周长扩大为原来的9倍B、周长扩大为原来的6倍C、周长扩大为原来的3倍D、周长不变3.圆的半径不变,圆心角扩大为原来的2倍,则()A、弧长扩大为原来的4倍B、弧长扩大为原来的2倍C、弧长不变D、弧长缩小为原来的一半4.圆的半径扩大为原来的3倍()A、面积扩大为原来的9倍B、面积扩大为原来的6倍C、面积扩大为原来的3倍D、面积不变5.圆的面积扩大为原来的四倍,则半径()A、扩大为4倍;B、扩大为16倍;C、不变;D、扩大为2倍6.一个扇形的半径扩大2倍,圆心角扩大3倍,则扇形的面积()A、扩大5倍B、扩大6倍C、扩大18倍D、扩大12倍7.一个扇形的圆心角扩大3倍,弧长扩大6倍,则扇形的面积()A、扩大5倍B、扩大6倍C、扩大18倍D、扩大12倍8.扇形的面积是157平方厘米,它所在的圆面积是1256平方厘米,则扇形的圆心角是度。
扇形的面积公式和周长公式弧度制

扇形的面积公式和周长公式弧度制在咱们学习数学的奇妙旅程中,扇形可是个有趣的小家伙。
今天咱们就来好好唠唠扇形的面积公式和周长公式,还有那个有点神秘的弧度制。
先来说说扇形的面积公式。
这就好比你去买披萨,扇形的披萨块儿大小怎么算呢?扇形的面积公式是 S = (n/360)×πr² ,这里的 n 表示扇形圆心角的度数,r 是扇形所在圆的半径。
举个例子,有一个扇形,圆心角是 90 度,半径是 5 厘米。
那它的面积就是(90/360)×π×5² = 1/4 × 25π = 6.25π 平方厘米。
这就好像是把整个圆平均分成了 360 份,扇形占了其中的 n 份,所以面积就是相应的比例乘以整个圆的面积。
再聊聊扇形的周长公式。
这就像是给扇形围个漂亮的“篱笆”,得知道需要多长的材料。
扇形的周长公式是 C = L + 2r ,这里的 L 是扇形的弧长,r 还是扇形所在圆的半径。
弧长 L 又等于(n/180)×πr 。
比如说有个扇形,圆心角是 120 度,半径是 8 厘米。
先算弧长 L = (120/180)×π×8 = 16π/3 厘米,那周长 C 就是16π/3 + 2×8 = 16π/3 + 16 厘米。
接下来讲讲弧度制,这可是个有点特别的东西。
咱们平常习惯用角度来衡量圆心角,比如说 30 度、60 度。
但弧度制就不太一样啦,它用弧长和半径的比值来表示圆心角的大小。
还记得有一次我在课堂上讲这些知识,有个同学一脸迷茫地问我:“老师,这弧度制到底有啥用啊?”我笑着回答他:“就好比你用尺子量东西,角度制是一种刻度,弧度制又是另一种刻度,各有各的用处呀。
”然后我给他举了个例子,比如在研究三角函数的时候,弧度制就特别方便,能让计算更简洁呢。
其实在生活中,扇形的面积和周长公式以及弧度制也都有不少用处。
比如说设计师在设计扇子的时候,就得用到扇形的知识,算一算面积和周长,才能做出美观又实用的扇子。
扇形的面积和周长计算

扇形的面积和周长计算扇形是我们在数学中经常会遇到的一个图形,它由圆的一部分构成,具有独特的面积和周长计算方法。
今天,咱们就来详细聊聊扇形的面积和周长到底怎么算。
咱们先来说说扇形的定义。
扇形呢,是由圆心角的两条半径和圆心角所对的弧围成的图形。
形象点说,就像是把一个圆像切蛋糕一样切下了一块。
那扇形的面积怎么算呢?这得先从圆的面积说起。
我们都知道,圆的面积公式是 S =πr² ,其中 r 是圆的半径。
而扇形呢,其实就是圆的一部分,它的面积和圆心角的大小有关系。
如果圆心角的度数是 n 度,扇形所在圆的半径是 r ,那么扇形的面积 S 扇就可以用下面这个公式来计算:S 扇=n/360 × πr² 。
打个比方,如果一个扇形的圆心角是 90 度,半径是 5 厘米,那么这个扇形的面积就是 90/360 × 314 × 5²= 19625 平方厘米。
再来说说扇形的周长。
扇形的周长可不像面积那么简单,它由两部分组成,一部分是扇形的弧长,另一部分是扇形的两条半径。
那扇形的弧长怎么算呢?我们先想想圆的周长,圆的周长 C =2πr 。
而扇形的弧长呢,其实就是圆周长的一部分。
如果圆心角是 n 度,半径是 r ,那么扇形的弧长 L 弧就可以用公式 L 弧=n/180 × πr 来计算。
所以,扇形的周长 C 扇就等于扇形的弧长加上两条半径,也就是 C 扇=n/180 × πr + 2r 。
比如说,一个扇形的圆心角是 120 度,半径是8 厘米,那么扇形的弧长就是120/180 × 314 × 8 ≈ 1675 厘米,扇形的周长就是 1675 + 2×8 = 3275 厘米。
为了更好地理解扇形的面积和周长计算,咱们来做几道实际的题目。
例 1:有一个扇形,半径为 6 厘米,圆心角为 60 度,求它的面积和周长。
先算面积,根据公式 S 扇= 60/360 × 314 × 6²= 1884 平方厘米。
圆和扇形周长与面积

为“祖冲之圆周率”,简称“祖率”。
刘徽——割圆术
魏晋时期数学家 所谓“割圆术”就是圆内接正多边形的周长去无限 逼近于圆的周长,并以此求圆周率的方法。
割之弥细,所失弥少。 割之又割,以至于不可割。 则与圆合体而无所失矣。
圆周率
圆周率用字母π (读作pài)表示,约等于 3.141592654……,是个无限不循环小数。
360分之1
l 1 2πr 1 πr
1° R
360
180
n°圆心角所对弧长是圆周长 的几分之几,弧长是多少?
360分之n
l n 2πr n πr
360
180
判断
1、圆心角相等,所对弧的长也相等。( )
2、如果一条圆弧所对的圆心角是45°,
那么这条圆弧的长与所在圆的周长的
比的比值是 1
2. 弧长
弧长
圆上 A、B 两点之间的部分就叫做弧,
记作: AB 读作:弧AB 。
∠AOB称为圆心角。
圆心角就是以圆心为顶点,以半径 为两边所组成的角。
记作: AOB
读作:角AOB
B
圆心角 O
A
90°圆心角所对的弧长是圆 周长的几分之几?
90° R
1°圆心角所对弧长是圆周长 的几分之几,弧长是多少?
解:R轨=500+6400=6900 C轨=2πR轨=2×3.14×6900 =43332 14C轨=43332×14=606648(千米)
答:卫星围绕地球一共飞行了约606648千米.
例题3:有一个圆环,圆环的外圆周长 C1=250cm,内圆周长C2=150cm,求圆环的宽度 d(精确到0.1cm)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形。
扇形是圆的一部分
扇形的圆心角占这个圆周角的几分之几 扇形的弧长 C =2360n r π⨯ 扇形的面积 S =2360
n r π⨯ 扇形的周长=2360
n
r π⨯
+2×半径 (易错点是把扇形的周长等同于扇形的弧长)
弓形: 弓形一般不要求周长,主要求面积。
一般来说,弓形面积=扇形面积-三角形面积。
(除了半圆)
“弯角”:弯角的面积=正方形-扇形
“谷子”:“谷子”的面积=弓形面积×2
(第6届“迎春杯”决赛试题)
圆和扇形的周长与面积(二)
如图中扇形的半径OA=OB=6厘米,∠AOB=45°,AC垂直OB于C,那么图中阴
影部分的面积是平方厘米。
(π≈3.14)
45°
O C B
A
如图,直角三角形ABC中,AB是圆的直径,且AB=20,阴影甲的面积比阴影乙的面积大7,求BC长。
(π取3.14)
乙
甲
C
B
A
如图是一个直径为3cm的半圆,让这个半圆以A点为轴沿逆时针方向旋转60°,此时B点移动到B'点,求阴影部分的面积。
(图中长度单位为cm,圆周率按3计算)。
B'
60
(2008年北大附中“资优博雅杯”数学竞赛)
如下图,在以AB为直径的半圆上取一点,分别以AC和BC为直径在△ABC外作半圆AEC和BFC。
已知AC的长度为4,BC的长度为3,AB的长度为5。
试求阴影部分的面积。
(2008年北大附中“资优博雅杯”数学竞赛)
如图,阴影正方形的顶点分别是大正方形EFGH各边的中点,分别以大正方形各边的一半为直径向外做半圆,再分别以阴影正方形的各边为直径向外作半圆,再分别以阴影正方形的各边为直径向外作半圆,形成8个“月牙形”。
这8个“月牙形”的总面积为32平方厘米,问大正方形EFGH的面积是多少平方厘米?
1.圆的周长与面积
2.扇形的周长与面积
3.常用的数学思想
常用的思想:
转化思想
等积变形
借来还去
容斥
外围入手
在线测试题
温馨提示:请在线作答,以便及时反馈孩子的薄弱环节。
1.如下图所示,扇形的半径OA=OB=6cm,∠AOB=45°,AC垂直OB于C,那么途中阴影部分的面积是( )2
cm ( π取3)
A.3 B.4.5 C.6 D.9
2.如下图所示,甲比乙的面积大2
50cm,20
=,那么BC的长为( )cm( π
AB cm
取3)
A.5 B.8 C.10 D.15
A
3.下图是由直径分别为4cm,6cm和10cm的三个半圆所组成的图形,图中阴影部分的面积是( )cm2 ( π取3)
A.30 B.31.4 C.43.5 D.60
4.如下图所示,大半圆半径为4cm,小半圆直径为4cm,那么图中阴影部分的面积是( )2
cm( π取3)
A.5 B.6 C.10 D.18
5.如下图所示,大圆半径为6,那么阴影部分的面积是( )(π取3)
A.36 B.48 C.60 D.72。
