中考数学一轮复习第一章数与式第四节因式分解同步测试题及答案.doc

合集下载

（完整版）初中数学因式分解单元测试试题含答案

（完整版）初中数学因式分解单元测试试题含答案因式分解单元测试数学考试一、单选题（共12 题；共36 分）1.若(x-3)(x+5)是x2+px+q 的因式，则p 为( )A. -15B. -2C. 8D. 22.在有理数范围内，下列各多项式能用公式法进行因式分解的是（）。

A. a2－6aB. a2－ab+b2C. a2－ab+b2D. a2－ab+b23.下列多项式的各项中,公因式是5a2b 的是( )A. 15a2b-20a2b2B. 30a2b3-15ab4-10a3b2C. 10a2b2-20a2b3+50a4b5D. 5a2b4-10a3b3+15a4b24.下列分解因式中，完全正确的是（）A. x3-x=x（x2-1）B. 4a2-4a+1=4a（a-1）+1C. x2+y2=（x+y）2D. 6a-9-a2=-（a-3）25.（2017?台湾）若a，b 为两质数且相差2，则ab+1 之值可能为下列何者（）A. 392B. 402D. 4226.任何一个正整数n 都可以进行这样的分解：n=s×t（s，t 是正整数，且s≤t），如果p×q 在n 的所有这种分解中两因数之差的绝对值最小，我们就称p×q 是n 的最佳分解，并规定：F（n）=．例如18 可以分解成1×18，2×9，3×6 这三种，这时就有F（18）==．给出下列关于F（n）的说法：（1）F（2）=；（2）F（24）= ；（3）F（27）=3；（4）若n 是一个完全平方数，则F（n）=1．其中正确说法的个数是（）A. 1 个B. 2 个C. 3 个D. 4 个7.下列分解因式正确的是（）A. x3﹣x=x（x2﹣1）B. x2+y2=（x+y）（x﹣y）C. （a+4）（a﹣4）=a2﹣16D. m2+m+ =（m+ ）28.把2x -4x 分解因式，结果正确的是( )A. (x+2)(x-2)B. 2x(x-2)C. 2(x -2x)D. x(2x-4)9.（2017?盘锦）下列等式从左到右的变形，属于因式分解的是（）A. x2+2x﹣1=（x﹣1）2B. （a+b）（a﹣b）=a2﹣b2C. x2+4x+4=（x+2）2D. ax2﹣a=a（x2﹣1）10.若x2﹣4x+3 与x2+2x﹣3 的公因式为x﹣c，则c 之值为何？（）B. ﹣1C. 1D. 311.多项式x2y2-y2-x2+1 因式分解的结果是（）A. （x2+1）（y2+1）B. （x-1）（x+1）（y2+1）C. （x2+1）（y+1）（y-1）D. （x+1）（x-1）（y+1）（y-1）12.已知a，b，c 为△ABC 三边，且满足a2c2-b2c2=a4-b4，则它的形状为（）A.等边三角形B. 直角三角形C. 等腰三角形D. 等腰三角形或直角三角形二、填空题（共6 题；共16 分）13.因式分解-x3+2x2y-xy2=14.因式分解：=15.分解因式：a2+ab=．16.因式分解：a2（x﹣y）﹣4b2（x﹣y）= ．17.分解因式：﹣2x3+4x2y﹣2xy2＝．18.若是完全平方式，那么= .三、计算题（共1 题；共6 分）19.先将代数式因式分解，再求值：2x（a﹣2）﹣y（2﹣a），其中a=0.5，x=1.5，y=﹣2．四、解答题（共6 题；共42 分）20.若a+b=﹣3，ab=1．求a3b+a2b2+ ab3的值．21.已知x2+y2+2x﹣6y+10=0，求x+y 的值．22.已知：（2x﹣y﹣1）2+ =0，（1）求的值；（2）求4x3y﹣4x2y2+xy3的值．23.先化简，再求值：（2a+3b）2﹣（2a﹣3b）2，其中a=．24.a4b﹣5a2b+4b．25.生活中我们经常用到密码，例如支付宝支付时．有一种用“因式分解”法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式：x3+2x2﹣x﹣2 可以因式分解为（x﹣1）（x+1）（x+2），当x=29 时，x﹣1=28，x+1=30，x+2=31，此时可以得到数字密码283031．（1）根据上述方法，当x=15，y=5 时，对于多项式x3﹣xy2分解因式后可以形成哪些数字密码？（2）已知一个直角三角形的周长是24，斜边长为11，其中两条直角边分别为x、y，求出一个由多项式x3y+xy3分解因式后得到的密码（只需一个即可）．答案解析部分一、单选题1.【答案】D【解析】【解答】解：, 左右恒等，故P=- 2，q=15.故答案为：D【分析】根据整式的运算把左式展开，合并同类项，因左右恒等，则x 的同次项系数相等求得P 值。

中考第一轮复习--第一章数与式

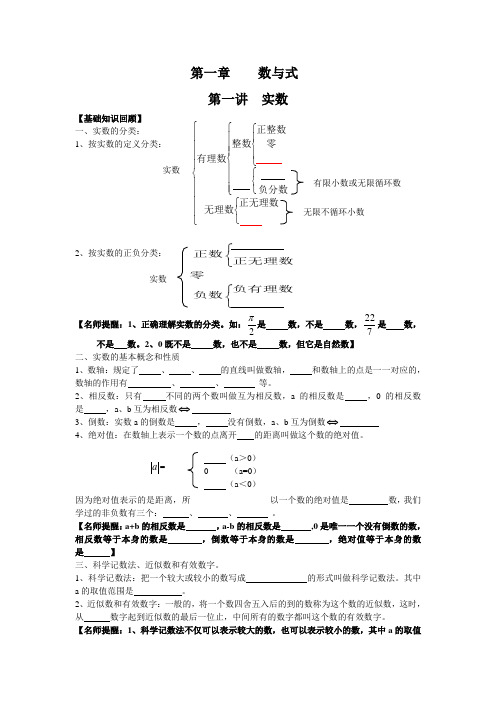
第一章数与式第一讲实数【基础知识回顾】一、实数的分类： 1、按实数的定义分类：实数有限小数或无限循环数2、按实数的正负分类：实数【名师提醒：1、正确理解实数的分类。

如：2π是数，不是数，722是数，不是数。

2、0既不是数，也不是数，但它是自然数】二、实数的基本概念和性质1、数轴：规定了、、的直线叫做数轴，和数轴上的点是一一对应的，数轴的作用有、、等。

2、相反数：只有不同的两个数叫做互为相反数，a 的相反数是，0的相反数是，a 、b 互为相反数⇔3、倒数：实数a 的倒数是，没有倒数，a 、b 互为倒数⇔4、绝对值：在数轴上表示一个数的点离开的距离叫做这个数的绝对值。

a =因为绝对值表示的是距离，所以一个数的绝对值是数，我们学过的非负数有三个：、、。

【名师提醒：a+b 的相反数是，a-b 的相反数是 ,0是唯一一个没有倒数的数，相反数等于本身的数是，倒数等于本身的数是，绝对值等于本身的数是】三、科学记数法、近似数和有效数字。

1、科学记数法：把一个较大或较小的数写成的形式叫做科学记数法。

其中a 的取值范围是。

2、近似数和有效数字：一般的，将一个数四舍五入后的到的数称为这个数的近似数，这时，从数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字。

【名师提醒：1、科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数无理数负分数零正整数整数有理数无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零负有理数负数（a ＞0）（a ＜0） 0 （a=0）范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）。

2020年中考数学第一轮复习第四节因式分解知识点+真题(后含答案)

2020年中考数学第一轮复习第一章数与式第四节因式分解【基础知识回顾】一、因式分解的定义：1、把一个式化为几个整式的形式，叫做把一个多项式因式分解。

2、因式分解与整式乘法是运算，即：多项式整式的积【注意：判断一个运算是否是因式分解或判断因式分解是否正确，关键看等号右边是否为的形式。

】二、因式分解常用方法：1、提公因式法：公因式：一个多项式各项都有的因式叫做这个多项式各项的公因式。

提公因式法分解因式可表示为：ma+mb+mc= 。

【注意：1、公因式的选择可以是单项式，也可以是，都遵循一个原则：取系数的，相同字母的。

2、提公因式时，若有一项被全部提出，则括号内该项为，不能漏掉。

3、提公因式过程中仍然要注意符号问题，特别是一个多项式首项为负时，一般应先提取负号，注意括号内各项都要。

】2、运用公式法：将乘法公式反过来对某些具有特殊形式的多项式进行因式分解，这种方法叫做公式法。

①平方差公式：a 2-b 2= ,②完全平方公式：a 2±2ab+b 2= 。

【注意：1、运用公式法进行因式分解要特别掌握两个公式的形式特点，找准里面的a 与b 。

如：x 2-x+14符合完全平方公式形式，而x 2- x+12就不符合该公式的形式。

】三、因式分解的一般步骤1、一提：如果多项式的各项有公因式，那么要先。

2、二用：如果各项没有公因式，那么可以尝试运用法来分解。

3、三查：分解因式必须进行到每一个因式都不能再分解为止。

【注意：分解因式不彻底是因式分解常见错误之一，中考中的因式分解题目一般为两步，做题时要特别注意，另外分解因式的结果是否正确可以用整式乘法来检验】【中考真题考点例析】考点一：因式分解的概念A ．a （x-y ）=ax-ayB ．x +2x+1=x （x+2）+1C ．（x+1）（x+3）=x 2+4x+3D ．x 3-x=x （x+1）（x-1）考点二：因式分解例2. （2019山东东营）因式分解：x(x-3)-x+3= ．对应练习2－1．（2019年济南）分解因式：244m m -+=_____．（）（）对应练习2－2．（2019年莱芜）分解因式：a 3﹣4ab 2= ．考点三：因式分解的应用例1. 答案：6，1对应练习1－1．答案：D考点二：因式分解例2. 答案：B对应练习2－1．答案：2(2)m -对应练习2－2．答案：a （a+2b ）（a ﹣2b ）考点三：因式分解的应用例3. 答案：4对应练习3－1．答案：18【聚焦中考真题】一、选择题：1．（2019年山东临沂）将a 3b －ab 进行因式分解，正确的是（）A ．a(a 2b －b)B ．ab(a －1)2C ．ab(a+1)(a －1)D ．ab(a 2－1)2．（2019潍坊）下列因式分解正确的是（）A ．3ax 2－6ax=3(ax 2－2ax)B ．x 2+y 2=(－x+y)(－x －y)C ．a 2+2ab －4b 2=(a+2b)2D ．－ax 2+2ax －a=－a(x －1)23.（南昌）下列因式分解正确的是（） A ．x 2-xy+x=x （x -y ） B ．a 3-2a 2b+ab 2=a （a -b ）2C ．x 2-2x+4=（x -1）2+3D ．ax 2-9=a （x+3）（x -3）4．（张家界）下列各式中能用完全平方公式进行因式分解的是（）A ．x 2+x+1B ．x 2+2x-1C ．x 2-1D ．x 2-6x+95．（佛山）分解因式a 3-a 的结果是（）A ．a （a 2-1）B ．a （a-1）2C ．a （a+1）（a-1）D ．（a 2+a ）（a-1）6．（恩施州）把x 2y-2y 2x+y 3分解因式正确的是（）A ．y （x 2-2xy+y 2）B ．x 2y-y 2（2x-y ）C ．y （x-y ）2D ．y （x+y ）2二、填空题：7.（2019年威海）分解因式:2x 2－2x ＋＝ .8．（2019年淄博）分解因式：=++x x x 6523 ．A ．3x -6x=x （3x-6）B ．-a +b =（b+a ）（b-a ）C．4x2-y2=（4x+y）（4x-y）D．4x2-2xy+y2=（2x-y）233．（内江）若m-n=6，且m-n=2，则m+n= ．参考答案一、选择题：1-5 CDBDC 6 C二、填空题：6.答案：()221 12x-7.答案：()()32++xxx8.答案：m(x+y)(x-y)9.答案：m(m-5)10.答案：B11.答案：2)2 (-ba12.答案：x(2-x)(2+x)13. 答案：5(x+2)(x -2)14. 答案：m(m+2)(m -2)15. 答案：b(a+2b)(a -2b)17. 答案：-91(3x+1)(3x -1)16. 答案：3(a+2b)(a -2b)17. 答案：2x(x -2)18. 答案：2m(m+2)(m -2)19. 答案：2（a+2b ）(a -2b)20. 答案：22）（-x21. 答案：a(b+1)(b -1)22. 答案：(x -1)23. 答案：a(a -2)24. 答案：x(x+y)25. 答案：(a+3)(a -3)26. 答案：x -227. 答案：(x+y)(x -y)28. 答案：(x+3y)(x -3y)29. 答案：a(m+2n)(m -2n)30. 答案：))((22x y x y y x -+ 31. 答案：332. 答案：2433. 答案：x(x+1)(x -1)34. 答案：-31。

中考数学一轮复习整式与因式分解中考真题训练 (有答案)

2020年中考数学一轮复习整式与因式分解中考真题训练一．选择题1.（2019•荆州）下列计算正确的是( )A.（－3x）3＝－27x3B.（x－2）2＝x4C.x2÷x－2＝x2D.x－1·x－2＝x22.（2019·百色）下列运算正确的是( )A.a2·a3＝a6B.（a2）3＝a5C.－a2·a＝－a3D.a5÷a3＝23.（2019•舟山）下列式子正确的是( )A.（a－b）2＝a2－2ab＋b2B.（a－b）2＝a2－b2C.（a－b）2＝a2＋2ab＋b2D.（a－b）2＝a2－ab＋b24.（2019•朝阳）下列运算正确的是( )A.a2·a4＝a8B.3x＋4y＝7xyC.（x－2）2＝x2－4D.2a·3a ＝6a25.（2019•河南）分解因式：16－x2＝( )A.（4－x）（4＋x）B.（x－4）（x＋4）C.（8＋x）（8－x）D.（4－x）26（2019•绵阳）用代数式表示：a的2倍与3 的和，下列表示正确的是( )A.2a－3B.2a＋3C.2（a－3）D.2（a＋3）7.（2019•苏州）苹果原价是每斤a元，现在按8折出售，假如现在要买一斤，那么需要付费( )A.0.8a元B.0.2a元C.1.8a元D.（a＋0.8）元8（2019•贺州）把多项式4a2－1分解因式，结果正确的是( )A.（4a＋1）（4a－1）B.（2a＋1）（2a－1）C.（2a－1）2D.（2a＋1）29.（2019•兰州）下列因式分解正确的是( )A.x2＋1＝（x＋1）2B.x2＋2x－1＝（x－1）2C.2x2－2＝2（x＋1）（x－1）D.x2－x＋2＝x（x－1）＋210.（2019•广州）下列计算正确的是( )A.x4÷x3＝xB.3x－x＝2C.（－x2）3＝x6D.（x＋y）2＝x2＋y211.（2019•青岛中考）下列运算正确的是( )A.2a＋3b＝5abB.3x2y－2x2y＝1C.（2a2）3＝6a6D.5x3÷x2＝5x12.（2019·桂林）下列计算正确的是( )A.a2·a3＝a6B.a8÷a2＝a4C.a2＋a2＝2a2D.（a＋3）2＝a2＋913.（2019•西宁）因式分解x－4x3的最后结果是( )A.x（1－2x）2B.x（2x－1）（2x＋1）C.x（1－2x）（2x＋1）D.x（1－4x2）14.（2019•承德）下列多项式中，不能因式分解的是( )A.a2＋1B.a2－6a＋9C.a2＋5aD.a2－115.（2019•石家庄）因式分解3ax2＋24axy＋48ay2的最后结果是( )A.3（ax2＋8axy＋16ay2）B.3a（x＋4y）2C.3a（x＋16y）2D.3a（x2＋8xy＋16y2）16.（2019•包头）如图是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒，…，则第n个图案中小棒根数是( )A.5nB.5n －1C.5n ＋1D.5n －317. （2019•赣州）观察以下一列数的特点：0，1，－4，9，－16，25，…，则第11个数是( )A.－121B.－100C.100D.12118．(2019•泰州)若2a －3b ＝－1，则代数式4a2－6ab ＋3b 的值为( )A ．－1B ．1C ．2D ．319．(2019•柳州)定义：形如a ＋bi 的数称为复数(其中a 和b 为实数，i 为虚数单位，规定i2＝－1)，a 称为复数的实部，b 称为复数的虚部．复数可以进行四则运算，运算的结果还是一个复数．例如(1＋3i)2＝12＋2×1×3i ＋(3i)2＝1＋6i ＋9i2＝1＋6i －9＝－8＋6i ，因此，(1＋3i)2的实部是－8，虚部是6.已知复数(3－mi)2的虚部是12，则实部是( )20．(2019•三门峡)我国南宋数学家杨辉所著的《详解九章算术》一书中，用如图的三角形解释二项式(a ＋b)n 的展开式的各项系数，此三角形称为“杨辉三角”．根据“杨辉三角”请计算(a ＋b)8的展开式中从左起第四项的系数为 ( )A ．84B ．56C ．35D ．28二．填空题21. (2019•齐齐哈尔)已知ab ＝a ＋b ＋1，则（a －1）（b －1）＝ .22. (2019•三亚)已知a ＋b ＝3，a －b ＝5，则代数式a 2－b 2的值是 .23.（2019·岳阳）已知x －3＝2，则代数式（x －3）2－2（x －3）＋1的值为 .24. (2019•黄冈)观察一列数：－3，0，3，6，9，12，…，按此规律，这一列数的第21个数是 .25. (2019•温州)观察以下一列数：3，54，79，916，1125，…，则第20个数是 . 26.（2019•天水）观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2 019个图形共有_________个○.…27.（2019•洛阳）观察下列一组数：32，－1，710，－917，1126，根据该组数的排列规律可推出第10个数是_________28.（2019•四平）观察下列各式的规律：（a－b）（a＋b）＝a2－b2，（a－b）（a2＋ab＋b2）＝a3－b3，（a－b）（a3＋a2b＋ab2＋b3）＝a4－b4，……可得到（a－b）（a2 019＋a2 018b＋…＋ab2 018＋b2 019）＝______________.29.（2019·达州）a是不为1的有理数，我们把11－a称为a的差倒数，如2的差倒数为11－2＝－1，－1的差倒数11－（－1）＝12.已知a1＝5，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，依此类推，a2 019的值是______________30.（2019·甘肃）如图，每一幅图中有若干个大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，如果第n幅图中有2 019个菱形，则n＝.三．解答题31. 先化简，再求值：（1）(2019·怀化) (2a－1)2－2(a＋1)(a－1)－a(a－2)，其中a＝2＋1.（2）(2019•沈阳)3a2－4ab＋[a2－2(a2－3ab)]，其中|a＋1|＋(b－12)2＝0.32. 分解因式：(1)(2019•开封)9x2－1；(2)(2019·贺州)m3(x－2)＋m(2－x)；(3)(2019·恩施)a2b－10ab＋25b.33. (2019•白城)已知a2＋b2＋6a－10b＋34＝0，求a＋b的值．参考答案一、选择题1-5 ACADA 6-10BABCA 11-15 DCCAB 16-20 CBBCB二、填空题21. 222. 1523. 124. 5725. 41 40026. 6 05827. －2110128. a2 020－b2 02029. 4 530. 1 010三、解答题31. （1））解：原式＝4a2－4a＋1－2a2＋2－a2＋2a＝a2－2a＋3，当a＝2＋1时，原式＝3＋22－22－2＋3＝4.＝9.(2)解：∵|a＋1|＋(b－12)2＝0，∴a＋1＝0，b－12＝0，∴a＝－1，b＝12.原式＝3a2－4ab＋(a2－2a2＋6ab)＝3a2－4ab＋a2－2a2＋6ab＝2a2＋2ab，当a＝－1，b＝12时，原式＝2×(－1)2＋2×(－1)×12＝2－1＝1.32. （1）解：原式＝(3x＋1)(3x－1)．(2)解：原式＝m(m＋1)(m－1)(x－2)．(3)解：原式＝b(a－5)2.33. 解：∵a2＋b2＋6a－10b＋34＝0，∴a2＋6a＋9＋b2－10b＋25＝0，即(a＋3)2＋(b－5)2＝0，∴a＋3＝0且b－5＝0，∴a＝－3，b＝5，∴a＋b＝－3＋5＝2.。

初中数学因式分解单元测试题(含答案)

1、2、、选择题:3、4、因式分解单元测试题F列运算中，正确的是( )A、x2x3=x6B、(ab)3=a3b3C、3a+2a=5a2下列各式从左到右的变形中，是因式分解的为( )x(a -b) = ax _bxx2 -1=(x 1)(x -1)F列各式是完全平方式的是( B、x2 -1 y2 =(x-1)(x 1)ax bx c = x(a b) c2 1 2x—x B、1 4x4F列多项式中能用平方差公式分解因式的是(A、a2 ( -b)2B、5m2-20mn c、- x2 - y2运用公式法计算992，应该是()A. (100 —1)2 B . (100 + 1)(100 1)25、6、把多项式m2(a - 2) ■ m(2 - a)分解因式等于((a-2)(m2 m) B 、(a-2)(m2-m)C m(a-2)(m-1)5D、(x3) 2= x y2a2ab b2D、D、x29-1)0. (99 + 1)(99 - 1)D. (99D m(a-2)(m+1)7、分解因式x4-1 得A(x2 1)(x2 -1)B(x 1)2(x-1)2C(x-1)(x 1)(x2 1) D (x-1)(x 1)38、无论x、y取何值，x2+ y2—2x + 12y + 40的值都是()A .正数E.负数C零D.非负数9、一个正方形的边长增加了2cm，面积相应增加了32cm2，则这个正方形的边长为( )A、6cmB、5cmC、8cmD、7cm二.填空1、在括号前面填上“ + ”或“—”号，使等式成立：(1)(y-x)2二(x-y)2; (2) (1-x)(2-x)二(x-1)(x-2)。

2、若a _2 +b2 _2b +1 = 0,贝U a2b +ab2= _________________________3、若x2—mx+16 = (x -4 f，那么m= ________________ 。

4、如果x y = 0, xy = -7, 贝卩x2y xy2二__________________ , x2y2二_________________________________________________________ < 5、利用因式分解简便计算：7.292—2.712二。

2024成都中考数学一轮复习专题因式分解 (含解析)

2024成都中考数学一轮复习专题因式分解一、单选题1．（2023·浙江杭州·统考中考真题）分解因式：241a -=（）A ．()()2121a a -+B ．()()22a a -+C ．()()41a a -+D ．()()411a a -+2．（2023·山东·统考中考真题）下列各式从左到右的变形，因式分解正确的是（）A ．22(3)69+=++a a a B ．()24444a a a a -+=-+C ．()()22555ax ay a x y x y -=+-D ．()()22824a a a a --=-+二、填空题3．（2023·辽宁丹东·校考二模）因式分解：24m m -=______．4．（2023·广东·统考中考真题）因式分解：21x -=______.5．（2022春·浙江杭州·七年级统考期末）分解因式：22x y -=__________6．（2023·山东临沂·统考二模）分解因式：24m -=_____．7．（2020秋·重庆沙坪坝·九年级重庆一中校考阶段练习）分解因式：222a a -=____________．8．（2023·四川成都·统考中考真题）因式分解：m 2﹣3m ＝__________．9．（2023·广东东莞·东莞市东莞中学初中部校考三模）因式分解221x x -+=______．10．（2018秋·广东湛江·八年级校考期末）分解因式：a 2+5a =________________.11．（2023·湖南张家界·统考中考真题）因式分解：22x y xy y ++=______．12．（2023·黑龙江绥化·统考中考真题）因式分解：2x xy xz yz +--=_______．13．（2023·四川眉山·统考中考真题）分解因式：3244x x x -+=______．14．（2023·甘肃武威·统考中考真题）因式分解：22ax ax a -+=________．15．（2023·浙江台州·统考中考真题）因式分解：x 2﹣3x =_____．16．（2023·湖南常德·统考中考真题）分解因式：3222a a b ab ++=_______．17．（2023·上海·统考中考真题）分解因式：29n -=________．18．（2023·湖北黄冈·校联考二模）分解因式：24xy x -=__________．19．（2021春·广西南宁·八年级南宁三中校考期中）因式分解：a 2+a b=_____．20．（2023·湖南永州·统考二模）分解因式：x 3﹣xy 2=_____．21．（2023·湖北十堰·统考中考真题）若3x y +=，2y =，则22x y xy +的值是___________________．22．（2020·江苏连云港·统考二模）分解因式：3a 2+6a b+3b 2=________________．23．（2023·内蒙古赤峰·统考中考真题）分解因式：3x 9x -=____.24．（2022春·上海奉贤·九年级校考期中）计算：（a +1）2﹣a 2=_____．25．（2023·江苏无锡·统考三模）分解因式：2242a a -+=_____．26．（2023春·广东茂名·八年级校考阶段练习）因式分解：x 2+x =_____．27．（2023·浙江·统考中考真题）分解因式：x 2－9＝______．28．（2023·广东广州·广州市第一中学校考二模）分解因式：x 3﹣6x 2+9x =___．29．（2023·浙江嘉兴·统考中考真题）一个多项式，把它因式分解后有一个因式为(1)x +，请你写出一个符合条件的多项式：___________．30．（2023·广东深圳·统考中考真题）已知实数a ，b ，满足6a b +=，7ab =，则22a b ab +的值为______．31．（2023·山东·统考中考真题）已知实数m 满足210m m --=，则32239m m m --+=_________．参考答案一、单选题1．【答案】A【分析】利用平方差公式分解即可．【详解】()()()2241212121a a a a -=-=+-．故选：A ．【点拨】此题考查了因式分解的方法，解题的关键是熟练掌握因式分解的方法．因式分解的方法有：提公因式法，平方差公式法，完全平方公式法，十字相乘法等．2．【答案】C【分析】根据因式分解的概念可进行排除选项．【详解】解：A.22(3)69+=++a a a ，属于整式的乘法，故不符合题意；B.()24444a a a a -+=-+，不符合几个整式乘积的形式，不是因式分解；故不符合题意；C.()()22555ax ay a x y x y -=+-，属于因式分解，故符合题意；D.因为()()22242828a a a a a a -+=+-≠--，所以因式分解错误，故不符合题意；故选：C ．【点拨】本题主要考查因式分解，熟练掌握因式分解的概念是解题的关键．二、填空题3．【答案】()4-m m 【分析】直接提取公因式m ，进而分解因式即可．【详解】解：m 2-4m =m (m -4)．故答案为：m (m -4)．【点拨】本题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．4．【答案】()()11x x +-【分析】利用平方差公式进行因式分解即可得．【详解】解：()()2111x x x -=+-，故答案为：()()11x x +-．【点拨】本题考查了利用平方差公式进行因式分解，熟记平方差公式是解题关键．5．【答案】()()x y x y +-【详解】解：()()22,x y x y x y -=+-故答案为：()()x y x y +-.6．【答案】(2)(2)m m +-【分析】直接根据平方差公式进行因式分解即可.【详解】24(2)(2)m m m -=+-，故答案为：(2)(2)m m +-.【点拨】本题考查利用平方差公式进行因式分解，解题关键在于熟练掌握平方差公式.7．【答案】2(1)a a -．【分析】利用提公因式法进行解题，即可得到答案．【详解】解：2222(1)a a a a -=-．故答案为：2(1)a a -．【点拨】本题考查了因式分解，解题的关键是掌握提公因式法进行解题．8．【答案】()3m m -【分析】题中二项式中各项都含有公因式m ，利用提公因式法因式分解即可得到答案．【详解】解：()233m m m m -=-，故答案为：()3m m -．【点拨】本题考查整式运算中的因式分解，熟练掌握因式分解的方法技巧是解决问题的关键．9．【答案】()21x -【分析】直接利用乘法公式分解因式得出答案．【详解】解：221x x -+=（x ﹣1）2．故答案为：（x ﹣1）2．【点拨】此题主要考查了公式法分解因式，正确应用乘法公式是解题关键．10．【答案】a (a+5)【分析】提取公因式a 进行分解即可．【详解】a 2+5a =a （a +5）．故答案是：a （a +5）．【点拨】考查了因式分解-提公因式法：如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法．11．【答案】()21+y x 【分析】先提取公因式，然后利用完全平方公式因式分解即可．【详解】解：2222(21)(1)x y xy y y x x y x ++=++=+，故答案为：2(1)y x +．【点拨】题目主要考查因式分解的方法，熟练掌握提公因式法及公式法是解题关键．12．【答案】()()x y x z +-【分析】先分组，然后根据提公因式法，因式分解即可求解．【详解】解：2x xy xz yz +--=()()()()x x y z x y x y x z +-+=+-，故答案为：()()x y x z +-．【点拨】本题考查了因式分解，熟练掌握因式分解的方法是解题的关键．13．【答案】2(2)x x -【分析】首先提取公因式x ，然后利用完全平方式进行因式分解即可．【详解】解：3244x x x-+()244x x x =-+2(2)x x =-，故答案为：2(2)x x -．【点拨】本题考查了提公因式法，公式法分解因式，提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．14．【答案】()21a x -【分析】先提取公因式，再利用平方差公式分解因式即可．【详解】解：()()2222211ax ax a a x x a x -+=-+=-，故答案为：()21a x -.【点拨】本题考查的是综合提公因式与公式法分解因式，掌握因式分解的方法与步骤是解本题的关键．15．【答案】x （x ﹣3）【详解】试题分析：提取公因式x 即可，即x 2﹣3x =x （x ﹣3）．故答案为：x （x ﹣3）.16．【答案】()2a ab +【分析】首先提公因式，原式可化为22(2)a a ab b ++，再利用公式法进行因式分解可得结果．【详解】解：3232222(2)()a a b b a a ab b a a b ++=++=+，故答案为：2()a a b +．【点拨】本题主要考查的是因式分解的运算，掌握因式分解运算的顺序“一提，二套，三分组，十字相乘做辅助”，利用合适方法进行因式分解，注意分解要彻底．17．【答案】()()33n n -+【分析】利用平方差公式进行因式分解即可．【详解】解：()()29=33n n n --+，故答案为：()()33n n -+．【点拨】本题考查因式分解，熟练掌握平方差公式是解题的关键．18．【答案】()(22)x y y +-【分析】先提公因式再利用平方差公式分解因式即可．【详解】解：24xy x-24()x y =-()(2)2x y y =+-故答案为：()(22)x y y +-．【点拨】本题考查利用提公因式、平方差公式分解因式等知识，是重要考点，难度较易，掌握相关知识是解题关键．19．【答案】a （a +b ）．【分析】直接提公因式a 即可.【详解】a 2+a b=a （a +b ）．故答案为：a （a +b ）．20．【答案】x （x +y ）（x -y ）【分析】先提取公因式x ，再对余下的多项式利用平方差公式继续分解．【详解】解：x 3-x y 2=x （x 2-y 2）=x （x +y ）（x -y ），故答案为：x(x +y)(x -y)．【点拨】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．21．【答案】6【分析】先提公因式分解原式，再整体代值求解即可．【详解】解：22x y xy +()xy x y =+，∵3x y +=，2y =，∴1x =，∴原式123=⨯⨯6=，故答案为：6．【点拨】本题主要考查因式分解，熟练掌握因式分解的方法，利用整体思想方法是解答的关键．22．【答案】3（a +b ）2【分析】先提取公因式3，再根据完全平方公式进行二次分解．完全平方公式：a 2+2a b+b 2=（a +b ）2．【详解】3a 2+6a b+3b 2=3（a 2+2a b+b 2）=3（a +b ）2．故答案为：3（a +b ）2．【点拨】本题考查了提公因式法，公式法分解因式．提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．23．【答案】()()x x 3x 3+-【分析】先提取公因式x 后继续应用平方差公式分解即可．【详解】()()()22x 9x x x 9x x 3x 3-=-=+-．故答案为：()()x x 3x 3+-.24．【答案】2a +1【详解】【分析】原式利用完全平方公式展开，然后合并同类项即可得到结果．【详解】（a +1）2﹣a 2=a 2+2a +1﹣a 2=2a +1，故答案为2a +1.【点拨】本题考查了整式的混合运算，熟练掌握完全平方公式以及合并同类项的法则是解题的关键.25．【答案】()221a -【详解】解：先提取公因式2后继续应用完全平方公式分解即可：原式()()2222121a a a =-+=-，故答案为：()221a -．26．【答案】()1x x +【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式，若有公因式，则把它提取出来，之后再观察是否是完全平方公式或平方差公式，若是就考虑用公式法继续分解因式．因此，直接提取公因式x 即可．【详解】解：()21x x x x +=+故答案为：()1x x +.27．【答案】(x ＋3)(x －3)【详解】解：x 2-9=（x +3）（x -3），故答案为：（x +3）（x -3）.28．【答案】x （x ﹣3）2【详解】解：x 3﹣6x 2+9x=x （x 2﹣6x +9）=x （x ﹣3）2故答案为：x （x ﹣3）2.29．【答案】21x -（答案不唯一）【分析】根据平方差公式或完全平方公式等知识解答即可．【详解】解：∵()()2111x x x -=+-，因式分解后有一个因式为(1)x +，∴这个多项式可以是21x -（答案不唯一）；故答案为：21x -（答案不唯一）．【点拨】本题考查了多项式的因式分解，熟练掌握分解因式的方法是解此题的关键．30．【答案】42【分析】首先提取公因式，将已知整体代入求出即可．【详解】22a b ab +()ab a b =+76=⨯42=．故答案为：42．【点拨】此题考查了求代数式的值，提公因式法因式分解，整体思想的应用，解题的关键是掌握以上知识点．31．【答案】8【分析】由题意易得21m m -=，然后整体代入求值即可．【详解】解：∵210m m --=，∴21m m -=，∴32239m m m --+()2229m m m m m --=-+229m m m -=-+29m m =-+()29m m =--+19=-+8=；故答案为8．【点拨】本题主要考查因式分解及整体思想，熟练掌握利用整体思维及因式分解求解整式的值．。

中考数学复习《数与式》考点及测试题(含答案)

中考数学复习《数与式》考点及测试题（含答案）【专题分析】本专题的主要考点有实数的有关概念，科学记数法，非负数的性质，实数的运算；幂的运算，整式的运算，因式分解；分式的概念，分式的加减，分式的混合运算；二次根式的有关概念，二次根式的性质，二次根式的运算等．中考中数与式的考查一般以客观张题为主，但分式的化简求值经常有开放型题目．数与式的考查常见题型以选择题或填空题为主，整式和分式的化简求值一般以解答题的形式进行考查．数与式在中考中所占比重约为20%～25%. 【解题方法】解决数与式问题的常用方法有数形结合法，特殊值法，分类讨论法，整体代入法，设参数法，逆向思维法等. 【知识结构】【典例精选】：计算：2－1－3tan 60°＋(π－2 015)0＋⎪⎪⎪⎪⎪⎪－12.【思路点拨】根据负整数指数幂、特殊角的三角函数、零次幂以及绝对值的概念计算即可．【自主解答】解：原式＝12－3×3＋1＋12＝－1.把x 2y －2y 2x ＋y 3分解因式正确的是( )A．y(x2－2xy＋y2) B．x2y－y2(2x－y)C．y(x－y)2 D．y(x＋y)2【思路点拨】首先提取公因式y，再利用完全平方公式进行二次分解即可．答案：C规律方法：利用两种方法结合的分解因式题目，提公因式后不要忘记利用公式法二次分解，分解因式要在规定的范围内分解彻底.先化简，再求值：(x＋3)(x－3)＋2(x2＋4)，其中x＝ 2.【思路点拨】原式第一项利用平方差公式展开，第二项去括号，合并同类项得到最简结果，将x的值代入计算即可求出代数式的值．【自主解答】解：原式＝x2－9＋2x2＋8＝3x2－1.当x＝2时，原式＝3×(2)2－1＝5.规律方法：整式的计算，要根据算式的特点选择合适的方法，可先选择乘法公式展开，然后合并；或先因式分解，然后计算.先化简，再求值：m－33m2－6m÷⎝⎛⎭⎪⎫m＋2－5m－2，其中m是方程x2＋3x＋1＝0的根．【思路点拨】在化简时要先算括号里面的，再把除法变为乘法，然后分解因式并约分，最后相乘．【自主解答】解：原式＝m－33m m－2÷m2－9m－2＝m－33m m－2×m－2m＋3m－3＝13m m＋3.∵m是方程x2＋3x＋1＝0的根，∴m2＋3m＋1＝0，∴m2＋3m＝－1，即m(m＋3)＝－1，∴原式＝13×－1＝－13.规律方法：1.本题采用了整体代入法求解，这是求代数式的值常用的方法，体现了整体思路的应用.2.分式的化简求值是先化简，再求值；化简时一定要化到最简，结果是最简分式或整式.【能力评估检测】一、选择题1．已知空气的单位体积质量是0.001 239 g/cm 3，则用科学记数法表示该数为( A )A ．1.239×10－3g/cm 3B ．1.239×10－2 g/cm 3C ．0.123 9×10－2 g/cm 3D ．12.39×10－4 g/cm 3 2．下列运算错误的是( B )A. ⎝ ⎛⎭⎪⎫120＝1 B ．x 2＋x 2＝2x 4C ．|a |＝|－a | D. ⎝ ⎛⎭⎪⎫b a 23＝b3a63．下列运算错误的是( D )A.a －b 2b －a2＝1 B.－a －ba ＋b＝－1 C. 0.5a ＋b 0.2a －0.3b ＝5a ＋10b 2a －3b D. a －b a ＋b ＝b －a b ＋a4．下列二次根式中，不能与2合并的是( C ) A.12B. 8C. 12D.18 5．若m ＝22×(－2)，则有( C )A ．0<m <1B ．－1<m <0C ．－2<m <－1D ．－3<m <－26．(2015·绍兴鲁迅中学模拟)下列三个分式12x 2，5x －14m －n ，3x的最简公分母是( D )A ．4(m －n )xB ．2(m －n )x 2C. 14x2m －nD ．4(m －n )x 27．已知x －1x ＝3，则4－12x 2＋32x 的值为( D )A ．1 B. 32 C. 52 D. 72【解析】把x －1x ＝3两边同乘x ，得x 2－1＝3x ，即x 2－3x ＝1，所以4－12x 2＋32x ＝4－12(x 2－3x )＝4－12×1＝72. 8．下面每个表格中的四个数都是按相同规律填写的：根据此规律确定x 的值为( )A ．135B ．170C ．209D ．252【解析】观察前四个表格中的数字，第1个表格中 9＝2×4＋1，第2个表格中20＝3×6＋2，第3个表格中35＝4×8＋3，第4个表格中54＝5×10＋4，且每个表格中左下角的数字是右上角数字的一半，左上角的数字比左下角数字小1，所以b ＝12×20＝10，a ＝b －1＝9，x ＝20×10＋9＝209.故选C.答案: C9.实数a ，b 在数轴上对应的点的位置如图所示，计算|a －b |的结果为( C )A ．a ＋bB ．a －bC ．b －aD ．－a －b【解析】由图可知，a <0，b >0，所以a －b <0，所以 |a －b |＝－(a －b )，C 正确．10．如图，在边长为2a 的正方形中央剪去一边长为 (a ＋2)的小正方形(a ＞2)，将剩余部分剪开密铺成一个平行四边形，则该平行四边形的面积为( C )第1个第2个第3个第4个 … … …A ．a 2＋4B ．2a 2＋4aC ．3a 2－4a －4D ．4a 2－a －2【解析】平行四边形的面积为(2a )2－(a ＋2)2＝4a 2－(a 2＋4a ＋4)＝4a 2－a 2－4a －4＝3a 2－4a －4.故选C.11．张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x ＋1x(x >0)的最小值是2”，其推导方法如下：在面积是1的矩形中设矩形的一边长为x ，则另一边的长为1x，矩形的周长为2⎝ ⎛⎭⎪⎫x ＋1x ；当矩形成为正方形时，就有x ＝1x (x >0)，解得x ＝1.这时矩形的周长2⎝ ⎛⎭⎪⎫x ＋1x ＝4最小，因此x ＋1x (x >0)的最小值是2.模仿张华的推导，你求得式子x 2＋9x(x >0)的最小值是( )A ．2B ．4C ．6D ．10【解析】∵x >0，∴在原式中分母分子同除以x ，即x 2＋9x ＝x ＋9x ，在面积是9的矩形中设矩形的一边长为x ，则另一边长为9x ，矩形的周长为2⎝⎛⎭⎪⎫x ＋9x ；当矩形成为正方形时，就有x ＝9x (x >0)，解得x ＝3.这时矩形的周长2⎝⎛⎭⎪⎫x ＋9x ＝12最小，因此x ＋9x(x >0)的最小值是6.故选C.答案: C 二、填空题12．分解因式：9x 3－18x 2＋9x ＝9x (x －1)2 . 13．若式子2－xx有意义，则实数x 的取值范围是x ≤2且x ≠0 .14．计算：－36＋214＋327＝－32. 15．已知(a ＋6)2＋b 2－2b －3＝0，则2b 2－4b －a 的值为12.【解析】由题意知，∵(a ＋6)2≥0，b 2－2b －3≥0.而(a ＋6)2＋b 2－2b －3＝0，∴(a ＋6)2＝0且b 2－2b －3＝0.整理，得a ＝－6，b 2－2b ＝3，∴2b 2－4b －a ＝2(b 2－2b )－a ＝2×3－(－6)＝12.三、解答题16．计算：||－3－12＋2sin 60°＋⎝ ⎛⎭⎪⎫13－1.解：原式＝3－23＋2×32＋3＝3. 17．先化简，再求值：(x ＋y )(x －y )－(4x 3y －8xy 3)÷2xy ，其中x ＝－1，y ＝33. 解：原式＝x 2－y 2－2x 2＋4y 2＝－x 2＋3y 2. 当x ＝－1，y ＝33时，原式＝－1＋1＝0. 18．先化简，再求值：⎝⎛⎭⎪⎫1－1x ＋2÷x 2＋2x ＋1x ＋2，其中x ＝3－1. 解：原式＝x ＋1x ＋2÷x ＋12x ＋2＝x ＋1x ＋2·x ＋2x ＋12＝1x ＋1. 当x ＝3－1时，原式＝13－1＋1＝13＝33.19．探究下面的问题：(1)在图甲中，阴影部分的面积和为a 2－b 2(写成两数平方差的形式)； (2)将图甲中的第①块割下来重新与第②块拼成如图乙所示的一个长方形，那么这个长方形的长是a ＋b ，宽是 a －b ，它的面积是(a ＋b )(a －b )(写成两个多项式的形式)；(3)由这两个图可以得到的乘法公式是(a ＋b )(a －b )＝a 2－b 2(用式子表示)；(4)运用这个公式计算：(x －2y ＋3z )(x ＋2y －3z )．(x －2y ＋3z )(x ＋2y －3z )＝[x －(2y －3z )]·[x ＋(2y －3z )]＝x 2－(2y －3z )2＝x 2－4y 2＋12yz －9z 2.20．如果10b ＝n ，那么b 为n 的劳格数，记为b ＝d (n )，由定义可知：10b＝n 与b ＝d (n )所表示的b ，n 两个量之间的同一关系．(1)根据劳格数的定义，填空：d (10)＝1，d (10－2)＝－2； (2)劳格数有如下运算性质：若m ，n 为正数，则d (mn )＝d (m )＋d (n )，d ⎝ ⎛⎭⎪⎫m n ＝d (m )－d (n )．根据运算性质，填空：d a 3d a＝3(a 为正数)，若d (2)＝0.301 0，则d (4)＝0.602 0，d (5)＝0.6990，d (0.08)＝－1.097.(3)如表中与数x 对应的劳格数d (x )有且只有两个是错误的，请找出错误的劳格数，说明理由并改正.x 1.5 3 5 6 8 9 12 27 d (x ) 3a －b ＋c 2a －ba ＋c1＋a －b －c3－3a －3c4a －2b3－b －2c6a －3b解：(1)1 －2(2)d a 3d a ＝3d a d a＝3.由运算性质可得，d (4)＝0.602 0，d (5)＝d (10)－d (2)＝ 1－0.301 0＝0.699 0，d (0.08)＝－1.097.(3)若d (3)≠2a －b ，则d (9)＝2d (3)≠4a －2b ，d (27)＝3d (3)≠6a －3b ，从而表中有三个劳格数是错误的，与题设矛盾，∴d (3)＝2a －b ；若d (5)≠a ＋c ，则d (2)＝1－d (5)≠1－a －c ， ∴d (8)＝3d (2)≠3－3a －3c ，d (6)＝d (3)＋d (2)≠1＋a －b －c ，表中也有三个劳格数是错误的，与题设矛盾．∴d(5)＝a＋c.∴表中只有d(1.5)和d(12)的值是错误的，应纠正为：d(1.5)＝d(3)＋d(5)－1＝3a－b＋c－1，d(12)＝d(3)＋2d(2)＝2－b－2c.。

2022~2023学年中考数学一轮复习专题03因式分解附解析

2022~2023学年中考数学一轮复习专题03因式分解附解析一、单选题1．（2022·济宁）下面各式从左到右的变形，属于因式分解的是（）A．x2−x−1=x(x−1)−1B．x2−1=(x−1)2C．x2−x−6=(x−3)(x+2)D．x(x−1)=x2−x2．（2022八下·光明期末）下列由左边到右边的变形是因式分解的是（）A．(a+3)(a−3)=a2−9B．a2−b2+1=(a+b)(a−b)+1C．a2+b2=(a+b)2D．4a2−9=(2a+3)(2a−3) 3．（2020·柳州）下列多项式中，能用平方差公式进行因式分解的是（）A．a2﹣b2B．﹣a2﹣b2C．a2+b2D．a2+2ab+b2 4．（2022七下·合肥期末）下列分解因式正确的是()A．x2−3x+1=x(x−3)+1B．x2−2x+1=x(x−2+1x)C．(m+n)2=m2+2mn+n2D．−a3+a=−a(a+1)(a−l) 5．（2022·台湾）多项式39x2+5x−14可因式分解成(3x+a)(bx+c)，其中a、b、c均为整数，求a+2c之值为何？（）A．-12B．-3C．3D．126．（2022七上·长沙开学考）已知多项式2x3−x2+m分解因式后有一个因式是x+1，则m的值为（）A．3B．-3C．1D．-17．（2022八下·长安期末）我们知道6−√2的小数部分b为2−√2，如果用a代表它的整数部分，那么ab2−a2b的值是（）A．8B．－8C．4D．－4二、填空题8．（2022·益阳）已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m2﹣n2的值是．9．（2022·绵阳）因式分解：3x3−12xy2=．10．（2022·内江）分解因式：a4﹣3a2﹣4＝.11．（2022·赤峰）分解因式：2x3+4x2+2x=．12．（2022·绥化）因式分解：(m+n)2−6(m+n)+9=．13．（2022·怀化）因式分解：x2−x4=.14．（2022·乐山）已知m2+n2+10=6m−2n，则m−n=.三、综合题15．（2022八上·莱西期中）某校数学社团的小亮、小颖两个同学利用分组分解法进行的因式分解：小亮：m2−mn+2m−2n=(m2−mn)+(2m−2n)=m(m−n)+2(m−n)=(m−n)(m+2)小颖：4x2−y2−z2+2yz=4x2−(y2+z2−2yz)=2x2−(y−z)2=(2x+y−z)(2x−y+z)．请你在他们解法的启发下，解决下面问题；（1）因式分解a3−3a2−9a+27；（2）因式分解x2−4xy+4y2−16；（3）已知a，b，c是ΔABC的三边，且满足a2−ab+c2=2ac−bc，判断ΔABC的形状并说明理由．16．（2022·六盘水）如图，学校劳动实践基地有两块边长分别为a，b的正方形秧田A，B，其中不能使用的面积为M．（1）用含a，M的代数式表示A中能使用的面积；（2）若a+b=10，a−b=5，求A比B多出的使用面积．17．如图，将一张矩形纸板按照图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m>n，(以上长度单位：cm)（1）观察图形，可以发现代数式2m2＋5mn＋2n2可以因式分解为；（2）若每块小矩形的面积为10 cm2，四个正方形的面积和为58 cm2，试求图中所有裁剪线(虚线部分)长之和．18．（2022·西宁）八年级课外兴趣小组活动时，老师提出了如下问题：将2a−3ab−4+6b因式分解．【观察】经过小组合作交流，小明得到了如下的解决方法：解法一：原式=(2a−3ab)−(4−6b)=a(2−3b)−2(2−3b)=(2−3b)(a−2)解法二：原式=(2a−4)−(3ab−6b)=2(a−2)−3b(a−2)=(a−2)(2−3b)【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）（1）【类比】请用分组分解法将x2−a2+x+a因式分解；（2）【挑战】请用分组分解法将ax+a2−2ab−bx+b2因式分解；（3）【应用】“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理．如图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形．若直角三角形的两条直角边长分别是a 和b(a>b)，斜边长是3，小正方形的面积是1．根据以上信息，先将a4−2a3b+2a2b2−2ab3+b4因式分解，再求值．19．（2022八上·莱西期中）［阅读材料]下面是某同学对多项式(x2−4x+2)(x2−4x+6)+4进行因式分解的过程．设x2−4x=y原式=(y+2)(y+6)+4（第一步）=y2+8y+16（第二步）=(y+4)2（第三步）=(x2−4x+4)2（第四步）请问：（1）该同学因式分解的结果是否符合题意？若不符合题意，请直接写出因式分解的最后结果．（2）请你模仿以上方法尝试对多项式(a2−2a)(a2−2a+2)+1进行因式分解．20．（2022八下·枣庄期末）阅读下列因式分解的过程，再回答所提出的问题：1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3（1）上述分解因式的方法是．（2）若分解1+x+x(x+1)+x(x+1)2+⋯+x(x+1)2021，则结果是．（3）依照上述方法分解因式：1+x+x(x+1)+x(x+1)2+⋯+x(x+1)n（n为正整数）．21．（2022八上·永春期中）先阅读下面的内容，再解决问题．如果一个整式A等于整式B与整式C之积，则称整式B和整式C为整式A的因式．如：①因为36=4×9，所以4和9是36的因数；因为x2−x−2=(x+1)(x−2)，所以x+1和x−2是x2−x−2的因式．②若x+1是x2+ax−2的因式，则求常数a的值的过程如下：解：∵x+1是x2+ax−2的因式，∴存在一个整式(mx+n)，使得x2+ax−2=(x+1)(mx+n)，∵当x=−1时，(x+1)(mx+n)=0，∴当x=−1时，x2+ax−2=0，∴1−a−2=0，∴a=−1．（1）若x+5是整式x2+mx−10的一个因式，则m=．（2）若整式x2−1是3x4−ax2+bx+1的因式，求√a+2017b的值．22．（2021八上·密山期末）先阅读下列材料：我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等．拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法．如：x2＋2x﹣3＝x2＋2x＋1﹣4＝（x＋1）2﹣22＝（x＋1＋2）（x＋1﹣2）＝（x＋3）（x﹣1）请你仿照以上方法，探索并解决下列问题：（1）分解因式：x2﹣6x﹣7；（2）分解因式：a2＋4ab﹣5b223．如图1，有若干张边长为α的小正方形①，长为b、宽为α的长方形②以及边长为b的大正方形3的纸片.（1）已知小正方形1与大正方形3的面积之和为169，长方形②的周长为34，求长方形2的面积；（2）如果现有小正方形①2张，大正方形31张，长方形②3张，请你将它们拼成一个大长方形(在图2虚线框内画出图形)，并运用面积之间的关系，将多项式2a2+3ab+b2分解因式.24．（2021八上·长春期末）如图，将一张大长方形纸板按图中虚线裁剪成9块，其中有2块是边长为a厘米的大正方形，2块是边长都为b厘米的小正方形，5块是长为a厘米，宽为b厘米的相同的小长方形，且a>b．（1）观察图形，可以发现代数式2a2+5ab+2b2可以因式分解为．（2）若图中阴影部分的面积为20平方厘米，大长方形纸板的周长为24厘米，求图中空白部分的面积．答案解析部分1．【答案】C【解析】【解答】把一个多项式化成几个整式积的形式，这种变形叫做因式分解．A、右边不是整式积的形式，故不是因式分解，不符合题意；B、形式上符合因式分解，但等号左右不是恒等变形，等号不成立，不符合题意；C、符合因式分解的形式，符合题意；D、从左到右是整式的乘法，从右到左是因式分解，不符合题意；故答案为：C．【分析】利用因式分解法的定义对每个选项一一判断即可。

中考数学一轮复习因式分解考点讲义及练习(含解析)-人教版初中九年级全册数学试题

因式分解【中考真题】【2019某某中考】分解因式4x2−y2的结果是A．(4x+y)(4x−y)B．4(x+y)(x−y)C．(2x+y)(2x−y)D．2(x+y)(x−y) 【答案】C【解析】直接利用平方差公式分解因式得出答案．4x2−y2＝(2x+y)(2x−y)．透析考纲精选好题【考向01】因式分解的概念【试题】【2019某某中考复习】下列各式由左到右的变形中，属于分解因式的是A．a(m+n)＝am+an B．a2−b2−c2＝(a−b)(a+b)−c2C．10x2−5x＝5x(2x−1)D．x2−16+6x＝(x+4)(x−4)+6x解题关键【好题变式练】1．【2019某某期末】下列由左到右的变形中，属于因式分解的是A．(x+4)(x−4)＝x2−16B．ax2+axy+ax＝ax(x+y)C．m2−2mn+n2＝(m+n)(m−n)D．4−a2＝(2+a)(2−a)2．【2019某某期中】下列各式中从左到右的变形，是因式分解的是A ．(a +3)(a −3)=a 2−9B ．x 2+x −5=(x −2)(x +3)+1C ．a 2b +ab 2=ab(a +b)D ．x 2+1=x(x +1x )【考向02】因式分解的方法【试题】【2019•某某】把2a 2–8分解因式，结果正确的是A ．2（a 2–4）B ．2（a –2）2C ．2（a +2）（a –2）D ．2（a +2）2【好题变式练】1．【2019某某期末】分解因式：−3a +12a 2−12a 3＝________．2．分解因式(a −b)2+4ab 的结果是________．【考向03】因式分解的应用【试题】【2019某某期中】若一个长、宽分别为a ，b 的长方形的周长为14，面积为8，则a 2b +ab 2=________．解题技巧【好题变式练】1．【2019秋•泉港区期中】如果代数式x2+mx+9=（ax+b）2，那么m的值可为A．3B．6C．±3D．±62．【2019某某月考】计算：5652×24−4352×24=________．过关斩将1．【2019某某期中】下列从左到右的变形，是因式分解的是A．(a+3)(a−3)=a2−9B．x2+x−5=x(x+1)−5C．a(m−n)=am−an D．x2+4x+4=(x+2)22．【2019某某期末】数348−1能被30以内的两位整数a整除，则a可能是A．28，26B．26，24C．27，25D．25，233．已知三角形的三边长分别是a，b，c，且满足a2+b2+c2=ab+bc+ca，则此三角形是解题技巧A．直角三角形B．等腰三角形．等腰直角三角形D．等边三角形4．若多项式x2−kx+1能用完全平方公式进行因式分解，则k的值为A．2B．−2C．±2D．±15．【2019某某中考】因式分解：ab−7a＝________．x因式分解的结果是________．6．多项式x3−x2+147．如果a+b=5,ab=3,求：a3b+ab3的值．8．【2019某某中考模拟】常用的分解因式的方法有提取公因式法、公式法，但有一部分多项式只单纯用上述方法就无法分解，如x2−2xy+y2−16，我们细心观察这个式子，会发现，前三项符合完全平方公式，进行变形后可以与第四项结合，再应用平方差公式进行分解．过程如下：x2−2xy+y2−16＝(x−y)2−16＝(x−y+4)(x−y−4)这种分解因式的方法叫分组分解法．利用这种分组的思想方法对下面这个多项式进行因式分解：9a2+4b2−25m2−n2+12ab+10mn．参考答案过关斩将1．D【解析】A，(a+3)(a−3)=a2−9，是多项式乘法运算，故此选项错误；B，x2+x−5=x(x+1)−5，右边不是等式乘积的形式，不是因式分解，故此选项错误；C，a(m−n)=am−an，是多项式乘法运算，不是因式分解，故此选项错误；D，x2+4x+4=(x+2)2，是因式分解，故此选项正确．故选D．2．A【解析】348−1＝(324+1)(324−1)＝(324+1)(312+1)(312−1)＝(324+1)(312+1)(36+1)(36−1)＝(324+1)(312+1)(36+1)(33+1)(33−1)＝(324+1)(312+1)×(73×10)×28×26＝(324+1)(312+1)×73×2×5×2×2×7×2×13，∵348−1能被30以内的两位数a（整数）整除，则a可能是28或26等．3．D【解析】已知等式整理得：2a2+2b2+2c2=2ab+2bc+2ca，即(a−b)2+(b−c)2+(a−c)2=0，可得a=b=c，则此三角形是等边三角形．故选D．4．C【解析】∵多项式x2−kx+1能用完全平方公式进行因式分解，∴k=±2．故选C．5．a(b−7)【解析】直接提公因式a即可．原式＝a(b−7)．6．x(x−12)2【解析】原式=x(x2−x+14)=x(x−12)2．7．57【解析】a3b+ab3=ab(a2+b2)=ab[(a+b)2−2ab]，当a+b=5，ab=3时，原式=3×(25−6)=57．8．(3a+2b+5m−n)(3a+2b−5m+n)【解析】9a2+4b2−25m2−n2+12ab+10mn＝(9a2+12ab+4b2)−(25m2−10mn+n2)＝(3a+2b)2−(5m−n)2＝(3a+2b+5m−n)(3a+2b−5m+n)．。

中考数学第一轮因式分解考点专题测试题及答案

中考一轮复习之因式分解精典例题：【例1】分解因式：（1）33xyy x -（2）x x x 2718323+-（3）()112---x x（4）()()3224x y y x ---分析：①因式分解时，无论有几项，首先考虑提取公因式。

提公因式时，不仅注意数，也要注意字母，字母可能是单项式也可能是多项式，一次提尽。

②当某项完全提出后，该项应为“1” ③注意()()nna b b a 22-=-，()()1212++--=-n n a b b a④分解结果（1）不带中括号；（2）数字因数在前，字母因数在后；单项式在前，多项式在后；（3）相同因式写成幂的形式；（4）分解结果应在指定范围内不能再分解为止；若无指定范围，一般在有理数范围内分解。

答案：（1）()()y x y x xy -+；（2）()233-x x ；（3）()()21--x x ；（4）()()y x y x -+-222【例2】分解因式：（1）2 2103yxyx--（2）32231222xyyxyx-+（3）()222164xx-+分析：对于二次三项齐次式，将其中一个字母看作“末知数”，另一个字母视为“常数”。

首先考虑提公因式后，由余下因式的项数为3项，可考虑完全平方式或十字相乘法继续分解；如果项数为2，可考虑平方差、立方差、立方和公式。

（3）题无公因式，项数为2项，可考虑平方差公式先分解开，再由项数考虑选择方法继续分解。

答案：（1）()()yxyx52-+；（2）()()yxyxxy232-+；（3）()()2222+-xx【例3】分解因式：（1）22244zyxyx-+-；（2）babaa2 322-+-（3）322222--++-yxyxyx分析：对于四项或四项以上的多项式的因式分解，一般采用分组分解法，。

四项式一般采用“二、二”或“三、一”分组，五项式一般采用“三、二”分组，分组后再试用提公因式法、公式法或十字相乘法继续分解。

人教版中考第一轮复习九年级第一章：数与式(含答案)

第一章：数与式 1.1：实数考点一：实数的相关概念实数 ✧实数的分类⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧负无理数负分数负有理数负实数零正无理数正整数正有理数正实数实数✧ 实数大小的比较在数轴上表示两个数的点，右边的点表示的数，左边的点表示的数。

正数大于零，负数小于零；两个正数，绝对值大的较；两个负数，绝对值大的较。

设a 、b 是任意两实数：若0>-b a 。

则a b ；若0=-b a 。

则b a =；若0<-b a 。

则a b ；数轴： ✧数轴的三要素为、正方向和单位长度。

数轴上的点与一一对应。

相反数、倒数、绝对值 ✧ 实数a 、b 互为相反数，则=+b a 。

实数a 、b 互为倒数，则=ab 。

✧绝对值：()()⎩⎨⎧<≥=00a a a aa 的集合意义是数轴上表示数a 的点与原点的距离。

数的乘方与开方 ✧ 负数的奇次幂是负数，负数的偶次幂是正数，正数的任何次幂都是正数，0的任何正整数次幂都是0； ✧ 正数有两个平方根，负数没有平方根，0的平方根是0，正数的正的平方根叫做。

✧ 若a b =3，则b 叫做a 的立方根。

考点1 正数、负数的意义1.（2019 滨州）2.（2019 云南）若零上8℃记作+8℃，则零下6℃记作 ℃．3.（2019 乐山）某天早晨的气温是℃,到中午升高了℃，晚上又降低了℃.则晚上的温度是 .4.（2019 乐山）4.一定是( )A. 正数B. 负数C.0D.以上选项都不正确考点2 实数及其分类1．(2019·玉林)下列各数中，是有理数的是( )A ．ΠB ．1.2 C. 2 D.33 2．(2018·重庆)下列四个数中，是正整数的是( ) A ．－1 B ．0 C.12D ．13．(2018·菏泽)下列各数：－2，0，13，0.020 020 002…，π，9，其中无理数的个数是( )A ．4B ．3C ．2D ．1（2018巴中）1. 下列各数：，0，，023，，，0.30003……，中无理数个数为（）A ． 2个B ． 3个C ．4个D ．5个4．(2019·桂林)若海平面以上1 045米，记作＋1 045米，则海平面以下155米，记作( ) A ．－1 200米 B ．－155米 C ．155米 D ．1 200米考点3 数轴、相反数、绝对值、倒数 5．(2019·威海)－3的相反数是( )A ．－3B ．3 C.13 D ．－136．(2019·德州)－12的倒数是( )A ．－2 B.12 C ．2 D ．17．(2019·遂宁)－|－2|的值为( )A. 2 B ．－ 2 C ．± 2 D ．28．(2019·陇南)如图，数轴的单位长度为1，如果点A 表示的数是－1，那么点B 表示的数是( )A．0 B．1 C．2 D．39．(2018·攀枝花)如图，实数－3，x，3，y在数轴上的对应点分别为M，N，P，Q，这四个数中绝对值最小的数对应的点是( )A．点M B．点N C．点P D．点Q10．(2019·成都)若m＋1与－2互为相反数，则m的值为．考点4 科学记数法和近似数11．(2019·荆门)已知一天有86 400秒，一年按365天计算共有31 536 000秒，用科学记数法表示31 536 000正确的是( )A．3.153 6×106 B．3.153 6×107 C．31.53 6×106 D．0.315 36×10812．(2019·潍坊)“十三五”以来，我国启动实施了农村饮水安全巩固提升工程．截止去年9月底，各地已累计完成投资1.002×1011元．数据1.002×1011可以表示为( )A．10.02亿 B．100.2亿 C．1 002亿 D．10 020亿13．(2019·烟台)某种计算机完成一次基本运算的时间约为1纳秒(ns)，已知1纳秒＝0.000 000 001秒，该计算机完成15次基本运算，所用时间用科学记数法表示为( )A．1.5×10－9秒 B．15×10－9秒 C．1.5×10－8秒 D．15×10－8秒14．(2019·攀枝花)用四舍五入法将130 542精确到千位，正确的是( )A．131 000 B．0.131×106 C．1.31×105 D．13.1×104【能力提升】15．(2019·天水)已知|a|＝1，b是2的相反数，则a＋b的值为( )A．－3 B．－1 C．－1或－3 D．1或－316．(2019·枣庄)点O，A，B，C在数轴上的位置如图所示，O为原点，AC＝1，OA＝OB.若点C所表示的数为a，则点B所表示的数为( )A．－(a＋1) B．－(a－1) C．a＋1 D．a－117．(2019·泰安)2018年12月8日，我国在西昌卫星发射中心成功发射“嫦娥四号”探测器，“嫦娥四号”进入近地点约200公里、远地点约42万公里的地月转移轨道，将数据42万公里用科学记数法表示为( )A．4.2×109米 B．4.2×108米 C．42×107米 D．4.2×107米第2讲实数的运算【基础过关】考点1 平方根、算术平方根、立方根1．(2018·安顺)4的算术平方根是( )A ．± 2 B. 2 C ．±2 D ．2 2．(2019·烟台)－8的立方根是( )A ．2B ．－2C ．±2D ．－2 2 3．(2019·南京)面积为4的正方形的边长是( ) A ．4的平方根 B ．4的算术平方根 C ．4开平方的结果 D ．4的立方根 4．(2019·通辽)16的平方根是( )A ．±4B ．4C ．±2D ．＋2 考点2 实数的大小比较5．(2019·菏泽)下列各数中，最大的数是( )A ．－12 B.14 C ．0 D ．－26．(2019·常德)下列各数中比3大比4小的无理数是( )A.10B.17 C ．3.1 D.1037．(2019·宜昌)如图，A ，B ，C ，D 是数轴上的四个点，其中最适合表示无理数π的点是( )A ．点AB ．点BC ．点CD ．点D 考点3 实数的运算8．(2019·淄博)比－2小1的数是( )A ．－3B ．－1C ．1D ．3 9．(2019·天津)计算(－3)×9的结果等于( )A ．－27B ．－6C ．27D ．6 10．(2019·聊城)计算：(－13－12)÷54＝．11．(2019·十堰)计算：(－1)3＋|1－2|＋38.12．(2019·黄石)计算：(2 019－π)0＋|2－1|－2sin45°＋(13)－1.【能力提升】13.(2019·广东)实数a ，b 在数轴上的对应点的位置如图所示，下列式子成立的是( )A ．a>bB ．|a|<|b|C ．a ＋b>0 D.ab <014.(2019·贺州)计算11×3＋13×5＋15×7＋17×9＋…＋137×39的结果是( )A.1937 B.1939 C.3739 D.383915．(2018·潍坊)用教材中的计算器进行计算，开机后依次按下3x 2＝，把显示结果输入如图的程序中，则输出的结果是．16.64的算术平方根是。

2020中考数学大一轮复习训练04：因式分解(含答案)

第4课时因式分解1．(2017·常德)下列各式由左到右的变形，属于分解因式的是( )A ．a (m ＋n )＝am ＋anB ．a 2－b 2－c 2＝(a －b )(a ＋b )－c 2C ．10x 2－5x ＝5x (2x －1)D ．x 2－16＋6x ＝(x ＋4)(x －4)＋6x2．(2019·安徽亳州模拟)下列各式中，能用完全平方公式因式分解的是( )A ．y 2－x 2＋2xyB ．x 2＋y 2＋xyC ．25y 2＋15y ＋9D ．4x 2＋9－12x3．(2019·潍坊)下列因式分解正确的是( )A ．3ax 2－6ax ＝3(ax 2－2ax )B ．－x 2＋y 2＝(－x ＋y )(－x －y )C ．a 2＋2ab ＋4b 2＝(a ＋2b )2D ．－ax 2＋2ax －a ＝－a (x －1)24．(2019·湘西州)分解因式：ab －7a ＝________.5．(2018·自贡)分解因式：ax 2＋2axy ＋ay 2＝________.6．(2019·张家界)分解因式：x 2y －y ＝_____________________.7．(2018·潍坊)分解因式：(x ＋2)x －x －2＝________________.8．(2018·东营)分解因式：x 3－4xy 2＝____________________________________.9．(2019·武威)因式分解：xy 2－4x ＝_____________________________________.10．(2018·威海)分解因式：－12a 2＋2a －2＝_______________________________.11．(2019·淄博)分解因式：x 3＋5x 2＋6x ＝______________________________.12．分解因式：x 2－2x ＋(x －2)＝_____________________________________.13．(2018·齐齐哈尔)分解因式：6(a －b )2＋3(a －b )．14．(2017·山西)分解因式：(y＋2x)2－(x＋2y)2.15．已知a－b＝5，ab＝3，求代数式a3b－2a2b2＋ab3的值．16．(2017·百色)用“十字相乘法”分解因式2x2－x－3的方法如下．(1)二次项系数：2＝1×2.(2)常数项：－3＝－1×3＝1×(－3)．图4-1是对“交叉相乘之和”的验算．图4-1①1×3＋2×(－1)＝1；②1×(－1)＋2×3＝5；③1×(－3)＋2×1＝－1；④1×1＋2×(－3)＝－5.(3)发现第③个“交叉相乘之和”的结果等于一次项系数－1.即(x＋1)(2x－3)＝2x2－3x＋2x－3＝2x2－x－3，则2x2－x－3＝(x＋1)(2x－3)．像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x2＋5x－12＝_______________________.17．(2017·河北)已知任意五个连续整数的平方和是5的倍数．(1)(－1)2＋02＋12＋22＋32的结果是5的几倍？(2)设五个连续整数的中间一个数为n，写出它们的平方和，并说明是5的倍数．18．(2018·临安区)阅读下列题目的解题过程：已知a，b，c为△ABC的三边长，且满足a2c2－b2c2＝a4－b4，试判断△ABC的形状．解：∵a2c2－b2c2＝a4－b4，(①)∴c2(a2－b2)＝(a2＋b2)(a2－b2)，(②)∴c2＝a2＋b2，(③)∴△ABC是直角三角形．问：(1)上述解题过程，从哪一步开始出现错误？请写出该步的代号：________；(2)错误的原因：________________________________；(3)本题正确的结论：_______________________________________.参考答案1．C 2.D 3.D 4.a (b －7)5．a (x ＋y )2 6.y (x ＋1)(x －1)7．(x ＋2)(x －1) 8.x (x ＋2y )(x －2y )9．x (y ＋2)(y －2) 10.－12(a －2)211．x (x ＋3)(x ＋2) 12.(x ＋1)(x －2)13．3(a －b )(2a －2b ＋1) 14.3(x ＋y )(x －y )15．75 16.(x ＋3)(3x －4)17．(1)3倍 (2)5(n 2＋2)，证明略18．(1)③ (2)没有考虑a ＝b 的情况 (3)△ABC 是等腰三角形或直角三角形。

2021年九年级数学中考一轮复习知识点基础达标测评：因式分解(附答案)

2021年九年级数学中考一轮复习基础达标测评：因式分解（附答案）1．下列各式分解因式结果是（a﹣2）（b+3）的是（）A．﹣6+2b﹣3a+ab B．﹣6﹣2b+3a+abC．ab﹣3b+2a﹣6D．ab﹣2a+3b﹣62．若多项式x2﹣ax﹣1可分解为（x﹣2）（x+b），则a+b的值为（）A．2B．1C．﹣2D．﹣13．分解因式b2（x﹣3）+b（x﹣3）的正确结果是（）A．（x﹣3）（b2+b）B．b（x﹣3）（b+1）C．（x﹣3）（b2﹣b）D．b（x﹣3）（b﹣1）4．若多项式﹣6ab+18abx+24aby的一个因式是﹣6ab，那么另一个因式是（）A．1﹣3x﹣4y B．﹣1﹣3x﹣4y C．1+3x﹣4y D．﹣1﹣3x+4y 5．下列各式：①﹣x2﹣y2；②﹣a2b2+1；③a2+ab+b2；④﹣x2+2xy﹣y2；⑤﹣mn+m2n2，用公式法分解因式的有（）A．2个B．3个C．4个D．5个6．现有一列式子：①552﹣452；②5552﹣4452；③55552﹣44452…则第⑧个式子的计算结果用科学记数法可表示为（）A．1.1111111×1016 B．1.1111111×1027 C．1.111111×1056 D．1.1111111×10177．将a3b﹣ab进行因式分解，正确的是（）A．a（a2b﹣b）B．ab（a﹣1）2C．ab（a+1）（a﹣1）D．ab（a2﹣1）8．下列各式：①4x2﹣y2；②2x4+8x3y+8x2y2；③a2+2ab﹣b2；④x2+xy﹣6y2；⑤x2+2x+3其中不能分解因式的有（）A．1个B．2个C．3个D．4个9．下列多项式已经进行了分组，能接下去分解因式的有（）（1）（m3+m2﹣m）﹣1；（2）﹣4b2+（9a2﹣6ac+c2）；（3）（5x2+6y）+（15x+2xy）；（4）（x2﹣y2）+（mx+my）A．1个B．2个C．3个D．4个10．把多项式4x2﹣2x﹣y2﹣y用分组分解法分解因式，正确的分组方法应该是（）A．（4x2﹣y）﹣（2x+y2）B．（4x2﹣y2）﹣（2x+y）C．4x2﹣（2x+y2+y）D．（4x2﹣2x）﹣（y2+y）11．有下列说法：①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；②无论k取任何实数，多项式x2﹣ky2总能分解成两个一次因式积的形式；③若（t﹣3）3﹣2t＝1，则t可以取的值有3个；④关于x，y的方程组为，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，当a每取一个值时，就有一个确定的方程，而这些方程总有一个公共解，则这个公共解是．其中正确的说法是（）A．①④B．①③④C．②③D．①②12．把多项式（x﹣y）2﹣2（x﹣y）﹣8分解因式，正确的结果是（）A．（x﹣y+4）（x﹣y+2）B．（x﹣y﹣4）（x﹣y﹣2）C．（x﹣y﹣4）（x﹣y+2）D．（x﹣y+4）（x﹣y﹣2）13．若多项式x2﹣mx+n（m、n是常数）分解因式后，有一个因式是x﹣3，则3m﹣n的值为．14．已知关于x的三次三项式2x3+3x﹣k有一个因式是2x﹣5，则另一个因式为．15．2x3y2与12x4y的公因式是．16．多项式6a2b+9ab2﹣15ab的公因式是．17．分解因式：x2﹣4x＝．18．因式分解：a2+3a＝．19．若|x+y﹣5|+（x﹣y+1）2＝0，则x2﹣y2＝．20．多项式x2+mx+25能用完全平方公式分解因式，则m＝．21．因式分解：﹣3x2+27＝．22．把多项式4mx2﹣my2因式分解的结果是．23．仔细阅读下面例题，解答问题：例题：已知二次三项式x2﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．解：设另一个因式为（x+n），得x2﹣4x+m＝（x+3）（x+n）则x2﹣4x+m＝x2+（n+3）x+3n∴．解得：n＝﹣7，m＝﹣21∴另一个因式为（x﹣7），m的值为﹣21问题：仿照以上方法解答下面问题：已知二次三项式2x2+3x﹣k有一个因式是（2x﹣5），求另一个因式以及k的值．24．1637年笛卡儿（R．Descartes，1596﹣1650）在其《几何学》中，首次应用待定系数法最早给出因式分解定理．关于笛卡尔的“待定系数法”原理，举例说明如下：分解因式：x3+2x2﹣3．观察知，显然x＝1时，原式＝0，因此原式可分解为（x﹣1）与另一个整式的积．令：x3+2x2﹣3＝（x﹣1）（x2+bx+c），而（x﹣1）（x2+bx+c）＝x3+（b ﹣1）x2+（c﹣b）x﹣c，因等式两边x同次幂的系数相等，则有：，得，从而x3+2x2﹣3＝0．根据以上材料，理解并运用材料提供的方法，解答以下问题：（1）若x+1是多项式x3+ax+1的因式，求a的值并将多项式x3+ax+1分解因式．（2）若多项式3x4+ax3+bx﹣34含有因式x+1及x﹣2，求a，b的值．25．分解因式：（1）x2y﹣xy；（2）x2﹣4y2．26．计算：分解因式：m3n﹣mn327．已知，求下列各式的值：（1）x2+2xy+y2（2）x2﹣y2．28．请仔细阅读下面某同学对多项式（x2﹣4x+2）（x2﹣4x+6）+4进行因式分解的过程，然后回答问题：解：令x2﹣4x+2＝y，则：原式＝y（y+4）+4（第一步）＝y2+4y+4（第二步）＝（y+2）2（第三步）＝（x2﹣4x+4）2（第四步）（1）该同学第二步到第三步运用了因式分解的；A．提取公因式B．平方差公式C．两数和的完全平方公式D．两数差的完全平方公式（2）另外一名同学发现第四步因式分解的结果不彻底，请你直接写出因式分解的最后结果；（3）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x+2）+1进行因式分解．29．对下列代数式分解因式：（1）n2（m﹣2）﹣n（2﹣m）；（2）（x﹣1）（x﹣3）+1．30．因式分解：4x2﹣4．31．常用的分解因式的方法有提取公因式法、公式法及十字相乘法，但有更多的多项式只用上述方法就无法分解，如x2﹣4y2﹣2x+4y，我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了．过程为：x2﹣4y2﹣2x+4y＝（x+2y）（x﹣2y）﹣2（x ﹣2y）＝（x﹣2y）（x+2y﹣2）．这种分解因式的方法叫分组分解法．利用这种方法解决下列问题：（1）分解因式x2﹣2xy+y2﹣16；（2）△ABC三边a，b，c满足a2﹣ab﹣ac+bc＝0，判断△ABC的形状．32．把下列多项式因式分解（要写出必要的过程）：（1）﹣x2y+6xy﹣9y；（2）9（x+2y）2﹣4（x﹣y）2；（3）1﹣x2﹣y2+2xy．参考答案1．解：（a﹣2）（b+3）＝﹣6﹣2b+3a+ab．故选：B．2．解：∵（x﹣2）（x+b）＝x2+bx﹣2x﹣2b＝x2+（b﹣2）x﹣2b＝x2﹣ax﹣1，∴b﹣2＝﹣a，﹣2b＝﹣1，∴b＝0.5，a＝1.5，∴a+b＝2．故选：A．3．解：b2（x﹣3）+b（x﹣3），＝b（x﹣3）（b+1）．故选：B．4．解：﹣6ab+18abx+24aby＝﹣6ab（1﹣3x﹣4y），所以另一个因式是（1﹣3x﹣4y）．故选：A．5．解：①﹣x2﹣y2＝﹣（x2+y2），因此①不能用公式法分解因式；②﹣a2b2+1＝1﹣（ab）2＝（1+ab）（1﹣ab），因此②能用公式法分解因式；③a2+ab+b2不符合完全平方公式的结果特征，因此③不能用公式法分解因式；④﹣x2+2xy﹣y2＝﹣（x2﹣2xy+y2）＝﹣（x﹣y）2，因此④能用公式法分解因式；⑤﹣mn+m2n2＝（﹣mn）2，因此⑤能用公式法分解因式；综上所述，能用公式法分解因式的有②④⑤，故选：B．6．解：根据题意得：第⑧个式子为5555555552﹣4444444452＝（555555555+444444445）×（555555555﹣444444445）＝1.1111111×1017．故选：D．7．解：a3b﹣ab＝ab（a2﹣1）＝ab（a+1）（a﹣1），故选：C．8．解：①原式＝（2x+y）（2x﹣y），能分解因式；②原式＝2x2（x+2y）2，能分解因式；③两个数的平方项，且异号，不能分解因式；④原式＝（x+3y）（x﹣2y），能分解因式；⑤不能化为两个整式积的形式，故不能分解因式．则不能分解因式的有2个．故选：B．9．解：（1）分组错误，无法继续分解因式；（2）﹣4b2+（9a2﹣6ac+c2）可用完全平方公式和平方差公式分解；（3）分组错误，无法继续分解因式；（4）（x2﹣y2）+（mx+my）用平方差公式和提公因式法继续分解因式．故选：B．10．解：原式＝4x2﹣2x﹣y2﹣y，＝（4x2﹣y2）﹣（2x+y），＝（2x﹣y）（2x+y）﹣（2x+y），＝（2x+y）（2x﹣y﹣1）．故选：B．11．解：①按照平行公理可判断在同一平面内，过直线外一点有且只有一条直线与已知直线平行，故本选项正确；②当k为负值时，多项式x2﹣ky2不能分解成两个一次因式积的形式，故本选项不正确；③当t＝4、时，（t﹣3）3﹣2t＝1，故本选项不正确；④新方程为（a﹣1）x+（a+2）y＝2a﹣5，∵a每取一个值时，就有一个方程，而这些方程总有一个公共解，∴当a＝1时，y＝﹣1，当a＝﹣2时，x＝3，∴公共解是．综上正确的说法是①④．故选：A．12．解：（x﹣y）2﹣2（x﹣y）﹣8，＝（x﹣y﹣4）（x﹣y+2）．故选：C．13．解：设另一个因式为x+a，则（x+a）（x﹣3）＝x2+（﹣3+a）x﹣3a，∴﹣m＝﹣3+a，n＝﹣3a，∴m＝3﹣a∴3m﹣n＝3（3﹣a）﹣（﹣3a）＝9﹣3a+3a＝9，故答案为：9．14．解：设另一个因式为x2+ax+b，则2x3+3x﹣k＝（2x﹣5）（x2+ax+b）＝2x3+（2a﹣5）x2+（2b﹣5a）x﹣5b，所以，解得：a＝2.5，b＝，即另一个因式为x2+2.5x+，故答案为：x2+2.5x+．15．解：∵2x3y2＝2x3y•y，12x4y＝2x3y•6x，∴2x3y2与12x4y的公因式是2x3y，故答案为：2x3y．16．解：多项式6a2b+9ab2﹣15ab的公因式是3ab，故答案为：3ab．17．解：x2﹣4x＝x（x﹣4）．故答案为：x（x﹣4）．18．解：a2+3a＝a（a+3）．故答案为：a（a+3）．19．解：∵|x+y﹣5|+（x﹣y+1）2＝0，∴，则原式＝（x+y）（x﹣y）＝﹣5，故答案为：﹣520．解：∵多项式x2+mx+25能用完全平方公式分解因式，∴m＝±10．故答案为：±10．21．解：原式＝﹣3（x2﹣9）＝﹣3（x+3）（x﹣3），故答案为：﹣3（x+3）（x﹣3）22．解：原式＝m（4x2﹣y2）＝m（2x+y）（2x﹣y），故答案为：m（2x+y）（2x﹣y）23．解：设另一个因式为（x+a），得（1分）2x2+3x﹣k＝（2x﹣5）（x+a）（2分）则2x2+3x﹣k＝2x2+（2a﹣5）x﹣5a（4分）∴（6分）解得：a＝4，k＝20（8分）故另一个因式为（x+4），k的值为20（9分）24．解：（1）令x3+ax+1＝（x+1）（x2+bx+c），而（x+1）（x2+bx+c）＝x3+（b+1）x2+（c+b）x+c，∵等式两边x同次幂的系数相等，即x3+（b+1）x2+（c+b）x+c＝x3+ax+1∴解得∴a的值为0，x3+1＝（x+1）（x2﹣x+1）（2）（x+1）（x﹣2）＝x2﹣x﹣2令3x4+ax3+bx﹣34＝（x2﹣x﹣2）（3x2+cx+d），而（x2﹣x﹣2）（3x2+cx+d）＝3x4+（c﹣3）x3+（d﹣c﹣6）x2﹣（2c+d）x﹣2d，∵等式两边x同次幂的系数相等，即3x4+（c﹣3）x3+（d﹣c﹣6）x2﹣（2c+d）x﹣2d＝3x4+ax3+bx﹣34∴解得答：a、b的值分别为8、﹣39．25．解：（1）x2y﹣xy，＝xy（x﹣1）．解：（2）x2﹣4y2，＝x2﹣（2y）2，＝（x+2y）（x﹣2y）．26．解:m3n﹣mn3＝mn（m2﹣n2）＝mn（m+n）（m﹣n）；27．解：x+y＝2，xy＝（）2﹣（）2＝4，x﹣y＝2（1）x2+2xy+y2＝（x+y）2＝（2）2＝24；（2）x2﹣y2＝（x+y）（x﹣y）＝2×2＝8．28．解：（1）运用了C，两数和的完全平方公式；故答案为：C；（2）x2﹣4x+4还可以分解，分解不彻底；（x2﹣4x+4）2＝（x﹣2）4．故答案为：（x﹣2）4．（3）设x2﹣2x＝y．（x2﹣2x）（x2﹣2x+2）+1，＝y（y+2）+1，＝y2+2y+1，＝（y+1）2，＝（x2﹣2x+1）2，＝（x﹣1）4．29．解：（1）n2（m﹣2）﹣n（2﹣m），＝n2（m﹣2）+n（m﹣2），＝n（m﹣2）（n+1）；（2）（x﹣1）（x﹣3）+1，＝x2﹣4x+4，＝（x﹣2）2．30．解：4x2﹣4＝4（x2﹣1）＝4（x+1）（x﹣1）．31．解：（1）x2﹣2xy+y2﹣16＝（x﹣y）2﹣42＝（x﹣y+4）（x﹣y﹣4）；（2）∵a2﹣ab﹣ac+bc＝0∴a（a﹣b）﹣c（a﹣b）＝0，∴（a﹣b）（a﹣c）＝0，∴a＝b或a＝c，∴△ABC的形状是等腰三角形．﹣3）2；。

最新中考一轮数与式复习：《因式分解》基础知识测试(附答案)

中考一轮数与式复习：《因式分解》基础知识测试满分100分姓名：___________班级：___________座号：___________题号一二三总分得分一．选择题（共12小题，满分36分）1．下面运算正确的是（）A．3ab+3ac＝6abc B．4a2b﹣4b2a＝0C．2x2+7x2＝9x4D．3y2﹣2y2＝y22．多项式12ab3c+8a3b的各项公因式是（）A．4ab2B．4abc C．2ab2D．4ab3．代数式x4﹣81，x2﹣9与x2﹣6x+9的公因式为（）A．x+3B．（x+3）2C．x﹣3D．x2+94．下列分解因式中，完全正确的是（）A．x3﹣x＝x（x2﹣1）B．4a2﹣4a+1＝4a（a﹣1）+1C．x2+y2＝（x+y）2D．6a﹣9﹣a2＝﹣（a﹣3）25．将2x2a﹣6xab+2x分解因式，下面是四位同学分解的结果，其中，正确的是（）①2x（xa﹣3ab），②2xa（x﹣3b+1），③2x（xa﹣3ab+1），④2x（﹣xa+3ab﹣1）．A．①B．②C．③D．④6．把x2﹣y2+2y﹣1分解因式结果正确的是（）A．（x+y+1）（x﹣y﹣1）B．（x+y﹣1）（x﹣y+1）C．（x+y﹣1）（x+y+1）D．（x﹣y+1）（x+y+1）7．下列分解因式错误的是（）A．15a2+5a＝5a（3a+1）B．﹣x2﹣y2＝﹣（x+y）（x﹣y）C．ax+x+ay+y＝（a+1）（x+y）D．a2﹣bc﹣ab+ac＝（a﹣b）（a+c）8．下列各式中，从左到右的变形是因式分解的是（）A．（a+2）（a﹣2）＝a2﹣4B．ab+ac+d＝a（b+c）+dC．x2﹣9＝（x﹣3）2D．a2b﹣ab2＝ab（a﹣b）9．下列多项式能用公式法分解因式的有（）①x2﹣2x﹣1；②﹣x+1；③﹣a2﹣b2；④﹣a2+b2；⑤x2﹣4xy+4y2A．1个B．2个C．3个D．4个10．下列各式中，能用平方差公式分解因式的有（）①x2+y2；②x2﹣y2；③﹣x2+y2；④﹣x2﹣y2；⑤；⑥x2﹣4A．3个B．4个C．5个D．6个11．下列各式从左到右的变形是分解因式的是（）A．2a2﹣b2＝（a+b）（a﹣b）+a2B．2a（b+c）＝2ab+2acC．x3﹣2x2+x＝x（x﹣1）2D．x2+x＝x2（1+）12．下列因式分解正确的是（）A．3x+3y+3＝3（x+y）B．a2﹣4a+4＝（a+2）2C．x2﹣4y2＝（x﹣4y）（x+4y）D．x2+2x＝x（x+2）二．填空题（共8小题，满分24分）13．在实数范围内分解因式：x2﹣3x﹣2＝．14．因式分解3xy﹣6y＝．15．分解因式：9m2﹣n2＝．16．分解因式：a2b+ab2﹣a﹣b＝．17．因式分解：2x2y﹣8y3＝．18．多项式ax2﹣a与多项式2x2﹣4x+2的公因式是．19．因式分解：x2﹣5x﹣36＝．20．若关于x的多项式ax3+bx2﹣2的一个因式是x2+3x﹣1，则a+b的值为．三．解答题（共6小题，各小题具体分值在题号后，满分40分）21．（6分）分解因式：12b2﹣3．22．（6分）分解因式：x4﹣（3x﹣2）2．23．（6分）分解因式：（1）xy﹣x+y﹣1；（2）a（a﹣2b）+（b﹣1）（b+1）．24．（7分）对下列代数式分解因式：（1）n2（m﹣2）﹣n（2﹣m）；（2）（x﹣1）（x﹣3）+1．25．（7分）已知：A＝3x2﹣12，B＝5x2y3+10xy3，C＝（x+1）（x+3）+1，问多项式A、B、C是否有公因式？若有，求出其公因式；若没有，请说明理由．26．（8分）仔细阅读下面例题，解答问题：例题：已知二次三项式x2﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．解：设另一个因式为（x+n），得x2﹣4x+m＝（x+3）（x+n）则x2﹣4x+m＝x2+（n+3）x+3n∴．解得：n＝﹣7，m＝﹣21∴另一个因式为（x﹣7），m的值为﹣21问题：仿照以上方法解答下面问题：已知二次三项式2x2+3x﹣k有一个因式是（2x﹣5），求另一个因式以及k的值．参考答案一．选择题1．D 2．D 3．C 4．D 5．C 6．B 7．B 8．D 9．C 10．B 11．C 12．D 二．填空题13．14．3y（x﹣2）15．（3m+n）（3m﹣n）16．（ab﹣1）（a+b）17．2y（x+2y）（x﹣2y）18．（x﹣1）19．（x﹣9）（x+4）20．26 三．解答题21．解：原式＝3（4b2﹣1）＝3（2b+1）（2b﹣1）；22．解：原式＝（x2）2﹣（3x﹣2）2＝（x2+3x﹣2）（x2﹣3x+2）＝（x2+3x﹣2）（x﹣1）（x﹣2）．23．解：（1）原式＝x（y﹣1）+（y﹣1）＝（x+1）（y﹣1）．（2）原式＝a2﹣2ab+b2﹣1＝（a﹣b）2﹣1＝（a﹣b+1）（a﹣b﹣1）．24．解：（1）n2（m﹣2）﹣n（2﹣m），＝n2（m﹣2）+n（m﹣2），＝n（m﹣2）（n+1）；（2）（x﹣1）（x﹣3）+1，＝x2﹣4x+4，＝（x﹣2）2．25．解：多项式A、B、C有公因式．∵A＝3x2﹣12＝3（x2﹣4）＝3（x+2）（x﹣2），B＝5x2y3+10xy3＝5xy3（x+2），C＝（x+1）（x+3）+1＝x2+4x+3+1＝x2+4x+4＝（x+2）2．∴多项式A、B、C的公因式是：x+2．26．解：设另一个因式为（x+a），得2x2+3x﹣k＝（2x﹣5）（x+a）则2x2+3x﹣k＝2x2+（2a﹣5）x﹣5a ∴解得：a＝4，k＝20，故另一个因式为（x+4），k的值为20。

2020年中考数学冲刺复习第一章数与式第四节代数式与整式(含因式分解)

单项式的系数
单项式的次数同类项算
整式的运算
幂的运算整式的乘除
代数式与整式（含因式分解）
因式分解
提公因式法基本方法公式法
十字相乘法步骤
第四节代数式与整式（含因式分解）
返回目录
考点精讲
列代数式及代数式求值
列代数式
把问题中与数量有关的词语，用含有数、字母和运算符号的式子表示出来，如： 1. 原量a增加10%为a(1＋10%) ；原量a减少10%为 a(1－10%) ；比原量a的n倍多m为 an＋m ；比原量a的n倍少m为 an－m ； 2. 原价a的八五折为0.85a；原价a的八折为0.8a；按成本a提高x%后再打七五折为 0.75a(1＋x%) ；
5. (2014江西3题3分)下列运算正确的是( D ) A. a2＋a3＝a5 B. (－2a2)3＝－6a6 C. (2a＋1)(2a－1)＝2a2－1 D. (2a3－a2)÷a2＝2a－1
返回目录
第四节代数式与整式（含因式分解）
拓展训练
6. 计算下列结果． (1)a6÷a－3＝__a_9_____； (2)a2＋a2＝__2_a_2____； (3)a3·a3＝__a_6_____； (4)(m－n)2＝_m_2_－__2_m_n__＋__n_2 ； (5)(3a－b)2＝_9_a_2－__6_a_b_＋__b_2_； (6)－a2b2·3ab3＝_－__3_a_3b_5__； (7)(－ab3)2＝_a_2_b_6____．
②常见的非负数有： a （a≥0），|a|，a2，若|a|＋b2＋ c ＝0，
则a＝b＝c＝0.
返回思维导图
第四节代数式与整式（含因式分解）
返回目录