第六章 自相关参考答案
计量经济学课后答案第六章 自相关

第六章课后答案6.1(1)收入—消费模型为Se = (2.5043) (0.0075)t = (-3.7650) (125.3411)R2 = 0.9978,F = 15710.39,d f = 34,DW = 0.5234(2)对样本量为36、一个解释变量的模型、5%显著水平,查DW统计表可知,d L=1.411,d U= 1.525,模型中DW<d L,显然消费模型中有自相关。
(3)采用广义差分法查5%显著水平的DW统计表可知d L = 1.402,d U = 1.519,模型中DW= 2.0972>d U,说明广义差分模型中已无自相关。
同时,判定系数R2、t、F统计量均达到理想水平。
由差分方程式可以得出:所以最终的消费模型为:6.2(1)给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中不存在自相关。
(2)自相关可能由于模型6.1的误设,因为它排除了趋势的平方项。
(3)虚假自相关是由于模型的误设造成的,因此就要求对可能的函数形式有先验知识。
真正的自相关是可以通过广义差分法等方法来修正。
6.3(1)收入—消费模型为(2)DW=0.575,取,查DW上下界,说明误差项存在正自相关。
(3)采用广义差分法使用普通最小二乘法估计的估计值,得DW=1.830,已知,模型中因此,在广义差分模型中已无自相关。
由差分方程式可以得出:因此,修正后的回归模型应为6.4(1)回归结果如下:(2)模型检验:从回归结果可以看出,参数均显著,模型拟和较好。
异方差的检验:通过white检验可以得知模型不存在异方差。
DW检验:给定n=25, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
(3)采用广义差分法修正模型中存在的自相关问题:给定n=24,,在的显著水平下,查DW统计表可知,。
计量经济学 第六章 自相关

计量经济学
第六章
自相关
6
一阶自相关系数
自相关系数 的定义与普通相关系的公式形式相同
n
utut-1
t=2
n
n
ut2
u2 t 1
t2
t2
的取值范围为 -1 1
(6.1)
式(6.1)中 ut-1是 ut 滞后一期的随机误差项。 因此,将式(6.1)计算的自相关系数 称为一阶 自相关系数。
模型中
ut
是
-1
ut
滞后一期的值,因此称为一阶。
此式中的 也称为一阶自相关系数。
18
如果式中的随机误差项 vt 不是经典误差项,即
其中包含有 ut 的成份,如包含有 ut2 则需将 vt
显含在回归模型中,其为
ut = 1ut-1 + 2ut-2 + vt
其中,1 为一阶自相关系数,2为二阶自相关系
另外回归模型中的解释变量在不同时期通常是
正相关的,对于
Xt和
X
t
来说
j
Xt Xt+j 是大于0的。
33
因此,普通最小二乘法的方差 Var(ˆ2) = 2 Σxt2
通常会低估 ˆ2 的真实方差。当 较大和 Xt 有
较强的正自相关时,普通最小二乘估计量的方 差会有很大偏差,这会夸大估计量的估计精度, 即得到较小的标准误。 因此在有自相关时,普通最小二乘估计 ˆ2 的标 准误就不可靠了。
许多农产品的供给呈现为 蛛网现象,供给对价格的 反应要滞后一段时间,因 为供给需要经过一定的时
间才能实现。如果时期 t
的价格 Pt 低于上一期的 价格 Pt-1 ,农民就会减少 时期 t 1 的生产量。如
第六章 自相关 思考题

第六章 自相关 思考题6.1 如何使用 DW 统计量来进行自相关检验 ? 该检验方法的前提条件和局限性有哪些 ?6.2 当回归模型中的随机误差项为 AR(1) 自相关时 , 为什么仍用OLS 法会低估的ˆjβ标准误差 ? 6.3 判断以下陈述的真伪,并给出合理的解释。
1) 当回归模型随机误差项有自相关时 , 普通最小二乘估计量是有偏误的和非有效的。
2)DW 检验假定随机误差项i u 的方差是同方差。
3) 用一阶差分法消除自相关是假定自相关系数ρ为-1。
4)当回归模型随机误差项有自相关时 , 普通最小二乘估计的预测值的方差和标准误差不再是有效的。
6.4 对于四个解释变量的回归模型011223344t t t t t t Y X X X X u βββββ=+++++如果样本量 n=50, 当 DW 统计量为以下数值时 , 请判断模型中的自相关状况。
1)DW=1.05 2)DW=1.40 3)DW=2.50 4)DW=3.97 6.5 如何判别回归模型中的虚假自相关 ? 6.6 在回归模型12t t t Y X u ββ=++中 ,t u 无自相关。
如果我们错误地判定模型中有一阶自相关 , 即1t t t u u v ρ-=+, 并使用了广义差分模型1121(1)()t t t t t Y Y X X v βρβρ---=-+-+ 将会产生什么问题 ? 练习题 6.1 表 6.6 给出了美国 1960~1995 年 36 年个人实际可支配收入 X 和个人实际消费支出Y 的数据。
1) 用普通最小二乘法估计收入-消费模型 ;12t t t Y X u ββ=++表 6.6 美国个人实际可支配收入和个人实际消费支出 ( 单位 :1010 美元 )资料来源:Economic Report of the Prsident 注 : 数据为 1992 年价格2) 检验收入 -消费模型的自相关状况 (5% 显著水平 ): 3) 用适当的方法消除模型中存在的问题。
第六章 自相关 答案

第六章 自相关一、判断题1.模型中的解释变量含有滞后被解释变量的时候可以使用DW 检验法检验自相关。
(F ) 2.可以作残差对某个解释变量的散点图来大概判断是否存在自相关。
(F ) 3.存在序列相关时,使用标准公式估计的随机扰动项的方差不再具有无偏性。
(T ) 4.杜宾—瓦尔森检验能够检验出任何形式的自相关。
( F ) 5.不存在负的自相关关系。
(F ) 6.LM 检验与DW 检验结果不一致是很有可能的。
(T ) 7. 存在序列相关时,有可能会高估或者低估随机扰动项的真实方差,但通常会低估。
(T )二、单项选择题1.如果模型t t 10t u x y ++=ββ存在序列相关,则( D )。
A. ()0x u Cov t t =,B. ()()s t 0u u Cov s t ≠=,C. ()0x u Cov t t ≠,D. ()()s t 0u u Cov s t ≠≠,2.DW 检验的零假设是(ρ为随机误差项的一阶相关系数)( B )。
A .DW =0B .0=ρC .DW =1D .1=ρ3.下列哪个序列相关可用DW 检验(t v 为具有零均值,常数方差且不存在序列相关的随机变量)( A )。
A . t 1t t v u u +=-ρB .t 2t 21t t v u u u +++=-- ρρC .t t v u ρ= ++=-1t 2t t v v u ρρ4.DW 的取值范围是( D )。
A .-1≤DW≤0B .-1≤DW≤1C .-2≤DW≤2D .0≤DW≤45.当DW =4时,说明( D )。
A .不存在序列相关B .不能判断是否存在自相关C .存在完全的正的自相关D .存在完全的负的自相关6.根据20个观测值估计的结果,一元线性回归模型的DW =2.3。
在样本容量n=20,解释变量k=1,显著性水平为0.05时,查得d L =1,d U =1.41,则可以决断( A )。
A .不存在自相关B .存在正的自相关C .存在负的自相关D .无法确定7.当模型存在序列相关现象时,适宜的参数估计方法是( C )。
六章自相关

Econometrics 2005
18
6.3 自相关的检验
6.3.1 图解法
时间序列图(Time Sequence plot):将残差对时间描点。 如图(a)所示,扰动项的估计值呈循环形,并不频繁 地改变符号,而是相继若干个正的以后跟着几个负的。 表明存在正自相关。
t
t
Econometrics 2005
小于临界值,表示存在序列相关。
Econometrics 2005
28
6.4 自相关的补救1: ( 已知)广义差分法
以双变量回归模型和AR(1)为例。
Yutt
1 2 X t ut1 t
ut
Yt 1 2 X t ut
(1)
Yt1 1 2 X t1 ut1
( 2)
(1) (2) :
Yt Yt1 b0 (1 ) b1( X t X t1) t
差分形式
Yt b0 (1 ) Yt1 b1X t b1X t1 t
a0 b0 (1 )
a1 b1
Yt a0 Yt1 a1 X t a2 X t1 t
a2 b1
往也是正的。于是在不同的样本点之间,随机误差项出现了相关
性,这就产生了序列相关性。
Econometrics 2005
16
再如,以绝对收入假设为理论假设、以时间序列数据
作样本建立居民总消费函数模型:
Ct 0 1 I t t
t=1,2,…,n
消费习惯没有包括在解释变量中,其对消费量的影响被
包含在随机误差项中。如果该项影响构成随机误差项的
类似一阶自相关的定义, 若rs Cov(ut ,uts ) 0, s 2 则称为是高阶自相关。
Econometrics 2005
《随机过程》第6章习题及参考答案

湖南大学本科课程《随机过程》第6章习题及参考答案主讲教师:何松华 教授1. 给定实数x 和一个平稳随机过程()X t ,定义理想门限系统的特性为1()()0()X t xY t X t x≤⎧=⎨>⎩ 试证:(1) [()]()X E Y t F x =;(2) ()](,,)Y X R F x x ττ=证:(1) ()Y t 在任意时刻为只有两种取值1,0的随机变量,则[()]1{()1}0{()0}{()1}{()}(,)() ()X X E Y t P Y t P Y t P Y t P X t x F x t F x =⨯=+⨯====≤==根据平稳性(2)根据相关函数定义,有()][()()]11{()1,()1}01{()0,()1} 10{()1,()0}00{()0,()0}{()1,()1}{(),()}(,;,)(,;) ()Y X X R E Y t Y t P Y t Y t P Y t Y t P Y t Y t P Y t Y t P Y t Y t P X t x X t x F x x t t F x x ττττττττττ=+=⨯⨯+==+⨯⨯+==+⨯⨯+==+⨯⨯+===+===+≤≤=+=根据平稳性2.设平方律检波器的传输特性为2y x =,在检波器输入端加入一窄带高斯随机过程()X t ,其概率密度函数为22()()}2X Xx a f x σ-=- 在检波器后联接一个理想低通滤波器,求低通滤波器输出过程的一维概率密度和均值;当0a =时结果有何变化。
解:根据题意,()X t 为非零均值的中频窄带随机过程,可以表示为:00()()cos()()sin()C S X t a A t t A t t ωω=+-其中()C A t 、()S A t 为零均值窄带随机过程的同向分量以及正交分量,都服从均值为0、方差为2X σ的正态分布,且在同一时刻互不相关,则检波器输出信号22002222200000()[()cos()()sin()]1111()()2()cos()()cos(2)()cos(2)2222 2()sin()()()sin(2)C S C S C C S S C S X t a A t t A t t a A t A t aA t t A t t A t t aA t t A t A t t ωωωωωωω=+-=++++--- 通过理想低通滤波后,滤波器输出信号为2221()[()()]2C S Z t a A t A t =++由于随机变量()C A t 、()S A t 为互不相关(正态分布情况与独立等价)的正态随机变量,则22122()()()C S XXA t A t Z t σσ=+服从自由度为2的卡方分布,即11121/22/211221()22(2/2)z z Z z ef z e ---==Γ 221()()2X Z t Z t a σ=+,2122[()]()[()]XZ t a Z t h Z t σ-==,根据随机变量函数的概率密度关系,()Z t 的一维概率密度分布函数为22122()1()[()] ()X z a Z Z Xdh z f z f h z e z a dz σσ--==≥2222222211[()]{[()()]}[]22C S X X X E Z t E a A t A t a a σσσ=++=++=+当0a =时,221() (0)X zZ Xf z e z σσ-=≥,2[()]X E Z t σ=。
《计量经济学》第六章精选题及答案

第六章自相关二、问答题1、那些原因可以造成自相关;2、存在自相关时,参数的OLS估计具有哪些性质;3、如何检验是否存在自相关;4、当存在自相关时,如何利用广义差分法进行参数估计;5、当存在自相关时,如何利用广义最小平方估计法进行参数估计;6、异方差与自相关有什么异同;三、计算题1、证明:当样本个数较大时,)d。
≈-1(2ρα2、通过D-W检验,判断下列模型中是否存在自相关,显著性水平%5=(1)样本大小:20;解释变量个数(包括常数项):2;d=0.73;(2)样本大小:35;解释变量个数(包括常数项):3;d=3.56;(3)样本大小:50;解释变量个数(包括常数项):3;d=1.87;(4)样本大小:80;解释变量个数(包括常数项):6;d=1.62;(5)样本大小:100;解释变量个数(包括常数项):5;d=2.41;3、假定存在下表所示的时间序列数据:请回答下列问题:(1)利用表中数据估计模型:t t t x y εββ++=10;(2)利用D-W 检验是否存在自相关?如果存在请用d 值计算估计自相关系数ρ;(3)利用广义差分法重新估计模型:'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。
第三部分 参考答案二、问答题1、那些原因可以造成自相关?答:造成自相关的原因大致包括以下六个方面:(1)经济变量的变化具有一定的倾向性。
在实际的经济现象中,许多经济变量的现值依赖于他的前期值。
也就是说,许多经济时间序列都有一个明显的相依性特点,这种现象称作经济变量所具有的惯性。
(2)缺乏应有变量的设定偏差。
(3)不正确的函数形式的设定错误。
(4)蛛网现象和滞后效应。
(5)随机误差项的特征。
(6)数据拟合方法造成的影响。
2、存在自相关时,参数的OLS 估计具有哪些性质?答:当存在自相关,即I D ≠ΩΩ=,)(2σε时,OLS 估计的性质有:(1)βˆ是观察值Y 和X 的线性函数;(2)βˆ是β的无偏估计;(3)βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ;(4)βˆ不是β的最小方差线性无偏估计;(5)如果nX X n Ω'∞→lim存在,那么βˆ是β的一致估计;(6)2σ 不是2σ的无偏估计;(7)2σ不是2σ的一致估计。
统计学第六章课后题及答案解析

第六章一、单项选择题1.下面的函数关系是( )A现代化水平与劳动生产率 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D亩产量与施肥量2.相关系数r的取值范围( )A -∞< r <+∞B -1≤r≤+1C -1< r < +1D 0≤r≤+13.年劳动生产率x(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4.若要证明两变量之间线性相关程度高,则计算出的相关系数应接近于( )A +1B -1C 0.5D 15.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建立线性回归方程ŷ=a+bx。
经计算,方程为ŷ=200—0.8x,该方程参数的计算( )A a值是明显不对的B b值是明显不对的C a值和b值都是不对的D a值和b值都是正确的7.在线性相关的条件下,自变量的均方差为2,因变量均方差为5,而相关系数为0.8时,则其回归系数为:( )A 8B 0.32C 2D 12.58.进行相关分析,要求相关的两个变量( )A都是随机的 B都不是随机的C一个是随机的,一个不是随机的 D随机或不随机都可以9.下列关系中,属于正相关关系的有( )A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究( )A变量之间的数量关系 B变量之间的变动关系C变量之间的相互关系的密切程度 D变量之间的因果关系11.在回归直线y c=a+bx,b<0,则x与y之间的相关系数 ( )A r=0B r=lC 0< r<1D -1<r <012.当相关系数r=0时,表明( )A现象之间完全无关 B相关程度较小C现象之间完全相关 D无直线相关关系13.下列现象的相关密切程度最高的是( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关系数为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8114.估计标准误差是反映( )A平均数代表性的指标 B相关关系的指标C回归直线方程的代表性指标 D序时平均数代表性指标二、多项选择题1.下列哪些现象之间的关系为相关关系( )A家庭收入与消费支出关系 B圆的面积与它的半径关系C广告支出与商品销售额关系D商品价格一定,商品销售与额商品销售量关系2.相关系数表明两个变量之间的( )A因果关系 C变异程度 D相关方向 E相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C可能存在着y依x和x依y的两个回归方程D回归系数只有正号4.可用来判断现象线性相关方向的指标有( )A相关系数 B回归系数 C回归方程参数a D估计标准误5.单位成本(元)依产量(千件)变化的回归方程为y c=78- 2x,这表示( ) A产量为1000件时,单位成本76元B产量为1000件时,单位成本78元C产量每增加1000件时,单位成本下降2元D产量每增加1000件时,单位成本下降78元6.估计标准误的作用是表明( )A样本的变异程度 B回归方程的代表性C估计值与实际值的平均误差 D样本指标的代表性7.销售额与流通费用率,在一定条件下,存在相关关系,这种相关关系属于( ) A完全相关 B单相关 C负相关 D复相关8.在直线相关和回归分析中( )A据同一资料,相关系数只能计算一个B据同一资料,相关系数可以计算两个C据同一资料,回归方程只能配合一个D据同一资料,回归方程随自变量与因变量的确定不同,可能配合两个9.相关系数r的数值( )A可为正值 B可为负值 C可大于1 D可等于-110.从变量之间相互关系的表现形式看,相关关系可分为( )A正相关 B负相关 C直线相关 D曲线相关11.确定直线回归方程必须满足的条件是( )A现象间确实存在数量上的相互依存关系B相关系数r必须等于1C y与x必须同方向变化D现象间存在着较密切的直线相关关系12.当两个现象完全相关时,下列统计指标值可能为( )A r=1B r=0C r=-1D S y=013.在直线回归分析中,确定直线回归方程的两个变量必须是( )A一个自变量,一个因变量 B均为随机变量C对等关系 D一个是随机变量,一个是可控制变量14.配合直线回归方程是为了( )A确定两个变量之间的变动关系 B用因变量推算自变量C用自变量推算因变量 D两个变量都是随机的15.在直线回归方程中( )A在两个变量中须确定自变量和因变量 B一个回归方程只能作一种推算C要求自变量是给定的,而因变量是随机的。
计量经济学练习题答案(第六章)
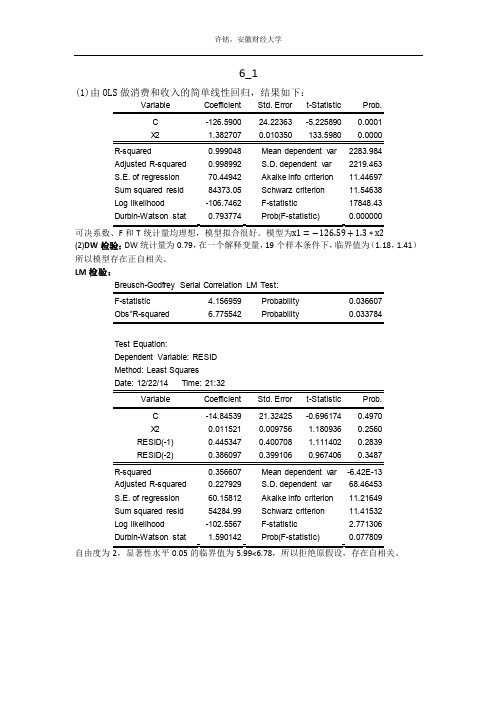
6_1(1)由OLS做消费和收入的简单线性回归,结果如下:Variable Coefficient Std. Error t-Statistic Prob.C -126.5900 24.22363 -5.225890 0.0001R-squared 0.999048 Mean dependent var 2283.984Adjusted R-squared 0.998992 S.D. dependent var 2219.463S.E. of regression 70.44942 Akaike info criterion 11.44697Sum squared resid 84373.05 Schwarz criterion 11.54638Log likelihood -106.7462 F-statistic 17848.43Durbin-Watson stat 0.793774 Prob(F-statistic) 0.000000可决系数、F和T统计量均理想,模型拟合很好。
模型为x1=−126.59+1.3∗x2(2)DW检验:DW统计量为0.79,在一个解释变量,19个样本条件下,临界值为(1.18,1.41)所以模型存在正自相关。
LM检验:F-statistic 4.156959 Probability 0.036607Test Equation:Dependent Variable: RESIDMethod: Least SquaresDate: 12/22/14 Time: 21:32C -14.84539 21.32425 -0.696174 0.4970X2 0.011521 0.009756 1.180936 0.2560RESID(-1) 0.445347 0.400708 1.111402 0.2839RESID(-2) 0.386097 0.399106 0.967406 0.3487R-squared 0.356607 Mean dependent var -6.42E-13Adjusted R-squared 0.227929 S.D. dependent var 68.46453S.E. of regression 60.15812 Akaike info criterion 11.21649Sum squared resid 54284.99 Schwarz criterion 11.41532Log likelihood -102.5567 F-statistic 2.771306Durbin-Watson stat 1.590142 Prob(F-statistic) 0.077809自由度为自相关分析:解释变量和被解释变量有显著二阶自相关。
第六章自相关性详解

y A bx vt
* t * t
其中,A=a(1- ρ )。
ˆ /(1 利用OLS法估计A、b,进而得到: a ˆA
若ρ =1,则可得到一阶差分模型 yt-yt-1=b(xt-xt-1) +υ 如果为高阶自回归形式: ε t=ρ 1ε t-1+ρ 2ε t-2+…+ρ pε
(2)构造检验统计量:
DW
(e
2
n
t
et 1 )
2
2 e t 1
n
DW统计量与ρ 之间的关系: 因为对于大样本,
2 2 e e t et 1 2 t 1 2 2 n n n
所以:
DW
2
2 2 ( e 2 e e e t t t 1 t 1 )
e
2 t
2 2 e 2 e e e t t t 1 t 1 ) 2 e t
2( e t et et 1 )
2 e t
et et 1 21 2 2 1 et
Байду номын сангаас
e
et et 1
2 t
ˆ) S (b
2
( xt x )
2
ˆ2 ( xt x ) 2
三、t检验失效。 四、模型的预测精度降低。
第三节 自相关性的检验
一、残差图检验 二、德宾-沃森(Durbin-Watson,DW)检验 适用条件:随机项一阶自相关性;解释变量 与随机项不相关;不含有滞后的被解释变量, 截距项不为零;样本容量较大。 基本原理和步骤: (1) 提出假设 H0: ρ =0一
③在大样本情况下,有 nR2~χ 2(p) 给定α ,若nR2大于临界值,拒绝H0。 EViews软件操作:在方程窗口中点击View\ Residual Test \Serial Correlation LM Test。
统计学第六章课后题及答案解析

第六章一、单项选择题1.下面的函数关系是( )A现代化水平与劳动生产率 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D亩产量与施肥量2.相关系数r的取值范围( )A -∞< r <+∞B -1≤r≤+1C -1< r < +1D 0≤r≤+13.年劳动生产率x(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4.若要证明两变量之间线性相关程度高,则计算出的相关系数应接近于( )A +1B -1C 0.5D 15.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建立线性回归方程ŷ=a+bx。
经计算,方程为ŷ=200—0.8x,该方程参数的计算( )A a值是明显不对的B b值是明显不对的C a值和b值都是不对的D a值和b值都是正确的7.在线性相关的条件下,自变量的均方差为2,因变量均方差为5,而相关系数为0.8时,则其回归系数为:( )A 8B 0.32C 2D 12.58.进行相关分析,要求相关的两个变量( )A都是随机的 B都不是随机的C一个是随机的,一个不是随机的 D随机或不随机都可以9.下列关系中,属于正相关关系的有( )A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究( )A变量之间的数量关系 B变量之间的变动关系C变量之间的相互关系的密切程度 D变量之间的因果关系11.在回归直线y c=a+bx,b<0,则x与y之间的相关系数 ( )A r=0B r=lC 0< r<1D -1<r <012.当相关系数r=0时,表明( )A现象之间完全无关 B相关程度较小C现象之间完全相关 D无直线相关关系13.下列现象的相关密切程度最高的是( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关系数为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8114.估计标准误差是反映( )A平均数代表性的指标 B相关关系的指标C回归直线方程的代表性指标 D序时平均数代表性指标二、多项选择题1.下列哪些现象之间的关系为相关关系( )A家庭收入与消费支出关系 B圆的面积与它的半径关系C广告支出与商品销售额关系D商品价格一定,商品销售与额商品销售量关系2.相关系数表明两个变量之间的( )A因果关系 C变异程度 D相关方向 E相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C可能存在着y依x和x依y的两个回归方程D回归系数只有正号4.可用来判断现象线性相关方向的指标有( )A相关系数 B回归系数 C回归方程参数a D估计标准误5.单位成本(元)依产量(千件)变化的回归方程为y c=78- 2x,这表示( ) A产量为1000件时,单位成本76元B产量为1000件时,单位成本78元C产量每增加1000件时,单位成本下降2元D产量每增加1000件时,单位成本下降78元6.估计标准误的作用是表明( )A样本的变异程度 B回归方程的代表性C估计值与实际值的平均误差 D样本指标的代表性7.销售额与流通费用率,在一定条件下,存在相关关系,这种相关关系属于( ) A完全相关 B单相关 C负相关 D复相关8.在直线相关和回归分析中( )A据同一资料,相关系数只能计算一个B据同一资料,相关系数可以计算两个C据同一资料,回归方程只能配合一个D据同一资料,回归方程随自变量与因变量的确定不同,可能配合两个9.相关系数r的数值( )A可为正值 B可为负值 C可大于1 D可等于-110.从变量之间相互关系的表现形式看,相关关系可分为( )A正相关 B负相关 C直线相关 D曲线相关11.确定直线回归方程必须满足的条件是( )A现象间确实存在数量上的相互依存关系B相关系数r必须等于1C y与x必须同方向变化D现象间存在着较密切的直线相关关系12.当两个现象完全相关时,下列统计指标值可能为( )A r=1B r=0C r=-1D S y=013.在直线回归分析中,确定直线回归方程的两个变量必须是( )A一个自变量,一个因变量 B均为随机变量C对等关系 D一个是随机变量,一个是可控制变量14.配合直线回归方程是为了( )A确定两个变量之间的变动关系 B用因变量推算自变量C用自变量推算因变量 D两个变量都是随机的15.在直线回归方程中( )A在两个变量中须确定自变量和因变量 B一个回归方程只能作一种推算C要求自变量是给定的,而因变量是随机的。
概率论与数理统计第六章课后习题及参考答案

概率论与数理统计第六章课后习题及参考答案1.已知总体X ~),(2σμN ,其中2σ已知,而μ未知,设1X ,2X ,3X 是取自总体X 的样本.试问下面哪些是统计量?(1)321X X X ++;(2)μ31-X ;(3)222σ+X ;(4)21σμ++X ;(5)},,max{321X X X ;(6)σ221++X X ;(7)∑=3122i i X σ;(8)2μ-X .解:(1)(3)(4)(5)(6)(7)是,(2)(8)不是.2.求下列各组样本值的平均值和样本差.(1)18,20,19,22,20,21,19,19,20,21;(2)54,67,68,78,70,66,67,70.解:(1)9.19)21201919212022192018(101101101=+++++++++==∑=i i x x ;43.1)(9110122=-=∑=i i x x s .(2)5.67)7067667078686754(1018181=+++++++==∑=i i x x ;018.292)(718122=-=∑=i i x x s .3.(1)设总体X ~)1,0(N ,则2X ~)1(2χ.(2)设随机变量F ~),(21n n F ,则F1~),(12n n F .(3)设总体X ~),(2σμN ,则X ~),(2n N σμ,22)1(S n σ-~)1(2-n χ,nS X /μ-~)1(-n t .(4)设总体X ~)10(2χ,Y ~)15(2χ,且X 与Y 相互独立,则=+)(Y X E 25,=+)(Y X D 50.4.设随机变量X 与Y 都服从标准正态分布,则(C )A .Y X +服从正态分布B .22Y X +服从2χ分布C .2X 与2Y 均服从2χ分布D .22YX 服从F 分布5.在总体X ~)3.6,52(2N 中随机抽取一容量为36的样本,求样本平均值X 落在8.50到8.53之间的概率.解:因为X ~)3.6,52(2N ,即52=μ,223.6=σ,因为36=n ,22205.1363.6==n σ,所以X ~)05.1,52(2N .由此可得)8.538.50(≤≤X P 05.1528.50()05.1528.53(-Φ--Φ=8302.0)1429.1()7143.1(=-Φ-Φ=.6.设总体X ~)1,0(N ,1X ,2X ,…,10X 为总体的一个样本,求:(1))99.15(1012>∑=i i X P ;(2)写出1X ,2X ,…,10X 的联合概率密度函数;(3)写出X 的概率密度.解:(1)由题可知∑==1012i i X X ~)10(2χ,查2χ分布表有99.15)10(210.0=χ,可得10.0=α,即10.0)99.15(1012=>∑=i i X P .(2)1X ,2X ,…,10X 相互独立,则联合概率密度函数为}exp{321}21exp{21),,,(1012510121021∑∏==-=-=i i i i x x x x x f ππ .(3)X Y =~)1.0,0(N ,所以有2251.02)0(e 5e1.021)(y y y f -⋅--==ππ.7.设总体X ~)1,0(N ,1X ,2X ,…,5X 为总体的一个样本.确定常数c ,使25242321)(XX X X X c Y +++=~)3(t .解:因为i X ~)1,0(N ,5,,2,1 =i ,所以21X X +~)2,0(N ,)(2121X X +~)1,0(N ,252423X X X ++~)3(2χ,因为25242321252423212632XX X X X X X X X X +++=+++~)3(t ,所以有23=c .8.设1X ,2X ,3X ,4X 是来自正态总体)4,0(N 的样本.已知243221)43()2(X X b X X a Y -+-=为服从自由度为2的2χ分布,求a ,b 的值.解:由题可知i X ~)4,0(N ,4,3,2,1=i ,故有0)2(21=-X X E ,20)2(21=-X X D ,所以212X X -~)20,0(N .同理4343X X -~)100,0(N .而20)2(221X X -~)1(2χ,100)43(221X X -~)1(2χ,故有100)43(20)2(243221X X X X -+-~)2(2χ,比较可知201=a ,1001=b .9.设总体X ~)3.0,(2μN ,1X ,2X ,…,n X 为总体的一个样本,X 是样本均值,问样本容量n 至少应取多大,才能使95.0)1.0(≥<-μX P .解:易知X ~)3.0,(2nN μ,由题意有95.013(2/3.01.0/3.0()1.0(≥-Φ=<-=<-nnnX P X P μμ,即应有975.0)3(≥Φn,查正态分布表知975.0)96.1(=Φ,所以取96.13≥n,即5744.34≥n ,取35=n .10.设总体X ~)16,(μN ,1X ,2X ,…,10X 为总体的一个样本,2S 为样本方差,已知1.0)(2=>αS P ,求α的值.解:由抽样分布定理知22)1(σS n -~)1(2-n χ,因为10=n ,故有2249S ~)9(2χ,得1.0)169169()(22=>=>ααS P S P ,查2χ分布表得684.14)9(21.0=χ,即684.14169=α,解得105.26=α.11.设(1X ,2X ,…,1+n X )为来自总体X ~),(2σμN 的一个样本,记∑==n i i n X n X 11,∑=--=n i in X X n S 122(11,求证:nn n S X X n n T -⋅+=+11~)1(-n t .证:由题可知n X ~),(2nN σμ,n n X X -+1~)11(,0(2σn N +,标准化得σnX X nn 111+-+~)1,0(N .又因为∑=-=-ni inX XS n 1222)(1)1(σσ~)1(2-n χ,从而有nn nnn S XX n n n S n n X X -+=--+-++122111)1(11σσ~)1(-n t ,即nnn S X X n n T -⋅+=+11~)1(-n t .。
自相关试题及答案

自相关试题及答案一、选择题1. 自相关函数是描述什么特性的统计量?A. 随机变量的分布特性B. 随机过程的统计特性C. 随机变量的独立性D. 随机过程的独立性答案:B2. 自相关函数的计算公式是什么?A. R(τ) = E[X(t)X(t+τ)]B. R(τ) = E[X(t) - μ][X(t+τ) - μ]C. R(τ) = E[X(t)X(t-τ)]D. R(τ) = E[X(t) + μ][X(t+τ) + μ]答案:B3. 自相关函数的值在什么范围内?A. -∞ 到+∞B. 0 到+∞C. -1 到 1D. 0 到 1答案:B二、简答题1. 什么是自相关函数,它在信号处理中有什么应用?答:自相关函数是一种描述信号或随机过程在不同时间点上值之间相关程度的统计量。
在信号处理中,自相关函数用于分析信号的周期性,检测信号中的重复模式,以及估计信号的功率谱。
2. 请简述自相关函数和互相关函数的区别。
答:自相关函数是描述同一信号在不同时间点上的值之间的相关性,而互相关函数是描述两个不同信号在不同时间点上的值之间的相关性。
自相关函数通常用于分析单个信号的特性,而互相关函数用于分析两个信号之间的相似性或时延。
三、计算题1. 给定一个离散时间信号 x[n] = {1, 2, 3, 4, 3, 2},请计算其自相关函数 R(0) 和 R(1)。
解:根据自相关函数的定义R(τ) = E[x[n]x[n-τ]],计算得:R(0) = (1*1 + 2*2 + 3*3 + 4*4 + 3*3 + 2*2) / 6 = 40 / 6 =20/3R(1) = (1*2 + 2*3 + 3*4 + 4*3 + 3*2 + 2*1) / 6 = 38 / 6 ≈ 6.33332. 如果一个随机过程 X(t) 的自相关函数为R(τ) = e^(-|τ|),请说明该过程的性质。
解:该自相关函数表明,随着时间延迟τ 的增加,随机过程 X(t) 的值之间的相关性指数级衰减。
计量经济学题库第6章自相关

第6章 自相关习 题一、单项选择题 1.设为随机误差项,则一阶线性自相关是指( )2.已知样本回归模型残差的一阶自相关系数接近于1,则DW 统计量近似等于( )A. 0B. 1C. 2D. 43.在序列自相关的情况下,参数估计值仍是无偏的,其原因是( )A. 无多重共线性假定成立B. 同方差假定成立C. 零均值假定成立D. 解释变量与随机误差项不相关假定成立4.应用DW 检验方法时应满足该方法的假定条件,下列不是其假定条件的为( )A. 解释变量为非随机的B. 被解释变量为非随机的C. 线性回归模型中不能含有滞后内生变量D. 随机误差项服从一阶自回归 5.广义差分法是( )的一个特例A. 加权最小二乘法B. 广义最小二乘法C. 普通最小二乘法D. 两阶段最小二乘法6.在下列引起序列自相关的原因中,不正确的是( )A. 经济变量具有惯性作用B. 经济行为的滞后性C. 设定偏误D. 解释变量之间的共线性 7.已知模型的形式为,在用实际数据对模型的参数进行估计的时候,测得DW 统计量为0.6453,则广义差分变量是( )A . t u 1211221.cov(,)0()...t s t t t t t t tt t t A u u t s B u u C u u u D u u ρερρερε----≠≠=+=++=+011t t t Y X u ββ=++11110.6453,0.6453tt t t Y Y X X ----B .C .D .8.在修正序列自相关的方法中,能修正高阶自相关的方法是( )A. 利用DW 统计量值求出B. Cochrane-Orcutt 法C. Durbin 两步法D. 移动平均法9.在DW 检验中,当d 统计量为2时,表明( )A. 存在完全的正自相关B. 存在完全的负自相关C. 不存在自相关D. 不能判定 10.在给定的显著性水平之下,若DW 统计量的下和上临界值分别为dL 和du,则当dL<DW<du 时,可认为随机误差项( )A. 存在一阶正自相关B. 存在一阶负相关C. 不存在序列相关D. 存在序列相关与否不能断定 11. 在序列自相关的情况下,参数估计值的方差不能正确估计的原因是( )12.在DW 检验中,当d 统计量为0时,表明( )A.存在完全的正自相关B.存在完全的负自相关C.不存在自相关D.不能判定 13.在DW 检验中,存在正自相关的区域是( )A. 4-﹤﹤4B. 0﹤﹤C. ﹤﹤4-D. ﹤﹤,4-﹤﹤4-14.如果回归模型违背了无自相关假定,最小二乘估计量是( )A .无偏的,有效的 B. 有偏的,非有效的 C .无偏的,非有效的 D. 有偏的,有效的 15.广义差分法是对( )用最小二乘法估计其参数。
第06章 自相关(讲稿)

第6章自相关1. 自相关定义1)非自相关由第2节知回归模型的假定条件之一是,Cov(u i,u j )=E(u i u j) =0, (i, j∈T, i ≠ j),(1.1)即误差项u t的取值在时间上是相互无关的。
称误差项u t非自相关。
2)自相关如果Cov (u i ,u j ) ≠ 0, (i ≠ j)则称误差项u t存在自相关。
自相关又称序列相关。
原指一随机变量在时间上与其滞后项之间的相关。
这里主要是指回归模型中随机误差项u t 与其滞后项的相关关系。
自相关也是相关关系的一种。
2.自相关类型1)自相关按滞后阶数可分为两类。
(1)一阶自回归形式当误差项u t只与其滞后一期值有关时,即u t = f (u t - 1),称u t具有一阶自回归形式。
(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关,而且与其前若干期的值都有关系时,即u t = f (u t – 1, u t – 2 , … ), 则称u t 具有高阶自回归形式。
2)按函数形式分为线性自相关和非线性自相关 (1)线性自相关 f 为线性函数形式 (2)非线性自相关 f 为非线性函数形式 3.一阶线性自相关通常假定误差项的自相关是线性的。
因计量经济模型中自相关的最常见形式是一阶自回归形式,所以下面重点讨论误差项的线性一阶自回归形式,即 u t =1a u t -1 + v t (1.2)其中1a 是自回归系数,v t 是随机误差项。
v t 满足通常假设E(v t ) = 0, t = 1, 2 …, T, Var(v t ) = σv 2, t = 1, 2 …, T,Cov(v i , v j ) = 0, i ≠ j, i, j = 1, 2 …, T, Cov(u t-1, v t ) = 0, t = 1, 2 …, T,依据普通最小二乘法公式,模型(1.2)中 1 的估计公式是,1ˆa= ∑∑=-=-Tt t Tt t tuuu 22121 (1ˆβ=∑∑---2)())((x x x x y y t t t ) (1.3)其中T 是样本容量。
北方民族大学计量期末习题第六章 自相关

一、单项选择题1.在给定的显著性水平之下,若DW 统计量的下和上临界值分别为dL 和dU,则当L U d d d <<时,可认为随机误差项( )A.存在一阶正自相关B.存在一阶负相关C.不存在序列相关D.存在序列相关与否不能断定2.在序列自相关的情况下,参数估计值的方差不能正确估计的原因是( )A22() i E u σ≠ B ()0() i j E u u i j ≠≠ C ()0 i i E x u ≠ D ()0 i E u ≠ 3.在检验异方差的方法中,不正确的是( )A. Goldfeld-Quandt 方法B. X-Y 散点图检验法C. White 检验法D. DW 检验法4.在DW 检验中,当d 统计量为0时,表明( )A.存在完全的正自相关B.存在完全的负自相关C.不存在自相关D.不能判定5.在下列产生序列自相关的原因中,不正确的是( )A.经济变量的惯性作用B.经济行为的滞后作用C.设定偏误D.解释变量的共线性6.加权最小二乘法是( )的一个特例A.广义差分法B.普通最小二乘法C.广义最小二乘法D.两阶段最小二乘法8.设为随机误差项,则一阶线性自相关是指( )A cov(,)0()t s u u t s ≠≠B 1t t t u u ρε-=+C 1122t t t t u u u ρρε--=++ D21t t t u u ρε-=+ 9.在自相关情况下,常用的估计方法( )A .普通最小二乘法 B. 广义差分法 C .工具变量法 D. 加权最小二乘法10.在DW 检验中,不能判定的区域是( )A 0,44l l d d d d <<-<<B 4u u d d d <<-C ,44l u u l d d d d d d <<-<<-D 上述都不对11.用于检验序列相关的DW 统计量的取值范围是( )。
A.0≤DW ≤1B.-1≤DW ≤1C.-2≤DW ≤2D.0≤DW ≤412.已知DW 统计量的值接近于2,则样本回归模型残差的一阶自相关系数ρˆ近似等于( )。
自相关性习题集与答案解析

自相关性一、名词解释1 序列相关性2 虚假序列相关3 差分法4 广义差分法5 自回归模型6 广义最小二乘法7 DW 检验 8 科克伦-奥克特跌代法 9 Durbin 两步法10 相关系数二、单项选择题1、如果模型y t =b 0+b 1x t +u t 存在序列相关,则()(x t , u t )=0 (u t , u s )=0(t ≠s) C. cov(x t , u t )≠0 D. cov(u t , u s ) ≠0(t ≠s)2、DW 检验的零假设是(ρ为随机误差项的一阶相关系数)A 、DW =0B 、ρ=0C 、DW =1D 、ρ=13、下列哪个序列相关可用DW 检验(v t 为具有零均值,常数方差且不存在序列相关的随机变量)A .u t =ρu t -1+v tB .u t =ρu t -1+ρ2u t -2+…+v tC .u t =ρv tD .u t =ρv t +ρ2 v t-1 +…4、DW 的取值范围是()A 、-1≤DW ≤0B 、-1≤DW ≤1C 、-2≤DW ≤2D 、0≤DW ≤45、当DW =4时,说明()A 、不存在序列相关B 、不能判断是否存在一阶自相关C 、存在完全的正的一阶自相关D 、存在完全的负的一阶自相关6、根据20个观测值估计的结果,一元线性回归模型的DW =。
在样本容量n=20,解释变量k=1,显著性水平为时,查得dl=1,du=,则可以决断()A 、不存在一阶自相关B 、存在正的一阶自相关C 、存在负的一阶自D 、无法确定7、当模型存在序列相关现象时,适宜的参数估计方法是()A 、加权最小二乘法B 、间接最小二乘法C 、广义差分法D 、工具变量法8、对于原模型y t =b 0+b 1x t +u t ,广义差分模型是指()0t 1t t t 01t t t t-101t t-1t t-1b B. y =b x uC. y =b +b x uD. y y =b (1-)+b (x x )(u u )ρρρρ++++--+- 9、采用一阶差分模型一阶线性自相关问题适用于下列哪种情况()A 、ρ≈0B 、ρ≈1C 、-1<ρ<0D 、0<ρ<110、假定某企业的生产决策是由模型S t =b 0+b 1P t +u t 描述的(其中S t 为产量,P t 为价格),又知:如果该企业在t-1期生产过剩,经营人员会削减t 期的产量。
概率统计第六章习题参考答案

概率统计第六章参考答案1.~(0,)X U b 101()2bbE X x dx A X b ====⎰2bX = ,b =1.69 2. 22()()3E X x xdx X θθθθ=-==⎰, 3X θ= 3. ~(,)X B m p111(1)101()(1)(1)kkm kk k m k mm k k E X kC p p pm C pp pm ∞∞-------===-=-=∑∑=X 22()(1)(1)(1)(1)k km kk km k mm k k E X k k C p p kC p p pm p X ∞∞--===--+-=-+∑∑=2A 4.~()X πλ {}!k e P X k k λλ-==()!k k e E X kX k λλλ-∞====∑ 所以 x λ= 11()()!nii x n nii e L p x λλ=-=∑=∏, 11ln ()ln ln ()!n niii i L p x n x λλ===--∑∏1(ln ())0nii x dL p n dp λ==-=∑ 解得 X λ=且2221(ln ())0d L p dp λ=-<所以 x λ=利用此式计算(2)5.1{}(1)x P X x p p -==-,1()()(1)ni i x n n L p p p =-∑=-1ln(())()ln(1)ln ni i L p x n p n p ==--+∑1(ln ())1ni i x n d nL p dp p p=-=-+-∑=0 解得1p = 利用此式解(2)6.2~(,)X N μσ (1) 参数2σ已知,估计μ解:由于),(~2σμN X ,故其概率密度函数为:),;(σμx f =()22221σμσπ--⋅x e⇒似然函数为),;,,,(21σμn n x x x L =∏=ni 1),;(σμi x f =∏=ni 1()22221σμσπ--⋅i x e=()21221σμσπ--∑=⋅⎪⎪⎭⎫⎝⎛⋅i ni x ne=()()212122μσσπ----∑=⋅⋅i ni x n n e两边取对数有:ln L =()()()212212ln ln 2ln μσσπ----∑=++i ni x nn e=()()212221ln 2ln μσσπ-∑--=-i ni nx n(l n ())dL d μμ=2(1)0ni i x n μ=-=∑ ⇒ˆx μ= (2) 参数μ已知,估计2σ22(ln ())d L d σσ=()2130ni i x nμσσ=-∑-+=⇒()2211ˆni i x x n σ==-∑ 7. (1) /21,0()0,x xe x f x θθ-⎧>⎪=⎨⎪ ⎩其他1/1222111()(),nii i x nx i n ni L x ex x x eθθθθθ=--=∑==∏121(())2()()()/nn i i Ln L nLn nLn x x x x θθθ==-+-∑(ln ())d L d θθ=1202nii x n θθ=-+=∑ ⇒ 2X θ=(2) 32/1,0()20,x x e x f x θθ-⎧>⎪=⎨⎪ ⎩其他1/221233111()(),22nii i x nx i n n n i L x e x x x e θθθθθ=--=∑==∏2121(())23()()()/nn i i Ln L nLn nLn nLn x x x x θθθ==--+-∑(ln ())d L d θθ=1203nii x n θθ=-+=∑⇒ 3X θ= (3) ~(,)X B m p 参数m 已知估计p ,{}(1)k kn k n P X k C p p -==-()L p =1(1)ii i nx x m x ni Cp p -=-(())Ln L p =111()ln(1)i nnnx ni i i i i Ln C x Lnp nm x p ===++--∑∑(ln ())dL p dp=1101nniii i xnm x pp==--=-∑∑⇒1ni i x =∑=nmp ⇒Xp m= 8.22()2(1)L θθθθθ=- 直接对其求导数=0 得到 56θ= 9.利用第六题中的结论可知道Y Xαβαβ⎧-=⎪⎨+=⎪⎩解得 22X Y α=+, 22X Y β=-10.(1) 证明:()(2)2()E E X E X θθ===(2) ()()E Y E Y λ==22()(3)3()()()E Z E Y Y E Y E Y D Y =+=++=24λλ+(3) 22111()(3)3()()()ni i E U E Y Y E Y nE Y E Z nn==+=+⋅=∑11 .T1和T3是无偏估计量 T3最有效 22212210()36936D T θθθ=+= 222222149164()252525255D T θθθθθ=+++= 2231()40.2516D T θθ=⋅= 12.(,1296)X N μ 27,36n σ==置信区间是22(,)X Z X Z αα-+(1) 210.95, 1.96Z αα-==, (2) 210.9, 1.645Zαα-==13. (1) 用第6题结论 (2)置信区间是22(,)X Z X Z αα-+,210.95, 1.96Z αα-==14.(1)根据P140中结论计算 (2)置信区间是2((1))X n a?,230,10.9, 1.6973n t a a =-== 15.置信区间是2((1))X n a?,9.4,12,s n == 210.95, 2.1788t a a -== 16.置信区间是2((1))X n a?, 19.06875,32, 3.256x n S === 210.95, 2.1788t a a -==17.置信区间是2((1))X n a?, 214.71, 6.144,13,10.95, 2.1788x S n t a a ===-==18.置信区间是122((2)X Y t n n S a -?-其中: W S =221281.31,78.61,60.76,48.24X Y S S ====1229,15,10.95,(23) 1.7139n n t a a ==-==19. 置信区间是2211222/21221/21211(,)(1,1)(1,1)S S S F n n S F n n a a -----129,11,n n == 22120.344,0.456S S ==/212(1,1) 3.85F n n a --=, 11/212 4.3(1,1)F n n a ---=20.单侧置信上限:221122221121()(1,1)S S F n n a s s -=--其中10.95a -=,21S =6.798 , 22S = 9.627 , 112(1,1)F n n a ---=3.29单侧置信上限22121(1)(1)n S n a s c --=- 21(1)n a c --=2.16721.单侧置信下限:(1)X n a m =+- 14.71, 6.144,13,10.95,(12)x S n t a a ===-==1.782322.单侧置信上限12(2)X Y t n n S a m =-++-222112212(1)(1)2wn S n S S n n -+-=+-,221281.31,78.61,60.76,48.24X Y S S ====12(2) 1.71t n n a +-=,。
计量经济学第六章部分课后题(庞皓(第三版))

计量经济学第六章作业思考题:6.1 如何使用DW统计量来进行自相关检验?该检验方法的前提条件和局限性有哪些?答:(1)DW 检验是J.Durbin(杜宾)和G.S.Watson(沃特森)于1951年提出的一种适用于样本容量大于等于15的检验自相关的方法,许多计量经济学和统计学计算机软件都可以计算出DW 值。
给定显著水平α,依据样本容量n和解释变量个数k’(不包括常数项),查D.W.分布表可得临界值(d统计量的上界d U和下界d L),当0<DW<d L时,表明存在一阶正自相关,而且正自相关的程度随DW向0的靠近而增强。
当d L<DW<d U时,表明为不能确定是否存在自相关。
当d U<DW<4-d U时,表明不存在一阶自相关。
当4-d U<DW<4-d L时,表明不能确定是否存在自相关。
当4-d L<DW<4时,表明存在一阶负自相关,而且负自相关的程度随DW向4的靠近而增强。
(2)DW检验的前提条件:<1>解释变量是非随机的(因此与随机扰动项不相关);<2>随机扰动项是一阶自回归形式,即u t=ρu t-1 +v t (v t满足古典假定);<3>线性模型的解释变量中不包含滞后的被解释变量,如不应出现下列形式:Y t =β1 +β2 X t +β 3 Y t-1 +u t;<4>截距项不为零,即只适用于有常数项的回归模型;<5>数据序列无缺失项,样本比较大。
(3)DW检验的局限性:<1>DW检验有两个不能确定的区域,一旦DW值落在这两个区域,就无法判断。
这时,只有增大样本容量或选取其他方法;<2>DW统计量的上、下界表要求n≥15, 这是因为样本如果再小,利用残差就很难对自相关的存在性做出比较正确的诊断;<3> DW检验不适应随机误差项具有高阶序列相关的检验;<4> DW检验有运用的前提条件,只有符合这些条件DW检验才是有效的。
自相关性习题集与答案解析

自相关性2虚假序列相关 3差分法5自回归模型 6广艾置小二乘法8科克伦-奧克特跌代法 9 Durbin 两步法二. 单项选择题1>如果模型y t =bo+bix t +ut 存在序列相关,则0(xt, ut) =0 (ut, u 5) =0 (t=^s) C. cov (xt, Ut) #=0 D. cov (ut, uj HOCtHs)2、 DW 检验的零假设是(p 为随机误差项的一阶相关系数) A 、DW=O B 、p =0 C 、DW=1 D 、p =13、 下列哪个序列相关可用DW 检脸(治为具有零均值,常数方差且不存在序列相关的随机变 量) A. ut= p Ut-i+vt B. Ut= p ut-i+ p 2ut-2+ C ・ u t = p v tD ・ u t = p v t + p Vt-i + …4、 DW 的取值范国是()A 、-1WDWW0 B> TWDWW1 C 、-2WDWW2 D> 0WDWW45、 当DW=4时■说明()A 、不存在序列相关B 、不能判斷是否存在一阶自相关C 、存在完全的正的一阶自相关D.存在完全的负的一阶自相关 6、 根据20个观测值估计的结果,一元线性回归模型的DW = o 在样本容量n=20,解释变董 k=1,显著性水平为时,査得dl=1,du=,則可以决斷() A 、不存在一阶自相关B 、存在正的一阶自相关 C 、存在负的一阶自D 、无法确定 7、 当模型存在序列相关现象时,适宜的参数估计方法是() A 、加权最小二乘法 B 、间接最小二乘法 C 、广乂差分法D 、工具变量法 8、 对于原模型y t =bo+bix t +u t ,广义差分模型是指()C.心二b ()+bgXt +AU tD ・ y t -py t4=b {)(\-p)+b l (x l -px tJ ) + (u t -pu,.,)9、 釆用一阶差分模型一阶线性自相关问题适用于下列哪种请况0 A 、p 心0 B 、p ^1 C 、-1 < p <0 D 、0< p <110、 假定某企业的生产决疑是由模型St=bo+biPt+ut 描述的(其中St 为产量,久为价格),又 知:如果该企业在tT 期生产过剩,经营人员会削减t 期的产量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习题6.1参考解答:
(1)收入—消费模型为
Se = (2.5043) (0.0075)
t = (-3.7650) (125.3411)
R2 = 0.9978,F = 15710.39,d f = 34,DW = 0.5234
(2)对样本量为36、一个解释变量的模型、5%显著水平,
查DW统计表可知,d L=1.411,d U= 1.525,模型中DW<d L,显然
消费模型中有自相关。
(3)采用广义差分法
查5%显著水平的DW统计表可知d L = 1.402,d U = 1.519,模型中
DW= 2.0972>d U,说明广义差分模型中已无自相关。
同时,判
定系数R2、t、F统计量均达到理想水平。
由差分方程式可以得出:
所以最终的消费模型为:
练习题6.2参考解答:
(1)给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中不存在自相关。
(2)自相关可能由于模型6.1的误设,因为它排除了趋势的平方项。
(3)虚假自相关是由于模型的误设造成的,因此就要求对可能的函数形式有先验知识。
真正的自相关是可以通过广义差分法等方法来修正。
练习题6.3参考解答:
(1)收入—消费模型为
(2)DW=0.575,取
,查DW上下界
(3)采用广义差分法
使用普通最小二乘法估计
的估计值
,得
DW=1.830,已知,模型中因此,在广义差分模型中已无自相关。
由差分方程式可以得出:
因此,修正后的回归模型应为
6.4参考解答:
(1)回归结果如下:
(2)模型检验:
从回归结果可以看出,参数均显著,模型拟和较好。
异方差的检验:
通过white检验可以得知模型不存在异方差。
DW检验:
给定n=25, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
(3)采用广义差分法修正模型中存在的自相关问题:
给定n=24,,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中不存在自相关。
由差分方程式可以得出:
所以修正后的模型为:
6.5参考答案
(1)进口需求模型为
给定n=19,,在的显著水平下,查DW统计表可知,。
模型中,所以可以
(2)采用科克伦-奥克特迭代法(此题多次迭代后仍然存在自相关)6.6参考解答:
(1)回归结果如下:
给定n=21,,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
(2)采用科克伦-奥克特迭代法修正自相关:
给定n=20,,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断广义差分模型中不存在自相关。
由差分方程式可以得出:
所以修正后的模型为:
(3)变换数据后的回归结果如下:
给定n=20,,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断变化数据后的模型中不存在自相关。
