高中数学必修二第二章复习优质 课件
合集下载
高中数学必修2第二章点、直线、平面之间的位置关系课件2.3.1直线与平面垂直的判定

则该直线与此平面垂直.
la l b a b a b A
品质来自专业 信赖源于诚信
判定定理:一条直线与一个平面内的两条相交直线都垂直,
l
l
b
A
a
作用: 判定直线与平面垂直. 思想: 直线与平面垂直 直线与直线垂直
5
金太阳教育网
典型例题
如果直线 l 与平面 内的任意一条直线都垂直,我 记作 l . 们说直线 l 与平面 互相垂直,
平面 的垂线
垂足
l
P
直线 l 的垂面
3
金太阳教育网
直线与平面垂直
品质来自专业 信赖源于诚信
Байду номын сангаас
除定义外,如何判断一条直线与平面垂直呢?
l
P
4
直线与平面垂直判定定理 金太阳教育网
16
n
又因为 b // a 所以 b m, b n. 又 m , n , m, n 是两条相交直线, 所以 b .
6
金太阳教育网
随堂练习
品质来自专业 信赖源于诚信
如图,直四棱柱 ABCD ABCD (侧棱与底面垂直的 ABCD 棱柱成为直棱柱)中,底面四边形 满足什么条件 AC BD 时, ?
金太阳教育网
品质来自专业 信赖源于诚信
2.3.1直线与平面垂直的判定
1
金太阳教育网
实例引入
品质来自专业 信赖源于诚信
生活中有很多直线与平面垂直的实例,你能举出几 个吗?
旗杆与底面垂直
2
金太阳教育网
直线与平面垂直
品质来自专业 信赖源于诚信
la l b a b a b A
品质来自专业 信赖源于诚信
判定定理:一条直线与一个平面内的两条相交直线都垂直,
l
l
b
A
a
作用: 判定直线与平面垂直. 思想: 直线与平面垂直 直线与直线垂直
5
金太阳教育网
典型例题
如果直线 l 与平面 内的任意一条直线都垂直,我 记作 l . 们说直线 l 与平面 互相垂直,
平面 的垂线
垂足
l
P
直线 l 的垂面
3
金太阳教育网
直线与平面垂直
品质来自专业 信赖源于诚信
Байду номын сангаас
除定义外,如何判断一条直线与平面垂直呢?
l
P
4
直线与平面垂直判定定理 金太阳教育网
16
n
又因为 b // a 所以 b m, b n. 又 m , n , m, n 是两条相交直线, 所以 b .
6
金太阳教育网
随堂练习
品质来自专业 信赖源于诚信
如图,直四棱柱 ABCD ABCD (侧棱与底面垂直的 ABCD 棱柱成为直棱柱)中,底面四边形 满足什么条件 AC BD 时, ?
金太阳教育网
品质来自专业 信赖源于诚信
2.3.1直线与平面垂直的判定
1
金太阳教育网
实例引入
品质来自专业 信赖源于诚信
生活中有很多直线与平面垂直的实例,你能举出几 个吗?
旗杆与底面垂直
2
金太阳教育网
直线与平面垂直
品质来自专业 信赖源于诚信
高中数学必修2全册复习课件

圆台
结构特征
用一个平行于圆 锥底面的平面去截圆 锥,底面与截面之间的 部分是圆台.
O’ O
球
结构特征
以半圆的直径所 在直线为旋转轴,半 圆面旋转一周形成的 旋转体.
半径 O 球心
空间几何体的表面积和体积 圆柱的侧面积: S 2 rl 圆锥的侧面积: S rl 面积 圆台的侧面积: S ( r r ) l
答:不一定是.如图所示,不是棱柱.
棱柱的性质
1.侧棱都相等,侧面都是平 行四边形; 2.两个底面与平行于底面的 截面都是全等的多边形; 3.平行于侧棱的截面都是平 行四边形;
棱柱的分类
1、按侧棱是否和底面垂直分类: 棱柱 斜棱柱 2、按底面多边形边数分类: 三棱柱、四棱柱、 五棱柱、· · · · · ·
a
八个定理
3.线面垂直 ①定义:若一条直线垂直于平面内的任意一条直线, 则这条直线垂直于平面。 符号表述:若任意 a , 都有 l a ,且 l ,则 l .
a, b a b O ②判定定理: l l (线线垂直 线面垂直) la l b
例1:在棱长为1的正方体ABCD—A1B1C1D1中,
(1)求异面直线A1B与B1C所成的角的大小; (2)求直线A1B与平面BB1D1D所成的角; (3)求二面角A—BD—A1的正切值; (4)求证:平面A1BD//平面CB1D1;
A1
D1 B1 D
C
1
(5)求证 : 直线AC1 平面A1BD;
球的表面积:
S 4 R
3
2
柱体的体积: V Sh 体积 锥体的体积: V 1 Sh 台体的体积:V 1 ( S
高中数学必修二课件:圆的一般方程(42张PPT)
此方程表示以(1,-2)为圆心,2为半径长的圆.
问题2:方程x2+y2+2x-2y+2=0表示什么图形?
提示:对方程x2+y2+2x-2y+2=0配方得
(x+1)2+(y-1)2=0,即x=-1且y=1. 此方程表示一个点(-1,1). 问题3:方程x2+y2-2x-4y+6=0表示什么图形? 提示:对方程x2+y2-2x-4y+6=0配方得 (x-1)2+(y-2)2=-1. 由于不存在点的坐标(x,y)满足这个方程,所以这 个方程不表示任何图形.
3.若方程x2+y2+2mx-2y+m2+5m=0表示圆,求 (1)实数m的取值范围; (2)圆心坐标和半径.
解:(1)根据题意知D2+E2-4F=(2m)2+(-2)2- 1 4(m +5m)>0,即4m +4-4m -20m>0,解得m<5,
2 2 2
1 故m的取值范围为(-∞,5).
(2)将方程x2+y2+2mx-2y+m2+5m=0写成标准 方程为(x+m)2+(y-1)2=1-5m, 故圆心坐标为(-m,1),半径r= 1-5m.
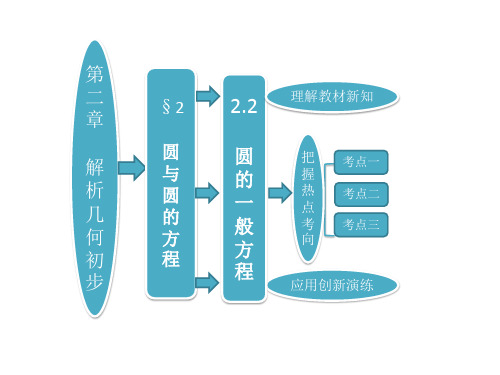
第 二 章 解 析 几 何 初 步
§2 圆 与 圆 的 方 程
2.2
圆 的 一 般 方 程
理解教材新知
把 握 热 点 考 向
考点一 考点二 考点三
应用创新演练
把圆的标准方程(x-a)2+(y-b)2=r2展开得,x2+y2 -2ax-2by+a2+b2-r2=0,这是一个二元二次方程的形 式,那么,是否一个二元二次方程都表示一个圆呢? 问题1:方程x2+y2-2x+4y+1=0表示什么图形? 提示:对x2+y2-2x+4y+1=0配方得 (x-1)2+(y+2)2=4.
1.若x2+y2-x+y-m=0表示一个圆的方程,则m的取值 范围是 1 A.m>-2 1 C.m<-2 1 B.m≥-2 D.m>-2 ( )
数学必修2第二章复习总结知识点PPT课件

简记为:线线垂直,则线面垂直。
3.直线与平面垂直的另一种判定方法
两条平行直线中的一条垂直一个平面,则另
一202条1/7/2直4 线也垂直这个平面.
11
直线和平面垂直的判定与性质
4.直线与平面所成的角 定义:平面的一条斜线和它在平面上的射影所 成的锐角,叫做这条直线和这个平面所成的角. 直线与平面所成的角的范围α: 00≤α ≤900
若两个平面平行,则一个平面内的所有
直2021线/7/24都平行于另一个平面.
10
直线和平面垂直的判定与性质
1.直线与平面垂直的概念
如果直线 l 与平面内的任意一条直线都 垂直,我们说直线 l 与平面 互相垂直,
2.直线与平面垂直的判定定理
一条直线与一个平面内的两条相交直线都垂直, 则该直线与此平面垂直.
2021/7/24
18
简记为:线面平行,则线线平行。
2021/7/24
9
平面和平面平行的判定与性质
1.判定定理:一个平面内的两条相交直线与 另一个平面平行,则这两个平面平行.
简记为:线面平行,则面面平行.
2.性质定理:如果两个平行平面同时和 第三个平面相交,那么它们的交线平行.
简记为:面面平行,则线线平行.
3.两个平面平行的一个性质:
6.平面与平面垂直的性质定理
定理:两个平面垂直,则一个平面内垂直于交线 的直线与另一个平面垂直.
简记为:面面垂直,则线面垂直
7.另一个性质:两个平面垂直,过一个平面的一点
作202另1/7/2一4 个平面的垂线,必在第一个平面内.
14
一些常用结论 1.三条两两相交的直线可确定1个或3个平面. 2.不共面的四点可确定4个平面. 3.三个平面两两相交,交线有1条或3条. 4.正方体各面所在平面将空间分成27个部分.
高中数学必修2第2章212第二课时两点式课件(_1

化,形成用联系的观点看问题的习惯.
1.直线的两点式方程
(1)条件:P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2). (2)方程:_y_y2-_-_yy_11_=__xx2_--_x_x1_1 __ 2.直线的截距式方程 (1)条件:A(a,0),B(0,b)且___a_b_≠__0_______ (2)方程:__xa_+__by_=__1______
1.在例1的条件下,求过点B且平行于AC的直线方程. 解:设所求的直线为 l,由于 l 与直线 AC 平行,则这两条直线 的倾斜角相等,所以 kl=kAC=3-0--22=-25, 故直线 l 的方程为 y-2=-25(x-3).
直线的截距式方程 求过定点P(2,3)且在两轴上截距相等的直线方程.
(本题满分 12 分)求过点 A(4,2),且在两坐标轴上的 截距的绝对值相等的直线 l 的方程.
[解] 当直线过原点时 ,它在 x 轴、y 轴上的截距都是 0, 满足题意,此时,直线的斜率为12,所以直线方程为 y=12x.2 分 当直线不过原点时 ,由题意可设直线方程为xa+by=1,又过 点 A,所以4a+2b=1①,4 分 因为直线在两坐标轴上的截距的绝对值相等,所以|a|=|b| ②,
[错因与防范] (1)方程xa+by=1 中的 a 与 b 是直线在 x 轴与 y 轴上的截距,而不是距离,所以由三角形面积为 4,应该有12|a||b| =4. (2)直线的截距是指直线在坐标轴上对应的坐标,因此可为正、 可为负、可为零;而距离是线段的长度,是非负的.截距不是 距离,解题中应注意准确把握两者的区别.
2.求过点 A(3,4),且在坐标轴上截距互为相反数的直线 l 的 方程. 解:(1)当直线 l 在坐标轴上截距互为相反数且不为 0 时,可 设直线 l 的方程为xa+-ya=1.又 l 过点 A(3,4), 所以3a+-4a=1,解得 a=-1.
1.直线的两点式方程
(1)条件:P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2). (2)方程:_y_y2-_-_yy_11_=__xx2_--_x_x1_1 __ 2.直线的截距式方程 (1)条件:A(a,0),B(0,b)且___a_b_≠__0_______ (2)方程:__xa_+__by_=__1______
1.在例1的条件下,求过点B且平行于AC的直线方程. 解:设所求的直线为 l,由于 l 与直线 AC 平行,则这两条直线 的倾斜角相等,所以 kl=kAC=3-0--22=-25, 故直线 l 的方程为 y-2=-25(x-3).
直线的截距式方程 求过定点P(2,3)且在两轴上截距相等的直线方程.
(本题满分 12 分)求过点 A(4,2),且在两坐标轴上的 截距的绝对值相等的直线 l 的方程.
[解] 当直线过原点时 ,它在 x 轴、y 轴上的截距都是 0, 满足题意,此时,直线的斜率为12,所以直线方程为 y=12x.2 分 当直线不过原点时 ,由题意可设直线方程为xa+by=1,又过 点 A,所以4a+2b=1①,4 分 因为直线在两坐标轴上的截距的绝对值相等,所以|a|=|b| ②,
[错因与防范] (1)方程xa+by=1 中的 a 与 b 是直线在 x 轴与 y 轴上的截距,而不是距离,所以由三角形面积为 4,应该有12|a||b| =4. (2)直线的截距是指直线在坐标轴上对应的坐标,因此可为正、 可为负、可为零;而距离是线段的长度,是非负的.截距不是 距离,解题中应注意准确把握两者的区别.
2.求过点 A(3,4),且在坐标轴上截距互为相反数的直线 l 的 方程. 解:(1)当直线 l 在坐标轴上截距互为相反数且不为 0 时,可 设直线 l 的方程为xa+-ya=1.又 l 过点 A(3,4), 所以3a+-4a=1,解得 a=-1.
高中数学必修2第二章点直线平面之间的位置关系211平面及其表示法(含习题课)PPT课件

1,2,3(1)(2)
21
补充练习金太:阳教育网
l 1、A为直线 l上的点,又点A不在平面
与 的公共点最多有 _______1个.
品质来自专业 信赖源于诚信
内,则
2、四条直线过同一点,过每两条直线作一个平
面,则可以作_____1_或___4_或___6个不同的平面 .
22
金太阳教育网
品质来自专业 信赖源于诚信
2
金实太阳教例育网引入
品质来自专业 信赖源于诚信
观察活动室里的地面,它呈现出怎样的形象?
3
一.平面金太的阳教育概网 念:
品质来自专业 信赖源于诚信
光滑的桌面、平静的湖面等都是我们
熟悉的平面形象,数学中的平面概念是现
实平面加以抽象的结果。
二.平面的特征:
平面没有大小、厚薄和宽窄,平面在空 间是无限延伸的。
文字语金言太阳:教育网 公理1.如果一条直线上两点品信质赖在来源自于专诚一业信 个平面内,那么这条直线在此平
面内(即这条直线上的所有的点
23
点、线金、太阳面教之育网间的位置关系及语言表达
品质来自专业
信赖源于诚信
文字语言表达 图形语言表达 符号语言表达
点A在直线a上 点A不在直线a上
A
a
A
a
A∈a A∈a
点A在平面α上 点A不在平面α上 直线a在平面α内
α
A
α
α
A
a a
A∈α A∈ α
aα
a b∩α=A
直线a在平面α外 α
A α
a∩α=φ 或 a∥α24
B A
B
CαA
C
公理2.过不在同一直线上的三点,有且只有一个平面.
《面面垂直的判定》人教版高中数学必修二PPT课件(第2.3.2课时)

新知探究
2.在立体几何中,"异面直线所成的角"是怎样定义的? 直线a、b是异面直线,在空间任选一点O,分别引直线a' //a, b'// b,我们把相交直线a' 和 b'所成 的锐角 (或直角)叫做异面直线所成的角。 3.在立体几何中,"直线和平面所成的角"是怎样定义的? 平面的一条斜线和它在平面上的射影所成的锐角, 叫做这条直线和这外,如何判定两个平面互相垂直呢? (2)日常生活中平面与平面垂直的例子? 为什么教室的门转到任何位置时,门所在平面都与地面垂直?
新知探究
如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直。 已知:AB⊥β,AB∩β=B,AB α
∪ ∪
∪
求证:α⊥β.
α
A
C
B
D
人教版高中数学必修二
第2章 关系 点、直线、平面之间的位置关系
感谢你的凝听
MENTAL HEALTH COUNSELING PPT
讲授人: 时间:20XX.6.1
A
新知探究
练习: 指出下列各图中的二面角的平面角:
A, B l
AC
BD
AC⊥l BD ⊥l
Bl
C
D
AO
二面角 --l--
D’
C’
A
A’ D
A
B’ O
CB B
D
O
E
C
二面角B--B’C--A
二面角A--BC-D
新知探究
二面角的计算: 1、找到或作出二面角的平面角 2、证明 1中的角就是所求的角 3、说明此角即为所求二面角的平面角 4、 求出此角的大小 5、回答此角的大小
深圳优质课件 人教版高一数学必修2第二章点直线平面之间的位置关系

你能再举出校园生活中几个可以近似 看成直线与平面垂直的例子吗?
二、观察思考
问题2:
(1)在阳光下观察直立于地面 旗杆AB及它在地面的影子BC,旗 杆所在直线与影子所在直线的位
A 置关系是什么?随着时间的推移, 这些影子所在直线有什么共同特 征?
B (2)旗杆AB与地面上任意一条 不过旗杆底部B的直线B1C1的位置 又是什么?
C1
三、抽象概括
定义:如果直线l 与平面 内的任意一条直线都垂直,我 们就说直线 l 与平面 互相垂直.记作:l .直线l 叫做平 面 的垂线,平面 叫做直线 l 的垂面.直线与平面垂直时, 它们唯一的公共点 P 叫做垂足. 画法:画直线与平面垂直时,通常把直线画成与表示平 面的 平行四边形的一边垂直.
概念辨析
下列命题是否正确,为什么?
(1)如L果O一R条E直M线I垂PS直U于M一个D平O面LO内R的无数条直
线,那么这条直线与这个平面垂直. (2)如果一条直线不垂直一个平面,那么这条直 线不可能与这个平面内的无数条直线垂直.
问题4:我们该如何检验学校广场上的旗杆是否与地 面垂直?用直线与平面垂直的定义方便检验吗?
合情猜想
一条直线与一个平面内的两条相交直线都垂直, 则该直线与此平面垂直
合情猜想
一条直线与一个平面内的两条相交直线都垂直, 则该直线与此平面垂直
l
m
n
五、证明猜想
(镜面对称法)
证明:设直线 l 与平面 的交点为点 B=m n ,在直线 l 上取点 A 和点 A' 使得 AB A'B , 在直线 m 与直线 n 再取 C 点和 D 点,连结 AC、AD、A'C、A'D
旗杆AB及它在地面的影子BC,旗
二、观察思考
问题2:
(1)在阳光下观察直立于地面 旗杆AB及它在地面的影子BC,旗 杆所在直线与影子所在直线的位
A 置关系是什么?随着时间的推移, 这些影子所在直线有什么共同特 征?
B (2)旗杆AB与地面上任意一条 不过旗杆底部B的直线B1C1的位置 又是什么?
C1
三、抽象概括
定义:如果直线l 与平面 内的任意一条直线都垂直,我 们就说直线 l 与平面 互相垂直.记作:l .直线l 叫做平 面 的垂线,平面 叫做直线 l 的垂面.直线与平面垂直时, 它们唯一的公共点 P 叫做垂足. 画法:画直线与平面垂直时,通常把直线画成与表示平 面的 平行四边形的一边垂直.
概念辨析
下列命题是否正确,为什么?
(1)如L果O一R条E直M线I垂PS直U于M一个D平O面LO内R的无数条直
线,那么这条直线与这个平面垂直. (2)如果一条直线不垂直一个平面,那么这条直 线不可能与这个平面内的无数条直线垂直.
问题4:我们该如何检验学校广场上的旗杆是否与地 面垂直?用直线与平面垂直的定义方便检验吗?
合情猜想
一条直线与一个平面内的两条相交直线都垂直, 则该直线与此平面垂直
合情猜想
一条直线与一个平面内的两条相交直线都垂直, 则该直线与此平面垂直
l
m
n
五、证明猜想
(镜面对称法)
证明:设直线 l 与平面 的交点为点 B=m n ,在直线 l 上取点 A 和点 A' 使得 AB A'B , 在直线 m 与直线 n 再取 C 点和 D 点,连结 AC、AD、A'C、A'D
旗杆AB及它在地面的影子BC,旗
人教A版高中数学选择性必修第二册精品课件 复习课 第2课时 一元函数的导数及其应用
故 f(x)在区间(0,+∞)内单调递增.
②当 Δ=0,即 a=2√2时,仅当 x=√2时,
有f'(x)=0,对其余的x>0都有f'(x)>0.
故函数f(x)在区间(0,+∞)内单调递增.
③当 Δ>0,即 a>2√2时,方程 g(x)=0 有两个不同的实根,
即
-√ 2 -8
+√ 2 -8
f'(x)=0 有两个不同的实根,x1= 2 ,x2= 2 ,0<x1<x2.
1 4
,
4 5
.
反思感悟 1.极值和最值是两个不同的概念,前者是函数的“局部”性质,而
后者是函数的“整体”性质.另函数有极值未必有最值,反之亦然.
2.判断函数“极值”是否存在时,务必把握以下原则:
(1)确定函数f(x)的定义域.
(2)求方程f'(x)=0的根.
(3)检验f'(x)=0的根的两侧f'(x)的符号.
的一个是最大值,最小的一个是最小值.
9.解决实际问题的基本思路
实际问题→用函数表示的数学问题
↓
实际问题的答案←用导数解决数学问题
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)函数在闭区间上的极大值就是最大值.( × )
(2)在闭区间[a,b]上连续的函数f(x)必存在最大值与最小值.( √ )
x2
0
极小值
(x2,+∞)
+
单调递增
【例3】
已知函数f(x)=x2+
求a的取值范围.
(x≠0,a∈R),若f(x)在区间[2,+∞)内单调递增,
②当 Δ=0,即 a=2√2时,仅当 x=√2时,
有f'(x)=0,对其余的x>0都有f'(x)>0.
故函数f(x)在区间(0,+∞)内单调递增.
③当 Δ>0,即 a>2√2时,方程 g(x)=0 有两个不同的实根,
即
-√ 2 -8
+√ 2 -8
f'(x)=0 有两个不同的实根,x1= 2 ,x2= 2 ,0<x1<x2.
1 4
,
4 5
.
反思感悟 1.极值和最值是两个不同的概念,前者是函数的“局部”性质,而
后者是函数的“整体”性质.另函数有极值未必有最值,反之亦然.
2.判断函数“极值”是否存在时,务必把握以下原则:
(1)确定函数f(x)的定义域.
(2)求方程f'(x)=0的根.
(3)检验f'(x)=0的根的两侧f'(x)的符号.
的一个是最大值,最小的一个是最小值.
9.解决实际问题的基本思路
实际问题→用函数表示的数学问题
↓
实际问题的答案←用导数解决数学问题
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)函数在闭区间上的极大值就是最大值.( × )
(2)在闭区间[a,b]上连续的函数f(x)必存在最大值与最小值.( √ )
x2
0
极小值
(x2,+∞)
+
单调递增
【例3】
已知函数f(x)=x2+
求a的取值范围.
(x≠0,a∈R),若f(x)在区间[2,+∞)内单调递增,
高一数学2015北师大版高中数学必修二第二章 解析几何初步复习课件

BS · 数学
必修2
已知点 P(x, y)满足关系式: x2+y2-6x-4y+12 =0,求: y (1) 的最大值和最小值; x (2)x2+y2 的看作是圆(x,y)与原点连线的斜 x 率,(2)x2+y2 可看作是(x,y)与原点距离的平方.
BS · 数学
BS · 数学
必修2
(2)设圆的一般方程为 x2+y2+Dx+Ey+F=0, 1+144+D+12E+F=0, 则49+100+7D+10E+F=0, 81+4-9D+2E+F=0, 解得 D=-2,E=-4,F=-95. ∴所求圆的方程为 x2+y2-2x-4y-95=0.
BS · 数学
必修2
从点 P(3,-2)发出的光线 l,经过直线 l1:x+y -2=0 反射,若反射光线的反向延长线恰好通过点 Q(5,1), 求 l 的方程.
【思路点拨】 求直线 l 的方程,已知点 P 在 l 上,只需 在 l 上再求出一个点即可.
BS · 数学
必修2
【思路点拨】 设点 P(3,-2)关于 l1:x+y-2=0 对称 的点 P1 的坐标为(x,y),则直线 l1 为线段 PP1 的垂直平分线, 可得方程组 y+2 =1, x-3 x+3 y-2 + 2 -2=0, 2 1).
(1)
|3 k-2|
BS · 数学
必修2
(2)设 u= x2+y2,则 u 为圆 C 上的点到原点的距离,如 图(2)所示.连接 OC 并延长交圆于 A、B 两点,圆心 C(3,2) 与原点 O 的距离是 |OC|= 13. ∴|OA |= 13-1,|OB |= 13+1.
2 2 ∴u2 = | OB | = ( 13 + 1) =14+2 13, max 2 2 u2 min=|OA | =( 13-1) =14-2 13.
人教A高二数学必修二第二章点直线平面之间的位置关系212空间中直线与直线之间的位置关系课件共36

H E 2
2 3 D 2 3
G F C B
在Rt△EFG中,求得∠EGF = 45°,
所以 BC与EG所成的角为45°. (2)因为BF∥AE,
A
所以∠FBG(或其补角)为所求.
在Rt△BFG中,求得∠FBG = 60°,
相交直线 空间两直线的位置关系
平行直线
异面直线
异面直线的定义
异面直线
异面直线的画法 两异面直线所成的角 一作(找)二证三求
边形叫做空间四边形ABCD.
A
相对顶点A与C,B与D的连线AC, BD叫做这个空间四边形的对角线.
B
C
D
【即时训练】
如图所示,在正方体 ABCD-A1B1C1D1 中,判断下列直线的位置关系:
平行 ; (1)直线 A1B 与直线 D1C 的位置关系是________ 异面 ; (2)直线 A1B 与直线 B1C 的位置关系是________ 相交 ; (3)直线 D1D 与直线 D1C 的位置关系是________ 异面 . (4)直线 AB 与直线 B1C 的位置关系是________
b a′ ? O a b′ a′
θ
O
平 移
若两条异面直线所成的角为90°,则称它们互相垂直. 异面直线a与b垂直也记作a⊥b. 异面直线所成的角θ 的取值范围: 0 o < 90 o
例2
如图,已知正方体ABCD-A′B′C′D′.
(1)哪些棱所在直线与直线BA′是异面直线?
(2)直线BA′和CC′的夹角是多少? ( 3 )哪些棱所在的直线与直线AA′垂直? 解 : (1)由异面直线的定义可知, 与直线BA′成异面直线的有直线 B′C′,AD,CC′,DD′,DC,D′C′.
2 3 D 2 3
G F C B
在Rt△EFG中,求得∠EGF = 45°,
所以 BC与EG所成的角为45°. (2)因为BF∥AE,
A
所以∠FBG(或其补角)为所求.
在Rt△BFG中,求得∠FBG = 60°,
相交直线 空间两直线的位置关系
平行直线
异面直线
异面直线的定义
异面直线
异面直线的画法 两异面直线所成的角 一作(找)二证三求
边形叫做空间四边形ABCD.
A
相对顶点A与C,B与D的连线AC, BD叫做这个空间四边形的对角线.
B
C
D
【即时训练】
如图所示,在正方体 ABCD-A1B1C1D1 中,判断下列直线的位置关系:
平行 ; (1)直线 A1B 与直线 D1C 的位置关系是________ 异面 ; (2)直线 A1B 与直线 B1C 的位置关系是________ 相交 ; (3)直线 D1D 与直线 D1C 的位置关系是________ 异面 . (4)直线 AB 与直线 B1C 的位置关系是________
b a′ ? O a b′ a′
θ
O
平 移
若两条异面直线所成的角为90°,则称它们互相垂直. 异面直线a与b垂直也记作a⊥b. 异面直线所成的角θ 的取值范围: 0 o < 90 o
例2
如图,已知正方体ABCD-A′B′C′D′.
(1)哪些棱所在直线与直线BA′是异面直线?
(2)直线BA′和CC′的夹角是多少? ( 3 )哪些棱所在的直线与直线AA′垂直? 解 : (1)由异面直线的定义可知, 与直线BA′成异面直线的有直线 B′C′,AD,CC′,DD′,DC,D′C′.
北师大版高中数学必修2第二章解析几何初步第二节《圆与圆的方程》ppt课件

O
X
1)写出过圆x2+y2=13上一点M(2,3)的
切线的方程。
2)已知圆x2+y2=3,求过点(-3,0)的圆的切 线方程。
小结
1)圆心为C(a,b),半径为r的圆的标准方程是 ;当圆心在原点时,a=0,b=0,那么圆的 方程就是x2+y2=r2。
x a2 y b2 r 2
试一试 : 1)已知一个圆的圆心在原点, 并且与直线4x+3y-70=0相切,求圆的方程。
例2 1) :已知圆心在Y轴上,且过点(10,0) 和(0,4)的圆的方程. 解
练习: 过点C(-1,1)和D(1,3),圆
心在X轴上,求圆的方程。解
某圆拱桥的一孔圆拱,其跨度为20m,高度为4m,在 建造时每隔4m需用一个支柱支撑,求支柱的长度。
2 -1-a 2 +12=r 2 2 1-a +3 2=r
解得
a=2,r2=10
2 2 +y= x- 10 2
所以这个圆的方程是
例2; 2) 如图是某圆拱桥的一孔圆拱的示意图,该圆拱的 跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱 支撑,求支柱A2P2的长度(精确到0.01m) y P2 P
A
A1 A2
O
A3 A4 Y
M
B
x
例3:已知圆的方程是x2+y2=r2,求 经过圆上一点M(xo,yo)的切线 的方程.
(x+3)2+(y+4)2=1
2)方程(x-1)2+(y+4)2 = 25 表示 的圆的圆心和半 径是?
圆心:(1,-4),半径:5
2 2 3) 圆x a y b r 的圆心和半径分别是什么?
高中数学必修2第二章点、直线、平面之间的位置关系课件2.1.2空间中直线与直线之间的位置关系

D
A
B
E
B1
C
等角定理2:如果一个角的两边和 另一个角的两边分别平行且方向 相同,那么这两个角相等
A1
D1 E1 C1
10
金太阳教育网
异面直线
品质来自专业 信赖源于诚信
3、判定方法: (1)、定义法:由定义判定两直线不可能在 同一平面内.(借助反证法) (2)、判定定理:过平面外一点与平面内一点 的直线,和平面内不经过该点的直线是异面 直线
b b
b
a
a
a
5
金太阳教育网
如图所示:正方体的棱所在的 直线中,与直线A1B异面的有 哪些? 答案 : 1 1 D C
B1 D C B
品质来自专业 信赖源于诚信
A1
D1C1、C1C、CD D1D、 AD、 B1C1
6
A
金太阳教育网
平行公理
品质来自专业 信赖源于诚信
例2、如图,在长方体中,已知AA1=AD=a, AB= 3 a,求AB1与BC1所成的角的余弦值
D1
A1 D A B
15
C1
B1
C
金太阳教育网
空间两条直线的位置关系: 相交、平行、异面 ⑴空间两条直线的位置关系归纳为:
位置关系 是否共面 公共点情况 相交直线 在同一个平面内 有且只有一个公共点
两路相交
B
C
立交桥
立交桥中, 两条路线AB, CD 既不平行,又不相交
2
金太阳教育网
定义 不同在任何一个平面内的两 条直线叫做异面直线。
位置关系
相交
品质来自专业 信赖源于诚信
公共点个数
高中数学必修二优质课件:第2章 1.4 两条直线的交点

答案:(1) 相交 交点坐标为( 9 ,- 46) . (2) 平行 17 17
(3) 垂直 交点坐标为 (5 2 + 4 , 6 + 2 )
4
4
2.经过直线2x+3y-7=0与7x+15y+1=0的交点,且平行 于直线x+2y-3=0的直线方程是_3_x_+_6_y_-_2_=_0__. 3.直线mx-y+2m+1=0经过一定点,则该点的坐标 是( A ) A.(-2,1) B.(2,1) C.(1,-2) D.(1,2) 4.经过两直线2x-3y-3=0 和x+y+2=0 的交点且与直 线3x+y-1=0 垂直的直线方程为__5_x_-_1_5_y_-_1_8_=_0___.
【提升总结】 两条直线的公共点个数与两条直线的位置关系
方程组
A1x+B1y+C1=0 的解
A2x+B2y+C2=0
一组 无数组 无解
两条直线l1, l2的公共点
一个 无数个 零个
直线l1, l2间的位置关系
相交 重合 平行
例1.求下列两条直线的交点:
l1: x + 2y + 1= 0,
l 2 :- x + 2y + 2 = 0.
1.4 两条直线的交点
我们知道,平面内任意一条直线都会与一个二元 一次方程对应,即直线上的点的坐标是这个方程的解, 反之亦成立.那么两条直线是否有交点与它们对应的 方程所组成的方程组是否有解有没有关系,如果有, 是什么关系?
1.理解两直线的位置关系与方程组解的个数之间的 关系.(重点) 2.能用解方程组的方法求两直线的交点坐标.(难 点)
高中数学 第二章2.3.1直线与平面垂直的判定课件 新人教A版必修2

除定义外,如何判定一条直线与平面垂直呢? 除定义外,如何判定一条直线与平面垂直呢?
A A 如图,准备一块三角形的纸片,做一个试验: 如图,准备一块三角形的纸片,做一个试验: A
l
C
A
D
α
B B
D D
P
C
C
α C α
B B
D
边上的高时, 所在直 当且仅当折痕 AD 是 BC 边上的高时,AD所在直 的顶点A翻折纸片 得到折痕AD, 翻折纸片, 过 ∆ABC 的顶点 翻折纸片,得到折痕 ,将翻 α 垂直. 线与桌面所在平面 垂直. 折后的纸片竖起放置在桌面上( , 于桌面接触 于桌面接触) 折后的纸片竖起放置在桌面上(BD,DC于桌面接触)
⊥ α ,求证 b ⊥ α .
b
n
证明: 证明:在平面 α 内作 a 两条相交直线m, . 两条相交直线 ,n. 因为直线 a ⊥ α, 根据直线与平面垂直的定义知 α m a ⊥ m, a ⊥ n. 又因为 b // a 所以 b ⊥ m, b ⊥ n. 是两条相交直线, 又 m ⊂ α , n ⊂ α , m, n 是两条相交直线, 所以 b ⊥ α .
线面垂直
知识探究( 知识探究(二):直线与平面垂直的判定
思考1 对于一条直线和一个平面, 思考1:对于一条直线和一个平面,如果 根据定义来判断它们是否垂直, 根据定义来判断它们是否垂直,需要解 决什么问题?如何操作? 决什么问题?如何操作?
思考2 思考2:我们需要寻求一个简单可行的办 法来判定直线与平面垂直. 法来判定直线与平面垂直. 如果直线l与平面 内的一条直线垂直, 如果直线 与平面α内的一条直线垂直, 与平面 内的一条直线垂直 能保证l⊥α吗? 能保证 ⊥ 吗 如果直线l与平面 内的两条直线垂直, 与平面α内的两条直线垂直 如果直线 与平面 内的两条直线垂直, 能保证l⊥ 吗 能保证 ⊥α吗?
北师大版高中数学选择性必修第二册-第2章-导数及其应用-章末复习课【课件】

当x∈(0,a)时,f′(x)>0,函数f(x)是递增的;
当x∈(a,1)时,f′(x)<0,函数f(x)是递减的;
当x∈(1,+∞)时,f′(x)>0,函数f(x)是递增的.
此时x=a是f(x)的极大值点,x=1是f(x)的极小值点.
②当a>1时,
当x∈(0,1)时,f′(x)>0,函数f(x)是递增的;
(1)当a=0时,若x<0,则f′(x)<0;若x>0,则f′(x)>0.
所以当a=0时,函数y=f(x)在(-∞,0)上为减函数,在(0,+∞)上为增函数.
2
2
(2)当a>0时,由2x+ax2>0,解得x<- 或x>0;由2x+ax2<0,解得- <x<0.
a
所以当a>0时,函数y=f(x)在区间 −∞, −
∴f(x)在x=3处的切线方程为y+10=6(x-3),
即6x-y-28=0.
考点二 利用导数研究函数的单调性
1.借助导数研究函数的单调性,尤其是研究含有ln x,ex,-x3等线
性函数(或复合函数)的单调性,是近几年高考的一个重点.其特点是
导数f′(x)的符号一般由二次函数来确定;经常同一元二次方程、一元
章末复习课
考点一 导数几何意义的应用
1.利用导数的几何意义可以求出曲线上任意一点处的切线方程y-
y0 =f′(x0)(x-x0),明确“过点P(x0 ,y0)的曲线y=f(x)的切线方程”与
“在点P(x0,y0)处的曲线y=f(x)的切线方程”的异同点.
2.通过对求切线方程的考查,提升学生的数学抽象、数学运算素
为减函数,在区间(0,+∞)上为增函数.
当x∈(a,1)时,f′(x)<0,函数f(x)是递减的;
当x∈(1,+∞)时,f′(x)>0,函数f(x)是递增的.
此时x=a是f(x)的极大值点,x=1是f(x)的极小值点.
②当a>1时,
当x∈(0,1)时,f′(x)>0,函数f(x)是递增的;
(1)当a=0时,若x<0,则f′(x)<0;若x>0,则f′(x)>0.
所以当a=0时,函数y=f(x)在(-∞,0)上为减函数,在(0,+∞)上为增函数.
2
2
(2)当a>0时,由2x+ax2>0,解得x<- 或x>0;由2x+ax2<0,解得- <x<0.
a
所以当a>0时,函数y=f(x)在区间 −∞, −
∴f(x)在x=3处的切线方程为y+10=6(x-3),
即6x-y-28=0.
考点二 利用导数研究函数的单调性
1.借助导数研究函数的单调性,尤其是研究含有ln x,ex,-x3等线
性函数(或复合函数)的单调性,是近几年高考的一个重点.其特点是
导数f′(x)的符号一般由二次函数来确定;经常同一元二次方程、一元
章末复习课
考点一 导数几何意义的应用
1.利用导数的几何意义可以求出曲线上任意一点处的切线方程y-
y0 =f′(x0)(x-x0),明确“过点P(x0 ,y0)的曲线y=f(x)的切线方程”与
“在点P(x0,y0)处的曲线y=f(x)的切线方程”的异同点.
2.通过对求切线方程的考查,提升学生的数学抽象、数学运算素
为减函数,在区间(0,+∞)上为增函数.
高中人教版必修2数学课件第二章2.1.2精选ppt课件

() A.2 对
B.3 对
C.6 对
D.12 对
解析:选 C.如图所示,在长方体 AC1 中,与对角线 AC1 成异面 直线位置关系的是:A1D1、BC、BB1、DD1、A1B1、DC,所以 组成 6 对异面直线.
3.如图,点 G、H、M、N 分别是三棱柱的顶点或所在棱的中 点,则表示直线 GH,MN 是异面直线的图形是________.
(1)判断两直线平行仍是立体几何中的一个重要组成部分,除了 平面几何中常用的判断方法以外,公理 4 也是判断两直线平行的 重要依据. (2)证明角相等,利用空间等角定理是常用的思考方法;另外也 可以通过证明两个三角形全等或相似来证明两角相等.在应用等 角定理时,应注意说明这两个角同为锐角、直角或钝角.
(2)异面直线所成的角 两条异面直线所成的角是由两条相交直线所成的角扩充而成的, 由平移原理可知,当两条异面直线在空间的位置确定后,它们所 成的角的大小也就随之确定了.
1.分别在两个平面内的两条直线间的位置关系是( )
A.异面
B.平行
C.相交
D.以上均有可能
答案:D
2.长方体的一条体对角线与长方体的棱所组成的异面直线有
章 点、直线、面之间的位置关系
2.1.2 空间中直线与直线之间的位置关系
第二章 点、直线、平面之间的位置关系
1.会判断空间两直线的位置关系. 2.理解两异面直线的 定义,会求两异面直线所成的角. 3.能用公理 4 解决一些简单的相关问题.
1.空间直线的位置关系 (1)异面直线 ①定义:把不同在_任__何__一__个__平面内的两条直线叫做异面直线. ②画法:(通常用平面衬托)
A.6 C.5 答案:B
B.4 D.8
3.若正方体 ABCD-A1B1C1D1 中∠BAE=25°.
人教A版高一数学必修2人教版精品课件第2章 2.1 2.1.1《平面》

高中数学人教版必修2课件
2.下列命题正确的是( C ) A.因为直线向两方无限延伸,所以直线不可能在平面内 B.如果线段的中点在平面内,那么线段在平面内 C.如果线段上有一个点不在平面内,那么线段不在平面内 D.当平面经过直线时,直线上可以有不在平面内的点 3.下列说法中正确的是( C ) A.两个平面相交有两条交线 B.两个平面可以有且只有一个公共点 C.如果一个点在两个平面内,那么这个点在两个平面的交 线上 D.两个平面一定有公共点
高中数学人教版必修2课件
例 4:如图 5,在正方体 ABCD-A′B′C′D′中,E、F 分别是 AA′、AB 上一点,且 EF∥CD′,求证:平面 EFCD′、 平面 AC 与平面 AD′两两相交的交线 ED′、FC、AD 交于一点.
图5
高中数学人教版必修2课件
错因剖析:遇到此类证明多线共点问题,找不到解决问题 的突破口.
高中数学人教版必修2课件
正确地用图形和符号表示点、直线、平面以 及它们之间的关系.点看成是元素,线、面看成是点的集合, 所以点与线、面的关系用“∈、∉”表示,线与线、线与面及面 与面的关系用“⊂、⊄”表示.
1-1.试用集合符号表示下列各语句,并画出图形: (1)点 A 在平面α内,但不在平面β内; (2)直线 l 经过平面α外一点 P,且与平面α相交于点 M; (3)平面α与平面β相交于直线 l,且 l 经过点 P.
高中数学人教版必修2课件
高中数学课件
(金戈铁骑 整理制作)
高中数学人教版必修2课件
第二章 点、直线、平面之间的位置关系
2.1 空间点、直线、平面之间的位置关系
2.1.1 平面
高中数学人教版必修2课件
1.下列命题正确的是( C ) A.画一个平面,使它的长为 14 cm,宽为 5 cm B.一个平面的面积可以是 16 m2 C.平面内的一条直线把这个平面分成两部分,一个平面把 空间分成两部分 D.10 个平面重叠起来,要比 2 个平面重叠起来厚
高中数学必修二第二章复习课件

本 章回 顾
本章主 要 研究了平面直角坐标系 中直线 和圆的有关知识以及 空间坐标系.学习本 章时, 应充分体会用坐标法研 究问题的基 本思想, 就是用坐标、方程等代 数语言描 述直线和圆的几何要素 及其关系, 进而将 直线和圆的有关问题转 化为代数问题.
平面解析几何初步
简单的平面曲线
结 特征
语言描述 建立方程
性质 用方程研究曲线
直线
结构特征 斜率
圆
位置关系、点 到直线的距离
结构特征 圆的 直线与圆、圆 圆心、半径 方程 与圆的位置关系
直线 方程
坐标法不仅是研究几何问题 的重要 方法, 而且是一种广泛用于其 他领域 的重要数学方法 .通过坐标系 , 把点和 坐标、曲线和方程等联 系起来, 沟通 了几何与代数之间的联 系, 体现了数 形结合的重要数学方法 .
本章主 要 研究了平面直角坐标系 中直线 和圆的有关知识以及 空间坐标系.学习本 章时, 应充分体会用坐标法研 究问题的基 本思想, 就是用坐标、方程等代 数语言描 述直线和圆的几何要素 及其关系, 进而将 直线和圆的有关问题转 化为代数问题.
平面解析几何初步
简单的平面曲线
结 特征
语言描述 建立方程
性质 用方程研究曲线
直线
结构特征 斜率
圆
位置关系、点 到直线的距离
结构特征 圆的 直线与圆、圆 圆心、半径 方程 与圆的位置关系
直线 方程
坐标法不仅是研究几何问题 的重要 方法, 而且是一种广泛用于其 他领域 的重要数学方法 .通过坐标系 , 把点和 坐标、曲线和方程等联 系起来, 沟通 了几何与代数之间的联 系, 体现了数 形结合的重要数学方法 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12. 直线与平面垂直的性质定理 垂直于同一个平面的两条直线平行.
l1⊥a,
l2⊥a,
l1//l2.
由线面垂直得线线平行.
13. 二面角及它的平面角 从一条直线出发的两个半平面所组成的图 形叫做二面角. 以二面角的棱上任意一点为端点, 在两个 半面内分别作垂直于棱的两条射线, 这两条射 线所成的角叫做二面角的平面角.
9. 线面垂直的判定定理 ⊕如果一条直线和一个平面内的两条 相交直线都垂直, 那么这条直线垂直于这 个平面. l⊥a, l⊥b, l⊥a. aa, ba, a∩b=P, ⊕两平行线中的一条垂直于一个平 面, 那么另一条也垂直于这个平面.
10. 三垂线定理 如果平面内的一条直线垂直平面的斜线, 则这条直线垂直斜线在平面上的射影;
3. 证明: 两两相交且不过同一点的三条直线必 在同一个平面内. 如图, 已知直线 a∩b=A, b∩c=B, c∩a=C. 求证 a, b, c 共面. b a a 证明: ∵ a∩b = A, A ⇒ a、b 确定平面, 设为 a, B 则 aa, ba, 又 c∩a = C, c∩b = B, 得 Ca, Bb, 于是得 Ca, Ba, 即得 ca, ∴ a、b、c 共面于 a.
二面角的大小由它的平面角确定.
14. 两平面垂直的判定 一个平面过另一个平面的垂线, 则这两 个平面垂直. l⊥a, ⇒ ba. l b,
b
l
a
15. 平面与平面垂直的性质 ⊕两个平面垂直, 则一个平面内垂直 于交线的直线与于另一个平面垂直.
ab, a∩b = m, l a,
l⊥m,
l a
返回目录
2. 线线之间的位置关系
相交 平行
异面ห้องสมุดไป่ตู้
共面
判定两直线平行的公理 4: 平行于同一条直线的两直线互相平行.
3. 两异面直线所成的角 ① 角的范围 (0, 90]. ② 由定义找角: 相交非钝角, 且两边分别平行两异面直线. ③ 垂直 异面垂直, 无垂足.
4. 线面平行的判定定理 b a, a a, ⇒ b∥a. b//a, 由线线平行得线面平行. 5. 线面平行的性质定理 l∥a, ⇒ l∥m. l b, b∩a = m 由线面平行得线线平行.
⇒ l ⊥b .
m
b
⊕两平面垂直, 平行于一平面的直 线垂直于另一平面.
返回目录
复习参考题 A 组 1. 三个平面可将空间分成几部分? 你能画出它 们的直观图吗? 答: 三个平面可将空间分成 4个、或 6个、或 7个、 或 8个部分. 4部分
a b g
6部分
g a b
7部分
8部分
g
g
a
b
a
b
2. 如图, 一块正方体形木料的上底面上有一点 E, 经过点 E 在上底面上画一条直线与 CE 垂直, 怎样画? 画法: ① 连结C1E, D1 M C1 E ② 在平面A1C1内, · A1 N B1 过点 E 作 MN⊥C1E. 则 MN就是所要求作的直线. D C 其理由: A B ∵ CC1⊥平面A1C1, MN平面A1C1, ∴ MN⊥CC1. 所作 MN⊥C1E, 则 MN⊥平面C1EC, 得 MN⊥CE.
如果平面内的一条直线垂直平面的一条 斜线在平面上的射影, 则这条直线垂直斜线.
11. 直线和平面所成的角 ⊕斜线与斜线在平面上的射影的夹角(锐角). ⊕垂线与平面所成的角为90. ⊕平行线或在平面内的直线与平面所成的 角为 0. ⊕斜线和平面所成的角是斜线和平面内所 有直线所成角中最小的. ⊕两条平行线和同一个平面所成的 角相等.
O
B
5. 如图, 正方体 ABCD-A1B1C1D1中, AE=A1E1, AF=A1F1, 求证 EF//E1F1, 且 EF=E1F1. 证明: 连结EE1, FF1, 在正方体中, AE∥A1E1, AF∥A1F1, 又知 AE=A1E1, AF=A1F1, ∴ AEE1A1和AFF1A1是□, 则 EE1//AA1, 且EE1=AA1, FF1//AA1, 且FF1=AA1, 得 EE1//FF1, 且EE1=FF1, ∴ 四边形EE1F1F是□, 则 EF//E1F1, 且EF=E1F1.
C
c
4. 如图, 正方体的棱长是 a, C, D 分别是两条 棱的中点. (1) 证明四边形 ABCD 是一个梯形; (2) 求四边形 ABCD 的面积. D A
证明: (1) 如图, 连结上底面 对角线AB, ∵C, D是两棱中点, ∴CD//AB, 且
而 AB//AB, 且AB=AB, ∴CD//AB, 且CD≠AB, 则ABCD是梯形.
本章内容
2.1 空间点、直线、平面之间的位置关系 2.2 直线、平面平行的判定及其性质
2.3 直线、平面垂直的判定及其性质 第二章 小结
知识要点
复习参考题
自我检测题
1. 三个公理 公理1: 如果一条直线上的两点在一个平面 内, 那么这条直线在此平面内. 公理2: 过不在一条直线上的三点, 有且只 有一个平面. 三推论: ①两相交直线确定平面; ②两平行 直线确定平面; ③直线外的点与直线确定平面. 公理 3: 如果两个不重合的平面有 一个公共点, 那么它们有且只有一条过 该点的公共直线.
6. 面面平行的判定定理 aa, ba, a∩b, ⇒ a∥b. 由线面平行得面面平行. a∥b, b∥b, 7. 面面平行的性质定理 ab, g a =a , ⇒ a∥b. g b =b , 由面面平行得线线平行.
8. 线面垂直的定义 ⊕若直线 l 垂直平面 a 内的任意一直 线, 则叫 l⊥a. 应用: 若 l⊥a, 则 l 垂直平面 a 内的任意一直线. l⊥a, l⊥m. ma, ⊕过空间任意一点, 有且只有一条直 线和已知平面垂直.
A
B C
B
4. 如图, 正方体的棱长是 a, C, D 分别是两条 棱的中点. (1) 证明四边形 ABCD 是一个梯形; (2) 求四边形 ABCD 的面积. D E E A O (2) 解: 在底面正方形中求得 B C
A
如图, 在Rt△OOE中可求得 梯形的高 OE= ∴梯形ABCD的面积为
