petri网的原理及应用
Petri网

迁移的使能条件:
对于Petri网N={P,T,F,K,W,M},如果:
(∀p1)p1∈.t=>M(p1)≧W(p1,t)且 (∀p2)p2∈t.=>K(p2)≧M(p2)+W(t,p2)
则称t在M下使能,记为M[T>。
迁移的引发规则:
对于,如果∀p∈P,M'(P)可通过下式计算:M'(p)=
Petri网是一种适合于并发、异步、分布式软件系统规格与分析的形式 化方法。
Petri网分为位置/迁移Petri网和高级Petri网。
高级Petri网包括:谓词/迁移Petri网、有色Petri网、计时Petri网等。
位置/迁移Petri网
基本定义
Petri网结构——三元组结构N={P,T,F},其中:
前集和后集:
对于一个Petri网结构N={P,T,F},设x=(PUT), 令:
.x={y|∃y:(y,x)∈F} x.={y|∃y:(x,y)∈F} 称.x为x的前集或输入集 x.为x的后集或输出集。
子网结构:
对于N1={P1,T1,F1},N2={P2,T2,F2},如果:
P1⊆P2;
M(p)-W(p,t),
若p∈.t-t.
M(p)+W(t,p),
若p∈t.-.t
M(p)-W(p,t)+W(t,p),
若p∈t.∩.t
M(p)
若p∉t.U.t
例子:
如下所示Petri网,令牌的变化可能存在3种方式: 对于图(a),t1和 t2是使能的。
引发t1
注:给定Petri网初始
活性(续):
放宽对活性的限制,Petri网迁移t的活性成分如下5级:
第七章Petri网基础

18
§7.2.1 共享资源模型6
p active1
p active 2
t request 1
prequesting 1
trequest2 pidle
p requesting 2
t start 1
pacces sin g 1
t start 2
pacces sin g 2 pbusy
事件之间的同步距离(synchronic distance)
公平性(fairness)
4
§7.1 Petri 网发展概述5
Petri网模型的主要分析方法依赖于: 可达树(reachability tree) 关联矩阵和状态方程(incidence matrix and state equation) 不变量(invariants) 分析化简规则 Petri网的的纵向扩展: 条件/事件(C/E)网
PetriNets-owner@daimi.au.dk]] PetriNets-request@daimi.au.dk]]
[[World Wide Web URL:
http://www.daimi.au.dk/PetriNets/pnl/]]
[[Read before posting:http://www.daimi.au.dk/PetriNets/pnl/faq.html]]
9
§7.2 Petri网模型简介1
直观理解什么是Petri网,它们如何应用。 一个PN的结构元素包括: 位置(place):描述可能的系统局部状态(条件或状 况),例如,队列、缓冲、资源等。 变迁(transition):描述修改系统状态的事件、动 作,例如,信息处理、发送、资源的存取等。 弧(arc):使用两种方法规定局部状态和事件之间 的关系:引述事件能够发生的局部条件状态;由 事件所引发的局部状态的转换。
Petri网详细介绍与学习

模型改进
针对传统Petri网的不足,研究者们不断尝试对其进行改 进和优化,以提高其适用性和性能。例如,通过引入新 的元素或规则,改进Petri网的表达能力;优化Petri网的 推理算法,提高其推理速度等。
有界性、安全性与死锁
01
03
有界性
Petri网中的每个库所至多 包含有限个标记,且每个 变迁最多可以消耗和产生 有限个标记。
安全性
Petri网中不存在死锁状态 ,即对于任意一个状态, 总存在一个后继状态。
死锁
当Petri网中存在一个状态 ,从该状态无法通过任何 变迁到达其他状态时,称 该状态为死锁状态。
Petri网与其他建模方法的融合
融合方法
为了更好地描述和分析复杂系统,研究者们尝试将 Petri网与其他建模方法进行融合。例如,将Petri网与 流程图、状态图等图形化建模方法相结合,可以更直 观地描述系统的结构和行为。
融合优势
通过融合不同的建模方法,可以取长补短,提高对复 杂系统的描述和分析能力。同时,这种融合也有助于 推动不同领域之间的交叉和融合,促进多学科研究的 开展。
实例分析学习
案例分析
分析不同类型Petri网的特点和适用场景,如同步Petri 网、时间Petri网和有色Petri网等。
通过学习经典的Petri网实例,深入理解Petri网的实际 应用和建模技巧。
对比不同Petri网实例的建模效果,提高对Petri网的实 际操作能力和应用水平。
实践应用学习
Petri网的应用

经典Petri网
注意! 有向弧是有方向的 两个库所或变迁之间不允许有弧 库所可以拥有任意数量的令牌 有两个变迁都被允许的可能,但是一次只能发生一个变迁
Petri网的定义
定义2.1 PN的结构是由4要元描述的一有向图: PNS=(P,T,I,O) 此处: (1)P={p1,…,pn}是库所的有限集合,n>0为库所的个数; (2)T={t1,…,tm}是变迁的有限集合,m>0为库所的个数; P∩T=⊙(空集) (3)I:P×T→N是输入函数,它定义了从P到T的有向弧的重复数或权 (Weight)的集合,这里N={0,1…}为非负整数集; (4)O:T×P→N是输出函数,它定义了从T到P的有向弧的重复数或权的集 合。
4.可逆性和主宿状态(Reversibility and homestate)。 可逆性表明了一个物理系统可以由当前状态返回到初始状态。在自动制 造系统中常用于系统故障的修复以使系统从故障状态回到初始状态。 如果对于任意的M∈R(M0),M′是从M可达的,就称M′为主宿状态。这种情 况对应于一个实际的物理系统可以从当前某个状态返回到一个指定状态, 而不是初始状态。 5.可覆盖性(Coverability)。如果对于M∈R(M0)和M′∈R(M0)有 M′(p)≥M(p),就称M是可覆盖的。
Petri网的运行规则
在PN中,我们以变迁t表示一事件,用变迁的使能(enabling)表示事 件因前提条件得以满足而能够发生。我们还用t的输入库所(通过指向t 的弧连接的库所)表示该事件的发生所需要的前提局部状态,用由输入 库所至t的输入函数定义这些要求局部前提状态实现的次数,而局部状 态的实现情况由库所中所包含的令牌(token)数目来表示。
2.有界性(Boundedness)和安全性(safty)。 在一个Petri网中的每一个位置中,令牌数不超过一个有限整数k,即 p∈P, M(p)≤k,称Petri网是k有界的,k=1时称为安全的。 通常,库所用于表示制造系统中的工件、工具、托盘以及AGV的存放区, 还用于表示资源的可利用情况。确认这些存放区是否溢出或资源的容量 是否溢出是非常重要的。PN的有界性是检验被描述的系统是否存在溢出 的有效尺度。
《Petri网原理与应用》读书笔记

《Petri网原理与应用》读书笔记1 传统Petri 网介绍Carl Adam Petri 教授于1962 年在博士论文《用自动机理论通信》中首次提出的一种自动机网状结构模型,拥有能恰当处理因果上的不存在依赖性的并行现象和表示不确定性的选择的能力,以及以系统模型用网状图形表示的方法。
传统的Petri 网是简单的过程模型,由两种节点:库所和变迁,有向弧,以及令牌等元素组成的。
相关概念:(1)transition enabled(变迁的就绪):当且仅当transition 的每一个输入place 都至少有一个token 的时候,变迁就绪,可以实施。
(2)transition firing(变迁的实施):变迁实施的时候它的每一个输入库所托肯减少一个,并使它的每一个输出库所的托肯增加一个。
图1.1 显示了Petri 网的基本建模,其中圆圈表示place;矩形表示transition;存在于place 中用的token 用黑点表示。
用简单图形较好的表示并发、同步、因果等关系。
以网图的方式简洁、直观的模拟离散事件系统。
目前已得到广泛应用,有限状态机、通信协议、同步控制、生产系统、形式语言、多处理器系统等建模中。
通讯协议的验证是Petri 网应用最为成功的领域之一最初应用在70年代初期,由于Petri网以形式语言作为基础,可形式化地对通信协议进行正确性验证。
随着计算机网络技术和信息技术的发展,对网络进行性能分析的需要,不仅出现于企业内部的生产控制的局域总线网,而且出现于光纤局域网或ATM网中。
图1.1 Petri 网基本模型由于产品开发中的竞争和革新需要,导致产品开发者面临巨大压力。
在软件工程中Petri网主要用于软件系统的建模和分析,比较成熟的是加色Petri网,可以用于大型软件系统的设计、说明、仿真、确认和实现,在软件开发生命周期的各个阶段,Petri网都可以得到很好的应用。
Petri网可用于Al中的知识表达和推理的形式化模型的建立,可以表达各个活动之间的各种关系,如顺序关系、与关系、或关系等,并可在模型基础上通过已知的初始状态和初始条件进行逻辑推理。
[汇编]petri网原理与应用综述
![[汇编]petri网原理与应用综述](https://img.taocdn.com/s3/m/7d42bf24a8956bec0875e327.png)
[汇编]petri网原理与应用综述petri网原理与应用综述摘要:本文概述了Petri网的历史、发展、研究方法及应用领域,同时介绍了Petri网的基本原理,并给出了1个计算机网络链路层数据传输协议——停等协议的Petri网模型。
最后,概述了Petri网研究和应用中出现的问题,展望了Petri网的发展方向。
关键字:Petri网;状态变迁模型;并发;停等协议中图法分类号:TP312Research Surveys of the Petri NetWU QiangDepartment of Electronics and Information Engineering,Henan Vocational College of Agriculture,Zhengzhou,Henan Province 451450,ChinaAbstract: The article summarizes the history, thedevelopment, the research methods, the application areas and the basic principle of Petri net, and gave a Petri net model of stop-and-wait protocol。
Meanwhile, according to the problem of Petri net research and application, the paper gave some ideas。
Key words: Petri net; States transition model; Concurrency;Stop-and-wait protocol1。
历史和发展Petri网的概念最早是在1962年Carl Adam Petri 的博士论文中提出来的,后来该模型就成为理论计算机科学包括自动机模型和形式语言理论的1个分支。
Petri网的应用.ppt

经典Petri网
注意! ❖ 有向弧是有方向的 ❖ 两个库所或变迁之间不允许有弧 ❖ 库所可以拥有任意数量的令牌 ❖ 有两个变迁都被允许的可能,但是一次只能发生一个变迁
Petri网的定义
▪定义2.1 PN的结构是由4要元描述的一有向图: PNS=(P,T,I,O)
此处: (1)P={p1,…,pn}是库所的有限集合,n>0为库所的个数; (2)T={t1,…,tm}是变迁的有限集合,m>0为库所的个数; P∩T=⊙(空集) (3)I:P×T→N是输入函数,它定义了从P到T的有向弧的重复数或权 (Weight)的集合,这里N={0,1…}为非负整数集; (4)O:T×P→N是输出函数,它定义了从T到P的有向弧的重复数或权的集 合。
Petri网及其应用
一、Petri网的起源与发展 二、基本Petri网
1. Petri网的定义 2. Petri网的结构 3. Petri网的运行规则 三、基本PN的性能 四、PN的基本分析方法 五、Petri网的特点 六、PN的应用及难点
Petri网的起源与发展
Petri网最早是由卡尔·A·佩特里于1962年在他的博士论文 提出的,用来描述计算机系统事件之间的因果关系。早期 Petri网主要应用于计算机与信息处理领域,后来具有工程 背景的研究人员将Petri网方法用在工程系统尤其是自动制 造系统的研究。40多年来, Petri网不断的充实和发展,日 臻完善,在计算机、自动化、通信、交通、电力与电子、服 务以及制造等领域得到广泛的应用。
可达性 有界性与安全性 活性 可逆性与主宿状态 守衡性
……
1.可达性(Reachability)。若从初始标识m0开始激发一个变迁序列mr, 则称mr是从m0可达的。
Petri网详细介绍与学习

21
Petri网模型结构
Petri网具有丰富的结构描述能力,下图给出了顺序、并发、 冲突、混惑结构下的Petri网模型。
22
各类关系
23
各类关系
24
实例1:工业生产线的Petri网模型
有一工业生产线,要完成两项操作,分别为变迁t1和t2表示,变迁t1 将进 入生产线的半成品s1s2用两个部件s3固定在一起,后形成中间件s4。然后 第2个变迁t2 将s4 和s5用3个部件s3固定在一起形成中间件s6。完成t1和t2 都需要用到工具s7 假设受空间限制s2 s5最多不能超过100件, s4最多不能超过5件,s3最多 不能超过1000件。 K=1000 K=100 K=100
54
使用可覆盖性树可研究Petri网的特性(2)
对于一个有界的Petri网,其可覆盖性树被称为可达性树。这是 因为它包括所有可能到达的标识。在这种情况下,前面计讨论 的所有行为特性的分析问题都可以通过可达性树来解决,这是 一种穷举法 但在通常情况下,由于使用符号会使一些信息丢失,所以可 达性和活性问题不可能单单利用可覆盖性树方法来解决。我们 可看下页所示的两个不同的Petri网,它们有相同的可覆盖性树。 但其中一个是活的Petri网,而另一个不是活的,因为该网在发 生t1、t2和t3以后再也没有可发生的转移
如果一个Petri网的每一个迁移都是Lk活的,则称该Petri网为 Lk活的(k=0,1,2,3,4)。如果一个潜意识Lk活的而不是L(k+1)活 的,则称该迁移是严格Lk活的。 L4 ⇒L3 ⇒L2 ⇒L1,L0实际上是永不引发的。
37
Petri网的行为性质
第3章Petri网..

(1) Petri网结构 (2) 普通网 (3) 位置/迁移Petri网
(二) Petri网的性质
(1) 行为性质 (2) 结构性质
(三) Petri网分析技术
(1) 结构化简 (2) 可达树、覆盖树 (3) 状态方程、不变量
(四) Petri网规格的例
(1) 哲学家就餐问题 (2) 生产者-消费者问题
2 3
p3 t5 p4
t2
t1
4
t4
p6
6
p1
t1
p2
2
t2
3
p4
4
t4
p6
6
t3
p3 t5
3 3
p5
4
t3 p3 t5
3 3
p5
4
顺序、并发、冲突、混惑结构的Petri网模型:
顺序关系:设M为Petri网PN的一个标识,若存在t1和t2使得M[t1 M, 且M[t2,M [t2,亦即,在 M标识下, t1使能,而 t2不使能, 且 t1的引发会使t2使能,即t2的使能以t1的引发为条件,则称t1 和t2在M下有顺序关系。 并发关系:设 M 为 Petri网 PN 的一个标识,若存在 t1和 t2使得 M[t1和 M[t2 ,并满足 M[t1M1 M1[t2 ,且 M[t2 M2 M2[t1 ,则称 t1和 t2在M下并发。就是说在 M标识下, t1和t2都使能,且它们当 中任一个迁移的引发都不会使另一个迁移不使能。 冲突关系:设 M 为 Petri网 PN 的一个标识,若存在 t1和 t2使得 M[t1和 M[t2 ,并满足 M[t1M1 M1[t2 ,且 M[t2M2 M2[t1 ,则 称t1和t2在M下冲突。就是说M 标识下,t1和t2都使能,但它们当 p1 中任一个迁移引发都会使另一个迁移不使能。 t1 p2 p1
Petri网

例子:
顺序(图a)、并发(图b)、冲突(图c)及混惑(图d)
Petri网的性质
Petri网具有两类性质:
行为性质--与初始标识有关 结构性质--与初始标识无关
行为性质:
可达性:
可达性是研究任何系统动态行为的基础。 对于初始M0 ,如果存在一系列迁移t1、t2、t3、···、tn的引发
使得M0转换为Mn,则称标识Mn是从M0可达的。
有界性和安全性:
在PN=(N,M0)中,∃k∈Z+,对∀M∈R(M0),都有k≥M(p),则称位 置p为k有界。
Thanks!
例子:
对于P={p1,p2,p3,p4,p5,p6},T={t1,t2,t3,t4}和 F={(p1,t1),(t1,p2),(t1,p3),(p2,t2),(p3,t3),(t2,p4),(t3,p5),(p4,t4),(p5,t4),(t4,p6),(p 6,t5),(t5,p1)}的Petri网结构的图形表示如下:
前集和后集:
对于一个Petri网结构N={P,T,F},设x=(PUT), 令:
.x={y|∃y:(y,x)∈F} x.={y|∃y:(x,y)∈F} 称.x为x的前集或输入集 x.为x的后集或输出集。
子网结构:
对于N1={P1,T1,F1},N2={P2,T2,F2},如果:
P1⊆P2;
Petri网是一种适合于并发、异步、分布式软件系统规格与分析的形式 化方法。
Petri网分为位置/迁移Petri网和高级Petri网。
高级Petri网包括:谓词/迁移Petri网、有色Petri网、计时Petri网等。
petri网 (2)

Petri网Petri网是一种图形模型,用于描述并发系统中的并发过程和状态迁移。
它由物理学家Carl Adam Petri在1962年提出,是一种形式化的工具,用于模拟和分析各种并发系统。
1. Petri网的基本概念Petri网由两种基本元素组成:库所(Place)和变迁(Transition)。
库所可以看作是存储资源的位置,变迁表示发生的事件。
这两种元素都是用圆圈表示,并使用有向弧线连接。
•库所:用一个圆圈表示,通常用于存储资源或表示系统的状态。
每个库所都有一个或多个标记(token),表示资源的数量或状态。
•变迁:用矩形或虚线矩形表示,表示一个事件或活动。
变迁可以使得库所中的资源发生变化,即在库所之间转移标记。
此外,Petri网还有一些辅助元素:•弧线:表示库所和变迁之间的关系。
用于指示资源的流动或变迁的触发条件。
•权重:用于限制资源的流动或变迁的触发条件。
2. Petri网的特性Petri网具有以下几个重要的特性:2.1 可视化Petri网通过图形化的方式描述并发系统,并使用直观的图形元素表示资源和事件之间的关系。
这种可视化的特性使得Petri网更容易理解和分析,并且可以有效地交流和共享。
2.2 模块化Petri网可以进行模块化设计,即将一个复杂的系统分解为多个简单的子系统,并使用库所和变迁进行连接。
这样可以方便地对子系统进行分析和调试,并且可以更好地理解整个系统的结构和功能。
2.3 并发性Petri网能够描述并发系统的行为。
通过在变迁周围放置多个库所,可以实现多个资源之间的并发操作。
这样可以提高系统的并发性,提高系统的性能和效率。
2.4 死锁检测Petri网可以用于检测系统中的死锁问题。
当库所和变迁之间的资源流动形成闭环时,可能会导致死锁的发生。
通过分析Petri网的结构和标记状态,可以检测到潜在的死锁情况,并采取相应的措施解决问题。
3. Petri网的应用领域Petri网在各个领域都有广泛的应用,以下是其中一些典型的应用领域:3.1 并发系统分析Petri网可以用于描述和分析各种并发系统,如操作系统调度算法、并行计算系统、通信协议等。
Petri网

Petri网是对离散并行系统的数学表示。
Petri网是1960年代由卡尔·A·佩特里发明的,适合于描述异步的、并发的计算机系统模型。
Petri网既有严格的数学表述方式,也有直观的图形表达方式,既有丰富的系统描述手段和系统行为分析技术,又为计算机科学提供坚实的概念基础。
由于Petri网能够表达并发的事件,被认为是自动化理论的一种。
研究领域趋向认为Petri 网是所有流程定义语言之母。
* 经典Petri网经典的Petri网是简单的过程模型,由两种节点:库所和变迁,有向弧,以及令牌等元素组成的。
o Petri网的结构(1) Petri网的元素:+ 库所(Place)圆形节点+ 变迁(Transition)方形节点+ 有向弧(Connection)是库所和变迁之间的有向弧+ 令牌(Token)是库所中的动态对象,可以从一个库所移动到另一个库所。
(2) Petri网的规则是:+ 有向弧是有方向的+ 两个库所或变迁之间不允许有弧+ 库所可以拥有任意数量的令牌o 行为如果一个变迁的每个输入库所(input place)都拥有令牌,该变迁即为被允许(enable)。
一个变迁被允许时,变迁将发生(fire),输入库所(input place)的令牌被消耗,同时为输出库所(output place)产生令牌。
+ 变迁的发生是原子的+ 有两个变迁都被允许的可能,但是一次只能发生一个变迁+ 如果出现一个变迁,其输入库所的个数与输出库所的个数不相等,令牌的个数将发生变化+ Petri网络是静态的+ Petri网的状态由令牌在库所的分布决定o Petri网的形式化定义一个经典的Petri网由四元组(库所,变迁,输入函数,输出函数)组成。
任何图都可以映射到这样一个四元组上,反之亦然。
o Petri网流程建模一个流程的状态是由在场所中的令牌建模的,状态的变迁是由变迁建模的。
令牌表示事物(人,货物,机器),信息,条件,或对象的状态;库所代表库所,通道或地理位置;变迁代表事件,转化或传输。
Petri网的任务分解原理概述

【 关键词 】 人工智能;模糊P e t r i 网;任务分解
集 ,用P ( p i ) 表示。
1 . 模糊P e t r i 网分解原理
根据 任 务分 解 的规 则产 生 式 的推理 过程 可 以采 用模 糊P e t r i 网建 模 的方 法进 行分 析 。P e t r i 网是 一种 形 式化 系 统模 型 ,它有 很 强 的模 拟 能力 和严 格 的数 学定 义 , 同时 又 具有 图形 化 的表示 , 由于 它有 着 异 步 、并发 的特 性 ,是 描述 动态 并 发系 统 的有力 工 具 ,也 因此在 各 个 领域 有着 广泛 应 用 。模糊 P e t r i 网是 一般 网 的模 糊化 ,它更 能有 效 地 处理 含有 模糊 特 性 的 问题 。任 务 分解 是一 个复 杂 困难 的过 程 ,有 很 强 的模糊 性 和不 确 定性 。我 们可 以通 过P e t r i 网相 关 的分析 来判 断 任 务 的分解 是 否 正确 ,通 过P e t r i 网 的动态 性 能找 到 完成 总任 务而 要 采 取 的计划 ,为 以后 的任 务动 态分 配打 下基 础 。 不 同的文 献对 模糊 P e t r i 网有 不 同的 定义 ,下面 介绍 一种 用 于模 糊 推理 的模 糊P e t r i 网。 定义2 . 1 :模 糊P e t r i 网是 一个 五元 组
E L E C T R ONI C S WORL D・ j 5 霹 与习 露
P e t r i 网的任务 分解 原 理概 述
沈 阳理 工 大学 自动化 与 电气工程 学院 董 冲冲
对 于一个 不能被 任 何基 础机 构单独 完成 的 复杂任 务 ,为 了实现任 务 目 【 摘要 】 近年来随着人工智能的发展 ,任务分解受到越来越 多的关注。 运 用形 式 化的 方法 对任务 分 解进行 描 述和验证 是 十分 必要 的。 标 ,必须进 行 模糊 P e t r i 的任 务 分解 。任 务的 分解 是 实现任 务 的关键 ,
Petri网:模型、理论与应用

Petri网:模型、理论与应用Petri网,也称为Petri图,是一种用来描述系统事件并发性、同步性和序列性的有向图。
Petri网模型被广泛应用于计算机科学、系统工程、控制工程和化学工程等领域,成为了目前最流行的并发系统建模工具之一。
Petri网的基本元素Petri网由一组有向弧和节点组成,包括以下几个基本元素:1.库所(Place):代表系统中的状态或原料库存等。
2.变迁(Transition):代表系统中的事件或操作,用于改变状态或消耗库存。
3.有向弧(Arc):连接库所和变迁,表示状态之间的转移或原料的消耗。
4.标志(Marking):库所内的标志表示库存的数量或状态。
Petri网的基本形式Petri网可以表示为二元组N=(P, T, F),其中:1. P为库所的集合;2. T为变迁的集合;3. F为弧集合,由以下两种类型的弧组成:a)输入弧(Inhibitor arc):表示一个库所是变迁的前置条件,但是库所中的标志数量必须为零。
b)常规弧(Regular arc):表示一个库所是变迁的前置条件,库所中的标志数量可以为任意值。
Petri网的理论Petri网理论主要研究Petri网的语法、分析和应用。
Petri网具有以下特点:1. 易于可视化:Petri网可以用于描述具有并发性、同步性和序列性的系统,比传统的文本模型更直观。
2. 模型简单:Petri网只包含库所、变迁和有向弧三种基本元素,是一种简单、易于理解的模型。
3. 通用性强:Petri网模型可以表示各种类型的系统,例如工作流、协作系统、并发系统和控制系统等。
Petri网的应用Petri网在计算机科学、系统工程、控制工程和化学工程等领域的应用非常广泛。
1. 生产调度:Petri网可以应用于生产调度中,用于描述生产流程中的各个节点及其状态转移。
2. 工作流管理:Petri网可以应用于工作流管理中,用于描述任务分配、任务执行和任务完成的过程。
Petri网详细介绍与学习.ppt

Petri网起源:数学家Carl Adam Petri在1962年提出Petri 网理论
Petri网现状:广泛应用于离散事 件系统建模、分析等领域
添加标题
添加标题
添加标题
添加标题
添加 标题
添加 标题
变迁(Transition ):Petri网中的变迁 对应于系统中的某个事件或操作,它能 够将一个库所中的资源转移到另一个库 所中。
流关系(Flow Relation):Petri网中 的流关系表示库所和变迁之间的关系, 它能够描述系统在某个事件发生时资源 的变化情况。
Petri网定义: 由库所、变 迁和有向弧 组成的网状
Petri网在计算机科学 中的应用
Petri网在金融领域的 应用
Petri网在交通领域的 应用
Petri网在物联网领域 的应用
Peri网定义、特点与 分类
Petri网在生产制造领 域的应用
Petri网在医疗领域的 应用
Petri网在人工智能领 域的应用
Petri网在网络安全领 域的应用
在线教育平台: 提供Petri网的 入门和进阶教程, 适合初学者和有 一定基础的学员
学术搜索引擎: 通过搜索关键词 获取Petri网的 学术论文和研究 资料,深入了解 Petri网的理论 和应用
社交媒体群组: 加入相关的社交 媒体群组,与其 他学习者交流心 得和经验,共同 进步
Petri网建模与仿真实践 基于Petri网的自动化控制系统设计 Petri网在生产调度中的应用实践 Petri网在物流管理中的应用实践
,a click to unlimited possibilities
基于Petri网的柔性制造系统控制器设计

基于Petri网的柔性制造系统控制器设计基于Petri网的柔性制造系统控制器设计一、引言柔性制造系统(Flexible Manufacturing System, 简称FMS)是一种高度自动化的生产系统,通过柔性配置的机械、设备、计算机等组成,能够根据市场需求和产品变化快速灵活地进行生产。
FMS的核心是控制系统,它负责协调和控制整个生产过程。
本文将基于Petri网的控制器设计,介绍柔性制造系统控制器的基本原理和设计方法。
二、Petri网基本原理Petri网是由德国科学家Carl Adam Petri于1962年提出的一种图论模型,主要应用于描述并发处理过程中的事件与系统之间的关系。
它由两个基本元素组成:库所(place)和变迁(transition)。
库所表示系统中的状态,变迁表示状态之间的转移。
Petri网通过定义库所和变迁之间的弧(Arc)来描述状态转移的条件和行为规则。
Petri网具有时序可控性、并发性和死锁检测等特点,非常适用于描述和分析柔性制造系统的控制关系。
三、柔性制造系统控制器设计方法1. 建立Petri网模型首先,需要根据柔性制造系统的具体需求和工艺流程建立Petri网模型。
库所代表系统的状态,如机床、零件、工序等;变迁代表状态之间的转移,如加工、搬运、报警等。
根据FMS的特点,要考虑到并发处理、死锁避免等因素,将它们作为Petri网模型的一部分。
2. 设计控制策略根据柔性制造系统的生产需求和控制要求,设计控制策略。
控制策略包括资源调度、任务分配、状态监测等。
通过设置库所和变迁的权重和延时等属性,可以调整和优化控制策略。
3. 状态监测与转移在柔性制造系统中,需要实时监测各个工序的状态,并进行合适的状态转移。
可通过Petri网模型中的变迁,设置相应的触发条件和执行动作,实现状态的自动转移和控制。
4. 故障检测和处理柔性制造系统中,可能会出现设备故障、工艺异常等问题,需要及时检测和处理。
Petri网与应用
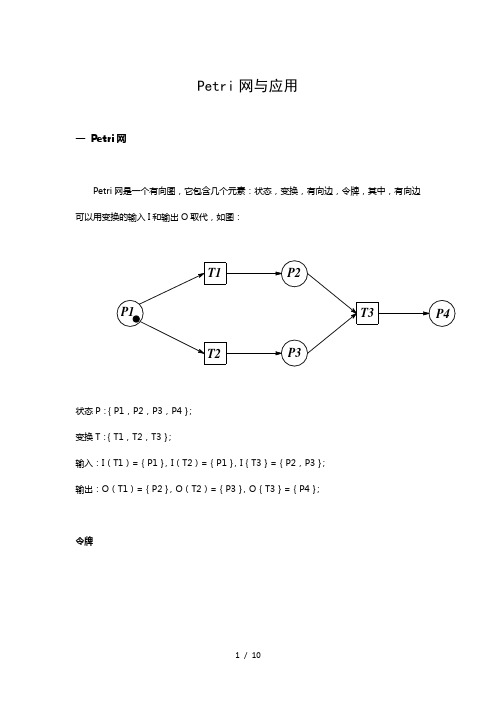
Petri网与应用一Petri网Petri网是一个有向图,它包含几个元素:状态,变换,有向边,令牌,其中,有向边可以用变换的输入I和输出O取代,如图:状态P:{P1,P2,P3,P4};变换T:{T1,T2,T3};输入:I(T1)={P1},I(T2)={P1},I{T3}={P2,P3};输出:O(T1)={P2},O(T2)={P3},O{T3}={P4};令牌令牌是状态中的动态对象,可以从一个状态所移动到另一个状态,通常当每个输入位置所拥有的令牌数大于等于从该位置到转换的线数时,就允许转换,当T1被激发时,P2和P4上各有一个权标被移出,而P1上则增加一个权标,Petri 网中权标总数不是固定的,在下例中两个权标被移出,而P1上只能增加一个权标,如图:转换前转换后二 Petri 网在电梯上的应用P3P31 假设人在f 层等电梯,电梯停在g 层,那么可以用下图表示:2 当按下电梯按钮的时候会亮灯,可以用令牌来表示,为了使多次按下按钮而不影响令牌数量的情况下,引入禁止线,如图所示,禁止线是用一个小圆圈而不是用箭头标记的输入线,通常当每个输入线上至少有一个权标,而禁止线上没有权标的时候,相应的转换才是允许的,在图中, P3上有一个权标而 P2 上没有权标,因此转换 t1 可以被激发:E fP gP f电梯运行中P1T1P3P2对以上的电梯进行完善:由于禁止线的作用,当再次按下按钮的时候,E f 中的令牌数不会增加,每部电梯有 m 个按钮,每层对应一个按钮,当按下一个按钮时该按钮指示灯亮,指示电梯 移往相应的楼层,当电梯到达指定的楼层时,按钮将熄灭;3 除了第一层与顶层之外,每个楼层都有两个按钮,一个要求电梯上行,另一个要求电梯下 行,这些按钮在按下时发亮,当电梯到达该层并将向 指定方向移动时,相应的按钮才会熄灭:E fP gP f按下按钮电梯运行4 在Petri 网中,变换是瞬时的,但在电梯中,从g 层到f 层是需要时间的,所以变换T 要加入时限,由于从g 层到f 层的时间time 是固定的,所以只需要把这个时间添加到对应的变换上即可:变换执行时间:time(电梯运行)=time (g ,f );time (g ,f )是g 层到f 层所用时间;5 一般情况下,一栋大楼有2部电梯,那么控制哪部运行,就要看电梯所在楼层与目的E fP gP f按下“上”按钮电梯运行E fP f按下“下”按钮电梯运行楼层的距离哪个最短:当电梯分别在a 和b 楼层中,设|a-b|为a 层和b 层的距离,如果|f-a|≤|f-b|,那么P c 中例牌传递给P b ,那么在优先判断之后,距离较大的电梯就可以依然保持1个令牌,原地待命的状态;E fP gP f按下“上”按钮电梯运行E fP f按下“下”按钮电梯运行P aP b楼层判断楼层判断 优先判断6 从上图中可以看出,一个状态可能会与多个变换有关,那么该如何执行变换的先后顺序呢?(1) 把同类变换分成一组;(2) 限制每组变换的输入;假如函数Itok 为输入变换的令牌数量,那么限定 Itok (最优楼层判断)=1; Itok (上下行判断)=1;P aP bP c P fP f楼层判断 楼层判断不动楼层最优楼层判断上下行判断上下行状态电梯运行电梯运行7为了能使上题中的令牌更有区别性完成以上操作,需要将令牌特征化,也就是令牌的着色,可以将1个令牌标记为绿色,记为楼层令牌,将另一个令牌标记为红色,记为方向令牌,那么可以限定最优楼层判断值接受绿色令牌,上下行判断只接受红色令牌:P aP bP cP fP f 楼层判断楼层判断不动楼层最优楼层判断上下行判断上下行状态电梯运行电梯运行8 将以上的问题整合起来:图中:优先判断的输出令牌为红色; 最优楼层判断的输入令牌为绿色; 上下行判断的输入令牌为红色; 其他判断不设置要求;三 参考文献1安阳师范学院网络教学资源/jsj/wlkc/rjgc1,2,3/3/4.3.htm 2 Petri 网-维基百科/wiki/Petri%E7%BD%91#.E4.BB.A4.E7.89.8C.E7.9D.80.EE fP aP bP c P fP fE f ’楼层判断楼层判断不动楼层最优楼层判断优先判断按下“上”按钮按下“下”按钮上下行状态上下行判断电梯运行电梯运行8.89.B2[文档可能无法思考全面,请浏览后下载,另外祝您生活愉快,工作顺利,万事如意!]。
第5讲 PETRI网模拟原理

逻辑关系图:死锁关系
P1 t1 P2 t2 P3
P4
t3
P5
t4
P6
C/E系统
基本逻辑关系表达:顺序、并发、冲突、 异或、死锁 事例与进程,进程的合成 C/E基本例子:生产者/消费者Petri网
逻辑关系图:顺序关系
P1 t1 P2 t2 P3
逻辑关系图:并发关系
P2 t1 t2 P3
P1
P4
t3
P5
逻辑关系图:互斥冲突关系
P2 t1 P3 t2
P1
P4
t3
逻辑关系图:异或关系
实例:工业生产线的Petri网模型
有一工业生产线,要完成两项操作,分别为 变迁t1和t2表示,变迁t1 将进入生产线的半成 品s1s2用两个部件s3固定在一起,后形成中间 件s4。然后第2个变迁t2 将s4 和s5用3个部件 s3固定在一起形成中间件s6。完成t1和t2 都需 要用到工具s7 假设受空间限制s2 s5最多不能超过100件, s4最多不能超过5件,s3最多不能超过1000件。
第5讲 PETRI网模拟原理
Petri网
1962年德国学者Carl A.Petri在其博士论文 中提出的描述事件和条件关系的网络 用简单图形较好的表示并发、同步、因果 等关系。以网图的方式简洁、直观的模拟 离散事件系统 目前已得到广泛应用,有限状态机、通信协 议、同步控制、生产系统、形式语言、多 处理器系i网类型
基本Petri网:每个库所容量为1,这样库所可称为 条件,变迁可称为事件。故又称为条件/事件系统 C/E 低级Petri网:库所容量和权重为>=1的任意整数, 称为库所/变迁网。简作P/T网 定时Petri网:将各事件的持续时长标在库所旁边, 库所中新产生的标记经过一须时间后才加入到网 中,或是标在变迁上,经过时间延迟后发生。 高级Petri网:谓词/事件网、染色网、随机网等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Petri网的原理及应用
1. 什么是Petri网
Petri网是一种用于描述并发系统和并发性行为的图形化工具和形式化方法。
它由德国数学家Carl Adam Petri于1962年提出,被广泛应用于系统建模、并发
系统分析、协议验证等领域。
Petri网可以模拟并发系统的并发行为、状态转换以
及资源分配等关键方面,通过图形化的方式直观地展示系统的结构和行为,并支持形式化的数学分析。
2. Petri网的基本元素
Petri网由以下基本元素组成:
2.1. 位置(Place)
位置表示系统中的状态或者条件,通常通过一个圆圈表示。
位置可以存储某种
资源或者表示某种变量的取值。
2.2. 过渡(Transition)
过渡表示系统中的某种事件或者操作,通常通过一个矩形表示。
过渡可以触发
或消耗位置中的资源,改变系统的状态。
2.3. 弧(Arc)
弧表示位置和过渡之间的联系,通常通过一条带箭头的线表示。
弧可以表示资
源的流动或者触发条件的关系,连接位置和过渡。
2.4. 标识(Marking)
标识是位置中的资源的数量,可以通过在位置内部的小圆圈中填写数字来表示。
标识表示系统的状态,在Petri网中可以不断变化。
3. Petri网的建模方法
Petri网可以通过以下步骤完成建模:
3.1. 确定系统的功能和行为
首先,需要明确系统的功能和行为,清楚系统中的位置、过渡以及它们之间的
关系。
例如,一个简单的交通信号灯系统中可以有位置表示红绿灯状态、过渡表示信号灯变换的事件或操作。
3.2. 绘制Petri网图
根据系统的功能和行为,使用标识符绘制位置和过渡,并用弧表示它们之间的联系。
根据需要,可以使用不同的符号和颜色来表示不同类型的位置和过渡。
3.3. 设定初始标识
确定初始状态下位置中的资源数量,填写在位置的小圆圈中。
这可以表示系统的初始状态,即Petri网的初始标识。
3.4. 定义触发条件和行为规则
根据系统的功能和行为,定义位置和过渡之间的触发条件和行为规则。
触发条件可以用于控制过渡的触发时机,行为规则可以用于描述触发过渡后的系统行为。
3.5. 模拟系统行为和状态转换
通过对Petri网进行模拟和分析,可以了解系统的行为和状态转换。
可以观察位置中资源的流动和过渡的触发情况,以及系统的状态变化。
4. Petri网的应用
Petri网在并发系统建模和分析、协议验证等领域有广泛的应用。
以下是一些常见的应用场景:
4.1. 并发系统建模和分析
Petri网可以用于描述并发系统的行为和状态转换,通过模拟和分析,可以评估系统的性能、可靠性和安全性,发现并发问题并进行优化。
4.2. 工作流建模和优化
Petri网可以用于建模和优化工作流,通过定义位置和过渡之间的触发条件和行为规则,可以模拟工作流的流程和资源分配,发现瓶颈和优化机会。
4.3. 协议验证和安全分析
Petri网可以用于描述协议的行为和安全性要求,通过模拟和分析,可以验证协议的正确性和安全性,发现潜在的漏洞和攻击。
4.4. 软件系统建模和测试
Petri网可以用于建模和测试软件系统,通过定义位置和过渡之间的触发条件和行为规则,模拟系统的行为和状态转换,发现潜在的错误和性能问题。
总结
Petri网是一种用于描述并发系统和并发性行为的图形化工具和形式化方法。
它通过位置、过渡和弧这些基本元素来表示系统的结构和行为,并支持模拟和分析。
Petri网的应用包括并发系统建模和分析、工作流建模和优化、协议验证和安全分析、软件系统建模和测试等领域。
通过使用Petri网,可以更好地理解并发系统的
行为和状态转换,发现问题并进行优化。
