【完整版毕业论文】巴特沃斯有源低通滤波器的设计
五阶巴特沃斯有源低通滤波器的设计

可以写成多个双二次函数的连乘形式 其中: 表 1 归一化的巴特沃斯低通滤波器传 递函数的分母多项式 在表 1 的 归 一 化 巴 特 沃 斯 低 通 滤 波 器 传 递 函 数 的 分 母 多 项 式 中 ,S 上式中的每一个双二次函数都可以用 运算放大器电阻和电容构成的有源滤波器 来 实 现 ,我 们 将 这 种 双 二 次 函 数 对 应 的 实 现电路,称 为 有 源 滤 波 器 的 基 本 节 电 路 。 下面是级联法的原理图:
222
一线技术
浅谈静电的危害及其消除
文⊙ 陈中银 盛宗生(南阳理工学院)
静电防灾己发展成为专门的科学,它 不 仅 限 于 静 电 工 程 学 ,而 且 广 泛 地 涉 及 到 燃 烧 化 学 工 程 学 、环 境 工 程 学 、材 料 工 程 学 和 系 统 工 程 学 。静 电 危 害 的 实 质 将 随 着 科 学 技 术 的 发 展 而 变 化 。所 以 ,了 解 静 电 的 危 害 ,熟 悉 静 电 的 消 除 方 法 显 得 越 来 越 重要了。 一、静电的危害 大家知道,物体带了静电,其周围空 间 即 存 在 静 电 场 。在 电 场 力 作 用 下 ,可以 产 生 种 种 物 理 现 象 。这 些 物 理 现 象 ,有的 有 利 ,有 的 有 危 害 。由 静 电 引 起 的 危 害 主 要有三个方面: (一)静电对生产的危害 由于静电对轻小物体有明显的力学作 用,因 而 在 某 些 生 产 部 门 中 会 引 起 严 重 的 障碍。如 在 某 些 粉 末 状 物 体 生 产 过 程 中 , 静 电 力 能 使 筛 孔 或 管 道 堵 塞;静 电 吸 引 灰 尘,使纺织品颜色灰暗,丝 质 脆 而 易 断; 感 光 胶 片 涂 膜 不 匀 ,出 现 拉 丝 、划痕;在 薄 膜 、纸 品 生 产 中 ,静 电 斥 力 能 使 产 品 离 散 而 无 法 整 理 ,而 静 电 引 力 又 能 使 产 品 互 相吸附而无法分离;静电力能吸引尘埃, 因而会严重影响某些电器外壳的喷涂质 量,也 会 影 响 某 些 超 净 工 作 场 所 环 境 的 净 化;车 间 工 人 由 于 在 地 面 上 行 走 、操 作 绝 缘 材 料 、在 椅 凳 和 工 作 台 面 上 移 动 、接近 或 触 及 其 它 带 电 体 、沾 附 带 电 粉 体 或 液 滴 等活动而带电,且人体充电电位一般为 1 k V 左右,最高可达 5 0 k V ,这足以影响比 较 精 密 的 电 器 设 备 、微 电 子 元 件 、计 算 机 等正常生产与工作。例如: 较新的集成电 路采用 H M O S 、S O S 等工艺,其静电敏感 度只有 3 0 ~4 0 V ,因而在制造和应用集成 电路时,必须从生产、运输、保管、组装、 调试、维修等场合采用一系列的保护措 施,防 止 人 体 静 电 电 位 的 产 生 而 带 来 的 影 响。 美国一家公司认为,一个价值 5 0 美分 (上接 222 页) 的集成电路,如果在生产和调测时忽略了 防静电措施,它将会出现极不稳定的特 性,因而大大降低了设备的可靠性,这时 的维修费用将会是 5 0 0 美元,即需要用原 旧件的一千倍的代价才能挽回质量和信 誉。美国的一些公司在采取防静电措施 后,元件失效率降低了 1 0 0 / n 。节约了上 百万的资金,其效益是投资购买防静电器 材的 1 0 倍以上。 (二)静电泄放的危害 对于电阻率特别大( ρ> 1 0 1 2 Ω m ) 的物 质,静电电荷不易散逸,静电电位越积越 高,在一定条件下导致火花放电瞬时功率 可达几十千瓦。把电能转变成热能,使易 燃易爆物引燃引爆,是十分危险的。例如: 干燥的制粉厂由于防尘设备不好,粉尘飞 扬,往往就会引燃粉尘,造成强烈爆炸,甚 至因拖擦车间地面油渍,使拖把因磨擦起 电而放电,引起充满汽油气的车间爆炸。 国内外因静电引起火灾、爆炸等事故屡见 不鲜。据有关资料统计,1 9 6 2 年~1 9 7 1 年 间,日本由于静电引起的火灾平均每年达 1 0 0 起;1 9 6 7 年~1 9 7 1 年间,加拿大空军 由于静电引起的燃油和油车着火达 1 1 次; 1 9 6 9 年 1 2 月份的两个星期内,连续发生 在英国、荷兰、挪威三国三艘 2 0 万吨级油 轮,因为冲洗船舱的水滴喷离水管或货油 流离油管时所带的电荷放电,引起严重的 爆炸事故,震惊了世界航运界。我国石油 工业从 6 0 年代以来迅猛发展,伴随而来的 因静电引起的火灾、爆炸等也时有发生。 在火化工厂里,静电事故率约为 1 0 % 。 (三)静电放电引起电击的危害 人在绝缘良好的地毯上行走,可带上 3 ~5 k V 的静电。一按触门把,使人感受到 电击而有惊悸和痛感;在其它生产现场, 如卷绕绝缘薄膜,收送印刷品、粉体装袋 作业等,都会发生电击伤害事故;静电电 击虽难以直接致人死亡,但由此而引起的 此外为了减少输入偏置电流及其漂移 对电路的影响,应使: 与 联立求解,可得: 恐怖情绪会使生产效率下降,精神受到 损。此 外 ,静 电 电 击 引 起 的 二 次 伤 害 事 故 也是不可忽视的。 二、消除静电的方法 为了防止电荷的积累,避免给国家和 个 人 生 活 带 来 的 严 重 危 害 ,就 必 须 采 取 行 之有效的措施,消除静电。其基本方法有: (一)接地法消除静电 如消除人体静电积累,将人体予以接 地,使人体电位不超过规定的 l 0 V 以下的 安 全 值 。人 体 接 地 的 主 要 方 法 要 看 地 面 的 导 电 性 ,一 般 水 泥 砂 浆 、大 理 石 、菱 苦 土 地 面 均 属 导 电 地 面;其 次 是 人 着 导 电 鞋 和 导 电 的 工 作 衣 、工 装 用 器 件 等 。在 操 作 高 静 电 敏 感 的 火 工 品 或 电 子 元 件 的 场 所 ,还 需要用电镯套,以降低人体电位至安全 值。人 在 操 作 时 动 作 要 小 心 谨 慎 ,严 禁 突 发 性 的 活 动 与 磨 擦 。对 于 存 在 金 属 外 壳 的 容 器 、设 备 、管 道 来 讲 ,也 要 采 取 接 地 或 跨接( 即各容器、管道、与设备之间用金属 线相连) 的方法消除静电。 (二)采取先进技术手段消除静电 各种高分子合成纤维材料是优良的绝 缘 材 料 ,容 易 积 累 静 电 ,现 今 我 国 已 研 制 出 各 种 新 型 的 抗 静 电 合 成 化 纤 材 料 。如为 防 止 石 油 输 送 过 程 中 ,由 于 石 油 在 管 道 内 流 动 摩 擦 而 产 生 的 电 荷 积 累 ,可 以 控 制 流 速 和 改 变 加 油 方 式 ,避 免 水 、空 气 和 油 品 的混合等措施减少摩擦产生的电荷积累, 同时采用抗静电添加剂。 (三)湿度控制法除静电 考虑到工作中的环境因素,应注意提 高空气湿度,使相对湿度控制在 4 5 % ~ 7 0 % 范围内,以减小物体表面的电阻率,增 加物体的漏电能力,防止电火花的产生; 减 少 粉 末 、纤 维 等 的 不 必 要 吸 附 。在 某 些 特 殊 环 境 条 件 工 作 的 设 备 上 ,还 应 安 装 放 电 尖 端 ,及 时 泄 漏 电 荷 的 积 累 ,防 止 产 生 电火花而引起火灾或爆炸事故。 三、仿真结果 使用 M u l t i s i m 进行仿真,很容易就可 以得到电路幅频特性和相频特性。在 B o d e P l o t t e r 仪表 I N 接系统输入端,O U T 接系 统 输 出 端 。打 开 仿 真 运 行 器 即 可 看 到 响 应 曲线。在 G r a p h e r 查看器中可以看到曲线 细节部分。 四、结束语 传统滤波器设计都是按照固定的模式 进 行 的 。本 文 就 给 出 了 一 个 低 通 滤 波 器 实 现 的 实 例 。但 经 典 滤 波 器 设 计 理 论 在 处 理 一 些 如 算 术 对 称 滤 波 器 的 设 计 、线 性 相 位 与 理 想 低 通 衰 减 相 结 合 等 问 题 时 ,却 存 在 较 大 困 难 。为 此 ,通 过 计 算 机 优 化 进 行 滤 波器设计的方法得到越来越广泛的应用。
【完整版毕业论文】巴特沃斯有源低通滤波器的设计

巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展,各种科技产品在人类社会中随处可见,极大的丰富了人们的日常生活。
物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。
就目前而言,在几乎所有的电子产品中,各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用,例如可穿戴设备的语音信号输入系统中,运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除,来提高系统的音质和语音识别精准度等。
本论文通过对各种低通滤波器的通频带、增益和截止频率的分析,采用通频带最大扁平度技术(巴特沃斯技术)来设计实现四阶高性能低通滤波器,通过Multisum仿真软件,验证了设计的正确性。
在这基础上,本文还对如何提高该滤波器的响应速度进行了研究,提出了一种有效的提高响应速度的方案,并通过仿真软件得以验证。
这在低通滤波器的理论以及实际工程应用中,都具有非常重要的意义。
关键词:有源低通滤波器,巴特沃斯,运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS:active low-pass filter,butterworth,amplifier1绪论1.1 引言在近现代的科技发展中,滤波器作为一种必不可少的组成成分,在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。
设计一个巴特沃斯模拟低通滤波器

1. 设计一个巴特沃斯模拟低通滤波器,要求通带截止频率为Hz f p 25=,通带最大衰减dB a p 3=,阻带起始频率Hz f s 50=,阻带最小衰减dB a s 25=。
解:根据已知条件确定巴特沃斯低通滤波器的阶数N :053.01010202520===--s a s δ()()2355.46021.05502.22lg 21053.01lg lg211lg 22==⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-≥p s s ΩΩδN取N =5。
低通滤波器3dB 截止频率为)/(157502s rad πf πΩΩp p c ====则五阶巴特沃斯滤波器的传输函数为:1021.010719.110095.110326.510048.111236.3236.4236.4236.31)(2436495112345++⨯+⨯+⨯+⨯=+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=----s s s s s Ωs Ωs Ωs Ωs Ωs s H c c ccc2. 设计一个切比雪夫模拟低通滤波器,要求通带截止频率为kHz f p 3=,通带最大衰减dB a p 2.0=,阻带起始频率kHz f s 12=,阻带最小衰减dB a s 50=。
解:由()2.01lg 20-=-p δ,求得9772.0101202.0==--p δ。
则2171.019772.011)1(122=-=--=p δε 由50lg 20-=s δ,求得0032.0102050==-s δ,则23.31610032.011122=-=-=s δδ 所需滤波器的阶数为:()()()()8604.30634.29770.7312arccos 2171.0/23.316arccos arccos arccos ===≥h h ΩΩh εδh N p s取N =4。
则该模拟低通滤波器的幅度表示为:⎪⎭⎫ ⎝⎛⨯⨯+=⎪⎪⎭⎫⎝⎛+=32422210322171.01111)(πΩC ΩΩC εΩj H p Na归一化的系统函数表示为:∏∏==--=-⋅=Nk k Nk k N a p p p p εp H 111)(7368.11)(21)(其中极点k p 为:0715.14438.01j p +-=,4438.00715.12j p +-=,4438.00715.13j p --=,0715.14438.01j p --=将)(p H a 去归一化,求得实际滤波器的系统函数)(s H a()()()8428426414107790.4100394.4107791.4106731.1102687.77368.1)()(⨯+⨯+⨯+⨯+⨯=-==∏==s s s s p Ωs Ωp H s H k k p pΩs p a a p3. 设计一个巴特沃斯模拟高通滤波器,要求通带截止频率为kHz f p 20=,通带最大衰减dB a p 3=,阻带起始频率kHz f s 10=,阻带最小衰减dB a s 15=。
巴特沃斯低通滤波器分析

巴特沃斯低通滤波器分析巴特沃斯低通滤波器课程论文班级: 1311电科学号: 2013111164 姓名:张梦雪摘要:本篇论文叙述了数字滤波器的基本原理、IIR数字滤波器的设计方法和IIR数字高通滤波器设计在MATLAB上的实现与IIR数字滤波器在实际中的应用。
无限脉冲响应(IIR)数字滤波器是冲激响应函数h(t)包含无限个抽样值的滤波器,一般是按照预定的模拟滤波器的逼近函数来转换成相应的数字滤波器,现有的逼近函数如巴特沃斯、切比雪夫。
设计IIR数字滤波器在工程上常用的有两种:脉冲响应不变法、双线性变换法。
其设计过程都是由模拟滤波器的系统函数H(s)去变换出相应的数字滤波器的系统函数H(z)。
关键词:数字滤波器 MATLAB 巴特沃斯切比雪夫双线性变换法Abstract:Digital filter is described in this paper basic principles, IIR digital filter design method of IIR digital high-pass filter design in MATLAB realization of IIR digital filter and application in practice. Infinite Impulse response (IIR) digital filter is the impulse response h (t) includes unlimited sampling filter, usually according to the analog filter approximating function to convert into digital filters, such as Butterworth, Chebyshev approximation functions. Design of IIR digital filters there are two commonly used in engineering: impulse response method, the bilinear transformation method. The design process are by the analog filter system function h (s) to transform the digital filter of the system function h (z).Key words: Digital filter MATLAB Butterworth ChebyshevBilinear transformation methed目录目录 (6)1.前言................... 错误!未定义书签。
有源低通滤波器的设计

有源低通滤波器的设计有源滤波器是一种使用有源元件(如运放)来构成的滤波器。
有源滤波器具有较低的输出阻抗和较高的增益,并且能够提供较大的增益和较低的失真。
有源低通滤波器是一种能够通过滤除高频信号而传递低频信号的滤波器。
它可以应用于音频信号处理、视频信号处理和通信系统中,用于去除噪音、改善信号品质等。
本文将介绍有源低通滤波器的设计原理和步骤,以供读者参考。
1.确定滤波器的截止频率:首先,根据需要滤除的高频信号范围,确定滤波器的截止频率。
截止频率是决定滤波器的性能的重要参数之一,它决定了滤波器在不同频率范围内的衰减特性。
2.选择合适的滤波器类型:根据应用场景和信号要求,选择合适的有源滤波器类型。
常见的有源滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
不同的滤波器类型具有不同的性能和设计要求,需要根据具体情况选择。
3.设计滤波器的电路结构:根据选择的滤波器类型和截止频率,设计滤波器的电路结构。
有源低通滤波器通常由运放、电阻和电容组成。
根据电路结构设计电容和电阻的数值,以满足滤波器的要求。
4.计算反馈电阻和输入电阻:根据电路结构和信号要求,计算滤波器的反馈电阻和输入电阻的数值。
反馈电阻决定了滤波器的增益和频率响应,输入电阻影响了滤波器的输入阻抗和信噪比。
5.选择适当的运放:根据滤波器的增益要求和频率响应,选择合适的运放器件。
不同的运放器件具有不同的增益、带宽和失真等特性,需要根据具体要求选择。
6.绘制电路图并进行仿真:根据设计的滤波器电路结构和参数,绘制电路图,并进行仿真分析。
通过仿真可评估滤波器的性能,如增益、相位延迟和截止频率等。
7.电路实现和调试:根据仿真结果,实现电路并进行调试。
调试过程中需要注意电路的稳定性和可靠性,同时还需要进行频率响应测试和输出波形观察,以验证设计结果。
总结:有源低通滤波器是一种常见的滤波器类型,其设计步骤包括确定截止频率、选择滤波器类型、设计电路结构、计算反馈电阻和输入电阻、选择适当的运放器件、绘制电路图并进行仿真分析,最后实现电路和调试。
巴特沃斯低通滤波器的设计
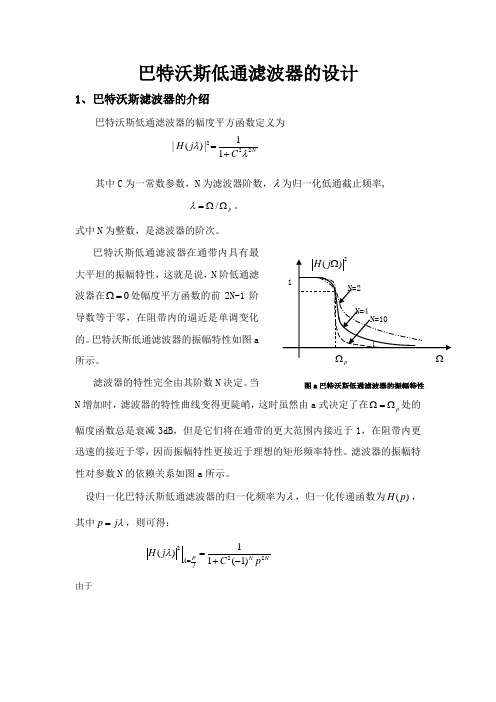
巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数,N 为滤波器阶数,λ为归一化低通截止频率,/p λ=ΩΩ。
式中N 为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图a 所示。
滤波器的特性完全由其阶数N 决定。
当N 增加时,滤波器的特性曲线变得更陡峭,这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N 的依赖关系如图a 所示。
设归一化巴特沃斯低通滤波器的归一化频率为λ,归一化传递函数为()H p ,其中p j λ=,则可得:2221()1(1)N NpjH j C pλλ==+- 由于p图a 巴特沃斯低通滤波器的振幅特性221()()()1()a a jsNcH s H s A s j Ω=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。
2、常用设计巴特沃斯低通滤波器指标p λ:通带截止频率; p α:通带衰减,单位:dB ;s λ:阻带起始频率;s α:阻带衰减,单位:dB 。
说明:(1)衰减在这里以分贝(dB )为单位;即222110lg10lg 1()NC H j αλλ⎡⎤==+⎣⎦(2)当3dB α=时p C Ω=Ω为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率/C λ=ΩΩ,即1,p sp s ppλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下:(1)计算归一化频率1p p pλΩ==Ω,ss pλΩ=Ω。
(2) 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ;注意当3p dB α=时 C=1。
巴特沃斯低通滤波器的设计精编资料

巴特沃斯低通滤波器的设计巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数,N 为滤波器阶数,λ为归一化低通截止频率,/p λ=ΩΩ。
式中N 为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图a 所示。
滤波器的特性完全由其阶数N 决定。
当N 增加时,滤波器的特性曲线变得更陡峭,这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N 的依赖关系如图a 所示。
设归一化巴特沃斯低通滤波器的归一化频率为λ,归一化传递函数为()H p ,其中p j λ=,则可得:2221()1(1)N Np jH j C pλλ==+-p 图a 巴特沃斯低通滤波器的振幅特性由于221()()()1()a a jsNcH s H s AsjΩ=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。
2、常用设计巴特沃斯低通滤波器指标pλ:通带截止频率;pα:通带衰减,单位:dB;sλ:阻带起始频率;sα:阻带衰减,单位:dB。
说明:(1)衰减在这里以分贝(dB)为单位;即222110lg10lg1()NCH jαλλ⎡⎤==+⎣⎦(2)当3dBα=时p CΩ=Ω为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率/Cλ=ΩΩ,即1,p sp sp pλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下:(1)计算归一化频率1p p pλΩ==Ω,ss pλΩ=Ω。
(2) 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ;注意当3p dB α=时 C=1。
Butterworth (巴特沃斯)滤波器设计参考

高通滤波器:
1 z 1 s C1 , 1 1 z
C1 c tan
c
2
,
c 1
(Note: 参考 陈佩青《数字信号处理教程》第二版 291 页 表 6-8)
2
其他带通、带阻滤波器频率变换式参考表 6-8 (下图)
3
参考设计: 1. 1 阶 Butterworth LPF 设计
频响如下
8
Butterworth 1~2 阶 LPF & HPF Filter Coefficients 以及制作成 Excel 表格分享在: /s/1hqw2mby 可以下载使用,选择对应的类型,设定相应的 fs & fc 就能自动计算出 Filter Coefficients。
(Note: 参考 陈佩青《数字信号处理教程》第二版 266 页 表 6-4)
上面的表达式是 s 域的表达式,下面是变化到 z 域的方法。
低通滤波器:
1 1 z 1 s C 1 1 z 1 C 1 c tan c 2 c 1, c 2 f c / f s
Butterworth (巴特沃斯)滤波器设计参考
-- By Water 在嵌入式音频产品开发过程中经常会到 LPF(Low Pass Filter 低通滤波器)和 HPF(High Pass Filter 高通滤 波器),一般情况下都是离线用工具(如: Matlab)设计好滤波器的参数(Filter Coefficients)再应用到产品中 去。但有些状况下需要用户自己根据需求来实时(Real-time)调整 Filter Frequency Response (滤波器频率响应), 这种情形下就需要在嵌入式系统中实时根据客户的设定需求来产生相应的 Filter Coefficients。 下文就汇总出了 N 阶 IIR LPF & HPF Butterworth 滤波器系数的设计方法, 具体的算法原理推导可以参考陈佩 青《数字信号处理教程》一书,此处只给出工程上可以应用的结论。
毕业设计(论文)-基于MATLAB做巴特沃斯低通滤波器

分类号编号烟台大学毕业论文基于MATLAB设计巴特沃斯低通滤波器The Design of Butterworth Low-passing Filter Based on MA TLAB申请学位:院系:专业:姓名:学号:指导老师:2011年05 月26日烟台大学基于MA TLAB设计巴特沃斯低通滤波器姓名:导师:2011年05月26日烟台大学烟台大学毕业论文任务书院(系):光电信息科学技术学院[摘要]滤波器设计是数字信号处理的重要内容。
在MATLAB软件中有丰富的滤波器设计的相关命令,掌握相关的方法后可以提高我们的工作效率。
首先对巴特沃斯低通滤波器的特性进行研究,然后用MATLAB信号处理工具箱提供的函数设计出巴特沃斯低通滤波器模型,并对具体实例进行分析,使得巴特沃斯滤波器的设计更加快捷、直观、简单。
[关键词]巴特沃斯低通滤波器; MATLAB仿真;[Abstract]First,analyse the characteristics of Butterworth low-pass filter, second use MATLAB signal processing toolbox design the mode of Butterworth low - pass filter ,to study it though an explme. The method makes the design of Butterw orth filter quicklier ,more intuitively,and simp -lier.[Keywords] Butterworth low-pass filter; MATLAB simulation;目录1 绪论 (1)1.1 引言 (1)1.2 数字滤波器的设计原理 (1)1.3数字滤波器的应用 (2)1.4MATLAB的介绍 (3)1.5本文的工作及安排 (3)2 滤波器分类及比较 (5)2.1滤波器的设计原理 (5)2.2 滤波器分类 (5)2.3四种类型模拟滤波器的比较 (9)3巴特沃斯低通滤波器 (11)3.1巴特沃斯低通滤波器的设计原理 (11)4 MATLAB仿真及分析 (15)4.1 MATLAB工具箱函数 (15)4.2 巴特沃斯低通滤波器的MATLAB仿真 (15)5 结论与展望 (19)5.1 总结 (19)5.2 展望 (19)致谢 (20)参考文献 (21)1 绪论1.1 引言凡是有能力进行信号处理的装置都可以称为滤波器。
巴特沃斯低通滤波电路设计

巴特沃斯低通滤波电路设计:
巴特沃斯低通滤波电路的设计主要包括以下几个步骤:
1.确定系统函数的极点:巴特沃斯滤波器的极点位于Z平面的单位圆上,因此可以通
过选取适当的滤波器阶数和电气参数,使得滤波器的极点位于单位圆上。
2.设计传递函数:根据滤波器的性能要求,如通带增益、阻带增益、过渡带宽度等,
设计出传递函数。
巴特沃斯滤波器的传递函数具有固定的形式,可以通过选取电气参数来调整其性能。
3.实现电路结构:将设计好的传递函数转换为实际电路结构。
根据不同的电路形式,
可以选择不同的电路元件和结构,如运算放大器、RC电路等。
4.参数调整:对电路中的元件参数进行适当调整,以保证滤波器的性能符合设计要求。
参数调整是滤波器设计中非常关键的一步,需要通过实验和仿真反复验证和调整。
5.测试和验证:对设计好的滤波器进行测试和验证,包括频率响应、相位响应、群延
迟等性能指标的测试。
如果测试结果不符合设计要求,需要对电路或参数进行调整。
一种巴特沃斯低通滤波器构成的PWM转DAC设计

一种巴特沃斯低通滤波器构成的P WM 转D A C设计*龙顺宇,何程,杨伟,吴建奇(海南热带海洋学院海洋信息工程学院,三亚572022)*基金项目:海南省2020年教育发展专项资金项目(H n j g202091);海南热带海洋学院2020年校级教育教学改革研究项目(R H Y j gz d 202004);海南热带海洋学院2019年校级教改项目(R H Y J G 201908)㊂摘要:本文提出一种巴特沃斯有源低通滤波器构成的P WM 转D A C 设计,利用S T C 8单片机片内12位分辨率的P WM发生器产生了频率为10k H z ㊁占空比可变的P WM 信号㊂将信号送入巴特沃斯低通滤波器后,P WM 信号转换为直流电压,电压幅度与P WM 信号占空比呈正比变化,转换得到的直流电压纹波小于0.2m V ,转换分辨率可达1/12位㊂转换电路线性度较高㊁纹波小㊁谐波抑制比较高㊂相比于专用D A C 芯片或P A C 芯片而,该方案性价比高,可以适配于分辨率要求高㊁建立时间要求一般的应用场景㊂关键词:脉宽调制;数/模转换器;P A C 转换器;巴特沃斯滤波器中图分类号:T P 31 文献标识码:AP WM t o D A C D e s i g n C o m p o s e d o f B u t t e r w o r t h L o w -pa s s F i l t e r L o n g S h u n y u ,H e C h e n g ,Y a n g W e i ,W u J i a n qi (C o l l e g e o f O c e a n o g r a p h i c I n f o r m a t i o n E n g i n e e r i n g ,H a i n a n T r o p i c a l O c e a n U n i v e r s i t y ,S a n ya 572022,C h i n a )Ab s t r ac t :I n t h e p a p e r ,a P WM t o D A Cde s i g n i s p r o p o s e d ,w h i c h i s c o m p o s e d of B u t t e r w o r t h a c t i v e l o w -pa s s f i l t e r .I t u s e s t h e 12b i t r e s -o l u t i o n P WM g e n e r a t o r o n t h e S T C 8m ic r o c o n t r o l l e r t o g e n e r a t e a P WM s i g n a l w i t h a f r e q u e n c y o f 10k H z a nd a v a r i a b le d u t y c yc l e .A f -t e r s e nd i n g t he s i g n a l t o t h e B u t t e r w o r t h l o w -p a s sf i l t e r ,t h e P WM s ig n a l i s c o n v e r t e d i n t o a D C v o l t a g e ,a n d th e v o l t a g e a m pl i t u d e c h a n -g e s i n p r o p o r t i o n t o t h e P WM s i g n a l d u t y c y c l e .T h e c o n v e r t e d D C v o l t a g e r i p pl e i s l e s s t h a n 0.2m V ,a n d t h e c o n v e r s i o n r e s o l u t i o n c a n r e a c h 1/12b i t .T h e c o n v e r s i o n c i r c u i t h a s h i g h l i n e a r i t y ,s m a l l r i p p l e a n d h i g h h a r m o n i c s u p p r e s s i o n .C o m pa r e d w i t h a d e d i c a t e d D A C c h i p o r a P A C c h i p ,t h i s s o l u t i o n i s c o s t -e f f e c t i v e a n d c a nb e a d a p t e d t o a p p l ic a t i o n s c e n a r i o s w i t h h i g h r e s o l u t i o n r e q u i r e m e n t s a nd ge n e r -a l s e t u p t i m e r e qu i r e m e n t s .K e yw o r d s :P WM ;D A C ;P A C c o n v e r t e r ;B u t t e r w o r t h f i l t e r 0 引 言通用型8位㊁16位㊁32位微控制器芯片中通常不带D A C 资源,无法凭借芯片自身实现数/模转换[1-2]㊂若需要程控输出高精度模拟电压,大多采用专用D A C 芯片,该类专用芯片在价格㊁分辨率㊁建立时间㊁内部结构㊁电压范围㊁输出通道数量及通信接口形式上存在较大差异,价格不低甚至超过了主控单片机的成本[3-4]㊂基于此类场景的实际需求,将P WM 信号转换为D A C 的方法得以广泛使用,只需将P WM 信号通过一阶R C 或L C 低通滤波器即可得到直流电压,此类电路虽然简单但转换质量不高,无源滤波形式下会严重影响D A C建立时间指标,导致输出信号滞后,线性度差[5-6]㊂故而本文改进了滤波器形式,选用M C P 6002运算放大器设计一种巴特沃斯低通滤波器,在此基础上采用了S T C 8增强型P WM 资源,对转换原理㊁过程㊁实现进行探究,使得系统指标满足一般场景的需求㊂1 P WM 转D A C 的基本原理以单极性P WM 信号为例,从时域上进行分析,该信号的周期保持固定,只是高/低电平所占的脉宽(即占空比)发生了改变,理论研究时可以将P WM 信号进行时域分解,变成一个直流分量加平均幅值为零的方波形式,直流分量幅值与占空比呈正比变化[7-8]㊂若占空比变化,则直流分量也会跟随改变,若在P WM 输出后级连接低通滤波器就可以衰减交流成分,得到幅值随占空比变化而变化的模拟电压,虽然交流成分不可能完全去除,但得到的模拟电压已经较为平滑,其转换过程如图1所示㊂若从频域理解P WM 信号,可以结合傅里叶级数的相关方法㊂将周期不变㊁占空比变动的P WM 信号进行分图1 P WM 转D A C 基本原理解,可以将其看作是基波频率和无限多个整数倍谐波的总和,信号函数f (t)级数展开之后有:f (t )=U 0+ðɕn =1U n ˑc o s 2πn t T+V n ˑs i n 2πn t T(1) 式中,U 0为PWM 信号的直流分量,数值等于P WM 信号的实际幅度与占空比的积:U 0=12T ʏT-Tf (t )d t (2) 式中,U n 和V n 就是PWM 信号的交流分量,数值等于P WM 信号的载波频率乘以整数倍之后的高频谐波,可以将其表达为:U n =12T ʏT-T f (t )c o s 2πn tTd t (3)V n=12TʏT-T f (t )s i n 2πn tT d t (4) 设U m 代表P WM 信号的幅度,D 为P WM 信号的占空比,代入式(2)~式(4),可以得到此时P WM 信号的直流分量U 0为:U 0=U m ˑD(5) 此时P WM 信号的交流分量U n 和V n 为:U n =U m ˑ1n πs i n (n πD )-si n2n π1-D2(6)V n =0(7) 式(5)和式(6)中的D 必须合理取值,只有在合适的占空比范围内才能得到细分电压,U n 和V n 是P WM 信号的整数倍正弦高次谐波,对于输出的模拟电压而言是应该去除的成分,所以应用中需要设计低通滤波器(L P F ),L P F 尽可能衰减谐波导致的纹波,只保留直流分量,即P WM 转换后输出电压U D A C 应该为:U D A C =U m ˑD(8)2 硬件L P F 单元设计将P WM 信号转换为D A C 本质就是尽可能地去除交流分量,处理得到的直流分量部分与占空比大小呈正比变化,这样就能用P WM 信号占空比调节间接得到直流电压的幅度调节,最终实现P A C 转换(即P WM 到D A C 的转换)㊂通常情况下,硬件采用一阶或多阶R C ㊁L C 低通滤波器,此类无源滤波电路较为简单,但输出阻抗较大,对于多阶的组成形式而言阻抗更大,P WM 信号虽然可以得到处理,但是输出的直流电压带载能力大大降低,很容易被拉低幅值,影响使用㊂而用运算放大器构成的L P F 有很大改善,不存在负载驱动问题,还可以方便地扩展为多阶滤波形式,其线性度㊁频幅特性以及抗干扰性都更好㊂在设计具体硬件滤波器之前需确定相关参数,设定供电电压U m 为5V ,即P WM 信号高电平幅值为5V ,低电平为0V ㊂实验中单片机系统时钟为27MH z ,P WM 信号输出分辨率为12位,若要求输出电压精度为12位,则P WM 信号的输出频率应配置为单片机系统时钟除以输出电压精度再除以2分频系数,即27MH z /212/2=3.3k H z ㊂然后根据傅里叶级数计算L P F 所需的衰减倍数,当P WM 信号占空比D 为0.5时,基波的幅度U 0最大,此时L P F 能将基波以上的多次谐波幅度衰减至1/2个L S B 以下㊂在P WM 信号的交流分量中,n =1时的基波频率最低,将n =1代入式(6),可得基波幅度:U n =1=2ˑU m π=2ˑ5π=3.18309886V ʈ3.1831V (9) 则L P F 所需的最低衰减倍数U f 为:U f =12ˑU m 212ˑ1U n =1=52ˑ4096ˑ3.1831=0.0001917(10) 结合式(9)和式(10)可知,输出12位精度的直流电压时,L P F 衰减倍数U f 应为0.0001917,约-74.34d B ㊂从理论上计算至少需要4阶L P F 单元,可采用两级两阶巴特沃斯L P F 滤波器级联得到㊂按照相关计算在L T s pi c e 软件中进行电路仿真,取交流1V ㊁相位0ʎ㊁10H z~10k H z 扫描频率范围,得到的频率响应如图2所示,在3.3k H z 处的衰减约为-81d B ,满足大于-74.34d B 的需求,这样就可以留有一些裕量去衰减高频谐波,输出相位滞后于输入P WM 信号相位约400ʎ,因输出信号为直流电压,故相位滞后不产生实际影响㊂得到必要的参数后即可设计硬件电路,综合考虑运算放大器带宽㊁成本及电路复杂度之后,实际使用了一级三阶巴特沃斯L P F 滤波器构成所需电路,电路原理如图3所示㊂电路由单5V 供电,P WM _I N 为P WM 信号输入端子(由S T C 8产生),经施密特触发器74L V C 1G 14芯片整形㊁去毛刺之后送入由M C P 6002运放构成的三阶巴特沃斯L P F 滤波器,最后得到的D C _O U T 端子即为输出电压㊂3 系统软件设计实验中选取S T C 8A 8K 64S 4A 12产生了频率为图2 两级两阶巴特沃斯L P F滤波器频率响应图3 三阶巴特沃斯低通L P F 滤波器电路原理图10k H z ㊁分辨位数12位㊁占空比可在0至100%变化的P WM 信号㊂因设计具有通用性,单片机的选择并无特殊要求,有的单片机具备高级定时/计数器单元㊁P C A 单元或者增强型P WM 发生器,产生的P WM 信号支持4㊁6㊁8㊁12㊁16乃至32位(如意法半导体公司生产的S TM 32F 334可产生32位分辨率高精度P WM 信号),此类微控制器产生的P WM 信号就更加细分,从原理上分析,转换后的D A C 精度会更高,但在实际应用中也要考虑运放性能㊁干扰等实际原因,从而进行合理选择㊂为了方便控制P WM 输出脉宽,单片机系统中分配3个I /O 口用作P WM 信号输出使能(K 1按键)㊁P WM 信号脉宽增加(K 2按键)㊁P WM 信号脉宽减小(K 3按键),其软件流程如图4所示㊂当K 1按键按下时,单片机使能P WM 信号输出,所得P WM 占空比默认为50%,在此基础上按下K 2或K 3按键即可分别控制脉宽的增加或减小,P WM 配置部分源码如下:v o i d m a i n (){ //主函数 P _S W 2=0x 80;//访问扩展寄存器P WM C K S =0x 00;//系统时钟图4 软件控制P WM 调整流程图 P WM C =0x 0400;//设置P WM 周期 P WM 0C R=0x 80;//使能P WM 输出 P _S W 2=0x 00;//关闭访问扩展寄存器P WM C R=0x C 0; //启动P WM 模块 W h i l e (1){K E Y _I n i t();}//循环按键处理}4 系统测试与分析按照图4所示硬件电路原理图绘制P C B并打样贴片后可以得到实物样式如图5所示,由于M C P 6002芯片内部自带两个运算放大器单元,为此做了图5 设计实物样式双通道P WM 信号转D A C 单元㊂模块实物做好后用锂电池组为其供电,实测供电电压为4.8V ,然后将S T C 8A 8K 64S 4A 12产生的P WM 信号送入模块相关端子并测量输出电压,P WM 信号占空比与输出电压的实测数据如表1所列㊂从数据误差上看,转换后的D A C 线性度优于1%㊂该模块参数与12位精度的专用P A C 芯片G P 8500(即客益电子生产的P WM 信号转换为D A C 的专用芯片)以及专用的D A C 芯片T L C 5618(即T I 公司生产的12位D A C )做了指标对比,结果如表2所列㊂表1P WM信号占空比及输出电压数据表表2三种不同方案的D A C指标对比指标项P WM转D A C模块(本设计)G P8500芯片(P A C专用芯片)T L C5618芯片(D A C专用芯片)P WM信号频率10H z~300k H z50H z~50k H z-P WM信号占空比0~100%0~100%-建立时间4~10m s<20μs<2.5μs分辨率约12位12位12位从指标项的对比结果看,本设计中的P WM信号转D A C模块在分辨率上接近于专用芯片,性价比也有明显优势,但在D A C的建立时间指标项上还是相对较慢,比较适合做低速非隔离型D A C应用㊂5结语本设计作为单片机类电子工艺实训项目在实际实验中取得了较好的效果,在实测中发现了P WM信号载波频率及谐波分量会影响D A C的分辨率,若贸然降低P WM信号的载波频率,则基波频率和谐波频率也会发生变化㊂应先确定L P F参数,再考虑P WM信号配置,合理设计L P F结构才能达到指标要求㊂L P F阶数会影响D A C建立时间参数及输出线性度,因此需要根据实际需求进行设计适配㊂参考文献[1]吴财源,周华,钟球盛,等.基于双通信的多通道P WM式D A C模块设计[J].机电工程技术,2017,46(6):710.[2]陈启武,吴新春,王飞.基于S TM32的P WM D A C实现精密程控电压源的设计[J].今日电子,2016(6):5457.[3]游乙龙.基于单片机的P WM转D A C实现通用变频器的自动控制[J].机电工程技术,2015,44(6):9092.[4]赵月丽.P WM模拟D A C的关键参数分析[J].微型机与应用,2014,33(18):2022.[5]吴桂清,李泓霖,戴瑜兴,等.微控制器P WM接口实现高分辨率D/A转换器方法研究[J].电子学报,2012,40(8):16311634.[6]辛德环.传统数模转换器的优缺点分析及高性能P WMD A C的基本设计思想[J].机械工程师,2011(10):2933.[7]W S t e p h e n W o o d w a r d.几乎没有纹波的快速稳定同步P WM D A C滤波器[J].电子设计技术,2008(8):101.[8]秦健.一种基于P WM的电压输出D A C电路设计[J].现代电子技术,2004(14):8183.龙顺宇(实验师),主要研究方向为嵌入式应用㊁单片机智能㊁物联网技术应用㊂通信作者:龙顺宇,t l o n g s y@163.c o m㊂(责任编辑:薛士然收稿日期:2020-11-02)4结语为提高工地信息化管理水平,降低安全生产施工发生率,依托于智慧工地建设理念开展了基于人脸识别和检测的工地管理系统平台研究㊂智慧工地系统平台应紧密结合工程实际操作流程,尽量减少人工干预的可能性;同时,人脸识别数据采集应智能化,并且集成自动分析㊁自动记录功能㊁证据备份和检索功能㊂参考文献[1]吉林省住房和城乡建设厅关于推进智慧工地建设的指导意见[J].北方建筑,2020,5(5):8182.[2]王瑜,叶子明.基于B I M技术的智慧工地平台方案架构探讨[J].江西建材,2020(9):181182.[3]樊则森.建筑工业化与智能建造融合发展的几点思考[J].中国勘察设计,2020(9):2527.[4]谢佳霓,黄玉贤,沈玉香.智慧工地平台管控中B I M技术的应用研究[J].低温建筑技术,2020,42(8):124126.[5]黄凯,张梅,王涛,等.大型综合体项目智慧工地信息化平台建设关键技术[J].施工技术,2020,49(16):3639.[6]杜黎明,王燃.物联网技术在智慧工地中的应用研究[J].核动力工程,2020,41(S1):9295.[7]王淮.5G与人工智能在航道建设智慧监管上的应用[J].珠江水运,2020(15):1516.[8]王秋茗,孙广玲,陆小锋,等.智慧工地中低分辨率的安全帽状态识别[J].电子测量技术,2020,43(15):6367.[9]陈巨坤.智慧工地中的智能安全帽及其管理平台研究[D].广州:华南理工大学,2019.[10]董荣.基于智慧工地理念的塔机租赁公司定制化E R P设计[D].北京:中国矿业大学,2019.李建奎㊁陈阳㊁黄小星(工程师),李辉(助理工程师):主要研究方向为建筑工程项目管理㊂通信作者:李建奎,t k j g j i h d u9852@163.c o m㊂(责任编辑:薛士然收稿日期:2020-10-29)。
巴特沃斯低通滤波器公式 巴特沃斯低通滤波器设计原理

巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
关于“巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理”的详细说明。
1.巴特沃斯低通滤波器公式
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:
其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
2.巴特沃斯低通滤波器设计原理
巴特沃斯型低通滤波器在现代设计方法设计的滤波器中,是最为有名的滤波器,由于它设计简单,性能方面又没有明显的缺点,又因它对构成滤波器的元件Q值较低,因而易于制作且达到设计性能,因而得到了广泛应用。
其中,巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。
滤波器的截止频率的变换是通过先求出待设计滤波器的截止频率与基准滤波器的截止频率的比值M,再用这个M去除滤波器中的所有元件值来实现的,其计算公式如下:M=待设计滤波器的截止频率/基准滤波器的截止频率。
滤波器的特征阻抗的变换是通过先求出待设计滤波器的特征阻抗与基准滤波器的特征阻抗的比值K,再用这个K去乘基准滤波器中的所有电感元件值和用这个K去除基准滤波器中的
所有电容元件值来实现的。
巴特沃斯数字低通滤波器的设计课题论文

电子技术课程设计----巴特沃斯数字低通滤波器的设计专业年级:姓名:学号:指导教师:日期:巴特沃斯数字低通滤波器的设计一、选题依据滤波器是能够过滤波动信号的电路, 它可以从具有各种不同频率成分的信号中, 取出具有特定频率成分的信号。
滤波器在信号处理、数据采集和传输、干扰抑制方面应用非常广泛, 其性能优劣直接影响整个系统的性能, 所以滤波器的设计在很多领域必不可少, 而且至关重要。
由于理想滤波器的特性难以实现, 在设计滤波器时关键是选择一个合适的逼近函数, 使其频率特性满足所需滤波器的所有要求。
目前比较成熟的逼近函数有巴特沃斯、切比雪夫、椭圆函数和贝塞尔滤等。
但是无论用哪种逼近函数设计滤波器都要经过繁琐的计算, 而且通过综合设计确定实现这个传递函数的电路及其元器件的方法也很复杂。
本文介绍了一种利用归一化表经过简单的计算就可以快速设计滤波器的方法。
模拟滤波器可以分为有源滤波和无源滤波两大类, 其中有源滤波器是由R、C 元件和OP 放大器构成。
与无源滤波器相比, 它具有易集成、易标准化、易制造、输出电阻低且不受负载影响, 体积小等优点。
因此得到了更加广泛的应用。
目前可实现的滤波器中巴特沃斯滤波器具有通带内响应平坦, 衰减特性和相位特性好, 对构成滤波器的器件的要求不甚严格, 易于得到符合设计值的特性, 适应性强, 在不知道使用哪种函数合适的情况下, 可以选择巴特沃斯型滤波器, 本文设计的就是巴特沃斯低通滤波器。
滤波器从广义上来说对特定的频点或频点以外的频率进行有效滤波的电路,这种电路保留输入信号中的有用信息,滤除不需要的信息,从而达到信号的检测、提取、识别等不同的目的。
如果处理的信号是时域离散信号,那么相应的处理系统就称为数字滤波器,由于在实际工作中被处理的信号都是幅度量化的数字信号,因此,数字滤波器实际上是用有限精度的算法实现一个线性时不变的时域离散系统。
目前,数字滤波器的应用越来越广泛,它已深入到很多领域,如图象处理、医学生物信息处理、地质信号处理和模式识别处理等。
巴特沃兹有源低通滤波器设计
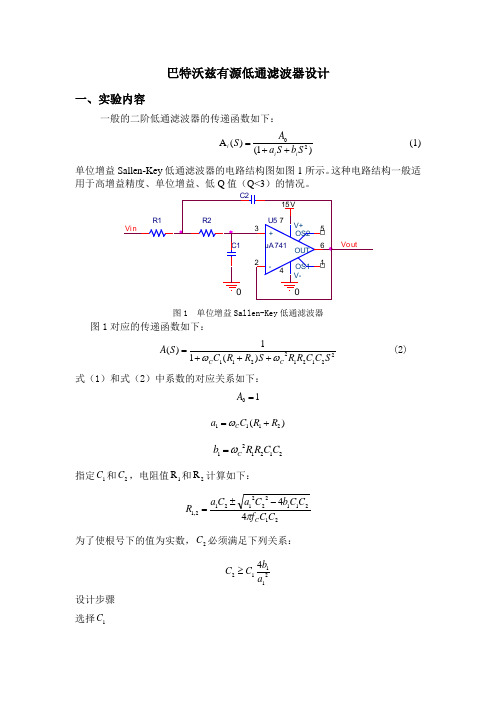
巴特沃兹有源低通滤波器设计一、实验内容一般的二阶低通滤波器的传递函数如下:)1()(A 2S b S a A S i i i ++=(1) 单位增益Sallen-Key 低通滤波器的电路结构图如图1所示。
这种电路结构一般适用于高增益精度、单位增益、低Q 值(Q<3)的情况。
图1 单位增益Sallen-Key 低通滤波器图1对应的传递函数如下: 221212211)(11)(SC C R R S R R C S A C C ωω+++=(2) 式(1)和式(2)中系数的对应关系如下:10=A )(2111R R C a C +=ω212121C C R R b C ω=指定1C 和2C ,电阻值1R 和2R 计算如下:212112221212,144C C f C C b C a C a R C π-±=为了使根号下的值为实数,2C 必须满足下列关系:211124a b C C ≥ 设计步骤 选择1C计算212⨯=C C 计算1R 和2R :Cf C ⨯⨯⨯1221π选择1C C C OUT IN ==的100~1000倍VinVout图2 低通滤波器所选的滤波器是一个具有巴特沃兹响应的单位增益Sallen-Key 低通滤波器。
注意在增加IN C 和OUT C 后,滤波器不再是纯粹的低通滤波器,而是一个宽带通滤波器;但是通过选择IN C 和OUT C 的容量,滤波器的高通频率可以远低于关心的频率区域。
如果需要直流响应,电路应当更改为双电源工作。
2.1频率特性巴特沃斯低通滤波器的幅频特性为:nc uou A j A 211)(⎪⎪⎭⎫ ⎝⎛+=ωωω (1)其中Auo 为通带内的电压放大倍数,ωC 为截止角频率,n 称为滤波器的阶。
从(1)式中可知,当ω=0时,(1)式有最大值1;ω=ωC 时,(1)式等于0.707,即Au 衰减了 3dB ;n 取得越大,随着ω的增加,滤波器的输出电压衰减越快,滤波器的幅频特性 越接近于理想特性。
五阶巴特沃斯有源低通滤波器的设计

五阶巴特沃斯有源低通滤波器的设计
文⊙ 谭红君(四川工程职业技术学院)
有 源 滤 波 器 为 广 泛 的 应 用 领 域 提 供 了 (2 )式中可知,当 = 0 时, )式有最大 (2 轻巧的信号处理部件。例如在通讯、遥测、 值 1 ; = C 时, )式等于 0 . 7 0 7 ,即 (2 生 物 电 子 学 、雷 达 、声 纳 和 地 震 分 析 等 领 A u 衰减了 3 d B ;n 取得越大,随着 的增 域内进行声频和视频信号处理。 加,滤波器的输出电压衰减越快,滤波器 在有源滤波器设计中,一般来说,采 的幅频特性越接近于理想特性。 用 有 源 R C 电 路 ,可 有 两 种 方 法 实 现 转 移 函数,第一种方法为级联法。这种方法,首 先是把要实现的转移函数分解成一阶与 / 当 >> C 时, (3 ) 或 二 阶 项 的 乘 积 ,然 后 每 一 项 分 别 由 一 有 源 R C 电 路 实 现 ,最 后 再 把 各 个 实 现 级 联 起 来 以 实 现 总 的 转 移 函 数 。第 二 种 方 法 称 两边取对数,得: 为 直 接 法 ,即 用 一 个 单 一 电 路 来 实 现 总 的 转 移 函 数 。本 文 将 介 绍 采 用 级 联 法 设 计 滤 (4) 波 器 的 方 法 以 及 需 要 注 意 的 问 题 ,而 且 实 例运用级联法设计了一个巴特沃斯高阶低 表 1 列出了归一化的、n 为 1 ~8 阶的 通滤波器,使用 M u l t i s i m 仿真验证设计指 巴特沃斯低通滤波器传递函数的分母多项 标。 式。 一、高阶有源滤波器设计方法和设计 步骤 所谓高阶滤波器,我们是指阶次大于 或等于 4 的滤波器。 如前所述,实现高阶滤波器的方法也 可 以 采 用 直 接 综 合 法 和 级 联 法 ,但 应 用 最 广 的 是 级 联 法 。我 们 知 道 一 个 高 阶 的 转 移 函数 T(s), 根据阻带衰减速率要求,确定滤波器 的阶数 n 。 选择具体的电路形式。 根 据 电 路 的 传 递 函 数 和 表 1 归一化滤 波 器 传 递 函 数 的 分 母 多 项 式 ,建 立 起 系 数 的方程组。 解方程组求出电路中元件的具体数 值。 运用计算机仿真软件进行仿真,使电 路的性能满足指标要求。 对于有源滤波器而言,其动态范围是 其 最 大 的 一 个 问 题 ,所 以 在 设 计 中 注 意 动 态 范 围 非 常 重 要 。在 用 级 联 法 实 现 转 移 函 数 时 ,我 们 一 定 要 保 证 滤 波 器 的 动 态 范 围 最 大 、同 时 通 带 内 损 失 最 小 。也 就 是 要 保 证 最 适 当 的 零 极 点 组 合 方 式 、最 适 当 的 各 节增益系数、最适当的链接顺序。 二、设计实例 要 求 设 计 一 个 有 源 低 通 滤 波 器 ,指标 为: 截止频率 f C =10kHz , 通带电压放大倍数:A u o = 1 , 在 f = 5 f c 时,要求幅度衰减大于 60dB 。 本 例 中 采 用 巴 特 沃 斯 低 通 滤 波 器 ,首 先需确定阶数 n : 根据巴特沃斯低通滤波器的幅频特性 公式(1 ) ,设计要求在 f = 5 f c 时,要求幅 度衰减大于 60dB ,即 2 0 <60
低通滤波器论文报告

目录引言 (1)一设计任务和要求 (1)1.1设计任务 (1)1.2设计要求 (1)二滤波器的设计原理依据及元器件的选择 (1)2.1滤波器的介绍 (1)2.2 有源滤波器的设计 (2)2.3滤波器类型及阶数的选择 (2)2.4 Ua741的封装介绍 (5)三multisim辅助设计及修正 (6)结束语 (7)引言课程设计是理论联系实际的重要实践教学环节,是对学生进行的一次综合性专业设计训练。
本次课程设计意在培养学生正确的设计思想方法以及思路,理论联系实际的工作作风,严肃认真、实事求是的科学态度,培养学生综合运用所学知识与生产实践经验,分析和解决工程技术问题的能力。
作为一名大学生不仅需要扎实的理论知识,还需要过硬的动手能力,所以认真做好课程设计,对提高我们的动手能力有很大的帮助做到。
一设计任务和要求1.1设计任务设计一个有源低通滤波器。
1.2设计要求(1)截止频率fc=3KHz;(2)增益Av=1;(3)阻带衰减速率大于等于40dB/10倍频程;(4)调整并记录滤波器的性能参数及幅频特性。
二滤波器的设计原理依据及元器件的选择2.1滤波器的介绍滤波器是一种用来消除干扰杂讯的器件,将输入或输出经过过滤而得到纯净的直流电。
对特定频率的频点或该频点以外的频率进行有效滤除的电路,就是滤波器,其功能就是得到一个特定频率或消除一个特定频率。
滤波器分为无源滤波器与有源滤波器两种:①无源滤波器:由电感L、电容C及电阻R等无源元件组成②有源滤波器:一般由集成运放与RC 网络构成,它具有体积小、性能稳定等优点,同时,由于集成运放的增益和输入阻抗都很高,输出阻抗很低,故有源滤波器还兼有放大与缓冲作用。
利用有源滤波器可以突出有用频率的信号,衰减无用频率的信号,抑制干扰和噪声,以达到提高信噪比或选频的目的,因而有源滤波器被广泛应用于通信、测量及控制技术中的小信号处理。
低通滤波器是一个通过低频信号而衰减或抑制高频信号的部件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展,各种科技产品在人类社会中随处可见,极大的丰富了人们的日常生活。
物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。
就目前而言,在几乎所有的电子产品中,各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用,例如可穿戴设备的语音信号输入系统中,运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除,来提高系统的音质和语音识别精准度等。
本论文通过对各种低通滤波器的通频带、增益和截止频率的分析,采用通频带最大扁平度技术(巴特沃斯技术)来设计实现四阶高性能低通滤波器,通过Multisum仿真软件,验证了设计的正确性。
在这基础上,本文还对如何提高该滤波器的响应速度进行了研究,提出了一种有效的提高响应速度的方案,并通过仿真软件得以验证。
这在低通滤波器的理论以及实际工程应用中,都具有非常重要的意义。
关键词:有源低通滤波器,巴特沃斯,运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS:active low-pass filter,butterworth,amplifier1绪论1.1 引言在近现代的科技发展中,滤波器作为一种必不可少的组成成分,在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。
滤波器作为一门学科已经有了仅一百年的历史了,自从德国的Wagner和美国的Campbell在1915年提出了滤波器的概念至今,它经历了由简单到复杂,由分立器件到单片集成,由有源到无源,由模拟到数字的发展历程[1]。
1.2 滤波器的发展历程及研究现状早期的滤波器基本上是由分立器件电感、电阻、电容等无源器件搭建而成,这就是最原始的无源滤波器。
最常应用的就是LC梯形无源滤波,因为它的性能对元器件的变化不太敏感。
并且LC无源滤波器还存在着体积大、Q值低、重量大和无法集成等缺点。
自60年代起由于计算机技术、集成电路技术和半导体材料技术的迅速发展,滤波器的发展上了一个新的台阶,并且朝着低功耗、高精度、小体积、多功能、稳定可靠和价廉方向努力,其中小体积、多功能、高精度、稳定可靠已经成为了70年代以后的主攻方向,导致RC 有源滤波器、数字滤波器、开关电容滤波器和电荷转移器等各种滤波器的飞速发展。
到70年代后期,上述几种滤波器的单片集成已被研制出来并得到应用[2]。
80年代,致力于各类新型滤波器的研究,努力提高性能并逐渐扩大应用范围。
90年代至今主要致力于把各类滤波器应用于各类产品的开发和研制。
当然,对滤波器本身的研究仍在不断进行,对高性能低通滤波器的研究和生产历来为各国所重视,一直是国内外研究热门之一,特别是研究采用开关技术实现的高性能低通滤波器,研究的滤波级数越来越高,10级、12级等高级别开关电容低通滤波器不断涌现[3]。
我国广泛使用滤波器是50 年代后期的事,当时主要用于话路滤波和报路滤波。
经过半个世纪的发展,我国滤波器在研制、生产和应用等方面已纳入国际发展步伐,但由于缺少专门研制机构,集成工艺和材料工业跟不上来,使得我国许多新型滤波器的研制应用及集成化与国际发展有一段距离。
1.3 选题背景及研究意义通过前面的论述可以清楚的看到,在长期的发展中,滤波器技术已经奠定了其在信息处理等领域无法替代的地位。
然而在许多的实际生产生活和科研等应用场合,需要采用低通滤波器来运载信息。
低通滤波器被广泛地应用于噪声情况下的低频信号的提取与抗干扰设计,无源滤波器也有着其固有的缺点,难以集成、器件容易老化、无法满足不同的工程需求等。
但是随着集成工艺和半导体技术的发展,通信设备日益小型化,各种无感滤波器相继问世,其中最具代表性的就是有源滤波器,其最大值可以高达1000,最高频率可达MHz数量级[4]。
目前采用的直接综合,多级级联,多环反馈等方法实现的有源滤波器,由于直接串联在信道中,无一例外地会在信道中引入由有源器件而产生的附加漂移。
在海洋监测,生物医学和电化学等领域的低频微弱信号传感和监测系统和高精度仪器仪表中,系统的灵敏度常达到uV和nV级别,这时附加漂移是同噪声一样严重的问题[5]。
为抑制噪声的同时又不引起新的附加漂移问题,对于滤波系统使用的放大器必然提出非常苟刻的要求,有时甚至是不可实现的。
因此本文就这一问题,提出了一种面向高精度传感与检测系统的无信道附加漂移的有源低通滤波系统。
对于低通滤波器而言,滤波器的频带越窄,滤除噪声的能力也就越强,但是滤波器的阶跃响应时间相应的变长,即阶跃信号通过滤波器输出达到稳定状态所需要的时问变长。
然而有一些应用场合,既需要低漂移高精度的窄带低通滤波器,也需要该滤波器有尽可能快的阶跃响应速度,即要具有好的实时性[6]。
本文在提出了一种低漂移窄带低通有源滤波系统之后,研究了如何提高该滤波器的阶跃响应速度,一方面,具有一定的实际工程应用价值;另一方面,这对于创新滤波器理论和抗干扰设计方法都具有普遍的意义。
2滤波器理论基础2.1 滤波器简介滤波,本质上是从被噪声畸变和污染了的信号中提取原始信号所携带的信息的过程。
滤波器是一种能使一定频率范围内的信号顺利通过,而使其他频率的信号受到较大的衰减的电路,主要用于滤除干扰信号[7]。
一般在微弱信号放大的同时附加滤波功能或在信号采样前使用滤波器。
2.2 滤波器的分类2.2.1 按所处理的信号按照所处理的信号不同可以分为模拟滤波器和数字滤波器。
利用模拟电路直接对模拟信号进行处理则构成模拟滤波器。
模拟滤波器可以分成两大类即无源滤波器和有源滤波器。
从20世纪20年代到20世纪60年代末,许多滤波器是由无源元件如电阻、电容和电感组成。
而其中的无源LC梯形网络是一种非常有用的结构,因为它对元件的变化不太敏感。
20世纪50年代人们发现,用有源电路来代替体积大而且价格昂贵的电感可以大大地减小电路的尺寸和降低电路的成本。
20世纪60年代中期高质量的有源器件如运算放大器开始出现。
20世纪70年代中期有源滤波器开始流行,人们开始考虑将滤波器进行集成。
在最近二十年,有源集成滤波器在信号处理应用中幵始变得越来越重要。
在这样的电路中,有源器件是单片集成的。
与由分立有源元件构成的滤波器相比,这些卑片集成电路有着许多优点,减少了系统中元件的数目,由于芯片上元件的良好匹配性使得滤波器的设计简化了不少。
此外,自动调谐电路能够减少工艺和温度变化所带来的误差,与分立无源滤波器相比,集成滤波器大大地减少了寄生电容。
数字滤波器是对数字信号进行滤波处理以得到期望的响应特性的离散时系统。
与模拟滤波器相比较,数字滤波器在体积、重量、精度、稳定性、可靠性、存储功能、灵活性以及性能价格比等方面都显示明显的优点。
模拟滤波器完全工作在模拟信号域,而数字滤波器工作在数字信号域,它处理的对象是经由采样器件将模拟信号转换而得到的数字信号。
数字滤波器除了可以利用硬件电路实现之外,还可以借助计算机以软件编程方式实现,无论哪种方法,数字滤波器实现的基本考虑有两点:1、把数字滤波器的输入输出关系转换成一种算法。
2、用一组基本运算或数字硬件(延时器,相加器和乘法器)来实现这种算法。
随着技术的进步与发展,数字滤波器的性能不断提升,成本逐渐下降,其应用的领域也不断拓宽。
按照数字滤波器的特性,它可以被分为线性与非线性、因果与非因果、无限脉冲响应(IIR)与有限脉冲响应(FIR)等等。
