大学物理课件第三章2
合集下载
大学物理-第3章-静电场中的导体

R2 R1
在金属球壳与导体球之间(r0 < r < R1时):
q r0
作过 r 处的高斯面S1
q
S1 E2 dS 0
得
E2 r
q
40r 2
q
E2 40r 2 er
在金属球壳内(R1< r < R2时):电场 E3 0
在金属球壳外( r > R2时): 作过 r 处的高斯面 S 2
S2
E4
dS
在它形成的电场中平行放置一无限大金属平板。求:
金属板两个表面的电荷面密度?
解:带电平面面电荷密度0 ,导体两面感应电荷面密度分 别为1 和 2,由电荷守恒有
1 2 0 (1)
导体内场强为零(三层电荷产生)
σ0 σ1
σ2
E0 E1 E2 0
(2)
E0
0 1 2 0
(3)
20 20 20
导体表面任一点的电场强度都与导体表面垂 直。
20
2.导体在静电平衡状态下 的一些特殊性质
❖ 导体是等势体,导体表面是等势面。
在导体内部任取两点P和Q,它们之间的电势差可以表示为
VP VQ
Q
E
dl
0
P
❖ 导体表面的电场强度方向与导体的表面相垂直。
❖ 导体上感应电荷对原来的外加电场施加影响,改
Q1
Q2
0
q
q
0
得
E4r
q
4 0 r 2
E4
q
4 0 r 2
er
43
思考:(3)金属球壳和金属球的电势各 为多少?
解:设金属球壳的电势为U壳 ,则:
U壳
R2 E4 dl
大学物理课件3章第二讲

容,解释电阻的定义和计算方法,以及电阻
率的概念和应用。
电源与电动势
03
讲解电源的作用和分类,电动势的定义和物理意义,以及闭合
电路欧姆定律的内容和应用。
磁场与电磁感应
1 2
磁场与磁感线
介绍磁场的形成和描述方式,磁感线的绘制方法 和物理意义,以及磁场强度和磁通量的概念。
势能
物体由于位置或状态而具有的能量,如重力势能、弹性 势能等。
ABCD
动能
物体由于运动而具有的能量,与物体的质量和速度平方 成正比。
机械能守恒定律
在只有重力或弹力做功的物体系统内,动能与势能可以 相互转化,而总的机械能保持不变。
03 振动与波动
简谐振动
简谐振动的定义
物体在一定位置附近所做的往复运动,如果回复力与位移成正比且方向相反,则称这种振 动为简谐振动。
机械波的产生与传播
机械波的产生
机械波是由物体振动产生的,振动的物体称为波源。波源振动时,会使其周围的介质产生周期性的压缩和稀疏,从而 形成机械波。
机械波的传播
机械波在介质中传播时,介质中的质点并不随波迁移,而是在各自平衡位置附近做振动。波的传播方向与质点的振动 方向垂直的波称为横波,波的传播方向与质点的振动方向平行的波称为纵波。
安培环路定理与磁矩
阐述安培环路定理的内容,解释磁矩的定义和计 算方法,以及磁场对电流的作用力情况。
3
法拉第电磁感应定律
讲解法拉第电磁感应定律的内容和应用,感应电 动势的计算方法,以及楞次定律的内容和应用。
06 光学基础
光的干涉
干涉现象
两列或多列相干光波在空间某些区域相遇时,光强在空间作周期 性变化的现象。
波在传播过程中遇到障碍物或孔时, 会绕过障碍物或穿过孔继续传播的现 象称为波的衍射。衍射现象表明波具 有绕过障碍物继续传播的能力,这是 波动性的重要表现之一。
率的概念和应用。
电源与电动势
03
讲解电源的作用和分类,电动势的定义和物理意义,以及闭合
电路欧姆定律的内容和应用。
磁场与电磁感应
1 2
磁场与磁感线
介绍磁场的形成和描述方式,磁感线的绘制方法 和物理意义,以及磁场强度和磁通量的概念。
势能
物体由于位置或状态而具有的能量,如重力势能、弹性 势能等。
ABCD
动能
物体由于运动而具有的能量,与物体的质量和速度平方 成正比。
机械能守恒定律
在只有重力或弹力做功的物体系统内,动能与势能可以 相互转化,而总的机械能保持不变。
03 振动与波动
简谐振动
简谐振动的定义
物体在一定位置附近所做的往复运动,如果回复力与位移成正比且方向相反,则称这种振 动为简谐振动。
机械波的产生与传播
机械波的产生
机械波是由物体振动产生的,振动的物体称为波源。波源振动时,会使其周围的介质产生周期性的压缩和稀疏,从而 形成机械波。
机械波的传播
机械波在介质中传播时,介质中的质点并不随波迁移,而是在各自平衡位置附近做振动。波的传播方向与质点的振动 方向垂直的波称为横波,波的传播方向与质点的振动方向平行的波称为纵波。
安培环路定理与磁矩
阐述安培环路定理的内容,解释磁矩的定义和计 算方法,以及磁场对电流的作用力情况。
3
法拉第电磁感应定律
讲解法拉第电磁感应定律的内容和应用,感应电 动势的计算方法,以及楞次定律的内容和应用。
06 光学基础
光的干涉
干涉现象
两列或多列相干光波在空间某些区域相遇时,光强在空间作周期 性变化的现象。
波在传播过程中遇到障碍物或孔时, 会绕过障碍物或穿过孔继续传播的现 象称为波的衍射。衍射现象表明波具 有绕过障碍物继续传播的能力,这是 波动性的重要表现之一。
大学物理第三章2
1 2 2 mv ( e 1 ) 0 2
第三章动量守恒定律和能量守恒定律
3-5 保守力与非保守力 势能
一
m 以 m ' 为参考系, 的位置矢量为 r . m' 对 m 的万有引力为
m 'm F G 3 r r
万有引力、重力、弹性力作功的特点 1) 万有引力作功
b
2mg k R
B
Ep 0
所以
03-4 第三章动量守恒定律和能量守恒定律
例 如图所示,轻质弹簧劲度系数为 k,两端各固定一 质量均为M的物块A和B,放在水平光滑桌面上静止。 今有一质量为 m 的子弹沿弹簧的轴线方向以速度 0 射 入一物块而不复出,求此后弹簧的最大压缩长度。
解:第一阶段:子弹射入到相对静止于物块中。由于 时间极短,可认为物块还没有移动,应用动量守恒定 律,求得物块A的速度A 0
作定积分,得:
r
0
vd v ( ) d s
r
v 0
v
v ln r 即: v e v0 r v0
由质点的动能定理得:
故: v v 0e
1 2 1 2 1 2 2 2 m ( v e v A mv mv 0 0) 0 2 2 2
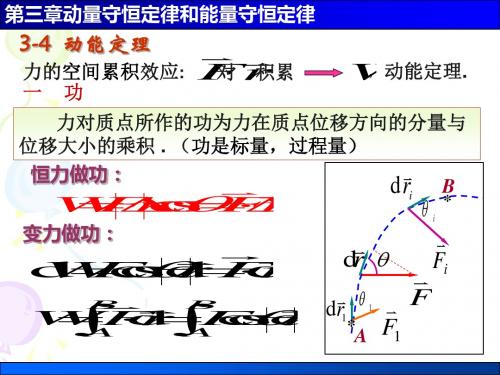
3-4 动能定理
一 功
力的空间累积效应: F 对r 积累
,动能定理. W
力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积 . (功是标量,过程量) 恒力做功: d ri B
W F r c o s F r
变力做功:
i
*
d W F c o sd r F d r
( M m ) m A 0
大学物理第三章刚体和流体运动

2
返回
退出
对刚体内各个质点的相应式子,相加得:
F r sin f
i i i i i
i i
r sin i ( mi ri )
2 i
对于成对的内力,对同一转轴的力矩之和为零,则:
f
i
i
ri sin i 0
2 i i i
F r sin ( m r
r
问题中包括平动和转动。
T1 m1 g m1a m2 g T2 m2a T2 r T1r M r J
轮不打滑: 联立方程,可解得 T1 ,T2,a, 。
此装置称阿特伍德机——可用于测量重力加速度 g
返回
退出
例3-4 一半径为R,质量为m匀质圆盘,平放在粗糙的 水平桌面上。设盘与桌面间摩擦系数为 ,令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转,问它 经过多少时间才停止转动? 解: 把圆盘分成许多环形 质元,每个质元的质量 dm=rddre , e 是 盘 的 厚 度,质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为:
刚体定轴转动的动能定理:总外力矩对刚体所做的功 等于刚体转动动能的增量。
返回
退出
四、刚体的重力势能 以地面为势能零点,刚体和地 球系统的重力势能:
z
i
O
返回
退出
例3-5 一质量为m ,长为 l 的均质细杆,转轴在O点, 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动,求(1)水平位置的角速度和角加速度。(2)垂直位 置时的角速度和角加速度。
第三章 刚体和流体的运动
§3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系
返回
退出
对刚体内各个质点的相应式子,相加得:
F r sin f
i i i i i
i i
r sin i ( mi ri )
2 i
对于成对的内力,对同一转轴的力矩之和为零,则:
f
i
i
ri sin i 0
2 i i i
F r sin ( m r
r
问题中包括平动和转动。
T1 m1 g m1a m2 g T2 m2a T2 r T1r M r J
轮不打滑: 联立方程,可解得 T1 ,T2,a, 。
此装置称阿特伍德机——可用于测量重力加速度 g
返回
退出
例3-4 一半径为R,质量为m匀质圆盘,平放在粗糙的 水平桌面上。设盘与桌面间摩擦系数为 ,令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转,问它 经过多少时间才停止转动? 解: 把圆盘分成许多环形 质元,每个质元的质量 dm=rddre , e 是 盘 的 厚 度,质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为:
刚体定轴转动的动能定理:总外力矩对刚体所做的功 等于刚体转动动能的增量。
返回
退出
四、刚体的重力势能 以地面为势能零点,刚体和地 球系统的重力势能:
z
i
O
返回
退出
例3-5 一质量为m ,长为 l 的均质细杆,转轴在O点, 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动,求(1)水平位置的角速度和角加速度。(2)垂直位 置时的角速度和角加速度。
第三章 刚体和流体的运动
§3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系
大学物理课件 第3章 动量 角动量

例 如图所示,一个有四分之一圆弧光滑槽的大物体,质量为 M, 置于 光滑的水平面上。另一质量为m的小物体从圆弧顶点由静止开始下滑。 求当小物体m滑到底时,M滑槽在水平上移动的距离。
解 以 M和 m 为研究对象,其在水平方向不受外力(所受外力都 在竖直方向),故水平方向动量守恒。
设在下滑过程中,m相对于M的滑动速度为m , M 对地速 度为 M ,并以水平方向右为正,则有
t
问题 结果与m与槽M间是否存在摩擦有关系吗?
3. 质心运动定理
C
mii mc m i 1 质点系的动量 p mc
i 1
m
n
rC
mi ri
n i 1
m
n
i i
质点系的动量等于质点系的质量乘以质心的速度。 注 质点系的动量的两种表达式
n p mii , p mc
pA m j ,
pB mi
y
B
I AB pB pA m (i j )
C
pC m j
o
A
x
I AC pC pA 2m j
质点的动量定理
例 一质量为10kg的物体沿x轴无摩擦地运动,设t=0时,物体 位于原点,速度为零。设物体在力(F=3+4t)N作用下运动了3秒, 求此时它的速度和加速度。 解
3.2
角动量定理 角动量守恒定律
3.2.1 质点的角动量定理及守恒定律
1. 力矩
讨论
力F 对定点O 的力矩 Mo F r F
单位:牛 米(N m)
(1)力矩的大小和方向
所组成的平面,指向是由 180 的角转到 F 时的右手螺旋前进的方向
①方向垂直于 r 和 F o
r 经小于
x 方向: m sin m0 sin 0 y 方向: ( f mg )t m cos m0 cos sin 由第一式 0 sin
大学物理学教案第三章 刚体和流体幻灯片PPT

[例2]求质量为m、半径为R、厚为l 的均匀圆盘的转动
惯量。轴与盘平面垂直并通过盘心。
解:取半径为r宽为dr的薄圆环,
dm 2πrdrl
d Jr2 d m 2 π l3 rd r l R
r dr
JdJ0R2πlr3dr
1 πR4l
2
m πR2l
J 1 mR2 2
可见,转动惯量与l 无关。所以,实心圆柱对其轴的 转动惯量也是 mR2/2。
解:分别对物体m和轮M看运动、
分析力,图中T1 用T表示。
和T2
大小相等,
定轴0
N
T2 T1
R
T1
α
T2
R
am
mg h
G T1
mg
动力学关系:
对M: TRJ1MR2 (1)
对m:
2 mgTma
(2)
运动学关系:
aR (3)
v 2ah (4)
联立以上四式,解得
a
m
m M
g
v 2ah 4mgh 2mM
W 1 2 M d 1 2 J d d td 1 2 Jd 1 2 J 2 2 1 2 J 1 2
即 WEK2EK 1 ┉┉定轴转动动能定理
定轴转动动能定理:合外力矩对一个绕固定轴转动的 刚体所做的功等于刚体的转动动能的增量。
➢ 刚体的重力势能
一个质元:mi ghi 整个刚体:
解:子弹和木棒组成的系统对轴O的 角动量守恒
1
m
0vl
m 4
0vl
Jω
M
其 中J 1 Ml2
3
3m
0vl
9m
0v
4J 4Ml
v0
mv
大学物理课件第3章-刚体

F
T
m
o
x
例4. 质量为M =16 kg的实心滑轮,半径为R = 0.15 m。 一根细绳绕在滑轮上,一端挂一质量为m的物体。
求(1)由静止开始1秒钟后,物体下降的距离。(2) 绳子的张力。
解: TR
a
1 2
MR
2
a R
T
1 2
Ma
2
mg T ma
M
T
mg mM 2
注: 可以用质点动力学 的方法来处理刚体 的平动问题。
转动:
刚体上所有质点都绕同一直线作圆 周运动。这种运动称为刚体的转动。这 条直线称为转轴。
定轴转动:
转轴固定不动的转动。
刚体的转动动能
mn
rn
o
r1
m1
r2
m2
令
I mi ri
i
2
kg m
2
I 为刚体对 z 轴的转动惯量。
结论: 刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 对于质量连续分布的刚体:
2
2
( mi ri )
Ek
1 2
J
2
设在外力矩 M 的作用下,刚体绕定轴发生角位移d 元功:
dA Md
A I
d dt
A
由转动定律 有
d dt
d I d
1 2 1 2
dA I
2
1
I d
I 2 -
2
I 1
2
刚体绕定轴转动的动能定理 :合外力矩对刚体所 做的功等于刚体转动动能的增量。
l a v
o
30°
机械能守恒:
11 l 2 2 2 Ml ma mga1 cos 30 Mg 1 cos 30 23 2
T
m
o
x
例4. 质量为M =16 kg的实心滑轮,半径为R = 0.15 m。 一根细绳绕在滑轮上,一端挂一质量为m的物体。
求(1)由静止开始1秒钟后,物体下降的距离。(2) 绳子的张力。
解: TR
a
1 2
MR
2
a R
T
1 2
Ma
2
mg T ma
M
T
mg mM 2
注: 可以用质点动力学 的方法来处理刚体 的平动问题。
转动:
刚体上所有质点都绕同一直线作圆 周运动。这种运动称为刚体的转动。这 条直线称为转轴。
定轴转动:
转轴固定不动的转动。
刚体的转动动能
mn
rn
o
r1
m1
r2
m2
令
I mi ri
i
2
kg m
2
I 为刚体对 z 轴的转动惯量。
结论: 刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 对于质量连续分布的刚体:
2
2
( mi ri )
Ek
1 2
J
2
设在外力矩 M 的作用下,刚体绕定轴发生角位移d 元功:
dA Md
A I
d dt
A
由转动定律 有
d dt
d I d
1 2 1 2
dA I
2
1
I d
I 2 -
2
I 1
2
刚体绕定轴转动的动能定理 :合外力矩对刚体所 做的功等于刚体转动动能的增量。
l a v
o
30°
机械能守恒:
11 l 2 2 2 Ml ma mga1 cos 30 Mg 1 cos 30 23 2
大学物理课课件第3章_刚体的定轴转动

G2 G1
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
(支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统,忽略轴摩擦,脱离驱动力矩后,系 统受合外力矩为零,角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间,系统在
铅直位置,受合外力矩为零,角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体(上某点)的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
(支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统,忽略轴摩擦,脱离驱动力矩后,系 统受合外力矩为零,角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间,系统在
铅直位置,受合外力矩为零,角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体(上某点)的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
大学物理第三章刚体力学PPT课件

精选
7
F is iin fis iin m ir i
两边同乘ri,得
F ir i siin fir i siin m ir i2
上式左边第一项为外力Fi对转轴的力矩,而第二项是 内力fi 对转轴的力矩。对刚体的所有质点都可写出类 似上式的方程,求和得
F ir is ii n fir is ii n ( m ir i 2 )
密度为,则dm=dx,有:
Ox
dx
l
J0r2dm ll2 2x2dx1l32 1 1m 22 l
(2)当转轴通过棒的一端A并与棒垂直时:
JAr2dm0 lx2dx3 l31 3m2l
精选
12
例2 求质量为m、半径为R、厚 为h的均质圆盘对通过盘心并与 盘面垂直的轴的转动惯量。
解:如图所示,将圆盘看成许多薄圆环组成。取任一 半径为r,宽度为dr的薄圆环,它的转动惯量为:
转动惯量与刚体的大小形状、质量分布以及转
轴的位置等有关。
精选
9
一般的情况下刚体质量是连 续分布的,把它分割成无限多个 微小部分,其中质量为dm的小块 到转轴的垂直距离为r,则它对该 转轴的转动惯量为
dJr2dm
r dm
积分得到整个刚体对相应转轴的转动惯量为
J r2dm
精选
10
常见刚体的转动惯量
MF 2dF 2rsin
精选
5
若F位于转动平面内,则上式简化为
MFd Fsri n
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
M rF
《大学物理》第3章 二、三维运动

经过的水平距离)为:
xmax
v02 sin 2
g
上页 下页 返回 退出
飞行的射高(即高出抛射点的距离)为
ymax
v02
sin 2
2g
若 0 ,则 ymax 0 , 此时为平抛运动;
若
4
,则 xmax
v02 g
,此时射程最大;
若
2
,则 xmax
0 ,此时为竖直抛体运动.
在t=0时刻坐标
原点重合,对于同一
o'
个质点P,在任意时
刻两个坐标系中的质 点对应的位置矢量: zz'
v
r
x'
P
r
x
上页 下页 返回 退出
K'系rr原 点rr相对RRK系原r点的vt位矢Ry t t
P点在K系和K'系的空间坐 标、时间坐标的对应关系 o
(4) t=2s内的平均速度 (5) t=2s末的速度及速度大小 (6) t=2s末加速度及加速度大小
解:(1) 先写运动方程的分量式
x 2t
y
2
t
2
消去 t 得轨迹方程: y 2 x2
4
抛物线
上页 下页 返回 退出
(2)
位置矢量:
r
2j
t os
r 4i 2 j
(6)加速度
a dv 2 j
dt
a 2 j
t2s
a =2 m / s2 沿 -y 方向,与时间无关。
上页 下页 返回 退出
例题 3-5 位置是时间的函数 质点的位置是时间的函 数,表示为
大学物理:第三章 理想光学系统

2. 像的大小;
3. 物右移200mm,像移动多大距离?
例:有一光组将物放大3倍,成像在影屏上,当透镜向物 体方向移动18mm时,物象放大率为4倍。求光组焦距。
三、由多个光组组成的理想光学系统
相应于高斯公式:
l2 l1 d1
………
d1 H1H 2
lk …lk1 d k1 (主面间隔)
相应于牛顿公式:
l HA,l H A
由图,有: x l f , x l f
代入牛顿公式,得: lf lf ll
f f 1 l l
n n n n l l f f
放大率公式为:
f f f f l nl
x f x f l n l
x f f f f f x f
x2 x1 1
………
1 F1F2
xk … xk 1 k1 (光学间隔)
光学间隔Δ和主面间隔d 的关系为:
1 d1 f1 f 2
………
k 1 …d k 1 f k1 f k 1
垂轴放大率为: yk y1 y2 yk
y1 y1 y2
yk
1 2 k
四、光学系统的光焦度
f h tgU
象方主点H′到象方焦点F′的距离称为象方 焦距(后焦距或第二焦距)
f h tgU
说明:
1)对于理想光学系统,不管其结构(r,d,n)如何,只 要知道其焦距值和焦点或主点的位置,其光学性质就确 定了。
2) f n n =n′ f f
fn
h ltgU ltgU
x f tgU x f tgU
§ 3-2 理想光学系统的基点、基面
1. 焦点、焦平面 物方焦点:对应像点在像方光轴上无限远处
焦点 像方焦点:对应物点在物方光轴上无限远处
3. 物右移200mm,像移动多大距离?
例:有一光组将物放大3倍,成像在影屏上,当透镜向物 体方向移动18mm时,物象放大率为4倍。求光组焦距。
三、由多个光组组成的理想光学系统
相应于高斯公式:
l2 l1 d1
………
d1 H1H 2
lk …lk1 d k1 (主面间隔)
相应于牛顿公式:
l HA,l H A
由图,有: x l f , x l f
代入牛顿公式,得: lf lf ll
f f 1 l l
n n n n l l f f
放大率公式为:
f f f f l nl
x f x f l n l
x f f f f f x f
x2 x1 1
………
1 F1F2
xk … xk 1 k1 (光学间隔)
光学间隔Δ和主面间隔d 的关系为:
1 d1 f1 f 2
………
k 1 …d k 1 f k1 f k 1
垂轴放大率为: yk y1 y2 yk
y1 y1 y2
yk
1 2 k
四、光学系统的光焦度
f h tgU
象方主点H′到象方焦点F′的距离称为象方 焦距(后焦距或第二焦距)
f h tgU
说明:
1)对于理想光学系统,不管其结构(r,d,n)如何,只 要知道其焦距值和焦点或主点的位置,其光学性质就确 定了。
2) f n n =n′ f f
fn
h ltgU ltgU
x f tgU x f tgU
§ 3-2 理想光学系统的基点、基面
1. 焦点、焦平面 物方焦点:对应像点在像方光轴上无限远处
焦点 像方焦点:对应物点在物方光轴上无限远处
大学物理第三章PPT课件

第3章刚体力学基础
刚体是一个理想模型,指物体受到力的作用时完全不 会发生形变。因此运动过程中刚体内部任意两点之间 的距离始终保持不变。
§3.1 刚体运动的描述
一、刚体运动基本形式和自由度
自由度:完全描述运动所需的独立坐标数
(决定物体空间位置)
1 平动(平移):刚体内任意两质点连线的 方向保持不变
自由度 i 3 (xc yc zc )
Lz Liz rimivi
i
i
( miri2 ) J
i
式中 J miri2
i
称为刚体对转轴 z 的转动惯量
代入
Mz
dLz dt
得到 M dJ
dt
J为常量 M = J dω J
dt
刚体定轴转动定理
z o
Li
ri
vi
mi
Ri
x o
y
F ma
M dL dt
L J
2
0
F
.y
O
F x
Fy mg
l0 C .
Fx
3l0 2l
1F
F .A
mg
M J
M J
l0F J
3l0F ml 2
F mg (Fx i Fy j ) mac
Fx
3l0 2l
1F
讨论
F
.y
O
F x
l0 C .
F .A
mg
(1) Fx
0, l0
2l 3
(2) Fx
0, l0
2 3
二、定 轴 转 动 定 理
刚体是一个质点系,描述质点系转动的动力
学方程
M
dL
z
dt
刚体是一个理想模型,指物体受到力的作用时完全不 会发生形变。因此运动过程中刚体内部任意两点之间 的距离始终保持不变。
§3.1 刚体运动的描述
一、刚体运动基本形式和自由度
自由度:完全描述运动所需的独立坐标数
(决定物体空间位置)
1 平动(平移):刚体内任意两质点连线的 方向保持不变
自由度 i 3 (xc yc zc )
Lz Liz rimivi
i
i
( miri2 ) J
i
式中 J miri2
i
称为刚体对转轴 z 的转动惯量
代入
Mz
dLz dt
得到 M dJ
dt
J为常量 M = J dω J
dt
刚体定轴转动定理
z o
Li
ri
vi
mi
Ri
x o
y
F ma
M dL dt
L J
2
0
F
.y
O
F x
Fy mg
l0 C .
Fx
3l0 2l
1F
F .A
mg
M J
M J
l0F J
3l0F ml 2
F mg (Fx i Fy j ) mac
Fx
3l0 2l
1F
讨论
F
.y
O
F x
l0 C .
F .A
mg
(1) Fx
0, l0
2l 3
(2) Fx
0, l0
2 3
二、定 轴 转 动 定 理
刚体是一个质点系,描述质点系转动的动力
学方程
M
dL
z
dt
大学物理课件第3章 动量与角动量

§3.3 动量守恒定律 质点系所受合外力为零, Σ 时间改变,即
Fi = 0 总动量不随
N P pi 常矢量
i 1
1. 合外力为零,或外力与内力相比小很多;
2. 合外力沿某一方向为零;
p i
i
const .
3. 只适用于惯性系; 4. 比牛顿定律更普遍的最基本的定律。
M r F
力
M F d F r sin
提问:力矩为0的情况?
力矩
Lrp
动量
N m 矢量性: r F
单位:
三、角动量定理
pr p v pr F Lr 角动量定理: r F M (力矩)
q
v
V
v sinq
v cosq V
解:设车相对地面的反冲速度为V,方向水平向左 炮弹相对地面的速度水平分量为 v cosq V mv cosq 水平方向动量守恒 m(v cosq V ) MV 0 解得V
炮弹相对地面的速度竖直分量为 v sinq
m M
v sinq tg v cosq V
t2
mg
3秒时物是否被拉起?
F cos f 0 N F sin mg 0 f N t1 1.9 s
I x 0.62 Kgm / s
t1
F
x
dt 1.12t (cos sin ) mg dt
3
I x mvx 0 0.62Kgm / s
6
h
v
0
N =
m 2gh
τ
m 工件
mg
大学物理(上)课件-第03章刚体的定轴转动3-2

解 : (1) 棒在任意位置时的重力矩 l M = mg cos θ 2 1 3g M = Jβ = ml 2 β β= cos θ 3 2l
N
o
c
⋅
θ
dθ
⋅
1 1 dω (2) mg cos θ = ml 2 2 3 dt 1 dω dθ 1 2 dω = ml 2 = ml ω 3 dθ dt 3 dθ
ω
o
r1
r2 v1
∆m1
E
27
K
1 2 = J ω ——刚体定轴转动的动能 2
3. 刚体定轴转动的动能定理
设在外力矩 M 的作用下,刚体绕定轴发生角位移 dθ 元功:
dA = Mdθ
dω 由转动定律 M = J β = J dt dω 有 dA = J dθ = Jω dω dt
A=
∫ω
ω2
1
1 1 2 2 = J ω - J ω Jω d ω 2 1 2 2
28
刚体绕定轴转动的动能定理 :合外力矩对刚体所做的 功等于刚体转动动能的增量。
ω = (2 β h r )1 2 = 9.08 rad ⋅ s −1
§3.3 定轴转动刚体的功与能
1.力矩的功 � 刚体在力 F 作用绕轴转过一微小角位移 dθ � � � � 力 F 作功为dA = F ⋅ dr = F cos(π − ϕ ) dr
2 = F sin ϕ dr = F sin ϕds = Fr sin ϕdθ � 力F使刚体由θ 0转到θ 时, 力矩的功为
2
4 2 19 2 65 2 J = J1 + J 2 = mr + mr = mr 3 2 6
22
例1 一个质量为M、半径为R的定滑 轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂 一质量为m的物体而下垂。忽略轴处 摩擦,求物体m由静止下落高度h时 的速度和此时滑轮的角速度。 解:
N
o
c
⋅
θ
dθ
⋅
1 1 dω (2) mg cos θ = ml 2 2 3 dt 1 dω dθ 1 2 dω = ml 2 = ml ω 3 dθ dt 3 dθ
ω
o
r1
r2 v1
∆m1
E
27
K
1 2 = J ω ——刚体定轴转动的动能 2
3. 刚体定轴转动的动能定理
设在外力矩 M 的作用下,刚体绕定轴发生角位移 dθ 元功:
dA = Mdθ
dω 由转动定律 M = J β = J dt dω 有 dA = J dθ = Jω dω dt
A=
∫ω
ω2
1
1 1 2 2 = J ω - J ω Jω d ω 2 1 2 2
28
刚体绕定轴转动的动能定理 :合外力矩对刚体所做的 功等于刚体转动动能的增量。
ω = (2 β h r )1 2 = 9.08 rad ⋅ s −1
§3.3 定轴转动刚体的功与能
1.力矩的功 � 刚体在力 F 作用绕轴转过一微小角位移 dθ � � � � 力 F 作功为dA = F ⋅ dr = F cos(π − ϕ ) dr
2 = F sin ϕ dr = F sin ϕds = Fr sin ϕdθ � 力F使刚体由θ 0转到θ 时, 力矩的功为
2
4 2 19 2 65 2 J = J1 + J 2 = mr + mr = mr 3 2 6
22
例1 一个质量为M、半径为R的定滑 轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂 一质量为m的物体而下垂。忽略轴处 摩擦,求物体m由静止下落高度h时 的速度和此时滑轮的角速度。 解:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
春的气息
合肥研究院首届青年才艺大赛摄影作品展
第二节 弯曲液面的附加压强
现象
液面不是平对于弯曲液面来说,由于液体表面张力的存在,在 靠近液面的两侧就形成一压强差,称为附加压强。
首先分析水平液面
P0
f Δs
f
P1=P0
表面张力的合力 f合 的方向与凸面法
解:
h
代入数据,可得
d
P =1.186×105Pa
知识回顾 Knowledge Review
凹球形液面内液体压强为
f
P0
Δs
Ps
f
P3=P0+Ps
球形液泡内的气体压强分析(以肥皂泡为例)
球形液膜具有两个球形面,且两个 半径近似相等 液膜外表面为凸液面,有
A CB
液膜内表面为凹液面,有
附加压强为
例:如图所示的装置中,连通管活塞关闭,左右两端吹成 一大一小两个气泡。(假设肥皂薄膜厚度为定值) 问:如果打开连通管,气体会怎么运动? 解:由肥皂泡内外气体压强差
线方向相反, 凸形液面
P0
Δs
Ps P2=P0+Ps
表面张力的合力 f合 的方向与凹面法
线方向相反,
f
凹形液面
P0
Δs
Ps
f
P3=P0+Ps
2. 球形液面的附加压强
B C
dl df//
取一线段元dL,则作用在其上的 表面张力大小为
A
r
df⊥ df
R
方向垂直并与球面相切
将表面张力分解成两个分力,分
别与半径 r 垂直和平行
圆周对称性
水平分力 相互抵消
故表面张力的合力为
f 作用在底面积为 的圆面上
对于凹状液面
弯曲液面的附加压强为作用在单位面积上的表面张力的合 力;与表面张力系数成正比,与液面的曲率半径成反比
如果液面外大气压为P0,在平衡状态下, 凸球形液面内液体压强为
P0
Δs
Ps P2=P0+Ps
因此,打开连通管后气体将从 B 流向 A
如果两个气泡的表面张力系数相同,大气泡膨胀,小气泡收缩。
例:在水下深度为 30cm 处有一直径d = 0.02mm的空气泡。设
水面压强为大气压 P0= 1.013×105Pa, ρ水= 1.0×103kg·m-3,
α水= 72×10-3 N·m-1。
P0
求:气泡内空气的压强。
合肥研究院首届青年才艺大赛摄影作品展
第二节 弯曲液面的附加压强
现象
液面不是平对于弯曲液面来说,由于液体表面张力的存在,在 靠近液面的两侧就形成一压强差,称为附加压强。
首先分析水平液面
P0
f Δs
f
P1=P0
表面张力的合力 f合 的方向与凸面法
解:
h
代入数据,可得
d
P =1.186×105Pa
知识回顾 Knowledge Review
凹球形液面内液体压强为
f
P0
Δs
Ps
f
P3=P0+Ps
球形液泡内的气体压强分析(以肥皂泡为例)
球形液膜具有两个球形面,且两个 半径近似相等 液膜外表面为凸液面,有
A CB
液膜内表面为凹液面,有
附加压强为
例:如图所示的装置中,连通管活塞关闭,左右两端吹成 一大一小两个气泡。(假设肥皂薄膜厚度为定值) 问:如果打开连通管,气体会怎么运动? 解:由肥皂泡内外气体压强差
线方向相反, 凸形液面
P0
Δs
Ps P2=P0+Ps
表面张力的合力 f合 的方向与凹面法
线方向相反,
f
凹形液面
P0
Δs
Ps
f
P3=P0+Ps
2. 球形液面的附加压强
B C
dl df//
取一线段元dL,则作用在其上的 表面张力大小为
A
r
df⊥ df
R
方向垂直并与球面相切
将表面张力分解成两个分力,分
别与半径 r 垂直和平行
圆周对称性
水平分力 相互抵消
故表面张力的合力为
f 作用在底面积为 的圆面上
对于凹状液面
弯曲液面的附加压强为作用在单位面积上的表面张力的合 力;与表面张力系数成正比,与液面的曲率半径成反比
如果液面外大气压为P0,在平衡状态下, 凸球形液面内液体压强为
P0
Δs
Ps P2=P0+Ps
因此,打开连通管后气体将从 B 流向 A
如果两个气泡的表面张力系数相同,大气泡膨胀,小气泡收缩。
例:在水下深度为 30cm 处有一直径d = 0.02mm的空气泡。设
水面压强为大气压 P0= 1.013×105Pa, ρ水= 1.0×103kg·m-3,
α水= 72×10-3 N·m-1。
P0
求:气泡内空气的压强。
