北约自主招生数学试题
高考专题自主招生模拟试卷(北约).docx

2015年自主招生模拟试卷(北约)1. 已知等腰直角△PQR 的三个顶点分别在等腰直角△ABC 的三条边上,记△PQR ,△ABC 的面积分别为S △PQR ,S △ABC ,则PQR ABCS S ∆∆的最小值为 .解答:如图5-1所示,图5-1 图5-2(1)当PQR ∆的直角顶点在ABC ∆的斜边上,则,,,P C Q R 四点共圆,180,APR CQR BQR ∠=∠=-∠o 所以sin sin .APR BQR ∠=∠在,APR BQR ∆∆中分别应用正弦定理得,sin sin sin sin PR AR QR BR A APR B BQR==.又45,A B ∠=∠=o故PR QR =,故AR BR =即R 为AB 的中点.过R 作RH AC ⊥于H ,则12PR RH BC ≥=,所以22221()124PQR ABC BC S PR S BC BC ∆∆=≥=,此时PQR ABCS S ∆∆的最大值为14. (2)当PQR ∆的直角顶点在ABC ∆的直角边上,如图5-2所示,设1,(01),(0)2BC CR x x BRQ παα==≤≤∠=<<,则90.CPR PRC BRQ α∠=-∠=∠=o在Rt CPR ∆中,,sin sin CR xPR αα== 在BRQ ∆中,31,,sin 4x BR x RQ PR RQB QRB B ππαα=-==∠=-∠-∠=+, AB P H由正弦定理, 1sin 3sin sin sin sin()44xPQ RB xB PQB αππα-=⇔=⇔∠+1sin cos 2sin x ααα=+,因此2221111()()22sin 2cos 2sin PQR x S PR ααα∆===+.这样,PQR ABCS S ∆∆2222111()cos 2sin (12)(cos sin )5αααα=≥=+++,当且仅当arctan 2α=取等号,此时PQR ABCS S ∆∆的最小值为15.2. 若集合{}2015*(,)(1)(2)()10,,A m n m m m n m Z n N =++++++=∈∈L ,则集合A中的元素个数为 . 解答:由已知得20162015(21)25n n m ++=,因为,21n n m ++一奇一偶,所以,21n n m ++两者之一为偶数,即为2016201620162201620152,25,25,,25L 共有2016种情况,交换顺序又得到2016种情形,所以集合A 共有4032个元素. 3.若数列{}n a 的前n 项和nS =32n n -,*n N ∈,则20151182i i a i =+-∑= .答案:20156048. 解答:1211352,n n n i i i i a a a n n -===-=-+∑∑又10a =,故2*352()n a n n n N =-+∈, 20152015201511111111()823(1)31i i i i a i i i i i =====-=+-++∑∑∑20156048. 4.若22sin cos 161610xx +=,则cos4x = .答案:12-. 解答:设2sin 16,116xt t =≤≤,则22cos 1sin 161616x x t-==,代入方程得16102,t t t +=⇒=或8t =,即21sin 4x =或34,所以cos4x =12-。
“北约”自主招生数学试题及解答(2010-2012)

2010年“北约”自主招生数学试题及解答1.(仅文科做)02απ<<,求证:sin tan ααα<<. 【解析】 不妨设()sin f x x x =-,则(0)0f =,且当02x π<<时,()1cos 0f x x '=->.于是()f x 在02x π<<上单调增.∴()(0)0f x f >=.即有sin x x >. 同理可证()tan 0g x x x =->.(0)0g =,当02x π<<时,21()10cos g x x '=->.于是()g x 在02x π<<上单调增。
∴在02x π<<上有()(0)0g x g >=。
即tan x x >。
注记:也可用三角函数线的方法求解.2.AB 为边长为1的正五边形边上的点.证明:AB(25分) 【解析】 以正五边形一条边上的中点为原点,此边所在的直线为x 轴,建立如图所示的平面直角坐标系.⑴当,A B 中有一点位于P 点时,知另一点位于1R 或者2R 时有最大值为1PR ;当有一点位于O 点时,1max AB OP PR =<;⑵当,A B 均不在y 轴上时,知,A B 必在y 轴的异侧方可能取到最大值(否则取A 点关于y 轴的对称点A ',有AB A B '<).不妨设A 位于线段2OR 上(由正五边形的中心对称性,知这样的假设是合理的),则使AB 最大的B 点必位于线段PQ 上.且当B 从P 向Q 移动时,AB 先减小后增大,于是max AB AP AQ =或;对于线段PQ 上任意一点B ,都有2BR BA ≥.于是22max AB R P R Q == 由⑴,⑵知2max AB R P =.不妨设为x .下面研究正五边形对角线的长.IHG F E 1111x x-1如右图.做EFG ∠的角平分线FH 交EG 于H . 易知5EFH HFG GFI IGF FGH π∠=∠=∠=∠=∠=. 于是四边形HGIF 为平行四边形.∴1HG =. 由角平分线定理知111EFEH x FG x HG ===-.解得x =3.AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值.(25分)【解析】 不妨设过A 点的切线交x 轴于点C ,过B 点的切线交x 轴于点D ,直线AC 与直线BD 相交于点E .如图.设1122(,),(,)B x y A x y ,且有222211121,1,0y x y x x x =-=->>.由于2y x '=-,于是AC 的方程为2222x x y y =--;① BD 的方程为1122x x y y =--. ②联立,AC BD 的方程,解得121221(,1)2()y y E x x x x ---. 对于①,令0y =,得222(,0)2y C x -;对于②,令0y =,得112(,0)2y D x -. 于是221212121222112222y y x x CD x x x x --++=-=-. 121(1)2ECD S CD x x ∆=-.不妨设10x a =>,20x b -=>,则 2222111111()(1)(22)44ECD a b S ab a b a b ab a b a b∆++=++=+++++1111()(2)(2)44a b ab ab ab ab=+++⋅++≥ ③0s >,则有331111111(2)(.....)223399ECD S s s s s s s s s ∆=++=++++++ 6个 9个1243691616111116)]8()29s s s ⋅⋅[⋅(⋅()=⋅≥3218)3=⋅(= ④又由当12x a x b s ==-==时,③,④处的等号均可取到.∴min ()ECD S ∆ 注记:不妨设311()(2)2g s s s s=++,事实上,其最小值也可用导函数的方法求解. 由2211()(32)2g s s s '=+-知当2103s <<时()0g s '<;当213s <时()0g s '>.则()g s 在(0,上单调减,在)+∞上单调增.于是当s =时()g s 取得最小值. 4.向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ在0t 时取得最小值,问当0105t <<时,夹角的取值范围.(25分) 【解析】 不妨设OA ,OB 夹角为α,则1,2OP t OQ t =-=,令 222()(1)42(1)2cos g t PQ t t t t α==-+-⋅-⋅2(54cos )(24cos )1t t αα=++--+. 其对称轴为12cos 54cos t αα+=+.而12()54x f x x +=+在5(,)4-+∞上单调增,故12cos 1154cos 3αα+-+≤≤. 当12cos 1054cos 3αα++≤≤时,012cos 1(0,)54cos 5t αα+=∈+,解得223αππ<<. 当12cos 1054cos αα+-<+≤时,()g t 在[0,1]上单调增,于是00t =.不合题意. 于是夹角的范围为2[,]23ππ.5.(仅理科做)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.(25分) 【解析】 不存在;否则有(cos sin )(cos sin )cos sin cot tan sin cos x x x x x x x x x x-+-=-=, 则cos sin 0x x -=或者cos sin 1sin cos x x x x+=.若cos sin 0x x -=,有4x π=.而此时1,122不成等差数列;若cos sin 1sin cos x x x x+=,有2(sin cos )12sin cos x x x x =+.解得有sin cos 1x x =. 而11sin cos sin 2(0,]22x x x =∈,矛盾!2011年“北约”自主招生数学试题及解答2012年“北约”自主招生数学试题及解答《自主招生》三大系列《全国重点高校自主招生备考指南·高一、高二基础版》从从高高一一开开始始行行动动起起来来!!⊙专为高一、高二学生设计,细致分析自主招生关键信息,深入讲解自主招生备考方略。
清北学长精心打造——北约自主招生数学模拟试题及参考答案(五)

4. 已知方程|x-2n|=k x(n∈N*)在区间(2n-1,2n+1]上有两个不相等的实根,则 k 的取值范围 是( ) 1 (A)k>0 (B)0<k≤ 2n+1 1 1 (C) <k≤ 2n+1 2n+1 (D)以上都不是
解:由|x-2n|≥0,故 k≥0,若 k=0,可知在所给区间上只有 1 解.故 k>0. 1 由图象可得,x=2n+1 时,k x≤1.即 k≤ .故选 B. 2n+1 又解: y=(x-2n)2 与线段 y=k2x(2n-1<x≤2n+1)有两个公共点. x2-(4n+k2)x+4n2=0 有(2n-1, 2n+1] 2 2 2 2 2 2 上 有 两 个 根 . 故 △ =(4n+k ) - 16n >0 . 且 (2n - 1) - (4n+k )(2n - 1)+4n >0 , (2n+1)2 - 1 1 (4n+k2)(2n+1)+4n2≥0,2n-1<2n+ k2<2n+1. k≤ . 2 2n+1 5. logsin1cos1,logsin1tan1,logcos1sin1,logcos1tan1 的大小关系 是 (A) (B) (C) (D) logsin1cos1< logcos1sin1< logsin1tan1< logcos1tan1 logcos1sin1< logcos1tan1< logsin1cos1< logsin1tan1 logsin1tan1< logcos1tan1< logcos1sin1< logsin1cos1 logcos1tan1< logsin1tan1< logsin1cos1< logcos1sin1
2019年北约自主招生数学试题

2019年北约自主招生数学试题
1、求x 的取值范围使得12)(-+++=x x x x f 是增函数;
2、求1210272611=+-+++-+x x x x 的实数根的个数;
3、已知0)2)(2(2
2
=+-+-n x x m x x 的4个根组成首项为
4
1
的等差数列,求n m -;
4、如果锐角ABC ∆的外接圆的圆心为O ,求O 到三角形三边的距离之比;
5、已知点)0,2(),0,2(B A -,若点C 是圆0222=+-y x x 上的动点,求ABC ∆面积的最小值。
6、在2012,,2,1Λ中取一组数,使得任意两数之和不能被其差整除,最多能取多少个数?
7、求使得a x x x x =-3sin sin 2sin 4sin 在),0[π有唯一解的a ;
8、求证:若圆内接五边形的每个角都相等,则它为正五边形;
9、求证:对于任意的正整数n ,n )21(+必可表示成1-+s s 的形式,其中+∈N s
2019年自主招生北约联考数学试题解答。
“北约”“华约”自主招生数学模拟试题

“北约”“华约”2013年自主招生数学模拟试题(满分150分)5. 设P 是抛物线2440y y x --=上的动点,点A 的坐标为(0,1)-,点M 在直线PA 上, 且分PA uu u v 所成的比为2:1,则点M 的轨迹方程是 . 第二部分:解答题(共5小题 每题20分)1设集合()12log 32A x x ⎧⎫⎪⎪=-≥-⎨⎬⎪⎪⎩⎭,21a B x x a ⎧⎫=>⎨⎬-⎩⎭.若A B ≠∅I ,求实数a 的取值范围2. 为了搞好学校的工作,全校各班级一共提了P )(+∈N P 条建议.已知有些班级提出了相同的建议,且任何两个班级都至少有一条建议相同,但没有两个班提出全部相同的建议.求证该校的班级数不多于12-P 个3. 设平面向量3,1)a =-v ,13(,22b =v .若存在实数(0)m m ≠和角((,))22ππθθ∈-,使向量2(tan 3)c a b =+-v v v ,tan d ma b θ=-+u v v v ,且c d ⊥v u v .(I)求函数()m f θ=的关系式; (II)令tan t θ=,求函数()m g t =的极值.4. 已知双曲线的两个焦点分别为1F ,2F ,其中1F 又是抛物线24y x =的焦点,点A (1,2)-, B (3,2)在双曲线上.(I)求点2F 的轨迹方程; (II)是否存在直线y x m =+与点2F 的轨迹有且只 有两个公共点?若存在,求实数m 的值,若不存在,请说明理由.5. 已知a ,b 均为正整数,且,sin )(),20(2sin ,2222θπθθn b a A ba ab b a n n ⋅+=<<+=>其中求证:对一切*N ∈n ,n A 均为整数参考答案一、选择题1. 由tan 2α=,得sin 2cos αα=,有22sin 4cos αα=,即221cos 4cos αα-=. 则21cos 5α=,原式=222216cos 6cos 5cos 5cos 1αααα--==. 2. 设x a bi =+,,a b R ∈,代入原方程整理得22(2256)(45)0a b a b ab a b i --+-++-=有2222560450a b a b ab a b ⎧--+-=⎨+-=⎩,解得11a b =⎧⎨=⎩或3232a b ⎧=⎪⎪⎨⎪=-⎪⎩,所以1x i =+或3322x i =-. 3. 直接求x 的个位数字很困难,需将与x 相关数联系,转化成研究其相关数. 【解】令])22015()22015[(,)22015()22015(82198219+++=+-+-=y x y 则 ])22015()22015[(8219-+-+,由二项式定理知,对任意正整数n.)2201515(2)22015()22015(22Λ+⋅⋅+=-++-n n n n n C 为整数,且个位数字为零.因此,x y +是个位数字为零的整数.再对y 估值, 因为2.0255220155220150=<+=-<, 且1988)22015()22015(-<-, 所以.4.02.02)22015(201919<⨯<-<<y 故x 的个位数字为9.【评述】转化的思想很重要,当研究的问题遇到困难时,将其转化为可研究的问题.4. 解:被7除余2的数可写为72k +. 由100≤72k +≤600.知14≤k ≤85.又若某个k 使72k +能被57整除,则可设72k +=57n . 即5722877n n k n --==+. 即2n -应为7的倍数. 设72n m =+代入,得5716k m =+. ∴14571685m ≤+≤. ∴m =0,1.于是所求的个数为70.5. 设点P 00(,)x y ,M (,)x y ,有0203x x +⨯=,02(1)3y y +⨯-=,得03x x =,032y y =+ 而2000440y y x --=,于是得点M 的轨迹方程是291240y x --=.二、解答题1. 解:{}13A x x =-≤<,()(){}30B x x a x a =--<. 当0a >时,{}03B x a x a =<<<,由A B ≠∅I 得03a <<; 当0a <时,{}30B x a x a =<<<,由A B ≠∅I 得1a >-;当0a =时,{}20B x x =<=∅,与A B ≠∅I 不符.综上所述,()()1,00,3a ∈-U2. 证明:假设该校共有m 个班级,他们的建议分别组成集合m A A A ,,,21Λ。
自主招生试题汇总

2012年北约自主招生数学试题1、求x 的取值范围使得12)(-+++=x x x x f 是增函数.2、求1210272611=+-+++-+x x x x 的实数根的个数.3、已知0)2)(2(22=+-+-n x x m x x 的4个根组成首项为41的等差数列,求n m -.4、如果锐角ABC ∆的外接圆的圆心为O ,求O 到三角形三边的距离之比.5、已知点)0,2(),0,2(B A -,若点C 是圆0222=+-y x x 上的动点,求ABC ∆面积的最小值.6、在2012,,2,1 中取一组数,使得任意两数之和不能被其差整除,最多能取多少个数?7、求使得a x x x x =-3sin sin 2sin 4sin 在),0[π有唯一解的a .8、求证:若圆内接五边形的每个角都相等,则它为正五边形.9、求证:对于任意的正整数n ,n )21(+必可表示成1-+s s 的形式,其中+∈N s .2012年自主招生华约联考数学试题解答(前4题)2011年北约物理试题1.在平直的轨道上,有一辆静止的火车,假设它与地面没有摩擦力,车后有N 个组员和一个组长列队排列,沿这辆火车的直线跑步,组长在最后。
火车的质量为M ,人的质量为m ,假设M=2m 。
(1)组员和组长追火车的速度为0v ,随后组员们以02v 的速度跳上火车,则最后一个组长正好追不上火车,求N 是多少?(2)此后组长减速为20v ,为使组长能上车,组员相继以相对车厢速度u 向前跳出,求该过程至少消耗组员多少人体内能?解:(1)002)(mv N v Nm M ⋅=+解得N=2(2)设第一个人跳出后车对地的速度为1v ,第二个人跳出后车对地的速度为2v ,则 1103)(4mv u v m mv ++=2212)(3mv u v m mv ++=0221v v = 20202222219851421221)(21)(21mv mv mv v u m v u m E =-++++=∆2、两个相同的铁球,质量均为m ,由原长为l 、劲度系数为k 的弹簧连接,设法维持弹簧在原长位置由静止释放两球(两球连线竖直),设开始时下球距离桌面的高度为h ,而且下球与桌面的碰撞为完全非弹性的。
2008-2011北京大学(北约)自主招生数学试题(全附答案)
5
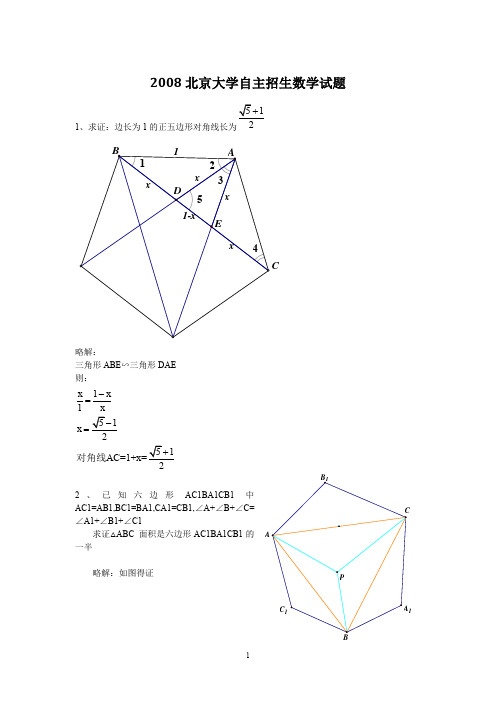
答案: 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号(9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号(55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的,因为 (m+499(k+m-2n))可能是负的,也就是当这是递减的等差数列的时候,那么 2009 就不在这个 数列中了。 3、 挺简单,设 a=tanx+(根 3),b=cotx+(根号 3),假设均为有理数。 那么由(a-(根号 3) ) (b-(根号 3) )=1 可得(a+b)根号 3=ab+2.若 a+b 非零,除过来就矛盾了。 所以必有 a+b=0,此时 ab+2 也是 0. 显然与 a,b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)(必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内,则可得 a^2≤8(b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤(a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况,显然 2 是 a+b 的最大值, 5、设优秀有 a 人,及格 b 人,不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000(这里都取各层次里的最少人,故用小于等于) 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题,矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数
北约2020年自主招生数学试题

2020年北约自主招生数学试题与答案2020-03-16(时间90分钟,满分120分)(33312(7)(232)2(63)40g a b c d e a b c d a b c =-+----+++++=702320a b c d e a b c d +---=⎧⇒⎨+++=⎩ 即方程组:420(1)20(2)70(3)2320(4)630(5)a c eb d a bcde a b c d a b c ++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩,有非0有理数解. 由(1)+(3)得:110a b c d ++-= (6) 由(6)+(2)得:1130a b c ++= (7) 由(6)+(4)得:13430a b c ++= (8) 由(7)-(5)得:0a =,代入(7)、(8)得:0b c ==,代入(1)、(2)知:0d e ==.于是知0a b c d e =====,与,,,,a b c d e 不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x 2312-2312为两根的有理系数多项式的次数最小为5.1. 在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车占一格,共有几种停放方法? A. 720 B. 20 C. 518400 D. 14400解析:先从6行中选取3行停放红色车,有36C 种选择.最上面一行的红色车位置有6种选择;最上面一行的红色车位置选定后,中间一行的红色车位置有5种选择;上面两行的红色车位置选定后,最下面一行的红色车位置有4种选择。
三辆红色车的位置选定后,黑色车的位置有3!=6种选择。
所以共有36654614400C ⨯⨯⨯⨯=种停放汽车的方法. 2. 已知2225,25x y y x =+=+,求32232x x y y -+的值. A. 10 B. 12 C. 14 D. 16 解析:根据条件知:32232(25)2(25)(25)(25)x x y y x y y x y x -+=+-++++1515450x y xy =---由2225,25x y y x =+=+两式相减得()()22x y x y y x -+=-故y x =或2x y +=-①若x y =则225x x =+,解得1x =±于是知1x y ==+1x y ==当1x y ==+3223222415()50430504(25)3870x x y y xy x y x x x x x -+=-++-=---=-----3870108x =--=--.当1x y ==3223222415()50430504(25)3870x x y y xy x y x x x x -+=--+-=---=-+---22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-3870108x =--=-+.(2)若x y ≠,则根据条件知:22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-,于是22(25)(25)2()106x y y x x y +=+-+=++=,进而知222()()12x y x y xy +-+==-. 于是知:32232415()5016x x y y xy x y -+=-+-=-.综上所述知,32232x x y y -+的值为108-±或16-.3. 数列{}n a 满足11a =,前n 项和为1,42n n n S S a +=+,求2013a . A. 3019⨯22020B. 3019⨯22020C. 3018⨯22020D.无法确定解析:根据条件知:1221221424244n n n n n n n n n a S a S a a a a a ++++++++==+=++⇒=-.又根据条件知:1212121,425a S a a a a ==+=+⇒=.所以数列{}1221:1,5,44n n n n a a a a a a ++===-.又212114422(2)n n n n n n n a a a a a a a +++++=-⇔-=-.令12n n n b a a +=-,则11212,23n n b b b a a +==-=,所以132n n b -=⋅.即11232n n n a a -+-=⋅.对11232n n n a a -+-=⋅,两边同除以12n +,有113224n n n n a a ++-=,即113224n n n n a a ++=+.令2n nn a c =,则134n n c c +=+,11122a c ==,于是知1331(1)244n n c n -=+-=.所以231,2(31)24nn n n a n --==-⋅.于是知:201120122013(320131)230192a =⨯-⋅=⋅.5.如图,ABC ∆中,AD 为BC 边上中线,,DM DN 分别,ADB ADC ∠∠的角平分线,试比较BM CN +与MN 的大小关系,并说明理由. A. BM+CN>MN B. MN +CN <MN C. BM+CN =MN D.无法确定解析:如图,延长ND 到E ,使得DE DN =,连接BE ME 、.易知BDE CDN ∆≅∆,所以CN BE =.又因为,DM DN 分别为,ADB ADC ∠∠的角平分线,所以90MDN ∠=︒,知MD 为线段EN 的垂直平分线,所以MN ME =.所以BM CN BM BE ME MN +=+>=.6.模长为1的复数A B C 、、,满足0A B C ++≠,求AB BC CAA B C++++的模长.A. -1/2B. 1C. 2D.无法确定 解析:根据公式z z z =⋅1,1,1A A B B C C ⋅=⋅=⋅=.于是知:AB BC CAAB BC CA AB BC CAA B CA B C A B C++++++=⋅++++++()()()()ABCC ABCC BCAA BCAA C ABB CABB AABB BBCC CCAA AB AB BC BC C A CA AA BB CC ++++++++=++++++++1==.所以AB BC CAA B C++++的模长为1.7.最多能取多少个两两不等的正整数,使得其中任意三个数之和都为素数. 解析:所有正整数按取模3可分为三类:3k 型、31k +型、32k +型.首先,我们可以证明,所取的数最多只能取到两类.否则,若三类数都有取到,设所取3k 型数为3a ,31k +型数为31b +,32k +型数为32c +,则3(31)(32)3(1)a b c a b c ++++=+++,不可能为素数.所以三类数中,最多能取到两类.其次,我们容易知道,每类数最多只能取两个.否则,若某一类3(012)k r r +=、、型的数至少取到三个,设其中三个分别为333a r b r c r +++、、,则(3)(3)(3)3()a r b r c r a b c r +++++=+++,不可能为素数.所以每类数最多只能取两个.结合上述两条,我们知道最多只能取224⨯=个数,才有可能满足题设条件. 另一方面,设所取的四个数为1、7、5、11,即满足题设条件. 综上所述,若要满足题设条件,最多能取四个两两不同的正整数.8.已知1232013a a a a R ∈L 、、、、,满足12320130a a a a ++++=L ,且122334201220132013122222a a a a a a a a a a -=-=-==-=-L ,求证:12320130a a a a =====L .解析:根据条件知:122334************(2)(2)(2)(2)()0a a a a a a a a a a a a -+-+-++-=-++++=L L ,(1)另一方面,令122334201312222a a a a a a a a m -=-=-==-=L ,则122334201312222a a a a a a a a ----L 、、、、中每个数或为m ,或为m -.设其中有k 个m ,(2013)k -个m -,则:12233420131(2)(2)(2)(2)(2013)()(22013)a a a a a a a a k m k m k m-+-+-++-=⨯+-⨯-=-L (2)由(1)、(2)知:(22013)0k m -= (3)而22013k -为奇数,不可能为0,所以0m =.于是知:12233420122013201312,2,2,,2,2a a a a a a a a a a =====L .从而知:2013112a a =⋅,即得10a =.同理可知:2320130a a a ====L .命题得证.9.对任意的θ,求632cos cos66cos 415cos 2θθθθ---的值. 解析:根据二倍角和三倍角公式知:632cos cos66cos 415cos 2θθθθ---622232cos (2cos 31)6(2cos 21)15(2cos 1)θθθθ=------63222232cos 2(4cos 3cos )162(2cos 1)115(2cos 1)θθθθθ⎡⎤⎡⎤=--------⎣⎦⎣⎦664242232cos (32cos 48cos 18cos 1)(48cos 48cos 6)(30cos 15)θθθθθθθ=--+---+--10=.10.已知有mn 个实数,排列成m n ⨯阶数阵,记作{}mxnija ,使得数阵中的每一行从左到右都是递增的,即对任意的123i m =L 、、、、,当12j j <时,都有12ij ij a a ≤.现将{}mxnija 的每一列原有的各数按照从上到下递增的顺序排列,形成一个新的m n ⨯阶数阵,记作{}mxnij a ',即对任意的123j n =L 、、、、,当12i i <时,都有12i j i j a a ''≤.试判断{}mxnija '中每一行的n 个数的大小关系,并说明理由.解析:数阵{}mxnija '中每一行的n 个数从左到右都是递增的,理由如下:显然,我们要证数阵{}mxnija '中每一行的n 个数从左到右都是递增的,我们只需证明,对于任意123i m =L 、、、、,都有(1)iji j a a +''≤,其中1231j n =-L 、、、、. 若存在一组(1)pq p q a a +''>.令(1)(1)k k q i q a a ++'=,其中123k m =L 、、、、,{}{}123,,,,1,2,3,,m i i i i m =L L .则当t p ≤时,都有(1)(1)(1)tti q i q t q p q pq a a a a a +++'''≤=≤<.也即在(123iq a i =L 、、、、m)中,至少有p 个数小于pq a ',也即pq a '在数阵{}mxnija '的第q 列中,至少排在第1p +行,与pq a '排在第p 行矛盾.所以对于任意123i m =L 、、、、,都有(1)iji j a a +''≤,即数阵{}mxnij a '中每一行的n 个数从左到右都是递增的.。
清北学长精心打造——北约自主招生数学模拟试题及参考答案(四)

绝密★启用前清北学长精心打造——北约自主招生数学模拟试题(四)考试范围:xxx ;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息<br/>2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(5*6=30分)1.已知函数()()432,,,f x x ax bx cx d a b c d =++++为实常数的图象经过三点12,2A ⎛⎫ ⎪⎝⎭,13,3B ⎛⎫ ⎪⎝⎭,14,4C ⎛⎫ ⎪⎝⎭,则()()15f f +的值等于() A .0B .1C .265D .252.已知函数()122,x f x -=-关于x 的方程()()220f x f x k -+=,下列四个命题中是假.命题的是()A .存在实数k ,使得方程恰有2个不同的实根;B .存在实数k ,使得方程恰有4个不同的实根;C .存在实数k ,使得方程恰有6个不同的实根;D .存在实数k ,使得方程恰有8个不同的实根;3.函数f 定义在正整数有序对的集合上,并满足(,),(,)(,),f x x x f x y f y x ==()(,)(,)x y f x y yf x x y+=+,则(14,52)f 的值为( )A .364B .182C .91D .无法计算4.二次函数c bx ax y ++=2的图象的一部分如图,则a 的取 值范围是 ( )A .01<≤-aB .1->aC .01<<-aD .1-≤a5.关于x 、y 的方程20071111=++xy y x 的正整数解(x ,y )的个数为( )A .16B .24C .32D .486.设圆O 1和圆O 2是两个定圆,动圆P 与这两个定圆都相切,则圆P 的圆心轨迹不可能是 ( )第II 卷(非选择题)二、填空题(6*6=36分)7.定义: 区间[](),c d c d <的长度为d c -. 已知函数3log y x =的定义域为[],a b , 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差等于________.8.设na 是(3+x )n的展开式中x 项的系数(n=2, 3, 4,… ), 则当n >100时,223a +333a +…+nn a 3的整数部分的值为.9. 平面上给定ΔA 1A 2A 3及点p 0,定义A s =A s-3,s ≥4,构造点列p 0,p 1,p 2,…,使得p k+1为绕中心A k+1顺时针旋转1200时p k 所到达的位置,k=0,1,2,…,若p 1986=p 0.则ΔA 1A 2A 3为 三角形。
北京大学(北约)2010~2014自主招生试题及答案(全)

2014年北京大学自主招生数学试题1. 圆心角为3π的扇形面积为6π,求它围成圆锥的表面积. 2. 将10个人分成3组,一组4人,两组每组3人,共有几种分法. 3. 2()2()(),(1)1,(4)733a b f a f b f f f ++===,求()2014f . 4.2()lg(2)f x x ax a =-+的值域为R ,求a 的取值范围.5. 已知1x y +=-,且,x y 都为负实数,求1xy xy+的取值范围. 6. 22()arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数,求C 的值. 一、求证:tan3Q ∉二、已知实系数二次函数()f x 与()g x ,()()f x g x =和()()30f x g x +=有两重根,()f x 有两相异实根,求证:()g x 没有实根.三、1213,a a a 是等差数列,{}113i j k M a a a i j k =++≤<<≤,问:7160,,23是否同在M 中,并证明你的结论.四、()01,2,,i x i n >=,且11n i i x ==∏,求证1)1)nn i i x =≥∏.答案1.π7; 2.2100; 3.4027)2024(12)(=⇒-=f x x f ; 4.1 00≥≤⇒≥∆a or a ;5.⎪⎭⎫⎢⎣⎡+∞,417;6.2arctan 0)0(-=⇒=C f 一、求证:Q ∉︒3tan解:若Q aab Q a ∈-=︒=⇒∈=︒2126tan 3tan ,Q ab b a c ∈-+=︒=⇒19tan Q bc cb d ∈-+=︒=⇒115tan 52518tan 41518sin 2-=︒⇒-=︒ 于是Q d d ∈-=⇒=-=︒233215tan ,从而矛盾。
二.实系数二次函数)(),(x g x f ,)()(x g x f =和0)()(3=+x g x f 有两重根,)(x f 有两相异根,求证:)(x g 无实数根。
北大自主招生数学试题

北大自主招生数学试题一、下列哪个数列不是等差数列?A. 1, 3, 5, 7, ...B. 2, 4, 8, 16, ...C. 10, 8, 6, 4, ...D. -1, 0, 1, 2, ...(答案:B)二、若复数z满足(1+i)z=2i,则z等于?A. 1-iB. 1+iC. -1+i(答案)D. -1-i三、设函数f(x) = x3 - 3x2 + 2,则f(x)的极小值点为?A. x = 0B. x = 1C. x = 2(答案)D. x = 3四、在三角形ABC中,若sinA:sinB = 3:4:5,则cosC的值为?A. 1/5B. -1/5(答案)C. 3/5D. 4/5五、已知向量a = (1, 2),b = (2, 1),则向量a与b的夹角θ的余弦值为?A. √5/5B. 2√5/5(答案)C. 1/√5D. -1/√5六、设集合A = {x | x2 - 5x + 6 = 0},B = {x | x2 - ax + a - 2 = 0},若B是A的子集,则a的取值范围是?A. a = 2或a = 3或a = 5B. a = 3或a = 5(答案)C. a = 2或a = 5D. a = 2或a = 3七、已知圆C的方程为x2 + y2 - 2x - 5 = 0,直线l的方程为2x - y - 1 = 0,则圆心C到直线l的距离为?A. √5B. 2√5/5C. √5/5(答案)D. 3√5/5八、若实数x, y满足约束条件x + y ≤ 2, x - y ≤ 1, x ≥ 0,则z = 2x + y的最大值为?A. 2B. 3C. 4D. 5(答案)九、设函数f(x) = ex - e(-x),则不等式f(x + 2) < f(1 - x)的解集为?A. (-∞, 3/2)B. (-3/2, +∞)(答案)C. (-∞, -1/2)D. (1/2, +∞)十、已知矩阵A = [1 2; 3 4],向量β = [5; 6],若向量α满足Aα = β,则α为?A. [-1; 2]B. [2; -1](答案)C. [1; 1]D. [-2; 1]。
华师附中“北约”自主招生强化训练试题四

华师附中“北约”自主招生强化训练四第一卷(选择题 共50分)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分)。
1.命题“存在2,20x Z x x m ∈++≤”的否定是 ( )A .存在2,20x Z x x m ∈++> B .不存在2,20x Z x x m ∈++> C . 对任意2,20x Z x x m ∈++≤ D .对任意2,20x Z x x m ∈++> 2.已知x 与y 之间的几组数据如下表:则y 与x 的线性回归方程y bx a =+必过 ( )A .()1,3B .()2,5C .()1.5,4D .()3,73. 已知()()1,10p q x a x a ≤---≤:.若p 是q 的充分不必要条件,则实数a 的取值范围是 ( ) A.10,2⎡⎤⎢⎥⎣⎦ B.10,2⎛⎫ ⎪⎝⎭ C.(]1,0,2⎡⎫-∞⋃+∞⎪⎢⎣⎭ D.()1,0,2⎛⎫-∞+∞ ⎪⎝⎭4.在数列{}n a 中,12i a =(i 为虚数单位),()()n 1n 1i 1i a a ++=-()n N *∈,则2012a 的值为 ( )A .-2B .0C .2D . 2i5.函数()cos xf x e x =,则此函数图像在点()()1,1f 处的切线的倾斜角为 ( )A.0 B.锐角 C.直角 D.钝角 6.已知集合{}22|4A x x y =+=,集合{}|sin ,B x x i tdt i x R π=+<∈⎰为虚数单位,集合A 与B 的关系是 ( )A .AB ⊂ B .B A ⊂C .A B A= D .A B =∅7.若变量,a b 满足约束条件6321a b a b a +≤⎧⎪-≤-⎨⎪≥⎩,23n a b =+,则n 取最小值时,21nx ⎛⎫ ⎪⎝⎭ 二项展开式中的常数项为 ( )A . -80B .80C .40D .-208.已知函数()()21,43,xf x eg x x x =-=-+- 若存在()()f a g b =,则实数b 的取值范围为 ( )A .[]1,3B .()1,3C .22,22⎡⎤-+⎣⎦D .()22,22-+9.在ABC ∆中, 已知向量cos18,cos 72AB =(), 2cos 63,2cos 27BC =(),则ABC ∆的面积为 ( ) A .22 B .24 C .32D .2 10. 已知点()1,0A -、()1,0B ,()00,P x y 是直线2y x =+上任意一点,以A 、B 为焦点的椭圆过点P .记椭圆离心率e 关于0x 的函数为()0e x ,那么下列结论正确的是 ( ) A .e 与0x 一一对应 B .函数()0e x 无最小值,有最大值 C .函数()0e x 是增函数 D .函数()0e x 有最小值,无最大值 二、填空题 (共5小题, 每题5分,计25分.将正确的答案填在题后的横线上) 11.观察下列式子:213122+<,221151+234+<, 222111712348+++<⋅⋅⋅,由此可归纳出的一般结论是 .12.阅读右面的程序,当分别输入3,5a b ==时, 输出的值a = .13.一质点受到平面上的三个力123,,F F F (单位:牛顿) 的作用而处于平衡状态.已知12,F F 成60角,且12,F F 大小 为2和4,则3F 的大小为 .14.如图,一个三棱锥的三视图的轮廓都是边长为1的正 方形,则此三棱锥外接球的表面积 . 15.(考生注意:请在下列三题中任选一题作答,如多做,则按所做的第一题评分)A .对于实数,x y ,若12x -≤,12y -≤,则21x y -+的最大值 .B .圆12cos ,:12sin ,x C y θθ⎧=+⎪⎨=+⎪⎩(θ为参数)的极坐标方程为 .C.如图,PC 切圆O 于点C ,割线PAB 经过圆心O ,4,8PC PB ==,则OBC S ∆= .三、解答题 (共6小题,计75分。
北约自主招生能力测试数学试题(含参考答案

综合性大学自主选拔录取联合考试自然科学基础——理科试卷数学部分(北约)一、选择题(每小题8分,合计48分)1.圆心角为3π的扇形的面积为6π,则它围成的圆锥的表面积为( B ).A .B .7πC .D .解:由2166S R ππ==扇形得6R =,由263r ππ=⨯得1r =,故它围成的圆锥的表面积为267r πππ+=.2.将10个人分为3组,一组4人,另两组各3人,共有( C )种分法.A .1070B .2014C .2100D .4200解:433106321002C C C N ==. 3.已知2()2()()33a b f a f b f ++=,(1)1f =,(4)7f =,则(2014)f =( A ). A .4027 B .4028 C .4029 D .4030 解:421(4)2(1)(2)()333f f f f +⨯+===,124(1)2(4)(3)()533f f f f +⨯+===,猜想*()21()f n n n N =-∈,假设()21f n n =-对3(1)n k k ≤≥都成立,则(31)3(1)2(1)2(31)1f k f k f k +=+-=+-,(32)3(2)2(2)2(32)1f k f k f k +=+-=+-,(33)3(3)2(3)2(33)1f k f k f k +=+-=+-,所以*()21()f n n n N =-∈.4.若2()lg(2)f x x ax a =-+的值域为R ,则a 的取值范围是( D ).A .01a ≤≤B .C .D .0a ≤或1a ≥解:由题知,{}2(0,)2y y x ax a +∞⊆=-+,故2(2)40a a ∆=--≥,解得:0a ≤或1a ≥.5.已知1x y +=-,且x 、y 均为负实数,则1xy xy+有( B ). A .最大值174 B .最小值174 C .最大值174- D .最小值174-解:1()()x y =-+-≥104xy <≤,而函数1()f t t t=+在(0,1)上单调递减,在(1,)+∞单调递增,故1()()4f xy f ≥,即1174xy xy +≥,当且仅当12x y ==-时取等号. 6.已知22()arctan14x f x C x +=+-在(,)44ππ-上为奇函数,则C =( B ). A .0 B .arctan 2- C .arctan 2 D .不存有解:由()0f x =得arctan(2)arctan 2C =-=-,此时()()f x f x +-22arctan14x x +=-22arctan 214x C x -+++4arctan()2arctan 203=--=,故arctan 2C =-符合题意.二、解答题(每题18分,共72分)7.证明:0tan3R ∉.证明:设0tan 3Q ∈,则0tan 6tan12tan 24tan 30tan(624)Q Q Q Q ∈⇔∈⇔∈⇔=+∈,这与0tan 303Q =矛盾. 8.已知实系数二次函数()f x 和()g x ,若方程()()f x g x =和3()()0f x g x +=都只有一个偶重根,方程()0f x =有两个不等的实根,求证:方程()0g x =没有实根. 解:设2()f x ax bx c =++,2()g x dx ex f =++,0ad ≠,所以2()4()()b e a d c f -=--,2(3)4(3)(3)b e a d c f +=++,所以223124b e ac df +=+,又240b ac ->,所以22()44(4)0g x e df b ac ∆=-=--<,所以方程()0g x =没有实根.9.已知1a ,2a ,…,13a 成等差数列,{}113i j k M a a a i j k =++≤<<≤,问:0,72,163是否能够同时在M 中?并证明你的结论.解:设该数列的公差为d ,∴p ∃,q ,*r N ∈,130a pd +=,173()2a p q d ++=,1163()3a p q r d +++=,∴2111q r =,∴21q ≥,11p ≥,又0123p ≥++=,∴35p q r ++≥, 又12111033p q r ++≤++=,与上式矛盾,故0,72,163不能够同时在M 中.10.i x (1i =,2,…,n )为正实数,且11nii x==∏,求证:1)1)nn i i x =≥∏.解:由AM GM -不等式得:11(n i n =≥,11(ni n =≥两式相加得:1≥,故1)1)nn i i x =≥∏.。
2013、2014年华约北约卓越自主招生数学试题

2013年“华约”自主招生数学试题1. 已知集合{}10A x Z x =∈≥,B 是A 的子集,且B 中元素满足下列条件: (a )数字两两不等;(b)任意两个数字之和不等于9;试求: (1)B 中有多少个两位数?多少个三位数? (2)B 中是否有五位数?是否有六位数?(3)将B 中元素从小到大排列,第1081个元素是多少? 2. 已知实数,x y 满足sin x +sin y =13, cos cos x y - =15,求sin()x y -,cos().x y +3. 已知0k >,从直线y kx =和y kx =-上分别选取点(,),(,)A A B B A x y B x y ,0A B x x >,满足21OA OB k =+,其中O 为坐标原点,AB 中点M 的轨迹为曲线C . (1)求曲线C 的方程;(2)抛物线22(0)x py p =>与曲线C 相切于两点,求证:两点在两条定直线上,并求出两条切线方程.4. 有7个红球8个黑球,从中任取四个. ⑴求恰有一个红球的概率;⑵设四个球中黑球个数为X ,求X 的分布列及数学期望Ex ; ⑶求当四个球均为一种颜色时,这种颜色为黑色的概率. 5. 已知数列{}n a 满足10a >,21n n n a a ca +=+,1,2...n =,,其中0c >, ⑴证明:对任意的0M >,存在正整数N ,使得对于n N >,n a M >;⑵设11n n b ca =+,n S 为n b 前n 项和,证明:{}n S 有界,且对0d >,存在正整数k ,当n k >时,110.n S d ca <-< 6. 已知,,x y z 是三个大于1的正整数,且xyz 整除(1)(1)(1),xy yz xz ---求,,x y z 的所有可能值.7. 已知()(1)1xf x x e =--, ⑴证明:当0x >时,()0f x <; ⑵若数列{}n x 满足11x =,11n n x x n x ee +=-.证明:数列{}n x 递减,且12nn x ⎛⎫> ⎪⎝⎭.2013年“华约”自主招生数学试题解析1.【试题分析】本题是集合元素的计数问题,需要用到排列组合的知识,对分步思维的理解要求较高。
2008-2011北京大学(北约)自主招生数学试题(全附答案)

形
=
舞ACBABA慧CB麓AC =/缓二C
。,
。/
l/
Dk
:::.?日 \、E。.・。
\I,・’
,‘1
.。.
BA 。,
。
口2丁,62丁,
.al一口2
bI—b2
B A +£ A B C +£C .,二 C
即证{一(口I+口2+bI+62)一(口l+d2+口,+
a 口l a 口2
2丁+口,
2丁一口'
【百189】+1=13分,而北方最高分的最大值为6+n
万方数据
14
中’?善i:.7(200s年第2期・高中版)
南方球队内部比赛总得分CⅢ2
,12
・解题研究・
=136,
一l=11分<13分,
.・.
冠军在南方队
北方球队内部比赛总得分c2=28,
北方胜南方得分=30—28=2, 北方球队最高得分=7+2=9, 因为9×17=153<270, 所以南方球队中至少有一支得分超过9分. 冠军在南方球队中.综上所述,冠军是一支南方 球队. 点评这道试题要注意突破口的选择,也需要 耐心和比较强的推理、分析能力. 5.(理科)0一xyz坐标系内xoy平面系内0≤,,≤ 2一石2绕),轴旋转一周构成一个不透光立体在点 (1,0,1)设置一光源,在xoy平面内有一以原点为圆 心的圆c被光照到的长度为2霄,求曲线C上未被照 到的长度.
c:+。+n(肛+9)≥召,c:≤A,
即3n2—22n一36。<0.
‘.・
’B=9A,
.・.c:+9+n(,l+9)≥B=9A1>9c:,
(1)
,’2
又总分为乞Ⅲ有10I乞小钴厶(1)得厅=6或8.
北约数学试题

2014年北约自主招生数学试题1. 圆心角为3π的扇形面积为π6,求它围成的表面积。
2. 将10个人分成三组,一组4人,两组各3人,求共有几种分法。
3. ()()3232b f a f b a f +=⎪⎭⎫ ⎝⎛+,()11=f ,()74=f ,求()2014f 。
4. ()()a ax x x f +-=2lg 2的值域为R ,求a 的取值范围。
5. 已知1=+y x ,且y x ,都为负实数,求xyxy 1+的取值范围。
6. ()C x x x f +-+=4122arctan 在⎪⎭⎫ ⎝⎛-41,41上为奇函数,求C 的值。
一、求证:Q ∉ 3tan 。
二、已知实系数二次函数()x f 与()x g ,()()x g x f =和()()03=+x g x f 有两重根,()x f 有两相异的实根,求证:()x g 没有实根。
三、1121,a a a ⋯⋯是等差数列,{}131≤<<≤++=k j i a a a M k j i ,问:316,27,0是否可以同时在M 中,并证明你的结论。
四、0>i x ,()n i ⋯⋯=2,1,11=∏=n i i x ,求证:()()nn i i x 1221+≥+∏=。
2013年北约自主招生数学试题一、选择题(每题8分,共48分)1.以2和312-为两根的有理系数多项式的最高次数最小为( )A. 2B. 3C. 5D. 62.在66⨯的表中停放3辆完全相同的红色和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车只占一格,共有 种停放方法.A. 720B. 20C. 518400D. 144003.已知225x y =+,225y x =+(x y ≠),则32232x x y y -+值为( )A. 10-B. 12-C. 14-D. 16-4.在数列{}n a 中,11a =,142n n S a +=+(1n ≥),则2013a 值为( )A. 201230192⨯B. 201330192⨯C. 201230182⨯D. 无法确定5.在ABC ∆中,D 为BC 中点,DM 平分ADB ∠交AB 于点M ,DN 平分ADC ∠交AC 于N ,则BM CN +与MN 的关系为( )A.BM CN MN +>B.MN CN MN +<C.BM CN MN +=D.无法确定 6.模长都为1的复数,,A B C 满足0A B C ++≠,则BC AC ABA B C ++++的模长为( )A.12- B. 1 C. 2 D. 无法确定 二、解答题(每题18分,共72分)7.最多能找多少个两两不相等的正整数使其任意三个数之和为质数,并证明你的结论.8.已知12320130a a a a ++++=,且122320131|2||2||2|a a a a a a -=-==-证明:12320130a a a a =====. 9.对于任意θ,求632cos cos66cos415cos2θθθθ---的值.10.有一个m n ⨯的数表,已知每一行的数均是由小到大排列.现在将每一列的数由小到大重新排列,则新的数表中每一行的数满足什么样的关系?请证明你的结论.2012年北约自主招生数学试题1.求x 的范围使得()12-+++=x x x x f 是增函数。
2013年“北约”自主招生训练题二

2013年“北约”自主招生训练题二1、函数sin cos y x x =+(x ∈R )的单调减区间是 .2、设函数()f x 的定义域为R ,若()1f x +与()1f x -都是关于x 的奇函数,则函数()y f x =在区间[]0,100上至少有 个零点.3、圆环形手镯上等距地镶嵌着4颗小珍珠,每颗珍珠镀金、银两色中的一种.其中镀2金2银的概率是 .4、在三棱锥A B C D -中,已知A C B C B A ∠=∠,A C D A D C B C D B D C ∠=∠=∠=∠θ=,且cos 10θ=.已知棱A B的长为,则此棱锥的体积为 .5、设复数列{}n x 满足1n x a ≠-,0,且11n n n a x x x +=+.若对任意n ∈N * 都有3n n x x +=,则a 的值是 .6、已知平面上两定点A (-3,0),B (0,-4),P 为曲线12(0)y x x=>上任意一点,过点P作PC ⊥x 轴,PD ⊥y 轴,垂足分别为C,D ,则四边形ABCD 面积S 的最小值为 7、函数()2f x x =-__________________________.8、函数22*()sincos()kkf x x x k N =+∈的最小值为9、设O 是平面上一个定点,A ,B ,C 是平面上不共线的三个点,动点P 满足||||A C A BO P O A A C A B λλ-=+,其中[0,)λ∈+∞,则点P 的轨迹为_________________. 10、函数21)(2+-=x x x f 的值域是__________________。
11、若ABC ∆为锐角三角形,满足)cos(sin sin B A BA +=,则A tan 的最大值是___________。
12、将9,,2,1 随机填入右图正方形ABCD 的九个格子中,则其每行三数,每列三数自上而下、自左至右顺次成等差数列的概率P=__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年北约自主招生数学试题与答案2013-03-16(时间90分钟,满分120分)(33312(7)(232)2(63)40g a b c d e a b c d a b c =-+----+++++=702320a b c d e a b c d +---=⎧⇒⎨+++=⎩ 即方程组:420(1)20(2)70(3)2320(4)630(5)a c eb d a bcde a b c d a b c ++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩,有非0有理数解. 由(1)+(3)得:110a b c d ++-= (6) 由(6)+(2)得:1130a b c ++= (7) 由(6)+(4)得:13430a b c ++= (8) 由(7)-(5)得:0a =,代入(7)、(8)得:0b c ==,代入(1)、(2)知:0d e ==.于是知0a b c d e =====,与,,,,a b c d e 不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x 2312-2312为两根的有理系数多项式的次数最小为5.1. 在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车占一格,共有几种停放方法? A. 720 B. 20 C. 518400 D. 14400解析:先从6行中选取3行停放红色车,有36C 种选择.最上面一行的红色车位置有6种选择;最上面一行的红色车位置选定后,中间一行的红色车位置有5种选择;上面两行的红色车位置选定后,最下面一行的红色车位置有4种选择。
三辆红色车的位置选定后,黑色车的位置有3!=6种选择。
所以共有36654614400C ⨯⨯⨯⨯=种停放汽车的方法. 2. 已知2225,25x y y x =+=+,求32232x x y y -+的值. A. 10 B. 12 C. 14 D. 16 解析:根据条件知:32232(25)2(25)(25)(25)x x y y x y y x y x -+=+-++++1515450x y xy =---由2225,25x y y x =+=+两式相减得()()22x y x y y x -+=-故y x =或2x y +=-①若x y =则225x x =+,解得1x =±于是知1x y ==+1x y ==当1x y ==+3223222415()50430504(25)3870x x y y xy x y x x x x x -+=-++-=---=-----3870108x =--=--.当1x y ==3223222415()50430504(25)3870x x y y xy x y x x x x -+=--+-=---=-+---22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-3870108x =--=-+.(2)若x y ≠,则根据条件知:22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-,于是22(25)(25)2()106x y y x x y +=+-+=++=,进而知222()()12x y x y xy +-+==-. 于是知:32232415()5016x x y y xy x y -+=-+-=-.综上所述知,32232x x y y -+的值为108-±或16-.3. 数列{}n a 满足11a =,前n 项和为1,42n n n S S a +=+,求2013a . A. 3019⨯22012B. 3019⨯22013C. 3018⨯22012D.无法确定解析:根据条件知:1221221424244n n n n n n n n n a S a S a a a a a ++++++++==+=++⇒=-.又根据条件知:1212121,425a S a a a a ==+=+⇒=.所以数列{}1221:1,5,44n n n n a a a a a a ++===-.又212114422(2)n n n n n n n a a a a a a a +++++=-⇔-=-.令12n n n b a a +=-,则11212,23n n b b b a a +==-=,所以132n n b -=⋅.即11232n n n a a -+-=⋅.对11232n n n a a -+-=⋅,两边同除以12n +,有113224n n n n a a ++-=,即113224n n n n a a ++=+.令2n nn a c =,则134n n c c +=+,11122a c ==,于是知1331(1)244n n c n -=+-=.所以231,2(31)24nn n n a n --==-⋅.于是知:201120122013(320131)230192a =⨯-⋅=⋅.5.如图,ABC ∆中,AD 为BC 边上中线,,DM DN 分别,ADB ADC ∠∠的角平分线,试比较BM CN +与MN 的大小关系,并说明理由. A. BM+CN>MN B. MN +CN <MN C. BM+CN =MN D.无法确定解析:如图,延长ND 到E ,使得DE DN =,连接BE ME 、.易知BDE CDN ∆≅∆,所以CN BE =.又因为,DM DN 分别为,ADB ADC ∠∠的角平分线,所以90MDN ∠=︒,知MD 为线段EN 的垂直平分线,所以MN ME =.所以BM CN BM BE ME MN +=+>=.6.模长为1的复数A B C 、、,满足0A B C ++≠,求AB BC CAA B C++++的模长.A. -1/2B. 1C. 2D.无法确定 解析:根据公式z z z =⋅1,1,1A A B B C C ⋅=⋅=⋅=.于是知:AB BC CAAB BC CA AB BC CAA B CA B C A B C++++++=⋅++++++()()()()ABCC ABCC BCAA BCAA C ABB CABB AABB BBCC CCAA AB AB BC BC C A CA AA BB CC ++++++++=++++++++1==.所以AB BC CAA B C++++的模长为1.7.最多能取多少个两两不等的正整数,使得其中任意三个数之和都为素数. 解析:所有正整数按取模3可分为三类:3k 型、31k +型、32k +型.首先,我们可以证明,所取的数最多只能取到两类.否则,若三类数都有取到,设所取3k 型数为3a ,31k +型数为31b +,32k +型数为32c +,则3(31)(32)3(1)a b c a b c ++++=+++,不可能为素数.所以三类数中,最多能取到两类.其次,我们容易知道,每类数最多只能取两个.否则,若某一类3(012)k r r +=、、型的数至少取到三个,设其中三个分别为333a r b r c r +++、、,则(3)(3)(3)3()a r b r c r a b c r +++++=+++,不可能为素数.所以每类数最多只能取两个.结合上述两条,我们知道最多只能取224⨯=个数,才有可能满足题设条件. 另一方面,设所取的四个数为1、7、5、11,即满足题设条件. 综上所述,若要满足题设条件,最多能取四个两两不同的正整数.8.已知1232013a a a a R ∈L 、、、、,满足12320130a a a a ++++=L ,且122334201220132013122222a a a a a a a a a a -=-=-==-=-L ,求证:12320130a a a a =====L .解析:根据条件知:122334************(2)(2)(2)(2)()0a a a a a a a a a a a a -+-+-++-=-++++=L L ,(1)另一方面,令122334201312222a a a a a a a a m -=-=-==-=L ,则122334201312222a a a a a a a a ----L 、、、、中每个数或为m ,或为m -.设其中有k 个m ,(2013)k -个m -,则:12233420131(2)(2)(2)(2)(2013)()(22013)a a a a a a a a k m k m k m-+-+-++-=⨯+-⨯-=-L (2)由(1)、(2)知:(22013)0k m -= (3)而22013k -为奇数,不可能为0,所以0m =.于是知:12233420122013201312,2,2,,2,2a a a a a a a a a a =====L .从而知:2013112a a =⋅,即得10a =.同理可知:2320130a a a ====L .命题得证.9.对任意的θ,求632cos cos66cos 415cos 2θθθθ---的值. 解析:根据二倍角和三倍角公式知:632cos cos66cos 415cos 2θθθθ---622232cos (2cos 31)6(2cos 21)15(2cos 1)θθθθ=------63222232cos 2(4cos 3cos )162(2cos 1)115(2cos 1)θθθθθ⎡⎤⎡⎤=--------⎣⎦⎣⎦664242232cos (32cos 48cos 18cos 1)(48cos 48cos 6)(30cos 15)θθθθθθθ=--+---+--10=.10.已知有mn 个实数,排列成m n ⨯阶数阵,记作{}mxnija ,使得数阵中的每一行从左到右都是递增的,即对任意的123i m =L 、、、、,当12j j <时,都有12ij ij a a ≤.现将{}mxnija 的每一列原有的各数按照从上到下递增的顺序排列,形成一个新的m n ⨯阶数阵,记作{}mxnij a ',即对任意的123j n =L 、、、、,当12i i <时,都有12i j i j a a ''≤.试判断{}mxnija '中每一行的n 个数的大小关系,并说明理由.解析:数阵{}mxnija '中每一行的n 个数从左到右都是递增的,理由如下:显然,我们要证数阵{}mxnija '中每一行的n 个数从左到右都是递增的,我们只需证明,对于任意123i m =L 、、、、,都有(1)iji j a a +''≤,其中1231j n =-L 、、、、. 若存在一组(1)pq p q a a +''>.令(1)(1)k k q i q a a ++'=,其中123k m =L 、、、、,{}{}123,,,,1,2,3,,m i i i i m =L L .则当t p ≤时,都有(1)(1)(1)tti q i q t q p q pq a a a a a +++'''≤=≤<.也即在(123iq a i =L 、、、、m)中,至少有p 个数小于pq a ',也即pq a '在数阵{}mxnija '的第q 列中,至少排在第1p +行,与pq a '排在第p 行矛盾.所以对于任意123i m =L 、、、、,都有(1)iji j a a +''≤,即数阵{}mxnij a '中每一行的n 个数从左到右都是递增的.。
