锐角三角函数章节练习
锐角的三角函数随堂练习3

欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;
唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,
只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
薄雾浓云愁永昼,瑞脑消金兽。佳节又重阳,玉枕纱厨,半夜凉初透。
东篱把酒黄昏后,有暗香盈袖。莫道不消魂,帘卷西风,人比黄花瘦。
锐角的三角函数练习
1.如图,在△ABC中,∠C=90°,BC=5,AC=12,则cosA等于().
A. B. C. D.
2.如图,一个钢球沿坡角31°的斜坡向上滚动了5m,此时钢球距地面的高度是(单位:m)().
A.5cos31°B.5sin31°
C. D.5tan31°
3.AE,CF是锐角△ABC的两条高,如果AE∶CF=3∶2,则sinA∶sinC等于().
参考答案
1解析:AB= =13,
所以cosA= .
答案:D
2答案:B
3解析:如图,sinA= ,sinC= ,
∴sinA∶sinC= ∶ =CF∶AE=2∶3.
答案:B
4答案:D
5解析:AB= =10,AD=DB=5,△AED∽△ABC.
∴ .∴ .
∴AE= .∴CE= .
∴tan∠CBE= .
5答案:C
A. B. C. D.
6. 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA= ,BC=10,则AB的值是().
A.9B.8C.6D.3
7.在平面直角坐标系中,有一点P(2,5),连接OP,且OP与x轴正半轴的夹角为α,则sinα=________,cosα=________,tanα=________.
人教版九年级下数学第二十八章锐角三角函数单元练习题(含答案)

《锐角三角函数》单元练习题一.选择题1.在Rt△ABC中,∠C=90°,如果∠A=α,AB=3,那么AC等于()A.3sinαB.3cosαC.D.2.在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为()A.B.C.D.3.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为()A.5 米B.5米C.2米D.4米4.如图,护林员在离树8m的A处测得树顶B的仰角为45°,已知护林员的眼睛离地面的距离AC 为1.6m,则树的高度BD为()A.8m B.9.6m C.(4)m D.(8+1.6)m5.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα=,则tanα=()A.B.C.D.6.如图,网格中小正方形的边长都为1,点A,B,C在正方形的顶点处,则cos∠ACB的值为()A.B.C.D.7.如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为()A.m B.m C.m D.m8.如图,在Rt△ABC中,∠ACB=90°,AC=24,AB=25,CD是斜边AB上的高,则cos∠BCD 的值为()A.B.C.D.9.如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为()A.千米B.千米C.千米D.千米10.如图,在△ABC中,∠C=90°,AC=5,若cos∠A=,则BC的长为()A.8B.12C.13D.1811.已知某条传送带和地面所成斜坡的坡度为1:2,如果它把一物体从地面送到离地面9米高的地方,那么该物体所经过的路程是()A.18米B.4.5米C.米D.米.12.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()A.cm B.cm C.64 cm D.54cm二.填空题13.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,若3a=4b,则sin B的值是.14.已知∠A是锐角,且cos A=,则tan A=.15.如图,在点A处测得点B处的仰角是.(用“∠1,∠2,∠3或∠4”表示)16.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD交BC于点E,如果AC=2,BC=4,那么cot∠CAE=.17.如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为米(结果保留根号).18.如图,某水库大坝的横假面是梯形ABCD,坝顶宽DC是10米,坝底宽AB是90米,背水坡AD和迎水坡BC的坡度都为1:2.5,那么这个水库大坝的坝高是米.三.解答题19.计算:2cos60°+4sin60°•tan30°﹣6cos245°.20.如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)(1)试问船B在灯塔P的什么方向?(2)求两船相距多少海里?(结果保留根号)21.如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值;(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.22.如图,已知:R t△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A 作AB的垂线交射线EC于点D,延长BC交AD于点F.(1)求CF的长;(2)求∠D的正切值.23.如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠F AE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据:≈1.73)24.“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.(1)求支点D到滑轨MN的距离(精确到1厘米);(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:≈1.41,≈1.73,≈2.45,≈2.65)25.被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大王米”的高度,他们制订了测量方案,并利用课余时间完成了实地测量.测量项目及结果如下表:项目内容课题测量郑州会展宾馆的高度的仰角是α,前进一段距离到达C点用测倾器CF测得楼β,且点A、B、C、D、E、F均在同一竖直平测量数据∠α的度数∠β的度数EC的长度,40°45°53米……请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)参考答案一.选择题1.【解答】解:∵∠A=α,AB=3,∴cosα=,∴AC=AB•cosα=3cosα,故选:B.2.【解答】解:∵AC=4,BC=3,∴tan A==,故选:A.3.【解答】解:作BC⊥地面于点C,设BC=x米,∵传送带和地面所成斜坡AB的坡度为1:2,∴AC=2x米,由勾股定理得,AC2+BC2=AB2,即(2x)2+x2=102,解得,x=2,即BC=2米,故选:C.4.【解答】解:在Rt△CBH中,∠HCB=45°,CH=8m,∴,∴HB=CH•tan∠HAB=8×tan45°=8m,∴HD=HB+AC=8+1.6=9.6.答:树的高度为9.6m.故选:B.5.【解答】解:如图,由sinα==可设PQ=4a,OP=5a,∵OQ=3,∴由OQ2+PQ2=OP2可得32+(4a)2=(5a)2,解得:a=1(负值舍去),∴PQ=4,OP=5,则tanα==,故选:C.6.【解答】解:如右图所示,∵网格中小正方形的边长都为1,∴CE==2,AC==,AE=3,CD=4,作AH⊥CE于点H,∵,∴,解得,AH=,∵AC=,AH=,∠AHC=90°,∴CH==,∴cos∠ACH=,即cos∠ACB=,故选:D.7.【解答】解:在Rt△ABD中,∵∠ADB=45°,∴BD=AB.在Rt△ABC中,∵∠ACB=30°,∴BC=AB.设AB=x(米),∵CD=14,∴BC=x+14.∴x+14=x∴x=7(+1).即铁塔AB的高为7(+1)米.故选:B.8.【解答】解:∵在Rt△ABC中,∠ACB=90°,AC=24,AB=25,∴BC=7,∵CD是斜边AB上的高,,∴CD==,∵CD⊥AB,∴∠CDB=90°,∴cos∠BCD===,故选:B.9.【解答】解:作PC⊥AB交AB于点C,如右图所示,AC=,BC=,∵m=AC﹣BC,∴m=﹣,∴PC==,故选:A.10.【解答】解:∵△ABC中,∠C=90°,AC=5,cos∠A=,∴=,∴AB=13,∴BC==12,故选:B.11.【解答】解:如图:由题意得:斜坡AB的坡度:i=1:2,AE=9米,AE⊥BD,∵i==,∴BE=18米,∴在Rt△ABE中,AB==9(米).故选:D.12.【解答】解:如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则Rt△ACE中,AE=AC=×54=27(cm),同理可得,BF=27cm,又∵点A与B之间的距离为10cm,∴通过闸机的物体的最大宽度为27+10+27=64(cm),故选:C.二.填空题(共6小题)13.【解答】解:因为在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,令b=3x,则a=4x,由勾股定理可得c=5x,所以sin B===,故答案为:.14.【解答】解:∵∠A为锐角,且cos A=,以∠A为锐角作直角三角形△ABC,∠C=90°.∴cos A==.设AC=5k,则AB=13k.根据勾股定理可得:BC=12k.∴tan A==.故答案为:.15.【解答】解:在点A处测得点B处的仰角是∠4,故答案为:∠4.16.【解答】解:∵∠ACB=90°,CD为AB边上的中线,∴AD=CD=BD,∴∠ACD=∠CAD,∠DCB=∠B,∵AE⊥CD,∴∠CAE+∠ACD=∠B+∠CAD=90°,∴∠CAE=∠B,∴cot∠CAE=cot B===2,故答案为:2.17.【解答】解:过点E作EG⊥AB于G,过点F作FH⊥AB于H,则四边形ECBG,HBDF是矩形,∴EC=GB=20,HB=FD,∵B为CD的中点,∴EG=CB=BD=HF,由已知得:∠EAG=90°﹣60°=30°,∠AFH=45°.在Rt△AEG中,AG=AB﹣GB=50﹣20=30米,∴EG=AG•tan30°=30×=10米,在Rt△AHP中,AH=HF•t an45°=10米,∴FD=HB=AB﹣AH=50﹣10(米).答:2号楼的高度为(50﹣10)米.故答案为:(50﹣10).18.【解答】解:如图所示:过点D作DM⊥AB于点M,作CN⊥AB于点N,设DM=CN=x,∵背水坡AD和迎水坡BC的坡度都为1:2.5,∴AM=BN=2.5x,故AB=AM+BN+MN=5x+10=90,解得:x=16,即这个水库大坝的坝高是16米.故答案为:16.三.解答题(共7小题)19.【解答】解:原式=2×+4××﹣6×()2=1+2﹣3=0.20.【解答】解:(1)过P作PC⊥AB交AB于C,在Rt△APC中,∠C=90°,∠APC=53°,AP=50海里,∴PC=AP•cos53°=50×0.60=30海里,在Rt△PBC中,∵PB=20,PC=30,∴cos∠BPC==,∴∠BPC=30°,∴船B在灯塔P的南偏东30°的方向上;(2)∵AC=AP•sin53°=50×0.8=40海里,BC=PB=10,∴AB=AC﹣BC=(40﹣10)海里,答:两船相距(40﹣10)海里.21.【解答】解:(1)∵P为AC的中点,AC=8,∴CP=4,∵∠ACB=90°,BC=6,∴BP=2,∵D是边AB的中点,P为AC的中点,∴点E是△ABC的重心,∴BE=BP=;(2)如图1,过点B作BF∥CA交CD的延长线于点F,∴,∵BD=DA,∴FD=DC,BF=AC,∵CE=2,ED=3,则CD=5,∴EF=8,∴=,∴=,∴=,设CP=k,则P A=3k,∵PD⊥AB,D是边AB的中点,∴P A=PB=3k∴BC=2k,∴AB=2k,∵AC=4k,∴cos A=;(3)∵∠ACB=90°,D是边AB的中点,∴CD=BD=AB,∵PB2=2CD2,∴BP2=2CD•CD=BD•AB,∵∠PBD=∠ABP,∴△PBD∽△ABP,∴∠BPD=∠A,∵∠A=∠DCA,∴∠DPE=∠DCP,∵∠PDE=∠CDP,∴△DPE∽△DCP,∴PD2=DE•DC,∵DE=3,DC=5,∴PD=.22.【解答】解:(1)∵∠ACB=90°,∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,∵AD⊥AB,∴∠BAC+∠CAF=90°,∴∠B=∠CAF,∴△ABC∽△F AC,∴=,即=,解得CF=;(2)如图,过点C作CH⊥AB于点H,∵AC=3,BC=4,∴AB=5,则CH==,∴AH==,EH=AE﹣AH=,∴tan D=tan∠ECH==.23.【解答】解:延长BD交AE于点G,作DH⊥AE于H,设BC=xm,由题意得,∠DGA=∠DAG=30°,∴DG=AD=6,∴DH=3,GH==3,∴GA=6,在Rt△BGC中,tan∠BGC=,∴CG==x,在Rt△BAC中,∠BAC=45°,∴AC=BC=x,由题意得,x﹣x=6,解得,x=≈14,答:大树的高度约为14m.24.【解答】解:(1)过C作CG⊥AB于G,过D作DH⊥AB于H,∵AC=20,∠CAB=60°,∴AG=AC=10,CG=AG=10,∵BC=BD﹣CD=30,∵CG⊥AB,DH⊥AB,∴CG∥DH,∴△BCG∽△BDH,∴=,∴=,∴DH=≈23(厘米);∴支点D到滑轨MN的距离为23厘米;(2)过C′作C′S⊥MN于S,∵A′C′=AC=20,∠C′A′S=45°,∴A′S=C′S=10,∴BS==10,∴A′B=10+10,∵BG==10,∴AB=10+10,∴AA′=A′B﹣AB≈6(厘米),∴滑块A向左侧移动的距离是6厘米.25.【解答】解:由题意可得:设BN=FN=x,则tan40°==≈0.84,解得:x=278.25,故AB=278.25+1.5≈280(m),答:郑州会展宾馆的高度为280m.。
锐角三角函数练习题及答案
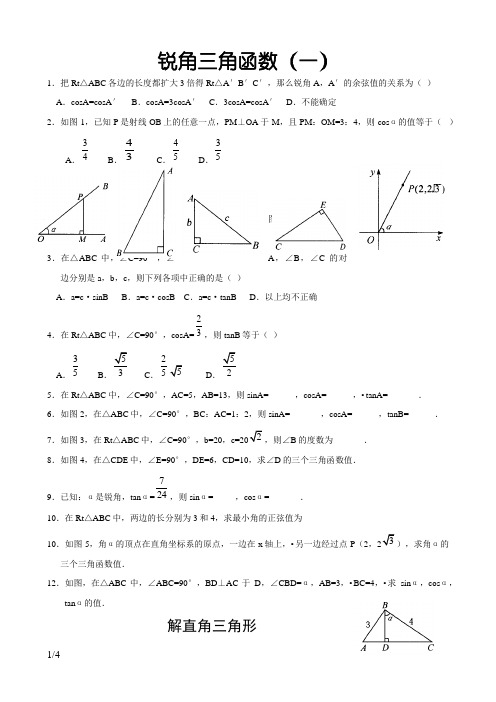
锐角三角函数(一)1.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A,A′的余弦值的关系为()A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定2.如图1,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值等于()A.34 B.43 C.45 D .35图 1 图 2 图3 图4图53.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是()A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确4.在Rt△ABC中,∠C=90°,cosA=23,则tanB等于()A.35 B.53 C.255 D.525.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinA=______,cosA=______,•tanA=_______.6.如图2,在△ABC中,∠C=90°,BC:AC=1:2,则sinA=_______,cosA=______,tanB=______.7.如图3,在Rt△ABC中,∠C=90°,b=20,c=202,则∠B的度数为_______.8.如图4,在△CDE中,∠E=90°,DE=6,CD=10,求∠D的三个三角函数值.9.已知:α是锐角,tanα=724,则sinα=_____,cosα=_______.10.在Rt△ABC中,两边的长分别为3和4,求最小角的正弦值为10.如图5,角α的顶点在直角坐标系的原点,一边在x轴上,•另一边经过点P(2,23),求角α的三个三角函数值.12.如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3,•BC=4,•求sinα,cosα,tanα的值.解直角三角形一、填空题1. 已知cosA=23,且∠B=900-∠A ,则sinB=__________.2. 在Rt △ABC 中,∠C 为直角,cot(900-A)=1.524,则tan(900-B)=_________.3. ∠A 为锐角,已知sinA=135,那么cos (900-A)=___________.4. 已知sinA=21(∠A 为锐角),则∠A=_________,cosA_______,tanA=__________.5. 用不等号连结右面的式子:cos400_______cos200,sin370_______sin420.6. 若cot α=0.3027,cot β=0.3206,则锐角α、β的大小关系是______________. 7. 计算: 2sin450-3tan600=____________. 8. 计算: (sin300+tan450)·cos600=______________.9. 计算: tan450·sin450-4sin300·cos450+6cot600=__________.10. 计算: tan 2300+2sin600-tan450·sin900-tan600+cos 2300=____________. 二、选择题:1. 在Rt △ABC 中,∠C 为直角,AC=4,BC=3,则sinA=( )A . 43;B . 34;C .53;D . 54.2. 在Rt △ABC 中,∠C 为直角,sinA=22,则cosB 的值是( )A .21;B .23;C .1;D .223. 在Rt △ABC 中,∠C 为直角,∠A=300,则sinA+sinB=( )A .1;B .231+;C .221+;D .414. 当锐角A>450时,sinA 的值( )A .小于22; B .大于22; C .小于23; D .大于235. 若∠A 是锐角,且sinA=43,则( )A .00<∠A<300; B .300<∠A<450;C .450<∠A<600;D . 600<∠A<9006. 当∠A 为锐角,且tanA 的值大于33时, ∠A( )A .小于300; B .大于300; C .小于600; D .大于6007. 如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan ∠BCD 等于( )A .43;B .34;C .53;D .548. Rt △ABC 中,∠C 为直角,AC=5,BC=12,那么下列∠A 的四个三角函数中正确的是( )A . sinA=135; B .cosA=1312; C . tanA=1213;D . cotA=1259. 已知α为锐角,且21<cos α<22,则α的取值范围是( )A .00<α<300;B .600<α<900;C .450<α<600;D .300<α<450.三、解答题1、 在△ABC 中,∠C 为直角,已知AB=23,BC=3,求∠B 和AC .2、在△ABC 中,∠C 为直角,直角边a=3cm ,b=4cm ,求sinA+sinB+sinC 的值.3、在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知b=3, c=14. 求∠A 的四个三角函数.4、在△ABC 中,∠C 为直角,不查表解下列问题: (1)已知a=5,∠B=600.求b ; (2)已知a=52,b=56,求∠A .5、在△ABC 中,∠C 为直角, ∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知a=25,b=215,求c 、∠A 、∠B .6、在Rt △ABC 中,∠C =90°,由下列条件解直角三角形: (1) 已知a =156, b =56,求c; (2) 已知a =20, c =220,求∠B ; (3) 已知c =30, ∠A =60°,求a ;(4) 已知b =15, ∠A =30°,求a .7、已知:如图,在ΔABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,若∠B =30°,CD =6,求AB 的长.8、已知:如图,在山脚的C 处测得山顶A 的仰角为︒45,沿着坡度为︒30︒=∠30DCB ,400=CD 米),测得A 的仰角为︒60,求山的高度DCAB9、会堂里竖直挂一条幅AB,如图5,小刚从与B成水平的C点观察,视角∠C=30°,当他沿CB方向前进2米到达到D时,视角∠ADB=45°,求条幅AB的长度。
《锐角三角函数》知识点及练习3篇

《锐角三角函数》知识点及练习3篇知识框架知识概念1.Rt△ABC(1)∠A的对边与斜边的比值是∠A的正弦,记作sinA=∠A的对边斜边(2)∠A的邻边与斜边的比值是∠A的余弦,记作cosA=∠A的邻边斜边(3)∠A的对边与邻边的比值是∠A的正切,记作tanA=∠A的对边∠A的邻边(4)∠A的邻边与对边的比值是∠A的余切,记作cota=∠A的邻边∠A的对边2.特殊值的三角函数1.求出下图中sinD ,sinE 的值.2.把Rt △ABC 各边的长度都扩大2倍得Rt △A ′B ′C ′,那么锐角A 、A ′的正弦值的关系为( )A .sinA =sinA ′B .sinA =2sinA ′C .2sinA =sinA ′D .不能确定 3.在Rt △ABC 中,∠C=90°,若AB =5,AC =4,则sinB 的值是( )A . 35B . 45C . 34D . 434.如图,△ABC 中,AB=25,BC=7,CA=24.求sinA 的值.25247C BA5.计算:sin30°·sin 60°+sin45°6.如图,B 是线段AC 的中点,过点C 的直线l 与AC 成60°的角,在直线上取一点P ,连接AP 、PB ,使sin ∠APB=12,则满足条件的点P 的个数是( ) A .1个 B .2个 C .3个 D .不存在7.如图,△ABC 中,∠A 是锐角,求证:1sin 2ABC S AB AC A ∆=⋅⋅8.等腰△ABC 中,AB=AC=5,BC=6,求sinA 、sinB .lCBA (第7题图)85F E D1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若b=3a,则tanA= .2.在△ABC中,∠C=90°,cosAc=4,则a=_______.3.如果a∠是等腰直角三角形的一个锐角,则cosα的值是()A.12B.2C.1D.4.如图,P是∠α的边OA上一点,且P点坐标为(2,3),则sinα=_______,cosα=_________,tanα=______ _.5.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=AB=tan∠ACD的值为()A.B. C D6.已知α是锐角,且cosα=34,求sinα、tanα的值.7.若α为锐角,试证明:sintancosααα=.8.如图,在Rt△ABC中,CD、CE分别为斜边AB上的高和中线,BC=a,AC=b(b>a),若tan∠DCE=12,求ab的值.9.如图,Rt△ABC中,∠C=90°,D为CA上一点,∠DBC=30°,DA=3,AB=,试求cosA与tanA的值.b aE DCBACBAD1.计算:(1)计算:()013sin 452007tan 30-+-(2) 先化简,再求值:()2221x xx x+-÷+1,其中,tan 60x = .2.如图,小明利用一个含60°角的直角三角板测量一栋楼的高度,已知他与楼之间的水平距离BD 为10m ,眼高AB 为1.6m (即小明的眼睛距地面的距离),那么这栋楼的高是( )A .(8105)m B .21.6m C ..85⎫+⎪⎪⎝⎭m3.已知AB 是半圆O 的直径,弦AD 、BC 相交于点P ,若∠DPB=α,那么CDAB等于( ) A .sin α B .COS α C .tan α D .1tan α4.如图,⊙O 的半径为3,弦AB 的长为5.求cosA 的值.5.如图,∠C=90°,∠DBC=45°,AB=DB ,利用此图求tan22.5°的值.E D CBA 第2题图第3题图。
【单元练】人教版初中九年级数学下册第二十八章《锐角三角函数》经典练习题(含答案解析)

一、选择题1.在ABC 中,若21cos |1tan |02A B ⎛⎫-+-= ⎪⎝⎭,则C ∠的度数是( ) A .45︒ B .60︒C .75︒D .105︒C解析:C 【分析】根据偶次方和绝对值的非负性可得1cos 02A -=,1tan 0B -=,利用特殊角的三角函数值可得A ∠和B 的度数,利用三角形内角和定理即可求解. 【详解】解:21cos |1tan |02A B ⎛⎫-+-= ⎪⎝⎭, 21cos 0,|1tan |02A B ⎛⎫∴-=-= ⎪⎝⎭,1cos 02A ∴-=,1tan 0B -=,则1cos 2A =,tan 1B =,解得:60A ∠=︒,45B ∠=︒, 则180604575C ∠=︒-︒-︒=︒. 故选:C . 【点睛】本题考查偶次方和绝对值的非负性、特殊角的三角函数值、三角形内角和定理,熟悉特殊角的三角函数值是解题的关键.2.如图,这是某市政道路的交通指示牌,BD 的距离为5m ,从D 点测得指示牌顶端A 点和底端C 点的仰角分别是60°和45°,则指示牌的高度,即AC 的长度是( )A .53mB .52mC .(5352mD .()535m D解析:D 【分析】由题意可得到BD=BC=5,根据锐角三角函数关系得出方程,然后解方程即可.【详解】解:由题意可得:∠CDB=∠DCB=45°, ∴BD=BC=5,设AC=x m ,则AB=(x +5)m , 在Rt △ABD 中,tan60°=AB BD, 则535x +=, 解得:535x =-, 即AC 的长度是()535m -; 故选:D . 【点睛】此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键. 3.下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度FE 为xm ,根据以上条件,可以列出的方程为 ( ) 题目测量铁塔顶端到地面的高度测量目标示意图相关数据10,45,50CD m αβ==︒=︒A .()10tan50x x =-︒B .()10cos50x x =-︒C .10tan50x x -=︒D .()10sin50x x =+︒A解析:A 【分析】过D 作DH ⊥EF 于H ,则四边形DCEH 是矩形,根据矩形的性质得到HE =CD =10,CE =DH ,求得FH =x−10,得到CE =x−10,根据三角函数的定义列方程即可得到结论. 【详解】过D 作DH ⊥EF 于H , 则四边形DCEH 是矩形, ∴HE =CD =10,CE =DH , ∴FH =x−10,∵∠FDH =α=45°, ∴DH =FH =x−10, ∴CE =x−10,∵tanβ=tan50°=EF CE =-10x x , ∴x =(x−10)tan 50°, 故选:A . 【点睛】本题考查了解直角三角形的应用,由实际问题抽象出边角关系的等式,正确的识别图形是解题的关键.4.下列计算中错误的是( ) A .sin60sin30sin30︒-︒=︒ B .22sin 45 cos 451︒+︒= C .sin 60tan 60sin 30︒︒=︒D .cos30tan 60cos60︒︒=︒A解析:A 【分析】根据特殊角的三角函数值、二次根式的运算即可得. 【详解】A、11sin 60sin 303022︒-︒==︒=,此项错误; B、222211sin 45 cos 45122︒+︒=+=+=⎝⎭⎝⎭,此项正确; C、sin 602tan 601sin 302︒︒===︒sin 60tan 60sin 30︒︒=︒,此项正确; D、cos302tan 601cos 602︒︒===︒cos30tan 60cos60︒︒=︒,此项正确; 故选:A . 【点睛】本题考查了特殊角的三角函数值、二次根式的运算,熟记特殊角的三角函数值是解题关键.5.如图,河坝横断面迎水坡AB 的坡比为1BC =3m ,则AB 的长度为( )A .6mB .33mC .9mD .63m A解析:A 【分析】根据坡比的概念求出AC ,根据勾股定理求出AB . 【详解】解:∵迎水坡AB 的坡比为1:3, ∴13BC AC =,即313AC =, 解得,AC =33, 由勾股定理得,AB 22BC AC =+=6(m ),故选:A . 【点睛】本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念是解题的关键. 6.如图,在A 处测得点P 在北偏东60︒方向上,在B 处测得点P 在北偏东30︒方向上,若2AB =米,则点P 到直线AB 距离PC 为( ).A .3米B 3米C .2米D .1米B解析:B 【分析】设点P 到直线AB 距离PC 为x 米,根据正切的定义用x 表示出AC 、BC ,根据题意列出方程,解方程即可. 【详解】解:设点P 到直线AB 距离PC 为x 米, 在Rt APC △中,3tan PCAC x PAC==∠,在Rt BPC △中,3tan PC BC x PBC ==∠,由题意得,3323x x -=, 解得,3x =(米),故选:B . 【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.7.如图,在平面直角坐标系中,边长为2的正方形ABCD 的对角线AC 在x 轴上,点A 的坐标是()1,0,把正方形ABCD 绕原点O 旋转180︒,则点B 的对应点B '的坐标是( )A .(-1,-1)B .()2,1C .()2,1--D .()2,1--D解析:D 【分析】根据题意,画出图形,连接BD ,交x 轴于E ,根据正方形的性质可得AB=2,BD ⊥x 轴,AE=BE ,∠BAE=45°,利用锐角三角函数即可求出AE 和BE ,从而求出OE ,即可求出点B 的坐标,然后根据关于原点对称的两点坐标关系即可求出结论. 【详解】解:把正方形ABCD 绕原点O 旋转180︒,如图所示,连接BD ,交x 轴于E∵四边形ABCD 2∴2,BD ⊥x 轴,AE=BE ,∠BAE=45° ∴AE=BE=AB·sin ∠BAE=1 ∴OE=OA +AE=2 ∴点B 的坐标为(2,1)∴点B 绕点O 旋转180°的对应点B '的坐标(-2,-1) 故选D . 【点睛】此题考查的是正方形的性质,锐角三角函数和关于原点对称的两点坐标关系,掌握正方形的性质,锐角三角函数和关于原点对称的两点坐标关系是解题关键. 8.如图,点A ,B ,C 在正方形网格的格点上,则sin ∠BAC=( )A .26B .2626C .2613D .1313B 解析:B 【分析】作BD ⊥AC 于D ,根据勾股定理求出AB 、AC ,利用三角形的面积求出BD ,最后在直角△ABD 中根据三角函数的意义求解. 【详解】解:如图,作BD ⊥AC 于D ,由勾股定理得,22223213,3332AB AC =+==+= ∵1113213222ABCSAC BD BD =⋅=⨯=⨯⨯, ∴2BD =, ∴2262sin 2613BD BAC AB ∠===. 故选:B . 【点睛】本题考查了勾股定理,解直角三角形,三角形的面积,三角函数的意义等知识,根据网格构造直角三角形和利用三角形的面积求出BD 是解决问题的关键.9.如图,在平面直角坐标系中,等边三角形OAB 的边长为4,点A 在第二象限内,将OAB 沿射线AO 平移,平移后点A '的横坐标为43,则点B ′的坐标为( )A .(63,2)-B .(63,23)-C .()6,2-D .(63,2)-D解析:D 【详解】如解图,过点A 作AC x ⊥轴,过点A '作A D x '⊥轴,∵AOB 是等边三角形,∴4AO BO ==,60AOB ∠=︒,∴30AOC ∠=︒,∴·cos 23CO OA AOC ==,2AC =,∴(23,2)A -,∵30AOD AOC ∠'=∠=︒,43OD =,∴·t 34343an A D OD A OD ⨯=∠'==',∴(43,4)A '-,∴点A '是将点A 向右平移63个单位,向下平移6个单位得到的,∴点B '也是将点B 向右平移63个单位,向下平移6个单位得到的,∵()0,4B ,∴B '的坐标为(63,2)-.10.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt △ACB 中,∠C =90°,∠ABC =30°,延长CB 使BD =AB ,连接AD ,得∠D =15°,所以tan15°()()12323232323AC CD -====-++-.类比这种方法,计算tan22.5°的值为( )A 21B 2﹣1C 2D .12B 解析:B 【分析】作Rt △ABC ,使∠C =90°,∠ABC =45°,延长CB 到D ,使BD =AB ,连接AD ,根据构造的直角三角形,设AC =x ,再用x 表示出CD ,即可求出tan22.5°的值. 【详解】解:作Rt △ABC ,使∠C =90°,∠ABC =90°,∠ABC =45°,延长CB 到D ,使BD =AB ,连接AD ,设AC =x ,则:BC =x ,AB =2x ,CD =()1+2x ,()22.5==211+2AC xC tan taD xn D =∠=-︒故选:B. 【点睛】本题考查解直角三角形,解题的关键是根据阅读构造含45°的直角三角形,再作辅助线得到22.5°的直角三角形.二、填空题11.已知ABC 与ABD △不全等,且3AC AD ==,30ABD ABC ∠=∠=︒,60ACB ∠=︒,则CD =________.或3【分析】如图△ABC ≌△ABP 当D′是PB 中点或点D″是BC 的中点时满足条件分别求解即可【详解】解:如图△ABC ≌△ABP ∴∴CAP 共线∴△BPC 是等边三角形当D′是PB 中点时AD′=BP=AC解析:3或3 【分析】如图,△ABC ≌△ABP ,当D′是PB 中点或点D″是BC 的中点时,满足条件,分别求解即可. 【详解】解:如图,△ABC ≌△ABP ,3AC AP ==,30ABP ABC ∠=∠=︒,60ACB ∠=︒,∴60APB ∠=︒,90CAB PAB ∠=∠=︒, ∴C ,A ,P 共线,BC BP AC AP ===, ∴△BPC 是等边三角形,当D′是PB 中点时,AD′=12BP=AC=3,此时ABC 与D'AB 满足条件, ∴D'90C P ∠=︒,∴CD′= PD′tan 60︒=3PD′=3,当点D″是BC 的中点时,此时ABC 与D AB "也满足条件, ∴CD″=3,∴满足条件的CD 的长为3或3. 故答案为:3或3. 【点睛】本题考查等边三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是画出符合题意的图形,用分类讨论的思想思考问题.12.小芳同学在学习了图形的镶嵌和拼接以后,设计了一幅瓷砖贴纸(图1),它是由图2这种基本图形拼接而成。
人教版九年级数学下册第28章《锐角三角函数》单元测试【含答案】

人教版九年级数学下册第28章《锐角三角函数》单元测试一.选择题(共10小题,满分30分)1.在Rt△ABC中,∠C=90°,若cos A=( )A.B.C.D.2.在边长相等的小正方形组成的网格中,点A,B,C都在格点上( )A.B.C.D.3.在Rt△ABC中,∠C=90°,BC=1,那么tan B的值是( )A.B.C.D.4.∠β为锐角,且2cosβ﹣1=0,则∠β=( )A.30°B.60°C.45°D.37.5°5.在Rt△ABC中,∠C=90°,AB=5,则tan A的值是( )A.B.C.D.6.如图,在Rt△ABC中,∠C=90°,则sin B=( )A.B.2C.D.7.若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是( )A.B.C.D.8.如图,AD是△ABC的高,AB=4,tan∠CAD=,则BC的长为( )A. +1B.2+2C.2+1D. +49.如图,半径为3的⊙O内有一点A,OA=,当∠OPA最大时,S△OPA等于( )A.B.C.D.110.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,∠C=42°,AB=60( )A.60sin50°B.C.60cos50°D.60tan50°二.填空题(共10小题,满分30分)11.在Rt△ABC中,∠C=90°,sin A= .12.用科学计算器计算: tan16°15′≈ (结果精确到0.01)13.在△ABC中,若,∠A,∠B都是锐角 三角形.14.在Rt△ABC中,∠C=90°,AC=6,那么AB的长为 .15.比较大小:sin80° tan50°(填“>”或“<”).16.在Rt△ABC中,∠C=90°,cos A= .17.在△ABC中,若|sin A﹣|+(﹣cos B)2=0,则∠C的度数是 .18.如图,在Rt△ABC中,CD是斜边AB上的中线,AC=6,则tan A的值为 .19.如图,在Rt△ABC中,∠ACB=90°,连接CD,过点B作CD的垂线,tan A=,则cos∠DBE的值为 .20.如图,河坝横断面迎水坡AB的坡比是1:(坡比是坡面的铅直高度BC与水平宽度AC之比),水平宽度AC=m 米.三.解答题(共7小题,满分6021.已知cos45°=,求cos21°+cos22°+…+cos289°的值.22.如图,在Rt△ABC中,∠C=90°,BC=5.求sin A,cos A和tan A.23.如图,在Rt△ABC中,∠C=90˚,BC=6,求AC的长和sin A的值.24.计算:cos60°﹣2sin245°+tan230°﹣sin30°.25.计算:(1);(2)sin245°+cos245°+tan30°tan60°﹣cos30°.26.2022年8月21日,重庆市北碚区缙云山突发山火,山火无情,各地消防迅速出动,冲锋在前,然后沿着坡比为5:12的斜坡前进104米到达B处平台,继续前进到达C,沿斜坡CD前行800米到达着火点D.(1)求着火点D距离山脚的垂直高度;(2)已知消防员在平地的平均速度为4m/s,求消防员通过平台BC的时间.(保留一位小数)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈,≈1.732)27.如图,已知∠ABC和射线BD P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.(1)若∠EBP=40°,∠FBP=20°,PB=m;(2)若∠EBP=α,∠FBP=β,α,β都是锐角,并给出证明.参考答案与试题解析一.选择题(共10小题,满分30分)1.解:如图,∵∠C=90°,∴设AC=5k,AB=13k,根据勾股定理得,BC==,所以,sin A===.故选:D.2.解:设点C到AB的距离为h,由勾股定理可知:AC==2=,由于S△ABC=32﹣×6×2﹣×7×3=9﹣8﹣3=4.∴AB•h=4,∴h=,∴sin∠BAC==,∴cos∠BAC=,故选:A.3.解:∵∠C=90°,∴tan B===.故选:D.4.解:∵∠β为锐角,且2cosβ﹣1=8,∴cosβ=,∴∠β=60°.故选:B.5.解:∵∠C=90°,AB=5,∴AC===4,∴tan A==,故选:D.6.解:∵∠C=90°,tan A=2,∴BC=2AC,∴,∴,故C正确.故选:C.7.解:若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是.故选:C.8.解:∵AD是△ABC的高,∴∠ADB=∠ADC=90°,在Rt△ABD中,cos∠BAD=,∴cos60°=,sin60°=,∴AD=4cos60°=7×=5=4,在Rt△ADC中,tan∠CAD=,∴=,解得CD=1,∴BC=BD+CD=2+1.故选:C.9.解:如图所示:∵OA、OP是定值,∴PA⊥OA时,∠OPA最大,在直角三角形OPA中,OA=,∴PA==,∴S△OPA=OA•AP=××=.故选:B.10.解:过点A作AD⊥BC于点D,如图所示:∵∠BAC=88°,∠C=42°,∴∠B=180°﹣88°﹣42°=50°,在Rt△ABD中,AD=AB×sin60×sin50°,∴点A到BC的距离为60sin50°,故A正确.故选:A.二.填空题(共10小题,满分30分)11.解:由sin A=知,可设a=6x,b=3x.∴tan A=.故答案为:.12.解: tan16°15′≈0.71,故答案为:4.71.13.解:∵,∴sin A=,cos B=,∴∠A=60°,∠B=60°,∴△ABC是等边三角形.故答案为:等边.14.解:∵cos A==,AC=7,∴AB==8,故答案为:8.15.解:∵tan50°>tan45°,tan45°=1,∴tan50°>1,又sin80°<2,∴sin80°<tan50°;故答案为:<.16.解:∵在△ABC中,∠C=90°,∴∠A+∠B=90°,∴sin B=cos A=.故答案为:.17.解:∵|sin A﹣|+(2=2,∴sin A﹣=4,,即sin A=,cos B=,∴∠A=30°,∠B=45°,∴∠C=180°﹣∠A﹣∠B=105°.故答案为:105°.18.解:在Rt△ABC中,CD是斜边AB上的中线,∴AB=2CD=10,∵AC=6,∴BC===8,∴tan A===,故答案为:.19.解:过点C作CF⊥AB,垂足为F,在Rt△ABC中,AC=3a=,∴BC=4a,AB=5a,∵D是AB的中点,∴CD=AB=a,∵△ABC的面积=AB•CF=,∴AB•CF=AC•CB,∴5aCF=3a×4a,∴CF=a,∴cos∠DCF==,∵BE⊥CD,∴∠E=90°,∴∠EDB+∠EBD=90°,∵∠FCD+∠CDF=90°,∠CDF=∠BDE,∴∠EBD=∠DCF,∴cos∠DBE=cos∠DCF=,故答案为:.20.解:∵河坝横断面迎水坡AB的坡比是1:,AC=m,∴=,∴BC=AC==3(m),在Rt△ABC中,由勾股定理得:AB==,故答案为:6.三.解答题(共7小题,满分60分)21.解:原式=(cos21°+cos289°)+(cos22°+cos588°)+…+(cos244°+cos246°)+cos445=(sin21°+cos51°)+(sin22°+cos22°)+…+(sin844°+cos244°)+cos245=44+()2=44.22.解:在Rt△ABC中,∠C=90°,BC=5.∴AB===13,∴sin A==,cos A==,tan A==.23.解:∵△ABC中,tan A=,∴=,∴AC=8,∴AB===10,∴sin A==24.解:原式=﹣4×()6+×()2﹣=﹣2×+×﹣=﹣2+﹣=﹣.25.解:(1)=﹣4﹣7+1=﹣4;(2)sin645°+cos245°+tan30°tan60°﹣cos30°===.26.(1)如图所示,过点B,C,D分别作水平线的垂线,F,G,延长BC交AG于点H,BHGE是矩形,依题意,,AB=104米,CD=800米,在Rt△ABE中,,设BE=8k米,∴AB=13k,∵AB=104米,∴k=8,∴BE=5×2=40(米),AE=12×8=96(米),在Rt△DCH中,CD=800米,∴DG=DH+HG=DH+BE=480+40=520(米),即着火点D距离山脚的垂直高度为520米;(2)依题意,∠DAG=30°,∴米,∵Rt△DCH中,CH=cos37°×CD=≈0.8×800=640(米),又AE=96米,∴(米),∵消防员在平地的平均速度为4m/s,∴消防员通过平台BC的时间为(秒).27.解:(1)在Rt△BPE中,sin∠EBP=在Rt△BPF中,sin∠FBP=又sin40°>sin20°∴PE>PF;(2)根据(1)得sin∠EBP==sinα=sinβ又∵α>β∴sinα>sinβ∴PE>PF.。
人教版九年级数学下册第二十八章: 锐角三角函数 练习(含答案)

第二十八章 锐角三角函数一、单选题1.在Rt △ABC 中,∠C=90°,AC=12,BC=5,则sinA 的值为( )A .B .C .D . 2.(2016甘肃省兰州市)在Rt △ABC 中,∠C =90°,sin A =35,BC =6,则AB =( ) A .4 B .6 C .8 D .103.在Rt △ABC 中,∠C=90°,sinB=513,则tanA 的值为( ) A .513 B .1213 C .512 D .1254.Rt ABC 中,C 90∠=,若BC 2=,AC 3=,下列各式中正确的是 ( ) A .2sinA 3= B .2cosA 3= C .2tanA 3= D .2cotA 3= 5.如图,过点C (﹣2,5)的直线AB 分别交坐标轴于A (0,2),B 两点,则tan ∠OAB=( )A .25B .23C .52D .326.如图,某超市自动扶梯的倾斜角 为 ,扶梯长 为 米,则扶梯高 的长为( )A.米B.米C.米D.米7.聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早期,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考≈3.162)()A.15.81米B.16.81米C.30.62米D.31.62米8.若某人沿坡角为α的斜坡前进100m,则他上升的最大高度是()A.100 αm B.100sinαm C.100cosαm D.100 αm9.某水坝的坡度i=1,坡长AB=20米,则坝的高度为()A.10米B.20米C.40米D.2010.如图,两建筑物的水平距离为32 m,从点A测得点C的俯角为30°,点D的俯角为45°,则建筑物CD的高约为()A.14 m B.17 m C.20 m D.22 m二、填空题11.2sin45°+2sin60°﹣=_____. 12.在Rt △ABC 中,∠C =90°,AB =5,BC =3,则sin A = .13.某同学沿坡比为1: 的斜坡前进了90米,那么他上升的高度是______米14.如图,在边长相同的小正方形网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 与CD 相交于点P ,则tan ∠APD 的值为______.三、解答题15.计算:|﹣2|﹣2cos60°+(16)﹣1﹣(π0. 16.如图,为了测得某建筑物的高度AB ,在C 处用高为1米的测角仪CF ,测得该建筑物顶端A 的仰角为45°,再向建筑物方向前进40米,又测得该建筑物顶端A 的仰角为60°.求该建筑物的高度AB .(结果保留根号)17.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=13,AD=1.(1)求BC的长;(2)求tan∠DAE的值.18.如图,为了测量出楼房AC的高度,从距离楼底C处D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据: 53°≈0.8, 53°≈0.6, 53°≈43,计算结果用根号表示,不取近似值).答案1.D2.D3.D4.C5.B6.A7.A8.A9.A10.A1112.3513.4514.215.|﹣2|﹣2cos60°+(16)﹣1﹣(π﹣ )0 =2﹣2×12+6﹣1 =6.16.解:设AM x =米,在Rt AFM ∆中,45AFM ︒∠=,∴FM AM x ==,在Rt AEM ∆中,AM tan EMAEM ∠=,则tan AM EM x AEM ==∠, 由题意得,FM EM EF -=,即40x x -=,解得,60x =+,∴61AB AM MB =+=+答:该建筑物的高度AB为(61+米.17.解:(1)在△ABC 中,∵AD 是BC 边上的高,∴∠ADB=∠ADC=90°。
初中锐角三角函数习题及详细答案
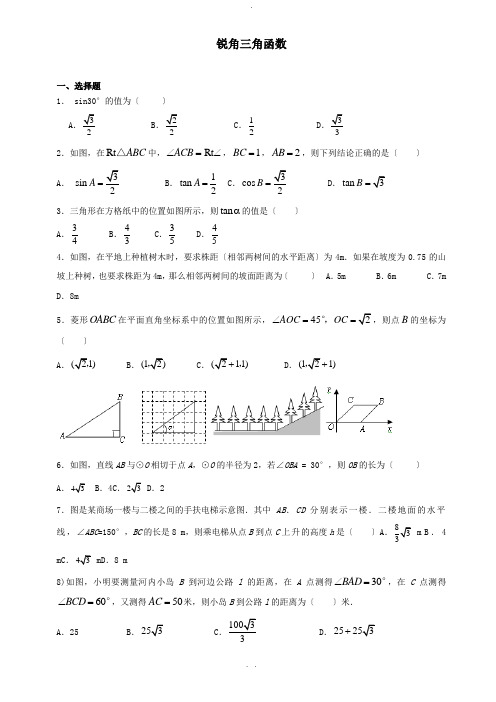
锐角三角函数一、选择题1. sin30°的值为〔 〕 A .32B .22C .12D .332.如图,在Rt ABC △中,ACB ∠=Rt ∠,1BC =,2AB =,则下列结论正确的是〔 〕 A . 3sin 2A =B .1tan 2A = C .3cos 2B = D .tan 3B =3.三角形在方格纸中的位置如图所示,则tan α的值是〔 〕 A .34B .43 C .35 D .454.如图,在平地上种植树木时,要求株距〔相邻两树间的水平距离〕为4m .如果在坡度为0.75的山坡上种树,也要求株距为4m ,那么相邻两树间的坡面距离为〔 〕 A .5m B .6m C .7m D .8m5.菱形OABC 在平面直角坐标系中的位置如图所示,452AOC OC ∠==°,,则点B 的坐标为〔 〕A .(21),B .(12),C .(211)+,D .(121)+,6.如图,直线AB 与⊙O 相切于点A ,⊙O 的半径为2,若∠OBA = 30°,则OB 的长为〔 〕 A .43.4C .23.27.图是某商场一楼与二楼之间的手扶电梯示意图.其中AB .CD 分别表示一楼.二楼地面的水平线,∠ABC =150°,BC 的长是8 m ,则乘电梯从点B 到点C 上升的高度h 是〔 〕A 833m B .4 mC .43 mD .8 m8)如图,小明要测量河内小岛B 到河边公路l 的距离,在A 点测得30BAD ∠=°,在C 点测得60BCD ∠=°,又测得50AC =米,则小岛B 到公路l 的距离为〔 〕米.A .25B .253C .10033D .253+9.如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为32,2AC =,则sin B 的值是〔〕A .23 B .32C .34D .4310.将宽为2cm 的长方形纸条折叠成如图所示的形状,那么折痕PQ 的长是〔〕A .233cmB .433cmC .5cmD .2cm 11.如图,在矩形ABCD 中,DE ⊥AC 于E ,∠EDC ∶∠EDA=1∶3,且AC=10,则DE 的长度是〔〕 A .3B .5C .25D .225 12.如图,已知△ABC 中,∠ABC =90°,AB =BC ,三角形的顶点在相互平行的三条直线l 1,l 2,l 3上,且l 1,l 2之间的距离为2 , l 2,l 3之间的距离为3 ,则AC 的长是〔 〕A .172B .52C .24D .713.如图4,在Rt ABC △中, 90=∠ACB ,86AC BC ==,,将ABC △绕AC 所在的直线k 旋转一周得到一个旋转体,则该旋转体的侧面积为〔 〕 A .30π B .40πC .50π D .60π14.在一次夏令营活动中,小亮从位于A 点的营地出发,沿北偏东60°方向走了5km 到达B 地,然后再沿北偏西30°方向走了若干千米到达C 地,测得A 地在C 地南偏西30°方向,则A .C 两地的距离为〔 〕 〔A 〕km 3310 〔B 〕km 335〔C 〕km 25 〔D 〕km 35 15.如图,在梯形ABCD 中,AD//BC ,AC ⊥AB ,AD =CD ,cos ∠DCA=54,BC =10,则AB 的值是〔 〕 A .3B .6C .8D .916.如图,AB 是O ⊙的直径,弦CD AB ⊥于点E ,连结OC ,若5OC =,8CD =,则tan COE ∠=〔 〕A .35 B .45 C .34 D .4317.为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道倾斜角α的正切值是〔 〕 A .14B .4C .117D .41718.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为〔 〕 A. αcos 5 B.αcos 5 C. αsin 5 D. αsin 519. 如图,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,54A cos =,则下列结论中正确的个数为〔 〕 ①DE=3cm ; ②EB=1cm ; ③2ABCD 15S cm =菱形.A .3个B .2个C .1个D .0个20.已知圆锥的底面半径为5cm ,侧面积为65πcm 2,设圆锥的母线与高的夹角为θ〔如图所示〕,则sinθ的值为〔 〕 〔A 〕125 〔B 〕135 〔C 〕1310 〔D 〕131221.如图,已知RtΔABC 中,∠ACB =90°,AC = 4,BC=3,以AB 边所在的直线为轴,将ΔABC 旋转一周,则所得几何体的表面积是〔 〕. A .π5168 B .π24C .π584D .π12 22.如图,在ABC △中,C ∠9060B D =∠=°,°,是AC 上一点,DE AB ⊥于E ,且21CD DE ==,,则BC 的长为〔 〕A .2B .433C .23D .4323.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角〔梯子与地面的夹角〕不能大于60°,否则就有危险,那么梯子的长至少为〔 〕 A .8米B.CD.3米 24.〕已知在Rt ABC △中,390sin 5C A ∠==°,,则tan B 的值为〔 〕 A .43B .45C .54D .3425. 2sin 30°的值等于〔 〕A .1 BCD .2 26.已知在Rt ABC △中,390sin 5C A ∠==°,,则tan B 的值为〔 〕 A .43B .45C .54D .3427.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角〔梯子与地面的夹角〕不能大于60°,否则就有危险,那么梯子的长至少为〔 〕 A .8米B.CD米 28.一根电线杆的接线柱部分AB 在阳光下的投影CD 的长为1米,太阳光线与地面的夹角60ACD ∠=°,则AB 的长为〔 〕 A .12米B米C.2米 D.3米 二、计算题〔每小题3分,共12分〕 1.计算:()1200911sin 602-⎛⎫-+-- ⎪⎝⎭°2.10120094sin 3022⎛⎫--+-- ⎪⎝⎭-(3.计算:0200912sin 603tan 30(1)3⎛⎫-++- ⎪⎝⎭°°.4.先化简.再求值.22 ()2111a a a a a ++÷+-- 其中a =tan60°-2sin30°.三、解答题1.〕如图,AC 是O ⊙的直径,PA ,PB 是O ⊙的切线,A ,B 为切点,AB =6,PA =5.求〔1〕O ⊙的半径;〔2〕sin BAC ∠的值.2.〔4分〕〔20XXXX 〕如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A 处测得灯塔C 在北偏西30°方向,轮船航行2小时后到达B 处,在B 处测得灯塔C 在北偏西60°方向.当轮船到达灯塔C 的正东方向的D 处时,求此时轮船与灯塔C 的距离.〔结果保留根号〕CDBA北60°30°CCAB60° 45°北北3.〕为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A 北偏西45︒并距该岛20海里的B 处待命.位于该岛正西方向C 处的某外国商船遭到海盗袭击,船长发现在其北偏东60︒的方向有我军护航舰〔如图9所示〕,便发出紧急求救信号.我护航舰接警后,立即沿BC 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该据:2 1.43 1.7≈,≈〕商船所在的位置C 处?〔结果精确到个位.参考数4.如图,某飞机于空中A 处探测到地平面目标B ,此时从飞机上看目标B 的俯角为α,若测得飞机到目标B 的距离AB 约为2400米,已知sin 0.52α=,求飞机飞行的高度AC 约为多少米?5.如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为︒60,看这栋高楼底部的俯角为︒30,热气球与高楼的水平距离为66 m ,这栋高楼有多高?〔结果精确到0.1 m ,参考数据:73.13≈〕BC AαC AB1.C 2. D 3。
《锐角三角函数》习题(含答案)

《锐⾓三⾓函数》习题(含答案)《锐⾓三⾓函数》⼀、选择题1. 4sin tan 5ααα=若为锐⾓,且,则为 ( )933425543A B C D ....2.在Rt△ABC 中,∠C = 90°,下列式⼦不⼀定成⽴的是()A .sinA = sinB B .cosA=sinBC .sinA=cosBD .∠A+∠B=90°3.直⾓三⾓形的两边长分别是6,8,则第三边的长为()A .10B .C .10或D .⽆法确定4.在Rt△ABC 中,∠C=90°,当已知∠A 和a 时,求c ,应选择的关系式是()A .c =B .c =C .c = a·tanAD .c = sin a A cos a A tan a A 5、的值等于()o o 45cos 45sin +A. B. C. D. 12213+36.在Rt△ABC 中,∠C=90°,tan A=3,AC 等于10,则S△ABC 等于( )A. 3B. 300C.D. 155037.当锐⾓α>30°时,则cosα的值是()A .⼤于B .⼩于CD 12128.⼩明沿着坡⾓为30°的坡⾯向下⾛了2⽶,那么他下降()A .1⽶B ⽶C .9.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=()(A )4 (B )5 (C )(D10.已知Rt△ABC 中,∠C=90°,tanA=,BC=8,则AC 等于()43 A .6 B . C .10 D .12323⼆、填空题11.计算2sin30°+2cos60°+3tan45°=_______.12.若sin28°=cosα,则α=________.13.已知△ABC 中,∠C=90°,AB=13,AC=5,则tanA=______.14.某坡⾯的坡度为1,则坡⾓是_______度.15.在△ABC 中,∠C =90°,AB =10cm ,sinA =,则BC 的长为_______cm .5416.如图,在⾼楼前点测得楼顶的仰⾓为,向⾼楼前进60⽶到点,⼜测得仰⾓为,则该⾼楼的D 30?C 45?⾼度⼤约为A.82⽶B.163⽶C.52⽶D.70⽶17.如图,⼩鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的⾼度CD =1m ,测得旗杆顶端B 的仰⾓=60°,则旗杆AB 的⾼度为.(计算结果保留根号)α(16题)三、解答题18.由下列条件解直⾓三⾓形:在Rt△ABC 中,∠C=90°:(1)已知a=4,b=8,(2)已知b=10,∠B=60°.(3)已知c=20,∠A=60°. (4) (2)已知a=5,∠B=35°19.计算下列各题.(1)s in 230°+cos 2sin60°·tan45°;(2)+ sin45°22cos 30cos 60tan 60tan 30?+四、解下列各题20.如图所⽰,平地上⼀棵树⾼为5⽶,两次观察地⾯上的影⼦,第⼀次是当阳光与地⾯成45°时,第⼆次是阳光与地⾯成30°时,第⼆次观察到的影⼦⽐第⼀次长多少⽶?(第21.如图,AB 是江北岸滨江路⼀段,长为3千⽶,C 为南岸⼀渡⼝,为了解决两岸交通困难,拟在渡⼝C 处架桥.经测量得A 在C 北偏西30°⽅向,B 在C 的东北⽅向,从C 处连接两岸的最短的桥长多少?(精确到0.1)22. 如图,点A 是⼀个半径为300⽶的圆形森林公园的中⼼,在森林公园附近有B 、C 两个村庄,现要在B 、C 两村庄之间修⼀条长为1000⽶的笔直公路将两村连通,经测得∠ABC=45o ,∠ACB=30o ,问此公路是否会穿过该森林公园?请通过计算进⾏说明。
锐角三角函数练习及答案

锐角三角函数练习及答案1.在Rt △ABC 中,∠C=90°,若AB=√5,BC=2,则sin B 的值为 ( ) A .√55B .2√55 C .12D .22.如图K24-1,已知△ABC 的三个顶点均在格点上,则cos A 的值为( )图K24-1A .√33B .√55C .2√33 D .2√553.如图K24-2,点A (t ,3)在第一象限,OA 与x 轴所夹的锐角为α,tan α=32,则t 的值是( )图K24-2A .1B .1.5C .2D .3 4.在Rt △ABC 中,已知∠C=90°,∠A=40°,BC=3,则AC= ( )A .3sin40°B .3sin50°C .3tan40°D .3tan50°5.如图K24-3,在矩形ABCD 中,AB=8,BC=12,点E 是BC 的中点,连接AE.将△ABE 沿AE 折叠,使点B 落在点F 处,连接FC ,则sin ∠ECF= ( )图K24-3A .34 B .43 C .35 D .456.如图K24-4,在Rt △ABC 中,∠ACB=90°,AC=8,BC=6,CD ⊥AB ,垂足为D ,则tan ∠BCD 的值是 .图K24-4图K24-57.如图K24-5,每个小正方形的边长都为1,点A,B,C都在小正方形的顶点上,则∠ABC的正弦值为.8.在△ABC中,∠A=45°,AB=√6,BC=2,则AC的长为.图K24-6,则▱ABCD的9.如图K24-6,在▱ABCD中,对角线AC,BD相交于点O.若AB=4,BD=10,sin∠BDC=35面积是.10.如图K24-7,根据图中数据完成填空,再按要求答题:图K24-7sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= ;(2)如图K24-8,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明你的猜想.图K24-8.锐角三角形ABC 11.如图K24-9,线段BC长为13,以C为顶点,CB为一边的∠α满足cosα=513.求△ABC的高BD及AB边的长,并结合你的的顶点A落在∠α的另一边l上,且满足sin A=45计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)图K24-9参考答案1.A2.D[解析] 如图,设小正方形的边长为1,AC与网格的一个交点为D,连接BD,由题意,得∠BDC=45°+45°=90°,∴∠BDA=90°,∵AD=√22+22=2√2,AB=√12+32=√10,∴cos A=AD AB =√2√10=2√55.故选D .3.C [解析] ∵点A (t ,3)在第一象限,∴AB=3,OB=t.又∵tan α=AB OB =32,∴t=2. 4.D [解析] ∵∠B=90°-∠A=90°-40°=50°,tan B=ACBC ,∴AC=BC ·tan B=3tan50°. 5.D [解析] ∵点E 是BC 的中点,BC=12,∴BE=6. ∵矩形ABCD ,∴∠B=90°, ∵AB=8,∴AE=10.由翻折的性质,得∠AEB=∠AEF ,BE=EF=CE. ∴∠ECF=∠EFC.∵∠BEF=∠ECF+∠EFC , ∴∠AEB=∠ECF ,∴sin ∠ECF=sin ∠AEB=AB AE =45.故选D .6.34 7.√228.√3+1或√3-19.24 [解析] 如图,作CE ⊥BD 于E ,在Rt △CDE 中,∵sin ∠BDC=35=CE CD =CE AB ,AB=4,∴CE=125,S ▱ABCD=2×12×BD ×CE=24.10.解:1 1 1 (1)1(2)证明:∵sin A=ac ,sin B=bc ,a 2+b 2=c 2,∴sin 2A+sin 2B=a 2c 2+b 2c 2=a 2+b 2c 2=1.11.解:如图,作BD ⊥l 于点D.在Rt △CBD 中,∠CDB=90°,BC=13,cos C=cos α=513,∴CD=BC ·cos C=13×513=5,∴BD=√BC 2-CD 2=√132-52=12.在Rt △ABD 中,∠ADB=90°,BD=12,sin A=45,∴AB=BD sinA =1245=15,AD=BD tanA =1243=9.作图:以点D 为圆心,9为半径作弧与射线l 交于点A ,连接AB.。
人教版九年级下册第二十八章 《锐角三角函数》单元练习题(含答案)

人教版九年级下册第二十八章《锐角三角函数》单元练习题(含答案)一、选择题1.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于()A.B.C.D.2.在Rt△ABC中,∠C=90°,AB=6,cos B=,则BC的长为()A.4B.2C.D.3.已知∠A为锐角,且tan A=,则∠A的取值范围是()A.0°<∠A<30°B.30°<∠A<45°C.45°<∠A<60°D.60°<∠A<90°4.把Rt△ABC各边的长度都缩小为原来的得Rt△A′B′C′,则锐角A、A′的余弦值之间的关系是()A.cos A=cos A′B.cos A=5cos A′C.5cos A=cos A′D.不能确定5.Rt△ABC中,∠C=90°,tan A=,AC=6 cm,那么BC等于()A.8 cmB.cmC.cmD.cm6.在△ABC中,∠C=90°,已知tan A=,则cos B的值等于()A.B.C.D.7.在Rt△ABC中,∠C=90°,AB=6,cos B=,则BC的长为()A.B.4C.2D.58.已知∠A为锐角,且sin A<,那么∠A的取值范围是()A.0°<∠A<30°B.30°<∠A<60°C.60°<∠A<90°D.30°<∠A<90°分卷II二、填空题9.在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为,则∠A=________.10.若tan (x+10°)=1,则锐角x的度数为__________.11.在△ABC中,∠C=90°,如果tan B=3,则cos A=__________.12.如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以20海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,我渔政船的航行路程是________海里.13.如图,某电视塔AB和楼CD的水平距离为100 m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为__________,楼高为__________.14.在Rt△ABC中,∠C=90°,且tan A=3,则cos B的值为__________.15.如图,将△ABC放在每个小正方形边长为1的网格中,点A,B,C均在格点上,则tan A 的值是__________.16.△ABC中,∠C=90°,cos ∠A=0.3,AB=10,则AC=__________.三、解答题17.如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i=∶3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:≈1.414,≈1.732)18.课堂上我们在直角三角形中研究了锐角的正弦,余弦和正切函数,与此类似,在Rt△ABC 中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot A=.(1)若∠A=45°,则cot 45°=__________;若∠A=60°,则cot 60°=__________;(2)探究tan A·cot A的值.19.已知Rt△ABC中,角A,B,C对应的边分别为a,b,c,∠C=90°,a:c=2:3,求tan A 的值.20.在Rt△ABC中,∠C=90°,∠A=30°,a=5,解这个直角三角形.21.如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF 交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°.(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60,sin 76°≈0.97.cos 76°≈0.24,tan 76°≈4.00)第二十八章《锐角三角函数》单元练习题答案解析1.【答案】D【解析】∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB===5.∴cos A==,故选D.2.【答案】A【解析】如图,∵∠C=90°,∴cos B=,∴BC=AB cos B=6×=4,故选A.3.【答案】C【解析】∵tan 45°=1,tan 60°=,锐角的正切值随角增大而增大,又1<<,∴45°<∠A<60°.故选C.4.【答案】【解析】∵Rt△ABC各边的长度都缩小为原来的得Rt△A′B′C′,∴Rt△ABC∽Rt△A′B′C′,∴∠A=∠A′,∴cos A=cos A′.故选A.5.【答案】A【解析】∵Rt△ABC中,∠C=90°,tan A=,AC=6 cm,∴tan A===,解得BC=8,故选A.6.【答案】A【解析】设BC=2x,∵tan A=,∴AC=x,∴AB=3,∴cos B==,故选A.7.【答案】B【解析】∵cos B=,∴BC=AB·cos B=6×=4.故选B.8.【答案】A【解析】∵∠A为锐角,且sin 30°=,又∵当∠A是锐角时,其正弦随角度的增大而增大,∴0°<A<30°,故选A.9.【答案】60°【解析】∵在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为,∴S=AC·BC=,∴AC=,∵tan A===,∴∠A=60°.10.【答案】20°【解析】∵tan (x+10°)=1,∴tan (x+10°)==,∴x+10°=30°,∴x=20°.11.【答案】【解析】由tan B=3,可以设∠B的对边是3k,邻边是k,则根据勾股定理,得斜边是k=k,故cos A=.12.【答案】30【解析】作CD⊥AB于点D,垂足为D,在Rt△BCD中,∵BC=20×1.5=30(海里),∠CBD=45°,∴CD=BC·sin 45°=30×=15(海里),则在Rt△ACD中,AC==15×2=30(海里).13.【答案】100m(100-100)m【解析】设CD=x m,则∵CE=BD=100,∠ACE=45°,∴AE=CE·tan 45°=100.∴AB=100+x.在Rt△ADB中,∵∠ADB=60°,∠ABD=90°,∴tan 60°=,∴AB=BD,即x+100=100,∴x=100-100,即楼高100-100 m,塔高100m.14.【答案】【解析】解法1:利用三角函数的定义及勾股定理求解.∵在Rt△ABC中,∠C=90°,tan A=3,设a=3x,b=x,则c=x,∴cos B===.解法2:利用同角、互为余角的三角函数关系式求解.又∵tan A==3,∴sin A=3cos A.又sin2A+cos2A=1,∴cos A=.∵A、B互为余角,∴cos B=sin (90°-B)=sin A=.15.【答案】【解析】作BD⊥AC于点D,∵BC=2,AC==3,点A到BC的距离为3,AB==,∴=,即=,解得BD=,∴AD===2,∴tan A===.16.【答案】3【解析】∵∠C=90°,AB=10,∴cos A===0.3,∴AC=3.17.【答案】解不需要移栽,理由:∵CB⊥AB,∠CAB=45°,∴△ABC为等腰直角三角形,∴AB=BC=5米,在Rt△BCD中,新坡面DC的坡度为i=∶3,即∠CDB=30°,∴DC=2BC=10米,BD=BC=5米,∴AD=BD-AB=(5-5)米≈3.66米,∵2+3.66=5.66<6,∴不需要移栽.【解析】根据题意得到三角形ABC为等腰直角三角形,求出AB的长,在直角三角形BCD中,根据新坡面的坡度求出∠BDC的度数为30,利用30度角所对的直角边等于斜边的一半求出DC的长,再利用勾股定理求出DB的长,由DB-AB求出AD的长,然后将AD+2与6进行比较,若大于则需要移栽,反之不需要移栽.18.【答案】解(1)由题意得:cot 45°=1,cot 60°=;(2)∵tan A=,cot A=,∴tan A·cot A=·=1.【解析】(1)根据题目所给的信息求解即可;(2)根据tan A=,cotA=,求出tan A·cot A的值即可.19.【答案】解设a=2k,c=3k.由勾股定理得b===k.则tan A===.【解析】设a=2k,c=3k,依据勾股定理可求得b的长度,然后依据锐角三角函数的定义解答即可.20.【答案】解在Rt△ABC中,∠B=90°-∠A=60°,∵tan B=,∴b=a×tan B=5×tan 60°=5,由勾股定理,得c==10.【解析】直角三角形的两个锐角互余,并且Rt△ABC中,∠C=90°则∠A=90-∠B=60°,解直角三角形就是求直角三角形中出直角以外的两锐角,三边中的未知的元素.21.【答案】解(1)如图,作DP⊥MN于点P,即∠DPC=90°,∵DE∥MN,∴∠DCP=∠ADE=76°,则在Rt△CDP中,DP=CD sin ∠DCP=40×sin 76°≈39(cm),答:椅子的高度约为39厘米;(2)作EQ⊥MN于点Q,∴∠DPQ=∠EQP=90°,∴DP∥EQ,又∵DF∥MN,∠AED=58°,∠ADE=76°,∴四边形DEQP是矩形,∠DCP=∠ADE=76°,∠EBQ=∠AED=58°,∴DE=PQ=20,EQ=DP=39,又∵CP=CD cos ∠DCP=40×cos 76°≈9.6(cm),BQ==≈24.4(cm),∴BC=BQ+PQ+CP=24.4+20+9.6≈54(cm),答:椅子两脚B、C之间的距离约为54 cm.【解析】(1)作DP⊥MN于点P,即∠DPC=90°,由DE∥MN知,∠DCP=∠ADE=76°,根据DP=CD sin ∠DCP可得答案;(2)作EQ⊥MN于点Q可得四边形DEQP是矩形,知DE=PQ=20,EQ=DP=39,再分别求出BQ、CP的长可得答案.人教版数学九年级下册第二十八章锐角三角函数 章末专题训练人教版数学九年级下册第二十八章锐角三角函数 章末专题训练一、选择题1.在Rt △ABC 中,∠C =90°,若将各边长度都扩大为原来的5倍,则∠A 的正弦值( D )A .扩大为原来的5倍B .缩小为原来的15C .扩大为原来的10倍D .不变2. 下列式子错误的是( D )A .cos40°=sin50°B .tan15°·tan75°=1 C.sin 225°+cos 225°=1 D .sin60°=2sin30°3. 如图所示,AB 为斜坡,D 是斜坡AB 上一点,斜坡AB 的坡度为i ,坡角为α,AC ⊥BM 于C ,下列式子:①i =AC ∶AB ;②i =(AC -DE)∶EC ;③i =tan α=DE BE;④AC =i ·BC.其中正确的有( C )A .1个B .2个C .3个D .4个4.河堤横断面如图所示,堤高BC =5米,迎水坡AB 的坡度是(坡度是坡面的铅直高度BC 与水平宽度AC 之比),则AC 的长是 ( A ) A.米B.米C. 15米D. 10米5.△ABC 在网格中的位置如图K -17-2所示(每个小正方形的边长都为1),AD ⊥BC 于点D ,下列选项中,错误..的是( C )图K-17-2A.sinα=cosα B.tanC=2C.sinβ=cosβ D.tanα=16.把Rt△ABC各边的长度都扩大3倍得到Rt△A′B′C′,那么锐角∠A、∠A′的余弦值的关系是( B )A.cosA=cosA′B.cosA=3cosA′C.3cosA=cosA′D.不能确定7. 如图,要在宽为22米的九洲大道AB两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直。
人教版九年级数学下《第二十八章锐角三角函数》单元练习题含答案

第二十八章锐角三角函数一、选择题1.在Rt△ABC中,∠C=90°,AB=6,cos B=,则BC的长为()A. 4B. 2C.D.2.在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,则sin A等于()A.B.C.D.3.在Rt△ABC中,∠C=90°,a=1,b=,则∠A等于()A. 30°B. 45°C. 60°D. 90°4.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)()A.B.C.D.h·cosα5.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是()A. 5米B. 6米C. 6.5米D. 12米6.Rt△ABC中,∠C=90°,AB=13,AC=5,则sin B的值为()A.B.C.D.7.在Rt△ABC中,∠C=90°,AB=6,AC=4,则cos A的值是()A.B.C.D.8.如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A 测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长()A. 2 kmB. (2+)kmC. (4-2) kmD. (4-) km9.在高为100米的楼顶测得地面上某目标的俯角为α,那么楼底到该目标的水平距离是() A. 100tanα米B. 100cotα米C. 100sinα米D. 100cosα米10.把△ABC三边的长度都扩大为原来的3倍,则锐角A的余弦函数值()A.不变B.缩小为原来的C.扩大为原来的3倍D.不能确定二、填空题11.若2cosα-=0,则锐角α=____________度.12.在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sin A=;②cos B=;③tan A=;④tan B=,其中正确的结论是__________(只需填上正确结论的序号)13.如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则sin ∠BAC=____________.14.已知∠A的补角是120°,则tan A=________.15.如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是____________.16.汽车沿着坡度为1∶7的斜坡向上行驶了50米,则汽车升高了____________米.17.已知0°<θ<30°,且sinθ=km+(k为常数且k<O),则m的取值范围是__________.18.在Rt△ABC中,∠C=90°,BC=3,sin A=,那么AB=__________.19.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则sin ∠ABC=________.20.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为________米.(精确到1米,参考数据:≈1.73)三、解答题21.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为(即AB∶BC=),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)22.南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?(参考数据:cos 75°=0.2588,sin 75°=0.9659,tan 75°=3.732,=1.732,=1.414)23.如图,图①是某电脑液晶显示器的侧面图,显示屏AO可以绕点O旋转一定的角度.研究表明:显示屏顶端A与底座B的连线AB与水平线BC垂直时(如图②),人观看屏幕最舒适.此时测得∠BAO=15°,AO=30 cm,∠OBC=45°,求AB的长度.(结果精确到0.1 cm)(参考数据:sin 15°≈0.259,cos 15°≈0.966,tan 15°≈0.268,≈1.414)24.小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据≈1.41,≈1.73)25.如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);(2)用方向和距离描述灯塔P相对于B处的位置.(参考数据:sin 53°=0.80,cos 53°=0.60,tan 53°=0.33,=1.41)26.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cos B的值.27.如图是某小区的一个健身器材,已知BC=0.15 m,AB=2.70 m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1 m).(参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)28.在△ABC中,∠C=90°,AC=7,BC=24,求sin A,sin B的值.答案解析1.【答案】A【解析】如图,∵∠C=90°,∴cos B=,∴BC=AB cos B=6×=4,故选A.2.【答案】B【解析】sin A==,故选B.3.【答案】A【解析】如图所示:∵在Rt△ABC中,∠C=90°,a=1,b=,∴tan A==.∴∠A=30°,故选A.4.【答案】B【解析】∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,∴∠CAD=∠BCD,在Rt△BCD中,∵cos ∠BCD=,∴BC==,故选B.5.【答案】A【解析】在如图AC=13,作CB⊥AB,∵cosα==,∴AB=12,∴BC===5,∴小车上升的高度是5 m.故选A.6.【答案】A【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=5,∴sin B==.故选A.7.【答案】B【解析】cos A===.故选B.8.【答案】C【解析】在CD上取一点E,使BD=DE,可得∠EBD=45°,AD=DC=2,∵从B测得船C在北偏东22.5°的方向,∴∠BCE=∠CBE=22.5°,∴BE=EC.设AB=x,则DE=BD=AD-AB=2-x,∴EC=BE=BD=(2-x),∵DE+EC=CD,∴2-x+(2-x)=2,解得x=4-2,即AB=4-2.故选C.9.【答案】B【解析】∵∠BAC=α,BC=100 m,∴AB=BC·cotα=100cotαm.故选B.10.【答案】A【解析】因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A的大小没改变,故锐角A的余弦函数值也不变.故选A.11.【答案】45°【解析】∵2cosα-=0,∴cosα=,又∵cos 45°=,∴锐角α=45°.12.【答案】②③④【解析】如图所示:∵在Rt△ABC中,∠C=90°,AB=2BC,∴sin A==,故①错误;∴∠A=30°,∴∠B=60°,∴cos B=cos 60°=,故②正确;∵∠A=30°,∴tan A=tan 30°=,故③正确;∵∠B=60°,∴tan B=tan 60°=,故④正确.故答案为②③④.13.【答案】【解析】∵A(0,1),B(0,-1),∴AB=2,OA=1,∴AC=2,由勾股定理,得OC==,∴在Rt△AOC中,sin ∠OAC=sin ∠BAC==.14.【答案】【解析】∵∠A的补角是120°,∴∠A=180°-120°=60°,∴tan A=tan 60°=.15.【答案】5∶12【解析】如图所示,由题意可知,PM=13 m,MC=5米,∴PC==12,∴MC∶PC=5∶12,故答案为5∶12.16.【答案】5【解析】∵坡度为1∶7,∴设坡角是α,则sinα==,∴上升的高度是50×=5(米).17.【答案】<m<【解析】∵0°<θ<30°,∴sin 0°<sinθ<sin 30°,即0<km+<,∴<km<,∴<m<.18.【答案】18【解析】在Rt△ABC中,∵∠C=90°,sin A==,∴AB=3×6=18.19.【答案】【解析】∵小正方形边长为1,∴AB2=8,BC2=10,AC2=2;∴AB2+AC2=BC2,∴△ABC是直角三角形,且∠CAB=90°,∴sin ∠ABC===.20.【答案】208【解析】由题意可得:tan 30°===,解得:BD=30,tan 60°===,解得DC=90,故该建筑物的高度为BC=BD+DC=120≈208(m).21.【答案】解∵AF⊥AB,AB⊥BE,DE⊥BE,∴四边形ABEF为矩形,∴AF=BE,EF=AB=2,设DE=x,在Rt△CDE中,CE===x,在Rt△ABC中,∵=,AB=2,∴BC=2,在Rt△AFD中,DF=DE-EF=x-2,∴AF===(x-2),∵AF=BE=BC+CE.∴(x-2)=2+x,解得x=6.答:树DE的高度为6米.【解析】由于AF⊥AB,则四边形ABEF为矩形,设DE=x,在Rt△CDE中,CE===x,在Rt△ABC中,得到=,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE 即可求出x的长.22.【答案】解过B作BD⊥AC,∵∠BAC=75°-30°=45°,∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,由勾股定理,得BD=AD=×20=10(海里),在Rt△BCD中,∠C=15°,∠CBD=75°,∴tan ∠CBD=,即CD=10×3.732=52.77048,则AC=AD+DC=10+10×3.732=66.91048≈67(海里),即我海监执法船在前往监视巡查的过程中行驶了67海里.【解析】过B作BD⊥AC,在直角三角形ABD中,利用勾股定理求出BD与AD的长,在直角三角形BCD中,求出CD的长,由AD+DC求出AC的长即可.23.【答案】解过O点作OD⊥AB交AB于D点.在Rt△ADO中,∵∠A=15°,AO=30,∴OD=AO·sin 15°≈30×0.259≈7.77(cm)AD=AO·co s 15°≈30×0.966≈28.98(cm)又∵在Rt△BDO中,∠OBC=45°,∴BD=OD=7.77(cm),∴AB=AD+BD=36.75≈36.8(cm).答:AB的长度为36.8 cm.【解析】过O点作OD⊥AB交AB于D点,根据∠A=15°,AO=30可知OD=AO·sin 15°,AD=AO·cos 15°,在Rt△BDO中根据∠OBC=45°可知,BD=OD,再根据AB=AD+BD即可得出结论.24.【答案】解∵在Rt△CBE中,sin 60°=,∴CE=BC·sin 60°=20×≈17.3 m,∴CD=CE+ED=17.3+1.75=19.05≈19.1 m.答:风筝离地面的高度是19.1 m.【解析】先根据锐角三角函数的定义求出CE的长,再由CD=CE+ED即可得出结论.25.【答案】解(1)如图,作PC⊥AB于C,在Rt△PAC中,∵PA=100,∠PAC=53°,∴PC=PA·sin ∠PAC=100×0.80=80,在Rt△PBC中,∵PC=80,∠PBC=∠BPC=45°,∴PB=PC=1.41×80≈113,即B处与灯塔P的距离约为113海里;(2)∵∠CBP=45°,PB≈113海里,∴灯塔P位于B处北偏西45°方向,且距离B处约113海里.【解析】(1)根据方向角的定义结合已知条件在图中画出点B,作PC⊥AB于C,先解Rt△PAC,得出PC=PA·sin ∠PAC=80,再解Rt△PBC,得出PB=PC=1.41×80≈113;(2)由∠CBP=45°,PB≈113海里,即可得到灯塔P位于B处北偏西45°方向,且距离B处约113海里.26.【答案】解∵∠C=90°,MN⊥AB,∴∠C=∠ANM=90°,∴∠A+∠B=90°,∠A+∠AMN=90°,∴∠B=∠AMN,又AN=3,AM=4,∴MN==,∴cos B=cos ∠AMN==.【解析】根据“同角的余角相等”,可得∠B=∠AMN,又AN=3,AM=4,由勾股定理得MN=,故 cos B=cos ∠AMN.27.【答案】解作AE⊥CD于E,BF⊥AE于F,则四边形EFBC是矩形,∵OD⊥CD,∠BOD=70°,∴AE∥OD,∴∠A=∠BOD=70°,在Rt△AFB中,∵AB=2.7,∴AF=2.7×cos 70°≈2.7×0.34=0.918,∴AE=AF+BC≈0.918+0.15=1.068≈1.1 m,答:端点A到地面CD的距离是1.1 m.【解析】作AE⊥CD于E,BF⊥AE于F,则四边形EFBC是矩形,求出AF、EF即可解决问题.28.【答案】解在△ABC中,∠C=90°,AC=7,BC=24,由勾股定理,得AB===25,sin A==,sin B==.【解析】根据勾股定理,可得AC的长,根据锐角的正弦为对边比斜边,可得答案.。
锐角三角函数单元测试(含答案)

初四数学假期作业锐角三角函数 命题人 班级 姓名 家长签名 一、填空题: 1、在Rt △ABC 中,∠C =90°,a =2,b =3,则cosA = ,sinB = ,tanB = 。
2、直角三角形ABC 的面积为24cm 2,直角边AB 为6cm ,∠A 是锐角,则sinA = 。
3、已知tan α=125,α是锐角,则sin α= 。
4、cos 2(50°+α)+co s 2(40°-α)-tan(30°-α)tan(60°+α)= ;5、如图1,机器人从A 点,沿着西南方向,行了个42单位,到达B 点后观察到原点O 在它的南偏东60°的方向上,则原来A 的坐标为 .(结果保留根号).(1) (2) (3)6、等腰三角形底边长10cm ,周长为36cm ,则一底角的正切值为 .7、某人沿着坡度i=1:3的山坡走了50米,则他离地面 米高。
8、如图2,在坡度为1:2 的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是 米。
9、在△ABC 中,∠ACB=90°,cosA=33,AB =8cm ,则△ABC 的面积为______ 。
10、如图3,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA 为a 米,此时,梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面墙上N ,此时梯子顶端距地面的垂直距离NB 为b 米,梯子的倾斜角45°,则这间房子的宽AB 是 _米。
二、选择题:11、sin 2θ+sin 2(90°-θ) (0°<θ<90°)等于( )A.0B.1C.2D.2sin 2θ12、在直角三角形中,各边的长度都扩大3倍,则锐角A 的三角函数值 ( )A.也扩大3倍B.缩小为原来的31 C. 都不变 D.有的扩大,有的缩小 13、以直角坐标系的原点O 为圆心,以1为半径作圆。
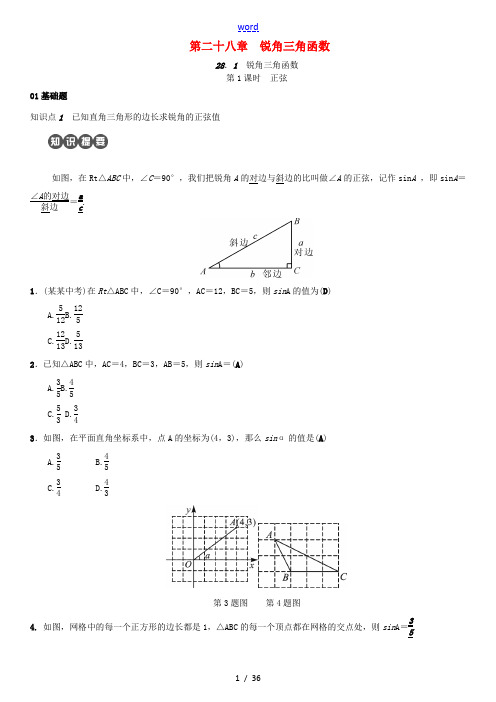
秋九年级数学下册 第二十八章 锐角三角函数练习 (新版)新人教版-(新版)新人教版初中九年级下册数学
第二十八章 锐角三角函数28.1 锐角三角函数第1课时 正弦01基础题知识点1 已知直角三角形的边长求锐角的正弦值如图,在Rt△ABC 中,∠C =90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦,记作sin A ,即sin A =∠A 的对边斜边=ac.1.(某某中考)在Rt △ABC 中,∠C=90°,AC =12,BC =5,则sin A 的值为(D )A.512B.125 C.1213D.5132.已知△ABC 中,AC =4,BC =3,AB =5,则sin A =(A )A.35B.45C.53D.343.如图,在平面直角坐标系中,点A 的坐标为(4,3),那么sin α的值是(A )A.35B.45C.34D.43第3题图 第4题图4. 如图,网格中的每一个正方形的边长都是1,△ABC 的每一个顶点都在网格的交点处,则sin A =35.5.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sin B 的值是34.6.根据图中数据,求sin C 和sin B 的值.解:在Rt△ABC 中,BC =AB 2+AC 2=34, ∴sinC =AB BC =53434,sinB =AC BC =33434.7.如图所示,在Rt △ABC 中,∠ACB=90°,a∶c=2∶3,求sin A 和sin B 的值.解:在Rt△ABC 中,∠ACB =90°,a∶c =2∶3,设a =2k ,c =3k.(k>0)∴b =c 2-a 2=5k. ∴sinA =a c =2k 3k =23,sinB =b c =5k 3k =53.知识点2 已知锐角的正弦值,求直角三角形的边长8.(来宾中考)在△ABC 中,∠C=90°,BC =6,sin A =23,则AB 边的长是9.9.(某某中考)在△ABC 中,AB =AC =5,sin ∠ABC=0.8,则BC =6.易错点 对正弦的概念理解不清10.把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦值(A )A .不变B .缩小为原来的13C .扩大为原来的3倍D .不能确定02中档题11.已知Rt △ABC∽Rt △A′B′C′,∠C=∠C′=90°,且AB =2A′B′,则sin A 与sin A′的关系为(B )A .sin A =2sin A ′ B.sin A =sin A ′ C .2sin A =sin A ′ D.不确定12.如图,在Rt △ABC 中,∠C=90°,AB =2BC ,则sin B 的值为(C )A.12B.22C.32D .1 13.在△ABC 中,∠C=90°,∠A,∠B,∠C 的对边分别为a ,b ,c ,c =3a ,则sin A 的值是(A )A.13B.233 C .3 D .以上都不对14.如图,在Rt △ABC 中,∠ACB=90°,CD⊥AB,垂足为点 D.若AC =5,BC =2,则sin ∠ACD 的值为(A )A.53 B.255 C.52 D.23第14题图 第16题图15.已知锐角A 的正弦sin A 是一元二次方程2x 2-7x +3=0的根,则sin A =12.16.(某某中考)如图,⊙O 的直径CD =10 cm ,且AB⊥CD,垂足为P ,AB =8 cm ,则sin ∠OAP=35.17.如图,直径为10的⊙A 经过点C(0,5)和点O(0,0),B 是y 轴右侧⊙A 优弧OC 上一点,求∠OBC 的正弦值.解:连接OA 并延长交⊙A 于点D ,连接CD.∴∠OBC =∠ODC, ∠OCD =90°.∴sin∠OBC =sin∠ODC =OC OD =510=12.03综合题18.(某某中考)如图,根据图中数据完成填空,再按要求答题:sin 2A 1+sin 2B 1=1;sin 2A 2+sin 2B 2=1;sin 2A 3+sin 2B 3=1.(1)观察上述等式,猜想:在Rt△ABC 中,∠C =90°,都有sin 2A +sin 2B =1;(2)如图4,在Rt△ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别是a ,b ,c ,利用三角函数的定义和勾股定理,证明你的猜想;(3)已知:∠A +∠B =90°,且sin A =513,求sin B .解:(2)∵在Rt△ABC 中,∠C =90°,sinA =a c ,sinB =b c ,∴sin 2A +sin 2B =a 2+b 2c2.∵∠C =90°, ∴a 2+b 2=c 2. ∴sin 2A +sin 2B =1.(3)∵sinA =513,sin 2A +sin 2B =1,且sinB >0,∴sinB =1-(513)2=1213.第2课时 锐角三角函数01基础题 知识点1 余弦如图,在Rt△ABC 中,∠C =90°,我们把锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cos A ,即cos A =∠A 的邻边斜边=bc.1.(某某中考)如图,在Rt △ABC 中,∠C=90°,AB =5,BC =3,则cos B 的值是(A )A.35B.45C.34D.432.在Rt △ABC 中,∠C=90°,cos A =35,AC =6 cm ,那么BC 等于(A )A .8 cm B.245 cmC.185 cm D.65cm 3.在△ABC 中,∠C=90°,AC =2,BC =1,求cos A 和cos B 的值.解:∵∠C =90°,AC =2,BC =1,∴AB =AC 2+BC 2=22+12= 5.cosA =AC AB =25=255,cosB =BC AB =15=55.知识点2 正切如图,在Rt△ABC 中,∠C =90°,我们把锐角A 的对边与邻边的比叫做∠A 的正切,记作tan A ,即tan A =∠A 的对边∠A 的邻边=a b.4.(某某中考)在Rt △ABC 中,∠C=90°,AB =5,BC =3,则tan A 的值是(A )A.34B.43C.35D.455.在4×4的正方形的网格中画出了如图所示的格点△ABC,则tan ∠ABC 的值为(D )A.31313 B.21313 C.32 D.23第5题图 第6题图6.(某某中考)如图,在△ABC 中,∠C=90°,AC =2,BC =1,则tan A 的值是12.7.已知等腰三角形的腰长为6 cm ,底边长为10 cm ,则底角的正切值为115.知识点3 锐角三角函数∠A 的正弦、余弦、正切都是∠A 的锐角三角函数.8.(某某中考)如图,在Rt △ABC 中,∠C=90°,BC =15,tan A =158,则AB =17.第8题图 第9题图9.(崇左中考)如图,在Rt △ABC 中,∠C=90°,AB =13,BC =12,则下列三角函数表示正确的是(A )A .sin A =1213B .cos A =1213C .tan A =512D .tan B =12510.在Rt △ABC 中,∠C=90°,AC =7,BC =24.(1)求AB 的长;(2)求sin A ,cos A ,tan A 的值. 解:(1)由勾股定理,得AB =AC 2+BC 2=72+242=25.(2)sinA =BC AB =2425,cosA =AC AB =725,tanA =BC AC =247.02中档题11.在△ABC 中,若三边BC ,CA ,AB 满足BC∶CA∶AB=5∶12∶13,则cos B =(C )A.512 B.125C.513 D.121312.(某某中考)在Rt △ABC 中,∠C=90°,若sin A =35,则cos B 的值是(B )A.45B.35C.34D.4313.将△AOB 按如图所示放置,然后绕点O 逆时针旋转90°至△A′OB′的位置,点A 的坐标为(2,1),则tan ∠A′OB′的值为(A )A.12B .2 C.55 D.255第13题图 第14题图14.(某某中考)如图,在Rt △ABC 中,∠ACB=90°,AC =8,BC =6,CD⊥AB ,垂足为D ,则tan ∠BCD 的值是34.15.(某某中考)如图,在半径为3的⊙O 中,直径AB 与弦CD 交于点E ,连接AC ,B D.若AC =2,则cos D =13.16.(某某中考)如图,在△ABC 中,CD⊥AB,垂足为D.若AB =12,CD =6,tan A =32,求sin B +cos B 的值.解:在Rt△ACD 中,CD =6,tanA =32,∴CD AD =6AD =32,即AD =4. 又AB =12,∴BD =AB -AD =8.在Rt△BCD 中,BC =CD 2+BD 2=10.∴sinB =CD BC =610=35,cosB =BD BC =810=45.∴sinB +cosB =35+45=75.17.如图,将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,如果AB BC =23,求tan ∠DCF 的值.解:∵四边形ABCD 是矩形,∴AB =CD ,∠D =90°. ∵AB BC =23,且由折叠知CF =BC , ∴CD CF =23.设CD =2x ,CF =3x (x>0),∴DF =CF 2-CD 2=5x. ∴tan∠DCF =DF CD =5x 2x =52.03综合题18.如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作c tan α,即c tan α=角α的邻边角α的对边=ACBC,根据上述角的余切定义,解下列问题:(1)c tan 30°=3;(2)如图,已知tan A =34,其中∠A 为锐角,试求c tan A 的值.解:∵tanA =34,且tanA =BC AC,∴设BC =3x ,AC =4x. ∴ctanA =AC BC =4x 3x =43.第3课时 特殊角的三角函数值01基础题知识点1 特殊角的三角函数值填写下表:30° 45° 60° sin α 12 22 32 cosα 32 22 12 tanα33131.已知∠A=30°,下列判断正确的是(A )A .sin A =12B .cos A =12C .tan A =12D .cot A =122.计算:cos 230°=(D )A.12B.14C.32D.34 3.(某某中考)计算:cos 245°+sin 245°=(B )A.12B .1 C.14 D.224.计算:tan 45°+2cos 45°=2. 5.计算:(1)sin 30°+cos 45°; 解:原式=12+22=1+22.(2)cos30°·tan30°-tan 245°; 解:原式=32×33-12=12-1=-12. (3)22sin45°+sin60°·cos45°. 解:原式=22×22+32×22=2+64.知识点2 由三角函数值求特殊角6.(某某中考)在△ABC 中,若|sin A -12|+(cos B -12)2=0,则∠C 的度数是(D )A .30° B.45° C.60° D.90° 7.如果在△ABC 中,sin A =cosB =22,那么下列最确切的结论是(C ) A .△ABC 是直角三角形 B .△ABC 是等腰三角形 C .△ABC 是等腰直角三角形 D .△ABC 是锐角三角形8.已知α为锐角,且cos (90°-α)=12,则α=30°.9.在△ABC 中,∠C=90°,AC =2,BC =23,则∠A=60°.知识点3 用计算器计算三角函数值10.用计算器计算cos 44°的结果(精确到0.01)是(B )A .0.90B .0.72C .0.6911.如图,在△ABC 中,∠ACB=90°,∠ABC=26°,BC =5.若用科学计算器求边AC 的长,则下列按键顺序正确的是(D )A .5÷tan26°=B .5÷sin26°=C .5×cos26°=D .5×tan26°=12.利用计算器求∠A =18°36′的三个锐角三角函数值.解:sinA =sin18°36′≈0.319 0,cosA =cos18°36′≈0.947 8, tanA =tan18°36′≈0.336 5.13.已知下列正(余)弦值,用计算器求对应的锐角(精确到0.1°).(1)sin α=0.822 1; 解:α≈55.3°.(2)cos β=0.843 4. 解:β≈32.5°.02中档题14.点M(-sin 60°,cos 60°)关于x 轴对称的点的坐标是(B )A.(32,12) B.(-32,-12)C.(-32,12) D.(-12,-32)15.李红同学遇到了这样一道题:3tan(α+20°)=1,你猜想锐角α的度数应是(D)A.40° B.30° C.20° D.10°16.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为(D)A.12B.33C.22D.3217.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=2,则点B的坐标为(C) A.(2,1) B.(1,2)C.(2+1,1) D.(1,2+1)第17题图第18题图18.(某某中考)如图,C为⊙O外一点,CA与⊙O相切,切点为A,AB为⊙O的直径,连接C B.若⊙O的半径为2,∠ABC=60°,则BC=8.19.计算:(1)(某某中考改编)2 0180+(-1)2-2tan45°+4;解:原式=1+1-2×1+2=2.(2)(-1)-2+|2-3|+(π-3.14)0-tan60°+8.解:原式=1+(3-2)+1-3+2 2=2+ 2.20.若tan A 的值是方程x 2-(1+3)x +3=0的一个根,求锐角A 的度数.解:解方程x 2-(1+3)x +3=0, 得x 1=1,x 2= 3.由题意知tanA =1或tanA = 3.∴∠A =45°或60°.21.(原创题)如图,在等腰△ABC 中,AB =AC =1.(1)若BC =2,求△ABC 三个内角的度数; (2)若BC =3,求△ABC 三个内角的度数.解:(1)∵AB =AC =1,BC =2,∴AB 2+AC 2=BC 2.∴∠BAC =90°,∠B =∠C =45°.(2)过点A 作AD⊥BC,垂足为D.∵AB =AC =1,AD⊥BC, ∴BD =12BC =32.∴cosB =BD AB =321=32.∴∠B =30°.∴∠C =30°,∠BAC =120°.03综合题22.(某某中考)一般地,当α,β为任意角时,sin (α+β)与sin (α-β)的值可以用下面的公式求得:sin (α+β)=sin α·cos β+cos α·sin β;sin (α-β)=sin α·cos β-cos α·sin β.例如:sin 90°=sin (60°+30°)=sin 60°·cos 30°+cos 60°·sin 30°=32×32+12×12=1.类似地,可以求得sin 15°的值是6-24. 解直角三角形及其应用 28. 解直角三角形01基础题知识点1 已知两边解直角三角形如图,已知两边:(1)已知a ,b ,则c =a 2+b 2,sin A =cos B =a c,sin B =cos A =bc ,tan A =a b ,tan B =b a;(2)已知a ,c ,则b =c 2-a 2,sin A =cos B =a c ,sin B =cos A =b c ,tan A =a b ,tan B =b a. 1.在△ABC 中,∠C=90°,AC =3,AB =4,欲求∠A 的值,最适宜的做法是(C )A .计算tan A 的值求出B .计算sin A 的值求出C .计算cos A 的值求出D .先根据sin B 求出∠B ,再利用90°-∠B 求出2.在Rt △ABC 中,∠C=90°,a =4,b =3,则cos A 的值是(A )A.35B.45C.43D.543.在Rt △ABC 中,∠C=90°,a =20,c =202,则∠A=45°,∠B =45°,b =20. 4.如图,在Rt △ABC 中,∠C=90°,已知BC =26,AC =62,解此直角三角形.解:∵tanA =BC AC =2662=33,∴∠A =30°.∴∠B =90°-∠A =90°-30°=60°,AB =2BC =4 6.知识点2 已知一边一锐角解直角三角形如图,已知一边一角:(1)已知a ,∠A ,则∠B =90°-∠A ,c =a sinA ,b =a tanA; (2)已知c ,∠A ,则∠B =90°-∠A ,a =c·sinA .5.(某某中考)如图,在Rt △ABC 中,∠C=90°,∠B=30°,AB =8,则BC 的长是(D )A.433B .4C .8 3D .4 36.在Rt △ABC 中,∠C=90°,tan A =43,BC =8,则△ABC 的面积为(C )A .12B .18C .24D .487.(某某中考)如图,在Rt △ABC 中,∠C=90°,∠B=37°,BC =32,则AC =24.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)8.(教材9下P 73例2变式)如图,在Rt △ABC 中,∠C=90°,∠B=55°,AC =4,解此直角三角形.(结果保留小数点后一位)解:根据题意,∠A =90°-∠B =90°-55°=35°. 根据正弦定义,sinB =AC AB,则AB =AC sinB =4sin55°≈4.9.根据正切的定义,tanB =AC BC,则BC =AC tanB =4sin55°≈2.8.所以△ABC 的另一个锐角度数为35°,另一条直角边长为2.8,斜边长为4.9. 易错点 忽视钝角三角形而致错9.在△ABC 中,AB =23,AC =2,∠B=30°,则BC 的长为2或4.02中档题10. 如图,在△AB C 中,∠C=90°,AC =8 cm ,AB 的垂直平分线MN 交AC 于D ,连接BD ,若cos ∠BDC=35,则BC的长是(A )A .4 cmB .6 cmC .8 cmD .10 cm11.(某某中考)在△ABC 中,AB =122,AC =13,cos B =22,则BC 边长为(D )A .7B .8C .8或17D .7或1712.(某某中考)如图,在△ABC 中,AC =6,BC =5,sin A =23,则tan B =43.第12题图 第13题图13.(某某中考)如图,在菱形ABCD 中,DE⊥AB 于点E ,cos A =35,BE =4,则tan ∠DBE 的值是2.14.(某某中考)如图,在△ABC 中,BD⊥AC,AB =6,AC =53,∠A=30°.(1)求BD 和AD 的长; (2)求tan C 的值.解:(1)∵BD⊥AC,∴∠ADB =∠BDC =90°.在Rt△ADB 中,AB =6,∠A =30°,∴BD =12AB =3.∴AD =3BD =3 3.(2)CD =AC -AD =53-33=23, 在Rt△BDC 中,tanC =BD CD =323=32.15.(某某中考)如图,在四边形ABCD 中,∠ABC=90°,∠ADC=90°,AB =6,CD =4,BC 的延长线与AD 的延长线交于点E.(1)若∠A=60°,求BC 的长; (2)若sin A =45,求AD 的长.解:(1)∵在Rt△ABE 中,∠ABE =90°,∠A =60°,AB =6,tanA =BE AB,∴BE =6·tan60°=6 3.∵在Rt△CDE 中,∠CDE =90°,∠E =90°-60°=30°, CD =4, ∴CE =2CD =8.∴BC =BE -CE =63-8.(2) ∵在Rt△ABE 中,∠ABE =90°,sinA =45,∴BE AE =45. 设BE =4x ,则AE =5x (x >0).∵AE 2-BE 2=AB 2,∴(5x )2-(4x )2=62.∴x =2. ∴BE =8,AE =10.∵在Rt△CDE 中,∠CDE =90°,CD =4,tanE =CD ED ,而在Rt△ABE 中,tanE =AB BE =68=34,∴CD ED =34. ∴ED =43CD =163.∴AD =AE -ED =143.03综合题16. 如图,在△ABC 中,CD 是边AB 上的中线,∠B 是锐角,且sin B =22,tan A =12,AC =3 5. (1)求∠B 的度数与AB 的长; (2)求tan ∠CDB 的值.解:(1)作CE⊥AB 于E ,设CE =x , 在Rt△ACE 中,∵tanA =CE AE =12,∴AE =2x.∴AC =x 2+(2x )2=5x. ∴5x =35,解得x =3. ∴CE =3,AE =6.在Rt△BCE 中,∵sinB =22, ∴∠B =45°.∴△BCE 为等腰直角三角形. ∴BE =CE =3. ∴AB =AE +BE =9.(2)∵CD 是边AB 上的中线,∴BD =12AB =4.5.∴DE =BD -BE =-3=1.5. ∴tan∠CDE =CEDE=错误!=2,即tan∠CDB 的值为2.28.2.2 应用举例第1课时 与视角有关的解直角三角形应用题01基础题知识点1 利用解直角三角形解决简单问题1. 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC =10米,∠B=36°,则中柱AD(D 为底边中点)的长是(C )A .5sin36°米B .5cos36°米C .5tan36°米D .10tan36°米第1题图 第2题图2.(教材9下P 74例3变式)如图,某航天飞船在地球表面P 点的正上方A 处,从A 处观测到地球上的最远点Q.若∠QAP=α,地球半径为R ,则航天飞船距离地球表面最近距离AP =Rsinα-R. 3.(某某中考)为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB 与MN 之间的距离).如图,在测量时,选定河对岸MN 上的点C 处为桥的一端,在河岸点A 处,测得∠CAB =30°,沿河岸AB 前行30米后到达B 处,在B 处测得∠CBA=60°.请你根据以上测量数据求出河的宽度.(参考数据:2≈1.41,3≈1.73;结果保留整数)解:过点C 作CD⊥AB,垂足为D.∵∠CAB =30°, ∴AD =3CD. ∵∠CBA =60°,∴DB =33CD. ∵AB =AD +DB =30,∴3CD +33CD =30. ∴CD =1523=152×1.73≈13(米).答:河的宽度约为13米.知识点2 解与视角有关的实际问题4.(教材9下P 75例4变式)(某某中考)如图,热气球的探测器显示,从热气球A 处看一栋楼顶部B 处的仰角为30°,看这栋楼底部C 处的俯角为60°,热气球A 处与楼的水平距离为120 m ,则这栋楼的高度为(A )A .160 3 mB .120 3 mC .300 mD .160 2 m5.(某某中考)如图,两幢建筑物AB 和CD ,AB⊥BD,CD⊥BD,AB =15 m ,CD =20 m ,AB 和CD 之间有一景观池,小南在A 点测得池中喷泉处E 点的俯角为42°,在C 点测得E 点的俯角为45°(点B ,E ,D 在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1 m ,参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)解:由题意,得∠AEB =42°,∠DEC =45°.∵AB⊥BD,CD⊥BD,∴在Rt△ABE 中,∠ABE =90°. ∵AB =15,∠AEB =42°, tan∠AEB =ABBE ,∴BE =15tan42°=503.在Rt△DEC 中,∠CDE =90°,∠DEC =45°,CD =20.∴ED =CD =20.∴BD =BE +ED =503+(m ).答:两幢建筑物之间的距离BD 约为36.7 m.易错点 混淆三点函数的数量关系而导致错误6.(某某中考)如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测得树顶A 的仰角∠ABO 为α,则树OA 的高度为(C )A.30tanα米 B .30sinα米 C .30tanα米 D .30cosα米 02中档题7. (某某中考)某某市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).解:延长AD交BC所在直线于点E.由题意,得BC=17米,AE=15米,∠CAE=60°,∠AEB=90°,在Rt△ACE中,tan∠CAE=CE AE ,∴CE=AE·tan60°=153米.在Rt△ABE中,tan∠BAE=BEAE=17+15315,∴∠BAE≈71°.答:第二次施救时云梯与水平线的夹角∠BAD约为71°.8.(某某中考)乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量:无人机在A处正上方97 m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测),无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.(1)求主桥AB的长度;(2)若两观察点P、D的连线与水平方向的夹角为30°,求引桥BC的长.(长度均精确到1 m,参考数据:3≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)解:(1)由题意知∠ABP=30°,AP=97,∴AB=APtan∠ABP =97tan30°=9733=973≈168.答:主桥AB的长度约为168 m.(2)∵∠ABP=30°,AP=97,∴PB=2PA=194.又∵∠DBC=∠DBA=90°,∠PB A=30°,∴∠DBP=∠DPB=60°.∴△PBD是等边三角形.∴DB=PB=194.在Rt△BCD中,∵∠C=80°36′,∴BC=DBtanC =194tan80°36′≈32.答:引桥BC的长约为32 m.03综合题9.(六盘水中考)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动.如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.活动中测得数据如下:①小明的身高DC=1.5米;②小明的影长CE=1.7米;③小明的脚到旗杆底部的距离BC=9米;④旗杆的影长BF=7.6米;⑤从D点看A点的仰角为30°.请你选择需要的数据,求出旗杆的高度.(计算结果精确到0.1米,参考数据:2≈1.414,3≈1.732)情况一:选用①,②,④.∵AB⊥FC,CD⊥FC,∴∠ABF=∠DCE=90°.又∵AF∥DE,∴∠AFB=∠DEC.则△ABF∽△DCE.∴ABDC=FBEC.又∵DC =1.5 m ,FB =7.6 m ,EC =1.7 m ,∴AB≈6.7 m.即旗杆高度约为6.7 m. 情况二: 选用①,③,⑤. 过D 点作DG⊥AB 于G 点, ∵AB⊥FC,DC⊥FC,∴四边形BCDG 为矩形. ∴CD =BG =1.5 m ,DG =BC =9 m.在Rt△AGD 中,∠ADG =30°,tan30°=AG DG,∴AG =3 3 m.又AB =AG +GB ,∴AB =33+(m).∴旗杆高度约为6.7 m.第2课时 与方位角、棱角有关的解直角三角形应用问题01基础题知识点1 解与方位角有关的实际问题1.如图,小雅家(图中点O 处)门前有一条东西走向的公路,经测得有一水塔(图中点A 处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB 是(A )A .250米B .2503米 C.50033米 D .5002米第1题图 第2题图2.如图,我国的一艘海监船在钓鱼岛A 附近沿正东方向航行,船在B 点时测得钓鱼岛A 在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.则船继续航行50海里与钓鱼岛A的距离最近.3.(某某中考)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,2≈1.41,3≈1.73)解:过P作PC⊥AB于C,在Rt△APC中,AP = 200 m,∠ACP =90°,∠PAC =60°.∴PC= 200×sin60°=200 ×32=1003(m).∵在Rt△PBC中,sin37°=PCPB ,∴PB=PCsin37°=错误!≈288(m).答:小亮与妈妈相距约288米.知识点2解与坡角有关的实际问题4.(聊城中考)河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1∶3,则AB的长为(A) A.12米 B.43米C.53米 D.63米第4题图第5题图5.如图,在坡度为1∶2的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是35米.6.(教材9下P77练习T2变式)如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:2≈1.414,3≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比)解:作BE⊥AD,CF⊥AD,垂足分别为点E,F,则四边形BCFE是矩形.由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1∶2.5,在Rt△ABE中,BEAE=错误!,∴AE=50米.在Rt△CFD中,∠D=30°,∴DF=3CF=203米.∴AD=AE+EF+FD=50+6+203(米).答:坝底AD的长度约为米.02中档题7.(某某中考)如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行200海里到达C处时,测得小岛A在船的北偏东30°的方向.已知在小岛周围170海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(3≈1.732)解:该轮船不改变航向继续前行,没有触礁危险.理由如下:由题意,得∠ABD=30°,∠ACD=60°.∴∠CAB=∠ABD.∴BC =AC =200海里.在Rt△ACD 中,设CD =x ,则AC =2x ,AD =AC 2-CD 2=(2x )2-x 2=3x. 在Rt△ABD 中,AB =2AD =23x ,BD =AB 2-AD 2=(23x )2-(3x )2=3x.又∵BD =BC +CD ,∴3x =200+x ,解得x =100.∴AD =3x =1003≈173.2.海里>170海里,且D 处距离A 处最近,∴轮船不改变航向继续向前行驶,轮船无触礁的危险.8.(某某中考)“蘑菇石”是我省著名自然保护区梵净山的标志,小明从山脚B 点先乘坐缆车到达观景平台DE 观景,然后再沿着坡角为29°的斜坡由E 点步行到达“蘑菇石”A 点,“蘑菇石”A 点到水平面BC 的垂直距离为1 790 m .如图,DE∥BC,BD =1 700 m ,∠DBC=80°,求斜坡AE 的长度.(结果精确到0.1 m )解:过点D 作DF⊥BC 于点F ,延长DE 交AC 于点M. 由题意,得EM ⊥AC,DF =CM ,∠AEM =29°, 在Rt△DFB 中,sin80°=DFBD,∴DF =BDsin80°.AM =AC -CM =1 790-1 700sin80°.在Rt△AME 中,sin29°=AM AE,∴AE =AM sin29°=1 790-1 700sin80°sin29°(m ),答:斜坡的长度约为238.9 m. 03综合题9.(黔东南中考)黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学测量学校附近一电线杆的高,如图,已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D 处测得电线杆顶端A 的仰角为30°,在C 处测得电线杆顶端A 的仰角为45°,斜坡与地面成60°角,CD =4 m ,请你根据这些数据求电线杆的高(AB).(结果精确到1 m ,参考数据:2≈1.4,3≈1.7)解:延长AD交BC的延长线于点G,过点D作DH⊥BG,垂足为点H,则∠G=30°.∵在Rt△DHC中,∠DCH=60°,CD=4,∴C H=CD·cos∠DCH=4×cos60°=2.DH=CD·sin∠DCH=4×sin60°=2 3.又∵DH⊥BG,∠G=30°,∴HG=DHtanG =23tan30°=6.∴CG=CH+HG=2+6=8.设AB=x m.又∵AB⊥BG,∠G=30°,∠BCA=45°,∴BC=x.∴BG=ABtanG =xtan30°=3x.∵BG-BC=CG,∴3x-x=8.解得x≈11 m.答:电线杆的高(AB)约为11 m.小专题17解直角三角形的实际应用1.(某某月考)如图,在一次测量活动中,小华站在离旗杆底部(B)处6 m的D处,仰望旗杆顶端A,测得仰角为60°,眼睛离地面的距离ED为1.5 m.试帮助小华求出旗杆AB的高度.(结果精确到0.1 m,3≈1.732)解:过点E作EC⊥AB于C.∵CE=BD=6 m,∠AEC=60°,∴AC=CE·tan60°=6×3=63(m).∴AB=AC+DE=+=(m).答:旗杆AB的高度约为11.9 m.2.钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我国海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.(1)请在图中作出该船在点B处的位置;(2)求钓鱼岛C到B处距离(结果保留根号).解:(1)如图.(2)AB=30×=15(海里).在Rt△ABC中,tan∠BAC=BC AB ,∴BC=AB·tan∠BAC=AB·tan30° =15×33=53(海里).答:钓鱼岛C 到B 处距离为53海里.3.(某某中考)为促进我市经济快速发展,加快道路建设,某高速公路建设工程中,需修建隧道A B.如图,在山外一点C 测得BC 距离为200 m ,∠CAB =54°,∠CBA =30°,求隧道AB 的长.(参考数据: sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,3≈1.73,结果精确到个位)解:过点C 作CD⊥AB 于D ,在Rt△BCD 中,∵∠B =30°,BC =200,∴CD =12BC =100,BD =1003≈173.在Rt△ACD 中,∵tan∠CAB =CD AD ,∴AD =100tan54°≈72.∴AB =AD +BD≈245.答:隧道AB 的长约为245米.4.(黔东南中考)如图,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数)(参考数据:sin 39°≈0.63,cos 39°≈0.78,tan 39°≈0.81,2,3≈1.73,4≈2.24)解:假设点D 移到D′的位置时,恰好∠α=39°,过点D 作DE⊥AC 于点E ,作D′E′⊥AC 于点E′,∵CD =12米,∠DCE =60°, ∴DE =CD·sin60°=12×32=63(米), CE =CD·cos60°=12×12=6(米).易知:四边形DEE′D′是矩形.∴DE =D′E′=63米. ∵∠D′CE′=39°,∴CE′=D′E′tan39°≈错误!≈12.8,∴EE′=CE′-CE =-6=(米). ∴DD′=EE′=米.答:学校至少要把坡顶D 向后水平移动米才能保证教学楼的安全.5.(某某中考)如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC =4米,AB =6米,中间平台宽度DE =1米,EN ,DM ,CB 为三根垂直于AB 的支柱,垂足分别为N ,M ,B ,∠EAB=31°,DF⊥BC 于F ,∠CDF=45°.求DM 和BC 的水平距离BM 的长度.(结果精确到0.1米,参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)解:设BM =x 米.∵∠CDF =45°,∠CFD =90°, ∴CF =DF =x 米.∴BF =BC -CF =(4-x )米. ∴EN =DM =BF =(4-x )米.∵AB =6米,DE =MN =1米,BM =x 米, ∴AN =AB -MN -BM =(5-x )米.在△AEN 中,∠ANE =90°,∠EAN =31°,∴EN =AN·tan31°,即4-x =(5-x ). ∴x =2.5.答:DM 和BC 的水平距离BM 的长度约为米.6.(某某中考)某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB 的长为3 m ,静止时,踏板到地面距离BD 的长为0.6 m (踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为h m ,成人的“安全高度”为2 m .(计算结果精确到0.1 m ,参考数据:2≈1.41,sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43)(1)当摆绳OA 与OB 成45°夹角时,恰为儿童的安全高度,则h =m ; (2)某成人在玩秋千时,摆绳OC 与OB 的最大夹角为55°,问此人是否安全?解:过C 点作CM⊥DF,CE⊥OD,垂足分别为M ,E ,∵在Rt△CEO 中,∠CEO =90°, ∠COE =55°, ∴cos∠COE =OEOC.∴OE =OC·cos∠COE =3·cos55°≈1.7 m. ∴ED =3+-=(m ).∴CM =ED =1.9 m <2 m.∴此人是安全的.章末复习(八) 锐角三角函数01分点突破知识点1 求锐角三角函数值1.如图,在Rt △ABC 中,∠BAC=90°,AD⊥BC 于点D ,则下列结论不正确的是(C )A .sinB =AD AB B .sin B =AC BC C .sin B =AD ACD .sin B =CD AC第1题图第3题图2.在Rt △ABC 中,∠C=90°,若斜边AB 是直角边BC 的3倍,则tan B 的值是(D )A.13B .3 C.24D .2 2 3.如图,在△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE ,若BE =9,BC =12,则cos C =23.知识点2 特殊角的三角函数值(某某2016T19、2015T19、2014T19) 4.在△ABC 中,若(3tan A -3)2+|2cos B -3|=0,则△ABC 为(A )A .直角三角形B .含60°角的任意三角形C .等边三角形D .顶角为钝角的等腰三角形5.(某某中考改编)计算:(π-2 016)0+|1-2|+2-1-2sin 45°=12.知识点3 解直角三角形及其应用(某某2017T22、2016T21、2015T21、2014T21、2013T21) 6.在△ABC 中,∠C =90°,AB =2,BC =3,则tan A 2=33.7.如图,在电线杆CD 上的C 处引拉线CE 、CF 固定电线杆,拉线CE 和地面所成的角∠CED=60°,在离电线杆6米的B 处安置高为1.5米的测角仪AB ,在A 处测得电线杆上C 处的仰角为30°,求拉线CE 的长.(结果保留小数点后一位,参考数据:2≈1.41,3≈1.73)解:过点A 作AH⊥CD,垂足为H. 则AB =DH =米,BD =AH =6米.在Rt△ACH 中,∵∠CAH =30°,tan∠CAH =CH AH,∴CH =AH·tan∠CAH =6·tan30°=23(米). ∴CD =CH +HD =(23+)米.在Rt△CDE 中,∵∠CED =60°,sin∠CED =CD CE,∴CE =CDsin60°=4+3(米).答:拉线CE 的长约为米.02中考题型演练8.(某某中考)如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cos α=1213,则小车上升的高度是(A )A .5米B .6米C .6.5米D .12米第8题图 第9题图9.(某某中考) △ABC 在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC 于D ,下列四个选项中,错误的是(C )A .sin α=cos αB .tanC =2 C .sin β=cos βD .tan α=110.(某某中考)如图,⊙O 是边长为2的等边△ABC 的内切圆,则⊙O 的半径为33.第10题图 第12题图11.(某某中考) △ABC 中,AB =12,AC =39,∠B=30°,则△ABC 的面积是213或153.12.(某某中考)如图,某城市的电视塔AB 坐落在湖边,数学老师带领学生隔湖测量电视塔AB 的高度,在点M 处测得塔尖点A 的仰角∠AMB 为22.5°,沿射线MB 方向前进200米到达湖边点N 处,测得塔尖点A 在湖中的倒影A′的俯角∠A′NB 为45°,则电视塔AB 的高度为1002米.(结果保留根号)13.(某某中考)如图,一楼房AB 后有一座假山,其坡度为i =1∶3,山坡坡面上E 点处有一休息亭,测得假山坡脚C 与楼房水平距离BC =25米,与亭子距离CE =20米,小丽从楼房顶测得E 点的俯角为45°,求楼房AB 的高.(注:坡度i 是指坡面的铅直高度与水平宽度的比)解:过点E 作EF⊥BC 的延长线于点F ,EH⊥AB 于点H , 在Rt△CEF 中,∵i =EFCF=13=tan∠ECF, ∴∠ECF =30°.∴EF =12CE =10米,CF =103米.∴BH =EF =10米,HE =BF =BC +CF =(25+103)米.在Rt△AHE 中,∵∠HAE =45°,∴AH =HE =(25+103)米. ∴AB =AH +HB =(35+103)米.答:楼房AB 的高为(35+103)米.14.(某某中考)今年,我国海关总署严厉打击“洋垃圾”某某行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为752海里.(1)求B点到直线CA的距离;(2)执法船从A到D航行了多少海里?(结果保留根号)解:(1)过点B作BH⊥CA,交CA的延长线于点H.∵∠MBC=60°.∴∠CBA=30°.∵∠NAD=30°,∴∠BAC=120°.∴∠C=180°-∠BAC-∠CBA=30°.∴BH=BC·sin∠BCA=150×12=75海里.答:B点到直线CA的距离是75海里.(2)∵在Rt△BDH中,BD=752海里,BH=75海里,∴DH=BD2-BH2=75海里,∵∠BAH=180°-∠BAC=60°,在Rt△ABH中,tan∠BAH=BHAH=3,∴AH=253海里.∴AD=DH-AH=(75-253)海里.答:执法船从A到D航行了(75-253)海里.。
锐角三角函数(全)

锐角三角函数 ( 1)一.问题: 为了绿化荒山,某地打算从位于山脚下的机井房沿山坡铺设水管,在山坡上修建一座扬 水站,对坡面的绿地进行喷灌 .现测得斜坡与水平面所成角的度数是 30 ,为使出水口的高度为 35m , 求需要准备多长的水管?探究:如图, Rt ABC 与 Rt ABC 中, C C 90 , A A , 探究 BC 与 BC 的关系AB A B结论:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠ A 的对边 与斜边的比是一个固定值 .※在 Rt ABC 中, C 90 ,我们把锐角 A 的对边与斜边的比叫做∠ A 的正弦 . 记作 sin ABC 如图, sinA A 的对边a A 的斜边 c AB 二.例题与练习: 1. 例题:如图,在 Rt ABC 中, C 90 ,求 sin A 和 sinB的值 . 同理: sinB B 的对边B 的斜边 2. 练习: 1. 三角形在正方形网格纸中的位置如图所示,则 3. 4 C . 3 . C . 35 Rt ABC 中, C 90 ,若 AB 5 , C .3 4 A . 42. 如图,在 A .3 5 B .45 3. 在 Rt ABC 中, C 90 , BC 2 , 4 3 AB 是⊙ O 的直径,点 ; sin ADC = 5.在 Rt ABC 中, ACB 90 , A . 13 B 4.如图,已知 则 sin BAC = sin ACD 的值为( ) A . 5B . 2 33D D ,则边 AC 的长是 ( ) .5 且 AB 5 , BC 3 . 则 sinA 的值是( 4 3 b c sin 的值是﹙ .4 5 AC 4, ACABsin A 23 C 、 D 在⊙ O 上, CD AB 于点 D . 已知 AC 5 , BC 2 , .5三.在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠ A 的邻边与 斜边的比是一个固定值,∠ A 的对边与邻边的比是一个固定值,※在 Rt ABC 中, C 90 ,我们把锐角 A 的邻边与斜边的比叫做∠ A 的余弦.记作 cosAA 的邻边 b ACB 的邻边 a BC 如图, cosA 同理: cosB A 的斜边 c AB B 的斜边 c AB ※在 Rt ABC 中, C 90 ,我们把锐角 A 的对边与邻边的比叫做∠ A 的正切.记作 tanABC AC 如图, tanA A A 的的邻对边边 a b 四.例题与练习: 同理: tanB B B 的的对邻边边b a AC BC 例题:如图,在 Rt ABC 中, 3 C 90 , BC 6 ,sin A ,求 cos A , tanB 的值 . 5练习: 1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值 2. 如图,在 Rt ABC 中, 五.课后作业:1. 在 Rt ABC 中, A . b a tan A2. 在 Rt ABC中, C 90 , AC 8 , 3 tan A 4 求 sin A 、 cosB 的值C 90 , a , b , c 分别是 A 、 B 、 C 的对边,则有( B . b c sinA C . a c cosBD C 90 ,如果 cosA 4,那么 tan B 的值为 5 c a sinA A . 3 5 3.如图: 4. 分别求出图中 A 、 B 的正弦值、余弦值和正切值 5 C . 3 44 P 是 的边 OA 上一点,且 4 3 P 点的坐标为( 3, 4),则 cos = (B 层)在 ABC 中, AB a , AC b , A ,求 ABC 的面积(用含有字母示)a ,b , 的式子表三 角 函 数(2).探究: 如图,在 Rt ABC 中, C 90 .⑴如图 1, A 30 ,求 sin A 、⑵如图 1, B 60 ,求sinB 、⑶如图 2, A 45 ,求 sin A 、⑶ A 的正切值随着 A 的角度的增大而三.例题与练习:例题 1:求下列各式的值:例题 2:⑴如图 1, 在 Rt ABC 中, C 90 , AB 6 , BC 3 ,求 A 的度数 . ⑵如图 2,已知圆锥的高 AO 等于圆锥的底面半径 OB 的 3倍, 求 .⑵ 3 tan 30 tan45 2 sin 60 ⑶ cos60 1二.结论: 1. 完成表格:2. ⑴ A 的正弦值随着 A 的角 度的增大而 .⑵ A 的余弦值随着 A 的角度 的增大而 .cosA 、 tanA 的值; cosB 、 tanB 的值; cosA 、 tan A 的值; ⑴ cos 260 sin 260cos45 sin45tan45 练习: 1. 求下列各式的值: ⑴ 1 2 sin 301 sin60 tan30 四.课堂检测:计算:cos260 cos245 2sin30 sin 451.将21 cosB 23 sin B改写成下列形式的式子,其中错误的是()A. sin30 cosB cos30 sinBB. sin30 cosB sin60 sinBC. cos60 cosB cos30 sinBD. cos60 cosB sin30 sinB2. 在 Rt ABC中, C 90 , a:b 3,则 sin A的值是()1A. 1B.2 22C. 32D.333. 在 ABC 中,A、 B 都是锐角,且sin A 1,,cosB 3,则 ABC 的形状为()2 2A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不能确定4. 化简tan30 12的结果为()3A.1B. 3 1C. 3 1D. 133 35. 已知2sin 3 0 ,则锐角的度数为 . B16.已知 B 是锐角,若sin B 1,则 tan B的值为.2237.在 Rt ABC中, C 90 ,sinB ,则 cos A的值为.238.已知 sin90 23,则锐角的度数为 .9.求下列各式的值:3⑴tan230 2 sin 60 tan45 tan60 cos230 ⑵ cos60 sin 245 tan230 cos 230 sin30410.在Rt ABC中, C 90 , tanA 3 ,且 AB 10cm ,求 AC 、BC的长.11.如图,一块为 ABC 的空地, AC 10m , BC 30m , C 150 ,现在这块空地上种植每平方米 a 元的草皮,求购买这种草皮至少需要多少钱?(B层)12.如图, A ,B两地之间有一座山,汽车原来从A地到B地须经 C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB 行驶. 已知 AC 10km, A 30 , B 45 ,求开通隧道后,汽车从 A 地到 B 地比原来少走多少千米?(结果保留根号)锐角三角函数 ( 3)二.课堂检测:1. 求下列锐角三角函数值(精确到 0.0001):⑴ sin25 30 = ; ⑵ cos62 18 =一.例题与练习:例题 1:用计算器计算下列锐角三角函数值(精确到 0.0001) ⑴ sin 20 ⑵ cos70 ⑶ sin15 32 ⑷ cos74 28 ⑸tan3 8⑹ tan80 25 43由⑴→⑷你能得到的猜想为 ,请利用下图验证你的猜想练习:用计算器计算下列锐角三角函数值(精确到 0.0001)⑸ tan36 20 ⑹ tan75 17例题 2:已知下列锐角三角函数值,用计算器求其相应的锐角 ⑴ sinA 0.6275 ⑵ cosA 0.6252 ⑶ tanA 4.8425 练习:⑴ sin A 0.0547⑵ cosA 0.1659 ⑶ tanA 0.8816⑷ sinA 0.9816 ⑸ cosA 0.8607 ⑹ tanA 0.1890例题 3:如图,要焊接一个高 3.5m ,底角为 32 的人字形钢架,约需要多长的钢材(结果保留小数点 后两位)练习:如图,一块平行四边形木板的两条邻边 AD 、 BC 的长分别为 62.31cm 和 35.24cm ,它们之间的 夹角 B 为 35 40 ,求这块木板的面积(结果保留小数点后两位)tan26 50 = .⑴ sinA 0.4723,A= ;⑵ cos A A= ;⑶ tanA 15.94 , A三.课后练1.计算 2sin 60 3 tan 30 的值)A .3B . 2 3C .3 3D .432.在 Rt ABC 各边的长度都扩 4 倍,那么 B 的正切值()A .扩大 4 倍B .扩大 2倍C .保持不变D .缩小4倍3.已知为锐角,tan 3 ,则c os 等于()A .1B .2C .3 D. 3 2 2 2 34.如果等腰三角形的底角为 30 ,腰长为 6cm ,那么这个三角形的面积为()A .4. 5cm2B .9 3 cm2C .18 3cm2D .36cm25Rt ABC C 90 , b a 则 cosB 等()5 .5.12 12A B cm C D .cm12 .12 .13 136已知 cos 则的度数为()A40 B .41 C .42 D .437.已知 cosA 0.5761,则 A ;若tanA 15.21,则 A ;若sin A 0.3562 ,则 A8. 某人沿倾斜角为 25 的斜坡前行了 100m ,则他上升的最大高度为(精确到 0.01 m )9.计算:⑴ 2cos60 6 sin 45 sin 60 ⑵ cos45 sin 301cos60 tan45210. 已知:如图,在 Rt ABC中, C 90 ,CD 是高,BC 10cm, B 53 6 ,?求CD 、 AC 、AB .(精确到 1cm)(B层)1.要求 tan30 的值,可构造如图所示的直角三角形进行计算:作Rt ABC ,使 C 90 ,斜边AB 2 ,直角边 AC 1,那么BC 3 , ABC 30 ,tan30 AC 1 3,在此图的基础上,BC 3 3 通过添加适当的辅助线,可求出 tan15 的值,请简要写出你添加的辅助线和求出 tan15 的值.2 如图,把矩形纸片 OABC 放入平面直角坐标系中,y 轴上,连接 OB ,将纸片 OABC 沿 OB 折叠,使点--6--锐角三角函数 ( 4)一.问题: 如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 满足 50 75 ,现有一个长 6m 的梯子,问: ⑴使用这个梯子最高可以攀上多高的墙(结果保留小数点后一位)? ⑵当梯子底端距离墙面 2.4m 时,这个人是否能够安全使用这个梯子? B 得 AC BC.解直角三角形:在 Rt ABC 中, C 90 ,AC ABB得 A 或由BCA AB三.例题与练习:例题 1:如图, Rt ABC 中, C 90 , AC 2 , BC 6 ,解这个直角三角形练习:如上图, Rt ABC 中, C 90 , BC 30 , AC 20 ,解这个直角三角形 .例题 2:如图,在 Rt ABC 中, C 90 , B 35 , AC 20 ,解这个直角三角形(结果保留小数点 后一位) 练习:如上图,在 Rt ABC 中, C 90 , A 72 , 后一位) . AB 14 ,解这个直角三角形(结果保留小数点四.课堂检测:在 Rt ABC中, C 90 , A 、 B 、 C 的对边分别为 解这个直角三角形 a 、b 和c ,若c 20,b 102 ,五.课后作业:1.在 Rt ABC 中, C 90 , A 、 B 、 C 的对边分别为 a 、b 和 c ,根据下列条件解直角三角形2.在 ABC 中, AD BC 于点 D ,且 B 30 , C 45 ⑴若 AD 5 ,求 BC 的长 ⑵若 BC =15,求 AD 的长3.为了测量塔高,小龙在距塔的中心点 B 50 米的C 处,用测角器量得仰角为 40 ,已知测角器的高度为 1.52 米,求塔高 AB 的长 .(精确到 0.1 米)4. 如图所示,在离铁塔 150米的 A 处用测角仪测得塔顶仰角 求铁塔高 BE . (精确到 0.1 米)5.如图所示,从某海岛上的观察所 A 测得海上某船只 B 的俯角为 8 18 ,若观察所 A 与海面的垂⑴ a 3 3 , c 6 ⑵ a 36 , B 30 ⑶ c 10 , b 6BAC 26 12 ,已知仪器高 AD 1.5 米,直高度 AC 50 米,求船只 B 到观察所的水平距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数检测11、 如图(1),在Rt △ABC 中,∠C=90°,求sinA=_____ sinB=______.2、 如图(2),在Rt △ABC 中,∠C=90°,求sinA=_____ sinB=_____ 3. 在△ABC 中,∠C=90°,BC=2,sinA=23,则边AC 的长是( )A .13B .3C .43D . 54.如图,已知点P 的坐标是(a ,b ),则sin α等于( )A .a bB .b aC 2222D a ba b ++5在Rt △ABC 中,∠C=900,sinA=53,求sinB 的值.6如图,Rt △ABC 中,∠C=900,CD ⊥AB 于D 点,AC=3,BC=4,求sinA 、sin ∠BCD 的值.7在Rt △ABC 中,∠C=900,AC=5cm,BC=3cm,则sinA=______,sinB=________.8在Rt △ABC 中,∠C=900,如果各边的长度都扩大2倍,那么锐角A 的正弦值( ) A 、扩大两倍 B 、缩小两倍 C 、没有变化 D 、不能确定9在Rt △ABC 中,∠C=900,AB=15,sinA=31,则AC=_______,S △ABC =_______.10在Rt △ABC 中,∠C=900,∠A=300,BD 平分∠ABC 交AC 边于D 点, 则sin ∠ABD 的值为___B A ABCDOABD·∠A的邻边b∠A的对边a 斜边c CBA图2图1134C ACB6CB A锐角三角函数检测21如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D 。
已知AC= 5 ,BC=2,那么sin ∠ACD =( )A .53B .23C .255D .522如图,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,且AB =5,BC =3.则sin ∠BAC= ;sin ∠ADC= . 1、 如图(1),在Rt △ABC 中,∠C=90°,求cosA=_____ ,cosB=______,tanA=_______,tanB=_______. 2、 如图(2),在Rt △ABC 中,∠C=90°,求cosA=_____ ,cosB=______,tanA=_______,tanB=_______. 3、在Rt △ABC中,∠C=90°,AC=•8,tanA=43,则BC=_____,AB=______,cosA=____tanB=_____. 4、在△ABC 中,AB=AC=5,BC=8,则tanB=______.5、在Rt △ABC 中,∠C=90°,sinB=53,求cosA 的值是___________.6如图,在Rt △ABC 中,∠C=90°,BC=•6,sinA=35,求cosA 、tanB 的值7.在△ABC 中,∠C =90°,a ,b ,c 分别是∠A 、∠B 、∠C 的对边,则有( )A .B .C .D .8在Rt △ABC 中,∠C =90°,如果cosA=45 那么tanB 的值为( )A .35B .54C .34D .43 9如图:P 是∠的边OA 上一点,且P 点的坐标为(3,4),则cos α=_____________.10在Rt △ABC 中,∠C =90°sinA:sinB=3:4,则tanB 的值是_______ 11在Rt △ABC 中,∠C =90°,BC=5,sinA=0.7,求cosA,tanA 的值.12如图(1)在Rt △ACB 中, ∠C=90°,∠A=30°,若BC=a,则AB=______,AC= _______, ∠B=____0,sinA=______,cosA=_______,tanA=_______ ,sinB=______,cosB=_______,tanB=_______ 13如图(2)在Rt △ACB 中,∠C=90°,若∠A =45°,BC=m ,则∠B=________AC= ________,AB=________, sinA=______,cosA=_______,tanA=_______。
a 30°Am 45°B CA 图2图121312BB锐角三角函数阶段检测31填表观察上表发现:(1)一个锐角的度数越大,它的正弦值_______,余弦值_______,正切值_______, (2) sinA 、 cosA 、 tanA 的取值围分别是________________________.2计算cos600=______ tan300=_______ 2sin450=_______ tan 2450=______ 3若sinA=21,则∠A=_____;若tanA=3,则∠A=_____;若cosA=22,则∠A=_____;4计算2sin30°-2cos60°+tan45°的结果是_______. 4、sin 272°+sin 218°的值是_________. 5求下列各式的值.(1)cos 260°+sin 260°. (2)cos 45sin 45︒︒-tan45°.6(1)如图(1),在Rt △ABC 中,∠C=90,AB=6,BC=3,求∠A 的度数. (2)如图(2),已知圆锥的高AO 等于圆锥的底面半径OB 的3倍,求a .7下列各式中不正确的是( ).A .sin 260°+cos 260°=1B .sin30°+cos30°=1C .sin35°=cos55°D .tan45°>sin45°8已知∠A 为锐角,且cosA ≤12,那么( )A .0°<∠A ≤60°B .60°≤∠A<90°C .0°<∠A ≤30°D .30°≤∠A<90°9在△ABC 中,∠A 、∠B 都是锐角,且sinA=12 ,cosB= 32,则△ABC 的形状是( )A .直角三角形B .钝角三角形C .锐角三角形D .不能确定10如图Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,BC=3,AC=4,设∠BCD=a ,则tana•的值为( ). A .43B .34 C .53 D .54 11当锐角a>60°时,cosa 的值( ). A .小于12 B .大于12 C .大于 3 2 D .大于112若( 3 tanA-3)2+│2cosB- 3 │=0,则△ABC ( ).A .是直角三角形B .是等边三角形C .是含有60°的任意三角形D .是顶角为钝角的等腰三角形 13设α、β均为锐角,且sin α-cos β=0,则α+β=_______.14已知,等腰△ABC•的腰长为4 3 ,•底为30•°,•则底边上的高为______,•周长为______.30° 45° 60° siaA cosA tanA35解直角三角形测试41.在△ABC 中,∠C=90°,若b=2,c=2,则tanB=__________2.在Rt △ABC 中,∠C=90°,sinA=54,AB=10,则BC=______.3.在△ABC 中,∠C=90°,若a:b=5:12则sinA= .4 在直角三角形ABC 中,∠C=90°,∠A=30°,斜边上的高h=1,则三边的长分别是_____________________.5如图,在Rt △ABC 中,∠C=90°,tanA=34, COSB=___________.6 如图,在Rt △ABC 中,∠C=90°,AB=6,AD=2,则sinA=____;tanB=____. 7如图在△ABC 中,∠C=900,∠A=300.D 为AC 上一点,AD=10,∠BDC=600,求AB 的长8在△ABC 中,∠C=900点D 在BC 上,BD=4,AD=BC,cos ∠ADC=35.,求(1)DC的长;(2)sinB 的值; 9Rt △ABC 中,若sinA=54,AB=10,那么BC=_____,tanB=______. 10在△ABC 中,∠C=90°,AC=6,BC=8,那么sinA=________.11在△ABC 中,∠C=90°,sinA= 则cosA 的值是 a=3,b=3,解这个三角形.12在Rt △ABC 中,∠C=90°,13 在△ABC 中,∠C 为直角,AC=6,BAC 的平分线AD=43,解此直角三角形。
BACDBACCDABACD EFB解直角三角形的应用练习51在山脚C 处测得山顶A 的仰角为45°。
问题如下:(1)沿着水平地面向前300米到达D 点,在D 点测得山顶A 的仰角为60 °,求山高AB 。
(2)沿着坡角为30 °的斜坡前进300米到达D 点,在D 点测得山顶A 的仰角为60 ° ,求山高AB 。
2直升飞机在高为200米的大楼AB 上方P 点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .3如图所示,小在广场上的A 处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D 处的仰角为30º,然后他正对大楼方向前进5m 到达B 处,又测得该屏幕上端C 处的仰角为45º.若该楼高为26.65m ,小的眼睛离地面 1.65m ,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离( 3 ≈1.732,结果精确到0.1m ).4某旅游区有一个景观奇异的望天洞,D 点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A 处观看旅游区风景,最后坐缆车沿索道AB 返回山脚下的B 处.在同一平面,若测得斜坡BD 的长为100米,坡角10DBC ∠=°,在B 处测得A 的仰角40ABC ∠=°,在D 处测得A 的仰角85ADF ∠=°,过D 点作地面BE 的垂线,垂足为C . (1)求ADB ∠的度数; (2)求索道AB 的长.(结果保留根号)5如图,太线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为________米.(结果保留根号) 6.王英同学从A 地沿北偏西60º方向走100m 到B 地,再从B 地向正南方向走200m 到C 地,此时王英同学离A 地 ( )A .150mB .350mC .100 mD .3100m7.如图所示,海上有一灯塔P ,在它周围3海里处有暗礁.一艘客轮以9海里/时的速度由西向东航行,行至A 点处测得P 在它的北偏东60°的方向,继续行驶20分钟后,到达B 处又测得灯塔P 在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险?A B CDE8如图,某货船以20海里/时的速度将一批重要物资由A 处运往正西方向的B 处,经16小时的航行到达,到达后必须立即卸货.此时.接到气象部门通知,一台风中心正以40海里/时的速度由A 向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均受到影响. (1)B 处是否会受到台风的影响?请说明理由.(2)为避免受到台风的影响,该船应在多少小时卸完货物?(供选用数据:2≈1.4,3 ≈1.7)9上午10点整,一渔轮在小岛O 的北偏东30°方向,距离等于10海里的A 处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O 的正向是什么时间?(精确到1分).10在东西方向的海岸线l 上有一长为1km 的码头MN (如图),在码头西端M 的正西19.5 km 处有一观察站A .某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A 相距40km 的B 处;经过1小时20分钟,又测得该轮船位于A 的北偏东60°,且与A 相距83km 的C 处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN 靠岸?请说明理由.NM 东北BCAl解直三角形应用自测61.一段坡面的坡角为60°,则坡度i=______; ______,坡角α______度.3.如图,一水坝横断面为等腰梯形ABCD ,斜坡AB 的坡度为1∶3,坡面AB 的水平宽度为33米,上底宽AD 为4米,求坡角B ,坝高AE 和坝底宽BC 各是多少?4某海港区为提高某段海堤的防海潮能力,计划将100米的一段堤(原海堤的横断面如图中的梯形ABCD )的堤面加宽1米,背水坡度由原来的1:1改成1:2。
