实验三动态规划求多段图问题
实验三-动态规划法求多段图问题

本科实验报告课程名称:算法设计与分析实验项目:动态规划法求多段图问题实验地点:专业班级:学号:学生姓名:指导教师:实验三动态规划法求多段图问题一、实验目的1.掌握动态规划算法的基本思想2.掌握多段图的动态规划算法3.选择邻接表或邻接矩阵方式来存储图4、分析算法求解的复杂度。
二、实验内容设G=(V,E)是一个带权有向图,其顶点的集合V被划分成k>2个不相交的子集Vi,1<i<=k,其中V1和Vk 分别只有一个顶点s(源)和一个顶点t(汇)。
图中所有边的始点和终点都在相邻的两个子集Vi和Vi+1中。
求一条s到t的最短路线。
参考讲义p136图5-24中的多段图,试选择使用向前递推算法或向后递推算法求解多段图问题。
三、实验环境程序设计语言:c++编程工具:microsoft visual studio 2010四、算法描述和程序代码#include <stdio.h>#include <stdlib.h>#include <conio.h>#include <iostream.h>#define MAX 100#define n 12#define k 5int c[n][n];void init(int cost[]) //初始化图{int i,j;for(i=0;i<13;i++){ for(j=0;j<13;j++){ c[i][j]=MAX;}}c[1][2]=9; c[1][3]=7; c[1][4]=3; c[1][5]=2; c[2][6]=4; c[2][7]=2; c[2][8]=1;c[3][6]=2; c[3][7]=7; c[4][8]=11; c[5][7]=11; c[5][8]=8; c[6][9]=6; c[6][10]=5;c[7][9]=4; c[7][10]=3; c[8][10]=5; c[8][11]=6; c[9][12]=4; c[10][12]=2;c[11][12]=5;}void fgraph(int cost[],int path[],int d[]) //使用向前递推算法求多段图的最短路径{ int r,j,temp,min;for(j=0;j<=n;j++)cost[j]=0;for(j=n-1;j>=1;j--){ temp=0;min=c[j][temp]+cost[temp]; //初始化最小值for(r=0;r<=n;r++){if(c[j][r]!=MAX){if((c[j][r]+cost[r])<min) //找到最小的r{ min=c[j][r]+cost[r];temp=r;} } }cost[j]=c[j][temp]+cost[temp];d[j]=temp; }path[1]=1; path[k]=n;for(j=2;j<k;j++)path[j]=d[path[j-1]];}void bgraph(int bcost[],int path1[],int d[])//使用向后递推算法求多段图的最短路径{ int r,j,temp,min;for(j=0;j<=n;j++)bcost[j]=0;for(j=2;j<=n;j++){ temp=12;min=c[temp][j]+bcost[temp];//初始化最小值for(r=0;r<=n;r++){if(c[r][j]!=MAX){if((c[r][j]+bcost[r])<min) //找到最小的r{min=c[r][j]+bcost[r];temp=r;} } }bcost[j]=c[temp][j]+bcost[temp];d[j]=temp;}path1[1]=1;path1[k]=n;for(int i=4;i>=2;i--){ path1[i]=d[path1[i+1]];} }void main(){int cur=-1;int cost[13],d[12],bcost[13];int path[k];int path1[k];cout<<"\t\t\t动态规划解多段图问题"<<endl;cout<<"\n\n";init(cost);fgraph(cost,path,d);cout<<"输出使用向前递推算法后的最短路径:\n\n";for(int i=1;i<=5;i++){ cout<<path[i]<<" ";}cout<<"\n";cout<<endl<<"最短路径为长度:"<<cost[1]<<endl;cout<<"\n";cout<<"\n输出使用向后递推算法后的最短路径:\n\n";bgraph(bcost,path1,d);for(i=1;i<=5;i++){ cout<<path1[i]<<" ";}cout<<"\n";cout<<endl<<"最短路径为长度:"<<bcost[12]<<endl;cout<<"\n";}五、实验结果截图六、实验总结七、。
动态规划算法详解及经典例题

动态规划算法详解及经典例题⼀、基本概念(1)⼀种使⽤多阶段决策过程最优的通⽤⽅法。
(2)动态规划过程是:每次决策依赖于当前状态,⼜随即引起状态的转移。
⼀个决策序列就是在变化的状态中产⽣出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。
假设问题是由交叠的⼦问题所构成,我们就能够⽤动态规划技术来解决它。
⼀般来说,这种⼦问题出⾃对给定问题求解的递推关系中,这个递推关系包括了同样问题的更⼩⼦问题的解。
动态规划法建议,与其对交叠⼦问题⼀次重新的求解,不如把每⼀个较⼩⼦问题仅仅求解⼀次并把结果记录在表中(动态规划也是空间换时间的)。
这样就能够从表中得到原始问题的解。
(3)动态规划经常常使⽤于解决最优化问题,这些问题多表现为多阶段决策。
关于多阶段决策:在实际中,⼈们经常遇到这样⼀类决策问题,即因为过程的特殊性,能够将决策的全过程根据时间或空间划分若⼲个联系的阶段。
⽽在各阶段中。
⼈们都须要作出⽅案的选择。
我们称之为决策。
⽽且当⼀个阶段的决策之后,经常影响到下⼀个阶段的决策,从⽽影响整个过程的活动。
这样,各个阶段所确定的决策就构成⼀个决策序列,常称之为策略。
因为各个阶段可供选择的决策往往不⽌⼀个。
因⽽就可能有很多决策以供选择,这些可供选择的策略构成⼀个集合,我们称之为同意策略集合(简称策略集合)。
每⼀个策略都对应地确定⼀种活动的效果。
我们假定这个效果能够⽤数量来衡量。
因为不同的策略经常导致不同的效果,因此,怎样在同意策略集合中选择⼀个策略,使其在预定的标准下达到最好的效果。
经常是⼈们所关⼼的问题。
我们称这种策略为最优策略,这类问题就称为多阶段决策问题。
(4)多阶段决策问题举例:机器负荷分配问题某种机器能够在⾼低两种不同的负荷下进⾏⽣产。
在⾼负荷下⽣产时。
产品的年产量g和投⼊⽣产的机器数量x的关系为g=g(x),这时的年完善率为a,即假设年初完善机器数为x,到年终时完善的机器数为a*x(0<a<1);在低负荷下⽣产时,产品的年产量h和投⼊⽣产的机器数量y 的关系为h=h(y)。
动态规划算法

动态规划算法
动态规划算法(Dynamic Programming)是一种解决多阶段最优化决策问题的算法。
它将问题分为若干个阶段,并按照顺序从第一阶段开始逐步求解,通过每一阶段的最优解得到下一阶段的最优解,直到求解出整个问题的最优解。
动态规划算法的核心思想是将问题划分为子问题,并保存已经解决过的子问题的解,以便在求解其他子问题时不需要重新计算,而是直接使用已有的计算结果。
即动态规划算法采用自底向上的递推方式进行求解,通过计算并保存子问题的最优解,最终得到整个问题的最优解。
动态规划算法的主要步骤如下:
1. 划分子问题:将原问题划分为若干个子问题,并找到问题之间的递推关系。
2. 初始化:根据问题的特点和递推关系,初始化子问题的初始解。
3. 递推求解:按照子问题的递推关系,从初始解逐步求解子问题的最优解,直到求解出整个问题的最优解。
4. 得到最优解:根据子问题的最优解,逐步推导出整个问题的最优解。
5. 保存中间结果:为了避免重复计算,动态规划算法通常会使
用一个数组或表格来保存已经求解过的子问题的解。
动态规划算法常用于解决最优化问题,例如背包问题、最长公共子序列问题、最短路径问题等。
它能够通过将问题划分为若干个子问题,并通过保存已经解决过的子问题的解,从而大大减少计算量,提高算法的效率。
总之,动态规划算法是一种解决多阶段最优化决策问题的算法,它通过将问题划分为子问题,并保存已经解决过的子问题的解,以便在求解其他子问题时不需要重新计算,从而得到整个问题的最优解。
动态规划算法能够提高算法的效率,是解决最优化问题的重要方法。
动态规划法的一般方法

动态规划法的⼀般⽅法在学习动态规划法之前,我们先来了解动态规划的⼏个概念1、阶段:把问题分成⼏个相互联系的有顺序的⼏个环节,这些环节即称为阶段。
2、状态:某⼀阶段的出发位置称为状态。
3、决策:从某阶段的⼀个状态演变到下⼀个阶段某状态的选择。
4、状态转移⽅程:前⼀阶段的终点就是后⼀阶段的起点,前⼀阶段的决策选择导出了后⼀阶段的状态,这种关系描述了由k阶段到k+1阶段状态的演变规律,称为状态转 移⽅程。
动态规划法的定义:在求解问题中,对于每⼀步决策,列出各种可能的局部解,再依据某种判定条件,舍弃那些肯定不能得到最优解的局部解,在每⼀步都经过筛选,以每⼀步都是最优解来保证全局是最优解,这种求解⽅法称为动态规划法。
⼀般来说,适合于⽤动态规划法求解的问题具有以下特点:1、可以划分成若⼲个阶段,问题的求解过程就是对若⼲个阶段的⼀系列决策过程。
2、每个阶段有若⼲个可能状态3、⼀个决策将你从⼀个阶段的⼀种状态带到下⼀个阶段的某种状态。
4、在任⼀个阶段,最佳的决策序列和该阶段以前的决策⽆关。
5、各阶段状态之间的转换有明确定义的费⽤,⽽且在选择最佳决策时有递推关系(即动态转移⽅程)。
动态规划设计都有着⼀定的模式,⼀般要经历以下⼏个步骤:1、划分阶段:按照问题的时间或空间特征,把问题分为若⼲个阶段。
2、确定状态:将问题发展到各个阶段时所处的各种客观情况⽤不同的状态表⽰出来。
3、确定决策并写出状态转移⽅程:因为决策和状态转移有着天然的联系,状态转移就是根据上⼀阶段的状态和决策来导出本阶段的状态,所以如果确定了决策,状态转移⽅程也就可以写出。
4、寻找边界条件:给出的状态转移⽅程是⼀个递推式,需要⼀个递推的终⽌条件或边界条件。
5、程序设计实现:动态规划的主要难点在于理论上的设计,⼀旦设计完成,实现部分就会⾮常简单。
根据以上的步骤设计,可以得到动态规划设计的⼀般模式:for k:=阶段最⼩值to 阶段最⼤值do {顺推每⼀个阶段}for I:=状态最⼩值to 状态最⼤值do {枚举阶段k的每⼀个状态}for j:=决策最⼩值to 决策最⼤值do {枚举阶段k中状态i可选择的每⼀种决策}f[ik]:=min(max){f[ik-1]+a[ik-1,jk-1]|ik-1通过决策jk-1可达ik}例如:多段图G=(V,E)是⼀个有向图。
(完整版)动态规划问题常见解法

(完整版)动态规划问题常见解法动态规划问题常见解法一、背包问题1. 0/1背包问题0/1背包问题是动态规划中的经典问题,解决的是在背包容量固定的情况下,如何选择物品放入背包,使得总价值最大化。
常见的解法有两种:记忆化搜索和动态规划。
记忆化搜索是一种自顶向下的解法,通过保存子问题的解来避免重复计算,提高效率。
动态规划是一种自底向上的解法,通过填表格的方式记录每个子问题的解,最终得到整个问题的最优解。
2. 完全背包问题完全背包问题是在背包容量固定的情况下,如何选择物品放入背包,使得总价值最大化,且每种物品可以选择任意个。
常见的解法有两种:记忆化搜索和动态规划。
记忆化搜索和动态规划的思路和0/1背包问题相似,只是在状态转移方程上有所不同。
二、最长公共子序列问题最长公共子序列问题是指给定两个序列,求它们之间最长的公共子序列的长度。
常见的解法有两种:递归和动态规划。
递归的思路是通过分别考虑两个序列末尾元素是否相等来进一步缩小问题规模,直至问题规模减小到边界情况。
动态规划的思路是通过填表格的方式记录每个子问题的解,最终得到整个问题的最优解。
三、最短路径问题最短路径问题是指在加权有向图或无向图中,求解从一个顶点到另一个顶点的最短路径的问题。
常见的解法有两种:Dijkstra算法和Bellman-Ford算法。
Dijkstra算法是通过维护一个距离表,不断选择距离最短的顶点来更新距离表,直至找到目标顶点。
Bellman-Ford算法是通过进行多次松弛操作,逐步缩小问题规模,直至找到目标顶点或发现负权环。
总结:动态规划是一种解决最优化问题的常见方法,它通过分组子问题、定义状态、确定状态转移方程和填表格的方式,来得到整个问题的最优解。
在解决动态规划问题时,可以采用记忆化搜索或者动态规划的策略,具体选择哪种方法可以根据问题的特点和优化的需要来决定。
算法实验3-最大子段和问题实验报告

昆明理工大学信息工程与自动化学院学生实验报告( 2011 — 2012 学年 第 1 学期 )课程名称:算法设计与分析 开课实验室:信自楼机房444 2012 年12月 14日一、上机目的及内容1.上机内容给定有n 个整数(可能有负整数)组成的序列(a 1,a 2,…,a n ),求改序列形如∑=jk ka1的子段和的最大值,当所有整数均为负整数时,其最大子段和为0。
2.上机目的(1)复习数据结构课程的相关知识,实现课程间的平滑过渡; (2)掌握并应用算法的数学分析和后验分析方法;(3)理解这样一个观点:不同的算法能够解决相同的问题,这些算法的解题思路不同,复杂程度不同,解题效率也不同。
二、实验原理及基本技术路线图(方框原理图或程序流程图)(1)分别用蛮力法、分治法和动态规划法设计最大子段和问题的算法; 蛮力法设计原理:利用3个for 的嵌套(实现从第1个数开始计算子段长度为1,2,3…n 的子段和,同理计算出第2个数开始的长度为1,2,3…n-1的子段和,依次类推到第n 个数开始计算的长为1的子段和)和一个if (用来比较大小),将其所有子段的和计算出来并将最大子段和赋值给summax1。
用了3个for 嵌套所以时间复杂性为○(n 3);分治法设计原理:1)、划分:按照平衡子问题的原则,将序列(1a ,2a ,…,na )划分成长度相同的两个字序列(1a ,…,⎣⎦2/n a )和(⎣⎦12/+n a ,…,na )。
2)、求解子问题:对于划分阶段的情况分别的两段可用递归求解,如果最大子段和在两端之间需要分别计算s1=⎣⎦⎣⎦)2/1(max2/n i an ik k≤≤∑=,s2=⎣⎦⎣⎦)2/(max12/n j n ajn k k≤≤∑+=,则s1+s2为最大子段和。
若然只在左边或右边,那就好办了,前者视s1为summax2,后者视s2 o summax2。
3)、合并:比较在划分阶段的3种情况下的最大子段和,取三者之中的较大者为原问题的解。
太原理工大学算法与分析实验报告

课程名称:算法设计与分析
实验项目:分治法,贪心法,动态规划法,回溯法
2016年6月6日
实验1分治法合并排序
一、实验目的
1.掌握合并排序的基本思想
2.掌握合并排序的实现方法
3.学会分析算法的时间复杂度
4.学会用分治法解决实际问题
二、实验内容
随机产生一个整型数组,然后用合并排序将该数组做升序排列,要求输出排序前和排序后的数组。
for(r=0;r<=n;r++)
{
if(c[j][r]!=MAX)
{
if((c[j][r]+cost[r])<min) //找到最小的r
{
min=c[j][r]+cost[r];
temp=r;
}
}
}
cost[j]=c[j][temp]+cost[temp];
d[j]=temp;
}
path[1]=1;
实验3动态规划法求多段图问题
一、实验目的
1.掌握动态规划算法的基本思想
2.掌握多段图的动态规划算法
3.选择邻接表或邻接矩阵方式来存储图
4.分析算法求解的复杂度
二、实验内容
设G=(V,E)是一个带权有向图,其顶点的集合V被划分成k>2个不相交的子集Vi,1<i<=k,其中V1和Vk分别只有一个顶点s(源)和一个顶点t(汇)。图中所有边的始点和终点都在相邻的两个子集Vi和Vi+1中。求一条s到t的最短路线。参考课本P124图7-1中的多段图,试选择使用向前递推算法或向后递推算法求解多段图问题。
using namespace std;
int c[n][n];
多段图的最短路劲问题,动态规划法 分析最优性原理

多段图的最短路劲问题,动态规划法分析最优性原理我们都知道,无论是初中还是高中,数理化的学习过程中都是非常重要的。
其中,最短路劲问题,是数学考试当中常考的题型之一。
它的难度在初中数学中是比较大的。
很多同学在学习该题的时候也十分头疼,因为该问题通常采用动态规划法求解即可。
所谓动态规划法,其实就是由求解方程组而得到结论最优的方法。
那么今天我们就来学习一下如何进行简单易操作并将其运用于实际之中吧!一、解题思路通过观察题目,我们可以得到题目中由图 a,图 b组成的最短路劲问题的求解法:求 a={a, b, c},其中 a、 b、 c表示两段图之间的相交点。
求 a最短路劲,我们可以根据不同的情况选择不同的方法来求解。
当我们在做题过程中遇到困难时,可以通过求解最短路劲问题来了解分析它所需要处理的基本数学原理,从而达到解决此题的目的。
根据题目中提供的信息可知,多段图对于图 b而言,最短路劲要求它具有不同的解题思路。
二、求最优解的基本方法最优解的求解方法有两种:一者为连续变量的最大值问题,二者为连续不变量。
这种问题的解决方法一般为:以图中 A点的起始位置(也就是 A与 B)作为计算基点,依次以 A点、 B 点进行一次求解方程组,再将方程组进行解析,得到最优解;或者以相同的方法求出各点的余数,得出最优解。
求解过程中需要注意两个问题:第一个问题是求方程组时不一定要选择整数、整列代入、整阶运算;第二个问题只要找到方程中关键的最优解即可。
所以在求最优解时需要掌握正确的方法,同时也要注意以下几个方面:三、动态规划法分析分析:将图中已知状态矩阵代入所求题中,可得到:设图中状态矩阵 B和状态矩阵 A是多段图中唯一正确状态的解,因此 B和 C是正确的解;设状态矩阵 A是已知状态矩阵-状态式解,则 AC和 AC是正确的解;由于状态矩阵 B和状态矩阵 A是正确方程组式外部分与状态矩阵 a、b、 c、 d四等分函数相关,因此 AC和 AC就是正确方程组。
动态规划_多阶段决策问题的求解方法

动态规划_多阶段决策问题的求解方法1.构造状态网络; :一:解决多阶段决策最优化的过程为动态规划方法在程序设计中,有一类活动的过程,由于它的特殊性,可将过程2.根据状态转移关系和状态转移方程建立最优值的分成若干个互相联系的阶段,在它的每一阶段都需要做出决策,从而3.按阶段的先后次序计算每个状态的最优值。
使整个过程达到最好的活动效果。
因此各个阶段决策的选取不能任逆向思维法是指从问题目标状态出发倒推回初始意确定,它依赖于当前面临的状态,又影响以后的发展。
当各个阶段态的思维方法。
动态规划的逆向思维法的要点可归纳为以决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条 1.分析最优值的结构,刻画其结构特征; 活动路线。
这种把一个问题看作是一个前后关联具有链状结构的多 2.递归地定义最优值; 阶段过程就称为多阶段决策过程,这种问题称为多阶段决策问题。
3.按自底向上或自顶向下记忆化的方式计算最优在多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列如果原问题可以分解成几个本质相同、规模较小的就是在变化的状态中产生出来的,故有"动态"的含义,我们称这种就会联想到从逆向思维的角度寻求问题的解决。
一般解决多阶段决策最优化的过程为动态规划方法。
策问题多采用动态规划逆向思维方法解决。
二、举:二:动态规划最优化原理 pascal 语例说明本文以信息学奥赛用语言——最优化原理是动态规划的基础。
任何一个问题,如果失去了这言为编程个最优化原理的支持,就不可能用动态规划方法计算。
这个“最优化说明,其他编程语言编写方法相同,语句类似。
原理”如果用数学化一点的语言来描述的话,就是:假设为了解决某 :一:问题描述一优化问题,需要依次作出 n 个决策 D1,D2,,Dn,如若这个决策设有 N 个不相同的整数组成的数列,记为: 序列是最优的,对于任何一个整数 k,1 < k < n,不论前面 k 个决策是怎样的,以后的最优决策只取决于由前面决策所确定的当前状态,即 ()且 ?? a1 a2 an aiajij以后的决策 Dk+1,Dk+2,,Dn 也是最优的。
实验三动态规划求多段图问题

成本值数组 存储最短路径的数组
void creatgraph() // { int i,j;
创建图的 ( 成本 ) 邻接矩阵
for(i=0;i<n;i++)
for(j=0;j<n;j++) scanf("%d",&cost[i][j]);//
获取成本矩阵数据
}
void printgraph() //
{ int i;
for(i=0;i<k;i++)
printf("%d ",path[i]);
}
int main()
{
creatgraph();
printgraph();
FrontPath();
printf(" 输出使用向前递推算法所得的最短路径 printpath();
:\n");
printf("\n
输出使用向后递推算法所得的最短路径 :\n");
printpath();
printf("\n");
return 0;
}
五、实验结果截图
六、实验总结
在做实验的过程中,要按部就班,首先明确实验目的,然后进行分析,写算法程序,最后
调试运行,不能粗枝大叶,做的过程要细心谨慎,自己不会的通过向别人请教,总之上机
编程工具: microsoft visual studio 2010
四、算法描述和程序代码 #include "stdio.h"
#define n 7 // 图的顶点数 #define k 4 // 图的段数 #define MAX 23767
多段图问题_动态规划法

多段图问题_动态规划法先简单叙述⼀下动态规划的步骤问题和思路代码如下1 #include<bits/stdc++.h>2 using namespace std;3 int cost[10];4 int path[10];5 int array1[10][10];6 int main()7 {8 memset(cost,0,sizeof(cost));9 memset(path,0,sizeof(path));10 memset(array1,0,sizeof(array1));11 cout << "请输⼊多段图的边数" << endl;12 int m;//1813 cin >> m;14 cout << "请依次输⼊多段图的起点终点和路径长度" << endl;15 int start;16 int stop;17 int length;18 for(int i=0;i<18;i++){19 cin >> start >> stop >> length;20 array1[start][stop]=length;21 }22 for(int i=8;i>=0;i--){23 cost[i]=9999;24 for(int j=i;j<10;j++){25 if(array1[i][j]!=0){//等于零表⽰之间没有路26 if(array1[i][j]+cost[j]<cost[i]){//此时找到⼀条更短的路27 path[i]=j;//更新path[i]28 cost[i]= array1[i][j]+cost[j];//更新从该节点出发的最短路径29 }30 }31 }32 }33 cout << "最短路径长度是" << cost[0];34 cout <<endl;35 cout << "最短路径为"<< endl;36 int i=0;37 cout << "0--->";38 while(true){39 cout << path[i];40 i=path[i];41 if(i==9){42 break;43 }44 cout << "--->" ;45 }46 return 0;47 }运⾏结果如下。
6.多段图问题

ForwardShortestPath(float c[][n], int k, int n) { float C[n]; int d[n], p[k]; C[0:n-2]=MAX; C[n-1]=0; for(i=n-2; i>=0; i--) for(j=i+1; j<=n-1; j++) if((c[i][j]>0)&&(c[i][j]+C[j]<C[i])) { C[i]=c[i][j]+C[j]; d[i]= j; } for(p[0]=0, p[k-1]=n-1, i=1; i<k-1; k++) p[i]=d[p[i-1]]; } 时间复杂度: 时间复杂度 邻接表 O(n+e) 邻接矩阵 O(n2)
向前递推算法
c[n][n]: <i,j>∈E, c[i][j]>0; < i,j >∉E, c[i][j]=-1; c[i][i]=0. ∈ C[n]: 各节点到汇点的最短路径, C[i] = min{c[i][ j] + C[ j]} 各节点到汇点的最短路径,
j∈ s V
d[n]: 各节点到 最小成本路径上的后向邻接节点 各节点到t最小成本路径上的后向邻接节点 p[k]: 存储 到t最小成本路径上的节点编号 存储s到 最小成本路径上的节点编号 最小成本路径上的节点编号.
xk ⇐(xk+1, L,xn-1,xn ), xk = opt{xi , Γk+1}, xi ∈Sk .
3) 向后递推
(x1, x2 ,L,xk-1) ⇒ xk , xk = opt{Γk−1, xi }, xi ∈Sk .
多段图 (multistage graph)
算法设计与分析-多段图最短路径问题

算法设计与分析-多段图最短路径问题关于多段图最短路径问题的探讨摘要:本⽂主要描述的是分别⽤动态规划法、贪⼼法和分⽀限界法来解决多段图最短路径问题时的情况,并在附录中附有实际问题的程序来辅助阐述观点。
⽂章⾸先阐述了各个⽅法的原理,主要的思路是通过输⼊⼀组数据,⽐较三者的输出结果的准确性以及运⾏时间,以之为基础来分析、讨论三者的性能区别。
另外,众所周知,多段图是有向图的⼀个简单的模型,它在有向图的基础上忽略了两点之间的线的双向性的问题,并且对点与点之间的线有很多的要求,从⽽把图简化为可分为⼏段的模式,⽂章最后讲述了若这⼏种⽅法运⾏到有向图中的情况,⼏种⽅法的对⽐和它们⽐较适应的使⽤情况的讨论,并给出了⾃⼰的建议。
关键字:多段图最短路径问题动态规划法分⽀限界法多段图与有向图的关系有向图最短路径算法引⾔:当前社会,关于最短路径的问题屡屡出现。
例如在开车⾃驾游的⼀个过程中,排除其他影响因素,从⼀个地点到另⼀点,这个时候必然是希望有⼀条距离最短的路程来尽量减少消耗的时间以及花费的(它们在模型中被称为代价),市场上对该问题的解决有很⼤的需求,因此,这⾥我将讨论多段图的最短路径的问题。
在早些时间的课程中,我们学习过数据结构这门课程,其中就包括最短路径这⽅⾯的讨论。
当时⽼师给我们介绍了分别⾯向单源(Dijkstra算法)与⾮单源(Floyd算法)两种问题的算法法---,这是我们最早的对最短路径⽅⾯的理解,也是我们接触的⽐较早的关于图的问题。
在这学期的算法课程中,我们学习了许多了⽅法,包括贪⼼法、动态规划法等算法,它们把以前学习的许多⽅法都命名并归纳分类起来,其中有许多算法都是可以⽤来解决这个最短路径的问题的,并且该问题作为⼀个图的问题,对该问题的继续探讨优化的需求很⼤,本⽂将就不同算法在解决该最短路径问题时的不同⽅法进⾏对⽐并给出该问题在不同基础上不同的最终解决⽅案。
由于时间的限制,本⽂将重点分析动态规划法下的情况,并会对图的情况加以简化、限制,最后会对其他的图做⼀些拓展。
多段图问题的动态规划算法与实现

多段图问题的动态规划算法与实现一、设计目的1.掌握有向网的成本邻接矩阵表示法;2.掌握多段图问题的动态规划递推算法;3.进一步掌握动态规划法的基本思想和算法设计方法;二、设计内容1.任务描述已知有向图有12个顶点,21条边,起点为S,终点为E,求从S到E的最小成本花费W。
(如图)起点终点花费起点终点花费起点终点花费1 2 9 4 8 11 9 12 41 3 7 5 7 11 10 12 21 4 3 5 8 8 11 12 51 52 6 9 62 6 4 6 10 52 7 2 7 9 42 8 1 7 10 103 6 2 8 10 153 7 7 8 11 162.主要数据类型与变量void ForwardShortestPath(int c[][N], int m)功能:运用动态规划的思想,逐级向后递推,找到最段的路径。
C[n]: 各节点到汇点的最短路径c[][N]:成本邻接矩阵, N为顶点数int m; /* 节点编号 */三、结果[输入要求]有多组测试数据,第一行输入S(1<=S<12),其中S为起点,E=12为终点,[输出要求]每组测试数据对应一个输出,输出S到终点E最小成本花费W[样例输入]12[样例输出]16源代码:#include<stdio.h>#define M 21#define N 12void ForwardShortestPath(int c[][N], int m){int i,j;int C[N]; //各节点到汇点的最短路径for(i=0;i<=N-1;i++)C[i]=100;C[N-1]=0;for( i=N-1; i>=0; i--){for( j=i+1; j<=N-1; j++)if((c[i][j]>0)&&(c[i][j]+C[j]<C[i]))C[i]=c[i][j]+C[j];if(i==m-1) printf("%d\n", C[m-1]);}}void main(){int i,j,vs=0,ve=0,cost=0;//vs,ve 顶点,cost成本。
算法设计与分析 多段图问题

多段图问题多段图是一种简单而经典的使用动态规划算法的模型,它既能有效地反映动态规划算法的基本特征,而且在实际问题中有较多的应用。
图6-2-1 多段图的动态规划算法执行过程最优值递推关系式为{}),1(),(min),(),(,1l i COST l j c j i COST El j V l i ++=∈∈+ (6.2.1)根据(6.2.1)式,我们可以由后向前逐步确定各阶段中的顶点到汇顶点t 的最短路径。
对于如上的5阶段网络图,蓝色字体标出了各顶点到汇顶点t 的最短距离。
图6-2-2 由前向后的处理方法(备忘录方法) 事实上,我们也可以由前向后逐步确定由源顶点s 到各阶段中顶点的最短路径,此时的递归关系为{}),(),1(min),(),(,1j l c l i BCOST j i BCOST Ej l V l i +-=∈∈- (6.2.2)上图中的红色字体标出了由源顶点s 到各顶点的最短距离。
程序6-2-2 多段图的动态规划算法伪代码MultiGraph(E, k, n, P) //有n 个顶点的k 段图G (按段序统一编号), //E 是边集,c(i, j)是边(i, j)的成本,P[1:k]是最小成本路径。
1 real COST(n); integer D(n-1),P(k), r, j, k, n;2 COST(n)=0;3 for j from n-1 by –1 to 1 do4设r 是这样一个顶点,(j, r)∈E 且使得c(j, r)+COST(r)取最小值18 5 427 7 5971615 7 V 1 V 2 V 3 V 4 V 51 t s 37 2 9224 6117811 345 26 5544 5 32 6 78 91011 1211 t s 3 72 9 2 24 611 7 8 11 3 4 5 2 6 5 5 4 9 2 3 7 9100111 160140 130 16 V 1 V 2 V 3 V 4 V 54 5 3 267 8 91011 12 15 COST(j)= c(j, r)+COST(r);6 D(j)=r;7endfor8P(1)=1; P(k)=n;9for j from 2 to k-1 do10 P(j)=D(P(j-1));11endfor12 end MultiGraph这里,D(j)将由j到汇顶点t的最短路径上j后面的顶点记录下来,P(j)则记录由源顶点s到汇顶点t的最短路径上处于第j阶段中的顶点。
求解多段图问题的并行动态规划算法

求解多段图问题的并行动态规划算法崔焕庆;王英龙【期刊名称】《计算机应用与软件》【年(卷),期】2011(028)012【摘要】Multistage graph problem is a special single-source shortest path problem. Based on two kinds of implementations of sequential dynamic programming method, two parallel algorithms with vertex-number-based task partition in cluster are given. Both of them are implemented by MPI. Experimental results indicated that these algorithms have lower time and communication complexity and higher speedup ratio. The algorithms can also be used in any structure of cluster and is of high universality.%多段图问题是一类特殊的单源最短路径问题.在串行动态规划算法的两种实现方法的基础上,根据图中顶点的编号,提出两种在集群环境下进行任务分割的并行化求解方法,并使用MPI进行实现.实验结果表明,所提出的算法具有较高的加速比和较低的通信复杂度、时间复杂度.算法不限于某种结构的集群,通用性强.【总页数】3页(P32-34)【作者】崔焕庆;王英龙【作者单位】山东科技大学信息科学与工程学院山东青岛266510;山东省计算机网络重点实验室山东济南250014;山东省计算中心山东济南250014;山东省计算机网络重点实验室山东济南250014;山东省计算中心山东济南250014【正文语种】中文【中图分类】TP30【相关文献】1.基于改进动态规划算法的复杂网络图最短路径求解 [J], 房茂燕;汪民乐;尹香麒2.求解并行加热炉群调度问题的三阶段算法 [J], 李铁克;王柏琳;赵艳艳3.求解最大团问题的并行多层图划分方法 [J], 顾军华;霍士杰;武君艳;尹君;张素琪4.基于二叉决策图的状态组合爆炸问题并行求解方法 [J], 叶雄;杨皓栋;;5.贪心核加速动态规划算法求解折扣{0-1}背包问题 [J], 史文旭;杨洋;鲍胜利因版权原因,仅展示原文概要,查看原文内容请购买。
动态规划_多段图_最小花费通路算法_C语言

动态规划_多段图_最小花费通路算法_C语言动态规划找出多段图的最小花费通路算法(C语言)//算法:#include#include#define MAX 50#define MAX_LEN 100 /*定义顶点之间最大花费(假设最大花费为100)*///结构体定义typedef struct edgenode{ /*定义边表结点结构体*/int adjvertex; /*邻接点编号*/int len; /*该结点与父结点之间的花费*/struct edgenode *next; /*指向下一个邻接点*/} EdgeNode;typedef struct vertexnode{ /*定义顶点结点结构体*/EdgeNode *firstedge; /*边表头指针*/} VertexNode;typedef struct { /*定义邻接表结构体*/VertexNode adjlist[MAX]; /*邻接表*/int vertexNum; /*顶点数*/int edgeNum; /*边数*/} ALGraph;//函数声明ALGraph * CreateALGraph(int vertexNum, int edgeNum);void MultistageGraph(ALGraph *G, int n, int route[], int *minCost);//主函数int main(){ALGraph *G = NULL;int vertexNum, edgeNum; /*顶点数和边数*/int *route; /*从源点到收点的最短路径上的顶点编号*/int minCost; /*最短路径的最小费用*/int i;printf("请输入顶点数和边数:\n");scanf("%d,%d", &vertexNum,&edgeNum);//初始化GG = CreateALGraph(vertexNum, edgeNum);if(!G){return 0;}//初始化route数组route = (int *)malloc(sizeof(int) * vertexNum);MultistageGraph(G, vertexNum, route, &minCost);//输出最小花费路径及最小花费printf("\n最小花费路径是:\n");for(i = 0; i < vertexNum; i ++){printf("%d —> ", route[i]);if(route[i] == (vertexNum - 1)){printf("\b\b\b\b \n");break;}}printf("\n最小花费是:%d\n", minCost);return 0;}/*********************************************************** 函数名称:GreateALGraph函数功能:初始化有向图的邻接表输入:顶点数ertexNum,边数edgeNum输出:指向已初始化完毕的有向图的邻接表指针***********************************************************/ ALGraph * CreateALGraph(int vertexNum, int edgeNum){ ALGraph *G = NULL;int i, j, u, v, info;G = (ALGraph *)malloc(sizeof(ALGraph));if(G){G->vertexNum = vertexNum;G->edgeNum = edgeNum;for(i = 0; i < vertexNum; i ++) {G->adjlist[i].firstedge = NULL;}//给边表结点分配内存空间printf("请输入分段图中各相邻结点的编号及其权值:\n");for(j = 0; j < edgeNum; j ++) {//初始化边结点EdgeNode *pnode = NULL;pnode = (EdgeNode *)malloc(sizeof(EdgeNode));pnode->next = NULL;//输入相邻结点的编号及其边上的权值scanf("%d,%d,%d", &u, &v, &info);if(pnode){pnode->next = G->adjlist[u].firstedge;G->adjlist[u].firstedge = pnode;pnode->adjvertex = v;pnode->len = info;}else{return NULL;}}}return G;}/***********************************************************函数名称:MultistageGraph函数功能:多段图中利用动态规划找出源点到收点的最小花费通路输入:指向有向图的邻接表指针G,结点个数n,保存最小花费通路结点的数组route,保存最小花费minCost输出:最小花费通路结点的数组route,最小花费minCost***********************************************************/void MultistageGraph(ALGraph *G, int n, int route[], int *minCost){int *cost; /*每个结点到收点的最小费用*/int *path; /*在阶段决策中,各个顶点到收点的最短路径上的前方顶点编号*/int i;//给cost、path、route指针分配n个int大小的内存空间cost = (int *)malloc(sizeof(int) * n);path = (int *)malloc(sizeof(int) * n);//初始化cost、path、route指向的内存空间for(i = 0; i < n; i ++) {cost[i] = MAX_LEN;path[i] = -1;route[i] = 0;}cost[n-1] = 0; /*收点到收点的距离为0*///动态规划过程for(i = i - 2; i >= 0; i --) {EdgeNode *pnode = G->adjlist[i].firstedge;while(pnode && (pnode->len + cost[pnode->adjvertex]) < cost[i]) { cost[i] = pnode->len + cost[pnode->adjvertex];path[i] = pnode->adjvertex;pnode = pnode->next;}}i = 0;while((route[i] != n-1) && (path[i] != -1)) {i ++;route[i] = path[route[i - 1]];}//最小花费*minCost = cost[0];//释放malloc申请的内存空间free(cost);free(path);return;}运行结果:。
多段图算法实验报告

算法分析与设计实验报告课题: 多段图******班级:计算机1101学号:**********目录一、实验目的二、实验内容三、实验要求四、概要设计五、详细设计六、实验心得一、实验目的加深理解动态规划策略,求出多段图中源点到各点的最短路径。
二、实验内容设G=(V,E)是一个赋权有向图,其顶点集V被划分成k>2个不相交的子集Vi: 1≤i≤k,其中,V1和Vk分别只有一个顶点s(称为源)和一个顶点t(称为汇),图中所有的边(u,v)的始点和终点都在相邻的两个子集Vi和Vi+1中:u∈Vi,v∈Vi+1。
找一条从s到t的最短路线。
三、实验要求在上机前写出全部源程序;能在机器上正确运行程序;四、概要设计图采用邻接矩阵表示设P(i,j)是一条从Vi中的结点j到汇点t的最小成本路径,COST(i,j)是这条路的成本。
则从Vi中节点j到t的最小代价为:cost((i,j)=min{cost(i+1,l)+c (j,l) }, l∈Vi+1 , j∈Vicost(i+1,l)是从Vi+1中节点l 到t的最小代价。
算法概要设计如下:多段图的向前处理算法procedure FGRAPH(G,k,n,P){//G有n个结点的k段图。
E是边集,c[i,j]是边<i,j>的成本。
P[1:k]是最小成本路径。
//COST[n], D[n一1],P[k],r,j,k,nCOST[n]← 0for j←n-1to 1 by -1 do //计算COST[j]//{设r是一个这样的结点,(j,r) E且使c[j,r]+COST[r]取最小值COST[j]←c[j,r]+COST[r]D[j]←r} //向前对j-1进行决策//P[1]←1P[k]←nfor j←2 to k-1 do //找路径上的第j个节点//P[j]←D [ P[j-1] ]五、详细设计:#include <stdio.h>#include <stdlib.h>#define N 12#define K 5#define MAX 23767int cost[N][N];int path[K];typedef struct node{int v;int w;struct node *next;}node;node L[N];void init(node *L[]){int i, j;node *p, *q;for (i = 0; i < N; i++)for (j = 0; j < N; j++)cost[i][j] = MAX;cost[0][1] = 9;cost[0][2] = 7;cost[0][3] = 3;cost[0][4] = 2;cost[1][5] = 4;cost[1][6] = 2;cost[1][7] = 1;cost[2][5] = 2;cost[2][6] = 7;cost[3][7] = 11;cost[4][6] = 11;cost[4][7] = 8;cost[5][8] = 6;cost[5][9] = 5;cost[6][8] = 4;cost[6][9] = 3;cost[7][9] = 5;cost[7][10] = 6;cost[8][11] = 4;cost[9][11] = 2;cost[10][11] = 5;/*生成邻接表*/for (i = 0; i < N; i++)L[i] = (node *)malloc(sizeof(node));for (i = 0; i < N; i++){q = L[i];for (j = 0; j < N; j++)if (cost[i][j] > 0 && cost[i][j] < MAX){p = (node *)malloc(sizeof(node));p->v = j;p->w = cost[i][j];q->next = p;q = p;}q->next = NULL;}}void Method1() /*使用邻接矩阵存储*/{int i, j, maxlen, temp, v[N], d[N];for (i = 0; i < N; i++)v[i] = 0;for (i = N - 2; i >= 0; i--){for (maxlen = MAX, j = i + 1; j <= N - 1; j++)if (cost[i][j] > 0 && cost[i][j] + v[j] < maxlen){maxlen = cost[i][j] + v[j];temp = j;}v[i] = maxlen;d[i] = temp;}path[0] = 0;path[K-1] = N - 1;for (i = 1; i <= K - 2; i++)path[i] = d[path[i-1]];}void Method2(node *L[]) /*使用邻接表存储*/ {int i, j, maxlen, temp, v[N], d[N];node *p;for (i = 0; i < N; i++)v[i] = 0;for (i = N - 2; i >= 0; i--){p = L[i]->next;maxlen = MAX;while (p){if (p->w + v[p->v] < maxlen){maxlen = p->w + v[p->v];temp = p->v;}p = p->next;}v[i] = maxlen;d[i] = temp;}path[0] = 0;path[K-1] = N - 1;for (i = 1; i <= K - 2; i++)path[i] = d[path[i-1]];}void print(){int i;for (i = 0; i < K; i++)printf("%d ", path[i] + 1);printf("\n");}int main(){init(&L);printf("最短路径:\n ");Method1();print();printf("最短路径:\n");Method2(&L);print();system("pause");return 0;}六.实验心得通过本次试验,掌握了动态规划的思想,即如果一个问题的最优解可以分解为找子问题的最优解,那么即可使用动态规划。
经典算法之多段图算法
每个点之间有无路径采用一个二维数组表示,即 mix[i][j]为从节点 i 到节点 j 的路径, 如பைடு நூலகம்不存在则 mix[i][j]=0; #include <iostream> using namespace std; void out(int mix[11][11]) {
};
out(mix); return 0; }
输出
最后一个值 14 即从首节点到目标节点的最短距离。 更多编程算法内容请登录 IT 部落格()
//思想是把每个节点假如进来,并且每加入一个节点,则更新值 int i=1; int len[11]={0}; while(i<11) {
//先找到该节点的所有前驱 int total=100000; for(int j=0;j<i;j++) {
if(mix[j][i]!=0) {
//判断是否存在到该节点的路径,如果有则根据路径长度更新 if(total>(mix[j][i]+len[j])) {
第一步,计算从第一层到首节点的距离,因为是第一层,因此不需要最小值函数,直 接记录首节点的距离即可。
第二步,展开第三层的节点,每个节点计算从前一层的可达路径,并且用 min 函数查 出最小值,并且记录最小值和取得最小值的前驱点。
重复上述过程。
重复上述过程。
在完成上述过程后,逆向查找前驱节点即可找到最短路径。
动态规划思想采用动态规划法从初始点开始每次更新最新的一段的节点距离得到最短距离重复该该过程直至达到目标节点
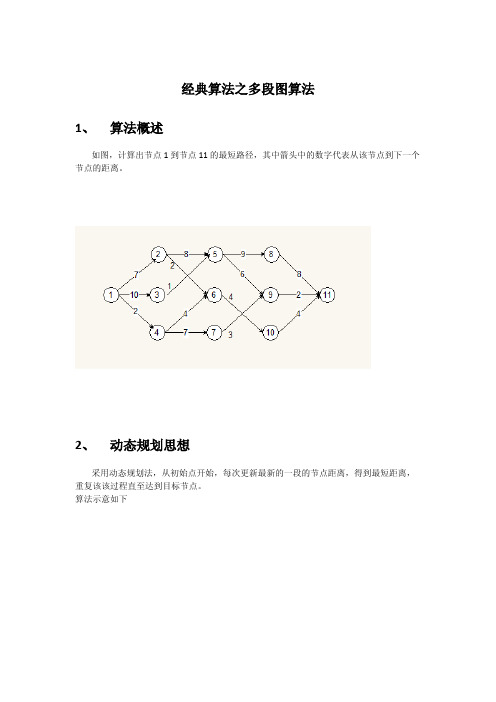
经典算法之多段图算法 1、 算法概述
如图,计算出节点 1 到节点 11 的最短路径,其中箭头中的数字代表从该节点到下一个 节点的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{inti,j;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&cost[i][j]);//获取成本矩阵数据
}
voidprintgraph() //输出图的成本矩阵
{inti,j;
printf("成本矩阵:\n");
}
path[0]=0;//起点
path[k-1]=n-1;//最后的目标
for(i=1;i<=k-2;i++) (path[i])=d[path[i-1]];//将最短路径存入数组中
}
voidprintpath()
{intห้องสมุดไป่ตู้;
for(i=0;i<k;i++)
printf("%d ",path[i]);
实验项目算法实验动态规划实验
一、实验目的
1.掌握动态规划算法的基本思想
2.掌握多段图的动态规划算法
3.选择邻接表或邻接矩阵方式来存储图
4、分析算法求解的复杂度。
二、实验内容
4.掌握动态规划算法的基本思想
5.掌握多段图的动态规划算法
6.选择邻接表或邻接矩阵方式来存储图
4、分析算法求解的复杂度。
三、实验环境
}
intmain()
{
creatgraph();
printgraph();
FrontPath();
printf("输出使用向前递推算法所得的最短路径:\n");
printpath();
printf("\n输出使用向后递推算法所得的最短路径:\n");
printpath();
printf("\n");
return 0;
}
五、实验结果截图
六、实验总结
在做实验的过程中,要按部就班,首先明确实验目的,然后进行分析,写算法程序,最后调试运行,不能粗枝大叶,做的过程要细心谨慎,自己不会的通过向别人请教,总之上机实践的过程会学到很多。
程序设计语言:c++
编程工具:microsoftvisual studio 2010
四、算法描述和程序代码
#include "stdio.h"
#define n 7 //图的顶点数
#define k 4 //图的段数
#define MAX 23767
intcost[n][n]; //成本值数组
intpath[k]; //存储最短路径的数组
for(i=0;i<n;i++)
{ for(j=0;j<n;j++)
printf("%d ",cost[i][j]);
printf("\n");
}
}
//使用向前递推算法求多段图的最短路径
voidFrontPath()
{inti,j,length,temp,v[n],d[n];
for(i=0;i<n;i++) v[i]=0;
for(i=n-2;i>=0;i--)
{ for(length=MAX,j=i+1;j<=n-1;j++)
if(cost[i][j]>0 && (cost[i][j])+v[j]<length)
{length=cost[i][j]+v[j]; temp=j;}
v[i]=length;
d[i]=temp;
