九年级数学下册_5.3_反比例函数(2后天).课件_青岛版
合集下载
青岛版九年级下册数学《反比例函数》PPT教学课件

3、已知北京市的总面积为16 800平方千米,人均占有 土地面积
以上三个问题的函数解析式为:
v 800 t
y 10 x
16 800 n
根据上述三个解析式回答: 1.你能说出它们的共同特征吗? 2.你能用一个一般形式表示出来吗?
一般地,形如 y k (k是常数,且k≠ 0)的函数, x
叫做反比例函数.
∴k=2
x
∴ y2
x
(2)当x=a时,y=2a,
当2a=3a+2时,解得a=4,
检验a=4是原分式方程的解,
∴当a=4时,点B在反比例函数图象上;
当a≠4 时,点B不在反比例函数图象上.
反比例函数的图象和性质
1.形状 反比例函数的图象是由两支曲线组成的, 因此称反比例函数的图象为双曲线.
2.位置 当k>0时,两支曲线分别位于第一、三象限内;在 每一个象限内,y随x的增大而减小; 当k<0时,两支曲线分别位于第二、四象限内,y随 x的增大而增大.
y x
6y
y6
5
x
4
3
2
2
1
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x
-1
-1
-2
-2
-3
-3
-4
-4
-5
-5
-6
-6
作反比例函数图象时应注意哪些问题?
1.列表时,选取的自变量的值,既要易于计算,又要便于描点, 尽量多取一些数值(取互为相反数的一对一对的数),多描一些点, 这样既可以方便连线,又可以使图象精确. 2.描点时要严格按照表中所列的对应值描点,绝对不能把点的 位置描错. 3.一定要养成按自变量从小到大的顺序依次画线,连线时必须用 光滑的曲线连接各点,不能用折线连接. 4.图象是延伸的,注意不要画的有明确端点. 5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
以上三个问题的函数解析式为:
v 800 t
y 10 x
16 800 n
根据上述三个解析式回答: 1.你能说出它们的共同特征吗? 2.你能用一个一般形式表示出来吗?
一般地,形如 y k (k是常数,且k≠ 0)的函数, x
叫做反比例函数.
∴k=2
x
∴ y2
x
(2)当x=a时,y=2a,
当2a=3a+2时,解得a=4,
检验a=4是原分式方程的解,
∴当a=4时,点B在反比例函数图象上;
当a≠4 时,点B不在反比例函数图象上.
反比例函数的图象和性质
1.形状 反比例函数的图象是由两支曲线组成的, 因此称反比例函数的图象为双曲线.
2.位置 当k>0时,两支曲线分别位于第一、三象限内;在 每一个象限内,y随x的增大而减小; 当k<0时,两支曲线分别位于第二、四象限内,y随 x的增大而增大.
y x
6y
y6
5
x
4
3
2
2
1
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x
-1
-1
-2
-2
-3
-3
-4
-4
-5
-5
-6
-6
作反比例函数图象时应注意哪些问题?
1.列表时,选取的自变量的值,既要易于计算,又要便于描点, 尽量多取一些数值(取互为相反数的一对一对的数),多描一些点, 这样既可以方便连线,又可以使图象精确. 2.描点时要严格按照表中所列的对应值描点,绝对不能把点的 位置描错. 3.一定要养成按自变量从小到大的顺序依次画线,连线时必须用 光滑的曲线连接各点,不能用折线连接. 4.图象是延伸的,注意不要画的有明确端点. 5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
青岛版九年级数学下册第五章《反比例函数》公开课课件

有古
一人
个云
在:
路“
上读
。万
”卷
从书
古,
至行
今万
,里
学路
习。
和”
旅今
行人
都说
是:
相“
辅要
相么
You made my day!
成读 的书
两,
件要
事么
。旅
。行
,
身
体
和
灵
魂
总
要
我们,在路上……
函数解析式又是什么呢?
B O
PA
B O
PA
例3 如图5-12,已知C、P的坐 y
标分别为(2,y)和(x,3√2 )
在反比例函数解析式
y=
12 x
B
C P
上,过C、P作x轴的垂线,垂
R
足分别为点A,Q.过C、P作y
O AQ
x
轴的垂线,垂足分别为点B,
R.
图5-12
(1)矩形OACB与矩形OQPR 的面积分别是多少?
(2)设CA与PR交于点D,求矩 形OACB与矩形OQPR的公共 部分的面积?
例4 如图5-13,已知反比例函数 y k x
的图像与y=ax+b相交于点
A(-2,3),B (3,m)。 求k及a,b的值。
A3
3
-2 0 B
图5-13
练习:1.如图,已知一次函数y=kx+b(k≠0)的图象与x 轴,
S1、S2有什么关系?为什么?
任取一点向两坐标轴作垂线得到的
矩形面积是一个定值,为|k |.
想一想
y k x
•P
Q
• S1 S2
2022年青岛版九下《反比例函数2》立体精美课件

6 x
反比例函数的性质:
① 当k>0时, 两支曲线各在哪个象限? 每个象限内,y随x的增大有什么变化? ② 当k<0呢?
y
y=
6 x
0x
y
0
x
y=
6 x
反比例函数的性质
反比函数双曲线, 所有都不过原点; k正一三负二四, 两轴是它渐近线; k正左高右边低, 一三象限滑下山; k负左低右边高, 二四象限如爬山.
5.2 反比例函数(2)
学习目标
1.会画反例函数的图象; 2.理解并探索k>0和k<0时,反比例函数图 象所在的象限及图象的变化情况。
一、画反比例函数 6 和 y = x
6 x
的图象。
回顾一下一次函数图
象的画法及图象特征, 同学们请说一说
函数图象画法
列 表
描
连
点线
x . . . -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ...
注意:①列表时,自变量x取值 要均匀和对称;② x≠0;
x
y
=
6 x
y= 6 x
… -6 -5 -4 -3 -2
… -1 -1.2-1.5 -2 -3 …
1 1.2 1.5 2 3
y
6
5 4
y
=
6 x
3
2
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x -1
-2 -3
-4 -5
21 4
=
9 4
3 2
25 =5 25 =5
判断:
(1) (2) (3) (4) (5) (6)
(7)
9的平方根是 3。 (×)
新青岛版九年级数学下册第五章《反比例函数复习》公开课课件

y2
小
zxxkw
请领导老师: 点评指正!
在每个象限内
y随x增大而增大
增减性 在每个象限内
性 质
求解析式
实际应用
K的几 何意义
S矩形 k
待定系数法 自变量取值范围
y
性
D:
x
o
x
图 像
K的范围 K>0 y 图像大 致形状 o
y=kx-1 ;xy=k;(k≠0) 对 K<0 y 称
zxxkw
• 1、(2) • 3、(1) 4
2、B
4 (2)y x
变式:
1、D
2、C 3、k<0
一
zxxkw
y
k<0
√
y2 y1
x1 x2
×
o
y1
x
y2zxxkw来自考点2:K的几何意义与中心对称的 考查
y
A
D o B
x
C
zxxkw zxxkw
两不同函数的值比较大 y1 小的方法:
y2
1、过交点作垂线,
将图像分区
-1 2 、看图高低
定值大小
y1
zxxkw
大
小 大
zxxkw
zxxkw
1、能够构建反比例函数的知识网络。 2、熟记反比例函数的定义及三种表 达形式,并能确定反比例函数的 关系式。(重点) 3、能利用反比例函数的图像与性质 解决有关问题。(难点)
•构建知识网络
函数解析式
zxxkw
y
k (k 0) x
x
D:
o
象限
一、三
y随x增大而减小
二、四
最新青岛版九年级数学下册全册完整课件

最新青岛版九年级数学下册全册 完整课件目录
0002页 0021页 0052页 0054页 0084页 0130页 0162页 0186页 0245页 0281页 0333页 0403页
第5章 对函数的再探索 5.2 反比例函数 5.4二次函数的图像与性质 5.7二次函数的应用 6.1随机事件 6.3频数直方图 6.5事件的概率 6.7利用画树状图和列表计算概率 7.1几种常见的几何体 7.3圆柱的侧面展开图 第8章 投影与识图 8.2平行投影
最新青岛版九年级数学下册全册完 整课件
第5章 对函数的再探索
最新青青岛版九年级数学下册全册完 整课件
5.2 反比例函数
最新青岛版九年级数学下册全册完 整课件
5.3二次函数
最新青岛版九年级数学下册全册完 整课件
5.4二次函数的图像与性质
0002页 0021页 0052页 0054页 0084页 0130页 0162页 0186页 0245页 0281页 0333页 0403页
第5章 对函数的再探索 5.2 反比例函数 5.4二次函数的图像与性质 5.7二次函数的应用 6.1随机事件 6.3频数直方图 6.5事件的概率 6.7利用画树状图和列表计算概率 7.1几种常见的几何体 7.3圆柱的侧面展开图 第8章 投影与识图 8.2平行投影
最新青岛版九年级数学下册全册完 整课件
第5章 对函数的再探索
最新青青岛版九年级数学下册全册完 整课件
5.2 反比例函数
最新青岛版九年级数学下册全册完 整课件
5.3二次函数
最新青岛版九年级数学下册全册完 整课件
5.4二次函数的图像与性质
2019青岛版初中数学九年级下册5.2反比例函数课件(共20张PPT)

青岛版义务教育教科书数学九年级(下)
史海漫游
诸葛亮先生家住茅草屋 中,途中有一片十几米的 烂泥湿地,如果徒步行走 会陷入泥潭中。 刘备心生一计让其好兄 弟关羽张飞在途中铺设了 若干块木板并且顺利抵达 诸葛亮家中。 关羽张飞一脸迷茫的问 道刘备:“大哥,这是何 故?”
1.理解反比例函数的概念和意义; 2.能用待定系数法求反比例函数关系式; 3.体会函数在解决实际问题中的作用.
我们再回顾刚才三顾茅庐的问题
当压力F一定时,压强p与受力面积s的函数关系是
测 学
使 你 自 知
F p S
通过本节课的学习,
你有什么收获?
还有什么困惑?
一设
二代
三解
四写
转化
三种表示方法
数学方法
数学思想
反比例函数的定义
反 比 例 函 数
当堂检测
1.D 2.3 3.X≠-2 1 1 4. y ,
k 一般地,形如 y (k是常数,且k≠ 0)的函数叫做反比例函 x
使 你 提 高
注: ① k≠ 0,x ≠ 0,y ≠ 0
② y=
1 k= x
kx-1 (k≠ 0)
xy = k( k≠ 0)
6
机会属于开拓者
你能举出反比例函数的例子吗?
胜利属于坚持者
三角形的面积为36cm2,底边长y(cm)与该底边的高(cm)
新知探究
1.面积为84m2的矩形花圃,写出矩形 的宽y(m)和长x(m)之间的函数 表达式。
84 y x
自 学
2.甲乙两地之间相距200km,写出汽 车行驶的时间t(h)与汽车的平均 速度v(km)之间的函数表达式
3.两个实数的乘积为-10,写出其中 一个因数q与另一个因数p之间的函 数表达式
史海漫游
诸葛亮先生家住茅草屋 中,途中有一片十几米的 烂泥湿地,如果徒步行走 会陷入泥潭中。 刘备心生一计让其好兄 弟关羽张飞在途中铺设了 若干块木板并且顺利抵达 诸葛亮家中。 关羽张飞一脸迷茫的问 道刘备:“大哥,这是何 故?”
1.理解反比例函数的概念和意义; 2.能用待定系数法求反比例函数关系式; 3.体会函数在解决实际问题中的作用.
我们再回顾刚才三顾茅庐的问题
当压力F一定时,压强p与受力面积s的函数关系是
测 学
使 你 自 知
F p S
通过本节课的学习,
你有什么收获?
还有什么困惑?
一设
二代
三解
四写
转化
三种表示方法
数学方法
数学思想
反比例函数的定义
反 比 例 函 数
当堂检测
1.D 2.3 3.X≠-2 1 1 4. y ,
k 一般地,形如 y (k是常数,且k≠ 0)的函数叫做反比例函 x
使 你 提 高
注: ① k≠ 0,x ≠ 0,y ≠ 0
② y=
1 k= x
kx-1 (k≠ 0)
xy = k( k≠ 0)
6
机会属于开拓者
你能举出反比例函数的例子吗?
胜利属于坚持者
三角形的面积为36cm2,底边长y(cm)与该底边的高(cm)
新知探究
1.面积为84m2的矩形花圃,写出矩形 的宽y(m)和长x(m)之间的函数 表达式。
84 y x
自 学
2.甲乙两地之间相距200km,写出汽 车行驶的时间t(h)与汽车的平均 速度v(km)之间的函数表达式
3.两个实数的乘积为-10,写出其中 一个因数q与另一个因数p之间的函 数表达式
青岛版九年级数学下册第五章《反比例函数复习》公开课课件

• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/312021/7/312021/7/312021/7/31
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
• 11、一个好的教师,是一个懂得心理学和教育学的人。2021/7/312021/7/312021/7/31Jul-2131-Jul-21
九年级数学下册 5.2 反比例函数课件青岛青岛级下册数学课件

12/11/2021
如果反比例函数 y 1的3图m象位于第二、
x
四象限,那么m的范围为
.
m>
1 3
由1-3m<0 得-3m<- 1
∴
m>
1 3
12/11/2021
已知反比例函数 y (kk≠0) 当x<0时,y随x的增大x而减小,k>0 则一次函数y=kx-k的图象不经过第二 象限.
k>0 ,-k<0
哪些是反比例函数?
① y = 3x-1 ② y = 2x2
③ y=
1 x
④
y
=
2x 3
⑤ y = 3x
⑥ y=
5 x
⑦
y
=
2 3x
12/11/2021
已知点A(-2,y1),B(-1,y2)
都在反比例函数
y
y
k x
4x(k的<图0) 象上,则y1
与y2的大小关系(从大到小)为
.
yy11>< yy22
t 50 v
12/11/2021
1.再次全面深入思考预习案中设置的问题, 将需
要重点探讨的问题做好标记 2.有展示任务的小组迅速到黑板展示。 注:重点是反比例函数的概念、图象的画法
和图象的变化规律
1.按照课前培训重点讨论反比例函数的概念、图象的画法 和图象的变化规律; 2.先一对一讨论,再组内、组间讨论; 3.讨论完毕,组长组织整理讨论成果和例1,例2的自纠和 拓展。
y
o
x
12/11/2021
12/11/2021
已知点AA(-(2x1,y,y11)),,BB(x-12,,yy22))且x1<0<
都在反比例x2函数
y
y
k x
如果反比例函数 y 1的3图m象位于第二、
x
四象限,那么m的范围为
.
m>
1 3
由1-3m<0 得-3m<- 1
∴
m>
1 3
12/11/2021
已知反比例函数 y (kk≠0) 当x<0时,y随x的增大x而减小,k>0 则一次函数y=kx-k的图象不经过第二 象限.
k>0 ,-k<0
哪些是反比例函数?
① y = 3x-1 ② y = 2x2
③ y=
1 x
④
y
=
2x 3
⑤ y = 3x
⑥ y=
5 x
⑦
y
=
2 3x
12/11/2021
已知点A(-2,y1),B(-1,y2)
都在反比例函数
y
y
k x
4x(k的<图0) 象上,则y1
与y2的大小关系(从大到小)为
.
yy11>< yy22
t 50 v
12/11/2021
1.再次全面深入思考预习案中设置的问题, 将需
要重点探讨的问题做好标记 2.有展示任务的小组迅速到黑板展示。 注:重点是反比例函数的概念、图象的画法
和图象的变化规律
1.按照课前培训重点讨论反比例函数的概念、图象的画法 和图象的变化规律; 2.先一对一讨论,再组内、组间讨论; 3.讨论完毕,组长组织整理讨论成果和例1,例2的自纠和 拓展。
y
o
x
12/11/2021
12/11/2021
已知点AA(-(2x1,y,y11)),,BB(x-12,,yy22))且x1<0<
都在反比例x2函数
y
y
k x
新青岛版九年级数学下册第五章《 反比例函数(3)》公开课课件

d/天 d/天 d/天 d/天 1×10³
1×10³
2×10³
2 t/h
1×10³
2 t/h
2 2 t/h
o
o
o
0
t/h
A
B
C
D
必做题:习题5.2 13、17题
选做题:习题5.2 16题
同学们, 再见!
2000
1000
O
0.1
0.2
0.3 S/ ㎡
(1)求P与S之间的函数表达式? P=100/s (s ﹥0) (2)求当S=0.5㎡时的物体承受的压强P? 200Pa 3、某种品牌的电脑显示屏的使用寿命大约为 2×10³ h,如果该显示屏工作天数为d(天),平均每 天工作时间为t(h),那么能正确表示d与t之间函数 关系的图像是( c )
y/(mg/m³ )
6 3 O 4 8 16 x/min
y/(mg/m³ )
解: (1)当药物燃尽时,y是x的正比例 函数,设它的关系式为y=kx,(0 ≤x ≤8) 将分段点(8,6)代入上式,得 6=8k,解得k=3/4.所以,药物燃烧时, y与x之间的函数关系式为:y=3/4x, (0 ≤x ≤8)
想一想
k y x
P
S1 S3 S2
Q
S1、S2等于多少? S3 等于多少?
例1. 一辆汽车以80km/h的平均速度从甲 地驶往乙地,用5h到达。 (1)当汽车按原路返回时,如果规定该车 限速120km/h,写出返回甲地所用时间t 与平均速度v的函数关系式,并画出它的 图像? (2)如果汽车必须在4h内回到甲地,求返 程时的平均速度的范围?
6 3பைடு நூலகம்
O 4 8 16 x/min
(2)当药物燃尽后,y是x的反比例函数,设它的关系式是y=k/x, (x ﹥8).将分段点(8,6)代入上式得 6=k/8,解得k=48.所以, 药物燃尽后,y与x之间的函数关系式为:y=48/x ( x ﹥8) (3).将y=1.6代入y=48/x,得x=30(min).所以,从灭蚊开始至 少经过30min,学生才能进入教室. (4).将y=3分别代入y=3/4x和y=48/x,分别得x1=4,x2=16,因此, 从药物点燃4min到16min时,室内每立方米空气中含药量超过 3mg,由于x2-x1=12(min) ﹥10(min),所以此次灭蚊有效.
1×10³
2×10³
2 t/h
1×10³
2 t/h
2 2 t/h
o
o
o
0
t/h
A
B
C
D
必做题:习题5.2 13、17题
选做题:习题5.2 16题
同学们, 再见!
2000
1000
O
0.1
0.2
0.3 S/ ㎡
(1)求P与S之间的函数表达式? P=100/s (s ﹥0) (2)求当S=0.5㎡时的物体承受的压强P? 200Pa 3、某种品牌的电脑显示屏的使用寿命大约为 2×10³ h,如果该显示屏工作天数为d(天),平均每 天工作时间为t(h),那么能正确表示d与t之间函数 关系的图像是( c )
y/(mg/m³ )
6 3 O 4 8 16 x/min
y/(mg/m³ )
解: (1)当药物燃尽时,y是x的正比例 函数,设它的关系式为y=kx,(0 ≤x ≤8) 将分段点(8,6)代入上式,得 6=8k,解得k=3/4.所以,药物燃烧时, y与x之间的函数关系式为:y=3/4x, (0 ≤x ≤8)
想一想
k y x
P
S1 S3 S2
Q
S1、S2等于多少? S3 等于多少?
例1. 一辆汽车以80km/h的平均速度从甲 地驶往乙地,用5h到达。 (1)当汽车按原路返回时,如果规定该车 限速120km/h,写出返回甲地所用时间t 与平均速度v的函数关系式,并画出它的 图像? (2)如果汽车必须在4h内回到甲地,求返 程时的平均速度的范围?
6 3பைடு நூலகம்
O 4 8 16 x/min
(2)当药物燃尽后,y是x的反比例函数,设它的关系式是y=k/x, (x ﹥8).将分段点(8,6)代入上式得 6=k/8,解得k=48.所以, 药物燃尽后,y与x之间的函数关系式为:y=48/x ( x ﹥8) (3).将y=1.6代入y=48/x,得x=30(min).所以,从灭蚊开始至 少经过30min,学生才能进入教室. (4).将y=3分别代入y=3/4x和y=48/x,分别得x1=4,x2=16,因此, 从药物点燃4min到16min时,室内每立方米空气中含药量超过 3mg,由于x2-x1=12(min) ﹥10(min),所以此次灭蚊有效.
5.2.3反比例函数的应用教学课件-2023—-2024学年青岛版九年级数学下册
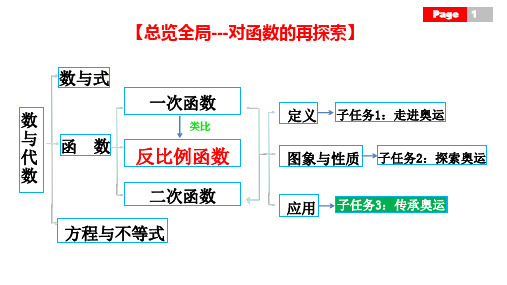
【总览全局---对函数的再探索】
Page 1
数与式
数
与 代
函数
数
一次函数
类比
反比例函数
二次函数
方程与不等式
定义 子任务1:走进奥运 图象与性质 子任务2:探索奥运 应用 子任务3:传承奥运
初中数学 九年级下册 青岛出版社
Page 2
§5.2.3 反比例函数的应用
【学习目标】
Page 3
1.通过分析实际问题中变量之间的关系,建立反比例函数 模型解决问题,提高运用函数的图象、性质的综合能力. 2.经历分析问题的过程,能够根据实际问题确定自变量的 取值范围,体会数学与现实生活的紧密联系.
【传承奥运---变式训练】
在奥运会游泳比赛中,为了保证运 动员身体健康,换水和消毒工作一 直是非常重要的环节,通常采用循 环使用含氯消毒剂对游泳池进行消 毒.
Page 8
【传承奥运---变式训练】
Page 9
消毒剂溶解时,游泳池内每立方米水中含消毒剂量y (克/立方米)与消毒剂溶解的时间x(分钟)成正比 例,消毒剂完全溶解后,y与x成反比例(如图所示). 已知消毒剂8分钟完全溶解,此时每立方米水中含消毒 剂量为6克.
【课堂小结---反比例函数的应用】
Page 15
请你回顾任务2中我 们应掌握的内容:
从知识上——
反比例函数
从方法上——
从思想上——
还有……
定义 子任务1:走进奥运 图象与性质 子任务2:探索奥运 应用 子任务3:传承奥运
Page 17
【课后作业---拓展提升】
Page 18
任务作业: 根据对奥运会情况的分析,思考刚刚结束的残
A.小于1.25m3 C.不小于0.8m3
Page 1
数与式
数
与 代
函数
数
一次函数
类比
反比例函数
二次函数
方程与不等式
定义 子任务1:走进奥运 图象与性质 子任务2:探索奥运 应用 子任务3:传承奥运
初中数学 九年级下册 青岛出版社
Page 2
§5.2.3 反比例函数的应用
【学习目标】
Page 3
1.通过分析实际问题中变量之间的关系,建立反比例函数 模型解决问题,提高运用函数的图象、性质的综合能力. 2.经历分析问题的过程,能够根据实际问题确定自变量的 取值范围,体会数学与现实生活的紧密联系.
【传承奥运---变式训练】
在奥运会游泳比赛中,为了保证运 动员身体健康,换水和消毒工作一 直是非常重要的环节,通常采用循 环使用含氯消毒剂对游泳池进行消 毒.
Page 8
【传承奥运---变式训练】
Page 9
消毒剂溶解时,游泳池内每立方米水中含消毒剂量y (克/立方米)与消毒剂溶解的时间x(分钟)成正比 例,消毒剂完全溶解后,y与x成反比例(如图所示). 已知消毒剂8分钟完全溶解,此时每立方米水中含消毒 剂量为6克.
【课堂小结---反比例函数的应用】
Page 15
请你回顾任务2中我 们应掌握的内容:
从知识上——
反比例函数
从方法上——
从思想上——
还有……
定义 子任务1:走进奥运 图象与性质 子任务2:探索奥运 应用 子任务3:传承奥运
Page 17
【课后作业---拓展提升】
Page 18
任务作业: 根据对奥运会情况的分析,思考刚刚结束的残
A.小于1.25m3 C.不小于0.8m3
5.2.3反比例函数的应用教学课件-2023—-2024学年青岛版九年级数学下册
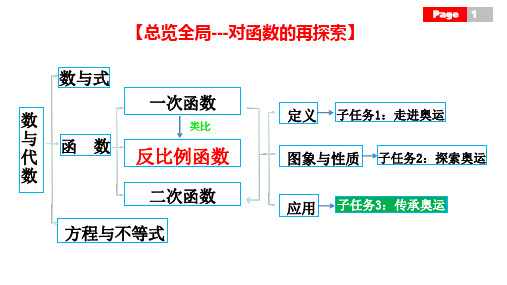
【总览全局---对函数的再探索】
Page 1
数与式
数
与 代
函数
数
一次函数
类比
反比例函数
二次函数
方程与不等式
定义 子任务1:走进奥运 图象与性质 子任务2:探索奥运 应用 子任务3:传承奥运
初中数学 九年级下册 青岛出版社
Page 2
§5.2.3 反比例函数的应用
【学习目标】
Page 3
1.通过分析实际问题中变量之间的关系,建立反比例函数 模型解决问题,提高运用函数的图象、性质的综合能力. 2.经历分析问题的过程,能够根据实际问题确定自变量的 取值范围,体会数学与现实生活的紧密联系.
Page 5
【传承奥运---情境重现】
Page 6
奥运会前期需要往游泳池内注水,当该游泳池以每小时150立 方米的速度注水时,经15小时能将游泳池注满.设注水的速度 为x立方米/时,将池内注满水需y小时.已知该游泳池每小时 的最大注水速度为250立方米/时。
问题2:下面选项中符合题意的图象是?
【传承奥运---情境重现】
问题5:求消毒剂溶解时, y与x之间的函数表达式;
【传承奥运---变式训练】
Page 10
消毒剂溶解时,游泳池内每立方米水中含消毒剂量y (克/立方米)与消毒剂溶解的时间x(分钟)成正比 例,消毒剂完全溶解后,y与x成反比例(如图所示). 已知消毒剂8分钟完全溶解,此时每立方米水中含消毒 剂量为6克.
【传承奥运---情境重现】
奥运会前期需要往游泳池内注水,当该游 泳池以每小时150立方米的速度注水时,经 15小时能将 游 泳 池 注 满 .设 注 水 的速度为x 立方米/时,将池内 注 满 水需y小时.已知 该游泳池每小时的最大注水速度为250立方 米/时。
Page 1
数与式
数
与 代
函数
数
一次函数
类比
反比例函数
二次函数
方程与不等式
定义 子任务1:走进奥运 图象与性质 子任务2:探索奥运 应用 子任务3:传承奥运
初中数学 九年级下册 青岛出版社
Page 2
§5.2.3 反比例函数的应用
【学习目标】
Page 3
1.通过分析实际问题中变量之间的关系,建立反比例函数 模型解决问题,提高运用函数的图象、性质的综合能力. 2.经历分析问题的过程,能够根据实际问题确定自变量的 取值范围,体会数学与现实生活的紧密联系.
Page 5
【传承奥运---情境重现】
Page 6
奥运会前期需要往游泳池内注水,当该游泳池以每小时150立 方米的速度注水时,经15小时能将游泳池注满.设注水的速度 为x立方米/时,将池内注满水需y小时.已知该游泳池每小时 的最大注水速度为250立方米/时。
问题2:下面选项中符合题意的图象是?
【传承奥运---情境重现】
问题5:求消毒剂溶解时, y与x之间的函数表达式;
【传承奥运---变式训练】
Page 10
消毒剂溶解时,游泳池内每立方米水中含消毒剂量y (克/立方米)与消毒剂溶解的时间x(分钟)成正比 例,消毒剂完全溶解后,y与x成反比例(如图所示). 已知消毒剂8分钟完全溶解,此时每立方米水中含消毒 剂量为6克.
【传承奥运---情境重现】
奥运会前期需要往游泳池内注水,当该游 泳池以每小时150立方米的速度注水时,经 15小时能将 游 泳 池 注 满 .设 注 水 的速度为x 立方米/时,将池内 注 满 水需y小时.已知 该游泳池每小时的最大注水速度为250立方 米/时。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
O A x
B
y O x
y O
C x
D
y o x
D
9.老师给出一个函数,甲、乙、丙三位同
学分别指出了这个函数的一个性质:
甲:函数的图象经过第二象限;
乙:函数的图象经过第四象限;
丙:在每个象限内,y随x的增大而增大.
请你根据他们的叙述构造满足上述性质的 一个函数: .
(10)反比例函数y=k/x(k≠0),当k>0时,函数的图 象的两个分支分别应在( ) A.第一、第三象限 B.第一、第二象限 C.第二、四象限 D.第三、四象限 (11)反比例函数y=-4/x的图象大致是(
y3 >y1>y2
4 y x
的图象上,
则y1、y2与y3的大小关系(从大到小)
.
-2
y
-1 y3
A
B
o y1 y2
C 4
x
1.若正比例函数 k1 x ( k1 0)与反比例函数 y y
k2 x
( k 2 0) 的函数值都随 的增大而增大 x ,
那么它们在同一直角坐 标系内的大致图 象是 _ _ _ _.
y
6 y=x
0 x
y y x
0
6 y= x
反比例函数的性质
1. 当k>0时, 图象的两
y
6 y=x
0 x
个分支分别在第一、
三象限内。y随x的增
大而减小
2. 当k<0时, 图象的两 个分支分别在第二、 四象限内。y随x的增 大而增大
y
0
6 y= x
x
反比例函数的图象既是轴对称图形又是中心对称图形。 有两条对称轴:直线y=x和 y=-x。对称中心是:原点
k
0
12
x
填一填
2 1.函数 y 是 反比例 函数,其图象为双曲线 , x
其中k= 2 ,自变量x的取值范围为 x≠ 0
.
6 2.函数 y 的图象位于第一、三 象限, x
在每一象限内,y的值随x的增大而 减小 , 当x>0时,y > 0,这部分图象位于第 一 象限.
复习回顾
1.什么是反比例函数? k 一般地,形如 y = — ( k是常数, k = 0 ) 的函数 x 叫做反比例函数. 2.反比例函数的定义中需要注意什么?
(1)k 是非零常数;
(2)自变量 x 是 分母, (3)xy = k 3.反比例函数的图象是什么?有些什么性质?
你还记得一次函数的图象与性质吗?
注意:①列表时,自变量x取值 要均匀和对称;② x≠0;
x
y =6 x
y= 6 x
a
… -6 -5 -4 -3 … -1 -1.2-1.5 -2 … 1 1.2 1.5 2
y
6 5 4 3 2 1
-2 -1 -3 3 -6
1 6
2 3 3
4
5
6 …
2
6 -6 -3 -2
y= 6 x
1 … -1.5 -1.2 -1 …
1.5 1.2
y
6 5 4 3 2 1
y= 6 x
-6
-5
-4
-3
-2
-1 -1 -2 -3 -4 -5 -6
0
1
2
3
4
5
6
x
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
x
-1
-2 -3 -4 -5 -6
请大家结合反比例函数 6 和 6 y= y= x x 的函数图象,围绕以下 两个问题分析反比例函 数的性质: ① 当k>0时, 两支曲线 各在哪个象限?每个象 限内,y随x的增大有什 么变化? ② 当k<0呢?
m+2m-16
2
, y 随 x 的减小而增大,
4.已知函数y=k/x 的图象如下右图,则 y=k x-2 的图象大致是(D )
y o x o (B) y y o o x x x o y y
(A)
x
(C)
(D)
同学们, 再见!
6 3.函数 y 的图象位于第二、四象限, x
在每一象限内,y的值随x的增大而 增大 , 当x>0时,y < 0,这部分图象位于第 四 象限.
思考: 试归纳反比例函数的概念、图象与性质, 并与正比例函数作比较.
函数
解析式
图象形状
正比例函数
y=kx ( k≠0 ) 直线
位 置
经过一三象限
反比例函数
练习
5 二,四 1.函数 y = x 的图象在第_____象限,在每 减小 个象限内,y 随 x 的增大而_____ . y 1 1 2. 双曲线 y = 3x 经过点(-3,___) 9 x m-2 3.函数 y = x 的图象在二、四象限,则m的 m<2 取值范围是 ____ . 1 减小 4.对于函数 y = 2x ,当 x<0时,y 随x的_____ 三 而增大,这部分图象在第 ________象限. 5.函数 y =(2m+1)x 则m= ____. 3
第二、四象限,那么m的范围为 m> 3 .
由1-3m<0 得-3m<- 1
1 ∴ m> 3
2.下列函数中,图象位于第二、四象限 的有(3)、(4) ;在图象所在象限内,y的 值随x的增大而增大的有 (2)、(3)、(5) .
2 2x (1)y (2)y 3x 3 (5)y 2x 3 2 (3)y 3x 2x (4)y 3
则y1与y2的大小关系(从大到小)
为
y2> y1
.
6.已知点A(-2,y1),B(-1,y2) 1<0<x2 A(x1,y1),B(x2,y2)且x
k4 都在反比例函数 y y x(k<0) 的图象上, x
则y1与y2的大小关系(从大到小)
为
y1 >0>y2
.
A
y
y1
o
x2
x
B
x1
y2
7.已知点A(-2,y11),B(-1,y2),C(4,y3) A(-2,y ),B(-1,y2) 都在反比例函数 为
(1)如果反比例函数y=k/x的图象过点(3,-4), 那么函数的图象应在( ) A.第一、三象限 B.第一、第二象限 C.第二、四象限 D.第三、四象限 (2)当x<0时,函数y=x与y=1/x在同 一坐标系中的图象在大致是( )
Y Y Y Y
X
X
X
X
A
B
C
D
k 3.已知反比例函数 y (k≠0) x
一次函数y=kx+b(k≠0)的图象是一条 直线,称直线y=kx+b.
当k>0时,
y
当k<0时,
y
b<0
o
b>0 b=0
x
b>0 b=0
o
b<0
x
y随x的增大而增大; y随x的增大而减小. •
6 作反比例函数 y = x 和 y =
函数图象画法
6 x 的图象。
描 点 连 线
列 表
x . . . -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ...
k y = x ( k≠0 )
填表 分析 正比 例函 数和 反比 例函 数的 异同
双曲线
K>0
位于一三象限
增 减 性
y随x的增大而增大
在每个象限内 y随x的增大而减小
K<0
位 置
增 减 性
经过二四象限
位于二四象限
y随x的增大而减小
在每个象限内 y随x的增大而增大
做一做(二)
1 3m 1.如果反比例函数 y 的图象位于 x 1
Y Y Y Y
)
X
X
X
X
A
B
C
D
k 反比例函数 y = — 有下列性质: x k 1.反比例函数的图象y 是由两支曲线组成的。因此 x 称反比例函数的图象为双曲线 2.(1)当 k>0 时,两支曲线分别位于 第___、___象限,y随x的增大而_____ 一 三 (2)当 k<0 时,两支曲线分别位于 二 四 第___、___象限, y随x的增大而_____
当x<0时,y随x的增大而减小, k>0
则一次函数y=kx-k的图象不经过第 二 象限. k>0 ,-k<0
y
o
x
4.已知点A(-2,y1),B(-1,y2) 都在反比例函数 为
y1> y2
4 y x
的图象上,
则y1与y2的大小关系(从大到小)
.
5.已知点A(-2,y1),B(-1,y2)
k4 都在反比例函数 y y x(k<0) 的图象上, x
