网格法平整场地土方量计算公式
方格网计算土方量原理

方格网计算土方量原理方格网法是一种用于测量土地表面不规则形状的土方量的方法。
它是一种简单而有效的方法,可以帮助工程师和土木工程师快速准确地计算土地表面的土方量。
接下来,我们将介绍方格网法的原理和计算步骤。
方格网法的原理是将土地表面划分为一个个小方格,并通过对每个小方格的测量来计算土方量。
首先,需要在土地表面建立一个方格网,网格的大小可以根据实际情况来确定,一般情况下,网格大小为1米×1米或2米×2米。
然后,对每个小方格的高程进行测量,可以使用全站仪或其他测量仪器来进行高程测量。
通过对每个小方格的高程测量,可以得到土地表面的高程数据。
在进行高程测量之后,需要对每个小方格的面积进行测量。
可以通过测量每个小方格的边长来计算出每个小方格的面积。
在测量完所有小方格的高程和面积之后,就可以利用这些数据来计算土方量了。
土方量的计算公式为,土方量 = Σ(高程差×面积)。
其中,Σ表示对所有小方格进行求和,高程差表示每个小方格的最大高程和最小高程之差,面积表示每个小方格的面积。
通过对所有小方格的高程差和面积进行求和,就可以得到土地表面的土方量。
在实际应用中,方格网法可以帮助工程师和土木工程师快速准确地计算土地表面的土方量,特别是对于不规则形状的土地表面,方格网法可以更加方便地进行土方量的计算。
通过合理设置方格网的大小和密度,可以得到更加精确的土方量计算结果。
总之,方格网法是一种简单而有效的土方量计算方法,通过对土地表面进行方格划分和测量,可以快速准确地得到土方量的计算结果。
在工程实践中,方格网法可以帮助工程师和土木工程师更加方便地进行土方量的计算,为工程设计和施工提供重要的参考依据。
土方方格网计算公式图示及推导
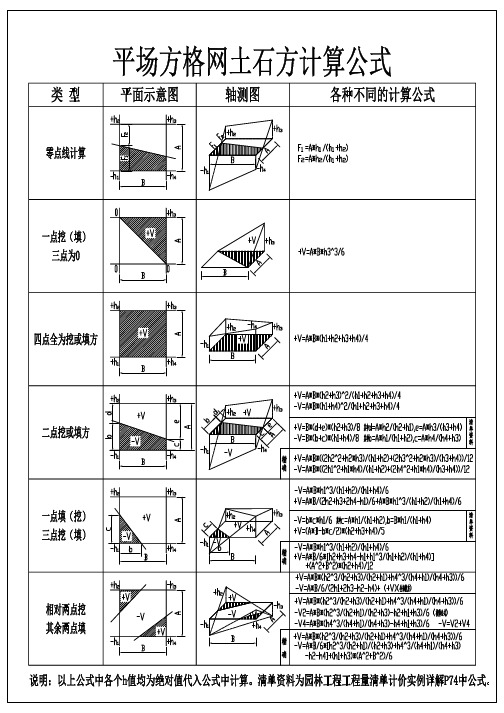
方格网土方计算公式推导:1、两点开挖工程量计算公式:如上图示:d=A*h2/(h1+h2); e=A*h3/(h3+h4); S1=d*h2/2; S2=e*h3/2S0=(d+e)/2*(h2+h3)/2/2根据拟柱体体积计算公式:V=B/6*(S1+4*S0+S2)将上面已知数代入公式可得:V=B/6*{A*h2/(h1+h2)*h2/2+4*[A*h2/(h1+h2)+A*h3/(h3+h4)]/2*(h2+h3)/2/2+h3*A*h3/(h3+h4)/2}=A*B/6*{h2*h2/(h1+h2)+ h2*(h2+h3)/(h1+h2)+ h3*(h2+h3)/(h3+h4)+h3*h3/(h3+h4)}/2=A*B/12*{(2h2^2+h2*h3)/ (h1+h2)+(2*h3^2+h2*h3)/(h3+h4)}2、三点开挖的挖方量计算公式:由图分解可得,挖方体积=v1+v2-(v3-v4),由拟柱体体积计算公式可以得出:V1={A*(h3+h4)/2+4*A/2*(h3+h2+h2+h4)/4}*B/6=A*B/12*{h3+h4+2*h2+h3+h4}=A*B*(h2+h3+h4)/6V2、V3、V4分别按四棱锥、三棱锥、三棱锥体积计算公式进行计算(体积=底面积*高/3)V2= [√(A^2+B^2)]*1/2*1/3*[√(A^2+B^2)]*(h2+h4)/2= (A^2+B^2)*(h2+h4) /12V3=A*B/2/3*h1=A*B*h1/6V4=h1/3*(B*h1/(h1+h4)*A*h1/(h1+h2)/2=A*B/6*h1^3/(h1+h2)/(h1+h4)V=V1+V2-V3+V4= A*B*(h2+h3+h4)/6+(A^2+B^2)*(h2+h4) /6+A*B/6*h1^2/(h1+h2)/(h1+h4)- A*B*h1/6= A*B /6*[ h2+h3+h4-h1+h1^3/(h1+h2)/(h1+h4)] +(A^2+B^2)*(h2+h4) /123、不机邻两点回填方量计算公式推导:如图示:从h1和h3处将图形分成平面为两个直角三角形体:h4侧的体积公式如下:Vh4=V1+V3-V2根据锥体体积公式:底面积*高/3可得V1=(h1+h3)/2*[√(A^2+B^2)] /3*[√(A^2+B^2)]/2=(h1+h3)*(A^2+B^2) /12 V2=A*B/2*h4/3= A*B*h4/6V3= h4/3*(B*h4/(h4+h1)*A*h4/(h4+h3)/2=A*B/6*h4^3/(h4+h1)/(h4+h3) V=(h1+h3)*(A^2+B^2) /12- A*B*h4/6+ A*B/6*h4^3/(h4+h1)/(h4+h3)= A*B/6*[h4^3/(h4+h1)/(h4+h3)-h4]+ (h1+h3)*(A^2+B^2) /12h2侧的体积公式推导方法h4侧的体积公式:Vh2=A*B/6*[h2^3/(h2+h1)/(h2+h3)-h2]+ (h1+h3)*(A^2+B^2) /12V=Vh2+Vh4=A*B/6*[h2^3/(h2+h1)/(h2+h3)-h2]+ (h1+h3)*(A^2+B^2) /12+ A*B/6*[h4^3/(h4+h1)/(h4+h3)-h4]+ (h1+h3)*(A^2+B^2) /12= A*B/6*[ h2^3/(h2+h1)/(h2+h3) + h4^3/(h4+h1)/(h4+h3) -h2-h4]+ (h1+h3)*(A^2+B^2) /6。
网格法土方量计算公式

网格法平整场地土方量计算公式:1、方格四个角点全部为填土式挖方,其土方量:2a)h?h?(h?h?Vh,h,h,h为角点填方高度,为绝对值。
)(注:4321432142、方格的相邻两角点为挖方,另两角点为填方。
其挖方部分工程量:21)??(V4h?hh?h3214222hha其222hha填方部分工程量:34)(?V?4h?hh?h3421h,hhh,为需填方角点填方高度。
皆为绝对值。
(注:为需挖方角点挖方高度,)43213、方格的三个角点为挖方,另一个角点为填方。
其填方部分工程量:4?V46(h?h)(h?h)43142a其挖方32ha部分工程量:V?h)??2hh?2hV?(4143,1,2326hhh,h,为需填方角点填方高度。
皆为绝对值。
)(注:为需挖方角点挖方高度,43124、方格的一个角点为挖方,相对的角点为填方。
另两个角点为零点时2a(零线为方格的对角线),其挖填方工程量为:hV?b4/ 142 /常用方格网计算公式2.计算公式项目图示一点填方或挖方(三角形)当时,二点填方或挖方(梯)形三点填方或挖方(五角形)四点填方正(或挖方方形)4/ 3注:1)a——方格网的边长,m;b、c——零点到一角的边长,m;h,h,h,h方格网四角点的施工高程,m,用绝对值代入;Σh——填方或挖方施工高程的——1423)本表公式是按各计算图形底面积乘以平均施工高程而得出的。
2。
挖方或填方体积,用绝对值代入; ,m总和——,m4/ 4。
方格网计算土方量原理

方格网计算土方量原理
方格网计算土方量原理即通过在地面上划分方格网,并计算每个方格中的土方体积,进而得出总的土方量。
具体原理可分为以下几步:
1. 划分方格网:首先在待测量区域的地面上进行方格网的划分,通常使用水平标杆和粉笔线等工具,将地面划分为等大的方格。
2. 计算单个方格的土方体积:对每个方格进行土方体积的计算。
土方体积的计算可以通过以下公式进行:
土方体积 = 方格面积 ×层高
其中,方格面积为方格的水平投影面积,层高为该方格内土
方堆积的高度,可以通过测量或估算得出。
3. 累加各个方格的土方体积:将所有方格内的土方体积累加起来,得到总的土方体积。
可以通过逐个方格计算土方体积,并将其累加到总体积中的方法来实现。
4. 随机抽查方格:为了验证计算结果的准确性,可以随机抽取部分方格进行测量和计算,然后与计算结果进行对比。
需要注意的是,在进行方格网计算土方量时,应当注意以下几点:
- 方格的大小应根据实际情况进行选择,一般应适当缩小,以
提高计算精度。
- 方格网的划分应在待测量区域的整个范围内进行,确保所有
区域被覆盖。
- 土方体积计算中的方格面积和层高都应该准确测量或者经过合理估算。
- 测量时要确保准确性,避免误差的产生,可选用高精度的测量工具,并进行多次测量取平均值。
综上所述,方格网计算土方量原理是通过划分方格网,计算每个方格内的土方体积,累加得到总的土方体积。
该方法可以提高土方量计算的准确性和效率。
网格法--土方量计算公式

网格法平整场地土方量计算公式:1、方格四个角点全部为填土式挖方,其土方量:2(hi h2 h3 h4)(注:0山2山3山4为角点填方高度,为绝对值。
)42、方格的相邻两角点为挖方,另两角点为填方。
其挖方部分工程量:V=M(-卫匹)4 +h4h2+h3其填方部分工程量:V二’(丄匹)4 0 +h4h2+h3(注:h i,h2为需挖方角点挖方高度,h3,h4为需填方角点填方高度。
皆为绝对值。
)3、方格的三个角点为挖方,另一个角点为填方。
其填方部分工程量:V^- S6 m +h4)(h3 +h4)2其挖方部分工程量:乂,2,3 =玄(20 +h2+2h3 - h4)+V46(注:h|, h2, h s为需挖方角点挖方高度,入为需填方角点填方高度。
皆为绝对值。
)4、方格的一个角点为挖方,相对的角点为填方。
另两个角点为零点时2(零线为方格的对角线),其挖填方工程量为:V二話h2.常用方格网计算公式项目图示一点填方或挖方(三角形)1计算公式F亠H竺12 315当!- -门时,■-- 二点填方或挖方(梯形)三点填方或挖方(五角形)四点填方或挖方(正方形)注:1) a ----- 方格网的边长,m; b、c ------ 零点到一角的边长,m; hi,h 2,h 3,h 4―方格网四角点的施工高程,m,用绝对值代入;2 h---------- 填方或挖方施工高程的总和,m ,用绝对值代入;y——挖方或填方体积,m。
2)本表公式是按各计算图形底面积乘以平均施工高程而得出的。
场地平整土方工程量的计算方法

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时,常需要进行土方工程量的计算。
计算方法有方格网法和横断面法两种。
(1)方格网法用于地形较平缓或台阶宽度较大的地段。
计算方法较为复杂,但精度较高,其计算步骤和方法如下:1)划分方格网根据已有地形图(一般用1:500的地形图)将欲计算场地划分成若干个方格网,尽量与测量的纵、横坐标网对应,方格一般采用20m×20m或40m×40m,将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。
将自然地面标高与设计地面标高的差值,即各角点的施工高度(挖或填),填在方格网的左上角,挖方为(-),填方为(+)。
2)计算零点位置在一个方格网内同时有填方或挖方时,应先算出方格网边上的零点的位置,并标注于方格网上,连接零点即得填方区与挖方区的分界线(即零线)。
零点的位置按下式计算(图6-3):(6-8)式中x1、x2——角点至零点的距离(m);h1、h2——相邻两角点的施工高度(m),均用绝对值;a——方格网的边长(m)。
图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算,亦可采用图解法直接求出零点位置,如图6-4所示,方法是用尺在各角上标出相应比例,用尺相接,与方格相交点即为零点位置。
这种方法可避免计算(或查表)出现的错误。
3)计算土方工程量按方格网底面积图形和表6-31所列体积计算公式计算每个方格内的挖方或填方量,或用查表法计算,有关计算用表见表6-31。
常用方格网点计算公式表6-31注:1.a——方格网的边长(m);b、c——零点到一角的边长(m);h1、h2、h3、h4——方格网四角点的施工高程(m),用绝对值代入;Σh——填方或挖方施工高程的总和(m),用绝对值代入;V——挖方或填方体积(m3)。
2.本表公式是按各计算图形底面积乘以平均施工高程而得出的。
4)计算土方总量将挖方区(或填方区)所有方格计算土方量汇总,即得该场地挖方和填方的总土方量。
方格网土方计算公式讲解学习
11.2.1方格网法土方计算
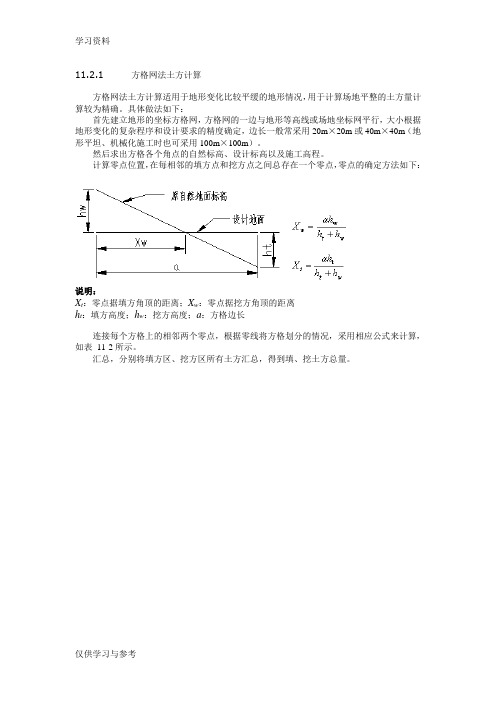
方格网法土方计算适用于地形变化比较平缓的地形情况,用于计算场地平整的土方量计算较为精确。
具体做法如下:
首先建立地形的坐标方格网,方格网的一边与地形等高线或场地坐标网平行,大小根据地形变化的复杂程序和设计要求的精度确定,边长一般常采用20m×20m或40m×40m(地形平坦、机械化施工时也可采用100m×100m)。
然后求出方格各个角点的自然标高、设计标高以及施工高程。
计算零点位置,在每相邻的填方点和挖方点之间总存在一个零点,零点的确定方法如下:
说明:
X t:零点据填方角顶的距离;X w:零点据挖方角顶的距离
h t:填方高度;h w:挖方高度;a:方格边长
连接每个方格上的相邻两个零点,根据零线将方格划分的情况,采用相应公式来计算,如表11-2所示。
汇总,分别将填方区、挖方区所有土方汇总,得到填、挖土方总量。
四个角点全填方(或全挖方)
一个角点填方(或挖方),另外三个角点挖方(或填方)
一侧两个角点填方(或挖方),另一侧两个角点挖方(或填方)相对两个角点填方(或挖方),另外相对两个角点挖方(或填方)说明:
a:方格边长(m)
h1、h2、h3、h4:方格网角点的施工高度,正值代表填方,负值代表挖方V+、V-:填方(或挖方)的体积(m3)。
土方工程量计算--方格网法

所谓零点就是既不挖土也不填土的点,将零
点互相连接起来的线就是零点线。零点线是
挖方和填方区的分界线,它是土方计算的重
要依据。
2021/10/10
8
(6)土方量计算
根据方格网中各 个方格的填挖情况, 分别计算出每一方 格土方量。由于每 一方格内的填挖情 况不同,计算所依 据的图式也不同。 计算中,应按方格 内的填挖具体情况, 选用相应的图式, 并分别将标高数字 代入相应的公式中 进行计算。
(1)求积仪法
运用求积仪进行测量,此法比较简便,精确度也比较 高。
(2)方格纸法
用方格纸蒙在图纸上,通过数方格数,再乘以每个方 格的面积而求取。此法方格网越密,精度越大。
一般在数方格数时,测量对象占方格单元超过1/2, 按一整个方格计;小于1/2者不计。最后进行方格数 的累加,再求取面积既可。
2021/10/10
4∑h4′1=(x-0.3+x-0.6)×4 =8x-3.6m H0′=4*8 (6x-6.4+12x-7.4+6x-4.2+8x-3.6)= x-0.675
H0′=X-0.675=H0
∵ H ≈ 2021/10/010 20.06 ∴ X=20.06+0.675≈20.74
16
6.求施工标高 施工标高=原地形标高-设计标高 得数 “+”号者为挖方,“-”号者为填方。
(如果有较精确的地形图,可用插入法由图上直接求得 各角点的原地形标高,并标记在图上。)
2021/10/10
11
上图所示的角点1—1属于上述第一种情况,过点1—1作相 邻二等高线间的距离最短的线段。用比例尺量得L=12.6m, x=7.4m, 等高差h=0.5m,代人前面插入法求两相邻等高线 之间任意点高程的公式,得 Hx=Ha+xh/L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网格法平整场地土方量计算公式:
1、方格四个角点全部为填土式挖方,其土方量:
)(4
43212
h h h h a V +++= (注:4321,,,h h h h 为角点填方高度,为绝对值。
)
2、方格的相邻两角点为挖方,另两角点为填方。
其挖方部分工程量:
)(43
22241212
h h h h h h a V +++= 其填方部分工程量:
)(43
22341242
h h h h h h a V +++= (注:21,h h 为需挖方角点挖方高度,43,h h 为需填方角点填方
高度。
皆为绝对值。
)
3、方格的三个角点为挖方,另一个角点为填方。
其填方部分工程量:
)
)((643413424h h h h h a V ++= 其挖方部分工程量:
4432123,2,1)22(6
V h h h h a V +-++=
(注:321,,h h h 为需挖方角点挖方高度,4h 为需填方角点填方
高度。
皆为绝对值。
)
4、方格的一个角点为挖方,相对的角点为填方。
另两个角点为零点时(零线为方格的对角线),其挖填方工程量为: h b a V 2。
