三角形等高模型 例题+巩固+答案
(小学奥数)三角形等高模型与鸟头模型(二)

板塊一 三角形等高模型我們已經知道三角形面積的計算公式:三角形面積=底⨯高2÷從這個公式我們可以發現:三角形面積的大小,取決於三角形底和高的乘積. 如果三角形的底不變,高越大(小),三角形面積也就越大(小);如果三角形的高不變,底越大(小),三角形面積也就越大(小);這說明當三角形的面積變化時,它的底和高之中至少有一個要發生變化.但是,當三角形的底和高同時發生變化時,三角形的面積不一定變化.比如當高變為原來的3倍,底變為原來的13,則三角形面積與原來的一樣.這就是說:一個三角形的面積變化與否取決於它的高和底的乘積,而不僅僅取決於高或底的變化.同時也告訴我們:一個三角形在面積不改變的情況下,可以有無數多個不同的形狀. 在實際問題的研究中,我們還會常常用到以下結論: ①等底等高的兩個三角形面積相等;②兩個三角形高相等,面積比等於它們的底之比; 兩個三角形底相等,面積比等於它們的高之比; 如左圖12::S S a b =s 2s 1baDCBA③夾在一組平行線之間的等積變形,如右上圖ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,則可知直線AB 平行於CD .④等底等高的兩個平行四邊形面積相等(長方形和正方形可以看作特殊的平行四邊形);⑤三角形面積等於與它等底等高的平行四邊形面積的一半;⑥兩個平行四邊形高相等,面積比等於它們的底之比;兩個平行四邊形底相等,面積比等於它們的高之比. 板塊二 鳥頭模型兩個三角形中有一個角相等或互補,這兩個三角形叫做共角三角形.例題精講4-3-2.三角形等高模型與鳥頭模型共角三角形的面積比等於對應角(相等角或互補角)兩夾邊的乘積之比. 如圖在ABC △中,,D E 分別是,AB AC 上的點如圖 ⑴(或D 在BA 的延長線上,E 在AC 上),則:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBADECBA圖⑴ 圖⑵【例 1】 如圖在ABC △中,,D E 分別是,AB AC 上的點,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方釐米,求ABC △的面積.EDCBAEDCBA【考點】三角形的鳥頭模型 【難度】2星 【題型】解答 【解析】 連接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,設8ADE S =△份,則35ABC S =△份,16ADE S =△平方釐米,所以1份是2平方釐米,35份就是70平方釐米,ABC △的面積是70平方釐米.由此我們得到一個重要的定理,共角定理:共角三角形的面積比等於對應角(相等角或互補角)兩夾邊的乘積之比 . 【答案】70【鞏固】如圖,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE的面積等於1,那麼三角形ABC 的面積是多少?EDCBA ABC D E【考點】三角形的鳥頭模型 【難度】2星 【題型】解答 【解析】 連接BE .∵3EC AE =∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==. 【答案】15【鞏固】如圖,三角形ABC 被分成了甲(陰影部分)、乙兩部分,4BD DC ==,3BE =,6AE =,乙部分面積是甲部分面積的幾倍?乙甲E DCBAABCD E甲乙【考點】三角形的鳥頭模型 【難度】2星 【題型】解答 【解析】 連接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【答案】5【例 2】如圖在ABC △中,D 在BA 的延長線上,E 在AC 上,且:5:2AB AD =, :3:2AE EC =,12ADE S =△平方釐米,求ABC △的面積.EDCBA EDCBA【考點】三角形的鳥頭模型 【難度】3星 【題型】解答【解析】 連接BE,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△ []::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△, 所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,設6ADE S =△份,則25ABC S =△份,12ADE S =△平方釐米,所以1份是2平方釐米,25份就是50平方釐米,ABC △的面積是50平方釐米.由此我們得到一個重要的定理,共角定理:共角三角形的面積比等於對應角(相等角或互補角)兩夾邊的乘積之比 【答案】50【例 3】如圖所示,在平行四邊形ABCD 中,E 為AB 的中點,2AF CF =,三角形AFE (圖中陰影部分)的面積為8平方釐米.平行四邊形的面積是多少平方釐米?【考點】三角形的鳥頭模型 【難度】2星 【題型】解答【解析】 連接FB .三角形AFB 面積是三角形CFB 面積的2倍,而三角形AFB 面積是三角形AEF 面積的2倍,所以三角形ABC 面積是三角形AEF 面積的3倍;又因為平行四邊形的面積是三角形ABC 面積的2倍,所以平行四邊形的面積是三角形AFE 面積的326⨯=()倍.因此,平行四邊形的面積為8648⨯=(平方釐米).【答案】48【例 4】已知DEF △的面積為7平方釐米,,2,3BE CE AD BD CF AF ===,求ABC △的面積.FED CBA【考點】三角形的鳥頭模型 【難度】3星 【題型】解答【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△設24ABC S =△份,則4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方釐米,所以24ABC S =△平方釐米 【答案】24【例 5】如圖16-4,已知.AE=15AC ,CD=14BC ,BF=16AB ,那麼DEF ABC三角形的面积三角形的面积等於多少?【考點】三角形的鳥頭模型 【難度】3星 【題型】解答 【關鍵字】迎春杯,決賽,第一題,9題【解析】 如下圖,連接AD ,BE ,CF.有△ABE ,△ABC 的高相等,面積比為底的比,則有ABE ABCSS=AEAC,所以ABE S=AEAC×ABC S =15ABCS同理有AEF S=AFABABE S ,即=AEF S=15×56ABC S =16ABCS .類似的還可以得到CDE S=14×45ABC S =15ABC S ,BDF S=16×13ABC S =18ABCS.所以有DEF S =ABC S -(AEF S +CDE S +BDF S )=(1-16-15-18)ABC S =61120ABC S .即DEF ABC 三角形的面积三角形的面积為61120. 【答案】61120【例 6】如圖,三角形ABC 的面積為3平方釐米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面積是多少?AB EC DDC EB A【考點】三角形的鳥頭模型 【難度】2星 【題型】解答 【解析】 由於180ABC DBE ︒∠+∠=,所以可以用共角定理,設2AB =份,3BC =份,則5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,設6ABC S =△份,恰好是3平方釐米,所以1份是0.5平方釐米,25份就是250.512.5⨯=平方釐米,三角形BDE 的面積是12.5平方釐米【答案】12.5【例 7】如圖所示,正方形ABCD 邊長為6釐米,13AE AC =,13CF BC =.三角形DEF 的面積為_______平方釐米.【考點】三角形的鳥頭模型 【難度】3星 【題型】解答 【關鍵字】走美杯,五年級,初賽 【解析】 由題意知13AE AC =、13CF BC =,可得23CE AC =.根據”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方釐米).【答案】10【例 8】如圖,已知三角形ABC 面積為1,延長AB 至D ,使BD AB =;延長BC 至E ,使2CE BC =;延長CA 至F ,使3AF AC =,求三角形DEF 的面積.FEDCB A ABCDEF【考點】三角形的鳥頭模型 【難度】3星 【題型】解答【解析】 (法1)本題是性質的反復使用.連接AE 、CD . ∵11ABC DBCSS=,1ABCS =,∴S 1DBC =.同理可得其他,最後三角形DEF 的面積18=. (法2)用共角定理∵在ABC和CFE中,ACB ∠與FCE ∠互補,∴111428ABC FCES AC BC SFC CE ⋅⨯===⋅⨯. 又1ABC S =,所以8FCE S =. 同理可得6ADF S =,3BDE S =.所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=. 【答案】18【例 9】如圖,把四邊形ABCD 的各邊都延長2倍,得到一個新四邊形EFGH 如果ABCD 的面積是5平方釐米,則EFGH 的面積是多少平方釐米?【考點】三角形的鳥頭模型 【難度】4星 【題型】解答【解析】 方法一:如下圖,連接BD ,ED ,BG ,有EAD 、ADB 同高,所以面積比為底的比,有2EADABDABDEA SS SAB==.同理36EAHEADEADABDAHSS SSAD===.類似的,還可得6FCG BCD S S =,有()66EAH FCG ABDBCDABCD S S SSS +=+==30平方釐米.連接AC ,AF ,HC ,還可得6EFBABCS S=,6DHGACDSS=,有()66EFB DHG ABCACDABCD S S SSS +=+==30平方釐米.有四邊形EFGH 的面積為EAH,FCG,EFB,DHG,ABCD 的面積和,即為30+30+5=65(平方釐米.)方法二:連接BD ,有EAH 、△ABD 中∠EAD+∠BAD=180° 又夾成兩角的邊EA 、AH ,AB 、AD 的乘積比,EA AHAB AD⨯⨯=2×3=6,所以EAHS=6ABDS.類似的,還可得FCGS =6BCDS,有EAHS +FCGS=6(ABDS +BCDS)=6ABCD S =30平方釐米.連接AC ,還可得EFB S=6ABC S ,DHG S=6ACDS,有EFBS+DHGS=6(ABCS+ACDS)=6ABCD S =30平方釐米.有四邊形EFGH 的面積為△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面積和,即為30+30+5=65平方釐米. 【答案】65【例 10】 如圖,平行四邊形ABCD ,BE AB =,2CF CB=,3GD DC =,4HA AD =,平行四邊形ABCD 的面積是2, 求平行四邊形ABCD 與四邊形EFGH 的面積比.HGAB CD EFHGA B CDEF【考點】三角形的鳥頭模型 【難度】4星 【題型】解答 【解析】 連接AC 、BD .根據共角定理∵在ABC △和BFE △中,ABC ∠與FBE ∠互補,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△. 所以213618ABCDEFGHS S ==. 【答案】118【例 11】 如圖,四邊形EFGH的面積是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四邊形ABCD 的面積.H GFED CB A A B CDEGH【考點】三角形的鳥頭模型 【難度】4星 【題型】解答 【解析】 連接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGFCDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形連接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如圖,將四邊形ABCD 的四條邊AB 、CB 、CD 、AD 分別延長兩倍至點E 、F 、G、H ,若四邊形ABCD 的面積為5,則四邊形EFGH 的面積是 .A B CD E F GHA B CD EF GH【考點】三角形的鳥頭模型 【難度】4星 【題型】解答 【解析】 連接AC 、BD .由於2BE AB =,2BF BC =,於是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 於是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由於3AE AB =,3AH AD =,於是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 於是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那麼491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如圖,在ABC △中,延長AB 至D ,使BD AB =,延長BC 至E ,使12CE BC =,F 是AC 的中點,若ABC △的面積是2,則DEF △的面積是多少?A BCDEF【考點】三角形的鳥頭模型 【難度】3星 【題型】解答 【解析】 ∵在ABC △和CFE △中,ACB ∠與FCE ∠互補,∴224111ABCFCES AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =,所以0.5FCE S =. 同理可得2ADF S =△,3BDE S =△. 所以20.532 3.5DEF ABC CEF DEB ADFS S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如圖,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCBA【考點】三角形的鳥頭模型 【難度】3星 【題型】解答 【解析】 本題題目本身很簡單,但它把本講的兩個重要知識點融合到一起,既可以看作是”當兩個三角形有一個角相等或互補時,這兩個三角形的面積比等於夾這個角的兩邊長度的乘積比”的反復運用,也可以看作是找點,最妙的是其中包含了找點的3種情況.最後求得FGS S △的面積為4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如圖所示,正方形ABCD 邊長為8釐米,E 是AD 的中點,F 是CE 的中點,G是BF 的中點,三角形ABG 的面積是多少平方釐米?ABC DEF GABCDEF G【考點】三角形的鳥頭模型 【難度】4星 【題型】解答【解析】 連接AF 、EG . 因為218164BCF CDE S S ==⨯=△△,根據”當兩個三角形有一個角相等或互補時,這兩個三角形的面積比等於夾這個角的兩邊長度的乘積比”8AEF S =,8EFG S =,再根據”當兩個三角形有一個角相等或互補時,這兩個三角形的面積比等於夾這個角的兩邊長度的乘積比”,得到16BFC S =,32ABFE S =,24ABF S =,所以12ABG S =平方釐米.【答案】12【例 16】 四個面積為1的正六邊形如圖擺放,求陰影三角形的面積.【考點】三角形的鳥頭模型 【難度】4星 【題型】解答【解析】 如圖,將原圖擴展成一個大正三角形DEF ,則AGF ∆與CEH ∆都是正三角形.假設正六邊形的邊長為為a ,則AGF ∆與CEH ∆的邊長都是4a ,所以大正三角形DEF 的邊長為4217⨯-=,那麼它的面積為單位小正三角形面積的49倍.而一個正六邊形是由6個單位小正三角形組成的,所以一個單位小正三角形的面積為16,三角形DEF 的面積為496. 由於4FA a =,3FB a =,所以AFB ∆與三角形DEF 的面積之比為43127749⨯=. 同理可知BDC ∆、AEC ∆與三角形DEF 的面積之比都為1249,所以ABC ∆的面積占三角形DEF 面積的1213134949-⨯=,所以ABC ∆的面積的面積為4913136496⨯=. 【答案】136【鞏固】已知圖中每個正六邊形的面積都是1,則圖中虛線圍成的五邊形ABCDE 的面積是 .BDCEA【考點】三角形的鳥頭模型【難度】4星【題型】解答【解析】從圖中可以看出,虛線AB和虛線CD外的圖形都等於兩個正六邊形的一半,也就是都等於一個正六邊形的面積;虛線BC和虛線DE外的圖形都等於一個正六邊形的一半,那麼它們合起來等於一個正六邊形的面積;虛線AE外的圖形是兩個三角形,從右圖中可以看出,每個三角形都是一個正六邊形面積的16,所以虛線外圖形的面積等於11132363⨯+⨯=,所以五邊形的面積是12103633-=.【答案】263【例 17】僅用下圖這把刻度尺,最少測量次,就能得出三角形ABC和三角形BCD的面積比。
小学奥数:三角形等高模型与鸟头模型(一).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =baS 2S 1DCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.【考点】三角形的等高模型 【难度】1星 【题型】解答 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一:例题精讲4-3-1.三角形等高模型与鸟头模型CD BAABFCABDGC⑵ 如下图,答案不唯一,以下仅供参考:(1)(2)(3)(4)(5)⑶如下图,答案不唯一,以下仅供参考:【答案】⑴答案不唯一:CD BAABF CABDGC⑵ 答案不唯一:(1)(2)(3)(4)(5)⑶答案不唯一:【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上. ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍?DCBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等.于是:三角形ABD 的面积12=⨯高26÷=⨯高 三角形ABC 的面积124=+⨯()高28÷=⨯高 三角形ADC 的面积4=⨯高22÷=⨯高所以,三角形ABC 的面积是三角形ABD 面积的43倍;三角形ABD 的面积是三角形ADC 面积的3倍.【答案】43、3【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是 平方厘米.ED CA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 图中阴影部分的面积等于长方形ABCD 面积的一半,即4326⨯÷=(平方厘米). 【答案】6【巩固】(2009年四中小升初入学测试题)如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 根据面积比例模型,可知图中空白三角形面积等于平行四边形面积的一半,所以阴影部分的面积也等于平行四边形面积的一半,为50225÷=平方厘米.【答案】25【巩固】如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .ACDE F【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 根据面积比例模型可知阴影部分面积等于长方形面积的一半,为120121202⨯⨯=.【答案】120【例 4】 如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.E BAE BA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 本题是等底等高的两个三角形面积相等的应用.连接BH 、CH . ∵AE EB =,∴AEH BEH S S =△△.同理,BFH CFH S S =△△,S =S CGH DGH V V ,∴11562822ABCD S S ==⨯=阴影长方形(平方厘米).【答案】28【巩固】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E GCBBCG E【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 把另外三个三等分点标出之后,正方形的3个边就都被分成了相等的三段.把H 和这些分点以及正方形的顶点相连,把整个正方形分割成了9个形状各不相同的三角形.这9个三角形的底边分别是在正方形的3个边上,它们的长度都是正方形边长的三分之一.阴影部分被分割成了3个三角形,右边三角形的面积和第1第2个三角形相等:中间三角形的面积和第3第4个三角形相等;左边三角形的面积和第5个第6个三角形相等.因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一,因此全部阴影的总面积就等于正方形面积的三分之一.正方形的面积是144,阴影部分的面积就是48. 【答案】48【例 5】 长方形ABCD 的面积为36,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?EEE【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 (法1)特殊点法.由于H 为AD 边上任意一点,找H 的特殊点,把H 点与A 点重合(如左上图),那么阴影部分的面积就是AEF ∆与ADG ∆的面积之和,而这两个三角形的面积分别为长方形ABCD 面积的18和14,所以阴影部分面积为长方形ABCD 面积的113848+=,为33613.58⨯=.(法2)寻找可利用的条件,连接BH 、HC ,如右上图.可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=,即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=;而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影.【答案】13.5【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米. (法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【答案】15【例 6】 如右图,E 在AD 上,AD 垂直BC ,12AD =厘米,3DE =厘米.求三角形ABC 的面积是三角形EBC 面积的几倍?ED CBA【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 因为AD 垂直于BC ,所以当BC 为三角形ABC 和三角形EBC 的底时,AD 是三角形ABC的高,ED 是三角形EBC 的高,于是:三角形ABC 的面积1226BC BC =⨯÷=⨯三角形EBC 的面积32 1.5BC BC =⨯÷=⨯所以三角形ABC 的面积是三角形EBC 的面积的4倍.【答案】4【例 7】 如图,在平行四边形ABCD 中,EF 平行AC ,连结BE 、AE 、CF 、BF 那么与△BEC等积的三角形一共有哪几个三角形?F DECBA【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 △AEC 、△AFC 、△ABF . 【答案】△AEC 、△AFC 、△ABF .【巩固】如图,在△ABC 中,D 是BC 中点,E 是AD 中点,连结BE 、CE ,那么与△ABE 等积的三角形一共有哪几个三角形?ED C BA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 3个,△AEC 、△BED 、△DEC . 【解析】 【答案】3个,△AEC 、△BED 、△DEC .【巩固】如图,在梯形ABCD 中,共有八个三角形,其中面积相等的三角形共有哪几对?ODC B A【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 △ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO . 【答案】△ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO【例 8】 如图,三角形ABC 的面积为1,其中3AE AB =,2BD BC =,三角形BDE 的面积是多少?AB ECD DCEB A【考点】三角形的等高模型 【难度】2星 【题型】解答 【关键词】迎春杯 【解析】 连接CE ,∵3AE AB =,∴2BE AB =,2BCE ACB S S =V V又∵2BD BC =,∴244BDE BCE ABC S S S ===V V V .【答案】4【例 9】 如右图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC ∆的面积是 平方厘米.AA【考点】三角形的等高模型 【难度】2星 【题型】解答 【关键词】2008年,四中考题【解析】 连接CD .根据题意可知,DEF ∆的面积为DAC ∆面积的13,DAC ∆的面积为ABC ∆面积的12,所以DEF ∆的面积为ABC ∆面积的111236⨯=.而DEF ∆的面积为5平方厘米,所以ABC ∆的面积为15306÷=(平方厘米).【答案】30【巩固】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?CB【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 ABD V ,ABC V 等高,所以面积的比为底的比,有12ABD ABC S BD S BC ==V V , 所以ABDS V =111809022ABC S ⨯=⨯=V (平方厘米).同理有190303ABE ABD AE S S AD =⨯=⨯=V V (平方厘米),34AFE ABE FE S S BE =⨯=V V 3022.5⨯= (平方厘米).即三角形AEF 的面积是22.5平方厘米. 【答案】22.5【巩固】如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果24AB =厘米,8BC =厘米,求三角形ZCY 的面积. ABC DZ Y【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 ∵Y 是BD 的中点,Z 是DY 的中点,∴1122ZY DB =⨯⨯,14ZCY DCB S S =V V ,又∵ABCD 是长方形,∴11124442ZCY DCB ABCD S S S ==⨯=V V Y (平方厘米).【答案】24【巩固】如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FED CBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 三角形ADC 的面积是三角形ABC 面积的一半24212÷=, 三角形ADE 又是三角形ADC 面积的一半1226÷=.三角形FED 的面积是三角形ADE 面积的一半,所以三角形FED 的面积623=÷=. 【答案】3【巩固】如图,在三角形ABC 中,8BC =厘米,高是6厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?FE CBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 ∵F 是AC 的中点 ∴2ABC ABF S S =V V 同理2ABF BEF S S =V V∴486246BEF ABC S S =÷=⨯÷÷=V V (平方厘米).【答案】6【例 10】 如图所示,A 、B 、C 都是正方形边的中点,△COD 比△AOB 大15平方厘米。
小学奥数:三角形等高模型与鸟头模型(二).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1baDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADECBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC BA AB CDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D C BAAB CDE 甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD . ∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FEDCBA【考点】三角形的鸟头模型【难度】3星【题型】解答【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC=⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABCS S CE CF CB CA=⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABCS S AD AF AB AC=⨯⨯=⨯⨯=△△设24ABCS=△份,则4BDES=△份,4ADFS=△份,9CEFS=△份,244497DEFS=---=△份,恰好是7平方厘米,所以24ABCS=△平方厘米【答案】24【例 5】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型【难度】3星【题型】解答【关键词】迎春杯,决赛,第一题,9题【解析】如下图,连接AD,BE,CF.有△ABE,△ABC的高相等,面积比为底的比,则有ABEABCSSVV=AEAC,所以ABES V=AEAC×ABCS V=15ABCS V同理有AEFS V=AFAB ABES V,即=AEFS V=15×56ABCS V=16ABCS V.类似的还可以得到CDES V=14×45ABCS V=15ABCS V,BDFS V=16×13ABCS V=18ABCS V.所以有DEFS V=ABCS V-(AEFS V+CDES V+BDFS V)=(1-16-15-18)ABCS V=61120ABCS V.即DEF ABC 三角形的面积三角形的面积为61120.【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米 【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】(法1)本题是性质的反复使用.连接AE、CD.∵11ABCDBCSS=VV,1ABCS=V,∴S1DBC=V.同理可得其它,最后三角形DEF的面积18=.(法2)用共角定理∵在ABCV和CFEV中,ACB∠与FCE∠互补,∴111428ABCFCES AC BCS FC CE⋅⨯===⋅⨯VV.又1ABCS=V,所以8FCES=V.同理可得6ADFS=V,3BDES=V.所以186318DEF ABC FCE ADF BDES S S S S=+++=+++=V V V V V.【答案】18【例 9】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】方法一:如下图,连接BD,ED,BG,有V EAD、V ADB同高,所以面积比为底的比,有2EAD ABD ABDEAS S SAB==V V V.同理36EAH EAD EAD ABDAHS S S SAD===V V V V.类似的,还可得V6FCG BCDS S=V V,有()66EAH FCG ABD BCD ABCDS S S S S+=+=V V V V=30平方厘米.连接AC,AF,HC,还可得6EFB ABCS S=V V,6DHG ACDS S=V V,有()66EFB DHG ABC ACD ABCDS S S S S+=+=V V V V=30平方厘米.有四边形EFGH的面积为V EAH,V FCG,V EFB,V DHG,ABCD的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD,有V EAH 、△ABD中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAH S V =6ABD S V .类似的,还可得FCG S V =6BCD S V ,有EAH S V +FCG S V =6(ABD S V +BCD S V )=6ABCD S=30平方厘米.连接AC ,还可得EFB S V =6ABC S V ,DHG S V =6ACD S V ,有EFB S V +DHG S V =6(ABC S V +ACD S V )=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米. 【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】如图,将原图扩展成一个大正三角形DEF,则AGF∆与CEH∆都是正三角形.假设正六边形的边长为为a,则AGF∆与CEH∆的边长都是4a,所以大正三角形DEF的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF的面积为496.由于4FA a=,3FB a=,所以AFB∆与三角形DEF的面积之比为4312 7749⨯=.同理可知BDC∆、AEC∆与三角形DEF的面积之比都为1249,所以ABC∆的面积占三角形DEF面积的1213134949-⨯=,所以ABC∆的面积的面积为4913136496⨯=.【答案】13 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】2 6 3【例 17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD 的面积比。
人教版 八年级数学 上册第11章 三角形 综合巩固训练(含答案)

人教版八年级数学第11章三角形综合巩固训练一、选择题(本大题共10道小题)1. 如图,在△ABC中,AC边上的高是()图A.线段DA B.线段BAC.线段BC D.线段BD2. 在△ABC中,∠A=95°,∠B=40°,则∠C的度数是()A. 35°B. 40°C. 45°D. 50°3. 如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为()A. 40°B. 50°C. 60°D. 70°4. 下列各组数中,不可能成为一个三角形三边长的是()A. 2,3,4B. 5,7,7C. 5,6,12D. 6,8,105. 在△ABC中,∠A,∠C与∠B处的外角的度数如图所示,则x的值是()A.80 B.70 C.65 D.606. 若一个正多边形的每一个外角都等于40°,则它是()A.正九边形B.正十边形C.正十一边形D.正十二边形7. 把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是()A.六边形B.五边形C.四边形D.三角形8. 若在n边形内部任意取一点P,将点P与各顶点连接起来,可以把n边形分成n个三角形,利用这个事实,可以探索到n边形的内角和为()A.180°×n B.180°×n-180°C.180°×n+180°D.180°×n-360°9. (2019•大庆)如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM 的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是A.15°B.30°C.45°D.60°10. 如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为()A.70°B.108°C.110°D.125°二、填空题(本大题共8道小题)11. 如图,已知AB,CD相交于点O,且∠A=38°,∠B=58°,∠C=44°,则∠D =________°.12. 如图所示,x的值为________.13. 如图,若A表示四边形,B表示正多边形,则阴影部分表示________.14. 若一个等腰三角形两边的长分别为2 cm,5 cm,则它的周长为________cm.15. 如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.16. 如图,在△ABC中,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若AC=4,AD=3,BE=2,则BC=________.17. 如图,在四边形ABCD中,AB∥CD,将四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B=________°.18. 如图,在△ABC中,点D在BC的延长线上,∠A=m°,∠ABC和∠ACD 的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2019BC和∠A2019CD的平分线交于点A2020,则∠A2020=________°.三、解答题(本大题共4道小题)19. 某单位修建正多边形花台,已知正多边形花台的一个外角的度数比一个内角度数的多12°.(1)求出这个正多边形的一个内角的度数;(2)求这个正多边形的边数.20. 如图,AE,BO,CO分别平分∠BAC,∠ABC,∠ACB,OD⊥BC于点D. 求证:∠1=∠2.21. 探究与证明如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.(1)猜测∠1与∠2的关系,并说明理由;(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?22. 已知:多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.(1)若多边形为四边形ABCD.①如图 (a ),∠A =50°,∠C =100°,BM 与DN 交于点P ,求∠BPD 的度数; ②如图(b ),猜测当∠A 和∠C 满足什么数量关系时,BM ∥DN ,并证明你的猜想. (2)如图(c ),若多边形是五边形ABCDG ,已知∠A =140°,∠G =100°,∠BCD =120°,BM 与DN 交于点P ,求∠BPD 的度数.人教版 八年级数学 第11章 三角形 综合巩固训练-答案一、选择题(本大题共10道小题)1. 【答案】D2. 【答案】C【解析】根据三角形内角和为180°,∠C =180°-∠A -∠B =45°.3. 【答案】B【解析】∵AB ∥CD ,∴∠A =∠ACD =40°,∵∠ACB =90°,∴∠B =90°-∠A =90°-40°=50°.4. 【答案】C 【解析】若三条线段的长满足三角形的三边,则这三条线段长满足最小的两边之和大于地三边,由题意,A ,B ,D 都能构成三角形,C 中5+6=11<12,不能构成三角形.5. 【答案】B6. 【答案】A[解析] 由于正多边形的外角和为360°,且每一个外角都相等,因此边数=360°40°=9.7. 【答案】A[解析] 剪去一个角的方法有三种:经过两个顶点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条.所以一个n 边形剪去一个角后,剩下的形状可能是n 边形或(n +1)边形或(n -1)边形.8. 【答案】D9. 【答案】B【解析】∵BE是∠ABC的平分线,∴∠EBM=12∠ABC,∵CE是外角∠ACM的平分线,∴∠ECM=12∠ACM,则∠BEC=∠ECM–∠EBM=12×(∠ACM–∠ABC)=12∠A=30°,故选B.10. 【答案】C[解析] ∵在△ABC中,∠ACB=70°,∠1=∠2,∴∠2+∠BCP=∠1+∠BCP=∠ACB=70°.∴∠BPC=180°-∠2-∠BCP=180°-70°=110°.二、填空题(本大题共8道小题)11. 【答案】64[解析] 由三角形内角和定理可知∠A+∠D+∠AOD=180°,∠B +∠C+∠BOC=180°.∵∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.∴∠D=64°.12. 【答案】55°[解析] 由多边形的外角和等于360°,得360°-105°-60°+x+2x=360°,解得x=55°.13. 【答案】正方形14. 【答案】12[解析] 分两种情况讨论:①当腰长为5 cm时,三边长分别为5 cm,5 cm,2 cm,满足三角形三边关系,周长=5+5+2=12(cm).②当腰长为2 cm时,三边长分别为5 cm,2 cm,2 cm.∵2+2=4<5,∴5 cm,2 cm,2 cm不满足三角形的三边关系.综上,它的周长为12 cm.15. 【答案】三角形三个内角的和等于180°16. 【答案】83 [解析] ∵S △ABC =12AC·BE =12BC·AD ,∴BC =AC·BE AD =4×23=83.17. 【答案】114[解析] 因为AB ∥CD ,所以∠BAB′=∠1=44°.由折叠的性质知∠BAC =12∠BAB′=22°.在△ABC 中,∠B =180°-(∠BAC +∠2)=114°.18. 【答案】(m22020)三、解答题(本大题共4道小题)19. 【答案】解:(1)设这个多边形的一个内角的度数是x °,则与其相邻的外角度数是x °+12°. 由题意,得x+x+12=180,解得x=140. 即这个正多边形的一个内角的度数是140°.(2)这个正多边形的每一个外角的度数为180°-140°=40°,所以这个正多边形的边数是=9.20. 【答案】证明:∵AE ,BO ,CO 分别平分∠BAC ,∠ABC ,∠ACB , ∴∠ABO =12∠ABC ,∠BAE =12∠BAC ,∠OCD =12∠ACB. ∵∠1=∠ABO +∠BAE ,∴∠1=12∠ABC +12∠BAC =12(180°-∠ACB)=90°-12∠ACB. 又∵∠2=90°-∠OCD =90°-12∠ACB ,∴∠1=∠2.21. 【答案】解:(1)∠1=∠2.理由如下: ∵AD ⊥BC ,CE ⊥AB ,∴△ABD 和△BCE 都是直角三角形.∴∠1+∠B =90°,∠2+∠B =90°. ∴∠1=∠2.(2)(1)中的结论仍然成立.理由如下: ∵AD ⊥BC ,CE ⊥AB , ∴∠D =∠E =90°.∴∠2+∠ABD =90°,∠1+∠CBE =90°. 又∵∠ABD =∠CBE , ∴∠1=∠2.22. 【答案】解:(1)①∵∠A =50°,∠C =100°, ∴在四边形ABCD 中,∠ABC +∠ADC =360°-∠A -∠C =210°. ∴∠CBE +∠CDF =150°.∵外角∠CBE 和∠CDF 的平分线分别为BM ,DN , ∴∠PBC +∠PDC =12∠CBE +12∠CDF =75°. ∴∠BPD =360°-50°-210°-75°=25°. ②当∠A =∠C 时,BM ∥DN. 证明:如图(a),连接BD.∵BM ∥DN ,∴∠BDN +∠DBM =180°.∴∠FDN +∠ADB +∠ABD +∠MBE =360°-180°=180°, 即12(∠FDC +∠CBE)+(∠ADB +∠ABD)=180°. ∴12(360°-∠ADC -∠CBA)+(180°-∠A)=180°. ∴12(360°-360°+∠A +∠C)+(180°-∠A)=180°. ∴∠A =∠C.(2)∵∠A =140°,∠G =100°,∠BCD =120°,∠A+∠ABC+∠BCD+∠CDG+∠G=540°,∴∠ABC+∠CDG=180°.∴∠CBE+∠CDF=180°.∵BP平分∠CBE,DP平分∠CDF,∴∠CBP+∠CDP=12(∠CBE+∠CDF)=90°.如图(b),延长DC交BP于点Q.∵∠BCD=∠CBP+∠CQB,∠CQB=∠QDP+∠BPD,∴∠BCD=∠CBP+∠QDP+∠BPD.∴∠BPD=120°-90°=30°.。
等高模型

例题讲解
练一练6:如图,三角形ABC中,D、E分别是BE、BC的中点 ,F是AC的三等分点 ,已知三角形 DEG的面积比三角形AGF的面积小1,求三角形ABC的面积.
例题讲解
例7:如图,正方形ABCD中,E是AB的四等分点 ,F是BD的五等分点 ,已知正方形ABCD的面积 是10,求三角形CEF的面积.
巩固提升
作业3:如图,等腰三角形ABC被分成面积相等的5个小三角形,已知AB=AC=15厘米,求AD、AG 的长.
巩固提升
作业4:如图,正三角形ABC被分成面积相等的15个小三角形,已知正三角形ABC的边长是112, 求AD+BE+CF的长.
巩固提升
作业5:如图,正方形ABCD被分成面积相等的8个三角形,已知BI=5厘米,求正方形ABCD被的面 积.
例题讲解
练一练3:如图,三角形ABC中,D、E、F是各边的三等分点,已知三角形ABC的面积是1平方厘 米,求三角形ABC的面积.
例题讲解
例4:如图,三角形ABC中,BC=3BD,AC=3CE,AF=FG,DF=FH=HE,已知三角形ABC的面积 是10,求三角形GHE的面积.
例题讲解
练一练4:如图,三角形ABC中,D、E、F、G是BC边的五等分点,H、I、J是AB边的四等分点, 已知三角形EFI的面积是1,求三角形ABC的面积.
SABD:SACD BD:CD SABD:SABC BD:BC SACD:SABC CD:BC
例题讲解
例题讲解
例1:如图,三角形ABC中,AE:CE=2:3,BD:CD=3:4,已知三角形ADE的面积是12平方厘米, 求三角形ABC的面积.
分析:图中涉及到多组等高模型,根据已知C被分成7块面积相等的小三角形,其中AC=90厘米,BC=84厘米,求线段 EF和GH的长度.
小学奥数:三角形等高模型与鸟头模型(一).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =baS 2S 1DCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.【考点】三角形的等高模型 【难度】1星 【题型】解答 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一:例题精讲4-3-1.三角形等高模型与鸟头模型CD BAABFCABDGC⑵ 如下图,答案不唯一,以下仅供参考:(1)(2)(3)(4)(5)⑶如下图,答案不唯一,以下仅供参考:【答案】⑴答案不唯一:CD BAABF CABDGC⑵ 答案不唯一:(1)(2)(3)(4)(5)⑶答案不唯一:【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上. ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍?DCBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等.于是:三角形ABD 的面积12=⨯高26÷=⨯高 三角形ABC 的面积124=+⨯()高28÷=⨯高 三角形ADC 的面积4=⨯高22÷=⨯高所以,三角形ABC 的面积是三角形ABD 面积的43倍;三角形ABD 的面积是三角形ADC 面积的3倍.【答案】43、3【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是 平方厘米.ED CA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 图中阴影部分的面积等于长方形ABCD 面积的一半,即4326⨯÷=(平方厘米). 【答案】6【巩固】(2009年四中小升初入学测试题)如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 根据面积比例模型,可知图中空白三角形面积等于平行四边形面积的一半,所以阴影部分的面积也等于平行四边形面积的一半,为50225÷=平方厘米.【答案】25【巩固】如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .ACDE F【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 根据面积比例模型可知阴影部分面积等于长方形面积的一半,为120121202⨯⨯=.【答案】120【例 4】 如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.E BAE BA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 本题是等底等高的两个三角形面积相等的应用.连接BH 、CH . ∵AE EB =,∴AEH BEH S S =△△.同理,BFH CFH S S =△△,S =S CGH DGH V V ,∴11562822ABCD S S ==⨯=阴影长方形(平方厘米).【答案】28【巩固】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E GCBBCG E【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 把另外三个三等分点标出之后,正方形的3个边就都被分成了相等的三段.把H 和这些分点以及正方形的顶点相连,把整个正方形分割成了9个形状各不相同的三角形.这9个三角形的底边分别是在正方形的3个边上,它们的长度都是正方形边长的三分之一.阴影部分被分割成了3个三角形,右边三角形的面积和第1第2个三角形相等:中间三角形的面积和第3第4个三角形相等;左边三角形的面积和第5个第6个三角形相等.因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一,因此全部阴影的总面积就等于正方形面积的三分之一.正方形的面积是144,阴影部分的面积就是48. 【答案】48【例 5】 长方形ABCD 的面积为36,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?EEE【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 (法1)特殊点法.由于H 为AD 边上任意一点,找H 的特殊点,把H 点与A 点重合(如左上图),那么阴影部分的面积就是AEF ∆与ADG ∆的面积之和,而这两个三角形的面积分别为长方形ABCD 面积的18和14,所以阴影部分面积为长方形ABCD 面积的113848+=,为33613.58⨯=.(法2)寻找可利用的条件,连接BH 、HC ,如右上图.可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=,即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=;而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影.【答案】13.5【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米. (法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【答案】15【例 6】 如右图,E 在AD 上,AD 垂直BC ,12AD =厘米,3DE =厘米.求三角形ABC 的面积是三角形EBC 面积的几倍?ED CBA【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 因为AD 垂直于BC ,所以当BC 为三角形ABC 和三角形EBC 的底时,AD 是三角形ABC的高,ED 是三角形EBC 的高,于是:三角形ABC 的面积1226BC BC =⨯÷=⨯三角形EBC 的面积32 1.5BC BC =⨯÷=⨯所以三角形ABC 的面积是三角形EBC 的面积的4倍.【答案】4【例 7】 如图,在平行四边形ABCD 中,EF 平行AC ,连结BE 、AE 、CF 、BF 那么与△BEC等积的三角形一共有哪几个三角形?F DECBA【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 △AEC 、△AFC 、△ABF . 【答案】△AEC 、△AFC 、△ABF .【巩固】如图,在△ABC 中,D 是BC 中点,E 是AD 中点,连结BE 、CE ,那么与△ABE 等积的三角形一共有哪几个三角形?ED C BA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 3个,△AEC 、△BED 、△DEC . 【解析】 【答案】3个,△AEC 、△BED 、△DEC .【巩固】如图,在梯形ABCD 中,共有八个三角形,其中面积相等的三角形共有哪几对?ODC B A【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 △ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO . 【答案】△ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO【例 8】 如图,三角形ABC 的面积为1,其中3AE AB =,2BD BC =,三角形BDE 的面积是多少?AB ECD DCEB A【考点】三角形的等高模型 【难度】2星 【题型】解答 【关键词】迎春杯 【解析】 连接CE ,∵3AE AB =,∴2BE AB =,2BCE ACB S S =V V又∵2BD BC =,∴244BDE BCE ABC S S S ===V V V .【答案】4【例 9】 如右图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC ∆的面积是 平方厘米.AA【考点】三角形的等高模型 【难度】2星 【题型】解答 【关键词】2008年,四中考题【解析】 连接CD .根据题意可知,DEF ∆的面积为DAC ∆面积的13,DAC ∆的面积为ABC ∆面积的12,所以DEF ∆的面积为ABC ∆面积的111236⨯=.而DEF ∆的面积为5平方厘米,所以ABC ∆的面积为15306÷=(平方厘米).【答案】30【巩固】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?CB【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 ABD V ,ABC V 等高,所以面积的比为底的比,有12ABD ABC S BD S BC ==V V , 所以ABDS V =111809022ABC S ⨯=⨯=V (平方厘米).同理有190303ABE ABD AE S S AD =⨯=⨯=V V (平方厘米),34AFE ABE FE S S BE =⨯=V V 3022.5⨯= (平方厘米).即三角形AEF 的面积是22.5平方厘米. 【答案】22.5【巩固】如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果24AB =厘米,8BC =厘米,求三角形ZCY 的面积. ABC DZ Y【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 ∵Y 是BD 的中点,Z 是DY 的中点,∴1122ZY DB =⨯⨯,14ZCY DCB S S =V V ,又∵ABCD 是长方形,∴11124442ZCY DCB ABCD S S S ==⨯=V V Y (平方厘米).【答案】24【巩固】如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FED CBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 三角形ADC 的面积是三角形ABC 面积的一半24212÷=, 三角形ADE 又是三角形ADC 面积的一半1226÷=.三角形FED 的面积是三角形ADE 面积的一半,所以三角形FED 的面积623=÷=. 【答案】3【巩固】如图,在三角形ABC 中,8BC =厘米,高是6厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?FE CBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 ∵F 是AC 的中点 ∴2ABC ABF S S =V V 同理2ABF BEF S S =V V∴486246BEF ABC S S =÷=⨯÷÷=V V (平方厘米).【答案】6【例 10】 如图所示,A 、B 、C 都是正方形边的中点,△COD 比△AOB 大15平方厘米。
小学奥数教程:三角形等高模型与鸟头模型 _全国通用(含答案)

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1bDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBADE CBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.例题精讲4-3-2.三角形等高模型与鸟头模型EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC B A AB C DE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D CBAA BCDE甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.ED CBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【答案】24【例 5】 如图16-4,已知.AE=15AC ,CD=14BC ,BF=16AB ,那么DEF ABC 三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】迎春杯,决赛,第一题,9题 【解析】 如下图,连接AD ,BE ,CF.有△ABE ,△ABC 的高相等,面积比为底的比,则有ABE ABCSS=AEAC,所以ABE S =AEAC×ABC S =15ABC S同理有AEF S=AFABABE S ,即=AEF S=15×56ABC S =16ABC S . 类似的还可以得到CDE S =14×45ABC S =15ABC S ,BDF S =16×13ABC S =18ABC S .所以有DEF S =ABC S -(AEF S +CDE S +BDF S )=(1-16-15-18)ABC S =61120ABC S . 即DEF ABC 三角形的面积三角形的面积为61120. 【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.EDC【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得, ():():()12:(33)2:9CEF ABCS S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 (法1)本题是性质的反复使用.连接AE 、CD . ∵11ABC DBC S S =,1ABC S =, ∴S 1DBC =.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯. 又1ABCS=,所以8FCES=.同理可得6ADFS =,3BDES =.所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=.【答案】18【例 9】 如图,把四边形ABCD 的各边都延长2倍,得到一个新四边形EFGH 如果ABCD 的面积是5平方厘米,则EFGH 的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】4星【题型】解答 【解析】 方法一:如下图,连接BD ,ED ,BG ,有EAD 、ADB 同高,所以面积比为底的比,有2EADABDABD EASS SAB==.同理36EAHEAD EAD ABD AHSS S S AD===. 类似的,还可得6FCG BCD S S =,有()66EAH FCG ABDBCDABCD S SSSS +=+==30平方厘米.连接AC ,AF ,HC ,还可得6EFBABCSS=,6DHGACDSS=,有()66EFBDHGABCACDABCD SSSSS +=+==30平方厘米.有四边形EFGH 的面积为EAH,FCG ,EFB,DHG ,ABCD 的面积和,即为30+30+5=65(平方厘米.) 方法二:连接BD ,有EAH 、△ABD 中∠EAD+∠BAD=180° 又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAHS=6ABDS.类似的,还可得FCGS =6BCDS,有EAHS+FCG S=6(ABDS +BCDS)=6ABCD S =30平方厘米.连接AC ,还可得EFBS=6ABC S,DHG S=6ACDS,有EFBS+DHG S=6(ABC S +ACDS)=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CDEF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABCS=,所以0.5FCES=.同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABC DEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS=,32ABFE S =,24ABF S =,所以12ABG S =平方厘米.【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【答案】136【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .B DCEA【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE 外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】263【例 17】 仅用下图这把刻度尺,最少测量 次,就能得出三角形ABC 和三角形BCD 的面积比。
等高三角形练习题及答案

等高三角形练习题及答案等高三角形是初中数学中常见的几何图形,它有着独特的性质和特点。
本文将介绍一些关于等高三角形的练习题,并提供详细的答案解析,以帮助读者加深对等高三角形的理解和掌握。
练习题1. 在等高三角形ABC中,若AB = 6 cm,BC = 8 cm,AC = 10 cm,求角A的大小。
2. 在等高三角形DEF中,已知∠F = 40°,DF = 5 cm。
求EF的长度。
3. 在等高三角形PQR中,已知PR = 12 cm,QR = 9 cm。
求∠Q的大小。
4. 在等高三角形XYZ中,如果YZ = 5 cm,∠X = 60°,则XY的长度是多少?5. 在等高三角形LMN中,已知∠M = 90°,MN = 12 cm。
求LN的长度。
答案与解析1. 根据等高三角形的性质,等腰三角形的底角相等,即∠A = ∠C。
由此可知,角A的大小为60°。
2. 在等高三角形DEF中,由于∠D = ∠F,根据等高三角形的性质可知,∠E = 180° - ∠D -∠F = 180° - 40° - 40° = 100°。
由正弦定理可得:EF/DF = sin∠E/sin∠F。
代入已知条件可得:EF/5 = sin100°/sin40°。
解得EF ≈ 7.13 cm。
3. 在等高三角形PQR中,由于∠P = ∠R,根据等高三角形的性质可知,∠Q = 180° - ∠P -∠R = 180° - ∠P - ∠P = 180° - 2∠P。
由正弦定理可得:PR/sin∠Q = QR/sin∠P。
代入已知条件可得:12/sin∠Q = 9/sin∠P。
由此可得sin∠Q/sin∠P = 12/9 = 4/3。
根据正弦函数的性质,当正弦值相等时,角度相等。
因此,sin∠Q = 4/3,sin∠P = 3/4。
小学奥数 三角形等高模型与鸟头模型(二) 精选练习例题 含答案解析(附知识点拨及考点)

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1bDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADE CBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBA ABCDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S =又∵5AB AD = ∴515ADEABEABCSSS=÷=÷,∴1515ABCADESS==.【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD .∵3BE =,6AE = ∴3AB BE =,3ABDBDES S=又∵4BD DC ==,∴2ABCABDSS=,∴6ABCBDESS=,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【答案】24【例 5】 如图16-4,已知.AE=15AC ,CD=14BC ,BF=16AB ,那么DEF ABC 三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】迎春杯,决赛,第一题,9题 【解析】 如下图,连接AD ,BE ,CF.有△ABE ,△ABC 的高相等,面积比为底的比,则有ABE ABCSS=AEAC,所以ABE S =AEAC×ABC S =15ABC S同理有AEF S=AFABABE S ,即=AEF S=15×56ABC S =16ABC S . 类似的还可以得到CDE S =14×45ABC S =15ABC S ,BDF S =16×13ABC S =18ABC S .所以有DEF S =ABC S -(AEF S +CDE S +BDF S )=(1-16-15-18)ABC S =61120ABC S . 即DEF ABC 三角形的面积三角形的面积为61120. 【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC E B A【考点】三角形的鸟头模型 【难度】2星 【题型】解答【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△ 故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 (法1)本题是性质的反复使用.连接AE 、CD .∵11ABC DBC S S =,1ABC S =, ∴S1DBC=.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯.又1ABCS=,所以8FCES=.同理可得6ADFS =,3BDES=.所以186318DEFABCFCEADFBDESS SS S=+++=+++=.【答案】18【例 9】 如图,把四边形ABCD 的各边都延长2倍,得到一个新四边形EFGH 如果ABCD 的面积是5平方厘米,则EFGH 的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 方法一:如下图,连接BD ,ED ,BG ,有EAD 、ADB 同高,所以面积比为底的比,有2EADABDABD EASS SAB==.同理36EAHEAD EAD ABD AHSS S S AD===. 类似的,还可得6FCG BCD S S =,有()66EAH FCG ABDBCDABCD S SSSS +=+==30平方厘米.连接AC ,AF ,HC ,还可得6EFBABCS S=,6DHGACDSS=,有()66EFBDHGABCACDABCD SSSSS +=+==30平方厘米.有四边形EFGH 的面积为EAH,FCG ,EFB,DHG ,ABCD 的面积和,即为30+30+5=65(平方厘米.) 方法二:连接BD ,有EAH 、△ABD 中∠EAD+∠BAD=180° 又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAHS=6ABDS.类似的,还可得FCGS =6BCDS,有EAHS+FCG S=6(ABDS +BCDS)=6ABCD S =30平方厘米.连接AC ,还可得EFBS=6ABC S,DHG S=6ACDS,有EFBS+DHG S=6(ABC S +ACDS)=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米.【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CDEF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABCS=,所以0.5FCES=.同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCD EF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS =,32ABFE S =,24ABFS=,所以12ABGS=平方厘米.【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型 【难度】4星 【题型】解答【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【答案】136【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】263【例17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD的面积比。
三角形等高模型训练(二)例题+巩固带答案
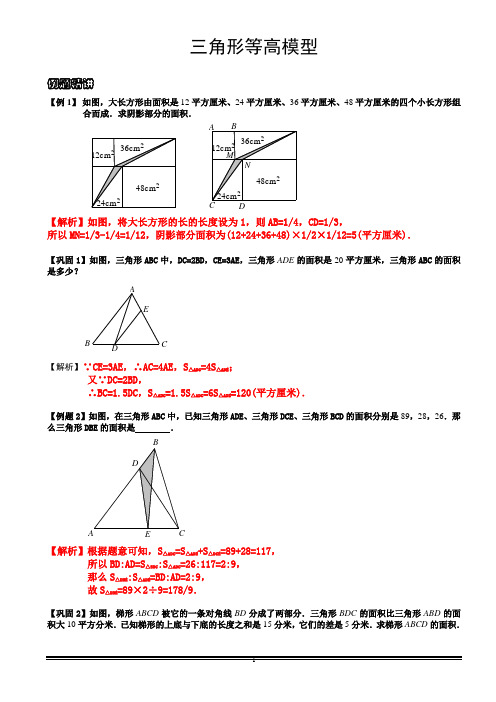
三角形等高模型例题精讲【例 1】 如图,大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成.求阴影部分的面积.【解析】如图,将大长方形的长的长度设为1,则AB=1/4,CD=1/3,所以MN=1/3-1/4=1/12,阴影部分面积为(12+24+36+48)×1/2×1/12=5(平方厘米).【巩固1】如图,三角形ABC 中,DC=2BD ,CE=3AE ,三角形ADE 的面积是20平方厘米,三角形ABC 的面积是多少?EDCBA【解析】 ∵CE=3AE ,∴AC=4AE ,S △ADC =4S △ADE ;又∵DC=2BD ,∴BC=1.5DC ,S △ABC =1.5S △ADC =6S △ADE =120(平方厘米).【例题2】如图,在三角形ABC 中,已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89,28,26.那么三角形DBE 的面积是 .【解析】根据题意可知,S △ADC =S △ADE +S △DCE =89+28=117,所以BD:AD=S △SDC :S △ADC =26:117=2:9, 那么S △DBE :S △ADE =BD:AD=2:9, 故S △DBE =89×2÷9=178/9.【巩固2】如图,梯形ABCD 被它的一条对角线BD 分成了两部分.三角形BDC 的面积比三角形ABD 的面积大10平方分米.已知梯形的上底与下底的长度之和是15分米,它们的差是5分米.求梯形ABCD 的面积.DCBA【解析】如右图,作AB 的平行线DE .三角形BDE 的面积与三角形ABD 的面积相等,三角形DEC 的面积就是三角形BDC 与三角形ABD 的面积差(10平方分米).从而,可求出梯形高(三角形DEC 的高)是:2×10÷5=4(分米),梯形面积是:15×4÷2=30(平方分米).【例题3】图中三角形AOB 的面积为15平方厘米,线段OB 的长度为OD 的3倍,求梯形ABCD 的面积.OCBDA【解析】在△ABD 中,因为S △AOB=15平方厘米,且OB=3OD , 所以有S △AOD =S △AOB ÷3=5平方厘米.因为△ABD 和△ACD 等底等高,所以有S △ABD =S △ACD .从而S △OCD =15平方厘米,在△BCD 中,S △BOC =3S △OCD =45平方厘米, 所以梯形面积:15+5+15+45=80平方厘米.【巩固3】如图,把四边形ABCD 改成一个等积的三角形.DBAA′ABCD【解析】本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右上图把顶点A 移到CB 的延长线上的A′处,△A′BD 与 △ABD 面积相等,从而△A′DC 面积与原四边形ABCD 面积也相等.这样就把四边形ABCD 等积地改成了三角形△A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB 平行的直线与CB 的延长线交于A′点. 具体做法:⑴ 连接BD ;⑵ 过A 作BD 的平行线,与CB 的延长线交于A′. ⑶ 连接A′D,则△A′CD 与四边形ABCD 等积.【例题4】一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的15%,黄色三角形面积是21平方厘米.问:长方形的面积是多少平方厘米?红绿黄红【解析】黄色三角形与绿色三角形的底相等都等于长方形的长,高相加为长方形的宽,所以黄色三角形与绿色三角形的面积和为长方形面积的59%,而绿色三角形面积占长方形面积的15%,所以黄色三角形面积占长方形面积的50%-15%=35%.已知黄色三角形面积是21平方厘米,所以长方形面积等于21÷35%=60(平方厘米).【巩固4】O 是长方形ABCD 内一点,已知三角形OBC 的面积是5平方厘米,三角形OAB 的面积是2平方厘米,求三角形0BD 的面积是多少?【解析】由于ABCD 是长方形,所以S △AOD +S △BOC =长方形面积的一半,而S △ABD =长方形面积的一半,所以S △AOD +S △BOC =S △ABD ,则S △BOC =S △OAB +S △OBD ,所以S △OBD - S △OAB =5-2=3(平方厘米).【例题5】如右图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若三角形PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?CHCH【解析】根据差不变原理,要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差,相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差. 如右上图,连接CP 、AP .由于S △BCP +S △ADP =S △ABP +S △BDP +S △ADP =平行四边形ABCD 面积的一半 ,所以S △BCP - S △ABP =S △BDP .而S △BCP =平行四边形BCFE 面积的一半 S △ABP =平行四边形ABHG 的一半,所以S BCFE -S ABHG =2(S △BCP -S △ABP )=2S △BDP =16(平方分米)【巩固5(1)】如右图,正方形ABCD 的面积是20,正三角形三角形BPC 的面积是15,求阴影三角形BPD 的面积.BAAB【解析】连接AC 交BD 于O 点,并连接PO .如下图所示,可得PO//DC ,所以△DPO 与△CPO 面积相等(同底等高),所以有:S △BPO +S △CPO =S △BPO +S △PDO =S △BPD ,因为S △BOC =正方形ABCD 面积÷4=5, 所以S △BPD =15-5=10.【巩固5(2)】如右图,正方形ABCD 的面积是12,正三角形BOC 的面积是5,求阴影三角形BPD 的面积.BAAB D【解析】连接AC 交BD 于O 点,并连接PO .如右上图所示,可得PO//DC ,所以△DPO 与△CPO 面积相等(同底等高),所以有:S △BPO +S △CPO =S △BPO +S △PDO =S △BPD因为S △BPC =正方形ABCD 面积÷4=3,所以S △BPD =5-3=2.【例题6】在长方形ABCD 内部有一点O ,形成等腰三角形AOB 的面积为16,等腰三角形DOC 的面积占长方形面积的18%,那么阴影三角形AOC 的面积是多少?D【解析】先算出长方形面积,再用其一半减去△DOC 的面积(长方形面积的18%),再减去△AOD 的面积,即可求出△AOC 的面积.根据模型可知S △COD +S △AOB =长方形ABCD 面积的一半, 所以S ABCD =16÷(1/2-18%)=50,又△AOD 与△BOC 的面积相等,它们的面积和等于长方形面积的一半, 所以△AOD 的面积等于长方形面积的1/4,所以S △AOC =S △ACD -S △AOD -S △COD =1/2S ABCD =25%S ABCD -18%ABCD =25-12.5-9=3.5【巩固6】如右图所示,在梯形ABCD 中,E 、F 分别是其两腰AB 、CD 的中点,G 是EF 上的任意一点,已知三角形ADG 的面积为15平方厘米,而三角形BCG 的面积恰好是梯形ABCD 面积的7/20,则梯形ABCD 的面积是 平方厘米。
小学奥数:三角形等高模型与鸟头模型(一).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =baS 2S 1DCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.【考点】三角形的等高模型 【难度】1星 【题型】解答 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一:例题精讲4-3-1.三角形等高模型与鸟头模型CD BAABFCABDGC⑵ 如下图,答案不唯一,以下仅供参考:(1)(2)(3)(4)(5)⑶如下图,答案不唯一,以下仅供参考:【答案】⑴答案不唯一:CD BAABF CABDGC⑵ 答案不唯一:(1)(2)(3)(4)(5)⑶答案不唯一:【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上. ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍?DCBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等.于是:三角形ABD 的面积12=⨯高26÷=⨯高 三角形ABC 的面积124=+⨯()高28÷=⨯高 三角形ADC 的面积4=⨯高22÷=⨯高所以,三角形ABC 的面积是三角形ABD 面积的43倍;三角形ABD 的面积是三角形ADC 面积的3倍.【答案】43、3【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是 平方厘米.ED CA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 图中阴影部分的面积等于长方形ABCD 面积的一半,即4326⨯÷=(平方厘米). 【答案】6【巩固】(2009年四中小升初入学测试题)如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 根据面积比例模型,可知图中空白三角形面积等于平行四边形面积的一半,所以阴影部分的面积也等于平行四边形面积的一半,为50225÷=平方厘米.【答案】25【巩固】如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .ACDE F【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 根据面积比例模型可知阴影部分面积等于长方形面积的一半,为120121202⨯⨯=.【答案】120【例 4】 如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.E BAE BA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 本题是等底等高的两个三角形面积相等的应用.连接BH 、CH . ∵AE EB =,∴AEH BEH S S =△△.同理,BFH CFH S S =△△,S =S CGH DGH V V ,∴11562822ABCD S S ==⨯=阴影长方形(平方厘米).【答案】28【巩固】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E GCBBCG E【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 把另外三个三等分点标出之后,正方形的3个边就都被分成了相等的三段.把H 和这些分点以及正方形的顶点相连,把整个正方形分割成了9个形状各不相同的三角形.这9个三角形的底边分别是在正方形的3个边上,它们的长度都是正方形边长的三分之一.阴影部分被分割成了3个三角形,右边三角形的面积和第1第2个三角形相等:中间三角形的面积和第3第4个三角形相等;左边三角形的面积和第5个第6个三角形相等.因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一,因此全部阴影的总面积就等于正方形面积的三分之一.正方形的面积是144,阴影部分的面积就是48. 【答案】48【例 5】 长方形ABCD 的面积为36,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?EEE【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 (法1)特殊点法.由于H 为AD 边上任意一点,找H 的特殊点,把H 点与A 点重合(如左上图),那么阴影部分的面积就是AEF ∆与ADG ∆的面积之和,而这两个三角形的面积分别为长方形ABCD 面积的18和14,所以阴影部分面积为长方形ABCD 面积的113848+=,为33613.58⨯=.(法2)寻找可利用的条件,连接BH 、HC ,如右上图.可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=,即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=;而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影.【答案】13.5【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米. (法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【答案】15【例 6】 如右图,E 在AD 上,AD 垂直BC ,12AD =厘米,3DE =厘米.求三角形ABC 的面积是三角形EBC 面积的几倍?ED CBA【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 因为AD 垂直于BC ,所以当BC 为三角形ABC 和三角形EBC 的底时,AD 是三角形ABC的高,ED 是三角形EBC 的高,于是:三角形ABC 的面积1226BC BC =⨯÷=⨯三角形EBC 的面积32 1.5BC BC =⨯÷=⨯所以三角形ABC 的面积是三角形EBC 的面积的4倍.【答案】4【例 7】 如图,在平行四边形ABCD 中,EF 平行AC ,连结BE 、AE 、CF 、BF 那么与△BEC等积的三角形一共有哪几个三角形?F DECBA【考点】三角形的等高模型 【难度】3星 【题型】解答 【解析】 △AEC 、△AFC 、△ABF . 【答案】△AEC 、△AFC 、△ABF .【巩固】如图,在△ABC 中,D 是BC 中点,E 是AD 中点,连结BE 、CE ,那么与△ABE 等积的三角形一共有哪几个三角形?ED C BA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 3个,△AEC 、△BED 、△DEC . 【解析】 【答案】3个,△AEC 、△BED 、△DEC .【巩固】如图,在梯形ABCD 中,共有八个三角形,其中面积相等的三角形共有哪几对?ODC B A【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 △ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO . 【答案】△ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO【例 8】 如图,三角形ABC 的面积为1,其中3AE AB =,2BD BC =,三角形BDE 的面积是多少?AB ECD DCEB A【考点】三角形的等高模型 【难度】2星 【题型】解答 【关键词】迎春杯 【解析】 连接CE ,∵3AE AB =,∴2BE AB =,2BCE ACB S S =V V又∵2BD BC =,∴244BDE BCE ABC S S S ===V V V .【答案】4【例 9】 如右图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC ∆的面积是 平方厘米.AA【考点】三角形的等高模型 【难度】2星 【题型】解答 【关键词】2008年,四中考题【解析】 连接CD .根据题意可知,DEF ∆的面积为DAC ∆面积的13,DAC ∆的面积为ABC ∆面积的12,所以DEF ∆的面积为ABC ∆面积的111236⨯=.而DEF ∆的面积为5平方厘米,所以ABC ∆的面积为15306÷=(平方厘米).【答案】30【巩固】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?CB【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 ABD V ,ABC V 等高,所以面积的比为底的比,有12ABD ABC S BD S BC ==V V , 所以ABDS V =111809022ABC S ⨯=⨯=V (平方厘米).同理有190303ABE ABD AE S S AD =⨯=⨯=V V (平方厘米),34AFE ABE FE S S BE =⨯=V V 3022.5⨯= (平方厘米).即三角形AEF 的面积是22.5平方厘米. 【答案】22.5【巩固】如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果24AB =厘米,8BC =厘米,求三角形ZCY 的面积. ABC DZ Y【考点】三角形的等高模型 【难度】2星 【题型】解答【解析】 ∵Y 是BD 的中点,Z 是DY 的中点,∴1122ZY DB =⨯⨯,14ZCY DCB S S =V V ,又∵ABCD 是长方形,∴11124442ZCY DCB ABCD S S S ==⨯=V V Y (平方厘米).【答案】24【巩固】如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FED CBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 三角形ADC 的面积是三角形ABC 面积的一半24212÷=, 三角形ADE 又是三角形ADC 面积的一半1226÷=.三角形FED 的面积是三角形ADE 面积的一半,所以三角形FED 的面积623=÷=. 【答案】3【巩固】如图,在三角形ABC 中,8BC =厘米,高是6厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?FE CBA【考点】三角形的等高模型 【难度】2星 【题型】解答 【解析】 ∵F 是AC 的中点 ∴2ABC ABF S S =V V 同理2ABF BEF S S =V V∴486246BEF ABC S S =÷=⨯÷÷=V V (平方厘米).【答案】6【例 10】 如图所示,A 、B 、C 都是正方形边的中点,△COD 比△AOB 大15平方厘米。
小学数学 几何模型之 等高模型 PPT+详细答案

A
E
F
B
C
例题10 如图ABCD是一个长方形,点E、F和G分别是它们所在边的中 点.如果长方形的面积是36个平方单位,求三角形EFG的面 积是多少个平方单位.
练习10 如图,长方形ABCD的面积是1,M是QD边的中点,N在AB边上 ,且2AN=BN.那么,阴影部分的面积是多少?
A
M
D
A
M
D
N
N
B
C
B
C
(3) 如下图,答案不唯一,以下仅供参考:
例题1 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三 角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.
⑶如下图,答案不唯一,以下仅供参考
:
练习1
如图,BD长12厘米,DC长4厘米,B、C和D在同一条直线上. ⑴ 求三角形ABC的面积是三角形ABD面积的多少倍? ⑵ 求三角形ABD的面积是三角形ADC面积的多少倍?
例题1 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三 角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.
⑴ 如下图,D、E是BC的三等分点,F、G分别是对应线段的中点,答案 不唯一:
例题1 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三 角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.
方形ABCD的长是20,宽是12,则它内部阴影部分的面积是
多少?
A
B
F
E
D
C
例题3
如图,长方形ABCD的面积是56平方厘米,点E、F、G分别是 长方形ABCD边上的中点,H为AD边上的任意一点,求阴影部 分的面积.
练习3
图中的EFG分别是正方形ABCD三条边的三等分点,如果正方 形的边长是12,那么阴影部分的面积是多少.
《等高(等底)模型》课后作业

《等高(等底)模型》课后作业
1、如图,在三角形ABC 中,8BC =厘米,高是6厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?
2、如图,直角三角形ABC 中AB=2,BC=2,其中AE=3AB,BD=2BC,三角形BDE 的面积是多少?
3、如下图,AD DB =,AE EF FC ==,已知阴影部分面积为6平方厘米,
ABC ∆的面积是多少平方厘米?
F
E C
B
A D
A
4、图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的2倍.那么三角形AEF 的面积是多少平方厘米?
5. 正图长方形ABCD 的面积是32平方厘米,E 、F 都是所在边的中点,三角形AEF 的面积是多少?
6. 右图是由大、小两个正方形组成的,大正方形的边长是6厘米,小正方形的边长是4厘米,求三角形ABC 的面积.
F E
D
C
B
A G
4A
B C
D
E
F
7、如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。
(1)求三角形ABD 的面积是三角形ADC 面积的多少倍? (2)求三角形ABC 的面积是三角形ADC 面积的多少倍?
8、如图,在长方形ABCD 中,AB=8,AD=10,AE=4,BF=5,三角形DEF 面积是多少?
9、如图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为1平方厘米.求三角形ABC 的面积.
G
A
B
C
D E F (H )。
三角形等高模型训练(二)例题+巩固带答案

三角形等高模型例题精讲【例 1】 如图,大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成.求阴影部分的面积.【解析】如图,将大长方形的长的长度设为1,则AB=1/4,CD=1/3,所以MN=1/3-1/4=1/12,阴影部分面积为(12+24+36+48)×1/2×1/12=5(平方厘米).【巩固1】如图,三角形ABC 中,DC=2BD ,CE=3AE ,三角形ADE 的面积是20平方厘米,三角形ABC 的面积是多少?EDCBA【解析】 ∵CE=3AE ,∴AC=4AE ,S △ADC =4S △ADE ;又∵DC=2BD ,∴BC=1.5DC ,S △ABC =1.5S △ADC =6S △ADE =120(平方厘米).【例题2】如图,在三角形ABC 中,已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89,28,26.那么三角形DBE 的面积是 .【解析】根据题意可知,S △ADC =S △ADE +S △DCE =89+28=117,所以BD:AD=S △SDC :S △ADC =26:117=2:9, 那么S △DBE :S △ADE =BD:AD=2:9, 故S △DBE =89×2÷9=178/9.【巩固2】如图,梯形ABCD 被它的一条对角线BD 分成了两部分.三角形BDC 的面积比三角形ABD 的面积大10平方分米.已知梯形的上底与下底的长度之和是15分米,它们的差是5分米.求梯形ABCD 的面积.DCBA【解析】如右图,作AB 的平行线DE .三角形BDE 的面积与三角形ABD 的面积相等,三角形DEC 的面积就是三角形BDC 与三角形ABD 的面积差(10平方分米).从而,可求出梯形高(三角形DEC 的高)是:2×10÷5=4(分米),梯形面积是:15×4÷2=30(平方分米).【例题3】图中三角形AOB 的面积为15平方厘米,线段OB 的长度为OD 的3倍,求梯形ABCD 的面积.OCBDA【解析】在△ABD 中,因为S △AOB=15平方厘米,且OB=3OD , 所以有S △AOD =S △AOB ÷3=5平方厘米.因为△ABD 和△ACD 等底等高,所以有S △ABD =S △ACD .从而S △OCD =15平方厘米,在△BCD 中,S △BOC =3S △OCD =45平方厘米, 所以梯形面积:15+5+15+45=80平方厘米.【巩固3】如图,把四边形ABCD 改成一个等积的三角形.DBAA′ABCD【解析】本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右上图把顶点A 移到CB 的延长线上的A′处,△A′BD 与 △ABD 面积相等,从而△A′DC 面积与原四边形ABCD 面积也相等.这样就把四边形ABCD 等积地改成了三角形△A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB 平行的直线与CB 的延长线交于A′点. 具体做法:⑴ 连接BD ;⑵ 过A 作BD 的平行线,与CB 的延长线交于A′. ⑶ 连接A′D,则△A′CD 与四边形ABCD 等积.【例题4】一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的15%,黄色三角形面积是21平方厘米.问:长方形的面积是多少平方厘米?红绿黄红【解析】黄色三角形与绿色三角形的底相等都等于长方形的长,高相加为长方形的宽,所以黄色三角形与绿色三角形的面积和为长方形面积的59%,而绿色三角形面积占长方形面积的15%,所以黄色三角形面积占长方形面积的50%-15%=35%.已知黄色三角形面积是21平方厘米,所以长方形面积等于21÷35%=60(平方厘米).【巩固4】O 是长方形ABCD 内一点,已知三角形OBC 的面积是5平方厘米,三角形OAB 的面积是2平方厘米,求三角形0BD 的面积是多少?【解析】由于ABCD 是长方形,所以S △AOD +S △BOC =长方形面积的一半,而S △ABD =长方形面积的一半,所以S △AOD +S △BOC =S △ABD ,则S △BOC =S △OAB +S △OBD ,所以S △OBD - S △OAB =5-2=3(平方厘米).【例题5】如右图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若三角形PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?CHCH【解析】根据差不变原理,要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差,相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差. 如右上图,连接CP 、AP .由于S △BCP +S △ADP =S △ABP +S △BDP +S △ADP =平行四边形ABCD 面积的一半 ,所以S △BCP - S △ABP =S △BDP .而S △BCP =平行四边形BCFE 面积的一半 S △ABP =平行四边形ABHG 的一半,所以S BCFE -S ABHG =2(S △BCP -S △ABP )=2S △BDP =16(平方分米)【巩固5(1)】如右图,正方形ABCD 的面积是20,正三角形三角形BPC 的面积是15,求阴影三角形BPD 的面积.BAAB【解析】连接AC 交BD 于O 点,并连接PO .如下图所示,可得PO//DC ,所以△DPO 与△CPO 面积相等(同底等高),所以有:S △BPO +S △CPO =S △BPO +S △PDO =S △BPD ,因为S △BOC =正方形ABCD 面积÷4=5, 所以S △BPD =15-5=10.【巩固5(2)】如右图,正方形ABCD 的面积是12,正三角形BOC 的面积是5,求阴影三角形BPD 的面积.BAAB D【解析】连接AC 交BD 于O 点,并连接PO .如右上图所示,可得PO//DC ,所以△DPO 与△CPO 面积相等(同底等高),所以有:S △BPO +S △CPO =S △BPO +S △PDO =S △BPD因为S △BPC =正方形ABCD 面积÷4=3,所以S △BPD =5-3=2.【例题6】在长方形ABCD 内部有一点O ,形成等腰三角形AOB 的面积为16,等腰三角形DOC 的面积占长方形面积的18%,那么阴影三角形AOC 的面积是多少?D【解析】先算出长方形面积,再用其一半减去△DOC 的面积(长方形面积的18%),再减去△AOD 的面积,即可求出△AOC 的面积.根据模型可知S △COD +S △AOB =长方形ABCD 面积的一半, 所以S ABCD =16÷(1/2-18%)=50,又△AOD 与△BOC 的面积相等,它们的面积和等于长方形面积的一半, 所以△AOD 的面积等于长方形面积的1/4,所以S △AOC =S △ACD -S △AOD -S △COD =1/2S ABCD =25%S ABCD -18%ABCD =25-12.5-9=3.5【巩固6】如右图所示,在梯形ABCD 中,E 、F 分别是其两腰AB 、CD 的中点,G 是EF 上的任意一点,已知三角形ADG 的面积为15平方厘米,而三角形BCG 的面积恰好是梯形ABCD 面积的7/20,则梯形ABCD 的面积是 平方厘米。
小学奥数:三角形等高模型与鸟头模型(二).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1baDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADECBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC BA AB CDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D C BAAB CDE 甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD . ∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FEDCBA【考点】三角形的鸟头模型【难度】3星【题型】解答【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC=⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABCS S CE CF CB CA=⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABCS S AD AF AB AC=⨯⨯=⨯⨯=△△设24ABCS=△份,则4BDES=△份,4ADFS=△份,9CEFS=△份,244497DEFS=---=△份,恰好是7平方厘米,所以24ABCS=△平方厘米【答案】24【例 5】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型【难度】3星【题型】解答【关键词】迎春杯,决赛,第一题,9题【解析】如下图,连接AD,BE,CF.有△ABE,△ABC的高相等,面积比为底的比,则有ABEABCSSVV=AEAC,所以ABES V=AEAC×ABCS V=15ABCS V同理有AEFS V=AFAB ABES V,即=AEFS V=15×56ABCS V=16ABCS V.类似的还可以得到CDES V=14×45ABCS V=15ABCS V,BDFS V=16×13ABCS V=18ABCS V.所以有DEFS V=ABCS V-(AEFS V+CDES V+BDFS V)=(1-16-15-18)ABCS V=61120ABCS V.即DEF ABC 三角形的面积三角形的面积为61120.【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米 【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】(法1)本题是性质的反复使用.连接AE、CD.∵11ABCDBCSS=VV,1ABCS=V,∴S1DBC=V.同理可得其它,最后三角形DEF的面积18=.(法2)用共角定理∵在ABCV和CFEV中,ACB∠与FCE∠互补,∴111428ABCFCES AC BCS FC CE⋅⨯===⋅⨯VV.又1ABCS=V,所以8FCES=V.同理可得6ADFS=V,3BDES=V.所以186318DEF ABC FCE ADF BDES S S S S=+++=+++=V V V V V.【答案】18【例 9】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】方法一:如下图,连接BD,ED,BG,有V EAD、V ADB同高,所以面积比为底的比,有2EAD ABD ABDEAS S SAB==V V V.同理36EAH EAD EAD ABDAHS S S SAD===V V V V.类似的,还可得V6FCG BCDS S=V V,有()66EAH FCG ABD BCD ABCDS S S S S+=+=V V V V=30平方厘米.连接AC,AF,HC,还可得6EFB ABCS S=V V,6DHG ACDS S=V V,有()66EFB DHG ABC ACD ABCDS S S S S+=+=V V V V=30平方厘米.有四边形EFGH的面积为V EAH,V FCG,V EFB,V DHG,ABCD的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD,有V EAH 、△ABD中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAH S V =6ABD S V .类似的,还可得FCG S V =6BCD S V ,有EAH S V +FCG S V =6(ABD S V +BCD S V )=6ABCD S=30平方厘米.连接AC ,还可得EFB S V =6ABC S V ,DHG S V =6ACD S V ,有EFB S V +DHG S V =6(ABC S V +ACD S V )=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米. 【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】如图,将原图扩展成一个大正三角形DEF,则AGF∆与CEH∆都是正三角形.假设正六边形的边长为为a,则AGF∆与CEH∆的边长都是4a,所以大正三角形DEF的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF的面积为496.由于4FA a=,3FB a=,所以AFB∆与三角形DEF的面积之比为4312 7749⨯=.同理可知BDC∆、AEC∆与三角形DEF的面积之比都为1249,所以ABC∆的面积占三角形DEF面积的1213134949-⨯=,所以ABC∆的面积的面积为4913136496⨯=.【答案】13 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】2 6 3【例 17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD 的面积比。
小学奥数:三角形等高模型与鸟头模型(二).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1baDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADECBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC BA AB CDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D C BAAB CDE 甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD . ∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FEDCBA【考点】三角形的鸟头模型【难度】3星【题型】解答【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC=⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABCS S CE CF CB CA=⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABCS S AD AF AB AC=⨯⨯=⨯⨯=△△设24ABCS=△份,则4BDES=△份,4ADFS=△份,9CEFS=△份,244497DEFS=---=△份,恰好是7平方厘米,所以24ABCS=△平方厘米【答案】24【例 5】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型【难度】3星【题型】解答【关键词】迎春杯,决赛,第一题,9题【解析】如下图,连接AD,BE,CF.有△ABE,△ABC的高相等,面积比为底的比,则有ABEABCSSVV=AEAC,所以ABES V=AEAC×ABCS V=15ABCS V同理有AEFS V=AFAB ABES V,即=AEFS V=15×56ABCS V=16ABCS V.类似的还可以得到CDES V=14×45ABCS V=15ABCS V,BDFS V=16×13ABCS V=18ABCS V.所以有DEFS V=ABCS V-(AEFS V+CDES V+BDFS V)=(1-16-15-18)ABCS V=61120ABCS V.即DEF ABC 三角形的面积三角形的面积为61120.【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米 【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】(法1)本题是性质的反复使用.连接AE、CD.∵11ABCDBCSS=VV,1ABCS=V,∴S1DBC=V.同理可得其它,最后三角形DEF的面积18=.(法2)用共角定理∵在ABCV和CFEV中,ACB∠与FCE∠互补,∴111428ABCFCES AC BCS FC CE⋅⨯===⋅⨯VV.又1ABCS=V,所以8FCES=V.同理可得6ADFS=V,3BDES=V.所以186318DEF ABC FCE ADF BDES S S S S=+++=+++=V V V V V.【答案】18【例 9】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】方法一:如下图,连接BD,ED,BG,有V EAD、V ADB同高,所以面积比为底的比,有2EAD ABD ABDEAS S SAB==V V V.同理36EAH EAD EAD ABDAHS S S SAD===V V V V.类似的,还可得V6FCG BCDS S=V V,有()66EAH FCG ABD BCD ABCDS S S S S+=+=V V V V=30平方厘米.连接AC,AF,HC,还可得6EFB ABCS S=V V,6DHG ACDS S=V V,有()66EFB DHG ABC ACD ABCDS S S S S+=+=V V V V=30平方厘米.有四边形EFGH的面积为V EAH,V FCG,V EFB,V DHG,ABCD的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD,有V EAH 、△ABD中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAH S V =6ABD S V .类似的,还可得FCG S V =6BCD S V ,有EAH S V +FCG S V =6(ABD S V +BCD S V )=6ABCD S=30平方厘米.连接AC ,还可得EFB S V =6ABC S V ,DHG S V =6ACD S V ,有EFB S V +DHG S V =6(ABC S V +ACD S V )=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米. 【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】如图,将原图扩展成一个大正三角形DEF,则AGF∆与CEH∆都是正三角形.假设正六边形的边长为为a,则AGF∆与CEH∆的边长都是4a,所以大正三角形DEF的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF的面积为496.由于4FA a=,3FB a=,所以AFB∆与三角形DEF的面积之比为4312 7749⨯=.同理可知BDC∆、AEC∆与三角形DEF的面积之比都为1249,所以ABC∆的面积占三角形DEF面积的1213134949-⨯=,所以ABC∆的面积的面积为4913136496⨯=.【答案】13 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】2 6 3【例 17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD 的面积比。
小学奥数:三角形等高模型与鸟头模型(二).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1baDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADECBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC BA AB CDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D C BAAB CDE 甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD . ∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FEDCBA【考点】三角形的鸟头模型【难度】3星【题型】解答【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC=⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABCS S CE CF CB CA=⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABCS S AD AF AB AC=⨯⨯=⨯⨯=△△设24ABCS=△份,则4BDES=△份,4ADFS=△份,9CEFS=△份,244497DEFS=---=△份,恰好是7平方厘米,所以24ABCS=△平方厘米【答案】24【例 5】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型【难度】3星【题型】解答【关键词】迎春杯,决赛,第一题,9题【解析】如下图,连接AD,BE,CF.有△ABE,△ABC的高相等,面积比为底的比,则有ABEABCSSVV=AEAC,所以ABES V=AEAC×ABCS V=15ABCS V同理有AEFS V=AFAB ABES V,即=AEFS V=15×56ABCS V=16ABCS V.类似的还可以得到CDES V=14×45ABCS V=15ABCS V,BDFS V=16×13ABCS V=18ABCS V.所以有DEFS V=ABCS V-(AEFS V+CDES V+BDFS V)=(1-16-15-18)ABCS V=61120ABCS V.即DEF ABC 三角形的面积三角形的面积为61120.【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米 【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】(法1)本题是性质的反复使用.连接AE、CD.∵11ABCDBCSS=VV,1ABCS=V,∴S1DBC=V.同理可得其它,最后三角形DEF的面积18=.(法2)用共角定理∵在ABCV和CFEV中,ACB∠与FCE∠互补,∴111428ABCFCES AC BCS FC CE⋅⨯===⋅⨯VV.又1ABCS=V,所以8FCES=V.同理可得6ADFS=V,3BDES=V.所以186318DEF ABC FCE ADF BDES S S S S=+++=+++=V V V V V.【答案】18【例 9】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】方法一:如下图,连接BD,ED,BG,有V EAD、V ADB同高,所以面积比为底的比,有2EAD ABD ABDEAS S SAB==V V V.同理36EAH EAD EAD ABDAHS S S SAD===V V V V.类似的,还可得V6FCG BCDS S=V V,有()66EAH FCG ABD BCD ABCDS S S S S+=+=V V V V=30平方厘米.连接AC,AF,HC,还可得6EFB ABCS S=V V,6DHG ACDS S=V V,有()66EFB DHG ABC ACD ABCDS S S S S+=+=V V V V=30平方厘米.有四边形EFGH的面积为V EAH,V FCG,V EFB,V DHG,ABCD的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD,有V EAH 、△ABD中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAH S V =6ABD S V .类似的,还可得FCG S V =6BCD S V ,有EAH S V +FCG S V =6(ABD S V +BCD S V )=6ABCD S=30平方厘米.连接AC ,还可得EFB S V =6ABC S V ,DHG S V =6ACD S V ,有EFB S V +DHG S V =6(ABC S V +ACD S V )=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米. 【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】如图,将原图扩展成一个大正三角形DEF,则AGF∆与CEH∆都是正三角形.假设正六边形的边长为为a,则AGF∆与CEH∆的边长都是4a,所以大正三角形DEF的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF的面积为496.由于4FA a=,3FB a=,所以AFB∆与三角形DEF的面积之比为4312 7749⨯=.同理可知BDC∆、AEC∆与三角形DEF的面积之比都为1249,所以ABC∆的面积占三角形DEF面积的1213134949-⨯=,所以ABC∆的面积的面积为4913136496⨯=.【答案】13 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】2 6 3【例 17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD 的面积比。
小学奥数:三角形等高模型与鸟头模型(二).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1baDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADECBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC BA AB CDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D C BAAB CDE 甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD . ∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FEDCBA【考点】三角形的鸟头模型【难度】3星【题型】解答【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC=⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABCS S CE CF CB CA=⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABCS S AD AF AB AC=⨯⨯=⨯⨯=△△设24ABCS=△份,则4BDES=△份,4ADFS=△份,9CEFS=△份,244497DEFS=---=△份,恰好是7平方厘米,所以24ABCS=△平方厘米【答案】24【例 5】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型【难度】3星【题型】解答【关键词】迎春杯,决赛,第一题,9题【解析】如下图,连接AD,BE,CF.有△ABE,△ABC的高相等,面积比为底的比,则有ABEABCSSVV=AEAC,所以ABES V=AEAC×ABCS V=15ABCS V同理有AEFS V=AFAB ABES V,即=AEFS V=15×56ABCS V=16ABCS V.类似的还可以得到CDES V=14×45ABCS V=15ABCS V,BDFS V=16×13ABCS V=18ABCS V.所以有DEFS V=ABCS V-(AEFS V+CDES V+BDFS V)=(1-16-15-18)ABCS V=61120ABCS V.即DEF ABC 三角形的面积三角形的面积为61120.【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米 【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】(法1)本题是性质的反复使用.连接AE、CD.∵11ABCDBCSS=VV,1ABCS=V,∴S1DBC=V.同理可得其它,最后三角形DEF的面积18=.(法2)用共角定理∵在ABCV和CFEV中,ACB∠与FCE∠互补,∴111428ABCFCES AC BCS FC CE⋅⨯===⋅⨯VV.又1ABCS=V,所以8FCES=V.同理可得6ADFS=V,3BDES=V.所以186318DEF ABC FCE ADF BDES S S S S=+++=+++=V V V V V.【答案】18【例 9】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】方法一:如下图,连接BD,ED,BG,有V EAD、V ADB同高,所以面积比为底的比,有2EAD ABD ABDEAS S SAB==V V V.同理36EAH EAD EAD ABDAHS S S SAD===V V V V.类似的,还可得V6FCG BCDS S=V V,有()66EAH FCG ABD BCD ABCDS S S S S+=+=V V V V=30平方厘米.连接AC,AF,HC,还可得6EFB ABCS S=V V,6DHG ACDS S=V V,有()66EFB DHG ABC ACD ABCDS S S S S+=+=V V V V=30平方厘米.有四边形EFGH的面积为V EAH,V FCG,V EFB,V DHG,ABCD的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD,有V EAH 、△ABD中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAH S V =6ABD S V .类似的,还可得FCG S V =6BCD S V ,有EAH S V +FCG S V =6(ABD S V +BCD S V )=6ABCD S=30平方厘米.连接AC ,还可得EFB S V =6ABC S V ,DHG S V =6ACD S V ,有EFB S V +DHG S V =6(ABC S V +ACD S V )=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米. 【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】如图,将原图扩展成一个大正三角形DEF,则AGF∆与CEH∆都是正三角形.假设正六边形的边长为为a,则AGF∆与CEH∆的边长都是4a,所以大正三角形DEF的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF的面积为496.由于4FA a=,3FB a=,所以AFB∆与三角形DEF的面积之比为4312 7749⨯=.同理可知BDC∆、AEC∆与三角形DEF的面积之比都为1249,所以ABC∆的面积占三角形DEF面积的1213134949-⨯=,所以ABC∆的面积的面积为4913136496⨯=.【答案】13 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】2 6 3【例 17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD 的面积比。
小学奥数:三角形等高模型与鸟头模型(二).专项练习及答案解析

板块一 三角形等高模型我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =s 2s 1baDCBA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.板块二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△例题精讲4-3-2.三角形等高模型与鸟头模型EDCBADECBA图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【答案】70【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E DC BA AB CDE【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【答案】15【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D C BAAB CDE 甲乙【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD . ∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【答案】5【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【答案】50【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【答案】48【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FEDCBA【考点】三角形的鸟头模型【难度】3星【题型】解答【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC=⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABCS S CE CF CB CA=⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABCS S AD AF AB AC=⨯⨯=⨯⨯=△△设24ABCS=△份,则4BDES=△份,4ADFS=△份,9CEFS=△份,244497DEFS=---=△份,恰好是7平方厘米,所以24ABCS=△平方厘米【答案】24【例 5】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【考点】三角形的鸟头模型【难度】3星【题型】解答【关键词】迎春杯,决赛,第一题,9题【解析】如下图,连接AD,BE,CF.有△ABE,△ABC的高相等,面积比为底的比,则有ABEABCSSVV=AEAC,所以ABES V=AEAC×ABCS V=15ABCS V同理有AEFS V=AFAB ABES V,即=AEFS V=15×56ABCS V=16ABCS V.类似的还可以得到CDES V=14×45ABCS V=15ABCS V,BDFS V=16×13ABCS V=18ABCS V.所以有DEFS V=ABCS V-(AEFS V+CDES V+BDFS V)=(1-16-15-18)ABCS V=61120ABCS V.即DEF ABC 三角形的面积三角形的面积为61120.【答案】61120【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米 【答案】12.5【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【答案】10【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCB AAB CDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】(法1)本题是性质的反复使用.连接AE、CD.∵11ABCDBCSS=VV,1ABCS=V,∴S1DBC=V.同理可得其它,最后三角形DEF的面积18=.(法2)用共角定理∵在ABCV和CFEV中,ACB∠与FCE∠互补,∴111428ABCFCES AC BCS FC CE⋅⨯===⋅⨯VV.又1ABCS=V,所以8FCES=V.同理可得6ADFS=V,3BDES=V.所以186318DEF ABC FCE ADF BDES S S S S=+++=+++=V V V V V.【答案】18【例 9】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】方法一:如下图,连接BD,ED,BG,有V EAD、V ADB同高,所以面积比为底的比,有2EAD ABD ABDEAS S SAB==V V V.同理36EAH EAD EAD ABDAHS S S SAD===V V V V.类似的,还可得V6FCG BCDS S=V V,有()66EAH FCG ABD BCD ABCDS S S S S+=+=V V V V=30平方厘米.连接AC,AF,HC,还可得6EFB ABCS S=V V,6DHG ACDS S=V V,有()66EFB DHG ABC ACD ABCDS S S S S+=+=V V V V=30平方厘米.有四边形EFGH的面积为V EAH,V FCG,V EFB,V DHG,ABCD的面积和,即为30+30+5=65(平方厘米.)方法二:连接BD,有V EAH 、△ABD中∠EAD+∠BAD=180°又夹成两角的边EA 、AH ,AB 、AD 的乘积比,EA AHAB AD⨯⨯=2×3=6,所以EAH S V =6ABD S V .类似的,还可得FCG S V =6BCD S V ,有EAH S V +FCG S V =6(ABD S V +BCD S V )=6ABCD S=30平方厘米.连接AC ,还可得EFB S V =6ABC S V ,DHG S V =6ACD S V ,有EFB S V +DHG S V =6(ABC S V +ACD S V )=6ABCD S =30平方厘米.有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【答案】118【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【答案】13.2【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=. 于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==. 【答案】60【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【考点】三角形的鸟头模型 【难度】3星 【题型】解答【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【答案】3.5【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【答案】110【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米. 【答案】12【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】如图,将原图扩展成一个大正三角形DEF,则AGF∆与CEH∆都是正三角形.假设正六边形的边长为为a,则AGF∆与CEH∆的边长都是4a,所以大正三角形DEF的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF的面积为496.由于4FA a=,3FB a=,所以AFB∆与三角形DEF的面积之比为4312 7749⨯=.同理可知BDC∆、AEC∆与三角形DEF的面积之比都为1249,所以ABC∆的面积占三角形DEF面积的1213134949-⨯=,所以ABC∆的面积的面积为4913136496⨯=.【答案】13 6【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【考点】三角形的鸟头模型【难度】4星【题型】解答【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.【答案】2 6 3【例 17】仅用下图这把刻度尺,最少测量次,就能得出三角形ABC和三角形BCD 的面积比。
等高模型答案解析

4 如图是由大、小两个正方形组成的,它们的边长分别是 厘米和 厘米,求三角形
积是
.
的面
答案
解析 如图连结 ,可以看出,
,
考点
几何 四边形
一半模型 等积变形
5 如图,正方形 厘米,则正方形
和正方形 的面积为
中, 在同一条直线上,且阴影三角形面积为 平方 ?
答案 16
解析 连结 ,那么 平行 ,所以,阴影面积 三角形
考点
几何 三角形 等高模型 等高模型综合
2 已知三角形 的面积是
的面积是 平方厘米, 的长为 厘米, 的长为 厘米,则三角形 平方厘米.
答案
解析 因为三角形 和三角形 的高相等,所以面积之比等于底边边长之比, 是 的 倍,则三角形 的面积是三角形 面积的 倍,因此三角形 的面积为 (平方厘米)
考点
几何 三角形 等高模型 等高模型综合
3 已知三角形 的面积是
的面积是 平方厘米, 平方厘米.
的长为 厘米,
的长为 厘米,则三角形
答案
解析 因为三角形 和三角形 的高相等,所以面积之比等于底边边长之比, 是 的 倍,则三角形 的面积是三角形 面积的 倍,因此三角形 的面积为
平方厘米.
考点
几何 三角形 等高模型 等高模型综合
大练兵-等高模型
1 如图, 长 厘米, 长 厘米, 、 和 在同一条直线上.
求三角形 的面积是三角形 面积的
倍.
答案
解析 因为三角形 、三角形 和三角形 在分别以 、 和 为底时,它们的高
都是从 点向 边上所作的垂线,也就是说三个三角形的高相等.
于是:三角形 的面积
高
高,
三角形 的面积 高
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的等高模型例题精讲在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =baS 2S 1 DC BA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.【例题1】你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形.【解析】⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一:CEDBAFC DB A G DB A⑵ 如下图,答案不唯一,以下仅供参考:⑸⑷⑶⑵⑴⑶如下图,答案不唯一,以下仅供参考:【例题2】如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上.⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍?CDBA【解析】因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等. 于是:三角形ABD 的面积=12高÷2=6×高 三角形ABC 的面积=(12+4)×高÷2=8×高 三角形ADC 的面积=4×高÷2=2×高所以,三角形ABC 的面积是三角形ABD 面积的4/3倍; 三角形ABD 的面积是三角形ADC 面积的3倍.【例题3】如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是 平方厘米.【解析】图中阴影部分的面积等于长方形ABCD 面积的一半,即4×3÷2=6(平方厘米).【巩固1】如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.【解析】根据面积比例模型,可知图中空白三角形面积等于平行四边形面积的一半,所以阴影部分的面积也等于 平行四边形面积的一半,为50÷2=25平方厘米.【巩固2】如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .F E CBA【解析】 根据面积比例模型可知阴影部分面积等于长方形面积的一半,为20×12÷120.【例题4】如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.E BAE BA【解析】本题是等底等高的两个三角形面积相等的应用.连接BH 、CH .∵AE=EB , ∴S △AEH =S △BEH同理,S △BFH =S △CFH ,S △CGH =S △DGH ,∴S 阴影=S 长ABCD ÷2=56÷2=28(平方厘米).【巩固3】图中的EFG 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E D GCFBBF CG E【解析】把另外三个三等分点标出之后,正方形的3个边就都被分成了相等的三段.把H 和这些分点以及正方形的顶点相连,把整个正方形分割成了9个形状 各不相同的三角形.这9个三角形的底边分别是在正方形的3个边上,它们 的长度都是正方形边长的三分之一.阴影部分被分割成了3个三角形,右边三角形的面积和第1第2个三角形相等:中间三角形的面积和第3第4个 三角形相等;左边三角形的面积和第5个第6个三角形相等.因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一,因此全部阴影的总面积就等于正方形面积的三分之一.正方形的面积是144,阴影部分的面积就是48.【例题5】长方形ABCD 的面积为36平方厘米,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?E【解析】寻找可利用的条件, 连接BH 、HC ,如下图:E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++= 即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=;而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影【巩固4】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,△求阴影部分面积.【解析】连接PA 、PC .由于△PAD 与△PBC 的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的1/4,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的1/6,所以阴影部分的面积为6×6×(1/4+1/6)=15平方厘米.【例题6】如右图,E 在AD 上,AD 垂直BC ,AD=12厘米,DE=3厘米.求三角形ABC 的面积是三角形EBC 面积的几倍?EDCBA【解析】因为AD 垂直于BC ,所以当BC 为三角形ABC 和三角形EBC 的底时,AD 是三角形ABC 的高,ED 是三角形EBC 的高, 于是:三角形ABC 的面积=BC×12÷2=BC×6 三角形EBC 的面积=BC×3÷2=BC×1.5所以三角形ABC 的面积是三角形EBC 的面积的4倍.【巩固5】如图,在三角形ABC 中,D 是BC 中点,E 是AD 中点,连结BE 、CE ,那么与三角形ABE 等积的三角形一共有哪几个三角形?ED C BA【解析】3个,△AEC 、△BED 、△DEC .【例题7】如图,在平行四边形ABCD 中,EF 平行AC ,连结BE 、AE 、CF 、BF 那么与三角形BEC 等积的三角形一共有哪几个三角形?F DECBA【解析】△AEC 、△AFC 、△ABF .【巩固6】如图,在梯形ABCD 中,共有八个三角形,其中面积相等的三角形共有哪几对?ODBA【解析】△ABD 与△ACD ,△ABC 与△DBC ,△ABO 与△DCO .【例题8】如图,三角形ABC 的面积为1,其中AE=3AB ,BD=2BC ,三角形BDE 的面积是多少?AB EC DC E B A【解析】连接CE ,∵AE=3AB ,∴BE=2AB ,S △BCE=2S △ACB 又∵BD=2BC ,∴S △BDE =2△BCE =4S △ABC =4.【巩固7】如右图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,三角形ABC 的面积是 平方厘米.AA【解析】连接CD .根据题意可知,△DEF 的面积为△DAC 面积的1/3, △DAC 的面积为△ABC 面积的1/2,所以△DEF 的面积为△ABC面积的1/2×1/3=1/6.而△DEF 的面积为5平方厘米,所以△ABC 的面积为5÷1/6=30(平方厘米).【例题9】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?CB【解析】,△ABD,△ABC 等高,所以面积的比为底的比,有S △ABD :S △ABC =BD:BC=1:2, 所以S △ABD =S △ABC ÷2=180÷2=90(平方厘米).同理有S △ABE =90 S △ABE =90×1/3=30(平方厘米),S △AEF =30×3/4=22.5 (平方厘米). 即三角形AEF 的面积是22.5平方厘米.【巩固8】如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果AB=24厘米,BC=8厘米,求三角形ZCY 的面积.ABC DZ Y【解析】∵Y 是BD 的中点,Z 是DY 的中点,∴ZY=1/2×1/2×DB,S △ZCY =S △DCB ÷4, 又∵ABCD 是长方形,∴S △ZCY =S △DCB ÷4=1/4×1/2×S 长BCD=24 (平方厘米).【例题10】如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FE DCBA【解析】三角形ADC 的面积是三角形ABC 面积的一半24÷2=12, 三角形ADE 又是三角形ADC 面积的一半12÷2=6.三角形FED 的面积是三角形ADE 面积的一半,所以三角形 FED 的面积6÷2=3.【巩固9】如图,在三角形ABC 中,BC=8厘米,高是6厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?FE CBA【解析】∵F 是AC 的中点 ∴S △ABC=2S △ABF 同理S △ABF =2S △BEF∴S △BEF =S △ABC ÷4=8×6÷2÷4=6(平方厘米).【例题11】如图ABCD 是一个长方形,点E 、F 和G 分别是它们所在边的中点.如果长方形的面积是36个平方单位,求三角形EFG 的面积是多少个平方单位.FE GD C B AFEGD C B A【解析】如右图分割后可得,S △EFG =S 长方形DEFG ÷2=S 长方形ABCD ÷4=36÷4=9(平方单位).【巩固10】如图,长方形ABCD 的面积是1,M 是QD 边的中点,N 在AB 边上,且2AN=BN.那么,阴影部分的面积是多少?ANBDCCDBNA【解析】连接BM,因为M是中点所以△ABM的面积为1/4又因为2AN=BN,所以△BDC的面积为1/4×1/3=1/12,又因为△BDC面积为1/2,所以阴影部分的面积为:1-1/12-1/2=5/12.。
