方差分析2
第十讲 第五章 方差分析2

B与C比:23-18=5<5.07,不显著
D与C比:24-18=6>5.23,显著
结论:只有处理D和C的差异在a=0.05水平显著, 其余皆不显著。
2.q检验:
q检验与SSR检验相似,其区别仅在a,而是查qa。
查qa值后,即有:
LSR= s x ×qa
3.各方法的异同
课堂练习:完全随机试验设计试验结果的统计分析
.
[例4] 研究6种氮肥施用方法(K=6)对小麦的效应,每种施 肥方法种5盆小麦(n=5),完全随机设计,最后测定它们的含 氮量,其结果如下表.试作方差分析
表 6种施肥法小麦植株含氮量
处理
施 12
氮法 34 5
6 总和
2.9 4 2.6 0.5 4.6 4
第五章 方差分析2 三、多重比较
F检验是一个整体的概念。仅能测出不同处理效应的平均 数的显著差异性。但是,是否各个平均数间都有显著差异性? 还是仅有部分平均数间有显著差异而另一部分平均数间没有 显著差异?它不曾提供任何信息。
要明确各个平均数间的差异显著性,还必须对各平均数 进行多重比较。
多重比较的方法主要有两大类: (一)LSD法:t检验法 (二)LSR法:分为SSR法、q检验法
表8 新复极差检验的LSR值
p
2
3
4
5
SSR0.05 SSR0.01 LSR0.05 LSR0.01
2.92 3.96 0.304 0.412
3.07 4.14 0.319 0.431
3.15 4.24 0.328 0.441
3.22 4.33 0.335 0.450
6 3.28 4.39 0.341 0.457
(二)平方和分解
方差分析(2)

ST = S1 + S2
上式表明, 上式表明,总的偏差平方和可以分解为组间偏差平方和 与组内偏差平方和之和。 与组内偏差平方和之和。前者表征了由于因素水平的改变而 引起的数据波动, 引起的数据波动,后者则表征了由于试验存在随机误差而引 起的数据波动。 起的数据波动。
列数据计算表
水 平 重 复 数 1 2… x12… x22… j… x1j… x2j… k 合 计 平均值
f2 = fT − f 1
(5)显著性 ) 为分析条件误差的显著性,常使用 检验 试验的F值 检验。 为分析条件误差的显著性,常使用F检验。 试验的 值 因素方差(组间) 因素方差(组间) 误差方差(组内) 误差方差(组内)
V S1 / f1 F= 1 = V2 S2 / f2
根据F值的大小及给定的显著度 α ,就可判断因素对 根据 值的大小及给定的显著度 值的大小及给定的 试验指标的影响相对于试验误差对试验指标的影响是否显 值越大, 著。F值越大,因素的影响越显著。 值越大 因素的影响越显著。 可从F分布表中查得 根据自由度 f 1 、 f 2 及显著水平α ,可从 分布表中查得 在这些条件下的临界F值 若实际的F值大于此临 在这些条件下的临界 值—— F 。若实际的 值大于此临 α 界值 Fα ,则可认为有 (1 − α ) 的把握说因素对试验指标有显 著影响。 著影响。
计算表中的数据按以下公式计算: 计算表中的数据按以下公式计算:
Ti = ∑xij
j=1
k
1 1 k xi = T = ∑xij i k k j=1 T = ∑Ti = ∑∑xij
i=1 i=1 j=1 m m k
1 1 m 1 m k 1m k x= T = ∑xi = ∑∑xij = n∑∑xij m k m i=1 m i=1 j=1 k i=1 j=1
第六章方差分析(二)

1.46
1.03
1.62
1.27
31.50
28.97
合计
2.08 2.97
2.08 2.49
2.06 2.91
2.30 3.08
2.24 2.58
SST SSA SSB
2.自由度的分解
总自由度:dfT ab 1
A的自由度:dfA a 1 B的自由度:dfB b 1
组内自由度:dfe (a 1)(b 1)
3. 方差计算:
s
2 A
SS A df A
sB2
SSB df B
se2
SSe dfe
方差分析表
变异来源 df A因素 a-1 B因素 b-1
SSR值与LSR值(dfe = 27)
M SSR0.05 SSR0.01 LSR0.05 LSR0.01
2 2.905 3.925 9.267 12.521
3 3.055 4.095 9.745 13.063
光照(A)
5h/d 10h/d 15h/d
平均数
Tij
90 -9 -17
差异显著性
α=0.05 α=0.01
…
Xabn
T•b
T
x•b
x
线性数学模型:
A、B的交互作用
随机误差,独立,正态分布
xijk i i ( )ij+ ijk
A因素的效应
B因素的效应
1. 总变异
自由度 平方和
2. A因素引起的变异
自由度 平方和
3. B因素引起的变异
自由度 平方和
4. A、B因素的交互作用引起的变异
自由度 平方和
1. 平方和的分解
矫正数:C T 2 ab
方差分析2(双因素方差分析、多元方差分析、可视化)

⽅差分析2(双因素⽅差分析、多元⽅差分析、可视化)1 双因素⽅差分析1.1 双因素⽅差分析的实战dat<-ToothGrowthdatattach(dat)table(dat$supp,dat$dose)aggregate(len,by=list(dat$supp,dat$dose),FUN=mean)解释:根据投⽅式(橙汁OJ,维C素VC)supp和剂量dose来对⽛齿的长度len进⾏求均值dose<-factor(dose)解释:为了避免把dose变量认为是数值变量,⽽是把dose认为成分组变量,所以设置成因⼦类型factorfit<-aov(dat$len~dat$supp*dat$dose)解释:aov()做⽅差分析,把 + 换成了 * ,这两项dat$supp和dat$dosee就变成了交互项summary(fit)结果分析:可以看出P值很⼩,三个P值都⼩于0.05,说明不同的投喂⽅式supp对⽛齿的⽣长长度len是有显著影响的;说明不同的剂量dose对⽛齿的⽣长长度len是有显著影响的;说明在两种投喂⽅式下,不同的投喂⽅式supp和剂量dose的交互效应对⽛齿的⽣长长度len是有显著影响的1.2 可视化⽅法1interaction.plot(dat$dose,dat$supp,dat$len,type = "b",col=c("red","blue"),pch=c(16,18),main="XX")1.3 可视化⽅法2library(gplots)plotmeans(dat$len~interaction(dat$supp,dat$dose,sep=" "),connect=list(c(1,3,5),c(2,4,6)),col=c("red","blue"),main="XX",xlab="xlab")1.4 可视化⽅法3library(HH)interaction2wt(dat$len~dat$supp*dat$dose)2 重复测量⽅差分析dat<-CO2CO2$conc<-factor(CO2$conc)w1b1<-subset(CO2,Treatment=="chilled")uptake是植物光合作⽤对⼆氧化碳的吸收量,是因变量y,type是组间因⼦,是互斥的,表⽰的是两个不同地区的植物类型,要么是加拿⼤的植物,要么是美国的植物,不可能两个地⽅都是,conc是不同的⼆氧化碳的浓度,每⼀种植物都在所有的⼆氧化碳浓度下,所以conc是组内因⼦研究不同地区的植物作⽤,在某种⼆氧化碳的浓度作⽤下,对植物的光合作⽤效果有没有影响2.1 含有单个组内因⼦w和单个组间因⼦B的重复测量ANOVAfit<-aov(uptake~conc*Type+Error(Plant/(conc)),w1b1)summary(fit)结果分析:⼆氧化碳浓度和类型对植物光合作⽤都有显著影响2.2 可视化图形呈现(1)⽅式⼀par(las=2)par(mar=c(10,4,4,2))with(w1b1,interaction.plot(conc,Type,uptake,type = "b",col=c("red","blue"),pch=c(16,18)))(2)⽅式⼆boxplot(uptake~Type*conc,data=w1b1,col=c("red","blue"))3 多元⽅差分析library(MASS)attach(UScereal)dat<-UScerealshelf<-factor(shelf)y<-cbind(calories,fat,sugars)fit<-manova(y~shelf)summary(fit)结果分析:不同的货架shelf上,⾷物的热量calories,脂肪含量fat和含糖量sugars是⾮常显著不同的3.1 多元正态性center<-colMeans(y)n<-nrow(y) #⾏数p<-ncol(y) #列数cov<-cov(y) #计算⽅差d<-mahalanobis(y,center,cov)coord<-qqplot(qchisq(ppoints(n),df=p),d) #画图abline(a=0,b=1) #画参考线identify(coord$x,coord$y,labels = s(UScereal)) #给出交互式标出离群点3.2 稳健多元⽅差分析install.packages("rrcov")library(rrcov)wilks.test(y,shelf,method="mcd")结果分析:P值⼩于0.05,说明结果是显著性的,即不同货架上⾷物的热量calories,脂肪含量fat和含糖量sugars是⾮常显著不同的4 ⽤回归来做ANOVAlibrary(multcomp)dat<-cholesterollevels(dat$trt)fit.aov<-aov(response~trt,data=dat)summary(fit.aov)结果分析:aov⽅差分析,trt对response的影响⾮常显著fit.lm<-lm(response~trt,data=dat)summary(fit.lm)结果分析:lm回归分析,trt对response的影响⾮常显著,并且trt的每⼀项都显⽰出来了。
方差分析第2部分单因素试验资料的方差分

(一)两因素单独观测值试验资料的方差分析 对于A、B两个试验因素的全部ab个水 平组合,每个水平组合只有一个观测值, 全
试验共有ab个观测值,其数据模式如表620所示。
上一张 下一张 主 页 退 出
表6-20 两因素单独观测值试验数据模式
表6-20中
x i.
x
j 1
bБайду номын сангаас
ij
, x. j x..
Cx /N
2 ..
SST x C
2 ij
dfT N 1
df t k 1 df e dfT df t
上一张 下一张 主 页 退 出
SSt xi2 . / ni C
SSe SST SSt
【例6.4】 5个不同品种猪的育肥试验,后期30天增 重(kg)如下表所示。试比较品种间增重有无差异。
这是一个单因素试验,k=5,n=5。
上一张 下一张 主 页 退 出
1、计算各项平方和与自由度
C
2 SST xij C (82 132 142 132 ) 2809.00
2 x..
/ kn 265 /(5 5) 2809 .00
2
2945.00 2809.00 136.00 1 1 2 2 SSt xi. C (51 412 60 2 482 652 ) 2809.00 n 5 2882.20 2809.00 73.20
系统分组方差分析两种,现分别介绍如下。
上一张 下一张 主 页 退 出
一、交叉分组资料的方差分析
设试验考察A、B两个因素,A因素分a个水
平,B因素分b个水平 。 所谓交叉分组是指A因
第三章正交试验设计中的方差分析2例题分析

第三章_正交试验设计中的方差分析2-例题分析第三章中的例题分析是关于正交试验设计中的方差分析的。
本例题分析主要涉及到两个因素和一个响应变量,通过正交试验设计的方法,对这两个因素的影响进行分析。
首先,我们需要了解正交试验设计的基本原理。
正交试验设计是一种实验设计方法,通过选择合适的试验因素和水平,使得每个试验条件都能够得到充分的信息,从而降低试验误差,提高试验效率。
在正交试验设计中,试验因素之间是相互独立的,这样可以更好地分析每个因素对响应变量的影响。
在本例题中,我们有两个因素,分别记作因素A和因素B,每个因素有两个水平。
我们还有一个响应变量Y,需要确定因素A、因素B和Y之间的关系。
接下来,我们需要进行方差分析。
方差分析是一种用于比较不同因素对响应变量的影响的统计方法。
在本例题中,我们可以使用两因素方差分析来分析因素A和因素B对响应变量Y的影响。
首先,我们需要计算总平方和(SST),表示响应变量的总变异。
然后,我们需要计算因素A的平方和(SSA),表示因素A对响应变量的影响,以及因素B的平方和(SSB),表示因素B对响应变量的影响。
同时,我们还需要计算交互作用的平方和(SSAB),表示因素A和因素B之间的交互作用对响应变量的影响。
接下来,我们可以计算各个平方和的自由度和均方差,从而得到F值。
F值可以用来判断因素对响应变量的影响是否显著。
如果F值大于临界值,则说明该因素对响应变量的影响是显著的。
最后,我们可以进行多重比较,比较每个因素水平之间的差异。
多重比较可以帮助我们确定哪些因素水平之间的差异是显著的。
通过以上的分析,我们可以得出因素A、因素B和响应变量Y之间的关系。
同时,我们还可以根据多重比较的结果,确定哪些因素水平之间的差异是显著的。
总结起来,本例题分析主要涉及到正交试验设计中的方差分析。
通过对两个因素和一个响应变量进行分析,我们可以确定因素对响应变量的影响是否显著,并确定哪些因素水平之间的差异是显著的。
方差分析(2次)

它除了推断k个样本所代表的总体均数µ1 ,µ2 , µ3 ,…是否相等外,还要推断b个区组所代表 的总体均数是否相等。由于从总变异中分离出 配伍组变异,考虑了个体变异对处理的影响, 使误差更能反映随机误差的大小,因而提高了 研究效率。
SS总 = SS处理 + SS配伍 + SS误差 df总 = df处理 + df配伍 + df误差
第一节
完全随机设计的方差分析
试验设计时,将受试对象随机分配到两组或 多组中进行实验观察,这里只涉及一个因素, 该因素的各个水平就是各个处理组。
单因素方差分析
或称单向方差分析(one way analysis of variance)或 成组设计(完全随机设计)方差分析,是指试验研究 的处理因素,或调查研究资料的分类方式只有一种。 这个处理因素(或分类方式)包含有多个离散的水平, 分析在不同水平上应变量的平均值是否来自相同总体
Xi = ∑ Xij ni
j =1
ni
X = ∑∑ Xij N = ∑ni Xi N
i =1 j =1 i =1
k
ni
k
SS总 = ∑∑ Xij − X
i=1 j =1
k
ni
(
)
2
ν总 = N −1
2、组间变异 、
SS组间 = ∑ni Xi − X
k
ν组间 = k −1
3、组内变异
i =1
(
)
2
MS组间 = SS组间 ν组间
一、基本思想
*
Xij表示第i个处理组的第j个观察值,i=1,2,…k, j=1,2,…ni
方差分析基本思想示意图
变异原因
第六章 方差分析2

Dft=k–1 Dfe=N–k DfT=N–1
SSt MSt dft SSe MSe dfe
MSt MSe
F分布
• 设想作一个抽样试验,即在一正态总体N(μ, σ2)中随机抽取样本含量为n的样本k个,将各样 本观测值整理成表6-1的形式。此时所谓的各处理 没有真实差异,各处理只是随机分的组。 SS SSt 都是误差方差σ 2的估计量 2 2 Se e St
(3)再求一个组内的离均差平方和相加得:
( X ij X ) ( X ij X i ) ni ( X i X )
2 2 j 1 j 1
因为:
ni
ni
2
2( X
j 1
ni
ij
X i )( X i X ) 2( X i X ) ( X ij X i ) 0
• HA: 至少有两个均数不等 或 至少有一个 a 0
(2)检验统计量,列方差分析表
SSt dft MSt F ~ F (dft , dfe ) SSe dfe MSe
MSt: 组间均方, MSe:组内均方
当 H0 成立时,
E ( MSt ) 2 n 2 0
6.1.3期望均方
试验中各处理所属总体的本质差异体现在处理效 应αi的差异上。
a
2 i
/(k 1) ( i ) /(k 1) 效应方差
2
它也反映了各处理观测值总体平均数μ的变异程 度,记为σα2 2 2 i
k 1
6.1.3期望均方
(x
i.
x.. ) /(k 1)
x i.
10.2 8.2 12 9.6 13
解:
方差分析二:双向方差分析

Yijk
ik
S j
Yij2k
ik
20 557
20 596
20 659
16613
18000
22843
华中科技大学同济医学院 宇传华制作,2004,9
60 1812
57456
21
两因素析因分析的方差分析步骤
1.整理数据:求出处理因素 A、B 及其交互项 AB 的观
察值之和,一个因素的观察值平方和、总和、总平方和等。
110447.5 6
变异分解
(1) 总变异: 所有观察值之间的变异
(2) 处理间变异:处理因素+随机误差
(3) 区组间变异:区组因素+随机误差
(4) 误差变异:
随机误差
S S 总 S S 处 理 S S 区 组 S S 误 差
总 处 理 区 组 误 差
华中科技大学同济医学院 宇传华制作,2004,9
双向方差分析前面内容回顾析因设计factorialdesignanova所关心的问题析因设计的4个实例析因设计的特点2个或以上处理因素factor分类变量本节只考虑两个因素每个因素有2个或以上水平level每一组合涉及全部因素每一因素只有一个水平参与几个因素的组合中至少有2个或以上的观察值观测值为定量数据需满足随机独立正态等方差的anova条件三交互作用三交互作用图第三节两因素析因设计方差分析中的多重比较第四节裂区设计splitplotdesign资料的方差分析裂区设计资料的特点一级单位大区间主区家庭学校二级单位小区内即裂区家庭成员学生两因素裂区设计资料的方差分析方法先按随机区组析因设计的方法分析因素a家庭拥挤程度区组家庭的主效应及其交互作用
变异来源 处理 区组 误差 总
离均差平方和 SS 283.83
第四章方差分析2

H A0 : µ1 = µ2 = L = µr ; H A1 : 至少存在一对µi ≠ µ j ,
1 s 1 设 : x i ⋅ = ∑ x ij , ( i = 1, 2, L , r ), x ⋅ j = s j =1 r 1 x = rs
H B 0 : µ1 = µ 2 = L = µr ; H B1 : 至少存在一对µi ≠ µ j ,
Y i ~ N ( µ i , σ 2 ), ( i = 1, 2 , L , r ), 且 相 互 独 立 , y ij 是 Y ij的 样 本 值 , 在 同 一 Y i 下 , 样 本 Y ij ~ N ( µ i , σ 2 )( j = 1, 2 , L , n i ) 也 相 互 独 立 ,
∴ µ i的 1 − α 置 信 区 间 为 : Yi ⋅ − tα / 2 ( n − r )
2 SE , Yi ⋅ + tα / 2 ( n − r ) ni ( n − r ) 2 SE ni ( n − r )
9
结束
就例1而言 就例 而言, 而言
αˆ 1 = y 1 ⋅ − y = 1 7 3 . 5 − 1 9 0 . 3 3 = − 1 6 . 8 3 , αˆ 2 = y 2 ⋅ − y = 1 8 7 . 7 5 − 1 9 0 . 3 3 = − 2 . 5 8 , αˆ 3 = y 3 ⋅ − y = 2 0 9 . 7 5 − 1 9 0 . 3 3 = 1 9 . 4 2 .
2 A
2 A
( r − 1) , S = S
2 E
2 E
2 SA ( n − r ) , F = 2 ~ F ( r − 1, n − r ). SE
6
方差分析2:原理

课程名称:统计学•从方差分析的目的看,是要检验四种颜色的饮料的销售均值是否相等,我们可用方差比较的方法来判断。
(接前例)超市编号无色粉色橘黄色绿色126.5 31.2 27.9 30.8228.7 28.3 25.1 29.6325.1 30.8 28.5 32.4429.1 27.9 24.2 31.7527.2 29.6 26.5 32.8均值27.3 29.6 26.4 31.5首先,四种颜色的销售情况可看作为分为四个组,分析各组间的差异。
差异的产生来自两个方面:•一方面是由不同颜色的差异造成的,既不同的饮料颜色对销售量产生了影响•另一方面是由于抽选样本的随机性而产生的差异,即各颜色内的随机误差,如相同颜色的饮料在不同的商场销售量也不同。
◆由此可知:差异的产生来自两个方面:◆一方面是由不同颜色的差异造成的,既不同的饮料颜色对销售量产生了影响◆另一方面是由于抽选样本的随机性而产生的差异,即各颜色内的随机误差,如相同颜色的饮料在不同的商场销售量也不同。
•这两个方面产生的差异可以用两个方差来计量:•水平之间的方差既包括系统性因素,也包括随机性因素;•水平内部方差仅包括随机性因素。
•方差分析就是通过不同方差的比价,做出拒绝原假设或不能拒绝原假设的判断。
•水平间的方差和水平内方差之比是一个统计量,这个统计量服从F分布:▪将统计量的值F与给定的显著性水平α的临界值F进行比较(或计算出α统计量的P值),做出决策▪若P<α,拒绝原假设H0,表明均值之间的差异是显著的,所检验的因子对观察值有显著影响▪若F>F,不拒绝原假设H0,无证据表明所检验的因子对观察α值有显著影响◆的总体随机抽取的样本;◆各组的观察数据,是从具有的相互的总体中抽取得到的。
谢谢观看。
第5章方差分析2
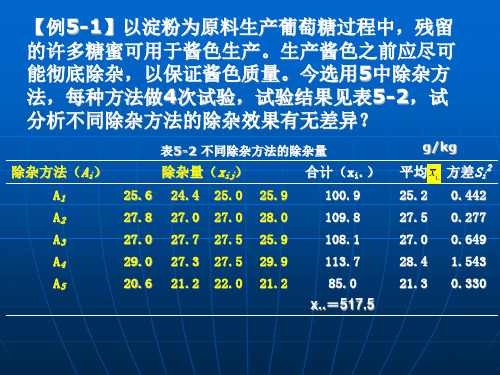
除杂方法(Ai)
A1 A2 A3 A4 A5
表5-2 不同除杂方法的除杂量
除杂量(xij)
(1)总偏差平方和的分解 在表5-1中,反映全部观测值总变异的
总偏差平方和是各观测值xij与总平均数 x..
的离均差平方和,记为SST。即
kn
SST
( xij x.. )2
i1 j1
上一张 下一张 主 页 退 出
k n
kn
(xij x..)2
(xi. x..) (xij xi.) 2
(xij xi. ) 2
i1 j1
SST =SSt+SSe
(5-8)
所以
总偏差平方和=处理间偏差平方和+处理内偏差平方和
或 =因素偏差平方和+误差偏差平方和
上一张 下一张 主 页 退 出
各偏差平方和计算公式:
kn
SST
xi2j C
i1 j 1
SS t
1 n
k i 1
xi2.
C
(5-9)
来表示,则
xij x.. (xi. x.. ) (xij xi. ) x.. ti e(ij 5-6) 与(5-4)式比较可知, x.. 、(xi. x.. ) ti 、
(xij xi. ) eij 分 别是μ、(μi-μ)= 、i
(xij- i ) = ij 的估计值。
13518.7875 13390.3125 128.4750
7医学统计--方差分析2(重复测量)课件

统计量
组数
q 界值
q
a
0.05
0.01
5.42
3
3.58
4.64
0.96
2
2.95
4.02
4.46
2
2.95
4.02
P值
<0.01 >0.05 <0.01
按照=0.05水准,甲厂与乙厂、乙厂与丙厂比较时均 拒绝H0,接受H1,可认为灭蚊效果上,甲厂、丙厂均 低于乙厂,但不能认为甲厂与丙厂间有差别。
二、 LSD-t 检验
总
n 1
处理组间 区组间 误差
MS处理组间
SS处理组间
处理组间
MS误差
SS误差
误差
MS区组间
SS区组间
区组间
随机区组设计方差分析的计算公式
变异来 源
SS
df
MS
F
处理组
k-1
区组 误差
b-1
N-k-b+1或 (k-1)(b-1)
总
N-1
➢处理组间变异(处理因素的影响) 用MS处理表示
➢区组间变异(配伍因素的影响) 用MS区组表示
第四节 多个样本均数间的多重比较
2020/4/5
医学统计学
24
• 多个总体均数不全相同,即多个总体均 数中至少有两个不同。
• 要了解哪些组均数间有差别,哪些组均 数间没有差别,需进一步作两两比较。
• t检验多次利用,会增大犯Ⅰ类错误的概 率。
• 探索性研究:在研究设计阶段未预料到多个 总体不全相等时,常用SNK-q检验,它用于 多个样本均数间的任两组比较。
表 7.3 甲厂
3.34 3.63 3.70 4.29 5.07 2.51 3.03 5.12 4.69 5.18 4.54 11 4.10 0.91
第九章方差分析2

交互作用:当一个因素的水平在另一个因素的不同水平 上变化趋势不一致时,称两个因素之前存在交互作用。 当一个因素的水平在另一个因素的不同水平上变化趋势 一致时,表明两个因素是相互独立的,即不存在交互作 用
(三)事后检验 1、二因素方差分析主效应显著,但交互作用不显著, 必须进行主效应事后检验 2、二因素交互作用显著,两个主效应也显著或某个主 效应显著,进行主效应事后检验已经不重要,而进行交 互作用的事后检验(称为简单效应分析)非常重要,即 限定其中一个因素的某个水平上,看另一个因素对因变 量的影响。
两因素(A、B)方差分析的流程图
进行方差分析 检验A因素 简单效应
交互作用 是否存在
不存在
存在 分析完成 检验B因素 简单效应
检验主效应
67600 32400 36100 78400
1350 1822500
265900
1960 3841600
1350 1822500
312100
变异来源 平方和
自由度
均方
F
P
组间效应 3878.8
2
1939.4
1.37
>0.05
组内效应 26848.5
19
1413.1
总变异
30727.3
21
ቤተ መጻሕፍቲ ባይዱ
第三节单因素随机区组设计的方差分析 一、什么叫随机区组设计 (一)随机区组设计又叫重复测量设计或组内设计,源 于农业试验 (二)特点:把被试划分为几个区组,再根据实验变量 的水平数在每一个区组内划分为若干个小区,同一个区 组随机接受不同的实验处理。 (三)原则:同一区组内的被试尽量同质
SAS学习系列29. 方差分析Ⅱ—ANOVA,GLM过程步

28. 方差分析Ⅱ—ANOVA,GLM过程步SAS提供了ANOV A和GLM过程步进行方差分析。
ANOV A过程步主要处理均衡数据(分类变量的每个水平的观察数是相等),该过程考虑到均衡设计的特殊构造,处理起来速度更快更省内存,也可以处理拉丁方设计、若干不完全的均衡区组设计数据等。
若试验设计不均衡,也不是前面几种实验设计数据,则应该使用GLM过程。
(一)PROC ANOV A过程步一、基本语法PROC ANOV A data=数据集<可选项> ;CLASS 分类变量列表;MODEL 因变量=效应变量列表</可选项>;<MEANS 效应变量列表</可选项> ;><TEST <H=效应变量列表> E=效应变量列表;>说明:(1)CLASS语句是必不可少的,必须放在MODEL语句之前,用来指定分类、区组变量(单因素方差分析只有一个变量);(2)MODEL语句也是必不可少的,该语句用来规定因变量和自变量效应(单因素方差分析的自变量就是分类变量)。
若没有规定自变量的效应,则只拟合截距,假设检验为因变量的均值是否为0. Model语句的主要形式有4种:①主效应模型model y=a b c;②含有交叉因素的模型model y=a b c a*b a*c b*c a*b*c;③嵌套模型model y=a b c(a b);④包含嵌套、交叉和主效应的模型model y=a b(a) c(a) b*c(a);(3)MEANS语句必须出现在MODEL语句之后,用来计算在效应变量所对应的因变量均值,但这些均值没有针对模型中的效应进行修正。
若要计算修正的均值需要用GLM过程步的LSMEANS语句;(4)MEANS语句的可选项主要有两个内容,一是选择多重比较的检验方法,二是设定这些检验的参数(只能用于主效应);bon——对所有主效应均值之差进行Bonferroni的t检验;duncan——对所有主效应均值进行Duncan的多重极差检验;smm|gt2——当样本量不等时,基于学生化最大模和Sidak不相关t不等式,等到Hochberg的GT2方法,对主效应均值进行两两对比检验;snk——对所有主效应均值进行Student-Newman-Keuls的多重极差检验;t|lsd——对所有主效应均值进行两两t检验,它相当于在单元观察数相等时Fisher的最小显著差检验;tukey——对所有主效应均值进行Tukey的学生化极差检验;waller——对所有主效应均值进行Waller-Duncan的k比率检验;……alpha=p——设置显著水平;clm——对变量的每个水平的均值按置信区间形式输出;e=效应变量——指定在多重对比检验中所使用的误差均方。
方差分析(二)

M 误 = 4 1 4, X24h =12.76, X0 = 8 04, n h = n =10 S 差 . 8 . 24 0
1 1 SXi −Xj = M 误 ( + ) = S 差 ni nj
LSDLSD- t =
1 1 41 ( + ) = 09 5 . 84 . 1 1 0 10
泸州医学院流行病与卫生统计教研室
一、SNK-q检验 SNK-
SNK(Student-Newman-Keuls)检验,亦称q检验
Xi − Xj SXi−X j
M误 1 1 S 差 , ν= ν 误 差 , SX −X = + i j 2 n nj i
q=
Xi , ni 和 Xj , nj 为两对比组的样本均数和样本例数。
泸州医学院流行病与卫生统计教研室
例 4 -3 续例 4 -1 试比较三个组两两之间的差别。 解:1 . 建立假设并确定检验水准 α ; 2. 计算 q 值 H0 : µi = µj H : µi ≠ µj ; α = 0.05 1 将三个样本均数从小到大排列,并赋予秩次 均数 8.04 9.25 12.76 组别 A 组 C 组 B 组 SXi −Xj = 4.184( 1 + 1 ) = 0.647 2 10 10 秩次 1 2 3 表 4-7 多个均数两两比较 q 值表 比较组秩次 (1 ) 1 , 2 1 , 3 2 , 3
①建立假设并确定检验水准 α ;
H0 : µ24h = µ96h ; H : µ24h ≠ µ96h ; α = 0.05 1
LSD②求 LSD- t 值
M 误 = 4.184, X24h =12.76, X96h = 9.25, n24h = n =10 S 差 96
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析是用于两个及两个以上样本均数差别的显著性检验。
由于各种因素的影响,研究所得的数据呈现波动状,造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
方差分析的基本思想是:通过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
方差分析主要用途:①均数差别的显著性检验,②分离各有关因素并估计其对总变异的作用,③分析因素间的交互作用,④方差齐性检验。
在科学实验中常常要探讨不同实验条件或处理方法对实验结果的影响。
通常是比较不同实验条件下样本均值间的差异。
例如医学界研究几种药物对某种疾病的疗效;农业研究土壤、肥料、日照时间等因素对某种农作物产量的影响;不同化学药剂对作物害虫的杀虫效果等,都可以使用方差分析方法去解决。
方差分析原理方差分析的基本原理是认为不同处理组的均数间的差别基本来源有两个:(1) 随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示,记作SS w,组内自由度df w。
(2) 实验条件,实验条件,即不同的处理造成的差异,称为组间差异。
用变量在各组的均值与总均值之偏差平方和表示,记作SS b,组间自由度df b。
总偏差平方和 SS t = SS b + SS w。
组内SS t、组间SS w除以各自的自由度(组内dfw =n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MS w和MS b,一种情况是处理没有作用,即各组样本均来自同一总体,MS b/MS w≈1。
另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体。
那么,MS b>>MS w(远远大于)。
MS b/MS w比值构成F分布。
用F值与其临界值比较,推断各样本是否来自相同的总体。
方差分析的假设检验假设有m个样本,如果原假设H0:样本均数都相同即μ1=μ2=μ3=…=μm=μ,m个样本有共同的方差。
则m个样本来自具有共同的方差和相同的均数u的总体。
零假设H0:m组样本均值都相同,即μ1= μ2=....= μm如果,计算结果的组间均方远远大于组内均方(MS b>>MS w),F>F0.05(dfb,dfw), p<0.05,拒绝零假设,说明样本来自不同的正态总体,说明处理造成均值的差异有统计意义;否则, F<F0.05((dfb,dfw), p>0.05不能拒绝零假设,说明样本来自相同的正态总体,处理间无差异。
SPSS中方差分析过程1)One-Way ANOVA过程One-Way过程是单因素简单方差分析过程。
它在Analyze菜单中的Compare Means过程组中。
用0ne-Way ANOVA菜单项调用,可以进行单因素方差分析、均值多重比较和相对比较。
2)General Linear Model 过程组在SPSS主菜单“Analyze”项调用。
这些过程可以完成简单的多因素方差分析和协方差分析,不但可以分析各因素的主效应,还可以分析各因素间的交互效应。
该过程允许指定最高阶次的交互效应,建立包括所有效应的模型。
如果想建立包括某些特定的交互效应的模型也可以通过过程中的“Method”对话框中的选择项实现。
在General Linear Model菜单项的下一级菜单中有四项过程,每个菜单项分别完成不同类型的方差分析任务。
这些过程的主要功能分别是:① Univariate 过程Univariate过程完成一般的单因变量、多因素方差分析。
可以指定协变量,即进行协方差分析。
在指定模型方面有较大的灵活性并可以提供大量的统计输出。
② Multivar iate过程Multivariate过程进行多因变量的多因素分析。
当研究的问题具有两个或两个以上相关的因变量时,要研究一个或几个因素变量与因变量集之间的关系时,才可以选用Multivariate过程。
例如,当你研究数学、物理的考试成绩是否与教学方法、学生性别、以及方法与性别的交互作用有关时,使用此菜单项。
如果只有几个不相关的因变量或只有一个因变量,应该使用Univariate过程。
③ Repeated Measure过程Repeated Measure过程进行重复测量方差分析。
当一个因变量在不只一种条件下进行测度,要检验有关因变量均值的假设应该使用该过程。
④ Variance Component 过程Variance Component过程进行方差估计分析。
通过计算方差估计值,可以帮助我们分析如何减小方差。
单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-A过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几之间彼此不独立,应该用Repeated Measure过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表5-1所示。
表5-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“DATA5-1.SAV”文件中,变量格式如图5-1。
图5-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图5-1所示。
或者打开已存文件“DATA5-1.SAV”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统单因素方差分析设置窗口如图5-2。
图5-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图5-3所示的对话框。
该对话框用于设置均值的多项式比较。
图5-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图5-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设组均值的1.1倍与第二组的均值相等。
单因素方差分析的“0ne-Way ANOVA”过程允许进行高达5次的均值多项式比较。
多项式的系由读者自己根据研究的需要输入。
具体的操作步骤如下:① 选中“Polynomial”复选项,该操作激活其右面的“Degree”参数框。
② 单击Degree参数框右面的向下箭头展开阶次菜单,可以选择“Linear”线性、“Quadratic”二次、“Cubic”三次、“4th”四h”五次多项式。
③ 为多项式指定各组均值的系数。
方法是在“Coefficients”框中输入一个系数,单击Add按钮,“Coefficients”框中的系数进的方框中。
依次输入各组均值的系数,在方形显示框中形成—列数值。
因素变量分为几组,输入几个系数,多出的无意义。
如果多包括第一组与第四组的均值的系数,必须把第二个、第三个系数输入为0值。
如果只包括第一组与第二组的均值,则只需要输入前,第三、四个系数可以不输入。
可以同时建立多个多项式。
一个多项式的一组系数输入结束,激话“Next”按钮,单击该按钮后“Coefficients”框中清空,准备组系数数据。
如果认为输入的几组系数中有错误,可以分别单击“Previous”或“Next”按钮前后翻找出错的一组数据。
单击出错的系数,该系编辑框中,可以在此进行修改,修改后单击“Change”按钮在系数显示框中出现正确的系数值。
当在系数显示框中选中一个系数时话“Remove”按钮,单击该按钮将选中的系数清除。
④单击“Previous”或“Next”按钮显示输入的各组系数检查无误后,按“Continue”按钮确认输入的系数并返回到主对话框。
要的输入,单击“Cancel”按钮;需要查看系统的帮助信息,单击“Help”按钮。
子不做多项式比较的选择,选择缺省值。
5)设置多重比较在主对话框里单击“Post Hoc”按钮,将打开如图5-4所示的多重比较对话框。
该对话框用于设置多重比较和配对比较。
方差分析各组均值间存在差异显著,多重比较检测可以求出均值相等的组;配对比较可找出和其它组均值有差异的组,并输出显著性水平为值比较矩阵,在矩阵中用星号表示有差异的组。
图5-4 “Post Hoc Multiple Comparisons”对话框(1)多重比较的选择项:①方差具有齐次性时(Equal Variances Assumed),该矩形框中有如下方法供选择:LSD (Least-significant difference) 最小显著差数法,用t检验完成各组均值间的配对比较。
对多重比较误差率不进行调整Bonferroni (LSDMOD) 用t检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
Sidak 计算t统计量进行多重配对比较。
可以调整显著性水平,比Bofferroni方法的界限要小。
Scheffe对所有可能的组合进行同步进入的配对比较。
这些选择项可以同时选择若干个。
以便比较各种均值比较方法的结果。
R-E-G-WF (Ryan-Einot-Gabriel-Welsch F) 用F检验进行多重比较检验。
R-E-G-WQ (Ryan-Einot-Gabriel-Welsch range test) 正态分布范围进行多重配对比较。
S-N-K (Student-Newmnan-Keuls) 用Student Range分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了“Harmonic average of all groups”即用所有各组样本含量的调和平均数进行样本量估计时还用逐步过程进行齐次子集(差异小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小按顺序排列,最先比较最末端的差异。
Tukey (Tukey's,honestly signicant difference) 用Student-Range统计量进行所有组间均值的配对比较,用所有配对比较差率作为实验误差率。
Tukey's-b用“stndent Range”分布进行组间均值的配对比较。
其精确值为前两种检验相应值的平均值。
Duncan (Duncan's multiple range test) 新复极差法(SSR),指定一系列的“Range”值,逐步进行计算比较得出结论。
