最新专题训练(十)角的计算word版本

合集下载

(完整word版)三角形中有关角度的计算

三角形中有关角度的计算一.直接求角度1.如图，在锐角△ABC 中，CD 、BE 分别是AB 、AC 上的高,• 且CD 、BE 交于一点P ，若∠A=50°，求∠BPC的度数。

2。

所示，在△ABC 中，∠BAC=90°，AD ⊥BC 于D ，∠ACB 的平分线交AD 于E ，•交AB 于F ，请猜测∠AEF 与∠AFE 之间有怎样的数量关系，并说明理由．3.把一副三角板按如图方式放置,则两条斜边所形成的钝角α=_______度．4。

如图,在△ABC 中，∠B=66°，∠C=54°,AD 是∠BAC 的平分线，DE 平分∠ADC 交AC 于E,则∠BDE=_________．5。

如图,△ABC 中,∠ABC=∠C=72°，BD 平分∠ABC,求∠ADB 的度数.EFDACB 45α30D CBA6。

如图,△ABC 中，∠A=80°，∠B 、∠C 的角平分线相交于点O,∠ACD=30°，•求∠DOB 的度数。

7。

△ABC 的两条高AD ，CE 相交于点M ，已知∠A=30°，∠C=75°,求∠AMC8。

（1）在△ABC 中，AB=AC ，∠BAC=100°，ME 和NF 分别垂直平分AB 和AC ，求∠MAN•的度数．（2)在（1)中，若无AB=AC 的条件，你还能求出∠MAN 的度数吗？若能，请求出；•若不能,请说明理由．9.如图，在△ABC 中，∠ABC 的角平分线BE 和 ∠ACD 的角平分线CE 相交于点E ，（1）如果∠A=60°，∠ABC=50°，求∠E 的大小．（2）如果∠A=70°，∠ABC=40°,求∠E 的大小．（3）根据（1）和（2）的结论,试猜测一般情况下，∠E 和∠A 的大小关ODCBAME D CAEDCA系，并简要说明理由．二.设未知数求角度10.在△ABC 中，AB=AC ，CD 平分∠C ，∠ADC=150°，求∠B11.如图,△ABC 中，∠A=90°，∠C 的平分线交AB 于D ，已知∠DCB=2∠B 。

角的计算专项练习60题(有答案)ok

角的计算专项练习60题(有答案)ok角的计算练习60题（附参考答案）1．如图，已知∠BOC=2∠AOB，OD平分∠AOC，∠BOD=14°，求∠AOB的度数．2．已知∠1=35°，∠2= _________ ．3．计算出下列各角的度数．4．算一算，下面是一个直角三角形．∠1= _________∠2= _________∠3= _________ ．9．求下面各个三角形中∠A的度数10．如图中，已知∠1=43°，∠2= _________ ，∠3= _________ ．11．计算三角形中角的度数．∠1= _________ ，∠2= _________ ，∠3=_________ ．12．算一算：∠1= _________ ；∠2= _________ ；∠3=_________ ．13．算一算，这些角各是多少度．已知∠2=40°求得：∠1= _________ °，∠3= _________ °，∠4= _________ °．14．求出如图所示各角的度数．15．如图，已知∠l=20°，∠2=46°，求∠3的度数．16．如图所示，∠BOC=110°，∠AOB=∠DOC，∠AOB是几度？17．如图：∠1=48°；∠2= _________ ．18．算一算．已知∠1=65°，求出：∠2、∠3、∠4的度数．19．求下面各角的度数．图1，∠1= _________ ∠2= _________图2，∠1= _________ ．20．求下面各角的度数．已知∠1=30°，∠2=90°．∠3= _________ ；∠4= _________ ；∠5= _________ ．21．∠1=32゜，∠2=36゜，∠3= _________ ．22．如图已知∠1=35°，∠2= _________ ，∠3=_________ ，∠4= _________ ．23．如图所示，已知∠1=30°．求：∠2、∠3和∠4的度数．24．已知∠1=25°，∠2= _________ °，∠3= _________ °，∠4= _________ °．25．算一算：∠1= _________ ；∠2= _________ ；∠3=_________ ．26．角的计算（1）如图1所示，已知：∠1=72°，∠2=45°，求：∠AOB= _________ ？（2）如图2所示，已知：∠1=35°，求∠2= _________ ？27．用量角器量出图中∠2的度数，再求∠1、∠3和∠4的度数．28．如图，已知∠1=130°，求∠2、∠3的度数．29．如图中，∠AOB=14°，∠COB=∠COD，求∠COD．30．在直角∠AOB内有射线OC、OD．∠AOC=∠BOD=60°，求∠COD的大小．31．求下面各角的度数．∠A= _________ ∠B= _________ ∠B=∠C=_________ ∠C= _________ ．32．（1）如图1，已知：∠1=45°，求：∠2（2）如图2，已知：∠1=90°，∠2=30°求：∠3等于多少度？（3）如图3，已知：∠1=135°求：∠2、∠3、∠4各等于多少度？33．如图，已知∠1=70°，∠2=25°，∠3=50°，求∠5=？34．如图是一张长方形纸折起来以后的图形，已知么∠2是65°，∠1是多少度？35．已知∠1=28°求∠2、∠3、∠4和∠5各是多少度？36．算一算∠1=65°∠2= _________ ∠3= _________ ∠4=_________ ∠1+∠2+∠3+∠4= _________ ．37．求角的度数．（1）AB=AC（如图1）∠1= _________∠2= _________（2）三角形ABC是等腰三角形（如图2）∠1= _________∠2= _________ ．38．如图中∠1=30°，∠2= _________ ，∠3=_________ ，∠4= _________ ，∠5= _________ ．39．如图所示，∠1=55．，请分别求出∠2、∠3、∠4的度数．40．图中，已知∠1=37°∠2= _________ ；∠3= _________ ；∠4=_________ ．41．如图，已知∠1=40°，∠2= _________ ，∠3=_________ ，∠4= _________ ，∠3+∠4= _________42．图中∠1= _________ ，∠2= _________ ，∠3= _________ ，∠1+∠2= _________ ．43．已知∠1=50°，求∠2=？∠3=？44．算一算．已知∠1=36°；∠2= _________ ；∠3= _________ ；∠4= _________ ；∠5= _________ ．45．图中，∠1=55°，∠2是直角，你能求∠3、∠4、∠5各是多少度吗？46．先量一量，再填空．①∠1= _________ ，是_________ 角；∠2=_________ ，是_________ 角；∠3= _________ ，是_________ 角．②画出∠1，使∠1=75°．47．算一算如图：已知∠1=35°∠3= _________ ∠4= _________∠2= _________ ∠1+∠2+∠3= _________ ．48．如图1，已知∠1=40°，∠2= _________ ，∠3= _________ ，∠4= _________ ．如图2，已知∠1=30°，∠2= _________ ，∠3=_________ ，∠4= _________ ，∠5=_________ ．49．求各个角的度数．（1）图1中：已知∠1=60°∠2= _________∠3= _________∠4= _________∠5= _________（2）图2中：已知∠1=75°∠2= _________∠3= _________∠4= _________ ．50．分别量出图中4个角的度数，再求出这4个角的和．∠1= _________ ；∠2= _________ ；∠3=_________ ；∠4= _________ ；∠1+∠2+∠3+∠4= _________ ．51．∠1= _________ ；∠2= _________ ；∠3=_________ ．52．∠1= _________ ；∠2= _________ ；∠3=_________ ．53．已知∠1=90°，∠2=50°，求∠3、∠4和∠5的度数．54．如图，求∠1和∠2的度数．55．已知：∠1=∠3，∠2=40°求：∠ADE=？56．在下面三角形中，∠1=38°，∠2+∠3=90°，求∠3和∠4各是多少度？57．在三角形ABC中，∠l=60°，∠3=50°，求∠2、∠4的度数．58．如图，已知：∠2=30°，∠3是直角，则∠2+∠3=_________ ，∠1+∠2+∠4= _________ ，∠1+∠2+∠3+∠4= _________ ．59．求图中各角的度数．图1：∠2= _________ ∠3= _________ 图2：∠1= _________ ∠2= _________ ∠3= _________ ．60．看图填数．①如图一，已知∠1=75°，那么∠2= _________ ∠3= _________ ∠4= _________ ．②如图二，∠1= _________ ∠2= _________ ∠3= _________ ．角的计算参考答案：1．设∠AOB=x，∠BOC=2x．则∠AOC=3x．又OD平分∠AOC，因为∠AOD=x．所以∠BOD=∠AOD﹣∠AOB=x ﹣x=14°因为x=28°即∠AOB=28°．答：∠AOB的度数是28°2．∠2=180°﹣∠1，∠2=180°﹣35°，∠2=145°．故答案为：145°．3．（1）（180°﹣50°）÷2，=130°÷2，=65°．答：角的度数是65°．（2）180°﹣40°=140°．答：角的度数是140°4．∠2=90°﹣60°=30°；∠3=180°﹣50°=130°；∠1=180°﹣∠2﹣∠3=180°﹣30°﹣130°=20°．故答案为：20°；30°；130°5．在直角三角形ABD中，因为∠ADB=90°，所以∠2=180°﹣90°﹣42°，∠2=48°；在直角三角形ADC中，∠ADC=90°，所以∠3=180°﹣90°﹣36°，∠3=54°答：∠2和∠3分别是48°和54°．6．（1）∠1=180°﹣90°﹣25°=65°；（2）180°﹣25°﹣20°=135°；∠2=135°﹣90°=45°；（3）∠3=180°﹣∠1=180°﹣65°=115°．故答案为：65°，45°，115°7．∠1与∠2组成了一个平角，所以∠2=180°﹣30°=150°；∠1与∠3组成一个直角，所以∠3=90°﹣30°=60°；故答案为：150°；60°8．根据题干分析可得：∠1=180﹣90﹣45=45（度），∠3=180﹣45=135（度），∠2=180﹣135=45（度），故答案为：45°，45°，135°9．∠ABC=90°，∠ACB=60°．所以，∠BAC=90°﹣∠BAC=90°﹣60°=30°；∠A=180°﹣∠B﹣∠C=180°﹣135°﹣20°=25°10．（1）∠2=90°﹣∠1=90°﹣43°=47°；（2）∠3=180°﹣∠2=180°﹣47°=133°．故答案为：47°，133°11．（1）根据题干分析可得：∠2=65°；则∠1=180°﹣65°﹣65°=50°；（2）∠3=90°﹣41°=49°；故答案为：50°；65°；49°12．∠1=180°﹣45°﹣90°=45°；∠2=180°﹣45°=135°；∠3=180°﹣135°=45°．故答案为：45°；135°；45°．13．根据题干分析可得：∠1=90°﹣40°=50°；∠3=180°﹣40°=140°；∠4=180°﹣140°=40°；故答案为：50；140；40．14．∠A=180°﹣40°﹣85°=55°；∠B=180°﹣90°﹣35°=55°；∠C=180°﹣20°﹣47°=113°．如图所示：故答案为：55°、55°、113°15．∠4=180°﹣∠1﹣∠2，=180°﹣20°﹣46°，=114°，∠3=180°﹣∠4，=180°﹣114°，=66°．答：∠3是66°16．根据题干分析可得：（180﹣110）÷2，=70÷2，=35（度），答：∠AOB的度数是35度．17．∠2=90°﹣48°=42°，故答案为：42°18．∠1与∠3是对顶角，所以∠3也是65°；因为∠1与∠2组成了一个平角，∠2与∠4又是对顶角，所以∠2=∠4=180°﹣65°=115°，答：∠2=115°，∠3=65°，∠4=115°．19．（1）∠1=∠2=（180°﹣120°）÷2=30°；（2）90°﹣40°=50°；所以∠1=50°；故答案为：30°；30°；50°20．∠1和∠5组成了一个直角，所以∠5=90﹣30=60（度），∠5与∠4组成了一个平角，所以∠4=180﹣60=120（度）；因为∠5与∠3是一组对顶角，所以∠3=∠5=60（度），故答案为：60°；120°；60°21．180°﹣32°﹣36°=112°；故答案为：112°22．∠2=90°﹣∠1=90°﹣35°=55°，∠3=180°﹣∠2=180°﹣55°=125°，∠4=180°﹣∠3=180°﹣125°=55°，故答案为：55°，125°，55°．23．∠2=90°﹣30°=60°，∠3=180°﹣60°=120°，∠4=180°﹣120°=60°．答：∠2的度数是60°，∠3的度数是120°，∠4的度数是60°24．∠2=180°﹣∠1=155°，∠3=180°﹣∠2=25°，∠4=180°﹣∠1=155°．故答案为：155，25，155．25．∠1=180°﹣35°=145°；∠2=180°﹣90°=90°；∠3=180°﹣125°=55°．故答案为：145°；90°；55°26．（1）∠AOB=∠1+∠2=72°+45°=117°；（2）∠2=180°﹣90°﹣∠1=55°．故答案为：117°；55°．27．经测量可得∠2=35°，则∠1=90°﹣35°=55°，∠3=180°﹣35°=145°，∠4=180°﹣145°=35°．答：∠1的度数是55°，∠3的度数是145°，∠4的度数是35°28．∠2=180°﹣∠1=180°﹣130°=50°；∠3=90°﹣∠2=90°﹣50°=40°；答：∠2是50度，∠3是40度．29.（90°﹣14°）÷2，=76°÷2，=38°；答：∠COD=38°30．∠COD=∠AOC+∠BOD﹣∠AOB，=60°+60°﹣90°，=30°．答：∠COD的大小是30°．31．（1）∠A=90°﹣34°=56°；（2）∠C=180°﹣90°﹣18°=72°，∠B=180°﹣60°﹣72°=48°；（3）∠B=∠C=（180°﹣48°）÷2=66°；（4）∠A=180°﹣119°=61°，∠C=90°﹣61°=29°．故答案为：56°；48°；66°；29°32．（1）∠2=180°﹣∠1=180°﹣45°=135°．（2）∠3=180°﹣∠1﹣∠2=180﹣90°﹣30°=60°．（3）∠3=180°﹣∠1=180°﹣135°=45°，∠4=180°﹣∠1=180°﹣135°=45°，∠2=180°﹣∠3=180°﹣45°=135°33．在小三角形里最大的角=180°﹣∠2﹣∠3=105°，∠4=180°﹣105°=75°，∠5=180°﹣∠1﹣∠4，=180°﹣70°﹣75°，=35°．答：∠5是35°34．180°﹣65°×2=180°﹣130°=50°．答：∠1是50度．35．∠4=90°，∠5=90°﹣∠1=90°﹣28°=62°，∠2=180°﹣∠1=180°﹣28°=152°，∠3=180°﹣∠2=180°﹣152°=28°；答：∠2=152°，∠3=28°，∠4=90°，∠5=62°．36．（1））∠2=90°﹣∠1，=90°﹣65°，=25°；（2））∠3=180°﹣∠2，=180°﹣25°，=155°；（3））∠4=180°﹣∠3，=180°﹣155°，=25°；（4））∠1+∠2+∠3+∠4=360°﹣90°，=270°．或∠1+∠2+∠3+∠4=65°+25°+155°+25°=270°．故答案为：25°；155°；25°；270°37．（1）∠C=180°﹣120°=60°，∠1=90°﹣∠C=90°﹣60°=30°；∠2=180°﹣60°×2=60°；（2）∠1=90°﹣60°=30°；∠2=180°﹣∠1×2﹣90°，=180°﹣30°×2﹣90°，=30°．故答案为：（1）30°，60°；（2）30°，30°38．根据题干分析可得：∠3=90°；∠2=90°﹣30°=60°；∠4=∠1=30°；∠5=180°﹣30°=150°；故答案为：60°；90°；30°；15039．如图：∠4=90°﹣∠1，=90°﹣55°，=35°，∠3=180°﹣∠4﹣∠5，=180°﹣35°﹣90°，=55°，∠2=180°﹣∠3，=180°﹣55°，=125°，答：∠2是125°、∠3是55°、∠4是35°40．∠2=90°﹣∠1=90°﹣37°=53°，∠3=180°﹣∠2=180°﹣53°=127°，∠4=180°﹣∠3=180°﹣127°=53°故答案为：53°，127°，53°41．∠2=∠4=180°﹣40°=140°，∠3=180°﹣∠2=40°，∠3+∠4=180°．故答案为：140°，40°，140°，180°42．∠1=90﹣50=40（度）；∠2=90﹣40=50（度）；∠3=180﹣50=130（度）；∠1+∠2=90（度）；故答案为：40°；50°；130°；90°43．∠2=180°﹣50°=130°，∠3=180°﹣90°=90°．答：∠2=130°，∠3=90°．44．根据题干分析可得：∠3是直角，是90°；∠2=90°﹣36°=54°；∠4=90°﹣54°=36°；∠5=180°﹣36°=144°，故答案为：54°；90°；36°；144°45．∠3=90°﹣55°=35°，∠5=180°﹣55°=125°，∠4=180°﹣125°=55°．答：∠3=35°、∠4=55°、∠5=125°46．（1）经过测量可知∠1=50°，是锐角，∠2=40°，是锐角，∠3=120°，是钝角；（2）根据分析画图如下：故答案为：50°；锐；4°；锐；120°；钝47．∠2=180°﹣∠1=180°﹣35°=145°，∠3=180°﹣∠2=180°﹣145°=35°，∠4=90°，∠1+∠2+∠3=35°+145°+35°=215°．故答案为：35°，90°，145°，215°48．图一：因为，∠1=40°．所以，∠2=180°﹣40°=140°；∠3=180°﹣140°=40°；∠4=180°﹣40°=140°；图二：因为，∠1=30°．所以，∠2=90°﹣30°=60°；∠3=90°；∠4=180°﹣60°﹣90°=30°；∠5=180°﹣30°=150°；故答案为：140°，40°，140°，60°，90°，30°，150°49．（1）因为∠2=90°，平角=180°，所以，∠3=180°﹣∠1﹣∠2=180°﹣90°﹣60°=30°；∠5=180°﹣∠1=180°﹣60°=120°；∠4=180°﹣∠5=180°﹣120°=60°；（2）因为∠1=75°，平角=180°，所以，∠2=180°﹣∠1=180°﹣75°=105°；∠4=180°﹣∠1=180°﹣75°=105°；∠3=180°﹣∠4=180°﹣105°=75°；故答案为：90°，30°，60°，120°，105°，75°，105°50．测量可得图中∠1=90°，∠2=45°，∠3=90°，∠4=135°．∠1+∠2+∠3+∠4=90°+45°+90°+135°=360°．故答案为：90°，45°，90°，135°．360°51．观察图形可知：∠3=90°；∠1=180﹣35=145（度）；∠2=90﹣30=60（度）；故答案为：145°；60°；90°52．因为∠1是等腰直角三角形底角，所以∠1=90°÷2=45°；因为正方形的两条对角线互相垂直，所以∠2=∠3=90°．故答案为：45°；90°；90°53．（1）∠3=180°﹣∠2=180°﹣50°=130°；（2）∠4=180°﹣∠3=180°﹣130°=50°；（3）∠5=180°﹣∠1﹣∠2=180°﹣90°﹣50°=40°．故答案为：∠3=130°，∠4=50°，∠5=40°54．∠1=180°﹣90°﹣65°=25°；∠2=180°﹣120°=60°．答：∠1的度数是25°；∠2的度数是60°．55．∠ADE=（180°﹣40°）÷2+40°，=140°÷2+40°，=70°+40°，=110°．答：∠ADE是110°．56．∠4=180°﹣∠1﹣（∠2+∠3），∠4=180°﹣38°﹣90°，∠4=52°；∠3=180°﹣90°﹣∠4，∠3=180°﹣90°﹣52°，∠3=38°．答：∠3是38°，∠4是52°57．因为∠1+∠3+∠4=180°，∠l=60°，∠3=50°，所以∠4=180°﹣60°﹣50°=70°；因为∠6=90°，所以∠2=90°﹣∠3，=90°﹣50°，=40°58．∠2+∠3=30°+90°=120°；∠1+∠2+∠3+∠4=360°；∠1+∠2+∠4=360°﹣90°=270°．故答案为：120°，270°，360°．59.（1）∠2=90°=50°=40°；∠3=180°﹣（40°+30°）=110°；（2）∠1=180°﹣120°=60°；∠2=180°﹣（60°+45°），=180°﹣105°，=75°；∠3=180°﹣75°=105°．故答案为：40°、110°；60°、75°、60．因为∠1+∠2=180°，∠1=75°，所以75°+∠2=180°，75°﹣75°+∠2=180°﹣75°，∠2=105°；因为∠1与∠3，∠2与∠4，分别是对顶角，所以∠1=∠3=75°，∠2=∠4=105°；（2）因为∠1+35°=180°，∠1+35°﹣35°=180°﹣35°，∠1=145°；因为∠2+30°=90°，∠2+30°﹣30°=90°﹣30°，∠2=60°；因为∠3是一个直角，所以∠3=90°；故答案为：（1）105°，75°，105°．（2）145°，60°，90°．。

(完整word版)数学小学四年级角的运算

一、填空题。

1.从一点引出两条()所构成的图形叫做角，这个点叫做角的() ，这两条射线叫做角的()。

2.角的两边在一条直线上，这样的角叫做()角，它有 ()度。

3.量角的大小，要用到（）、计量角的单位是(),用符号（）来表示。

把半圆均匀分红（
每一份所对的角的大小是（），记做（），五份表示（）。

），
4.角的两条边在一条直线上，
5.1 周角 =()平角 =(
这样的角叫做（）。

一条射线绕着它的端点旋转一周所成的角叫做
)直角 =()45°的角。

（）。

6、３时整，钟面上的时针与分针成（）；６时整成（），钟面上（）时，时针与分针所成的角度是１５０度的角。

7.∠ 1+ ∠ 2+∠3=180 °，此中∠1=52°，∠2=46°，那么∠3=()。

8.∠1 是∠ 2的 3 倍，∠ 1=120°，∠2=() 。

9、三角板上的角有（）度、（）度、（）度、（）度。

(word完整版)角的度量练习题 (1)

角的度量练习题一、填空1.从一点引出两条（ )所组成的图形叫做角,这个点叫做角的（），这两条射线叫做角的( )。

2。

计量角的大小的单位是（ )。

3.在一个直角三角形中，有两个相等的角，那么这两个角都是( )。

4.用一副三角尺中( )度和（）度的角可以拼成105度的角。

二、精心挑选1.度量一个角，角的一条边对着量角器上内圈“0"的刻度，另一条边对着内圈刻度“60",这个角是（）.A。

60度 B.180度 C.20度2.一个5倍的放大镜看一个15度的角，这个角是( ）。

A。

15度 B.20度 C.75度3。

度量一个角，角的一条边对着量角器上内圈“180"的刻度，另一条边对着内圈刻度“60"，这个角是( ）.A。

60度 B。

120度 C.无法确定三、量一量1.量出下面各角的度数。

（）度 ( ）度 ( )度（）度 ( ）度 ( ）度2。

量出下面各图中角的度数。

三个角的度数和是（ ) 三个角的度数和是( )四个角的度数和是（ ) 四个角的度数和是( ）1．下图中④是直线，①是射线，②是线段．⑦是锐角,⑧是平角，⑨是周角，⑥是钝角．2．从一点引出两条射线，所组成的图形叫作角．这两条射线叫作角的边，角通常用符号∠来表示．．量角时，量角器的中心与重合，零刻度与重合,角的另一条边所对的量角器上的刻度，就是这个角的．重合，零刻度与重合，角的另一条边所对的量角器上的刻度，就是这个角的11．看图计算．①如图∠1=50°,求∠2、∠3、∠4的度数．②已知,图中∠1=30°，∠3=90°，求∠2、∠4、∠5、∠6各是多少度？③已知图中∠1=30°，∠3=40°，求∠2、∠4、∠5各是多少度？12．下图是一个大型花池中小路的平面图，你能否不重复地一次走完所有的小路?进口、出口应分别设在什么地方?一、填空题（每空1分，共20分)1、角是从一点引出的两条（ )所组成的图形，这一点是角的( ）,两条射线是角的（）。

新人教版七年级数学上册专题训练：角的计算(含答案).优选

因为∠AOB＝2∠BOC，所以∠BOC＝2x°. 所以 3x＋3x＋2x＋x＝360. 解得 x＝40. 所以∠AOB＝40°，∠COD＝120°.
类型 4 利用分类讨论思想求解在角度计算中，如果题目中无图，或补全图形时，常需分类讨论，确保答案的完整性． 2
8．已知∠AOB＝75°，∠AOC＝3∠AOB，OD 平分∠AOC，求∠BOD 的大小． 2
专题训练角的计算
类型 1 利用角度的和、差关系找出待求的角与已知角的和、差关系，根据角度和、差来计算．
1．如图，已知∠AOC＝∠BOD＝75°，∠BOC＝30°，求∠AOD 的度数．
解：因为∠AOC＝75°，∠BOC＝30°，所以∠AO B＝∠AOC－∠BOC＝75°－30°＝45°. 又因为∠BOD＝75°，所以∠AOD＝∠AOB＋∠BOD＝45°＋75°＝120°.
数，建立方程，通过解方程使问题得以解决． 2
5．一个角的余角比它的补角的3还少 40°，求这个角的度数．解：设这个角的度数为 x°，根据题意，得 2 90－x＝3(180－x)－40. 解得 x＝30. 所以这个角的度数是 30°.
6．如图，已知∠AOE是平角，∠DOE＝20°，OB 平分∠AOC，且∠COD∶∠BOC＝2∶3，求∠BOC的度数．
专题训练整式的加减运算
计算： (1)(钦南期末)a2b＋3ab2－a2b；解：原式＝3ab2.
(2)2(a－1)－(2a－3)＋3；解：原式＝4.
(3)2(2a2＋9b)＋3(－5a2－4b)；解：原式＝－11a2＋6b.
(4)3(x3＋2x2－1)－(3x3＋4x2－2)；解：原式＝2x2－ 1.
解：(1)因为 OC 是∠AOB 的平分线， 1

角的计算题20道初一

角的计算题20道初一1.已知一个角的补角是它的余角的3倍，求这个角的度数。

2.已知一个角的余角比它的补角的31还小10°，求这个角。

3.一个角的补角比它的余角的2倍大90°，求这个角。

4.已知一个角的余角等于45∘，求这个角。

5.已知一个角的补角是130∘，求这个角。

6.一个角的补角与它的余角的和等于180∘，求这个角。

7.已知两个角的和是180∘，其中一个角比另一个角的3倍还多10∘，求这两个角的度数。

8.一个角的补角与它的余角的2倍的和等于270∘，求这个角的余角。

9.一个角的补角比它的余角的4倍少15∘，求这个角的度数。

10.一个角的余角比它的补角的61大10∘，求这个角的余角及补角。

11.一个角的补角与它的余角的3倍的和等于90∘，求这个角的度数。

12.两个角的和是90∘，其中一个角是另一个角的4倍，求这两个角的度数。

13.一个角的补角是它的3倍，求这个角的余角。

14.已知一个角的补角比它的余角的2倍多45∘，求这个角的度数。

15.一个角的余角比它的补角小54∘，求这个角的度数。

16.两个角的和是180∘，且它们的差是30∘，求这两个角的度数。

17.一个角的补角比它的余角的5倍还多20∘，求这个角的度数。

18.已知两个角的和是90∘，且其中一个角是另一个角的2倍多15∘，求这两个角的度数。

19.一个角的补角比它的余角的6倍小30∘，求这个角的度数。

20.一个角的补角是它的余角的7倍，求这个角的度数。

角的度量练习题带答案

角的度量练习题带答案角的度量是数学中的一个重要概念，它涉及到角度的计算和度量单位。

以下是一些角的度量练习题及其答案，以帮助学生更好地理解和掌握这一概念。

练习题1：一个角的度数是30°，另一个角是它的两倍，求另一个角的度数。

答案：30° × 2 = 60°练习题2：如果一个角的度数是90°，它是一个直角。

那么一个角的度数是45°，它是什么角？答案：45°是一个锐角。

练习题3：一个角的度数是120°，它比直角大多少度？答案：120° - 90° = 30°练习题4：一个角的度数是360°，它是一个周角。

如果将它平均分成4个相等的角，每个角的度数是多少？答案：360° ÷ 4 = 90°练习题5：一个角的度数是180°，它是一个平角。

如果将它平均分成3个相等的角，每个角的度数是多少？答案：180° ÷ 3 = 60°练习题6：一个角的度数是15°，它是一个锐角。

如果将它扩大到原来的3倍，新的角的度数是多少？答案：15° × 3 = 45°练习题7：一个角的度数是150°，它是一个钝角。

如果将它缩小到原来的一半，新的角的度数是多少？答案：150° ÷ 2 = 75°练习题8：如果一个角的度数是75°，它是一个钝角。

那么一个角的度数是75°的三分之一，这个角的度数是多少？答案：75° ÷ 3 = 25°练习题9：一个角的度数是300°，它是一个周角的四分之三。

求这个周角的度数。

答案：300° ÷ (3/4) = 400°练习题10：一个角的度数是40°，另一个角的度数是它的补角。

求角的度数的练习题

求角的度数的练习题一、基础题1. 已知∠A = 30°，求∠A的补角。

2. 已知∠B = 135°，求∠B的余角。

3. 在等腰三角形ABC中，若∠A = 70°，求∠B的度数。

4. 已知平行线l1和l2，∠1 = 55°，求同旁内角∠2的度数。

5. 在直角三角形DEF中，若∠D = 90°，∠E = 35°，求∠F的度数。

二、进阶题1. 在四边形ABCD中，已知∠A + ∠B = 180°，∠C = 100°，求∠D的度数。

2. 已知等边三角形XYZ的边长为6cm，求∠X的度数。

3. 在梯形MNOP中，MN ∥ OP，∠M = 120°，求∠P的度数。

4. 已知圆的周角∠SOR = 50°，求圆心角∠SOT的度数。

5. 在五边形ABCDE中，已知∠A + ∠B + ∠C + ∠D + ∠E = 540°，且∠A = ∠B = ∠C，求∠A的度数。

三、综合题1. 在凸六边形ABCDEF中，已知∠A = 120°，∠B = 100°，∠C = 110°，∠D = 90°，求∠E和∠F的度数。

2. 已知等腰梯形GHJK中，GH ∥ KJ，∠G = 105°，求∠H和∠K 的度数。

3. 在正五边形ABCDE中，求一个内角的度数。

4. 已知圆的半径为r，圆心角∠AOB = 80°，求弧AB所对应的圆心角的度数。

5. 在平行四边形STUV中，已知∠S = 120°，求其他三个角的度数。

四、挑战题1. 在正七边形ABCDEF中，求一个外角的度数。

2. 已知凸多边形有10个内角，且所有内角之和为1440°，求该多边形一个内角的度数。

3. 在圆中，已知弧MN的长度是弧PQ长度的两倍，求弧MN所对应的圆心角的度数。

4. 在矩形WXYZ中，已知∠W = 90°，求其他三个角的度数。

2019年年秋人教版七年级数学上册(河南专版)作业课件：专题训练(十) 角的计算(共19张PPT)精品物理

8．已知∠AOB＝60°，从点O引射线OC，使∠AOC＝40°，作∠AOC 的角平分线OD，
(1)依题意画出图形； (2)求∠BOD的度数．
解：(1)分两种情况讨论：当∠AOC 在∠AOB 的外部时，如图①；当∠AOC 在∠AOB 的内部时，如图②
(2)如图①，∵射线 OD 平分∠AOC，∴∠AOD＝12∠AOC＝20°，∴∠BOD
解：∵∠AOB＝90°，OC 平分∠AOB，∴∠BOC＝12∠AOB＝45°，∵ ∠BOD＝∠COD－∠BOC＝90°－45°＝45°，∠BOD＝3∠DOE，∴∠DOE ＝15°，∴∠COE＝∠COD－∠DOE＝90°－15°＝75°
类型二：方程思想 4 ．如图，已知 ∠ AOE 是平角， ∠ DOE ＝ 20° ， OB 平分 ∠ AOC ，且 ∠COD∶∠BOC＝2∶3，求∠BOC的度数．
人教版
第四章几何图形初步
专题训练(十) 角的计算
类型一：直接计算 1．如图，∠AOC＝∠BOD，∠AOD＝120°，∠BOC＝70°，求∠AOB 的度数．
解：∵∠AOB＝AOC－∠BOC，∠DOC＝∠BOD－∠BOC，又∵∠AOC ＝∠BOD，∴∠AOB＝∠COD，∵∠AOB＋∠BOC＋∠COD＝∠AOD，∴∠ AOB＝12(∠AOD－∠BOC)＝12(120°－70°)＝25°
解：设∠COD＝2x°，则∠BOC＝3x°，∵OB平分∠AOC，∴∠AOB ＝3x°.∴2x＋3x＋3x＋20＝180.解得x＝20.∴∠BOC＝3×20°＝60°
5．如图，已知BC平分∠DBE，BA分∠DBE成3∶4两部分，若∠ABC＝ 8°，求∠DBE的度数．
解：设∠DBA＝3x°，则∠ABE＝4x°，∠DBE＝7x°，∵BC 平分∠DBE， ∴∠DBC＝12∠DBE＝72x°，∴∠ABC＝∠DBC－∠DBA＝72x°－3x°＝12x°， ∵∠ABC＝8°，∴12x°＝8°，解得 x＝16，∴∠DBE＝7x°＝7×16°＝112 °

角的相关计算和证明学案,附练习题含详细参考答案

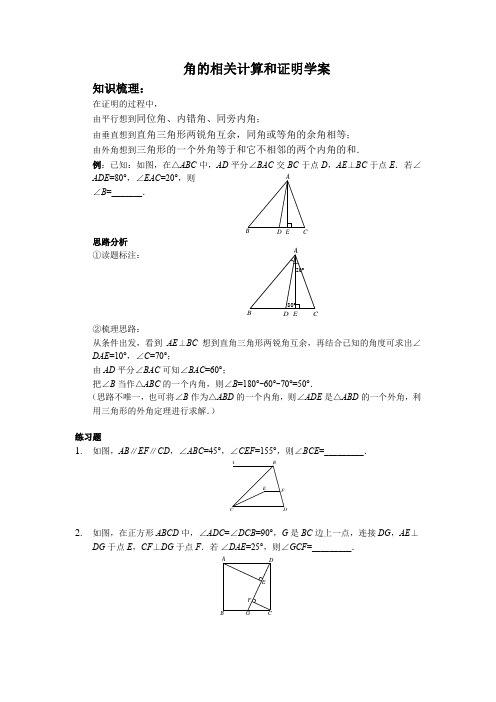
角的相关计算和证明学案知识梳理：在证明的过程中，由平行想到同位角、内错角、同旁内角；由垂直想到直角三角形两锐角互余，同角或等角的余角相等；由外角想到三角形的一个外角等于和它不相邻的两个内角的和．例：已知：如图，在△ABC 中，AD 平分∠BAC 交BC 于点D ，AE ⊥BC 于点E ．若∠ADE =80°，∠EAC =20°，则 ∠B =_______．思路分析 ①读题标注：②梳理思路：从条件出发，看到AE ⊥BC 想到直角三角形两锐角互余，再结合已知的角度可求出∠DAE =10°，∠C =70°；由AD 平分∠BAC 可知∠BAC =60°；把∠B 当作△ABC 的一个内角，则∠B =180°-60°-70°=50°．（思路不唯一，也可将∠B 作为△ABD 的一个内角，则∠ADE 是△ABD 的一个外角，利用三角形的外角定理进行求解．）练习题1. 如图，AB ∥EF ∥CD ，∠ABC =45°，∠CEF =155°，则∠BCE =_________．2. 如图，在正方形ABCD 中，∠ADC =∠DCB =90°，G 是BC 边上一点，连接DG ，AE ⊥DG 于点E ，CF ⊥DG 于点F ．若∠DAE =25°，则∠GCF =_________．F EDCBAG FE DCB AB D E CA20°80°ACE D B3. 已知：如图，在Rt △ABC 中，∠BAC =90°，∠C =45°，在Rt △AFG 中，∠G =90°，∠F AG =45°，∠CAG =20°，则∠AEB =_______，∠ADC =________．4. 如图，点F 是△ABC 边BC 延长线上一点，EF ∥AC ，过点E 作ED ⊥AB 于点D ，交AC于点G ．若∠A =35°，则∠DEF =______．5. 如图，在△ABC 中，∠B =60°，P 为BC 上一点，且∠1=∠2，则∠APD =________．6. 已知：如图，直线BD 交CF 于点D ，交AE 于点B ，连接AD ，BC ，∠1+∠2=180°，∠A =∠C ．求证：DA ∥CB ．证明：如图，∵∠1+∠2=180° （__________________________） ∠2+∠CDB =180° （__________________________） ∴_______=_______（__________________________）∴______∥________ （__________________________） ∴∠A +∠CDA =180° （__________________________） ∵∠A =∠C （__________________________） ∴______+______=180°（__________________________）∴DA ∥CB （__________________________）7. 已知：如图，E ，F 分别在AB ，CD 上，EC ⊥AF ，垂足为点O ，∠1+∠C =90°，∠2=∠D ．求证：AB ∥CD ．GFE DCBAG FEDCBA21PDCBA 21O E FDCBA第6题图21F EDCBA8. 如图，在△ABC 中，∠B =35°，∠C =75°，AD ⊥BC 于D ，AE 平分∠BAC ，求∠EAD 的度数．9. 已知：如图，点E 是△ABC 边BC 延长线上一点，BP 平分∠ABC ，CP 平分△ABC 的外角∠ACE ．求证：∠A =2∠P ．证明：如图，设∠PBC =α，∠PCE =β ∵BP 平分∠ABC （_____________________） ∴∠ABC =2∠PBC =2α （_____________________） ∵CP 平分∠ACE（_____________________）∴∠ACE =______=_______ （_____________________） ∵∠ACE 是△ABC 的一个外角（_____________________） ∴∠ACE =∠ABC +∠A （_____________________） ∴2β=2α+∠A（_____________________）∴∠A =2(β-α) （_____________________） ∵∠PCE 是△BCP 的一个外角（_____________________） ∴∠PCE =∠PBC +∠P（_____________________）∴β=______+_______ （_____________________） ∴∠P =β-α （_____________________） ∴∠A =2∠P （_____________________）10. 已知：如图，在△ABC 中，∠B =∠ACB ，CD ⊥AB ，垂足D ．求证：∠A =2∠BCD ．E DC APEC B AD CBA11. 已知：如图，在△ABC 中，∠A =30°，∠B =70°，CE 平分∠ACB ，CD ⊥AB 于D ，DF ⊥CE 于F ，则∠FDE 的度数是_______．12. 已知：如图，CD ∥AB ，∠DCB =70°，∠CBF =20°，∠F =130°．求证：EF ∥AB ．证明：如图，13. 已知：如图，AB ⊥BD 于点B ，ED ⊥BD 于点D ，C 是线段BD 上一点．若AC ⊥CE ，∠A =30°，则∠E =______．第13题图第14题图 14. 已知：如图，△ABC 为直角三角形，∠C =90°，若沿图中虚线剪去∠C ，则∠1+∠2=____________．15. 已知：如图，∠A =32°，∠B =45°，∠C =38°，则∠DFE =（）A ．120°B ．115°C ．110°D ．105°第15题图第16题图16. 已知：如图，在△ABC 中，∠A :∠B =1:2，DE ⊥AB 于E ，且∠FCD =60°，则∠D =（）A ．50°B ．60°C ．70°D ．80°EF D CBAAB C DE21C B AD AF EBC FD AFEDC BA17. 已知：如图，在△ABC 中，BD 平分∠ABC ，CD 平分∠ACB ．求证：．证明：如图，设∠DBC =α，∠DCB =β ∵BD 平分∠ABC （__________________________） ∴∠ABC =2∠DBC =2α （__________________________） ∵CD 平分∠ACB（__________________________）∴∠ACB =______=_____ （__________________________） ∵∠ABC +∠ACB +∠A =180°（________________________） ∴2α+2β+∠A =180°（等量代换）∴α+β=_______________ （等式性质） ∵∠DBC +∠DCB +∠D =180° （_______________________） ∴____________________（__________________________） ∴α+β=______________（__________________________）∴ （等量代换） ∴ （等式性质）18. 已知：如图，AB ∥DE ，∠1=∠ACB ，AC 平分∠BAD ．求证：AD ∥BC ．19. 已知：如图，在△ABC 中，AD 平分∠BAC ，EF ⊥AD 于点P ，交BC 的延长线于点M ．已知∠ACB =70°，∠B =40°，求∠M 的度数．1902D A ∠=︒+∠190=1802A D ︒-︒-∠∠1902D A ∠=︒+∠A BCDA B CDE F1BCDMPF AE【参考答案】1. 20°2. 25°3. 65°，70°4. 125°5. 60°6.已知，平角的定义，∠1，∠CDB ；同角的补角相等AB ，CD ；同位角相等，两直线平行，两直线平行，同旁内角互补已知，∠C ，∠CDA ；等量代换，同旁内角互补，两直线平行 7. 证明：如图，∵EC ⊥AF（已知）∴∠COF =90° （垂直的定义） ∴∠C +∠2=90° （直角三角形两锐角互余） ∵∠1+∠C =90 （已知）∴∠1=∠2（同角的余角相等） ∵∠2=∠D （已知） ∴∠1=∠D （等量代换）∴AB ∥CD（内错角相等，两直线平行）8. 解：如图，在△ABC 中，∠B =35°，∠C =75° （已知）∴∠BAC =180°-∠B -∠C=180°-35°-75° =70°（三角形的内角和等于180°） ∵AE 平分∠BAC（已知）∴∠BAE =12∠BAC=12×70° =35°（角平分线的定义）∵∠AED 是△ABE 的一个外角（外角的定义） ∴∠AED =∠B +∠BAE=35°+35° =70° （三角形的一个外角等于和它不相邻的两个内角的和） ∵AD ⊥BC（已知） ∴∠ADE =90°（垂直的定义）21O E FD CBAE DCBA∴∠EAD =90°-∠AED=90°-70° =20°（直角三角形两锐角互余）9. 已知，角平分线的定义，已知2∠PCE ，2β；角平分线的定义，外角的定义三角形的一个外角等于和它不相邻的两个内角的和，等量代换等式性质，外角的定义三角形的一个外角等于和它不相邻的两个内角的和，α，∠P ；等量代换等式性质，等量代换 10. 证明：如图，设∠B =∠ACB =α，在△ABC 中，∠B =∠ACB =α（已知） ∴∠A =180°-∠B -∠ACB=180°-2α（三角形的内角和等于180°） ∵CD ⊥AB （已知）∴∠BDC =90°（垂直的定义）∴∠B +∠BCD =90°（直角三角形两锐角互余） ∴∠BCD =90°-∠B=90°-α（等式的性质）∴∠A =2∠BCD （等量代换） 11. 20°12. 证明：如图，∵CD ∥AB （已知）∴∠DCB =∠ABC （两直线平行，内错角相等） ∵∠DCB=70° （已知） ∴∠ABC =70° （等量代换） ∵∠CBF =20°（已知） ∴∠FBA =∠ABC -∠CBF =70°-20°=50°（等式的性质） ∵∠F =130° （已知）∴∠FBA+∠F=50°+130°=180°（等式的性质） ∴EF ∥AB （同旁内角互补，两直线平行）13. 60° 14. 270° 15. BFEDCBA D CBA16.A17.已知，角平分线的定义，已知，2∠DCB，2β；角平分线的定义三角形的内角和等于180°，1902A︒-∠，三角形的内角和等于180°α+β+∠D=180°，等量代换，180°-∠D，等式性质18.证明：如图，∵AB∥DE（已知）∴∠1=∠BAC（两直线平行，同位角相等）∵AC平分∠BAD（已知）∴∠DAC=∠BAC（角平分线的定义）∴∠1=∠DAC（等量代换）∵∠1=∠ACB （已知）∴∠DAC=∠ACB（等量代换）∴AD∥BC （内错角相等，两直线平行）19.解：如图，在△ABC中，∠ACB=70°，∠B=40°（已知）∴∠BAC=180°-∠ACB-∠B=180°-70°-40°=70°（三角形的内角和等于180°）∵AD平分∠BAC（已知）∴∠DAC=12∠BAC=12×70°=35°（角平分线的定义）∵EF⊥AD（已知）∴∠APF=90°（垂直的定义）∴∠AFP+∠DAC=90°（直角三角形两锐角互余）∴∠AFP=90°-∠DAC=90°-35°=55°（等式性质）∵∠CFM=∠AFP（对顶角相等）∴∠CFM=55°（等量代换）∵∠ACB是△CFM的一个外角（外角的定义）∴∠ACB=∠CFM+∠M（三角形的一个外角等于和它不相邻的两个内角的和）∴∠M=∠ACB-∠CFM=70°-55°=15°（等式性质）。

角的计算精选练习题

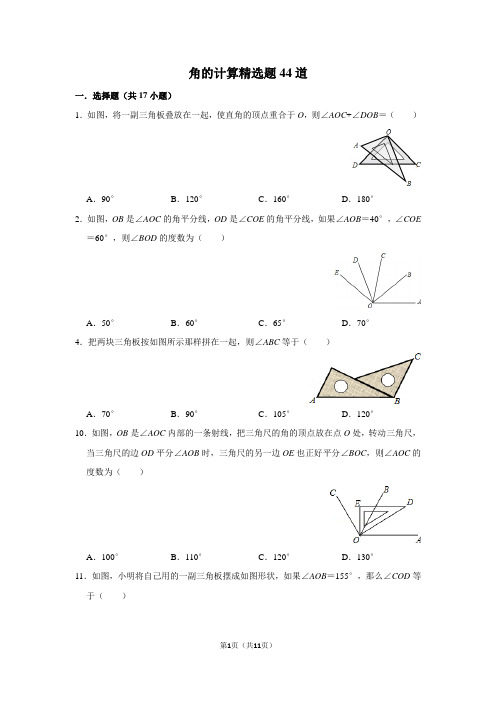
角的计算精选题44道一．选择题（共17小题）1．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB＝（）A．90°B．120°C．160°D．180°2．如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB＝40°，∠COE ＝60°，则∠BOD的度数为（）A．50°B．60°C．65°D．70°4．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°10．如图，OB是∠AOC内部的一条射线，把三角尺的角的顶点放在点O处，转动三角尺，当三角尺的边OD平分∠AOB时，三角尺的另一边OE也正好平分∠BOC，则∠AOC的度数为（）A．100°B．110°C．120°D．130°11．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB＝155°，那么∠COD等于（）A．15°B．25°C．35°D．45°16．如图，是一副特制的三角板，用它们可以画出一些特殊角．在下列选项中，不能画出的角度是（）A．18°B．55°C．63°D．117°12．如图，两块直角三角板的直角顶点O重合在一起，若∠BOC=17∠AOD，则∠BOC的度数为（）A．22.5°B．30°C．45°D．60°6．将长方形纸片按如图所示的方式折叠，BC、BD为折痕，若∠ABC＝35°，则∠DBE的度数为（）A．55°B．50°C．45°D．60°3．如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（）A．90°＜α＜180°B．0°＜α＜90°C．α＝90°D．α随折痕GF位置的变化而变化5．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°7．如图，已知∠AOB＝120°，∠COD在∠AOB内部且∠COD＝60°，则∠AOD与∠COB 一定满足的关系为（）A．∠AOD＝∠COB B．∠AOD+∠COB＝180°C．∠AOD=12∠COB D．∠AOD+∠COB＝120°8．如图所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）A．20°B．25°C．30°D．70°9．如图，将三个同样的正方形的一个顶点重合放置，如果∠1＝α，∠2＝β，那么∠3的度数是（）A．90°﹣α﹣βB．90°﹣α+βC．90°+α﹣βD．α﹣β13．如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．若∠DOC ＝70°，则∠BOE的度数是（）A．30°B．40°C．25°D．20°14．如图，∠AOD＝150°，∠BOC＝30°，∠BOC绕点O逆时针在∠AOD的内部旋转，其中OM平分∠AOC，ON平分∠BOD，在∠BOC从OB与OA重合时开始到OC与OD 重合为止，以每秒2°的速度旋转过程中，下列结论其中正确的是（）（1）射线OM的旋转速度为每秒2°；（2）当∠AON＝90°时间为15秒；（3）∠MON的大小为60°．A．（1）（2）（3）B．（2）（3）C．（1）（2）D．（3）15．如图，点O为直线AB上一点，∠COB＝27°29′，则∠1＝（）A．152°31′B．153°31′C．162°31′D．163°31′17．如图，已知∠AOB＝26°，∠AOE＝120°，OB平分∠AOC，OD平分∠AOE，则∠COD 的度数为（）A．8°B．10°C．12°D．18°二．填空题（共17小题）18．如图，将一副直角三角板叠在一起，使直角顶点重合于点O，则∠AOB+∠DOC＝度．24．一副三角板如图放置，将三角板ADE绕点A逆时针旋转α（0°＜α＜90°），使得三角板ADE的一边所在的直线与BC垂直，则α的度数为．25．将一副三角板如图摆放，若∠BAE＝135°17′，则∠CAD的度数是．33．如图，一副三角板如图示摆放，∠α与∠β的度数之间的关系应为．19．将矩形ABCD沿AE折叠，得到如图的图形．已知∠CEB′＝50°，则∠AEB′＝°．20．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕．若∠ABE＝30°，则∠DBC 为度．22．如图，将三个同样的正方形的一个顶点重合放置，那么∠1的度数为．23．将一张长方形纸片折叠成如图所示的形状，则∠ABC的度数．26．如图，在正方形网格中，点O、A、B、C、D均是格点．若OE平分∠BOC，则∠DOE 的度数为°．27．将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为．34．把一张长方形纸条按图的方式折叠后，量得∠AOB′＝110°，则∠B′OC＝．28．小明将一张正方形纸片按如图所示顺序折叠成纸飞机，当机翼展开在同一平面时（机翼间无缝隙），∠AOB的度数是．29．以∠AOB的顶点O为端点引射线OC，使∠AOC：∠BOC＝5：4，若∠AOB＝27°，则∠AOC＝．21．如图，点A、O、B在一条直线上，且∠AOC＝50°，OD平分∠AOC，则∠BOD＝度．30．如图，∠AOD＝135°，∠AOC＝75°，∠DOB＝105°，则∠BOC＝．31．如图，一纸片沿直线AB折成的V字形图案，已知图中∠1＝62°，则∠2的度数＝．32．如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB，∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“巧分线”，如图2，若∠MPN＝α，且射线PQ是∠MPN的“巧分线”，则∠MPQ＝（用含α的式子表示）．三．解答题（共10小题）35．点O为直线AB上一点，过点O作射线OC，使∠BOC＝65°，将一直角三角板的直角顶点放在点O处．（1）如图①，将三角板MON的一边ON与射线OB重合时，则∠MOC＝；（2）如图②，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；（3）将三角板MON绕点O逆时针旋转至图③时，∠NOC=14∠AOM，求∠NOB的度数．36．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM是∠BOC 的平分线．（1）求∠MON的大小；（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？37．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板（∠M＝30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．（1）将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．如图2，经过t秒后，OM恰好平分∠BOC．①求t的值；②此时ON是否平分∠AOC？请说明理由；（2）在（1）问条件的基础上，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC平分∠MON？请说明理由；（3）在（2）问条件的基础上，经过多长时间OC平分∠MOB？请画图并说明理由．38．如图，点O为直线AB上一点，过点O作射线OC，使∠BOC＝135°，将一个含45°角的直角三角尺的一个顶点放在点O处，斜边OM与直线AB重合，另外两条直角边都在直线AB的下方．（1）将图1中的三角尺绕着点O逆时针旋转90°，如图2所示，此时∠BOM＝；在图2中，OM是否平分∠CON？请说明理由；（2）紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示，使得ON在∠AOC的内部，请探究：∠AOM与∠CON之间的数量关系，并说明理由；（3）将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为（直接写出结果）．39．如图，∠AOB是平角，∠DOE＝90°，OC平分∠DOB．（1）若∠AOE＝32°，求∠BOC的度数；（2）若OD是∠AOC的角平分线，求∠AOE的度数．40．已知，点O是直线AB上一点，OC、OD为从点O引出的两条射线，∠BOD＝30°，∠COD=87∠AOC．（1）如图①，求∠AOC的度数；（2）如图②，在∠AOD的内部作∠MON＝90°，请直接写出∠AON与∠COM之间的数量关系；（3）在（2）的条件下，若OM为∠BOC的角平分线，试说明∠AON＝∠CON．41．如图，以直线AB上一点O为端点作射线OC，使∠BOC＝70°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE＝90°）（1）如图①，若直角三角板DOE的一边OD放在射线OB上，则∠COE＝°；（2）如图②，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OC恰好平分∠BOE，求∠COD的度数；（3）如图③，将直角三角板DOE绕点O转动，如果OD始终在∠BOC的内部，试猜想∠BOD和∠COE有怎样的数量关系？并说明理由．42．已知，O为直线AB上一点，∠DOE＝90°．（1）如图1，若∠AOC＝130°，OD平分∠AOC．①求∠BOD的度数；②请通过计算说明OE是否平分∠BOC．（2）如图2，若∠BOE：∠AOE＝2：7，求∠AOD的度数．43．如图：AB，CD，EF相交于O点，AB⊥CD，OG平分∠AOE，∠FOD＝30°，求∠BOE 及∠AOG的度数．44．如图，∠AOB＝120°，射线OC从OA开始，绕点O逆时针旋转，旋转的速度为每分钟20°；射线OD从OB开始，绕点O逆时针旋转，旋转的速度为每分钟5°，OC和OD同时旋转，设旋转的时间为t（0≤t≤15）．（1）当t为何值时，射线OC与OD重合；（2）当t为何值时，射线OC⊥OD；（3）试探索：在射线OC与OD旋转的过程中，是否存在某个时刻，使得射线OC，OB 与OD中的某一条射线是另两条射线所夹角的角平分线？若存在，请求出所有满足题意的t的取值，若不存在，请说明理由．第11页（共11页）。

(完整word版)量角、算角的专项练习

角的专项练习姓名_________ 学号____
1.先看看下面各角是什么角，再用量角器量一量，度数标在角内。

2. 用量角器分别画出48°、65°、160°、105°、85 °、150°的角。

3.量一量下面各图中每一个角的度数。

⑴ ⑵ ∠1＝（）∠2＝（） ∠1＝（）∠2＝（）
∠3＝（）∠4＝（） ∠3＝（）∠4＝（）
你发现了什么？
答：长方形
平行四边形
4. ⑴以下面的射线为角的一条边。

35°的角 80°的角 160°的角
（2）以O 为顶点，OA 为一条边，画一个125°的角。

5.不用量角器，用一副三角尺分别画出75°、120°、150°、15°的角。

（在图中注明是由哪几个度数的角拼成的）
1234
341
2
六.计算下面各角的度数。

（5、6、8写出计算过程）
1.
7.
8.下图是一张长方形纸折起来以后的图形。

已知∠2＝72°，你能推算出∠1的度数吗？
七.数一数12。

部编三年级小学下册角计算专项练习60题(有)

角的计算练习60 题（附参照答案）1．如图，已知∠BOC=2∠ AOB， OD均分∠ AOC，∠ BOD=14°，求∠ AOB的度数．2．已知∠ 1=35°，∠ 2= _________．3．计算出以下各角的度数．4．算一算，下边是一个直角三角形．∠1= _________∠2= _________∠3= _________ ．5．三角形ABC的一条高将∠ BAC分红角度为42°和 36°的两个角（如图）．∠ 2 和∠ 3 分别是多少度？6．求以下图中各角的度数．∠1= _________∠2= _________∠3= _________ ．7．如图中，已知∠1=30°，∠ 2= _________，∠ 3=_________．8．如图，∠ 1= _________，∠ 2=_________，∠ 3=_________．9．求下边各个三角形中∠A的度数10．如图中，已知∠1=43°，∠ 2= _________，∠ 3=_________．11．计算三角形中角的度数．∠ 1= _________，∠ 2=_________，∠ 3=_________．12．算一算：∠1= _________ ；∠ 2= _________ ；∠ 3= _________ ．13．算一算，这些角各是多少度．已知∠ 2=40°求得：∠ 1= _________°，∠ 3=_________°，∠ 4=_________°．14．求出以下图各角的度数．15．如图，已知∠l=20 °，∠ 2=46°，求∠ 3 的度数．16．以下图，∠BOC=110°，∠ AOB=∠ DOC，∠ AOB是几度？17．如图：∠ 1=48°；∠ 2= _________．18．算一算．已知∠ 1=65°，求出：∠ 2、∠ 3、∠ 4 的度数．19．求下边各角的度数．图 1，∠ 1= _________∠2=_________图 2，∠ 1= _________ ．20．求下边各角的度数．已知∠ 1=30°，∠ 2=90°．∠ 3= _________；∠ 4=_________；∠ 5=_________．21．∠ 1=32゜，∠ 2=36゜，∠ 3= _________．22．如图已知∠ 1=35°，∠ 2= _________，∠ 3=_________，∠ 4=_________．23．以下图，已知∠1=30°．求：∠ 2、∠ 3 和∠ 4 的度数．24．已知∠ 1=25°，∠2= _________ °，∠3= _________ °，∠4= _________ °．25．算一算：∠1= _________ ；∠ 2= _________ ；∠ 3= _________ ．26．角的计算（1）如图 1 所示，已知：∠ 1=72°，∠ 2=45°，求：∠ AOB= _________ ？（2）如图 2 所示，已知：∠ 1=35°，求∠ 2= _________ ？27．用量角度量出图中∠ 2 的度数，再求∠1、∠ 3 和∠ 4 的度数．28．如图，已知∠1=130°，求∠ 2、∠ 3 的度数．29．如图中，∠ AOB=14°，∠ COB=∠ COD，求∠ COD．30．在直角∠ AOB内有射线OC、 OD．∠ AOC=∠ BOD=60°，求∠ COD的大小．31．求下边各角的度数．∠ A= _________∠ B=_________∠ B=∠ C=_________∠ C=_________．32．（ 1）如图 1，已知：∠ 1=45°，求：∠ 2（2）如图 2，已知：∠ 1=90°，∠ 2=30°求：∠ 3 等于多少度？（3）如图 3，已知：∠ 1=135°求：∠ 2、∠ 3、∠ 4 各等于多少度？33．如图，已知∠1=70°，∠ 2=25°，∠ 3=50°，求∠ 5=？34．如图是一张长方形纸折起来此后的图形，已知么∠ 2 是 65 °，∠ 1 是多少度？35．已知∠ 1=28°求∠ 2、∠ 3、∠ 4 和∠ 5 各是多少度？36．算一算∠1=65°∠ 2= _________ ∠ 3= _________ ∠ 4= _________ ∠ 1+∠ 2+∠ 3+∠ 4= _________ ．37．求角的度数．（1）AB=AC（如图1）∠ 1= _________∠2= _________（2）三角形 ABC是等腰三角形（如图 2）∠ 1= _________∠2= _________ ．38．如图中∠ 1=30°，∠ 2= _________，∠ 3=_________，∠ 4=_________，∠ 5=_________．39．以下图，∠1=55．，请分别求出∠2、∠ 3、∠ 4 的度数．40．图中，已知∠1=37°∠ 2= _________；∠ 3=_________；∠ 4=_________．41．如图，已知∠1=40°，∠ 2= _________，∠ 3=_________，∠ 4=_________，∠ 3+∠ 4=_________42．图中∠ 1= _________，∠ 2=_________，∠ 3=_________，∠ 1+∠ 2=_________．43．已知∠ 1=50°，求∠ 2=？∠ 3=？44．算一算．已知∠ 1=36°；∠ 2= _________；∠ 3=_________；∠ 4=_________；∠ 5=_________．45．图中，∠ 1=55°，∠ 2 是直角，你能求∠3、∠ 4、∠ 5 各是多少度吗？46．先量一量，再填空．①∠ 1= _________，是_________角；∠ 2=_________，是_________角；∠ 3=_________，是_________角．②画出∠ 1，使∠ 1=75°．47．算一算如图：已知∠ 1=35°∠3= _________ ∠ 4= _________∠2= _________ ∠ 1+∠ 2+∠ 3= _________ ．48．如图 1，已知∠ 1=40°，∠ 2= _________，∠ 3=_________，∠ 4=_________．如图 2，已知∠ 1=30°，∠ 2= _________，∠ 3=_________，∠ 4=_________，∠ 5=_________．49．求各个角的度数．（1）图 1 中：已知∠ 1=60°∠ 2= _________∠3= _________∠4= _________∠5= _________（2）图 2 中：已知∠ 1=75°∠ 2= _________∠3= _________∠4= _________ ．50．分别量出图中 4 个角的度数，再求出这 4 个角的和．∠1= _________ ；∠ 2= _________ ；∠ 3= _________ ；∠ 4= _________ ；∠ 1+∠2+∠ 3+∠4=_________ ．51．∠ 1= _________；∠ 2=_________；∠ 3=_________．52．∠1= _________ ；∠ 2= _________ ；∠ 3= _________ ．53．已知∠ 1=90°，∠ 2=50°，求∠ 3、∠ 4 和∠ 5 的度数．54．如图，求∠ 1 和∠ 2 的度数．55．已知：∠ 1=∠ 3，∠ 2=40°求：∠ ADE=？56．在下边三角形中，∠1=38°，∠ 2+∠ 3=90°，求∠ 3 和∠ 4 各是多少度？57．在三角形ABC中，∠ l=60 °，∠ 3=50°，求∠ 2、∠ 4 的度数．58．如图，已知：∠2=30°，∠ 3 是直角，则∠2+∠ 3= _________，∠ 1+∠ 2+∠ 4=_________，∠ 1+∠ 2+∠3+∠ 4= _________．59．求图中各角的度数．图 1：∠ 2= _________∠3=_________图2：∠ 1=_________∠ 2=_________∠ 3=_________．60．看图填数．①如图一，已知∠1=75°，那么∠ 2= _________∠ 3=_________∠ 4=_________．②如图二，∠ 1= _________∠ 2=_________∠ 3=_________．角的计算参照答案：1．设∠ AOB=x，∠ BOC=2x．则∠ AOC=3x．又 OD均分∠ AOC，由于∠ AOD=x．因此∠ BOD=∠ AOD﹣∠ AOB=x﹣x=14 °由于 x=28°即∠ AOB=28°．答：∠ AOB的度数是 28°2．∠ 2=180°﹣∠ 1，∠2=180°﹣ 35°，∠2=145°．故答案为： 145°．3．（ 1）（ 180°﹣ 50°）÷ 2，=130°÷ 2，=65°．答：角的度数是65°．（2） 180°﹣ 40°=140°．答：角的度数是140°4．∠ 2=90°﹣ 60° =30°；∠3=180°﹣ 50° =130°；∠1=180°﹣∠ 2﹣∠ 3=180°﹣ 30°﹣ 130°=20°．故答案为： 20°； 30°； 130°5．在直角三角形 ABD中，由于∠ ADB=90°，因此∠ 2=180°﹣ 90°﹣ 42°，∠2=48°；在直角三角形 ADC中，∠ ADC=90°，因此∠ 3=180°﹣ 90°﹣ 36°，∠3=54°答：∠ 2 和∠ 3 分别是 48°和 54°．6．（ 1）∠ 1=180°﹣ 90°﹣ 25°=65°；（2） 180°﹣ 25°﹣ 20° =135°；∠2=135°﹣ 90° =45°；（3）∠ 3=180°﹣∠ 1=180°﹣ 65°=115°．故答案为： 65°， 45°， 115°7．∠ 1 与∠ 2 构成了一个平角，因此∠ 2=180°﹣ 30°=150°；∠ 1 与∠ 3 构成一个直角，因此∠ 3=90°﹣ 30°=60°；故答案为： 150°； 60°8．依据题干剖析可得：∠1=180﹣ 90﹣45=45（度），∠3=180﹣ 45=135（度），∠2=180﹣ 135=45（度），故答案为： 45°， 45°， 135°9．∠ ABC=90°，∠ ACB=60°．因此，∠ BAC=90°﹣∠ BAC=90°﹣ 60°=30°；∠A=180°﹣∠ B﹣∠ C=180°﹣ 135°﹣ 20° =25°10．（ 1）∠ 2=90°﹣∠ 1=90°﹣ 43° =47°；（2）∠ 3=180°﹣∠ 2=180°﹣ 47° =133°．故答案为： 47°， 133°11．（ 1）依据题干剖析可得：∠ 2=65°；则∠ 1=180°﹣ 65°﹣ 65° =50°；（2）∠3=90°﹣41°=49°；故答案为： 50°； 65°； 49°12．∠ 1=180°﹣ 45°﹣ 90° =45°；∠2=180°﹣ 45° =135°；∠3=180°﹣ 135° =45°．故答案为： 45°； 135°； 45°．13．依据题干剖析可得：∠1=90°﹣ 40°=50°；∠3=180°﹣ 40° =140°；∠4=180°﹣140°=40°；故答案为： 50；140； 40．14．∠ A=180°﹣ 40°﹣ 85° =55°；∠B=180°﹣ 90°﹣ 35° =55°；∠C=180°﹣ 20°﹣ 47°=113°．以下图：故答案为： 55°、 55°、 113°15．∠ 4=180°﹣∠ 1﹣∠ 2，=180°﹣20°﹣46°，=114°，∠3=180°﹣∠ 4，=180°﹣ 114°，=66°．答：∠ 3 是 66°16．依据题干剖析可得：（ 180﹣ 110）÷ 2，=70÷ 2，=35（度），答：∠ AOB的度数是 35 度．17．∠ 2=90°﹣ 48° =42°，故答案为： 42°18．∠ 1 与∠ 3 是对顶角，因此∠ 3 也是 65°；由于∠ 1 与∠ 2 构成了一个平角，∠ 2 与∠ 4 又是对顶角，因此∠ 2=∠ 4=180°﹣ 65° =115°，答：∠ 2=115°，∠ 3=65°，∠ 4=115°．19．（ 1）∠ 1=∠2=（ 180°﹣ 120°）÷ 2=30°；（2）90°﹣40°=50°；因此∠ 1=50°；故答案为： 30°； 30°； 50°（ 4）∠ A=180°﹣ 119° =61°，∠ C=90°﹣ 61°=29°．20．∠ 1 和∠ 5 构成了一个直角，因此∠5=90﹣30=60故答案为： 56°； 48°； 66°； 29°（度），32．（ 1）∠ 2=180°﹣∠ 1=180°﹣ 45° =135°．∠ 5 与∠ 4 构成了一个平角，因此∠ 4=180﹣ 60=120（度）；（ 2）∠ 3=180°﹣∠ 1﹣∠ 2=180﹣90°﹣ 30° =60°．由于∠ 5 与∠ 3 是一组对顶角，因此∠3=∠ 5=60（度），（ 3）∠ 3=180°﹣∠ 1=180°﹣ 135° =45°，故答案为： 60°； 120°； 60°∠ 4=180°﹣∠ 1=180°﹣ 135° =45°，21． 180°﹣ 32°﹣ 36° =112°；∠ 2=180°﹣∠ 3=180°﹣ 45° =135°故答案为： 112°33．在小三角形里最大的角 =180°﹣∠ 2﹣∠ 3=105°，22．∠ 2=90°﹣∠ 1=90°﹣ 35°=55°，∠ 4=180°﹣ 105° =75°，∠ 3=180°﹣∠ 2=180°﹣ 55°=125°，∠ 5=180°﹣∠ 1﹣∠ 4，∠ 4=180°﹣∠ 3=180°﹣ 125° =55°，=180°﹣ 70°﹣ 75°，故答案为： 55°， 125°， 55°．=35°．23．∠ 2=90°﹣ 30°=60°，答：∠ 5 是 35°∠ 3=180°﹣ 60° =120°，34． 180°﹣ 65°× 2∠ 4=180°﹣ 120° =60°．=180°﹣ 130°答：∠ 2 的度数是 60°，∠ 3 的度数是120°，∠ 4 的度=50°．数是 60°答：∠ 1是 50度．24．∠ 2=180°﹣∠ 1=155°，35．∠ 4=90°，∠ 3=180°﹣∠ 2=25°，∠ 5=90°﹣∠ 1=90°﹣ 28° =62°，∠ 4=180°﹣∠ 1=155°．∠ 2=180°﹣∠ 1=180°﹣ 28° =152°，故答案为： 155， 25， 155．∠ 3=180°﹣∠ 2=180°﹣ 152° =28°；25．∠ 1=180°﹣ 35° =145°；答：∠ 2=152°，∠ 3=28°，∠ 4=90°，∠ 5=62°．∠ 2=180°﹣ 90° =90°；36．（ 1））∠ 2=90°﹣∠ 1，∠ 3=180°﹣ 125° =55°．=90°﹣ 65°，故答案为： 145°； 90°； 55°=25°；26．（ 1）∠ AOB=∠ 1+∠ 2=72°+45° =117°；（ 2））∠ 3=180°﹣∠ 2，（ 2）∠ 2=180°﹣ 90°﹣∠ 1=55°．=180°﹣ 25°，故答案为： 117°； 55°．=155°；27．经丈量可得∠ 2=35°，（ 3））∠ 4=180°﹣∠ 3，则∠ 1=90°﹣ 35° =55°，=180°﹣ 155°，∠ 3=180°﹣ 35° =145°，=25°；∠ 4=180°﹣ 145° =35°．（ 4））∠ 1+∠ 2+∠ 3+∠ 4=360°﹣ 90°，答：∠ 1 的度数是 55°，∠ 3 的度数是145°，∠ 4 的度=270°．数是 35°或∠ 1+∠ 2+∠ 3+∠ 4=65°+25° +155° +25°=270°．28．∠ 2=180°﹣∠ 1=180°﹣ 130° =50°；故答案为： 25°； 155°； 25°； 270°∠ 3=90°﹣∠ 2=90°﹣ 50° =40°；37．（ 1）∠ C=180°﹣ 120° =60°，答：∠2是50度，∠3是40度．∠ 1=90°﹣∠ C=90°﹣ 60° =30°；29. （ 90°﹣ 14°）÷ 2，∠ 2=180°﹣ 60°× 2=60°；=76°÷ 2，（ 2）∠ 1=90°﹣ 60° =30°；=38°；∠ 2=180°﹣∠ 1× 2﹣ 90°，答：∠ COD=38°=180°﹣ 30°× 2﹣ 90°，30．∠ COD=∠ AOC+∠BOD﹣∠ AOB，=30°．=60° +60°﹣ 90°，故答案为：（ 1）30°， 60°；=30°．（ 2） 30°， 30°答：∠ COD的大小是 30°．38．依据题干剖析可得：∠ 3=90°；31．（ 1）∠ A=90°﹣ 34° =56°；∠ 2=90°﹣ 30°=60°；（ 2）∠ C=180°﹣ 90°﹣ 18°=72°，∠ 4=∠ 1=30°；∠ B=180°﹣ 60°﹣ 72° =48°；∠ 5=180°﹣ 30° =150°；（ 3）∠ B=∠ C=（ 180°﹣ 48°）÷ 2=66°；故答案为： 60°； 90°； 30°； 15039．如图：因此，∠ 2=180°﹣ 40° =140°；∠ 3=180°﹣ 140° =40°；∠ 4=90°﹣∠ 1，∠ 4=180°﹣ 40° =140°；=90°﹣ 55°，图二：由于，∠ 1=30°．=35°，因此，∠ 2=90°﹣ 30° =60°；∠ 3=180°﹣∠ 4﹣∠ 5，∠ 3=90°；=180°﹣ 35°﹣ 90°，∠ 4=180°﹣ 60°﹣ 90° =30°；=55°，∠ 5=180°﹣ 30° =150°；∠ 2=180°﹣∠ 3，故答案为： 140°， 40°， 140°， 60°， 90°， 30°，=180°﹣ 55°，150°=125°，49．（ 1）由于∠ 2=90°，平角 =180°，答：∠ 2 是 125°、∠ 3 是 55°、∠ 4 是 35°因此，∠ 3=180°﹣∠ 1﹣∠ 2=180°﹣ 90°﹣ 60°40．∠ 2=90°﹣∠ 1=90°﹣ 37°=53°，=30°；∠ 3=180°﹣∠ 2=180°﹣ 53°=127°，∠ 5=180°﹣∠ 1=180°﹣ 60° =120°；∠ 4=180°﹣∠ 3=180°﹣ 127° =53°∠ 4=180°﹣∠ 5=180°﹣ 120° =60°；故答案为： 53°， 127°， 53°（ 2）由于∠ 1=75°，平角 =180°，41．∠ 2=∠4=180°﹣ 40° =140°，因此，∠ 2=180°﹣∠ 1=180°﹣ 75° =105°；∠ 3=180°﹣∠ 2=40°，∠ 4=180°﹣∠ 1=180°﹣ 75° =105°；∠ 3+∠ 4=180°．∠ 3=180°﹣∠ 4=180°﹣ 105° =75°；故答案为： 140°， 40°， 140°， 180°故答案为： 90°， 30°， 60°， 120°， 105°， 75°，42．∠ 1=90﹣ 50=40（度）；105°∠ 2=90﹣ 40=50（度）；50．丈量可得图中∠ 1=90°，∠ 2=45°，∠ 3=90°，∠∠ 3=180﹣ 50=130（度）；4=135°．∠ 1+∠ 2=90（度）；∠ 1+∠ 2+∠ 3+∠4=90° +45° +90°+135° =360°．故答案为： 40°； 50°； 130°； 90°故答案为： 90°， 45°， 90°， 135°． 360°43．∠ 2=180°﹣ 50° =130°，51．察看图形可知：∠ 3=90°；∠ 3=180°﹣ 90° =90°．∠ 1=180﹣ 35=145（度）；答：∠ 2=130°，∠ 3=90°．∠ 2=90﹣ 30=60（度）；44．依据题干剖析可得：故答案为： 145°； 60°； 90°∠ 3 是直角，是 90°；52．由于∠ 1 是等腰直角三角形底角，因此∠1=90°÷∠ 2=90°﹣ 36° =54°；2=45°；∠ 4=90°﹣ 54° =36°；由于正方形的两条对角线相互垂直，因此∠2=∠∠ 5=180°﹣ 36° =144°，3=90°．故答案为： 54°； 90°； 36°； 144°故答案为： 45°； 90°； 90°45．∠ 3=90°﹣ 55°=35°，53．（ 1）∠ 3=180°﹣∠ 2=180°﹣ 50° =130°；∠ 5=180°﹣ 55° =125°，（ 2）∠ 4=180°﹣∠ 3=180°﹣ 130° =50°；∠ 4=180°﹣ 125° =55°．（ 3）∠ 5=180°﹣∠ 1﹣∠ 2=180°﹣ 90°﹣ 50°=40°．答：∠ 3=35°、∠ 4=55°、∠ 5=125°故答案为：∠ 3=130°，∠ 4=50°，∠ 5=40°46．（ 1）经过丈量可知∠ 1=50°，是锐角，∠ 2=40°，54．∠ 1=180°﹣ 90°﹣ 65° =25°；是锐角，∠ 3=120°，是钝角；∠ 2=180°﹣ 120° =60°．（ 2）依据剖析绘图以下：答：∠ 1 的度数是 25°；∠ 2 的度数是 60°．55．∠ ADE=（ 180°﹣ 40°）÷ 2+40°，故答案为： 50°；锐； 4°；锐； 120°；钝=140°÷ 2+40°，47．∠ 2=180°﹣∠ 1=180°﹣ 35° =145°，=70° +40°，∠ 3=180°﹣∠ 2=180°﹣ 145° =35°，=110°．∠ 4=90°，答：∠ ADE是 110°．∠ 1+∠ 2+∠3=35° +145° +35° =215°．56．∠ 4=180°﹣∠ 1﹣（∠ 2+∠ 3），故答案为： 35°， 90°， 145°， 215°∠ 4=180°﹣ 38°﹣ 90°，48．图一：由于，∠ 1=40°．∠ 4=52°；部编三年级小学下册角计算专项练习60题(有)∠ 3=180°﹣ 90°﹣∠ 4，=75°；∠ 3=180°﹣ 90°﹣ 52°，∠ 3=180°﹣ 75° =105°．∠ 3=38°．故答案为：40°、 110°； 60°、 75°、答：∠3 是 38°，∠ 4 是 52°60．由于∠1+∠2=180°，∠ 1=75°，57．由于∠ 1+∠ 3+∠4=180°，∠ l=60 °，∠ 3=50°，因此 75° +∠ 2=180°，因此∠ 4=180°﹣ 60°﹣ 50°=70°；75°﹣ 75° +∠ 2=180°﹣ 75°，由于∠ 6=90°，∠ 2=105°；因此∠ 2=90°﹣∠ 3，由于∠ 1 与∠ 3，∠ 2 与∠ 4，分别是对顶角，=90°﹣ 50°，因此∠ 1=∠ 3=75°，∠ 2=∠ 4=105°；=40°（ 2）由于∠ 1+35° =180°，58．∠2+∠3=30° +90° =120°；∠ 1+35°﹣35°=180°﹣ 35°，∠ 1+∠2+∠3+∠ 4=360°；∠ 1=145°；∠ 1+∠2+∠4=360°﹣ 90° =270°．由于∠ 2+30° =90°，故答案为： 120°， 270°， 360°．∠ 2+30°﹣30°=90°﹣ 30°，59. （ 1）∠ 2=90° =50° =40°；∠ 2=60°；∠ 3=180°﹣（ 40° +30°） =110°；由于∠ 3 是一个直角，（ 2）∠ 1=180°﹣ 120° =60°；因此∠ 3=90°；∠ 2=180°﹣（ 60° +45°），故答案为：（1）105°，75°，105°．（2）145°，60°，=180°﹣ 105°，90°．。

角的计算初二练习题

角的计算初二练习题在初中数学学习中，角的计算是一个非常重要的内容。

通过熟练地掌握角的计算方法，可以帮助我们解决各种与角相关的问题。

下面是一些初二角的计算练习题，希望对你巩固这一知识点有所帮助。

1. 已知∠ABC=120°，求补角和余补角的度数。

解析：补角是与已知角相加等于90°的角，余补角是与已知角相加等于180°的角。

因此，补角的度数是90°-120°=60°，余补角的度数是180°-120°=60°。

2. 已知∠DEF为直角，求其补角和余补角的度数。

解析：直角的补角是90°-90°=0°，即补角是一个度数为0°的角。

余补角的度数是180°-90°=90°。

3. 已知∠MNO的补角为40°，求∠MNO的度数。

解析：由题意可知∠MNO的补角为40°，根据补角的概念可得∠MNO+∠X=90°，其中∠X为补角。

代入已知条件可得∠MNO+40°=90°，解方程可得∠MNO=50°。

4. 已知∠PQR和∠QRS的度数分别为70°和110°，求∠PQS的度数。

解析：首先根据角的性质可知∠PQR+∠QRS+∠PQS=180°，代入已知条件可得70°+110°+∠PQS=180°，解方程可得∠PQS=180°-70°-110°=0°。

因此，∠PQS的度数为0°。

5. 已知∠ABC的余角是75°，求∠ABC的补角的度数。

解析：余角是与已知角相加等于180°的角，补角是与已知角相加等于90°的角。

根据已知条件可知∠ABC+75°=180°，解方程可得∠ABC=180°-75°=105°。

角的训练题

角的训练题以下是文字描述的问题，您可以根据需要绘制图形来解答。

1.在直角三角形中，一个角是90度，另一个角是30度，那么第三个角是多少度？2.如果两条线段互相垂直，它们之间的夹角是多少度？3.一把尺子被放置在平面上，尺子与水平线的夹角是60度，那么尺子与垂直线的夹角是多少度？4.两条平行线被一条横穿线相交，交点处的夹角是多少度？5.如果一个角的度数是其补角度数的两倍减去30度，求该角的度数。

6.如果一个角的度数是其补角度数的三倍加上15度，求该角的度数。

7.一个锐角的度数是其补角度数的一半减去10度，求该角的度数。

8.一条射线从原点开始，沿着正x轴方向旋转，它所经过的角度是多少度？9.一个角的度数是120度，它的补角度数是多少度？10.一个角的度数是80度，它的补角度数是多少度？11.一个角的度数是45度，它的补角度数是多少度？12.一个角的度数是60度，它的余角度数是多少度？13.一个锐角的度数是30度，它的余角度数是多少度？14.如果两个角互为补角，其中一个角的度数是35度，求另一个角的度数。

15.如果两个角互为补角，其中一个角的度数是75度，求另一个角的度数。

16.如果两个角互为补角，其中一个角的度数是120度，求另一个角的度数。

17.如果两个角互为补角，其中一个角的度数是x度，求另一个角的度数（用x 表示）。

18.如果两个角互为补角，其中一个角的度数是2x度，求另一个角的度数（用x表示）。

19.如果两个角互为补角，其中一个角的度数是3x度，求另一个角的度数（用x表示）。

20.如果两个角互为补角，其中一个角的度数是y度，求另一个角的度数（用y 表示）。

希望以上问题能帮助到您进行角的训练！。