结构力学 静定梁与静定刚架习题共81页文档
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第3章 静定梁与静定刚架【圣才出品】

第3章 静定梁与静定刚架
3.1 复习笔记【知识框架】
【重点难点归纳】
一、单跨静定梁 ★★★★
1.内力
表3-1-1 内力的基本概念
图3-1-1
图3-1-22.内力与外力间的微分关系及积分关系(1)由平衡条件导出的微分关系式
计算简图如图3-1-3所示,微分关系式为
(Ⅰ)
d d d d d d s
s N
F q x
x M F
x F p x
x ⎧=⎪⎪⎪=
⎨⎪⎪=-⎪⎩-()()
图3-1-3
(2)荷载与内力之间的积分关系
如图3-1-4
所示,结合式(Ⅰ)可得梁的内力积分公式,积分公式及其几何意义见表3-1-2。
图3-1-4
表3-1-2 内力的积分公式及几何意义
3.叠加法作弯矩图
表3-1-3 常用叠加法及其作图步骤
图3-1-5
图3-1-6
二、多跨静定梁 ★★★★
多跨静定梁是由构造单元(如简支梁、悬臂梁)多次搭接而成的几何不变体系,其计算简图见图3-1-7,几何构造、计算原则、传力关系见表3-1-4。
结构力学 第三章 静定梁和静定刚架

C A
θ
x
VC
ql 2
第三章 静定梁和静定刚架
q
B
M图 图 ql
ql 2 8
C
ql 2
2
cos θ
V图 图
ql cos θ 2 ql sin θ 2
0
A
θ
l
ql 2
NC = −ql sin θ 2 + qx sin θ VC = ql cos θ 2 − qx cos θ
N图 图
第三章 静定梁和静定刚架
3、多跨静定梁实例
企口
多跨静定梁简图
基、附关系层叠图
第三章 静定梁和静定刚架 4、计算顺序:先附属部分,后基本部分 计算顺序:先附属部分,
P2
B A
P1
C D
P2 VB P1 VB VC VC
作用于基本部分上的荷载,只使该基本部分受力, 作用于基本部分上的荷载,只使该基本部分受力,不传 递给附属部分; 递给附属部分; 作用于在附属部分上的荷载,除附属部分受力外,还将 作用于在附属部分上的荷载,除附属部分受力外, 传递给基本部分。 传递给基本部分。
第三章 静定梁和静定刚架
练习: 练习: 作梁的 V、M 图。
q=20kN/m
40kN
A
4m 70kN
B
C
2m
2m 50kN
V kN)
70 + 3.5m 10 50
M(kN▪m)
2 ql1 = 40 8
122.5 120
Pl2 = 40 4
第三章 静定梁和静定刚架
练习:作梁的V 练习:作梁的V、M 图
第三章 静定梁和静定刚架
第三章
静定梁和静定刚架
长沙理工结构力学期末考试题库和答案第二章静定梁与钢架 结构力学超静定

长沙理工结构力学期末考试题库和答案第二章静定梁与钢架结构力学超静定第二章静定梁及静定刚架一、判断题1.静定结构在荷载作用下产生的内力与杆件弹性常数、截面尺寸无关。
( O )2.计算位移时,对称的静定结构是指杆件几何尺寸、约束、刚度均对称的结构。
( O ) 3.静定结构在支座移动、变温及荷载分别作用下,均产生位移和内力。
( X )4.几何不变体系一定是静定结构。
( X )25.图示结构 MK = ql/2(内侧受拉)。
( X )q6.图示结构中 AB 杆弯矩为零。
( X ) q7.图示结构中 |MAC|=|MBD|。
( O )|8.图示结构中 |MAC|=|MBD。
( O )l9.图示结构 M 图的形状是正确的。
( X ) M 图 10.图示结构|MC|=0 。
( O)11.图示结构中 A、B 支座反力均为零。
d二、选择题12.静定结构有变温时:( C )A. 无变形,无位移,无内力;B. 有变形,有位移,有内力;C. 有变形,有位移,无内力;D. 无变形,有位移,无内力。
13.静定结构在支座移动时:( D )A. 无变形,无位移,无内力;B. 有变形,有位移,有内力;C. 有变形,有位移,无内力; D 无变形,有位移,无内力。
O )(14.静定结构的内力计算与( A )A. EI 无关;B. EI 相对值有关;C. EI 绝对值有关;D. E 无关, I 有关。
15.图示结构MA 、MC (设下面受拉为正)为:( C )A.MA =0 ,MC=Pa/2 ;B.MA =2Pa ,MC=2Pa ;C.MA =Pa ,MC=Pa ;D.MA =-Pa,MC=Pa 。
16.图示结构 MA、 MB (设以内侧受拉为正)为:( DA. MA=-Pa , MB =Pa;B. MA=0 , MB =-Pa ;C. MA=Pa ,MB =Pa ;D.MA=0 , MB =Pa 。
17.图示结构 B 点杆端弯矩(设内侧受拉为正)为:( C )A.MBA = Pa, MBC = -Pa ;B.MBA = MBC = 2Pa;C. MBA = MBC = Pa ;D.MBA = MBC = 0 。
材料力学静定梁与静定刚架

8
第三章 静定梁与静定刚架
§3-1 单跨静定梁
1)求支座反力(如图): 2)分段建立Q、M方程,分成三段: AC段:
Q( X 1 ) V A 7.75KN (0 X 1 2)
M ( X 1 ) VA X 1 7.75 X 1
Q( X 2 ) VA 5 2.75KN CD段: M ( X 2 ) V A X 2 5( X 2 2) 2.75 X 2 10 (2 X 2 5)
§3-3 静定平面刚架
(1)求反力。 切断C铰,考虑右边平衡,再分析左 边部分。求得反力如图所示:
C
53
第三章 静定梁与静定刚架
§3-3 静定平面刚架
(2)作M图 (3)做Q、N图 (4)校核
M图
N图
Q图
54
第三章 静定梁与静定刚架
§3-3 静定平面刚架
例3 (1)求反力 (2)绘M图 (3)绘Q图 (4)绘N图 (5)校核 M M
DB段:
Q( X 3 ) VA 5 3( X 3 5) 17.75 3 X 3
(5 X 3 10)
9
M ( X 3 ) VA X 3 5( X 3 2) 3/ 2( X 3 5)2 1.5 X 32 17.75 X 3 27.5
第三章 静定梁与静定刚架
44
第三章 静定梁与静定刚架
§3-3 静定平面刚架
(4)内力记号:
NAB-AB杆A端的轴力。 QAB-AB杆A端的剪力。 MAB-AB杆A端的弯矩。
45
第三章 静定梁与静定刚架
§3-3 静定平面刚架
2、内力图:N、Q、M (1)分杆列N、Q、M方程。 (2)分杆利用q、Q、M微分关系 (3)叠加法绘制Q、M图 ((2)、(3)联合运用。) 静定刚架的内力图绘制方法: 一般先求反力,然后求控制弯矩,用区 段叠加法逐杆绘制,原则上与静定梁相同。
李廉锟《结构力学》(上册)配套题库【课后习题】(静定梁与静定刚架)【圣才出品】

第3章静定梁与静定刚架复习思考题1.用叠加法作弯矩图时,为什么是竖标的叠加,而不是图形的拼合?答:因为有时叠加弯矩图时的基线与杆轴不重合,如果用图形拼合,不能完全保证叠加后弯矩值是实际同一点的两个弯矩相加后的值。
2.为什么直杆上任一区段的弯矩图都可以用简支梁叠加法来作?其步骤如何?答:(1)因为根据内力分析可以求出直杆任一区段两端的内力,所以直杆任一区段两端均可以看成两端有外力(集中力或集中力偶)的简支梁。
(2)设有直杆任一区段简支梁AB,具体步骤如下①分解作用区段AB上的荷载;②分别作出分解荷载下的弯矩图;③求解出区段AB两端的弯矩M A和M B;④将两端弯矩M A和M B绘出并连以直线(虚线);⑤以步骤④中的虚线为基线叠加各个分解荷载下的弯矩图(竖标叠加),得最终弯矩图。
3.试判断图3-1所示刚架中截面A、B、C的弯矩受拉边和剪力、轴力的正负号。
图3-1答:轴力以受压为负,受拉为正;剪力以使截面顺时针旋转为正。
(1)截面A:左边受拉,剪力为负,轴力为负;(2)截面B:右边受拉,剪力为正,轴力为正;(3)截面C:左边受拉,剪力为正,轴力为正。
4.怎样根据静定结构的几何构造情况(与地基按两刚片、三刚片规则组成,或具有基本部分与附属部分等)来确定计算反力的顺序和方法?答:(1)与地基按两刚片,例如简支梁,支座反力只有三个,对某一端点取矩直接解除约束反力。
(2)与地基按三刚片规则组成,例如三铰刚架,支座反力有四个,考虑结构整体的三个平衡方程外,还需再取刚架的左半部(或右半部,一般取外荷载较少部分)为隔离体建立一个平衡方程方可求出全部反力。
(3)具有基本部分与附属部分时,按先附属后基本的计算顺序,求解支座反力。
5.当不求或少求反力而迅速作出弯矩图时,有哪些规律可以利用?答:当不求或少求反力而迅速作出弯矩图时,如下规律可以利用(1)结构上若有悬臂部分及简支梁部分(含两端铰接直杆承受横向荷载)弯矩图可先行绘制出;(2)直杆的无荷区段弯矩图为直线和铰处弯矩为零;(3)刚结点的力矩平衡条件;(4)外力与杆轴重合时不产生弯矩;(5)外力与杆轴平行及外力偶产生的弯矩为常数;(6)对称性的合理利用;(7)区段叠加法作弯矩图。
结构力学 第三章 静定梁和静定平面钢架

2、截面法 若要求某一横截面上的内力,假想用一平面沿杆轴垂直方向将该 截面截开,使结构成两部分;在截开后暴露的截面上用力(内力)代 替原相互的约束。
对于截开后结构的两部分上,截面上的内力已成为外力,因此,
由任一部分的静力平衡条件,均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
3、截面内力 截开一根梁式杆件的截面上有三个内力(分量),即:轴力FN 、 剪力FQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系: DFN=-FPx
DFQ=-FPy
DM=m
1)微分关系及几何意义: dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy (1)在无荷载区段,FQ图为水平直线;
当FQ≠0时,Μ图为斜直线;
右右为正。
FQ=截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正, 右下为正。
Μ =截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图(a)所示简支梁在图示荷载下截面的内力。
解:1)支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=-60kN (← ) 由 ∑Fy= 0 校核,满 足。
(下侧受拉)
区段叠加法求E、D截面弯矩; ΜE=20×42/8+120/2=100kNm ΜD=40×4/4+120/2=100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明:集中力或集中力偶作用点,注意对有突变的 分两侧截面分别计算。
结构力学 静定梁与静定刚架习题

M BC 2kNm
3、取AB为研究对象
MBA
或 取B节点为研究对象
2 kNm 2 kNm MBA
MBA=0
-4 kN
练习题
2
M
2
B
A 2m 1m
D
2m L P L L L L L
P
练习题
L
P L
P
L
P L
练习题
C
1kN/m
VC A VA 4m D
3、取AD为研究对象 B 4m
4m
VA
MDA VDA
3 kNm
3、取BCD为研究对象
2 kN
B
A 2m
C
D
1m
1m
MBC
1m
MBC= -1 kNm,上侧 1
MBA
1、取整体为研究对象
VC=4 kN
HA=2 kN 2、取AB为研究对象 MBA= - 2 kNm ,右侧受拉
B
2 A
C
D
练习题 2kN/m
C
8kN
20kNm 2m
3、BC为悬臂部分 MBC= 4 kNm,左侧
20 kN/m
4m
VB
MCB
MCD=90
MCF=135
VF
3.基本部分的计算,为悬臂杆。
VB=135
ME=135×3=405 kNm,左侧受拉
4. 作出弯矩图。
90 90
405
135
45
[习题3] 作弯矩图,剪力图,轴力图。
1.取整体为研究对象, ∑MA=0 ,VC×94×5-2×5×2.5=0 , 解得VC= 5 kN , ∑Y=0,VA=5 kN ∑X=0,HA=8 kN 8 kN 4 kN 2 kN/m HA VA VC
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学2-静定梁及刚架
1、悬臂刚架
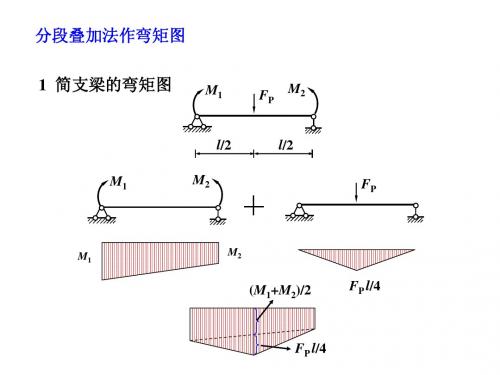
例. 试计算下图所示悬臂刚架的支座反力,并绘制M、FQ和FN图。
解:(1)计算支座反力
2qa2 q E
Fx 0 2 q 4 a F xA 0
C
3a
6qa
Fx A 8 q a
Fy 0 F yA 6 qa q 4 a 0
D 2q B
Fy A 10qa
2
B B
2 qa
2
2 qa
2
2 qa
2
4 qa
2
4 qa
2
2
A
14 qa
14 qa
2
也可直接从悬臂端开始计算杆件
2qa2
8 qa
2
q
10 qa
2
弯矩图
10 B
8 2qa2
6qa 2q
4 qa
14 qa
2
2
2 qa
2
2
M图
(4)绘制结构FQ图和FN图 2qa2 2qa2 C 6qa q E
2
8 qa
85
15
20
45
FQ 图(k N)
例 确定x值,使支座B处弯矩与AB跨中弯矩相等,画弯矩图
q A E B D l/2 x l-x C
解
M
B
1 2 1
qx
2
1 2 1
q l x x
1
q lx
l/2
M
q
E
ql
2
M
8
M M
2
B
2 1 2 1 q l q lx 8 4
f
f
Fx 0
结构力学章节习题及参考答案

习题2.1(6)图
习题2.2填空
(1)习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2)习题2.2(2)图所示体系为__________体系。
习题2-2(2)图
习题2.2(5)图
(6)习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图
(7)习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图
习题2.3对习题2.3图所示各体系进行几何组成分析。
习题2.3图
第3章静定梁与静定刚架习题解答
习题7.2(4)图
习题9.3用力矩分配法计算习题7.3图所示连续梁,作弯矩图和剪力图,并求支座B的反力。
(1)(2)
习题7.3图
习题9.4用力矩分配法计算习题7.4图所示连续梁,作弯矩图。
(1)(2)
习题7.4图
习题9.5用力矩分配法计算习题7.5图所示刚架,作弯矩图。
(1)(2)
习题7.5图
第11章影响线及其应用习题解答
习题11.1是非判断题
(1)习题8.1(1)图示结构BC杆轴力的影响线应画在BC杆上。( )
习题8.1(1)图习题8.1(2)图
(2)习题8.1(2)图示梁的MC影响线、FQC影响线的形状如图(a)、(b)所示。
(3)习题8.1(3)图示结构,利用MC影响线求固定荷载FP1、FP2、FP3作用下MC的值,可用它们的合力FR来代替,即MC=FP1y1+FP2y2+FP3y3=FR 。( )
结构力学静定梁与静定刚架

第三章静定梁与静定刚架
§3-1 单跨静定梁
§3-2 多跨静定梁
§3-3 静定平面刚架 §3-4 少求灾不求反力绘制巷矩图 §3-5 静定结构的特性 习题
----静定梁与静定刚架
3-1 单跨静定梁
一、单跨静定梁的反力
二、用截面法求指定梁的内力
轴力的数值等于截面一侧所有的外力沿截面法线方向的投影代数和 剪力的数值等于截面一侧所有的外力沿截面切线方向的投影代数和 弯矩的数值等于截面一侧所有的外力对截面形心的力矩代数和
` 4
4
`
4KN/m 2KNM 7.5 2
4
8.5
` 4KNm
4 2
`
----静定梁与静定刚架
例3-1 作图示梁的剪力弯矩图
RA
Rb
----静定梁与静定刚架
----静定梁与静定刚架
----静定梁与静定刚架
----静定梁与静定刚架
例3-2
(a)
A
4KN B
10KN
C
D E F
B A
C F D E
10KN Hb=0 Ma=18KN.m A B Va=9KN
----静定梁与静定刚架
----静定梁与静定刚架
三、利用微分关系作内力图
基线:平行于杆轴线的坐标表示截面的位置
竖标:垂直于杆轴线的坐标表示内力的数值
----静定梁与静定刚架
用简易法绘内力图的一般步骤是: (1)求反力 (2)分段 内力不连续处 (3)定点 根据内力图形状,
选定控制截面,求出内力值
(4)联线 直线或曲线
四、用叠加法作弯矩图
C
B
Hc=0 Vb=5KN Vc=5KN
第三章:静定梁和静定刚架

二.多跨静定梁 多跨静定梁
第三章 静定梁与静定钢架 二.多跨静定梁 多跨静定梁 基本部分--能独立 基本部分--能独立 1.多跨静定梁的组成 承载的部分。 1.多跨静定梁的组成 承载的部分。 附属部分--不能独 附属部分--不能独 立承载的部分。 立承载的部分。
基、附关系层叠图
练习:区分基本部分和附属部分并画出关系图 练习 区分基本部分和附属部分并画出关系图 第三章 静定梁与静定钢架
ql 2 / 2
Q=0的截面为抛 Q=0的截面为抛 物线的顶点. 物线的顶点.
ql / 2
ql
2
M图 Q图
第三章 静定梁与静定钢架
例: 作内力图
ql 2 / 2
M图 Q图
第三章 静定梁与静定钢架
1.无荷载分布段(q=0),Q图为水平线,M图为斜直线. 1.无荷载分布段 无荷载分布段(q=0),Q图为水平线 图为斜直线 图为水平线,M图为斜直线. 2.均布荷载段(q=常数),Q图为斜直线,M图为抛物线, 2.均布荷载段 常数 图为斜直线 图为抛物线 均布荷载段(q=常数),Q图为斜直线,M图为抛物线, 且凸向与荷载指向相同. 且凸向与荷载指向相同. 3.集中力作用处,Q图有突变,且突变量等于力值; M 3.集中力作用处 图有突变 且突变量等于力值; 集中力作用处,Q图有突变, 图有尖点,且指向与荷载相同. 图有尖点,且指向与荷载相同.
P
1 Pl 4 1 Pl 4
P 1 Pl
4
l/2
q
l/2
l/2
1 2 ql 4
l/2
l/2
ql 1 ql 2 4
l/2
l/2
l 静定梁与静定钢架
§3-2 静定刚架受力分析
一. 刚架的受力特点
结构力学3静定梁与静定刚架

要求灵活运用隔离体的平衡条件 灵活运用隔离体的平衡条件, 主要任务 :要求灵活运用隔离体的平衡条件,熟练掌握静定 梁内力图的作法。 梁内力图的作法。 分析方法:按构造特点将结构拆成杆单元, 分析方法:按构造特点将结构拆成杆单元,把结构的受力分析 问题转化为杆件的受力分析问题。 问题转化为杆件的受力分析问题。 §3-1 单跨静定梁的内力分析
1m
4m
4m
4m
1m
§3-3 静定平面刚架的组成特点及类型 平面刚架结构特点: 一、平面刚架结构特点:
刚架是由梁和柱以刚性结点相连组成的, 刚架是由梁和柱以刚性结点相连组成的,其优点是将梁柱形成一个刚性 整体,使结构具有较大的刚度,内力分布也比较均匀合理,便于形成大空间。 整体,使结构具有较大的刚度,内力分布也比较均匀合理,便于形成大空间。 下图是常见的几种刚架: 下图是常见的几种刚架:图(a)是车站雨蓬,图(b)是多层多跨房屋, )是车站雨蓬, )是多层多跨房屋, 图(c)是具有部分铰结点的刚架。 )是具有部分铰结点的刚架。
A C E A E C
C
E
A
(a)
(b)
(c)
二、分析多跨静定梁的一般步骤
对如图所示的多跨静定梁,应先从附属部分 开始分析 将支座C 开始分析: 对如图所示的多跨静定梁,应先从附属部分CE开始分析:将支座 的支反 力求出后,进行附属部分的内力分析、画内力图, 力求出后,进行附属部分的内力分析、画内力图,然后将支座 C 的反力反向 加在基本部分AC 的C 端作为荷载,再进行基本部分的内力分析和画内力图, 端作为荷载,再进行基本部分的内力分析和画内力图, 加在基本部分 将两部分的弯矩图和剪力图分别相连即得整个梁的弯矩图和剪力图 。
R A = 17 kN
《结构力学》第三章 静定梁和静定刚架.

返19回
§3—4 少求或不求反力绘制弯矩图
弯矩图的绘制,以后应用很广,它是本课最 重要的基本功之一。
静定刚架常常可少求或不求反力绘制弯矩图。
例如:1. 悬臂部分及简支梁部分,弯矩图可先绘出。
2. 充分利用弯矩图的形状特征(直线、零值)。
3.刚结点处的力矩平衡条件。
4. 用叠加法作弯矩图。
5. 平行于杆轴的力及外力偶产生的弯矩为常数。 6. 与杆轴重合的力不产生弯矩等。
满足投影平衡条件。
0 24kN C 0
22kN
24kN 22kN (返1b8 回)
例题 3—6 作三铰刚架的内力图
→HA VA↑ 26.7 20 6.7
解(:1)求反力
←HB
↑VB
由(∑2Y由)=V刚0A求VH作得架=AA杆=弯整1=30H体端矩0Bk8平4=弯图N6衡↑矩.,66,以,7kV∑D3NMB0C(=kBN杆1=→0o↑为k可←N例得↑)
M图: 通常检查刚结点处是否满足力矩的平衡条件。
例如取结点C为隔离体(图a),有:
∑MC=48-192+144=0 满足这一平衡条件。
48kN·m
C
192kN·m
Q(N)图:可取刚架任何一部分为隔
离体,检查∑X=0 和 ∑Y=0 是否满足。 144kN·m (a)
例如取结点C为隔离体(图b), 有: ∑X=24-24=0 ∑Y=22-22=0
dQ q(x) dx
dM Q dx
d2M dx2
q(x)
据此,得直梁内力图的形状特征
梁上情况 q=0
q=常数
q↓ q↑
P 作用处
m 铰或
作用处 自由端 (无m)
水平线
结构力学 静定梁与静定刚架习题
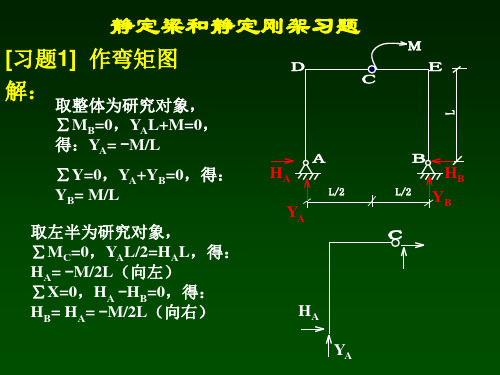
MCD
MBA
MCD=4 kNm,左侧受拉
练习题
4kNm A 2kN D 2m 2kN B C 2m
1kN/m
6m
4、由B、C节点的平衡
MBA MBC MCD
A
4 2
பைடு நூலகம்
D
MCB
B
C
MBC=4 kNm,下侧; MCB= 4 kNm,上侧。
4
4
练习题
30kN
D
E
F
G 20kN/m H 2m 2m
A 3m 3m
4×2m × 2.由对称性, 由对称性, 由对称性 YA=YB=6 kN 3. 计算 计算DFH部分 部分 3 kN 3 kN 6 kN 3 kN 3 kN 6 kNm
同理, 部分的弯矩图与DEH部分对称。 部分对称。 同理,GAEC部分的弯矩图与 部分的弯矩图与 部分对称 4.计算中间工字型 计算中间工字型 6 kN 3 kN 3 kN 3 kN 3 kN 3 kN 3 kN 3 kN 6 kNm 6 kN 3 kN 6 kNm
20 kN/m HB A B C D 4m E 3m 3m 3m
*MCF=YF×3=135 kNm ,下侧受拉 *CD、AB是悬臂杆,直接写出弯矩 、 是悬臂杆 是悬臂杆, MBA=90 kNm, , MCD=90 kNm, , 上侧受拉。 上侧受拉。
B YB
C
F YF
F
取整体为研究对象, 取整体为研究对象, ∑MB=0, , YF×6+20×3×1.5-20×6×3=0 × × . - × × 得:YF = 45 kN ∑Y=0,得:YB=135 kN , ∑X=0,得:HB=0 ,
B 2m 30kN 2m
03静定梁--习题

0G
15 kN
F
80
67 kN 32
H
25
I
kN
8
结构力学电子教程
3 静定梁
2kN m
0C
D0
4kN
1kN 1kN
0A
9 kN 4
3、作剪力图
9/4
B 3 kN 0 0
4
E
25 kN 32
1kN/m
0G
15 kN
F
80
67 kN 32
H
25
I
kN
8
15/ 8
Q (kN) A
4、作弯矩图
A M (kN·m)
接画出M图。
P
B
CD
E
F
A
【解】
a
a
a
a
a
a
a
Pa
Pa
B
CD
E
A
Pa
结构力学电子教程
3 静定梁
结构力学(第二版)
包世华 主编
结构力学电子教程
3 静定梁
3.1 用叠加法作图示单跨静定梁的弯矩图。
(a)
A
P
Pl / 2
Pl/4
B
C
M
l/2
l/2
Pl / 4
【解】
Pl/4
A
B
C
P
A
B
C
Pl / 4 Pl / 4
3 静定梁
3.20 用分段叠加法作图示梁的弯矩图,并计算C点的弯矩值。
2kN/m
10kN
3kN
D
2m
A
C
2m 2m
B
E
结构力学自测题静定梁刚架内力计算
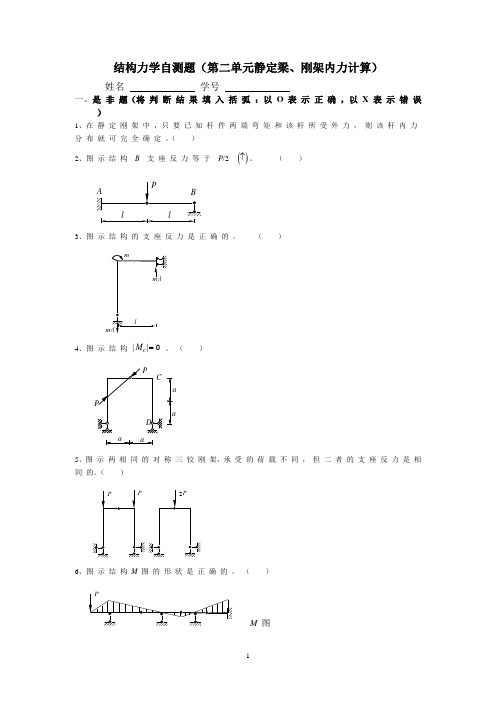
结构力学自测题(第二单元静定梁、刚架内力计算)姓名 学号一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 )1、在 静 定 刚 架 中 ,只 要 已 知 杆 件 两 端 弯 矩 和 该 杆 所 受 外 力 , 则 该 杆 内 力 分 布 就 可 完 全 确 定 。
( )2、图 示 结 构 B 支 座 反 力 等 于 P /2 ()↑。
( )3、图 示 结 构 的 支 座 反 力 是 正 确 的 。
( )m 4、图 示 结 构 ||M C =0 。
( )a a5、图 示 两 相 同 的 对 称 三 铰 刚 架,承 受 的 荷 载 不 同 ,但 二 者 的 支 座 反 力 是 相 同 的。
( )6、图 示 结 构 M 图 的形 状 是 正 确 的 。
( )M 图二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )1、对 图 示 的 AB 段 , 采 用 叠 加 法 作 弯 矩 图 是 :A. 可 以 ;B. 在 一 定 条 件 下 可 以 ;C. 不 可 以 ;D. 在 一 定 条 件 下 不 可 以 。
( )2、图 示 两 结 构 及 其 受 载 状 态 , 它 们 的 内 力 符 合 。
A. 弯 矩 相 同 , 剪 力 不 同 ;B. 弯 矩 相 同 , 轴 力 不 同 ;C. 弯 矩 不 同 , 剪 力 相 同 ;D. 弯 矩 不 同 , 轴 力 不 同 。
( )P P ll l3、 图 示 结 构 M K ( 设 下 面 受 拉 为 正 ) 为 :A. qa 22 ; B -qa 22 ;C. 3qa 22 ;D. 2qa 2 。
( )2 a4、图示 结 构 M DC (设 下 侧 受 拉 为 正 )为 :A. - Pa ;B. Pa ;C. -Pa ;D. Pa 2。
()三、填 充 题 ( 将 答 案 写 在 空 格 内 )1、在 图 示 结 构 中, 无 论 跨 度,高 度 如 何 变 化,M CB 永 远 等 于 M BC 的 倍 ,q使 刚 架 侧 受 拉 。
