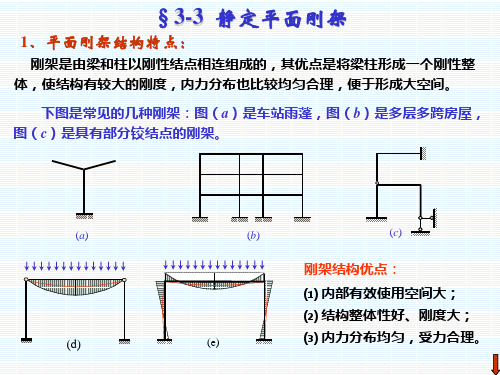
3,《结构力学》静定刚架
合集下载
03结构力学 第三章 静定结构的内力计算3.3 静定刚架的内力计算(邓军)
剪力图： 剪力符号规定与直梁中的规定相同；剪力图可画在杆件的任一 侧，但剪力图上要标明正负号。 轴力图：
轴力仍以受拉为正，受压为负；轴力图可画在杆件的任一侧或 与纵坐标对称地画在杆件的两边，但需在轴力图上标明正负号。
§3.3 静定刚架的计算
例1 绘制如图所示门式刚架在半跨均布荷载作用下的内力图。
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
静定刚架的组成及类型
平面刚架是由直杆（梁和柱）组成的平面结构。
刚架中的结点部分或全部是刚节点。
在刚节点处，各杆件连成一个整体，杆件之间不能发生相对 移动和相对转动，刚架变形时各杆之间的夹角保持不变，因 此刚节点能够承受弯矩、剪力和轴力。
解：
1）求支座反力 由整体平衡方程可得
M A 0, 6 3 12FyB 0 M B 0, 6 9 12FyA 0
X 0, FxA FxB 0
取铰C右边部分为隔离体
MC 0, 6.5FxB 6FyB 0
求得
FyB =1.5kN() FyA=4.5kN() FxA =1.384 kN()
§3.3 静定刚架的计算
2）作弯矩图
求出杆端弯矩（设弯矩方正向为使刚架内侧受拉）后，画于受 拉一侧并连以直线，再叠加简支梁的弯矩图。
以DC杆为例
M DC 1.384 4.5 6.23kN m, MCD 0
CD中点弯矩为 1.3845.5 133 1 1 4.5 6 1.388kN m 22
（2）为计算静定刚架位移和分析超静定刚架打下基础。
2）刚架各杆内力的求法
从力学观点看，刚架是梁的组合结构，因此刚架的内力求法 原则上与梁的内力计算相同。 通常是利用刚架的整体或个体的平衡条件求出各支座反力和 铰接点处的约束反力，然后用截面法逐个计算杆件内力。
轴力仍以受拉为正，受压为负；轴力图可画在杆件的任一侧或 与纵坐标对称地画在杆件的两边，但需在轴力图上标明正负号。
§3.3 静定刚架的计算
例1 绘制如图所示门式刚架在半跨均布荷载作用下的内力图。
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
静定刚架的组成及类型
平面刚架是由直杆（梁和柱）组成的平面结构。
刚架中的结点部分或全部是刚节点。
在刚节点处，各杆件连成一个整体，杆件之间不能发生相对 移动和相对转动，刚架变形时各杆之间的夹角保持不变，因 此刚节点能够承受弯矩、剪力和轴力。
解：
1）求支座反力 由整体平衡方程可得
M A 0, 6 3 12FyB 0 M B 0, 6 9 12FyA 0
X 0, FxA FxB 0
取铰C右边部分为隔离体
MC 0, 6.5FxB 6FyB 0
求得
FyB =1.5kN() FyA=4.5kN() FxA =1.384 kN()
§3.3 静定刚架的计算
2）作弯矩图
求出杆端弯矩（设弯矩方正向为使刚架内侧受拉）后，画于受 拉一侧并连以直线，再叠加简支梁的弯矩图。
以DC杆为例
M DC 1.384 4.5 6.23kN m, MCD 0
CD中点弯矩为 1.3845.5 133 1 1 4.5 6 1.388kN m 22
（2）为计算静定刚架位移和分析超静定刚架打下基础。
2）刚架各杆内力的求法
从力学观点看，刚架是梁的组合结构，因此刚架的内力求法 原则上与梁的内力计算相同。 通常是利用刚架的整体或个体的平衡条件求出各支座反力和 铰接点处的约束反力，然后用截面法逐个计算杆件内力。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第3章 静定梁与静定刚架【圣才出品】
第3章 静定梁与静定刚架
3.1 复习笔记【知识框架】
【重点难点归纳】
一、单跨静定梁 ★★★★
1．内力
表3-1-1 内力的基本概念
图3-1-1
图3-1-22．内力与外力间的微分关系及积分关系（1）由平衡条件导出的微分关系式
计算简图如图3-1-3所示，微分关系式为
（Ⅰ）
d d d d d d s
s N
F q x
x M F
x F p x
x ⎧=⎪⎪⎪=
⎨⎪⎪=-⎪⎩-（）（）
图3-1-3
（2）荷载与内力之间的积分关系
如图3-1-4
所示，结合式（Ⅰ）可得梁的内力积分公式，积分公式及其几何意义见表3-1-2。
图3-1-4
表3-1-2 内力的积分公式及几何意义
3．叠加法作弯矩图
表3-1-3 常用叠加法及其作图步骤
图3-1-5
图3-1-6
二、多跨静定梁 ★★★★
多跨静定梁是由构造单元（如简支梁、悬臂梁）多次搭接而成的几何不变体系，其计算简图见图3-1-7，几何构造、计算原则、传力关系见表3-1-4。
结构力学3静定刚架受力分析
C
∑F = 0,
x
XB + XC = 0, XC = −P(↓)
XC
YC
B
XB
YB
3)取整体为隔离体 取整体为隔离体 ∑Fy = 0,YA +YB = 0,YA = −YB = −P(↓) l ∑ M A = 0, M A + P × 2 − YB × l = 0, 1 M A = Pl (顺时针转 ) 2
Pl
Pl
P
l
l
l
练习: 练习 试找出图示结构弯矩图的错误
练习: 练习 试找出图示结构弯矩图的错误
本章小结
一. 刚架的受力特点 二. 刚架的支座反力计算 三. 刚架指定截面内力计算 四.刚架弯矩图的绘制 五.计算结果的校核
作业
3-3 (a) 3-7(a) 3-8(c)
P
P
Pl
P
P
P
P
Pl
P
P
连接两个杆端的刚结点, 连接两个杆端的刚结点 §3-3 静定刚架受力分析 ,若 结点上无外力偶作用, 结点上无外力偶作用,则两 三. 刚架指定截面内力计算 个杆端的弯矩值相等, 个杆端的弯矩值相等,方向 与梁的指定截面内力计算方法相同. 与梁的指定截面内力计算方法相同. 相反. 相反.
第三章 静定结构受力分析
§3-3 静定刚架受力分析
§3-3 静定刚架受力分析
一. 刚架的受力特点
刚架是由梁柱组成的含有刚结点的杆件结构
1 2 ql l 8
梁
桁架
1 2 ql 8
弯矩分布均匀 可利用空间大
刚架
§3-3 静定刚架受力分析
二. 刚架的支座反力计算
静定刚架的分类: 静定刚架的分类 三铰刚架 (三铰结构 三铰结构) 三铰结构
结构力学 第三章 静定梁和静定平面钢架
２、截面法 若要求某一横截面上的内力，假想用一平面沿杆轴垂直方向将该 截面截开，使结构成两部分；在截开后暴露的截面上用力（内力）代 替原相互的约束。
对于截开后结构的两部分上，截面上的内力已成为外力，因此，
由任一部分的静力平衡条件，均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
３、截面内力 截开一根梁式杆件的截面上有三个内力（分量），即：轴力ＦN 、 剪力ＦQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系： DFN=-FPx
DFQ=-FPy
DM=m
１）微分关系及几何意义： dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy （１）在无荷载区段，ＦQ图为水平直线；
当ＦQ≠０时，Μ图为斜直线;
右右为正。
ＦQ＝截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正， 右下为正。
Μ ＝截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图（a）所示简支梁在图示荷载下截面的内力。
解：1）支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=－60kN (← ) 由 ∑Ｆy= 0 校核，满 足。
(下侧受拉)
区段叠加法求Ｅ、Ｄ截面弯矩； ΜE＝20×42/8＋120/2＝100kNm ΜＤ＝40×4/4＋120/2＝100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明：集中力或集中力偶作用点，注意对有突变的 分两侧截面分别计算。
结构力学 第3章静 定梁、平面刚架受力分析
工程中，斜梁和 斜杆是常遇到的，如楼梯梁、刚架中的斜梁等。斜梁 受均布荷载时有两种表示方法： （1）按水平方向分布的形式给出（人群、雪荷载等），用 q 表示。 （2）按沿轴线方向分布方式给出（自重、恒载），用 q’ 表示。
q 与 q’间的转换关系：
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
（1）求支座反力：
解：
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核：
Y
qj 6
qj 6
ql 3
0
第3章
（2）AC段受力图：
（3）AD段受力图：
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
（1）在无荷区段q(x)＝０，剪力图为水平直线，弯矩图为斜直线。
（2）在q(x)＝常量段，剪力图为斜直线，弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
（3）集中力作用点两侧，剪力值有突变、弯矩图形成尖点；集中力偶作用点两 侧，弯矩值突变、剪力值无变化。
解：
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
（1）计算支座反力
q 与 q’间的转换关系：
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
（1）求支座反力：
解：
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核：
Y
qj 6
qj 6
ql 3
0
第3章
（2）AC段受力图：
（3）AD段受力图：
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
（1）在无荷区段q(x)＝０，剪力图为水平直线，弯矩图为斜直线。
（2）在q(x)＝常量段，剪力图为斜直线，弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
（3）集中力作用点两侧，剪力值有突变、弯矩图形成尖点；集中力偶作用点两 侧，弯矩值突变、剪力值无变化。
解：
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
（1）计算支座反力
《静定梁与静定刚架》课件
优化材料分布
根据刚架的受力特点，合理分布材 料，使材料得到充分利用，降低成 本。
注意事项
注意梁的挠度和侧弯
根据载荷大小和分布，合理选择截面尺寸和材料，以控制梁的挠度和侧弯在允许 范围内。
考虑施工条件限制
在设计和施工过程中，应充分考虑施工条件限制，如施工空间、吊装能力等。
注意事项
• 注意载荷变化的影响：载荷的大小和分布可能会 发生变化，应在设计时充分考虑这些因素对梁的 影响。
静定刚架的应用实例
工业厂房
静定刚架在工业厂房中应用广泛，如厂房的柱、梁、支撑等 结构，能够承受较大的荷载，保证厂房的正常运行。
设备支撑
在大型设备或机械的支撑结构中，静定刚架也得到了广泛应 用，能够提供稳定可靠的支撑，确保设备的正常运行和使用 寿命。
静定梁与静定刚架的比较与选择
受力特点
静定梁和静定刚架在受力特点上有所不同。静定梁主要承受弯矩和剪力作用，而静定刚架 则主要承受轴力和弯矩作用。因此，在选择时需要根据实际需求和受力特点进行比较。
静定梁在受力时，其支座反力的 大小和方向可以通过截面的平衡
条件求出。
静定梁的内力计算
静定梁的内力计算可以通过截面的平衡条件进行，不需要引入未知数和求解方程组 。
静定梁的内力包括剪力和弯矩，可以通过截面的平衡条件求出剪力和弯矩的大小和 方向。
静定梁的内力计算可以通过手算或使用计算软件进行，手算需要掌握截面的平衡条 件和内力的计算方法。
BIG DATA EMPOWERS TO CREATE A NEW ERA
04
静定梁与静定刚架的应用实例
静定梁的应用实例
桥梁结构
静定梁广泛应用于桥梁设计中，如简 支梁桥、连续梁桥等，具有结构简单 、受力明确、施工方便等优点。
根据刚架的受力特点，合理分布材 料，使材料得到充分利用，降低成 本。
注意事项
注意梁的挠度和侧弯
根据载荷大小和分布，合理选择截面尺寸和材料，以控制梁的挠度和侧弯在允许 范围内。
考虑施工条件限制
在设计和施工过程中，应充分考虑施工条件限制，如施工空间、吊装能力等。
注意事项
• 注意载荷变化的影响：载荷的大小和分布可能会 发生变化，应在设计时充分考虑这些因素对梁的 影响。
静定刚架的应用实例
工业厂房
静定刚架在工业厂房中应用广泛，如厂房的柱、梁、支撑等 结构，能够承受较大的荷载，保证厂房的正常运行。
设备支撑
在大型设备或机械的支撑结构中，静定刚架也得到了广泛应 用，能够提供稳定可靠的支撑，确保设备的正常运行和使用 寿命。
静定梁与静定刚架的比较与选择
受力特点
静定梁和静定刚架在受力特点上有所不同。静定梁主要承受弯矩和剪力作用，而静定刚架 则主要承受轴力和弯矩作用。因此，在选择时需要根据实际需求和受力特点进行比较。
静定梁在受力时，其支座反力的 大小和方向可以通过截面的平衡
条件求出。
静定梁的内力计算
静定梁的内力计算可以通过截面的平衡条件进行，不需要引入未知数和求解方程组 。
静定梁的内力包括剪力和弯矩，可以通过截面的平衡条件求出剪力和弯矩的大小和 方向。
静定梁的内力计算可以通过手算或使用计算软件进行，手算需要掌握截面的平衡条 件和内力的计算方法。
BIG DATA EMPOWERS TO CREATE A NEW ERA
04
静定梁与静定刚架的应用实例
静定梁的应用实例
桥梁结构
静定梁广泛应用于桥梁设计中，如简 支梁桥、连续梁桥等，具有结构简单 、受力明确、施工方便等优点。
[精品]李廉锟版结构力学课件3静定梁与静定刚架
![[精品]李廉锟版结构力学课件3静定梁与静定刚架](https://img.taocdn.com/s3/m/b8a4912d04a1b0717ed5dd19.png)
FSⅣ B
MⅣ
FyB =36 kN
天水师范学院
School of Civil
结构力学 第三章 静定梁与静定刚架
§3-1 单跨静定梁 §3-2 多跨静定梁 §3-3 静定平面刚架 §3-4 少求或不求反力绘制弯矩图 §3-5 静定结构的特性
天水师范学院
School of Civil
15:21
§3-1 单跨静定梁
结构力学
静定结构定义
在荷载等因素作用下，其全部支座反力和任意 一截面的内力均可由静力平衡方程唯一确定的结构。
M Ⅳ 4410 208 15 4 4 32 72 kN =0
CD Ⅰ
FyA= 44 kN 2m 2m
15 kN/m Ⅱ
4m
3m
3m
32 kN m
EG
B
ⅢⅣ
FyB = 36 kN
2m 2m
也可以由截面Ⅳ-Ⅳ以
右隔离体的平衡条件 求得。
20 kN Fs1
可以判定所有截面的轴力均为零, 取截面Ⅰ-Ⅰ以左为
隔离体。
20 kN
15 kN/m
32 kN m
AC
D
FxA =0
Ⅰ
Ⅱ
EG
B
ⅢⅣ
FyA= 44 kN
FyB = 36 kN
2m 2m
4m
3m
3m
2m 2m
由 MⅠ 0
2200 kkNN
FFSsⅠ1
有
AC
44 kN
MM1Ⅰ
由
44 kN
15 kN/m
44 3 20 1 MⅠ 0 MⅠ 44 3 20 1 112 kN m
44 kN
FyB 36 kN
结构力学-静定梁与静定钢架
4：斜梁例题
M图
Q图 1、求支座反力：VA=ql/6，HA=0， VB=ql/6 2、作M、Q、N图
N图
对简支斜梁内力计算的总结
1 简支斜梁计算支座反力和内力的方法仍然是隔离体平衡和截面 法。
2 在竖向荷载作用下，简支斜梁的支座反力和相应的平梁的支座 反力是相同的。
3 在竖向均布荷载作用下，简支斜梁的弯矩图和相应平梁的弯矩图 是相同的。
静定空间刚架例题
试求图a所示的空间刚架制作界面A的内力？
解： (1)由已知图做出此刚架的A截面的 内力图如图b所示
B
A VAY VAZ
MAZ Z
NA MAX x
D C
y （b）
D B
C A
（a）
(2) 由空间一般力系的平衡条件可得以下方程求得结果：
∑X=0，NA+4×2=0， NA=-8kN
∑Y=0，VAY-5=0， VAY=5kN
结构力学第三章
静定梁和静定钢架
成员： 刘锦伟 侯智译 于涛 潘琦 杨宏宇
内容概要：（一） 简支斜梁的计算
（二） 静定空间刚架
（1）简支斜梁的计算
1：工程应用实例、斜梁荷载
沿水平方向均布q：活载（人群、雪载）
梁式楼梯、板式楼梯、 屋面斜梁、及具有斜杆 的刚架等。
沿杆轴线均布q′：恒载(自重)，
（2）：水平方向均布荷载作用
∑Z=0,
VAZ=0
∑MX=0,MAX-5×2=0, MAX=10KN.M
∑MY=0,MAY-4×2×2×1/2=0, MAY=8KN.M ∑MZ=0,MAZ-4×2×3+5×3=0, MAZ=9KN.M
NA MAX x
(b)
D C
结构力学(一)第三版龙驭球第三章3.3静定刚架
结点处有不同的杆端截面。各截面上的内力用该杆两端 字母作为下标来表示，并把该端字母列在前面。 注意结点的平衡条件！
2m
1m
4.3 用截面法求静定刚架杆端截面内力 【例4.3 】计算图示刚架刚结点处各杆杆端截面的内力。
1kN/m
2kN
B C D
9
3kN 2kN
B
1kN/m
C
MCA
3kN
QCA D NCA
2qa2
4qa2
14qa
2
M图
QDC 0
QDB 0
QBD 6qa
N DC 0
3.2qa
QBE 3.2qa
QBA 0
6qa 8qa
Q图
N DB 0 N BD 0 N BE 2.4qa N BA 10qa
YA 10qa()
2.4qa
10qa
N图
X A 8qa()
1kN/m
C
2m
C D A 2kN 4kN B E
2
4 4 D A
2 4 E 4
2m
4m
4m
2kN 4kN
M图（kN· ） B m
4.5 三铰刚架及多层多跨静定刚架的内力图 【例4.8 】作出图示两跨静定刚架的弯矩图。
2kN/m
D
15
8 E
F
G
4m
1kN
A
B
C
1kN
D 4
4 E F
4
G 4
2m
2m
M CA 12 4 3 4 2 24kN m NCD 12 3 4 0
4kN
C
D
3kN/m
12kN 4kN
2m
1m
4.3 用截面法求静定刚架杆端截面内力 【例4.3 】计算图示刚架刚结点处各杆杆端截面的内力。
1kN/m
2kN
B C D
9
3kN 2kN
B
1kN/m
C
MCA
3kN
QCA D NCA
2qa2
4qa2
14qa
2
M图
QDC 0
QDB 0
QBD 6qa
N DC 0
3.2qa
QBE 3.2qa
QBA 0
6qa 8qa
Q图
N DB 0 N BD 0 N BE 2.4qa N BA 10qa
YA 10qa()
2.4qa
10qa
N图
X A 8qa()
1kN/m
C
2m
C D A 2kN 4kN B E
2
4 4 D A
2 4 E 4
2m
4m
4m
2kN 4kN
M图（kN· ） B m
4.5 三铰刚架及多层多跨静定刚架的内力图 【例4.8 】作出图示两跨静定刚架的弯矩图。
2kN/m
D
15
8 E
F
G
4m
1kN
A
B
C
1kN
D 4
4 E F
4
G 4
2m
2m
M CA 12 4 3 4 2 24kN m NCD 12 3 4 0
4kN
C
D
3kN/m
12kN 4kN
《结构力学》_龙驭球_第3章_静定结构的受力分析(2)
一、求支座反力
40 kN
在支座反力的计算过程中，应尽可能建立 独立方程。
B
D
C
20 kN/m
4m
MA 0 FY 0
FDY 4 40 2 (20 4) 2 0 FDY 60kN () FAY 40 60 0 FAY 20kN ()
FX 0 FAX 80kN ()
二、绘制内力图
⑴ 分段：根据荷载不连续点、结点；
解，本题剪力很容易用投影方程求得。
4kN/m
1kN
C
MDE D
E
8
14kN
4m
1kN B 4m
2kN
28 24
4
4D
8
E
F
A
B
M 图（kN·m）
14
D
E
2
2
16
1
F
A
B
FQ 图（kN）
③ 作FN 图 各杆轴力可以用投影方程求
解。也可根据剪力图， 取各结点 为隔离体，用投影方程求轴力。
④ 校核
16
14
40
载和B端外力偶作用的简支梁(图C)。
画M图时，将 B 端弯矩竖标画在受拉 80 A
侧，连以虚直线，再叠加上横向荷载产生
20
的简支梁的弯矩图，如图(d)示。
(b)
A
A
(c)
(d)
B 160
D
160
120
20 60
120
20
A M图 (kN·m）
80 F Q 图（kN)
F N 图（kN)
练习3-3.1：试计算图示简支刚架的支座反力，并绘制Ｍ、F Q 和 F N 图。
Fx 0, FBx 2 11kN()
结构力学3静定刚架
（）
速绘弯矩图
Pa
P
a
2m/3 m/3
m m/3
m 2m/3
a
a
a
a
↑↑↑↑↑
P
Pa a
P Pa
a
qa2/2 l
a
a
P
m
m Pa/2
m
Oa
a
m
m/2 m
m/2a
a
Pa/2
m
m/2a
m
a
m/2
m/2
m/2
0
m/2a
a
a m/2
a
a
P
2Pa Pa
2P
0
Pa
a
a
a
Pa
a
2P
m
2Pa Pa
P
Pa P
h
E
D
B
2q A
2a 2a
4a
4）杆AB
N BA
M BA
B QBA
2q 14qa2
A 8qa
10qa
3)杆BE q
M BE
N BE
QBE 4a
8qa 2
M图NBBiblioteka = 10qa QBA = 0 M BA = 2qa2
x=0
NBE q 4a sin = 0
N BE
=
4qa
1、悬臂刚架
可以不求反力，由自由端开始直接求作内力图。
q
2q
½qL²↓↓↓↓↓↓↓↓↓
qL²
2q
↓↓↓↓↓
L
q
qL²
2m
2m
L
6q
2、简支型刚架弯矩图
简支型刚架绘制弯矩图时，往
速绘弯矩图
Pa
P
a
2m/3 m/3
m m/3
m 2m/3
a
a
a
a
↑↑↑↑↑
P
Pa a
P Pa
a
qa2/2 l
a
a
P
m
m Pa/2
m
Oa
a
m
m/2 m
m/2a
a
Pa/2
m
m/2a
m
a
m/2
m/2
m/2
0
m/2a
a
a m/2
a
a
P
2Pa Pa
2P
0
Pa
a
a
a
Pa
a
2P
m
2Pa Pa
P
Pa P
h
E
D
B
2q A
2a 2a
4a
4）杆AB
N BA
M BA
B QBA
2q 14qa2
A 8qa
10qa
3)杆BE q
M BE
N BE
QBE 4a
8qa 2
M图NBBiblioteka = 10qa QBA = 0 M BA = 2qa2
x=0
NBE q 4a sin = 0
N BE
=
4qa
1、悬臂刚架
可以不求反力，由自由端开始直接求作内力图。
q
2q
½qL²↓↓↓↓↓↓↓↓↓
qL²
2q
↓↓↓↓↓
L
q
qL²
2m
2m
L
6q
2、简支型刚架弯矩图
简支型刚架绘制弯矩图时，往
结构力学-静定梁与静定刚架
A BC
D
130 210
E
F
140
340
280 M图（kN·m）
130 D
120
40
A B C 30
E
F
FS 图（kN）
190
26
小结： 1）弯矩叠加是指竖标以基线或杆轴为准叠加，而非 图形的简单拼合； 2）应熟悉简支梁在常见荷载下的弯矩图； 3）先画M 图后画FS图，注意荷载与内力之间的微分 关系。
B (qlcosθ)/2
B (qlcosθ)/2
32
3) 作内力图。
(qlcosθ)/2 (qlsinθ)/2
ql2/8 M图 FQ 图
FN 图
(qlcosθ)/2 (qlsinθ)/2
33
例3-1-3 作图示斜梁的内力图。
x FxA A θ
FyA
q
l /cosθ
C qlcosθ
l
ql θ qlsinθ
1.荷载与内力之间的微分关系
qy
M FN
FS
o qx dx
M+dM x
FN+dFN
FS dFS
y
Fy 0, F SdS F qyd xF S0ddFxS q y .
MO 0, M M dM F Sd 2 xF SdF Sd 2 x0,
dM dxFS,
3）定点：求控制截面在全部荷载作用下的 M 值， 将各控制面的 M 值按比例画在图上，在各控制截 面间连以直线——基线。
4）连线叠加：对于各控制截面之间的直杆段，在 基线上叠加该杆段作为简支梁时由杆间荷载产生的 M图。
18
例3-1-1 作图示静定单跨梁的M图和FS图。
8kN
结构力学3静定结构的受力分析-刚架
1 结构力学多媒体课件1、刚架由梁和柱组成的结构，其结点全部或部分是刚结点。
2、刚架的形式2）简支刚架1）悬臂刚架2、刚架的形式3)三铰刚架4)主从刚架3、刚架的特点1）杆数少，净空大，便于使用3、刚架的特点2）刚结点的特点①变形：刚结点处的各杆端不能发生相对移动和相对转动，因而受力变形后，各杆杆端转动了同一角度，即各杆之间的夹角保持不变。
②受力：刚结点可承受和传递弯矩保持角度不变3、刚架的特点3）横梁和竖柱连成整体，使整体刚度增大，弯矩的峰值减少二、刚架中各杆的杆端内力1、支座反力的计算⑴求反力时要先根据支座的性质正确定出反力未知量个数，不能多、不能少。
⑵假定反力方向，由平衡方程确定其数值。
⑶应尽量利用一个平衡方程求一个未知力。
⑷求出反力后要有没有用过的平衡方程校核。
l /2l /2l /2l /2CBAPF AY =0.5PF BY =0.5PF AX=0.75P F BX =0.25P2m 2m 4mCBA4m2kN/mGFEDF AX =1KNF CX =1KNF CY =3KNF BY =7KN2、杆端内力的计算⑴方法：截面法⑵内力符号结点处有不同的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示，并把该端字母列在前面。
——AB杆A端的轴力。
FN AB——AB杆A端的剪力。
FQ AB——AB杆A端的弯矩。
MAB2、杆端内力的计算⑶内力的正负规定轴力FN：以拉力为正，压力为负。
剪力FQ：以绕隔离体顺时针转为正,反之为负。
弯矩M：不规定正负，但弯矩图画在受拉侧。
F N FNF Q F QM AB M BAF NF NF QF Q MBAM AB 竖杆剪力图和轴力图可画在任一侧，但必须标出正负；弯矩图画在受拉一侧，可不标正负。
2、杆端内力的计算 ⑷正确选取脱离体⑸注意结点平衡∑F X =0 ∑F Y =0 ∑M D ＝0一般先求出支座反力及铰结点处的内约束力，然后将刚架拆成杆件，逐杆绘制其内力图，将各杆的内力图合在一起就是刚架的内力图。
结构力学第4章静定刚架的内力计算
GDCB部分： 见图(c)右。计算如下：
FX 0
FCx 1kN (←)
MC 0
FBy
1 (q 6 3 8 6 1 4 4
FP
2)
30kN(↑)
MB 0
FCy
1 4
(q
4
2
q
2
1
8
2
1
4
FP
2) 2kN(↑)
2）作内力图：
结构力学
结构力学教研室
青岛理工大学工程管理系
第四章
静定刚架的内力分析
§4.1 概 述
组成刚架的杆件主要产生弯曲变形， 可承受弯矩。
刚架的构造特点: 具有刚结点
(a)
(b)
(c)
刚结点的特点:
能传递力矩 （弯矩）
静定刚架有如下几种最简形式, 较复杂的刚架一般是由若干简 单刚架按基本组成规则构成的。
由 M A 0 得：
1 L L qL
FBy
q L
2
4
8
(↑)
(a)
由 M B 0 得：
FAy
1 q L
L (L 24
L) 2
3qL 8
(↑)
(b)
如取截面I-I以右部分，由 MC 0
得：
FBx
1 L
FBy
L 2
qL(←)
16
再由整体的平衡方程 FX 0
（右侧受拉）
结点C：
MCD
FNCD FQCD MCB
FQCB
结构力学3静定刚架
在支座反力的计算过程中，应尽可能建立独立方程。 下图所示两跨刚架可先建立投影方程 Y =0计算RC ，再对 RC 和 RB的交点 O取矩，建立力矩方程M O =0 ，计算RA，最后建立投影方程 X = 0 计算RB 。
y x
0
C
A
B
.
O
如图（a）三铰刚架，具有四个支座反力，可以利用三个整
体平衡条件和中间铰结点C 处弯矩等于零的局部平衡条件，一共
1、悬臂刚架
可以不求反力，由自由端开始直接求作内力图。
q
2q
½qL²↓↓↓↓↓↓↓↓↓
qL²
2q
↓↓↓↓↓
L
q
qL²
2m
2m
L
6q
2、简支型刚架弯矩图
简支型刚架绘制弯矩图时，往
↓↓↓↓↓↓↓↓↓↓↓↓
q
往只须求出一个与杆件垂直的
ql2/2
l/2
支座反力，然后由支座作起。
q
D
qa2/2
l
C
l/2
qL2/2
ql2/8
ql2/8
ql2/8ຫໍສະໝຸດ hl/2l/2
静定刚架的M图正误判别
利用上述内力图与荷载、支承和联结之间的对应关系，可在绘制内力图时 减少错误，提高效率。 另外，根据这些关系，常可不经计算直观检查 M 图的轮廓是否正确。 ①M图与荷载情况不符。 ②M图与结点性质、约束情况不符。 ③作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件。
P
2P
a
a
2P
Ph Ph
a
2Ph
Ph 2Ph
2Ph
Ph
aa
2a
h aaa
↓↓↓↓↓↓↓↓↓↓↓↓↓
y x
0
C
A
B
.
O
如图（a）三铰刚架，具有四个支座反力，可以利用三个整
体平衡条件和中间铰结点C 处弯矩等于零的局部平衡条件，一共
1、悬臂刚架
可以不求反力，由自由端开始直接求作内力图。
q
2q
½qL²↓↓↓↓↓↓↓↓↓
qL²
2q
↓↓↓↓↓
L
q
qL²
2m
2m
L
6q
2、简支型刚架弯矩图
简支型刚架绘制弯矩图时，往
↓↓↓↓↓↓↓↓↓↓↓↓
q
往只须求出一个与杆件垂直的
ql2/2
l/2
支座反力，然后由支座作起。
q
D
qa2/2
l
C
l/2
qL2/2
ql2/8
ql2/8
ql2/8ຫໍສະໝຸດ hl/2l/2
静定刚架的M图正误判别
利用上述内力图与荷载、支承和联结之间的对应关系，可在绘制内力图时 减少错误，提高效率。 另外，根据这些关系，常可不经计算直观检查 M 图的轮廓是否正确。 ①M图与荷载情况不符。 ②M图与结点性质、约束情况不符。 ③作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件。
P
2P
a
a
2P
Ph Ph
a
2Ph
Ph 2Ph
2Ph
Ph
aa
2a
h aaa
↓↓↓↓↓↓↓↓↓↓↓↓↓
结构力学刚架
§2
静定刚架支座反力的计算
刚架分析的步骤一般是先求出支座反力，再求出各杆控制
截面的内力，然后再绘制各杆的弯矩图和刚架的内力图。
在支座反力的计算过程中，应尽可能建立独立方程。
下图所示两跨刚架可先建立投影方程 Y = 0 计算RC ，再对 RC 和RB 的交点 O取矩，建立力矩方程 MO = 0 ，计算R A，最后建立投影方程 X = 0 计算 R 。
• • • • 2. 计算步骤： 1） 求出支座反力； 2） 将刚架拆成单个单元； 3） 用截面法计算各杆杆端截面的内力 值； • 4） 利用微分关系和叠加法逐杆绘制内 力图； • 将各杆内力图组合在一起。
例1.作内力图 ⑴ 求反力（利用平衡条件）： ∑FX=0 HD=30×4=120kN(←) ∑MD=0
4m
VA=-40kN(↓)
∑FY=0 VD=－VA=-40kN（↑）
⑵ 分析绘制M图（列方程） AB 杆 （ 0<x1<4 ） ： M(X1)=
30 2 X 1 = 15 X 12 2
4m
CD杆(0<x3<4)：无荷载，直 线 M(X3)=120 X3 MCD=480kN· m BC杆：M图为直线
160
B 4m
20 kN/m
40
A (d) M图
H A = 80
VA = 20
A 2m (a)
80
A
20
A ( c)
2m
(b)
40kN
N BD
M BD
B 2m
160kN· m
40kN
B D
40kN B 20kN/m C D 4m
2m
D
60
QBD
X =0 N BD = 0
《结构力学》静定刚架
2qa2 q 4a 2a 6qa 2a
2q 4a 2a M A 0
M A 14qa2
（2）计算各杆端截面力，绘制各杆M图
2qa2
q
1）杆CD
2qa2
C 6qa
E
2qa2
3a
D
B
F SDC 0
C
2q A
2a 2a
4a
结点D
4a
F
NDC
0
D
F SDC
M DC 2qa2 M DC
M图
2）杆DB
20kN·m
30kN
D CE
40kN·m
D
40kN·m
E
4m
10kN A 2m
10kN
20 M DC 20
D
B
10kN
2m 20kN
10kN A 10kN
M EC 40 E
20 40
B 10kN 20kN
40
40
20kN·m
40kN·m 40
D
C
E
M图（kN·m）
例4. 求绘图示结构的弯矩图。
3.3 静定平面刚架的内力计算
1、平面刚架的基本形式： 1、悬臂刚架
2、简支刚架
3、三铰刚架
4、主从刚架
2、平面刚架结构特点：
把简支梁折弯即成简支刚架。刚架与梁明显的区别刚架具有 刚结点。
1）刚结点的变形特点：刚架受力前后，刚结点上各杆之间 的夹角保持不变。
2）刚结点的受力特点：图示刚架取C结点作受力分析
内力符号的标注：为了区分汇交于同一结点的各杆端截面内
力，在内力符号下面引用两个脚标，第一个表示内力所属截
面，第二个表示该截面所属杆件的另一端。
2q 4a 2a M A 0
M A 14qa2
（2）计算各杆端截面力，绘制各杆M图
2qa2
q
1）杆CD
2qa2
C 6qa
E
2qa2
3a
D
B
F SDC 0
C
2q A
2a 2a
4a
结点D
4a
F
NDC
0
D
F SDC
M DC 2qa2 M DC
M图
2）杆DB
20kN·m
30kN
D CE
40kN·m
D
40kN·m
E
4m
10kN A 2m
10kN
20 M DC 20
D
B
10kN
2m 20kN
10kN A 10kN
M EC 40 E
20 40
B 10kN 20kN
40
40
20kN·m
40kN·m 40
D
C
E
M图（kN·m）
例4. 求绘图示结构的弯矩图。
3.3 静定平面刚架的内力计算
1、平面刚架的基本形式： 1、悬臂刚架
2、简支刚架
3、三铰刚架
4、主从刚架
2、平面刚架结构特点：
把简支梁折弯即成简支刚架。刚架与梁明显的区别刚架具有 刚结点。
1）刚结点的变形特点：刚架受力前后，刚结点上各杆之间 的夹角保持不变。
2）刚结点的受力特点：图示刚架取C结点作受力分析
内力符号的标注：为了区分汇交于同一结点的各杆端截面内
力，在内力符号下面引用两个脚标，第一个表示内力所属截
面，第二个表示该截面所属杆件的另一端。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
只有两杆汇交的刚结点，若结 点上无外力偶作用，则两杆端 弯矩必大小相等，且同侧受拉。
40
80
D
FNDE FNED
E
30
30
FNDC
FNEB
FQ
40 kN
FN 30 kN
80 kN
静定刚架内力的概念分析，除用到以上介 绍的三条知识点外，补充另两点：
1、计算刚架的水平反力。 2、刚结点满足力偶矩的平衡条件。
静定平面刚架(frame)
悬臂刚架
静
A
D
定
刚
简支刚架
架
B
C
三铰刚架
D
E
刚架--具有刚结点的由 直杆组成的结构。
有基、附关系的刚架
附属部分
基本部分
刚结点处的 变形特点
保持角度不变
超静定刚架
一个多余约束
三个多余约束
静定刚架的内力图绘制方法：
一般先求反力，然后求控 制弯矩，用区段叠加法逐杆 绘制，原则上与静定梁相同。
例一、试作图示刚架的内力图
求反力
(单位：kN . m)
48
144
192
126
12
图示刚架的内力图 FQ (单位：kN . m)
48
144
192
126
12
42 kN
FN
48 kN
22 kN
例二、试作图示刚架的内力图
快速作
弯矩图
3F0Bx
求反力
40 FAy
80 FBy
静定的对称结构指：结构的几何尺寸、支 承情况关于某轴对应相同。
对称结构作用荷载可分解为;正对称荷载与 反对称荷载。
对称结构在正对称荷载作用下，弯矩图、 轴力图是正对称图形，剪力图是反对称图形。
例三、试作图示三铰刚架的内力图
整体对A、B
取矩，部分
20
对C取矩。 20
FBx
FBx
80 FAy
80 FBy
例五、不经计算画图示结构弯矩图
FP
FP
FP
FP
FPa
FPa
FPa
FPa 2FP FPa 2FP FPa
60
180
240
FAx FAy
40 40
FBy
M图 kN .m
FPa
2FPa a
FPa a
FPa
FPa
FP a
2FP
a
a
平行
20 20
40
75
30
45 5kN
FN FQ
关键是注意： 取斜杆对杆端取矩求剪力
这样可不解联立方程
例四、试作图示刚架的弯矩图
附属 部分
基本 部分
弯矩图如何?
少求或不求反力绘制弯矩图
根
1.弯矩图的形状特征（微分关系） 2.刚结点力矩平衡
3.外力与杆轴关系(平行,垂直,重合)
4.特殊部分(悬臂部分,简支部分)
据 5.区段叠加法作弯矩图