第八章_RLC电路与常微分方程的解法_郑大昉

0 Qn+1 = Qn + f (Qn , tn )∆t
(8-18)
此方法称向后的欧拉法 此方法称向后的欧拉法. 向后的欧拉法 但向后的欧拉法并未给出其误差的改进(?). 但向后的欧拉法并未给出其误差的改进
改进的欧拉方法 折线斜率选其在 处的平均值 平均值, 若折线斜率选其在 Q(tn ) 和 Q(tn+1) 处的平均值 即:
6
其中(推导从略 其中 推导从略): 推导从略
k1 = f (Qn , tn ) ∆t k2 = f (Qn + k1, t 1 ) n+ 2 2 ∆t k3 = f (Qn + k2 , t 1 ) n+ 2 2 k4 = f (Qn + ∆tk3, tn+1)
(8-22) (8-23) (8-24) (8-25)
dQn+1 0 0 0 = f (Qn+1, In+1, tn ) = In+1 dt 0 0 dIn+1 Qn+1 0 1 0 0 = g(Qn+1, In+1, tn ) = (Va − − In+1R) dt L C
(8-38) (8-39)
0 0 Qn+1, In+1 , 由欧拉法预测出 欧拉法预测出.
欧拉方法
(8-4)
基本思路: 差分代替其微分,并通过递推法求解 代替其微分 并通过递推法求解. 基本思路 用差分代替其微分 并通过递推法求解 (8-4) 改写为 改写为: 另: 即:
∆Q = f (Q, t)∆t
(8-5) (8-6) (8-7)
∆Q Q(t + ∆t) − Q(t) = ∆t ∆t
注意: 的解对其参数的依赖十分敏感 参数的依赖十分敏感. 注意 (8-29) 的解对其参数的依赖十分敏感 即解的形式依赖于阻尼度： 即解的形式依赖于阻尼度： 阻尼度
λ=
若： 若： 若：
R C 2 L
(8-30)
λ >1, λ =1, λ <1,
称过阻尼; 过阻尼 称临界阻尼; 临界阻尼; 称阻尼振荡; 阻尼振荡
t = tn 处展成泰勒级数 处展成泰勒级数 泰勒级数:
Qn+1 = Qn + f (Qn , tn )∆t
即为欧拉法. 即为欧拉法
欧拉法的局部截断误差为: O[(∆t)2 ],其整体截断误差为: O[∆t]. 欧拉法的局部截断误差为 整体截断误差为 局部截断误差
向后的欧拉方法 折线斜率选在 若折线斜率选在 Q(tn+1) 处,即: 即
第八章 RLC电路与常微分方程的解法 电路与常微分方程的解法
RC电路及一阶常微分方程解法 电路及一阶常微分方程解法
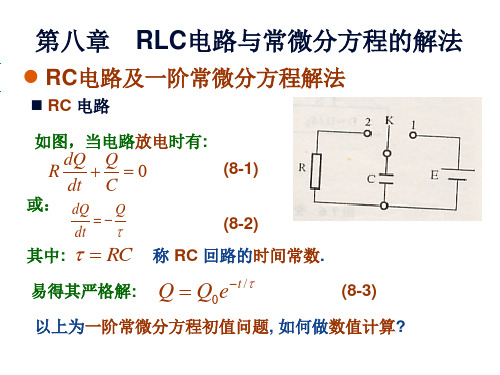
RC 电路 如图，当电路放电时有 如图，当电路放电时有: 放电时有
dQ Q + =0 R dt C
或： dQ Q =− dt τ 其中: 其中 τ = RC 易得其严格解: 易得其严格解
∆Q = Q(t + ∆t) − Q(t)
(8-5),(8-7) 得:
Q(t + ∆t) = Q(t) + f (Q, t)∆t
(8-8)
令:
tn+1 −tn ≡ ∆t = 常量
Qn+1 = Qn + f (Qn , tn )∆t
f (Qn , tn ) = −
Qn+1 = Qn − Qn
(8-9)
Q0 =1.0,τ =10, ∆t =1
(8-13)
可见, 增加而增加. 可见 其误差随 n 的增加而增加 另一方面, 减少而提高. 另一方面 结果精度将随 ∆t 的减少而提高 减少将增加机时,且有可能导入舍入误差. 且有可能导入舍入误差 但 ∆t 的减少将增加机时 且有可能导入舍入误差
欧拉解法的几何意义 欧拉解法的几何意义: 几何意义 (1)实质为折线法 即差分法 实质为折线法 即差分法). 实质为折线法(即差分法
则得递推解 则得递推解: 递推解
(8-10)
本例子中: 本例子中 即:
Qn
τ
,τ = RC
(8-11)
τ
∆t
(8-12)
若给定初始条件 若给定初始条件: Q , 常数 初始条件 0 常数:
τ , 步长 ∆t 步长:
可递推出任意时刻 的解. 则依 (8-10) 可递推出任意时刻 tn+1 的解
例如, 例如 设: 则易递推得: 则易递推得
龙格-库塔 龙格 库塔(R-K)方法 库塔 方法 此时,四阶 方法为 此时 四阶R-K方法为: 四阶 方法
1 Qn+1 = Qn + 6 (k1 + 2k2 + 2k3 + k4 )∆t I = I + 1 (l + 2l + 2l + l )∆t n 1 2 3 4 n+1 6 Q(t0 ) = Q0 I (t ) = I 0 0
欧拉方法
(8-31)
对上述RLC充电电路 充电电路: 对上述 充电电路
Q0 = 0, I0 = 0
(8-32) (8-33)
f (Q, I , t) = I 1 Q g(Q, I , t) = (Va − − IR) L C
其欧拉算法? 欧拉算法
事实上,其差分思想仍可直接应用 即 事实上 其差分思想仍可直接应用,即 思想仍可直接应用 dQn Qn+1 = Qn + dt ∆t I = I + dIn ∆t n+1 n dt Q(t0 ) = Q0 I (t ) = I 0 0 其中: 其中 dQn
(8-1) (8-2) 回路的时间常数 时间常数. 称 RC 回路的时间常数
−t /τ
Q = Q0e
(8-3)
以上为一阶常微分方程初值问题 如何做数值计算 数值计算? 以上为一阶常微分方程初值问题, 如何做数值计算 一阶常微分方程初值问题
dQ = f (Q, t) 上述方程的一般形式 一般形式: 上述方程的一般形式 dt Q(t0 ) = Q0
其中: 其中
(8-45)
k1 = f (Qn , In , tn )
(8-46) (8-47)
l1 = g(Qn , In , tn )
以及: 以及
∆t ∆t k2 = f (Qn + k1, In + l1, t 1 ) n+ 2 2 2 ∆t ∆t l2 = g(Qn + k1, In + l1, t 1 ) n+ 2 2 2 ∆t ∆t k3 = f (Qn + k2 , In + l2 , t 1 ) n+ 2 2 2 ∆t ∆t l3 = g(Qn + k2 , In + l2 , t 1 ) n+ 2 2 2 k4 = f (Qn + ∆tk3, In + ∆tl3, tn+1)
其解如图示: 其解如图示 因此对其数值计算的要求也更高. 因此对其数值计算的要求也更高
dQ dt = f (Q, I , t) 上述方程的一般形式 一般形式: 上述方程的一般形式 dI = g(Q, I , t) dt Q(t0 ) = Q0 I (t ) = I 0 0
(8-34)
dt dIn 1 Qn = g(Qn , In , tn ) = (Va − − In R) (8-36) dt L C 因此,给定 0 便可递推算出 递推算出任意时刻的 因此 给定 Q , I0, 便可递推算出任意时刻的 Qn+1, In+1.
= f (Qn , In , tn ) = In
改进的欧拉方法 进一步地,改进的欧拉方法 改进的欧拉方法为 进一步地 改进的欧拉方法为:
0 1 dQn dQn+1 + )∆t Qn+1 = Qn + ( 2 dt dt 0 1 dIn dIn+1 + )∆t In+1 = In + ( 2 dt dt Q(t0 ) = Q0 I (t0 ) = I0
1 0 Qn+1 = Qn + [ f (Qn , tn ) + f (Qn+1, tn+1)]∆t 2 0 其中: 其中 Qn+1 = Qn + f (Qn , tn )∆t
(8-19) (8-20)
可以证明(略 此方法的局部截断误差数量级为: 局部截断误差数量级为 可以证明 略), 此方法的局部截断误差数量级为 O[(∆t)3 ] (事实上 欧拉法与向后的欧拉法其误差符号相反 因此相 事实上, 欧拉法与向后的欧拉法其误差符号相反, 事实上 互抵消,从而提高其结果精度 从而提高其结果精度). 互抵消 从而提高其结果精度 以上方法称改进的欧拉法 以上方法称改进的欧拉法, 改进的欧拉法 也称两点欧拉法 两点欧拉法, 也称两点欧拉法 中点欧拉法, 或中点欧拉法 梯形法. 或梯形法 如何实现其数值计算? 如何实现其数值计算 提醒: 提醒 (8-20) 中的 Q 是 n 改进后的值 的值. 改进后的值
VR +VL +VC = Va
(8-26)
dI Q + = Va (8-27) 即：IR + L dt C
又： I = dQ dt (8-28) (8-29)
d 2Q dQ Q 得： L +R + = Va 2 dt dt C
(8-29)即为二阶常微分方程 它由两个一阶的方程 即为二阶常微分方程,它由两个一阶的方程 即为二阶常微分方程 它由两个一阶的方程(8-27) 构成. 和(8-28)构成 构成
或
dQn+1 Qn+1 = Qn + ∆t dt Qn+1 = Qn + f (Qn+1, tn+1)∆t