第三章 应力和应变
《应力与应变》课件

目录
CONTENTS
• 应力概述 • 应变概述 • 应力与应变的关系 • 应力与应变的应用 • 实验与演示 • 总结与展望
01 应力概述
CHAPTER
定义与概念
定义
应力定义为物体内部单位面积上 所承受的力,用于描述物体受力 状态。
概念
应力是物体受力时内部各部分之 间的相互作用,是物体抵抗变形 和破坏的内在能力。
压缩实验
总结词
通过观察物体在压缩过程中的形变,了解应 力和应变的基本性质。
详细描述
压缩实验是应力与应变研究中另一种重要的 实验方法。在实验中,我们将物体的一端固 定,另一端施加逐渐增大的压力,使物体发 生压缩形变。通过测量压缩量,我们可以计 算出物体的应力和应变。通过观察和记录实 验数据,学生可以了解应力和应变的基本性
应力分类
按作用方式
可分为正应力和剪应力。正应力表示 垂直于受力面的力,剪应力表示与受 力面平行且垂直于切线方向的力。
按作用效果
可分为拉应力和压应力。拉应力表示 使物体拉伸的力,压应力表示使物体 压缩的力。
应力单位与表示方法
单位
应力的单位是帕斯卡(Pa),国际单位制中的基本单位。
表示方法
应力的表示方法通常采用符号“σ”或“σxx”(xx表示方向),例如正应力的 表示符号为σ或σxx,剪应力的表示符号为τ或τxy(xy表示剪切方向)。
进步。
谢谢
THANKS
压缩试验
测定材料的抗压强度、弹性模量等指 标,了解材料在受压状态下的性能表 现。
有限元分析
模型建立
根据实际结构或系统建立有限元 模型,将复杂结构离散化为有限
个单元。
加载与约束
河海大学 材料力学 第三章 杆件横截面上的应力、应变分析第一节

点K处的应力(stress) DF p=lim pm= lim —— DA→0 DA→0 DA
p 正应力s :沿截面法向 n 切应力t :沿截面切向 s p 2= s 2 + t 2
应力单位:Pa(帕斯卡、帕) MPa(兆帕)
1 Pa = 1 N/m2 1MPa =106 Pa
注意:
t
K
s
以上分析可见,应力是受力物体内某个截面上某 一点上内力分布集度。通常情况下,物体内各点 应力是不同的,对于同一点不同方位截面上应力 亦不同。这样,应力离开它的作用点是没有意义 的,同样,离开它的作用面亦是没有意义的。
(shearing strain) 单位: rad。
四、胡克定律
s
s
du e= — dx
u
u+du
如果仅在单方向正应力s 作用下,且正应力不超过某 一限值(比例极限),则正应力与正应变成正比,即
s = Ee ——胡克定律(Hooke's law)
E ——弹性模量。(elastic modulus)
如何描述一点处的应力?
二、一点的应力状态、单元体:
K K
围绕K点取一微小的六面体,称为单元体。
六个面都表示通过同一点K的面,只是方向不同而已。
如果所取的单元体在空间方位不同,则单元体上各面 的应力分量亦不相同。
sy
y
tyz
tyx txy txz sx
x
tzy
z
sz
tzx
若从一复杂受力构件内某点取一单元体,一般 情况下单元体各面上均有应力,且每一面上同时存 在三个应力分量:一个法向分量——正应力;两个 切向分量——切应力。这样,单元体上共有9个应力 分量。
第三章应力分析应变分析屈服准则复习讲诉

a 0 0
1 ij
0
b
0
0 0 0
ab
2
ab 2
0
2 ij
a
b 2
ab 2
0
0
0 0
一、应力张量不变量及其应用
例题解答
对于
1 ij
J1 a b0 a b
J2
a 0
0b
b0
00
00
0
a
ab
a00 J3 0 b 0 0
000
同理,对于
2 ij
J1
a
2
b
a
2
b
0
a
b
ab
J2
试问上述应变场在什么情况下成立?
例题解答
2 xy xy
1 2
2 x y 2
2 y x2
(1)
2 xy 2 (2bxy) 2b xy xy
1
2
2 x y 2
2 y x2
1
2
2
a x2 y2 y 2
2
axy
x2
a
a 2b 即当a 2b时,上述应变场存在。
应变分析问题小 结
max min
2
C
2.2 单向拉伸时的Tresca屈服准则
2.2 Tresca yield criterion in uniaxial stretch test
三、应变连续方程问题
知识要点回顾
小应变几何方程
2 x y2
2 y2
u x
2 xy
u
y
(1)
2 y x2
2 x2
v y
2 v xy x
(2)
2应力应变分析

JJ J
1 2
应该是单值的,不随坐标
3
而变,因此把
JJ J
1 2
3
分别称为应力张量的
第一、第二和第三不变量,存在不变量也是张
量的特性之一。
15
例题
• 设某点的应力状态如图所示,试求其主应力(应力 单位:牛顿/平方毫米)
16
• 解:
x
yx
zx
2; 3;
4;
ij
xy y
2
2
2
2
xy
yz
zx
x
yz
y
xz
z
xy
2
2
2
18
• 将应力张量不变量带入应力状态特征方程中得:
J 1 J 2 J 3 0
3 3 2
•
9;
1
15 60 54 0
2
9 6 6 0
2 2
3 3;
ζ
ζ η ζ
ζ 主剪切应力平面
21
• 一对相互垂直的主剪应力平面,它们分别与一个主平面 垂直并与另两个主平面成45度,而且每对正交主剪平面 上的主剪应力都相等。如下图所示:
22
三个主剪应力为: τ σ σ 2 23 2 3
τ 31 σ 3 σ1 2
τ12 σ1 σ 2 2
张量的特性:一个对称张量有三个相互垂直的方向, 叫做主方向,在主方向上,下标不同的分量均为零, 只剩下下标相同的分量,叫做主值。
在应力张量中,主值就是主方向上的三个正应力, 叫做主应力;与三个主方向垂直的微分面叫主平面, 主平面上没有剪应力。也就是说τ=0。
第三章 应力-应变及其基本方程

一点的应力状态
z
xx
z
zx zy
xz yz
xy
yx
y y
ij yxx
xy y
xz yz
zx zy z
应力分量的值与坐标系的
选取有关. 3
在空间应力状态下,如适当的选择坐标轴, 使其在该坐标系内的剪应力为零而只剩正应力。 则这样三个相互垂直的坐标轴的方向就是应力 张量的主方向,与主方向垂直的面叫主平面, 该面上存在的正应力叫主应力。三个主应力的 大小与坐标轴的选择无关。
22
应力路径
➢几种加载方式的说明
单调加载和循环加载:
23
应变张量的分解
物体内部 任意一点 的变形状态可以由六 个应变分量来表示:
三个正应变: x , y , z 三个剪应变: xy , yz , zx
24
应变张量的分解
=
+
立方体变形
纯体积变形
m ( x y z ) / 3
纯畸变变形
应力张量分解及其不变量
体积变形
剪切变形
应力张量 ij 球应力张量 m 偏应力张量 Sij
ij Sij m ij
m 0 0
0
m
0
mij
0 0 m
m (1 2 3 ) / 3
Sij ij mij Syxx
xy Sy
xz yz
zx zy Sz
平面上法向应变:
3m
平面上剪应变:
2 2 2 J2
应变空间与应变平面
26
各种剪应变
➢ 八面体上正应变:
8
1 3
(1
x
ij
1 2
yx
1
2 xy
1 2
连续介质力学第三章(分析“应力”文档)共110张PPT

x xy xz
ij
y
yz
=
(对称)
z
x
1 2
xy
y
(对称 )
u
x
1 2
u y
v x
1 2
u z
w x
=
v y
1 2
v z
w y
(对称)
w
z
1
2 1
2
xz yz
z
◆ 几何方程:
x
u x
;
y
v y
性体变,从而出现奇异屈服面。
⑩.平衡(或运动)微分方程
◆ 平衡微分方程:
x
x
yx
y
zx
z
F
x 0
2u t2
xy
x
y
y
zy
z
F
y
0
2v t2
xz
x
yz
y
z
z
F
z 0
2w t2
ij'j Fi 0
◆ 一个客观的弹性力学问题,在物体体内任意一点的 应力分量和体力分量必定满足这组方程。
xxyssii n n xyycco o s sq q00sci on s xy
(xyq0)ctg (xyq0) tg
yxtan
左边界:据圣文南原理和平衡的原理得:
Fx 0 , Fy 0 , M0 0 ,
h
hxdy 0
h
hxydy P0
h
h x ydy M 0
h xdy 0
理论上可证明:当一点的应力状态确定时,经推导 必可求出三个实根,即为主应力,且主应力彼此正交。
河海大学 材料力学 第三章 杆件横截面上的应力、应变分析第三节

切应力互等定理:在两个相互垂直的平面上,垂 直于两平面交线的切应力必成对存在,其数值相等, 方向或同时指向交线,或同时背离交线(定理具有普 遍意义,不管该平面上是否同时存在正应力) 反之,一个面上没有垂直于两平面交线的切应力, 另一面上也没有相应的切应力。 纯剪切应力状态(纯切应力状态)/纯剪切 (shearing state of stresses) ——单元体四个侧面上均只有切应力而无正应力。 圆扭转时横截面上的应力状态均为纯剪切应力状态
a dy
t´ t
b
t
t´ d d z
dx
t
c
例1 圆轴,Mx=2.15kN•m, D=50mm,求(1)距轴心 r=10mm处t , (2) t max, (3) 若采用d/D1=0.5 , t max不 变 , D =? 4 3 pD pD Mx t max 解: Ip= —— Wp= —— 32 16 Mx O (2) t max = —— = 87.6MPa Wp (1) t r= t max×r /R = 87.60×10/25 = 35.04MPa
§3-3 圆轴扭转时横截面上的切应力
轴(shaft)
横截面上的应力的三个问题? (1)应力形式? t (2)应力分布? (3)应力大小? 从几何(变形)、物理、静力学三个方面分析
一、试验现象与平面假设 1、试验现象
(1)纵向线仍为直线,且都 倾斜同一微小角度g 。圆 周表面所有矩形网格,变 形后错动为平行四边形网 格。 (2)圆周线形状不变,仅绕 轴线作相对转动,不同截 面转过不同角度;变形很 小时,圆周线大小、间距 均不改变。
2、圆轴扭转的平面假设:
平面假设:圆轴扭转变形前为平面的横截面,变形后仍 为大小相同的平面,其半径仍保持为直线;且相邻两 横截面之间的距离不变。 (1)各横截面如同刚性圆片,仅绕轴线作相对旋转。 (2)圆轴无轴向正应变和横向正应变,因而扭转圆轴横截 面上无正应力,只可能存在切应力。 (3)倾斜的角度g 就是圆轴表面处的切应变。
第三章 应力分析、应变分析和屈服条件-第二部分

1 2 ′ J2 = σ S = C 在单向拉伸时, 在单向拉伸时, 3
2 在纯剪切时, 在纯剪切时, J2 =τ S = C ′
比较这二者可知,采用 比较这二者可知,采用Mises条件就意味着 条件就意味着
σs = 3τ s
屈服条件
π平面上 平面上Mises圆同 圆同Tresca六边形的几何关系 平面上 圆同 六边形的几何关系
两点假设
1、材料是初始各向同性的,即屈服条件与坐标的取向无关。 材料是初始各向同性的,即屈服条件与坐标的取向无关。 材料是初始各向同性的 可表示为三个主应力的函数: 可表示为三个主应力的函数: 或应力不变量来表示: 或应力不变量来表示: 2、静水应力不影响材料的塑性性质。 静水应力不影响材料的塑性性质。 静水应力不影响材料的塑性性质 这时,屈服条件只与应力偏量有关: 这时,屈服条件只与应力偏量有关: f (s1, s2 , s3 ) = 0,
F(J1, J2 , J3 ) = 0
′ ′ 也可由应力偏张量的不变量表示: 也可由应力偏张量的不变量表示: f (J2 , J3 ) = 0
屈服条件
二、屈服曲线
主应力空间中任一点P代表一个应力状态, 主应力空间中任一点 代表一个应力状态, 代表一个应力状态 直线和π平面分解 平面分解: 向量 OP可参照L直线和 平面分解:
弹性力学-第三章 应力张量 应变张量-1

上述方程为
的齐次线性方程组, 且常数项都为
零。因为:
,故
不能同时为零,
所以方程组的系数行列式应为零,即
将行列式展开,得到求解主应力 的三次方程,称为 应力张量 的特征方程。
式中
设特征方程的三个根为 展开后有
比较上两式,有
,则 (特征方程)
对一个给定的应力状态,其主应力的大小和方向是确定的,
球形张量应力(静水应力)作用下,物体只产生各向 相同的线应变而无剪应变。对应物体的体积改变,而形状 不变。
应力偏量代表各面正应力中偏离静水应力的量,是正应力 之和为零的应力状态。该应力状态下,物体的体积不改变 而形状改变。
静水压力实验研究表明,在均匀受力情况下,即使应力达到 很大值,材料也不产生塑性变形。 故:应力球形张量不产生材料的塑性变形; 应力偏量是产生塑性变形的真正原因。
对应于经过主轴之一,而平分其他两主轴夹角(与主平面成45°)的 平面,
设
,最大剪应力为:
(2)两主应力相等,设 由第二式,得
方程的解为
表示通过oz轴的平面,该组平面上,剪应力为零。
表示任一个与圆锥面相切的微分面。在该组 面上剪应力取最大值。
(3)三个主应力相等
空间任一方向都为主方向,即任一平面都是主平面, 剪应力均为零。
应力偏量也是一种应力状态,同样存在着不变量。
用
表示。
式中:
问:是否存在一特定的斜截面,其上应力矢量T与截 面法线同向。即T为该截面上的正应力 ,
而剪应力为零。
设斜截面法线方向余弦为: 应力矢量T在坐标轴上的投影为:
由斜面应力(Cauchy)公式
故 或 将上式展开
当斜面法线方向满足上述方程时,该斜面上只有正应 力,没有剪应力,称该平面为主平面;主平面上的正 应力称为主应力;主应力方向(即主平面法线方向) 称为主方向。
塑性力学第3章-应力和应变分析

yz
zx
应变张量
x ij yx zx
xy y zy
xz yz z
x 1 2 yx 1 2 zx
1 2
xy y 1 2 zy
1 2 1 2
xz yz z
主 剪 应 力
任意斜截面上的应力,可由以三个圆周为 界限的阴影区中的某一点来表示。
移轴: 平均正应力与应力偏张量
在已知的应力状态上叠加一个静水应力
1 OO ( 1 2 3 ) m 3 OP 1 1 m S1 OP2 2 m S 2 OP3 3 m S3
xy y zy
xz m yz 0 z 0
m
0
ij m ij eij
应变张量的不变量 主应变:
1 , 2 , 3
I1 x y z
2 2 2 I 2 x y y z z x xy yz zx
第 3章
应力和应变分析
指标表示法 张量定义 应力张量
应力张量 的分解
应力(偏)张量 等效应力 等效剪应力 的不变量
三向Mohr圆 应力空间 Lode应力参数
指标表示法
指标表示
求和约定
求导简记Βιβλιοθήκη 克氏符号张量定义坐标变换
张量:如果某些量依赖于坐标轴的选择。在坐标变换时, 按以下指定的形式变化,称这些量的总体为张量。
已知某点的应力状态为:
s x 50 , s y 10 , m 50 ,
xy 0, yz 20 ,
zx 0
求:主应力和应力强度(等效应力)。
应力和应变之间的关系

应力和应变的关系曲线
描述
应力和应变的关系曲线是描述应力与应变之间关系的图形表示。
形状
在弹性范围内,曲线呈直线上升;超过弹性极限后,曲线出现弯曲。
应用
通过应力和应变的关系曲线,可以确定材料的弹性模量、屈服点和 极限强度等机械性能参数。
04
应力和应变的应用
弹性力学
弹性力学是研究弹性物体在外力作用下 变形和内力的规律的科学。在弹性力学 中,应力和应变是描述物体变形和受力 状态的基本物理量。
公式
σ=Eεsigma = E varepsilonσ=Eε
解释
σ为应力,E为弹性模量,ε为应变。 当应力增加时,应变也相应增加, 且两者成正比关系。
非线性关系
描述
当材料受到超过其弹性极限的应力时 ,应力与应变之间的关系不再是线性 的,而是呈现非线性关系。
特征
在非线性阶段,应变随应力的增加而 急剧增加,可能导致材料发生屈服或 断裂。
设计优化
优化结构设计
通过对应力和应变的分析,优化结构设计,提高结构的承载能力 和稳定性。
考虑材料特性
在设计过程中,充分考虑材料的力学特性和性能,合理选择和使 用材料,以降低应力和应变对结构的影响。
引入减震和隔震措施
通过引入减震和隔震措施,降低地震等外部载荷对结构产生的应 力和应变,提高结构的抗震性能。
时间
蠕变
在长期恒定应力作用下,材料会发生 缓慢的塑性变形,即蠕变。蠕变会影 响材料的应力和应变关系,特别是在 高温和长期载荷作用下。
时间依赖性
某些材料的力学性能会随时间发生变 化,对应力和应变的关系产生影响。 例如,疲劳和时效等现象会导致材料 性能随时间发生变化。
07
应力和应变在工程实践中的 注意事项
第3章 平面应力和平面应变

P
σy τ yx
dx dy ds
x
A XN
的关于坐标轴的方向余弦: 斜面外法线 N 的关于坐标轴的方向余弦:
τ xy
B YN
cos(N, x) = l cos(N, y) = m
由微元体平衡: 由微元体平衡: ∑Fx = 0, σ xdy ×1τ yxdx ×1+ X N ds ×1 = 0
dx = ds m dy = ds l
因为任一横截面均可视为对称面, 因为任一横截面均可视为对称面,则有 平面。 所有各点的位移矢量都平行于 x y 平面。 —— 平面位移问题
w≡ 0
εz ≡ 0 γ zy = γ yz ≡ 0 γ zx = γ xz ≡ 0
εx = εx (x, y) —— 平面应变问题 ε y = ε y (x, y) γ xy = γ yx = γ xy (x, y)
如图所示三种情形,是否都属平面问题? 如图所示三种情形,是否都属平面问题?是平 面应力问题还是平面应变问题? 面应力问题还是平面应变问题?
平面应力问题
平面应变问题
非平面问题
3. 平面问题的求解
问题: 已知:外力(体力、面力)、边界条件, )、边界条件 问题: 已知:外力(体力、面力)、边界条件, 求: σ x ,σ y ,τ xy
y
τ xy τ N
B
dx dy ds
A XN
σN
s
N
YN
求解得: 求解得:
m σ σ x = l τ yx
τ yx m = l σ σ y
σ x σ y 2 +τ xy 2
2
X N = lσ x + mτ yx YN = mσ y + lτ xy
弹塑性力学第三章 应力与应变讲解

式中:n和s分别为微分面的法线和切线方向的单位 矢量。全应力和应力分量之间有
n pn n
n pn s
pn2
2 n
(3.3)
研究具体问题时,总是在一个可以选定坐标系里进 行。对给定的直角坐标系,全应力还可以沿坐标系 方向进行分解。
p 的单位法向量,它与三个坐标轴之间的夹角余弦为 l1、l2、l3
则该主平面上的应力矢量 n 可表示为
pn n (3.14)
或
px py
l1 l2
(3.15)
pz
l3
式中: 表示主应力
将应力分量表达式(3.7)代入上式,经移项并整理后得
(
x
)l1
设给定的坐标系Oxyz下,某点M的应力张量为
ij yxx
xy y
xz yz
zx zy z
现让该坐标系原点不动,坐标轴任意旋转一个角度而得 到新坐标系Ox’y’z’,新旧坐标关系如下表:
x
y
z
X’ l11 cos(x ', x) l12 cos(x ', y) l13 cos(x ', z)
要使主方向存在,也即要使方程组(3.17)或(3 .18)有 非零解,则其系数行列式必须为零。
x yx zx
xy y
zy
xz yz 0 z
(3.19a)
方程组(3.19)也可以写成
det ij ij 0
(3.19b)
式(3.19)展开后,得
对面)上有9个应力分量。这9个应力分量的整
应力与应变的关系

应力与应变的关系
应力与应变是相互关联的概念,有着密切的关系。
下文将对应力与应变的关系
作详细的解释。
首先,需要了解应力和应变的概念,应力是一种外力对材料的作用,包括张力,剪力,扭转力和摩擦。
应变本质上是材料力学特性的变化,是以体积为例子的变形,受应力的强大影响而形成的。
其次,应力和应变的关系本质上是一种“折中”的关系,材料对某种外力的反
应强度不定;受应力越大,应变就会越大,物体越有可能变形;受应力越小,应变就会越小,这就说明应力和应变之间呈现出正比的关系。
正是基于这种关系,受应力的大小可以通过测量材料的应变来表示,这是测定应力的一种重要方式。
最后,由于应力与应变之间的密切关系,对其进行计算模拟可以有效预测在应
力作用下材料的表现,科学上精确的计算模型可以模拟出完整的应力、应变关系并用于进行预测。
总之,应力与应变之间的关系是相互关联的,相互影响的关系。
它具有很强的
可预测性、可算法化的特点,可以更好地解释材料行为,并且为预测带来很大的方便。
第三章 杆件横截面上的应力应变分析

第三章杆件横截面上的应力应变分析利用截面法可以确定静定问题中的杆件横截面上的内力分量,但内力分量只是横截面上连续分布内力系的简化结果,仅根据内力并不能判断杆件是否有足够的强度。
如用同一种材料制成粗细不同的两根杆,在相同的拉力作用下,两杆的轴力是相同的,当拉力增大时,细杆必定先被拉断。
这说明拉杆的强度不仅与轴力大小有关,还与横截面面积有关,因此还必须引入内力集度的概,即应力的概念。
本章在此基础上分别讨论了杆件在拉压、扭转和弯曲三种基本变形和组合变形下横截面上应力的分布规律,导出了应力计算公式,为后面对杆件进行强度计算打下了基础。
第一节应力、应变及其相互关系一、正应力、剪应力观察图3-1a所示受力杆件,在截面上围绕K点取微小面积,其上作用有微内力,于是在上内力的平均集度为:(3-1)亦称为面积上的平均应力。
一般来说截面上的内力并不均匀分布,因此平均应力随所取ΔA的不同而变化。
当ΔA趋向于零时,的大小方向都将逐渐趋于某一极限。
(3-2)式中,p称为K点的应力,它反映内力系在K点的强弱程度。
p是一个矢量,一般说既不与截面垂直,也不与截面相切。
通常将其分解为垂直于截面的应力分量和相切于截面的应力分量(图3-1b)。
称为正应力,称为切应力。
在国际单位制中,应力的单位是牛顿/米2(N/M2),称为帕斯卡,简称帕(Pa)。
由于这个单位太小,通常使用兆帕(MPa),1MPa = 106Pa。
二、正应变、切应变杆件在外力作用下,其尺寸或几何形状将发生变化。
若围绕受力弹性体中任意点截取一个微小正六面体(当六面体的边长趋于无限小时称为单元体),六面体的棱边边长分别为Δx 、Δy 、Δz (图3-2 )。
把该六面体投影到xy平面(图3-2b)。
变形后,六面体的边长和棱边夹角都将发生变化(图3-2c)。
变形前长为Δx的线段MN,变形后长度为Δx+Δs。
相对变形(3-3)表示线段MN单位长度的平均伸长或缩短,称为平均应变。
当Δx趋向于零,即点N趋向于M点时,其极限为(3-4)式中,ε称为M点沿x方向的线应变或正应变,ε为无量纲量。
应力与应变

应力与应变概念解释在物理学和材料科学领域中,应力(stress)和应变(strain)是两个重要的概念。
应力描述的是物体内部的力状态,而应变描述的是物体对于应力的响应。
理解应力和应变的关系对于材料强度和工程设计具有重要意义。
应力是指物体内部的力,可以描述为单位面积上施加的力。
它通常用符号σ(sigma)表示,单位为帕斯卡(Pa)。
应力可以分为正应力(tensile stress)和剪应力(shear stress)两种类型。
正应力指作用在物体上的拉伸或压缩力。
拉伸应力是指物体被拉伸的力,压缩应力是指物体被压缩的力。
正应力的大小等于作用力除以物体横截面的面积。
剪应力指作用在物体上的剪切力,是指物体内部各点上的两个互相垂直的力之间的比例。
剪应力的大小等于剪切力除以物体横截面的面积。
应变是指物体对于应力的响应,是单位长度的长度变化。
应变可以描述为物体在单位长度上的变形程度。
应变可以分为线性应变(linear strain)和剪应变(shear strain)两种类型。
线性应变指物体的长度变化与原始长度的比例。
它是一个无量纲的物理量,通常用符号ε(epsilon)表示。
线性应变可以是拉伸应变,也可以是压缩应变。
拉伸应变是指物体在拉伸力作用下产生的应变,压缩应变是指物体在压缩力作用下产生的应变。
剪应变指物体产生的平面变形,在受到平行力作用的情况下,物体的形状会发生变化。
剪应变可以通过一个无量纲数值来表示物体的错位程度。
应力-应变关系应力和应变之间存在一种关系,称为应力-应变关系。
它描述了物体在受到应力作用时的应变程度。
应力-应变关系可以是线性的,也可以是非线性的。
在线性应力-应变关系中,应力和应变之间存在简单的比例关系。
例如,在拉伸应力作用下,当应力增加时,应变也会以同样的比例增加。
这种关系可以由胡克定律(Hooke's law)来描述。
胡克定律是一种线性弹性模型,描述了应力和应变之间的关系。
根据胡克定律,应力与应变之间的比例常数被称为弹性模量(elastic modulus)。
应力与应变的关系
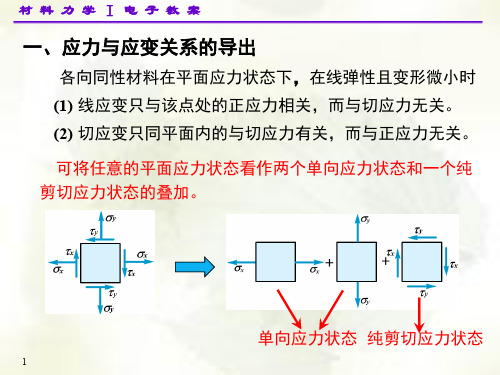
一、应力与应变关系的导出
各向同性材料在平面应力状态下,在线弹性且变形微小时 (1) 线应变只与该点处的正应力相关,而与切应力无关。 (2) 切应变只同平面内的与切应力有关,而与正应力无关。 可将任意的平面应力状态看作两个单向应力状态和一个纯 剪切应力状态的叠加。
单向应力状态 纯剪切应力状态
6
材料力学Ⅰ电子教案
解:1. 构件的自由表面上无任何应力,故知该点处 于平面应力状态。
2. 根据平面应力状态的胡克定律有
ex
=
1 E
s x
ns y ,e y
=
1 E
s
y
ns x
联立求解此二式得
s
x
=
E
1n
2
e x ne y
= 210109 Pa 1 0.32
ex
=
sx
E
n
sy
E
ey
=
sy
E
n
sx
E
xy
=
tx
G
3
材料力学Ⅰ电子教案
平面应力状态中的应力和应变的关系
ex
=
sx
E
n
sy
EeBiblioteka y=syE
n
sx
E
xy
=
tx
G
G
=
E
21 n
上式即为平面应力状态下的广义胡克定律。
4
材料力学Ⅰ电子教案
例题1 平面应力状态下是否有z轴方向的线应变?
sy
ty
tx
sx
平面应力状态下有 z轴方向的线应变
ez
=
应变和应力关系

应变和应力关系嘿,朋友们!咱今儿来聊聊应变和应力这对“好哥们儿”。
你想想啊,这应变就像是个爱调皮捣蛋的小孩子,遇到点情况就变来变去的。
比如说你拉一根橡皮筋,轻轻一拉,它就变长了,这就是它的应变呀。
而应力呢,就像是家长,时刻管着应变这个小家伙,可不能让它随便乱变。
咱生活中到处都能看到应变和应力的影子呢。
就好比你走在路上,不小心踩了个坑,脚就得变形来适应这个坑吧,这就是应变。
而你的身体为了保持平衡,肌肉和骨头就会产生应力来对抗这种变形。
要是没有应力,那你不就直接摔个大跟头啦!再比如说,建房子的时候,那钢材啊、砖块啊都得承受各种力。
要是没有足够的应力来对抗,这房子不就摇摇晃晃的,谁敢住进去呀!这就好像是一场拔河比赛,应变在一边拼命想把东西弄变形,而应力就在另一边紧紧拉住,不让它得逞。
你说这应变和应力是不是很有意思?它们俩就像是一对欢喜冤家,相互制约又相互依存。
没有应变,很多东西都没法变形适应环境;没有应力,那这世界还不得乱了套呀!咱再换个角度想想,人不也一样嘛!我们在生活中会遇到各种各样的困难和挑战,这就像是给我们施加了应力。
我们得像那些坚强的材料一样,产生足够的应力来应对这些应变,不能轻易就被困难给打败了。
有时候我们可能会觉得压力山大,就好像应力太大了,感觉自己都要被压垮了。
但咱可不能就这么轻易放弃呀!得像弹簧一样,压力越大,反弹的力量就越大。
等挺过了这一段,你就会发现自己变得更强大了。
而且呀,我们还得学会灵活应变。
就像水一样,遇到什么形状的容器就能变成什么形状。
不能太死板,要懂得根据不同的情况调整自己。
总之呢,应变和应力这俩家伙可真是无处不在,它们的关系可重要啦!我们得好好了解它们,利用它们,让我们的生活变得更加美好。
别小看了它们,它们可是能决定很多事情的呢!所以呀,我们在生活中要时刻留意应变和应力,让它们为我们服务,而不是让我们被它们牵着鼻子走。
你说是不是这个理儿?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3 14) (3 15) (3 16)
其中应力偏张量的第二不变量 J 2 今后用得最多。 再介绍它的其他几个表达式:
2 2 2 2 2 2 1 J2 ( s s s 2 s 2 s 2 s ) 11 22 33 12 23 31 2
1 s s 2 ij ij ,
(3 - 3)
( 3 - 7)
2 2 l12 + l 2 + l3 = 1,即l i l i = 1.
应有
ij ij 0,
11 12 13 21 22 23 0 31 32 33
(3 8)
或即
(3 8)
将这个行列式展开得到
N
O
SN
采用张量下标记号,可简写成
S Ni = ij l j
说明:
(3 - 3)
x1 i)重复出现的下标叫做求和下标,相当于
j 1
3
,这称为求和约定;
x2
ii)不重复出现的下标i叫做自由下标,可取i=1,2,3;
(4) 应力张量的分解
11 = 22 = 33 = 1.静水“压力”:
13 11 12 13 m 0 0 11 m 12 0 0 m 22 m 23 21 22 23 21 32 33 m 31 32 33 0 0 m 31
若八面体面上的应力向量用F8表示,则按(3-3)式有 1 2 2 2 2 2 2 2 F8 ( 1l1 ) ( 2l2 ) ( 3l3 ) ( 1 2 3 ) (3 21) 3
八面体面素上的正应力为
2 2 2 8 1l12 2l2 3 l3 1 ( 1 2 3 ) m (3 22) 3
(3 10) (3 11) (3 12)
应力偏张量Sij显然也是一种应力状态即J1=0的应力状态。 不难证明,它的主轴方向与应力主轴方向一致,而主值 (称为主偏应力)为:
s j j m , ( j 1,2,3)
应力偏张量也有三个不变量:
(3 13)
s1 s2 s3 1 2 3 3 M 0 J1 1 2 2 2 J 2 ( s1s2 s2 s3 s3 s1 ) ( s1 s2 s3 ) 2 s1s2 s3 J3
3 J12 J 2 J 3 0,
其中 J , 1 kk
(3 9)
(3 10) (3 11) (3 12)
1 J 2 ii kk ik ki , 2 J 3 ij .
2. 应力张量的不变量
当坐标轴方向改变时,应力张量的分量 ij均将改变,但主应力的 大小不应随坐标轴的选取而改变.因此,方程(3-9)的系数 J 1、J 2、J 3 的值与坐标轴的取向无关,称为应力张量的三个不变量。
在静水压力作用下,应力—应变间服从弹性规律,且不会屈 服、不会产生塑性变形。
不产生塑性变形的部分 应力 产生塑性变形的部分
反映静水“压力”:
2.平均正应力:
1 1 m = ( 11 + 22 + 33 ) = kk 3 3 (3 - 4)
3.应力张量的分解:
应力张量可作如下分解:
而没有剪应力的状态。
应力偏张量
m m ij 0 0
0
m
0
0 0 m
S ij ——应力偏张量 12 13 11 m S ij 21 22 m 23 32 33 m 31
用张量符号表示: 其中:
ij m ij sij ,
(3 5)
1 0 0 ij 0 1 0 0 0 1
1,当i j, ij 0,当i j,
(3 6)
或
应力球张量
——与单元体的体积变形有关
ij ——单位球张量 m ij ——应力球张量,它表示各方向承受相同拉(压)应力
2.Lode应力参数
[分析]
由图3-4可见,若在已知应力状态上 叠加一个静水压力,其效果仅使三 个 Mohr圆一起沿 轴平移一个距离 ,该距离等于所叠加的静水应力, 并不改变Mohr圆的大小。 [结论]
三点中的任意两点为直径端点, 可作出三个Mohr圆,如图3-3. 其半径为:
P 2 1P 2 1 3, 2 2 P2 P3 2 3 1, 2 2 P3 P 3 1 1 2. 2 2
O P3
M P2
P 1
3
2
1
图 3-3
1、 2、 3 ——称为主剪应力 max ——最大剪应力
标志着所考察的偏应力状态与材料未受力(或只受静水应 力)状态的距离或差别的大小。
联系到(3-17)式, J 2
1 s s 2 ij ij
不难看出 代表 S ij 空间的中的广义距离
4. 等效剪应力
1 0, 2 0, 3 0,
J2
2 J 联系到(3-19)式,可知 2 或
八面体面素上的剪应力为
2 2 2 8 F8 82 1 ( ) ( ) ( ) 1 2 2 3 3 1 . 3 2
8
说明:
2 3
. J2
(3 23)
八面体面上的应力向量可分解为两个分量:
i)垂直于八面体面的分量,即正应力 8 m ,它与应力球张 量有关,或者说与 J1 有关; ii)沿八面体面某一切向的分量,即剪应力 8 2 J 2 ,与应力 偏张量的第二不变量 J 2 有关。
(3 2)
(3) 斜截面上的应力与应力张量的关系
在xj坐标系中,考虑一个法线为N的斜平面。 N是单位向量,其方向作弦为 l1 , l 2 , l 3 ,
则这个面上的应力向量SN的三个分量与应力张量 ij 之间的关系 x3
s N 1 11 12 13 l1 S N 2 21 22 23 l 2 S l 3 32 33 N 3 31
8
(3 26)
说明:
这些量的引入,使我们有可能把复杂应力状态化作“等效”( 在
J
' 意义下等效)的单向应力状态,从而有可能对不同应力 2
状态的“强度”作出定量的描述和比较。
五、三向Mohr圆和Lode应力参数 1.三向Mohr圆
在 平面上 P 1 ( 1 ,0), P 2 ( 2 ,0), P 3 ( 3 ,0)
(Байду номын сангаас 17)
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ], (3 18) J2 6 1 2 2 [ 12 2 J2 3 1 2 2 3 3 1 ] (3 19) 3
说明: 在第四章中将看到, 在屈服条件中起重要作用。至于 J 3 可以注 J2 意它有这样的特点:不管 sij 的分量多么大,只要有一个主偏应力 在屈服条件中不可能起决定作用。 为零,就有 J 3 0 。这暗示 J 3
写法: 采用张量下标记号的应力写法 把坐标轴x、y、z分别 用x1、x2、x3表示, 或简记为xj (j=1,2,3),
(3 1)
上式中左边是工程力学的习惯写法,右边是弹性力学的习惯写法
11 12 13 , 22 23 ij ji 21 31 32 33
2.等效应力 的特点
与空间坐标轴的选取无关;
J2
意义下衡量的
各正应力增加或减少同一数值(也就是叠加一个静水应力
状态)时 数值不变,即与应力球张量无关;
j ( j 1,2,3)全反号时 的数值不变。
3. S ij 空间
S ij 空间指的是以 S ij 的九个分量为坐标轴的九维偏应力空间;
3
四、等效应力 1.定义: 相等的两个应力状态的力学效应相同,那么 如果假定 J 2
对一般应力状态可以定义:
3J 2
1 2
1 2 2 2 3 2 3 1 2
(3 24)
—— 在塑性力学中称为应力强度或等效应力
注意:这里的“强度”或“等效”都是在
;
(2)应力主向
所在的平面 —— 称为主平面; 主应力 所在平面的法线方向 —— 称为应力主向;
主应力
根据主平面的定义,SN与N重合。若SN的大小为 ,则它在各 坐标轴上的投影为 S Ni = li 代入(3-3)式
S Ni = ij l j
( ij - ij )l j = 0.
三、等斜面上的应力
等斜面:通过某点做平面 ,该平面的法线与三个应力主轴
夹角相等 设在这一点取 x1 , x2 , x3 坐标轴与三个应力主轴一致, 3 则等斜面法线的三个方向余弦为
l1 l2 l3 1 / 3
八面体面:
(3 20)
2
1
满足(3-20)式的面共有八个,构成 一个八面体,如图所示。 等斜面常也被叫做八面体面。
说明: 材料进入塑性后,单元体的体积变形是弹性的,只与 应力球张量有关;而与形状改变有关的塑性变形则是 由应力偏张量引起的 。应力张量的这种分解在塑性力
学中有重要意义。
二、主应力和应力不变量
1. 一点的主应力与应力主向 (1)主应力
力 若某一斜面上
N 称为该点一个主应力
N 0 ,则该斜面上的正应
