人教新课标版数学高一- 必修2作业直线与平面平行的判定

合集下载

高一数学新人教A版必修2第二章直线和平面平行的判定

高一数学新人教A版必修2第二章直线和平面平行的判定复习引入直线与平面有几种位置关系？直线与平面有几种位置关系？有三种位置关系：在平面内，相交、有三种位置关系：在平面内，相交、平行．其中平行是一种非常重要的关系，其中平行是一种非常重要的关系，不仅应用较而且是学习平面和平面平行的基础．多，而且是学习平面和平面平行的基础．引入新课怎样判定直线与平面平行呢？怎样判定直线与平面平行呢？与平面平行呢根据定义，判定直线与平面是否平行，只需判根据定义，判定直线与平面是否平行，定直线与平面有没有公共点．但是，直线无限延长，定直线与平面有没有公共点．但是，直线无限延长，平面无限延展，如何保证直线与平面没有公共点呢？平面无限延展，如何保证直线与平面没有公共点呢？aα实例感受在生活中，注意到门扇的两边是平行的．当门扇在生活中，注意到门扇的两边是平行的．绕着一边转动时，绕着一边转动时，另一边始终与门框所在的平面没有公共点，公共点，此时门扇转动的一边与门框所在的平面给人以平行的印象．以平行的印象．实例感受门扇转动的一边与门框所在的平面之间的位置关系．实例感受将一本书平放在桌面上，翻动书的硬皮封面，将一本书平放在桌面上，翻动书的硬皮封面，封面边缘AB所在直线与桌面所在平面具有什么样封面边缘所在直线与桌面所在平面具有什么样的位置关系？的位置关系？实例感受将一本书平放在桌面上，翻动书的硬皮封面，将一本书平放在桌面上，翻动书的硬皮封面，封面边缘AB所在直线与桌面所在平面具有什么样封面边缘所在直线与桌面所在平面具有什么样的位置关系？的位置关系？实例感受将一本书平放在桌面上，翻动书的硬皮封面，将一本书平放在桌面上，翻动书的硬皮封面，封面边缘AB所在直线与桌面所在平面具有什么样封面边缘所在直线与桌面所在平面具有什么样的位置关系？的位置关系？AABB直线与平面平行与平面α平行吗平行吗？下图中的直线a与平面平行吗？aα直线与平面平行平行，如果平面α内有直线b与直线a平行，那么直线a的位置关系如何？与平面α的位置关系如何？平行？是否可以保证直线a与平面α平行？abα直线与平面平行平面α外有直线a平行于平面α内的直线b．（1）这两条直线共面吗？）这两条直线共面吗？共面（2）直线a与平面α相交吗？不可能相交相交吗？）aαb直线与平。

高一数学必修2直线平面平行的判定及其性质知识点讲解

性质
判定
a′∩b′＝
a，b⊂βa P′a∩b＝P
无公
条件
∩b＝P a∥ a∥a′b∥b′
共点
αb∥α
a′，b′⊂βa，
b⊂α
结论 α∥β α∥β
α∥β
性质
α∥ββ ∩γ＝ α∥β bα∩γ＝ a⊂β
a
a∥b a∥α
[究疑点] 1．若一直线平行于平面α，那么平面α内的任一条直线
与它有何位置关系？提示：平行或异面． 2．若两平面平行，那么在一个平面内的任一条直线与另一个平面内的任一条直线有何位置关系？提示：平行或异面．
直线、平面平行的判定及其性质以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的判定定理与有关性质．
[理要点] 一、直线与平面平行的判定与性质
判定
图形
性质
条件 a与α无交点结论 a∥α
b∥α
a∥α
a∥αa⊂βα ∩β＝b
a∩α＝ ∅
a∥b
二、面面平行的判定与性质判定
图形
()
A．若a∥α，b∥a，则b∥α
B．a∥α，b∥α，a⊂β，b⊂β，则β∥α
C．若α∥β，b∥α，则b∥β
D．若α∥β，a⊂α，则a∥β
解析：A、C中b都可能在面内故错，B中α与β相交
也可行．
答案：D
AB∥CD，AD⊥DC，CD＝2，DD1＝AB＝1，P、Q分别是CC1、C1D1的中点．求证：AC∥平面BPQ.
条件变为E、F、G满足“DF∶D1F＝1∶2，DG∶DA＝1∶3， BE∶BB1＝2∶3”，求证平面AD1E∥平面BGF.
证明：∵D1F∶DD1＝2∶3 BE∶BB1＝2∶3 DD1＝BB1，∴D1F＝BE 又D1F∥BE，∴四边形D1FBE为平行四边形， ∴D1E∥BF 又DG∶GA＝1∶2 DF∶FD1＝1∶2 ∴GF∥AD1 又AD1∩D1E＝D1，GF∩BF＝F ∴平面AD1E∥平面GFB

人教课标版高中数学必修2知识归纳：直线、平面平行的判定及其性质

2.2 直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
1.判定定理的符号表示为：.
2.证明线面平行的根本问题是要在平面内找一直线与已知直线平行，此时常用中位线定理、成比例线段、射影法、平行移动、补形等方法，具体用何种方法要视条件而定.
2.2.2 平面与平面平行的判定
1.面面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．用符号表示为：
.
2.垂直于同一条直线的两个平面平行.
3.平面α上有不在同一直线上的三点到平面β的距离相等，则α与β的位置关系是平行或相交.
2.2.3 直线与平面平行的性质
1.线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.
即：.
2.直线和平面平行的判定定理及性质定理在解题时往往交替使用．证线面平行往往转化为证线线平行，而证线线平行又将转化为证线面平行．循环往复直至证得结论为止.
2.2.4 平面与平面平行的性质
1.面面平行的性质：如果两个平行平面同时与第三个平面相交，那么它们的交线平行.用符号语言表示为：.
2. 其它性质：
①；
②；
③夹在平行平面间的平行线段相等.。

高一数学人教版必修2课件：2.2.1直线与平面平行的判定

A 求解线线平行的常用方法2：
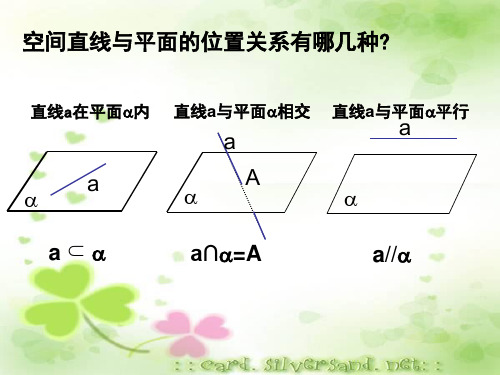
利用等比分点对应边成比 E
F
例
B
D C
例2.在长方体 ABCDA1B1C1D 1中，E是线段 A 1 A 的中点，证明:直线 B E //平面DCC1D1
求解线线平行的常用方法3：作辅助线构造平行四边形
小结：
1.直线与平面平行的判定： (1)运用判定定理：线线平行线面平行 (2)运用定义；
2.应用判定定理判定线面平行时应注意六个字:
〔1〕面外，〔2〕面内，〔3〕平行。
3.应用判定定理判定线面平行的关键是找平行线
方法一：利用等比分点对应边成比例〔三角形的中位线定理〕；方法二：平行四边形的平行关系。
小结： 4.转化思想:把空间问题转化为平面问题解决
如图，正方体 AB CA1B D 1C1D 中1 ，P 是棱A1B1 的中点，过点 P 画一条直线使之与截面A1BCD1 平行.
D1
C1
A1
P• B1
D A
C B
猜测探究
a
如图，平面外的直线a
平行于平面内的直线b
b
（1）这两条直线共面吗？
（2
a 抽象概括：直线与平面平行的判定定理： b
假设平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行.
①判定定理的实质：线线平行线面平行〔转化〕
②两条直线的特点：面内，面外，平行
所E 以F //平B 面C.D
中位线定理
学以致用
变式 1 、把 “ 例 1 中的 E 、 F 分别为边 A B 、 A D 上的中点 ” 改为三等分点，即 A E A F 2 , 如图所示，试证明直线 E F //平面 B C D .

人教新课标版数学高一-人教A版必修2 课时提升 -2 直线与平面平行的判定1

关闭Word文档返回原板块。

课时提升作业(十)直线与平面平行的判定平面与平面平行的判定(25分钟60分)一、选择题(每小题5分,共25分)1.(2015·福州高一检测)平面α与△ABC的两边AB,AC分别交于点D,E,且AD︰DB=AE︰EC,如图,则BC与α的位置关系是( )A.平行B.相交C.平行或相交D.异面【解析】选A.因为AD︰DB=AE︰EC,所以DE∥BC,又DE⊂α,BC⊄α,所以BC∥α.2.有以下三种说法,其中正确的是( )①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③直线a,b满足a∥α,a∥b,且b⊂α,则a平行于经过b的任何平面.A.①②B.①③C.②③D.①【解析】选D.①正确,若在α内存在一条直线b,使a∥b,则a∥α与“a 与平面α相交”矛盾,故①正确,②错误,反例如图(1)所示,③错误,反例如图(2)所示,a,b可能在同一平面内.3.若正n边形的两条对角线分别与平面α平行,则这个正n边形所在的平面一定平行于平面α,那么n的取值可能是( )A.12B.8C.6D.5【解题指南】考虑平面与平面平行的判定定理,只需判断正n边形的两条对角线是否一定相交.【解析】选D.正五边形的两条对角线必相交,而其余正多边形的两条对角线不一定相交.4.点E,F,G,H分别是空间四面体ABCD的棱AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是( )A.0条B.1条C.2条D.3条【解析】选C.因为E,F分别为AB,BC的中点,所以EF∥AC,又AC⊄平面EFGH,EF⊂平面EFGH,所以AC∥平面EFGH,同理BD∥平面EFGH.5.正方体EFGH-E1F1G1H1中,下列四对截面中,彼此平行的一对截面是( )A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G【解析】选A.在平面E1FG1与平面EGH1中,因E1G1∥EG,FG1∥EH1,且E1G1∩FG1=G1,EG∩EH1=E,故平面E1FG1∥平面EGH1.二、填空题(每小题5分,共15分)6.过三棱柱ABC-A1B1C1任意两条棱的中点作直线,其中与平面ABB1A1平行的直线有________条.【解析】如图,EF,FG,GH,HE,EG,HF都与平面ABB1A1平行,共6条.答案:67.(2015·广州高一检测)P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下列四种说法:①OM∥平面PCD;②OM∥平面PBC;③OM∥平面PDA;④OM∥平面PBA.其中正确的为________(填序号).【解析】因为OM∥PD,故OM∥平面PCD,OM∥平面PDA,所以①③正确.答案:①③8.(2015·杭州高二检测)如图所示,在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是________.【解析】连接AM并延长,交CD于点E,则E为CD的中点,连接BE,则BE过点N.因为M,N分别为△ACD和△BCD的重心,所以==,所以MN∥AB,所以可得MN∥平面ABC,MN∥平面ABD.答案:平面ABC,平面ABD【拓展延伸】三角形的“四心”及主要性质(1)三角形的三条中线的交点叫三角形的重心.重心到顶点的距离等于到对边中点距离的2倍.(2)三角形三边垂直平分线的交点叫三角形的外心.外心到三角形三个顶点的距离相等.(3)三角形三条高线的交点叫三角形的垂心.(4)三角形三个角的角平分线的交点叫三角形的内心.内心到三角形三边的距离相等.三角形的“四心”在数学中应用非常广泛,要熟练掌握.三、解答题(每小题10分,共20分)9.(2014·山东高考改编)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD 是梯形,AB=2CD=2,M是线段AB的中点.求证:C1M∥平面A1ADD1.【证明】连接AD1,因为ABCD-A1B1C1D1为四棱柱,所以CD∥C1D1,CD=C1D1,又因为M为AB的中点,所以AM=1,所以CD∥AM,CD=AM,所以AM∥C1D1,AM=C1D1,所以四边形AMC1D1为平行四边形,所以AD1∥MC1,又因为C1M⊄平面A1ADD1,AD1⊂平面A1ADD1,所以C1M∥平面A1ADD1.【补偿训练】(2014·天津高考改编)如图,四棱锥P-ABCD的底面ABCD 是平行四边形,E,F分别是棱AD,PC的中点.证明:EF∥平面PAB.【证明】如图,取PB的中点M,连接MF,AM.因为F为PC中点,故MF∥BC且MF=BC.由已知有BC∥AD,BC=AD.又由于E为AD中点,因而MF∥AE且MF=AE,故四边形AMFE为平行四边形,所以EF∥AM.又AM⊂平面PAB,而EF⊄平面PAB,所以EF∥平面PAB.10.(2015·厦门高一检测)在正方体ABCD-A1B1C1D1中,M,N,P分别是AD1,BD和B1C的中点.求证:(1)MN∥平面CC1D1D.(2)平面MNP∥平面CC1D1D.【证明】(1)连接AC,CD 1,因为ABCD为正方形,N为BD的中点,所以N为AC的中点,又因为M为AD1的中点,所以MN∥CD1,因为MN⊄平面CC1D1D,CD1⊂平面CC1D1D,所以MN∥平面CC1D1D.(2)连接BC1,C1D,因为B1BCC1为正方形,P为B1C的中点,所以P为BC1的中点,又因为N为BD的中点,所以PN∥C1D,因为PN⊄平面CC1D1D,C1D⊂平面CC1D1D,所以PN∥平面CC1D1D.由(1)知MN∥平面CC1D1D且MN∩PN=N,所以平面MNP∥平面CC1D1D.(20分钟40分)一、选择题(每小题5分,共10分)1.已知m,n是两条直线,α,β是两个平面,有以下说法:①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;②若m∥α,m∥β,则α∥β;③若m∥α,n∥β,m∥n,则α∥β.其中正确说法的个数是( )A.0B.1C.2D.3【解析】选B.设m∩n=P,则直线m,n确定一个平面,设为γ,由面面平行的判定定理知,α∥γ,β∥γ,因此,α∥β,即①正确;如图,在长方体ABCD-A1B1C1D1中,直线EF平行于平面ADD 1A1和平面A1B1C1D1,即满足②的条件,但平面A1B1C1D1与平面ADD1A1不平行,因此②不正确;图中,EF∥平面ADD1A1,BC∥平面A1B1C1D1,EF∥BC,但平面ADD1A1与平面A1B1C1D1不平行,所以③也不正确.2.(2015·青岛高一检测)在正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,P在对角线BD1上,且BP=BD1,给出下面四个命题:(1)MN∥平面APC;(2)C1Q∥平面APC;(3)A,P,M三点共线;(4)平面MNQ ∥平面APC.正确的序号为( )A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4) 【解析】选C.(1)MN∥AC,连接AM,CN,易得AM, CN交于点P,即MN⊂平面PAC,所以MN∥平面APC是错误的;(2)平面APC延展,可知M,N在平面APC上,AN∥C1Q,所以C1Q∥平面APC,是正确的;(3)由BP=BD1,以及相似,可得A,P,M三点共线,是正确的;(4)直线AP延长到M,则M在平面MNQ内,又在平面APC内,所以平面MNQ∥平面APC,是错误的.二、填空题(每小题5分,共10分)3.(2015·太原高二检测)下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是________.(将你认为正确的都填上)【解析】在④中NP平行所在正方体的那个侧面的对角线,从而平行AB,所以AB∥平面MNP;在①中设过点B且垂直于上底面的棱与上底面交点为C,则由NP∥CB,MN∥AC,可知平面MNP∥平行平面ABC,即AB∥平面MNP.答案:①④4.(2015·菏泽高一检测)如图,在正方体ABCD-A 1B1C1D1中,E,F分别是AB和AA1的中点,则下列命题:①E,C,D1,F四点共面;②CE,D1F,DA三线共点;③EF和BD1所成的角为90°;④A1B∥平面CD1E.其中正确的是________(填序号).【解析】由题意EF∥CD 1,故E,C,D1,F四点共面;由EF CD1,故D1F与CE相交,记交点为P,则P∈平面ADD1A1,P∈平面ABCD,所以点P在平面ADD1A1与平面ABCD的交线AD上,故CE,D1F,DA三线共点;∠A1BD1即为EF与BD1所成角,显然∠A1BD1≠90°;因为A1B∥EF,EF⊂平面CD1E,A1B⊄平面CD1E,所以A1B∥平面CD1E.答案:①②④三、解答题(每小题10分,共20分)5.(2014·四川高考)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.【解析】存在点M是AB的中点.取线段AB的中点M,连接A1M,MC,A1C,AC1.设O为A 1C,AC1的交点.由已知,O为AC1的中点,连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,所以MD AC,OE AC,因此MD OE,连接OM,从而四边形MDEO为平行四边形,则DE∥MO.因为直线DE⊄平面A1MC,MO⊂平面A1MC,所以直线DE∥平面A1MC.即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC. 【延伸探究】本题若加上条件“F是A1C1的中点”其他条件不变,问在AB上是否存在一点M,使平面DEF∥平面A1MC,并证明.打印版【解析】存在点M是AB的中点,证明如下:由本题证明知DE∥平面A1MC,又F为A1C1的中点,E为CC1的中点,所以EF∥A1C,又EF⊄平面A1MC,A1C⊂平面A1MC,所以EF∥平面A1MC,又EF∩DE=E,所以平面DEF∥平面A1MC.故AB上存在一点M(AB中点),使平面DEF∥平面A1MC.6.(2015·福州高一检测)已知直三棱柱ABC-A1B1C1,点N在AC上且CN=3AN,点M,P,Q分别是AA1,A1B1,BC的中点.求证:直线PQ∥平面BMN.【证明】如图,取AB中点G,连接PG,QG分别交BM,BN于点E,F,则E,F分别为BM,BN的中点.而GE∥AM,GE=AM,GF∥AN,GF=AN,且CN=3AN,所以=,==,所以==,所以EF∥PQ,又EF⊂平面BMN,PQ⊄平面BMN,所以PQ∥平面BMN.关闭Word文档返回原板块高中数学。

高一数学必修二2.2.1直线与平面平行的判定2.2.2平面与平面平行的判定练习题(解析版)

2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定一、选择题1.下列说法中正确的是 ( )A.如果一个平面内有一条直线和另一个平面平行,那么这两个平面平行B.如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行C.如果一个平面内任意一条直线和另一个平面平行,那么这两个平面平行D.若果两个平面平行于同一条直线,那么这两个平面平行2.下列命题中,正确的个数为 ( )①若a ∥b ,α⊂b ,则a ∥α②若a ∥α,b ∥α,则a ∥b③若a ∥b ,b ∥α,则a ∥α④若a ∥α,α⊂b ,则a ∥bA.0B.1C.2D.33.已知三条互相平行的直线c b a ,,中，,,βα⊂⊂c b a 、则两个平面βα,的位置关系是（）A.平行B.相交C.平行或相交D.重合4.与两个相交平面的交线平行的直线和这两个平面的位置关系是（）A.都平行B.都相交C.在这两个平面内D.至少和其中一个平面平行5.下列说法正确的是（）①若一个平面内的任何直线都与另一个平面无公共点，则这两个平面平行②过平面外一点有且仅有一个平面和已知平面平行③过平面外两点不能作平面与已知平面平行④若一条直线和一个平面平行，经过这条直线的任何平面都与已知平面平行A. ①③B. ②④C. ①②D. ②③④二、填空题6.若直线b a =A ，a ∥α，则b 与α的位置关系是＿＿＿＿＿＿＿7.若直线a b a 满足，与平面βα,∥b ,a ∥α,b ∥β,则平面α与平面β的位置关系是＿＿＿＿＿＿＿＿8.过平面外一点有＿＿＿条直线与已知平面平行,过平面外一点有且只有＿＿＿个平面与已知平面平行.9.正方体1111D C B A ABCD -中,的平面与过的中点，则为E C A BD DD E ,,11的位置关系是＿＿＿＿＿＿三、解答题10.正方体1111D C B A ABCD -中个，F E N M ,,,分别为棱11111111,,,D C C B D A B A 的中点。

高中数学必修2立体几何常考题型：直线与平面、平面与平面平行的判定全面版

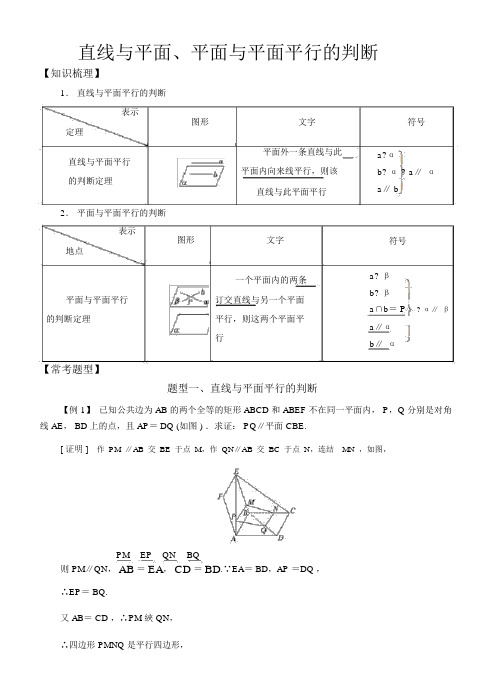
直线与平面、平面与平面平行的判断【知识梳理】1．直线与平面平行的判断表示图形文字定理直线与平面平行平面外一条直线与此平面内向来线平行，则该的判断定理直线与此平面平行2．平面与平面平行的判断表示图形文字地点一个平面内的两条平面与平面平行订交直线与另一个平面的判断定理平行，则这两个平面平行符号a?αb? α ? a∥ αa∥ b符号a? βb? βa∩b＝ P? α∥ βa∥αb∥ α【常考题型】题型一、直线与平面平行的判断【例 1】已知公共边为 AB 的两个全等的矩形 ABCD 和 ABEF 不在同一平面内， P，Q 分别是对角线 AE， BD 上的点，且 AP＝ DQ (如图 ) ．求证： PQ∥平面 CBE.[ 证明 ]作PM∥AB交BE于点M，作QN∥AB交BC于点N，连结MN，如图，PM EP QN BQ则 PM∥QN，AB＝EA，CD＝BD.∵EA＝ BD，AP ＝DQ ，∴EP＝ BQ.又 AB＝ CD ，∴PM 綊 QN，∴四边形 PMNQ 是平行四边形，∴PQ∥MN .又 PQ?平面 CBE， MN? 平面 CBE，∴PQ∥平面CBE.【类题通法】利用直线和平面平行的判断定理证明线面平行的重点是在平面内找一条直线与已知直线平行，常利用平行四边形、三角形中位线、平行公义等．【对点训练】1.如图，在四棱锥 P－ABCD 中，底面 ABCD 是矩形， E，F 分别是 PB ，PC 的中点．证明： EF∥平面 PAD.证明：在△PBC 中， E， F 分别是 PB， PC 的中点，∴EF∥BC.又 BC ∥AD ，∴EF ∥AD .∵AD ? 平面 PAD， EF?平面 PAD，∴EF∥平面PAD .题型二、面面平行的判断【例 2】如图，在正方体ABCD — A1B1C1D1中， M、 E、F、N 分别是 A1B1、 B1C1、 C1D1、 D 1A1的中点．求证： (1) E、 F 、B、 D 四点共面；(2) 平面 MAN ∥平面 EFDB .[证明 ] (1)连结 B1D1，∵E、 F 分别是边B1 C1、 C1D1的中点，∴EF∥B1D 1.而 BD∥B1D 1，∴BD∥EF.∴E、 F 、 B、 D 四点共面．(2) 易知 MN ∥B1D1， B1D 1∥BD，∴MN ∥BD .又 MN?平面 EFDB ， BD? 平面 EFDB .∴MN ∥平面EFDB .连结 MF .∵M、 F 分别是 A1B1、 C1D1的中点，∴MF ∥A1D 1，MF ＝ A1D1.∴MF ∥AD ， MF ＝AD .∴四边形 ADFM 是平行四边形，∴ AM ∥DF .又 AM?平面 BDFE ， DF ? 平面 BDFE ，∴AM ∥平面BDFE .又∵AM∩MN ＝M，∴平面 MAN ∥平面EFDB .【类题通法】两个平面平行的判断定理是确立面面平行的重要方法．解答问题时必定要追求好判断定理所需要的条件，特别是订交的条件，即与已知平面平行的两条直线一定订交，才能确立面面平行．【对点训练】2.如图，已知四棱锥 P－ ABCD 中，底面 ABCD 为平行四边形，点 M， N， Q 分别在 PA， BD ，PD 上，且 PM ∶MA＝ BN∶ ND ＝PQ∶ QD.求证：平面 MNQ ∥平面PBC.证明：∵PM ∶MA＝ BN∶ND ＝PQ∶QD ，∴MQ ∥AD ， NQ∥BP.∵BP? 平面 PBC， NQ?平面 PBC，∴NQ∥平面PBC.又底面 ABCD 为平行四边形，∴BC∥AD ，∴MQ ∥BC.∵BC? 平面 PBC， MQ?平面 PBC ，∴MQ ∥平面PBC.又 MQ ∩ NQ＝Q，依据平面与平面平行的判断定理，得平面MNQ ∥平面PBC.题型三、线线平行与面面平行的综合问题【例 3 】如图，在四棱锥O－ ABCD 中，底面ABCD 是边长为 1 的菱形， M 为 OA 的中点， N 为 BC 的中点．证明：直线MN ∥平面 OCD .[证明 ]如图，取OB中点E，连结ME，NE，则ME∥AB .又∵AB∥CD ，∴ME ∥CD .又∵ME?平面 OCD ， CD? 平面 OCD ，∴ME ∥平面OCD .又∵NE∥OC，且 NE?平面 OCD ， OC? 平面 OCD ，∴NE∥平面OCD .又∵ME∩ NE＝ E，且 ME ，NE? 平面 MNE，∴平面 MNE ∥平面OCD .∵MN ? 平面 MNE ，∴MN∥平面OCD .【类题通法】解决线线平行与面面平行的综合问题的策略(1)立体几何中常有的平行关系是线线平行、线面平行和面面平行，这三种平行关系不是孤立的，而是互相联系、互相转变的．判断判断(2) 线线平行――→ 线面平行――→ 面面平行所以平行关系的综合问题的解决一定灵巧运用三种平行关系的判断定理．【对点训练】3.如图，在正方体 ABCD － A1B1C1D 1中， S 是 B1D1的中点， E， F ，G 分别是 BC， DC ，SC 的中点．求证： (1) 直线 EG∥平面 BDD 1B1；(2) 平面 EFG ∥平面 BDD 1B1.证明： (1) 如图，连结 SB，∵E， G 分别是 BC， SC 的中点，∴EG∥SB.又∵SB? 平面 BDD 1B1， EG?平面 BDD 1B1.∴直线 EG∥平面BDD 1B1.(2) 连结 SD，∵F， G 分别是 DC， SC 的中点，∴FG ∥SD.又∵SD? 平面 BDD 1B1，FG ?平面 BDD 1B1，∴FG ∥平面BDD 1B1.又 EG∥平面BDD 1B1，且 EG? 平面 EFG ，FG ? 平面 EFG ，EG∩ FG ＝ G，∴平面 EFG ∥平面BDD 1 B1 .【练习反应】1．若一个平面内的两条直线分别平行于另一个平面内的两条直线，则这两个平面的地点关系是 ()A ．必定平行B ．必定订交C．平行或订交D．以上判断都不对分析：选 C可借助于长方体判断两平面对应平行或订交．2．能保证直线 a 与平面α平行的条件是 ()A ． b? α， a∥ bB ．b? α， c∥ α， a∥b， a∥ cC．b? α， A、B∈ a，C、 D∈ b，且 AC∥ BDD． a?α， b? α， a∥b分析：选 D由线面平行的判断定理可知， D 正确．3．正方体ABCD － A1B1C1D1中， E 为 DD 1的中点，则 BD1与过 A，C，E 三点的平面的位置关系是 ________．分析：如右图所示，连结BD 交 AC 于点 O.在正方体中简单获得点O为 BD 的中点．又由于 E 为 DD 1的中点，所以OE∥BD 1.又∵OE? 平面 ACE，BD 1?平面 ACE，∴BD 1∥平面ACE.答案：平行4．以下命题真命题序号为________①若一个平面内有两条直线都与另一个平面平行，则这两个平面平行；②若一个平面内有无数条直线都与另一个平面平行，则这两个平面平行；③若一个平面内任何一条直线都平行于另一个平面，则这两个平面平行；④若一个平面内的两条订交直线分别平行于另一个平面，则这两个平面平行．分析：①错，应为一平面内两订交直线与另一平面平行；②当两平面订交时，一面内也有无数条直线均与另一平面平行，②也不对；③中随意直线都与另一平面平行，也有两订交直线与另一平面平行，故③为真；④为两平面平行的判断定理，故④也为真．答案：③④5.如图，正方形ABCD 和四边形ACEF 所在平面订交．EF ∥ AC，AB ＝2，EF ＝ 1.求证： AF ∥平面 BDE.证明：设 AC， BD 交于点 G，由于 EF∥AC，且 EF＝ 1，易得 AG＝12AC＝1，所以四边形AGEF 为平行四边形，所以AF∥EG.由于 AF?平面 BDE ，EG? 平面 BDE，所以 AF ∥平面BDE .你曾落的泪，最都会成阳光，照亮脚下的路。

人教新课标版数学高一-必修2训练直线与平面平行、平面与平面平行判定

数学·必修2(人教A 版)2.2 直线、平面平行的判定及其性质2．2.1 直线与平面平行、平面与平面平行的判定基础达标1．a 、b 、c 为三条不重合的直线，α，β，γ为三个不重合的平面，现给出下列命题：⎭⎪⎬⎪⎫①a ∥γ b ∥γ⇒a ∥b ；② ⎭⎪⎬⎪⎫α∥c β∥c ⇒α∥β；③ ⎭⎪⎬⎪⎫a ∥γα∥γ⇒a ∥α. 其中正确命题的个数是( ) A ．0个 B ．1个 C ．2个 D ．3个解析：①错，a 与b 可平行、相交、异面．②错，c 可平行于α与β的交线．③错，a ⊂α也可能．答案：A2．如图，在正方体ABCD—A1B1C1D1中，E为A1B1的中点，则直线AE与平面BB1D1D的位置关系是______．答案：相交3．经过平面外的两点作该平面的平行平面可以作()A．0个B．1个C．0个或1个D．1个或2个解析：连接平面外的两点的直线，当该直线与平面平行时，过该直线的平面有1个，当该直线与平面相交时，过该直线的平面有0个．故选C.答案：C4．经过两条异面直线a、b之外的一点P，可作________个平面与a、b都平行．答案：15．(1)直线在平面外，这条直线一定与平面平行对吗？答案：错(2)直线与平面平行，那么该直线与平面内每条直线都平行对吗？答案：错(3)直线与平面平行，那么该直线与平面内每条直线都没有公共点对吗？答案：对(4)三棱柱的棱和面之间可以形成多少对线面平行？答案：9对(5)正方体的棱和面之间可以形成多少对线面平行？答案：24对6．正四棱柱ABCD-A1B1C1D1中，E是DD1的中点．求证：BD1∥平面ACE.证明：如右图所示，连接BD，交AC于点O，则O是BD的中点，连接OE，因为E 是DD1的中点，EO∥BD1，因为BD1⊄平面ACE，EO⊂平面ACE，所以BD1∥平面ACE.巩固提升7．如图，正方体木块ABCDA1B1C1D1中，P是平面ABCD上的一点，现需过点P画一条与平面ADC1B1平行的直线，应该怎样去完成？解析：过点P作一条直线a与AD平行即可．∵AD⊂平面ADC1B1，a⊄平面ADC1B1，∴a∥平面ADC1B1.8．如图所示，已知四棱锥PABCD底面ABCD为平行四边形，E，F分别为AB，PD的中点．求证：AF∥平面PCE.证明：如图所示，取CD中点M，连接MF，MA，则在△PCD中，MF∥PC，又MF⊄平面PCE，PC⊂平面PCE，∴MF∥平面PCE.又∵ABCD为平行四边形，E，M分别为AB，CD中点，∴AE綊CM，∴四边形EAMC为平行四边形，∴MA∥CE，又MA⊄平面PCE，CE⊂平面PCE.∴MA∥平面PCE.又MA∩MF＝M，∴平面MAF∥平面PCE.又∵AF⊂平面MAF，∴AF∥平面PCE.9．在正方体ABCDA1B1C1D1中，M，N，E，F分别是棱A1B1，A1D1，B1C1，C1D1的中点，O是底面ABCD的中心．求证：平面AMN∥平面OEF.证明：连接A1C1交EF于点G，交MN于点H，连接AC，显然O为AC的中点．在平面A1ACC1中，∵A 1C 1∥AC ，∴GH ∥AO .∵M ，N ，E ，F 分别是A 1B 1，A 1D 1，B 1C 1，C 1D 1的中点，GH ＝12A 1C 1，AO ＝12AC ，∴GH ＝AO . 连接AH ，OG ，则四边形AOGH 是平行四边形． ∴AH ∥OG .连接B 1D 1，则MN ∥B 1D 1，EF ∥B 1D 1，∴MN ∥EF .又MN ，AH ⊂平面AMN ，且MN ∩AH ＝H ， EF ，OG ⊂平面EOF ，且EF ∩OG ＝G ，∴平面AMN ∥平面OEF .。

数学课件-高一-直线与平面平行的判定

四、教学过程设计
创设情境导入新课线面平行判定定理的探究线面平行判定定理的应用
课堂练习巩固提高归纳总结提高认识
分析实例—猜想定理合作探究—确认定理
布置作业自主探究板书设计
1、创设情境导入新课
设计意图：让学生直观感知直线与
提出问题：
平面平行的位置关系，激发学生的学习兴趣。
（１）直线与平面有什么
面内面外平行
2、用定理证明线面平行时,在寻找平行直线时可
以通过三角形的中位线、对应边成比例、平行四
边形中的平行关系等来完成。
３、数学思想方法：转化的思想.
转化为
线线平行
线面平行
空间问题转化为平面问题
６、布置作业自主探究
必做题:
１、教材Ｐ56 练习２; ２、教材Ｐ61 习题2.2 Ａ组３、４.
三、教学方法分析
1、教法采用“尝试指导法和引导发现法”，让学生真正成为课堂的主人。
2、学法
强调“观察实验－合理猜想－操作确认 ” 的探究式学习方法，培养学生自主探究和解决问题的能力。
三、教学方法分析
3、教学手段
多媒体辅助教学
教学手段的现代化有利于提高课堂效率，通过问题探究为学生提供丰富、生动、直观的观察材料，可有效激发学生参与学习的积极性和主动性。
样的位置关系？
（２）观察图片：你能找
出这三种位置关系吗？
（３）你得到平行的依据是什么呢？
地面
（４）你如何保证它们没
有公共点呢？
2.线面平行判定定理的探究
（１）分析实例猜想定理
将课本的一边AB紧靠桌面，并绕AB转动， C
D
观察AB的对边CD在各个位置时，与桌面

人教新课标版数学高一必修2课件直线与平面平行的判定

由a∥b，且a∥α，知b与α平行或b⊂α.
反思与感悟
解析答案
探究点2 直线与平面平行的判定定理的应用例2 已知公共边为AB的两个全等的矩形ABCD和ABEF不在同一平面内， P ， Q 分别是对角线 AE ， BD 上的点，且 AP ＝ DQ( 如图 ). 求证： PQ∥平面CBE.
连接D1H，在△DD1H中，
∵DDOH＝23＝DDDG1，∴GO∥D1H，又GO⊄平面D1EF，D1H⊂平面D1EF， ∴GO∥平面D1EF.
1 23 4
解析答案
课堂小结
1.判断或证明线面平行的常用方法 (1)定义法：证明直线与平面无公共点(不易操作). (2)判定定理法：(a⊄α，b⊂α，a∥b⇒a∥α). (3)排除法：证明直线与平面不相交，直线也不在平面内. 2.证明线线平行的常用方法 (1)利用三角形、梯形中位线的性质. (2)利用平行四边形的性质. (3)利用平行线分线段成比例定理.
解析答案
1 23 4
2.以下说法(其中a，b表示直线，α表示平面)正确的个数为__0__. ①若a∥b，b⊂α，则a∥α； ②若a∥α，b∥α，则a∥b； ③若a∥b，b∥α，则a∥α；④若a∥α，b⊂α，则a∥b. 解析 ①a⊂α也可能成立； ②a，b还有可能相交或异面； ③a⊂α也可能成立； ④a，b还有可能异面.
答案
问题2 如图，平面α外的直线a平行于平面α内的直线b.这两条直线共面吗？直线a与平面α相交吗？答案由于直线a∥b，所以两条直线共面，直线a与平面α不相交.
答案
探究点1 直线与平面平行的判定定理
例1 如果两直线a∥b，且a∥α，则b与α的位置关系是( D )
A.相交
B.b∥α

人教版必修二高一数学：直线、平面平行的判定及其性质

人教版必修二高一数学：直线、平面平行的判定及其性质一、直线与平面平行的判定定理语言文字_______一条直线与此平面内的一条直线________，则该直线与此平面平行图形语言符号语言a⊄α，b⊂α，且a∥b⇒a∥α作用证明直线与平面______________二、平面与平面平行的判定定理语言文字一个平面内的两条________直线与另一个平面________，则这两个平面平行图形语言符号语言a⊂β，b⊂β，__________，a∥α，b∥α⇒α∥β作用证明两个平面__________1．要证明两平面平行，需要在其中一个平面内找到两条相交直线平行于另一个平面，注意“相交”二字不能丢．2．可以通过证明线线平行来证明面面平行．三、直线与平面平行的性质定理（1）自然语言：一条直线与一个平面______________，则过这条直线的任一平面与此平面的______________与该直线平行．（2）图形语言：如图．（3）符号语言：,,a a b a b αβαβ⊂=⇒∥∥．（4）直线与平面平行的性质定理的作用①作为证明线线平行的依据．当证明线线平行时，可以证明其中一条直线平行于一个平面，另一条直线是过第一条直线的平面与已知平面的交线，从而得到两条直线平行．②作为画一条直线与已知直线平行的依据．如果一条直线平行于一个平面，要在平面内画一条直线与已知直线平行，可以通过已知直线作一个平面与已知平面相交，交线就是所要画的直线．四、平面与平面平行的性质定理（1）自然语言：如果______________同时和第三个平面______________，那么它们的交线平行．（2）图形语言：如图．（3）符号语言：,,.∥∥a b a b αβαγβγ==⇒1．已知两个平面平行，虽然一个平面内的任意一条直线都平行于另一个平面，但是这两个平面内的所有直线并不一定互相平行，它们可能是平行直线，也可能是异面直线，但不可能是相交直线． 2．应用该定理证明线线平行．五、两个平面平行的其他性质（1）两个平面平行，其中一个平面内的任意一条直线都平行于另一个平面．（2）夹在两个平行平面间的平行线段相等．（3）经过平面外一点有且只有一个平面与已知平面平行．（4）两条直线被三个平行平面所截，截得的对应线段成比例．（5）如果两个平面分别平行于第三个平面，那么这两个平面互相平行．答案一、平面外平行平行二、相交平行a b P平行三、（1）平行交线四、（1）两个平行平面相交帮—重点1．直线与平面平行的判定、平面与平面平行的判定；2．掌握直线与平面平行的性质定理，明确由线面平行可推出线线平行；3．掌握平面与平面平行的性质定理，并会应用性质定理解决问题．帮—难点1．线面平行、面面平行的综合应用；2．掌握直线与直线、直线与平面、平面与平面之间的平行关系的相互转化．帮—易错1．忽略线面平行、面面平行的判定定理使用的前提条件；2．忽略定理的必备条件致误．1．直线与平面平行的判定应用判定定理证明线面平行的步骤：上面的第一步“找”是证题的关键，其常用方法有：利用三角形、梯形中位线的性质；利用平行四边形的性质；利用平行线分线段成比例定理．1）如图，下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB ∥平面MNP的图形序号是( )A ．①③B ．①④C ．②③D ．②④【答案】B【解析】①连接AC ，AC ∥MN ，BC ∥PN 可得出面ACB ∥面MPN .∴AB ∥面MPN ；④AB ∥PN ，∴AB ∥面PMN ；②③中，AB 与面PMN 不平行．2）如图所示，在三棱柱111ABC A B C -中，AC BC =，点D 是AB 的中点. 求证：1BC ∥平面1CA D ．【答案】证明详见解析．【解析】如图所示，连接1AC ，交1A C 于点O ，连接OD ，则O 是1AC 的中点． ∵点D 是AB 的中点， ∴1∥OD BC ．又∵OD ⊂平面1CA D ，1BC ⊄平面1CA D ， ∴1BC ∥平面1CA D ．3）如图所示的几何体中，△ABC 是任意三角形，AE ∥CD ，且AE ＝AB ＝2a ，CD ＝a ，F 为BE 的中点，求证：DF ∥平面ABC .【证明】如图所示，取AB 的中点G ，连接FG ，CG ，∵F ，G 分别是BE ，AB 的中点，∴FG ∥AE ，FG ＝12AE .又∵AE ＝2a ，CD ＝a ，∴CD ＝12AE .又AE ∥CD ，∴CD ∥FG ，CD ＝FG ，∴四边形CDFG 为平行四边形，∴F ∥CG .又CG ⊂平面ABC ，DF ⊄平面ABC ，∴DF ∥平面ABC . 2．平面与平面平行的判定平面与平面平行的判定方法有如下三种：（1）根据定义：证明两个平面没有公共点，但有时直接证明非常困难．（2）根据判定定理：要证明两个平面平行，只需在其中一个平面内找两条相交直线，分别证明它们平行于另一个平面，于是这两个平面平行，或在一个平面内找到两条相交的直线分别与另一个平面内两条相交的直线平行．（3）根据平面平行的传递性：若两个平面都平行于第三个平面，则这两个平面互相平行．已知m ，n 是两条直线，α，β是两个平面，有以下结论：①m ，n 相交且都在平面α，β外，m ∥α，m ∥β，n ∥α，n ∥β，则α∥β；②若m ∥α，m ∥β，则α∥β； ③若m ∥α，n ∥β，m ∥n ，则α∥β. 其中正确结论的个数是( ) A ．0 B ．1 C ．2 D ．3【答案】B【解析】设m ∩n ＝P ，则直线m ，n 确定一个平面，设为γ，由面面平行的判定定理知，α∥γ，β∥γ，因此，α∥β，即命题①正确；如图，在长方体中，直线EF 平行于平面ADD 1A 1和平面A 1B 1C 1D 1，即满足命题②的条件，但平面A 1B 1C 1D 1与平面ADD 1A 1不平行，因此命题②不正确；图中，EF ∥平面ADD 1A 1，BC ∥平面A 1B 1C 1D 1，EF ∥BC ，但平面ADD 1A 1与平面A 1B 1C 1D 1不平行，所以命题③也不正确．2）如图，在长方体ABCD A B C D -''''中，,,,E F E F ''分别是,,,AB CD A B C D ''''的中点．求证：平面A EFD ''∥平面BCF E ''．【答案】证明详见解析．【解析】∵E E '，分别是AB A B ''，的中点，∴=A E BE ''∥．∴四边形A EBE ''为平行四边形， ∴A E BE ''∥．∵A E '⊄平面BCF E ''，BE '⊂平面BCF E ''，∴A E '∥平面BCF E ''．同理，A D ''∥平面BCF E ''．又A EA D A '''='，∴平面A EFD ''∥平面BCF E ''．利用判定定理证明两个平面平行的一般步骤：第一步：在一个平面内找出两条相交直线；第二步：证明这两条相交直线分别平行于另一个平面；第三步：利用平面与平面平行的判定定理得出结论． 3．线面平行、面面平行的综合应用在立体几何中，常见的平行关系有线线平行、线面平行和面面平行，这三种平行关系不是孤立的，而是相互联系，并且可以相互转化的．在解决问题的过程中，要灵活运用平行关系的判定定理．一般地，证明线面平行可以转化为证明线线平行；证明面面平行可以转化为证明线面平行；证明线线平行可以利用线面平行或面面平行的性质定理来实现．1）如果AB 、BC 、CD 是不在同一平面内的三条线段，则经过它们中点的平面和直线AC 的位置关系是( )A ．平行B ．相交C ．AC 在此平面内D ．平行或相交【答案】 A【解析】把这三条线段放在正方体内如图，显然AC ∥EF ，AC ⊄平面EFG .EF ⊂平面EFG ，故AC ∥平面EFG .故选A.2）如图所示，在四棱锥C ABED -中，四边形ABED 是正方形，点,G F 分别是线段,EC BD 的中点.（1）求证：∥平面GF ABC ；（2）线段BC 上是否存在一点H ，使得平面∥GFH 平面ACD ，若存在，请找出点H 并证明；若不存在，请说明理由.【答案】（1）见解析；（2）见解析.【解析】（1）由四边形ABED 为正方形可知，连接AE 必与BD 相交于中点F ，故∥GF AC . ∵GF ⊄平面ABC ，∴∥GF 平面ABC .（2）线段BC 上存在一点H 满足题意，且点H 是BC 的中点. 理由如下：由点,G H 分别为,CE CB 中点可得：∥∥GH EB AD .∵GH ⊄平面ACD ，∴∥GH 平面ACD .由（1）可知，∥GF 平面ACD ，且GF GH G =，.故平面∥GFH 平面ACD .本题考查线面位置关系的判定与证明，熟练掌握空间中线面位置关系的定义、判定、几何特征是解答的关键，其中垂直、平行关系证明中应用转化与化归思想的常见类型：证明线面、面面平行，需转化为证明线线平行，着重考查了推理与论证能力． 4．直线与平面平行的性质定理的应用应用线面平行的性质定理时，关键是过已知直线作辅助平面与已知平面相交，所得交线与已知直线平行．还可以利用交线判断已知平面内任意一条直线与已知直线的位置关系，即在已知平面内所有与交线平行的直线都与已知直线平行，所有与交线相交的直线都与已知直线异面．1）若直线a平行于平面α，则下列结论错误的是（）A．直线a上的点到平面α的距离相等B．直线a平行于平面α内的所有直线C．平面α内有无数条直线与直线a平行D．平面α内存在无数条直线与直线a成90°角【答案】B【分析】直线a与平面α内的所有直线平行或异面．【解答】解：由直线a平行于平面α，知：在A中，直线a上的点到平面α的距离相等，故A正确；在B中，直线a与平面α内的所有直线平行或异面，故B错误；在C中，平面α内有无数条直线与直线a平行，故C正确；在D中，平面α内存在无数条直线与直线a成90°角，故D正确．故选：B．2）已知m，n表示两条不同的直线，α表示平面．下列说法正确的是（）A．若m∥α，n∥α，则m∥n B．若m⊥α，n⊥α，则m∥nC．若m⊥α，m⊥n，则n∥αD．若m∥α，m⊥n，则n⊥α【答案】B【分析】在A中，m与n相交、平行或异面；在B中，由线面垂直的性质定理得m∥n；在C中，n∥α或n ⊂α；在D中，n与α相交、平行或n⊂α．【解析】由m，n表示两条不同的直线，α表示平面，知：在A中，若m∥α，n∥α，则m与n相交、平行或异面，故A错误；在B中，若m⊥α，n⊥α，由线面垂直的性质定理得m∥n，故B正确；在C中，若m⊥α，m⊥n，则n∥α或n⊂α，故C错误；在D中，若m∥α，m⊥n，则n与α相交、平行或n⊂α，故D错误．故选：B．3）在如图所示的几何体中，三个侧面AA1B1B，BB1C1C，CC1A1A都是平行四边形，则平面ABC与平面A1B1C1平行吗？______(填“是”或“否”)．【答案】是【解析】因为侧面AA 1B 1B 是平行四边形，所以AB ∥A 1B 1，因为AB ⊄平面A 1B 1C 1，A 1B 1⊂平面A 1B 1C 1，所以AB ∥平面A 1B 1C 1，同理可证：BC ∥平面A 1B 1C 1.又因为AB ∩BC ＝B ，AB ⊂平面ABC ，BC ⊂平面ABC ，所以平面ABC ∥平面A 1B 1C 1.4）如图，在三棱柱111ABC A B C -中，点E ，F 分别是棱CC 1，BB 1上的点，点M 是线段AC 上的动点，EC =2FB =2，若∥MB 平面AEF ，试判断点M 的位置．【答案】M 是AC 的中点时，MB ∥平面AEF ．【解析】如图，过F ，B ，M 作平面FBMN ，交AE 于N ．因为∥BF 平面11AAC C ，BF ⊂平面FBMN ，平面FBMN 平面11AAC C MN =，所以∥BF MN ．又∥MB 平面AEF ，MB ⊂平面FBMN ，平面FBMN 平面AEF FN =，所以∥MB FN ，所以四边形BFNM 是平行四边形，所以MN =BF =1．又EC ∥FB ，EC =2FB =2，所以MN ∥EC ，MN =12EC ，故MN 是△ACE 的中位线．所以M 是AC 的中点时，MB ∥平面AEF ． 5．平面与平面平行的性质定理的应用利用面面平行的性质定理判断两直线平行的步骤：（1）先找两个平面，使这两个平面分别经过这两条直线中的一条；（2）判定这两个平面平行；（3）再找一个平面，使这两条直线都在这个平面上；（4）由定理得出结论．1）设平面α∥平面β，A ∈α，B ∈β，C 是AB 的中点，当点A 、B 分别在平面α，β内运动时，动点C ( )A ．不共面B ．当且仅当点A 、B 分别在两条直线上移动时才共面C ．当且仅当点A 、B 分别在两条给定的异面直线上移动时才共面D ．无论点A ，B 如何移动都共面【答案】 D【解析】无论点A 、B 如何移动，其中点C 到α、β的距离始终相等，故点C 在到α、β距离相等且与两平面都平行的平面上．2）下列命题中不正确的是( )A ．两个平面α∥β，一条直线a 平行于平面α，则a 一定平行于平面βB ．平面α∥平面β，则α内的任意一条直线都平行于平面βC ．一个三角形有两条边所在的直线平行于一个平面，那么三角形所在平面与这个平面平行D ．分别在两个平行平面内的两条直线只能是平行直线或者是异面直线【答案】 A【解析】选项A 中直线a 可能与β平行，也可能在β内，故选项A 不正确；三角形两边必相交，这两条相交直线平行于一个平面，那么三角形所在的平面与这个平面平行，所以选项C 正确；依据平面与平面平行的性质定理可知，选项B ，D 也正确，故选A.3）设α∥β，A 、C ∈α，B 、D ∈β，直线AB 与CD 交于S ，若AS ＝8，BS ＝9，CD ＝34，则CS 的长是________．【答案】272或16【解析】有两种情况，当点S 在α，β面同侧时，如图(a )所示，∵α∥β，平面SBD ∩α＝AC ，平面SBD ∩β＝BD ，∴AC ∥BD ，AS BS ＝CSDS ，且AS AB ＝CS CD， ∴CS ＝AS ·CD AB ＝8×349－8＝272.同理，当点S 在α，β两平面之间，如图(b )所示，可证得AC ∥DB 及SA SB ＝CSDS ，∴CS CD －CS ＝89. ∴9CS ＝8CD －8CS ，∴CS ＝8CD 17＝8×3417＝16.4）已知三个平面α、β、γ满足α∥β∥γ，直线a 与这三个平面依次交于点A 、B 、C ，直线b 与这三个平面依次交于点E 、F 、G ．求证：AB EFBC FG=．【答案】证明详见解析．【解析】如图，连接AG 交β于H ，连接BH 、FH 、AE 、CG ．∵∥βγ，平面ACG ∩β＝BH ，平面ACG CG γ=，∴BH ∥CG ．同理AE ∥HF ， ∴AB AH EF BC HG FG ==，即AB EFBC FG=． ①当a 与b 共面时，有AE ∥BF ∥CG ．上述证明过程也是正确的，只是此时B 、H 、F 三点共线． ②连接CE ，可同理证明．③当a 与b 异面时，可过A （或B 、C ）作b 的平行线或过E （或F 、G ）作a 的平行线，再利用面面平行的性质定理可证得结论．以上思路都遵循同一个原则，即“化异为共”．6．忽略定理使用的前提条件致错如果两条平行直线a，b中的a∥α，那么b∥α．这个命题正确吗？为什么？【错解】这个命题正确．∵a∥α，∴在平面α内一定存在一条直线c，使a∥c．又∵a∥b，∴b∥c，∴b∥α．【错因分析】忽略了b⊂α这种情况，从而导致错误，本题条件中的直线b与平面α有两种位置关系：b∥α和b⊂α．【正解】这个命题不正确．若b⊄α，∵a∥α，∴在平面α内必存在一条直线c，使a∥c．又∵a∥b，∴b∥c，∴b∥α．若b⊂α，则不满足题意．综上所述，b与α的位置关系是b∥α或b⊂α．【易错警示】错误的原因是利用线面平行的判定定理时，忽略了定理使用的前提条件必须是平面外的一条直线与平面内的一条直线平行．7．对平面与平面平行的性质定理理解不正确，忽略“第三个平面”这一条件如图，α∥β，AB，CD是夹在平面α和平面β间的两条线段，则AC所在的直线与BD所在的直线平行，这个说法正确吗？【错解】这个说法正确．【错因分析】忽略了AB，CD可能异面的情况．当AB，CD异面时，AC与BD不平行．【思路分析】AB，CD共面时，AC∥BD；AB，CD异面时，AC∥β，但AC与BD不平行．同理BD∥α，但BD与AC不平行．【正解】这个说法错误．【易错警示】使用定理证明或判断线线平行和线面平行时，一定要注意定理成立的条件，缺一不可．1.能保证直线a与平面α平行的条件是（）A．b⊂α，a∥bB．b⊂α，c⊂α，a∥b，a∥cC．b⊂α，A∈a，B∈a，C∈b，D∈b，且AC＝BDD．a⊄α，b⊂α，a∥b【答案】D【解答】在A中，b⊂α，a∥b，则直线a与平面α平行或a⊂α，故A错误；在B中，b⊂α，c⊂α，a∥b，a∥c，则直线a与平面α平行或a⊂α，故B错误；在C 中，b⊂α，A，B∈a，C，D∈b，且AC＝BD，则直线a与平面α平行、相交或a⊂α，故C错误；在D中，a⊄α，b⊂α，a∥b，由此利用线面平行的判定定理得直线a与平面α平行．故选：D．在A中，直线a与平面α平行或a⊂α；在B中，直线a与平面α平行或a⊂α；在C中，直线a与平面α平行、相交或a⊂α；在D中，利用线面平行的判定定理得直线a与平面α平行．2．在正方体ABCD–A1B1C1D1中，与平面ACC1A1平行的棱共有（）A．2条B．3条C．4条D．6条【答案】A【解析】如图所示，正方体ABCD–A1B1C1D1中，与平面ACC1A1平行的棱是BB1和DD1，共有2条．故选A．3.下列条件中，能判断平面α与平面β平行的是（）A．α内有无穷多条直线都与β平行B．α与β同时平行于同一条直线C．α与β同时要垂直于同一条直线D．α与β同时垂直于同一个平面【答案】C【解析】对于A，若α内有无穷多条平行的直线与β平行，则不能说明α平行β；对于B，平行于同一条直线的两个平面可能不平行，还可以相交；对于C，垂直于同一条直线的两平面平行；对于D，垂直于同一平面的两个平面不一定平行，还可以垂直．综上，选项C正确．故选：C．4．若平面α∥平面β，则（） A ．平面α内任一条直线与平面β平行B ．平面α内任一条直线与平面β内任一条直线平行C ．平面α内存在一条直线与平面β不平行D ．平面α内一条直线与平面β内一条直线有可能相交【答案】A【解析】根据平面与平面平行的性质可知，若a ⊂平面α，平面∥α平面β，则∥a 平面β.故选A. 5．已知a ，b 为不同的直线，α、β、γ为不同的平面.在下列命题中，正确的是（） A ．若直线//a 平面α，直线//a 平面β，则∥αβ B ．若平面α内有无穷多条直线都与平面β平行，则∥αβ C ．若直线a α⊂，直线b β⊂，且∥a β，∥b α，则∥αβ D ．若平面∥α平面γ，平面∥β平面γ，则∥αβ 【答案】D【解析】若∥a α且∥a β，则α和β平行或相交，A 错误；若平面α内的无数条相互平行的直线均平行于平面β，则α和β可能相交，B 错误；若∥a b ，此时直线a α⊂，直线b β⊂，且∥a β，∥b α，则α和β可能相交，C 错误；由平面平行的性质可知，平行于同一平面的两平面互相平行，D 正确.本题正确选项为D.本题考查空间中的平行关系，涉及线线关系、线面关系、面面关系.求解时，根据空间中平行关系的判定和性质依次判断各个选项即可得到结果.6．设α、β是两个平面，a 、b 是两条直线，下列推理正确的是（）A ．∥∥∥a b a b ⎫⇒⎬⎭ααB ．∥∥a a a b b ⊂⎫⎪⇒⎬⎪=⎭αβαβC ．∥∥a b a b ⊂⎫⎪⊂⇒⎬⎪⎭αβαβD ．∥∥a b a b ⊂⎫⎪⊂⇒⎬⎪⎭αβαβ 【答案】 B【解析】对于A ，也可能a α⊂，故A 错误，对于B ，根据线面平行的性质定理可知B 正确；对于C ，由α，β平行可知a ，b 没有公共点，故a ，b 平行或异面，故C 错误；对于D ，若α，β相交，a ，b 均与交线平行，显然结论不成立，故D 错误．故选B ．本题考查线线、线面、面面位置关系的判定及性质，属于基础题.求解时，根据空间线面位置关系的定义、判定定理和性质进行判断．7．如图，在平行六面体ABCD −1111A B C D 中，点,,M P Q 分别为棱,,AB CD BC 的中点，若平行六面体的各棱长均相等，给出下列说法：①1A M ∥1D P ； ②1A M ∥1B Q ； ③1A M ∥平面11DCC D ； ④1A M ∥平面11D PQB .则以上正确说法的个数为（） A ．1 B ．2 C ．3 D ．4【答案】C【解析】连接PM ，因为M 、P 分别为AB 、CD 的中点，故PM 平行且等于AD .由题意知AD 平行且等于11A D ，故PM 平行且等于11A D ，所以四边形11PMA D 为平行四边形，所以1A M ∥1D P ，故①正确. 显然1A M 与1B Q 为异面直线.故②错误.由①知1A M ∥1D P .由于1D P 在平面11DCC D 内，又在平面11D PQB 内，且1A M 不在平面11DCC D 内，又不在平面11D PQB 内.故1A M ∥平面11DCC D ，1A M ∥平面11D PQB ，故③④均正确. 所以正确说法的个数为3，故选C.本题主要考查线面平行的判断.其中通过证明平行四边形得到线线平行是解题的关键.8．如图，正方体ABCD A 1B 1C 1D 1中，过BD 1的平面，分别与AA 1，CC 1交于M ，N ，则四边形BND 1M 的形状为________．【答案】平行四边形【解析】由题意知，平面A1B∥平面C1D，∴MB∥D1N，同理，D1M∥BN. ∴四边形BND1M是平行四边形．9．若夹在两个平面间的三条平行线段相等，则这两个平面的位置关系为________.【答案】平行或相交【解析】三条平行线段共面时，两平面可能相交也可能平行；当三条平行线段不共面时，两平面一定平行. 故填平行或相交.10．三棱锥S−AB C中，G为△ABC的重心，E在棱SA上，且AE=2ES，则EG与平面SBC的关系为________.【答案】平行【解析】连接AG并延长交BC于点M，连接SM，则AG=2GM，又AE=2ES，所以EG∥SM，又EG⊄平面SBC，所以EG∥平面SB C.故填平行.11.如图是正方体的平面展开图，在这个正方体中，①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.以上四个结论中，正确结论的序号是________．【答案】①②③④【解析】展开图可以折成如图①所示的正方体．图①在正方体中，连接AN ，如图②所示，图②∵AB ∥MN ，且AB ＝MN ，∴四边形ABMN 是平行四边形．∴BM ∥AN ，∴BM ∥平面DE ，同理可证CN ∥平面AF ，∴①②正确；如图③所示，图③可以证明BM ∥平面AFN ，BD ∥平面AFN ，则平面BDM ∥平面AFN ，同理可证平面BDE ∥平面NCF ，所以③④正确．12．如图所示，在直四棱柱1111ABCD A B C D -中，已知122DC DD AD AB ===，AD DC ⊥，∥AB DC .设E 是DC 的中点，求证：1∥D E 平面1A BD .【答案】见解析. 【解析】连接BE .∵E 是DC 的中点，22DC AD AB ==，AD DC ⊥，∴四边形DABE 为正方形， ∴11BE AD A D ==，且11∥∥BE AD A D ，∴四边形11A D EB 为平行四边形，∴11∥D E A B ， ∵1D E ⊄平面1A BD ，1A B ⊂平面1A BD ，∴1∥D E 平面1A BD .本题主要考查线面平行的判定定理，属于中档题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行；②利用面面平行的性质，即两面平行，在其中一平面内的直线平行于另一面.13．如图所示，在三棱柱111ABC A B C -中，D 是BC 上一点，且1∥A B 平面1AC D ，1D 是11B C 的中点.求证：平面11A BD ∥平面1AC D . 【答案】见解析.【解析】连接1A C 交1AC 于点E ，连接ED ， ∵四边形11A ACC 是平行四边形，∴E 是1A C 的中点，1A B ∥平面1AC D ，平面1A BC 平面1AC D DE =，∴根据线面平行的性质定理，可得1ED A B ∥，E 是1A C 的中点，D ∴是BC 的中点，又1D 是11B C 的中点，11BD C D ∴∥且11BD C D =，∴四边形11C D BD 为平行四边形，11C D BD ∴∥，1BD ∴∥平面1AC D ，又11A BBD B =，∴平面11A BD ∥平面1AC D .本题主要考查了线面平行的性质定理的应用，以及面面平行的判定与证明，其中解答中把握几何体的结构特征，熟练应用线面平行的性质定理和面面平行的判定定理是解答的关键，着重考查了推理与论证能力，属于基础题．求解时，连接1A C 交1AC 于点E ，连接ED ，利用线面平行的性质定理，证得1ED A B ∥，又由四边形11C D BD 为平行四边形，得11C D BD ∥，证得1BD ∥平面1AC D ，利用面面平行的判定定理，可得平面11A BD ∥平面1AC D .14．已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：（1）1∥C O 平面11AB D ；（2）平面11∥AB D 平面1C BD . 【答案】（1）见解析；（2）见解析.【解析】（1）连接11A C 交11B D 于点1O ，连接1AO ，1111ABCD A B C D -是正方体，∴四边形11A ACC 是平行四边形，11∥A C AC ∴且11A C AC =，又1,O O 分别是11,A C AC 的中点，11∥O C AO ∴且11O C AO =，∴四边形11AOC O 是平行四边形，11,∥C O AO ∴又1AO ⊂平面11AB D ，1C O ⊄平面11AB D ，1∥C O ∴面11AB D .（2）1111ABCD A B C D -是正方体，1111,∥∥AB DC AD BC ∴，∴1∥AB 平面1,C BD 1∥AD 平面1C BD ，又11,AB AD A =1AD ⊂平面111,AB D AB ⊂平面11AB D ，∴平面11∥AB D 平面1C BD .本题主要考查直线与平面平行的证明，考查平面与平面平行的证明，属于中档题. 证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行；②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面.15.在正方体ABCD ﹣A 1B 1C 1D 1中，点O 是四边形ABCD 的中心，关于直线A 1O ，下列说法正确的是（） A ．A 1O ∥D 1C B ．A 1O ⊥BC C ．A 1O ∥平面B 1CD 1 D ．A 1O ⊥平面AB 1D 1【答案】C【解析】∵在正方体ABCD ﹣A 1B 1C 1D 1中，点O 是四边形ABCD 的中心，∴A 1D ∥B 1C ，OD ∥B 1D 1， ∵A 1D ∩DO ＝D ，B 1D 1∩B 1C ＝B 1，∴平面A 1DO ∥平面B 1CD 1， ∵A 1O ⊂平面A 1DO ，∴A 1O ∥平面B 1CD 1．故选：C ．推导出A 1D ∥B 1C ，OD ∥B 1D 1，从而平面A 1DO ∥平面B 1CD 1，由此能得到A 1O ∥平面B 1CD 1．16.如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是（）A ．B ．C ．D ．【答案】A【解析】对于B ，易知AB ∥MQ ，则直线AB ∥平面MNQ ；对于C ，易知AB ∥MQ ，则直线AB ∥平面MNQ ；对于D ，易知AB ∥NQ ，则直线AB ∥平面MNQ ．故排除B ，C ，D ，选A ．本题主要考查线面平行的判定定理以及空间想象能力，属容易题．证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．17．对于两条不同的直线m ，n 和两个不同的平面α，β，以下结论正确的是（）A ．若m ⊂α，∥n β，m ，n 是异面直线，则α，β相交B ．若m ⊥α，m ⊥β，∥n α，则∥n βC ．若m ⊂α，∥n α，m ，n 共面于β，则∥m nD ．若m ⊥α，n ⊥β，α，β不平行，则m ，n 为异面直线【答案】C【解析】正方体1111ABCD A B C D -中，取，m n 分别为棱11，BC C D ，平面α为平面，ABCD β为与平面1111A B C D 平行的平面，满足选项A 中的条件，但是∥αβ，选项A 错误；取，m n 分别为棱1，BB BC ，平面，αβ为1111，A B C D ABCD ，满足选项B 中的条件，但是n ⊂β，选项B 错误；取，m n 分别为棱1，AB AA ，平面，αβ分别为平面111111，BCC B A B C D ，满足选项D 中的条件，但是m n A =，选项D 错误.本题选择C 选项.18．如图所示，正方体1111ABCD A B C D -中，点E ，F ，G ，P ，Q 分别为棱AB ，11C D ，11D A ，1D D ，1C C 的中点.则下列叙述中正确的是（）A ．直线∥BQ 平面EFGB ．直线1∥A B 平面EFGC ．平面∥APC 平面EFGD ．平面1∥A BQ 平面EFG【答案】B【解析】过点,,E F G 的截面如图所示（,H I 分别为1,AA BC 的中点）1∥A B HE ，1A B ⊄平面EFG ，HE ⊂平面EFG ，1∥A B ∴平面EFG .本题正确选项为B.本题考查了直线与平面、平面与平面平行的判定，关键在于能够准确地找到截面，从而判断出结果.求解时，将平面EFG 扩展，可作出过,,E F G 的正方体的截面，易证得1∥A B 平面EFG .19.如图所示的四个正方体中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，能得出AB ∥平面MNP 的图形的序号为（）A ．①②B ．③④C ．①②③D ．②④【答案】C【解析】正方体中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，在图①中，∵BC ∥PN ，AC ∥PM ，AC ∩BC ＝C ，PN ∩PM ＝P ，∴平面ABC ∥平面PMN ， ∵AB ⊂平面ABC ，∴AB ∥平面MNP ，故①能得出AB ∥平面MNP ；在图②中，∵AC ∥MN ，BC ∥PN ，AC ∩BC ＝C ，MN ∩PN ＝N ，∴平面ABC ∥平面PMN ，∵AB ⊂平面ABC ，∴AB ∥平面MNP ，故②能得出AB ∥平面MNP ；在图③中，BC ∥MN ，AC ∥PN ，BC ∩AC ＝C ，MN ∩PN ＝N ，∴平面ABC ∥平面PMN ，∵AB ⊂平面ABC ，∴AB ∥平面MNP ，故③能得出AB ∥平面MNP ；在图④中，AB ∩PB ＝B ，PB ⊂平面PMN ，∴AB ∩平面PMN ＝B ，故④不能得出AB ∥平面MNP ．故选：C ．在图①中，由BC ∥PN ，AC ∥PM ，推导出AB ∥平面MNP ；在图②中，由AC ∥MN ，BC ∥PN ，推导出AB ∥平面MNP ；在图③中，由BC ∥MN ，AC ∥PN ，推导出AB ∥平面MNP ；在图④中，AB ∩平面PMN ＝B ．20．如图所示，在长方体1111ABCD A B C D -中，E F ，分别是棱1AA 和1BB 的中点，过EF 的平面EFGH 分别交BC 和AD 于点G H ，，则HG 与AB 的位置关系是（）A ．平行B ．相交C ．异面D ．平行或异面【答案】A 【解析】,E F 分别是11,AA BB 的中点，∥EF AB ∴.又AB ⊄平面EFGH ，EF ⊂平面EFGH ，AB ∴∥平面EFGH . 又AB平面ABCD ，平面ABCD平面EFGH GH =，AB GH ∴∥.本题考查线面平行的判定和性质，属于简单题.求解时，由EF AB ∥得到∥AB 平面EFGH ，从而得到AB GH ∥.21．正方体ABCD −A 1B 1C 1D 1的棱长为3，点E 在A 1B 1上，且B 1E =1，记图中阴影平面为平面α，平面α∥平面BC 1E ，若平面α∩平面AA 1B 1B =A 1F ，则AF 的长为（）A ．1B ．1.5C ．2D ．3【答案】A【解析】因为平面α∥平面BC 1E ，平面α∩平面AA 1B 1B =A 1F ，平面BC 1E ∩平面AA 1B 1B =BE ，所以A 1F ∥BE .又A 1E ∥BF ，所以四边形A 1EBF 是平行四边形，所以A 1E =BF =2，所以AF =1.故选A.本题考查平面与平面平行的性质定理.属于中档题.平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行;平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线互相平行.特别提醒：线线平行、面面平行有传递性，而线面平行没有传递性. 22．如图（1）所示，已知正方形ABCD 中，E F ，分别是AB ，CD 的中点，将△ADE 沿DE 折起，如图（2）所示，则BF 与平面ADE 的位置关系是________.【答案】平行【解析】∵E ，F 分别为AB ，CD 的中点，∴EB ＝FD ．又∵EB ∥FD ，。

人教课标版高中数学必修2《直线与平面平行的判定》名师课件2

a
b
a ,关b键词有, a哪/些/ b呢？a //.
线（平面外）线（平面内）平行线面平行
直线与平面平行（空间）
化归
直线平行（平面）
定理应用，形成技能
判断下列说法是否正确：
①若一条直线不在平面内，则该直线与此平面平行（）
②若一条直线与平面内无数条直线平行，则该直线与此平
面平行（）
b
③如图，a 是平面α内一条给定的
你的感觉可靠吗？
a
α
怎样判定直线与平面平行呢？
直线与平面平行的判定
a
问题引入
问题 1 怎样判断一条直线与平面平行？
如何判定无公共点？
定义直线与平面无公共点
用定义去判断比较抽象
创设情景活动：演示开门关门的过程。
问题 2 门的两边是什么位置关系？
l 问题 3 当门绕轴转动时，门转动的一边与门框所在的平面给人的感觉是什么位置关系？
一、复习回顾
在空间中，直线与平面有几种位置关系？
一、复习回顾
在空间中，直线与平面有几种位置关系？
文字语言图形语言
直线在
平面内 α a
直线与平面直线与的位置关系平面相交
符号语言
a
a A
直线与
a
平面平行 α
a //
二、列举实例直观感知
在日常生活中，哪些实例给我们以直线与平面平行的印象呢？
其中正确的是_①__②___③__(填序号)．
[解]由题意可知OM是△BPD的中位线，所以OM∥PD，①正确；由线面平行的判定定理可知②③都正确．OM与平面PBA及平面 PCB都相交，故④⑤不正确．故填①②③.
例题讲解

139.教案高一数学人教版必修二 2.2.1直线与平面平行的判定

双峰一中高一数学必修二教案科目：数学课题§2.2.1直线与平面平行的判定课型新课教学目标（1）理解并掌握直线与平面平行判定定理；（2）进一步培养学生观察、发现的能力和空间想象能力；（3）学生通过观察图形，借助已有知识，掌握直线与平面平行的判定定理教学过程教学内容备注一、自主学习1.直线与平面的位置关系有哪几种？2.在直线与平面的位置关系中，平行是一种非常重要的关系，它是空间线面位置关系的基本形态，那么怎样判定直线与平面平行呢？二、质疑提问思考1：根据定义，怎样判定直线与平面平行？图中直线l 和平面α平行吗？思考2：生活中，我们注意到门扇的两边是平行的. 当门扇绕着一边转动时，观察门扇转动的一边l 与门框所在平面的位置关系如何？思考3：若将一本书平放在桌面上，翻动书的封面，观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系？思考4：有一块木料如图，P为面BCEF内一点，要求过点P在平面BCEF内画一条直线和平面ABCD平行，那么应如何画线？思考5：如图，设直线b在平面α内，直线a在平面α外，猜想在什么条件下直线a与平面α平行？思考1：如果直线a与平面α内的一条直线b平行，则直线a与平面α一定平行吗？思考2：设直线b在平面α内，直线a在平面α外，若a//b，则直线a与直线b确定一个平面β，那么平面α与平面β的位置关系如何？此时若直线a 与平面α相交，则交点在何处？思考3：通过上述分析，我们可以得到判定直线与平面平行的一个定理，你能用文字语言表述出该定理的内容吗？定理若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.思考4：上述定理通常称为直线与平面平行的判定定理，该定理用符号语言可怎样表述？思考5：直线与平面平行的判定定理可简述为“线线平行，则线面平行”，在实际应用中它有何理论作用？通过直线间的平行，推证直线与平面平行，即将直线与平面的平行关系（空间问题）转化为直线间的平行关系（平面问题）.思考6：设直线a，b为异面直线，经过直线a可作几个平面与直线b平行？过a，b外一点P可作几个平面与直线a，b都平行？三、问题探究例1：在空间四边形ABCD中，E，F分别是AB，AD的中点，求证：EF//平面BCD.例2 在长方体ABCD—A1B1C1D1中.（1）作出过直线AC且与直线BD1平行的截面，并说明理由.（2）设E，F分别是A1B和B1C的中点，求证直线EF//平面ABCD.四、课堂检测五、小结评价〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f，对于集合A 中任何一个数x ，在集合B 中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a xb <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <．（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1． ⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零． ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值． ③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．。

线面平行的判定

一、教材分析
3、教学重点：
重点
线面平行的判定定理的探究和应用
难点
二、学情分析
学生已经掌握了证明线线平行的方法，了解了直线与平面的位置关系，有着强烈的探究欲望。但根据以往教学经验，学生的抽象概括和空间想象能力比较薄弱，动手实践与合作探究的能力不强。这也是确立本节课难点的依据。
三、教法、学法设计
选做题：如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,
A
F
D
F为AE的中点.
求证:AB//平面DCF。(04年天津高考)
E
O
C
B
5.设计说明
本节课的设计可概括为创设情境，让学生主动参与；动手实验，让学生探究质疑；适度点拨，让学生开拓创新；恰当选题，让学生自我评价与反思；归纳体验，让学生将知识系统化。这种教学模式的应用真正让学生动起来，使教材潜在的教育功能得到有效的开发，提高学习的有效性。
教法：根据建构主义学习理论,学生的学习过程是在原有认知的基础上,自主建构新知识的过程。因此，我将设计问题激励学生去思，启发学生去想，引导学生去疑，鼓励学生去探，让其应用已有知识去探索、建构、生成新知识。学法：观察猜想、动手操作、合作探究。
四、教学过程四、教学过程
复习引入
定理探究

b
（3）深化定理
判断下列命题是否正确，若不正确，请用
图形语言加以表达:
（ 1）（ 2）
a a
b a bb
若a , a // b, 则a //
若a , b , 则a // α
α
（ 3）
若b , a // b, 则a //

高中数学(人教版必修2)直线、平面平行的判定及其性质配套练习(有答案)

§2.2直线、平面平行的判定及其性质2.2.1直线与平面平行的判定一、基础过关1．直线m∥平面α，直线n∥m，则() A．n∥αB．n与α相交C．n⊂αD．n∥α或n⊂α2．棱台的一条侧棱所在的直线与不含这条侧棱的侧面所在的平面的位置关系是() A．平行B．相交C．平行或相交D．不相交3．已知a，b是两条相交直线，a∥α，则b与α的位置关系是() A．b∥αB．b与α相交C．b⊂αD．b∥α或b与α相交4．一条直线l上有相异三个点A、B、C到平面α的距离相等，那么直线l与平面α的位置关系是() A．l∥αB．l⊥αC．l与α相交但不垂直D．l∥α或l⊂α5. 如图，在长方体ABCD－A1B1C1D1的面中：(1)与直线AB平行的平面是______；(2)与直线AA1平行的平面是______；(3)与直线AD平行的平面是______．6．已知不重合的直线a，b和平面α.①若a∥α，b⊂α，则a∥b；②若a∥α，b∥α，则a∥b；③若a∥b，b⊂α，则a∥α；④若a∥b，a∥α，则b∥α或b⊂α，其中正确命题的个数是________．7．在正方体ABCD－A1B1C1D1中，E为DD1的中点，求证：BD1∥平面AEC.8. 如图，四棱锥A—DBCE中，O为底面正方形DBCE对角线的交点，F为AE的中点．求证：AB∥平面DCF.二、能力提升9．在空间四边形ABCD中，E、F分别是AB和BC上的点，若AE∶EB＝EF∶FB＝1∶3，则对角线AC和平面DEF的位置关系是()A．平行B．相交C．在内D．不能确定10．过直线l外两点，作与l平行的平面，则这样的平面() A．不存在B．只能作出一个C．能作出无数个D．以上都有可能11．过平行六面体ABCD－A1B1C1D1任意两条棱的中点作直线，其中与平面DBB1D1平行的直线共有________条．12．如图，在平行四边形ABCD中，E为线段AB的中点，将△ADE沿直线DE翻折成△A′DE，F为线段A′C的中点．求证：BF∥平面A′DE.三、探究与拓展13. 正方形ABCD与正方形ABEF所在平面相交于AB，在AE，BD上各有一点P，Q，且AP＝DQ.求证：PQ∥平面BCE.(用两种方法证明)答案1．D 2.B 3.D 4.D5．(1)平面A1C1和平面DC1(2)平面BC1和平面DC1(3)平面B1C和平面A1C1 6．17．证明如图，连接BD交AC于F，连接EF.因为F为正方形ABCD对角线的交点，所以F为AC、BD的中点．在三角形DD1B中，E、F分别为DD1、DB的中点，所以EF∥D1B.又EF⊂平面AEC，BD1⊄平面AEC，所以BD1∥平面AEC.8．证明连接OF，∵O为正方形DBCE对角线的交点，∴BO＝OE，又AF＝FE，∴AB∥OF，⎭⎬⎫AB⊄平面DCFOF⊂平面DCFAB∥OF⇒AB∥平面DCF.9．A10．D11．1212．证明取A′D的中点G，连接GF，GE，由条件易知FG∥CD，FG＝12CD，BE∥CD，BE＝12CD，所以FG∥BE，FG＝BE，故四边形BEGF为平行四边形，所以BF∥EG.因为EG⊂平面A′DE，BF⊄平面A′DE，所以BF∥平面A′DE.13．证明如图所示，连接AQ并延长交BC于K，连接EK.∵KB∥AD，∴DQBQ＝AQQK.∵AP＝DQ，AE＝BD，∴BQ＝PE.∴DQBQ＝APPE.∴AQQK＝APPE.∴PQ∥EK.又PQ⊄平面BCE，EK⊂平面BCE，∴PQ∥平面BCE.2.1.2 空间中直线与直线之间的位置关系一、基础过关1．分别在两个平面内的两条直线间的位置关系是( )A ．异面B ．平行C ．相交D ．以上都有可能2．若AB ∥A ′B ′，AC ∥A ′C ′，则有( )A ．∠BAC ＝∠B ′A ′C ′ B ．∠BAC ＋∠B ′A ′C ′＝180°C ．∠BAC ＝∠B ′A ′C ′或∠BAC ＋∠B ′A ′C ′＝180°D ．∠BAC ＞∠B ′A ′C ′3．空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是 ( )A ．空间四边形B ．矩形C ．菱形D ．正方形4．“a 、b 为异面直线”是指：①a ∩b ＝∅，且aD \∥b ；②a ⊂面α，b ⊂面β，且a ∩b ＝∅；③a ⊂面α，b ⊂面β，且α∩β＝∅；④a ⊂面α，b ⊄面α；⑤不存在面α，使a ⊂面α，b ⊂面α成立．上述结论中，正确的是( )A ．①④⑤B ．①③④C ．②④D ．①⑤5．如果两条直线a 和b 没有公共点，那么a 与b 的位置关系是________． 6．已知正方体ABCD —A ′B ′C ′D ′中： (1)BC ′与CD ′所成的角为________； (2)AD 与BC ′所成的角为________．7．如图所示，四边形ABEF 和ABCD 都是直角梯形，∠BAD ＝∠F AB＝90°，BC 綊12AD ，BE 綊12F A ，G 、H 分别为F A 、FD 的中点．(1)证明：四边形BCHG 是平行四边形； (2)C 、D 、F 、E 四点是否共面？为什么？8．如图，正方体ABCD －EFGH 中，O 为侧面ADHE 的中心，求：(1)BE 与CG 所成的角； (2)FO 与BD 所成的角．二、能力提升9.如图所示，已知三棱锥A －BCD 中，M 、N 分别为AB 、CD 的中点，则下列结论正确的是( )A ．MN ≥12(AC ＋BD )B ．MN ≤12(AC ＋BD )C ．MN ＝12(AC ＋BD )D ．MN <12(AC ＋BD )10．如果两条异面直线称为“一对”，那么在正方体的十二条棱中共有异面直线( )A ．12对B ．24对C ．36对D ．48对11．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：①AB ⊥EF ；②AB 与CM 所成的角为60°； ③EF 与MN 是异面直线； ④MN ∥CD .以上结论中正确的序号为________．12．已知A 是△BCD 平面外的一点，E ，F 分别是BC ，AD 的中点，(1)求证：直线EF 与BD 是异面直线；(2)若AC ⊥BD ，AC ＝BD ，求EF 与BD 所成的角．三、探究与拓展13．已知三棱锥A —BCD 中，AB ＝CD ，且直线AB 与CD 成60°角，点M 、N 分别是BC 、AD 的中点，求直线AB 和MN 所成的角．答案1．D 2．C 3．B 4．D 5.平行或异面 6．(1)60° (2)45°7．(1)证明由已知FG ＝GA ，FH ＝HD ，可得GH 綊12AD .又BC 綊12AD ，∴GH 綊BC ，∴四边形BCHG 为平行四边形．(2)解由BE 綊12AF ，G 为F A 中点知，BE 綊FG ，∴四边形BEFG 为平行四边形，∴EF ∥BG . 由(1)知BG 綊CH ，∴EF ∥CH ， ∴EF 与CH 共面．又D ∈FH ，∴C 、D 、F 、E 四点共面．8．解 (1)如图，∵CG ∥BF ，∴∠EBF (或其补角)为异面直线BE 与CG 所成的角，又△BEF 中，∠EBF ＝45°，所以BE 与CG 所成的角为45°.(2)连接FH ，BD ，FO ，∵HD 綊EA ，EA 綊FB ， ∴HD 綊FB ，∴四边形HFBD 为平行四边形， ∴HF ∥BD ，∴∠HFO (或其补角)为异面直线FO 与BD 所成的角．连接HA 、AF ，易得FH ＝HA ＝AF ， ∴△AFH 为等边三角形，又依题意知O 为AH 中点，∴∠HFO ＝30°，即FO 与BD 所成的角是30°.9．D 10．B 11．①③12．(1)证明假设EF 与BD 不是异面直线，则EF 与BD 共面，从而DF 与BE 共面，即AD 与BC 共面，所以A 、B 、C 、D 在同一平面内，这与A 是△BCD 平面外的一点相矛盾．故直线EF 与BD 是异面直线．(2)解取CD 的中点G ，连接EG 、FG ，则EG ∥BD ，所以相交直线EF 与EG 所成的角，即为异面直线EF 与BD 所成的角．在Rt △EGF 中，由EG ＝FG ＝12AC ，求得∠FEG ＝45°，即异面直线EF 与BD 所成的角为45°.13．解如图，取AC 的中点P .连接PM 、PN ，则PM ∥AB ，且PM ＝12AB ，PN ∥CD ，且PN ＝12CD ，所以∠MPN 为直线AB 与CD 所成的角(或所成角的补角)．则∠MPN ＝60°或∠MPN ＝120°，若∠MPN ＝60°，因为PM ∥AB ，所以∠PMN 是AB 与MN 所成的角(或所成角的补角)．又因AB ＝CD ，所以PM ＝PN ，则△PMN 是等边三角形，所以∠PMN ＝60°，即AB 与MN 所成的角为60°.若∠MPN ＝120°，则易知△PMN 是等腰三角形．所以∠PMN ＝30°，即AB 与MN 所成的角为30°.故直线AB 和MN 所成的角为60°或30°.2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系一、基础过关1．已知直线a∥平面α，直线b⊂α，则a与b的位置关系是() A．相交B．平行C．异面D．平行或异面2．直线l与平面α不平行，则() A．l与α相交B．l⊂αC．l与α相交或l⊂αD．以上结论都不对3．如果直线a∥平面α，那么直线a与平面α内的() A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线不相交4．如果平面α外有两点A、B，它们到平面α的距离都是a，则直线AB和平面α的位置关系一定是() A．平行B．相交C．平行或相交D．AB⊂α5．直线a⊂平面α，直线b⊄平面α，则a，b的位置关系是________．6．若a、b是两条异面直线，且a∥平面α，则b与α的位置关系是________．7．平面α内有无数条直线与平面β平行，那么α∥β是否正确？说明理由．8. 如图，直线a∥平面α，a⊂β，α∩β＝b，求证：a∥b.二、能力提升9．下列命题正确的是() A．若直线a在平面α外，则直线a∥αB．若直线a与平面α有公共点，则a与α相交C．若平面α内存在直线与平面β无交点，则α∥βD．若平面α内的任意直线与平面β均无交点，则α∥β10．教室内有一根直尺，无论怎样放置，在地面上总有这样的直线与直尺所在的直线() A．异面B．相交C．平行D．垂直11．若不在同一条直线上的三点A、B、C到平面α的距离相等，且A、B、CD/∈α，则面ABC 与面α的位置关系为________．12. 如图，平面α、β、γ满足α∥β，α∩γ＝a，β∩γ＝b，判断a与b、a与β的关系并证明你的结论．三、探究与拓展13．正方体ABCD—A1B1C1D1中，点Q是棱DD1上的动点，判断过A、Q、B1三点的截面图形的形状．答案1．D2．C3．D4．C5.平行、相交或异面6．b⊂α，b∥α或b与α相交7．解不正确．如图，设α∩β＝l，则在α内与l平行的直线可以有无数条，如a1，a2，…，a n，它们是一组平行线，这时a1，a2，…，a n与平面β平行，但此时α与β不平行，α∩β＝l.8．证明∵直线a∥平面α，∴直线a与平面α无公共点．∵α∩β＝b，∴b⊂α，b⊂β.∴直线a与b无公共点．∵a⊂β，∴a∥b.9．D10.D11.平行或相交12．解由α∩γ＝a知a⊂α且a⊂γ，由β∩γ＝b知b⊂β且b⊂γ，∵α∥β，a⊂α，b⊂β，∴a、b无公共点．又∵a⊂γ且b⊂γ，∴a∥b.∵α∥β，∴α与β无公共点，又a⊂α，∴a与β无公共点，∴a∥β.13．解由点Q在线段DD1上移动，当点Q与点D1重合时，截面图形为等边三角形AB1D1，如图(1)所示；当点Q与点D重合时，截面图形为矩形AB1C1D，如图(2)所示；图(1)图(2)当点Q不与点D，D1重合时，截面图形为等腰梯形AQRB1，如图(3)所示．图(3)2.2.2平面与平面平行的判定一、基础过关1．直线l∥平面α，直线m∥平面α，直线l与m相交于点P，且l与m确定的平面为β，则α与β的位置关系是() A．相交B．平行C．异面D．不确定2．平面α与平面β平行的条件可以是() A．α内的一条直线与β平行B．α内的两条直线与β平行C．α内的无数条直线与β平行D．α内的两条相交直线分别与β平行3．给出下列结论，正确的有()①平行于同一条直线的两个平面平行；②平行于同一平面的两个平面平行；③过平面外两点，不能作一个平面与已知平面平行；④若a，b为异面直线，则过a与b平行的平面只有一个．A．1个B．2个C．3个D．4个4．若正n边形的两条对角线分别与面α平行，则这个正n边形所在的平面一定平行于平面α，那么n的取值可能是() A．12 B．8 C．6 D．55．已知平面α、β和直线a、b、c，且a∥b∥c，a⊂α，b、c⊂β，则α与β的关系是________．6．有下列几个命题：①平面α内有无数个点到平面β的距离相等，则α∥β；②α∩γ＝a，α∩β＝b，且a∥b(α，β，γ分别表示平面，a，b表示直线)，则γ∥β；③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边，则α∥β；④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行，则α∥β.其中正确的有________．(填序号)7．如图所示，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF，求证：AE∥平面DCF.8. 在长方体ABCD—A1B1C1D1中，E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点．求证：平面A1EFD1∥平面BCF1E1.二、能力提升9．α、β是两个不重合的平面，a、b是两条不同的直线，在下列条件下，可判定α∥β的是() A．α，β都平行于直线a、bB．α内有三个不共线的点到β的距离相等C．a，b是α内两条直线，且a∥β，b∥βD．a、b是两条异面直线，且a∥α，b∥α，a∥β，b∥β10. 正方体EFGH—E1F1G1H1中，下列四对截面中，彼此平行的一对截面是()A．平面E1FG1与平面EGH1B．平面FHG1与平面F1H1GC．平面F1H1H与平面FHE1D．平面E1HG1与平面EH1G11. 如图所示，在正方体ABCD—A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足________时，有MN∥平面B1BDD1.12．已知在正方体ABCD—A1B1C1D1中，M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点．求证：(1)E、F、D、B四点共面；(2)平面AMN∥平面EFDB.三、探究与拓展13．如图所示，B为△ACD所在平面外一点，M、N、G分别为△ABC、△ABD、△BCD的重心．(1)求证：平面MNG∥平面ACD；(2)求S△MNG∶S△ADC.答案1．B 2．D 3．B 4.D 5．相交或平行 6．③7．证明由于AB ∥CD ，BE ∥CF ，故平面ABE ∥平面DCF .而直线AE 在平面ABE 内，根据线面平行的定义，知AE ∥平面DCF . 8．证明 ∵E 、E 1分别是AB 、A 1B 1的中点，∴A 1E 1∥BE 且A 1E 1＝BE .∴四边形A 1EBE 1为平行四边形． ∴A 1E ∥BE 1.∵A 1E ⊄平面BCF 1E 1， BE 1⊂平面BCF 1E 1. ∴A 1E ∥平面BCF 1E 1. 同理A 1D 1∥平面BCF 1E 1， A 1E ∩A 1D 1＝A 1，∴平面A 1EFD 1∥平面BCF 1E 1. 9．D 10.A 11.M ∈线段FH12．证明 (1)∵E 、F 分别是B 1C 1、C 1D 1的中点，∴EF 綊12B 1D 1，∵DD 1綊BB 1，∴四边形D 1B 1BD 是平行四边形， ∴D 1B 1∥BD . ∴EF ∥BD ，即EF 、BD 确定一个平面，故E 、F 、D 、B 四点共面． (2)∵M 、N 分别是A 1B 1、A 1D 1的中点， ∴MN ∥D 1B 1∥EF . 又MN ⊄平面EFDB ， EF ⊂平面EFDB . ∴MN ∥平面EFDB .连接NE ，则NE 綊A 1B 1綊AB . ∴四边形NEBA 是平行四边形．∴AN ∥BE .又AN ⊄平面EFDB ，BE ⊂平面EFDB .∴AN ∥平面EFDB . ∵AN 、MN 都在平面AMN 内，且AN ∩MN ＝N ， ∴平面AMN ∥平面EFDB .13．(1)证明连接BM 、BN 、BG 并延长交AC 、AD 、CD 分别于P 、F 、H .∵M 、N 、G 分别为△ABC 、△ABD 、△BCD 的重心，则有BM MP ＝BN NF ＝BGGH ＝2.连接PF 、FH 、PH ，有MN ∥PF . 又PF ⊂平面ACD ，MN ⊄平面ACD ， ∴MN ∥平面ACD .同理MG ∥平面ACD ，MG ∩MN ＝M ， ∴平面MNG ∥平面ACD .(2)解由(1)可知MG PH ＝BG BH ＝23，∴MG ＝23PH .又PH ＝12AD ，∴MG ＝13AD .同理NG ＝13AC ，MN ＝13CD .∴△MNG ∽△DCA ，其相似比为1∶3， ∴S △MNG ∶S △ADC ＝1∶9.2.2.3 直线与平面平行的性质一、基础过关1．a ，b 是两条异面直线，P 是空间一点，过P 作平面与a ，b 都平行，这样的平面( ) A ．只有一个 B ．至多有两个 C ．不一定有D ．有无数个2. 如图，在四面体ABCD 中，若截面PQMN 是正方形，则在下列命题中，错误的为( )A ．AC ⊥BDB ．AC ∥截面PQMNC ．AC ＝BDD ．异面直线PM 与BD 所成的角为45°3. 如图所示，长方体ABCD －A 1B 1C 1D 1中，E 、F 分别是棱AA 1和BB 1的中点，过EF 的平面EFGH 分别交BC 和AD 于G 、H ，则HG 与AB 的位置关系是( )A ．平行B ．相交C ．异面D ．平行和异面4．直线a ∥平面α，α内有n 条直线交于一点，则这n 条直线中与直线a 平行的直线( ) A ．至少有一条 B ．至多有一条 C ．有且只有一条D ．没有5．设m 、n 是平面α外的两条直线，给出三个论断：①m ∥n ；②m ∥α；③n ∥α.以其中的两个为条件，余下的一个为结论，构造三个命题，写出你认为正确的一个命题：______________.(用序号表示)6. 如图所示，ABCD —A 1B 1C 1D 1是棱长为a 的正方体，M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点，P 是上底面的棱AD 上的一点，AP ＝a3，过P ，M ，N 的平面交上底面于PQ ，Q 在CD 上，则PQ ＝________.7. ABCD 是平行四边形，点P 是平面ABCD 外一点，M 是PC 的中点，在DM 上取一点G ，过G 和AP 作平面交平面BDM 于GH ，求证：AP ∥GH .8. 如图所示，三棱锥A —BCD 被一平面所截，截面为平行四边形EFGH .求证：CD∥平面EFGH.二、能力提升9.如图所示，平面α∩β＝l1，α∩γ＝l2，β∩γ＝l3，l1∥l2，下列说法正确的是()A．l1平行于l3，且l2平行于l3B．l1平行于l3，且l2不平行于l3C．l1不平行于l3，且l2不平行于l3D．l1不平行于l3，但l2平行于l310．如图所示，已知A、B、C、D四点不共面，且AB∥平面α，CD∥α，AC∩α＝E，AD∩α＝F，BD∩α＝H，BC∩α＝G，则四边形EFHG的形状是________．10题图11题图11．如图所示，在空间四边形ABCD中，E、F、G、H分别是四边上的点，它们共面，并且AC∥平面EFGH，BD∥平面EFGH，AC＝m，BD＝n，当四边形EFGH是菱形时，AE∶EB ＝________.12. 如图所示，P为平行四边形ABCD所在平面外一点，M、N分别为AB、PC的中点，平面P AD∩平面PBC＝l.(1)求证：BC∥l；(2)MN与平面P AD是否平行？试证明你的结论．三、探究与拓展13．如图所示，三棱柱ABC—A1B1C1，D是BC上一点，且A1B∥平面AC1D，D1是B1C1的中点，求证：平面A1BD1∥平面AC1D.答案1．C 2．C 3．A 4．B5．①②⇒③(或①③⇒②) 6.223a7．证明如图所示，连接AC 交BD 于O ，连接MO ，∵ABCD 是平行四边形，ABCD 是平行四边形，点P 是平面ABCD 外一点，M 是PC 的中点，在DM 上取一点G ，过G 和AP 作平面交平面BDM 于GH ，求证：AP ∥GH .∴O 是AC 中点，又M 是PC 的中点， ∴AP ∥OM .根据直线和平面平行的判定定理，则有P A ∥平面BMD .∵平面P AHG ∩平面BMD ＝GH ，根据直线和平面平行的性质定理，则有AP ∥GH .8．证明 ∵四边形EFGH 为平行四边形， ∴EF ∥GH .又GH ⊂平面BCD ，EF ⊄平面BCD . ∴EF ∥平面BCD .而平面ACD ∩平面BCD ＝CD ，EF ⊂平面ACD ，∴EF ∥CD . 而EF ⊂平面EFGH ，CD ⊄平面EFGH ， ∴CD ∥平面EFGH . 9．A 10.平行四边形 11．m ∶n12．(1)证明因为BC ∥AD ，AD ⊂平面P AD ，BC ⊄平面P AD ，所以BC ∥平面P AD .又平面P AD ∩平面PBC ＝l ，BC ⊂平面PBC ，所以BC ∥l . (2)解 MN ∥平面P AD . 证明如下：如图所示，取PD 中点E . 连接EN 、AE .又∵N 为PC 中点，∴EN 綊12AB∴EN綊AM，∴四边形ENMA为平行四边形，∴AE∥MN.又∵AE⊂平面P AD，MN⊄平面P AD，∴MN∥平面P AD.13．证明连接A 1C交AC1于点E，∵四边形A1ACC1是平行四边形，∴E是A1C的中点，连接ED，∵A1B∥平面AC1D，平面A1BC∩平面AC1D＝ED，∴A1B∥ED，∵E是A1C的中点，∴D是BC的中点．又∵D1是B1C1的中点，∴BD1∥C1D，又∵C1D⊂平面AC1D，BD1⊄平面AC1D，∴BD1∥平面AC1D，又A1B∩BD1＝B，∴平面A1BD1∥平面AC1D.2.2.4 平面与平面平行的性质一、基础过关1．已知平面α∥平面β，过平面α内的一条直线a 的平面γ，与平面β相交，交线为直线b ，则a 、b 的位置关系是( ) A ．平行B ．相交C ．异面D ．不确定2．已知a 、b 表示直线，α、β表示平面，下列推理正确的是( )A ．α∩β＝a ，b ⊂α⇒a ∥bB ．α∩β＝a ，a ∥b ⇒b ∥α且b ∥βC ．a ∥β，b ∥β，a ⊂α，b ⊂α⇒α∥βD ．α∥β，α∩γ＝a ，β∩γ＝b ⇒a ∥b3. 如图所示，P 是三角形ABC 所在平面外一点，平面α∥平面ABC ，α分别交线段P A 、PB 、PC 于A ′、B ′、C ′，若P A ′∶AA ′＝2∶3，则S △A ′B ′C ′∶S △ABC 等于( )A ．2∶25B ．4∶25C ．2∶5D ．4∶54．α，β，γ为三个不重合的平面，a ，b ，c 为三条不同的直线，则有下列命题，不正确的是( )①⎭⎪⎬⎪⎫a ∥c b ∥c ⇒a ∥b; ② ⎭⎪⎬⎪⎫a ∥γb ∥γ⇒a ∥b ； ③⎭⎪⎬⎪⎫α∥c β∥c ⇒α∥β； ④ ⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β；⑤⎭⎪⎬⎪⎫α∥c a ∥c ⇒α∥a; ⑥⎭⎪⎬⎪⎫α∥γa ∥γ⇒a ∥α. A ．④⑥ B ．②③⑥ C ．②③⑤⑥ D ．②③5．分别在两个平行平面的两个三角形．(填“相似”“全等”) (1)若对应顶点的连线共点，那么这两个三角形具有______关系； (2)若对应顶点的连线互相平行，那么这两个三角形具有________关系．6．已知平面α∥β∥γ，两条直线l 、m 分别与平面α、β、γ相交于点A 、B 、C 与D 、E 、F .已知AB ＝6，DE DF ＝25，则AC ＝______.7.如图，在三棱柱ABC －A 1B 1C 1中，M 是A 1C 1的中点，平面AB 1M ∥平面BC 1N ，AC ∩平面BC 1N ＝N .求证：N 为AC 的中点．8. 如图所示，在底面是平行四边形的四棱锥P －ABCD 中，点E 在PD 上，且PE ∶ED ＝2∶1，在棱PC 上是否存在一点F ，使BF ∥平面AEC ？并证明你的结论．二、能力提升9．设α∥β，A ∈α，B ∈β，C 是AB 的中点，当A 、B 分别在平面α、β内运动时，得到无数个AB 的中点C ，那么所有的动点C( )A ．不共面B ．当且仅当A 、B 分别在两条直线上移动时才共面C ．当且仅当A 、B 分别在两条给定的异面直线上移动时才共面D ．不论A 、B 如何移动，都共面10．已知平面α∥平面β，P 是α，β外一点，过点P 的直线m 与α，β分别交于点A ，C ，过点P 的直线n 与α，β分别交于点B ，D ，且P A ＝6，AC ＝9，PD ＝8，则BD 的长为( )A ．16B ．24或245 C ．14 D ．2011．对于不重合的两个平面α与β，给定下列条件：①存在平面γ，使得α、β都垂直于γ；②存在平面γ，使α、β都平行于γ；③α内有不共线的三点到β的距离相等；④存在异面直线l ，m ，使得l ∥α，l ∥β，m ∥α，m ∥β.其中可以判断两个平面α与β平行的条件有________个．12. 如图所示，平面α∥平面β，△ABC 、△A ′B ′C ′分别在α、β内，线段AA ′、BB ′、CC ′共点于O ，O 在α、β之间，若AB ＝2，AC ＝1，∠BAC ＝90°，OA ∶OA ′＝3∶2. 求△A ′B ′C ′的面积．三、探究与拓展13．如图所示，在棱长为2的正方体ABCD－A1B1C1D1中，A1B1的中点是P，过点A1作与截面PBC1平行的截面，能否确定截面的形状？如果能，求出截面的面积．§2.3直线、平面垂直的判定及其性质2.3.1直线与平面垂直的判定一、基础过关1．已知直线a∥b，平面α∥β，a⊥α，则b与β的位置关系是() A．b⊥βB．b∥βC．b⊂βD．b⊂β或b∥β2．直线a⊥直线b，b⊥平面β，则a与β的关系是() A．a⊥βB．a∥βC．a⊂βD．a⊂β或a∥β3．空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是() A．垂直且相交B．相交但不一定垂直C．垂直但不相交D．不垂直也不相交4．如图所示，定点A和B都在平面α内，定点P∉α，PB⊥α，C是平面α内异于A和B的动点，且PC⊥AC，则△ABC为()A．锐角三角形B．直角三角形C．钝角三角形D．无法确定5. 在正方体ABCD－A 1B1C1D1中，(1)直线A1B与平面ABCD所成的角是________；(2)直线A1B与平面ABC1D1所成的角是________；(3)直线A1B与平面AB1C1D所成的角是______．6. 如图所示，在正方体ABCD－A1B1C1D1中，M、N分别是棱AA1和AB上的点，若∠B1MN是直角，则∠C1MN＝______.7．如图所示，在正方体ABCD—A1B1C1D1中，E、F分别是棱B1C1、B1B的中点．求证：CF⊥平面EAB.8. 如图所示，在四棱锥P—ABCD中，底面ABCD是矩形，侧棱P A垂直于底面，E、F分别是AB、PC的中点，P A＝AD.求证：(1)CD⊥PD；(2)EF⊥平面PCD.二、能力提升9. 如图所示，P A⊥平面ABC，△ABC中BC⊥AC，则图中直角三角形的个数为()A．4 B．3 C．2 D．110．已知矩形ABCD，AB＝1，BC＝2，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中() A．存在某个位置，使得直线AC与直线BD垂直B．存在某个位置，使得直线AB与直线CD垂直C．存在某个位置，使得直线AD与直线BC垂直D．对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直11．在直三棱柱ABC—A1B1C1中，BC＝CC1，当底面A1B1C1满足条件________时，有AB1⊥BC1(注：填上你认为正确的一种条件即可，不必考虑所有可能的情况)．12. 如图所示，在正方体ABCD－A1B1C1D1中，P为DD1的中点，O为ABCD的中心，求证：B1O⊥平面P AC.三、探究与拓展13．已知平面α外两点A、B到平面α的距离分别为1和2，A、B两点在α内的射影之间距离为3，求直线AB和平面α所成的角．答案1．A 2.D 3．C 4．B 5．(1)45° (2)30° (3)90° 6．90°7．证明在平面B 1BCC 1中， ∵E 、F 分别是B 1C 1、B 1B 的中点， ∴△BB 1E ≌△CBF ， ∴∠B 1BE ＝∠BCF ，∴∠BCF ＋∠EBC ＝90°，∴CF ⊥BE ，又AB ⊥平面B 1BCC 1，CF ⊂平面B 1BCC 1， ∴AB ⊥CF ，又AB ∩BE ＝B ， ∴CF ⊥平面EAB .8．证明 (1)∵P A ⊥底面ABCD ， ∴CD ⊥P A .又矩形ABCD 中，CD ⊥AD ，且AD ∩P A ＝A ，∴CD ⊥平面P AD ，∴CD ⊥PD .(2)取PD 的中点G ，连接AG ，FG .又∵G 、F 分别是PD 、PC 的中点，∴GF 綊12CD ，∴GF 綊AE ，∴四边形AEFG 是平行四边形，∴AG ∥EF . ∵P A ＝AD ，G 是PD 的中点， ∴AG ⊥PD ，∴EF ⊥PD ， ∵CD ⊥平面P AD ，AG ⊂平面P AD . ∴CD ⊥AG .∴EF ⊥CD .∵PD ∩CD ＝D ，∴EF ⊥平面PCD . 9．A 10．B 11．∠A 1C 1B 1＝90°12．证明连接AB 1，CB 1，设AB ＝1.∴AB 1＝CB 1＝2，∵AO ＝CO ，∴B 1O ⊥AC .连接PB1.∵OB21＝OB2＋BB21＝32，PB21＝PD21＋B1D21＝94，OP2＝PD2＋DO2＝34，∴OB21＋OP2＝PB21.∴B1O⊥PO，又∵PO∩AC＝O，∴B1O⊥平面P AC.13．解(1)如图①，当A、B位于平面α同侧时，由点A、B分别向平面α作垂线，垂足分别为A1、B1，则AA1＝1，BB1＝2，B1A1＝ 3.过点A作AH⊥BB1于H，则AB和α所成角即为∠HAB.而tan∠BAH＝2－13＝33.∴∠BAH＝30°.(2)如图②，当A、B位于平面α异侧时，经A、B分别作AA1⊥α于A1，BB1⊥α于B1，AB∩α＝C，则A1B1为AB在平面α上的射影，∠BCB1或∠ACA1为AB与平面α所成的角．∵△BCB1∽△ACA1，∴BB1AA1＝B1CCA1＝2，∴B1C＝2CA1，而B1C＋CA1＝3，∴B1C＝233.∴tan∠BCB1＝BB1B1C＝2233＝3，∴∠BCB1＝60°.综合(1)、(2)可知：AB与平面α所成的角为30°或60°.2.3.2平面与平面垂直的判定一、基础过关1．过两点与一个已知平面垂直的平面() A．有且只有一个B．有无数个C．一个或无数个D．可能不存在2．不能肯定两个平面一定垂直的情况是() A．两个平面相交，所成二面角是直二面角B．一个平面经过另一个平面的一条垂线C．一个平面垂直于另一个平面内的一条直线D．平面α内的直线a与平面β内的直线b是垂直的3．设有直线m、n和平面α、β，则下列结论中正确的是()①若m∥n，n⊥β，m⊂α，则α⊥β；②若m⊥n，α∩β＝m，n⊂α，则α⊥β；③若m⊥α，n⊥β，m⊥n，则α⊥β.A．①②B．①③C．②③D．①②③4．设l是直线，α，β是两个不同的平面，下列结论中正确的是() A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l⊥βD．若α⊥β，l∥α，则l⊥β5．过正方形ABCD的顶点A作线段AP⊥平面ABCD，且AP＝AB，则平面ABP与平面CDP 所成的二面角的度数是________．6．如图所示，已知P A⊥矩形ABCD所在的平面，图中互相垂直的平面有________对．7．在如图所示的几何体中，四边形ABCD是正方形，MA⊥平面ABCD，PD∥MA，E、G、F分别为MB、PB、PC的中点，且AD＝PD＝2MA.求证：平面EFG⊥平面PDC.8. 如图所示，四棱锥P—ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，P A⊥底面ABCD，P A＝ 3.(1)证明：平面PBE⊥平面P AB；(2)求二面角A—BE—P的大小．二、能力提升9．在边长为1的菱形ABCD 中，∠ABC ＝60°，把菱形沿对角线AC 折起，使折起后BD ＝32，则二面角B －AC －D 的余弦值为( )A.13B.12C.223D.32 10．在正四面体P －ABC 中，D 、E 、F 分别是AB 、BC 、CA 的中点，下面四个结论中不成立的是( )A ．BC ∥面PDFB ．DF ⊥面P AEC ．面PDF ⊥面ABCD ．面P AE ⊥面ABC11．如图，在直三棱柱ABC —A 1B 1C 1中，E 、F 分别是A 1B 、A 1C 的中点，点D 在B 1C 1上，A 1D ⊥B 1C . 求证：(1)EF ∥平面ABC ； (2)平面A 1FD ⊥平面BB 1C 1C .12．如图，在三棱锥P —ABC 中，P A ⊥底面ABC ，P A ＝AB ，∠ABC ＝60°，∠BCA ＝90°，点D 、E 分别在棱PB 、PC 上，且DE ∥BC .(1)求证：BC ⊥平面P AC .(2)是否存在点E 使得二面角A —DE —P 为直二面角？并说明理由．三、探究与拓展13．如图所示，三棱锥P —ABC 中，D 是AC 的中点，P A ＝PB ＝PC ＝5，AC ＝22，AB ＝2，BC ＝ 6.(1)求证：PD ⊥平面ABC ； (2)求二面角P —AB —C 的正切值．答案1．C 2.D 3.B 4.B5．45°6．57．证明因为MA⊥平面ABCD，PD∥MA，所以PD⊥平面ABCD.又BC⊂平面ABCD，所以PD⊥BC.因为四边形ABCD为正方形，所以BC⊥DC.又PD∩DC＝D，所以BC⊥平面PDC.在△PBC中，因为G、F分别为PB、PC的中点，所以GF∥BC，所以GF⊥平面PDC.又GF⊂平面EFG，所以平面EFG⊥平面PDC.8．(1)证明如图所示，连接BD，由ABCD是菱形且∠BCD＝60°知，△BCD是等边三角形．因为E是CD的中点，所以BE⊥CD.又AB∥CD，所以BE⊥AB.又因为P A⊥平面ABCD，BE⊂平面ABCD，所以P A⊥BE.而P A∩AB＝A，因此BE⊥平面P AB.又BE⊂平面PBE，所以平面PBE⊥平面P AB.(2)解由(1)知，BE⊥平面P AB，PB⊂平面P AB，所以PB⊥BE.又AB⊥BE，所以∠PBA是二面角A—BE—P的平面角．＝3，则∠PBA＝60°.在Rt△P AB中，tan∠PBA＝P AAB故二面角A—BE—P的大小是60°.9．B 10．C11．证明(1)由E、F分别是A1B、A1C的中点知EF∥BC.因为EF⊄平面ABC，BC⊂平面ABC.所以EF∥平面ABC.(2)由三棱柱ABC—A1B1C1为直三棱柱知CC1⊥平面A1B1C1.又A1D⊂平面A1B1C1，故CC1⊥A1D.又因为A1D⊥B1C，CC1∩B1C＝C，故A1D⊥平面BB1C1C，又A1D⊂平面A1FD，所以平面A1FD⊥平面BB1C1C.12．(1)证明∵P A⊥底面ABC，∴P A⊥BC.又∠BCA＝90°，∴AC⊥BC.又∵AC∩P A＝A，∴BC⊥平面P AC.(2)解∵DE∥BC，又由(1)知，BC⊥平面P AC，∴DE⊥平面P AC.又∵AE⊂平面P AC，PE⊂平面P AC，∴DE⊥AE，DE⊥PE.∴∠AEP 为二面角A —DE —P 的平面角． ∵P A ⊥底面ABC ，∴P A ⊥AC ， ∴∠P AC ＝90°.∴在棱PC 上存在一点E ，使得AE ⊥PC .这时∠AEP ＝90°，故存在点E ，使得二面角A —DE —P 为直二面角． 13．(1)证明连接BD ，∵D 是AC 的中点，P A ＝PC ＝5， ∴PD ⊥AC .∵AC ＝22，AB ＝2，BC ＝6， ∴AB 2＋BC 2＝AC 2.∴∠ABC ＝90°，即AB ⊥BC .∴BD ＝12AC ＝2＝AD .∵PD 2＝P A 2－AD 2＝3，PB ＝5， ∴PD 2＋BD 2＝PB 2.∴PD ⊥BD . ∵AC ∩BD ＝D ，∴PD ⊥平面ABC .(2)解取AB 的中点E ，连接DE 、PE ，由E 为AB 的中点知DE ∥BC ， ∵AB ⊥BC ，∴AB ⊥DE . ∵PD ⊥平面ABC ，∴PD ⊥AB .又AB ⊥DE ，DE ∩PD ＝D ，∴AB ⊥平面PDE ，∴PE ⊥AB . ∴∠PED 是二面角P —AB —C 的平面角．在△PED 中，DE ＝12BC ＝62，PD ＝3，∠PDE ＝90°，∴tan ∠PED ＝PDDE ＝ 2.∴二面角P —AB —C 的正切值为 2.2.3.3 直线与平面垂直的性质 2.3.4 平面与平面垂直的性质一、基础过关1．已知两个平面互相垂直，那么下列说法中正确的个数是( )①一个平面内的直线必垂直于另一个平面内的无数条直线；②一个平面内垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线； ③过一个平面内一点垂直于另一个平面的直线，垂足必落在交线上； ④过一个平面内的任意一点作交线的垂线，则此直线必垂直于另一个平面． A ．4B ．3C ．2D ．1 2．在圆柱的一个底面上任取一点(该点不在底面圆周上)，过该点作另一底面的垂线，则这条垂线与圆柱的母线所在直线的位置关系是( ) A ．相交B ．平行C ．异面D ．相交或平行3．若m 、n 表示直线，α表示平面，则下列命题中，正确命题的个数为( )①⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α； ② ⎭⎪⎬⎪⎫m ⊥αn ⊥α⇒m ∥n ； ③⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n; ④⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥α. A ．1 B ．2C ．3D ．4 4．在△ABC 所在的平面α外有一点P ，且P A ＝PB ＝PC ，则P 在α内的射影是△ABC 的( )A ．垂心B ．内心C ．外心D ．重心5. 如图所示，AF ⊥平面ABCD ，DE ⊥平面ABCD ，且AF ＝DE ，AD ＝6，则EF ＝________.6．若α⊥β，α∩β＝AB ，a ∥α，a ⊥AB ，则a 与β的关系为________． 7. 如图，在三棱锥P －ABC 中，P A ⊥平面ABC ，平面P AB ⊥平面PBC .求证：BC ⊥AB .8. 如图所示，在正方体ABCD —A 1B 1C 1D 1中，M 是AB 上一点，N 是A 1C 的中点，MN ⊥平面A 1DC . 求证：(1)MN ∥AD 1； (2)M 是AB 的中点．二、能力提升9. 如图所示，平面α⊥平面β，A ∈α，B ∈β，AB 与两平面α、β所成的角分别为π4和π6.过A 、B 分别作两平面交线的垂线，垂足分别为A ′、B ′，则AB ∶A ′B ′等于( )A ．2∶1B ．3∶1C ．3∶2D ．4∶310．设α－l －β是直二面角，直线a ⊂α，直线b ⊂β，a ，b 与l 都不垂直，那么( )A ．a 与b 可能垂直，但不可能平行B ．a 与b 可能垂直，也可能平行C ．a 与b 不可能垂直，但可能平行D ．a 与b 不可能垂直，也不可能平行11．直线a 和b 在正方体ABCD －A 1B 1C 1D 1的两个不同平面内，使a ∥b 成立的条件是________．(只填序号)①a 和b 垂直于正方体的同一个面； ②a 和b 在正方体两个相对的面内，且共面； ③a 和b 平行于同一条棱；④a 和b 在正方体的两个面内，且与正方体的同一条棱垂直． 12．如图所示，在多面体P —ABCD 中，平面P AD ⊥平面ABCD ，AB ∥DC ，△P AD 是等边三角形，已知BD ＝2AD ＝8，AB ＝2DC ＝4 5. (1)设M 是PC 上的一点，求证：平面MBD ⊥平面P AD ； (2)求四棱锥P —ABCD 的体积．三、探究与拓展13．如图，直三棱柱ABC －A 1B 1C 1中，AC ＝BC ＝12AA 1，D 是棱AA 1的中点，DC 1⊥BD . (1)证明：DC 1⊥BC ；(2)求二面角A 1－BD －C 1的大小．答案1．B 2.B 3．C 4．C 5．6 6．a ⊥β7．证明在平面P AB 内，作AD ⊥PB 于D . ∵平面P AB ⊥平面PBC ，且平面P AB ∩平面PBC ＝PB . ∴AD ⊥平面PBC . 又BC ⊂平面PBC ， ∴AD ⊥BC .又∵P A ⊥平面ABC ， BC ⊂平面ABC ，∴P A ⊥BC ，∴BC ⊥平面P AB . 又AB ⊂平面P AB ， ∴BC ⊥AB .8．证明 (1)∵ADD 1A 1为正方形， ∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1， ∴CD ⊥AD 1. ∵A 1D ∩CD ＝D ， ∴AD 1⊥平面A 1DC . 又∵MN ⊥平面A 1DC ， ∴MN ∥AD 1.(2)连接ON ，在△A 1DC 中， A 1O ＝OD ，A 1N ＝NC .∴ON 綊12CD 綊12AB ，∴ON ∥AM . 又∵MN ∥OA ，∴四边形AMNO 为平行四边形， ∴ON ＝AM . ∵ON ＝12AB ，∴AM ＝12AB ，∴M 是AB 的中点． 9．A 10．C 11．①②③12．(1)证明在△ABD 中，∵AD ＝4，BD ＝8，AB ＝45， ∴AD 2＋BD 2＝AB 2.∴AD ⊥BD .又∵面P AD ⊥面ABCD ，面P AD ∩面ABCD ＝AD ，BD ⊂面ABCD ，∴BD ⊥面P AD ，又BD ⊂面BDM ， ∴面MBD ⊥面P AD . (2)解过P 作PO ⊥AD ， ∵面P AD ⊥面ABCD ， ∴PO ⊥面ABCD ，即PO 为四棱锥P —ABCD 的高．又△P AD 是边长为4的等边三角形， ∴PO ＝2 3.在底面四边形ABCD 中，AB ∥DC ，AB ＝2DC ，∴四边形ABCD 为梯形．在Rt △ADB 中，斜边AB 边上的高为4×845＝855，此即为梯形的高． ∴S 四边形ABCD ＝25＋452×855＝24. ∴V P —ABCD ＝13×24×23＝16 3.13．(1)证明由题设知，三棱柱的侧面为矩形．由于D 为AA 1的中点，故DC ＝DC 1.又AC ＝12AA 1，可得DC 21＋DC 2＝CC 21，所以DC 1⊥DC .而DC 1⊥BD ，CD ∩BD ＝D ，所以DC 1⊥平面BCD .因为BC ⊂平面BCD ，所以DC 1⊥BC .(2)解 DC 1⊥BC ，CC 1⊥BC ⇒BC ⊥平面ACC 1A 1⇒BC ⊥AC ，取A 1B 1的中点O ，过点O 作OH ⊥BD 于点H ，连接C 1O ，C 1H ，A 1C 1＝B 1C 1⇒C 1O ⊥A 1B 1，面A 1B 1C 1⊥面A 1BD ⇒C 1O ⊥面A 1BD ，又∵DB ⊂面A 1DB ，∴C 1O ⊥BD ，又∵OH ⊥BD ，∴BD ⊥面C 1OH ，C 1H ⊂面C 1OH ，∴BD ⊥C 1H ，得点H 与点D 重合，且∠C 1DO 是二面角A 1－BD －C 的平面角，设AC ＝a ，则C 1O ＝22a ，C 1D ＝2a ＝2C 1O ⇒∠C 1DO ＝30°，故二面角A 1－BD －C 1的大小为30°.章末检测一、选择题1．下列推理错误的是() A．A∈l，A∈α，B∈l，B∈α⇒l⊂αB．A∈α，A∈β，B∈α，B∈β⇒α∩β＝ABC．l⊄α，A∈l⇒A∉αD．A∈l，l⊂α⇒A∈α2．长方体ABCD－A1B1C1D1中，异面直线AB，A1D1所成的角等于() A．30°B．45°C．60°D．90°3．下列命题正确的是() A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行4．在空间四边形ABCD的边AB，BC，CD，DA上分别取E、F、G、H四点，如果EF，GH交于一点P，则() A．P一定在直线BD上B．P一定在直线AC上C．P一定在直线AC或BD上D．P既不在直线AC上，也不在直线BD上5．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是() A．①和②B．②和③C．③和④D．②和④6．已知平面α⊥平面β，α∩β＝l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是() A．AB∥m B．AC⊥m C．AB∥βD．AC⊥β7．如图(1)所示，在正方形SG1G2G3中，E，F分别是G1G2及G2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G，如图(2)所示，那么，在四面体S－EFG中必有()。

高一数学必修2第二单元知识点：直线、平面平行的判定及其性质

高一数学必修2第二单元知识点：直线、平面平行的判定及其性质(实用版)编制人：__审核人：__审批人：__编制单位：__编制时间：__年__月__日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的实用资料，如工作总结、述职报告、心得体会、工作计划、演讲稿、教案大全、作文大全、合同范文、活动方案、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of practical materials for everyone, such as work summaries, job reports, insights, work plans, speeches, lesson plans, essays, contract samples, activity plans, and other materials. If you want to learn about different data formats and writing methods, please pay attention!高一数学必修2第二单元知识点：直线、平面平行的判定及其性质数学在科学发展和现代生活生产中的应用非常广泛，本店铺准备了高一数学必修2第二单元知识点，希望你喜欢。

人教新课标版数学高一人教A必修2学案直线与平面平行的判定

高中数学2.2.1 直线与平面平行的判定【学习目标】1、探究直线与平面平行的性质定理；2、体会直线与平面平行的性质定理的应用．【探索新知】1、空间中直线与平面的位置关系有_____________，_____________，______________。

2、线面平行的判定定理：（1）文字叙述：平面____的一条直线与此平面______的______条直线平行，则该直线与此平面平行。

（2（3）语言表示： ________________________________ α//a ________________【基础自测】1．已知两条相交直线a 、ｂ，a ∥平面α，则ｂ与平面α的位置关系 ( ) A ｂ∥α B ｂ与α相交 C ｂ⊂α D ｂ∥α或ｂ与α相交 2．不同直线,m n 和不同平面,αβ，给出下列命题： ( )① ////m m αββα⎫⇒⎬⊂⎭ ② //////m n n m ββ⎫⇒⎬⎭③,m m n n αβ⊂⎫⇒⎬⊂⎭异面其中假命题有A 0个B 1个C 2个D 3个3．若将直线、平面都看成点的集合，则直线l ∥平面α可表示为 ( ) A l ∉α B l ⊂α C l ≠α D l ∩α＝∅4．平行于同一个平面的两条直线的位置关系是 ( ) A 平行 B 相交 C 异面 D 平行或相交或异面5．已知直线l 1、l 2，平面α，l 1∥l 2，l 1∥α，则l 2与α的位置关系是 ( )a高中数学A l 2∥αB l 2⊂αC l 2∥α或l 2⊂αD l 2与α相交【合作学习】例1、如图，在四棱锥P —ABCD 中，底面ABCD 是矩形， E 为PC 的中点证明：PA //平面EDB【检测反馈】1、判断下列命题是否正确，若不正确，请用图形语言或模型加以表达（1）,//,//a a b a αα⊄若则（2）,,//a b a ααα⊄⊂若则（3）,//,//a b a αα⊂若b 则2、若AB 、BC 、CD 是不在同一平面内的三线段，则经过它们中点的平面和直线AC 的位置关系是（）A 、平行B 、相交C 、AC 在此平面内D 、平行或相交 3、如图，长方体ABCD —A 1B 1C 1D 1中， ①与AB 平行的平面是_______________②与AA 1平行的平面是________________ ③与AD 平行的平面是__________________4、如图，已知正三棱柱ABC —A 1B 1C 1中，D 为AC 的中点，求证：BD C AB 11//平面.5、如图，在四棱锥P ABCD -中，ABCD 是平行四边形，A1A 1B C1C 1D ABECD PNPAD BC1A 1B 1CM，N分别是AB，PC的中点．求证：MN//平面PAD．6、如图所示，正方体ABCD—A1B1C1D1中，侧面对角线AB1，BC1上分别有两点E，F，且B1E=C1F求证：EF∥平面ABCD.高中数学。