图论复习题
图论复习题

连通度: κ (G) = min{| V|| V是 G 的顶点割集} 。 完全图的连通度定义为κ (Kν) =ν − 1 。空图的连通度 定义为0。
v
2
1
证:(a)若 G 不连通,可分为两个顶点数分别为
v1,v2的互不连通子图 G1,G2。
易v知i 1,(i 1,2),v1 v2 v 于是
(G )
v1 2
v2 2
v1(v1 2
1)
v2 (v2 2
1)
(v
1)(v1 2
•确定下列给定图类的点连通度和边连通度.
(Pl ) (Pl ) 1 (Kn ) (Kn ) n 1
(Cn ) (Cn ) 2 (Kl,n ) (Kl,n ) l
• 由定义我们可以确定对于图的任一点和任意一条边, 有下列性质成立
定义为0。
注:(1)对平凡图或不连通图G, (G) 0 。 (2)若图G 是含有割边的连通图,则 (G) 1 。 (3)若 (G) k ,则称G 为k-边连通的。
(4)所有非平凡连通图都是1-边连通的。
(5)使得 E (G) 的边割集 E称为G 的最小边割
集。
(G) 1 (G x) (G) 1 (G xy) (G)
定理3.1 .
证明:先证 (G) (G) 。 若G 不连通,则 (G) (G) 0 。 若G 是完全图,则 (G) (G) 1 。
离散数学图论部分经典试题及答案
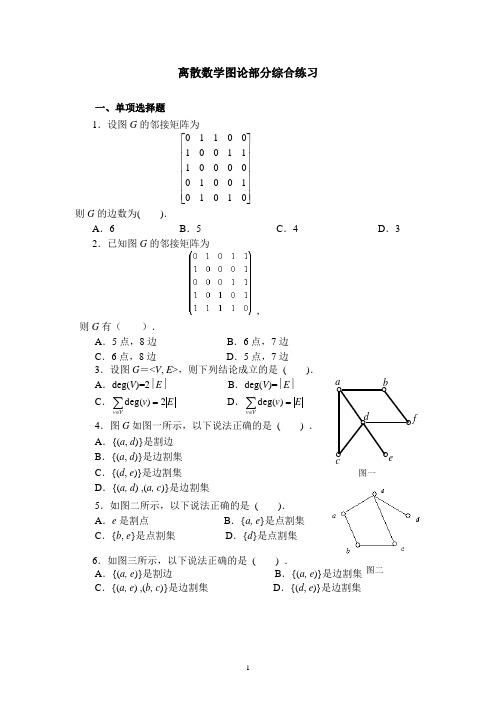
离散数学图论部分综合练习一、单项选择题1.设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010*******11100100110则G 的边数为( ).A .6B .5C .4D .32.已知图G 的邻接矩阵为, 则G 有( ).A .5点,8边B .6点,7边C .6点,8边D .5点,7边3.设图G =<V , E >,则下列结论成立的是 ( ).A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v Vv 2)deg(=∑∈ D .E v Vv =∑∈)deg(4.图G 如图一所示,以下说法正确的是 ( ) . A .{(a , d )}是割边 B .{(a , d )}是边割集 C .{(d , e )}是边割集 D .{(a, d ) ,(a, c )}是边割集5.如图二所示,以下说法正确的是 ( ). A .e 是割点 B .{a, e }是点割集 C .{b , e }是点割集 D .{d }是点割集6.如图三所示,以下说法正确的是 ( ) .A .{(a, e )}是割边B .{(a, e )}是边割集C .{(a, e ) ,(b, c )}是边割集D .{(d , e )}是边割集οο ο ο οca b edο f图一图二图三7.设有向图(a )、(b )、(c )与(d )如图四所示,则下列结论成立的是 ( ).图四A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的 应该填写:D8.设完全图K n 有n 个结点(n ≥2),m 条边,当( )时,K n 中存在欧拉回路.A .m 为奇数B .n 为偶数C .n 为奇数D .m 为偶数 9.设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ).A .e -v +2B .v +e -2C .e -v -2D .e +v +2 10.无向图G 存在欧拉通路,当且仅当( ). A .G 中所有结点的度数全为偶数 B .G 中至多有两个奇数度结点 C .G 连通且所有结点的度数全为偶数 D .G 连通且至多有两个奇数度结点11.设G 是有n 个结点,m 条边的连通图,必须删去G 的( )条边,才能确定G 的一棵生成树.A .1m n -+B .m n -C .1m n ++D .1n m -+ 12.无向简单图G 是棵树,当且仅当( ).A .G 连通且边数比结点数少1B .G 连通且结点数比边数少1C .G 的边数比结点数少1D .G 中没有回路.二、填空题1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 . 2.设给定图G (如图四所示),则图G 的点割ο οο οc a b f集是 .3.若图G=<V , E>中具有一条汉密尔顿回路, 则对于结点集V 的每个非空子集S ,在G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点 数|S|与W 满足的关系式为 .4.无向图G 存在欧拉回路,当且仅当G 连通 且 .5.设有向图D 为欧拉图,则图D 中每个结点的入度 . 应该填写:等于出度6.设完全图K n 有n 个结点(n 2),m 条边,当 时,K n 中存在欧拉回路.7.设G 是连通平面图,v , e , r 分别表示G 的结点数,边数和面数,则v ,e 和r 满足的关系式 .8.设连通平面图G 的结点数为5,边数为6,则面数为 . 9.结点数v 与边数e 满足 关系的无向连通图就是树.10.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去 条边后使之变成树.11.已知一棵无向树T 中有8个结点,4度,3度,2度的分支点各一个,T 的树叶数为 .12.设G =<V , E >是有6个结点,8条边的连通图,则从G 中删去 条边,可以确定图G 的一棵生成树.13.给定一个序列集合{000,001,01,10,0},若去掉其中的元素 ,则该序列集合构成前缀码.三、判断说明题1.如图六所示的图G 存在一条欧拉回路.2.给定两个图G 1,G 2(如图七所示):(1)试判断它们是否为欧拉图、汉密尔顿图?并说明理由. (2)若是欧拉图,请写出一条欧拉回路.v 123图六图七3.判别图G (如图八所示)是不是平面图, 并说明理由.4.设G 是一个有6个结点14条边的连 通图,则G 为平面图.四、计算题1.设图G =<V ,E >,其中V ={a 1, a 2, a 3, a 4, a 5},E ={<a 1, a 2>,<a 2, a 4>,<a 3, a 1>,<a 4, a 5>,<a 5, a 2>}(1)试给出G 的图形表示; (2)求G 的邻接矩阵;(3)判断图G 是强连通图、单侧连通图还是弱连通图?2.设图G =<V ,E >,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1, v 2),(v 1, v 3),(v 2, v 3),(v 2, v 4),(v 3, v 4),(v 3, v 5),(v 4, v 5) },试(1)画出G 的图形表示; (2)写出其邻接矩阵;(2)求出每个结点的度数; (4)画出图G 的补图的图形. 3.设G =<V ,E >,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1,v 3),(v 2,v 3),(v 2,v 4),(v 3,v 4),(v 3,v 5),(v 4,v 5) },试(1)给出G 的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出其补图的图形. 4.图G =<V , E >,其中V ={ a , b , c , d , e },E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (c , d ), (d , e ) },对应边的权值依次为2、1、2、3、6、1、4及5,试(1)画出G 的图形; (2)写出G 的邻接矩阵;(3)求出G 权最小的生成树及其权值.5.用Dijkstra 算法求右图中A 点到其它各点的最短路径。
图论部分复习题

图论部分一、选择题:1.欧拉回路是(B )A. 路径B. 简单回路C. 既是基本回路也是简单回路D.既非基本回路也非简单回路 2.哈密尔顿回路是(C )A. 路径B. 简单回路C. 既是基本回路也是简单回路D.既非基本回路也非简单回路 3.设G 是简单有向图,可达矩阵P(G)刻划下列关系中的是(C ) A 、点与边 B 、边与点 C 、点与点 D 、边与边4.下列哪一种图不一定是树(C )。
A.无简单回路的连通图B. 有n 个顶点n-1条边的连通图C. 每对顶点间都有通路的图D. 连通但删去一条边便不连通的图 5.下列哪个不是两个图同构的必要条件A. 结点数目相等B. 边数相等C. 度数相同的结点数目相同D. 两个图都是平面图 6.在有n 个结点的连通图中,其边数(B )A. 最多有n-1条B. 至少有n-1条C. 最多有n 条D. 至少有n 条 7.下列图为树的是(C )。
A 、>><><><=<},,,,,{},,,,{1d c b a a a d c b a G B 、>><><><=<},,,,,{},,,,{2d c d b b a d c b a G C 、>><><><=<},,,,,{},,,,{3a c d a b a d c b a GD 、>><><><=<},,,,,{},,,,{4d d c a b a d c b a G 二、填充题:1、n 阶无向完全图K n 的边数是(2)1(-n n ),每个结点的度数是(n-1)。
2、n 个结点的有向完全图边数是(n(n-1)),每个结点的度数是(2n-2)。
3、设有向图G = < V ,E >,},,,{4321v v v v V =的邻接矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=00010*******1010A , 则1v 的入度)(deg 1v -= 3 ,4v 的出度)(deg 4v +=1 ,从2v 到4v 的长度为2的路有 1 条。
图论复习题

图论复习题(二)图论复习题一、选择题1.设图G =<V , E >,v ∈V ,则下列结论成立的是 ( C ) . A .deg(v )=2∣E ∣ B . deg(v )=∣E ∣ C .E v Vv 2)deg(=∑∈ [PPT 23] D .Ev Vv =∑∈)deg(定理1 图G=(V ,E )中,所有点的次之和为边数的两倍 2.设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100100110则G 的边数为( B ).A .6B .5C .4D .33、 设完全图K n 有n 个结点(n ≥2),m 条边,当( C )时,K n 中存在欧拉回路.A .m 为奇数B .n 为偶数C .n 为奇数D .m 为偶数解释:K n 每个结点的度都为n -1,所以若存在欧拉回路则n -1必为偶数。
n 必为奇数。
4.欧拉回路是( B )A. 路径B. 简单回路[PPT 40]C. 既是基本回路也是简单回路D.既非基本回路也非简单回路5.哈密尔顿回路是( C )A. 路径B. 简单回路C. 既是基本回路也是简单回路D.既非基本回路也非简单回路[PPT 40]:哈密尔顿回路要求走遍所有的点,即是基本回路的点不重复,也可以是简单回路的边不重复。
6.设G 是简单有向图,可达矩阵P(G)刻划下列关系中的是( C ) A 、点与边 B 、边与点 C 、点与点 D 、边与边7.下列哪一种图不一定是树(C )。
A.无简单回路的连通图B. 有n 个顶点n-1条边的连通图C. 每对顶点间都有通路的图D. 连通但删去一条边便不连通的图8.在有n 个结点的连通图中,其边数(B )A.最多有n-1条B.至少有n-1条C.最多有n 条D.至少有n 条9.下列图为树的是(C )。
A 、>><><><=<},,,,,{},,,,{1d c b a a a d c b a GB 、>><><><=<},,,,,{},,,,{2d c d b b a d c b a GC 、>><><><=<},,,,,{},,,,{3a c d a b a d c b a GD 、>><><><=<},,,,,{},,,,{4d d c a b a d c b a G 10、下面的图7-22是(C )。
图论测试题及答案

图论测试题及答案一、选择题1. 在图论中,如果一个图的每个顶点的度数都是偶数,那么这个图一定存在欧拉路径吗?A. 是的B. 不一定C. 没有欧拉路径D. 无法确定答案:B2. 图论中的哈密顿路径是指什么?A. 经过图中所有顶点的路径B. 经过图中所有顶点的回路C. 经过图中某些顶点的路径D. 经过图中某些顶点的回路答案:A3. 如果一个图是完全图,那么它的边数是多少?A. 顶点数的一半B. 顶点数的平方C. 顶点数的两倍D. 顶点数减一答案:B二、填空题4. 在无向图中,如果存在一条路径,使得每个顶点只被经过一次,并且起点和终点相同,这样的路径被称为________。
答案:欧拉回路5. 图论中的二分图是指图中的顶点可以被分成两个不相交的集合,使得同一个集合内的顶点之间没有边,而不同集合之间的顶点之间有边,这种图也被称为________。
答案:二部图三、简答题6. 请简述图论中的最短路径问题,并给出解决该问题的一种算法。
答案:最短路径问题是在图中找到两个顶点之间的最短路径的问题。
解决该问题的一种算法是迪杰斯特拉算法(Dijkstra's algorithm),该算法通过维护一个顶点集合来记录已经找到最短路径的顶点,并迭代更新距离,直到找到从起点到所有顶点的最短路径。
7. 描述图论中的图着色问题,并说明其在实际生活中的应用。
答案:图着色问题是将图的顶点着色,使得任何两个相邻的顶点颜色不同。
在实际生活中,图着色问题可以应用于时间表的安排、频率分配、电路设计等领域,其中每个顶点代表一个任务或频道,而颜色则代表不同的时间段或频率。
结束语:以上是图论测试题及答案,希望能够帮助大家更好地理解和掌握图论的基本概念和算法。
图论复习题

图论及网络总复习题一、选择题1、设G是由5个顶点构成的完全图,则从G中删去()边可以得到树。
A.6 B.5 C.8 D.42、下面哪几种图不一定是树()。
A.无回路的连通图B.有n个结点,n-1条边的连通图C.对每对结点间都有通路的图D.连通但删去任意一条边则不连通的图。
3、5阶无向完全图的边数为()。
A.5 B.10 C.15 D.204、把平面分成x个区域,每两个区域都相邻,问x最大为()A.6 B.4 C.5 D.35、设图G有n个结点,m条边,且G中每个结点的度数不是k,就是k+1,则G中度数为k的节点数是()A.n/2 B.n(n+1) C.nk-2m D.n(k+1)-2m 6、图G1和G2的结点和边分别存在一一对应关系是G1和G2同构的()。
A.充分条件B.必要条件C.充分必要条件D.既不充分也不必要条件7、设G=<V,E>为有向图,V={a,b,c,d,e,f},E={<a,b>,<b,c>,<a,d>,<d,e>,<f,e>}是()。
A.强连通图B.单向连通图C.弱连通图D.不连通图8、无向图G中的边e是G的割边(桥)的充分必要条件是()。
A.e是重边B.e不是重边C.e不包含在G的任一简单回路中D.e不包含在G的某一简单回路中9、在有n个结点的连通图中,其边数()A.最多有n-1条B.至少有n-1条C.最多有n条D.至少有n条10.设无向简单图的顶点个数为n,则该图最多有()条边。
A.n-1 B.n(n-1)/2 C. n(n+1)/2 D.n211.n个结点的完全有向图含有边的数目()。
A.n*n B.n(n+1) C.n/2 D.n*(n-l)12.在一个无向图中,所有顶点的度数之和等于所有边数()倍。
A.1/2 B.2 C.1 D.413.连通图G是一棵树,当且仅当G中()A.有些边不是割边B.所有边都是割边C.无割边集D.每条边都不是割边14.4个顶点的完全图G,其生成树个数是()。
图论试题及答案解析图片

图论试题及答案解析图片一、选择题1. 图论中,图的基本元素是什么?A. 点和线B. 点和面C. 线和面D. 点和边答案:A2. 在无向图中,如果两个顶点之间存在一条边,则称这两个顶点是:A. 相邻的B. 相连的C. 相等的D. 相异的答案:A3. 在有向图中,如果从顶点A到顶点B有一条有向边,则称顶点A是顶点B的:A. 父顶点B. 子顶点C. 邻接顶点D. 非邻接顶点答案:B4. 一个图的度是指:A. 图中顶点的总数B. 图中边的总数C. 一个顶点的边数D. 图的连通性答案:C5. 一个图是连通的,当且仅当:A. 图中任意两个顶点都是相邻的B. 图中任意两个顶点都可以通过边相连C. 图中任意两个顶点都可以通过路径相连D. 图中任意两个顶点都可以通过子顶点相连答案:C二、填空题1. 在图论中,一个顶点的度数是该顶点的________。
答案:边数2. 如果一个图的任意两个顶点都可以通过边相连,则称该图为________。
答案:完全图3. 一个图中,如果存在一个顶点到其他所有顶点都有边相连,则称该顶点为________。
答案:中心顶点4. 图论中,最短路径问题是指在图中找到两个顶点之间的________。
答案:最短路径5. 如果一个图的任意两个顶点都可以通过有向路径相连,则称该图为________。
答案:强连通图三、简答题1. 请简述图论中的欧拉路径和哈密顿路径的定义。
答案:欧拉路径是指在图中经过每条边恰好一次的路径,而哈密顿路径是指在图中经过每个顶点恰好一次的路径。
2. 什么是图的着色问题?答案:图的着色问题是指将图中的顶点用不同的颜色进行标记,使得相邻的两个顶点颜色不同。
四、计算题1. 给定一个无向图G,顶点集为{A, B, C, D, E},边集为{AB, BC, CD, DE, EA},请画出该图,并计算其最小生成树的权重。
答案:首先画出图G的示意图,然后使用克鲁斯卡尔算法或普里姆算法计算最小生成树的权重。
图论期末复习题

17.任何简单平面图,均有. G 3
二、解答题
1.同构的判定及理由
3.左图称作什么图?两图是否同 构?为什么?
x
y
z
x
c
a
a
b
c
z
y b
2、给定图 :
(1)给出图 的一个生成树 。 (2)给出图 的顶点的最大度数 。
(3)给出图 的最长链。 (4)给出图 的一个边数最多的割集。
d
f
a
e1 b
在或不存在〕完美匹配.
35.在计算平面图面的次数之和时,每条边边计算了______ 次.
36.一个图是平面图当且仅当它既没有收缩到K5的子图, 也没有收缩到 的子图.
37.如果一个平面图有一个面的次数为4,那么该图______ 〔填是或不是〕极大平面图.
三、判断题
1.假设途径中的所有点互不相同,那么称此途径为一 条链.
31.设M1和M2是图G的两个不同匹配, 由M1 M2导出的G的边导出子图记作H, 那么H的任意连通分支是以下情况之一: (1)边在M1和M2中交错出现的偶圈;(2)边 在M1和M2中交错出现的 .
32.二部图G中假设满足V1= V2,那么G必有完美匹配. 33. (G)=2 G是 . 34.假设最大匹配的边数为p(G)/2,那么说明该图___〔填存
点连通度、边连通度与最小顶点的度数。
四、应用题
1. (蚂蚁比赛问题)甲、乙两只蚂蚁分别位于如以下图 中的顶点A,B处,并设图中的边长度是相等的。甲、 乙进行比赛:从它们所在的顶点出发,走过图中的所 有边最后到达顶点C处。如果它们的速度相同,问谁 先到达目的地?
甲A
乙
C
B
2.某地要兴建5个工厂,拟修筑道路连接这5 处。经勘测其道路可依如以下图无向边铺设。 为使这5处都有道路相通,问至少要铺几条路?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1设图G= <V, E >, v V,则下列结论成立的是(C ). A . deg(v )=2 E B . deg(v )二 EC.deg(v) 2 E [PPT 23]D.deg(v) Ev Vv V定理1 图G=(V, E )中,所有点的次之和为边数的两倍 2. 设无向图G 的邻接矩阵为0 10 0 1 0 10 10则G 的边数为(B ). A . 6B. 53、设完全图K n 有n 个结点(n 2) , m 条边,当(C )时,K n中存在 欧拉回路.解释:K n 每个结点的度都为n — 1所以若存在欧拉回路则n —1必为偶数。
n 必 为奇数。
4. 欧拉回路是(B )A.路径B.简单回路[PPT 40]C.既是基本回路也是简单回路D.既非基本回路也非简单回路 5 .哈密尔顿回路是(C ) A.路径 B.简单回路 C.既是基本回路也是简单回路 D.既非基本回路也非简单回路A. m 为奇数 B . n 为偶数 C. n 为奇数 D . m 为偶数0 1 1 01 0 1 0[PPT 40] :哈密尔顿回路要求走遍所有的点,即是基本回路的点不重复,也可以是简单回路的边不重复。
6. 设G是简单有向图,可达矩阵P(G)刻划下列关系中的是(C )A、点与边B、边与点C、点与点D、边与边7. 下列哪一种图不一定是树(C)。
A.无简单回路的连通图B. 有n个顶点n-1条边的连通图C. 每对顶点间都有通路的图D. 连通但删去一条边便不连通的图8. 在有n 个结点的连通图中,其边数(B)A. 最多有n-1 条B. 至少有n-1 条C. 最多有n 条D. 至少有n9. 下列图为树的是(C)。
A、G1{a,b,c,d},{a,a ,a,b ,c,d B、G2{a,b,c,d},{a,b ,b,d, c,d C、G3{a,b,c,d}, {a,b ,a,d, c,a D、G4{a,b,c,d},{a,b ,a,c ,d,d } } } }10、面的图7-22 是(C)。
A.完全图;B.平面图;C.哈密顿图;D.欧拉图。
二、填空题1无向完全图K6有15 条边。
[6 X( 6-1 ) ]/2=152. 设连通无向图G有k个奇顶点,要使G变成欧拉图,在G中至少要加k/2条边。
解:•••任何图中的奇点的个数为偶数在每对奇点处多加一条边形成了多重边,G图就成了欧拉图。
T连通无向图G有k个奇顶点•••有k/2对奇顶点.有多少对奇点就加多少条边n(n-1)3、n阶无向完全图K n的边数是( 2 —),每个结点的度数是(n-1)证明:•/ 1个顶点的图有o条边2个顶点的图有1条边•满足1 2( 2°2当3个顶点以上时假如n=k-1 k>=3时•/ k-1个顶点的图有(k 1)(k 2)- 3k1条边2 2 2k个顶点的图有坐9 匚兰条边2 2 2(2n- 2 )解:仿用握手定理 假设把每个顶点看成一个人 A 点到B 点相当于A 主动向B 伸手 每个点要与n-1个点握手。
因为是有向的,所以A 向B 伸手和B 向A 伸手有区别总共握手次数是n(n-1) 所以总共边数是n(n-1)0 1 0 1 5、设有向图G= < V , E >, V {V 1,V 2,V 3,V 4}的邻接矩阵A1 0 1 1 1 1 0 01 0 0 0则V 1的入度deg (v 1)= 3 ,V 4 的出度 deg (V 4) = 136、 一棵无向树的顶点数为n ,则其边数为 n-1 ,其结点度数之和是2(n-1)。
所有的次之和为边数的两倍7、 一个无向图有生成树的充分必要条件是(此图为连通图)。
8设T= < V,E 〉是一棵树,若|V|>1,则T 中至少存在(2 )片树叶. 9、 任何连通无向图G 至少有(1 )棵生成树,当且仅当G 是(树), G 的生成树只有一棵。
2 2* 3k “、 * k 、 | 彳 ( 1) ( ) k 1••• k -1个顶点的图与k 个顶点的图产生的边数为而又••• k-1个顶点的图的边数加上这条边 k-1恰好为k 2 2k(k 1)二一个具有N 个顶点的无向完全图的边数为n(n -1) 24、n 个结点的有向完全图边数是(n(n-1)),每个结点的度数是3k乙1) (k 1)2•••当n=k 时满足条件10、设T是一棵树,则T是一个连通且(无圈)的图。
11、设无向图G有18条边且每个顶点的度数都是3,则图G有(12)个顶点。
解:T 18条边的次之和为d(v) 2E 36,v V且每个顶点的度数都是3•••顶点数为36/3=12。
如图:12、任一有向图中,度数为奇数的结点有(偶数)个。
[PPT 23]13、一棵树有2个2度顶点,1个3度顶点,3个4度顶点,则其1度顶点为(9 )。
如图:14、设G是由5个顶点组成的完全图,则从G中删去(6 )条边可以得到树。
解:v 5个顶点组成的完全图边数为5 (5-1)10 2又V 树有5个顶点二树的边数应为4• ••完全图应删除10-4=6条边可以得到树1 0 00 1 1 0 0 0 0 0 1 0 1 0二、计算题1 .设 G=<V, E >, V ={ V 1, V 2, V 3, V 4, V 5} , E ={(V 1, V 3),(V 2,V 3), (V 2, V 4), ( V 3, V 4),(V 3, V 5),(V 4,V 5)},试(1) 给出G 的图形表示; (2) 写出其邻接矩阵;(3)求出每个结点的度数;VIY270 0 1 0 0叫0 0 1 1 0G (g j )5 51 1 0 1 1解: (1)V4(2) jc0 1 1 0 10 0 1 1 0(3)、每个结点的度数分别为15、已知图G 是相邻矩阵为 则G 的边数为(B )。
0 0 0 0 1 0 0 1V1—1、VP2、VI4、V4—3、VN22•图G=<V, E>,其中V={ a, b, c, d, e}, E={ (a, b), (a, c).(a, e), ( b, d), ( b, e), ( c, e), ( c, d), ( d, e) },对应边的权值依次为2、1、2、3、6、1、4及5,试四、问答题1、设无向图G=<V,E> |E|=12。
已知有6个3度顶点,其他顶点的度数均小于3。
问G中至少有多少个顶点?解:•••有6个3度顶点二它们的度数之和为6X 3=18.(1)画出G的图形; (2)写出G的邻接矩阵;0110110011G(g j)55 100110110111110G图最小生成树的权值为2+1+1+3=8(3)求出G权最小的生成树及其权值.又T所有点的度数之和为d(v) 2E 24 ,v V二度数均小于3的其余顶点的度数之和为24-18=6.•••其余顶点的度数均为2时,G的顶点最少二其余顶点有6/2=3个二G中至少有6+3=9个顶点2、判断下列图是否为欧拉图?说明理由,存在是否哈密尔顿回路解:(1)、是欧拉图。
理由:欧拉图判断条件:图中所有节度点均为偶数(2)、不存在哈密尔顿回路。
理由:哈密顿图是基本回路(点不能重复)。
哈密顿图遍历顶点3、下列各组数中,哪些能构成无向图①的度数列?哪些能构成无向简单图②的度数列?(1) 1,1,1, 2, 3(2) 2,2,2, 2, 2(3) 3,3,3, 3(4) 1,2,3, 4, 5①"②"①"②"①②(5) 1, 3, 3, 3解:1、构成图的度数列的条件: 度数(次)之和d(v) 2E为偶数,并且奇点有偶数个。
v VT⑴、(2)、(3)、⑷、(5)的度数(次)之和分别为8、10、12、15、10又T奇点的个数分别为4、0、4、3、4(4)不符合。
也不满足无向简单图。
• •• (1),⑵,(3),⑸ 都能构成无向图的度数列2、(5)虽然能构成无向图的度数列,但不能构成无向简单图的度数列。
若G是无向简单图,设G中顶点为a、b、c、d且d(a)=1、d(b)=d(c)=d(d)=3 显然,a只能与b、c、d其中一个顶点相邻,若设a与b相邻,则除b可以是3 度顶点,c、d都不能是3度顶点,这是矛盾的。
所以(5)中的度数列不能构成不是无向简单图。
4、[1] 哥尼斯堡的居民能否通过建一座新桥来找一条可接受的路线?如果可以,该怎么作?[2] 哥尼斯堡的居民能否通过建两座新桥来找一条可接受的路线?如果可以,该怎么作?[3] 哥尼斯堡的居民能否通过拆一座桥来找一条可接受的路线?如果可以,该怎么作?[4] 哥尼斯堡的居民能否通过拆两座桥来找一条可接受的路线?如果可以,该怎么作?解:•七桥示意图的每个节点度为奇数.它不是欧拉图,不能遍历边•••连通无向图G有n个奇点成为欧拉图的充要条件:在G中至少要添加或删掉n/2条边假设桥为图中的边,解答如下:(1)、(2)(2)(3)奇数个顶点,偶数个顶点,(4)奇数个顶点,偶数条边?画出一个有向欧拉图,要求:按数字顺序走遍所有的边,点可以重复。
蓝点是起点。
(1)偶数个顶点,偶数条边;(2)奇数个顶点,奇数条边;(3)偶数个顶点,奇数条边;(4)奇数个顶点,偶数条边。
默为起点•.•图中有4个奇点•••要使其变为欧拉回路,即可以在G中添加4/2=2条边•••( 1)不满足条件,路线不被接受,(2)的建议则被接受(3)、(4)(1)偶数个顶点,偶数条边;奇数条边;⑴⑺⑷3.根据如下的相邻矩阵,画出它所对应的图G顶点的个数分别是1、3、2、1,求G 的边数,试画 出满足条件的图形?解:由题可知,0 A (G ) !4、已知无向图 G 有12条边, 6个3度顶点,其余顶点的 度数均小于3,问图G 至少有几个顶点?并画出符合 条件的图形?解:T 无向图G 的|E|=12•••图G 的度数之和为 d(v) 2E 24v V又T 6个3度顶点如•••这6个3度顶点的度数之和为6X 3=18 •度数均小于3的其余顶点的度数之和为24-18=6当其余顶点的度数均为2时,图G 的顶点最少 二其余顶点数为6/2=3•••图G 至少有6+3=9个顶点。
5、在有7个结点的无向图 叶,2度、3度、 4度、5度2 红色为边数 7 黑色为度数3 37个顶点的度数之和为1 x 2+3X 3+2X 4+1X 5=24 • ••所有次之和为边数的两倍红色为边二G图的边数为24/2=12。
