八年级数学几种证明图示
勾股定理9种证明(有图)

勾股定理9种证明(有图)本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF.∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c2.∵ Rt ΔGDH ≌ Rt ΔHAE,∴ ∠HGD = ∠EHA.∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD,∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a.∴ BDPC是一个边长为a的正方形.同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P. 过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF.从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD. 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵ AF = AC ,AB = AD , ∠FAB = ∠GAD ,∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM的面积的一半,∴矩形ADLM的面积 =2a.同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积∴ 222b ac += ,即 222c b a =+. 【证法5】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R. 过B 作BP ⊥AF ,垂足为P. 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵ ∠BAD = 90º,∠PAC = 90º,∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c , ∴ Rt ΔDHA ≌ Rt ΔBCA.∴ DH = BC = a ,AH = AC = b.由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ,AP= a ,从而PH = b ―a. ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA. ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c. 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE. 又∵ ∠BTH = ∠BEA = 90º, BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a. 又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º,∴ ∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ,垂足是M. 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE.∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ,即 222c b a =+.【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,AC = BD = b,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+• 可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB.在ΔADC 和ΔACB 中, ∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++, ∴ 222c b a =+.。
勾股定理种证明(有图)

勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE=∠BEF.∵∠AEH+∠AHE=90º,∴∠AEH+∠BEF=90º. ∴∠HEF=180º―90º=90º.∴四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.∵Rt ΔGDH ≌Rt ΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90º, ∴∠EHA+∠GHD=90º. 又∵∠GHE=90º,∴∠DHA=90º+90º=180º.∴ABCD 是一个边长为a+b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+.∴222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c.把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于点P. ∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt Δ∴∠EGF=∠BED , ∵∠EGF+∠GEF=90°,∴∠BED+∠GEF=90°,∴∠BEG=180º―90º=90º. 又∵AB=BE=EG=GA=c ,∴ABEG 是一个边长为c 的正方形.∴∠ABC+∠CBE=90º.∵Rt ΔABC ≌Rt ΔEBD, ∴∠ABC=∠EBD.∴∠EBD+∠CBE=90º. 即∠CBD=90º.又∵∠BDE=90º,∠BCP=90º,BC=BD=a.∴BDPC 是一个边长为a 的正方形.同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴222c b a =+. 【证法3】(项明达证明) 做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P.过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵∠BCA=90º,QP ∥BC ,∴∠MPC=90º,∵BM ⊥PQ , ∴∠BMP=90º,∴BCPM 是一个矩形,即∠MBC=90º.∵∠QBM+∠MBA=∠QBA=90º,∠ABC+∠MBA=∠MBC=90º, ∴∠QBM=∠ABC ,又∵∠BMP=90º,∠BCA=90º,BQ=BA=c , ∴Rt ΔBMQ ≌Rt ΔBCA.同理可证Rt ΔQNF ≌Rt ΔAEF. 从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD.过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵AF=AC ,AB=AD ,∠FAB=∠GAD , ∴ΔFAB ≌ΔGAD ,∵ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴矩形ADLM 的面积=2a .同理可证,矩形MLEB 的面积=2b .∵正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 ∴222b a c +=,即222c b a =+. 【证法5】(杨作玫证明) 做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R.过B 作BP ⊥AF ,垂足为P.过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵∠BAD=90º,∠PAC=90º,∴∠DAH=∠BAC.又∵∠DHA=90º,∠BCA=90º, AD=AB=c , ∴Rt ΔDHA ≌Rt ΔBCA.∴DH=BC=a ,AH=AC=b.由作法可知,PBCA 是一个矩形, 所以Rt ΔAPB ≌Rt ΔBCA.即PB= CA=b ,AP=a ,从而PH=b ―a.∵Rt ΔDGT ≌Rt ΔBCA, Rt ΔDHA ≌Rt ΔBCA.∴Rt ΔDGT ≌Rt ΔDHA.∴DH=DG=a ,∠GDT=∠HDA. 又∵∠DGT=90º,∠DHF=90º,∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90º, ∴DGFH 是一个边长为a 的正方形. ∴GF=FH=a.TF ⊥AF ,TF=GT ―GF=b ―a. ∴TFPB 是一个直角梯形,上底TF=b ―a ,下底BP=b ,高FP=a+(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+∙-+=++21438=ab b 212-, 985S S S +=,∴824321S ab b S S --=+=812SS b --.② 把②代入①,得=922S S b ++=22a b +.∴222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c.做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上.用数字表示面积的编号(如图).∵∠TBE=∠ABH=90º, ∴∠TBH=∠ABE. 又∵∠BTH=∠BEA=90º,BT=BE=b , ∴Rt ΔHBT ≌Rt ΔABE. ∴HT=AE=a. ∴GH=GT ―HT=b ―a.又∵∠GHF+∠BHT=90º,∠DBC+∠BHT=∠TBH+∠BHT=90∴∠GHF=∠DBC.∵DB=EB ―ED=b ―a ,∠HGF=∠BDC=90º, ∴Rt ΔHGF ≌Rt ΔBDC.即27S S =.过Q 作QM ⊥AG ,垂足是M.由∠BAQ=∠BEA=90º,可知∠ABE =∠QAM ,而AB=AQ=c ,所以Rt ΔABE ≌Rt ΔQAM.又Rt ΔHBT ≌ Rt ΔABE.所以Rt ΔHBT ≌Rt ΔQAM.即58S S =.由Rt ΔABE ≌Rt ΔQAM ,又得QM=AE=a ,∠AQM=∠BAE. ∵∠AQM+∠FQM=90º,∠BAE+∠CAR=90º,∠AQM=∠BAE , ∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90º,QM=AR=a ,∴Rt ΔQMF ≌Rt ΔARC.即64S S =.∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ,即222c b a =+. 【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC=a ,AC=b ,斜边AB=c (如图).过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆.根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙, ∵AB=DC=c ,AD=BC=a , AC=BD=b , ∴222AC BC AB +=,即222b a c +=, ∴222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BCb ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知AD AB AC ∙≠2,或者BD AB BC ∙≠2.即AD :AC ≠AC :AB ,或者BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵∠A=∠A ,∴若AD :AC ≠AC :AB ,则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵∠B=∠B , ∴若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵∠ACB=90º,∴∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾.所以,222AB BC AC ≠+的假设不能成立.∴222c b a =+. 【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c.作边长是a+b 的正方形ABCD.把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+=22c ab +.∴22222c ab ab b a +=++,∴222c b a =+.。
初中数学八年级上册 1.3 证明(2) 课件
E
B C
D
F
本节课你学到什么
1.数学知识有:
三角形内角和定理:三角形的三个内角的和等于180°.
推论:
三角形的一个外角等于和它不相邻的两个内角的和. 三角形的一个外角大于任何一个和它不相邻的内角.
2.数学方法:添辅助线
3.证明几何命题的一般步骤:
(1)画出图形; (2)(2)写出“已知” 、“求证” ; (3)证明.
对于三角形,我们已经有哪些认识?
A
B
C
三角形三个内角的和等于180°
你能验证:三角形三个内角的和等于180°吗?
实验1: 将纸片三 角形顶角剪下,随意 将它们拼凑在一起。
2 B
1
A 1
31 2
C
D
实验2:先将纸片三角形一角折向其对边,使顶点 落在对边上,折线与对边平行(图1),然后把另处 两角相向对折,使其顶点与已折角的顶点相嵌合 (图2)、(图3),最后得到(图4)所示的结果.
一个人最炫耀什么,说明其内心最缺乏什么;一个人越在意的地方,也是其最自卑的地方。 青春一经“典当”,永不再赎。 你目前所拥有的都将随着你的死亡而成为他人的,那为何不现在就乐施给真正需要的人呢? 自己要先看得起自己,别人才会看得起你。 你今天必须做别人不愿做的事,好让你明天可以拥有别人不能拥有的东西。 有两种人是忘不了的,一种是你爱的人,再就是你恨的人,不过往往他们是同一个人。 君子成人之美,不成人之恶。——《论语》 勤奋是学习的枝叶,当然很苦,智慧是学习的花朵,当然香郁。 语言是心灵和文化教养的反映。 受惠的人,必须把那恩惠常藏心底,但是施恩的人则不可记住它。--西塞罗 工作中,你要把每一件小事都和远大的固定的目标结合起来。 一切节省,归根到底都归结为时间的节省。——马克思
八年级数学 勾股定理证明方法
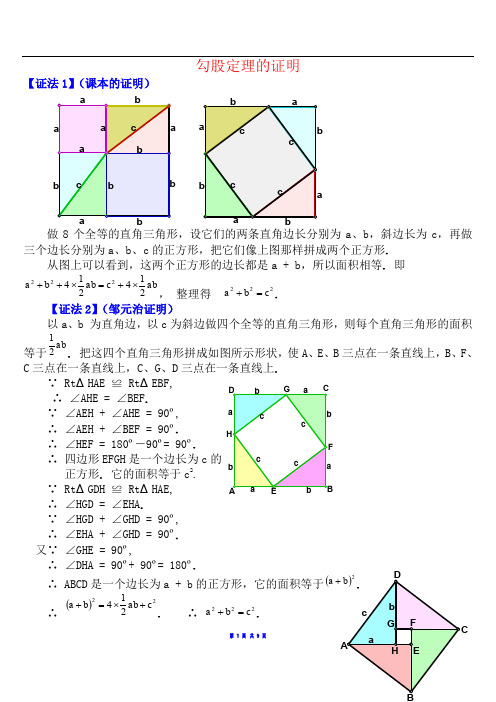
勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于(a +∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º, BC = BD = a . ∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221aΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC ∙=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC ∙=2.∴ ()222AB AB DB AD BC AC =∙+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c .再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º,AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC ∙=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a c b -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC ∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)D设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图). 在EH = b 上截取ED = a ,连结DA 、则 AD = c .∵ EM = EH + HM = b + a , ED = a ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
浙教版八年级数学上册《证明》课件(36张ppt)

如果是假命题,请添加适当的条件,使它成为 真命题.你有几种不同的添加方法?
E
A
B
C
图1
A
S
N
P
Q
R
B
M
T
C
图3
A
F E
B
D
图2
S
N
P
Q
C
A R
M
B
C
T
图4
❖不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月11日星期一2022/4/112022/4/112022/4/11 ❖书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/112022/4/112022/4/114/11/2022 ❖正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/112022/4/11April 11, 2022 ❖书籍是屹立在时间的汪洋大海中的灯塔。
例2 已知
想一想: 证明几何命题的基本思路是什么?
证明几何命题的基本思路: 顺推分析 从条件 逆推分析 从结论
结论 条件
已知:如图BC AC于点C,CD ∠1=∠A
求证:BE//CD
E
AB于点D,
证“明证命明题” 的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
合作探索
对于三角形,我们已经有哪些认识?
定义
A
分类
内角和
…………
B
C
例1、求证:三角形的三个内角的和等于180°.
已知:如图,∠A,∠B,∠C是△ABC
人教版八年级数学下册17.1勾股定理的证明(比较全的证明方法)ppt课件
b
a
∵ S梯 形 AB CD = = 1
1 2
B
a+b 2
2 又 ∵S梯 形 AB CD =S AED +S EBC+S 1 1 1 1 = ab+ ba+ c2= (2ab+c2) 2 2 2 2 比 较上 面 二 式得 c2=a2+b2
(a2+2ab+b2)
CED
向常春的证明方法
S梯形ABCD 1 1 2 1 ( a b b )( a b ) a ab 2 2 2
那么:
朱实 中 黄实 b a
返回
( b- a) 2
ab c 4 ( b a )2 2
2
得: c2 =a2+ b2.
证明1:
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
a c b
a
2 c 大正方形的面积可以表示为 ; 1 2 (b a ) 4 ab 也可以表示为 2 c 1 2 ∵ c2= (b a ) 4 ab 2 2 2 =b -2ab+a + 2ab b =a2+b2
G
已知:如图,以在Rt△ABC中, ∠ACB=90°,分别以a、b、c为边向外作 正方形.
K
H C b A c a B
F
求证:a2 +b2=c2.
D E
传说中毕达哥拉斯的证法
证明:从Rt△ABC的三边向外各作一个正方形(如图),作CN⊥DE交AB于M,那么正方形 ABED被分成两个矩形.连结CD和KB. ∵由于矩形ADNM和△ADC同底(AD),等高(即平行线AD和CN间的距离),
八年级数学证明课件1(PPT)2-2

徐光启于公元1603年在南京与利玛窦结识。公 元1604年,他到翰林院做官后,就专门拜利玛 窦为师,跟他学习西洋的天文历法、几何数学、 武器制造等知识。 徐光启对数学非常有兴趣。 他认为数学原则可以应用于各种实验科学,对 于解决天文历法、测量建筑、武器制造等等都 是有用的,好多学问都离不开数学。
复习回顾
下列语句是命题吗? 是真命题吗? 同角的补角相等. 过点P作直线AB的垂线. 对顶角相等. 内错角相等. 内错角相等,两直线平行.
•
;/ 特许经营 连锁加盟展会 中国特许展 特许经营 特许加盟
•
•
分类地位,放在恐龙里才最合适。个体小于始祖鸟和孔子鸟但稍大于中国鸟等九佛堂组中的反鸟类。头骨短、高,吻短,上颌骨背突细长且构成整个外鼻孔的后缘,鼻骨短宽,上颌骨齿小于前颌骨齿。颈部长,颈椎枚,荐椎愈合,可能由~8枚椎骨组成,尾综 骨长。叉骨Ⅴ形,具较长的锁下突,乌喙骨相对较短,末端宽;胸骨顶端不强烈向后凹陷,胸骨具单一、较短的后侧突。肱骨稍短于尺骨,腕掌骨短,第Ⅲ掌骨扩展但不与第Ⅱ掌骨末端愈合,第Ⅰ指骨细长,第Ⅰ、Ⅱ指爪较发达,第Ⅲ指仅残存近端的第指节, 其他指节及爪均退化消失。始反鸟略大于其他早白垩世反鸟类的事实,表明身体缩小的趋势在反鸟类进化中起着较为重要的作用。愈合的荐椎数目为8枚,尾综骨前半部具有三角形的背嵴;叉骨呈典型的Y字形且具有较长的锁下突;胸骨宽大,其后缘具有两对 后突,其中的侧后突长且其末端变宽;第Ⅱ、Ⅲ掌骨背面具有纵向的中央沟;第Ⅰ指第指节极为细弱,第Ⅱ指强壮,第Ⅲ指仅具一枚指节;耻骨纤细、弯曲,耻骨脚小、三角形且伸向背方;坐骨细,远端变尖,向背方弯曲;第Ⅱ骨的滑车略高于第Ⅲ骨滑车但 略低于第Ⅳ骨滑车,趾爪发育。完整个体,趾骨不全。为朝阳地区最早被发现的中生代鸟类之一,它个体小,头部骨骼很少愈合,头颅较大,吻较长而低,具牙齿。胸骨龙骨突低,但与乌喙骨关连的面宽阔,肱骨近端已有小的气窝,掌骨近端愈合,并有腕骨 滑车,指爪仅有两个且不发育,耻爪也不太钩曲。长翼鸟为一较为特殊的反鸟类,头骨相对较长,头长至少是头高的.倍,牙齿短圆锥状,9枚颈椎,中间的几枚颈椎已经演化为类似于现代鸟类的异凹型椎体,叉骨为典型反鸟类的Y字形,肋骨钩突至少发现对, 这在反鸟类中为首次发现,表明这一结构不是今鸟类的特有结构,前肢显著长于后肢,发达的前肢、较大的胸骨及较发育的龙骨突等表明长翼鸟比一般反鸟类具有更强的飞行能力,后肢较短,尤其胫跗骨相对较短,第Ⅳ骨长于其他骨,第Ⅰ趾较长,各趾爪亦 较发达,表明其具有较强的抓握能力。根据骨骼形态特征,长翼鸟具有类似于现代鸟类的稳固的胸廓,供发达的肌肉附着和具有发达的主动呼吸功能,它的翼发达,具有较强的飞行能力,嘴长,适应水中捕食,后肢的个骨滑车几乎在同一个平面上,第Ⅰ趾与 其他趾对握,适宜树栖。长翼鸟可能具有与现代翠鸟非常类似的生活方式,它可以靠有力的翅飞行,以长长的嘴捕食水中的鱼类,代表了一种独特的生态适应类型。水星是太阳系内与地球相似的颗类地行星之一,有着与地球一样的岩石个体。它是太阳系中最 小的
勾股定理9种证明(有图)
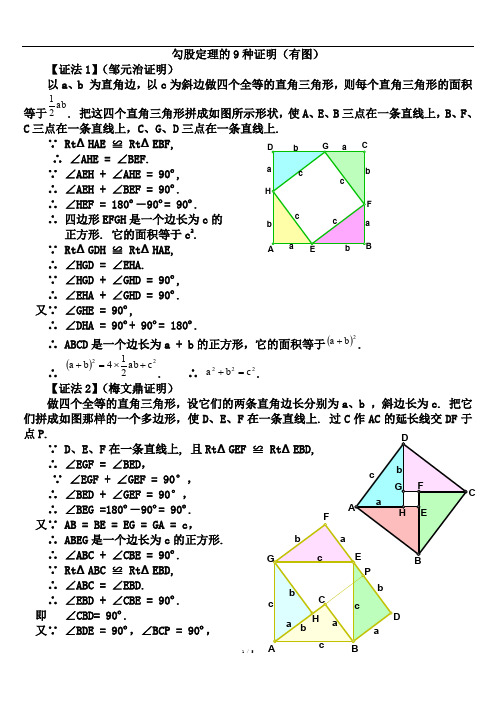
勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF.∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE,∴ ∠HGD = ∠EHA.∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a.∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P.过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵ ∠BCA = 90º,QP ∥BC ,∴ ∠MPC = 90º,∵ BM ⊥PQ , ∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF. 从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD. 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵ AF = AC ,AB = AD , ∠FAB = ∠GAD ,∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法5】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R. 过B 作BP ⊥AF ,垂足为P. 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵ ∠BAD = 90º,∠PAC = 90º,∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c , ∴ Rt ΔDHA ≌ Rt ΔBCA.∴ DH = BC = a ,AH = AC = b.由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ,AP= a ,从而PH = b ―a.∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA.∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c. 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE. 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a.又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ,垂足是M. 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE.∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC ∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.。
八年级数学证明课件1-P

2018秋人教版八年级数学上册课件:第三部分 专题探究 专题四 几何证明专题 (共20张PPT)

考点三中,AD⊥BC,垂 足为点D,E是线段AD上的点,且AD=BD,DE=DC. 求 证:∠BED=∠C.
证明:∵AD⊥BC,∴∠BDE=∠ADC=90°. 在△BDE和△ADC中,
∴△BDE≌△ADC (SAS). ∴∠BED=∠C.
考点四: 证明等边三角形 【例4】如图3-4-7,在Rt△ABC中,∠ACB=90°,BD 是△ABC的角平分线. (1)如图3-4-7①,若AD=BD,求∠A的度数; (2)如图3-4-7②,在(1)的条件下,作DE⊥AB于点 E,连接EC. 求证:△EBC是等边三角形.
(2)解:△ABE是等边三角形. 理由如下. ∵BC是线段AE的垂直平分线, ∴BA=BE,即△ABE是等腰三角形. 又∵∠CAB=60°, ∴△ABE是等边三角形.
5. 如图3-4-10,已知:在△ABC中,∠B,∠C的平分线 相交于点D,过点D作EF∥BC交AB于点E,交AC于点F, 求证:BE+CF=EF. 证明:∵BD平分∠ABC, ∴∠EBD=∠DBC. ∵EF∥BC,∴∠EDB=∠DBC. ∴∠EDB=∠EBD. ∴DE=BE. 同理,CF=DF. ∴EF=DE+DF=BE+CF, 即BE+CF=EF.
拓展提升
9. 如图3-4-14,在等边△ABC中,点P在△ABC内,点 Q在△ABC外,且∠ABP=∠ACQ,BP=CQ. 判断 △APQ的形状,并说明理由. 解:△APQ是等边三角形. 理由如下. ∵△ABC为等边三角形, ∴AB=AC.
在△ABP和△ACQ中,
∴△ABP≌△ACQ(SAS). ∴AP=AQ,∠BAP=∠CAQ. ∵∠BAC=∠BAP+∠PAC=60°, ∴∠PAQ=∠CAQ+∠PAC=60°. ∴△APQ是等边三角形.
八年级数学上册《三角形全等的证明》课件 (共14张PPT)

添加辅助线是几何证明 中很重要的一种思路
1、证明两个三角形全等 分析:现在我们已知
A→∠CAB=∠DAB
例1 :如图,点B在AE
S→ AB=AB(公共边) .
上,∠CAB=∠DAB,要使 ①用SAS,需要补充条件
归纳思考:
两个三角形全等,通常需要3个
条件,其中至少要有1组 边 对
应相等。
知识梳理:
A
A
B
C
SSA不能
A
判定全等
B
C
D
B D
证明题的分析思路:
①要证什么 ②已有什么 ③还缺什么 ④创造条件
注意1、证明两个三角形全等,要结合题目的条件 和结论,选择恰当的判定方法
2、全等三角形,是证明两条线段或两个角相 等的重要方法之一,证明时
①要证明PA=PC可将其 放在ΔAPB和ΔCPB 或ΔAPD和ΔCPD考虑
D ②已有两条边对应相等 (其中一条是公共边) ③还缺一组夹角对 应相等
析:
若能使∠ABP=∠CBP 或∠ADP=∠CDP 即可。
创造条件
例3已知:P是BD上的任意一点AB=CB,AD=CD. 求证PA=PC
证明:在△ABD和△CBD中
用适当方法解决三角形全 等的证明
知识点 三角形全等的证题思路:
找夹角 SAS 已知两边找直角 HL
找另一边 SSS
边为角的对边 找任一角 AAS 已知一边一角边为角的邻边找找找夹夹边角角的的的对另另角一一边角AASASASAS
已知两角找找夹任边一边ASAAAS
AB=CB
A
AD=CD
八年级数学几种证明图示

勾股定理9种证明(有图)

勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE=∠BEF.∵∠AEH+∠AHE=90o,∴∠AEH+∠BEF=90o. ∴∠HEF=180o ―90o=90o.∴四边形EFGH 是一个边长为c 的 正方形.它的面积等于c2.∵Rt ΔGDH ≌Rt ΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90o, ∴∠EHA+∠GHD=90o. 又∵∠GHE=90o,∴∠DHA=90o+90o=180o.∴ABCD 是一个边长为a+b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+.∴222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c.把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于点P. ∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt ∴∠EGF=∠BED , ∵∠EGF+∠GEF=90°,∴∠BED+∠GEF=90°,∴∠BEG=180o ―90o=90o. 又∵AB=BE=EG=GA=c ,∴ABEG 是一个边长为c 的正方形.∴∠ABC+∠CBE=90o.∵Rt ΔABC ≌Rt ΔEBD, ∴∠ABC=∠EBD.∴∠EBD+∠CBE=90o. 即∠CBD=90o.又∵∠BDE=90o ,∠BCP=90o ,BC=BD=a.∴BDPC 是一个边长为a 的正方形.同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴222c b a =+.【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b(b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P.过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵∠BCA=90o ,QP ∥BC ,∴∠MPC=90o ,∵BM ⊥PQ , ∴∠BMP=90o ,∴BCPM 是一个矩形,即∠MBC=90o.∵∠QBM+∠MBA=∠QBA=90o ,∠ABC+∠MBA=∠MBC=90o , ∴∠QBM=∠ABC ,又∵∠BMP=90o ,∠BCA=90o ,BQ=BA=c , ∴Rt ΔBMQ ≌Rt ΔBCA.同理可证Rt ΔQNF ≌Rt ΔAEF.从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD.过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵AF=AC ,AB=AD ,∠FAB=∠GAD , ∴ΔFAB ≌ΔGAD ,∵ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴矩形ADLM 的面积=2a . 同理可证,矩形MLEB 的面积=2b .∵正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 ∴222b a c +=,即222c b a =+. 【证法5】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b(b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R.过B 作BP ⊥AF ,垂足为P.过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵∠BAD=90o ,∠PAC=90o ,∴∠DAH=∠BAC.又∵∠DHA=90o ,∠BCA=90o , AD=AB=c , ∴Rt ΔDHA ≌Rt ΔBCA.∴DH=BC=a ,AH=AC=b.由作法可知,PBCA 是一个矩形, 所以Rt ΔAPB ≌Rt ΔBCA.即PB= CA=b ,AP=a ,从而PH=b ―a.∵Rt ΔDGT ≌Rt ΔBCA, Rt ΔDHA ≌Rt ΔBCA.∴Rt ΔDGT ≌Rt ΔDHA.∴DH=DG=a ,∠GDT=∠HDA. 又∵∠DGT=90o ,∠DHF=90o ,∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90o , ∴DGFH 是一个边长为a 的正方形.∴GF=FH=a.TF ⊥AF ,TF=GT ―GF=b ―a.∴TFPB 是一个直角梯形,上底TF=b ―a ,下底BP=b ,高FP=a+(b ―a ).用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+∙-+=++21438=ab b 212-, 985S S S +=,∴824321S ab b S S --=+=812SS b --.② 把②代入①,得=922S S b ++=22a b +.∴222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c.做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上.用数字表示面积的编号(如图).∵∠TBE=∠ABH=90o , ∴∠TBH=∠ABE. 又∵∠BTH=∠BEA=90o ,BT=BE=b , ∴Rt ΔHBT ≌Rt ΔABE. ∴HT=AE=a. ∴GH=GT ―HT=b ―a.又∵∠GHF+∠BHT=90o ,∠DBC+∠BHT=∠TBH+∠∴∠GHF=∠DBC.∵DB=EB ―ED=b ―a ,∠HGF=∠BDC=90o , ∴Rt ΔHGF ≌Rt ΔBDC.即27S S =.过Q 作QM ⊥AG ,垂足是M.由∠BAQ=∠BEA=90o ,可知∠ABE =∠QAM ,而AB=AQ=c ,所以Rt ΔABE ≌Rt ΔQAM.又Rt ΔHBT ≌ Rt ΔABE.所以Rt ΔHBT ≌Rt ΔQAM.即58S S =.由Rt ΔABE ≌Rt ΔQAM ,又得QM=AE=a ,∠AQM=∠BAE.∵∠AQM+∠FQM=90o ,∠BAE+∠CAR=90o ,∠AQM=∠BAE , ∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90o ,QM=AR=a ,∴Rt ΔQMF ≌Rt ΔARC.即64S S =.∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ,即222c b a =+.【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC=a ,AC=b ,斜边AB=c (如图).过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆.根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙, ∵AB=DC=c ,AD=BC=a , AC=BD=b ,∴222AC BC AB +=,即222b a c +=, ∴222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知AD AB AC ∙≠2,或者BD AB BC ∙≠2.即AD :AC ≠AC :AB ,或者BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵∠A=∠A ,∴若AD :AC ≠AC :AB ,则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵∠B=∠B , ∴若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵∠ACB=90o ,∴∠ADC ≠90o ,∠CDB ≠90o.这与作法CD ⊥AB 矛盾.所以,222AB BC AC ≠+的假设不能成立. ∴222c b a =+.【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c.作边长是a+b 的正方形ABCD.把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+=22c ab +.∴22222c ab ab b a +=++, ∴222c b a =+.。
八年级数学下册三角形的证明 PPT

上册第一章复习 ┃ 考点攻略
[解析] 根据线段垂直平分线得性质,线段垂直平分线上得点 到线段两端点得距离相等,所以EA=EC,∠A=∠ACE=30°,又 ∠ACB=80°,故∠BCE=80°—30°=50°、
大家学习辛苦了,还是要坚持
继续保持安静
上册第一章复习 ┃ 考点攻略
方法技巧 若题目中出现或经过构造出现线段垂直平分线,注意利用“线 段垂直平分线上的点到这条线段两个端点的距离相等”解决问 题.同时,我们在求一些边长、周长或角的度数时,如果能恰当地 运用线段垂直平分线性质,可以大大简化解题过程,同学们在学习 中要注意到这一点!
八年级数学下册三角形的证明
上册第一章复习 ┃ 知识归纳
┃知识归纳┃
1、等腰三角形得性质 性质(1):等腰三角形得两个底角 相等、 性质(2):等腰三角形顶角得 平分线 、底边上得 中线、底边上 得高互相重合、 2、等腰三角形得判定 (1)定义:有两条边 相等得三角形是等腰三角形、 (2)等角对等边:有两个角 相等得三角形是等腰三角形、
上册第一章复习 ┃ 考点攻略
► 考点二 全等三角形得证明 例2 如图S1-2,在△ABC和△DEF中,B,E,C,F在同一直线上,
下面有四个条件,请你从中选三个作为题设,余下得一个作为结论, 写出一个正确得命题,并加以证明、
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF、
上册第一章复习 ┃ 考点攻略
上册第一章复习 ┃ 知识归纳
3、用反证法证明得一般步骤 (1)假设命题得结论不成立; (2)从这个假设出发,应用正确得推论方法,得出与定义、公理、已 证定理或已知条件相矛盾得结果; (3)由矛盾得结果判定假设不正确,从而肯定命题得结论正确、 4、等边三角形得判定 (1)有一个角等于60°得 等腰 三角形是等边三角形;
八年级数学证明课件2(PPT)3-3

探索活动
❖ 让我们尝试从基本事实出发,证实我们曾探索、发 现的有关图形的许多性质的正确性。
❖ 本书选用下列真命题作为基本ห้องสมุดไป่ตู้实:
❖ 同位角相等,两直线平行
❖ 两直线平行,同位角相等。
❖ 两边和它们的夹角对应相等的两个三角形相 等
❖ 两角和它们的夹边对应相等的两个三角形全 等
❖ 三边对应相等的两个三角形全等
定后,注意水肥管理,产量才能提高;生育中期应注意水肥调控,要施缓肥,以保持根形的发育;此品种发芽后~8天长势茂盛,吸肥量剧增,第二时期肥料 应注意其延迟性,要后期起作用。 [] 改良新黑田五寸 生长势强,早期生育好,耐暑性、抗病性较强;肥大好,根部缩尾好,根形优秀;根色深红,根皮光 滑;夏季播种,秋、冬收; 微商货源 ; 获的丰产品种。 [] 超级红芯 属抽薹晚、收尾早、三红率高的超级品种。生长势强,耐 暑性、抗病性强;根部收尾好,长圆柱形,根长8~cm,单根重~g;着色好、肥大快商品率高,生育期天左右,亩产kg左右。 [] 汉城六寸 生长速度快, 根皮及芯部呈鲜红色;生长势强,不易抽 改良新黑田五寸、汉城六寸、超级红芯 改良新黑田五寸、汉城六寸、超级红芯(张) 薹,根形均匀一致,商品性好; 生育期约天,根型长圆筒型,根长8~cm,单根重g左右,根径.~.cm;抗病性强,高产品种,亩产kg以上。 [] 法国阿雅 属早熟性突出,根型好,心部颜 色佳的早熟品种。改良黑田五寸系列,大型高产品种;播种后天采收,根长~cm,肩宽.~cm;根形好,收尾渐细,根皮橘红色;耐热性好,抗萎缩病及叶 斑病。 [] 红映二号 引自日本的早熟杂交一代胡萝卜优种,播种后天即可收获。抗抽薹能力特强,适于早春覆膜播种。叶丛挺立,适于密植,产量高。生长 强健,肉质根肥大快,低温条件下成形、成色能力强;皮、肉、芯三红,颜色深,着色快,根形整齐,根皮光滑,收尾好,形状好看。 [] 宝冠 进口品种, 根形整齐,一般长~cm粗cm左右,尾部 宝冠 宝冠 收尖好,红心,红肉,红皮,中心轴细小,适于生产加工胡萝卜汁和胡萝卜粒原料,抗旱,耐暑,宜于 夏季播种,属高产增收型品种,播后天左右根重可达~g,播后天起可以开始上市,每亩(m)产成品可达kg。 [] 红芯六号 杂交种,地上部分长势强而不旺, 叶色浓绿生育期~天,抗抽薹性极强,适合中国大部分地区春季露地播种或南方地区小拱棚越冬栽培;肉质根光滑整齐,柱形;皮、肉、心浓鲜红色,心柱 细,口感好;肉质根长cm,粗约cm,单根重约g,m产量约kg;胡萝卜素含量为新黑田五寸的~倍,总胡萝卜素~mg/kg,其中β-胡萝卜素含量~mg/kg, 是适合鲜食与加工的理想品种。 [] 春红二号 生育期天左右,为早熟品种;根形为整齐的柱形,外表光滑 春红二号 春红二号 ,皮、肉、心均为鲜红色根长 8cm,直径~cm,是适合春夏栽培的早熟耐热品种,m产量~kg左右,适合中国
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Байду номын сангаас
五脏与五窍的关系密切,其中肾开窍于A.鼻B.耳C.口D.舌E.目 某患者右侧面部及颏部遭到重击后,出现开、闭口困难,伴右侧面部及耳颞部肿痛。检查见下颌中线偏右,左侧后牙早接触,左侧前牙开。对于该患者,应该采用的治疗措施()A.颌间牵引、固定B.手法复位、绷带固定C.咀嚼肌封闭D.局部理疗E.手术摘除髁状突及关节盘 用万用表测得某晶体二极管的正反向电阻值相差很大,则说明该管子。A.很好B.已失去单向导电性C.已经击穿D.内部已断路 正常人的腋窝温、口腔温和直肠温按温度由高至低排列顺序为A.口腔温,腋窝温,直肠温B.腋窝温,口腔温,直肠温C.口腔温,直肠温,腋窝温D.直肠温,腋窝温,口腔温E.直肠温,口腔温,腋窝温 单位工程施工组织设计由负责编制,并报上一级领导机关审批。A.建设单位B.监理单位C.施工单位D.设备供应商 对接受青霉素治疗的患者,如果停药几天以上,必须重新做过敏试验()A.1天B.2天C.3天D.4天E.5天 管理学家提供的激励方法有很多种,经常用于实际操作的方法主要有、奖励激励、考评激励、领导激励、与事业激励等五种。 下列听眦线组合,错误的是A.听眶线--听眦线约呈20°B.听眦线--听眶线约呈12°C.听鼻线--听眦线约呈25°D.听口线--听眦线约呈35°E.听眉线--听眦线约呈10° 在客户服务中心品质监控中电话监听通常可分为随机监听、、三种形式。 哪项不是心脏病孕妇发生心力衰竭的诱因A.妊娠32~34周心排血量明显增加B.妊娠末期血容量增加达高峰C.妊娠6周始心率平均增加10次/分D.妊娠早期以心排血量增加为主E.妊娠后期子宫增大心脏机械性负担 监理合同要求监理人必须完成的工作包括哪几类? 在静稳性曲线图上,GZ曲线与横轴的第二个交点对应的横倾角为。A.静倾角B.极限静倾角C.稳性消失角D.甲板浸水角 某女,60岁,有高度近视眼病史,近半年来眼前可见黑色漂浮物,视力较前降低,做了眼底镜检查患者的可能诊断是()A.玻璃体积血B.玻璃体液化C.玻璃体炎症D.玻璃体后脱离E.玻璃体混浊 土壤热通量 血吸虫病的基本病理变化是A.尾蚴性皮炎B.嗜酸性粒细胞增多C.肝脾肿大D.虫卵肉芽肿E.静脉炎和静脉周围炎 肾癌的三大典型症状是A.血尿、肿块和疼痛B.血尿、发热和疼痛C.血尿、肿块和高血压D.肿块、发热和高血压E.肿块、血沉快和高血压 造成碳化尾气压力大的原因是什么? 单位和个人的计算机信息网络直接进行国际联网时,可以自由选择信道进行国际联网。A.正确B.错误 下面哪种机械通气模式是"定容"型通气A.压力辅助通气P-ACVB.压力支持通气PSVC.同步间歇指令通气SIMVD.压力控制-同步间歇指令通气PC-SIMVE.压力控别通气PCV 牡蛎散中功专止汗的药物是A.煅牡蛎B.麻黄根C.生黄芪D.小麦E.山茱萸 案例分析题]某“冠心病”患者死后尸解。冠状动脉镜下改变如图所示,可见蓝色颗粒状物质沉积,这是发生了何种变性A.黏液样变性B.淀粉样变性C.玻璃样变性D.病理性色素沉着E.病理性钙化 男,36岁,胸痛半月伴发高热,胸片发现占位性病变,CT检查如图,最可能的诊断为A.左下肺肺脓肿B.左下肺癌并空洞形成C.左侧胸腔积脓D.左下肺囊肿E.左下肺肺炎 有关公账户余额管理价格再转授权规定正确的是A、横向可转授至二级分支行业务经营和管理部门B、纵向最低可再转授至县级行分管行领导C、横向再转授权由二级分支行自行确定D、纵向最低可再转授至县级行业务部门负责人或网点负责人 ()资料是调查的起点,其优点是成本低及可以立即使用。A.一手B.基础C.原始D.二手 渠道平时检查中,不包括。A、检查路口及交叉建筑物连接处是否合乎要求,检查干、支渠渠堤险工险段B、检查渠堤上有无雨淋沟、浪窝、洞穴、裂缝、滑坡、塌岸、淤积、杂草滋生等现象C、检查渠道保护区有无人为乱挖乱垦等破坏现象D、汛期检查 动车组列车安装好防护网、打开部分车门、由列车乘务人员防护的情况下允许限速运行,通过高站台时限速。 某运输企业投资一项目,预计6年后可获利800万元。按年利率12%计算,这笔收益的现值是()万元。A.428.28B.415.28C.405.28D.438.28 钩体病首次抗菌治疗过程中如出现高热、寒战加重伴血压下降,则应首先考虑A.抗生素剂量不足B.变态反应C.赫氏反应D.溶血反应E.中毒反应 主要发生于猫的常见疾病的是A.唾液腺炎B.咽炎C.食道梗塞D.齿龈炎E.喉炎 关于债券的描述,错误的是()。A.债券本身有一定的面值,通常它是债券投资者投入资金的量化表现B.债券的本质是证明债权债务关系的证书C.债券的流动意味着它所代表的实际资本也同样流动,债券与实际资本紧密关联D.债券代表债券投资者的权利,这种权利不是直接支配财产权,也不以 权表现,而是一种债权 下列不能作为系统性红斑狼疮的临床活动指标的是A.血白细胞降低、低补体血症、抗dsDNA抗体阳性B.皮肤黏膜损害C.血管炎D.明显血尿E.大量蛋白尿 当单元机组的汽轮机发电机跳闸时,要求锅炉维持运行,必须投入。A、灭火保护系统;B、协调控制系统;C、燃烧控制系统;D、旁路系统。 下列各项,不属正常舌象表现的是。A.舌体荣润B.舌质淡红C.舌苔薄白D.舌体淡嫩少苔E.舌体柔软 对风湿性心脏病孕妇分娩期的处理正确的是A.除有产科指征外,不需行剖宫产B.宫口开全时要防止产妇用力屏气C.忌用吗啡D.无感染征象不需使用抗生素E.肌注麦角新碱,预防产后出血 足底与地面接触并承受重力的时期称为A.支撑相B.摆动相C.迈步相D.迈步前期E.摆动中期 上海品牌设计:https:///
