奥数知识点图形计数.doc
小学奥数-三年级-图形计数

解:(1)以OA为一边的角有:3个; (2)以OB为一边的角有:2个; (3)以OC为一边的角有:1个; 因此,共有角:3+2+1=6(个).
【随堂练习1】 数一数,图中共有几个角?
⋮ ⋮ 4 3 2 1 10 9
解:9+8+7+6+5+4+3+2+1=45(个).
【例3】数一数,下图中有(
【例4】数一数,图中共有(
)个三角形。
上面三条粗线围起来的图形也是21个三角形。 下面三条粗线围起来的图形是6个三角形。
所以,一共有三角形:21+21+6=48 (个).
【例5】数一数,下图中有多少个长方形?
解法一: (1)单块长方形:4个; (2)两块组成的长方形:4个; (3)四块组成的长方形:1个; 因此,总共有4+4+1=9(个).
【例5】数一数,下图中有多少个长方形?
解法二: 长被分成2段,宽被分成2段,所以一共有(2+1)× (2+1)=9(个)长方形。
【随堂练习2】 数一数,图中共有多少个长方形?
解法一:(1)单块长方形:10个; (2)两块组成的长方形:13个; (3)三块组成的长方形:6个;(4)四块组成的长方形:8个; (5)五块组成的长方形:2个;(6)六块组成的长方形:3个; (7)八块组成的长方形:2个;(8)十块组成的长方形:1个 因此,总共有10+13+6+8+2+3+2+1=45(个).
收获
收获
【作业1】 数一数,下列各图中有多少个三角形?
(1)
(2)
(3)
奥数2年级图形计数

图形计数:计算某一图形的个数。
要求: 1、计数时不重复,即不能 把同一图
形计数两次。 2、不遗漏。 3、要按一定的顺序或按一某一个标
准统一分类去计算,即有规律地 计数。
图形计数方法: 1、线段端点法 2、基本图形数量法 3、分式法 4、分类法
典型例题 例1:下图中有多少条线段?
AB C
D
练习: 下图中有多少条线段?
练习: 下图中有多少条线段?
……
A C1 C2
C20 B
典型例题 例2:下图中有多少个三角形?
练习 下图中有多少个三角形?
典型例题 例3:下图中有多少个三角形?
A
D NM
BF E
CHale Waihona Puke 练习 下图中有多少个三角形?
典型例题 例4:下图中有多少个长方形?
练习 下图中有多少个长方形?
典型例题 例4:下图中有多少个正方形?
练习 下图中有多少个正方形?
从武汉到上海的客船,中途要停靠5 站,航运公司要为这艘客船准备多 少种不同的船票价?
有10个小朋友,每个小朋友都要和 其他小朋友拍手,这些小朋友一共 要拍多少次手?
小学奥数 图形计数 知识点+例题+练习 (分类全面)

一、图形计数
要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
例1、数出下图中有多少条线段?
巩固、数出下图中有几个长方形?
例2、数出图中有几个角?
D A B
C O
D C
B
A
巩固、数出图中有几个角?
例3、数出下图中共有多少个三角形?
巩固、数出图中共有多少个三角形?
例4、数出下图中有多少个长方形?
O C B A
P
C B A K G I H G F E A
D C B A
巩固、数出下图中有多少个正方形?
课后练习:
1、数出下图中有多少条线段?
2、数出图中有几个角?
E
A B C D E D
O
C B A
3、数出图中共有多少个三角形?
4、数出下图中有多少个长方形?
A
B A D
C B A。
(完整版)四年级奥数第一讲_图形的计数问题

第一讲图形的计数问题一、知识点:几何图形计数问题常常没有不言而喻的次序,并且要数的对象往常是重叠交织的,要正确计数就需要一些智慧了.实质上,图形计数问题,往常采纳一种简单原始的计数方法-一列举法.详细而言,它是指把所要计数的对象一一列举出来,以保证列举时无一重复、.无一遗漏,而后计算其总和.正确地解答较复杂的图形个数问题,有助于培育同学们思想的有序性和优秀的学习习惯.二、典例解析:例( 1)数出右图中总合有多少个角解析:在∠ AOB内有三条角分线 OC1、OC2、OC3,∠ AOB被这三条角分线分红 4 个基本角,那么∠ AOB内总合有多少个角呢?第一有这 4 个基本角,其次是包括有 2 个基本角构成的角有 3 个(即∠ AOC2、∠ C1OC3、∠ C2OB),而后是包括有 3 个基本角构成的角有 2 个(即∠ AOC3、∠C1OB),最后是包括有 4 个基本角构成的角有 1 个(即∠ AOB),因此∠ AOB内总合有角:4+3+2+1=10(个)解:4+3+ 2+ 1=10(个)答:图中总合有10 个角。
方法 2:用公式计算:边数×(边数—1)÷ 25 ×( 5-1 )÷ 2=10练一练:数一数右图中总合有多少个角?例( 2 )数一数共有多少条线段?共有多少个三角形?解析:①要数多少条线段:先看线段 AB、AD、AE、AF、AC纵向线段,再看 BC、MN、 GH 这 3 条横向线段:(4×3÷2)×5+(5×4÷2)×3=60(条)②要数有多少个三角形,先看在△ ABC中,被 GH和 MN分红了三层,每一层的三角形同样多,因此只需算出一层三角形个数就能够了。
(5 ×4÷2)×3=30(个)答:在△ ABC中共有线段60 条,共有三角形30 个。
练一练:图中共有多少个三角形?例( 3)数一数图中长方形的个数解析:长边线段有:6× 5÷ 2=15宽边线段有: 4 ×3÷2=6共有长方形: 15×6 = 90(个)答:共有长方形90 个。
三年级奥数教材第六讲之数图形
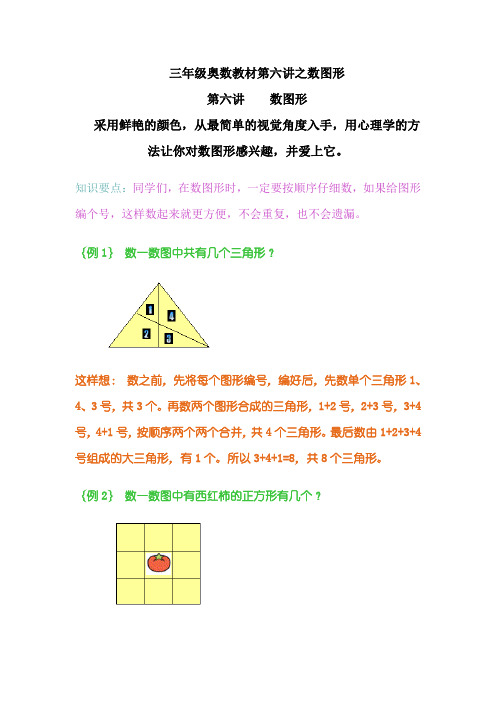
三年级奥数教材第六讲之数图形第六讲数图形采用鲜艳的颜色,从最简单的视觉角度入手,用心理学的方法让你对数图形感兴趣,并爱上它。
知识要点:同学们,在数图形时,一定要按顺序仔细数,如果给图形编个号,这样数起来就更方便,不会重复,也不会遗漏。
{例1}数一数图中共有几个三角形?这样想:数之前,先将每个图形编号,编好后,先数单个三角形1、4、3号,共3个。
再数两个图形合成的三角形,1+2号,2+3号,3+4号,4+1号,按顺序两个两个合并,共4个三角形。
最后数由1+2+3+4号组成的大三角形,有1个。
所以3+4+1=8,共8个三角形。
{例2}数一数图中有西红柿的正方形有几个?这样想:先数单个正方形,有西红柿的正方形有1个。
再数四个正方形合成的大正方形,有西红柿的大正方形有4个。
最后数由9个小正方形组成的大正方形,有1个。
所以1+4+1=6,有西红柿的正方形共6个。
{例3}数一数图中共有几个正方形?这样想:先数单个正方形1、2、3、4、5、6号,共6个。
再数四个正方形合成的大正方形,1+2+4+5号,2+3+5+6号,按顺序四个四个合并,共2个正方形。
所以6+2=8,共8个正方形。
{例4}数一数图中共有几个正方形?这样想:先数小正方形,共4个。
再数稍大的正方形,共5个。
最后数大正方形,有1个。
4+5+1=10,所以图中共有10个正方形。
{例5}数一数图中共有几个圆形?这样想:先数小圆,共5个。
再数大圆有1个。
图中共有6个圆。
数图形晚饭过后,妈妈给小小出了一道“试眼力”的题目:数数窗户上一共有多少个正方形。
小小一看,立即回答:“窗户上一共有6个正方形。
”妈妈笑了,爸爸在一旁也笑了,小小给弄了个“丈二和尚莫不着头脑”。
小朋友,你知道小小的爸爸妈妈为什么笑吗?小小数得难道不对吗?如果不对,那么窗户上究竟有几个正方形呢?下面我们就一起来研究数图形的问题。
典型例题例【6】下图中有多少条线段?A B C D E分析我们把图中的线段AB、BC、CD、DE看作是基本线段,那么:由1条基本线段构成的线段有AB、BC、CD、DE 4条;由2条基本线段构成的线段有AC、BD、CE 3条;由3条基本线段构成的线段有AD、BE 2条;由4条基本线段构成的线段有AE 1条。
小学奥数第五讲:图形的计数

小学奥林匹克数学第一集:第五讲:图形的计数一、数一数小朋友,你知道中有多少个三角形吗?我们可以这样想,图中的小三角形一共有4个,大三角形有1个,所以一共有5个三角形。
在数数时,要做到有次序,有条理,不遗漏也不重复,这样才能正确地数数。
例1:数一数下图各有几条线段?分析:我们可以照下面的方法数:解:共有线段4+3+2+1=10(条)例2:图中有多少个小正方体?分析:这个图形是由小正方体组成的。
可以采用数数的方法,按顺序数。
也可以根据图形的组成规律进行计算,如果每2个一摞,一共有4摞。
解:方法一:一个一个地数出8个正方体。
方法二:2×4=8(个)答:共有8个小正方体。
例3:将9个小正方体组成如图所示的“十”字形,再将表面涂成红色,然后将小正方体分开。
问(1)2面涂成红色的有几个?(2)4面涂成红色的有几个?(3)5面涂成红色的有几个?分析:整个图形表面涂成红色。
只有“粘在一起的”面没有涂色。
中间的一个小正方体2面涂色,四端的4个小正方体都是5面涂色,剩下的四个小正方体都是4面涂色。
解:(1)2面涂成红色的小正方体只有1个。
(2)4面涂成红色的小正方体有4个。
(3)5面涂成红色的小正方体有4个。
例4:亮亮从1写到100,他一共写了多少数字“1”?分析:在1到100这100个数中,“1”可能出现在个位、十位或百位上。
应分三种情况计数:“1”在个位上的数有:1、11、21、31、41、51、61、71、81、91共10个;“1”在十位上的数有:10、11、12、13、14、15、16、17、18、19共10个;“1”在百位上的数有:100 只有1个。
解:10+10+1=21(个)答:共写21个。
例5:27个小方块堆成一个正方体。
如果将表面涂成黄色,求:(1)3面涂成黄色的小方块有几块?(2)1面涂成黄色的小方块有几块?(3)2面涂成黄色的小方块有几块?分析:涂色的有26个小方块。
3面涂色的只有顶点上的8个小方块;1面涂色的只有六个面上中间的小方块;其余的必然是2面涂色的小方块。
奥数知识点-图形计数

巧数图形例1、数出下图中共有多少条线段。
分析与解:对于基础图形,用最小线段为单位,按序递增。
单拼:3(段),双拼:2(段),三拼:1(段)通过以上的计数方法可以发现:开小火车的方式解决。
最小线段(基础线段)的数量为火车头火车头为基础线段数3段:3+2+1=6(段){或者,线段个数=基础线段数×端点÷2(高阶)基础线段要求:手拉手,肩并肩对于相交的线段,分别计算各个方向,然后加总例2、数出下页左上图中锐角的个数。
分析与解:对于基础图形,可以使用开小火车的方式解决。
最小线段的数量为火车头。
/或者,角的个数=最小角个数×(最小角个数+1)÷2又,角的个数=射线的个数×(射线个数-1)÷2例3、下列各图形中,三角形的个数各是多少分析与解:对于基础图形,可以使用开小火车的方式解决,最小线段的数量为火车头。
所以,三角形个数=底边线段个数(每个底边基础线段构成一个基础三角形)或者,三角形的个数=最小三角形个数×(最小三角形个数+1)÷2(高阶)¥以上的内容基本是单层规整图形:数线段(数角,数三角形),解决方法:开小火车!对于多层规整的图形,应该以单层规整图形为基础,运用技术,算出多层规整图形的数量。
例4、下列图形中各有多少个三角形分析与解:方法(1)使用分层计数法:图(1)~图(2)上层:4+3+2+1=10(个)上层:4+3+2+1=10(个)下层: 0(个);中层:0(个)上下层:4+3+2+1=10(个)下层:0(个)[ 上中层:4+3+2+1=10(个)中下层:0(个)—上中下层:4+3+2+1=10总数:10+0+10=20(个)总数:—10+10+10=30(个)方法(2)公式法:第一层三角形的总数×层数公式法:第一层三角形的总数×层数图(1)图(2)第一层:4+3+2+1=10(个)4+3+2+1=10(个),第一层:层数: 2(层)层数: 3(层)总数:10×2=20(个)¥总数:10×3=30(个)例5、下列图形中各有多少个三角形分层法:;上层:4+3+2+1=10(个)下层: 4(个)(吹泡泡法)上下层:。
小学四年级数学 奥数 第17讲 数数图形

小学四年级数学奥数第17讲数数图形一、知识要点我们已经认识了线段、角、三角形、长方形等基本图形,当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。
要想准确地计数这类图形中所包含的某一种基本图形的个数,就需要仔细地观察,灵活地运用有关的知识和思考方法,掌握数图形的规律,才能获得正确的结果。
要准确、迅速地计数图形必须注意以下几点:1.线段上有n个端点,那么线段的条数为n+(n-1)+(n-2)+…+3+2+12.从一个顶点引n条射线,那么锐角的个数为n+(n-1)+(n-2)+…+3+2+13. 由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为:1×1+2×2+…+n×n。
4. 如果一个长方形的长被分成m等份,宽被分成n等份(长和宽的每一份都是相等的)那么正方形的总数为:mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)n.二、精讲精练【例题1】数出下面图中有多少条线段。
练习1:数出下列图中有多少条线段。
(2)【例题2】数一数下图中有多少个锐角。
练习2::下列各图中各有多少个锐角?【例题3】数一数下图中共有多少个三角形。
练习3::数一数下面图中各有多少个三角形。
【例题4】数一数下图中共有多少个三角形。
练习4::数一数下面各图中各有多少个三角形。
【例题5】数一数下图中有多少个长方形。
练习5::数一数下面各图中分别有多少个长方形。
【例题6】数一数下图中有多少个长方形?练习6:数一数,下面各图中分别有几个长方形?【例题7】数一数,下图中有多少个正方形?(每个小方格是边长为1的正方形)练习7::数一数下列各图中分别有多少个正方形?(每个小方格为边长是1的小正方形)【例题8】数一数下图中有多少个正方形?(其中每个小方格都是边长为1个长度单位的正方形)练习8:数一数下列各图中分别有多少个正方形。
【例题9】从广州到北京的某次快车中途要停靠8个大站,铁路局要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?练习9:1.从上海到武汉的航运线上,有9个停靠码头,航运公司要为这段航运线准备多少种不同的船票?2.从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?3.从成都到南京的快车,中途要停靠9个站,有几种不同的票价?【例题10】求下列图中线段长度的总和。
小学奥数与应用题——图形的计数

小学奥数与应用题——图形的计数一、数线段、数角、数三角形例1:数一数下列图形中各有多少条线段。
分析1:[左端点] 按照线段的左端点的顺序数图(1)线段最左边的端点是A ,以A 为左端点线段有AB 、AC ;以B 为左端点线段有BC ,所以图(1)中线段的总个数为2+1=3(条)。
同理:图(2)中线段的总个数为3+2+1=6(条)。
图(3)中线段的总个数为4+3+2+1=10(条)。
分析2:[基本线段]图(1)中基本线段有2条,则线段的总个数为2(21)32+=(条) 图(2)中基本线段有三条,AB 、BC 、CD ,包含三条基本线段有一条AD ,(1)包含两条基本线段有二条,AC 、BD ,(2)包含一条基本线段有三条AB 、BC 、CD (3),所以图(2)中线段的总个数为3+2+1=6(条) 图(3)基本线段有4条,则线段的总个数为4(41)102+=(条) 模型:一条大线段有n 条基本线段,则这条线段的总个数为 1+2+3+……+n=+1n (n )2练习:数一数下图中共有线段 条。
例2:数出下图中总共有多少个角。
分析1:角度:[射线]数出顶O 点的射线的个数(5条)过这个顶点的角的个数为(4+3+2+1)图中总共有角的个数为4+3+2+1=10(个)模型:一幅图中角的个数有多少首先看图中有几个顶点,其次看每个顶点射线(或线段)的条数n ,确定每一顶点角的个数(1)2n n -;最后求和。
分析2:角度[基本角]同基本线段相似,此图中有4个基本角,则角的个数为4+3+2+1=10(个)模型:一幅图中一个顶点有n 个基本角,则这个顶点角的总个数为1+2+3+……+n=+1n (n )2练习:数出下图中总共有多少个角。
例3:下图中,各个图形中各有多少个三角形?分析1:角度:[边共线]图(1)中以AB为边的三角形(△ABD,△ABE,△ABC)……三角形的个数(3+2+1)(1)(2)图(2)中以AB为边的三角形, (4)……图(2)中以AG为边的三角形(4)……图(2)中以AM为边的三角形(4)……图形中三角形的总个数为3×(4+3+2+1)=30分析2:[基本三角形]同前相似总结:数线段、数角、数三角形的总个数,就是等于从1开始的连续几个自然数的和这几个连续自然数的和的最大加数是基本线段(基本角、基本三角形),二、数长方形、正方形及数综合图形例4:如下图,数一数下列各图中长方形的个数。
小学奥数家教 计数问题一几何中的计数

计数问题一、数线段第一种:按照线段的端点顺序去数第二种:按照基本线段多少的顺序去数.线段的总条数等于从1开始的连续几个自然数的和,这个连续自然数的和的最大的加数是线段分点数加1或者是线段所有点数(包括线段的两个端点)减1.二、数角数角的方法可以采用数线段的方法来数,就是角的总数等于从1开始的几个连续自然数的和,这个和里面的最大的加数是角分线的条数加1三、数三角形1.共顶点只有一个公共底边的三角形数法:计算三角形的总数也等于从1开始的几个连续自然数的和,其中最大的加数就是三角形一边上的分点数加1,也就是三角形这边上分成的基本线段的条数.2.有多条底边的三角形数法:分开看各底边用之前方法进行计数小结:由本题可以推出一般情况:若周角中含有n个基本角,那么它上面角的总数是 n(n-1)+1.练习1.数一数下图中,各有多少条线段?2.数一数下图中各有多少角?3.数一数下图中,各有多少条线段?4.数一数下图中,各有多少条线段,各有多少个三角形?四、数长方形一般情况下,如果有类似图Ⅲ的任一个长方形一边上有n-1个分点(不包括这条边的两个端点),另一边上有m-1个分点(不包括这条边上的两个端点),通过这些点分别作对边的平行线且与另一边相交,这两组平行线将长方形分为许多长方形,这时长方形的总数为:(1+2+3+…+m)×(1+2+3+…+n).五、数正方形一般地,如果类似图Ⅳ中,一个大正方形的边长是n个长度单位,那么其中边长为1个长度单位的正方形个数有:n×n=n2(个),边长为2个长度单位的正方形个数有:(n-1)×(n-1)=(n-1)2(个)…;边长为(n-1)个长度单位的正方形个数有:2×2=22(个),边长为n个长度单位的正方形个数有:1×1=1(个).所以,这个大正方形内所有正方形总数为:12+22+32+…+n2(个)一般情况下,若一长方形的长被分成m等份,宽被分成n等份,(长和宽上的每一份是相等的)那么正方形的总数为(n<m):mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)·1六、数复杂图形中三角形尖朝上的三角形共有四种.每一种尖朝上的三角形个数都是由1开始的连续自然数的和,其中连续自然数最多的和中最大的加数就是三角形每边被分成的基本线段的条数,依次各个连续自然数的和都比上一次少一个最大的加数,直到1为止.尖朝下的三角形的个数也是从1开始的连续自然数的和,它的第一个和恰是尖朝上的第二个和,依次各个和都比上一个和少最大的两个加数,以此类推直到零为止.我们已对较基本、简单的图形的数法作了较系统的研究,寻找到了一般规律.而对于较复杂的图形即综合图形的数法,我们仍需遵循不重复、不遗漏的原则,采用能按规律数的,按规律数,能按分类数的就按分类数,或者两者结合起来就一定能把图形数清楚了. 35练习1.下图中有多少个正方形?2.下图中有多少个长方形?3.下图中有多少个长方形?4.下图(1)、(2)中各有多少个三角形?5.下图中有多少个三角形?6.下图中有多少个三角形?7.下图中有多少个正方形?解答:1.①在AB线段上有4个分点,所以它上面线段的总条数为:5+4+3+2+1=15(条).②在线段AB上有3个分点,所以它上面线段的总条数为4+3+2+1=10(条).在线段CD上有4个分点:所以它上面线段的总条数为:5+4+3+2+1=15(条).∴整个图(2)共有线段10+15=25(条).③在线段AB上有3个分点,它上面线段的条数为:4+3+2+1=10(条).在线段CD上有2个分点,它上面线段的条数为:3+2+1=6(条).在线段EF上有2个分点,它上面线段的条数为6条.所以图(3)上总共有线段10+6+6=22(条).2.①在∠AOB内有4条角分线,所以共有角:5+4+3+2+1=15(个);②在∠AOB 内有9条角分线,所以共有角:10+9+8+7+6+5+4+3+2+1=55(个);③周角内含有6个基本角,所以共有角:6×(6-1)+1=31(个).3.①(3+2+1)×7=42;②(6+5+4+3+2+1)×4+(4+3+2+1)×7=21×4+10×7=84+70=154.4.①有线段:(4+3+2+1)×3+(3+2+1)×5=30+30=60(条)有三角形:(4+3+2+1)×3=30(个);②有线段:(5+4+3+2+1)+5×2+(2+1)=15+10+3=28(条)有三角形:(5+4+3+2+1)×2+5=15×2+5=35(个).1.共有正方形54个.2.共有长方形136个.3.共有长方形133个.4.(1)共有三角形78个.(2)共有三角形58个.5.共有三角形45个.6.共有三角形36个.7.共有正方形24个.。
小学奥数模块教程几何计数(ABC级)

几何计数知识框架一、公式计算法几何计数内容很广,包括数线段的条数,角的个数,长方形、正方形、三角形、平行四边形、梯形等图形的个数,也包括数立体图形的个数。
图形的计数一般有两种思考方法:公式计算法和分类计数法。
三年级学习的线段、长方形和正方形的计数就属于公式计算法。
(1)一条线段有两个端点,若这条线段上有n个点,那么线段总数是(n-1)+(n+2)+…+3+2+1(2)如果一个长方形的长边上有n个小格,宽边上有m个小格,那么长方形的总数是(1+2+3+…+n)×(1+2+…+m)(3)如果把正方形各边都n等分,那么正方形的总数是n2+(n-1)2+(n-2)2+…+32+22+12上面计算线数的方法也可用于计算角的个数,而且,根据这些计数方法在以后还可以类推出立体图形的计算方法。
二、对应法将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.重难点(1)分类数图形。
(2)对应法数图形。
一、 分类数图形【例 1】 下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的.如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍,那么围成的图形有几层,共用了多少根小棍?【巩固】 如图所示,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?【例 2】 图中有______个正方形.例题精讲【巩固】 数一数:图中共有________ 个正方形。
【例 3】 右图中三角形共有 个.【巩固】 数一数图中有_______个三角形.【例 4】 图中共有多少个三角形?【巩固】 下图是由边长为1的小三角形拼成,其中边长为4的三角形有_____个。
CBA【例 5】如图,每个小正方形的面积都是l平方厘米。
则在此图中最多可以画出__________个面积是4平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。
四年级奥数-巧数图形个数

姓名:巧数图形个数“数图形的个数”是趣味图形问题的一种,由于几何图形千变万化,错综复杂,要想准确地数出图形中所包含的某一个几何图形的个数,关键是要掌握有条理有次序地数图形的方法。
数图形的个数时,既不能同一图形数两次,又不能把有的图形漏掉不数,常用的计算方法有按顺序和分类数两种。
下面举例介绍两种方法的运用规律:例:数一数下面图中有多少条线段。
第一:按含基本线段的顺序去数。
上图一共有5条小线段,这每条小线段就是基本线段,有5条基本线段,包含有两条基本线段的有4条……第二:按端点进行分类去数。
以线段最左边的点为第一个端点,第二个点为第二个端点……为了方便同学们计数,向大家介绍数线段、三角形、角数量的公式:1+2+…+(n-2)+(n-1)=2)1(nn一、试一试,看谁数得又对又快。
一共有()个三角形。
一共有()个角。
二、填空。
1. 算式中有乘法和加、减法,应先算();算式中有除法和加、减法,应先算();算式中有括号的,应先算()。
2. 在计算25+13×2时,先算( )法,再算( )法。
3. 在计算78÷16×3时,先算()法,再算()法。
4. 在算式50-20÷5里,如果要先算减法,那么算式应该是:()。
里填上“<”“>”或“=”。
20×5+×(5+3)48÷6÷÷(6×8)280-37-280-(37+163)60-24÷60-24)÷12小故事明明和沉沉都十分喜欢数学。
一天明明问沉沉:“你最喜欢几?”“我最喜欢9。
”“那你说说从1数到100,要说几次‘9’?”“啊!……这”沉沉被难住了,“这要数一数才能知道,一分钟时间。
”同学们,请你在一分钟内说出从1到100有多少个9?。
奥数-05图形计数+答案

( )个
( )个
4
( )个
【例 7】
下图中各有多少个三角形?
分层法: 上 层: 下 层: 上下层: 总 数:
下图中,有多少个正方形?
解析:利用开小火车法: 火车头为最小正
5
练习一 下图中,有多少个正方形?
1、
2、
3、
( )个
( )个
( )个
【例 2】
下图形中,长方形有多少个? 解析,先将<格 1>与<格 2>隐去,剩下的
练习一
2
【例 2】 数出右图中共有多少条线段。 解析:(加法原理)从基本图形(只包含
最短线段)的个数出发,按序递增,依次数 出它们的个数,并求出它们的和是多少。最 小线段(基础线段)的数量为火车头,有 3
条,由两条基础线段拼成的线段有 2 条,由三条基础线段拼成的线段有 1 条,共有 3+2+1=6(条)。
练习七 下列图形中各有多少个三角形?
按分类加法原理
4+3+2+1=10(个) 4(个) 4+3+2+1=10(个) 10+4+10=24(个)
【例 8】 下图中有多少个三角形? 解析:假设每一个最小三角形的边长为 1。按边
的长度来分类计算三角形的个数。 边长为 1 的三角形,从上到下一层一层地数,有
一、图形计数方法——分类计数法
它是指先把所要计数的对象按性质、特点进行分类,统计出每一类的个数,再求 各类之和。分类计数的理论基础是“加法原理”。
运用加法原理的关键问题:确定分类的方法。 举例:下图中共有多少个图形? 可以分成圆、正方形、三角形和长方形 4 类,统计出各类的个数,再相加。也可 以按位置分上、中、下分别统计,再求和。
初一奥数-几何图形的计数问题

• 同样,宽的一边上不同的线段也有10条.
• 所以,共有长方形10×10=100(个).
• (2)因为长的一边上的10条线段长分别为
• 5,17,25,26,12,20,21,8,9,1,
• 宽的一边上的10条线段长分别为
• 2,6,13,16,4,11,14,7,10,3.
• 所以,所有长方形面积和为
点能把原三角形分割成2×1999+1=3999个小三角形.
2021/4/14 星期三
28
• 1.填空:
• (1)在圆周上有7个点A,B,C,D,E,F和G,连接每 两个点的线段共可作出______条.
• (2)已知5条线段的长分别是3,5,7,9,11,若每次以 其中3条线段为边组成三角形,则最多可构成互不全等 的三角形_____个.
• 因此,5个圆和1条直线,最多将平面分成
22+10=32个部分.
2021/4/14 星期三
24
• 例10 、 平面上5条直线和一个圆, 最多能把平面分成多少个部分?
2021/4/14 星期三
25
• 解:首先,由例7知,5条直线最多将平 面分成16个部分.
• 现在加入一个圆,它最多与每条直线有 两个交点,所以,与5条直线最多有10个 交点.这10个交点将圆周分成10段圆弧,
2021/4/14 星期三
1
几何图形的计数问题
主讲:刘文峰
2021/4/14 星期三
2
专题简析
• 在几何中,有许多有趣的计数问题,如计 算线段的条数,满足某种条件的三角形的 个数,若干个图分平面所成的区域数等 等.这类问题看起来似乎没有什么规律可 循,但是通过认真分析,还是可以找到一 些处理方法的.常用的方法有枚举法、加 法原理和乘法原理法以及递推法等.
小学奥数讲义4年级-15-图形计数-难版

几何中的计数问题包括:数线段、数角、数长方形、数正方形、数三角形、数综合图形等。
在几何图形的计数问题中,各种图形的基本概念及其相关性质是计数过程中寻找规律的基础。
掌握图形的规律和方法多种多样,常用的有按顺序数和分类数两种。
分类方法如:按点分类,按边分类,按块分类等等还要注意分类的合理性,只有当所分的类型包含所有情况并且相互不重叠,这样才有可能做到不重复、不遗漏。
【例1】★数一数图1中有多少条线段?【解析】第一种可以按端点进行分类,如图1中,线段最左边的端点是A ,即以A 为左端点的线段有AB 、AC 、AD 、AE 、AF 共五条;以B 为左端点的线段有BC 、BD 、BE 、BF 共四条;以C 为左端点的线段有CD 、CE 、CF ,共三条;以D 为左端点的线段有DE 、DF 共二条;以E 为左端点的线段有EF ,一条。
这些线段的和就是图形中线段的条数。
第二种可以按含基本线段多少的顺序去数。
在此题中最长的线段AF 上有四个分点,将AF 分成了5条小线段,这每条小线段就是基本线段。
首先有5条基本线段,其次是包含有两条基本线段的有4条,然后是包含有三条基本线段的有3条,包含有四条基本线段的有2条,包含有五条基本线段的有1条。
则线段AF 上的线段条数可求。
5+4+3+2+1=15(条)典型例题知识梳理【例2】★数一数,右图中共有多少个角?【解析】我们规定:把相邻两条射线构成的角叫做基本角,我们可以这样分类数:由1个基本角构成的角有:∠AOB、∠BOC、∠COD、∠DOE、∠EOF共5个.由2个基本角构成的角有:∠AOC、∠BOD、∠COE、∠DOF共4个.由3个基本角构成的角有:∠AOD、∠BOE、∠COF共3个.由4个基本角构成的角有:∠AOE、∠BOF共2个.由5个基本角构成的角有:∠AOF共1个.角总数5+4+3+2+1=15(个).【小试牛刀】数出图2中总共有多少个角?【解析】10个【例3】★数一数,右图中共有多少个三角形?你有什么好方法?【解析】1个三角形组成的:△AOB、△BOC、△COD、△DOE、△EOF共5个;2个三角形组成的:△AOC、△BOD、△COE、△DOF共4个;3个三角形组成的:△AOD、△BOE、△COF共3个;4个三角形组成的:△AOE、△BOF共2个;5个三角形组成的:△AOF共1个;共有5+4+3+2+1=15(个).【例4】★★数一数:下面三个图中长方形分别有多少个?【解析】先数一数AB边上有多少条线段,每一条线段可以分别作为长方形的长,再数一数AD上有多少条线段,每一条线段可以分别作为长方形的宽,每一条长与一条宽搭配,就确定了一个长方形,这样就容易得出一共有多少个长方形了.先来看图(1),AB边上包含着的10条线段中的每一条(想一想为什么),都可与线段AD 对应,惟一确定一个长方形,所以图(1)中共有10×1=lO个长方形.再来看图(2),与图(1)不同的是在AD上增加了一个分点,这样就有3条线段时,这3条线段分别与AB边上不同的线段构成长方形,所以图(2)中共有10×3=30个长方形.最后看图(3),与上面的思路相同,由于AD边上有3+2+1=6条线段,所以图(3)中共有10×6=60个长方形.即:(1)(4+3+2+1)×1=10(个);(2)(4+3+2+1)×(2+1)=30(个);(3)(4+3+2+1)×(3+2+1)=60(个).【小试牛刀】数一数图4中长方形的个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3、下列各图形中, 三角形的个数各是多少
(最小三角形个数+1) +2(高阶)
巧数图形
例1、数出下图中共有多少条线段。
X—C D
分析与解:对于基础图形,用最小线段为单位,按序递增。
单拼:3 (段),双拼:2 (段),三拼:1 (段)通过以上的计数方法可
以发现:开小火车的方式解决。
最小线段(基础线段)的数量为火车头
火车头为基础线段数3段:3+2+1二6 (段)或者,线段个数二基础线段
数X端点(高阶)
基础线段要求:手拉手,肩并肩
对于相交的线段,分别计算各个方向,然后加总
例2、数出下页左上图中锐角的个数。
分析与解:对于基础图形,可以使用开小火车的方式解决。
最小线段的数量为火车头。
或者,角的个数二最小角个数X (最小角个数+1) +2
又,角的个数二射线的个数X (射线个数-1) -2
分析与解:对于基础图形,可以使用开小火车的方式解决,最小线段的数量为火车头。
所以,三角形个数二底边线段个数(每个底边基础线段构成一个基础三角形)
或者,三角形的个数二最小三角形个数
X
⑷(5)
以上的内容基本是单层规整图形:数线段(数角,数三角形),解决方法:开小火车! 对于多层规整的图形,应该以单层规整图形为基础,运用技术,算出多层规整图形的数量。
例4、下列图形中各有多少个三角形?
分析与解:方法(1)使用分层计数法:
图(1)
图(2)
上层:4+3+2+1=10 (个) 上层: 4+3+2+1=10 (个) 下层: 0 (个) 中层: 0 (个) 上下层:4+3+2+1=10 (个)
下层: 0 (个)
上中层: 4+3+2+1=10 (个)
中下层: 0 (个)
上中下层:4+3+2+1=10
总 数:10+0+10=20 (个) 总数: 10+10+10二30
(个) 方法(2)公式法:第一层三角形的总数X 层数
公式法:第一层三角形的总数X 层数 图(1) 第一层: 4+3+2+1=10 (个) 图(2)
第一层:4+3+2+1=10 (个)
层数: 2 (层) 总数:
10X2二20 (个)
层数:
3 (层)
总数:10X3=30 (个)
例5、下列图形中各有多少个三角形?
1
分层法:
上层:4+3+2+1=10 (个) 下层:
4 (个)(吹泡泡法)
上下层:4+3+2+1=10 (个) 总 数:10+4+10=24 (个)
例6、右图中有多少个三角形?
例7、右图中有多少个三角形?
分析与解:对于不规则的图形,数之前,先将每个图形编号,
编好后,先数单拼三角形1、4、3号,共3个。
再数两个图形合成的(双拼)三角形,1+2号,2+3号,
3+4号,4+1号,按顺序两个两个合并,共4个三角形。
最后数由1 +2+3+4号组成的(四拼)大三角形,有1个。
所以3+4+1=8,共8个三角形。
例8、下列各图形中,长方形的个数各是多少?
分析与解:对于(单层)基础图形,可以使用开小火车的方式解决。
每个长方形相当于最小线
段。
所以数单层的基础长方形,就是数基础线段数。
对于多层的长方形的个数=单层长方形的数量X 层数(个)
单层长方形的数量=长边上的线段数(个),层数=宽边上线段的个数(层)
例9、下列图形中,长方形的个数是多少个?
分析与解:对于基础图形,可以使用开小火车的方式解决。
单层长方形的数量二长边线段数二4+3+2+1二10 (个),
层数二宽边线段数=3+2+1=6 (层)
总数二(4+3+2+1) X (3+2+1) =60 (个)
例10、下列图形中,长方形的个数是多少个?
分析,先将〈格1>与〈格2>隐去,剩下的格3,
就是一个多层规整长方形=10X6=60 (个)
格1带来的长方形=4 (个)(吹泡泡法)
格2带来的长方形=5 (个)
总数=60+4+5=69 (个)
例11、下列图形中,长方形的个数是多少个?
分析与解:了解正方形的构成特点:四边相等。
方法(1)数格子:一格,四格,九格,十六格...
方法(2)开小火车法:最小正方形的个数为“火车头”,后面的“车厢”中的每个
乘数都减T,直至出现1为止(0乘任何数都等于0)
解:3X3+2X2+1X1=14 (个)
例12、下列图形中,正方形的个数是多少个?
分析与解:利用开小火车法:
火车头为最小9正方形数量:6X5
正方形个数二6X5+5X4+4X3+3X2+2X1 =70 (个)
例13、数下列图形中共有21个三角形,一共需要多少个小棒:
12345••••••21
357911••••••?
例10、在下图中,包含"*”号的长方形和正方形共有多少个?分析与解:对于不规整的图形,进行分类讨论。
左图中,应先进行分类:正正方形与斜正方形
正正方形=5+5=10 (个)
斜正方形二 5 (个)
总数二10+5二15 (个)
例11、如下图是由小立方体构成的塔,数一数有多少个小立方体?
分析与解:数立方体时,先从顶层数起。
公式:本层可见数+上层数
本题:1+ (3+1) + (5+4) + (7+9) =30 (个)
例12、数一数,下列图形中有多少个长方形?
OO OOOO OOOOO OOOO OO
方法(1):小讨厌法:
不包含小讨厌的多层规整图形:10X6=60 (个) 小讨厌m + a+0: 4+4+4=12,共:60+12=72 (个) *方法(2):重叠法(三年级): 横:10X6=60 (个),竖:3X10=30 (个)
中(重叠):3X6=18 (个),共:60+30-18=72 (个) 例13、数一•数,第10个图形应该有多少圆圈
组成?
OO
OO OOOO
OO
通过观察可以发现如下的规律:
例13、数一数,第10个图形应该有多少条线段?
通过观察可以发现如下的规律:
例14、数一•数,下列图形中包含★长方形有多少个? 方法(1)勾对角线法:将★的左上角的点和右下角的点相连: 通过加标字母A 、B 和a 、b 、c 、d 、e 、f,帮助我们数图形:
Aa> Ab> Ac> Ad> Ae 、 Af 、 Ba 、 Bb> Bc> Bd> Be> Bf>
*方法(2)公式法:经过★划十字线,左侧、右侧、上面、下面焦点数相乘:2X2X1X372(个)
例15、数一•数,下列图形中有多少条线段?有多少个三角形?
(1)
数线段:分方向:共:6X5+5=35 (条) (2)
数三角形:分方向
中间五角星(不用①③③④⑤):共10个三角形。
仅使用①③③④⑤中一条:每一条有4个三角形,共4X5=20 (条) 使用①③③④⑤中的两条:共4个三角形。
共:10+20+5二35 (个)。
