第十一章三相电路
《电路》邱关源第五版课后习题解答

电路习题解答第一章 电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得 U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上 式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=; ⑴ KCL :43211-=I I ;I 185=A ;U I I S =-⨯=218511V 或16.V ;或I I 12=-。
⑵ KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章电阻电路的等效变换【题1】:[解答]I=-+9473A=0.5A;U Ia b.=+=9485V;IU162125=-=a b.A;P=⨯6125.W=7.5W;吸收功率7.5W。
邱关源—电路—教学大纲—第十一章

(三)教学思路
1、一二节一块讲。先介绍三相电压,再讲三相电路的连接以及三相电路的一些 名词术语,然后讲线电压(电流)与相电压(电流)的关系。 2、讲对称三相电路的计算。先推出中性点等电位,再讲三相归结为一相计
(四)教学内容和要点
§11-1 三相电路 §11-2 线电压(电流)与相电压(电流)的关系
一、三相电压:指三个最大值相等,角频率相同而初相位不同的正弦电压。 若初相互差 120 时,则称为对称三相电压。 以 uA 为参考正弦量,它们的瞬时值表达式为
i
i
i
本章,无特殊说明,三相电源的相序均是顺序。 三、对称三相电路的联接 (一) 、星形联接: 1、联接方式: A
IA U _ A
.
.
A’ Z N’
.
+
.
UC
C +
.
_
_N
U AB
.
.
IN U CA IB IC
.
.
Z
UB +
B
Z B’ C’
U BC
.
2、常用术语:①端线:由电源始端引出的联接线
②中线:联接 N , N 的联接线 ③相电压:指每相电源(负载)的端电压。 ④线电压:指两端线之间的电压 ⑤相电流:流过每相电源(负载)的电流 ⑥线电流:流过端线的电流 ⑦中线电流:流过中线的电流 3、线电压与相电压的关系:
i i i 1 (U A + U B + U C ) Z + Zl = =0 1 1 + Z + Zl Z N
Z l I A' N ' + Z I A' N ' + U N ' N = U A
电路分析 选择题题库 第11章 正弦稳态功率和三相电路

第11章正弦稳态的功率和三相电路1、在三相交流电路中,负载对称的条件是()。
(a)Z Z ZA B C==(b)ϕϕϕA B C==(c)Z Z ZA B C==答案:(c)2、某三角形连接的三相对称负载接于三相对称电源,线电流与其对应的相电流的相位关系是()。
(a)线电流导前相电流30︒(b)线电流滞后相电流30︒(c)两者同相答案:(b)3、三角形连接的三相对称负载,接于三相对称电源上,线电流与相电流之比为()。
(a)3(b)2(c)1答案:(a)4、作星形连接有中线的三相不对称负载,接于对称的三相四线制电源上,则各相负载的电压()。
(a)不对称(b)对称(c)不一定对称答案:(b)5、对称三相电路的有功功率P U I l l=3λ,功率因数角ϕ为()。
(a)相电压与相电流的相位差角(b)线电压与线电流的相位差角(c)阻抗角与30︒之差答案:(a)6、对称三相电路的无功功率Q U I l l=3sinϕ,式中角ϕ为()。
(a)线电压与线电流的相位差角(b)负载阻抗的阻抗角(c)负载阻抗的阻抗角与30︒之和答案:(b)7、有一对称星形负载接于线电压为380V的三相四线制电源上,如图所示。
当在M点断开时,U1为()。
(a)220V (b)380V (c)190VABCNM答案:(a)18、一对称三相负载接入三相交流电源后,若其相电压等于电源线电压,则此三个负载是( )接法。
(a)Y (b)Y 0 (c)∆答案:(c)9、作三角形连接的三相对称负载,均为RLC 串联电路,且R =10Ω,X L =X C =5Ω,当相电流有效值为I P =1A 时,该三相负载的无功功率Q =( )。
(a)15Var (b)30Var (c)0Var答案:(c)10、正弦交流电路的视在功率定义为( )。
(a)电压有效值与电流有效值的乘积 (b)平均功率(c)瞬时功率最大值答案:(a)11、正弦交流电路的无功功率表征该电路中储能元件的( )。
电网第十一章三相正弦交流电路

UV U 120 0
U W U1200
11.1 三 相 正 弦 交 流 电 源
11.1.3 三相交流电源的“对称”和“相序” 1)若三相电源的最大值相等、频率相同、相位互差1200, 即称为“对称”
电源。 2)三相电源的对称性,是由三相绕组对称结构所保证的。 3)三相对称正弦量的三个电动势(或电流、电压)到达最大值 (或零值) 的
零线, 这种措施称为“保护接零”。 4)有中线的三相星形联结电路,称为三相四线制电路,记作Y0。
11. 2三 相 正 弦 交 流 电 源 的 联 结
11.2.2 电源星形联结的线电压和相电压 三相四线制电路对外输出两种电压:线电压和相电压。 图11-3是星形联结三相电源线电压与相电压的相量图。
11. 2三 相 正 弦 交 流 电 源 的 联 结
1.线电压
相线 (火线) 之间的电压, 称为线电压, 用uUV 、uVW 、uWU表示
(下标表示一定的顺序) , 由于电路对称, 三个线电压的有效值 是相等的, 记作U线或UL。 2.相电压 每相绕组的始端与末端之间的电压,即每相绕组两端的电压,也即是
火线与中线之间的电压,称为相电压, 用uU、uV、uW 表示, 由于
三相交流电之所以广泛应用, 是因为它比单相交流电,具有以下的主要优点: 1)制造三相发电机和三相变压器比制造单相的要省材料。 2)在输电距离、输送功率,负载的线电压,负载的功率因数、输电损耗以 及输电线材料等方面,在相同的条件下,用三相输电线的金属用量仅为用 单相输电时的75%。 3)三相电能产生旋转磁场, 从而能制成结构简单、性能良好的三相异步 电动机。 4)有星形和三角形两种联结方式,提供线电压和相电压两种电压,提供线 电流和相电流两种电流。
西安交大版电路第011章_三相电路

– N – –
& UA
+
& IB
& + & UB I C
& UC
+
& IN
=0
中线可视为短路。 ∴ N′N中线可视为短路。 中线可视为短路 & & & UA & = & = UC = αI & & = UB = α2I & IC IB 于是, 于是,IA A A Z1 + Z Z1 + Z Z1 + Z & & & 三者对称, & ∵三者对称, I N = −( I A + I B + I C ) = 0 ∴ 三相四线制电路的中线又 ∴对称Y-Y三相四线制电路的中线又可视为开路。 对称 - 三相四线制电路的中线 可视为开路。
而对星形电源(负载)而言, 而对星形电源(负载)而言,I l = I p
10
负载): 一、对称星形电源(负载 : 对称星形电源 负载
C N
& -UB
& U AB
30° ° A
C
+
& UA +
_ _
C A A N
& UA
& UC _
& UB
B
& UB
B + B
结论:对Y接法的对称三相电源 结论: 接法的对称三相电源 接法的 (1) 线电流等于对应的相电流 I l = I p 线电流等于对应的相电流: (2) 相电压对称,则线电压也对称; 相电压对称,则线电压也对称 (3) 线电压与相电压的大小关系 U l = 3U p . 线电压与相电压的大小关系: (4) 线电压相位超前对应相电压 °。 线电压相位超前对应相电压30° 超前对应相电压
天津理工电路习题及答案 第十一章 三相电路

第十一章 三相电路一 重点和难点1 三相对称的概念2 三相对称电路单相求解的方法3 三相对称电路功率的求解 星形联接:线电压与相电压的关系:.............(11120)330330330AB A B A A BC B CB CAC A CU U U U U U U U U U U U U =-=-∠-=∠=-=∠=-=∠①相电压对称,线电压也对称; ②3P LU U =;③线电压超前对应相电压30 ④线电流与相电流的关系:三角形联接:必须注意,如果任何一相定子绕组接法相反,三个相电压之和将不为零,在三角形联接的闭合回路中将产生根大的环行电流,造成严重恶果。
线电流与相电流的关系:''''''''''''...''...''...''330330330A B C A A B A B C A B B C B C A B C C A C I I I I I I I I I I I I •••=-=∠-=-=∠-=-=∠-①相电流对称,线电流也对称; ②3L P I I =;③线电流滞后对应相电流30 ④线电压与相电压的关系:P L U U =平均功率cos cos cos 3cos A B CAP AP ZA BP BP ZB CP CP ZC AP BP CPP AP BP CPPZA ZB ZCZP P ZP P P P U I U I U I U U U U I I I I P U I ϕϕϕϕϕϕϕϕ=++=++=======∴对称时: []23,3333cos ()3Re l P l Pl P l P P P l ll l Z Z P U U I I U U I I U I U I P U I P I Z ϕϕ=======星形:,三角形:故 为每相阻抗的阻抗角无功功率 对称时:[]23sin 3sin 3Im P P Z l l Z p Q U I U I I Z ϕϕ===视在功率 对称时:2233P P l l S P Q U I U I =+==三相功率的测量:(两瓦特表法)i A + i B + i C =0()()()()1()cos()cos()A AB BC C A A B B C A B A C A B C B TAC A BC B AC BC BAu u i i p t u i u i u i u i u i u i i u u i u u i P p t dt U I U I Tψψψψ=++=++--=-+-==-+-⎰可见等式右端两次分别对应两个瓦特表的读数。
《电路》邱关源第五版课后习题答案解析

电路答案——本资料由张纪光编辑整理(C2-241 内部专用)第一章电路模型和电路定律【题 1】:由UAB 5 V可得: I AC 2.5A: U DB0 : U S12.5V。
【题 2】: D。
【题 3】: 300; -100 。
【题 4】: D。
【题5】:a i i1i 2;b u u1u2;c u u S i i S R S;d i i S 1R Su u S。
【题 6】: 3;-5 ; -8。
【题 7】: D。
【题 8】:P US150 W ;P US26W;P US30 ; P IS115 W ; P IS214W ;P IS315W。
【题 9】: C。
【题 10】:3; -3 。
【题 11】:-5 ; -13 。
【题 12】:4(吸收); 25。
【题 13】:0.4 。
【题 14】:31I 2 3; I 1A 。
3【题 15】:I43A; I23A; I31A; I5 4 A。
【题 16】:I7A;U35 V;X元件吸收的功率为 P UI245W。
【题 17】:由图可得U EB 4 V;流过 2电阻的电流 I EB 2 A;由回路ADEBCA列KVL得U AC 2 3I ;又由节点D列KCL得 I CD 4I ;由回路CDEC列KVL解得;I 3 ;代入上式,得 U AC7 V。
【题 18】:P122 I12;故 I 22; I 1I 2;P2I 221I 2⑴ KCL:4I 13I 1;I 18;U S 2I1 1 I 18V或16.V;或I I。
2 5 A512⑵ KCL:4I 13I1;I18A;U S。
224 V第二章电阻电路的等效变换【题 1】:[解答 ]94A = 0.5 A ;U ab9I 4 8.5 V;I73U ab66 125. W = 7.5 W ;吸收I 12 1.25 A;P功率 7.5W。
【题 2】:[解答 ]【题 3】:[解答]C 。
【题 4】: [ 解答 ]等效电路如图所示,I 005. A。
(三相电路)习题解答

第十一章 (三相电路)习题解答一、选择题1.对称三相Y联接负载,各相阻抗为(3 j3),假设将其变换为等效联接负载,那么各相阻抗为 C 。
.(1 j1);.32 /450;.(9j9);.3(3 j3)A B C D2.如图 11— 1 所示电路中, S 闭合时为对称三相电路,设U A U /00V〔U A为A相电源的电压〕,那么 S 断开时,负载端 C 。
A.U AN U /00V,UBN U / 1200V;B.U AN U/00,UBN U /1800V;C.U AN 3U /300V,UBN3U/ 1500V;22D.U AN 3U/ 300V,U BN3U/ 300V 223.如图 11— 2 所示对称三相电路中,线电流I A为D。
U A;U A; C.U A; D.U AA.Z Z N B.Z Z 3Z N Z Z N34.对称三相电路总有功功率为P 3 lIlcos,式中的角是 B。
UA.线电压与线电流之间的相位差角;B.相电压与相电流之间的相位差角;C.线电压与相电流之间的相位差角;D.相电压与线电流之间的相位差角5.如图 11— 3 所示对称星形三相电路的线电流为 2 A,当S闭合后I A变为A。
A.;.;.43;.23A6 A B4AC AD解:设U A U /00,那么U B U / 1200, U C U /1200,UBA3U A/ 3003U A / 1500,U CA3U C/300,开关闭合后I A I B I CU BA U CA3U A /15003U C /300Z Z3U A/15003U A /1200/3003U A/1500/1500Z Z3U A326AZ二、填空题1.三相三线制电路中可用二瓦计法测量三相负载功率。
在不对称三相四线制电路中,可用三瓦计法测量三相负载功率。
2.在图 11— 4 所示三相电路中电源对称,R X L X C,电流表A1的读数为5A,电流表 A2的读数为A,电流表 A3读数为 A。
《电路》第五版-第11章答案
流和电源发出总功率;(2)用两表法测电动机负载的功率,画接线图,求两表读
IA
IA 2
A
IA 1
B
D
C
电动机
Z1 数。 解:
(1)
UA N
2200
V
IA 1
UA N
2200
4.41 53.1 A 电动机负载:
Z 30 j40
P 3Ul IA2 cosφ 1700W
IA2
P 3Ul cos φ
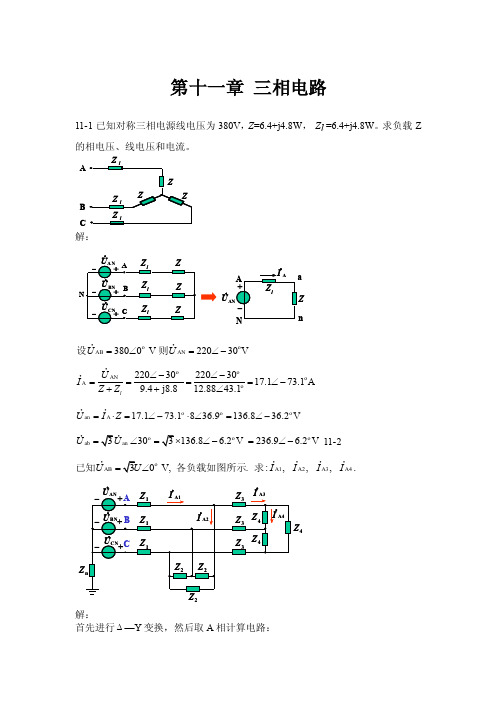
已知U AB
3U 0o
V,
各负载如图所示.
求
:
I A1
,
I A2 ,
I A3,
I A4 .
_
U AN +A
Z1
_ U BN+ B Z1
_ UCN+C Z1
I A1
I A2
Z3 I A3
Z3 Z4 Z3 Z4
I A4
Z4
Zn
Z2 Z2
Z2
解: 首先进行 —Y 变换,然后取 A 相计算电路:
U AN
1
U
AB
30o
U 30o
V
3
+
U AN _
Z1 I A1
I A2
Z3 I A3
Z 2/3
Z 4/3
负载化为 Y 接。根据对称性,中性电阻 Zn 短路。
I A1
Z1
1 3
U AN Z2 //(Z3
1 3
Z4 )
,
I A2 ,
I
A3
可由分流得到
相电流
I A4
1
I
A3
30o
3
11-3Ul =380V,Z1=30+j40W,电动机 P=1700W,cos=0.8(滞后)。求:(1)线电
电路原理复习知识点
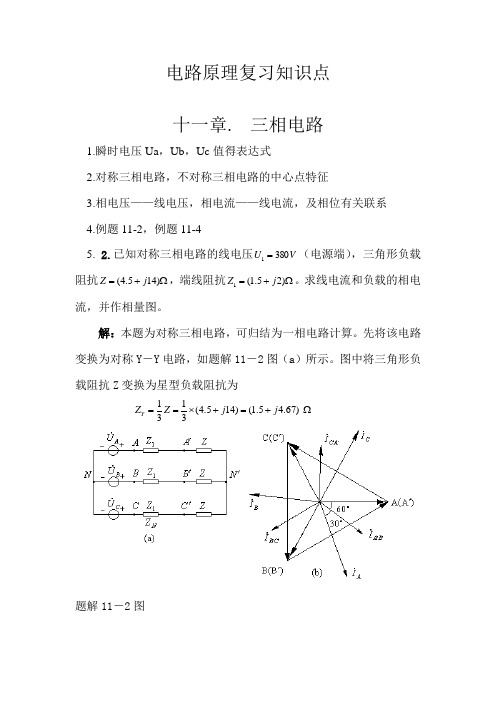
电路原理复习知识点十一章. 三相电路1.瞬时电压Ua ,Ub ,Uc 值得表达式2.对称三相电路,不对称三相电路的中心点特征3.相电压——线电压,相电流——线电流,及相位有关联系4.例题11-2,例题11-45. 2.已知对称三相电路的线电压V U 3801=(电源端),三角形负载阻抗Ω+=)145.4(j Z,端线阻抗Ω+=)25.1(1j Z 。
求线电流和负载的相电流,并作相量图。
解:本题为对称三相电路,可归结为一相电路计算。
先将该电路变换为对称Y -Y 电路,如题解11-2图(a )所示。
图中将三角形负载阻抗Z 变换为星型负载阻抗为 Ω+=+⨯==)67.45.1()145.4(3131j j Z ZY题解11-2图令VU U A︒∠=∠=0220031,根据一相( A 相)计算电路(见题解11-1图(b )中),有线电流A I 为 A78.6508.3067.6302201-∠=+∠=+=j Z Z U I YA A根据对称性可以写出 A 78.18508.302-∠==AB I a IA 22.5408.30∠==ACI a I利用三角形连接的线电流与相电流之间的关系,可求得原三角形负载中的相电流,有 A 78.3537.173031-∠=∠=''A B A I I而 A 78.15537.172 -∠==''''B A C B I a IA 22.8437.17∠==''''B A A C I a I电路的相量图如题解11-2图(b )所示。
6. 5图示对称Y -Y 三相电路中,电压表的读数为1143.16V ,Ω+=)31515(j Z ,Ω+=)21(1j Z 。
求图示电路电流表的读数和线电压ABU 。
题11-5图解:图示电路为对称Y -Y 三相电路,故有0='NN U,可以归结为一相(A 相)电路的计算。
电路分析基础(第十一章 三相电路)要点PPT课件

二、三相电源的连接方式
星形 (Y)连接
A
+
•
UA
– X
Y
Z
•
C UC
•
UB
名词介绍:
•
IA
A
•
•
•
IB
U A B U CA
N
B
B
•
•
I C U BC
C
三角形 ()连接
ZA
•
UC
•
UA
C
X
Y– •
+
B
UB
•
IA
A
•
IB
U U •
•
A B CA
B
•
•
I C U BC
C
(1) 端线(火线):始端A, B, C 三端引出线。
A +
•
IA
A
设
•
U
AN(1)
U相• A电 U压对0o称
线电压U•对A 称;
•
U
B
N
(2)
U线•B电 U压模是12相0o电压模的
3 X–倍Y,即
Z
Ul
•
I B
•
U AB 3Up
•
U CA ;N
•
UC
N
(3)
U线•C电 U压相12位0o超前对应相C 电U• 压C 30Uo。• B
B
•
•
I C U BC
四、三相电路的连接方式
三相电源
三相负载ห้องสมุดไป่ตู้
A +
•
UA
– X
Y
•
IA
A
a
三相• 电路• 的连接方式:I •a
电路第五版邱关源原著电路教案第11章

第十一章三相电路一、教学基本要求1、掌握三相电路的概念及对称三相电路的计算方法2、了解不对称三相电路的概念3、会计算三相电路的功率二、教学重点与难点1. 教学重点: (1).三相电路的概念;(2). 星形连接、三角形连接下的线电压(电流)与相电压(电流)的关系(3). 对称三相电路归结为一相电路的计算方法(4). 三相电路的功率分析(5). 不对称三相电路的概念2.教学难点:(1).三相电路的计算及相量图的应用(2).三线三相制电路功率测量的二瓦特计法三、本章与其它章节的联系:三相电路可以看成是三个同频率正弦电源作用下的正弦电流电路,对它的计算,第九章正弦电流电路中所阐述的方法完全适用。
四、学时安排总学时:6五、教学内容§11.1三相电路三相电路是由三个频率相同、振幅相同、相位彼此相差120°的正弦电动势作为供电电源的电路。
三相电力系统由三相电源、三相负载和三相输电线路三部分组成。
三相电路具有如下优点:(1)发电方面:比单项电源可提高功率50%;(2)输电方面:比单项输电节省钢材25%;(3)配电方面:三相变压器比单项变压器经济且便于接入负载;(4)运电设备:具有结构简单、成本低、运行可靠、维护方便等优点。
以上优点使三相电路在动力方面获得了广泛应用,是目前电力系统采用的主要供电方式。
研究三相电路要注意其特殊性,即:(1)特殊的电源;(2)特殊的负载;(3)特殊的连接;(4)特殊的求解方式。
1. 对称三相电源通常由三相同步发电机产生对称三相电源。
如图11.1所示,其中三相绕组在空间互差120°,当转子以均匀角速度ω转动时,在三相绕组中产生感应电压,从而形成图11.2 所示的对称三相电源。
其中A、B、C三端称为始端,X、Y、Z三端称为末端。
图 11.1 图 11.2三相电源的瞬时值表达式为:为参考正弦量,三相电压波形图如图 11.3 所示。
式中以 A 相电压 uA图 11.3 图 11.4三相电源的相量表示为可以用图 11.4 所示的相量图表示。
第十一章三相电路优秀课件

IIC B Z ZU L U L C BZ Z44.4 .4 6.6 1 8o 7 7.A 1可33 以A 验证:IIB CI A I IA A IB 1 12I2 0C 00
uB 2Ucost(12)0
uC 2Ucost (24)0
2Ucost(120)
uAuBuC0
U AU0 U BU120 U CU120
U AU BU C0
(2)三相电源的接线: 三相电源的接线只有两种接线形式:
Y形和△形。
Y形连接:三个相电源的尾端(负极X、Y、Z)连接在一起, 而三个首端(正极A、B、C)对外引出。
A B
U P0 U P 120
•
UB
U AB
U C U P 120
①线电压: U AB U AU B 3 U P 3 0 3 U A 3 0 U l 3 0
U BCU BU C 3 U B 30 U l 90
U CAU CU A 3U C 30U l 15 0
结论:相电压对称则线电压亦对称,且Y接时: 即:线电压有效值为相电压有效值的 3 倍,相位超前相应相电
Y形连接存 在中性点N 和中性线。
△形连接:三个相电源依次首尾相连,从三个首端(A、B、C) 向外引出。
特别说明:* Y接必须是三尾相接形成中性点N;
*△接必须是首尾相接,一但接错,即会形成很大的 环路电流,足以烧毁电源 。
(3)相序和相量图
•
A 超 前 B 120° , B 超 前 C
UC
•
120°,同时C超前A 120°
流 30°. 线电压=相电压。
§11-3对称三相电路的计算
由三相电源和三相负载组成的电路称为三相电路。当电源 为三相对称电源,负载也为三相对称负载(三相负载相等) 时,称为三相对称电路;当电源为三相不对称电源,或负载 为三相不对称负载,或都不对称时,称为三相不对称电路。
第十一章三相电路

UB 2 IB IA Z Zl
同理: I U C I C A
Z Zl
N -
UA
+ A
IA
Zl Zl Zl
A’ B’ C’
Z Z Z N’
UB
+ B
+ C N
IB
UC
IC
IN
ZN
UB 2 IB IA Z Zl
U A U N 'N UA IA Z Zl Z Zl
3 个电源依次称为A相、B相和C相,它们的电压为:
u A 2U cos(t )
uB 2U cos(t 120) uC 2U cos(t 120)
u A uB uC = 0
u u A uB
uC
O
t
问题讨论
Z A
eC
C
•
eA
B X
•
Y
eB
•
三个电源串接 直流电源串接不行, 能否造成短路? 三相交流电源可以, 为什么? 直流电源行吗?
所以
U N 'N 0
-
UA
+ A
+ B + C N
IA
Zl
A’
B’
Z
N -
UB
IB
Zl
Zl
Z
Z
N’
UC
IC
C’
IN
ZN
IA ?
U N ' N - (Z Zl ) I A + U A
电路 第四版 第11章 三相电路

第11章 三相电路
第11章 三相电路
第11章 三相电路
图11-12 三相不对称电路
第11章 三相电路
第11章 三相电路
例11-3 如图11-13所示是一种相序指示器电路,图中的R
可以用两个相同的白炽灯泡代替。如果使
则可以
根据两个灯泡的亮度判断电源的相序。
图11-13 例11-3图
第11章 三相电路
第11章 三相电路
11.5 三相电路的功率
11.5.1 三相电路的功率 无论 Y 形接法还是△形接法,或者负载对称与否,都有三
相负载的瞬时功率等于各相负载瞬时功率之和。
第11章 三相电路
以 Y 形接法的感性对称负载为例,三相负载的瞬时功率 为
解 该电路的负载虽然是△形连接,但由于存在线路阻抗 Zl,所以不能用△形方法直接求解。其求解方法是,首先将△ 形负载变换成 Y 形负载,根据式(2 16)的变换公式,并注意由 时域变换到相量域,则有
第11章 三相电路
第11章 三相电路
11.4 不对称三相电路的计算
对于三相电路,只要有一部分不对称就称为不对称三相 电路。例如,三相负载不对称,对称三相电源的某一条端线断 开,或某一相负载发生短路或开路等,均为不对称三相电路。 本节只讨论三相负载不对称的情况。
6 所 示。当 ZA'B' =ZB'C'=ZC'A'=Z 时,称为对称三相负载。
图11-6 负载的三角形接法
第11章 三相电路
11.2.2 三相负载中的电流和电压 对于三相负载来说,负载两端的电压称为相电压,流过负
载的电流称为相电流,电源和负载端线的电流称为线电流,中 线的电流称为中线电流。负载连接端(或三相负载与外界的 连接端)之间的电压称为负载的线电压。如图11-5所示。
第十一章-三相电路

3Ua30O
Ubc 3Ub30O,Uca 3Uc30O
Uc
结 论 :UL 3UP3 0O 且U L 3U P
3、线电压之间的关系
Ubc Uab 120O,Uca Uab120O Ub
Ua Uab 7
二、对称三角形连接电源
1、 线 电 压 相 电 压(UL UP) 2、线电流与相电流的关系:
根据对称性:IB 5.18 69.440 A
IC 5.18170.560 A
21
2)求电源发出的复功率
IA
IA 1
A
B
IB IA 2 R
IC
R
C
~S 3~SA 3UA NI*A
IA 5.1850.560 A
R
UAN 2 2 000 ~S 3UA NIA*
3 41 8 5 0. 5 60 V .A
1)相电压:
Un'n 0 UAn' UAn UA
根据对称性:
n’
UB n ' UA n ' 1 2 00
UC n ' UA n '1 2 00
- UC +
Zn
2)线电压:
U AB
3U An
'3
00
3UA300
U BC
UAB
1200
U CA
UAB1200
11
3、求负载线电流(相电流) AZ
负载上的线电压: UAB 3UA300 236 .923.70V
UB‘C’ 236.9 96.30V
UC‘A’ 236 .9143 .70V
16
$11-5 三相电路的功率(256)(定义同前)
一、三相电路复功率:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以N为参考结点,可得:
1 ZN
Z
3
Z1
U
N N
Z
1 Z1
U A
U B
U C
由于 所以
UUAN
N
U B
0
UC
0
各相电源和负载中的电流等于线电流,它们是:
IA
U AU NN Z Z1
U A Z Z1
IB
U B Z Z1
a 2 IA
IC
U B Z Z1
aIA
中线电流: IN IA IB IC 0 所以在Y-Y三相电路中中线如同开路。 只要分析计算三相中的任一相,而其他两 相的电压、电流就能按对称顺序写出。
上图所示为一相计算电路(A相)。
注意
在一相计算电路中,连接N、N的是 短路线,与中线阻抗ZN无关。
2、其他连接方式 对于其他连接方式的对称三相电路,可
以根据星形和三角形的等效互换,化简成对 称的Y-Y三相电路,然后归结为一向的计算 方法。
例11-1 对称三相电路如图,已知:Z1=(1+j2) , Z=(5+j6),uAB 380 2 cos(t 30 )V 。试 求负载中各电流相量。
第十一章 三相电路
内容提要
本章主要内容有:三相电源和三 相电路的组成,对称三相电路及归结 为一相计算方法;电压和电流的相值 和线值之间的关系;三相电路的功率 和测量。简要介绍了不对称三相电路 的计算。
§11-1 三相电路 §11-2 线电压(电流)和相
电压(电流)的关系
§11-3 对称三相电路的计算 §11-4 不对称三相电路的概念 §11-5 三相电路的功率
§11-1 三相电路
一、三相电压
对称三相电源是由3个等幅值、同频率、 初相依次相差120的正弦电压源连接成星形 或三角形组成的电源,如图所示。
A、B、C相的电压分别为:
uA 2U cos(t) uB 2U cos(t 120 ) uC 2U cos(t 120 )
若以A相U的 A 电 U压为0 参考正弦量相量形式为:
1、负载的Y形连接方式 左图所示为三相四线制
2、负载的形连接方式
四、相序
相序的定义:对称三相电压到达正(负)最大 值的先后次序 。
A→B→C→A 顺序 A→C→B→A 逆序 本章若无特殊说明,三相电源的相序均是顺序。
§11-2 线电压(电流)和相 电压(电流)的关系
一、线电压和相电压的关系
1、Y形电源
2、形连接方式
把三相电压源依次连接成一个回路,再从 端子A、B、C引出端线,就成为三相电源的三 角形连接,简称三角形或形电源。三角形电 源的线电压、相电压、线电流和相电流的概念 与星形电源相同。三角形电源不能引出中线。
三、负载的Y形和形连接方式
3个阻抗连接成星形(三角形)就构成星形 (三角形)负载。三相负载的相电压和相电流 是指各阻抗的电压和电流。三相负载的3个端 子A 、B 、C向外引出的导线中的电流称 为负载的线电流;任两个端子之间的电压则 称为负载的线电压。
解 该电路可以变换
为对称的Y-Y电路,如 下图所示。
Z Z 19.2 j14.4
3
3
(6.4 j4.8)
令
U
A
220 0。根据一相计算电路有
IA
U A Z1 Z
17.1 43.2
3IAB 30 3IBC 30
IC
ICA
IBC
(1 a)ICA
3ICA 30
另有 IA IB IC 0
所以上面3个方程中只有2个是独立的。
线电流和对称相电流 之间的关系可以用图 示的电流相量图表示。
从图中可以看出,线电流与对称相电流
之间的关系,可以用一个电流正三角形说明,
相电流对称时,线电流也一定对称,它是相
线电压与对称相电压之间 的关系可以用图示电压正 三角形说明。相电压对称 时,线电压也必依序对称, 它是相电压 3倍,依次超 前U A、U B、UC的相位为 30,实际计算时,只要 算U出BCUABa,2U就AB可,U以CA依 a序U写AB出
2、形电源
对于三角形电源,有
U AB U A ,U BC U B ,UCA UC
U B U 120 a2U A UC U120 aU A
其中a 1120,为单位相量算子。
对称三相电压各相的波形和相量图如下图所示。 对称三相电压满足:
uA uB uC 0或U A U B UC 0
二、电源的Y形和形连接方式
1、Y形连接方式
从3个电压源正极性端子A、 B、C向外引出的导线称为端 线,从中(性)点N引出的导 线称为中线。端线A、B、C 之间(即端线之间)的电压称 为线电压。电源每一相的电 压称为相电压。端线中的电 流称为线电流,各相电压源 中的电流称为相电流。
电流的 倍,3依次滞后
IAB、IBC、的I相CA位
为30。实际计算时,只要计算出 ,就IA 可以
依次写出
IB a2IA, I。C aIA
上述方法也适用于三角形电源。
§11-3 对称三相电路的计算
1、三相四线制
Z1为端线阻抗, ZN为中线阻抗。 N和N为中点。 先用结点法求 出中点N和N之 间的电压。
解
U A
U AB 3
30
ห้องสมุดไป่ตู้
220 0V
根据一相计算电路,可以得出
IA
U A Z Z1
2200 6 j8
A
22 53.1 A
根据对称性可以得出:
IB a2IA 22 173.1 A IC aIA 2266.9 A
例11-2 对称三相电路如图所示。已知: Z=(19.2+j14.4), Z1=(3+j4),对称线电压 UAB=380V。求负载端的线电压和线电流。
即线电压等于相电压,相电压对称时, 线电压也一定对称。
以上有关线电压和相电压的关系也适 用于对称星形负载和三角形负载。
二、线电流和相电流的关系
1、星形连接
线电流等于相电流。
2、三角形连接
以图示三角形负载 为例,列出KCL。
IA IB
IAB IBC
ICA IAB
(1 a)IAB (1 a)IBC
U AB U A U B (1 a2 )U A U BC U B UC (1 a2 )U B UCA UC U A (1 a2 )UC
3U A30 3U B30 3U C 30
而 U AB U BC UCA 0
故3个方程中只有2个是独立的。
对称的Y形三相电源端的线电压与相电压之间 的关系,可以用下面的电压相量表示。
