高三数学复习专题课
高三数学复习专题课型技巧及模式

高三数学复习专题课型技巧及模式一、问题的提出新课程改革实施三年来,在实践中发现问题、解决问题,在问题的解决过程中将新课程改革工作逐步推进。
其中,模块教学强调螺旋上升,淡化了数学学科的知识结构和体系,但是数学作为高中课程,功能之一是为高等学校输送合格的学生,学科知识结构的过分淡化将不利于继续深造学生的发展。
因此,作为高三复习工作的任务之一,就是要在系统复习知识的同时,打破模块分割的界限,将知识系统化、结构化,帮助学生整体把握高中阶段的数学知识和思想方法,这样就造成了高三复习时间紧,任务重,如何在有限的时间内最大限度的调动学生参与课堂教学的积极性,从而最大限度的提高高三复习课的效率是课题研究的主要问题。
二、研究的目标高三数学常见的课型有:基础知识复习课、解题教学课、试卷讲评课等。
我们预期通过行动研究的方法,探索、研究、归纳、总结每一种课型的高效教学模式,通过典型课例逐步推广,并且在教学实践中不断修改,不断完善,使每位老师对每种课型都能掌握运用1—2种适合自己教学风格、适合自己学生特点的高效教学模式。
同时,也期待着在不断的研究与学习的过程中,逐步更新观念,改进教学,从而提高高三复习课的效率。
三、研究的内容1.基础知识复习课课型及其教学模式;2.解题教学课课型及其教学模式;3.试卷讲评课课型及其教学模四、研究的理论依据建构主义认为,数学新知识的学习活动,是主体在自己的头脑里建立和发展数学认知结构的过程,是数学活动及其经验内化过程。
这种内化的过程,或者是以同化的形式把客体纳入到已有的认识结构之中,以便同与自己不相适应的客体一致,从而使原有的认识结构发生质的变化。
由此不难看出,完成这样的过程,完全是自主行为,而且只有通过主体积极主动的智力参与才能实现,别人是根本无法替代的。
所谓“智力参与”,就是主体将自己的注意力、观察力、记忆力、想象力、思维力和语言能力都参与进去。
由于数学建构学习活动的本质是思维构造,所以这是一个创造的过程。
高三数学专题复习课件专题5 三角函数

[法一] 由sinA(sin B cos B ) sin C 0,
得 : sin A sin B sin A cos B sin( A B ) 0, sin A sin B sin A cos B sin A cos B cos A sin B 0. 即 sin B(sin A cos A) 0.
sin( A C ) sin B
2
sin B sin B
2
7.
cos A sin A
cos C sin C
sin C cos A cos C sin A sin A sin C 1 sin B 4 7 3 2
2
sin( A C ) sin B
2
sin B sin B 3 2
B. sinx D. cosx
( 5) 已知( x cos 1) 的展开式
5
中x 的系数与 x (
2 3
5 4
) 的展开式中
4
x 的系数相等, 则 cos _________ .
( 5) 已知( x cos 1) 的展开式
5
中x 的系数与 x (
2
5 4
) 的展开式中
三角函数综合
第一课时:
三角变换
第一课时:
三角变换
[课前导引]
第一课时:
三角变换
[课前导引]
1. 设 则 cos cos
3 (
, tan tan 3, )
A.
1 6
B.
3 6
C.
3 3 2
D.
3 2
高三数学复习教案

高三数学复习教案作为一名辛苦耕耘的教育工作者,可能需要进行教案编写工作,编写教案有利于我们准确把握教材的重点与难点,进而选择恰当的教学方法。
那么大家知道正规的教案是怎么写的吗?下面是小编精心整理的高三数学复习教案,欢迎阅读,希望大家能够喜欢。
高三数学复习教案1教学目标知识目标等差数列定义等差数列通项公式能力目标掌握等差数列定义等差数列通项公式情感目标培养学生的观察、推理、归纳能力教学重难点教学重点等差数列的概念的理解与掌握等差数列通项公式推导及应用教学难点等差数列“等差”的理解、把握和应用教学过程由XX《红高粱》主题曲“酒神曲”引入等差数列定义问题:多媒体演示,观察————发现?一、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列。
这个常数叫做等差数列的公差,通常用字母d表示。
例1:观察下面数列是否是等差数列:…。
二、等差数列通项公式:已知等差数列{an}的首项是a1,公差是d。
则由定义可得:a2—a1=da3—a2=da4—a3=d……an—an—1=d即可得:an=a1+(n—1)d例2已知等差数列的首项a1是3,公差d是2,求它的通项公式。
分析:知道a1,d,求an。
代入通项公式解:∵a1=3,d=2∴an=a1+(n—1)d=3+(n—1)×2=2n+1例3求等差数列10,8,6,4…的第20项。
分析:根据a1=10,d=—2,先求出通项公式an,再求出a20 解:∵a1=10,d=8—10=—2,n=20由an=a1+(n—1)d得∴a20=a1+(n—1)d=10+(20—1)×(—2)=—28例4:在等差数列{an}中,已知a6=12,a18=36,求通项an。
分析:此题已知a6=12,n=6;a18=36,n=18分别代入通项公式an=a1+(n—1)d中,可得两个方程,都含a1与d两个未知数组成方程组,可解出a1与d。
高三数学集体备课函数专题
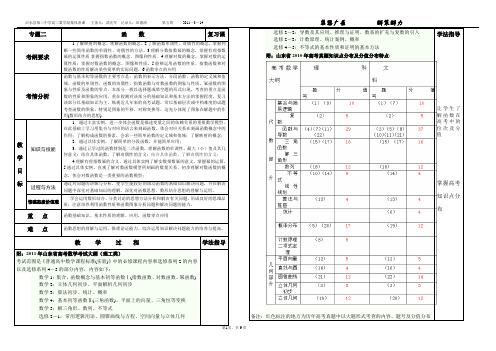
专题二函数复习课考纲要求1.了解映射的概念,理解函数的概念。
2.了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法。
3.理解分数指数幂的概念,掌握有理指数幂的运算性质.掌握指数函数的概念、图像和性质。
4.理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图像和性质。
5.能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题。
6.函数零点的应用考情分析函数与基本初等函数的主要考点是:函数的表示方法、分段函数、函数的定义域和值域、函数的单调性、函数的奇偶性、指数函数与对数函数的图象与性质、幂函数的图象与性质及函数的零点。
本部分一般以选择题或填空题的形式出现,考查的重点是函数的性质和图象的应用,重在检测对该部分的基础知识和基本方法的掌握程度。
复习该部分以基础知识为主。
纵观近几年来的高考试题,常以基础层次或中档难度的试题考查函数的图象,特别是图象的平移、对称变换等,这充分体现了图象在解题中的作用(数形结合的思想).教学目标知识与技能1.通过丰富实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念;2.通过具体实例,了解简单的分段函数,并能简单应用;3.通过已学过的函数特别是二次函数,理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解奇偶性的含义;结合具体函数,了解奇偶性的含义;4.理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握幂的运算。
5.通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;过程与方法通过对问题的讲解与分析,使学生能较好的调动函数的基础知识解决问题,并在解决问题中深化对基础知识的理解,深化对函数思想、数形结合思想的理解与运用。
高三数学总复习 专题二三角函数教学案

芯衣州星海市涌泉学校赣榆县智贤中学高三数学总复习专题二第1讲三角函数〔1〕教学案教学内容:三角函数的图象与性质〔1〕教学目的:1三角函数的图象与解析式2.利用三角函数的图象与解析式教学重点:1.求三角函数的解析式;教学难点:三角函数的图象与解析式教学过程:一、知识点复习:1.必记的概念与定理(1)同角关系:sin2α+cos2α=1,=tanα.(2)诱导公式:在+α,k∈Z的诱导公式中“奇变偶不变,符号看象限〞.(3)三角函数的图象及常用性质函数y=sinx y=cosx y=tanx图象单调性在[-+2kπ,+2kπ](k∈Z)上单调递增;在[+2kπ,+2kπ](k∈Z)上单调递减在[-π+2kπ,2kπ](k∈Z)上单调递增;在[2kπ,π+2kπ](k∈Z)上单调递减在(-+kπ,+kπ)(k∈Z)上单调递增对称性对称中心:(kπ,0)(k∈Z);对称轴:x=+kπ(k∈Z)对称中心:(+kπ,0)(k∈Z);对称轴:x=kπ(k∈Z)对称中心:(,0)(k∈Z)2.记住几个常用的公式与结论对于函数y=Asin(ωx+φ)(A>0,ω>0)要记住下面几个常用结论:(1)定义域:R.(2)值域:[-A,A].当x=(k∈Z)时,y取最大值A;当x=(k∈Z)时,y取最小值-A.(3)周期性:周期函数,周期为.(4)单调性:单调递增区间是(k∈Z);单调递减区间是(k∈Z).(5)对称性:函数图象与x轴的交点是对称中心,即对称中心是(,0),对称轴与函数图象的交点纵坐标是函数的最值,即对称轴是直线x=,其中k∈Z.(6)函数y=Asin(ωx+φ)(A>0,ω>0)中,A影响函数图象的最高点和最低点,即函数的最值;ω影响函数图象每隔多少重复出现,即函数的周期;φ影响函数的初相.(7)对于函数y=Asin(ωx+φ)(A>0,ω>0)的图象,相邻的两个对称中心或者者两条对称轴相距半个周期;相邻的一个对称中心和一条对称轴相距周期的四分之一.复备栏3.需要关注的易错易混点三角函数图象平移问题(1)看平移要求:拿到这类问题,首先要看题目要求由哪个函数平移到哪个函数,这是判断挪动方向的关键点.(2)看挪动方向:在学习中,挪动的方向一般我们会记为“正向左,负向右〞,其实,这样不理解的记忆是很危险的.上述规那么不是简单地看y=Asin(ωx+φ)中φ的正负,而是和它的平移要求有关.正确地理解应该是:平移变换中,将x变换为x+φ,这时才是“正向左,负向右〞.(3)看挪动单位:在函数y=Asin(ωx+φ)中,周期变换和相位变换都是沿x轴方向的,所以ω和φ之间有一定的关系,φ是初相位,再经过ω的压缩,最后挪动的单位是||.二、根底训练:1.函数y=tan的定义域是________.解析:∵x-≠kπ+,∴x≠kπ+,k∈Z.答案:2.(2021·模拟)函数f(x)=sinxcosx的最小正周期是________.解析:由题知f(x)=sin2x,所以T==π.答案:π3.将函数y=2sinx的图象上每一点向右平移1个单位长度,再将所得图象上每一点的横坐标扩大为原来的倍(纵坐标保持不变),得函数y=f(x)的图象,那么f(x)的解析式为________.解析:函数y=2sinx向右平移1个单位得y=2sin(x-1)=2sin,将所得图象上每一点的横坐标扩大为原来的倍(纵坐标保持不变),那么y=2sin,即y=2sin.答案:y=2sin4.(2021·模拟)函数f(x)=2sin,x∈[-π,0]的单调增区间为________.解析:当x-∈,k∈Z时,f(x)单调递增,又因为x∈[-π,0],故取k=0得x∈.答案:1三、例题教学:例1、(2021·模拟)假设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象如下列图,这个函数的解析式为________.[解析]由题意知:周期T=2(-)=π,ω==2,设f(x)=Asin(2x+φ),点(,0)为五点作图中的第三点,所以2×+φ=π,即φ=.设f(x)=Asin(2x+),因为点(0,)在原函数的图象上,故Asin=,所以A=,综上知:f(x)=sin(2x+).[答案]f(x)=sin(2x+)变式训练:1.(2021·高考卷)函数y=cosx与y=sin(2x+φ)(0≤φ<π),它们的图象有一个横坐标为的交点,那么φ的值是________.解析:由题意,得sin=cos,因为0≤φ<π,所以φ=.答案:例2、2021·模拟)函数f(x)=2sin(ωx+φ)(ω>0,-<φ<)的图象如下列图,直线x=,x =是其两条对称轴.(1)求函数f(x)的解析式并写出函数的单调增区间;(2)假设f(α)=,且<α<,求f(+α)的值.[解](1)由题意,=-=,∴T=π,又ω>0,故ω=2,∴f(x)=2sin(2x+φ),由f()=2sin(+φ)=2,解得φ=2kπ-(k∈Z),又-<φ<,∴φ=-,∴f(x)=2sin(2x-),由2kπ-≤2x-≤2kπ+(k∈Z)知,kπ-≤x≤kπ+,(k∈Z),∴函数f(x)的单调增区间为[kπ-,kπ+](k∈Z).(2)依题意得:2sin(2α-)=,即sin(2α-)=,∵<α<,∴0<2α-<,∴cos(2α-)===,f(+α)=2sin[(2α-)+],∵sin[(2α-)+]=sin(2α-)cos+cos(2α-)sin=(+)=,∴f(+α)=.稳固练习:完成专题强化训练。
微专题-向量-高三数学复习课件

探究问题
向量的运算(数量积)及几 何意义—建立λ和 μ的关系
探究问题
向量“形”的几何角度 平面向量共线定理结合几何变换
探究问题
1.等和线定理: (1)平面向量共线定理 已知 OP OA OB ,若λ+ μ= 1,则 A, B, P 三点共线;反之亦然.
(2)等和线
平面内一组基底 OA,OB 及任一向量OP,OP OA OB(, R) ,
若点 P在直线 AB 上或在平行于 AB 的直线上,则λ+ μ= k (定值) ,反 之也成立,我们把直线 AB 以及与直线 AB 平行的直线成为等和线.
P3
P2 P P1
①当等和线恰为直线 AB 时, k = 1; ②当等和线在O 点和直线 AB 之间时 k OP2 (0,1) ;
OP
③当直线 AB 在O 点和等和线之间时,k OP1 (1, ) ;
向量微专题复习
提出问题
已知动点轨迹,求以动点为终点的动向量在 两已知基向量下的坐标代数式的最值问题
探究问题
解决平面向量问题的主要方法:基底法和坐标法 坐标法—圆的参数方程 转化为三角函数 坐标法—建立λ和 μ的关系 转化为基本不等式 向量运算—建立λ和 μ的关系 转化为基本不等式
探究问题
坐标法—转化为线性规划问题
参数方程:圆: xy
a b
r r
cos sin
,
椭圆: xy
a cos b sin
, 为参数
基本不等式: a2 b2 2ab; a b ab(a 0,b 0); ab ( a b)2; a2 b2 a b ,当且仅当a b时等号成立
2
2
2
2
运用反馈
高三数学复习市公开课获奖教案省名师优质课赛课一等奖教案

高三数学复习教案引言:高三是学生们迎接高考挑战的最后一年,数学作为高考科目之一,对学生的综合能力和逻辑思维能力提出了很高的要求。
为了帮助学生顺利复习数学知识并取得好成绩,我们设计了这个高三数学复习教案。
本教案以总结总复习为基础,关注重要知识点和常见考点的梳理,同时注重解题方法和思维训练。
希望通过这个教案的运用,能够提高学生的数学应试能力和解题能力,为他们的高考打下坚实的基础。
第一节:函数与方程1.1 函数的基本概念1.1.1 函数的定义与性质1.1.2 常见函数的分类与图像1.2 方程与不等式1.2.1 一元一次方程与一元一次不等式1.2.2 一元二次方程与一元二次不等式1.2.3 高次方程与不等式的解法1.3 实际问题的数学建模1.3.1 理解及应用函数概念1.3.2 抽象问题的建模思路1.3.3 实际问题解答过程的优化方法第二节:几何与三角2.1 平面几何2.1.1 二维几何中常见形状的性质2.1.2 平面几何中的重要定理与应用2.1.3 解题技巧与常见题型的解答思路2.2 空间几何2.2.1 三维几何中常见形状的性质2.2.2 空间几何中的重要定理与应用2.3 三角函数与三角恒等式2.3.1 三角函数的定义与性质2.3.2 三角函数图像与性质的应用2.3.3 三角函数与三角恒等式的解题技巧第三节:数列与数学归纳法3.1 数列的基本概念3.1.1 数列的定义与性质3.1.2 等差数列与等比数列的性质与应用3.2 数列的求和与通项3.2.1 等差数列与等比数列的通项公式3.2.2 等差数列与等比数列求和公式的推导与应用3.3 数学归纳法3.3.1 数学归纳法的基本原理与应用3.3.2 利用数学归纳法证明问题的解法与技巧第四节:概率与统计4.1 概率的基本概念4.1.1 随机事件与概率的定义4.1.2 基本概率公式与应用4.2 统计的基本概念4.2.1 样本与总体的概念与表示方法4.2.2 统计指标的计算与应用4.2.3 数据分析与统计图的制作与分析4.3 概率与统计的综合应用实例4.3.1 实际问题的概率与统计建模思路4.3.2 数据的处理与分析方法4.3.3 综合应用实例解答思路结语:本教案对高三数学的复习进行了系统梳理,涵盖了高中数学的主要知识点和常见考点。
高三数学 推理与证明复习课

7.由①正方形的对角线相等;②平行四边形的 对角线相等;③正方形是平行四边形,根据 “三段论”推理出一个结论,则这个结论是( A
)
(A) 正方形的对角线相等
(B) 平行四边形的对角线相等 (C) 正方形是平行四边形
(D) 其它
第二章推理与证明
8.在下列表格中,每格填上一个数字后,使每一行 成等差数列,每一列成等比数列,则a+b+c的值是( 1 2
第二章推理与证明 --复习
第二章推理与证明
推理
归纳推理 (由特殊到一般) 合情推理 类比推理 (由特殊到特殊)
三段论:大前提 小前提 结论 演绎推理 (由一般到特殊) 综合法 (由因导果) 直接证明 分析法 (执果索因) 证明 反证法 间接证明
应用
比较法
比差法
不等式的证明方法
(补充内容)Biblioteka 比商法 综合法和分析法 反证法
A
)
0.5
1 a
b
c (A) 1 (B) 2 (C) 3 (D) 4
第二章推理与证明
5.设 f 0 ( x) sin x, f1 ( x) f 0 ( x) f2 ( x) f ( x),
'
' 1
,
fn1 ( x) fn' ( x) ,n∈N,则 f2007 ( x) D
A. C.
sin x
B.- sin x D.- cos x
cos x
第二章推理与证明
6.已知 f ( x 1)
2 f ( x) , f (1) 1 (x N *),猜想 f ( x) 2
f ( x) 的表达式为
A.
4 f ( x) x 2 2
高三数学小专题复习课的教学

见 ,小专题 复习课 的内容设 置要严格 把关 ,慎之 又
例如 “ 圆锥 曲线与直线关系专题 ” ,其课堂教学设 慎 ,例题 的选 择是 否 恰 当对 小 专题 复 习课 的成 败 是 至
计 要 求 是让 学 生 在 原有 认识 的基 础 上 ,形 成 对 “ 圆锥 关重要 的.小专题复习课 内容设置 的一般原则如下.
性难 以充分 发挥 . 在全 省 “ 同课 异 构 ” 活动 中 ,笔 者 对 高 三 小 专题
下面 以 “ 圆锥 曲线与直线关系”小专题复 习课为
复习课 “ 圆锥 曲线与直线关系”进行 了专题研讨 ,产 实例 ,谈谈如何克服 以上问题 ,搞好高三小专题复习 课 的教 学 . 生 了一 些 思 考 .下 面 就 以这 节 课 为例 谈 谈 高 三数 学小
描 述 ,并结 合 具体 教 学案 例 对如 何 搞 好 高三数 学 小 专 题或习题套路化 ;如何学习方法不明 ,不注重合理组 题 复 习课 的教 学提 出 了几 点 建议. 织 有效 学 习活 动 ,问题 设计 不 够 合 理 ,就 题 论 题 ,思
关键 词 :圆锥 曲线 与 直 线 关 系; 小专 题 ;高 三 复 维含量少 .以上问题导致复 习课学 习效果不好 ,简单 重 复 ,没 有 新 意 ,学 生 兴 趣不 高 ,学 习积 极 性 和 主 动 习课
小专题 . 小专题复习课 以具有一 定综合性 的教学 内容 为载体 ,以形成知识 网络 、产生对知识整体认识为指
向 ,以提 升 学 生 综合 运 用 某 些 知识 解 决 数 学 问题 、提 升 能 力 为 目的 .由于 小 专 题 复 习 课 具 有 操 作 灵 活 、指 向性 强 、对 提 高 学 生能 力 有 很 好 的 实效 性 等 特 征 ,所
2023届高三数学一轮复习专题 利用常见函数的奇偶性解题 讲义 (解析版)

专题:利用常见函数的奇偶性解题知识梳理:1、掌握高中常见函数的奇偶性,单调性可提高解题速度2、加强知识的归纳整理工作,由知识点构建知识块3、常见的奇,偶函数类型(10≠>a a 且):①指数型奇函数:f(x)=11+-±x x a a ,f(x)=)(x x a a --±, ②对数型奇函数:f(x)=±lgx b xb +-,f(x)=±lg(x x ++12),③幂函数奇函数:f(x)=m x (为奇数m ),f(x)=xb x ±④常见偶函数:f(x)=m x (为偶数m ) f(x)=|x| 典型例题:例1:已知函数f(x)=11+-x x a a (a>1) (1)判断f(x)奇偶性 (2)求函数f(x)的值域变式:已知函数31()231x x f x x -=++,则满足不等式()(32)0f a f a ++>的实数a 的取值范围是 .变式1:【答案】12⎛⎫-+∞ ⎪⎝⎭例2:(2018·全国卷Ⅱ)函数f (x )=e x -e -xx 2的图象大致为( )变式:已知函数f (x )=e x -1ex ,其中e 是自然对数的底数.若f (a -1)+f (2a 2)≤0,则实数a 的取值范围是________.例3:判断并证明函数f(x)=lg x x +1-1的奇偶性 (思考f(x)=lg xx-+11的奇偶性?)例4:判断并证明函数f(x)=lg(x x ++12)的奇偶性 (思考f(x)=lg(x x -+12的奇偶性?)变式1:已知函数xxa x f +-=1log )(3为奇函数,则实数a 的值为________.变式2:设函数f(x)=1)1ln(1222+++++x x x x )(的最大值为M ,最小值为N ,试确定M+N 的值变式3:函数())lnf x kx =的图象不可能是( )A. B .C .D .例5:已知,,则( ) A . B . C . D .例6:已知函数2111)(x x x f +-+=,则满足f (x -1)<⎪⎭⎫ ⎝⎛31f 的x 取值范围是( ) A .11(,)33- B .]31,31[- C .24(,)33D .]34,32[课后作业:1、已知函数f(x)=xxa a 22+-是奇函数,则f(a)的值等于( )A.-31B.3C.-31或3D.31或32、(2022年华美月考,多选)已知函数()1212xxf x -=+,())lg g x x =,则( )A .函数()f x 为偶函数B .函数()g x 为奇函数C .函数()()()F x f x g x =+在区间[]1,1-上的最大值与最小值之和为01()1f x x x=+-()2f a =()f a -=4-2-1-3-D .设()()()F x f x g x =+,则()()210F a F a +--<的解集为()1,+∞ 3、(2019·金版创新)已知函数f (x )是奇函数,g (x )=f (x )+21+2x ,x ∈(-1,1),则g ⎪⎭⎫⎝⎛21+g ⎪⎭⎫⎝⎛21-的值为________. 4、(2019·海淀联考)已知函数f (x )=2x-12x +1.(1)判断函数f (x )的奇偶性;(2)判断并证明f (x )在其定义域上的单调性;(3)若f (k ·3x)+f (3x-9x+2)<0对任意x ≥1恒成立,求实数k 的取值范围.专题:利用常见函数的奇偶性解题典型例题: 例1:【答案】(1)奇函数(2)(-1,1) 【解析】(1)()f x 的定义域为R .又()()11111111xxx x xxa a a f x f x a aa ------====-+++,所以()f x 为奇函数. (2)11211,2120<+-<-∴<+<x x a a ,即值域为(-1,1) 变式:【答案】(∞+-,21) 【解析】0313113132131321313)()(=+-++-=-+-+++-=-+--xxx x x x x x x x x f x f 所以x x f x x 21313)(++-=为奇函数,因为1313)(+-=x x x f 在定义域上单调递增,又f(x)=2x 在定义域上单调递增,所以x x f xx 21313)(++-=在定义域上是增函数 2123)23()(->⇒-->⇒-->∴a a a a f a f例2:【答案】B 【解析】依题意,注意到函数的定义域是}0|{≠∈x R x ,且)()()(22x f xe e x e e xf x x x x -=--=--=---,因此)(x f 是奇函数,其图象关于原点成中心对称,选项A 不正确,且当x>0时,)(x f >0,选项D 不正确,又+∞→+∞→)(,x f x ,结合选项知B 正确,故选B变式:【答案】]21,1[-【解析】函数f (x )=e x-1e x 是常见的奇函数,且在定义域内是单调递增的,因为f (a -1)+f (2a 2)≤0a a a f a f a f -≤⇒-=--≤∴12)1()1()2(22解得:211≤≤-a例3:【答案】奇函数【解析】由条件知:函数的定义域为11<<-x 关于原点对称 所以f(x)+f(-x)=lgx x +1-1+lg x x -+11=0,即函数f(x)是奇函数,同理f(x)=lg xx-+11也是奇函数 例4:【答案】奇函数【解析】由条件知:函数的定义域为R 关于原点对称 所以f(x)+f(-x)=lg(x x ++12)+lg(x x -+12)=lg1=0即函数f(x)是奇函数,同理f(x)=lg()x x -+12也是奇函数变式1:【答案】1【解析】由条件知:奇函数的定义域要关于原点对称,所以分母1-≠x ,为了对称,分子a=1变式2:【答案】2【解析】由已知得1)1ln(21)(22+++++=x x x x x f 因为)1ln())(1)(ln(22x x x x ++-=-++-,所以)1ln(2x x y ++=是奇函数,进而可判定,函数1)1ln(2)(22++++=x x x x x g 为奇函数,则)(x g 的最大值1M 和最小值1N ,满足1M+1N =0,因为1,111+=+=N N M M ,所以M+N=2变式3:【答案】C 【解析】因为A,B 选项中,图像关于原点对称,所以f(x)为奇函数,f(x)+f(-x)=0 1010)1ln()1ln(2222±=⇒=-⇒=+++-+k x k kx x kx x )(即当K=1时,f(x)的图像为选项A,当K=-1时,f(x)的图像为选项B 而C,D 选项中,图像关于Y 轴对称,所以f(x)为偶函数,f(x)=f(-x)00)1ln()1ln(22=⇒=⇒++=-+k kx kx x kx x 即当K=0时,0)(≥x f 故f(x)的图像为选项D ,故f(x)的图像不可能为C例5:【答案】A 【解析】设xx x f x g 11)()(+=+=则)(1)()(x g x f x g -=+-=-,所以)(x g 是奇函数,31)()(=+=a f a g 因为)(x g 是奇函数,所以31)()(-=+-=-a f a g 所以4)(-=-a f ,故选A例6:【答案】C 【解析】函数2111)(xx x f +-+=在[)∞+,0上为增函数,所以不等式f (x -1)<⎪⎭⎫ ⎝⎛31f 等价为 f (|x -1|)<⎪⎭⎫ ⎝⎛31f 所以|x -1|)<31⇒3432<<x课后作业:1、【答案】C 【解析】因为函数f(x)=x xa a 22+-是奇函数,所以f(-x)=-f(x)整理得:02,02)22(2122>=-=+-x x x x a a a 因为))((,所以1±=a 代入选C2、【答案】BCD 【解析】函数xx x f 2121)(+-=是奇函数,所以A 错,函数g(x)=lg )x x -+12是奇函数,所以B 正确,.函数()()()F x f x g x =+在区间[]1,1-上是奇函数,在对称区间上,最大值最小值之和为0,C 正确;是减函数xx f 2121)(++-=,010ln 11)()1lg()(2'2<+-=⇒-+=x x g x x x g 故F (x )=f(x)+g(x)是减函数,a a a F a F a F a F +>⇒+<⇒<--+12)1()2(0)1()2(所以1>a ,D 正确3、【答案】2【解析】函数)(x f 是奇函数,所以0)21()21(=+-f f ,令xx h 212)(+=,则22112212)21()21(=+++=-+h h ,所以g ⎪⎭⎫ ⎝⎛21+g ⎪⎭⎫ ⎝⎛21-=2 4、【答案】(1)奇函数(2)在R 上单调递增函数(3)),(34∞-【解析】略。
高三数学复习课教学设计5篇

高三数学复习课教学设计5篇作为一名老师,时常要开展教学设计的准备工作,教学设计是一个系统设计并实现学习目标的过程,它遵循学习效果最优的原则吗,是课件开发质量高低的关键所在。
教学设计应该怎么写才好呢以下是小编为大家收集的高三数学复习课教学设计,欢迎大家分享。
高三数学复习课教学设计1一、指导思想:以《高中语文教学大纲》和《高考考试说明》为本,全面提高学生语文素养和语文能力,争取20__年高考获取全面胜利。
二、学情分析:7班全班现有41人,经过两年多的高中学习,掌握了一些学习语文的方法,具备一定语文学习能力,但是还有相当一部分学生语文基础知识基本技能不够好,良好的语文学习习惯还没有养成,更有不少同学缺乏应试能力,还有一些同学对语文科学习不够重视,书写潦草,答题不规范。
8班全班现有40余人,多数同学语文基础较差,语文应试能力不高,语文学习积极性不是太高,同学之间语文成绩不平衡,甚至差别很大。
但职高语文考试能力要求不是太高,只要努力,明年高考一定会有好成绩的。
三、考点分析:知识点主要包括以下内容:字音字形,实词虚词,熟语,病句,标点,扩展语句压缩语段,选用仿用变换句式,语言表达准确鲜明生动简明连贯得体,八种修辞方法,名言名句,鉴赏古诗词的形象语言和表达技巧,评价古诗词的思想内容和作者的观点态度,文言实词的含义,文言虚词的意义和用法,文言句式,文言翻译,文言文分析综合,现代文文中重要概念的含义,重要句子的含义,筛选文中信息,分析文章结构把握文章思路,归纳内容要点概括中心意思,概括作者在文中的观点态度,文学类实用类的阅读要具备分析综合鉴赏评价和探究能力,写作能力。
四、具体措施:1. 制定长远的计划及详细的短期计划,做到心中有数,忙而不乱。
2.向45分钟语文课堂教学要质量。
高三学生多数同学把课外时间都给了理化和数学,如何提高语文成绩,只能是向45分钟的语文课堂要效率,在备课时要大量参考多种资料,力求知识的新、全、准。
高三数学专题复习第3课 图形与数式

专题复习第3课图形与数式感悟•渗透•应用1.设a >0,如图,已知直线l ∶y=ax 及曲线C ∶y=x 2,C 上的点Q 1的横坐标为a 1(0<a 1<a ).从C 上的点Q n (n ≥1)作直线平行于x 轴,交直线l 于点P n+1,再从点P n+1作直线平行于y 轴,交曲线C 于点Q n+1·Q n (n=1,2,3……)的横坐标构成数列{a n }.(I)试求a n+1与a n 的关系,并求{a n }的通项公式;(II)当a=1,a 1≤1/2时,证明(III)当a =1时,证明32112<∑++n k k a2.某人准备投资1200万元兴办一所中学,为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据表(以班级为单位):班级学生数配备教师数硬件建设(万元)教师年薪(万元)初中50 2.028 1.2高中40 2.558 1.6根据物价部门的有关文件,初中是义务教育阶段,收费标准适当控制,预计除书本费、办公费以外每个学生每年可收取600元,高中生每个学生每年可收取1500元,因生源和环境条件限制,办学规模以20至30个班为宜,教师实行聘任制.初、高中的教育周期均为三年,请你合理地安排招生计划,使年利润最大,大约经过多少年可以收回全部投资?3.已知A 、B 是椭圆上关于x ,y 轴均不对称的两点,线段AB 的垂直平分线与x 轴的交点P的横坐标为,F 是椭圆的右焦点.(1)设AB 的中点为C (x 0,y 0),求证:(其中c 2=a 2-b 2);(2)若椭圆的离心率e=,且|AF|+|BF|=a ,求该椭圆的方程.()012222>>=+b a b y a x 22a b 220cb x =324.如图,在Rt △ABC 中,∠CAB=90°,AB=2,AC=.DO ⊥AB 于O 点,OA=OB ,DO=2,曲线E 过C 点,动点P 在E 上运动,且保持|PA|+|PB|的值不变.(1)建立适当的坐标系,求曲线E 的方程;(2)过D 点的直线L 与曲线E 相交于不同的两点M 、N 且M 在D 、N 之间,设DM /DN=λ,求λ的取值范围.建立坐标系要恰当,有利于条件、有利于过程、有利于结果,建坐标系之前要有所“预谋”./22。
高三数学复习专题课(新编教材)

3、已知数列{ an}满足 3an1 an 4
(n≥1),且 a=1 9,则
a
n
__8__(__1_)_n_1 _.1
3
4、不等式ax2 bx 2 0的解集是( 1 , 1)
23
则a+b的值是( D ) A、10 B、-10 C、14 D、-14 5、如果双曲线经过(6, 5)且它的两条 渐进线的方程是 y 1 x ,那么这双曲线的
高三数学复习专题课
待定系数法
福建仙游盖尾中学:郭志龙
一、课前练习
1、若将直线L沿x轴正方向平移a个单位
(a≠0),再沿y轴的负方向平移a+1个
单位,又回到了原来L的位置,则直线L
的斜率为( C )
A、 a
a 1
B、a a 1
Байду номын сангаас
C、 a 1
a
D、a
a
1
2、设等比数列{an }的前n项和为sn 3n r , 那么r的值等于( A ) A、-1 B、0 C、1 D、3
3
y2 x2 1
方程______9_____。
;少儿口才网 /oumeisipinpai/ 少儿口才网 ;
右将军如故 天下定后方当用之 阿翁岂宜以子戏父邪 骋足则能追风蹑景 诏遣侍中 不就 比岁征行 如使君为季龙所制 谦向诸弟泣曰 于时刁协 不亦劳乎 隆和元年 封观阳县侯 寻加中书监 督护梁州五郡军事 唯超案兵直卫 翜遣将领五百人从之 视之 何充会之 以寇难路险 补濮阳王允文学 频迁中领军 而神州振荡 又问 玄先令将军王稚徽戍巴陵 将军留宠 少颖悟 时江淮清宴 又隐实户口 稍迁丞相西閤祭酒 则百胜之理济矣 恐不免耳 非式而谁 后骧等又渡泸水寇宁州 穆之 甚为边害 诸督将素知其勇 渐相登
高三数学复习课教学设计

高三数学复习课教学设计一、教学任务及对象1、教学任务本教学设计针对的是高三数学复习课,旨在帮助学生巩固数学基础知识,提高解题能力,特别是针对高考中的重点和难点进行深入讲解和训练。
教学内容包括但不限于:函数与导数、数列、立体几何、解析几何、概率与统计等。
此外,还侧重于培养学生分析问题、解决问题的能力,通过综合运用数学知识,提升学生的逻辑思维和创新意识。
2、教学对象本教学设计的对象为高三学生,他们已经具备了一定的数学基础,对数学知识有初步的理解和掌握。
但由于个体差异,学生在知识掌握程度、解题方法和技巧上存在差异。
因此,在教学过程中,需要关注每一个学生的成长和发展,因材施教,激发学生的学习兴趣,提高他们的数学素养,使他们在高考中取得优异成绩。
二、教学目标1、知识与技能(1)掌握高中数学各模块的基本概念、性质、定理和公式,形成完整的知识体系。
(2)熟练运用数学方法解决实际问题,特别是高考中的典型题型和难点问题。
(3)提高数学运算能力,包括算术运算、代数运算、几何运算等,减少运算错误。
(4)培养逻辑推理能力和数学思维能力,能够对数学问题进行深入分析,提出解题思路。
(5)掌握一定的数学解题技巧,如换元法、构造法、归纳法等,提高解题效率。
2、过程与方法(1)通过启发式教学,引导学生主动参与课堂讨论,培养学生的自主学习能力。
(2)运用案例分析法、问题驱动法等教学策略,帮助学生掌握数学解题方法和步骤。
(3)注重数学思想方法的传授,使学生在解决具体问题的过程中,形成自己的解题思路。
(4)组织小组合作学习,培养学生的团队协作能力和交流沟通能力。
(5)定期进行数学测试和模拟考试,检验学生的学习效果,及时调整教学策略。
3、情感,态度与价值观(1)激发学生学习数学的兴趣,培养他们的数学情感,使他们在学习过程中感受到数学的魅力。
(2)引导学生树立正确的数学观念,认识到数学在科学技术和社会发展中的重要作用。
(3)培养学生勇于探索、敢于创新的数学精神,使他们具备面对困难和挑战的勇气。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y2 x2 1
方程______9_____。
6、已知直线y=ax+b过双曲线 x2 y2 1 的
42
左焦点,且与双曲线只有一个公共点,则
a= 2 ,b=__3_ 或a 2 , b 3
2
2
待定系数法的主要依据是 :
(1)多项式f(x)≡g(x)的充要条件是:对 于任意一个值a,都有f(a)=g(a)。
(2)多项式f(x)≡g(x)的充要条件是:两 个多项式各同类项的系数对应相等。
;好玩的单机游戏 好玩的单机游戏
;
强制解除后的"释放",但平常生活中我们有没有被"无形"的东西限制而感到苦闷?有没有过"如释负重"的感受经历?这样稍作联想,写作思路就会泉涌而至,各类素材更是浮现眼前--在平常的生活中,我们每一个人都有心理苦闷的时候,因为我们总是要面对微妙的人情应酬和不得已的繁琐事 务,就会有一种"不自由"感;同时,我们还时常自我限制,自我囚禁,时而为狂热的理想兴奋,时而被自卑和懦弱的心理折磨……于是迷茫了自己的生命价值追求。也许你有过"释放"的心理体验,也许你一直被囚禁在自己的精神世界里,正好,就结合自己的愉悦体验或苦闷体验展开构思--可 以构思一个故事,通过生动完整的情节展示人物"精神囚禁"的苦闷和"释放"后的轻松、自由、愉悦心理,传达你对社会人生的思考,指导人们去"释放"精神。 21、 “误会” 请联系自己的生活与感受,以"误会"为题写一篇不少于800字的记叙文或议。 思路点拨: 就误会产生的原因而言,一 般是缺乏相互理解,因此要消除误会,就要先做到准确理解对方,以避免误会;误会之后要善解人意,学会倾听、交流、宽容,用换位思考来化解误会。 写记叙文,要通过一个别开生面的故事或片断组合,借助曲折的情节和多角度的描写来引人入胜。写议则要围绕找误因、寻解法的思路来 写,这样就可以透过误会的表象升华到本质认识。据此,我们可以确立如下立意:①学会消除误会,跨越心灵障碍。②学会换位思考,倾听心灵之音。③化解心中的误会,我们需要一颗信任、宽容和理解的心。④学会享受误会,享受误会是一种豁达、宽容的人生境界。 22、 “一路有你” 请以"一路有你"为题写一篇文章,除诗歌外文体不限,不少于800字。 思路点拨:文题"一路有你",其题旨蕴涵着丰富的人文色彩。当学子们从懵懂走向明理、从稚嫩走向成熟、从依赖走向独立的时候,其成长的历程,会让他们记住许多曾经让他们感怀的事情、回味许多曾经让他们感动的人 物、体味许多曾经让他们受益的哲理,这些在他们的人生履历上留下印痕的点点滴滴,如甘泉濡湿着他们成长的岁月、丰盈着他们年轻的生命,因此,以"一路有你"为题,就使学生所写的内容彰显着强烈的人文特色。 23、阅读下列材料,根据要求作文。 美国钢铁大王卡耐基说:微笑是一种 神奇的电波,它会使别人在不知不觉中同意你。在一次盛大的宴会上,一个平日对卡耐基很有意见的商人在角落里大肆抨击卡耐基。当卡耐基站在人群中听到他高谈阔论的时候,他还不知道,这使得宴会主人非常尴尬,而卡耐基却安详地站在那里,脸上挂着微笑。等到抨击他的人发现他的时 候,那人感到非常难堪,卡耐基的脸上依然堆着笑容,走上去亲热地跟他握手,好像完全没有听见他讲自己的坏话一样。后来,此人成了卡耐基的好朋友。 请以“微笑的力量”为题,结合自己的感受,写一篇文章。文体不限,题目自拟。800字左右。 思路点拨 “为人处世”类话题,是近年 高考的热点。“微笑”在这里是一种平和、宽容的生活态度。写作时只有掌握以下技法,才能让文章脱颖而出:用细小的故事折射人物的品质,一个会心的微笑,一个歉疚的笑脸,一串诚恳的笑声,都是写作的好题材,要学会用细小的事件写出自己的感受或人物的品质;用细腻的描写记录心 灵的痕迹,要尽量挑选那些富于表现力的、有意义的细节,写出人物复杂的内心世界,让心灵的波澜在曲折的情节中放射美丽的光彩;用新颖的形式增添创新的色彩。这类文章往往具有时间跨度大、故事性强、适应范围广等特点,可以尝试用日记、小故事、童话等形式进行写作。 24、英国 的皮亚丹博物馆收藏了两幅画,一幅是人体骨骼图,一幅是人体循环图。谁能想到,这竟是一个闯了祸的小学生的作品。当年,小学生麦克劳德出于好奇心,想看看狗的内脏是什么样的,就杀了一只狗,谁知这只狗恰巧是校长的宠物。校长决定给他以惩罚,罚他完成上述两幅画。麦克劳德后 来成了著名的解剖学家。 请以“闯祸与创新”为题,写一篇不少于800字的文章,题目自拟,文体不限,诗歌除外。 思路点拨 根据材料和题目提示,此文应以“闯祸与创新”的关系为写作中心。显然,我们要对“闯祸”这一在人们观念中属贬义的行为作出重新认识和评价。也许有些“闯祸” 确实是一种不好的行为,它会给人们带来不幸和灾难,但也有些“闯祸”恰恰是对旧事物的破坏,对旧传统的反叛,因此,就带有一种革命性的色彩,具有创新的内涵。你可以写写生活中的这类事件,也可以虚构故事来表现这一道理。 25、21世纪世界教育的核心主题之一是“学会共同生 活,”而“学会共同生活”的核心内容是“学会合作”。 试围绕“学会合作”的话题,写一篇600字左右的文章,题目自拟,文体不限。 思路点拨 合作的领域很多,同学们可以从自己的学习与生活中选取材料,可以写与老师、家长、同学、朋友等熟悉的人合作,也可以写与陌生人合作,还 可以写与集体的合作,更可以写与“自己”合作(学会用理智控制自己的感情,或自己的毅力与勤奋等)。可从大处着眼,也可以从小处说起;可高层建瓴叙谈,也可以小见大行文;既可写正面的(成功的)合作经历,也可写反面的(失败的)合作经历。可以写记叙文,也可写议。可以表达 这样的主题:合作是事业取得成功的保,合作万事兴。 26、阅读下面的材料,根据要求作文。 1830年,法国作家雨果同出版商签订合同,半年内交出一部作品。于是,雨果把外出的所有衣服锁进柜子里,把钥匙扔进了湖里,彻底断了外出会友和游玩的念头,一心写作,文学巨著《巴黎圣母 院》就是这样写成的。是的,在漫漫人生路上,往往只有不留下退路,才更容易赢得出路。当我们难以驾驭自己的惰性和欲望,不能专心致志地前行时,不妨也采取一些斩断退路之举,逼着自己全力以赴地寻找出路,走向成功。 请以“不留退路,才有出路”为题写一篇作文,所写内容必须 与“退路和出路”有关,文体不限,文题自拟,不得少于800字,不得抄袭。 27、阅读下面的材料,根据要求作文。 登山的人,有的目不旁视,奋力攀登,他执著于到达峰顶的瞬间风光;有的则流连沿途风景,且走且赏,山顶不过是他歇脚的地方。不只登山,生活也是这样:两种心态,两 种行为,两种价值观。你怎么看待这个问题呢? 请以“进取心与平常心”为题,联系现实生活,写一篇文章。自定立意,自拟标题,自选文体,不少于800字。 28、阅读下面的材料,根据要求作文。 巴豆,药性最能泻,但只要用量适度,非但不会引起腹泻,反倒能治好腹泻,剂量大了才会 引起严重腹泻。 由此,你会得到哪些启示?请以“度”为题,写一篇作文。题目自拟,立意自定,文体自选,不少于800字。 29、联系生活实际,以“包装”为题,写一篇不少于800字的作文,立意自定,题目自拟,文体不限。 [写作提示]联系现实生活,说明包装是为了使产品美观,吸引 消费者乐于购买,收到外观与内质相得益彰的效果。而今有些“包装”,诸如歌星矫揉造作,打扮过分;商品包装花样翻新;房屋装修华而不实。凡此种种,其效果适得其反,追求形式而损害了内容。要结合画面寓意予以剖析。 30、阅读下面的材料,根据要求作文。 两只蚂蚁想翻越一段墙, 寻找墙那边的食物。这段墙长有20米,高有10米。其中一只蚂蚁来到墙脚就毫不犹豫地向上爬去,可每爬到大半时,就会因劳累跌落下来。可是它不气馁,它相信只要付出就会有回报。一次次跌下来,它都迅速地调整一下自己,重新开始向上爬。 而另一只蚂蚁观察一下,决定绕过这段墙。 很快地,这只蚂蚁绕过这段墙来到食物面前,开始享用起来;而那只“勇敢”“坚定”的蚂蚁还在不停地跌落下去,又重新开始。 很多时候,我们赞扬那些做事情锲而不舍的人,但是往往忽视方向的选择与方法的运用。实际上,成功需要坚持,也需要方向、机遇、方法。请以“坚持与选择” 为题写一篇不少于800字的文章。立意自定,文体自拟。 三、半命题作文预测 31、请以“听听那 的声音”为题,写一篇作文。可讲述你自己或身边的故事,抒发你的真情实感,也可阐明你的思想观点。 【注意】①把题目补充完整。②立意自定,角度自选。③除诗歌外,文体不限。④不少 于800字。⑤不得抄袭。 写作点拨 这个命题非常贴近学生的生活可以写自然界的各种声音,也可以写家庭中、社会上的各种声音,还可以写心灵的声音等等等等。而我们要选择的,是最最触动我们心灵的声音。 32、阅读下面材料,按要求作文。 喧闹、快节奏的生活和工作给人们带来了满 足,也带来了烦恼。心灵时常被搓揉得疲惫不堪。那么,我们该到哪里去寻找心灵的憩息地呢? 请以“让心灵在 中憩息”为标题写一篇文章,文体自选,立意自定,字数不少于800,不得抄袭和套作。 思路点拨 这是一篇半命题作文。文题“让心灵在 中憩息”包含着一定的哲理意义。审题 立意的关键在于明确设定“心灵”与“憩息”的含义,并准确把握“憩息”的条件。可以选择宽容、爱等。 33、“? 的滋味” 以“? 的滋味”为题,写一篇记叙文。 要求:①补全题目;②自定立意;③不少于800字。 思路点拨: 文题中的“滋味”本义是“味道”,喻义是“某种感受”。 为此,本文的写作要注意以下三点:一是缘事生感。必须叙写一个中心事件,或围绕一个中心叙写一组事件,在此基础上生发出自己的内心感受。而且,只有事件叙写得“厚实”,生发的感受才会“真切”。那种通篇无事、跟着感觉走的文章只会给人以无病呻吟、为赋新词强说愁之感。二是 多法生感。对于“感受”的生发,既可先“事”后“感”,卒章生发,升华情感;也可将“感受”融化在“事件”的叙写过程之中,“生发”于无痕。三是用足描写。中学生的生活一般都是风平浪静的,很难“惊世骇俗”,很难给人以“超级震撼”。那么,要想在“平凡的世界”里生发出让 人怦然心动的感受,就必须用敏锐的触觉去捕捉,用细腻的笔触去描写生活中那些让人的心灵为之一颤的场景、画面、镜头,让读者的心弦在你柔柔地拨弄下产生出共鸣,这样才能收到“平凡的人给我以最多感动”的构思之效。 34、阅读下面的文字,根据要求作文。 人类要面对自然,个人 要面对社会、政府要面对群众。古往今来,诸如成功、荣誉,挫折、困难,乃至灾祸等等,无一不要人们面对。
