平行四边形讲义
平行四边形及其性质讲义讲义

学习必备 欢迎下载辅导讲义平行四边形及其性质1理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.2理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.1平行四边形对角线互相平分的性质,以及性质的应用.3平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.教学内容,基础知识(1)定义:两组对边分别平行的四边形是平行四边形. (2)表示:平行四边形用符号“来表示.如图,在四边形ABCD 中,AB // DC , AD // BC ,那么四边形ABCD 是平行四边形.平行四边形ABCD 记作“Q ABCD ,读作 平行四边形ABCD .① ••• AB//DC ,AD//BC ,二四边形ABCD 是平行四边形(判定); ② •••四边形ABCD 是平行四边形••• AB//DC , AD//BC (性质).注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边, 邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角(3)由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为 补角.(4)、平行四边形的对边相等、对角相等证明结论:重点、难点2综合运用平行四边形的性质进行有关的论证和计算2.教学目标2、能综合考点及考试要求平行四边形性质,有关的论证和计算A已知:如图口ABCD ,求证:AB = CD , CB = AD , / B = / D, / BAD =/ BCD .分析:作口ABCD的对角线AC,它将平行四边形分成△ ABC和^CDA,证明这两个三角形全等即可得到结论.(作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.)证明:连接AC,AB // CD, AD // BC ,/ 1 = / 3,/ 2=/4.又AC = CA ,△ ABC CDA (ASA ).AB = CD, CB = AD , / B = / D .又 / 1 + / 4=/ 2+/3,/ BAD = / BCD .由此得到:平行四边形性质1 平行四边形的对边相等.平行四边形性质2 平行四边形的对角相等.五、例习题分析例1如图,在平行四边形ABCD中,AE=CF, 求证:AF=CE .分析:要证AF=CE,需证△ ADF◎△ CBE,由于四边形ABCD是平行四边形,因此有/ D= / B ,AD=BC , AB=CD,又AE=CF,根据等式性质,可得BE=DF .由“边角边” 可得出所需要的结论.证明:六、随堂练习1. 填空:在口ABCD 中,/ A=50。
平行四边形讲义

平行四边形一、知识梳理1.平行四边形:(1)平行四边形的定义:两组对边分别平行的四边形是平行四边形.平行四边形用符号示.平行四边形ABCD记作QLECD,读作平行四边形ABCD.2.平行四边形的性质:(1)平行四辿形的对这平行且相等.(2).平行四边形的对角相等,邻角互补。
(3)平行四边形的对角线互相平分.(4)若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交. 点,且这条直线二等分平行四边形的面积.例1. = ABCD中,ZA的平分线分BC成4cm和3cm两条线段,则Q ABCD的周长为.例2.在U7ABCD 中,ZC=6O°,DE1AB 于E,DF丄BC 于F.(1)则ZEDF= __________ ;rt ----------- (-(2)如图,若AE=4, CF=7, //则UABCD周长= _______________ ;/ Y F例3.在平行四边形ABCO中,已知NA=40° ,则NB = 例4.ZZ7ABCD.中,周长为20cm,对角线AC交BD于点O, AOAB比△OBC的周长多4,则边AB =,BC=变式训练•如图,在平行四诊形ABCD中,已知对角线A匚和BD相交于点0, A AOB的周长为15, AB = 6,那么又角线AC 和BD的和是多少?例5、如图,在cABCD^,。
是对角线的交点,过。
的宜线交厶8于£,交DC于F,图中全等三角形共有(A. 2对B. 3对C. 6对D. 8对3.两条平行线间的距离,(1〕定义,两条平行线中,一条宜线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.(2)两平行线间的距离处处相等.例6、有以下四个说怯;①两点的距离,点;到直线的距离,两条平行线间的距离,都是指某种线段的长.②如果两点的位置固定,那么它们的距离是定值.③如果一点和一条直线的位置固定,那么它们的距离是定值.④两条平行线间的距离不是定值其中正确说法的个数是A. 1B. 2C. 3D. 44-平行四边形的面积:⑴如图①,S^ABCI =BC * AE=CD • AF .① ②(2)同底(等底)同高(等高)的平行四边形面积相等.如图②,必ECD与U7EBCF有公共边BC,则Scwm = SaHRm.例7、如图.四边形ABCD是平行四边形.AB=10, AD=8, AC J. BC.求AC、OA以及平行四边形ABCD的面积变式训练:1、平行四边形两邻边分别是4和6.其中一位上的高是*则平行四苞形的面积是.2、平行四边形的周长为20皿,AE丄BC于E, AF1CD于F, AE=2 cm, AF=3 cm.求平行四边形旭CD的面积。
平行四边形标准讲义.doc

学习好资料欢迎下载(1) 演变关系 :(2)从属关系:(一)平行四边形的性质1.平行四边形的定义:有两组对边分别平行的四边形叫做平行四边形2.平行四边形的性质:(1)平行四边形的对边平行且相等 ;(2)平行四边形的对角相等 , 邻角互补 ;(3)平行四边形的对角线互相平分 .(4)平行四边形是中心对称图形 , 对角线的交点是它的对称中心 ;3.平行四边形的面积平行四边形的面积等于它的底和该底上的高的积.( 二) 平行四边形的判定1.平行四边形的判定方法 5 种:两组对边分别平行从边看一组对边平行且相等两组对边分别相等的四边形是平行四边形从角看 ------两组对角分别相等从对角线看 --- 对角线互相平分2.三角形中位线定理定义 :连接三角形两边中点的线段叫做三角形中位线.定理 :三角形的中位线平行于三角形的第三边,并且等于第三边的一半.结论 :三角形共有三条中位线,并且它们又重新构成一个新的三角形其周长是原三角形周长的一半,面积是原三角形面积的四分之一;(三)矩形1.矩形定义:有一个角是直角的平行四边形叫做矩形.2.矩形的性质:矩形具有平行四边形的所有性质(1)矩形对边平行且相等;( 2)矩形四个角都是直角; (3) 矩形对角线互相平分且相等;(4)矩形是轴对称图形 , 有2条对称轴,对称轴是对边中点所在直线;是中心对称图形,对称中心是两条对角线的交点.3.直角三角形的性质:直角三角形斜边上的中线等于斜边的一半4.矩形的判定方法(1)有一个角是直角的平行四边形 ;(2)有三个角是直角的四边形 ;(3)对角线相等的平行四边形 .5.矩形的面积公式(类比平行四边形):矩形面积=底×高(四)菱形1.定义 : 有一组邻边相等的平行四边形叫做菱形.2.性质 : 菱形具有平行四边形的一切性质:(1)菱形四条边都相等; ( 2)菱形对角相等(3)菱形对角线互相垂直平分,并且每一条对角线平分一组对角;(4)菱形是轴对称图形 , 有2条对称轴,对称轴是对角线所在直线;是中心对称图形,对称中心是两条对角线的交点 .3.判定 : (1)有一组邻边相等的平行四边形是菱形;(2)四条边都相等的四边形;(3)对角线互相垂直的平行四边形;4.菱形的面积 :(1)类比平行四边形面积公式:底×高(2)两条对角线乘积的一半. 若a、b分别表示两条对角线的长,则S菱形=1ab2(五)正方形1.定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形.2.性质:( 1)边 ------- 四条边都相等 , 对边平行 ;(2)角 -------四个角都相等且都是直角;( 3)对角线 ----① 相等;② 互相垂直平分;③ 每一条对角线平分一组对角;④两条对角线将它分成四个全等的等腰直角三角形.(4)是轴对称图形 , 有 4 条对称轴;是中心对称图形 , 对称中心是两条对角线的交点 .3.判定:( 1)先证它是矩形 , 再证一组邻边相等;( 2)先证它是菱形 , 再证一个角是直角 .4.面积:( 1)正方形的面积等于边长的平方;(2)正方形的面积等于两条对角线的乘积的一半.结论:周长相等的四边形中,正方形的面积最大.(六)梯形知识点1.定义:一组对边平行,另一组对边不平行的四边形叫做梯形.特殊梯形的定义:①等腰梯形:两腰相等的梯形叫做等腰梯形;②直角梯形:有一个角是直角的梯形叫做直角梯形.2.等腰梯形的性质 : ( 1)等腰梯形两腰相等 , 两底平行;(2)等腰梯形同一底上的两个角相等;(3)等腰梯形两条对角线相等;(4)等腰梯形是轴对称图形 , 有一条对称轴 , 过两底中点的直线是它的对称轴 .3.等腰梯形的判定 : ( 1)定义:即先判定梯形 , 再证明两腰相等;(2)同一底上的两角相等的梯形;(3)对角线相等的梯形 .4.梯形的中位线定理( 1)定义:连结梯形两腰中点的线段叫做梯形的中位线.※( 2)结论:梯形的中位线平行于两底, 且等于两底和的一半 .5. 梯形的面积公式 : (1)S= 1( 上底+下底) ×高2※( 2)S= 中位线×高解决梯形问题常用的方法在研究梯形的问题中,常通过添加辅助线将其转化为三角形和特殊的四边形.梯形中常用的辅助线:① 平移腰② 作高③ 平移对角线④ 延长两腰⑤有一腰中点时 ,作另一腰的平行线⑥有一腰中点时 ,常把一底的端点与中点连接并延长,与另一底的延长线相交⑦有底的中点时 ,常过中点作两腰的平行线A DE A DMMB FC B C EAD A DEB EC B C练习 11 .菱形的定义: __________________ 的平行四边形叫做菱形.2 .菱形的性质:菱形是特殊的平行四边形,它具有四边形和平行四边形的______ :还有:菱形的四条边 ______ ;菱形的对角线 ______ ,并且每一条对角线平分______ ;菱形的面积等于 __________________ ,它的对称轴是______________________________ .3.若菱形的两条对角线长分别是 6cm , 8cm ,则它的周长为 ______cm ,面积为______cm 2.4.如图,在菱形 ABCD中, E、F 分别是 AB、AC 的中点,如果 EF=2,那么菱形ABCD的周长是5.如图,在菱形 ABCD中, E 是 AB 的中点,且 DE⊥ AB, AB=4.求: (1) ∠ABC的度数; (2) 菱形ABCD的面积.6、菱形的两条对角线的长分别是6cm和 8cm,求菱形的周长和面积7、如图,已知四边形ABCD是菱形,点 E、 F 分别是边 CD、AD的中点,求证: AE=CFA FDEB C练习 21.正方形的定义:有一组邻边______ 并且有一个角是______ 的平行四边形叫做正方形,因此正方形既是一个特殊的有一组邻边相等的______ ,又是一个特殊的有一个角是直角的 ______ .2.正方形的性质:正方形具有四边形、平行四边形、矩形、菱形的一切性质,正方形的四个角都 ______ ;四条边都 ______ 且__________________;正方形的两条对角线 ______ ,并且互相 ______ ,每条对角线平分______ 对角.它有 ______ 条对称轴.3.若正方形的边长为 a,则其对角线长为______4、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为cm2.5、如图,正方形ABCD的边 CD在正方形ECGF的边 CE上,连接 BE、 DG,求证: BE=DGE FA DB C G6、已知:如图,正方形中,点、、N 分别在、、边上,=,ABCD E M AB BC AD CE MN ∠MCE=35°,求∠ANM的度数.7.已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交 BC于F.求证: BF=EC.练习 31.梯形有关概念:一组对边平行而另一组对边______ 的四边形叫做梯形,梯形中平行的两边叫做底,按______ 分别叫做上底、下底(与位置无关 ) ,梯形中不平行的两边叫做 ______ ,两底间的 ______ 叫做梯形的高.一腰垂直于底边的梯形叫做______ ;两腰 ______ 的梯形叫做等腰梯形.2. 已知:如图,在梯形ABCD中, AD∥BC,∠B=72°,∠C=36°,AD=6cm,BC=15cm,求 CD的长A DB C3.在梯形 ABCD中, AD∥BC,对角线 AC⊥BD,且 AC=5cm, BD=12cm,则梯形中位线的长等于多少4. 如图所示,在直角梯形ABCD 中,已知底AD=6cm ,BC=11cm ,腰 CD=12cm ,求这个直角梯形的周长.练习题 41.等腰梯形的性质:等腰梯形中 ______ 的两个角相等,两腰 ______ ,两对角线______ ,等腰梯形是轴对称图形,只有一条对称轴,______ 就是它的对称轴.2.等腰梯形的判定:______ 的梯形是等腰梯形;同一底上的两个角______ 的梯形是等腰梯形.3.等腰梯形的上、下底和腰分别是4cm、 10cm和 5cm,则此梯形的高为 ___________,面积为 ____________4、等腰梯形两底之和是10,两底差是4,一底角是45°,则其面积是多少 ?5、已知:如图,梯形ABCD中, AD∥BC, AB=CD,延长 CB到 E,使 EB= AD,连结AE.求证: AE=CA.四边形期末复习一、选填题1、如图,在平行四边形ABCD中,∠A=130°,在AD上取 DE=DC,则∠ECB的度数是.2、如图,在ABCD中,已知 AB=9㎝, AD=6㎝, BE平分∠ABC交 DC边于点 E,则 DE等于㎝.2 题1题3、已知四边形ABCD ,有以下四个条件:①AB // CD ;② AB CD ;③ BC // AD ;④ BC AD .从这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法种数共有()(A)6 种(B)5种(C)4种(D)3种4、如图,在△ ABC 中,点D、 E、 F 分别在边AB 、BC 、 CA 上,且DE ∥CA ,DF ∥ BA .下列四种说法:①四边形AEDF 是平行四边形;②如果BAC 90 ,那么四边形AEDF 是矩形;③如果AD 平分BAC ,那么四边形AEDF 是菱形;④如果AD BC 且AB AC ,那么四边形AEDF 是菱形其中,正确的有. (只填写序号)5、如图,矩形ABCD中,对角线AC、BD交于 O, AE⊥ BD于 E,∠DAE∶∠ BAE=3∶1,则∠EAC=_______.6、矩形ABCD的对角线AC、 BD交于 O,若△ ABC的周长比△ AOB的周长大10cm,则边AD的长是 _______.7、如图 , 菱形 ABCD边长为 4, ∠A=60°,E 、 F 分别为 AD、 BD的中点,点G在 DC上,△EGF的面积为.AECF.若AB=3,则BC的长为8、将矩形纸片ABCD按如图所示的方式折叠,得到菱形()2D.3A.1 B.2 C.学习好资料欢迎下载DCGE FA B5题7 题8 题9、等腰梯形的下底是上底的 3 倍,上底与高相等,则下底角的度数为.10、等腰梯形中位线等于它的腰长,若腰长等于5,则等腰梯形的周长是.11、等腰梯形ABCD中, AD∥BC, BD平分∠ ABC, BD⊥ CD于 D,若梯形的周长为35cm,则AD的长为cm.12、如图,三个边长均为 2 的正方形重叠在一起,O1、 O2是其中两个正方形的中心,则阴影部分的面积是.O2O113、如图,正方形ABCD 中,M 是BC的中点, CM 2 ,点P是BD上一动点,则PM PC 的最小值是.14、如图,平行四边形中, E 是 CD的中点, F 是 AE的中点,FC与 BE交于 G.求证: GF= GC.15、若矩形ABCD的一条角平分线BE分 AD边为5cm和4cm两部分,求BE长和矩形 ABCD的面积 .学习好资料欢迎下载A D17、如图,在矩形ABCD中, E、 F 分别是边 BC、AB上的点,且EF=ED, EF⊥ ED.GEB FC求证: AE平分∠BAD.18、 Rt △ABC,∠A=90°,∠B 的平分线交AC于 D,自 A 作 BC的垂线交BD于 E,自 D?作 DF?⊥BC,求证:四边形AEFD为菱形.19 、如图,已知ABCD 中,AE平分BAD,交DC于 E,DF BC于F,交AE于 G,且DF AD .(1)试说明DE BC ;(2 )试问 AB 与DG FC之间有何数量关系?写出你的结论,并说明理由.20、如图,等腰梯形ABCD中, AD∥BC, AB=DC, AC⊥ BD,过 D 点作 DE∥AC交 BC的延长线于A DE点。
平行四边形课件ppt

判定
有一个角是直角的菱形是 正方形;对角线相等的菱 形是正方形。
03
CATALOGUE
平行四边形的应用
在几何作图中的应用
总结词:基础应用
详细描述:平行四边形是几何学中最基础的图形之一,它在证明定理、解决几何 问题等方面有着广泛的应用。通过平行四边形的性质和判定,可以解决各种几何 问题,如面积计算、线段长度比较等。
。
掌握平行四边形的面积和周长的 计算方法。
加深对平行四边形的应用的理解 ,如对称问题、最值问题等。
THANKS
感谢观看
进一步提高孩子们对平行四边形性质的理解和应用能力。
详细描述
给出一个不规则的图形,让孩子们通过重新排列或剪切得到一个平行四边形,并说明理由。
06
CATALOGUE
总结与回顾
主要概念总结
平行四边形定义
两组对边分别平行的四边形叫做 平行四边形。
平行四边形性质
平行四边形的对边相等且平行、 对角相等、对角线互相平分。
对角线互相平分的四边形是平行四边 形。
一组对边平行且相等的四边形是平行 四边形。
两组对角分别相等的四边形是平行四 边形。
02
CATALOGUE
平行四边形的特殊形式
矩形
定义
有一个角是直角的平行四边形是 矩形。
性质
矩形的四个角都是直角,矩形的对 角线相等。
判定
有一个角是直角的平行四边形是矩 形;对角线相等的平行四边形是矩 形。
平行四边形属于中心 对称图形,其对称中 心是两条对角线的交 点。
平行四边形的性质
01
02
03
04
对边平行:平行四边形的对边 平行且相等。
对角相等:平行四边形的对角 相等,邻角互补。
人教版初二下册数学第18章《平行四边形》讲义第12讲平行四边形-复习训练(有答案)
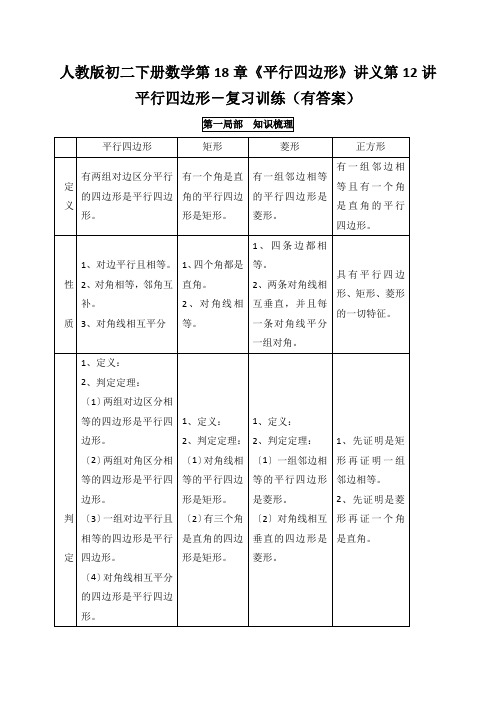
人教版初二下册数学第18章《平行四边形》讲义第12讲平行四边形-复习训练(有答案)对称 中心对称 中心对称轴对称图形 中心对称 轴对称图形 中心对称 轴对称图形第二局部 考点精讲精练考点一、平行四边形的性质及判定【知识要点】〔1〕、平行四边形的边、角、对角线性质, 对称性〔2〕、平行四边形判定方法〔3〕、三角形中位线【典型例题】例1、以下图形中是中心对称图形,但不是轴对称图形的是〔 〕A 、菱形B 、矩形C 、正方形D 、平行四边形例2、如图,□ABCD 与□DCFE 的周长相等,且∠BAD=60°,∠F=110°,那么∠DAE 的度数为 例3、如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延伸线交于点E,与DC 交于点F,且点F 为边DC 的中点,DG ⊥AE,垂足为G,假定DG=1,那么AE 的长为〔 〕 A 、2 B 、4 C 、4 D 、8例4、平面直角坐标系中,□ABCD 的顶点,A ,B ,D 的坐标区分是〔0,0〕〔5,0〕,〔2,3〕,那么顶点C 的坐标是〔 〕A 、〔3,7〕B 、(5,3)C 、(7,3)D 、 (8,2)〔例2〕 〔例3〕 〔例4〕例5、如图,E 是平行四边形内任一点, 假定S平行四边形ABCD =8,那么图中阴影局部的面积是〔 〕A 、3B 、4C 、5D 、6 例6、如图,将平行四边形ABCD 纸片沿EF 折叠,使点C 与点A 重合,点D 落在点G A yB CD处。
〔1〕求证:AE =AF〔2〕求证:△ABE ≌△AGF例7、如下图:四边形ABCD 是平行四边形,DE 平分BF ADC ,∠平分ABC ∠.试证明四边形BFDE 是平行四边形.例8、如图,在△ABC 中,AB =4,AC =3,BC =5,以三边为边,在BC 的同侧区分作三个等边三角形即△ABD 、△BCE 、△ACF 。
〔1〕求证:四边形EFAD 是平行四边形;〔2〕求四边形EFAD 的面积。
平行四边形的判定--讲义

平行四边形的判定主讲教师:傲德重难点易错点辨析题一:如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( ) A.AD=BC B.OA=OCC.AB=CD D.∠ABC+∠BCD=180°B考点:平行四边形的判定金题精讲题一:在四边形ABCD中,AC与BD相交于点O,要使四边形ABCD是平行四边形应符合下列条件中的( ) A.AB∥CD,BC=AD B.AB=CD,OA=OCC.AB∥CD,OA=OC D.AB=CD,AC=BD考点:平行四边形的判定[:题二:已知,平面直角坐标系内有A、B、C三点,坐标分别为A(2,2),B(3,0),C(1,0),若四边形ABCD 为平行四边形,则点D的坐标是.[:考点:平行四边形的判定题三:如图,四边形ABCD中,AD=BC,AE⊥BD,CF⊥BD,垂足为E、F,AE=CF,求证:四边形ABCD是平行四边形.B C考点:平行四边形的判定题四:如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.考点:平行四边形的判定思维拓展题一:如图所示,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC、BC于点E、F,作GH∥BC分别交AB、AC于点G、H,作MN∥AC分别交AB、BC于点M、N.试求EF+GH+MN的值.BF N考点:平行四边形的判定[:[:数理化][:平行四边形的判定讲义参考答案重难点易错点辨析题一:C.金题精讲题一:C.题二:(6,2)、(2,2)、(0,2).题三:略.题四:略.思维拓展题一:8.。
平行四边形的判定公开课ppt讲义公开课获奖课件百校联赛一等奖课件

A
E
D
B
F
C
例1:已知:平行四边形ABCD中,E, F分别是边AD,BC旳中点(如图)
求证:EB=DF
A
E
D
B
F
C
例1:已知:平行四边形ABCD中,E, F分别是边AD,BC旳中点(如图)
求证:EB=DF
E
D
证明:∵四边形ABCD
是平行四边形 B
F
C
∴AD BC
∵ED=1/2AD BF=1/2BC ∴ED BF ∴四边形EBFD是平行四边形
∵AB=CD AC=CA
∴△ABC≌△CDA (SAS)
∴BC=AD
A
D
∴四边形ABCD是平行四边形 B
C
(两组对边分别相等旳四边形是平行四边形)
平行四边形旳鉴定定理1:
一组对边平行且相等旳四边形是平行四边 形
例1:已知:平行四边形ABCD中,E, F分别是边AD,BC旳中点(如图)
求证:EB=DF
(一组对边平行且相等旳四边形是平行四边形)
∴EB=DF
A
E
D
B
F
C
例2:画平行四边形ABCD,使∠B=45°,
AB=2CM,BC=3CM
小结:平行四边形旳三个鉴定措施:
从边看:
两组对边分别平行 两组对边分别相等
一组对边平行且相等
旳四 边形 是平 行四 边形
边有什么关系?
平行四边形旳对边平行且相等,这种 关系可记作AB =//CD,
问题:请猜测“一组对边平行且相 等旳四边形是平行四边形”这个命 1 题是真命题还是假命题?
已知:如图 ,在四边形ABCD中,AB=//CD 求证:四边形ABCD是平行四边形
平行四边形(讲义).doc

q一q — qD MOB — ° MiOC — ° ^COD 平行四边形【知识要点】一、平行四边形1.平行四边形的概念:两组对边分别的四边形叫做平行四边形.2.平行四边形的性质(1)平行四边形的对边;(2)平行四边形的对角;(3)平行四边形的对角线.注意:平行四边形是以对角线的交点为中心的对称图形,但不一定是轴对称图形.3.平行四边形的判定(1)两组对边分别相等的四边形是平行四边形;(2)对角线的四边形是平行四边形;(3)两组对角分别相等的四边形是平行四边形;(4)一组对边的四边形是平行四边形.注意:(1)平行四边形的定义既可以作为性质,乂可以作为判定;(2)一组对边平行,一组对角相等的四边形是平行四边形;(3)一组对边平行,另一组对边相等的四边形不一定是平行四边形,有可能是等腰梯形.(2)如图所示,四边形ABCD是平行四边形,则有C — C — C — C — J_ c。
MBC —□ MiCD— D ACDA — ° 2)AB ~ ABCD4.两平行线间的距离定义:两条平行线中一条直线上任意一点到另一条直线的距离叫做两条平行线间的距离.二、矩形1、定义:有一个角是的平行四边形叫做知形.2、性质:(1)矩形的四个角是;(2)矩形的对角线.注意:(1)矩形的定义可作为性质;(2)平行四边形的所有性质矩形都具备.3、判定:(1)有三个角是直角的四边形是;(2)对角线相等的平行四边形是.注意:矩形的定义可作为判定.证明方法:(1)先证明一个四边形是平行四边形,再证明它有一个角是直角;(2)先证明一个四边形是平行四边形,再证明它的对角线相等.三、菱形1、定义:有一组邻边的平行四边形是菱形.2、性质:(1)菱形的四条边;(2)菱形的对角线,并且每一条对角线. 注意:(1)菱形的定义可作为性质;(2)平行四边形的所有性质菱形都具备;(3)菱形既是中心对称图形,又是轴对称图形,有条对称轴.3、判定:(1)四条边都相等的四边形是_____ ;(2)对角线互相垂直的平行四边形是・注意:(1)菱形的定义可作为判定;(2)对角线平分一组对角的平行四边形是菱形.证明方法:(1)先证明一个四边形是平行四边形,再证明它的一•组邻边相等或者对角线互相垂直;(2)可以证明一个四边形的四条边相等.4、面积:(1)可用平行四边形的面积计算公式,即底X高;(2)两条对角线乘积的一半,即若菱形的两条对角线的长为。
(完整版)平行四边形专题讲义

平行四边形专题讲义一、学习目标 复习平行四边形、特殊平行四边形性质与判定,能利用它们进行计算或证明. 二、学习重难点 重点:性质与判定的运用;难点:证明过程的书写。
三、本章知识结构图1.平行四边形是特殊的 ;特殊的平行四边形包括 、 、 。
2.梯形 (是否)特殊平行四边形, (是否)特殊四边形。
3.特殊的梯形包括 梯形和 梯形。
4、本章学过的四边形中,属于轴对称图形的有 ;属于中心对称图形的有 。
四、复习过程 (一)知识要点1:平行四边形的性质与判定1.平行四边形的性质:(1)从边看:对边 ,对边 ; (2)从角看:对角 ,邻角 ; (3)从对角线看:对角线互相 ; (4)从对称性看:平行四边形是 图形。
2、平行四边形的判定:(1)判定1:两组对边分别 的四边形是平行四边形。
(定义)(2)判定2:两组对边分别 的四边形是平行四边形。
(3)判定3:一组对边 且 的四边形是平行四边形。
(4)判定4:两组对角分别 的四边形是平行四边形。
(5)判定5:对角线互相 的四边形是平行四边形。
【基础练习】1.已知□ABCD 中,∠B =70°,则∠A =____,∠C =____,∠D =____.2.已知O 是ABCD 的对角线的交点,AC =38 mm ,BD =24 mm,AD =14 mm ,那么△BOC 的周长等于__ __.3.如图1,ABCD 中,对角线AC 和BD 交于点O ,若AC =8,BD =6,则边AB 长的取值范围是( ). A.1<AB <7 B.2<AB <14 C.6<AB <8 D.3<AB <44.不能判定四边形ABCD 为平行四边形的题设是( ) A.AB=CD,AD=BC B.ABCD C.AB=CD,AD ∥BC D.AB ∥CD,AD ∥BC5.在ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F ,AE=4,AF=6,ABCD 的周长为40,则ABCD 的面积是 ( ) A 、36 B 、48 C 、 40 D 、24【典型例题】例1、若平行四边形ABCD 的周长是20cm,△AOD 的周长比△ABO 的周长大6cm.求AB,AD 的长. F DA OA B CDOA DDC AB E F M NBE F C AD例2、 如图,已知四边形ABCD 是平行四边形,∠BCD 的平分线CF 交边AB 于F ,∠ADC 的平分线DG 交边AB 于G 。
平行四边形的性质及判定(四边形)讲义

EOABD C平行四边形的性质及判定一、知识提要1.定义有两组对边分别平行的四边形叫做平行四边形.平行四边形用“□”表示,平行四边形ABCD记作□ABCD.2.平行四边形的性质:对边相等,对角相等,对角线互相平分.3.三角形的中位线平行于三角形的第三边,且等于第三边的一半.4.两条平行线间的任何两条平行线段都是相等的,其中,两条平行线间最短的线段长度叫做平行线间的距离.5.平行四边形的判定:共5个①两组对边分别平行的四边形是平行四边形;②两组对角分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.二、精讲精练1.(2011广东)已知□ABCD的周长为32,AB=4,则BC=()A. 4B. 12C. 24D. 282.在平行四边形中,四个角之比可以成立的是( )A.1:2:3:4 B.2:2:3:3 C.2:3:3:2 D.2:3:2:33.(2011江苏)在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于________.4.(2011山东)如图,在□ABCD中,AC,BD相交于点O,点E是AB的中点,3OE cm,则AD的长是__cm.5.(2011湖南)如图所示,在□ABCD中,对角线AC、BD相交于点O,且AB≠AD,则下列式子不.正确..的是( )A.AC⊥BD B.AB=CDC.BO=OD D.∠BAD=∠BCD6.在平行四边形ABCD中,∠B-∠A=20°,则∠D的度数是_______.7.平行四边形的两邻边分别为3,4,那么其对角线必( )A.大于1 B.大于1且小于7C.小于7 D.大于7或小于1A DCOB8. 以长为5cm, 4cm, 7cm 的三条线段中的的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是 ( ) A. 1 B. 2 C. 3 D. 49. 已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______.10. 在□ABCD 中,AB =3,BC =5,∠B 的平分线AE 交AD 于点E ,则DE 的长为__________.11. 在平面内和直线l 距离为8 cm 的直线有______条. 12. 平行四边形的一组对角的平分线( )A .一定相互平行B .一定相交C .可能平行也可能相交D .平行或共线13. (2011湖南)如图.下列四组条件中.不能..判定四边形ABCD 是平行四边形的是( )A .AB =DC , AD =BCB .AB ∥DC ,AD ∥BC C .AB ∥DC ,AD =BCD .AB ∥DC ,AB =DC14. 如图,平行四边形ABCD 中,AE =CG , DH =BF ,连结E ,F ,G ,H ,E ,则四边形EFGH 是_____.15. 如图,平行四边形ABCD 中,E ,F 是对角线AC 上的两点,且AE =CF ,则四边形BEDF 是___________.16. 如图,平行四边形ABCD 中,E ,F 分别为边BC ,AD 的中点,则图中共有平行四边形的个数是( ) A . 3 B . 4 C . 5 D . 617. (2011天津)如图,点D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点,连接DE 、EF 、FD .则图中平行四边形的个数为__________.18. 已知四边形ABCD ,有以下四个条件,①AB ∥CD ;②AB =CD ;③BC ∥AD ;④BC =AD .从这四个条件中,任选两个,能使四边形ABCD 成为平行四边形的选法共有( ) A .3 B .4 C .5 D .6FEDCBA DCBAHGA BCDEFF EDCBA FA BCDEABECFD 19. 如图,在△ABC 中,∠ACB =90°,点E 为AB 中点,连结CE ,过点E 作ED ⊥BC 于点D ,在DE 的延长线上取一点F ,使AF =CE .求证:四边形ACEF 是平行四边形.20. (2011湖北)如图,在平行四边形ABCD 中,E 为CD 中点,BE 的延长线与AD 的延长线相交于点F . (1)证明:∠DFE =∠CBE ; (2)证明:△DFE ≌△CBE .21. 如图,四边形ABCD 是平行四边形,AD =12,AB =13,BD ⊥AD ,求BC ,CD及OB 的长.22. (2011四川)如图,平行四边形ABCD 的对角线AC 、BD 交于点O ,E 、F 在AC 上,G 、H 在BD 上,且AF =CE ,BH =DG ,求证:EG ∥HF .OD CBAH G O E DCBA F E DCB A F三、测试提高【板块一】平行四边形的性质1. (2011重庆)如图,在平行四边形 ABCD 中(AB ≠BC ),直线EF 经过其对角线的交点O ,且分别交AD 、BC 于点M 、N ,交BA 、DC 的延长线于点E 、F ,下列结论:①AO =BO ;②OE =OF ; ③△ODM ≌△OBN ; ④△EAO ≌△CNO ,其中正确的是( ) A. ①② B. ②③ C. ②④ D. ③④2. (2011辽宁)如图,在□ABCD 中,点E 、F 分别在边AD 、BC 上,且BE ∥DF ,若∠EBF =45°,则∠EDF 的度数是( ) A .30° B .45° C .55° D .75°3. (2011浙江)如图,已知E 、F 是□ABCD 对角线AC 上的两点,且BE ⊥AC ,DF ⊥AC ,对角线AC ,BD 相交于点O ,则图中有几对全等三角形( ) A .3 B .4 C .5 D .64. 如图,EF 过平行四边形ABCD 对角线的交点O ,并交AD 于点E ,交BC 于F ,若AB =4,BC =6,OE =2,那么四边形EFCD 的周长是( ) A .16 B .14 C .12 D .10N MFE ODC BAFEDCBA O ABCDE FF E ODCB A【板块二】平行四边形的判定5. (2011广西)如图,在平行四边形ABCD 中,EF ∥AD , HN ∥AB ,则图中的平行四边形的个数共有( ) A .12个 B .9个 C .7个 D .5个四、课后作业1. 在□ABCD 中,∠A = 2∠B ,则∠C =________.2. 在□ABCD 中,∠A ∶∠B ∶∠C ∶∠D 的值可以是( ). A.1∶2∶3∶4 B.1∶2∶2∶1 C.1∶1∶2∶2 D.2∶1∶2∶13. 已知平行四边形ABCD 的周长是100cm, AB :BC =4:1,则AB 的长是__________.4. 在平行四边形ABCD 中,∠A :∠B =3:2,则∠C =_______度,∠D =____度.5. 用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的短边长为____.6. 平行四边形ABCD 的周长32, 5AB =3BC ,则对角线AC 的取值范围为_______.7. 在平行四边形ABCD 中,∠A =65°,则∠D 的度数是_______8. 由等腰三角形底边上任一点(端点除外)作两腰的平行线,则所成的平行四边形的周长等于等腰三角形的 ( ).A.周长B. 一腰的长C.周长的一半D. 两腰的和 9. 能够判定一个四边形是平行四边形的条件是 ( ). A. 一组对角相等 B. 两条对角线互相平分 C. 两条对角线互相垂直 D. 一对邻角的和为180°10. 关于四边形ABCD :①两组对边分别平行②两组对边分别相等③有两组角相等④对角线AC 和BD 相等.以上四个条件中,可以判定四边形ABCD 是平行四边形的有______个.11. 四边形ABCD 中,AD ∥BC ,要判定ABCD 是平行四边形,那么还需满足 ( ). A. ∠A +∠C =180° B. ∠B +∠D =180° C. ∠A +∠B =180° D. ∠A +∠D =180°12. 已知平行四边形ABCD 中,AB = 12,AB 边上的高为3,BC 边上的高为6,则平行四边形ABCD 的周长为 .NHE D CBA F13.已知:如图,△ABC中,AB=AC,DE//AC,DF//AB.求证:DE+DF=AB14.如图,在□ABCD中,O是对角线AC、BD的交点,E,F是BD上的点,BE⊥EC,DF⊥AF,垂足分别为E、F.那么OE与OF是否相等?为什么?15.(2010江苏)如图,在□ABCD中,点E,F是对角线AC上两点,且AE=CF.求证:∠EBF=∠FDE.16.(2011福建)如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.求证:AE=CF.FAB C DE OEDCB AFC ABD EFB DAFCE。
(完整)平行四边形全部讲义

平行四边形1、平行四边形的性质考点一、平行四边形的概念(1)定义:两组对边分别平行的四边形叫做平行四边形.(2) "表示,平行四边形ABCD ABCD”,读作“平行四边形ABCD”。
平行四边形一定按顺时针或逆时针依次注明各顶点。
(3)平行四边形定义的作用:平行四边形的定义既是判定,又是性质.①由定义知平行四边形两组对边分别平行;②由定义可以得出只要四边形中两组对边分别平行,那么这个四边形就是平行四边形。
(4)平行四边形的基本元素:边、角、对角线。
例1中,EF∥AB,GH∥BC,EF、GH相交于点P,写出图中的平行四边形.A E DG P HB F C考点二、平行四边形的性质(1)边的性质:平行四边形的对边平行且相等。
(2)角的性质:平行四边形的邻角互补,对角相等。
(3)对角线性质:平行四边形的对角线互相平分。
例2中,∠A+∠C=160°,求∠A、∠B、∠C、∠D的度数.A BC D 考点三、平行四边形的对角线的性质(1)平行四边形的对角线互相平分.例3中,对角线AC 、BD 相交于O 点,若AC=14,BD=8,AB=10,则△OAB 的周长为_______。
练习题 一、感受理解1.已知 ABCD 的对角线交点,AC=10cm ,BD=18cm ,AD=•12cm ,•则△BOC•的周长是_______.2的对角线AC,BD 交于点O,△AOB 的面积为2,那么平行四边形ABCD 的面积为_____.3.已知平行四边形的两邻边之比为2:3,周长为20cm ,•则这个平行四边形的两条邻边长分别为___________.4.平行四边形的周长为30,两邻边的差为5,则其较长边是________. 5.平行四边形具有,而一般四边形不具有的性质是( ) A .外角和等于360° B .对角线互相平分 C .内角和等于360° D .有两条对角线6.如图,□ABCD 中,EF 过对角线的交点O ,AB =4,AD =3,OF =1。
平行四边形的概念和性质课件

平行四边形的性质
1 对角线
平行四边形的对角线互相平分,交点称为对 角线的中点。
2 边长相等
平行四边形的相邻边长相等。
3 对边平等且平行
平行四边形的对边相等且平行。
4 内角和为360°
平行四边形的内角和为360°。
平行四边形的应用
建筑设计
平行四边形的结构特性使其在 建筑设计中得到广泛应用,如 设计建筑外观、立面或屋顶。
特殊情况
若平行四边形是矩形或正方形,可使用其他相应的 面积公式。
平行四边形与其他几何形状的关系
矩形Байду номын сангаас
矩形是一种特殊的平行四边形,具有相等的内角和 直角。
菱形
菱形是一种特殊的平行四边形,具有相等的对角线 和内角。
平行四边形的判定方法
对边判定法
若一组对边相等且平行,则四边形是平行四边 形。
角判定法
若一组内角或外角相等,则四边形是平行四边 形。
平行四边形的概念和性质
平行四边形是具有两组对边平行的四边形。它们具有多种特征和性质,其理 解对于几何学的学习至关重要。
平行四边形的定义和特征
定义
平行四边形是具有两组对边 平行的四边形。
特征
平行四边形的对边相等且平 行,同一组内角相等,同一 组外角相等。
例子
例如,长方形和菱形都是平 行四边形的特例。
图案设计
平行四边形的简单几何形状常 用于图案设计,如地板瓷砖、 墙纸和纺织品。
数学研究
平行四边形是数学研究中的一 个重要概念,有助于推导和证 明其他几何形状的性质。
平行四边形的推论
1
推论1
相邻内角互补。
2
推论2
对角线平分平行四边形的内角。
平行四边形的概念和性质讲义

八年级平行四边形的概念和性质知识归纳一.平行四边形的定义两组对边分别平行的四边形是平行四边形.平行四边形用符号“□”表示.平行四边形ABCD记作□ABCD,读作平行四边形ABCD.要点诠释:平行四边形的定义即是它的一个性质,又是它的一种判定方法.二.平行四边形的性质1.从边看:平行四边形的对边平行且相等;2.从角看:平行四边形的对角相等、邻角互补;3.从对角线看:平行四边形的对角线互相平分.要点诠释:已知平行四边形,要根据推理证明的需要,合理选用其性质.题型:运用平行四边形的性质解决线段、角及面积计算问题例1.在□ABCD中,AB=3,BC=5,则它的周长为__________.(结论:平行四边形的一组邻边之和等于周长的一半,反之,周长等于2倍邻边之和).【变式】1.在□ABCD中,∠A的平分线分BC成4cm和3cm两条线段,则□ABCD的周长为.例2.如下左图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是________°.【变式】2-2.如上右图,在□ABCD中,∠C=60º,DE⊥AB于E,DF⊥BC于F.(1)则∠EDF= ;(2)若AE=4,CF=7,则□ABCD的周长为.例2-3.如右图,已知□ABCD的周长为20,对角线AC交BD于点O,△BOC比△AOB的周长多4,则边AB=____________,BC=____________.结论:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.【变式】2-3.在□ABCD中,对角线AC,BD相交于点O,已知△BOC与△AOB△的周长之差为3,平行四边形ABCD的周长为26,则BC的长度为_____________.例2-4.如图,□ABCD 的对角线AC 交BD 于点O ,分平行四边形为四个三角形,它们的面积有怎样的关系?结论:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.【变式】2-4.如图,直线EF 过平行四边形ABCD 对角线的交点O ,分别交AB 、CD 于E 、F ,那么阴影部分的面积是平行四边形ABCD 面积的( )A .51 B .41 C .31 D .21例2-5.如图,在□ABCD 中,对角线AC ,BD 相交于点O ,过点O 作直线EF ,分别交AD ,BC 于点E ,F .判断四边形ABFE 的面积与四边形FCDE 的周长和面积有何关系?试说明理由.结论:过平行四边形对角线交点的任一条直线都将平行四边形分成周长和面积相等的两部分.【变式】2-5.如图,□ABCD 的对角线AC ,BD 相交于O ,EF 过点O 与AD ,BC 分别相交于E ,F ,如果AB =4,BC =5,OE =1.5,那么四边形EFCD 的周长为( )A .16B .14C .12D .10题型三:运用平行四边形的性质进行证明例3-1.如图,在□ABCD 中,点E ,F 分别是边AD ,BC 的中点,求证:AF =CE .【变式】3-1.如图,在□ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q,求证:MP=QN.例3-2.如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.(1)求证:AB=AF;(2)若BC=2AB,△BCD=110°,求△ABE的度数.【变式】3-2.如图,在□ABCD中,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD;(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.例3-3.如图,AD△BC,AE△CD,BD平分△ABC,求证AB=CE.【变式】3-3.在□ABCD中,AE、BF分别平分△DAB和△ABC,交CD于E、F,AE、BF相交于点M.(1)求证:AE△BF;(2)求证:DF=CE.例3-4.如图,□ABCD的顶点A,C和□EBFD的顶点E,F在同一条直线上,求证:AE=CF.题型四:平行四边形的性质与勾股定理及其逆定理综合例4-1.如图,在□ABCD中,AB=10,AD=8,AC=6,AC交BD于点O,求OB以及□ABCD的面积.O【变式】4-1.如图,已知□ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,求AE的长.题型五:利用两平行线间的距离的性质解决面积问题例5-1. 如下左图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为_____________. .【变式】5-1.如上右图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB:CD=1:2,若△ABC的面积为5,则△BCD的面积为______.。
经典特殊的平行四边形讲义+家教专用

学科教师辅导讲义教学内容一、知识回顾矩形、菱形、正方形1菱形的性质:①菱形的四条边都相等•②菱形的对角线互相垂直,并且每条对角线平分一组对角.③具有平行四边形所有性质•2•菱形的判定:①对角线互相垂直的平行四边形是菱形•②一组邻边相等的平行四边形是菱形.③四条边都相等的四边形是菱形.3•矩形的性质:①矩形的四个角都是直角•②矩形的对角线相等•③矩形具有平行四边形的所有性质. 4•矩形的判定:①有一个角是直角的平行四边形是矩形•②对角线相等的平行四边形是矩形.③有三个角是直角的四边形是矩形.5. 正方形的性质:①正方形的四个角都是直角,四条边都相等.② 正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角.6. 正方形的判定:①有一个角是直角的柳是正方形.②有一组邻边相等的矩形是正方形.③ 对角线相等的菱形是正方形•④对角线互相垂直的矩形是正方形.课前练习:1 .已知平行四边形 ABCD 勺周长是28Cm CD-AD=2cm 那么AB= _________ Cm BC= 2•菱形的两条对角线分别是 6cm, 8cm,则菱形的边长为 __________ ,一组对边的距离为 _______ 3. 在菱形 ABCD 中,∠ ADC=120 ,贝U BD AC 等于 _________4. ________________________________________________________________ 已知正方形的边长为 a ,则正方形内任意一点到四边的距离之和为 ___________________________ .5.矩形ABCD 被两条对角线分成的四个小三角形的周长之和是 86cm ,对角线长是13cm ,ABCD 的周长是 __________6•如图,将一张等腰直角三角形纸片沿中位线剪开,可以拼出不同形状的四边形, 请写出其中两个不同的四边形的名称:7•如图,有一张面积为1的正方形纸片ABCD , M , N 分别是AD , BC 边的中点, 将C 点折叠至MN 上,落在P 点的位置,折痕为 BQ ,连结PQ ,则PQ =&如图,梯形 ABCD 中,AD // BC , AB=CD=AD =1,∙ B =60* ,直线 MN 为梯 形ABCD 的对称轴,P 为MN 上一点,那么PC PD 的最小值为9.如图,OBCt 是边长为1的正方形,∠ BOx=60°,则点C 的坐标为 _____________10•如图,把正方形 ABCD 沿着对角线 AC 的方向移动到正方形 ABCD •的位置,它们的重叠部分的面积是正方形ABCD 面积的一半,若 AC = '• 2 ,则正方形移动的距离 AA ■是Cm则矩形D Q C巩固练习1矩形的相邻两边的长分别是12 Cm和5 cm,则矩形的对角线的长是。
平行四边形性质和判定基础讲义

数学学科辅导讲义【知识点1平行四边形的对角线互相平分】 【例1】•如图,在口ABCD 中,O 是对角线AC ,BD 的交点,下列结论错误的是()A • AB #CD B • AB =CDC • AC =BD D • OA =OCBC=5,对角线AC ,BD 相交于点O ,则UOA 的取值范围是 解答题:如图所示,在ABCD 中,对角线AC 与BD相交于点O,点M, N 在对角线AC 上,且AM=CN,求证【例1】•如图,^^ABCD 中,O 是对角线AC ,BD 的交点,若^AOD 的面积是5,则口ABCD 的面积是()A •10 B. 15 C. 20 D. 25练1:如图,在口 ABCD 中,已知20口人=90 AC=10 cm ,BD = 6 cm ,则AD 的长为(A • 4 cmB. 5 cm C • 6 cm【例2】•如图,口ABCD 的对角线交于点O ,且AB = 5,AOCD 的周长为23,则口ABCD的两条对角线的和是(A • 18B. 28 C • 36 D. 46 练1. o ABCD 的对角线 AC BD 交于点O ,若两条对角线长的和为20 cm ,且BC 长为6 cm ,则4AOD 的周长为cm. 练 2. ^^ABCD 中,AB = 3 :BM 〃DN.知识点2 平行四边形的面积.3*练 2 •如图,^^ABCD 中,对角线 AC ,BD 交于点 O ,若 DO = 1.5 cm ,AB = 5 cm ,BC=4 cm.练3.如图,o ABCD 的对角线交于点O ,<AB = 5,AOCD 的周长为23,贝U^ABCD 的A -B. 28 C • D. 46【例2】•如图,=ABCD 面积为)A - 60 B C • 20 D. 16 cm 2 例1 •如图,o ABCD 中分的面积为A • 6 C. 12 D. 24B. 求D ABCD 的面积.D两条对角线的和是()H 口练1 •(柳州中考)如图,^^ABCD 的面积为20,BC=5,则边AD 与BC 间的距离为 A D ,AC ,BD 为对角线,BC=6,BC 边上的高为4,则阴影部 的对角线AC 的长为10 cm ,NCAB = 30° ,AB 的长为6 cm ,则=ABCD 的随堂检测△AEF 与4DFC 是否全等?为什么?课后练习1.如图,已知BE 〃DF,NADF=NCBE, AF=CE.求证:四边形DEBF 是平行四边形.1.已知□ABCD 的周长为32, AB=4,则U BC= ( A. 4B. 12C. 24 )D. 28 2.如图,OABCD 的对角线交于点O,且AB = 5,AOCD 的周长为23,则 ABCD 的两条对角线的和是 ()3.4. 5. 6. A. 18 C. 36 D. 46 在□ABCD 中,AB = 6 cm, BC = 8 cm 如图 如图 如图 在□ABCD 中,NA=120°,则ND = 在□ABCD 中,对角线AC 、BD 相交于点O,若AC=14, BD = 8, AB = 10,则^OAB 的周长为 四边形ABCD 是平行四边形,点E 在BA 的延长线上,且BE=AD,^ F 在AD 上,AF=AB.那么 Q2.如图,已知D是4ABC的边AB上一点,CE〃AB, DE交AC于点O,且OA=OC,猜想线段CD与线段 AE的大小关系和位置关系,并证明你的结论.第12。
平行四边形的判定讲义

5、 在平面直角坐标系内, 平行四边形 ABCD 的对角线的交点正好与坐标原点重合, 且点 A、 B 的坐标分别为 3,1, 7,5 求点 C、D 的坐标及平行四边形 ABCD 的周长。
A
E G
H
P
I
B
C D F
4、求证:平行四边形的四个内角平分线围成一个平行四边形
A
H L I J K
E
D
B
F
G
C
5、请设计一种方案,把三角形切割成一个与其面积相等的平行四边形,并说明理由
A
D.
.E
F
C
B
6、平行四边形 ABCD 中,△ACP 和△ACQ 是正三角形,求证:四边形 BPDG 是平行四边形
E
F A B
例 6、如图是某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE,EF=FC,甲乙两人 同时从 B 站乘车到 F 站,甲的路线是 B→A→E→F,乙的路线是 B→D→C→F,两车速度相同,无耽 E 误时间,谁先到 F 站?
D
A
F
B
C
例 7、已知 AD 是△ABC 的中线,E 为 AC 上一点,连线 BE 交 AD 于 F,且 AE=FE,求证:AC=BF
A
F B D
E C
G
例 8、六边形 ABCDEF,∠A=∠B=∠C=∠D=∠E=∠F=120°,AB=10,BC=70,CD=20,DE=40,求 AF 和 EF 的长
F E
N
ADΒιβλιοθήκη MBC三、练习 1、在平行四边形 ABCD 中,对角线 AC、BD 交于点 O,E、F 是对角线 AC 上的两点,当 E、F 满足 C 下列哪个条件时,四边形 DEBF 不一定是平行四边形?( ) D F A. AE=CF O B. ∠ADE=∠CBF E C. ∠AED=∠CFB A B D. DE=BF
平行四边形及其性质课件

04 平行四边形的面积计算
面积公式推导
底乘高
通过将平行四边形的一条底边与对应 的高相乘,可以得出面积。这是平行 四边形面积计算的基本公式。
转化思想
将平行四边形转化为矩形或三角形, 利用已知的矩形或三角形面积公式推 导出平行四边形的面积公式。
面积计算方法
01
02
03
直接计算
根据平行四边形的底和高 ,直接使用面积公式进行 计算。
理等。
代数方程
在代数方程中,平行四边形也常 被用于解决各种问题,如解线性
方程组、求矩阵的逆等。
微积分
在微积分中,平行四边形可用于 计算面积和体积,如在计算曲边 梯形和曲顶柱体的面积和体积时 ,可以利用平行四边形的性质进
行简化计算。
THANKS FOR WATCHING
感谢您的观看
平行四边形及其性质课件
目录
• 平行四边形的基本概念 • 平行四边形的性质 • 平行四边形的判定方法 • 平行四边形的面积计算 • 平行四边形的应用举例
01 平行四边形的基本概念
定义与分类
定义
两组对边分别平行的四边形叫做 平行四边形。
分类
根据对边是否相等或平行,平行 四边形可分为两组对边相等且平 行和一组对边平行且相等的两种 类型。
VS
证明
假设四边形ABCD中,AB平行于CD且BC 平行于AD。由于AB平行于CD且BC平行 于AD,所以∠ABC+∠BCD=180°且 ∠ADC+∠BCD=180°。因此, ∠ABC=∠ADC。由于AB平行于CD且BC 平行于AD,根据平行线的性质,BC是AB 和CD的中线。因此,四边形ABCD是平 行四边形。
对角线互相平分
定义
平行四边形全章知识讲解

平行四边形全章复习【知识网络】【要点梳理】要点一、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:边:(1)平行四边形的对边平行且相等;角:(2)平行四边形的对角相等;邻角互补;边与角:(3)平行四边形的对角线互相平分;对称性:(4)平行四边形不是轴对称图形.3.面积:高底平行四边形⨯=S4.判定:边:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形.角:(4)两组对角分别相等的四边形是平行四边形;(5)两组邻角分别互补的四边形是平行四边形.边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形; 对角线:(7)对角线互相平分的四边形是平行四边形.拓展:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等;(3)三角形的中位线平行于三角形的第三边,且等于第三边的一半.要点二、矩形1.定义:有一个角是直角的平行四边形叫做矩形.2.性质:边:(1)矩形的对边平行且相等;角:(2)矩形的四个角都是直角;对角线:(3)矩形的对角线互相平分且相等;对称性:(4)矩形是轴对称图形. 对称轴为____________________________;3.面积:宽=长矩形⨯S4.判定:角:(1)有一个角是直角的平行四边形是矩形.对角线:(2)对角线相等的平行四边形是矩形.角:(3)有三个角是直角的四边形是矩形.拓展:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半. 要点三、菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2.性质:边:(1)菱形的对边平行;边:(2)菱形的四条边相等;角:(3)菱形的对角相等;邻角互补;对角线:(4)菱形的两条对角线互相平分且垂直,并且每一条对角线平分一组对角; 对称性:(5)菱形是轴对称图形.对称轴为________________________________;3.面积:2对角线对角线高==底菱形⨯⨯S 4.判定:边:(1)一组邻边相等的平行四边形是菱形;对角线:(2)对角线互相垂直的平行四边形是菱形;边:(3)四边相等的四边形是菱形.要点四、正方形1. 定义:一组邻边相等的矩形叫做正方形;或:_______________________________.2.性质:边:(1)正方形的对边平行;边:(2)正方形的四条边都相等;角:(3)正方形的四个角都是直角;对角线:(4)对角线互相垂直平分且相等,对角线平分对角;对角线:(5)两条对角线把正方形分成四个全等的等腰直角三角形;对称性:(6)正方形是轴对称图形. 对称轴为____________________________;3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:边:(1)一组邻边相等的矩形是正方形;角:(2)有一个角是直角的菱形是正方形;对角线:(3)对角线互相垂直的矩形是正方形;对角线:(4)对角线相等的菱形是正方形;(5)四条边都相等,三个角都是直角的四边形是正方形;(6)对角线互相垂直平分且相等的四边形是正方形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形(讲义)
课前预习
1.已知:如图,在四边形ABCD中,AB∥CD,AD∥BC.
(1)求证:AB=CD且AD=BC.
(2)连接AC,BD,设AC,BD的交点为O.求证:OA=OC
1.平行四边形的定义:__________________________________.
2.平行四边形的性质
边:________________________________________________;
角:________________________________________________;
对角线:____________________________________________.3.平行四边形的判定
⎧⎨⎩①_____________________________________________;
边
②_____________________________________________.
角:________________________________________________.
对角线:____________________________________________.
4.夹在平行线之间的________________相等.
精讲精练
1. 已知□ABCD 的周长是100,且AB :BC =4:1,则AB 的长为______________.
2. 如图,在□ABCD 中,∠DAB 的平分线AE 交CD 于点E ,若AB =5,BC =3,
则EC 的长为( )
A .1
B .1.5
C .2
D .3
3. 在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )
A .1:2:3:4
B .1:2:2:1
C .1:1:2:2
D .2:1:2:1
4. 在□ABCD 中,对角线AC ,BD 相交于点O ,若△ABO 的周长为15,AB =6,
则AC +BD =____________.
5. 在周长为20cm 的□ABCD 中,AB <AD ,AC ,BD 相交于点O ,OE ⊥BD ,交
线段AD 于点E ,连接BE ,则△ABE 的周长为__________. 6. 如图,在□ABCD 中,已知AB =5,AD =3,AC ⊥BC ,则
BD =_______,□ABCD 的面积为_______.
7. 如图,□ABCD 的对角线AC ,BD 相交于点O ,EF 过点O 且与AB ,CD 分
别交于点E ,F .求证:OE =OF .
F
E
A B
C
D
O
8. 下列说法:
①如果一个四边形任意相邻的两个内角都互补,那么这个四边形是平行四边形;
②一组对边平行,另一组对边相等的四边形是平行四边形;
③如果AC ,BD 是四边形ABCD 的对角线,且AC 平分BD ,那么四边形ABCD 是平行四边形;
④一组对边平行,一组对角相等的四边形是平行四边形. 其中正确的有() A .1个
B .2个
C .3个
D .4个
O
D
C B A B
C
E
D A
9. 如图,点E ,F 在线段BC 上,若△ABE ≌△DCF .
求证:四边形AFDE 是平行四边形.
A
E
B
C
F
D
10. 如图,已知四边形ABCD 是平行四边形,E ,F 是对角线AC 上的两点,且
AE =CF .求证:四边形EBFD 是平行四边形.
11. 如图,在四边形ABCD 中,AD ∥BC ,AE ∥CD ,且AE 交BC 于点E ,BD 平
分∠ABC .求证:AB =EC .
A
B
C
D
E
12. 如图,在四边形ABCD 中,AB =CD ,BE =DF ,AE ⊥BD ,
CF ⊥BD ,垂足分别为点E ,F . (1)求证:△ABE ≌△CDF ;
(2)若AC 与BD 交于点O .求证:AO =CO .
A
E
B
C
F D
O
平行四边形(习题)
巩固练习
1. 在□ABCD 中,若∠A :∠B =5:4,则∠C 的度数为( ) A .80° B .120° C .100° D .110°
2. 在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )
A .1:2:3:4
B .1:2:2:1
C .1:1:2:2
D .2:1:2:1
3. 若□ABCD 的周长为40,△ABC 的周长为25,则对角线AC 的长为( )
A .5
B .15
C .6
D .16
4. 已知平行四边形的一边长为10,则其两条对角线的长可能是( )
A .3,8
B .20,30
C .6,8
D .8,12
5. 已知四边形ABCD 的对角线相交于点O ,以下条件能判定四边形ABCD 为平
行四边形的是( ) A .AB ∥CD ,BC =AD
B .AB ∥CD ,AO =CO
C .AB ∥C
D ,∠DAC =∠CAB D .AB =CD ,∠B =∠C
6. 如图,在平行四边形ABCD 中,EF ∥AD ,HN ∥AB ,则图中的平行四边形共
有( ) A .12个
B .9个
C .7个
D .5个
7. 已知平行四边形的周长为56,两邻边长之比为3:1,则这个平行四边形较长
的边长为____________.
8. 在□ABCD 中,已知AB ,BC ,CD 三条边的长度分别为3x +,4x -,16,则这个平行四边形的周长为___________.
9. 如图,在□ABCD 中,CE ⊥AB 于点E ,CF ⊥AD 于点F .若∠B =60°,则∠
ECF =___________.
F
E
D
C
B
A N H
F
E D
C B A
10.若□ABCD的周长为22,AC,BD相交于点O,△AOD的周长比△AOB的周
长小3,则AD=_________,AB=_________.
11.如图,在□ABCD中,O是AC,BD的交点,E,F,G,H分别是AO,BO,
CO,DO的中点,求证:四边形EFGH是平行四边形.
O
G H
F E
D
C
B
A
【思路分析】
①读题标注:
②梳理思路:
要证四边形EFGH是平行四边形,根据题目中已有的条件选择判定定理:________________________________________.
【过程书写】
12. 如图,在□ABCD 中,点E ,F ,G ,H 分别在边AB ,BC ,CD , AD 上,且
AE =CG ,BF =DH ,求证:四边形EFGH 是平行四边形.
G
H
F
E
D
C B
A
【思路分析】 ①读题标注: ②梳理思路:
要证四边形EFGH 是平行四边形,根据题目中已有的条件选择判定定理:_______________________________________.
【过程书写】。
