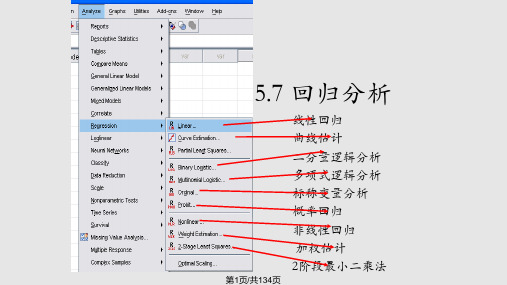
spss回归分析大全ppt课件
合集下载
软件SPSS的回归分析功能-PPT课件

“残差”复选框组:
“模型拟合度”复选框:
“R方变化”复选框:
• 模型拟合过程中进入、退出的变量的列表,以及一些有关拟合优度的检 验:R,R2和调整的R2, 标准误及方差分析表。 • 显示模型拟合过程中R2、F值和p值的改变情况。 • 提供一些变量描述,如有效例数、均数、标准差等,同时还给出一个自 变量间的相关矩阵。
【选项】按钮
• 注意:选项按钮只需要在选择方法为逐步回归后,才需要打开
• “步进方法标准”单选钮组:设置纳入和排除标准,可按P值或F 值来设置。 • “在等式中包含常量”复选框:用于决定是否在模型中包括常数 项,默认选中。 • “缺失值”单选钮组:用于选择对缺失值的处理方式,可以是不 分析任一选入的变量有缺失值的记录(按列表排除个案)而无论 该缺失变量最终是否进入模型;不分析具体进入某变量时有缺失 值的记录(按对排除个案);将缺失值用该变量的均数代替(使 用均值替代)。
“描述性”复选框:
“部分相关和偏相关性”复选框:
• 显示自变量间的相关、部分相关和偏相关系数。
“共线性诊断”复选框:
• 给出一些用于共线性诊断的统计量,如特征根(Eigenvalues)、方差 膨胀因子(VIF)等。
以上各项在默认情况下只有“估计”和“模型拟合度”复选框被选中。
【绘制】按钮
step4:线性回归结果
【Anova】 (analysisofvariance方差分析)
• 此表是所用模型的检验结果,一个标准的方差分析表。 • Sig.(significant )值是回归关系的显著性系数,sig.是F值的实际显著 性概率即P值。当sig. <= 0.05的时候,说明回归关系具有统计学意义。 如果sig. > 0.05,说明二者之间用当前模型进行回归没有统计学意义, 应该换一个模型来进行回归。 • 由表可见所用的回归模型F统计量值=226.725 ,P值为0.000,因此我 们用的这个回归模型是有统计学意义的,可以继续看下面系数分别检验 的结果。 • 由于这里我们所用的回归模型只有一个自变量,因此模型的检验就等价 与系数的检验,在多元回归中这两者是不同的。
《SPSS回归分析》ppt课件

.
-3.666
.002
从表中可知因变量与自变量的三次回归模型为: y=-166.430+0.029x-5.364E-7x2+5.022E-12x3
9.2 曲线估计
➢拟合效果图
从图形上看出其拟合效果非常好。
8.3 曲线估计
说明:
曲线估计是一个自变量与因变量的非线性回归过程,但 只能处理比较简单的模型。如果有多个自变量与因变量呈非 线性关系时,就需要用其他非线性模型对因变量进行拟合, SPSS 19中提供了“非线性”过程,由于涉及的模型很多,且 非线性回归分析中参数的估计通常是通过迭代方法获得的, 而且对初始值的设置也有较高的要求,如果初始值选择不合 适,即使指定的模型函数非常准确,也会导致迭代过程不收 敛,或者只得到一个局部最优值而不能得到整体最优值。
8.1 回归分析概述
(3)回归分析的一般步骤
第1步 确定回归方程中的因变量和自变量。 第2步 确定回归模型。 第3步 建立回归方程。 第4步 对回归方程进行各种检验。
➢拟合优度检验 ➢回归方程的显著性检验 ➢回归系数的显著性检验
第5步 利用回归方程进行预测。
主要内容
8.1 回归分析概述 8.2 线性回归分析 8.3 曲线估计 8.4 二元Logistic回归分析
8.3 曲线估计
(2) 统计原理
在曲线估计中,有很多的数学模型,选用哪一种形式的回 归方程才能最好地表示出一种曲线的关系往往不是一个简单的 问题,可以用数学方程来表示的各种曲线的数目几乎是没有限 量的。在可能的方程之间,以吻合度而论,也许存在着许多吻 合得同样好的曲线方程。因此,在对曲线的形式的选择上,对 采取什么形式需要有一定的理论,这些理论是由问题本质决定 的。
第章SPSS回归分析PPT课件

第八章 SPSS的回归分析
2020-01-10
1
8.1 SPSS在一元线性回归分析中的应用
8.1.1 一元线性回归的基本原理
1.方法概述
线性回归模型侧重考察变量之间的数量变化规律,并通过 线性表达式,即线性回归方程,来描述其关系,进而确定一 个或几个变量的变化对另一个变量的影响程度,为预测提供 科学依据。
2020-01-10
4
8.1.2 一元线性回归的SPSS操作详解
第一步:打开对话框
选择菜单栏中的【分析】→【回归】→【线性】命令, 弹出【线性回归】对话框,这是线性回归分析的主操作 窗口。
第二步:选择因变量
在【线性回归】对话框左侧的候选变量列表框中选择 一个变量,将其添加至【因变量】列表框中,即选择该 变量作为一元线性回归的因变量。
协方差矩阵:方差-协方差矩阵。
模型拟合度:模型拟合过程中进入、退出的变量的列表; 以及一些有关拟合优度的检验统计量,例如R、R2和调 整的R2、估计值的标准误及方差分析表。
R方变化:显示每个自变量进入方程后R2、F值和p值的 改
变情况。
描述性:显示自变量和因变量的有效数目、均值、标准
【预测值】为预测栏,用于选择输出回归模型的预测值。
未标准化(U):未标准化的预测值。
标准化(R):标准化的预测值。
调节(J):经调整的预测值。
均值预测值的S.E.(P):预测值的标准误差。
2020-01-10
12
【残差】为残差栏,包含以下选项。 未标准化(N):未标准化残差。 标准化(A):标准化残差。 学生化(S):学生化残差。 删除(L):剔除残差。 学生化已删除(E):学生化剔除残差。 【距离】为距离栏,包含以下选项。 Mahalanobis距离(H)。 Cook 距离(K)。 杠杆值(G)。
2020-01-10
1
8.1 SPSS在一元线性回归分析中的应用
8.1.1 一元线性回归的基本原理
1.方法概述
线性回归模型侧重考察变量之间的数量变化规律,并通过 线性表达式,即线性回归方程,来描述其关系,进而确定一 个或几个变量的变化对另一个变量的影响程度,为预测提供 科学依据。
2020-01-10
4
8.1.2 一元线性回归的SPSS操作详解
第一步:打开对话框
选择菜单栏中的【分析】→【回归】→【线性】命令, 弹出【线性回归】对话框,这是线性回归分析的主操作 窗口。
第二步:选择因变量
在【线性回归】对话框左侧的候选变量列表框中选择 一个变量,将其添加至【因变量】列表框中,即选择该 变量作为一元线性回归的因变量。
协方差矩阵:方差-协方差矩阵。
模型拟合度:模型拟合过程中进入、退出的变量的列表; 以及一些有关拟合优度的检验统计量,例如R、R2和调 整的R2、估计值的标准误及方差分析表。
R方变化:显示每个自变量进入方程后R2、F值和p值的 改
变情况。
描述性:显示自变量和因变量的有效数目、均值、标准
【预测值】为预测栏,用于选择输出回归模型的预测值。
未标准化(U):未标准化的预测值。
标准化(R):标准化的预测值。
调节(J):经调整的预测值。
均值预测值的S.E.(P):预测值的标准误差。
2020-01-10
12
【残差】为残差栏,包含以下选项。 未标准化(N):未标准化残差。 标准化(A):标准化残差。 学生化(S):学生化残差。 删除(L):剔除残差。 学生化已删除(E):学生化剔除残差。 【距离】为距离栏,包含以下选项。 Mahalanobis距离(H)。 Cook 距离(K)。 杠杆值(G)。
spss中的回归分析PPT课件
6、Statistics(统计)对话框 单击“Statistics”按钮,进入统计对话框如图:
第19页/共134页
Estimates(默认选择项):回归系数的估计值(B)及其标准误(Std.Error)、 常数(Constant);标准化回归系数(Beta);B的t值及其双尾显著性水平(Sig.)。
第5页/共134页
H0:1 0, 2 0,, k 0
Fα
第6页/共134页
(3)回归系数的显著性检验(t检验) 所谓回归系数的显著性检验,就是根据样 本估计的结果对总体回归系数的有关假设进行 检验。 之所以对回归系数进行显著性检验,是因 为回归方程的显著性检验只能检验所有回归系 数是否同时与零有显著性差异,它不能保证回 归方程中不包含不能较好解释说明因变量变化 的自变量。因此,可以通过回归系数显著性检 验对每个回归系数进行考察。
4、 Selection variable(选择变量):可从源变量栏中 选择一个变量,单击Rule后,通过该变量大于、小于或等于某 一数值,选择进入回归分析的观察单位。
5、Case Labels(个案标签):在左侧的源变量框中选择 一变量作为标签变量进入 Case Labels框中。
第18页/共134页
Model fit(默认选择项):列出进入或从模型中剔除的变量;显示下列拟合 优度统计量:复相关系数(R)、判定系数(R2)、调整 R2(Adjusted R Square)、 估计值的标准误以及方差分析表。
Confidence intervals:回归系数 B的 95%可信区间(95%Confidence interval for B)。
第7页/共134页
回归参数显著性检验的基本步骤。 ① 提出假设
[课件]SPSS回归分析过程详解()PPT
![[课件]SPSS回归分析过程详解()PPT](https://img.taocdn.com/s3/m/9975250eed630b1c59eeb5c4.png)
SPSS回归分析过程详解 (ppt)
回归分析的概念
寻求有关联(相关)的变量之间的关系 主要内容:
从一组样本数据出发,确定这些变量间的定 量关系式 对这些关系式的可信度进行各种统计检验 从影响某一变量的诸多变量中,判断哪些变 量的影响显著,哪些不显著 利用求得的关系式进行预测和控制
回归分析的模型
按是否线性分:线性回归模型和非线性回归模型 按自变量个数分:简单的一元回归,多元回归 基本的步骤:利用SPSS得到模型关系式,是否 是我们所要的,要看回归方程的显著性检验(F 检验)和回归系数b的显著性检验(T检验),还要 看拟合程度R2 (相关系数的平方,一元回归用R Square,多元回归用Adjusted R Square)
我们只讲前面3个简单的(一般教科书的讲法)
10.1 线性回归(Liner)
一元线性回归方程: y=a+bx
a称为截距 b为回归直线的斜率 用R2判定系数判定一个线性回归直线的拟合程度:用来说明用自变 量解释因变量变异的程度(所占比例)
b0为常数项 b1、b2、…、bn称为y对应于x1、x2、…、xn的偏回归系数 用Adjusted R2调整判定系数判定一个多元线性回归方程的拟合程度: 用来说明用自变量解释因变量变异的程度(所占比例)
逐步回归方法的基本思想
对全部的自变量x1,x2,...,xp,按它们对Y贡献的大小进 行比较,并通过F检验法,选择偏回归平方和显著的变 量进入回归方程,每一步只引入一个变量,同时建立 一个偏回归方程。当一个变量被引入后,对原已引入 回归方程的变量,逐个检验他们的偏回归平方和。如 果由于引入新的变量而使得已进入方程的变量变为不 显著时,则及时从偏回归方程中剔除。在引入了两个 自变量以后,便开始考虑是否有需要剔除的变量。只 有当回归方程中的所有自变量对Y都有显著影响而不需 要剔除时,在考虑从未选入方程的自变量中,挑选对Y 有显著影响的新的变量进入方程。不论引入还是剔除 一个变量都称为一步。不断重复这一过程,直至无法 剔除已引入的变量,也无法再引入新的自变量时,逐 步回归过程结束。
回归分析的概念
寻求有关联(相关)的变量之间的关系 主要内容:
从一组样本数据出发,确定这些变量间的定 量关系式 对这些关系式的可信度进行各种统计检验 从影响某一变量的诸多变量中,判断哪些变 量的影响显著,哪些不显著 利用求得的关系式进行预测和控制
回归分析的模型
按是否线性分:线性回归模型和非线性回归模型 按自变量个数分:简单的一元回归,多元回归 基本的步骤:利用SPSS得到模型关系式,是否 是我们所要的,要看回归方程的显著性检验(F 检验)和回归系数b的显著性检验(T检验),还要 看拟合程度R2 (相关系数的平方,一元回归用R Square,多元回归用Adjusted R Square)
我们只讲前面3个简单的(一般教科书的讲法)
10.1 线性回归(Liner)
一元线性回归方程: y=a+bx
a称为截距 b为回归直线的斜率 用R2判定系数判定一个线性回归直线的拟合程度:用来说明用自变 量解释因变量变异的程度(所占比例)
b0为常数项 b1、b2、…、bn称为y对应于x1、x2、…、xn的偏回归系数 用Adjusted R2调整判定系数判定一个多元线性回归方程的拟合程度: 用来说明用自变量解释因变量变异的程度(所占比例)
逐步回归方法的基本思想
对全部的自变量x1,x2,...,xp,按它们对Y贡献的大小进 行比较,并通过F检验法,选择偏回归平方和显著的变 量进入回归方程,每一步只引入一个变量,同时建立 一个偏回归方程。当一个变量被引入后,对原已引入 回归方程的变量,逐个检验他们的偏回归平方和。如 果由于引入新的变量而使得已进入方程的变量变为不 显著时,则及时从偏回归方程中剔除。在引入了两个 自变量以后,便开始考虑是否有需要剔除的变量。只 有当回归方程中的所有自变量对Y都有显著影响而不需 要剔除时,在考虑从未选入方程的自变量中,挑选对Y 有显著影响的新的变量进入方程。不论引入还是剔除 一个变量都称为一步。不断重复这一过程,直至无法 剔除已引入的变量,也无法再引入新的自变量时,逐 步回归过程结束。
《spss回归与相关》PPT课件

制作:王立芹
a
Met hod
St epwise
(Crit eria: Probabilit
y-of -
F-to-enter
.
<= .050,
Probabilit y-of -
F-to-remo
ve >= . 100).
St epwise
(Crit eria:
Probabilit y-of -
F-to-enter
1
Sig. (2-tailed)
.000
N
15
15
**. Correlation is significant at the 0.01 level (2-tailed).
23.11.2020 23:43:55
制作:王立芹
2.秩相关
例13-2 某医生收集12例急性脑梗死(AMI)病人, 记录了患者在抢救期间的总胆固醇,用爱丁堡-斯堪 的那维亚神经病学中SNSS量表评分标准评定患者 的神经功能缺损程度,试分析总胆固醇与神经功能 评分是否相关。
Model
B Std. Error Beta
t
1 (Consta6n.7t)74 .156
43.545
x3
.110 .027
.693 4.079
a.Dependent Variable: y
Sig. .000 .001
23.11.2020 23:43:57
制作:王立芹
R e g re s s io n S ta n d a rd iz e d R e s id u a l
23.11.2020 23:43:57
制作:王立芹 23.11.2020 23:43:57
Spss线性回归分析讲稿ppt课件

绘制各自变量与因变量之间的关系散点图,观
察其与因变量之间是否具有线性关系。然后,
将自变量进行组合,生成若干自变量的子集,再
针对每一个自变量的子集生成回归分析报告。
比较调整后的R2值,挑选最优的自变量子集,
生成回归分析模型。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
①一元线性回归:y=a+bx (有一个自变量)
②多元线性回归:
(有两个或两个以上的自变量)
(2)按回归曲线的形态分
①线性(直线)回归
②非线性(曲线)回归
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
回归分析
(二)回归分析的主要内容
即销售量的95%以上的变动都可以被该模型所解释,拟和优度较高。
表3
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
一元线性回归分析
表4给出了回归模型的方差分析表,可以看到,F统计量为
734.627,对应的p值为0,所以,拒绝模型整体不显著的
图1
奖金-销售量表
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
一元线性回归
以奖金-销售量表图1做回归分析
2、绘制散点图
打开数据文件,选择【图形】-【旧对话框】-【散点/点状】
图2
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
察其与因变量之间是否具有线性关系。然后,
将自变量进行组合,生成若干自变量的子集,再
针对每一个自变量的子集生成回归分析报告。
比较调整后的R2值,挑选最优的自变量子集,
生成回归分析模型。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
①一元线性回归:y=a+bx (有一个自变量)
②多元线性回归:
(有两个或两个以上的自变量)
(2)按回归曲线的形态分
①线性(直线)回归
②非线性(曲线)回归
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
回归分析
(二)回归分析的主要内容
即销售量的95%以上的变动都可以被该模型所解释,拟和优度较高。
表3
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
一元线性回归分析
表4给出了回归模型的方差分析表,可以看到,F统计量为
734.627,对应的p值为0,所以,拒绝模型整体不显著的
图1
奖金-销售量表
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
一元线性回归
以奖金-销售量表图1做回归分析
2、绘制散点图
打开数据文件,选择【图形】-【旧对话框】-【散点/点状】
图2
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
SPSS数据分析教程第8章线性回归分析ppt课件

53.00
66.00
53.00
59.00
精5选5.课00 件ppt 45.00
1.00
1.00
25.00 64
精选课件ppt
z1 61.00 59.00 55.00 56.00 59.00 60.00 52.00 56.00 68.00 60.00 64.00 67.00 56.00 53.00 53.00 60.00 54.00
38
精选课件ppt
表7-1 强度与拉伸倍数的试验数据
序号 1 2 3 4 5 6 7 8 9 10 11 12
拉伸倍数 2.0 2.5 2.7 3.5 4.0 4.5 5.2 6.3 7.1 8.0 9.0 10.0
强度(kg/mm2) 1.6 2.4 2.5 2.7 3.5 4.2 5.0 6.4 6.5 7.3 8.0 8.1
58.00
57.00
62.00
1.00
1.00
23.00
56.00
55.00
57.00
39.00
44.00
46.00
1.69
1.00
15.00
50.00
50.00
68.00
46.00
45.00
56.00
1.08
1.14
25.00
58.00
54.00
60.00
59.00
52.00
51.00
1.00
1.00
5
精选课件ppt
具体地说,回归分析主要解决以下几方面 的问题。
• 通过分析大量的样本数据,确定变量 之间的数学关系式。
• 对所确定的数学关系式的可信程度进 行各种统计检验,并区分出对某一特定变量影 响较为显著的变量和影响不显著的变量。
SPSS数据分析教程回归分析PPT课件

F
SSR / SSE /(n
p p
1)
SSR /1 SSE /(n 2)
MSR MSE
回归均方 残差均方
第19页/共41页
• SPSS在回归输出结果的ANOVA表中给出SSR,SSE,SST和F统计量的取值,同时给出F值的显著性值(即 p值)。
第20页/共41页
用回归方程预测
• 在一定范围内,对任意给定的预测变量取值,可以利用求得的拟合回归方程进行预测。其预测值为: • SPSS可以提供标准化的预测值和调整的预测值
第11页/共41页
简单回归方程的求解
•
我们希望根据观测值估计出简单回归方程中的待定系数 ¯0和¯1,它们使得回归方程对应的响应变量的误
差达到最小,该方法即为最小二乘法。
也就是求解¯0和 ¯1, 使 得
达到最小。
•
把得到的解记为
,则回归方程为
n
S(0, 1) ( yi 0 1xi )2 i 1
• 选择【分析】→【回归】→【线性】。把Units选入到自变量框中;把Minuts选入到因变量框中。其他选 项保留默认值。
第23页/共41页
SPSS回归分析
第24页/共41页
回归度检验
第26页/共41页
多元线性回归
• 实际应用中,很多情况要用到多个预测变量才能更好地描述变量间的关系,如果这些预测变量在预测方程 中的系数为线性,那么回归方程称为多元线性回归方程。就方法的实质来说,处理多个预测变量的方法与 处理一个预测变量的方法基本相同。
第30页/共41页
• F检验的 被拒绝,并不能说明所有的自变量都对因变量Y有显著影响,我们希望从回归方程中剔除那些统 计上不显著的自变量,重新建立更为简单的线性回归方程,这就需要对每个回归系数做显著性检验。
spss第五讲回归分析PPT课件

关于x的残差图 关于y的残差图 标准化残差图
2、用于判断误差的假定是否成立 3、检测有影响的观测值
34
残差图
(形态及判别)
残
差
0
残
残
差
差
0
0
x
(a)满意模式
x
(b)非常数方差
x
(c)模型不合适
35
二、检验正态性 标准化残差(standardized residual)
2. E(y0) 在1-置信水平下的置信区间为
yˆ0 t 2 (n 2)se
1
n
x0 x 2
n
xi x 2
i 1
式中:se为估计标准误差
29
个别值的预测区间
1. 利用估计的回归方程,对于自变量 x 的一个给定值 x0 ,求出因变量 y 的一个个别值的估计区间,这一
区间称为预测区间(prediction interval) 2. y0在1-置信水平下的预测区间为
一、变差 1、因变量 y 的取值是不同的,y 取值的这种波动称为变
差。变差来源于两个方面
由于自变量 x 的取值不同造成的 除 x 以外的其他因素(如x对y的非线性影响、测量误差等)
的影响
2、对一个具体的观测值来说,变差的大小可以通过该 实际观测值与其均值之差y y 来表示
16
误差分解图
y
(xi , yi )
32
一、检验方差齐性
残差(residual)
1、因变量的观测值与根据估计的回归方程求 出的预测值之差,用e表示
ei yi yˆi
2、反映了用估计的回归方程去预测而引起的 误差
3、可用于确定有关误差项的假定是否成立 4、用于检测有影响的观测值
2、用于判断误差的假定是否成立 3、检测有影响的观测值
34
残差图
(形态及判别)
残
差
0
残
残
差
差
0
0
x
(a)满意模式
x
(b)非常数方差
x
(c)模型不合适
35
二、检验正态性 标准化残差(standardized residual)
2. E(y0) 在1-置信水平下的置信区间为
yˆ0 t 2 (n 2)se
1
n
x0 x 2
n
xi x 2
i 1
式中:se为估计标准误差
29
个别值的预测区间
1. 利用估计的回归方程,对于自变量 x 的一个给定值 x0 ,求出因变量 y 的一个个别值的估计区间,这一
区间称为预测区间(prediction interval) 2. y0在1-置信水平下的预测区间为
一、变差 1、因变量 y 的取值是不同的,y 取值的这种波动称为变
差。变差来源于两个方面
由于自变量 x 的取值不同造成的 除 x 以外的其他因素(如x对y的非线性影响、测量误差等)
的影响
2、对一个具体的观测值来说,变差的大小可以通过该 实际观测值与其均值之差y y 来表示
16
误差分解图
y
(xi , yi )
32
一、检验方差齐性
残差(residual)
1、因变量的观测值与根据估计的回归方程求 出的预测值之差,用e表示
ei yi yˆi
2、反映了用估计的回归方程去预测而引起的 误差
3、可用于确定有关误差项的假定是否成立 4、用于检测有影响的观测值
第9章 SPSS 线性回归分析ppt课件

β0 、β1 都是模型中的未知参数,β0为回归常数, β1为y对x回归系数(即x每变动一个单位所引起 的y的平均变动) 。
ε称为随机误差。且满足:E(ε)=0,Var(ε)=σ2 。
.
一元线性回归方程:
E(y)=β0+β1x
表明x和y之间的统计关系是在平均意义下表 述的。
估计的一元线性回归方程:yˆ
b b b b c ˆ ˆ y ˆ ˆ n
2
一元二乘估计:Q( , ) = min (
)
0
1
b b, 0
1 i=1
i
0
1i
多元二乘估计(略)
.
9.3回归方程的统计检验
拟合优度检验 回归方程的显著性检验 回归系数的显著性检验 残差分析
.
9.3.1回归方程的拟合优度检验
用于检验样本数据点聚集在回归线周围的密集程 度,从而评价回归线对样本数据的代表程度。 思想:因变量y(儿子身高)取值的变化受两个因 素的影响:自变量x(父亲身高)不同取值的影响, 其他因素(环境、饮食等)的影响。 可表示如下: ➢ 因变量总变差 = 自变量引起的 + 其他因素引起的 ➢ 即因变量总变差= 回归方程可解释的+不可解释的 ➢ 即,因变量总离差平方和SST =回归平方和 SSA + 剩余平方和SSE
^y=β^0+β1^x 1 +β2x^ 2 …. +βpx^p
.
9.2.3回归参数的最小二乘估计
(ordinary least square estimation ,OLSE)
估计思想:
使每个样本点(xi , yi)与回归线上的对应点( xi , E (yi ))在垂直方向上偏差距离的二次方总和达 到最小的原则来估计参数 即,∑( yi - E(yi ))2 =最小
ε称为随机误差。且满足:E(ε)=0,Var(ε)=σ2 。
.
一元线性回归方程:
E(y)=β0+β1x
表明x和y之间的统计关系是在平均意义下表 述的。
估计的一元线性回归方程:yˆ
b b b b c ˆ ˆ y ˆ ˆ n
2
一元二乘估计:Q( , ) = min (
)
0
1
b b, 0
1 i=1
i
0
1i
多元二乘估计(略)
.
9.3回归方程的统计检验
拟合优度检验 回归方程的显著性检验 回归系数的显著性检验 残差分析
.
9.3.1回归方程的拟合优度检验
用于检验样本数据点聚集在回归线周围的密集程 度,从而评价回归线对样本数据的代表程度。 思想:因变量y(儿子身高)取值的变化受两个因 素的影响:自变量x(父亲身高)不同取值的影响, 其他因素(环境、饮食等)的影响。 可表示如下: ➢ 因变量总变差 = 自变量引起的 + 其他因素引起的 ➢ 即因变量总变差= 回归方程可解释的+不可解释的 ➢ 即,因变量总离差平方和SST =回归平方和 SSA + 剩余平方和SSE
^y=β^0+β1^x 1 +β2x^ 2 …. +βpx^p
.
9.2.3回归参数的最小二乘估计
(ordinary least square estimation ,OLSE)
估计思想:
使每个样本点(xi , yi)与回归线上的对应点( xi , E (yi ))在垂直方向上偏差距离的二次方总和达 到最小的原则来估计参数 即,∑( yi - E(yi ))2 =最小
