2020年三角函数w的取值问题
重难点专题18 三角函数中w取值范围问题八大题型汇总(原卷版) 备战2024年高考数学重难点突破

题型8新定义 (9)已知函数y =Asin(ωx +φ)(A >0,ω>0),在[x 1,x 2]上单调递增(或递减),求ω的取值范围第一步:根据题意可知区间[x 1,x 2]的长度不大于该函数最小正周期的一半,即x 2-x 1≤12T =πω,求得0<ω≤πx 2-x 1.第二步:以单调递增为例,利用[ωx 1+φ,ωx 2+φ]⊆[―π2+2kπ,π2+2kπ],解得ω的范围;第三步:结合第一步求出的ω的范围对k 进行赋值,从而求出ω(不含参数)的取值范围.结合图象平移求ω的取值范围1、平移后与原图象重合思路1:平移长度即为原函数周期的整倍数;思路2:平移前的函数=平移后的函数.2、平移后与新图象重合:平移后的函数=新的函数.3、平移后的函数与原图象关于轴对称:平移后的函数为偶函数;4、平移后的函数与原函数关于轴对称:平移前的函数=平移后的函数-;5、平移后过定点:将定点坐标代入平移后的函数中。
()f x ()g x ()f x ()g x y x ()f x ()g x三角函数两条相邻对称轴或两个相邻对称中心之间的“水平间隔”为T,相邻的对称轴和对2,也就是说,我们可以根据三角函数的对称性来研究其周期称中心之间的“水平间隔”为T4性,进而可以研究ω的取值。
三角函数的对称轴比经过图象的最高点或最低点,函数的对称中心就是其图象与x轴的交点(零点),也就是说我们可以利用函数的最值、零点之间的“差距”来确定其周期,进而可以确定ω的取值.已知三角函数的零点个数问题求ω的取值范围对于区间长度为定值的动区间,若区间上至少含有k个零点,需要确定含有k个零点的区间长度,一般和周期相关,若在在区间至多含有k个零点,需要确定包含k+1个零点的区间长度的最小值.三角函数的对称轴比经过图象的最高点或最低点,函数的对称中心就是其图象与x轴的交点(零点),也就是说我们可以利用函数的最值、零点之间的“差距”来确定其周期,进而可以确定ω的取值.ππ。
三角函数中的参数w的范围问题

三角函数中的参数问题三角函数中的参数范围问题是三角函数中中等偏难的问题,很多同学由于思维方式不对,导致问题难解。
此类问题主要分为四类,它们共同的方法是将相位看成整体,结合正弦函数或余弦函数的图像与性质进行求解。
【题型示例】1.已知,0ω函数在上单调递减,则ω的取值范围是()A. B. C. D.2.已知函数在上有且只有两个零点,则实数ω的取值范围为()A. B. C. D.3.已知函数,若的图象的任意一条对称轴与x轴的交点的横坐标都不属于区间,则ω的取值范围是()A、 B. C. D.4.已知函数,其中,,若且恒成立在区间上有最小值无最大值,则ω的最大值是()A.11B.13C. 15D.17【专题练习】1.已知函数在上单调递减,则ω的取值范围是()A. B. C. D.2.已知函数,若方程在上有且只有四个实根数,则实数ω的取值范围为()A. B. C. D.3.将函数的图像向右平移个单位后,所得图像关于y轴对称,则ω的最小值为()A.2B. 1C.D.4.已知函数的图象过点,若对恒成立,则ω的最小值为()A. 2B.10C.4D.165.已知函数,若对满足的,有,若对任意恒成立,则φ的取值范围是()A. B. C. D.6.将函数的图象向右平移个单位,得取函数的图象,若在上为减函数,则ω的最大值为()A.2B. 3C.4D.57.函数在内的值域为,则ω的取值范围为()A. B. C. D.8.已知函数,若且在区间上有最小值,无最大值,则ω的值为()A. B. C. D.。
16三角函数中w的取值范围问题-带答案

三角函数中w 的取值范围问题1, (2020烟台二模)将函数x x f cos )(=的图像向右平移π32个单位长度,再将各点的横坐标变为原来的()01>ωω,得到函数)(x g 的图像,若)(x g 在⎥⎦⎤⎢⎣⎡2,0π上的值域为⎥⎦⎤⎢⎣⎡-1,21,则ω范围为( )A .⎥⎦⎤⎢⎣⎡38,34 B. ⎥⎦⎤⎢⎣⎡35,31 C. ),34[+∞ D. ),38[+∞2, 将函数f (x )=cosωx 2(2sin ωx 2−2√3cosωx 2)+√3(ω>0)的图象向左平移π3ω个单位,得到函数y =g (x )的图像,若y =g (x )在[0,π4]上为增函数,则ω的最大值为( )A . 1B . 2C . 3D . 43, 若函数f(x)=4sinωx ⋅sin 2 (ωx 2+π4)+cos2ωx −1 (ω>0)在[−π3,π2]内有且仅有一个最大值,则ω的取值范围是( )A . [34,5) B . [1,5) C . [1,92) D . (0,34]4, 已知函数f (x )=2sin (ωx +φ)+1(ω>0,|φ|≤π2), 其图象与直线y =3相邻两个交点的距离为π,若f (x )>2对∀x ∈(π24,π3)恒成立,则φ的取值范围是( )A . (π6,π2) B . [π6,π3] C . (π12,π3) D . [π12,π6]5, (2019III ,12)设函数()()sin 05f x x πωω⎛⎫=+> ⎪⎝⎭,已知()f x 在[]02π,有且仅有5个零点,下述四个结论:①()f x 在()0,2π有且仅有3个极大值点 ②()f x 在()0,2π有且仅有2个极小值点 ③()f x 在0,10π⎛⎫ ⎪⎝⎭单调递增 ④ω的取值范围是1229,510⎡⎫⎪⎢⎣⎭ 其中所有正确结论的编号是A. ○1○4B.○2○3C.○1○2○3D.○1○3○46, (2020德州一模)若函数f (x )=sin(ωx +π6),(ω>0)在(0,5π18)上存在唯一极值点,且在(π2,π)上单调,则ω的取值范围为 。
三角函数中w取值范围研究

三角函数中w取值范围研究在三角函数中,我们常用的三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)。
在研究三角函数中w的取值范围时,我们可以从两个方面进行讨论,即角度角和弧度角两个方面。
首先,我们来讨论角度角的情况。
在角度角中,一个完整的圆周角为360°。
因此,我们可以将w看作一个角度值,而角度值的取值范围是从0°到360°之间。
即0°≤w≤360°。
在这个取值范围内,我们可以观察到一些特殊的取值点。
比如当w等于0°时,sin(w)和tan(w)都为0,而cos(w)为1、当w等于90°时,sin(w)和cos(w)都为1,而tan(w)不存在。
当w等于180°时,sin(w)为0,而cos(w)为-1,tan(w)不存在。
当w等于270°时,sin(w)和cos(w)都为-1,而tan(w)不存在。
最后,当w等于360°时,sin(w)和tan(w)都为0,而cos(w)为1、可以看出,在这些特殊的取值点上,三角函数会有一些特殊的性质。
接下来,我们来讨论弧度角的情况。
在弧度角中,一个完整的圆周角为2π(π≈3.14)。
因此,我们可以将w看作一个弧度值,而弧度值的取值范围是从0到2π之间。
即0≤w≤2π。
同样地,在这个取值范围内,我们可以观察到一些特殊的取值点。
比如当w等于0时,sin(w)和tan(w)都为0,而cos(w)为1、当w等于π/2时,sin(w)和cos(w)都为1,而tan(w)不存在。
当w等于π时,sin(w)为0,而cos(w)为-1,tan(w)不存在。
当w等于3π/2时,sin(w)和cos(w)都为-1,而tan(w)不存在。
最后,当w等于2π时,sin(w)和tan(w)都为0,而cos(w)为1总结起来,三角函数中w的取值范围在角度角中是0°≤w≤360°,在弧度角中是0≤w≤2π。
三角函数中ω的取值范围研究

三角函数中w 的求值及范围研究——从一道高考题引起的思考在三角函数图象中, w 对整个图象的性质影响巨大,因此,对 w 的取值范围的考察就是高考的热门考点之一,这部分考题呈现出综合性较强,对学生的逻辑推理,直观想象素养要求较高,比如2022全国甲卷理11,2021全国甲卷理16,2020年新高考10题,2020年全国Ⅰ卷理7,2019 年一卷 11 题、三卷 12 题,2018全国新课标Ⅱ理10等等,所以,对 w 的取值范围的系统研究,找到解题的通性通法对提高学生的整体数学素养有巨大的帮助.例(2020年新高考10)(多选)下图是函数y = sin(ωx +φ)的部分图像,则sin(ωx +φ)=( )A .πsin(3x +)B .πsin(2)3x -C .πcos(26x +)D .5πcos(2)6x -变式1:(2020年全国Ⅰ卷理7)设函数π()cos()6f x x ω=+在[−π,π]的图像大致如下图,则f (x )的最小正周期为( )A .10π9B .7π6 C .4π3 D .3π2变式2:已知函数()sin()(0)4f x x πωω=+>的图象向右平移23π个单位长度后,所得图象与原函数图象重合,则ω的最小值为__________:已知函数()sin()(0)4f x x πωω=+>的图象向右平移3π个单位长度后,与函数sin()6y x πω=+的图象重合,则ω的最小值为__________变式2.2:已知函数()sin()(0)4f x x πωω=+>的图象向右平移6π个单位长度后,与函数cos()4y x πω=+ 的图象重合,则ω的最小值为__________变式3:若函数)0(1sin 2)(>+=ωωx x f 在区间]32,2[ππ-上是增函数,求ω的取值范围。
变式3.1:已知函数)0(cos sin 3)(>+=ωωωx x x f 在)4,0(π上不单调,在)32,3(ππ上单调,则实数ω的取值范围为( )A.]2,1(B.]2,53( C.]2,1[ D.]2,34(变式4:(多选)函数)0(sin 2)(>=ωωx x f 在]4,3[ππ-∈x 上的最小值为2-,则实数ω的值可以取( )A.32 B.23C.2D.3 变式4.1:函数x x f ωsin 2)(=在]4,3[ππ-∈x 上的最小值为2-,则实数ω的取值范围为( )A.]23,(--∞B.),23[+∞C.),23[]2,(+∞⋃--∞D.),2[]23,(+∞⋃-∞变式4.2:若函数)0(sin 2)(>=ωωx x f 在]2,3[ππ-∈x 内有且仅有一个最大值2,则实数ω的取值范围为( )A.)5,43[ B.)5,1[ C.)291[, D.]43,0(:为了使函数)0(sin 2)(>=ωωx x f 在区间[0,1]上至少出现50次最大值,则ω的最小值为( )A .98πB .1972πC .1992π D .100π变式5:若函数*sin()()6y x N πωω=+∈图像的一条对称轴是直线6x π=,则ω的最小值是______变式5.1:若函数())(0)3f x x πωω=+>相邻两对称轴之间的距离为2,则ω=_____变式5.2:已知函数sin()(0)6y x πωω=+>的图象在 (0,π )上有且仅有两条对称轴,求w 的取值范围.变式 5.3:已知函数()f x cos x ω=(其中x R ∈,0ω>)的图象在[0]2π,上恰有四个对称中心点,求ω的取值范围。
三角函数之w的取值范围解析

三角函数之w 的取值范围解析一、单选题1.(2023·湖北·二模)已知0w >,函数()π3sin 24f x wx ⎛⎫=+- ⎪⎝⎭在区间π,π2⎡⎤⎢⎥⎣⎦上单调递减,则w 的取值范围是()A .10,2⎛⎤B .(]0,2C.13,24⎡⎤⎢⎥D .15,24⎡⎤⎢⎥2.(2017·山西太原·三模)已知函数()(0)f x sinwx w =->在()0,π上有且只有两个零点,则实数w 的取值范围为A .40,3⎛⎤ B .47,33⎛⎤ ⎥C .710,33⎛⎤ ⎥D .1013,33⎛⎤ ⎥3.(2019·安徽·三模)已知奇函数()sin())f x x x ωϕωϕ=+-+,(其中0ω>,ϕ∈R )在[1,1]x ∈-有7个零点,则实数w 的取值范围是A .(3,4]B .(3,4]ππC .[3,4)D .[3,4)ππ4.(19-20高三下·湖南·阶段练习)已知函数()()222sin cos sin 024f x x x ωωω⎛⎫=⋅-> ⎪⎝⎭在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数,且在区间[]0,π上恰好取得一次最大值1,则w 的取值范围是A .30,5⎛⎤ ⎥B .13,25⎡⎤⎢⎥C .13,24⎡⎤⎢⎥D .15,22⎡⎫⎪⎢5.(17-18高三·河南南阳·阶段练习)已知函数()21cos sin (0,)222wx f x wx w x R =+->∈,若()f x 在区间(,2)ππ内没有零点,则w 的取值范围是A .5(0,)12πB .5(0,]12πC .5(0,6D .5511(0,[,]126126.(2018·安徽合肥·一模)已知0w >,函数()cos()3f x wx π=+在(,)32ππ上单调递增,则w 的取值范围是()A .210(,33B .210[,]33C .10[2,]3D .5[2,3二、多选题7.(2024·贵州黔西·一模)已知()cos (0)f x wx wx w =+>,则下列说法正确的是()A .若()f x 的最小正周期为π,则()f x 的对称中心为ππ,0,62k k ⎛⎫-+∈ ⎪⎝⎭ZB .若()f x 在区间π0,4⎡⎤⎢⎥⎣⎦上单调递增,则w 的取值范围为40,3⎤⎛ ⎥⎝⎦C .若()01f x =,则02π1cos 32wx ⎛⎫+=⎝⎭D .若()f x 在区间[]0,π上恰好有三个极值点,则w 的取值范围为710,33⎡⎫⎪⎢三、填空题8.(21-22高一下·安徽池州·阶段练习)已知函数()2sin f x wx =在区间ππ,43⎡⎤-⎢⎥⎣⎦上的最小值为2-,则w 的取值范围是.9.(18-19高三上·天津武清·期中)已知函数()()sin (0,02f x wx w πϕϕ=+><<,若()f x 的图象的一条对称轴是3x π=,且在区间,64ππ⎛⎫- ⎪上单调递增,则w 的取值范围是10.(20-21高三上·江西抚州·期末)若函数()cos()(0)4f x wx w π=+>在[]0,π的值域为1⎡-⎢⎣⎦,则w 的取值范围是。
突破130--三角函数w的取值问题

2
2
4
k
x
4
k
k Z
而
3 2
,
2
是
4
k
, 4
k
k
Z
的
一个单调区间,且对于某个特定的 k 成立,则必有 k 0 ,
故:
2
4
4
3 2
即: 0
2
3
4
2k 2 2k
2
3
3 6k 2 2 4k
k Z
由于取值两个不等式的交集,故 k 只能是唯一的结果, k 0 即: 0 3 2
解法二:由题可知,将 x 看成一个整体,则 x
4 2k k Z 3 k k Z ,即当 k 1 时, 有最小值为 3 .
3
2
2
4
另解法二:当然我们也可以换一种思维向右平移 个单位以后,与原图重合,那么平移的
3
4
距离一定是一个周期的整数倍:则
3
kT
k
2
k Z
1 39.5
基本题型四:与单调性零点对称性最值有关的综合问题
例
1:已知函数
f
(x)
Asinx( A
0,
0) ,在区间 [
,
] 上是增函数,且在区间
43
0, 2 上恰好两次取得最大值 A ,则 的取值范围是__________.
三角函数中“ω”的取值范围(解析版)
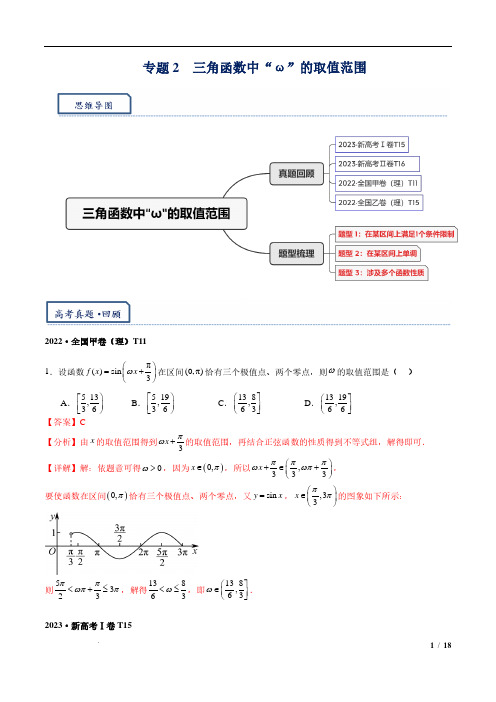
专题2 三角函数中“ω”的取值范围2022·全国甲卷(理)T11【分析】由x 的取值范围得到3x πω+的取值范围,再结合正弦函数的性质得到不等式组,解得即可.【详解】解:依题意可得0ω>,因为()0,x π∈,所以,333x πππωωπ +∈+, 要使函数在区间()0,π恰有三个极值点、两个零点,又sin y x =,,33x ππ∈的图象如下所示:则5323ππωππ<+≤,解得13863ω<≤,即138,63ω∈.2023·新高考Ⅰ卷T152.已知函数()cos 1(0)f x x ωω=−>在区间[]0,2π有且仅有3个零点,则ω的取值范围是 . 【答案】[2,3)【分析】令()0f x =,得cos 1x ω=有3个根,从而结合余弦函数的图像性质即可得解. 【详解】因为02x π≤≤,所以02x πωω≤≤, 令()cos 10f x x ω=−=,则cos 1x ω=有3个根, 令t x ω=,则cos 1t =有3个根,其中[0,2π]t ω∈,结合余弦函数cos y t =的图像性质可得4π2π6πω≤<,故23ω≤<,2023·新高考Ⅱ卷T16【分析】设1211,,,22A x B x,依题可得,21π6x x −=,结合1sin 2x =的解可得,()212π3x x ω−=,从而得到ω的值,再根据2π03f = 以及()00f <,即可得2()sin 4π3f x x =− ,进而求得()πf . 【详解】设1211,,,22A x B x,由π6AB =可得21π6x x −=,由1sin 2x =可知,π2π6xk =+或5π2π6x k =+,Z k ∈,由图可知, ()215π2ππ663x x ωϕωϕ+−+=−=,即()212π3x x ω−=,4ω∴=. 因为28ππsin 033f ϕ =+=,所以8ππ3k ϕ+=,即8ππ3k ϕ=−+,Z k ∈. 所以82()sin 4ππsin 4ππ33f x x k x k=−+=−+, 所以()2sin 4π3f x x =−或()2sin 4π3f x x=−− ,又因为()00f <,所以2()sin 4π3f x x =− ,()2πsin 4ππ3f ∴=− 2022·全国乙卷数学(理)T15【分析】首先表示出T ,根据()f T=求出ϕ,再根据π9x =为函数的零点,即可求出ω的取值,从而得解;【详解】解: 因为()()cos f x x ωϕ=+,(0ω>,0πϕ<<) 所以最小正周期2πT ω=,因为()()2πcos cos 2πcos f T ωϕϕϕω=⋅+=+==, 又0πϕ<<,所以π6ϕ=,即()πcos 6f x x ω=+, 又π9x =为()f x 的零点,所以ππππ,Z 962k k ω+=+∈,解得39,Z k k ω=+∈, 因为0ω>,所以当0k =时min 3ω=;1.已知函数()cos (0)6f x x πωω=−>在区间7,26ππω上有且只有3个零点,则ω的取值范围是____________.【答案】117,63解:7,2,2666x x πππωπωωπ∈⇒−∈π−由于()cos (0)6f x x πωω=−>在区间7,26ππω上有且只有3个零点,则有 226263πωω7ππ9π117≤−<⇒≤<,所以,w 的取值范围是117,63重点题型·归类精讲2023·湖南郴州·统考三模【分析】根据图象平移得π()sin()5f x x ω=+,结合零点个数及正弦型函数的性质可得1229510ω≤<,进而判断极值点个数判断B 、D ;代入法判断A ,整体法判断C. 【详解】由题设ππ()()sin()55f x g x x ωω=+=+,在[]0,2π上,若πππ[,2π]555t x ωω+∈+, 所以sin y t =在ππ[,2π]55ω+上有5个零点,则π5π2π6π5ω≤+<,解得1229510ω≤<,D 正确; 在()0,2π上ππ(,2π)55t ω∈+,由上分析知:极值点个数可能为5或6个,B 错误;πππ()sin()225f ω=+且ππ33π)2520ω+∈,故π()2f 不为0,A 错误; 在π0,10上πππ(,)5105t ω∈+,则ππ11π49π[,)10525100ω+∈,故sin y t =递增,即()f x 在π0,10上递增,C 正确. 故选:CD2024届·江苏省南京市六校联合调研(10月)3.(多选)已知函数()sin (0)f x x x ωωω=>,下列说法正确的是( )【答案】ACD【分析】化简()f x 的解析式,根据三角函数的值域、最值、周期、单调性、极值点等知识对选项进行分析,从而确定正确答案.【详解】已知函数()π2sin 3f x x ω=+,可知其值域为[]22−,,故选项A 正确; 若存在12,x x ∈R ,使得对x ∀∈R 都有()()()12f x f x f x ≤≤, 所以12x x −的最小值为π2T ω=,故选项B 错误; 函数()f x 的单调递增区间为πππ2π2π232k x k ω−≤+≤+,()5ππ2π2π66,Z k k x k ωω−+ ∈∈, 所以5π2ππ66π2ππ63k k ωω− ≤− + ≥ ,令0k =,则10,2ωω<≤∴的取值范围为10,2 ,故选项C 正确;若函数()f x 在区间()0,π上恰有3个极值点和2个零点,πππ,π333x ωω+∈+, 由如图可得:5ππ138π3π2363ωω<+≤⇒<≤,ω∴的取值范围为138,63,故选项D 正确 2024届·广东省六校第二次联考【分析】先将()f x 的函数式化简成形如sin()y A x k ωθ++的形式,根据()f x 在π5π,66−上为增函数,列出关于ω的不等式组求解即可.【详解】π1()4cos sin cos(π2)4sin sin cos 262f x x x x x x x x ωωωωωωω=++−=−−222sin 2sin cos sin 21x x x x x x ωωωωωω=−−+=−,当π5π,66x∈−时,π5π2,33x ωωω ∈−, 若函数()f x 在π5π,66 − 上为增函数,则ππ325ππ32ωω −≥− ≤ ,由0ω>,解得3010ω<≤, 则ω的最大值为310.2024届长郡中学月考(二) 5.已知函数211()sin sin (0)222xf x x ωωω=+−>,x R ∈.若()f x 在区间(,2)ππ内没有零点,则ω的取值范围是A .10,8B .150,,148 ∪C .50,8D .1150,,848 ∪【答案】D【分析】先把()f x化成()4f x x πω=−,求出()f x 的零点的一般形式为+4,k x k Z ππω∈,根据()f x 在区间(,2)ππ内没有零点可得关于k 的不等式组,结合k 为整数可得其相应的取值,从而得到所求的取值范围.【详解】由题设有1cos 11()sin 2224f x x x x πωωω−=+−=−, 令()0f x =,则有,4x k k Z πωπ−=∈即+4,k x k Z ππω∈.因为()f x 在区间(,2)ππ内没有零点, 故存在整数k ,使得5++442k k ππππππωω≤<<,即14528k k ωω ≥+ ≤+,因为0ω>,所以1k ≥−且15428k k +≤+,故1k =−或0k =,所以108ω<≤或1548ω≤≤,2024届浙江省名校协作体高三上学期适应性考T7【分析】令ππππ(,π)3333t x ωωω+∈++,将问题转化为sin y t =,πππ(,π)333t ωω∈++只有1个零点,则πππππ33πππππ3k k k k ωω−≤+<<+≤+(Z k ∈),从而讨论可求出结果. 【详解】令ππππ(,π)3333t x ωωω+∈++,因为函数π()sin()(0)3f x x ωω+>在π(π)3,上恰有1个零点,即转化为sin y t =,πππ(,π)333t ωω∈++只有1个零点,故可得πππππ33πππππ3k k k k ωω −≤+< <+≤+(Z k ∈),即34311233k k k k ωω−≤<− −<≤+ (Z k ∈), 又0ω>,要使上述方程组有解,则需13132343203310k k k k k k −<−−≤++> −> (Z k ∈),所以1733k <≤(Z k ∈),故1,2k =,当1k =时,2533ω<≤,当2k =时,283ω≤≤【分析】根据正弦型函数的最小值的性质,结合题意进行求解即可.【详解】因为函数()()πsin 04f x x ωω +> 在π7π,44内恰有两个最小值点,0ω>,所以最小正周期满足1711713πππππ=π,3442442T −=≤<− 所以42π7154,ππ+ππ312444Tωω<≤<≤,所以有:4413337π7ππ11π72442ωωω <≤ ⇒<≤<+≤8.已知函数π()cos sin (0)6f x x x ωωω =−+>,若()f x 在[0,π]上的值域为11,2 −,则ω的取值范围为( ) A. 2,13B. 24,33C. 74,63D. 27,36【答案】B 【解析】【分析】化简函数解析式可得π()cos 3f x x ω =+,求出π3x ω+的范围,再由函数的值域可得π5πππ33ω≤+≤,解不等式即可求解. 【详解】函数π()cos sin 6f x x x ωω=−+可化为ππ1π()cos sin coscos sin cos cos 6623f x x x x x x x ωωωωω=−−==+, 所以π()cos 3f x x ω=+, 因为0πx ≤≤,所以ππππ+333x ωω≤+≤, 因为()f x 在[0,π]上的值域为11,2−,所以π5πππ33ω≤+≤, 所以2433ω≤≤,所以ω的取值范围为24,33. 2024届山东联考9.若函数()()cos 05πf x x ωω =+>在区间π3π,22上恰有两个零点,则ω的取值范围是( )A .2311,155B .2311,155C .23111343,,155515D .23111343,,155515【答案】C【分析】利用整体思想,结合余弦函数得图象与性质列出不等式组,解之即可. 【详解】由题可知3ππ32222T T <−≤,解得13ω<≤,πππ3ππ25525x ωωω+<+<+. 因为函数()πcos 5f x x ω =+ 在区间π3π,22上恰有两个零点, 所以πππ3π,22525π3ππ7π,2252ωω ≤+< <+≤ 或3πππ5π,22527π3ππ9π,2252ωω ≤+<<+≤解得2311155ω<≤或1343515ω≤≤,即23111343,,155515ω ∈.2024届·长沙一中月考(二)10.函数()2sin()f x x ωϕ=+(0ω>,ππ2ϕ<<)的部分图象如图所示,若()()1gx f x =+在[]6,ππ上有且仅有3个零点,则ω的最小值为( )A .52B .3C .196D .92【答案】A【分析】先求得ϕ,然后根据()()1g x f x =+在[]6,ππ上有且仅有3个零点列不等式,从而求得ω的取值范围,进而求得正确答案.【详解】由图可知()0=2sin f ϕϕ 由于ππ2ϕ<<,所以2π=3φ,2π()2sin()3f x x ω=+ 令()2π=2sin 1=03g x x ω++,得2π1sin =32x ω+− ,由ππ6≤≤x 得π2π2π2ππ6333x ωωω+≤+≤+,依题意,()()1gx f x =+在[]6,ππ上有且仅有3个零点,故当ω取值最小时,有2ππ2π7π3636π2ππ3ππ4π636ωω <+≤ +≤+<−,解得532ω≤≤,所以ω的最小值为52.2024届·合肥一中高三上学期第一次检测(10月)11.已知函数()()2sin f x x ωϕ=+,其中0ω>,0πϕ<<,且()π3f x f ≤恒成立,若()f x 在区间π0,2上恰有3个零点,则ω的取值范围是( )【分析】分析可得π23f=,可得出()ππ2π23k k ωϕ=+−∈Z ,再结合题意可得出关于ω的不等式,结合k 的取值可求得ω的取值范围.【详解】因为()π3f x f≤恒成立,则ππ2sin 233f ωϕ=+=,所以,()ππ2π32k k ωϕ+=+∈Z ,则()ππ2π23k k ωϕ=+−∈Z , 当π02x <<时,π2x ωϕωϕϕ<+<+, 因为0πϕ<<,则()0sin 0f ϕ=>,因为()f x 在区间π0,2上恰有3个零点,则0ππ3π4π2ϕωϕ<< <+≤, 即ππ02ππ23π3π4π2k ωωϕ<+−< <+≤,k ∈Z ,解得33662215122112k k k k ωω −<<+ −<≤− ,k ∈Z ,假设ω不存在,则3621122k k −≥−或3615122k k +≤−,解得34k ≤或54k ≥,因为ω存在,则3544k <<,因为k ∈Z ,则1k =.所以,9152239ωω <<<≤ ,可得91522ω<< 2024届·广州市越秀区高三上学期月考(十月)12.函数()()sin 0f x x ωω=>,将()f x 的图象上所有的点纵坐标保持不变横坐标变为原来的ω倍,然后将()0,2π内恰有4个零点,则ω的取值范围是 .【答案】 cos x 3π5π,22【分析】根据三角函数图象平移可得()cos g x x =,再代入()()10f g x −=,数形结合求解即可 【详解】由题意()πsin cos 2g x x x=+=,又()()()1h x f g x =−在()0,2π内恰有4个零点, 故()cos 10f x −=,即()sin cos 1x ω=在()0,2π内恰有4个零点, 则()πcos 2π,Z 2x k k ω=+∈在()0,2π内恰有4个零点, 数形结合可得,当0k =时πcos 2x ω=有两根,当1k =−时3πcos 2x ω=−也有两根,故3π25π2ωω−<− ≤,即3π5π22ω<≤,故ω的取值范围是3π5π,22 .题型二 在某区间上单调2023武汉市华中师大附一中高三上期中【答案】16【分析】由π,π2x∈得到πππ2π,2π666x ωωω +∈++ ,结合正弦函数图象得到不等式组,求出21236k k ω−+≤≤+,Zk ∈,利用21236106k k k −+<+ +> ,求出0k =,从而得到106ω<≤,得到答案.【详解】π,π2x∈ ,则πππ2π,2π666x ωωω +∈++ ,因为0ω>,所以要想()f x 在π,π2上单调递增,需要满足πππ2π26k ω+≥−+且ππ2π2π62k ω+≤+,Z k ∈,解得:21236k k ω−+≤≤+,Z k ∈,所以21236106k k k −+<+ +> ,解得:1566k −<<,因为Z k ∈,所以0k =, 因为0ω>,所以106ω<≤, ω的最大值是16.【分析】由三角函数的图象与性质可得πππ33ω+>及2π3ππ242T ω=≥− ,继而可得3πππ2233ππ5π432ωω ≤+ +≤ ,计算可得结果.【详解】化简π()sin 2sin()3f x x x x ωωω==+, 在π0,3x∈ 时,ππππ,3333x ωω +∈+ ,该区间上有零点,故πππ233ωω+>⇒>,又π3π,24x ∈ 时()f x 单调,则2π3ππ2442T ωω≥−⇒≤ ,即(]2,4ω∈, 故4πππ7π3πππ7263233223,11π3ππ10π3ππ5π396433432ωωωωω <+≤≤+ ⇒⇒∈<+≤+≤ 总结:有难度,先通过无零点区间和周期求出ω大致范围,进一步确定单调区间的增减性,最终得出ω范围2023届杭州市二模T8【分析】通过对称轴与对称点得出ω的式子,再通过单调得出ω的范围,即可得出答案.【详解】()sin()f x x ωφ=+(0)>ω满足()14f π=,503f π=, 53442T nT ππ∴−=+,即()1736Tn n π=∈+N , ()61217nn ω+∴=∈N , ()f x 在5,46ππ上单调, 572641222T ππππω∴−≤,即127ω≤,∴当1n =时ω最大,最大值为1817, 故选:B.2024届·重庆市高三上学期入学调研【分析】三角函数在区间上单调,可知在区间内不含对称轴,构建不等式即可求得ω的取值范围.【详解】因为()πsin 2(0)3g x x ωω=+> ,令ππ22π,32x k ω+=+()k ∈Z ,可得对称轴方程1ππ26x k ω+()k ∈Z , 函数()πsin 2(0)3g x x ωω =+> 在区间π,π2上是单调的,∴1π22T ≥,且1πππ,π262x k ω=+∉ ,()k ∈Z ,∴12ππ222ω⋅≥即01ω<≤, 函数()πsin 2(0)3g x x ωω =+>在区间π,π2 上是单调的,所以()1πππ2621π1ππ26k k ωω +≤++≥ ,即6167612k k ω++≤≤()k ∈Z , 又01ω<≤, 可得1012ω<≤或17612ω≤≤2023·杭州二模T8(改)最大值为 . 【答案】3013【分析】由函数在区间π2π,43上单调,求出ω的取值范围,再由π14f = ,4π03f = 得到*2113π,N 412k T k −=∈,即可求出的取值集合,从而求出ω的最大值; 【详解】因为()f x 在区间π2π,43上单调,所以2ππ5π23412T ≥−=,5π6T ∴≥,2π5π60ωω ≥ ∴ >,解得1205ω<≤; 因为π14f=,4π()03f =,所以*214ππ13π,N 43412k T k −=−=∈,所以13π3(21)T k =−,所以2π13π3(21)k ω=−,所以*6(21),N 13k k ω−=∈; 当6(21)12135k ω−=≤,解得3110k ≤,所以max6(231)301313ω×−==.是 .【答案】1117,46【分析】利用辅助角公式化简函数()f x 的解析式,利用函数()f x 在区间π0,3上存在最值,以及函数()f x 在2π,π3上单调分别求出ω的取值范围,取交集可得ω的取值范围. 【详解】因为()sin π2sin 3s x x f x x ωωω−= ,当π03x <<时,因为0ω>,则ππππ3333x ωω−<−<−, 因为函数()f x 在π0,3上存在最值,则πππ332ω−>,解得52ω>,当2ππ3x <<时,2πππππ3333x ωωω−<−<−, 因为函数()f x 在2π,π3上单调,则()2πππππ,ππ,π33322k k k ωω −−⊆−+∈Z , 所以,2ππππ332ππππ32k k ωω −≥−−≤+,其中k ∈Z ,解得()315246k k k ω−≤≤+∈Z , 所以,315246k k −≤+,解得136k ≤,又因为0ω>,则{}0,1,2k ∈.当0k =时,506ω<≤;当1k =时,51146ω≤≤;当2k =时,111746ω≤≤.又因为52ω>,因此,实数ω的取值范围是1117,46题型三 涉及多个函数性质2024届深圳宝安区10月调研【答案】11,44【分析】先根据题目的要求平移伸缩对称变换得到()g x 的解析式,然后结合函数在2π0,3上恰有两个零点以及在ππ,1212−上单调递增,列出不等式组,即可求得本题答案.【详解】函数()f x 的图象向左平移2π3个单位长度,得到2πcos 3y x+的图象,再将图象上所有点的横坐标变为原来的1ω,纵坐标不变,得到2πcos 3yx ω+的图象,因为函数()g x 的图象与2πcos 3yx ω+的图象关于x 轴对称,所以2π()cos 3g x x ω=−+ 2ππsin 32x ω+−= πsin 6x ω +, 因为20π3x ≤≤,所以ππ2ππ6636x ωω≤+≤+, 又因为π()sin 6g x x ω =+ 在2π0,3 恰有2个零点,且()sin π0k =,Z k ∈, 所以2π2ππ3π36ω≤+<,解得1117<44ω≤, 令22πππ2π2π262k x k ω−+≤+≤+,2k ∈Z ,得222π2π2ππ33k k x ωωωω−+≤≤+,2k ∈Z ,令20k =,得()g x 在2ππ,33ωω − 上单调递增,所以ππ,1212 − 2ππ,33ωω⊆− , 所以2ππ312ππ312ωω −≤−≥ ,又0ω>,解得04ω<≤. 综上所述,1144ω≤≤,故ω的取值范围是11,4420.记函数()()cos (0,0π)f x x ωϕωϕ=+><<的最小正周期为T,若()f T =9x π=为()f x 的零点,则ω的最小值为 . 【答案】3【分析】首先表示出T ,根据()f T =求出ϕ,再根据π9x =为函数的零点,即可求出ω的取值,从而得解;【详解】解: 因为()()cos f x x ωϕ=+,(0ω>,0πϕ<<) 所以最小正周期2πT ω=,因为()()2πcos cos 2πcos f T ωϕϕϕω=⋅+=+==, 又0πϕ<<,所以π6ϕ=,即()πcos 6f x x ω=+, 又π9x =为()f x 的零点,所以ππππ,Z 962k k ω+=+∈,解得39,Z k k ω=+∈, 因为0ω>,所以当0k =时min 3ω=;故答案为:3湖北省黄冈市2023-2024学年高三上学期9月调研【分析】利用正弦型函数的对称性、奇偶性、单调性进行求解即可.【详解】因为函数()f x 在3π7π,88内单调递减,3π8x =是函数()f x 的一条对称轴, 所以有7π3π17π3π12π2882882T ωω−≤⇒−≤⋅⇒≤, 所以()()3ππ2πZ 182k k ωϕ⋅+=+∈, 因为ππsin 88y f x x ωωϕ=+=++是奇函数, 所以()()ππZ 28m m ωϕ+=∈,由()()12−可得:()422k m ω=−+,而2ω≤,所以2ω=±, 当2ω=时,()()2ππZ πZ 84m m m m πϕϕ+=∈⇒=−∈, 因为ππ22ϕ−<<,所以π4ϕ=−,即π()sin(2)4f x x =−, 当3π7π,88x∈ 时,ππ3π2,422x −∈ ,显然此时函数单调递减,符合题意,所以7π7πππ()sin(2)sin 242443f =×−==; 当2ω=−时,(()2πππZ πZ 84m m m m ϕϕ−+=∈⇒=+∈, 因为ππ22ϕ−<<,所以π4ϕ=,即π()sin(2)4f x x =+, 当3π7π,88x∈时,()π2π,2π4x +∈,显然此时函数不是单调递减函数,不符合题意2023·山东淄博·统考三模【答案】5π12【分析】先化简函数,利用零点求出ω,根据单调递增求出m 的值.【详解】因为()sin (0)f x x x ωωω=>,所以1π()2sin 2sin 23f x x x x ωωω ==−, 因为()f x 的零点是以π2为公差的等差数列,所以周期为π,即2π=πω,解得2ω=; 当[]0,x m ∈时,πππ2,2333x m−∈−−,因为()f x 在区间[]0,m 上单调递增,所以ππ232m −≤,解得5π12m ≤. 所以m 的最大值为5π12.。
破解高考三角函数中参数w取值范围必做题含详解

象,若对满足
f (x1) g(x2 )
4 的 x1、x2 ,有
x1 x2
的最小值为
6
.则
(
)
A. 6
B.
4
C.
3
D. 5π 12
25.将函数
y
sin
2x
的图象向右平移
0
2
个单位长度得到
f
x
的图象,若函
数
f
x
在区间
0,
3
上单调递增,且
f
x
的最大负零点在区间
5 12
, 6
3
cos
x
的图像向左平移
2
个单位长度,得函数
g
x
的图
像,若
g
x
在
0,
2
内只有两个最值(即最大值和最小值),则
的最大正整数值为(
)
A.6
B.5
C.4
D.3
13.将函数 f x cos 2x 图象向左平移 ( 0 )个单位后得到函数 g x 的图象,若
2
函数
g
x
在区间
6
,
6
上单调递减,且函数
2 的 x1 , x2 ,有
x1 x2 min
3
,则 (
)
5
A.
12
B.
3
C.
4
D.
6
6.将函数
f (x)
cos 4x 的图象向左平移
个单位长度后,得到
g x 的图象,若函数
8
y
g ( x)
在
12
,
4
上单调递减,则正数
三角函数w的取值范围答案

三角函数k x A y ++=)sin(ϕϖ中ϖ的取值范围一 内容回顾: 二 典型例题: 题组一1.已知函数2sin()(0)y x ωθω=+>为偶函数,0θπ<<,其图象与直线2y =的某两个交点的横坐标为1221,,||x x x x -若的最小值为π,则( )A .2,2πωθ==B .1,24πωθ== C .1,22πωθ== D .2,4πωθ== 解:2sin()y x ωθ=+为偶函数2k πθπ∴=+k z ∈ 又02πθπθ<<∴=由诱导公式得函数2cos y x ω=,又其图象与直线2y =某两个交点的横坐标分别为1x ,2x ,若21||x x -的最小值为π∴函数的周期为π 即22cos2y x ω=∴=∴函数在[,]2x k k k z πππ∈-+∈上为增函数故选:A .2.已知函数x x x f ωωcos sin )(+=,如果存在实数1x ,使得对任意的实数x ,都有)2014()()(11+≤≤x f x f x f成立,则ω的最小正值为 B A .20141 B . 2014π C .40281 D .4028π解:题意可得区间1[x ,12014]x +能够包含函数的至少一个完整的单调区间,利用两角和的正弦公式求得())4f x x πω+,由1220142πω,求得ω的最小值.()sin cos )4f x x x x πωωω++,由题意可得1220142πω,求得2014πω,故ω的最小正值为2014π,故选:B .3.将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像,若对满足12()()2f x g x -=的1x ,2x ,有12min 3x x π-=,则ϕ=( ) DA .512πB .3πC .4πD .6π解:()sin 2f x x =,()sin(22)g x x ϕ∴=-,由12|()()|2f x g x -=,可知1()f x 、2()g x 分别为两个函数的最大值和最小值(或最小值和最大值). 不妨设1222x k ππ=+,k Z ∈,22222x m πϕπ-=-+,m Z ∈,则12()2x x k m πϕπ-=-+-,由12||3min x x π-=,可得23ππϕ-=,解得6πϕ=,故选:D .4.函数()sin(),f x x ϕ=-且230()0,f x dx π=⎰则函数()f x 的图象的一条对称轴( )A .56x π=B .712x π=C .3x π=D .6x π= 解:因为3()0f x dx π=⎰,即且30sin()0x dx πϕ-=⎰,所以30cos()|cos()cos 03x ππϕϕϕ--=--+=,所以sin()06πϕ-=,解得6k πϕπ=+,k Z ∈;所以()sin()6f x x k ππ=--,所以函数()f x 的图象的对称轴是62x k k ππππ--='±,所以其中一条对称轴为23x π=; 故选:A .题组二1.(2012天津)将函数()sin f x x ω=(其中ω>0)的图像向右平移4π个单位长度,所得图像经过点3(,0)4π,则ω的最小值是 A .13 B .1 C .53D .2D 【解析】函数向右平移4π得到函数)4sin()4(sin )4()(ωπωπωπ-=-=-=x x x f x g ,因为此时函数过点)0,43(π,所以0)443(sin =-ππω,即,2)443(πωπππωk ==-所以Z k k ∈=,2ω,所以ω的最小值为2,选D .2.(2012新课标)已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=A .π4B .π3C .π2D .3π4A 【解析】由题设知,πω=544ππ-,∴ω=1,∴4πϕ+=2k ππ+(k Z ∈),∴ϕ=4k ππ+(k Z ∈),∵0ϕπ<<,∴ϕ=4π,故选A.3.(2012新课标)已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ单调递减,则ω的取值范围是A .]45,21[B .]43,21[C .]21,0( D .]2,0(A 【解析】函数)4sin()(πω+=x x f 的图像可看作是由函数()sin f x x =的图像先向左平移4π个单位得()sin()4f x x π=+的图像,再将图像上所有点的横坐标缩小到原来的1ω倍,纵坐标不变得到的,而函数()sin()4f x x π=+的减区间是5[,]44ππ,所以要使函数)4sin()(πω+=x x f 在),2(ππ上是减函数,需满足142514ππωππω⎧⨯⎪⎪⎨⎪⨯⎪⎩≤≥,解得1524ω≤≤.方法二 特值验证,21=ϖ,1=ϖ,()sin()4f x x π=+在),2(ππ单调递减,选A解法三:【利用三角函数的单调性求解】 函数()sin()4f x x πω=+在(,)2ππ单调递减,在0ω>的前提下,需同时满足:12222()24232()42k k Z k k Z πππωπππωππππωπ⎧-≤⋅⎪⎪⎪+≥+∈⎨⎪⎪+≤+∈⎪⎩,解得0214()252()4k k Z k k Z ωωω⎧⎪<≤⎪⎪≥+∈⎨⎪⎪≤+∈⎪⎩综上,12≤ω≤54,故选A . 4.(2011山东)若函数()sin f x x ω=(ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增,在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减,则ω=A .23B .32C .2D .3B 【解析】由于()sin f x x ω=的图象经过坐标原点,根据已知并结合函数图象可知,3π为函数()f x 的四分之一周期,故243ππω=,解得32ω=. 5.(2011安徽)已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若()()6f x f π≤对x R ∈ 恒成立,且()()2f f ππ>,则()f x 的单调递增区间是 A .,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ B .,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C .2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D .,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦C 【解析】因为当x R ∈时,()|()|6f x f π≤恒成立,所以()sin()163f ππϕ=+=±,可得26k πϕπ=+或526k πϕπ=-,k Z ∈, 因为()sin()sin ()sin(2)sin 2f f ππϕϕππϕϕ=+=->=+=故sin 0ϕ<,所以526k πϕπ=-,所以5()sin(2)6f x x π=-, 由5222262k x k πππππ-+-+≤≤(k Z ∈),得263k x k ππππ++≤≤(k Z ∈),故()f x 的单调递增区间是2[,]63k k ππππ++(k Z ∈)6.(2016年全国III)函数sin y x x =的图像可由函数sin y x x =的图像至少向右平移_____________个单位长度得到.32π【解析】函数sin 2sin()3y x x x π=-=-的图像可由函数sin y x =+2sin()3x x π=+的图像至少向右平移23π个单位长度得到. 7.(2016全国I )已知函数ππ()sin()(0),24f x x+x ωϕωϕ=>=-,≤为()f x 的零点,π4x =为()y f x =图像的对称轴,且()f x 在π5π()1836,单调,则ω的最大值为A .11B .9C .7D .5 B 【解析】因为4x π=-为函数()f x 的零点,4x π=为()y f x =图像的对称轴,所以2π24kT T=+(k Z ∈,T 为周期),得221T k π=+(k Z ∈).又()f x 在5(,)1836ππ单调,218365T≤-ππ, 所以11,62T k π,又当5k =时,11,4πωϕ==-,()f x 在5(,)1836ππ不单调;当4k =时,9,4πωϕ==,()f x 在5(,)1836ππ单调,满足题意,故9ω=,即ω的最大值为9.解析:由题意知:12π+π 4ππ+π+42k k ωϕωϕ⎧-=⎪⎪⎨⎪=⎪⎩则21k ω=+,其中k ∈Z ,()f x 在π5π,1836⎛⎫⎪⎝⎭单调,5π,123618122T ππω∴-=≤≤接下来用排除法.若11=ϖ时,,4111πϕπk =+-4111+=πϕk ,由2||πϕ≤,当31-=k ,得4πϕ-=,此时π()sin 114f x x ⎛⎫=- ⎪⎝⎭,)365,18(ππ∈x ,由411π-=x t ,可得ππ36463613≤≤t ,不满足()f x 在π5π,1836⎛⎫ ⎪⎝⎭单调若9=ϖ时,,491πϕπk =+ππϕ491-=k ,由2||πϕ≤,当21=k ,得4πϕ=π9,4ωϕ==,此时,)365,18(ππ∈x ,由49π+=x t ,可得ππ2343≤≤t ,满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调递减, 故选B .方法三 4221ππϕ++=k k .1)(212+-=k k ω,Z k k ∈21,2||πϕ≤4πϕ=∴或4πϕ-= ()f x 在π5π,1836⎛⎫⎪⎝⎭单调,5π,123618122T ππω∴-=≤≤,0>ϖ.120≤<∴ϖ若4πϕ=,则021=+k k ,142+=k ϖ,951,,=ϖ验证: 若4-πϕ=,则1-21=+k k ,342+=k ϖ,1173,,=ϖ验证:2020尖子生TOP300联考8.已知函数f (x )=sin(ωx +φ)(ω>0,|φ|≤π2),x =-π4,43π=x 为y =f (x )图象的两条对称轴,且f (x )在)12,0(π上单调函数,则ω的最大值为( )A .12B .11C .10D .9解:两条对称轴之间的距离是周期T 的)(2Z k k ∈倍,或者2T 的k 倍,ϖπππ22443⋅=+k ,k =ϖf (x )在)12,0(π上单调函数,故存在Z k ∈0,使得⎪⎪⎩⎪⎪⎨⎧≥++-≤+-12)1(40400πϖππϖππk k)1(3k 400+≤≤k ϖ,由)1(3k 400+≤k 可得30≤k ,这时的ω最大值为12同理,用43π=x 也可以算 方法二。
三角函数中ω的范围与最值问题【七大题型】(举一反三)(原卷版)—2025年新高考数学一轮复习

三角函数中ω的范围与最值问题专练【七大题型】【题型1 与三角函数的单调性有关的ω的范围与最值问题】 (2)【题型2 与三角函数的对称性有关的ω的范围与最值问题】 (2)【题型3 与三角函数的最值有关的ω的范围与最值问题】 (3)【题型4 与三角函数的周期有关的ω的范围与最值问题】 (4)【题型5 与三角函数的零点有关的ω的范围与最值问题】 (4)【题型6 与三角函数的极值有关的ω的范围与最值问题】 (5)【题型7 ω的范围与最值问题:性质的综合问题】 (5)1、三角函数中ω的范围与最值问题三角函数的图象与性质是高考的重要内容,在三角函数的图象与性质中,ω的求解是近几年高考的一个重点、热点内容,试题主要以选择题、填空题的形式呈现,但因其求法复杂,涉及的知识点多,历来是我们复习中的难点,学生在复习中要加强训练,灵活求解.【知识点1 三角函数中有关ω的范围与最值问题的类型】1.三角函数中ω的范围与最值的求解一般要利用其性质,此类问题主要有以下几个类型:(1)三角函数的单调性与ω的关系;(2)三角函数的对称性与ω的关系;(3)三角函数的最值与ω的关系;(4)三角函数的周期性与ω的关系;(5)三角函数的零点与ω的关系;(6)三角函数的极值与ω的关系.【知识点2 三角函数中ω的范围与最值问题的解题策略】1.利用三角函数的单调性求ω的解题思路对于已知函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集,其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解,另外,若是选择题,利用特值验证排除法求解更为简捷.2.利用三角函数的对称性求ω的解题策略三角函数两条相邻对称轴或两个相邻对称中心之间的“水平间隔”间的“水平间隔”为,这就说明,我们可根据三角函数的对称性来研究其周期性,解决问题的关键在于运用整体代换的思想,建立关于ω的不等式组,进而可以研究“ω”的取值范围.3.利用三角函数的最值求ω的解题策略若已知三角函数的最值,则利用三角函数的最值与对称轴或周期的关系,可以列出关于ω的不等式(组),进而求出ω的值或取值范围.4.利用三角函数的周期性求ω的解题策略若已知三角函数的周期性,则利用三角函数的周期与对称轴、最值的关系,列出关于ω的不等式(组),进而求出ω的值或取值范围.【题型1 与三角函数的单调性有关的ω的范围与最值问题】【例1】(2024·重庆·二模)若函数f(x)=sin(2x―φ)(0≤φ<π)在φ的最小值为()A.π12B.π6C.π4D.π3【变式1-1】(2024·湖北鄂州·一模)已知函数y=sin(ωx+φ)(ω>0,φ∈(0,2π))的一条对称轴为x=―π6,且f(x)在πω的最大值为()A.53B.2C.83D.103【变式1-2】(2024·全国·模拟预测)已知函数f(x)=sin(ωx+φ)(ω>0),若直线x=π4为函数f(x)图象的为函数f(x)图象的一个对称中心,且f(x)ω的最大值为()A.917B.1817C.1217D.2417【变式1-3】(2024·广东湛江·一模)已知函数f(x)=sinωxω>0)ω的取值范围是()A.[2,5]B.[1,14]C.[9,10]D.[10,11]【题型2 与三角函数的对称性有关的ω的范围与最值问题】【例2】(2023·广西·模拟预测)若函数f (x )=2sin (ωx +φ)(ω>0,|φ|<π2)满足f (2x )=―2x ,且f (0)=―1,则ω的最小值为( )A .1B .2C .3D .4【变式2-1】(2024·内蒙古呼和浩特·一模)已知函数f (x )=sin ωx >0)在区间[0,π]上有且仅有两条对称轴,则ω的取值范围是( )A B C D【变式2-2】(2023·云南大理·一模)函数f (x )=sin (ωx +φ)(ω>0,0<φ<π),若不等式f (x )≤|对∀x ∈R 恒成立,且f (x )的图像关于x =π8对称,则ω的最小值为( )A .1B .2C .3D .4【变式2-3】(2024·全国·模拟预测)已知函数f(x)=sin (ωx +φ)(ω>0)其图象关于直线x =―π36对称,且f (x )的一个零点是x =772π,则ω的最小值为( )A .2B .12C .4D .8【题型3 与三角函数的最值有关的ω的范围与最值问题】【例3】(2023·四川泸州·一模)已知函数f (x )=2sin ωx >0)在π上单调,则ω的取值范围是( )A .B .1,C D【变式3-1】(2024·浙江温州·一模)若函数f (x )=2sin ωx ―(ω>0),x ∈0,[―,则ω的取值范围是( )A BC D【变式3-2】(2024·四川绵阳·模拟预测)已知函数f (x )=4cos ωx >0),f (x )在区间0,值恰为―ω,则所有满足条件的ω的积属于区间( )A .(1,4]B .[4,7]C .(7,13)D .[13,+∞)【变式3-3】(2023·新疆乌鲁木齐·一模)已知函数f (x )=2sin (ωx +φ)(ω>0,0<φ<π)的图象过点(0,1),且在区间(π,2π)内不存在最值,则ω的取值范围是( )A .BC .∪D .∪【题型4 与三角函数的周期有关的ω的范围与最值问题】【例4】(2023·四川绵阳·模拟预测)记函数f (x )=cos (ωx +φ)(ω>0,0<φ<π)的最小正周期为T ,若f (T )=x =π9为f (x )的一个零点,则ω的最小值为( )A .32B .3C .6D .152【变式4-1】(2024·全国·模拟预测)已知函数f (x )=sin (2πωx )(ω>0)在区间(0,2)上单调,且在区间[0,18]上有5个零点,则ω的取值范围为( )A BC D 【变式4-2】(2024·全国·模拟预测)记函数f (x )=cos (ωx +φ)(ω>0,0<φ<π)的最小正周期为T ,若f (T )=―12,且x =π2为f (x )的一条对称轴,则ω的最小值为( )A .23B .43C .83D .103【变式4-3】(23-24高二下·江苏南京·期末)已知函数f (x )=sin (ωx +φ)ω>0,|φ|<=f (x )在区间[0,2]上恰有8个零点,则ω的取值范围是( )A πB .4πC .4π,D 【题型5 与三角函数的零点有关的ω的范围与最值问题】【例5】(2023·全国·一模)已知函数f (x )=sin ωx +>0)π上恰有3个零点,则ω的取值范围是( )A ∪4,B ∪C .[113,143)∪(5,173)D ,5∪【变式5-1】(2023·吉林长春·一模)将函数f(x)=cos x 图象上所有点的横坐标变为原来的1ω(ω>0),纵坐标不变,所得图象在区间―π12ω的取值范围为( )【变式5-2】(2024·全国·模拟预测)已知函数f(x)=sinωx+>0)π上至少有两个零点,则实数ω的取值范围是()A+∞B+∞C∪+∞D∪+∞【变式5-3】(2024·四川雅安·一模)已知函数f(x)=2cos(ωx+φ)(ω>0且―π2<φ<π2),设T为函数f(x)的最小正周期,=―1,若f(x)在区间[0,1]有且只有三个零点,则ω的取值范围是()A B236πC D【题型6 与三角函数的极值有关的ω的范围与最值问题】【例6】(2023·四川成都·二模)将函数f(x)=>0)的图象上所有点的横坐标缩短到原来的14,纵坐标不变,得到函数g(x)的图象.若g(x)在3个极值点,则ω的取值范围为()A B,4C.D,7【变式6-1】(2023·河南开封·模拟预测)已知将函数f(x)=ωx2―>0)的图象向右平移π2ω个单位长度,得到函数g(x)的图象,若g(x)在(0,π)上有3个极值点,则ω的取值范围为()A+∞B,4C D【变式6-2】(2024·陕西渭南·一模)已知函数f(x)=sinωx>0)在区间[0,π]上有且仅有4个极值点,给出下列四个结论:①f(x)在区间(0,π)上有且仅有3个不同的零点;②f(x)的最小正周期可能是π2;③ω④f(x).其中正确结论的个数为()A.1B.2C.3D.4【变式6-3】(2024·全国·模拟预测)将函数f(x)=sin x的图像向左平移5π6个单位长度后得到函数g(x)的图像,再将g(x)的图像上各点的纵坐标不变、横坐标变为原来的1ω(ω>0)倍,得到函数ℎ(x)的图像,且ℎ(x)在区间(0,π)上恰有两个极值点、两个零点,则ω的取值范围为()【题型7 ω的范围与最值问题:性质的综合问题】【例7】(2024·湖北武汉·模拟预测)若函数f (x )=3cos (ωx +φ)ω<0,―π2<φ<π,在区间―π6φ的取值范围是( )A B .―π2,―C D .【变式7-1】(2024·全国·模拟预测)已知函数f (x )=sin (2ωx ―φ)(ω>0)满足对任意的x ∈R ,均有f (x )≥f+x =x ,且f (x )ω的最大值为( )A .14B .12C .34D .45【变式7-2】(2024·天津·模拟预测)已知f (x )=sin ωx +π3+φω>0,|φ|<g (x )=sin(ωx +φ),则下列结论错误的个数为( )①φ=π6;②若g (x )的最小正周期为3π,则ω=23;③若g (x )在区间(0,π)上有且仅有3个最值点,则ω④若=ω的最小值为.A .1个B .2个C .3个D .4个【变式7-3】(2023·河南·模拟预测)已知函数f (x )=sin (ωx +φ)ω>0,0<φ<=f x且f ―π4―x +f ―π4+x =0,f (x )ω的最大值为( )A .1B .3C .5D .367一、单选题1.(2024·四川成都·模拟预测)若函数f(x)=sin (ωx)(ω>0)在0,ω的取值范围为( )A .B .(0,2)C .D .(0,2]2.(2024·重庆开州·模拟预测)已知函数f (x )=2sin ωx(ω>0),则“32<ω<3”是“f (x )的图象在区间―π6上只有一个极值点”的()A.充分条件B.必要条件C.充要条件D.非充分非必要条件3.(2024·湖北武汉·模拟预测)设ω>0,已知函数f(x)=sin3ωx2ωx(0,π)上恰有6个零点,则ω取值范围为()A B C D4.(2024·河北·模拟预测)已知函数f(x)=sin(ωx+φ)(ω>0),若f(0)=f=π,则ω的最小值为()A.3B.1C.67D.235.(2024·四川·模拟预测)已知函数f(x)=sinωx+ω>0)在区间1个零点,且当x∈―2π3f(x)单调递增,则ω的取值范围是()A B C,1D6.(2024·四川内江·三模)设函数f(x)=2sinωx>0),若存在x1,x2∈―π6x1≠x2,使得f(x1)=f(x2)=ω的取值范围是()A.(0,12]B.[10,+∞)C.[10,12]D.(6,10]7.(2024·河南南阳·模拟预测)若函数f(x)=cos(ωx+φ)ω>0,|φ|≤中心对称,且x=―π3是f(x)的极值点,f(x)在区间0,ω的最大值为()A.8B.7C.274D.2548.(2024·陕西安康·模拟预测)已知函数f(x)=cosωxω>0),π上单调递减,且f(x)在区间(0,π)上只有1个零点,则ω的取值范围是()A.B C D二、多选题9.(2024·浙江·模拟预测)已知函数f(x)=cosωx+ω>0),则()A.当ω=2时,f x x=π2对称B.当ω=2时,f(x)在C.当x=π6为f(x)的一个零点时,ω的最小值为1D.当f(x)在―π3ω的最大值为110.(2024·浙江温州·三模)已知函数f(x)=sin(ωx+φ)(ω>0),x∈,π的值域是[a,b],则下列命题正确的是()A.若b―a=2,φ=π6,则ω不存在最大值B.若b―a=2,φ=π6,则ω的最小值是73C.若b―a=ω的最小值是43D.若b―a=32,则ω的最小值是4311.(2023·浙江·三模)已知函数f(x)=cosωx>0),则下列判断正确的是()A.若f(x)=f(π―x),则ω的最小值为32B.若将f(x)的图象向右平移π2个单位得到奇函数,则ω的最小值为32C.若f(x)π单调递减,则0<ω≤34D.若f(x)π上只有1个零点,则0<ω<54三、填空题12.(2024·陕西安康·模拟预测)已知函数f(x)=cos2ωx>0)π上是单调的,则ω的最大值为.13.(2024·陕西西安·模拟预测)若函数f(x)=2cosωx―1(ω>0)在(0,π)上恰有两个零点,则ω的取值范围为.14.(2024·黑龙江哈尔滨·模拟预测)已知函数f(x)=2sinωxω>0),若∃x1,x2∈[0,π],使得f(x1) f(x2)=―4,则ω的最小值为.四、解答题15.(2023·河北承德·模拟预测)已知ω>1,函数f(x)=cosωx―(1)当ω=2时,求f(x)的单调递增区间;(2)若f(x)ω的取值范围.16.(23-24高一下·湖北恩施·期末)已知函数f(x)=2sinωx+>0).(1)若x+x=0,求ω的最小值;(2)若f(x)在区间0,[1,2],求ω的取值范围.17.(2024·全国·模拟预测)已知函数f(x)=2sin(ωx+φ)ω>0,|φ|≤(1)若f(x)的图象经过点,0,,2,且点B恰好是f(x)的图象中距离点A最近的最高点,试求f(x)的解析式;(2)若f(0)=―1,且f(x)π上单调,在ω的取值范围.18.(2024·全国·模拟预测)已知函数f(x)=3sin(ωx+φ)ω>0,|φ|<(1)当φ=π时,函数f(x)ω的取值范围.6(2)若f(x)的图象关于直线x=π对称且f=0,是否存在实数ω,使得f(x)4求出ω的值;若不存在,说明理由.19.(2023·山西·模拟预测)已知函数f(x)=A sin(ωx+φ)(A>0,ω>0)的图象是由y=2sinωx 个单位长度得到的.象向右平移π6(1)若f(x)的最小正周期为π,求f(x)y轴距离最近的对称轴方程;(2)若f(x)ω的取值范围.。
三角函数的w参数题型归类分析(学生版)

原点,若ΔOAB 为锐角三角形,则ω的取值范围为【1】已知函数f (x )=sin ωx (ω>0),点A ,B 分别为f (x )图像在y 轴右侧的第一个最高点和第一个最低点,O 1三角函数的性质与w 三角函数的w 参数题型归类分析的范围为坐标()A.0,3π2B.π2,3π2C.0,π2D.π2,+∞-1,⋅OB >0,AB ⋅AO∙BO4)(ω>0)的图象在[0,【2 】函数f (x )=sin (ωx +ππ4]内有且仅有一条对称轴,则实数ω的取值范围是()A.(1,5)B.(1,+∞)C.[1,5)D.[1,+∞)【解析】:当x =π4时,wx +π4=π4w +π4,当x =0,wx +π4=π4因为在0,π4 只有一条对称轴,可知π2≤π4w +π4<3π2,解得w ∈1,5 ,故选C .2),使得曲线y =cos ωx -π3【 3 】若存在唯一的实数t ∈(0,π(ω>0)关于点(t ,0)对称,则ω的取值范围是()A.[53,113]B.(53,113]C.(43,103]D.[43,103]【解析】:由题意,因为t ∈(0,π2),所以ωt -π3∈-π3,ωπ2-π3,因为存在唯一的实数t ∈(0,π2),使得曲线y =cos ωx -π3(ω>0)关于点(t ,0)对称,则π2<ωπ2-π3≤3π2,解得53<ω≤113,故选B .2【4】(★★★★☆)已知函数f (x )=sin (ωx +φ) ω>0,|φ|≤π,x =-π4为f (x )的零点,x =π4为f (x )的对称轴,且∀x ∈11π36,17π36,|f (x )|<1,则ω的最大值为()A.5B.4C.3D.2【解析】:因为x =-π4为f (x )的零点,所以ωx +φ=k 1π,(k 1∈Z ),∴-π4ω+φ=k 1π,(1),因为x=π4为y=f(x)图象的对称轴,所以ωx+φ=k2π+π2,(k2∈Z),∴π4ω+φ=k2π+π2,(2)(1)+(2)得2φ=(k1+k2)π+π2,∴φ=(k1+k2)π2+π4,因为|φ|≤π2,∴φ=±π4.(2)-(1)得π2ω=(k2-k1)π+π2,∴ω=2(k2-k1)+1=2n+1(n∈Z),当ω=5时,如果f(x)=sin(5x+π4),令5x+π4=kπ+π2,k∈Z,∴x=15kπ+120π,当k=2时,x=9π20∈(1136π,1736π),与已知不符.如果f(x)=sin(5x-π4),令5x-π4=kπ+π2,k∈Z,∴x=15kπ+320π,当k=1时,x=7π20∈(1136π,1736π),与已知不符.如果ω=3,如果f(x)=sin(3x+π4),令3x+π4=kπ+π2,k∈Z,∴x=13kπ+112π,当k=1时,x=5π12∈(1136π,1736π),与已知不符.如果f(x)=sin(3x-π4),令3x-π4=kπ+π2,k∈Z,∴x=13kπ+14π∉(1136π,1736π),与已知相符.故选:C若函数f(x)=wx-π32单调性与w的范围sin w>0在区间π,3π2上为单调递减函数(1)从周期上:T2≥3π2-π.这样可以缩小w的范围.(2)再从单调性上去解.有两种思路.一种是换元,一种不换元直接用x算.本质是一样的.3)(ω>0),若函数f(x)在区间(π,【1】已知函数f(x)=sin(ωx-π3π2)上为单调递减函数,则实数ω的取值范围是()A.[23,119]B.[56,119]C.[23,34]D.[23,56]【解析】:因为π<x<3π2,所以ωπ-π3<ωx-π3<3ωπ2-π3,由正弦函数的单调性可得{ωπ-π3≥π2+2kπ3ωπ2-π3≤3π2+2kπ,解得:56+2k≤w≤119+43k,k=0时,所以56≤ω≤119,应选答案B。
三角函数中w的取值范围训练

三角函数中ω的取值范围训练例1:已知函数()()03sin >⎪⎭⎫ ⎝⎛+=ωπωx x f ,⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12512ππf f ,且()x f 在⎪⎭⎫ ⎝⎛612ππ,上单调,则ω的最大值为________.答案:320例2:已知函数()()⎪⎭⎫ ⎝⎛≤>+=2,0sin 2πϕωϕωx x f ,对任意x 满足033=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+x f x f ππ,066=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+x f x f ππ,且()x f 在⎪⎭⎫ ⎝⎛103154ππ,上单调递增,则ω的最大值为()A.3 B.9 C.15 D.27答案:C例3:(2019全国卷Ⅲ)设函数()()05sin >⎪⎭⎫ ⎝⎛+=ωπωx x f ,已知()x f 在[]π2,0上有且仅有5个零点.下述四个结论:①()x f 在()π20,上有且仅有3个极大值点②()x f 在()π20,上有且仅有2个极小值点③()x f 在⎪⎭⎫⎝⎛100π,上单调递增④ω的取值范围是⎥⎦⎤⎢⎣⎡1029512,其中所有正确结论的编号是()A.①④ B.②③C.①②③D.①③④答案:D例4:(2016天津)已知函数()()R x x x x f ∈>-+=,0212sin 212sin 2ωωω.若()x f 在区间()ππ2,内没有零点,则ω的取值范围是()A.⎦⎤ ⎝⎛810, B.⎪⎭⎫⎢⎣⎡⋃⎦⎤ ⎝⎛185410,,C.⎦⎤ ⎝⎛850, D.⎥⎦⎤⎢⎣⎡⋃⎦⎤ ⎝⎛8541810,,答案:D例5:已知定义在⎦⎤⎢⎣⎡4,0π上的函数()()06sin >⎪⎭⎫ ⎝⎛-=ωπωx x f 的最大值为3ω,则正实数ω的取值个数最多为()A.4B.3C.2D.1答案:C例6:设函数()()ϕω+=x A x f sin (ϕω,,A 是常数,0,0>>ωA ).若()x f 在区间⎥⎦⎤⎢⎣⎡26ππ,上具有单调性,且⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,则()x f 的最小正周期为__________.答案:π例7:已知函数()()()03,0,0sin 3=⎪⎭⎫ ⎝⎛-<<>+=ππϕωϕωf x x f ,对任意R x ∈恒有()⎪⎭⎫ ⎝⎛≤3πf x f ,且在区间⎪⎭⎫ ⎝⎛515ππ,上有且只有一个1x ,使()31=x f ,则ω的最大值为()A.457 B.4111 C.4105 D.4117答案:C例8:已知函数()()04sin >⎪⎭⎫ ⎝⎛-=ωπωx x f ,若()x f 在区间()ππ2,上存在零点,则ω的取值范围为_________.答案:⎪⎭⎫ ⎝⎛∞+⋃⎪⎭⎫ ⎝⎛,854181例9:已知函数()⎪⎭⎫ ⎝⎛∈>⎪⎭⎫ ⎝⎛+=R x x x f ,416sin 2ωπω,若()x f 的任何一条对称轴与x 轴交点的横坐标都不属于区间()ππ2,,则ω的取值范围是__________.答案:⎦⎤⎢⎣⎡32,31例10:已知函数()()04sin >⎪⎭⎫ ⎝⎛+=ωπωx x f 在⎪⎭⎫ ⎝⎛312ππ,上有最大值,但没有最小值,则ω的取值范围是__________.答案:⎪⎭⎫ ⎝⎛343,。
专题13 三角函数中参数ω的取值范围问题(教师版)-2024年高考数学压轴专题复习

专题13 三角函数中参数ω的取值范围问题
目录
①ω的取值范围与单调性结合 (1)
②ω的取值范围与对称性相结合 (4)
③ω的取值范围与三角函数的最值相结合 (6)
④ω的取值范围与三角函数的零点相结合 (9)
⑤ω的取值范围与三角函数的极值相结合 (15)
①ω的取值范围与单调性结合
②ω的取值范围与对称性相结合
要使()g x 的图像在区间(0,π)上有且仅有两条对称轴和两个对称中心,则π5π2ππ32ω<+
≤,解得51336
ω<≤,因为*ω∈N ,所以2ω=.
③ω的取值范围与三角函数的最值相结合
④ω的取值范围与三角函数的零点相结合
所以,由上图可知,
9π11ππ22ωω<≤,解得911
22
ω<≤ ,所以,当1k =-时145k ω=-=,故选:B
5.(2023春·高一单元测试)已知函数()4cos f x x =,将函数
所以
24 24
ω
ω
ππ
π
ωω
>
⎧
⎪
⇒≤<⎨
≤<
⎪⎩
.
故答案为:[2,4).
⑤ω的取值范围与三角函数的极值相结合
由余弦函数()cos h t t =的性质可得:π
3ππ3
ω<+≤解得:811
33
ω<≤.。
三角函数中求w范围问题

三角函数中求w范围问题
在三角函数中,我们常常需要求解某个三角函数的定义域或值域。
现在,我们要解决的问题是求解函数w的范围。
首先,让我们来明确一下问题:函数w是一个三角函数,但具体是哪个三角函数呢?常见的三角函数有正弦函数、余弦函数和正切函数等。
由于未提供具体的三角函数名称,我们无法给出w的范围。
然而,对于常见的三角函数,我们可以给出它们的范围约定。
以下是一些常见三角函数的范围:
- 正弦函数(sin)的范围是[-1, 1],即w ∈ [-1, 1];
- 余弦函数(cos)的范围也是[-1, 1],即w ∈ [-1, 1];
- 正切函数(tan)的范围是整个实数集,即w ∈ (-∞, +∞)。
请注意,以上范围是根据常见定义所得,对于其他类型的三角函数,范围可能有所不同。
总之,要求准确确定函数w的范围,需要明确所给函数的具体名称。
根据常见定义,我们可以给出常见三角函数的范围,例如正弦函数和余弦函数的范围为[-1, 1],正切函数的范围为整个实数集。
二轮微专题研究之:三角函数中的w的求法(师)

二轮微专题研究之:三角函数中的w 的求法题型一:利用函数图象求w例1、已知函数f (x )=sin(ωx +φ)(ω>0,0≤φ≤π)是R 上的偶函数,其图像关于点M ⎝⎛⎭⎫3π4,0对称,且在区间⎣⎡⎦⎤0,π2上是单调函数,求φ和ω的值. 解:由f (x )是偶函数,得f (-x )=f (x ), 即函数f (x )的图像关于y 轴对称,∴f (x )在x =0时取得最值,即sin φ=1或-1. 依题设0≤φ≤π,∴解得φ=π2.由f (x )的图像关于点M 对称,可知 sin ⎝⎛⎭⎫3π4ω+π2=0, 则3π4ω+π2=k π,k ∈Z ,解得ω=4k 3-23(k ∈Z ), 又f (x )在⎣⎡⎦⎤0,π2上是单调函数, 所以T ≥π,即2πω≥π.∴ω≤2.又ω>0,∴k =1时,ω=23;k =2时,ω=2.故φ=π2,ω=2或23.题型二:利用单调性求w 的取值范围变式2-2、若函数在区间上单调递增,则ω的最大值为9 .【解答】解:函数在在区间上单调递增,则,k∈Z.解得:,∵ω∈N*.当k=1时,可得ω的最大值为:9.故答案为:9.题型五:代值验证例 4.(2016•新课标Ⅰ)已知函数()sin()(0f x x ωϕω=+>,||)2πϕ,4x π=-为()f x 的零点,4x π=为()y f x =图象的对称轴,且()f x 在(18π,5)36π上单调,则ω的最大值为( )A .11B .9C .7D .5解:4x π=-为()f x 的零点,4x π=为()y f x =图象的对称轴,∴2142n T π-=,即21242n ππω-=,()n N ∈即21n ω=-,()n N ∈,即ω为正奇数, 解:()f x 在(18π,5)36π上单调,则53618122T πππ-=≤,即26T ππω=≥,解得:12ω≤;当11ω=时,+2411k ππϕπ-=,k Z ∈,||2πϕ,4πϕ∴=-,此时由于对称轴+2411k x πππ+=,当0=k 时,35(,)441836x πππ=∈,()f x ∴在(18π,5)36π不单调,不满足题意;当9ω=时,+249k ππϕπ-=,k Z ∈,||2πϕ,4πϕ∴=,此时()f x 在(18π,5)36π单调,满足题意;故ω的最大值为9,故选:B . 变式:33.已知函数f(x)=﹣sin2ωx(ω>0)的图象关于点对称,且在区间上是单调函数,则ω的值为.【解答】解:由题意图象关于点对称,∴2ω×=kπ,k∈Z可得:ω=在区间上是单调函数,即T,可得:T≥2π,那么:2ω≤1,∴0<ω≤当k=1时,可得ω=.故答案为:.4、已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),若f(x)≤f()对于x∈R恒成立,f(x)的一个零点为,且在区间[,]上不是单调函数,则ω的最小值为9 .【解答】解:函数f(x)=Asin(ωx+φ)(A>0,ω>0),若f(x)≤f()对于x∈R恒成立,则ω•+φ=2kπ+,k∈Z.可得φ=﹣+2kπ.①f (x )的一个零点为,故有ω•+φ=k′π,k′∈Z .要使ω最小,即使周期最大,最近的一个零点,可得==﹣,∴ω=3, 那么φ=2kπ. ∴f (x )=Asin3x 在区间[,]上是单调函数,不满足题意;当x=与对称轴x=是第二个最近的一个零点,可得==﹣,∴ω=9, 那么φ=+2kπ.∴f (x )=﹣Acos9x 在区间[,]上不是单调函数,满足题意;则ω的最小值为9. 故答案为:9.5.(2020•碑林区校级模拟)已知()sin()(0f x x ωϕω=+>,0)ϕπ<是R 上的奇函数,若()f x 的图象关于直线4x π=对称,且()f x 在区间[,]2211ππ-内是单调函数,则()(6f π= )A .B .12-C .12D 6.(2019•开福区校级模拟)已知函数()3sin()(0f x x ωϕω=+>,0)ϕπ<<,()03f π-=,对x R ∈恒有()|()|3f x f π,且在区间(,)155ππ上有且只有一个1x 使1()3f x =,则ω的最大值为( )A .574B .1054C .1114D .11747、。
三角函数w范围

三角函数w范围三角函数在数学中是非常重要的一个概念,它对于解决各种问题和计算具有广泛的应用。
在我们学习三角函数的时候,常常会涉及到三角函数的定义域和值域,也就是三角函数的范围。
下面我将详细介绍三角函数的范围,并且从不同的角度进行讨论。
首先我们来看正弦函数sin(x)。
正弦函数的定义域是整个实数集R,也就是对于任意实数x都可以求得sin(x)的值。
那么,对于sin(x)的值域是多少呢?我们知道sin(x)的值介于-1和1之间,可以表示为-1≤sin(x)≤1。
也就是说,对于任意实数x,sin(x)的值都在-1和1之间。
接下来让我们来看余弦函数cos(x)。
余弦函数的定义域也是整个实数集R,对于任意实数x都可以求得cos(x)的值。
那么,对于cos(x)的值域是多少呢?我们知道cos(x)的值介于-1和1之间,可以表示为-1≤cos(x)≤1。
也就是说,对于任意实数x,cos(x)的值都在-1和1之间。
再来看正切函数tan(x)。
正切函数的定义域是x∈(2n-1)π/2≤x≤nπ/2 (n∈Z),这是因为对于tan(x)来说,分母是cos(x),当cos(x)等于0的时候,tan(x)是无穷大。
所以我们需要剔除这些点。
另外,tan(x)也是一个周期性函数,它的周期是π。
那么,对于tan(x)的值域是多少呢?我们知道tan(x)可以取到任何实数的值,也就是说,tan(x)的值域是整个实数集R。
接下来让我们来看余切函数cot(x)。
余切函数的定义域是x∈nπ<x<(n+1)π (n∈Z),与tan(x)类似,我们也需要除去分母为0的点。
另外,cot(x)的周期也是π,这是因为cot(x)等于tan(x)的倒数。
那么,对于cot(x)的值域是多少呢?我们知道cot(x)可以取到任何实数的值,也就是说,cot(x)的值域是整个实数集R。
最后我们来看正割函数sec(x)和余割函数csc(x)。
正割函数的定义域是x∈2nπ<x<(2n+1)π (n∈Z),与cos(x)=0时对应的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作者:败转头
作品编号44122544:GL568877444633106633215458 时间:2020.12.13
三角函数w 的取值问题
1.已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π
2,π上单调递减,则ω的取值范围是________. 答案:⎣⎡⎦⎤
12,54
答案:C
4.已知函数f (x )=sin (ωx +φ)(ω>0,0≤φ≤π)是R 上的偶函数,其图象关于点对称,且在区间上是单调函数,则ω的值为( ) A .
B .
C .
D .
解:由f (x )是偶函数,得f (﹣x )=f (x ),即sin (﹣ωx +∅)=sin (ωx +∅), 所以﹣cosφsinωx=cosφsinωx ,对任意x 都成立,且ω>0,所以得cosφ=0.
依题设0<φ<π,所以解得φ=,由f (x )的图象关于点M 对称,得f (﹣x )=﹣f
(
+x ),
取x=0,得f ()=sin (+
)=cos ,∴f ()=sin (+)=cos ,
∴cos
=0,又ω>0,得
=
+kπ,k=1,2,3,∴ω=(2k +1),k=0,1,2,
当k=0时,ω=,f (x )=sin (x +)在[0,]上是减函数,满足题意; 当k=1时,ω=2,f (x )=sin (2x +)在[0,]上是减函数;
当k=2时,ω=,f (x )=(
x +
)在[0,
]上不是单调函数;所以,综合得ω=或
2.故选D .
5.(2016年全国I 高考)已知函数ππ
()sin()(0),24
f x x+x ,
ωϕωϕ=>≤=-为()f x 的零点,π4x =
为()y f x =图像的对称轴,且()f x 在π5π
()1836
,单调,则ω的最大值为 (A )11 (B )9 (C )7 (D )5 解:∵x=﹣为f (x )的零点,x=为y=f (x )图象的对称轴, ∴
,即
,(n ∈N )即ω=2n +1,(n ∈N ) 即ω为正奇数,∵f (x )在(,
)则
﹣
=
≤,
即T=≥
,解得:ω≤12,当ω=11时,﹣
+φ=kπ,k ∈Z ,
∵|φ|≤,∴φ=﹣
,此时f (x )在(
,
)不单调,不满足题意;当ω=9时,
﹣
+φ=kπ,k ∈Z ,
∵|φ|≤,∴φ=
,此时f (x )在(
,
)单调,满足题意;故ω的最大值为9,
故选:B
6. 已知函数f (x )=2sin ωx (ω>0)在区间⎣⎡⎦⎤-π3,π
4上的最小值是-2,则ω的最小值等于________.
答案:
3
2
8. (第十三周周考题)函数()2sin()
3
f x x
π
ω
=-(
1
3
ω>,x R
∈),若()
f x的任意一个对称中心的横坐标都不属于区间()
,2
ππ,则ω的取值范围是.
答案:
12
,
33
⎛⎤
⎥
⎝⎦
9.(2016年天津高考改编)已知函数
2
())(0)
4
f x x
π
ωω
=->,R
x∈.若)
(x
f在区间)
2,
(π
π内没有零点,则ω的取值范围是()
(A)]
8
1
,0((B))1,
8
5
[
]
4
1
,0( (C)]
8
5
,0((D)]
8
5
,
4
1
[
]
8
1
,0(
答案:D
作者:败转头
作品编号44122544:GL568877444633106633215458 时间:2020.12.13。
