桁架结构优化设计
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析摘要:随着市场经济的发展以及工业化进程的加快,剧场演出的数量越来越多,规模也越来越大。
为了保证演出的安全性,可以将桁架结构应用在演出舞台搭建当中,而桁架结构不仅能够提高舞台的质量,还具有跨度大、成本低等特点,因此需要对舞台搭建中桁架结构的应用进行深入研究。
本文将对舞台搭建中桁架结构的优化设计进行简析。
关键词:舞台搭建;桁架结构;优化设计桁架结构是当前常用的一种梁式结构,具有结构布置灵活、抗弯性强、抗剪性强、应用范围广泛等特点。
将桁架结构应用在舞台搭建当中能够有效增强舞台的抗剪性、抗压性,有利于提高舞台的质量。
但是当前舞台搭建企业在应用桁架结构时还存在一些问题,需要不断对桁架结构进行优化设计才能够充分发挥桁架结构的作用。
1 舞台搭建中的桁架结构桁架结构是一种梁式结构,其中桁架是指桁架梁,也被称为屋架,比較适用于跨度较大的展览馆、厂房等建筑当中。
桁架结构的布置比较灵活,无论是抗弯性能还是抗剪性能都比较强,因此适用于各种跨度的建筑。
按照桁架的外形,可将桁架结构分为平行弦桁架、折弦桁架以及三角形桁架;按照桁架的几何组成方式可将桁架结构分为简单桁架、联合桁架以及复杂桁架;按照所受水平推力的不同可将桁架结构分为无推力的梁式桁架以及有推力的拱式桁架[1]。
桁架的外形不同,对杆件内力分布的影响也不同,比如说平行弦桁架弦杆的内力是由中间向两端逐渐减少的,而三角形桁架弦杆的内力则是由中间向两端逐渐增加的。
当前在实际演出过程中,舞台搭建的内部空间较大,受临时场地环境的影响,结构复杂,由于演出对光线等情况的要求,所以在实际的舞台搭建桁架结构施工过程中,对施工技术的要求也比较高,舞台桁架主要是为了支撑舞台的(如下图),在经过专业力学测试的情况下,舞台承重结构满足实际需求,所搭建起来的舞台稳定性都很好,同时也可以搭建成后台影视墙和顶层支架,可以悬挂背景布、灯光和音响。
舞台桁架结构2 舞台搭建中桁架结构的优化设计2.1 根据工程情况进行优化工程建筑企业必须根据舞台搭建工程的具体情况对桁架结构进行优化设计,只有这样才能够让桁架结构更符合舞台搭建的实际需要。
桁架机构的优化设计

空间桁架结构是将杆件按一定规律布置,通过节点连接瓤成的一种抒系结构,具有经济、跨越能力大以及形式活泼新颖等优点n3.由于是空间超静定结构,力学分析和结构设计都较为复杂,采用计算机辕韵优化设计,对减轻结构重遗、降低缕构造徐有饕重要意义.在桁架结构中根据锫杆件的受力,合理选择杆件截丽尺寸,使其在满足多种约束条件的前提下最大限凌缝承受骜载,就可以达裂减轻结构重量、降低结构造价的目的桁架结构优化问题可以表述如下:以雄杆桁架结构系统蠹研究对象,该系统基本参数<包括弹性模量、材料密度、最大容许应力、最大允许位移等)已知;问题是在给定的荷载条件下,确定桁架的最优截瑟瑟积,使结搀夔量最轻。
设各杆截面积为设计变量:工=[x 1,x 2,...,X n ]T ,目标函数可写为:min ʃ(x)= ρn i =1x t L i ; 约束包括:σt ≤σt a (i 一1,2,⋯,刀)“μj ≤μj a “; (j=1,2,⋯,n)A min ≤x t ≤A max (i=1,2,⋯,n)式中:x t 为第i 杆件的截面面积,L t 为第i 杆件的长度,ρ为材料密度,σt 、σt a 分别为第i 杆的应力和允许应力,μj 、μj a ;分别为第J 节点的位移和位移限值,A min 、A max ;分别为杆件截面积的上、下限.桁架与框架同属于杆系结构,在结构工程、工民建等有着广泛的应用,是常见但又 重要的结构形式。
杆系结构的失效模式很多,其中有代表性的是结构的整体和局部届曲 失稳。
随着设计和施工水平的不断进步,杆系结构正向着大跨度、轻柔化的方向发展, 因此对结构稳定性的要求越来越高,需要准确的稳定性理论分析和数值计算方法。
桁架结构的稳定性理论已有两种:几何非线性特征值稳定性理论和几何非线性临界 点理论。
其中几何非线性特征值稳定性理论出现的最早。
国内外的许多学者们一直沿用 这个理论来解决整体稳定性问题。
但是,近些年来,人们发现,用这套稳定性理论时会 出现一些问题,比如应力过高,有时甚至会超过材料的许用应力.结构在整体失稳之前 已经局部欧拉失稳或发生材料屈服。
桁架杆机构的优化设计

OCCUPATION2013 08108案例CASES桁架杆机构的优化设计文/宋育红摘 要:桁架结构优化设计中普遍存在约束的作用,现有优化设计一般采用满应力法、遗传优化或直接实验法搜索等优化方法,但其时间周期长、优化复杂。
本文主要采用复合形法,建立了桁架结构优化设计的数学模型,利用Fortran优化程序对其进行优化并获得最优解。
关键词:桁架结构 优化设计 复合形法一、优化目标及设计原则1.优化目标在工程力学教学当中,笔者利用复合形法对桁架杆进行优化设计,以求得到其最优解。
桁架杆设计的优化可以选择多种目标,如尺寸最小、质量最轻、强度最高等,一般应根据不同的需要选定。
笔者以桁架杆为例,以其质量最小为优化目标。
2.设计原则在桁架杆设计时我们首先要求两杆同时满足强度条件,其次要满足几何条件约束,进而确定目标函数,并对其优化。
二、复合形法优化设计简述复合形法的基本思路是在n 维空间的可行域中选取K 个设计点(通常取n +1≤K ≤2n )作为初始复合形(多面体)的顶点。
然后比较复合形各顶点目标函数的大小,其中把目标函数值最大的点作为坏点,以坏点之外其余各点的中心为映射中心,寻找坏点的映射点。
一般说来,此映射点的目标函数值总是小于坏点的,也就是说映射点优于坏点。
这时,以映射点替换坏点与原复合形除坏点之外其余各点构成K 个顶点的新的复合形。
如此反复迭代计算,在可行域中不断以目标函数值低的新点代替目标函数值最大的坏点从而构成新复合形,使复合形不断向最优点移动和收缩,直至收缩到复合形的各顶点与其形心非常接近、满足迭代精度要求时为止。
最后输出复合形各顶点中的目标函数值最小的顶点作为近似最优点。
三、建立数学模型1.已知参数如桁架杆的结构,已知l =2m,x B =1m,载荷ρ=100kN桁架材料的密度 ρ=7.5×10-5N/mm 3,许用拉应力[σ+ ]=150MPa,许用压应力[σ- ]=100MPa,y B 的范围为:0.5m≤y B ≤1.5m,求桁架杆在满足强度的条件下,其质量的最小值。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析舞台桁架结构是舞台搭建中的重要组成部分,它承载着舞台上的各种装置和设备,起到支撑和固定的作用。
在舞台设计中,桁架结构的优化设计是非常重要的,可以提高舞台的安全性和稳定性,同时也可以减少材料的使用量,降低成本。
本文将对舞台桁架结构的优化设计进行分析,探讨如何在保证舞台安全的前提下实现材料的节约和效益的最大化。
一、舞台桁架结构的构成和功能舞台桁架结构通常由立柱、横向梁和斜杆组成,它们共同构成了一个稳定的支撑系统,承载着舞台上的各种设备和装置。
立柱支撑着整个桁架结构的重量,横向梁则起到了连接和支撑的作用,而斜杆则增强了结构的稳定性和承载能力。
这些部件在舞台搭建过程中是紧密相连的,构成了一个整体的支撑系统。
二、舞台桁架结构的优化设计方法1. 选材优化在舞台桁架结构的设计中,选材是非常重要的一环。
选择合适的材料不仅可以达到承载要求,还可以降低材料成本和重量,提高结构的使用寿命。
在选材时,需要考虑材料的强度、刚度、耐腐蚀性、重量等因素,以及材料的可加工性和可维护性。
根据舞台桁架结构的实际需求和使用环境,选择合适的材料,如钢材、铝合金等,进行优化设计。
2. 结构优化舞台桁架结构的优化设计还包括对结构的优化布局和连接方式的设计。
通过合理的结构布局和连接方式,可以提高结构的承载能力和稳定性,减少结构的自重,增加整体结构的安全性和稳固性。
在设计中,可以采用一些新颖的设计理念和技术,如空间桁架结构、三维结构等,来实现结构的优化设计和目标的实现。
3. 节能减排在舞台桁架结构的设计中,还需要考虑节能减排和环保要求。
可以通过合理的设计和材料选择,减少结构的自重,降低能源消耗,减少二氧化碳的排放。
还可以考虑结构的再利用和循环利用,减少对自然资源的消耗,降低对环境的影响,实现舞台桁架结构设计的可持续发展。
以某大型室内演出场馆的舞台桁架结构为例,进行优化设计分析。
该场馆的舞台桁架结构由钢材组成,包括立柱、横向梁和斜杆,用于支撑舞台上的吊装设备和装置。
桥梁工程中桁架结构的设计与优化

桥梁工程中桁架结构的设计与优化桁架结构是桥梁工程中常用的一种结构形式,它由一系列的斜杆和水平杆件组成,形成一个稳定的三维网格结构。
在桥梁设计中,桁架结构有着重要的地位和作用。
本文将探讨桥梁工程中桁架结构的设计和优化方法。
桁架结构的设计是桥梁工程中的核心环节。
在设计之初,首先需要明确桥梁的功能和要求,包括跨越的距离、承载能力等。
根据这些要求,设计师可以选择适当的桁架结构形式,如平行桁架、倒桁架等。
同时还需要考虑桥梁所处环境的因素,如地质条件、风速等。
这些因素将直接影响桁架结构的设计。
设计过程中,桁架结构的稳定性是必须考虑的关键因素。
桁架结构的稳定性与其强度相辅相成,设计师需要采取合适的措施来保证桁架结构的稳定性。
一方面,设计师可以通过优化桁架结构的杆件尺寸,使其能够承受合适的荷载,并避免产生过大的变形;另一方面,设计师还可以通过布置适当的支撑结构来提高桁架结构的稳定性,如设置斜撑、加固节点等。
除了稳定性外,桁架结构的刚度也是需要考虑的因素之一。
刚度是指结构对外力作用下的变形程度,对于桥梁来说,合适的刚度可以提高行车的舒适性和安全性。
桁架结构的刚度主要由杆件的尺寸和节点的刚性决定。
设计师可以通过调整这些参数来控制桁架结构的刚度,以确保其满足工程要求。
在桁架结构的设计中,材料的选择也非常重要。
常用的材料包括钢材、混凝土等,每种材料都有其独特的物理性质和优缺点。
设计师需要根据实际情况选择最合适的材料,并考虑到材料的成本、可持续性等因素。
同时,设计师还需要考虑材料的疲劳性能,特别是对于长跨度桥梁来说,疲劳性能的考虑将是非常重要的。
桥梁工程中的桁架结构设计不仅仅局限于上述提到的几个方面,还包括了许多其他的考虑因素。
例如,在设计过程中,设计师还需要考虑桥梁的美观性、施工的可行性等方面。
此外,设计师还可以运用现代的计算机辅助设计软件,如AutoCAD、ANSYS等,来辅助完成桁架结构的设计工作。
在设计完成后,还需要对桁架结构进行优化。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析1. 引言1.1 背景介绍舞台桁架是承载舞台设备和布景的重要结构,其设计质量直接影响到舞台的稳定性和安全性。
随着舞台设计的需求不断提高,舞台桁架结构的优化设计成为了重要问题。
在传统的设计方法中,舞台桁架结构往往存在着一些问题,比如重量过大、材料利用率低等。
为了解决这些问题,必须进行舞台桁架结构的优化设计分析,以提高其性能表现。
目前,关于舞台桁架结构的优化设计分析研究还比较少,尤其是在材料选用和连接方式等方面的研究较为薄弱。
本文将围绕舞台桁架结构的设计原理、优化方法、材料选用与连接方式、结构应力分析以及荷载模拟与实验验证展开研究,希望通过本文的研究成果对舞台桁架结构的优化设计提供一定的参考和帮助。
本研究的目的在于通过对舞台桁架结构的优化设计分析,提出一套更加科学合理的设计方案,以满足舞台设计的要求,提高舞台桁架结构的安全性和稳定性。
本研究也将为舞台桁架结构的设计和应用提供新的思路和方法。
1.2 研究目的本研究的目的是通过对舞台桁架结构的优化设计分析,探索如何提高舞台桁架结构的性能和稳定性,实现更加高效和安全的舞台搭建。
舞台桁架结构在舞台搭建中起着至关重要的支撑作用,其设计是否合理直接影响到演出活动的进行和参与者的安全。
本研究旨在通过深入研究舞台桁架结构的设计原理、优化方法、材料选用与连接方式、结构应力分析以及荷载模拟与实验验证等方面,挖掘出最优的设计方案,为舞台搭建领域提供更加科学和可靠的技术支持。
通过本研究,我们希望能够为舞台行业的发展和舞台工程设计提供实用的指导,为舞台搭建的安全和稳定做出贡献。
1.3 研究意义舞台桁架结构作为舞台搭建的重要组成部分,其设计与优化在现代舞台工程中扮演着至关重要的角色。
在现代演艺行业中,舞台演出的要求越来越高,对舞台桁架结构的稳定性、安全性和美观性提出了更高的要求。
对舞台桁架结构的优化设计分析具有重要的研究意义。
舞台桁架结构的优化设计可以提高舞台的稳定性和安全性。
十杆桁架结构优化设计

十杆桁架结构优化设计首先,对于十杆桁架结构的优化设计,我们需要对其结构进行合理的剖析。
十杆桁架结构由十根杆件组成,杆件之间以节点连接。
在进行优化设计时,需要考虑到杆件与节点之间的连接强度和刚度,杆件的强度和稳定性等因素。
因此,选择适当的杆件形状和截面尺寸是优化设计的第一步。
其次,进行载荷分析对于优化设计非常重要。
十杆桁架结构主要承受水平和垂直方向的力。
水平方向的力可以来自于风荷载、地震荷载等外部荷载,垂直方向的力可以来自于自重、活载等。
通过对这些荷载进行分析,可以确定桁架结构的受力情况,进而进行优化设计。
在进行优化设计时,还需要考虑材料的选择。
优化设计的目的之一是减少材料的使用量,降低工程成本。
因此,在选择材料时,需要考虑到材料的强度、稳定性、重量等因素。
常用的材料有钢材、铝合金等,其强度和重量比较适合十杆桁架结构的优化设计。
优化设计的另一个重要方面是连接节点的设计。
节点连接的强度和刚度对于整个十杆桁架结构的稳定性和安全性起到了至关重要的作用。
在连接节点的设计中,需要考虑到连接的可靠性、刚度和简单性等因素。
合理的连接设计可以提高整个桁架结构的性能,降低结构的变形和振动。
此外,还需要进行结构的优化分析。
优化分析是通过数值模型和计算方法对十杆桁架结构进行全面的分析和优化,以确定最佳设计方案。
可以通过有限元分析等方法对结构进行应力分析、变形分析等,进而进行优化调整。
总之,十杆桁架结构的优化设计需要考虑到杆件形状和截面尺寸的选择、载荷分析、材料选择、节点连接的设计以及结构的优化分析等方面。
通过合理的优化设计,可以提高结构的性能,减少材料的使用量,降低工程成本。
最终实现结构的安全、稳定和经济的设计目标。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析舞台桁架结构作为舞台搭建的重要组成部分,在舞台搭建中起着承重、支撑和连接作用。
舞台桁架结构的优化设计是保障舞台搭建安全稳固的重要环节。
本文将从优化设计的角度对舞台桁架结构进行分析,探讨如何在设计中充分考虑结构的稳定性、承载能力和施工便捷性,从而达到最佳的搭建效果。
一、舞台桁架结构概述舞台桁架结构主要由横梁、竖柱和连接件组成,其作用是支撑舞台平台、灯光音响设备以及表演人员,同时也要承受各种外力和荷载。
桁架结构的设计必须符合建筑结构设计的相关规范标准,并且需要考虑到舞台搭建的实际使用情况和要求,确保桁架结构能够稳定支撑整个舞台系统。
二、舞台桁架结构的优化设计原则1. 结构稳定性舞台桁架结构在搭建过程中需要承受各种荷载,包括人员活动、设备重量、风荷载等。
结构的稳定性是设计的首要考虑因素。
为了确保结构的稳定性,需要在设计中合理配置各种构件,通过合理的连接方式和支撑方式,使得整个结构能够在外力作用下保持稳定。
2. 承载能力舞台桁架结构需要承载各种荷载,并且需要考虑到不同位置的荷载大小不同。
设计时需要根据实际使用情况和要求合理配置各个部位的支撑结构,并通过合理的布局和材料选择来提高结构的承载能力,确保其能够承受各种外力的作用。
3. 施工便捷性舞台桁架结构的优化设计不仅要考虑到结构的稳定性和承载能力,还要考虑到施工的便捷性。
在设计中需要合理配置各种连接件和支撑构件,确保结构在施工过程中能够快速、方便地搭建起来,并且能够在搭建完成后易于维护和管理。
在舞台桁架结构的优化设计中,需要进行详细的结构分析,包括受力分析、位移分析、振动分析等。
通过结构分析可以了解结构在各种外力作用下的受力情况,找出结构的薄弱环节,并且可以通过分析来确定结构的合理布局和材料选择。
2. 材料选择舞台桁架结构的优化设计需要根据实际使用情况和要求选择合适的材料。
在材料选择时需要考虑到强度、刚度、耐腐蚀性等因素,并且需要满足相关的建筑结构设计规范要求,以确保选择的材料能够满足结构的承载能力和稳定性要求。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析舞台桁架结构是指搭建在舞台上用于支撑灯光、音响和布景的桁架系统。
它在舞台装置中扮演着十分重要的角色,可以保障演出过程的安全和顺利进行。
对舞台桁架结构进行优化设计分析,对于提高舞台效率和提升演出质量具有重要意义。
舞台桁架结构的优化设计需要考虑到承重能力。
由于舞台上会安装灯光、音响和布景等设备,因此舞台桁架需要足够的承重能力来支撑这些设备的重量。
设计舞台桁架时需要考虑到每个点的承重能力,并根据实际情况进行合理分配和安排。
还需要考虑到桁架的连接方式和支撑方式,确保桁架能够稳固地支撑起上面的设备,保证演出过程的安全。
舞台桁架结构的优化设计还需要考虑到搭建和拆卸的便捷性。
舞台上的演出通常是临时性的,因此舞台桁架需要能够快速地搭建和拆卸。
设计舞台桁架时需要考虑到各个部件的连接方式和搭建顺序,以及桁架结构的稳固性和平衡性,确保能够在短时间内完成搭建和不需要过多的人力物力。
还需要考虑到桁架部件的材质选择,选择轻便耐用的材料,同时尽量减少部件的数量和复杂度,以提高搭建和拆卸的效率。
舞台桁架结构的优化设计还需要考虑到整体的美观性和灵活性。
舞台桁架作为舞台装置的一部分,它的美观性和灵活性对于舞台装置的整体效果至关重要。
在设计舞台桁架时需要考虑到其外观设计和颜色搭配,能够和舞台装置和舞台布景相协调。
还需要考虑到桁架的灵活性,能够适应不同的演出需求和布景要求,满足演出的多样化和个性化。
舞台桁架结构的优化设计还需要考虑到成本和节能环保。
在设计舞台桁架时需要兼顾到其造价和材料费用,确保在满足功能和质量要求的前提下能够尽量减少成本。
还需要考虑到节能环保的要求,选择可循环利用和节能环保的材料,并在设计时考虑到其使用寿命和后续处理问题,确保舞台桁架在使用过程中对环境的影响尽量减少。
在舞台桁架结构的优化设计过程中,需要综合考虑到承重能力、搭建和拆卸便捷性、美观性和灵活性、成本和节能环保等因素,从而设计出结构合理、功能完善、质量可靠的舞台桁架系统,为演出的顺利进行和舞台效果的提升提供保障。
大跨度钢结构桁架优化措施

大跨度钢结构桁架优化措施嘿,咱今儿就来聊聊大跨度钢结构桁架优化措施这档子事儿!你想想啊,那大跨度钢结构桁架,就像是建筑界的大力士,撑起了一片片广阔的空间。
可要是没弄好,那可不行呀!咱先说说设计这块儿。
这设计就好比是给桁架规划路线,得精心琢磨。
你不能随随便便就画个图,那可不行!得考虑各种因素,比如受力情况,就像人得知道自己能扛多重的东西,桁架也得清楚自己能承受多大的力呀。
还有啊,节点的设计也很关键,这就好比是人的关节,得灵活又牢固,不然怎么能活动自如呢?再讲讲材料的选择。
这材料就像是桁架的血肉呀,得挑好的。
不能贪便宜用那些质量不靠谱的,不然到时候出问题可就麻烦大了。
好的材料能让桁架更结实,更耐用,就像好马配好鞍一样。
然后呢,施工过程也不能马虎。
工人师傅们得像对待艺术品一样对待桁架的安装。
焊接得严丝合缝,安装得稳稳当当,这可不是闹着玩的。
要是这里歪一点,那里斜一点,那整个桁架不就变形了吗?还有啊,咱得注意后期的维护。
别以为建好就完事大吉了,还得时不时去看看,有没有生锈啊,有没有松动啊。
就像人要定期体检一样,桁架也需要我们的关心和照顾。
优化大跨度钢结构桁架,不就是为了让它更好地为我们服务吗?让那些大空间变得更加安全可靠,更加美观实用。
这可不是一件简单的事儿,但只要我们用心去做,肯定能做好呀!你想想看,如果一个大跨度钢结构桁架设计不合理,那会怎么样?肯定会存在安全隐患呀!那要是材料不好呢?说不定用不了多久就出问题了。
施工不仔细,后期不维护,那后果简直不堪设想!所以说呀,这些优化措施一个都不能少,都得认真对待。
咱们可不能小瞧了这大跨度钢结构桁架,它可是建筑领域的重要组成部分。
通过优化措施,让它发挥出更大的作用,这难道不是一件很有意义的事情吗?咱得把这事儿做好,让每一个大跨度钢结构桁架都能成为建筑中的亮点,成为我们生活中的可靠支撑!这就是咱对待大跨度钢结构桁架优化措施该有的态度,你说是不是呢?。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析舞台桁架结构是舞台搭建的主要结构之一,其主要作用是支撑舞台的悬挂灯光、音响等设备以及演员的表演用品。
优化设计舞台桁架可以提高舞台的安全性、稳定性和美观度,进而提高演出效果。
本文将从舞台桁架结构的特点和设计原则出发,探讨舞台桁架结构的优化设计分析。
一、舞台桁架结构的特点1. 轻型桁架多采用铝合金材料,重型桁架多使用钢材制作。
铝合金桁架重量轻,强度高,不易生锈,安装方便,具有良好的机械性能和耐腐蚀性能,在日常运用中具有较高的经济效益;钢铁桁架强度更高,是重型设备的选择。
2. 舞台桁架分为三角钢桁架和铝合金桁架两种形式。
三角钢桁架强度较高,适合用于较大面积和较高高度的场地;铝合金桁架则具有轻便、美观的特点,适合用于展览、商业活动等场合。
3. 舞台桁架结构可以根据需要进行组合和拆卸,具有可移动性和易于维护的优点。
桁架通过连接卡具或卡子与其它部件相接,便于组装、拆卸和调整。
1. 功能要求。
舞台桁架结构要保证足够的承载能力,能够支撑悬挂的各种设备和配件,满足舞台表演的要求。
2. 安全性。
桁架结构要保证舞台设备和器材安全可靠,同时也要考虑观众的安全和舞台工作人员的作业安全。
3. 美观度。
舞台桁架的结构应该保持整体美观,不仅要满足功能和安全要求,也要有良好的视觉效果,避免影响整个演出的美感。
4. 经济性。
舞台桁架的设计要兼顾经济因素,考虑到材料成本、制作工艺、运输成本等因素,使得整个舞台搭建成本可控。
1. 桁架的材质选择。
根据功能要求和经济性原则,对舞台桁架的材料作出选择。
轻型桁架多采用铝合金材料,而重型桁架多使用钢材制作,材料抗拉强度大约370-410MPa。
2. 桁架的横截面设计。
可以采用优化设计方法,根据舞台设计要求和承载能力要求,选择合适的截面形状。
截面形状选取的好坏将直接影响桁架的承载能力和稳定性。
一般情况下,桁架截面形式应选择圆形或方形截面。
3. 桁架的接头设计。
舞台桁架的接头是整个桁架结构的关键部分,是一个较容易发生失效的部分,因此关于接头的优化设计是必不可少的。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析随着文化产业的发展,舞台表演活动越来越受到人们的关注,舞台桁架结构作为舞台表演中重要的组成部分,其设计和施工质量不仅直接影响着表演效果,还关系到观众的安全。
因此,为了使舞台桁架结构更加坚固、安全和美观,需要对其优化设计进行分析。
一、舞台桁架结构的定义和组成舞台桁架结构通常由大量的桁架杆件组成,这些杆件的加工和连接方式也相对复杂。
桁架杆件通常由两种材料制成:铝合金和钢材。
舞台桁架结构的组成部分包括三个部分:载荷部分、桁架结构和支撑部分。
载荷部分是指舞台上的各个设备及演员的重量,这些载荷需要经过合理的计算和布置,以确保整个舞台的稳定性和安全性。
桁架结构是指舞台桁架结构中的各种支架、连杆和螺栓等零部件,这些零部件需要根据实际需要和设计要求进行制作和安装。
支撑部分是指舞台桁架结构中的各种支撑点和基座,这些支撑点和基座需要在实际安装时进行精确的调整和加固,以确保整个舞台的稳定性和安全性。
1、桁架杆件的选择桁架杆件的选择是舞台桁架结构优化设计中的重要环节。
对于桁架杆件的选择,需要结合实际的使用环境和要求,针对不同的应用场合选择合适的材料和规格。
常用的材料包括铝合金、碳钢、不锈钢等,其中铝合金更为常用,因为其重量轻、强度高、易于加工、美观等优点。
2、桁架结构的引入舞台桁架结构的引入是指将桁架结构组件引入到原有的建筑空间中,以达到稳定的支撑效果。
对于舞台桁架结构的引入,在实践中具体分析所需要的支撑点和建筑结构支撑点,并在设计中精确塑造支撑点,以确保桁架结构能够准确填补现有建筑结构的空间,并保证建筑结构的稳定性和安全性。
3、桁架杆件的加工和连接桁架杆件的加工和连接方式对于舞台桁架结构的设计和制作直接关系到其强度和稳定性。
因此,在桁架杆件的加工和连接方面,需要严格按照相关标准和规范进行制作,并且对于每个杆件都需要进行质量检查,以确保其强度和稳定性。
4、整体结构的强度和稳定性分析在舞台桁架结构的优化设计中,对整体结构的强度和稳定性进行分析是必要的。
超高层建筑桁架结构设计与优化

超高层建筑桁架结构设计与优化随着城市化进程的加快和人口的不断增加,越来越多的超高层建筑崛起于都市的天际线上。
而这些巨型建筑的设计与施工面临着前所未有的挑战。
其中,桁架结构的设计与优化是超高层建筑中最重要也是最复杂的一项工程。
本文将对超高层建筑桁架结构的设计与优化进行探讨,旨在揭示在这一领域的最新进展和未来发展趋势。
首先,我们将深入了解桁架结构的基本概念和工作原理。
桁架结构是由纵向和横向构件组成的网格状结构。
这种结构具有良好的抗震性能和承载能力,能够有效地分散建筑重量并抵抗外部冲击。
在超高层建筑中,桁架结构通常用于承担建筑的主要荷载,包括垂直荷载、水平荷载和风载。
因此,桁架结构的设计和优化对超高层建筑的安全性和稳定性至关重要。
接下来,我们将介绍现代桁架结构设计中的关键技术和方法。
在设计过程中,工程师需要考虑多种因素,如荷载分布、结构稳定性、结构材料等。
其中,荷载分析是桁架结构设计的基础。
工程师需要准确地计算各种荷载对桁架结构的影响,并确定各个构件的尺寸和连接方式。
此外,结构稳定性也是设计中的一个关键问题。
超高层建筑由于高度较大,容易受到风力的影响,因此需要使用抗风设计方法来确保结构的稳定性。
在现代桁架结构设计中,计算机辅助设计(CAD)和有限元分析(FEA)等工具已经得到广泛应用,有效地提高了设计的准确性和效率。
然后,我们将讨论桁架结构优化中的关键问题。
超高层建筑桁架结构的优化是一个复杂的问题,需要综合考虑结构的强度、稳定性、经济性和施工难度等因素。
在优化过程中,工程师需要寻找最佳的构件尺寸和连接方式,以最大限度地提高桁架结构的性能和效益。
此外,材料的选择也是优化的重要内容。
工程师需要在结构强度和经济性之间进行权衡,选择恰当的材料来提高超高层建筑的整体性能。
最后,我们将展望超高层建筑桁架结构设计与优化的未来发展趋势。
随着科学技术和工程实践的不断进步,桁架结构的设计和优化将迎来更多创新。
例如,新材料的引入和新型连接技术的研发将进一步提高桁架结构的性能和可靠性。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析
舞台桁架结构是指用于支撑舞台上的舞台灯光、音响设备等的支架系统。
它的优化设计可以提高结构的稳定性、安全性和可靠性,同时还能减少材料的使用、简化施工过程,并提高舞台的功能性和美观性。
1. 结构的稳定性:舞台桁架结构的设计应保证其在各种力的作用下具备足够的稳定性。
首先要进行结构强度计算和稳定性分析,确定合适的截面尺寸和连接方式,以保证结构的承载能力和稳定性。
2. 结构的安全性:舞台桁架结构的设计应满足建筑设计规范和安全标准要求,确保结构在正常使用和特殊情况下不发生失稳、破坏等事故。
应考虑结构的超载和地震反应能力,采取合适的防护措施,如设置适当的抗震支撑和连接件。
3. 结构的可靠性:舞台桁架结构的设计应考虑结构的可靠性,即在设计寿命内,结构不发生失效。
为了确保结构的可靠性,可以采用优质的材料,合理的结构连接设计,以及定期检测和维修。
4. 材料的节约和施工的简化:舞台桁架结构的优化设计应尽量减少材料的使用,以节约成本。
可以采用轻型材料或高强度材料,进行结构材料的优化选择。
在设计时要考虑施工的便利性,尽量减少构件的加工和安装工艺,简化施工过程。
5. 舞台的功能性和美观性:舞台桁架结构的设计应满足舞台的功能需求,并与舞台的整体设计风格相匹配。
在结构设计中应考虑悬挂吊点的位置和数量、舞台灯光和音响设备的布置等。
在进行舞台桁架结构的优化设计时,可以借助计算机辅助设计软件进行结构分析和优化计算。
通过对桁架结构的有限元分析和强度计算,可以得到最佳的设计参数和结构方案。
三杆桁架的优化设计

三杆桁架的优化设计本文旨在介绍三杆桁架优化设计的背景和目的。
三杆桁架是一种常用的结构形式,具有高强度、轻量化和刚性好的特点,广泛应用于建筑、航空航天等领域。
然而,在实际应用中,三杆桁架结构的设计效果往往会受到诸多因素的制约,包括材料选择、结构形式、荷载条件等。
因此,对三杆桁架进行优化设计,不仅可以提高结构的性能和稳定性,还可以降低材料的使用量,减少成本。
本文将分析三杆桁架优化设计的背景和目的,探讨优化设计的方法和策略,以期为相关领域的研究者和设计师提供参考和指导。
三杆桁架的结构分析三杆桁架是一种常见的结构形式,由三根杆件和若干个节点组成。
它具有简单的结构和良好的稳定性,在工程领域得到广泛应用。
三杆桁架的基本结构是由三根杆件连接而成的三角形,每个顶点都是一个节点,杆件在节点处连接。
三杆桁架的性质取决于杆件的材料特性和连接方式。
三杆桁架的优化设计在设计三杆桁架时,可以采用优化设计的方法来提高其性能和效率。
优化设计的目标是使得三杆桁架在给定约束条件下,达到最佳的结构性能。
优化设计中的关键是确定合适的优化目标和设计变量。
优化目标可以包括最小化杆件的重量、最大化桁架的刚度或最小化应力集中等。
而设计变量可以包括杆件的截面积、材料的选择等。
进行三杆桁架的优化设计时,可以采用数值计算方法,如有限元分析和遗传算法等。
通过建立数学模型和进行参数优化,可以找到最优的设计方案。
总之,三杆桁架的优化设计是一项复杂而重要的工作。
通过合理的优化设计,可以提升三杆桁架的性能,实现结构的优化和效率的提高。
本文将介绍三杆桁架的优化设计方法,包括有限元分析等相关内容。
通过优化设计,我们可以改善三杆桁架的性能和结构强度,以满足特定的工程需求。
三杆桁架的优化设计可以采用以下方法:1.确定设计目标在开始优化设计之前,需要明确设计目标。
这可以包括改善结构强度、减小重量、降低成本等方面。
明确设计目标可以帮助我们选择适当的优化方法和评估指标。
2.建立数学模型根据设计目标,我们需要建立三杆桁架的数学模型。
智能桁架梁结构优化设计及关键节点预测分析

智能桁架梁结构优化设计及关键节点预测分析近年来,随着工程技术的不断发展,人们对于结构设计的要求也越来越高。
特别是在建筑领域,结构设计的优化和节点预测分析对于确保工程质量和安全具有至关重要的作用。
本文将讨论智能桁架梁结构的优化设计以及关键节点的预测分析,并探讨其在实际工程中的应用。
1. 智能桁架梁结构优化设计桁架梁结构是一种由桁架组成的载荷传输系统,其特点是结构轻巧、刚性强,适用于大跨度建筑的设计。
然而,传统的桁架梁结构设计往往过于保守,没有充分利用材料的优势,造成了资源的浪费。
在智能化设计的背景下,结构优化设计成为了一个重要的研究领域。
在桁架梁结构的优化设计中,智能算法发挥了重要作用。
例如,遗传算法可以对桁架梁结构的构件进行适应性优化,通过不断迭代计算,找到最优的结构形式和截面尺寸。
此外,神经网络算法也可以应用于桁架梁结构的设计中,通过学习已有的结构案例,为新设计提供参考和指导。
2. 关键节点预测分析在桁架梁结构的设计中,关键节点的预测分析十分重要。
关键节点是指结构中受力较大、应力集中或易于破坏的节点。
通过预测这些节点,可以及早发现潜在的问题,并采取相应的措施进行改进。
预测分析可以借助有限元分析方法,为关键节点的受力情况进行模拟和计算。
在模拟中,需要考虑梁的材料性能、外界荷载和边界条件等因素。
通过数值计算,可以得到节点的应力分布、变形情况和破坏概率等参数。
根据这些参数,可以选择合适的材料和结构形式,以优化设计方案。
3. 实际工程应用智能桁架梁结构的优化设计和关键节点的预测分析已经在实际工程中得到了应用。
例如,在大型体育馆和会展中心的建设中,采用智能优化设计的桁架梁结构可以减轻结构自重,提高空间利用效率;同时,通过关键节点的预测分析,可以调整节点的位置和增强措施,确保结构的安全性和稳定性。
此外,智能桁架梁结构的优化设计和关键节点的预测分析也在桥梁工程中发挥了重要作用。
通过适当调整节点的位置和改变截面形状,可以减小结构自重,提高桥梁的承载能力和抗震性能。
桁架轻型化优化设计
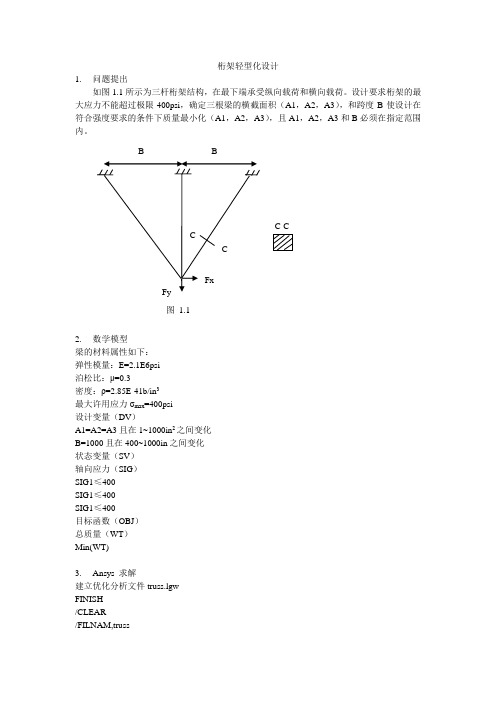
桁架轻型化设计1. 问题提出如图1.1所示为三杆桁架结构,在最下端承受纵向载荷和横向载荷。
设计要求桁架的最大应力不能超过极限400psi ,确定三根梁的横截面积(A1,A2,A3),和跨度B 使设计在符合强度要求的条件下质量最小化(A1,A2,A3),且A1,A2,A3和B 必须在指定范围内。
2. 数学模型梁的材料属性如下:弹性模量:E=2.1E6psi泊松比:μ=0.3密度:ρ=2.85E-41b/in 3最大许用应力σmax =400psi设计变量(DV )A1=A2=A3且在1~1000in 2之间变化B=1000且在400~1000in 之间变化状态变量(SV )轴向应力(SIG )SIG1≤400SIG1≤400SIG1≤400目标函数(OBJ )总质量(WT )Min(WT)3. Ansys 求解建立优化分析文件truss.lgwFINISH/CLEAR/FILNAM,truss FxFyB BCCC-C图 1.1B=1000A1=1000A2=1000A3=1000/PREP7ET,1,LINK1R,1,A1R,2,A2R,3,A3MP,EX,1,2.1E6MP,PRXY,1,0.3N,1,-B,0,0N,2,0,0,0N,3,B,0,0N,4,0,-1000,0/PNUM,NODE,1/NUMBER,0NPLOTREAL,1E,1,4REAL,2E,2,4REAL,3E,3,4FINISH/SOLUD,1,ALL,0,,3F,4,FX,200000F,4,FY,-200000SOLVEFINISH/POST1SET,LASTETABLE,EVOL,VOLUSSUM*GET,VTOT,SSUM,,ITEM,EVOL RHO=2.85E-4WT=RHO*VTOTETABLE,SIG,LS,1*GET,SIG1,ELEM,1,ETAB,SIG *GET,SIG2,ELEM,2,ETAB,SIG *GET,SIG3,ELEM,3,ETAB,SIG SIG1=ABS(SIG1)SIG2=ABS(SIG2)SIG3=ABS(SIG3)/ESHAPE,2/VIEW,1,1,1,1EPLOTFINISH在ANSYS中得到的模型如图3.1所示。
十杆桁架结构优化设计

题目:十杆桁架结构优化设计日期:2013.09.16目录1设计题目 (1)2设计过程 (2)2.1一、运用Abaqus求解各杆轴力应力 (2)2.1.1Abaqus计算流程 (2)2.1.2结果 (3)2.2二、利用材料力学知识求解 (4)2.2.1基本思路 (4)2.2.2解题过程 (4)2.2.3结果 (5)2.3三、编写有限元程序求解 (6)2.3.1程序基本步骤 (6)2.3.2Vs2012 中重要的程序段 (6)2.3.3程序输出文件 (9)2.3.4材料力学、有限元程序、Abaqus结果比较 (10)2.4四、装配应力计算 (11)2.4.1处理技巧 (11)2.4.2Abaqus处理技巧 (11)2.4.3不加外力(P1,P2,P3)时材力,Ansys与Abaqus结果 (12)2.4.4不加外力(P1,P2,P3)时材力,Ansys与Abaqus误差分析 (12)2.4.5加外力(P1,P2,P3)时 Ansys与Abaqus结果 (12)2.5五、优化设计 (14)2.5.1设计中变量的概念 (14)2.5.2优化步骤运用VS2012编写复合形法进行约束优化。
(14)2.5.3VS2012优化程序 (16)2.5.4优化结果 (20)2.5.5结果说明 (20)3设计感想 (20)4备注 (20)4.1参考书目 (20)4.2说明 (20)十字桁架结构优化设计现有十字桁架结构见图1,材料泊松比为0.3,E=2.1e11,密度为7.8×103kg/m3, 许用应力为160Mpa,P1=600k N ,P2=900k N ,P3=600k N,杆1-6面积为A1=0.03m2,杆7-10面积为A2=0.02m。
1、利用Abaqus计算各杆的应力;2、利用材料力学的知识求解,并与1计算出的结果做比较;3、编写有限元程序求解,与1和2计算结果进行比较;4、若杆5制作时短了0.001m,试求各杆的应力;5、若令2节点的位移小于0.005m,A1、A2为0.005~0.05m2,试对结构进行优化,使其重量最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
桁架结构优化设计
一般所谓的优化,是指从完成某一任务所有可能方案中按某种标准寻找最佳方案。
结构优化设计的基本思想是,使所设计的结构或构件不仅满足强度、刚度与稳定性等方面的要求,同时又在追求某种或某些目标方面(质量最轻,承载最高,价格最低,体积最小)达到最佳程度。
对于图1-1的结构,已知L=2m,x b=1m,载荷P=100kN,桁架材料的密度r=7.7x10-5N/mm3,[δt]=150Mpa,[δc]=100Mpa,y b的范围:0.5m≦y b≦1.5m。
图1-1 桁架结构
设计变量与目标函数(质量最小)
预定参数(设计中已确定,设计者不能任意修改的量):L , x b ,P ,r ,[δt ] ,[δc ]
设计变量(可由设计者调整的量)y b ,A 1,A 2 约束条件(对设计变量的约束条件) (1) 强度条件约束(截面、杆件的强度) (2) 几何条件约束(B 点的高度范围) 目标函数:桁架的质量W (最小)
解:1. 应力分析
0sin sin 02112=--=∑θθN N F x
0cos cos 02112=---=∑P N N F
y
θθ
由此得:
)sin(sin 2111θθθ+=
p N )
sin(sin 212
2θθθ+-
=p N
由正弦定理得:
l
y l x p
N B B 2
1)
(2
-+=
l
y x p
N B
B 2
22
+=
由此得杆1和2横截面上的正应力
1
2
1)
(2
lA y l x p
B B -+=
σ
2
2
22
lA y x p
B B +=
σ
2.最轻质量设计
目标函数(桁架的质量)
))((2
2
2
1
2
2
B B y x A y l x A W B B ++-+=γ
(1-1)
约束条件
[][]⎪
⎪
⎭
⎪⎪
⎬⎫⎪⎪⎩
⎪⎪⎨⎧≤+≤-+c B t B lA y x p lA y l x p B B σσ2
2
1
2
22
)
( (1-2)
0.5≦y b ≦1.5(m ) (1-3) (于是问题归结为:在满足上述约束条件下,确定设计变量y b ,A 1,A 2,使目标函数W 最小。
) 3.最优解搜索
采用直接实验法搜索。
首先在条件(1-3)所述范围内选取一系列y b 值,由强度条件(1-2)确定A 1与A 2,最后根据式(1-2)计算相应W ,在y b -W 曲线中选取使W 最小的y b 与相应的A 1与A 2,即为本问题的最优解。
4.利用MA TLAB 编程 (1)分析目标函数和约束条件
由已知L=2m ,x b =1m ,载荷P=100kN ,桁架材料的密度r=7.7x10-5N/mm 3,[δt ]=150Mpa ,[δc ]=100Mpa ,y b 的范围:0.5m ≦y b ≦1.5m 。
利用约束条件(1-2)。
可以分析最优解时:
A 1与A 2取最小面积时,约束条件即取等号。
即(1-2)中两不等式取等号。
如下
]
[]
[)
(2
2
2
1
2
2
c b b t b b lA y x p
lA y l x p
σσ=+=-+ (1-4)
代人已知条件得:
200
1300)
2(12
22
1b b y A y A +=
-+=
(1-5)
将(9-25)代人(9-21)得
)200
)1(300
)
)2(1((
107.72
2
4
b b y y W ++
-+⨯= (1-6)
0.5≦y b ≦1.5(m )
式(1-6)即为所求目标函数,求出其最小值,就是本问题的最优解。
所以采样二次插值法求极值 (3) 流程图 如图1-2
图1-2二次插值法程序框图
(3)MA TLAB程序
程序中F为目标函数W,而x为y b。
目标函数化为计算机认识的函数为:
F=256.66667*(5-4*x+x^2)^1.5+385*(1+x^2)^1.5;
利用二次插值法求极小值。
function eccz
syms x;%定义
f=256.66667*(5-4*x+x^2)+385*(1+x^2);%目标函数a1=0.5;a2=1.5;%区间0.5≦y b≦1.5
a3=1;%中间点
k=0;
while (abs(a3-a1)>1.0e-7)%精度为10-7
f1=subs(f,x,a1);%循环内为二次插值过程
f2=subs(f,x,a2);
f3=subs(f,x,a3);
C1=(f3-f1)/(a3-a1);
C2=((f2-f1)/(a2-a1)-C1)/(a2-a3);
ap=0.5*(a1+a3-C1/C2);
fp=subs(f,x,ap);
if ap>a2;
if f2>=fp
a1=a2;
f1=f2;
a2=ap;
f2=fp;
else
a3=ap;
f3=fp;
end
else
if f2>=fp;
a3=a2;
f3=f2;
a2=ap;
f2=fp;
else
a1=ap;
f1=fp;
end
end
k=k+1
a=ap
ff=subs(f,x,ap)%输出循环次数k,最优解x以及最小值ff)
end
MA TLAB程序输出最后结果如下:
k =
24
a =
0.8000
ff =
125.7667(最小值)
即目标函数最优解为:
y b=0.8m时,桁架重量最轻
W min=125.7667N
由(1-5)得
1,2杆横截面分为
A1=521mm2
A2=640mm2
下面程序为用MA TLAB画出Yb与W的函数关系曲线如图1-3 画图程序:
y=0:0.01:1.5;%范围及步长
w=25.666667*(5-4*y+y.^2)+38.5*(1+y.^2);%目标函数
plot(y,w,'-r')%坐标点
title('Yb与W的函数关系 ')%标题
xlabel('Yb的函数值')%x轴
ylabel('质量W的值')%y轴
图1-3 Yb与W的函数关系。
