基于MATLAB的桁架结构优化设计
MatLab与Fortran混合编程实现结构优化和可靠性分析

( auyo osutnE gnen D l nU irt o Tcnl y a a ,L oi 104 hn ) Fcl t fCnt co ni r g, ai n e i eho g ,D l n i n g 162 ,C i r i ei a v syf o i a n a
200 第 第 3 1卷 6月 12年 翅
Ju l f t eore adA cic 珀 oma 0 wa水利与建筑工程学报 e R sIcs n r t 】 r l heu
V 11 o3 o.0N .
J n ., 2 u 20 1
Ma a t b与 F r a L ot n混 合 编 程 实 现 r 结 构 优 化 和 可 靠 性 分 析
sr t uct e ur s.
K e wo d y r s:M a La a u g t b lng a e;Fo ta a g a e;m ii o r m m i g; sr c u a p i ia i n;sr t a ei rr n l n ug x ng pr g a n t u t r lo tm z to tucur lr l-
a ii nay i b l y a l ss t
M ta 化 工 具 箱 针 对 各 种 优 化 问题 给 出 了 aLb优 完整 的解 决方 案 l_ , 内容 涵盖 了包括最 值 问题 、 1 其 l
Fra 有 限元 程序成 功 连 接 ; or tn 然后 在 Ma a t b环 境 下 l
赵 秀 丽 , 平 易
( 大连理工大学 建设工程学部 , 辽宁 大连 162 ) 104
摘 要 : 为有效利用 Ma a t b和现有 F  ̄a 有 限元程 序 , L or n 采用 Ma a 与 Fra 合编程 。通过 Ma a 程 tb L or t tn 昆 tb L 序接 口, Ma a 与 F ̄a 有 限元 程序成功连接实现平 面桁架结 构 的静 力分析 ; 将 tb L or n 然后 在 M ta a ̄ lb环境下 运用优 化工 具箱 和统计工具箱编程实现 了平面桁架 的结 构优 化设 计和可靠指标的计算。 关键词 : a a 语言 ;o r 语 言 ; Mt b L F ̄a n 混合编程 ; 结构优化 ; 构可靠性 分析 结
桁架优化matlab算法

桁架优化matlab算法桁架优化Matlab 算法【引言】桁架是一种常见的结构体系,它由连接节点的杆件构成。
桁架通常在工程设计中用于支撑、加固或分散载荷。
优化桁架结构对于减少材料使用、提高结构强度和降低成本非常重要。
Matlab 是一种功能强大的计算软件,它提供了许多优化算法和工具。
本文将介绍如何使用Matlab 进行桁架优化的算法实现。
【第一步- 建立力学模型】桁架的力学模型是优化过程的基础。
在Matlab 中,可以使用矩阵表示力学模型。
首先,我们需要定义桁架的节点和杆件。
节点用坐标表示,杆件用节点之间的连接关系表示。
根据节点和杆件的定义,可以构建节点坐标矩阵和链接关系矩阵。
【第二步- 约束条件和目标函数】在进行桁架优化时,通常会遇到一些约束条件和目标函数。
典型的约束条件可能包括杆件的最大和最小尺寸限制、节点的最大和最小高度限制等。
目标函数可以是桁架的重量、刚度或模态频率等。
根据具体问题,我们需要定义合适的约束条件和目标函数。
【第三步- 优化算法】Matlab 提供了许多优化算法,如遗传算法、粒子群优化算法等。
我们需要选择合适的算法来解决桁架优化问题。
对于离散变量的优化,可以使用遗传算法。
对于连续变量的优化,可以使用粒子群优化算法。
选择合适的算法后,可以将约束条件和目标函数输入优化算法,得到优化结果。
【第四步- 结果分析】优化算法完成后,我们需要对结果进行分析。
可以通过绘制优化后的桁架结构来比较与原始结构的差异。
此外,还可以从目标函数的值来评估优化结果。
如果目标函数的值较小,则说明优化结果较优。
【第五步- 进一步优化】根据结果的分析,我们可以进一步优化桁架结构。
可以尝试使用不同的约束条件和目标函数,或者尝试其他优化算法。
通过多次迭代优化,逐步优化桁架结构,以得到更好的结果。
【第六步- 结论】通过以上的一步一步的回答,我们可以得出结论,桁架优化的Matlab 算法是一个有效的方法。
通过建立力学模型、定义约束条件和目标函数、选择合适的优化算法,我们可以获得优化后的桁架结构。
桁架杆机构的优化设计

OCCUPATION2013 08108案例CASES桁架杆机构的优化设计文/宋育红摘 要:桁架结构优化设计中普遍存在约束的作用,现有优化设计一般采用满应力法、遗传优化或直接实验法搜索等优化方法,但其时间周期长、优化复杂。
本文主要采用复合形法,建立了桁架结构优化设计的数学模型,利用Fortran优化程序对其进行优化并获得最优解。
关键词:桁架结构 优化设计 复合形法一、优化目标及设计原则1.优化目标在工程力学教学当中,笔者利用复合形法对桁架杆进行优化设计,以求得到其最优解。
桁架杆设计的优化可以选择多种目标,如尺寸最小、质量最轻、强度最高等,一般应根据不同的需要选定。
笔者以桁架杆为例,以其质量最小为优化目标。
2.设计原则在桁架杆设计时我们首先要求两杆同时满足强度条件,其次要满足几何条件约束,进而确定目标函数,并对其优化。
二、复合形法优化设计简述复合形法的基本思路是在n 维空间的可行域中选取K 个设计点(通常取n +1≤K ≤2n )作为初始复合形(多面体)的顶点。
然后比较复合形各顶点目标函数的大小,其中把目标函数值最大的点作为坏点,以坏点之外其余各点的中心为映射中心,寻找坏点的映射点。
一般说来,此映射点的目标函数值总是小于坏点的,也就是说映射点优于坏点。
这时,以映射点替换坏点与原复合形除坏点之外其余各点构成K 个顶点的新的复合形。
如此反复迭代计算,在可行域中不断以目标函数值低的新点代替目标函数值最大的坏点从而构成新复合形,使复合形不断向最优点移动和收缩,直至收缩到复合形的各顶点与其形心非常接近、满足迭代精度要求时为止。
最后输出复合形各顶点中的目标函数值最小的顶点作为近似最优点。
三、建立数学模型1.已知参数如桁架杆的结构,已知l =2m,x B =1m,载荷ρ=100kN桁架材料的密度 ρ=7.5×10-5N/mm 3,许用拉应力[σ+ ]=150MPa,许用压应力[σ- ]=100MPa,y B 的范围为:0.5m≤y B ≤1.5m,求桁架杆在满足强度的条件下,其质量的最小值。
桁架结构优化设计
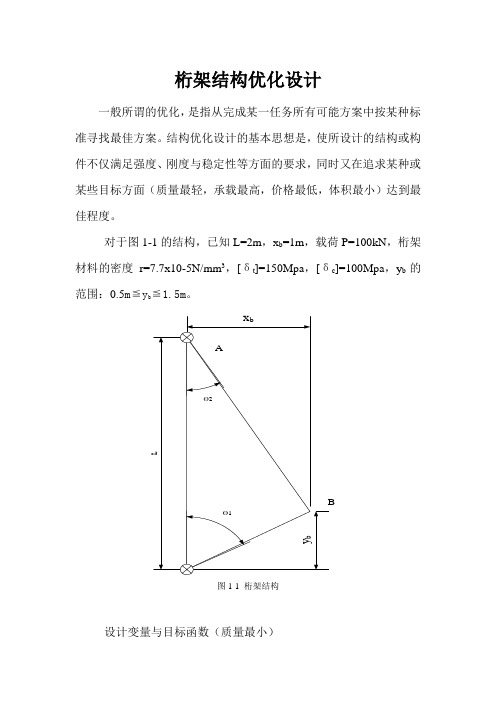
桁架结构优化设计一般所谓的优化,是指从完成某一任务所有可能方案中按某种标准寻找最佳方案。
结构优化设计的基本思想是,使所设计的结构或构件不仅满足强度、刚度与稳定性等方面的要求,同时又在追求某种或某些目标方面(质量最轻,承载最高,价格最低,体积最小)达到最佳程度。
对于图1-1的结构,已知L=2m,x b=1m,载荷P=100kN,桁架材料的密度r=7.7x10-5N/mm3,[δt]=150Mpa,[δc]=100Mpa,y b的范围:0.5m≦y b≦1.5m。
图1-1 桁架结构设计变量与目标函数(质量最小)预定参数(设计中已确定,设计者不能任意修改的量):L , x b ,P ,r ,[δt ] ,[δc ]设计变量(可由设计者调整的量)y b ,A 1,A 2 约束条件(对设计变量的约束条件) (1) 强度条件约束(截面、杆件的强度) (2) 几何条件约束(B 点的高度范围) 目标函数:桁架的质量W (最小)解:1. 应力分析0sin sin 02112=--=∑θθN N F x0cos cos 02112=---=∑P N N Fyθθ由此得:)sin(sin 2111θθθ+=p N )sin(sin 2122θθθ+-=p N由正弦定理得:ly l x pN B B 21)(2-+=ly x pN BB 222+=由此得杆1和2横截面上的正应力121)(2lA y l x pB B -+=σ2222lA y x pB B +=σ2.最轻质量设计目标函数(桁架的质量)))((222122B B y x A y l x A W B B ++-+=γ(1-1)约束条件[][]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤+≤-+c B t B lA y x p lA y l x p B B σσ221222)( (1-2)0.5≦y b ≦1.5(m ) (1-3) (于是问题归结为:在满足上述约束条件下,确定设计变量y b ,A 1,A 2,使目标函数W 最小。
平面桁架结构matlab

桁架结构计算第四章P56******************************************************************************* function y=plane_truss_element_stiffness(E,A,L,theta) %平面桁架单元刚度x=theta*pi/180;C=cos(x);S=sin(x);y=E*A/L*[C*C C*S -C*C -C*S;C*S S*S -C*S -S*S;-C*C -C*S C*C C*S;-C*S -S*S C*S S*S];%平面桁架刚度矩阵*******************************************************************************function y=plane_truss_assemble(K,k,i,j) %平面桁架组装K(2*i-1,2*i-1)=K(2*i-1,2*i-1)+k(1,1);K(2*i-1,2*i)=K(2*i-1,2*i)+k(1,2);K(2*i-1,2*j-1)=K(2*i-1,2*j-1)+k(1,3);K(2*i-1,2*j)=K(2*i-1,2*j)+k(1,4);K(2*i,2*i-1)=K(2*i,2*i-1)+k(2,1);K(2*i,2*i)=K(2*i,2*i)+k(2,2);K(2*i,2*j-1)=K(2*i,2*j-1)+k(2,3);K(2*i,2*j)=K(2*i,2*j)+k(2,4);K(2*j-1,2*i-1)=K(2*j-1,2*i-1)+k(3,1);K(2*j-1,2*i)=K(2*j-1,2*i)+k(3,2);K(2*j-1,2*j-1)=K(2*j-1,2*j-1)+k(3,3);K(2*j-1,2*j)=K(2*j-1,2*j)+k(3,4);K(2*j,2*i-1)=K(2*j,2*i-1)+k(4,1);K(2*j,2*i)=K(2*j,2*i)+k(4,2);K(2*j,2*j-1)=K(2*j,2*j-1)+k(4,3);K(2*j,2*j)=K(2*j,2*j)+k(4,4);y=K;*******************************************************************************function y=plane_truss_element_force(E,A,L,theta,u)%力的表达式x=theta*pi/180;C=cos(x);S=sin(x);y=E*A/L*[-C -S C S]*u;*******************************************************************************function y=plane_truss_element_stress(E,L,theta,u) %应力表达式x=theta*pi/180;C=cos(x);S=sin(x);y=E/L*[-C -S C S]*u;***************************************************************************************************** *****************************************************************************************************clear;clc;E= ;A= ;L1= ;%杆长度L2= ;L3= ;L4= ;%杆长度L5= ;L6= ;L7= ;L8= ;t1= ;%杆角度t2= ;t3= ;t4= ;%杆角度t5= ;t6= ;t7= ;t8= ;k1=plane_truss_element_stiffness(E,A,L1,t1) % 单位刚度矩阵k2=plane_truss_element_stiffness(E,A,L2,t2)k3=plane_truss_element_stiffness(E,A,L3,t3)k4=plane_truss_element_stiffness(E,A,L4,t4);% 单位刚度矩阵k5=plane_truss_element_stiffness(E,A,L5,t5); % 单位刚度矩阵k6=plane_truss_element_stiffness(E,A,L6,t6)k7=plane_truss_element_stiffness(E,A,L7,t7)k8=plane_truss_element_stiffness(E,A,L8,t8) % 单位刚度矩阵K=zeros( );%组装矩阵大小,节点位移个数Q,节点数乘以2K=plane_truss_assemble(K,k1, , ); %刚度矩阵的组装K=plane_truss_assemble(K,k2, , ); %后边为单元连接关系图中杆的指向顺序K=plane_truss_assemble(K,k3, , );K=plane_truss_assemble(K,k4, , );K=plane_truss_assemble(K,k5, , ); %刚度矩阵的组装K=plane_truss_assemble(K,k6, , ); %后边为单元连接关系图中杆的指向顺序K=plane_truss_assemble(K,k7, , );K=plane_truss_assemble(K,k8, , ) %注意( )中的数字参数B=K([ , , , , , , , ,],:) ; %取特定的行5 6 7 8 9 10 11 12k=B(:,[ , , , , , , , ]) %取特定的列5 6 7 8 9 10 11 12%得到k矩阵f=[ ]';u=k\f***************************************************************************** ***************************************************************************** 求得位移列矩阵为:u = [0 0 0 0 0.2133 0.4083 -0.1600 0.4617 0.4267 1.5008 -0.0533 1.6608]’;以下为求各个杆的应力大小:u1=[u( );u( );u( );u( )];%后边为单元连接关系图中杆的指向顺序sigma1=plane_truss_element_stress(E,L1,t1,u1) %element stress,u1是Q列向量u2=[u( );u( );u( );u( )];sigma2=plane_truss_element_stress(E,L2,t2,u2)u3=[u( );u( );u( );u( )];sigma3=plane_truss_element_stress(E,L3,t3,u3) %element stress,u1是Q列向量u4=[u( );u( );u( );u( )];sigma4=plane_truss_element_stress(E,L4,t4,u4)u5=[u( );u( );u( );u( )];sigma5=plane_truss_element_stress(E,L5,t5,u5) %element stress,u1是Q列向量u6=[u( );u( );u( );u( )];sigma6=plane_truss_element_stress(E,L6,t6,u6)u7=[u( );u( );u( );u( )];sigma7=plane_truss_element_stress(E,L7,t7,u7) %element stress,u1是Q列向量u8=[u( );u( );u( );u( )];sigma8=plane_truss_element_stress(E,L8,t8,u8)*******************************************************************************R=K*u; %求得支反力,从中选取支反力处的值R=[R( );R( );R( );R( )] %填入位置坐标。
桁架结构及有限元分析MATLAB

桁架结构及有限元分析MATLAB桁架结构是一种由杆件和节点连接而成的结构系统。
它的主要特点是具有良好的刚性和承载能力,适用于跨度较大的建筑物或桥梁。
桁架结构的设计和分析是工程领域中重要的课题。
有限元分析是一种常用的方法,用于对桁架结构进行力学和结构分析。
MATLAB是一种强大的数学建模和计算工具,可以方便地进行有限元分析。
在进行桁架结构的有限元分析之前,首先需要进行结构的建模。
可以使用MATLAB中的节点和杆件来建立桁架结构的几何模型。
节点代表结构中的连接点,杆件代表连接节点的杆件。
接下来,需要将结构分割为有限元网格。
在MATLAB中,可以使用二维和三维有限元网格生成函数来生成网格。
生成的网格可以根据需要的精度进行调整。
每个有限元包含一个或多个节点和杆件,用于描述局部的力学行为。
在有限元分析中,需要考虑材料的力学性质。
可以通过定义材料的模量、泊松比和密度等参数来描述材料的本构关系。
在MATLAB中,可以使用材料库函数来定义不同材料的力学性质。
进行有限元分析时,需要考虑结构的边界条件和加载条件。
边界条件包括固定边界和位移约束,加载条件可以是力、压力或扭矩等。
在MATLAB中,可以使用边界条件函数来定义结构的边界条件和加载条件。
在有限元分析的过程中,需要对结构进行求解。
可以使用线性或非线性求解算法来计算结构的位移和应力等。
MATLAB中提供了多种求解器和求解方法,可以根据需要选择适合的求解算法。
完成有限元分析后,可以进行结果的后处理。
可以使用MATLAB中的可视化工具来绘制结构的位移和应力云图,以及显示结构的反应力和形变等。
可以通过对结果进行分析和比较,评估结构的可靠性和安全性。
总之,使用MATLAB进行桁架结构的有限元分析可以帮助工程师深入了解结构的力学行为和性能。
它可以为结构的设计和优化提供依据,并帮助工程师制定提高结构性能的策略。
同时,MATLAB提供了丰富的功能和工具,使得桁架结构的分析和设计更加高效和准确。
有限元方法与MATLAB程序设计 第3章 桁架和刚架

Fe keUe
Ue TUe
结构坐标系下的 单元刚度方程
9
结构坐标系下单元刚度矩阵 ke T TkeT
c cos s sin
y
Fe keUe
y
i (xi , yi )
(xj, yj ) x j
x
结构坐标系
cos sin 0
0 1 0 1 0 e cos sin 0
0
ke
EA sin
Fyi
Fxj Fyj
EA l
0
1
0
0 0 0
0 1 0
0
vi
0 0
u v
j j
单元坐标系下的 1 0 1 0
单元刚度矩阵
ke
EA l
0
1
0 0
0 1
0 0
0
0
0
0
7
§3.1.3 整体坐标系下的单元刚度方程
Fxi Fxi cos Fyi sin Fyi Fxi sin Fyi cos Fxj Fxj cos Fyj sin
是结构坐标系x轴正方 向至单元坐标轴x 的角度
y
x
y Fxi i
Fxi Fyi Fyi
x
结构(整体)坐标系
Fyj Fxj sin Fyj cos
Fxi Fyi
Fxj
Fyj
e
cos
sin
0
0
sin cos
0 0
0 0
cos sin
0
e
Fxi
e0Fyi源自sin cosFxj
Fyj
Fe TFe Ue TUe
cos
T sin
0
0
sin cos
基于MATLAB的空间桁架梁的内力分析计算

基于MATLAB的空间桁架梁的内力分析计算韩刚;樊涛;卜培培【摘要】针对空间桁架梁杆件多、载荷工况复杂、计算量大、内力图多等特点,运用节点法总结并归纳出桁架梁的各个杆件的内力计算递推公式,并用MATLAB软件进行了仿真计算。
该方法是根据推导出的计算公式,运用数学变换来建立空间桁架梁数学模型,确定变量之间的函数关系,分步编制弦杆和腹杆的内力计算程序仿真输出数据和图形。
通过仿真得到桁架梁的各杆件在不同的载荷组合工况下的受力情况,找出在最不利工况下的受力杆件,为结构的轻量化研究提供理论基础。
%For the characteristics of the space truss beam such as many bars,complex load cases,large amounts of calculation,internal force diagram,the node method was used to summarize and deduce a recursive formula which was used for calculating each internal force of the truss rod,and its simulation calculation could be conducted with software MATLAB.According to the calculation formula deduced,this method uses mathematical transformation to build a space truss beam mathematical model,to determine the functional relationship between variables,and then to simulate output data and graphics through outputting the internal force calculation program of the chords and web members step-by-step.The stress state of the truss rod under different load combinations conditions can be obtained through the simulation results,and the force-bearing rod under the most unfavorable conditions was found out to provide a theoretical foundation for structural lightweight research.【期刊名称】《太原科技大学学报》【年(卷),期】2012(033)002【总页数】5页(P132-136)【关键词】桁架梁;数学模型;结构分析;受力计算;MATLAB仿真【作者】韩刚;樊涛;卜培培【作者单位】太原科技大学机械工程学院,太原030024;太原科技大学机械工程学院,太原030024;太原科技大学机械工程学院,太原030024【正文语种】中文【中图分类】TH222桁架梁的杆件由型钢和钢板组成,截面一般有槽形、工字形和箱形,常用铆接或焊接成型,主要承受轴向力。
桁架优化
桁架优化设计
*********
1.参数设置
给设计变量A1、A2、A3、B赋上一个初始值。
2.前处理
单元类型为杆单元
其值分别为A1、A2、A3)
2.3设置材料(弹性模量、泊松比、密度)
2.4.1创建节点
首先给各杆单元分配横截面积,然后连接节点创建单元,依次建立起三个单元。
2.5施加载荷
2.5.1施加位移载荷
2.5.2施加集中力载荷
3.求解
4.通用后处理4.1定义单元表格
将体积列表显示
对体积求和
取得结果数据(体积和)
将轴向应力列入表格
取得结果数据(三个杆单元的轴向应力zyl1、zyl2、zyl3)
将轴向应力值取正直
定义质量wt=7800*vall
创建一个优化的循环文件
命名
将优化循环分配到刚建好的lgw文件
定义设计变量的变化范围
定义状态变量的变化范围
定义目标函数
选择优化方法
运行
优化设计结果显示
以图表的形式显示优化过程
更改x 、y 轴的显示
结束。
桁架结构MATLAB编程

桁架结构% 变量说明% NPOIN NELEM NVFIX NFPOIN NFPRES% 总结点数,单元数, 约束个数, 受力结点数, 非结点力数% COORD LNODS YOUNG% 结构节点坐标数组, 单元定义数组, 弹性模量% FPOIN FPRES FORCE FIXED% 结点力数组,非结点力数组,总体荷载向量, 约束信息数组% HK DISP% 总体刚度矩阵,结点位移向量%**************************************************format short e%设定输出类型clear %清除内存变量FP1=fopen('6-6.txt','rt'); %打开初始数据文件%读入控制数据NELEM=fscanf(FP1,'%d',1); %单元数NPOIN=fscanf(FP1,'%d',1); %结点数NVFIX=fscanf(FP1,'%d',1); %约束数NFPOIN=fscanf(FP1,'%d',1); %结点荷载数NFPRES=fscanf(FP1,'%d',1); %非结点荷载数YOUNG=fscanf(FP1,'%f',1); %弹性模量% 读取结构信息LNODS=fscanf(FP1,'%f',[4,NELEM])'% 单元定义:左、右结点号,面积,惯性矩(共计 NELEM组)COORD=fscanf(FP1,'%f',[2,NPOIN])'% 坐标: x,y坐标(共计 NPOIN 组)FPOIN=fscanf(FP1,'%f',[3,NFPOIN])'% 节点力(共计 NFPOIN 组):结点号、X方向力(向右正),% Y方向力(向上正),FPRES=fscanf(FP1,'%f',[4,NFPRES])' % 均布力(共计% NFPRES 组):单元号、荷载类型、荷载大小、距离左端长度FIXED=fscanf(FP1,'%f',NVFIX)'% 约束信息:约束对应的位移编码(共计 NVFIX 组)%---------------------------------------------------------HK=zeros(2*NPOIN,2*NPOIN); % 张成总刚矩阵并清零FORCE=zeros(2*NPOIN,1); % 张成总荷载向量并清零%形成总刚for i=1:NELEM % 对单元个数循环% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵EKT=T'*EK*T; % 生成整体单刚(整体坐标系)% 组成总刚按2*2子块加入总刚中(共计4块)for j=1:2 %对行进行循环---按结点号循环N1=LNODS(i,j)*2; % j结点第2个位移的整体编码for k=1:2 %对列进行循环---按结点号循环N2=LNODS(i,k)*2; % k结点第2个位移的整体编码HK((N1-1):N1,(N2-1):N2)=HK((N1-1):N1,(N2-1):N2)...+EKT(j*2-1:j*2,k*2-1:k*2);endendend% 由结点力与非结点力生成总荷载向量列阵for i=1:NFPOIN % 对结点荷载个数进行循环N1=FPOIN(i,1); % 作用荷载的结点号N1=N1*2-2; % 该结点号对应第一个位移编码 - 1for j=1:2FORCE(N1+j)=FORCE(N1+j)+FPOIN(i,j+1);%取结点荷载endend% 计算由非结点荷载引起的等效结点荷载for i=1:NFPRES % 对非结点荷载个数进行循环F0=ele_FPRES(i,FPRES,LNODS,COORD); %计算单元固端力% 对单元局部杆端力要进行坐标转换T=zbzh(i,LNODS,COORD); % 坐标转换矩阵F0=T'*F0;ele=FPRES(i,1); % 取荷载所在的单元号NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号% 将单元固端力变成等效结点荷载(注意固端力与等效结点荷载符号相反)FORCE((3*NL-2):3*NL)=FORCE((3*NL-2):3*NL)-F0(1:3);FORCE((3*NR-2):3*NR)=FORCE((3*NR-2):3*NR)-F0(4:6);end% 总刚、总荷载进行边界条件处理for j=1:NVFIX % 对约束个数进行循环N1=FIXED(j);HK(1:2*NPOIN,N1)=0; HK(N1,1:2*NPOIN)=0; HK(N1,N1)=1;% 将零位移约束对应的行、列变成零,主元变成1FORCE(N1)=0;end%---------------------------------------------------------DISP=HK\FORCE % 方程求解,HK先求逆再与力向量左乘%---------------------------------------------------------% 求结构各个单元内力EDISP=zeros(4,1); % 单元位移列向量清零for i=1:NELEM % 对单元个数进行循环for j=1:2 %对杆端循环% i单元左右端结点号*2 = 该结点的最后一个位移编码N1=LNODS(i,j)*2;% 取一端的单元位移列向量EDISP(2*j-1:2*j)=DISP(N1-1:N1);end% 生成局部单刚(局部坐标) 右手坐标系EK=ele_EK(i,LNODS,COORD,YOUNG);T=zbzh(i,LNODS,COORD); % 坐标转换矩阵FE=EK*T*EDISP; %计算局部坐标杆端力(由结点位移产生)for j=1:NFPRESif FPRES(j,1) == i %成立时,当前单元上有非结点荷载F0=ele_FPRES(j,FPRES,LNODS,COORD);%单元固端力FE=FE+F0; % 考虑由非结点荷载引起的杆端力endendFE % 打印杆端力end%-------------------------------------------------------------------------------- % 计算桁架单元刚度矩阵函数 EK% 入口参数:单元号、单元信息数组、结点坐标、弹性模量% 出口参数:局部桁架单元刚度矩阵EKfunction EK=ele_EK(i,LNODS,COORD,YOUNG)NL=LNODS(i,1); NR=LNODS(i,2); %左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度A=LNODS(i,3); %面积;E=YOUNG;% 生成单刚(局部坐标) 右手坐标系EK =[E*A/L 0 -E*A/L 0 ;...0 0 0 0 ;...-E*A/L 0 E*A/L 0 ;...0 0 0 0 ];return%---------------------------------------------------------------------------------%计算单元固端力函数(正方向:X向右 Y向上 M逆时针)% 入口参数:荷载序号,荷载信息,单元信息,结点坐标% 出口参数:单元固端力——左右两端的轴力、剪力、弯矩function F0=ele_FPRES(iFPRES,FPRES,LNODS,COORD)ele=FPRES(iFPRES,1); %取荷载所在的单元号G=FPRES(iFPRES,3); %单元荷载大小C=FPRES(iFPRES,4); %单元荷载与左端距离NL=LNODS(ele,1); NR=LNODS(ele,2); %单元的左右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); %单元长度% 计算公式中一些常出现的项D=L-C; C1=C/L; C2=C1*C1; C3=C1*C2;B1=D/L; B2=B1/L;F0=[0;0;0;0;0;0]; %单元固端力清零switch FPRES(iFPRES,2)case 1 %均布荷载F0(2)=-G*C*(2-2*C2+C3)/2.0;F0(3)=-G*C*C*(6-8*C1+3*C2)/12.0;F0(5)=-G*C-F0(2);F0(6)=G*C*C*C1*(4-3*C1)/12.0;case 2 %横向集中力F0(2)=-G*B1*B2*(L+2*C);F0(3)=-G*C*B1*B1;F0(5)=-G*C2*(L+2*D)/L;F0(6)=G*D*C2;case 3 %纵向集中力F0(1)=-G*B1;F0(4)=-G*C1;endreturn%-------------------------------------------------------------------------------- % 形成第i单元的坐标转换矩阵函数 T(4,4)% 入口参数:单元号,单元信息,结点坐标% 出口参数:坐标转换矩阵(整体向局部投影)function T=zbzh(i,LNODS,COORD)NL=LNODS(i,1); %左结点号NR=LNODS(i,2); %右结点号dx=COORD(NR,1)-COORD(NL,1); % x 坐标差dy=COORD(NR,2)-COORD(NL,2); % y 坐标差L=sqrt(dx^2+dy^2); % 单元长度c=dx/L; % cos a (与 x 轴夹角余弦) s=dy/L; % sin aT=[ c s 0 0;...-s c 0 0;...0 0 c s0 0 -s c ];return6-6.txt文件数据:4 45 2 0 2.95e111 2 0.001 13 2 0.001 11 3 0.001 14 3 0.001 10 00.4 00.4 0.30 0.32 2e4 03 0 -2.5e41 2 4 7 8。
桁架优化matlab算法 -回复

桁架优化matlab算法-回复【桁架优化matlab算法】一步一步解析【引言】在工程设计中,桁架结构是一种常见的结构形式,具有轻量、高强度和刚度等优势。
然而,在实际应用中,如何对桁架结构进行优化设计仍然是一个挑战。
近年来,随着计算机技术的快速发展,使用计算机辅助设计工具如MATLAB 对桁架结构进行优化已经成为一种非常有效的途径。
本文将介绍一种基于MATLAB 的桁架优化算法,并一步一步解析其实现过程。
【主体】一、问题定义在进行桁架优化设计之前,首先需要明确问题的定义和目标。
例如,在设计一种承重桁架结构时,可能会面临以下问题:给定一组约束条件,如承重要求、材料限制等,如何确定桁架结构的杆件尺寸、形状以及连接方式等,使得其重量最小、刚度最大并满足所有约束条件?二、建立数学模型为了能够用数学方法进行桁架优化设计,首先需要建立桁架的数学模型。
通常采用力法进行计算,即将桁架结构转化为节点和杆件组成的力学系统。
在MATLAB 中,可以采用矩阵运算和方程求解的方法,建立桁架结构的总刚度矩阵和载荷向量。
三、确定优化算法在确定桁架的数学模型后,接下来需要选择适用的优化算法。
常用的优化算法有遗传算法、模拟退火算法等。
这些算法能够在解空间中搜索最优解,并在每一次迭代中更新设计变量。
在MATLAB 中,可以使用内置的优化工具箱或自定义函数来实现优化算法。
四、设计变量和约束条件在桁架优化设计中,设计变量通常包括杆件的尺寸、截面形状以及连接方式等。
约束条件可以是杆件的强度、刚度要求,总重量的限制等。
在MATLAB 中,可以使用向量或矩阵的方式来表示设计变量和约束条件,并在优化算法中进行限制。
五、编写MATLAB 代码根据桁架优化的数学模型、选择的优化算法和设计变量、约束条件,可以编写相应的MATLAB 代码。
首先,需要编写函数来计算桁架结构的总刚度矩阵和载荷向量。
其次,编写优化算法代码,包括初始化设计变量、设置优化参数和约束条件、迭代搜索等。
桁架结构遗传算法优化设计与安全性评判综述

遗传 算法 模拟 生 物适 者生存 、优 胜劣汰 的基本进化 原则,即在 所有可 能的解 中不断进 化得 到最适 合生 存的解,即最优解。 自然界, 各个个体对 环境 有不同的适应能力,较差个体 将被淘汰 ,优秀个 体的基因将遗传给后代。在
A X X X 4
1/2 3 21 t 1 3l
l l 1 2 l 1/3 1,2 1
(1)
通 过 式 (1)计 算 该 矩 阵 的最 大 特 征 值
特殊 的情况 下,基因产生有利突变,使群体朝 = 3.0092及特征 向量 ,然后得 归一化后的各
着更优方 向进化。此算法中,各个个体的染色 因素权向量为 w,
体 用二进 制串表述,通过遗传操作改善结构 , 使 目标函数值较优 。
c尺 : :0.0080< 0.1 JR,
其 中 :
有并行搜索特性 ,可大大减少 陷入局部最小 的
CR一 检 验 系数
可 能 。
cI一 一 次 性 指 标
随着科 技 的发 展,桥 梁结 构 要求越 来越
ANSYS软件 提供 了常用 的优化 算法 ,零
RI一 随 机 一 次 性 指 标
W=f0.242 0.449 0.128 O.195}
其中共有 4个影响因素 ,所 以 n=4,得
键词 】桁 架 遗传算 法 有限元 优化设计 目评 判
遗 传 算法优 点 是将变 量编 码成 二进 制 串 进行优化 ,不受约束条件 的限制 ;搜索过程从 问题解的一个集合开始 ,而不是单个个体 ,具
计算机技术应用 ·the Application of Computer Technology
桁架结构遗传算法优化设计 与安全性 评判综述
MATLAB在建筑工程与结构分析中的应用实践

MATLAB在建筑工程与结构分析中的应用实践一、引言MATLAB(Matrix Laboratory)是一种高级的技术计算软件,被广泛应用于工程和科学领域。
在建筑工程与结构分析领域,MATLAB不仅可以提供强大的数学计算和数据处理能力,还可以帮助工程师快速设计、分析和优化建筑结构。
本文将探讨MATLAB在建筑工程与结构分析中的应用实践,包括结构优化、地震响应分析以及结构设计等方面。
二、结构优化结构优化是建筑工程中的一个重要环节,通过改变结构参数和材料性能,以最大限度地满足设计要求。
MATLAB提供了多种数学优化算法,如遗传算法、模拟退火算法和粒子群算法等,可以对结构参数进行优化设计。
例如,对于悬臂梁的设计,可以通过编写MATLAB代码,定义设计变量、目标函数和约束条件,然后使用遗传算法对梁的跨度、截面尺寸进行优化。
通过不断调整参数,可以得到最优的结构方案。
三、地震响应分析地震是建筑结构的主要灾害载荷之一,了解结构在地震作用下的动态响应是十分重要的。
MATLAB提供了强大的信号处理和数值计算工具,可以用于地震响应分析。
例如,可以利用MATLAB中的频域分析工具来计算结构在地震中的加速度响应谱。
通过调整地震波的频率和振幅,可以预测结构的动态响应情况,为地震设计和防护提供科学依据。
四、结构设计MATLAB还可以用于建筑结构的设计和优化。
例如,在混凝土结构设计中,可以利用MATLAB编写代码,自动计算混凝土材料的强度和变形等性能,并根据结构的受力情况,自动生成合理的截面尺寸。
此外,还可以利用MATLAB进行钢结构的设计和优化。
通过定义设计变量、约束条件和目标函数,可以生成满足强度和刚度要求的钢结构方案。
MATLAB的优势在于,工程师可以自定义计算模块,灵活地进行结构设计。
五、实例应用为了更好地理解MATLAB在建筑工程与结构分析中的应用实践,下面将分享一个实例应用。
假设有一个跨度为30m的钢桁架桥需要进行设计优化。
基于Lingo和Matlab的空间桁架结构联合优化设计

22
23 24 25
1.334e-3 同前 同前 同前
对于以上算例,文献[5]采用自适应遗传算法进行离散 变量优化设计得到的结构重量为 268.237kg,这表明本文 方法得到的结果与其基本一致,且本文得到的优化结构比 初始结构大约减重 57%。
5 结论 本文通过对位移和应力约束下空间桁架结构尺寸优 化问题的求解,表明了基于 Lingo 和 Matlab 的联合求解 策略是有效的,而且方法实施简单、便利,很适合工程实 际中桁架结构尺寸优化问题的求解以及优化技术的推广 应用。
参考文献: [1]罗佑新,杨立军.基于全局优化设计的桁架结构优化设计 研究[J].空间结构,2009,15(2):65-67. [2]Y.W. Kwon, H.Bang. The finite element method using Matlab [M]. CRC Press, 1996. [3]隋允康,李善坡.结构优化中的建模方法概述[J].力学进展, 2008,38(2):190-200. [4]徐浩.基于 LINGO10 的单级圆柱齿轮减速器优化设计[J]. 装备制造技术,2008,(7):59-60. [5]李娜,祝晓燕.自适应遗传算法在桁架截面优化设计中的 应用[J].煤矿机械,2005,(11):28-30.
2010(2).
Value Engineering
· 107 ·
通过显式近似把位移约束表示成设计变量的近似显
函数,可以大幅度的提高优化设计求解的效率[3],因此利用
Σ 如下的近似公式对位移约束进行转化:ujl= i
n =
1
j
Nil Nil li Ei xi
(4)
上式中各符号表示的含义可参考相关文献。
优化设计问题数学模型的各个要素表示成矩阵、向量或者
桁架结构的有限元分析MATLAB

桁架结构的有限元分析MATLAB桁架结构是一种由直杆或斜杆连接而成的稳定结构,在工程应用中较为常见。
有限元分析(Finite Element Analysis,FEA)是一种利用数值方法解决结构力学问题的工具。
本文将介绍如何使用MATLAB进行桁架结构的有限元分析,并对其进行1200字以上的详细描述。
在进行桁架结构有限元分析前,需要先进行结构建模以及材料属性和加载条件的定义。
这些定义可以通过MATLAB命令行或者编写MATLAB脚本文件实现。
首先,我们需要定义桁架结构的节点和单元。
节点用于表示桁架结构的连接点,单元用于表示相邻节点之间的连接关系。
可以使用MATLAB中的矩阵表示节点和单元,如下所示:nodes = [x1, y1; x2, y2; ...; xn, yn];elements = [n1, n2; n3, n4; ...; nm, np];```其中,`nodes`是一个n行2列的矩阵,表示n个节点的坐标;`elements`是一个m行2列的矩阵,表示m个单元的节点连接关系。
接下来,我们需要定义材料属性和加载条件。
材料属性包括杨氏模量和截面面积等参数,加载条件包括节点的约束和外部加载。
可以使用MATLAB中的矩阵或者结构体表示材料属性和加载条件,如下所示:materials = struct('E', E1, 'A', A1; 'E', E2, 'A', A2; ...);constraints = [n1, d1x, d1y; ...; nm, dmx, dmy];loads = [n1, F1x, F1y; ...; nl, Flx, Fly];```其中,`materials`是一个结构体数组,每个结构体包含材料的杨氏模量(E)和截面面积(A);`constraints`是一个m行3列的矩阵,表示m个节点的约束,其中d1x和d1y分别表示节点的x方向和y方向位移约束;`loads`是一个l行3列的矩阵,表示l个节点的外部加载,其中F1x和F1y分别表示节点的x方向和y方向外部力。
基于MATLAB及参数化建模的起重机桁架式臂架结构优化设计

基于MATLAB 及参数化建模的起重机桁架式臂架结构优化设计张欢 徐长生(武汉理工大学物流工程学院 武汉 430063)摘要:本文针对起重机桁架式臂架结构设计计算,运用MATLAB 优化工具箱,分别采用了遗传算法和fmincon 优化函数对其结构的目标函数和约束条件进行优化处理,研究了结构的强度、刚度、总体稳定性、局部稳定性等静态特性,并对优化后的结果与优化之前的数值进行对比分析,并通过在ANSYS 中利用APDL 语言参数化建模直观地观察出两者之间的差别以及这种优化设计的优越性。
论文成果对起重机臂架的设计、制造具有较好的理论指导意义和实际应用价值。
关键字: MA TLAB ;遗传算法;桁架式臂架;优化设计;参数化 中图法分类号:TB1150 前言由于大型起重机桁架式臂架的弦杆一般采用费用较高的高强度钢管,故针对减少臂架自重的优化设计的重要性十分明显。
随着优化技术在机械设计上的深入研究,越来越多的优化方法被开发出来。
而在起重机桁架式臂架的优化问题中,由于设计变量多、优化约束条件复杂并且为非线性状态,使得优化的难度有所增加。
针对这种典型的非线性规划问题,本文采用了MA TLAB 优化工具箱中的遗传算法工具箱及fmincon 优化函数,以便能高效地求解出全局的最优解。
在得出优化后的设计变量后,将变量赋给用APDL 语言编写好的ANSYS 臂架模型文件,进行计算后能直接观察出应力分布情况以验证优化的正确性。
本文以300t-48m 船用甲板起重机的桁架式臂架为实例研究对象,通过以上优化方法和参数化建模,确定最优解,对快速确定设计方案以及降低制造成本有一定指导意义。
1起重机桁架式臂架结构优化设计数学模型1.1臂架优化数学模型的设计变量针对桁架式的单臂架,为了有效地表达整个桁架系统的几何要素,采用如表1的7个设计变量:()2211,,,,,,d D t d D B A X =表1 臂架结构设计变量及说明变量 说明 设 计 变 量A (mm ) 臂架高度B (mm )臂架宽度D 1 (mm ) 主弦杆外径 d 1 (mm ) 主弦杆内径 t (mm ) 腹杆节间距 D 2(mm ) 腹杆外径 d 2 (mm )腹杆内径变量所指代的各几何要素具体位置以及臂架外观可见图1、图2。
matlab中关于桁架问题的程序

clear; %清除内存变量ss1=input('give a data filename:','s');fp1=fopen(ss1,'r');ss2=input('give a result filename:','s');fp2=fopen(ss2,'w');%1.读入结构数据、建立累积约束表向量、建立结构刚度矩阵%1.1.结构参数和弹性模量[m,c]=fscanf(fp1,'%u',[1]); %杆件数[nj,c]=fscanf(fp1,'%u',[1]); %节点数[nrj,c]=fscanf(fp1,'%u',[1]); %约束节点[e,c]=fscanf(fp1,'%e',[1]); %弹性模量fprintf(fp2,'(1)结构参数和弹性模量\n');fprintf(fp2,'杆件数节点数约束节点数弹性模量\n');fprintf(fp2,'%3u %8u %8u %13.3e\n',m,nj,nrj,e);fprintf(fp2,'\n');%1.2. 节点坐标pc(1:2,1:nj)=0for jx=1:nj[k,c]=fscanf(fp1,'%u',[1]); %节点号[pc(:,k),c]=fscanf(fp1,'%f',[2]); %x坐标、y坐标endfprintf(fp2,'(2)节点坐标\n');fprintf(fp2,'节点号x坐标y坐标\n');fprintf(fp2,'%3u %13.3e %13.3e\n',[1:nj;pc(:,1:nj)]);fprintf(fp2,'\n');%1.3.杆件标号与截面特性jj(1:m)=0; jk(1:m)=0; ax(1:m)=0; iz(1:m)=0;for imx=1:m[k,c]=fscanf(fp1,'%u',[1]); %杆件号[jj(k),c]=fscanf(fp1,'%u',[1]); %j端点号[jk(k),c]=fscanf(fp1,'%u',[1]); %k端点号[ax(k),c]=fscanf(fp1,'%f',[1]); %截面积[iz(k),c]=fscanf(fp1,'%f\n',[1]); %杆件号endfprintf(fp2,'(3)杆件标号与截面特性\n');fprintf(fp2,'杆件号j端点号k端点号截面积截面惯性矩\n');fprintf(fp2,'%3u %8u%8u %13.3e%13.3e\n',[1:m;jj(1:m);jk(1:m);ax(1:m);iz(1:m)]); fprintf(fp2,'\n');%1.4.di和dj取值di(1:m)=0; dj(1:m)=0;for imx=1:m[k1(imx),c]=fscanf(fp1,'%u',[1]);[di(k1(imx)),c]=fscanf(fp1,'%f',[1]);[dj(k1(imx)),c]=fscanf(fp1,'%f',[1]);endfprintf(fp2,'(4)杆件标号与两端刚域\n');fprintf(fp2,'杆件号j端刚域k端刚域\n');fprintf(fp2,'%3u %13.3e %13.3e\n',[1:m;di(1:m);dj(1:m)]);fprintf(fp2,'\n');%1.5.节点约束情况fprintf(fp2,'(5)节点约束情况\n');fprintf(fp2,'受约束点号x向约束情况y向约束情况z约束情况\n');rl(1:3*nj)=0;for jx=1:nrj[k,c]=fscanf(fp1,'%u',[1]); %受约束节点号[rl(3*k-2:3*k),c]=fscanf(fp1,'%f',[3]); %x向约束情况y向约束情况z约束情况fprintf(fp2,'%5u %12u%12u%12u\n',k,rl(3*k-2:3*k));endfprintf(fp2,'\n');%1.6.建立累积约束表向量crl(1:3*nj)=0;[n,nr,crl]=Cu(3*nj,rl);fprintf(fp2,'(5)非约束位移数约束位移数\n');fprintf(fp2,'%10u %10u\n',n,nr);fprintf(fp2,'\n');H(1:6,1:6)=0;%1.7. 装配总节点刚度矩阵sj(1:3*nj,1:3*nj)=0;for imx=1:mH(1:6,1:6)=[1 0 0 0 0 0;0 1 di(k1(imx)) 0 0 0;0 0 1 0 0 0;0 0 0 1 0 0;0 0 0 0 1 -dj(k1(imx));0 0 0 0 0 1];sm=Psm(pc(:,jj(imx)),pc(:,jk(imx)),ax(imx),iz(imx),e);sm2=H(1:6,1:6)'*sm*H(1:6,1:6);RT=PRT(pc(:,jj(imx)),pc(:,jk(imx)));smd=RT'*sm2*RT;j=[3*jj(imx)-2:3*jj(imx),3*jk(imx)-2:3*jk(imx)]; %计算杆端位移对应的总节点位移标号sj(j(1:6),j(1:6))= sj(j(1:6),j(1:6))+smd(1:6,1:6);end%1.8. 对应非约束位移、约束位移、将总节点刚度矩阵sj重新排列s(crl(1:3*nj),crl(1:3*nj))=sj(1:3*nj,1:3*nj);%2. 读入荷载数据、构建约束杆端力、构建综合节点荷载%2.1. 读入荷载节点数、集中荷载杆件数、分布荷载杆件数[nlj,c]=fscanf(fp1,'%u',[1]); %荷载节点数[nla,c]=fscanf(fp1,'%u',[1]); %集中荷载杆件数[nlq,c]=fscanf(fp1,'%u',[1]); %分布荷载杆件数fprintf(fp2,'(7)荷载节点数集中荷载杆件数分布荷载杆件数\n');fprintf(fp2,'%10u %10u %10u\n',nlj,nla,nlq);fprintf(fp2,'\n');%2.2. 节点荷载fprintf(fp2,'(8)节点荷载\n');fprintf(fp2,'节点号x向线力y向线力z向力偶\n');ac(1:3*nj,1:1)=0;for jx=1:nlj[k,c]=fscanf(fp1,'%u',[1]); %受荷载节点号[aj,c]=fscanf(fp1,'%f',[3]); %x向线力y向线力z向力偶fprintf(fp2,'%3u %13.3e%13.3e%13.3e\n',k,aj);ac(3*k-2:3*k)=ac(3*k-2:3*k)+aj(1:3);endfprintf(fp2,'\n');%2.3.杆件上集中荷载fprintf(fp2,'(9)杆件上集中荷载\n');fprintf(fp2,'杆件号x向线力y向线力z向力偶作用点距杆j端距离\n');aml(1:6,1:m)=0;for imx=1:nla[ia,c]=fscanf(fp1,'%u',[1]); %杆件号[as,c]=fscanf(fp1,'%f',[3]); %x向线力y向线力z向力偶[xa,c]=fscanf(fp1,'%f',[1]); %集中荷载杆端距fprintf(fp2,'%3u %13.3e%13.3e%13.3e%13.3e\n',ia,as,xa);amx=PamlC(pc(:,jj(ia)),pc(:,jk(ia)),as,di(k1(imx)),dj(k1(imx)),xa);aml(:,ia)=aml(:,ia)+amx(:); %累加约束杆端力endfprintf(fp2,'\n');%2.4.杆件上分布荷载fprintf(fp2,'(10)杆件上分布荷载\n');fprintf(fp2,'杆件号起点x向集度终点x向集度起点y向集度终点y向集度起点距j端距离终点距j端距离\n');for imx=1:nlq[iq,c]=fscanf(fp1,'%u',[1]); %杆件号[q,c]=fscanf(fp1,'%f',[4]); %起点x向集度终点x向集度起点y向集度终点y向集度[xq,c]=fscanf(fp1,'%f',[2]); %起点距j端距离终点距j端距离fprintf(fp2,'%3u %14.3e%14.3e%14.3e%14.3e%14.3e\n',iq,q,xq);amx=PamlD(pc(:,jj(iq)),pc(:,jk(iq)),q,xq);aml(:,iq)=aml(:,iq)+amx(:); %累加约束杆端力endfprintf(fp2,'\n');fclose(fp1); %关闭输入数据文件fprintf(fp2,'(111)约束杆端力\n');fprintf(fp2,'杆件号j/k端号xm向线约束力ym向线约束力zm向约束弯矩\n');fprintf(fp2,'%3u %6u %14.3e%14.3e%14.3e\n %6u %14.3e%14.3e%14.3e\n',[1:m;jj(1:m);aml( 1:3,1:m);jk(1:m);aml(4:6,1:m)]);fprintf(fp2,'\n');%2.5.计算等效节点荷载,累加到综合节点荷载中for im=1:mRT=PRT(pc(:,jj(im)),pc(:,jk(im)));j=[3*jj(im)-2:3*jj(im) 3*jk(im)-2:3*jk(im)];ac(j(1:6))=ac(j(1:6))-RT'*aml(1:6,im);endfprintf(fp2,'(12)综合节点荷载\n');fprintf(fp2,'节点号x向线力y向线力z向力偶\n');for ja=1:njfprintf(fp2,'%3u %13.3e%13.3e%13.3e\n',ja,ac(3*ja-2:3*ja));endfprintf(fp2,'\n');%2.6.对应非约束位移、约束位移,将综合节点荷载ac重新排列ac(crl(1:3*nj))=ac(1:3*nj);%3.计算非约束位移、支座反力,并构建总节点位移向量[d,r]=St(n,nr,s,ac,crl);fprintf(fp2,'(13)节点位移与支座反力\n');fprintf(fp2,'节点号x向线位移y向线位移z向角位移x向支座反力y向支座反力z向支座反力矩\n');for je=1:njfprintf(fp2,'%3u %13.3e%13.3e%13.3e%13.3e%13.3e%13.3e\n',je,d(3*je-2:3*je),r(3*je-2:3*je)); endfprintf(fp2,'\n');%4.计算最终杆端力for im=1:mRT=PRT(pc(:,jj(im)),pc(:,jk(im)));j=[3*jj(im)-2:3*jj(im),3*jk(im)-2:3*jk(im)];aml(:,im)=aml(:,im)+sm2*RT*d(j(1:6));endfprintf(fp2,'(14)最终杆端力\n');fprintf(fp2,'杆件号j/k端号xm向轴力ym向剪力zm向弯矩\n');fprintf(fp2,'%3u %7u %14.3e%14.3e%14.3e\n %7u %14.3e%14.3e%14.3e\n',[1:m;jj(1:m);aml( 1:3,1:m);jk(1:m);aml(4:6,1:m)]);fclose(fp2); %关闭计算结果数据文件。
智能桁架梁结构优化设计及关键节点预测分析

智能桁架梁结构优化设计及关键节点预测分析近年来,随着工程技术的不断发展,人们对于结构设计的要求也越来越高。
特别是在建筑领域,结构设计的优化和节点预测分析对于确保工程质量和安全具有至关重要的作用。
本文将讨论智能桁架梁结构的优化设计以及关键节点的预测分析,并探讨其在实际工程中的应用。
1. 智能桁架梁结构优化设计桁架梁结构是一种由桁架组成的载荷传输系统,其特点是结构轻巧、刚性强,适用于大跨度建筑的设计。
然而,传统的桁架梁结构设计往往过于保守,没有充分利用材料的优势,造成了资源的浪费。
在智能化设计的背景下,结构优化设计成为了一个重要的研究领域。
在桁架梁结构的优化设计中,智能算法发挥了重要作用。
例如,遗传算法可以对桁架梁结构的构件进行适应性优化,通过不断迭代计算,找到最优的结构形式和截面尺寸。
此外,神经网络算法也可以应用于桁架梁结构的设计中,通过学习已有的结构案例,为新设计提供参考和指导。
2. 关键节点预测分析在桁架梁结构的设计中,关键节点的预测分析十分重要。
关键节点是指结构中受力较大、应力集中或易于破坏的节点。
通过预测这些节点,可以及早发现潜在的问题,并采取相应的措施进行改进。
预测分析可以借助有限元分析方法,为关键节点的受力情况进行模拟和计算。
在模拟中,需要考虑梁的材料性能、外界荷载和边界条件等因素。
通过数值计算,可以得到节点的应力分布、变形情况和破坏概率等参数。
根据这些参数,可以选择合适的材料和结构形式,以优化设计方案。
3. 实际工程应用智能桁架梁结构的优化设计和关键节点的预测分析已经在实际工程中得到了应用。
例如,在大型体育馆和会展中心的建设中,采用智能优化设计的桁架梁结构可以减轻结构自重,提高空间利用效率;同时,通过关键节点的预测分析,可以调整节点的位置和增强措施,确保结构的安全性和稳定性。
此外,智能桁架梁结构的优化设计和关键节点的预测分析也在桥梁工程中发挥了重要作用。
通过适当调整节点的位置和改变截面形状,可以减小结构自重,提高桥梁的承载能力和抗震性能。
基于MATLAB的桁架结构优化设计

基于MAT LAB 的桁架结构优化设计林 琳 张云波(华侨大学土木系福建泉州 362011) 【摘 要】 介绍了基于BP 神经网络的全局性结构近似分析方法,解决了结构优化设计问题中变量的非线性映射问题。
在此基础上,利用改进的遗传算法,对桁架结构在满足应力约束条件下进行结构最轻优化设计。
利用Matlab 的神经网络工具箱,编程求解了三杆桁架优化问题。
【关键词】 改进遗传算法;BP 神经网络;结构优化设计;满应力准则【中图分类号】 T U20114 【文献标识码】 A 【文章编号】 100126864(2003)01-0034-03TRUSS STRUCTURA L OPTIMIZATON BASE D ON MAT LABLI N Lin ZH ANG Y unbo(Dept.of Civil Engineering ,Huaqiao University ,Quanzhou ,362011) Abstract :Optimal structural design method based on BP neural netw ork and m odified genetic alg orithm were proposed in this paper.The high parallelism and non -linear mapping of BP neural netw ork ,an approach to the global structural approximation analysis was introduced.It can s olve the mapping of design variables in structural optimization problems.C ombining with an im proved genetic alg orithm ,the truss structure is optimized to satis fy the full stress criteria.Under the condition of MAT LAB 5.3,an exam ple of truss structure has been s olved by this method.K ey w ords :G enetic alg orithm ;BP neural netw ork ;Structural optimization design ;Full stress principle 结构优化设计,就是在满足结构的使用和安全要求的基础上,降低工程造价,更好地发挥投资效益。
基于MATLAB的桁架结构优化设计

基于MATLAB的桁架结构优化设计
林琳;张云波
【期刊名称】《低温建筑技术》
【年(卷),期】2003(000)001
【摘要】介绍了基于BP神经网络的全局性结构近似分析方法,解决了结构优化设计问题中变量的非线性映射问题.在此基础上,利用改进的遗传算法,对桁架结构在满足应力约束条件下进行结构最轻优化设计.利用Matlab的神经网络工具箱,编程求解了三杆桁架优化问题.
【总页数】3页(P34-36)
【作者】林琳;张云波
【作者单位】华侨大学土木系,福建泉州,362011;华侨大学土木系,福建泉
州,362011
【正文语种】中文
【中图分类】TU201.4
【相关文献】
1.基于Matlab和ANSYS的钢管桁架结构优化设计 [J], 秦林肖;潘颖
2.基于matlab的空间三维桁架结构受力分析通用程序设计 [J], 李罡
3.基于Lingo和Matlab的空间桁架结构联合优化设计 [J], 李姣玉;何建军
4.基于大跨度双坡重屋盖桁架结构优化设计 [J], 刘洋; 孙继杨
5.基于全局优化设计的桁架结构优化设计研究 [J], 罗佑新;杨立军
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MAT LAB 的桁架结构优化设计林 琳 张云波(华侨大学土木系福建泉州 362011) 【摘 要】 介绍了基于BP 神经网络的全局性结构近似分析方法,解决了结构优化设计问题中变量的非线性映射问题。
在此基础上,利用改进的遗传算法,对桁架结构在满足应力约束条件下进行结构最轻优化设计。
利用Matlab 的神经网络工具箱,编程求解了三杆桁架优化问题。
【关键词】 改进遗传算法;BP 神经网络;结构优化设计;满应力准则【中图分类号】 T U20114 【文献标识码】 A 【文章编号】 100126864(2003)01-0034-03TRUSS STRUCTURA L OPTIMIZATON BASE D ON MAT LABLI N Lin ZH ANG Y unbo(Dept.of Civil Engineering ,Huaqiao University ,Quanzhou ,362011) Abstract :Optimal structural design method based on BP neural netw ork and m odified genetic alg orithm were proposed in this paper.The high parallelism and non -linear mapping of BP neural netw ork ,an approach to the global structural approximation analysis was introduced.It can s olve the mapping of design variables in structural optimization problems.C ombining with an im proved genetic alg orithm ,the truss structure is optimized to satis fy the full stress criteria.Under the condition of MAT LAB 5.3,an exam ple of truss structure has been s olved by this method.K ey w ords :G enetic alg orithm ;BP neural netw ork ;Structural optimization design ;Full stress principle 结构优化设计,就是在满足结构的使用和安全要求的基础上,降低工程造价,更好地发挥投资效益。
传统的优化方法有工程法和数学规划法,其难以解决离散变量问题,对多峰问题容易陷入局部最优,且对目标函数要求有较好的连续性或可微性。
而近年来提出的基于生物自然选择与遗传机理的随机搜索遗传算法对所解的优化问题没有太多的数学要求,可以处理任意形式的目标函数和约束,对离散设计变量的优化问题尤为有效。
进化算子的各态历经性使得遗传算法能够非常有效地进行概率意义下的全局搜索,能高效地寻找到全局最优点。
但采用遗传算法时,进化的每一代种群成员必须要进行结构分析,因此所需的结构分析次数较多。
1 桁架结构优化设计问题的表述在满足应力约束条件下的桁架重量最轻优化问题为: min w (A )=Σni =1ρA i L i s.t 1 σi ≤[σi ] (i =1,2……n ) A min ≤A i ≤A maxw (A )为结构总重量,ρ为材料密度,L i 为第i 杆的长度,A i 为第i 杆件面积,σi 为第i 杆的应力,[σi ]为第i 杆的许用应力,A min 、A max 分别为杆件面积的下界与上界;n 为杆件总数。
2 神经网络结构近似分析方法人工神经网络是由大量模拟生物神经元功能的简单处理单元相互连接而成的巨型复杂网络,它是一个具有高度非线性的超大规模连续时间自适应信息处理系统,易处理复杂的非线性建模问题。
文献[1]在K olm og orov 多层神经网络映射存在定理的基础上,针对近似结构分析问题提出的多层神经网络映射存在定理,确定了近似结构分析的神经网络的基本模型。
从理论上证明一个三层神经网络可用来描述任一弹性结构的应力、位移等变量和结构设计变量之间的映射关系,为利用人工神经网络来进行结构近似分析提供理论基础。
211 BP 神经网络及其算法改进BP 神经网络,即误差反向传播神经网络。
其最主要的特性就是具有非线性映射功能。
1989年R obert Hecht -Niel 2s on 证明了对于任何闭区间内的一个连续函数,都可用一个隐含层的BP 网络来逼近。
因而一个三层BP 网络可完成任意的n 维到m 维的映照,它由输入层、隐层和输出层构成。
传统的BP 网络存在着局部极小问题和收敛速度较慢的问题,因此本文采用了动量法和学习率自适应调整的策略,提高了学习速度并增加了算法的可靠性。
动量法考虑了以前时刻的梯度方向,降低了网络对误差曲面局部细节的敏感性,有效地抑制了网络陷于局部极小。
w (k +1)=w (k )+α[(1-η)D (k )+ηD (k -1)]α(k )=2λα(k -1)λ=stg n[D (k )D (k -1)]w (A )为权值向量,D (k )=-5E5w (k )为k 时刻的负梯度,D (k -1)为k -1时刻的负梯度,η为动量因子,α为学习率。
43 低 温 建 筑 技 术 2003年第1期(总第91期)这种方法所加的动量项实质上相当于阻尼项,上一次权值的变化的影响可由动量常数来调节,它减小了学习过程的振荡过程,从而改善了收敛性。
自适应调整学习率的改进算法: w (k +1)=w (k )+α(k )D (k ) α(k )=2λα(k -1) λ=sig n[D (k )D (k -1)]在一个神经网络的设计中,网络要经过几个不同的学习速率的训练,通过观察每一次训练后的误差平方和的下降速率来判断所选定的学习速率是否合适。
学习速率选择的适当与否影响着BP 算法的收敛速度。
采用上述方法,当连续两次迭代其梯度方向相同时,表明下降太慢,这时可使步长加倍;当连续两次迭代其梯度方向相反时,表明下降过头,这时可使步长减半。
网络通过在不同阶段调节学习速度,不断变化学习速率以缩短学习时间。
212 训练样本选择BP 神经网络是通过对样本的学习来掌握蕴含在样本集中的问题的内在规律和相互关系。
因此,学习样本集的优劣将影响网络的学习时间与网络的泛化能力。
一般来说,当学习变量成正态分布时,数据对网络的学习最有效。
本文据文献,将学习变量在其取值范围内按n 等分分割,正交化的数据点作为试验的样本点。
BP 神经网络中的非线性活性函数S igm oid 函数在接近011的时候,曲线比较平缓,变化非常缓慢,影响网络的学习速度。
为减小网络学习时间,将输入的学习变量数据选择在[011,019]之间,则S igm oid 函数在此区间变化梯度比较大,网络收敛时间可大为减少,改善了网络的仿真性能。
模型精度分析图213 模型精度分析如上图所示:三杆超静定桁架,弹性模量为:E =1,密度为:ρ=1,L 1=L 3=2,L 2=1,结构的设计变量杆1和杆2的截面积A 1,A 2的设计区域为[011,019],且A 1=A 3,材料常数为许用拉应力为σ+=200MPa ,许用压应力σ-=150MPa 。
工况1:P 1=20K N ,P 2=0K N ;工况2:P 1=0K N ,P 2=20K N 。
求结构在荷载作用下,各杆的应力值。
针对以上问题本文构造了一个输入层为2个节点,隐层为5个节点,输出层为3个节点的三层BP 神经网络。
借助于Matlab 的神经网络工具箱,设置“tansig 、purelin ”分别为隐层和输出层的变换函数,网络学习采用动量法和学习率自适应调整法策略的“traingdx ”函数进行训练,网络结构如图所示。
利用此网络来解决输入变量A 1,A 2与输出变量三杆应力值σ1,σ2,σ3的数字逼近映射问题。
输出变量三杆应力值σ1,σ2,σ3的精确值由有限单元法求得。
采用上述正交化方法将输入变量A 1,A 2域值按n =3进行分割,产生训练样本集进行训练。
即:A 1=[011 013 016 019 011 013 016 019 011 013 016 019 011 013 016 019]A 2=[011 011 011 011 013 013 013 013 016 016 016 016 019 019 019 019]而后用训练好的BP 网络来识别和预测一组由计算机随机产生的16个样本点。
神经网络的预测值和精确值相对误差很小,效果良好,能达到工程要求。
3 改进的优化算法311 结合BP 神经网络用遗传算法进行结构优化过程中,不论是在可行域或非可行域的可能解都必须做结构分析。
涉及的设计点多,因此结构的应力、位移等的设计量非常大。
采用上述训练好的BP 神经网络建立设计变量与结构应力、位移等量的非线性映射关系,对遗传算法产生的可能解进行个体判别,只让可行域个体参与群体繁殖,缩小了个体搜索空间,群体进行更加有效。
312 稳定优选的遗传算法传统的遗传算法,每代种群的所有个体通过复制、杂交和变异在下一代中得以更新,种群中的所有个体须进行适应值重新计算。
对于种群规模较大的问题,要耗费较多的计算时间。
且据基因模式定理,好的基因模式和种群结构可能被破坏,使算法难以收敛。
采用稳定比例优选法的遗传算法,通过杂、变异等遗传操作产生一些新的个体,将这些新个体按适应值优劣从好到坏进行排序,按照它们在排序中的位置而不是原适应值来制定选择再生:对适应度优的个体进行保护,使适应度高的个体不受影响,直接进入下一代,只替换种群中的一部分适应度差的个体。
这样,能避免好的种群结构和基因模式遭受破坏,使遗传算法稳定地收敛。
同时,每代只计算替换适应度差的个体的适应值,可减少适应值计算的次数。
定义未被替换的个体占1/N 种群规模(M ),则每代可减少的适应度计算次数为M/N (初始代除外)。
313 改进的G A 流程(1) 编码:一般采用有长度的二进制串来表示求解问题的一个可能解,建立起位串与实际设计变量之间的对应关系。
对给定优化问题将目标函数min F (x )作为适应度函数。
(2) 产生初始种群:选择合适的原始群体规模,随机选取个体,采用BP 神经网络近似结构分析方法来识别初始可能解。
引入罚函数法,即对不等式约束的处理采用静态的惩罚函数,在设计点违反约束条件(即非可行域的可能解)时施以严重的惩罚,从而有效地将这一设计点排除在考虑范围之外。
