气体的pVT性质
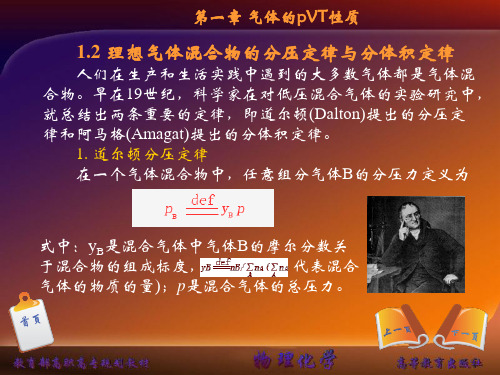
1.2理想气体混合物的分压定律与分体积定律
气体的pVT pVT性质 第一章 气体的pVT性质 设温度为T、压力为p的容器中,装有理想气体混合物, 混合气体的总体积为V,物质的量为n,则
将此式代入,得 因为 所以 上式右端nBRT/p的物理意义是,物质的量为nB的 理想气体B在温度为T、压力为p时所具有的体积。
气体的pVT pVT性质 第一章 气体的pVT性质 于是上式告诉我们:在理想气体混合物中,某组分气 体的体积等于在相同温度T和相同压力p时该气体单独存在 时所占有的体积。结合式 亦可得出如下结论:混合气体的总体积等于混合气体中各 组分气体在与混合气体具有相同温度和相同压力条件下单 独存在时所占有的体积之和。这就是阿马格分体积定律。 分体积定律同样只适用于理想气体混合物,对于真实气体, 其各组分的体积不等于它单独存在时所占有的体积,当然 分体积定律不能成立。在低压下的真实气体混合物近似服 从阿马格分体积定律。 例题解析
式中:yB是混合气体中气体B的摩尔分数关 于混合物的组成标度, 代表混合 气体的物质的量);p是混合气体的总压力。
气体的pVT pVT性质 第一章 气体的pVT性质 于是,对于一个由N种气体构成的气体混合物,则由于 ∑yB≡1,必有
B
即
这就是说,在气体混合物中,所有组分气体的分压 力之和等于混合气体的总压力。所 pVT性质 第一章 气体的pVT性质 分压力的定义是国际纯粹及应用化学联合会(IUPAC) 推荐的式 从上式中不难得出如下结论:混合气体的总压力等于混合 气体中各组分气体在与混合气体具有相同温度和相同体积条件 下单独存在时所产生的压力之和。这就是道尔顿分压定律。分 压定律只适用于理想气体混合物。理想气体分子之间没有相互 作用力,因而其中的每一种气体都不会由于其他气体的存在而 受到影响。 也就是说,每一种组分气体都是独立起作用的,对总压力 的贡献和它单独存在时的压力相同。对于真实气体,分子之间 有作用力,且在混合气体中的相互作用力与纯气体不同,于是 各组分气体的压力不等于它单独存在时的压力,即分压定律不 能成立。在低压下的真实气体混合物近似服从道尔顿分压定律。 例题解析
物理化学天津大学第四版答案

物理化学天津大学第四版答案【篇一:5.天津大学《物理化学》第四版_习题及解答】ass=txt>目录第一章气体的pvt性质 ....................................................................................................... (2)第二章热力学第一定律 ....................................................................................................... . (6)第三章热力学第二定律 ....................................................................................................... .. (24)第四章多组分系统热力学 ....................................................................................................... . (51)第五章化学平衡 ....................................................................................................... .. (66)第六章相平衡 ....................................................................................................... (76)第七章电化学 ....................................................................................................... (85)第八章量子力学基础 ....................................................................................................... . (107)第九章统计热力学初步 ....................................................................................................... ...... 111 第十一章化学动力学 ....................................................................................................... . (117)第一章气体的pvt性质1.1 物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
第一章气体的pVT性质

3. 阿马加分体积定律与分体积
Amagat Law and partial volume
1) 阿马加分体积定律
理想气体混合物的总体积V为各组分分体积VB*之和: V= VB*
2) 理想气体混合物中某一组分的分体积
V
nRT p
nB RT B
p
nB RT Bp
VB
n2
出口状态
因为
n1 = n2
所以
p1V1 p2V2 nR
T1
T2
得
V2
p1V1 T2 T1 p2
V1
p1 p2
T2 T1
26m 3
解题关键: 找出各状态参量之间的相互联系
§1.2 理想气体混合物
Mixtures of ideal gasas
• 1. 混合物的组成
components of mixtures
低压气体实验定律:
(1)玻义尔定律(R.Boyle,1662):
pV = 常数
(n,T 一定)
(2)盖.吕萨克定律(J. Gay-Lussac,1808):
V / T = 常数
(n, p 一定)
(3)阿伏加德罗定律(A. Avogadro, 1811)
V / n = 常数
(T, p 一定)
以上三式结合
具有的共性,体现了一种非常简单、非常理想的pVT行 为,
lim
p0
pVm
RT
3、理想气体模型及定义
the modle and definition of ideal gas (1)分子间力
吸引力 分子相距较远时,有范德华引力;
第一章 气体的pVT性质

30.31× 10−3 kg.mol −1 × 0.201 = 6.29 ≈ 6 1× 10−3 kg.mol −1 ∴ C2 H 6
3. 在生产中 用电石 CaC2 CaC2 分析碳酸氢氨产品中水分的含量 = C2H2 g +Ca OH
2
其反应式如下
s + 2H2O l
现称取 2.000g 碳酸氢氨样品与过量的电石完全作用 在 27 50.0cm3 解 试计算碳酸氢氨样品中水分的质量分数为多少
VB = yBV
VB =
nB RT p
压缩因子的定义
Z=
5 范德华方程
pV nRT
或
Z=
pVm RT
a p + 2 (Vm − b ) = RT Vm 二. 本章练习
(一) 选择题
n2a 或 p + 2 (V − nb ) = nRT V
1 对于实际气体,处于下列哪种情况时,其行为与理想气体相近
n=
2 pV p2V p2V = + RT1 RT1 RT2 2 p1T2 = 57900 Pa = 57.9kPa T2 + T1
p2 =
6. 298.15K 时 在一抽空的烧瓶中充入 2.00g 的 A 气体 此时瓶中压力为 1.00 105Pa 今若再充入 3.00g 的 B 气体 解 发现压力上升为 1.50 105Pa 试求两物质 A B 的摩尔量之比
充入气体质量为
0.3897g 时 解
试计算混合气体中乙烷和丁烷的摩尔分数与分压力
M = y1M 1 + y2 M 2 = =
mRT pV
0.3897 g × 8.314 J .K −1.mol −1 × 293.15 K = 46.87 g .mol −1 −4 3 101.325kPa × 2.00 ×10 m M 1 = 30 g / mol M 2 = 58 g / mol
高中物理 第一章气体的pVT性质

第一章 气体的PVT 性质主要内容1. 理想气体状态方程及微观模型2. Daltonp 定律与Amagat 定律3. 实际气体的PVT 性质4. 范德华方程5. 实际气体的液化与临界性质重点1. 重点掌握理想气体状态方程及微观模型2. 重点掌握Daltonp 定律与Amagat 定律3. 重点掌握实际气体的液化与临界性质难点1. 理想气体模型及其理论解释2. 实际气体的液化与临界性质教学方式1. 采用CAI 课件与黑板讲授相结合的教学方式2. 合理运用问题教学或项目教学的教学方法教学过程一、理想气体状态方程17世纪中期,为了寻找气体的状态方程,通过大量实验得出:状态方程: pV =nRT (其中压力越低越符合条件)R =0lim m p pV R T p T→=↓↑ R=8.314J/K ⋅mol 理想气体定义与模型定义:在任何温度及任何压力下都能严格服从上面的状态方程的气体就定义为理想气体。
上式就称为理想气体的状态方程。
模型:分子为质点,无体积;分子间无相互作用力。
二、Daltonp 定律与Amagat 定律1. Daltonp 定律与分压力混合气体的总压力等于混合气体中各组分气体在与混合气体有相同温度和相同体积条件下单独存在时所产生的压力之和(只适用于理想气体)。
B Bp p =∑ B B p y p =(适用于任何气体)分压力B p 是它的摩尔分数B y 与混合气体的总压力p 之积。
2. Amagat 定律混合气体的总压力等于混合气体中各组分气体在与混合气体有相同温度和相同体积条件下单独存在时所产生的压力之和(只适用于理想气体)。
BB V V =∑ (只适用于理想气体)//B B B V y nRT p n RT p ==(只适用于理想气体)三、实际气体的PVT 性质,///m m m m idV V Z pV nRT pV RT RT p V ==== m V 实际气体在某一确定状态下的摩尔体积,m id V 代表与实际有相同温度和相同压力的理想气体的摩尔体积用大小相等分子间的引力与斥力作比理想气体易压缩同温同压下,实际气体比理想气体难压缩同温同压下,实际气体111=<>Z四、范德华方程RT b V V a p m m=-+))((2 22()()n a p V nb nRT V+-= 五、实际气体的液化与临界性质 1. c T T >,任何p 均不液化同一温度,p ↑,偏离↑ 同一压力,T ↓,偏离↑ 2. c T T <3. c T T =,临界点定义 临界温度c T临界压力c P临界摩尔体积c V。
课件:第一章 气体的pVT性质

上一内容 下一内容 回主目录
返回
2018/11/9
4.阿马加定律ቤተ መጻሕፍቲ ባይዱ
1) 分体积 混合气体中,组分B单独存在,并且处于与混 合气体相同的温度和压力时,所产生的体积称组
分B的分体积。
nB RT V p
B
上一内容 下一内容 回主目录
返回
2018/11/9
§1.1 理想气体的状态方程
理想气体:分子间无相互作用,分子本身无体积
× ×
× ×
可无限压缩
在任何温度、压 力下均符合理想
× × × × × × × × ×
上一内容 下一内容
气体模型,或服
从理想气体状态
方程的气体为理
想气体
回主目录
返回
2018/11/9
§1.1 理想气体的状态方程 • 理想气体的状态方程是理想气体的宏 观外在表现
pVm=RT
m pV RT M
Vm=V/n ρ=m/V
或
用于p, V, T, n, m, M, ρ的计算
上一内容 下一内容 回主目录
返回
2018/11/9
§1.1 理想气体的状态方程 例:计算25℃,101325Pa时空气的密度。
(空气的分子量为29)
解: n p 101325 3 mol m V RT 8.315 273.15 25 3 40.87 mol m n 3 3 d空气= M 40.87 29 g m 1.185 kg m V
• 理想气体的微观模型反映了理想气体
的微观内在本质
• 理想气体是真实气体在 p→ 0 情况下
第1章气体的PVT性质

理想气体状态方程
p Pa; V m3; T K; n mol ;
R 摩尔气体常数 8.314J mol-1 K-1 理想气体状态方程也可表示为: pVm=RT pV = (m/M)RT pM= (m/V)RT=RT
理想气体状态方程也可表示为:
pVm= RT pV = (m/M)RT pM= (m/V)RT = RT
阿马加定律表明理想气体混合物的体积具有加和性,在 相同温度、压力下,混合后的总体积等于混合前各组分的体 积之和。 由二定律有:
pB VB nB yB p V n
高压下,混合前后气体体积一般将发生变化,阿马加定律 不再适用。这时需引入偏摩尔体积的概念进行计算。(见第 四章)
第三节 气体的液化和临界参数 一、理想气体 pV = nRT
理想气体混合物中某一组分B的分压 pB 等于该组分单独 存在于混合气体的T、V时产生的压力。
而理想气体混合物的总压等于各组分单独存在于混合气 体的T、V时产生的压力总和 道尔顿定律 对低压下真实气体混合物适用。在高压下,分子间的相互作
用不可忽视,且混合物不同分子间的作用与纯气体相同分子间
的作用有差别,所以某气体B的分压不再等于它单独存在时的 压力,所以分压定律不再适用
pV nRT nB RT B
及
pV = (m / Mmix) RT
式中:m 混合物的总质量; Mmix 混合物的摩尔质量; p,V 为混合物的总压与体积。
又 m = mB = nB MB = n yB MB = nMmix Mmix= m/n = yB MB 即混合物的摩尔质量又等于混合物的总质量除以混 合物的总的物质的量。 混合物的(平均)摩尔质量定义为: 混合物中各物质的摩尔 质量与其摩尔分数的乘积的和:
1.3真实气体与范德华方程
1.3真实气体与范德华方程
1、真实气体对理想气体的偏差
为了定量描述真实气体的pVT行为与理想 气体的偏离程度,定义压缩因子Z为
Z
def
pV m RT
或
Z
def
pV nRT
Z
Vm RT / p
Байду номын сангаас
Vm V m , id
式中,Vm为真实气体在某一确定状态下的摩尔体积, Vm,id 代表与真实气体具有相同温度和相同压力的理想气 体的摩尔体积。
第一章气体的pvt性质13真实气体与范德华方程1真实气体对理想气体的偏差为了定量描述真实气体的pvt行为与理想气体的偏离程度定义压缩因子z为pvzz?mdefpvzz?def?或rtnrtidmmmvvprtvz??式中vm为真实气体在某一确定状态下的摩尔体积vmid代表与真实气体具有相同温度和相同压力的理想气体的摩尔体积
第一章 气体的pVT性质
真实气体 1、低温低压:分子本身体积忽 略,分子间引力不忽略 2、高压:分子间距小,分子本 身体积不能忽略,分子间作用 力中斥力占主导 3、高温:分子热运动加剧,引 力作用可忽略,体积成为主导 因素 易压缩,Z<1
难压缩,Z>1
第一章 气体的pVT性质
范德华方程 为了能够比较准确地定量描述真实气体的 pVT行为,自19世纪以来,人们在大量实验的基 础上,提出了许多形式各异的真实气体状态方程, 它们的适用对象及精确程度也有所不同。 在众多的探索真实气体状态方程的科学家 中,荷兰科学家范德华(van der Waals J D)于1871 年首先从理论上建立了真实气体的微观模型,并 在此基础上对理想气体方程进行了修正,提出了 一个与实验结果比较一致的真实气体状态方程。 范德华提出:
物化(上)答案

第一章 气体pVT 性质1-3 0℃、101.325kPa 的条件常称为气体的标准状况。
试求甲烷在标准状况下的密度。
解:33714.015.273314.81016101325444--⋅=⨯⨯⨯=⋅=⋅=m kg M RT p M V n CH CH CH ρ 1-5 两个体积均为V 的玻璃球泡之间用细管连接,泡内密封着标准状况条件下的空气。
若将其中一个球加热到100℃,另一个球则维持0℃,忽略连接管中气体体积,试求该容器内空气的压力。
解:方法一:在题目所给出的条件下,气体的量不变。
并且设玻璃泡的体积不随温度而变化,则始态为 )/(2,2,1i i i i RT V p n n n =+=终态(f )时 ⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=+=f f ff f f f f f f T T T T R Vp T V T V R p n n n ,2,1,1,2,2,1,2,1 kPaT T T T T p T T T T VR n p f f f f i i ff f f f 00.117)15.27315.373(15.27315.27315.373325.1012 2,2,1,2,1,2,1,2,1=+⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=1-8二者均克视为理想气体。
(1压力。
(2)隔板抽去前后,H 2及N 2的摩尔体积是否相同?(3)隔板抽去后,混合气体中H 2及N 2的分压力之比以及它们的分体积各为若干? 解:(1)抽隔板前两侧压力均为p ,温度均为T 。
p dmRT n p dm RT n p N N H H ====33132222 (1) 得:223N H n n =而抽去隔板后,体积为4dm 3,温度为,所以压力为3331444)3(2222dmRT n dm RT n dm RT n n V nRT p N N N N ==+==(2) 比较式(1)、(2),可见抽去隔板后两种气体混合后的压力仍为p 。
第一章气体的PVT性质
§ 1.2 理想气体混合物的分压定律与分体积定律 3) 体积分数 混合气体中某组分 i 的分体积与总体积之比称该组 分i的体积分数。
Vi ni RT / P ni yi V nRT / P n
即体积分数等于该组分i的摩尔分数 此规律只近似应用于低压下的实际混合气体。
15-03-13 29
15-03-13 17
理想气体模型
理想气体: 凡在任何温度、压力下均服从理想气体状态方程 的气体称为理想气体. 分子是质点 理想气体的两个特征: (1)分子本身必定不占有体积; (2)分子间无相互作用. 解释: (1) T 恒定时, pVm = 常数, 意味着 p , Vm 0. (2) p = (n/V)RT, 表明在恒温下, 气体分子碰撞器壁的压 力与分子数密度成简单的比例关系, 而这只有在分子 间没有相互作用时才有可能.
摄氏温度 热力学温度
t T
℃ K -273.15K
T/K
=
t/℃ +273.15
绝对零度:在此温度下,构成物质的所有分子和原 子均停止运动。
15-03-13 8
§ 1.1 理想气体状态方程
在气液固三种聚集状态中, 气体最容易用分子模型进行研究.
联系 p、V、T 之间关系的方程称为状态方程 本章中主要讨论气体的状态方程 理想气体
§ 1.2 理想气体混合物的分压定律与分体积定律
及
pV = nRT = ( nB)RT
pV = (m/Mmix)RT
式中:m 混合物的总质量 Mmix 混合物的摩尔质量
又 m = mB = nB MB = n yB MB = nMmix
Mmix= m/n = mB / nB
Z>1,则Vm>Vmid,即同温同压下实际气体的摩尔体积 大于理想气体的摩尔体积——真实气体比理想气体 难于压缩 Z<1,则Vm<Vmid,即同温同压下实际气体的摩尔体积 大于理想气体的摩尔体积——真实气体比理想气体 易于压缩
第一章 气体的pVT性质-含答案

一、填空题1.温度为400K ,体积为2m 3的容器中装有2mol 的理想气体A 和8mol 的理想气体B ,则该混合气体中B 的分压力p B =( )KPa 。
13.3022.在300K ,100KPa 下,某理想气体的密度ρ=80.8275×10-3kg ·m -3。
则该气体的摩尔质量M=( )。
3.恒温100°C 下,在一带有活塞的气缸中装有3.5mol 的水蒸气H 2O (g ),当缓慢地压缩到压力p=( )KPa 是才可能有水滴H 2O (l )出现。
4.恒温下的理想气体,其摩尔体积随压力的变化率Tmp V ⎪⎪⎭⎫ ⎝⎛∂∂ =( )。
5,一定的范德华气体,在恒容条件下,其压力随温度的变化率()=∂∂V T /p .6.理想气体的微观特征是:( )7. 在临界状态下,任何真实气体的宏观特征为:( )8. 在n,T 在一定的条件下,任何种类的气体当压力趋近于零时均满足:()=→pV p lim 0( ).9.实际气体的压缩因子定义为Z=( )。
当实际气体的Z>1时,说明该气体比理想气体( )三、问答题理想气体模型的基本假设是什么?什么情况下真实气体和理想气体性质接近?增加压力真实气体就可以液化,这种说法对吗,为什么?第二章 热力学第一定律――附答案一、填空题1. 理想气体向真空膨胀过程 , 下列变量中等于零的有 : 。
2. 双原子理想气体经加热内能变化为 ,则其焓变为 。
3. 在以绝热箱中置一绝热隔板,将向分成两部分,分别装有温度,压力都不同的两种气体,将隔板抽走室气体混合,若以气体为系统,则此过程 。
4. 绝热刚壁容器内发生CH 4+2O 2=CO 2+2H 2O 的燃烧反应,系统的 Q ___ 0 ; W ___ 0 ;∆U ___ 0;∆H ___ 05. 某循环过程 Q = 5 kJ, 则 ∆U + 2W + 3 ∆(pV) = __________.6. 298K 时, S 的标准燃烧焓为-296.8 kJ ⋅mol -1, 298K 时反应的标准摩尔反应焓 ∆r H m = ________ kJ ⋅mol -1 .7. 已知 的 , 则 的 。
第一章气体的pVT性质详解

lim R
pVm 2494.35kJ mol1
p0 T
300K
8.314J mol1 K 1
1.0
20
40
60
80
100
P /MPa
300K下He、N2、CH4的PVm→P等温线图
13@2020/9/30
§1.2 理想气体混合物
1. 混合物组成表示 2. 理气状态方程对混合物的
应用 3. 道尔顿定律(分压定律) 4. 阿马加定律(分体积定律)
A
A
混合前纯 B体积 混合前各纯组分体积总
和
显然
B 1
B
18@2020/9/30
§1.2 理想气体混合物
• 质量摩尔浓度:
bB
nB mA
mol·kg-1
溶液中溶质B的物质的量nB除以溶剂的质量mA
19@2020/9/30
§1.2 理想气体混合物
2.理气状态方程对理气混合物的应用
pV nRT B nB RT
12@2020/9/30
§1.1 理想气体的状态方程
• 由于压力趋于零的实验条 4.5
件不易达到,所以,R值
4.0
的确定实际是采用外推法 3.5
求得的
3.0
pVm/KJ /mol
• 首先,测量恒温下气体的 2.5
pVm~p图,外推至p →0, 2.0
再由pVm=RT求出R值。
1.5
N2 He
CH4
根据反应式求出:所需NaN3的物质的量及质 量……
9@2020/9/30
§1.1 理想气体的状态方程
2.理想气体的模型
真实气体微观模型: •分子间有相互作用 •分子本身有体积
物理化学(天大第五版全册)课后习题答案

第一章 气体pVT 性质1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下:11TT p V p V VT V V ⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂=κα 试导出理想气体的V α、T κ与压力、温度的关系?解:对于理想气体,pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V pnRT V p p nRT V p V V T T T κ 1-5 两个体积均为V 的玻璃球泡之间用细管连接,泡内密封着标准状况条件下的空气。
若将其中一个球加热到100℃,另一个球则维持0℃,忽略连接管中气体体积,试求该容器内空气的压力。
解:方法一:在题目所给出的条件下,气体的量不变。
并且设玻璃泡的体积不随温度而变化,则始态为 )/(2,2,1i i i i RT V p n n n =+=终态(f )时 ⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=+=f f ff f f f f f f T T T T R Vp T V T V R p n n n ,2,1,1,2,2,1,2,1 kPaT T T T T p T T T T VR n p f f f f i i ff ff f 00.117)15.27315.373(15.27315.27315.373325.1012 2,2,1,2,1,2,1,2,1=+⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=1-8 如图所示一带隔板的容器中,两侧分别有同温同压的氢气与氮气,二者均克视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽去前后,H 2及N 2的摩尔体积是否相同?(3)隔板抽去后,混合气体中H 2及N 2的分压力之比以及它们的分体积各为若干? 解:(1)抽隔板前两侧压力均为p ,温度均为T 。
物理化学第一章气体的pVT性质

一、状态方程 :联系 p、V、T 之间关系的方 程称为状态方程。 二、理想气体状态方程 1. 理想气体状态方程 低压气体定律: (1)波义尔定律(R.Boyle,1662):
pV = 常数 V / T = 常数
( n ,T 一定) (n , p 一定)
(2)盖.吕萨克定律(J. Gay-Lussac,1808):
ρ ∝
a 内压力= V 2 = p i p
1 V
pi = p +
3. 范德华方程
(P +
a V2
a )(Vm b) = RT 2 Vm
n 2a (P + )( V nb ) = nRT V 2
§1-3
实际气体的PVT性质 实际气体的PVT性质 PVT
4.范德华常数及其单位 范氏方程里的两个常数a、b总称为范德华常数,常数a 标志了物质分子间所具有的相互吸引力,常数b则表示 了分子本身所具有的体积,故a与b都是与气体种类有 关的特性常数。
R=
或
PVm 1atm × 22.4140L mol = T 273.15K
= 0.082057atm L K 1 mol 1
1
(101325 N m 2 )( 22 . 4140 10 3 m 3 mol R= 273 .15 K
)
=8.3144NmK-1mol-1 =8.3144JK-1mol-1
第一章
气体的PVT性质 气体的PVT性质 PVT
§1-0 物质的聚集状态
聚集状态 1.定义:物质是由大量的不断流动着的分子、原子、 离子等微观粒子聚集而成的,所以物质所表现出来的 状态 。 2.产生原因:分子间相互作用力 运动 3.表示方法:气、液、固分别用于g、l、s表示。
物理化学模拟试题及答案

物理化学模拟试题及答案第一章气体的PVT性质选择题1.理想气体模型的基本特征是(A)分子不断地作无规则运动、它们均匀分布在整个容器中(B)各种分子间的作用相等,各种分子的体积大小相等(C)所有分子都可看作一个质点,并且它们具有相等的能量(D)分子间无作用力,分子本身无体积答案:D2.关于物质临界状态的下列描述中,不正确的是(A)在临界状态,液体和蒸气的密度相同,液体与气体无区别(B)每种气体物质都有一组特定的临界参数C)在以p、V为坐标的等温线上,临界点对应的压力就是临界压力(D)临界温度越低的物质,其气体越易液化答案:D3.对于实际气体,下面的陈述中正确的是(A)不是任何实际气体都能在一定条件下液化(B)处于相同对比状态的各种气体,不一定有相同的压缩因子(C)对于实际气体,范德华方程应用最广,并不是因为它比其它状态方程更精确(D)临界温度越高的实际气体越不易液化答案:C4.理想气体状态方程pV=nRT表明了气体的p、V、T、n、这几个参数之间的定量关系,与气体种类无关。
该方程实际上包括了三个气体定律,这三个气体定律是(A)波义尔定律、盖-吕萨克定律和分压定律(B)波义尔定律、阿伏加德罗定律和分体积定律(C)阿伏加德罗定律、盖-吕萨克定律和波义尔定律(D)分压定律、分体积定律和波义尔定律答案:C问答题1.什么在真实气体的恒温PV-P曲线中当温度足够低时会出现PV值先随P的增加而降低,然后随P的增加而上升,即图中T1线,当温度足够高时,PV值总随P的增加而增加,即图中T2线?答:理想气体分子本身无体积,分子间无作用力。
恒温时pV=RT,所以pV-p线为一直线。
真实气体由于分子有体积且分子间有相互作用力,此两因素在不同条件下的影响大小不同时,其pV-p曲线就会出现极小值。
真实气体分子间存在的吸引力使分子更靠近,因此在一定压力下比理想气体的体积要小,使得pV<RT。
另外随着压力的增加真实气体中分子体积所点气体总体积的比例越来越大,不可压缩性越来越显著,使气体的体积比理想气体的体积要大,结果pV>RT。
物理化学第一章气体的pVT性质

如两种气体混合 V = V*A + V*B
nB RT V p
* B
(3)适用于理想气体混合物,低压下的真实气体混合物;对高压下的混 合气体,需用偏摩尔体积取代摩尔体积。
=======分体积定律是理想气体的必然规律========
11
Physical Chemistry CAI
斥力
A B E E吸引+E排斥= 6 12 r r
对真实气体,通过降低温度和增加压力都
E
引力
E
可使气体的摩尔体积减小,即分子间距减小,
最终导致液化。
r0 r
图1-2 兰纳德-琼斯势能曲线
14
Physical Chemistry CAI
物理化学教学课件
2.真实气体p-Vm等温图
1869年,Andrews T,通过研究n一定的CO2气体的系列实验,采
物理化学教学课件
(3)沸点:
当液体的饱和蒸汽压等于外界压力(pex, External)时,液体开始沸 腾(汽化),此时的温度称为液体的沸点。
习惯上将101.325kPa(标准大气压)下的沸点成为正常沸点。
水(100℃),乙醇(78℃),苯(80℃)
在外压较低 (高原上, pex <101.325kPa)时, 沸点降低(水的沸点 < 100℃),所以在高原上煮鸡蛋不熟。 在外压较高(高压釜中, pex>101.325kPa)时,沸点升高(水的沸点 >100℃),所以用高压锅煮饭易熟。 部分液体的饱和蒸汽压-温度关系表(Page13-table 1-2)。
2. 液、固体的复杂性——液、固体的分子间作用力较大,研究较复杂,甚 至无法研究。 人们常利用气体的一些性质,并加以修正,来处理液、固体行为,亦 能得到令人满意结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 ︒C,另一个球则维持0 ︒C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 ︒C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals 方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算气(附录七)用van der Waals计算,查表得知,对于N2,用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.16 25 ︒C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7 kPa,于恒定总压下冷却到10 ︒C,使部分水蒸气凝结为水。
试求每摩尔干乙炔气在该冷却过程中凝结出水的物质的量。
已知25 ︒C及10 ︒C时水的饱和蒸气压分别为3.17 kPa及1.23 kPa。
解:该过程图示如下设系统为理想气体混合物,则1.17 一密闭刚性容器中充满了空气,并有少量的水。
但容器于300 K条件下大平衡时,容器内压力为101.325 kPa。
若把该容器移至373.15 K的沸水中,试求容器中到达新的平衡时应有的压力。
设容器中始终有水存在,且可忽略水的任何体积变化。
300 K时水的饱和蒸气压为3.567 kPa。
解:将气相看作理想气体,在300 K时空气的分压为由于体积不变(忽略水的任何体积变化),373.15 K时空气的分压为由于容器中始终有水存在,在373.15 K时,水的饱和蒸气压为101.325 kPa,系统中水蒸气的分压为101.325 kPa,所以系统的总压第二章热力学第一定律2.5 始态为25 ︒C,200 kPa的5 mol某理想气体,经途径a,b两不同途径到达相同的末态。
途经a先经绝热膨胀到 -28.47 ︒C,100 kPa,步骤的功;再恒容加热到压力200 kPa的末态,步骤的热。
途径b为恒压加热过程。
求途径b的及。
解:先确定系统的始、末态对于途径b,其功为根据热力学第一定律2.6 4 mol的某理想气体,温度升高20 C,求的值。
解:根据焓的定义2.10 2 mol某理想气体,。
由始态100 kPa,50 dm3,先恒容加热使压力体积增大到150 dm3,再恒压冷却使体积缩小至25 dm3。
求整个过程的。
解:过程图示如下由于,则,对有理想气体和只是温度的函数该途径只涉及恒容和恒压过程,因此计算功是方便的根据热力学第一定律2.13 已知20 ︒C液态乙醇(C2H5OH,l)的体膨胀系数,等温压缩率,密度,摩尔定压热容。
求20 ︒C,液态乙醇的。
解:由热力学第二定律可以证明,定压摩尔热容和定容摩尔热容有以下关系2.14 容积为27 m3的绝热容器中有一小加热器件,器壁上有一小孔与100 kPa的大气相通,以维持容器内空气的压力恒定。
今利用加热器件使器内的空气由0 ︒C加热至20 ︒C,问需供给容器内的空气多少热量。
已知空气的。
假设空气为理想气体,加热过程中容器内空气的温度均匀。
解:在该问题中,容器内的空气的压力恒定,但物质量随温度而改变注:在上述问题中不能应用,虽然容器的体积恒定。
这是因为,从小孔中排出去的空气要对环境作功。
所作功计算如下:在温度T时,升高系统温度 d T,排出容器的空气的物质量为所作功这正等于用和所计算热量之差。
2.15 容积为0.1 m3的恒容密闭容器中有一绝热隔板,其两侧分别为0 ︒C,4 mol 的Ar(g)及150 ︒C,2 mol的Cu(s)。
现将隔板撤掉,整个系统达到热平衡,求末态温度t及过程的。
已知:Ar(g)和Cu(s)的摩尔定压热容分别为及,且假设均不随温度而变。
解:图示如下假设:绝热壁与铜块紧密接触,且铜块的体积随温度的变化可忽略不计则该过程可看作恒容过程,因此假设气体可看作理想气体,,则(g)的摩尔2.16 水煤气发生炉出口的水煤气的温度是1100 ︒C,其中CO(g)和H2分数均为0.5。
若每小时有300 kg的水煤气由1100 ︒C冷却到100 ︒C,并用所收回的热来加热水,是水温由25 ︒C升高到75 ︒C。
求每小时生产热水的质量。
(g)的摩尔定压热容与温度的函数关系查本书附录,水的CO(g)和H2比定压热容。
(g)的物质量分别为解:300 kg的水煤气中CO(g)和H2300 kg的水煤气由1100 ︒C冷却到100 ︒C所放热量设生产热水的质量为m,则2.18 单原子理想气体A于双原子理想气体B的混合物共5 mol,摩尔分数,始态温度,压力。
今该混合气体绝热反抗恒外压膨胀到平衡态。
求末态温度及过程的。
解:过程图示如下分析:因为是绝热过程,过程热力学能的变化等于系统与环境间以功的形势所交换的能量。
因此,单原子分子,双原子分子由于对理想气体U和H均只是温度的函数,所以2.19 在一带活塞的绝热容器中有一绝热隔板,隔板的两侧分别为2 mol,0 ︒C 的单原子理想气体A及5 mol,100 ︒C的双原子理想气体B,两气体的压力均为100 kPa。
活塞外的压力维持在100 kPa不变。
今将容器内的隔板撤去,使两种气体混合达到平衡态。
求末态的温度T及过程的。
解:过程图示如下假定将绝热隔板换为导热隔板,达热平衡后,再移去隔板使其混合,则由于外压恒定,求功是方便的由于汽缸为绝热,因此2.20 在一带活塞的绝热容器中有一固定的绝热隔板。
隔板靠活塞一侧为2 mol,0 ︒C的单原子理想气体A,压力与恒定的环境压力相等;隔板的另一侧为6 mol,100 ︒C的双原子理想气体B,其体积恒定。
今将绝热隔板的绝热层去掉使之变成导热板,求系统达平衡时的T及过程的。
解:过程图示如下显然,在过程中A为恒压,而B为恒容,因此同上题,先求功同样,由于汽缸绝热,根据热力学第一定律2.23 5 mol双原子气体从始态300 K,200 kPa,先恒温可逆膨胀到压力为50 kPa,在绝热可逆压缩到末态压力200 kPa。
求末态温度T及整个过程的及。
解:过程图示如下要确定,只需对第二步应用绝热状态方程,对双原子气体因此由于理想气体的U和H只是温度的函数,整个过程由于第二步为绝热,计算热是方便的。
而第一步为恒温可逆2.24 求证在理想气体p-V图上任一点处,绝热可逆线的斜率的绝对值大于恒温可逆线的绝对值。
证明:根据理想气体绝热方程,得,因此。
因此绝热线在处的斜率为恒温线在处的斜率为。
由于,因此绝热可逆线的斜率的绝对值大于恒温可逆线的绝对值。
2.25 一水平放置的绝热恒容的圆筒中装有无摩擦的绝热理想活塞,活塞左、右两侧分别为50 dm3的单原子理想气体A和50 dm3的双原子理想气体B。
两气体均为0 C,100 kPa。
A气体内部有一体积和热容均可忽略的电热丝。
现在经过通电缓慢加热左侧气体A,使推动活塞压缩右侧气体B到最终压力增至200 kPa。
求:(1)气体B的末态温度。
(2)气体B得到的功。
(3)气体A的末态温度。
(4)气体A从电热丝得到的热。
解:过程图示如下由于加热缓慢,B可看作经历了一个绝热可逆过程,因此功用热力学第一定律求解气体A的末态温度可用理想气体状态方程直接求解,将A与B的看作整体,W= 0,因此2.25 在带活塞的绝热容器中有4.25 mol的某固态物质A及5 mol某单原子理想气体B,物质A的。
始态温度,压力。
今以气体B为系统,求经可逆膨胀到时,系统的及过程的。
解:过程图示如下将A和B共同看作系统,则该过程为绝热可逆过程。
作以下假设(1)固体B的体积不随温度变化;(2)对固体B,则从而对于气体BO, l)在100 ︒C的饱和蒸气压,在此温度、压2.26 已知水(H2力下水的摩尔蒸发焓。
求在在100 ︒C,101.325 kPa下使1 kg水蒸气全部凝结成液体水时的。
设水蒸气适用理想气体状态方程式。
解:该过程为可逆相变2.28 已知 100 kPa 下冰的熔点为 0 °C,此时冰的比熔化焓热J·g-1. 水的平均定压热容。
求在绝热容器内向1 kg 50 °C 的水中投入 0.1 kg 0 °C 的冰后,系统末态的温度。
计算时不考虑容器的热容。
解:经粗略估算可知,系统的末态温度T应该高于0 °C, 因此2.29 已知 100 kPa 下冰的熔点为0 °C,此时冰的比熔化焓热J·g-1. 水和冰的平均定压热容分别为及。
今在绝热容器内向1 kg 50 °C 的水中投入 0.8 kg 温度 -20 °C 的冰。
求:(1)末态的温度。
(2)末态水和冰的质量。
解:1 kg 50 °C 的水降温致0 °C 时放热0.8 kg -20 °C 的冰升温致0 °C 时所吸热完全融化则需热因此,只有部分冰熔化。
所以系统末态的温度为0 °C。
设有g的冰熔化,则有系统冰和水的质量分别为2.30 蒸汽锅炉中连续不断地注入 20 °C的水,将其加热并蒸发成 180 °C,饱和蒸汽压为 1.003 MPa 的水蒸气。
求生产 1 kg 水蒸气所需要的热量。
已知:水在 100 °C的摩尔蒸发焓,水的平均摩尔定压热容,水蒸气的摩尔定压热容与温度的函数关系见附录。
解:将过程看作是恒压过程(),系统的初态和末态分别为和。
