运筹学典型题型案例集
运筹学实例 含解析

案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。
其中有五项住宅工程,三项工业车间。
由于这些工程要求同时施工,而企业又没有能力同时承担,企业应根据自身的能力,分析这两类工程的盈利水平,作出正确的投标方案。
有关数据见下表:表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。
解:设承包商承包X 1项住宅工程,X 2项工业车间工程可获利最高,依题意可建立如下整数模型:目标是获利最高,故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性,有约束:利用WinSQB 建立模型求解:1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数,;,2121X X 3X 5X ≤≤综上,承包商对2项住宅工程,3项车间工程进行投标,可获利最大,目标函数Max z=340022 元。
案例2. 生产计划问题某厂生产四种产品。
每种产品要经过A,B两道工序加工。
设该厂有两种规格的设备能完成A工序,以A1 ,A2表示;有三种规格的设备能完成B工序,以B1 ,B2,B3 表示。
产品D可在A,B任何一种规格的设备上加工。
产品E可在任何规格的A设备上加工,但完成B工序时只能在B1设备上加工。
产品F可在A2及B2 ,B3上加工。
产品G可在任何一种规格的A设备上加工,但完成B工序时只能在B1 ,B2设备上加工。
已知生产单件产品的设备工时,原材料费,及产品单价,各种设备有效台时如下表,要求安排最优的生产计划,使该厂利润最大?设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费(元/件)单价(元/件)0.251.250.352.000.502.800.42.4解:设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3,得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 B3X1a1X1a2X1b1X1b2X1b3X2a1X2a2X2b1X3b2X3b3X3a1X3a2X3b1X3b2X3b3X4a1X4a2X4b1X4b2X4b3601110000400070004000原料费Ci (元/件) 单价Pi (元/件) 0.25 1.25 0.352.00 0.50 2.80 0.4 2.4其中,令X 3a 1,X 3b 1,X 3b 2,X 3b 3,X 4b 3=0 可建立数学模型如下: 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*(X 1a 1+X 1a 2)+1.65*(X 2a 1+X 2a 2)+2.30* X 3a 2+2.00*( X 4a 1+X 4a 2)约束条件:利用WinSQB 求解(X1~X4,X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量):4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ,且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上,最优生产计划如下:设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495,即最大利润为3495案例3. 高校教职工聘任问题 (建摸)由校方确定的各级决策目标为:P 1 要求教师有一定的学术水平。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
运筹学例题及解答

运筹学例题及解答一、市场对I、II两种产品的需求量为:产品I在1-4月每月需10000件,5-9月每月需30000件,10-12月每月需100000件;产品II在3-9月每月需15000件,其它月份每月需50000件。
某厂生产这两种产品成本为:产品I在1-5月内生产每件5元,6-12月内生产每件4.50元;产品II在1-5月内生产每件8元,6-12月内生产每件7元。
该厂每月生产两种产品能力总和应不超过120000件。
产品I容积每件0.2立方米,产品II容积每件0.4立方米,而该厂仓库容积为15000立方米,要求:(a)说明上述问题无可行解;(b)若该厂仓库不足时,可从外厂借。
若占用本厂每月每平方米库容需1元,而租用外厂仓库时上述费用增加为1.5元,试问在满足市场需求情况下,该厂应如何安排生产,使总的生产加库存费用为最少。
解: (a) 10-12月份需求总计:100000X3+50000X3=450000件,这三个月最多生产120000X3=360000件,所以10月初需要(450000-360000=90000件)的库存,超过该厂最大库存容量,所以无解。
••(b)考虑到生产成本,库存费用和生产费用和生产能力,该厂10-12月份需求的不足只需在7-9月份生产出来库存就行,则设xi第i个月生产的产品1的数量,yi第i个月生产的产品2的数量,zi,wi分别为第i个月末1,2的库存数s1i,s2i分别为用于第i+1个月库存的原有及租借的仓库容量m3,可建立模型:Lingo 程序为 MODEL: sets: row/1..16/:;!这里n 为控制参数; col/1..7/:; AZ(row,col):b,x; endsetsdata:12111277777787887898998910910109101110111110111211min (4.57)( 1.5)30000150003000015000300001500030000150003000015000.i i i i i i z x y s s x z y w x z z y w w x z z y w w x z z y w w x z z y w w st x z ===+++-=→-=+-=→+-=+-=→+-=+-=→+-=+-=→+-=+∑∑1211121100005000120000(712)0.20.415000(712)0i i i i i i iy w x z i z w s s s i ⎧⎪⎪⎪⎪⎪⎪⎪⎨=→+=⎪⎪+≤≤≤⎪+=+⎪⎪≤≤≤⎪⎪⎩变量都大于等于b=1.754167,1.737500,1.737500,1.770833,1.770833,1.762500,1.7 62500,1.667500,1.609167,1.609167,1.650833,1.650833,1.659167 ,1.659167,1.396667,1.380000,1.380000,1.438333,1.438333,1.41 3333,1.413333,1.658333,1.633333,1.633333,1.658333,1.658333, 1.658333,1.658333,1.546667,1.513333,1.513333,1.555000,1.555 000,1.546667,1.546667,1.538333,1.496667,1.496667,1.480000,1 .480000,1.505000,1.505000,1.562500,1.545833,1.545833,1.5791 67,1.579167,1.570833,1.570833,1.645833,1.604167,1.604167,1. 637500,1.637500,1.637500,1.637500,1.670833,1.645833,1.64583 3,1.645833,1.645833,1.654167,1.654167,1.454167,1.420833,1.4 20833,1.412500,1.412500,1.420833,1.420833,1.463333,1.480000 ,1.480000,1.421667,1.421667,1.430000,1.430000,1.682500,1.69 0833,1.690833,1.699167,1.699167,1.690833,1.690833,1.466667, 1.483333,1.483333,1.475000,1.475000,1.466667,1.466667,1.508 333,1.500000,1.500000,1.466667,1.466667,1.475000,1.475000,1 .552500,1.535833,1.535833,1.569167,1.569167,1.560833,1.5608 33,1.542500,1.509167,1.509167,1.550833,1.550833,1.542500, 1.542500;enddatamax=@sum(AZ(i,j): b(i,j)*x(i,j));@for(col(j): @sum(row(i):x(i,j))<=2);@for(col(j): @sum(row(i):x(i,j))>=1);@sum(AZ(i,j):x(i,j))=8;@for(row(i): @sum(col(j):x(i,j))=1);@for(AZ(i,j): @bin(x(i,j)));运行结果:Rows= 32 Vars= 112 No. integer vars= 112 ( all are linear)Nonzeros= 591 Constraint nonz= 448( 448 are +- 1) Density=0.163Smallest and largest elements in abs value= 1.00000 8.00000No. < : 7 No. =: 17 No. > : 7, Obj=MAX, GUBs <= 16Single cols= 0。
运筹学经典案例

运筹学经典案例案例一:鲍德西((B AWDSEY)雷达站的研究20世纪30年代,德国内部民族沙文主义及纳粹主义日渐抬头。
以希特勒为首的纳粹势力夺取了政权开始为以战争扩充版图,以武力称霸世界的构想作战争准备。
欧洲上空战云密布。
英国海军大臣丘吉尔反对主政者的“绥靖”政策,认为英德之战不可避免,而且已日益临近。
他在自己的权力范围内作着迎战德国的准备,其中最重要、最有成效之一者是英国本土防空准备。
1935年,英国科学家沃森—瓦特(R.Watson-Wart)发明了雷达。
丘吉尔敏锐地认识到它的重要意义,并下令在英国东海岸的Bawdsey建立了一个秘密的雷达站。
当时,德国已拥有一支强大的空军,起飞17分钟即可到达英国。
在如此短的时间内,如何预警及做好拦截,甚至在本土之外或海上拦截德机,就成为一大难题。
雷达技术帮助了英国,即使在当时的演习中已经可以探测到160公里之外的飞机,但空防中仍有许多漏洞,1939年,由曼彻斯特大学物理学家、英国战斗机司令部科学顾问、战后获诺贝尔奖金的P.M.S.Blachett为首,组织了一个小组,代号为“Blachett 马戏团”,专门就改进空防系统进行研究。
这个小组包括三名心理学家、两名数学家、两名应用数学家、一名天文物理学家、一名普通物理学家、一名海军军官、一名陆军军官及一名测量人员。
研究的问题是:设计将雷达信息传送给指挥系统及武器系统的最佳方式;雷达与防空武器的最佳配置;对探测、信息传递、作战指挥、战斗机与防空火力的协调,作了系统的研究,并获得了成功,从而大大提高了英国本土防空能力,在以后不久对抗德国对英伦三岛的狂轰滥炸中,发挥了极大的作用。
二战史专家评论说,如果没有这项技术及研究,英国就不可能赢得这场战争,甚至在一开始就被击败。
“Blackett马戏团”是世界上第一个运筹学小组。
在他们就此项研究所写的秘密报告中,使用了“Operational Research”一词,意指作战研究”或“运用研究”。
第七章---运筹学-运输问题案例

第七章运输问题7.1 一个农民承包了6块耕地共300亩,准备播种小麦、玉米、水果和蔬菜四种农产品,问如何安排种植计划,可得到最大的总收益。
解:这是一个产销平衡的运输问题。
可以建立以下的运输模型:代入产销平衡的运输模板可得如下结果:得种植计划方案如下表:7.2 某客车制造厂根据合同要求从当年开始起连续四年年末交付40辆规格型号相同的大型客车。
该厂在这四年内生产大型客车的能力及每辆客车的成本情况如下表:根据该厂的情况,假设制造出来的客车产品当年未能交货,每辆车每积压一年的存储和维护费用为4万元。
在签订合同时,该厂已储存了20辆客车,同时又要求四年期未完成合同后还需要储存25辆车备用。
问该厂如何安排每年的客车生产量,使得在满足上述各项要求的情况下,总的生产费用加储存维护费用为最少?解:得运价表〔产大于销的运输模型〕如下:第一季度正常上班生产20台,加班27台,拿出正常生产18台和加班2台,加上年前储存的20台,满足本季度的40台;第二季度正常生产38台,不安排加班。
加上第一季度储存的2台,满足本季度的40台;第三季度正常生产15台,不安排加班。
加上第一季度储存的25台,满足本季度的40台;第四季度正常生产42台。
加班生产23台。
拿出正常生产的17台的加班生产的23台满足本季度的40台。
剩余25台以后务用。
7.3 某企业生产有甲、乙、丙、丁四个分厂生产同一种产品,这四个分厂的产量分别为:200吨、300吨、400吨和100吨,这些产品供给给A、B、C、D、E、F六个地区,六个地区的需求量分别为:200吨、150吨、350吨、100吨、120吨、120吨。
由于工艺、技术的差异,各分厂运往各销售地区的单位运价〔万元/吨〕、各厂单位产品成本〔万元/吨〕和各销地的销售价格〔万元/吨〕如下表:12、如果E地区至少供给100吨,试确定该公司获利最大的产品调运方案。
2、如果E地区至少供给100吨,C地区的需要必须全部得到满足,试确定该公司获利最大的产品调运方案。
(典型例题)《运筹学》运输问题

xj0,yij0,zij0,(i=1,┈,4;j=1,┈,5)
2008/11
--22--
--《Ⅵ 产量
新购 1 第一天 M 第二天 M 第三天 M
第四天 M
1 1 1 1 0 5200
0.2 0.1 0.1 0.1 0 1000
2008/11
--21--
建立模型:
--《运筹学》 运输问题--
设 xj—第j天使用新毛巾的数量;yij—第i天送第j天使用快洗 餐巾的数量;zij—第i天送第j天使用慢洗餐巾的数量;
Min z=∑xj+∑∑0.2yij+∑∑0.1zij
第一天:x1=1000
需 第二天:x2+y12=700
求 约
m1
xij b j (j 1,2,...,n)
i1
x 0 (i 1,...,m,m 1; j 1,...,n) ij
2008/11
--16--
--《运筹学》 运输问题--
销>产问题单位运价表
产地销地 B1 B2 ┈
A1
C11 C12 ┈
A2
C21 C22 ┈
┊ ┆┊┈
Am Cm1 Cm2 ┈
2008/11
--8--
产销平衡表
--《运筹学》 运输问题--
单位运价表
B1 B2 B3 B4 产量
A1 (1) (2) 4 3 7 A2 3 (1) 1 (-1) 4 A3 (10) 6 (12) 3 9 销量 3 6 5 6
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
Ⅰ Ⅱ
示。又如果生产出来的柴
Ⅲ
运筹学 例子

x1 , x2 , x3 , x4 , x5
0 4 0 0 8 16 16 16 0 0 5 15 15 0 15 15
是否 可行
否 是 是 是 否 是 否 是
Z=w
对偶问题(DP)
是否可行
y1 , y2 , y3 , y4 , y5
17 15* 14 8 12 9 18 0
0 1/ 2 3/ 5 0 0 是 1 0 1/ 5 0 0 是 3/ 2 1/ 4 0 0 0 否 0 1/ 2 0 0 3 否 1 0 0 0 1 否 0 0 3/5 2 0 否 3/ 2 0 0 1 0 是 0 0 0 2 3 否
P1 P 3 P 4 P2 P3 P5 P2 P4 P5 P3 P4 P5 P1 P 3 P 5 P1 P 4 P 5 P2 P3 P4
P1 P 2 P 3
P1 P 2 P 4
P1 P 2 P 5
对于基矩阵 B1,x1, x 2, x 3基变量 x 4, x 5为非基变量。 令,则约束方程变为 2 x1 2 x 2 x 3 12 x1 4 4 x1 16 x2 3 x 3 1 5 x 2 15 所以相对于 B1的基本解是 X=(4, 3,-2, 0) 0, T 因为 x 3小于零,所以其不是基 代入目标函数得 Z= 17 本可行解。
阵
2 2 1 2 2 0 2 2 0 B1 4 0 0 ......B 2 4 0 1 ......B 3 4 0 0 0 5 0 0 5 0 0 5 1 2 1 0 2 0 0 2 1 0 B 4 4 0 0 ......B 5 4 1 0 ......B 6 0 0 1 0 0 1 0 0 1 5 0 0 2 0 0 1 0 0 B 7 0 1 0 ......B 8 0 1 0 5 0 1 0 5 1 2 1 0 2 1 0 B 9 4 0 1 ......B10 0 0 0 0 0 0 5 0 0 因为矩阵 B1-B 8的行列式不等于零,所 以为基矩阵 矩阵 B 9,B10的行列式等于零,所以 不是基矩阵。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
运筹学考试题型

运筹学考试题型一、图解法求解(见书)二、单纯形法例:12max 2Z x x =+ 123515x x +≤ 126224x x +≤ 120x x ≥、解:在上述问题的约束条件中加入松弛变量x3、x4,得到1234max 200Z x x x x =+++1233515x x x ++= 1246224x x x ++= 12340x x x x ≥、、、因为所有检验数都已为负或零,所以最优解TX *=(15/4,3/4,0,0) 目标函数值33/4Z *=三、加入人工变量(大 M 法,两阶段法)例:123max 235Z x x x =+-1237x x x ++=1232510x x x -+≥1230x x x ≥、、(1)采用大M 法解:在上述问题的约束条件中加入人工变量x4、剩余变量x5、人工变量x6,得到123456max 2350Z x x x Mx x Mx =+--+-12347x x x x +++=123562510x x x x x -+-+= 1234560x x x x x x ≥、、、、、其中M 为任意大的正数 用单纯形表进行计算,见下表:因为所有检验数都已负或零,所以最优解TX *=(45/7,4/7,0,0,0,0) 目标函数值102/7Z *=(2)采用两阶段法解:先在上述问题的约束条件中加入人工变量x4、剩余变量x5、人工变量x6,得到46max W x x =--第一阶段求得的结果0W =,得到的最优解TX *=(45/7,4/7,0,0,0,0) 因为人工变量460,0x x ==,所以T因为所有检验数都已负或零,所以最优解TX *=(45/7,4/7,0,0) 目标函数值102/7Z *=四、运输问题(伏格尔法)例采用闭回路法求检验数13759121a =-+-=- 2116912109a =-+-= 221091267a =-+-=32461053a =-+-=331059121057a =-+-+-= 3410121053a =-+-=因为检验数,所以须调整方案,调整后如下表所示采用闭回路法求检验数14129571a =-+-= 211657108a =-+-= 22105766a =-+-=32461053a =-+-= 331071058a =-+-= 34109571054a =-+-+-=因为所有空格的检验数都大于0, 所以此方案为最优。
2.6-运筹学应用实例汇总
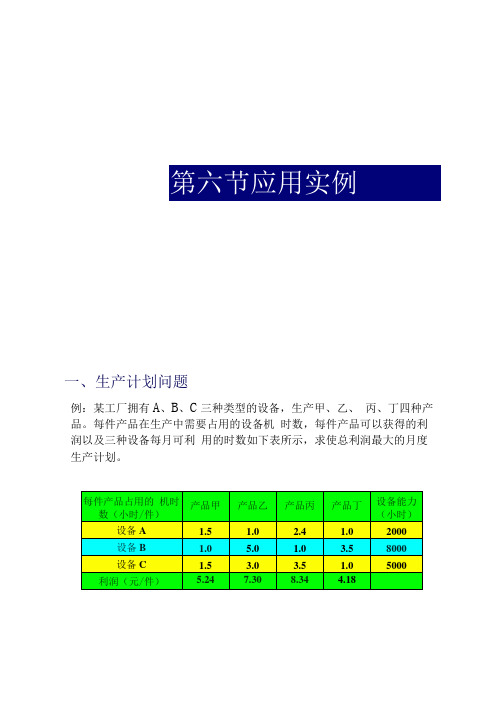
一、生产计划问题例:某工厂拥有A、B、C三种类型的设备,生产甲、乙、丙、丁四种产品。
每件产品在生产中需要占用的设备机时数,每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示,求使总利润最大的月度生产计划。
建模思路■用线性规划制订使总利润最大的生产计划。
■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。
在加工时间以及利润与产品产量成线性关系的假设下,可以建立如下的线性规划模型:建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习:某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
数据如下表。
问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?甲 .乙丙资源限制铸造工时(小时/件)51078000机加工工时(小时/件)64812000装配工时(小时/件)32210000自产铸件成本(兀/件)354外协铸件成本(兀/件)56一机加工成本(元/件)213装配成本(元/件)322产品售价(元/件)231816解:设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数,同,幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求占的利润:利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协,其余自制的利润产品乙全部自制的利润产品乙铸造外协,其余自制的利润产品丙的利润可得到毛(i = 1,2, 3,4,5)的利润分别为15、10、7、13、9=23-(3+2+3)=15 =23-(5+2+3)=13 =18-(5+1+2)=10 =18-(6+1+2)=9 =16-(4+3+2)=7通过以上分析,可建立如下的数学模型:目标函数:Max 15百+ 10电+ 7两+ 13题+ 9不约束条件:5为+ 10西+ 7玛<80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛,演,传,演,与12000 10000二、混合配料问题例:某工厂要用四种合金T1, T2, T3和T4为原料,经熔炼成为一种新的不锈钢G。
大学生运筹学例题案例

Lingo 软件实践练习 1.题目:已知6个发点8个收点的最小费用运输问题。
产销量及单位运价如下表。
求出结果。
分析过程:Min Z = Cij Xij∑=61i Xij <=bj (j=1...8) 销量约束∑=81j Xij = ai (i=1...6) 产量约束Xij ≥ 0(i=1...6;j=1...8)Lingo软件中输入data:capacity=55 47 42 52 41 32;demand=60 55 51 43 41 52 43 38;cost=6 2 9 7 4 2 5 94 5 5 3 8 5 3 25 2 1 3 7 4 8 37 6 7 9 9 2 7 12 3 6 5 7 2 6 55 9 2 2 8 1 4 3;enddataend软件出的结果:Global optimal solution found.Objective value: 473.0000 Infeasibilities: 0.000000 Total solver iterations: 9 Model Class: LP Total variables: 48Nonlinear variables: 0Integer variables: 0Total constraints: 15Nonlinear constraints: 0Total nonzeros: 144Nonlinear nonzeros: 0最终结果:Row Slack or Surplus Dual Price1 473.0000 -1.0000002 19.00000 0.0000003 0.000000 0.0000004 9.000000 0.0000005 0.000000 0.0000006 41.00000 0.0000007 6.000000 0.0000008 39.00000 0.0000009 0.000000 1.00000010 0.000000 -2.00000011 0.000000 -3.00000012 0.000000 -1.00000013 0.000000 -2.00000014 0.000000 -2.00000015 0.000000 -1.000000 求解结果:最小费用为 4732. Lingo软件实践练习某车间有长度180的钢管(数量充分多),今要从这钢管截得70的管料150跟,52的管料200根,35的管料80根,请建立数学模型解决:怎样的截法,既能完成任务,也能使剩下的余料最少?解答过程目标函数:minz=x1+x2+x3+x4+x5+x6+x7+x8约束条件:2x1+x2+x3+x4>1502x2+x3+3x5>2002x6+x7>80Lingo软件中输入:Min x1+x2+x3+x4+x5+x6+x7+x8s.t.2x1+x2+x3+x4>1502x2+x3+3x5>2002x6+x7>80运算结果:Global optimal soulation found at iteration: 0Objectionvalue: 193.0000Variable value reduc ed costX1 25.00000 0.0 00000X2 100.0000 0.0 00000X3 0.000000 0.2 500000X4 0.000000 0.5 000000X5 0.000000 0.2 500000X6 0.000000 1. 000000X7 68.00000 0. 000000X8 0.000000 1. 000000Row slack or surplus dual price1 193.0000 -1.0000002 0.000000 -0.50000003 0.000000 -0.250000004 0.000000 -1.000000剩余最少为 193既能完成任务,也能使剩下的余料最少?lingo软件使用3.线性规划问题一种汽油的特性可用两个指标描述:其点火性用“辛烷数”描述,其挥发性用“蒸汽压力”描述。
运筹学案例

运筹学案例(第一部分)案例1 高压电器强电流试验计划的安排某高压电器研究所属行业归口所,是国家高压电器试验检测中心,每年都有大量的产品试验、中试、出口商检等任务.试验计划安排及实施的过程一般如下:·提前一个月接受委托试验申请·按申请的高压电器类别及台数编制下月计划·按计划调度,试验产品进入试验现场·试验检测,出检测报告·试验完成,撤出现场高压电器试验分强电流试验和高压电试验两部分,该研究所承担的强电流实验任务繁重,委托试验的电器量很大,因此科学地计划安排试验计划显得非常重要。
高压电器分十大类,委托试验的产品有一定随机性,但是试验量最多的产品(占85%以上)是以下八类:1.35KV断路器2.10KV等级断路器3.35KV开关柜4.10KV等级开关柜5.高压熔断器6.负荷开关7.隔离开关8.互感器这八类产品涉及全国近千个厂家,市场广阔,数量庞大。
当前的强电流产品试验收费标准见表1—1。
表1-1 强电流产品试验收费标准由于强电流试验用的短路发电机启动时,会给城市电网造成冲击,严重影响市网质量,故只能在中午1点用电低谷时启动,从而影响全月连续试验工时只有约108小时,任务紧张时只能靠加班调节。
正常情况下各种试验所需试验工时见表8—2。
表1—2 各类产品试验所需工时强电流试验特点是开机时耗电量大,而每次实验短路时,只持续几秒钟,虽然短路容量在“0”秒时达2500 MVA,但瞬时耗电量却很小.每天试验设备提供耗电量限制为5000千瓦,每月135千千瓦,那麽每种产品耗量如表8-3所示。
各类产品的冷却水由两个日处理能力为14吨的冷却塔供给.每月按27天计,冷却水月供给量为14×27=378吨.每月各类产品冷却水处理量见表8-3。
表1—3 各类产品试验耗电量与冷却水处理量根据以往的经验和统计报表显示第一类产品和第二类产品每月最多试验台数分别为6台和4台,第三类和第四类产品则每月至少需分别安排8台和10台。
运筹学案例1
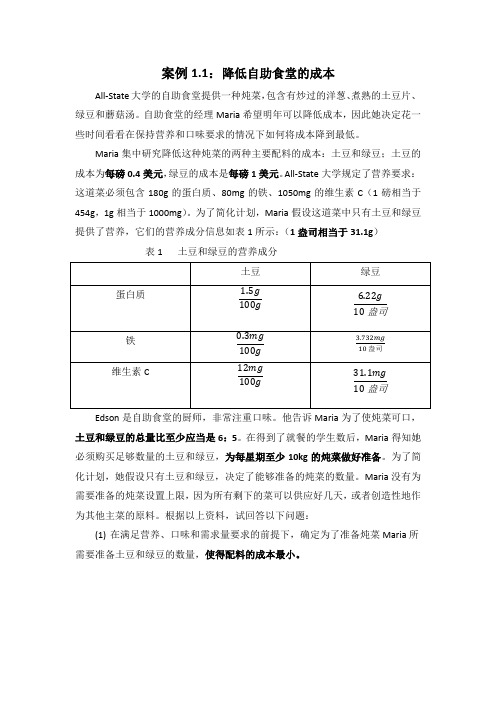
案例1.1:降低自助食堂的成本All-State大学的自助食堂提供一种炖菜,包含有炒过的洋葱、煮熟的土豆片、绿豆和蘑菇汤。
自助食堂的经理Maria希望明年可以降低成本,因此她决定花一些时间看看在保持营养和口味要求的情况下如何将成本降到最低。
Maria集中研究降低这种炖菜的两种主要配料的成本:土豆和绿豆;土豆的成本为每磅0.4美元,绿豆的成本是每磅1美元。
All-State大学规定了营养要求:这道菜必须包含180g的蛋白质、80mg的铁、1050mg的维生素C(1磅相当于454g,1g相当于1000mg)。
为了简化计划,Maria假设这道菜中只有土豆和绿豆提供了营养,它们的营养成分信息如表1所示:(1盎司相当于31.1g)表1 土豆和绿豆的营养成分Edson是自助食堂的厨师,非常注重口味。
他告诉Maria为了使炖菜可口,土豆和绿豆的总量比至少应当是6:5。
在得到了就餐的学生数后,Maria得知她必须购买足够数量的土豆和绿豆,为每星期至少10kg的炖菜做好准备。
为了简化计划,她假设只有土豆和绿豆,决定了能够准备的炖菜的数量。
Maria没有为需要准备的炖菜设置上限,因为所有剩下的菜可以供应好几天,或者创造性地作为其他主菜的原料。
根据以上资料,试回答以下问题:(1)在满足营养、口味和需求量要求的前提下,确定为了准备炖菜Maria所需要准备土豆和绿豆的数量,使得配料的成本最小。
(2)Maria没有太多地考虑炖菜的口味,她只考虑了满足营养要求和削减成本,因此她要求Edson改变配方,使得土豆和绿豆最低质量比可以为1:2。
在这种新的配方下,确定Maria每个星期需要购买的土豆和绿豆的数量。
(3)由于Maria认为其他配料,如洋葱和蘑菇汤也含有铁,因此她决定将铁含量的要求降低到65mg。
在这种新的配方下,确定Maria每个星期需要购买的土豆和绿豆的数量。
(4)Maria得知批发商有多余的绿豆,因此绿豆的价格降低到每磅0.5美元。
运筹学期末复习例题.doc

《运筹学》期末复习例题例1 :用图解法求解下面的LP问题:max z — 6%1 —2x2厂2兀1 —兀2 W 22%1 — 3%2 三 6xi W 6J1 ,兀2 $ 0解,由图知,该问题因为没有可行解,因而也没有最优解。
例2:某饲料厂用含蛋白质、葡萄糖、氨基酸的四种原料,配制一种新营养保健品。
四种原料中1 2 3 4成分蛋白质(%)30 40 20 15葡萄糖(%)20 30 25 40氨基酸(%)40 25 55 30单价(元)30 40 35 50要求该保健品中含蛋白质不少于20%,葡萄糖不少于35%,氨基酸不少于30%。
由于技术上的原因,原料2的用量不能少于30%,原料4不能超过40%。
试建立一个线性规划模型,以便求得成本最低而又合乎要求的新营养保健品(建模不计算)。
解:设单位产品中需要第j种原料的比例为心则可建立线性规划模型: min z=30%i + 40%2 + 35%3 + 50%4r30xi + 40%2 + 20%3 + 15%4》2020xi + 30%2 + 25%3 + 40%4》3540xi + 25%2 + 55%3 + 30%4》30〈疋》0.3 %4 < 0.4 兀1 +兀2 +兀3 +兀4 = 1 匕1,兀2,兀3,兀4》0例3:某工厂计划期内要安排生产A、B两种产品。
已知生产单位产品的利润与所需的资源如要求:(列出线性规划模型;(2)用图解法求解该问题的最优解;(3)用单纯形法求解最优解,并指出单纯形法的迭代步骤解与图解法顶点的关系。
例4:某工厂计划期内要安排生产A、B两种产品。
已知生产单位产品的利润与所需的资源如要求:(列出线性规划模型;(2)用图解法求解该问题的最优解;(3)用单纯形法求解最优解,并指出单纯形法的迭代步骤解与图解法顶点的关系。
问:1.表中解是否为最优解?为什么?写出该解。
2.若X4、*5、X6分别是原问题的松驰变量,请写出在该表中相应的对偶问题的解。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示.又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2—25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间.甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
四个运筹学案例
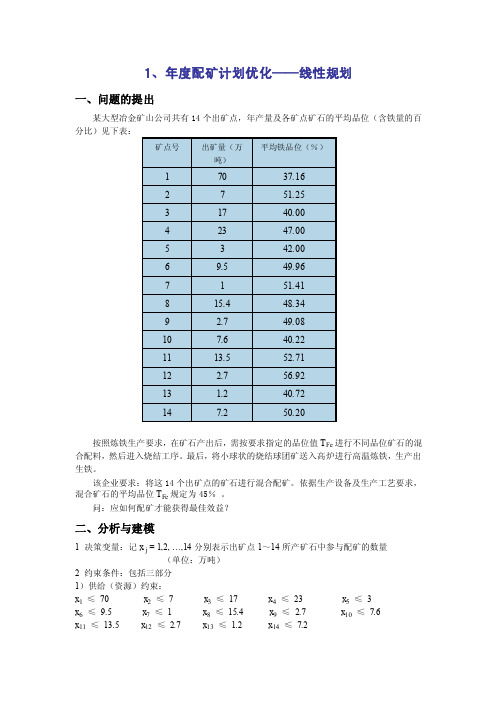
1、年度配矿计划优化——线性规划j(单位:万吨)2 约束条件:包括三部分1)供给(资源)约束:x1 ≤70 x2≤7 x3≤17 x4≤23 x5≤3 x6≤9.5 x7≤1 x8≤15.4 x9≤ 2.7 x10≤7.6 x11≤13.5 x12≤2.7 x13≤1.2 x14≤7.22)品位约束3)非负约束: x j ≥ 0 j = 1,2,3, … ,143 目标函数:此题目要求“效益最佳”有一定的模糊性,由于配矿后的混合矿石将作为后面 工序的原料而产生利润,故在初始阶段,可将目标函数选作配矿总量的极大化。
三、计算结果及分析1 计算结果利用单纯形法可得出该问题的最优解为:x1 = 31.121 x2 = 7 x3 = 17 x4 = 23 x5 = 3 x6 = 9.5 x7 = 1 x8 = 15.4 x9 = 2.7 x10 = 7.6 x11 = 13.5 x12 = 2.7 x13 = 1.2 x14 = 7.2 最优值:Z* = 141.921(万吨)2 分析与讨论1)计算结果是否可被该公司接受?——回答是否定因为:①在最优解中,除第1个采矿点有富裕外,其余13个采矿点的出矿量全部参与了配矿。
而矿点1在配矿以后尚有富余量 70 -31.12 =38.879 (万吨),但矿点1的矿石品位仅为37.16%,属贫矿。
②该公司花费了大量人力、物力、财力后,在矿点1生产的贫矿中却有近39万吨矿石被闲置,而且在大量积压的同时,还会对环境造成破坏,作为该公司的负责人或公司决策者是难以接受这样的生产方案的。
———原因何在?出路何在?2)解决问题的思路经过分析后可知:在矿石品位T Fe 及出矿量都不可变更的情况下,只能把注意力集中在 混合矿石的品位T Fe 要求上。
——不难看出,降低T Fe 的值,可以使更多的低品位矿石参与配矿。
问题:T Fe 的值有可能降低吗?在降低T Fe 的值,使更多的贫矿入选的同时,会产生什么影响?——以上问题就属于运筹学的灵敏度分析(优化后分析)3)经调查,以及与现场操作人员、工程技术人员、管理人员学习、咨询,拟定了三个T Fe 的新值:44% 、43% 、42%3 变动参数之后再计算,结果如下表所示:∑==+++++++++++++14114131211109875432145.0502.04073.05692.05271.04022.0408.04834.05141.064996.04200.04700.0400.05125.03716.0j jx x x x x x x x x x x x x x x ∑==141max j jx zFe境的破坏,故不予以考虑。
运筹学案例素材

例题1 合金制造问题有一家钢铁公司收到一份500吨造船用钢的订单.对这些造船用钢有如下要求:此公司储存有七种再现的原材料,都可以用于制造这种钢。
表6.2列出了这些析材料的品质,可用库存量,以及价格表6.2 原材料品质,可用库存量,与价格例题2 露天采矿探测发现了一个露天铀矿。
根据一些探测钻探的结果,发现这个矿可以分为若干个可开采区。
矿坑需要挖掘成阶梯形,以方便卡车开到矿坑底部。
铀矿呈东西方向分布。
在西面有一个村庄,在东面是山脉,因此矿坑大小要受到它们限制。
考虑了这些限制之后,确定有18个可开采区,呈三层分布。
总储蓄所量为10000吨,如下图,为挖掘一个可开采区,首露天矿山结构图挖开第一层的区块每吨需要耗费100欧元,挖开的二层的区块每吨需要耗费200欧元,挖开的二层的区块每吨需要耗费300欧元。
但是如果有区块是由含很多石英的石头组成(显示为斜线区域),那么由于这些石头非常硬,因此每吨需要耗费1000欧元。
只有以灰色显示的区块才含有铀(1,7,10,12,17,18)。
其市场价值分别为200,300,500,1000,和1200欧元/吨。
第18区块,尽管也含有大量矿石,但是此区块也和其他绘有斜线的区块一样,含水量有大量非常硬的石头。
为使总收益达到最大,应掘开那些区块?例题3 电力生产为满足每日电力需求(单位为兆瓦),可以选用四种不同类型的发电机。
每日电力需求如下表所示。
所有发电机都存在一个启动成本,以及工作于最小功率状态时势固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
这些数据均列于下表中。
表4 发电机描述出任何代价。
在任意时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。
问题是:在每个时段应分别作用哪些发电机才能够使每天的总成本电小?例题4 汽车租赁有一家小型汽车租赁公司,此公司有94辆可供出租的汽车,分布于10个代理点中。
运筹学课件例题集锦

优质资料欢迎下载1.1线性规划标准型max Z=c1x1+c2x2+…+c n x ns.t. a11x1+a12x2+…+a1n x n =b1a21x1+a22x2+…+a2n x n =b2a m1x1+a m2x2+….+a mn x n =b m x1,x2….x n≥ 0用两个变量的差值代替无约束变量,左边加一个变量将<变=,左边减一个变量将>变=。
目标函数左边乘-1将min Z变max Z1用对偶单纯形法解下列线性规划问题min S = x1 + 4x2 + 3x4s.t. x1+2x2- x3 +x4≥ 3-2x1 - x2+4x3 +x4≥ 2x1,x2,x3,x4≥ 0解:此题可用人工变量方法求,但也可用对偶单纯形法。
max S’ = -x1- 4x2 - 3x4s.t. -x1 -2x2+ x3 -x4 +x5= -3 2x1 + x2-4x3 -x4+x6 = -2常数项是负数且最小,确定出基变量x5。
用出基变量x5行的所有负数分别去除对应的检验数,最小值对应的为进基变量x1,交叉元素为主元(-1)主元运算:第一行乘(-1)【提示:表格同上,x5行对应数字乘-1,这里不抄】主元运算:第二行加上第一行乘(-2)【提示:是对应第二张表的,继续画出表3】计算检验数确定出基变量X确定进基变量X,主元(-2)计算检验数:全为非正。
但此时常数b已全大于零,最优解=(7,0,4,0)最优值S’= - 7 S=72用对偶单纯形法解下列线性规划问题min S = x1 + 2x2s.t. -x1+2x2 - x3≥ 1 -x1 -2x2+ x3≥ 6 x1,x2,x3≥ 0解:将原问题化成max S’ = -x1 - 2x2常数项最小出基变量X5,按比值无法比较。
常数项次小出基变量X4,按比值X2为进基变量。
主元(-2)主元运算:第一行乘(-1/2)【提示:表格同上X4行对应数字乘-1/2,画出表格2】主元运算:第二行加第一行乘(-2)【提示:是对表2而言的,画出表3】常数项为负数的行元素全大于零,原问题无可行解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学典型题型案例集第一章线性规划1 生产计划问题((摘自王治祯环境应用数学309页))某企业为了搞好综合利用,用三种废品生产三种副产品,生产情况和利润见下表,求最佳利润。
解:设ABC三种产品的产量为X1X2X3Max Z =5X1+8X2+2X310X1+5X2+3 X3<=4006X1+10X2+2 X3<=4004X1+5X2+4X3<=200经过求解X1=34.23,X2=8.19X3=5.37最大利润为274.412 投资问题解:用Xij表示第i年初(i=1,2,3)给项目j(A,B,C,D)的投资金额。
第一年资金量:30万,可投项目:A、B;故:X1A+X1B<=30。
第二年资金量:1.2*X1A,可投项目:A、C;故:X2A+X2C<=1.2*X1A。
第三年资金量:1.2*X2A+1.5*X1B,可投项目:A、B、D;故:X3A+X3B+X3D<=1.2*X2A+1.5*X1B。
其它条件:X1B<=20;X2C<=15;X3D<=10。
目标:第三年底收益最大。
因投资X3B在第3年底不能收回,故无收益。
则目标函数为:f(x)=0.2*(X1A+ X2A + X3A)+0.5*X1B+0.6* X2C+0.4* X3D LINGO Model如下:max =0.2*(X1A+ X2A + X3A)+0.5*X1B+0.6* X2C+0.4* X3D;X1A+X1B<=30;X2A+X2C<=1.2*X1A;X3A+X3B+X3D<=1.2*X2A+1.5*X1B;@bnd(0,X1B,20); @bnd(0,X3B,20); @bnd(0,X2C,15); @bnd(0,X3D,10);运行结果如下:Global optimal solution found.Objective value: 27.50000Total solver iterations: 2Variable Value Reduced CostX1A 12.50000 0.000000X2A 0.000000 0.6000000E-01X3A 16.25000 0.000000X1B 17.50000 0.000000X2C 15.00000 -0.1000000X3D 10.00000 -0.2000000X3B 0.000000 0.2000000Row Slack or Surplus Dual Price1 27.50000 1.0000002 0.000000 0.80000003 0.000000 0.50000004 0.000000 0.2000000投资计划解释:第一年年初投资A项目12.5万元,投资B项目17.5万元;第二年年初投资C项目15万元;第三年年初投资A项目16.25万元,投资D项目10万元;第三年年年末可获最大收益27.5万元。
3 志愿者排班问题志愿者排班问题解答解:(1)假设从早上8点开始,整点时有xi位志愿者开始工作,如下表:从20:00开始,工作时间由3小时调整为2小时,但接待时间到22:00为止,刚好为2小时,故此条件不构成限制。
为方便计算,假定x6=x7=0。
设每个时间段需要的工作人数为zi,则:2,([8,21])ij i xj zi i=-≥=∑;目标:所需志愿者最少。
LINGO Model如下:min= X8 +X9+ X10+ X11+ X12+ X13+ X14+ X15+ X16+ X17+ X18+ X19+ X20+ X21;X8>=4; X8+ X9>=4; X8+ X9+ X10>=6; X9+ X10+ X11>=6; X10+ X11+ X12>=8;X11+ X12+ X13>=8; X12+ X13+ X14>=6; X13+ X14+ X15>=6; X14+ X15+ X16>=4; X15+ X16+ X17>=4;X16+ X17+ X18>=6; X17+ X18+ X19>=6; X18+ X19+ X20>=8; X19+ X20+ X21>=8;运行LINGO软件得到问题的最优解(只列出非零变量):最优目标函数值=32.00000X8=4.000000 X10=4.000000 X11=2.000000 X12=2.000000X13=4.000000 X15=2.000000 X16=2.000000 X17=4.000000X19=2.000000 X20=6.000000根据运行结果,最优时间表确定如下,此时最少人数为32人(2)没有志愿者愿意在12:00和18:00开始工作,即增加约束条件:X12=0; X18=0。
LINGO Model如下:min= X8 +X9+ X10+ X11+ X12+ X13+ X14+ X15+ X16+ X17+ X18+ X19+ X20+ X21;X8>=4; X8+ X9>=4; X8+ X9+ X10>=6; X9+ X10+ X11>=6; X10+ X11+ X12>=8;X11+ X12+ X13>=8; X12+ X13+ X14>=6; X13+ X14+ X15>=6; X14+ X15+ X16>=4; X15+ X16+ X17>=4;X16+ X17+ X18>=6; X17+ X18+ X19>=6; X18+ X19+ X20>=8; X19+ X20+ X21>=8;X12=0; X18=0;运行LINGO软件得到问题的最优解(只列出非零变量):最优目标函数值=32.00000X8=4.000000 X10=6.000000 X11=2.000000 X13=6.000000 X16=4.000000 X17=2.000000 X19=4.000000 X20=4.000000根据运行结果,最优时间表确定如下,此时最少人数为32人第二章灵敏度分析解:(1)设每天生产A1产品用奶x1桶,生产A2产品用奶x2桶。
则LINGO Model 如下:max= 24*3*x1+ 16*4*x2;x1+ x2 <=50;12*x1+ 8*x2 <=480;3*x1 <=100;运行结果如下:Global optimal solution found.Objective value: 3360.000Total solver iterations: 2Variable Value Reduced CostX1 20.00000 0.000000X2 30.00000 0.000000Row Slack or Surplus Dual Price1 3360.000 1.0000002 0.000000 48.000003 0.000000 2.0000004 40.00000 0.000000灵敏度分析结果如下:Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient Increase Decrease X1 72.00000 24.00000 8.000000X2 64.00000 8.000000 16.00000Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 50.00000 10.00000 6.6666673 480.0000 53.33333 80.000004 100.0000 INFINITY 40.00000生产计划:每天用20桶奶生产A1产品,用30桶奶生产A2产品获利最大,每天可获利3360元。
附加问题:①由影子价格可知,原料增加1单位,利润增长48元,成本为35元,所以可以买。
由灵敏度分析结果,每天最多再购买10桶牛奶。
②由影子价格可知,时间增加1单位,利润增长2元,所以聘用临时工人的工资最多2元/小时。
③由灵敏度分析可知,x1系数范围是(72-8,72+24),当A1产品获利增加到30元/kg时,即x1系数为30*3=90<72+24,在允许范围内,所以不应改变生产计划。
2 课本81页2.12 林敏度分析第三章运输问题1产销平衡的运输问题(摘自王治祯环境应用数学330页)某城市有三个工厂,每个工厂生产都产出一定量的剩余物(通称为污染物),本着化害为宝的精神,需将各厂的废物分别输送到本市内其他单位搞综合利用,一直每厂的剩余物和各厂的需要量及运价表,试用表上作业法求满足现有条件的运费最少的分配方案.解:(中间过程略)最优运送方案表为此时总运费为20502 产销不平衡的运输问题解:(1)设xij(i,j=1,2,3)为产地i运往客户j的运量,列表如下(运量、运费):建立数学模型如下:min=10*x11+4*x12+12*x13+8*x21+10*x22+3*x23;目标x11+x12+x13<=3000;约束条件x21+x22+x23<=4000;约束条件x31+x32+x33<=1500;约束条件x11+x21+x31>=2000;约束条件x12+x22+x32>=1500;约束条件x13+x23+x33>=5000;约束条件运行结果如下:(只列出部分结果)Objective value: 33000.00Variable ValueX11 1500.000X12 1500.000X13 0.000000X21 0.000000X22 0.000000X23 4000.000X31 500.0000X32 0.000000X33 1000.000运输方案:产地1分别给客户1、2发货1500单位;产地2给客户3发货4000单位;产地3给客户1发货500单位,给客户3发货1000单位。
最低运费为33000。
3 课本104页3.9飞行安全问题转化的运输问题4 人员分配问题某检测站在一定时间内要化验一批水样,共分析16个项目,其中重金属A4项,有机物B5项,物理分析C3项,其他分析D4项,在分析期间,一部分人外出采样,站立仅仅有4人能够承担化验任务,根据每人世纪工作情况,化验员甲乙丙丁能完成4354项任务,每人完成不同任务注释:划横线为不能胜任此项工作此时用时最少为19.第四章整数规划与分配问题(摘自北京工业大学薛毅编写的数学建模实验)1监控摄像头的最优安装问题(0-1整数规划)3 指派问题1利用5种不同质量浓度的有机废水灌溉5块土质相同的草地,各质量浓度的污水灌溉草地收提示:此时最佳收获量为120+130+115+125+80=570第八章动态规划1 最短路径问题2电器安全可靠性问题(课本216页8.9)3招聘问题(课本216页8.12)第九章决策分析1风险型决策的决策树法(课本317页11.511.611.8类似)某厂因生产需要,考虑是否自行研制一个新的安全装置,首先,决定这个研制项目是否需要评审,如果需要评审,则需要评审费5000元,不评审,则可省去这笔评审费用,如进行评审,通过概率为0.8,不通过概率为0.2。
