运筹学部分课后习题集解答1
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
(完整版)运筹学》习题答案运筹学答案

《运筹学》习题答案一、单选题1.用动态规划求解工程线路问题时,什么样的网络问题可以转化为定步数问题求解()BA.任意网络B.无回路有向网络C.混合网络D.容量网络2.通过什么方法或者技巧可以把工程线路问题转化为动态规划问题?()BA.非线性问题的线性化技巧B.静态问题的动态处理C.引入虚拟产地或者销地D.引入人工变量3.静态问题的动态处理最常用的方法是?BA.非线性问题的线性化技巧B.人为的引入时段C.引入虚拟产地或者销地D.网络建模4.串联系统可靠性问题动态规划模型的特点是()DA.状态变量的选取B.决策变量的选取C.有虚拟产地或者销地D.目标函数取乘积形式5.在网络计划技术中,进行时间与成本优化时,一般地说,随着施工周期的缩短,直接费用是( )。
CA.降低的B.不增不减的C.增加的D.难以估计的6.最小枝权树算法是从已接接点出发,把( )的接点连接上CA.最远B.较远C.最近D.较近7.在箭线式网络固中,( )的说法是错误的。
DA.结点不占用时间也不消耗资源B.结点表示前接活动的完成和后续活动的开始C.箭线代表活动D.结点的最早出现时间和最迟出现时间是同一个时间8.如图所示,在锅炉房与各车间之间铺设暖气管最小的管道总长度是( )。
CA.1200B.1400C.1300D.17009.在求最短路线问题中,已知起点到A,B,C三相邻结点的距离分别为15km,20km,25km,则()。
DA.最短路线—定通过A点B.最短路线一定通过B点C.最短路线一定通过C点D.不能判断最短路线通过哪一点10.在一棵树中,如果在某两点间加上条边,则图一定( )AA.存在一个圈B.存在两个圈C.存在三个圈D.不含圈11.网络图关键线路的长度( )工程完工期。
CA.大于B.小于C.等于D.不一定等于12.在计算最大流量时,我们选中的每一条路线( )。
CA.一定是一条最短的路线B.一定不是一条最短的路线C.是使某一条支线流量饱和的路线D.是任一条支路流量都不饱和的路线13.从甲市到乙市之间有—公路网络,为了尽快从甲市驱车赶到乙市,应借用()CA.树的逐步生成法B.求最小技校树法C.求最短路线法D.求最大流量法14.为了在各住宅之间安装一个供水管道.若要求用材料最省,则应使用( )。
运筹学习题集(第一章)

判断题判断正误,如果错误请更正第1章线性规划1.任何线形规划一定有最优解。
2.若线形规划有最优解,则一定有基本最优解。
3.线形规划可行域无界,则具有无界解。
4.在基本可行解中非基变量一定为0。
5.检验数λj表示非基变量Xj增加一个单位时目标函数值的改变量。
6.minZ=6X1+4X2|X1-2X|︳<=10 是一个线形规划模型X1+X2=100X1>=0,X2>=07.可行解集非空时,则在极点上至少有一点达到最优解.8.任何线形规划都可以化为下列标准型Min Z=∑C j X j∑a ij x j=b1, i=1,2,3……,mX j>=0,j=1,2,3,……,n:b i>=0,i=1,2,3,……m9.基本解对应的基是可行基.10.任何线形规划总可用大M 单纯形法求解.11.任何线形规划总可用两阶段单纯形法求解。
12.若线形规划存在两个不同的最优解,则必有无穷多个最优解。
13.两阶段中第一阶段问题必有最优解。
14.两阶段法中第一阶段问题最优解中基变量全部非人工变量,则原问题有最优解。
15.人工变量一旦出基就不会再进基。
16.普通单纯形法比值规则失效说明问题无界。
17.最小比值规则是保证从一个可行基得到另一个可行基。
18.将检验数表示为λ=C B B-1A-的形式,则求极大值问题时基本可行解是最优解的充要条件为λ》=0。
19.若矩阵B为一可行基,则|B|≠0。
20.当最优解中存在为0的基变量时,则线形规划具有多重最优解。
选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。
第1章线性规划1.线形规划具有无界解是指:A可行解集合无界B有相同的最小比值C存在某个检验数λk>0且a ik<=0(i=1,2,3,……,m) D 最优表中所有非基变量的检验数非0。
2.线形规划具有多重最优解是指:A 目标函数系数与某约束系数对应成比例B最优表中存在非基变量的检验数为0 C可行解集合无界D存在基变量等于03.使函数Z=-X1+X2-4X3增加的最快的方向是:A (-1,1,-4)B(-1,-1,-4)C(1,1,4)D(1,-1,-4-)4.当线形规划的可行解集合非空时一定A包含原点X=(0,0,0……)B有界C 无界D 是凸集5.线形规划的退化基本可行解是指A基本可行解中存在为0的基变量B非基变量为C非基变量的检验数为0 D最小比值为06.线形规划无可行解是指A进基列系数非正B有两个相同的最小比值C第一阶段目标函数值大于0 D用大M法求解时最优解中含有非0的人工变量E可行域无界7.若线性规划存在可行基,则A一定有最优解B一定有可行解C可能无可行解D可能具有无界解E全部约束是〈=的形式8.线性规划可行域的顶点是A可行解B非基本解C基本可行解D最优解E基本解9.minZ=X1-2X2,-X1+2X2〈=5,2X1+X2〈=8,X1,X2〉=0,则A有惟一最优解B有多重最优解C有无界解D无可行解E存在最优解10.线性规划的约束条件为X1+X2+X3=32X1+2X2+X4=4X1,X2,X3,X4〉=0 则基本可行解是A(0,0,4,3)B(0,0,3,4)C(3,4,0,0)D(3,0,0,-2)计算题1.1 对于如下的线性规划问题MinZ= X1+2X2s.t. X1+ X2≤4-X1+ X2≥1X2≤3X1, X2≥0的图解如图所示。
规划数学(运筹学)第三版课后习题答案 习 题 1(1)

习 题 11 用图解法求解下列线性规划问题,并指出问题具有唯一最优解、无穷最优解、无界解还是无可行解。
⎪⎩⎪⎨⎧≥≥+≥++=0x x 42x 4x 66x 4x 3x 2x minz )a (21212121, ⎪⎩⎪⎨⎧≥≥+≤++=0x ,x 124x 3x 2x 2x 2x 3x maxz )b (21212121⎪⎩⎪⎨⎧≤≤≤≤≤++=8x 310x 512010x 6x x x maxz )c (212121⎪⎩⎪⎨⎧≥≤+-≥-+=0x ,x 23x 2x 2x 2x 6x 5x maxz )d (21212121 答案: (a)唯一解3*,)5.0,75.0(*==z X T); (b)无可行解;(c)唯一解16*,)6,10(*==z X T); (d)无界解)2 用单纯形法求解下列线性规划问题。
⎪⎩⎪⎨⎧≥≤+≤++=0x ,x 82x 5x 94x 3x 5x 10x maxz )a (21212121 ⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+=0x ,x 5x x 242x 6x 155x x 2x maxz )b (212121221 答案:(a)唯一解5.17*,)5.1,1(*==z X T),对偶问题5.17*,)786.1,357.0(*==w Y T; (b)唯一解5.8*,)5.1,5.3(*==z X T),5.8*,)5.0,25.0,0(*==w Y T3 用大M 法和两阶段法求解下列线性规划问题,并指出属于哪一类解。
⎪⎪⎩⎪⎪⎨⎧≥≥-≥+-≥+++-=0x x x 0x 2x 2x 2x 6x x x 2x x 2x maxz )a (3,2,13231321321 ⎪⎩⎪⎨⎧≥≥+≥++++=0x ,x ,x 62x 3x 82x 4x xx 3x 2x minz )b (32121321321答案:(a)无界解;(b)唯一解8*,)0,8.1,8.0(*==z X T),对偶问题8*,)0,1(*==w Y T4已知线性规划问题的初始单纯形表(如表1-54所示)和用单纯形法迭代后得到的表(如表1-55所示)如下,试求括弧中未知数a ~l 的值。
运筹学版熊伟编著习题答案

运筹学(第3版)习题答案P36 P74 P88 P105 P142 P173 P195 P218 P248 P277 P304 品P343 P371全书420页第1章 线性规划工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.产品 资源 A B C 资源限量 材料(kg) 4 2500 设备(台时) 3 1400 利润(元/件)101412310和130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:型号A 型号B 每套窗架需要材料长度(m ) 数量(根)长度(m) 数量(根)A 1:2 2B 1: 2 A 2:3 B 2:23需要量(套)300400问怎样下料使得(1)用料最少;(2)余料最少. 【解 方案 一 二 三 四 五 六 七 八 九 十 需要量 B1 2 1 1 1 0 0 0 0 0 0 800 B2 2 0 1 0 0 2 1 1 0 0 0 1200 A1 2 0 0 1 0 0 1 0 2 1 0 600 A2120 2 3 900 余料(m) 0 1 1 1 01设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ (2)余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩某企业需要制定1~6月份产品A 的生产与销售计划。
运筹学课后习题解答_1.(DOC)

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题min z=2x1 3x2a4x1 6x2 6 )2x2 4 st.. 4x1x1, x2 0解:由图 1 可知,该问题的可行域为凸集 MABCN,且可知线段 BA上的点都为最优解,即该问题有无量多最优解,这时的最优值为3z min =23 0 3 2P47 1.3 用图解法和纯真形法求解线性规划问题max z=10x1 5x 2a )3x1 4x2 95x1 2x2 8st..x1, x2 0解:由图 1 可知,该问题的可行域为凸集OABCO,且可知 B 点为最优值点,3x1 4x2x1 1 T 9 3,即最优解为x*1,3即2x2 8x2 2 5x1 2这时的最优值为 z max =10 1 5 3 35 2 2纯真形法:原问题化成标准型为max z=10x15x23x1 4 x2x39st.. 5x12x2x48x1 , x2 , x3 ,x4 010 5 0 0c jC B X B b x1 x2 x3 x49 3 4 1 0x38 [5] 2 0 1x410 5 0 0C j Z j21/5 0 [14/5] 1 -3/5 x38/5 1 2/5 0 1/5 10x10 1 0 -2C j Z j53/2 0 1 5/14 -3/14 x21 1 0 -1/7 2/7 10x10 0 -5/14 -25/14C j Z j1,3 T1015335因此有 x*, zmax2 2 2P78 2.4 已知线性规划问题:max z 2 x1 4x2 x3 x4x1 3x2 x4 82x1 x2 6x2 x3 x4 6x1 x2 x3 9x1 , x2 , x3,x4 0求: (1) 写出其对偶问题;(2)已知原问题最优解为X* (2,2,4,0) ,试依据对偶理论,直接求出对偶问题的最优解。
解:( 1)该线性规划问题的对偶问题为:min w 8 y1 6 y2 6 y3 9 y4y1 2 y2 y4 23y1 y2 y3 y4 4y3 y4 1y1 y3 1y1, y2 , y3 ,y4 0(2)由原问题最优解为X* ( 2,2,4,0) ,依据互补废弛性得:y1 2 y2 y4 23y1 y2 y3 y4 4y3 y4 1把 X * (2,2,4,0) 代入原线性规划问题的拘束中得第四个拘束取严格不等号,即 2 2 4 8 9 y4 0y1 2 y2 2进而有3y1 y2 y3 4y3 1得 y 4 , y2 3, y31, y 01 5 5 4( 4,3,1,0)T,最优值为w min16因此对偶问题的最优解为y*5 5P79 2.7考虑以下线性规划问题:min z 60x140x280x33x12x2x3 24x1x23x3 42x12x22x3 3x1, x2 , x30( 1)写出其对偶问题;( 2)用对偶纯真形法求解原问题;解:( 1)该线性规划问题的对偶问题为:max w 2y1 4 y23y33y1 4 y2 2 y3602 y1 y22y340y13y22y380y1, y2 , y30(2)在原问题加入三个废弛变量x4 , x5 , x6把该线性规划问题化为标准型:max z 60x1 40x2 80x33x1 2x2 x3 x4 24x1 x2 3x3 x5 42 x1 2x2 2x3 x6 3x j 0, j 1, ,6c j-60 -40 -80 0 0 0 C B X B b x1 x2 x3 x4 x5 x6x4-2 -3 -2 -1 1 0 0x5-4 [-4] -1 -3 0 1 0x6-3 -2 -2 -2 0 0 1 C j Z j-60 -40 -80 0 0 0x41 0 -5/4 5/4 1 -1/12 080x11 1 1/4 3/4 0 -1/4 0x6-1 0 [-3/2] -1/2 0 -1/2 1C j Zj0 -25 -35 0 -15 0x411/6 0 0 5/3 1 1/3 -5/680x15/6 1 0 2/3 0 -1/3 1/640x22/3 0 1 1/3 0 1/3 -2/3C j Zj0 0 -80/3 0 -20/3 -50/3x* ( 5 , 2 ,0) T , z max 60 5 40 2 80 0 2306 3 6 3 3P81 2.12某厂生产A、B、C三种产品,其所需劳动力、资料等相关数据见下表。
规划数学(运筹学)第三版课后习题答案-习-题-1(1)

习 题 11 用图解法求解下列线性规划问题,并指出问题具有唯一最优解、无穷最优解、无界解还是无可行解。
⎪⎩⎪⎨⎧≥≥+≥++=0x x 42x 4x 66x 4x 3x 2x minz )a (21212121, ⎪⎩⎪⎨⎧≥≥+≤++=0x ,x 124x 3x 2x 2x 2x 3x maxz )b (21212121⎪⎩⎪⎨⎧≤≤≤≤≤++=8x 310x 512010x 6x x x maxz )c (212121⎪⎩⎪⎨⎧≥≤+-≥-+=0x ,x 23x 2x 2x 2x 6x 5x maxz )d (21212121 答案: (a)唯一解3*,)5.0,75.0(*==z X T); (b)无可行解;(c)唯一解16*,)6,10(*==z X T); (d)无界解)2 用单纯形法求解下列线性规划问题。
⎪⎩⎪⎨⎧≥≤+≤++=0x ,x 82x 5x 94x 3x 5x 10x maxz )a (21212121 ⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+=0x ,x 5x x 242x 6x 155x x 2x maxz )b (212121221 答案:(a)唯一解5.17*,)5.1,1(*==z X T),对偶问题5.17*,)786.1,357.0(*==w Y T; (b)唯一解5.8*,)5.1,5.3(*==z X T),5.8*,)5.0,25.0,0(*==w Y T3 用大M 法和两阶段法求解下列线性规划问题,并指出属于哪一类解。
⎪⎪⎩⎪⎪⎨⎧≥≥-≥+-≥+++-=0x x x 0x 2x 2x 2x 6x x x 2x x 2x maxz )a (3,2,13231321321 ⎪⎩⎪⎨⎧≥≥+≥++++=0x ,x ,x 62x 3x 82x 4x x x 3x 2x minz )b (32121321321 答案:(a)无界解;(b)唯一解8*,)0,8.1,8.0(*==z X T),对偶问题8*,)0,1(*==w Y T4已知线性规划问题的初始单纯形表(如表1-54所示)和用单纯形法迭代后得到的表(如表1-55所示)如下,试求括弧中未知数a ~l 的值。
运筹学课后习题解答-1.

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a)12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA上的点都为最优解,即该问题有无穷多最优解,这时的最优值为min 3z=23032⨯+⨯= P47 1.3 用图解法和单纯形法求解线性规划问题a)12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集OABCO,且可知B点为最优值点,即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩,即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法: 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105B CB X b 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题:1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题;(2)已知原问题最优解为)0,4,2,2(*=X ,试根据对偶理论,直接求出对偶问题的最优解。
第五版运筹学课后习题答案

第五版运筹学课后习题答案【篇一:运筹学课后习题答案林齐宁版本北邮出版社】>1、某织带厂生产a、b两种纱线和c、d两种纱带,纱带由专门纱线加工而工厂有供纺纱的总工时7200h,织带的总工时1200h。
(1) 列出线性规划模型,以便确定产品的数量使总利润最大;(2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化?对模型的解是否有影响?解:(1)设a的产量为x1,b的产量为x2,c的产量为x3,d的产量为x4,则有线性规划模型如下:max f(x)=(168?42)x1 +(140?28)x2 +(1050?350)x3 +(406?140)x4=126 x1 +112 x2 +700 x3 +266 x4?3x1?2x2?10x3?4x4?7200?s.t. ? 2x3?0.5x4?1200?xi?0, i?1,2,3,4?(2)如果组织这次生产有一次性的投入20万元,由于与产品的生产量无关,故上述模型只需要在目标函数中减去一个常数20万,因此可知对模型的解没有影响。
2、将下列线性规划化为极大化的标准形式minf(x)?2x1?3x2?5x3解:将约束条件中的第一行的右端项变为正值,并添加松弛变量x4,在第二行添加人工变量? x1? x2? x3??5 ???6x1?7x2?9x3?16 x5,将第三行约束的绝对值号打开,变为两s.t. ?|19x1?7x2?5x3|?13个不等式,分别添加松弛变量x6, x7,并令??x,x?0, x?不限3?12x3?x3??x3??,则有max[?f(x)]= {?2 x1 ?3 x2 ?5(x3??x3??)+0 x4 ?m x5+0 x6 +0 x7} ?? x3???x4?5 ?x1 ?x2 ?x3 ???6x?7x?9x??9x?? ?x?1612335????5x3?? ?x6?13 s.t. ? 19x1?7x2?5x3??19x?7x?5x??5x?? ?x7?131233??,x3??,x4,x5,x6,x7?0?x1,x2,x3?3、用单纯形法解下面的线性规划maxf(x)?2x1?5x2?3x3?3x1?2x2?x3?610??x?6x?3x?125 ?123s. t. ???2x1?x2?0.5x3?420?x1,x2,x3?0, ?解:在约束行1,2,3分别添加x4, x5, x6松弛变量,有初始基础可行解和单纯形答:最优解为x1 =244.375, x2 =0, x3 =123.125, 剩余变量x6=847.1875;最优解的目标函数值为858.125。
运筹学习题答案(1)

第一章 线性规划及单纯形法(作业)1.4 分别用图解法和单纯型法求解下列线性规划问题,并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
(1)Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解:①图解法:由作图知,目标函数等值线越往右上移动,目标函数越大,故c 点为对应的最优解,最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点,解之得X=(15/4,3/4)T 。
Max z =33/4. ② 单纯形法:将上述问题化成标准形式有: Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为:P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵,构成一个基,对应变量向,x 3,x 4为基变量,令非基变量x 1,x 2为零,找到T 优解,代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题,并指出属哪一类。
(3)Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解:这种情况化为标准形式: Max z '=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z '=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法: Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段,将表中y 1,y 2去掉,目标函数回归到Max z '=-4x 1-x 2+0x 3+0x 4第二章 线性规划的对偶理论与灵敏度分析(作业)2.7给出线性规划问题:Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求:(1)写出其对偶问题;(2)已知原问题最优解为X *=(2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
规划数学(运筹学)第三版课后习题答案习题1(1)

习 题 11 用图解法求解下列线性规划问题,并指出问题具有唯一最优解、无穷最优解、无界解还是无可行解。
⎪⎩⎪⎨⎧≥≥+≥++=0x x 42x 4x 66x 4x 3x 2x minz )a (21212121, ⎪⎩⎪⎨⎧≥≥+≤++=0x ,x 124x 3x 2x 2x 2x 3x maxz )b (21212121⎪⎩⎪⎨⎧≤≤≤≤≤++=8x 310x 512010x 6x x x maxz )c (212121 ⎪⎩⎪⎨⎧≥≤+-≥-+=0x ,x 23x 2x 2x 2x 6x 5x maxz )d (21212121 答案: (a)唯一解3*,)5.0,75.0(*==z X T); (b)无可行解;(c)唯一解16*,)6,10(*==z X T); (d)无界解)2 用单纯形法求解下列线性规划问题。
⎪⎩⎪⎨⎧≥≤+≤++=0x ,x 82x 5x 94x 3x 5x 10x maxz )a (21212121 ⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+=0x ,x 5x x 242x 6x 155x x 2x maxz )b (212121221 答案: (a)唯一解5.17*,)5.1,1(*==z X T ),对偶问题5.17*,)786.1,357.0(*==w Y T ; (b)唯一解5.8*,)5.1,5.3(*==z X T ),5.8*,)5.0,25.0,0(*==w Y T3 用大M 法和两阶段法求解下列线性规划问题,并指出属于哪一类解。
⎪⎪⎩⎪⎪⎨⎧≥≥-≥+-≥+++-=0x x x 0x 2x 2x 2x 6x x x 2x x 2x maxz )a (3,2,13231321321 ⎪⎩⎪⎨⎧≥≥+≥++++=0x ,x ,x 62x 3x 82x 4x xx 3x 2x minz )b (32121321321 答案:(a)无界解;(b)唯一解8*,)0,8.1,8.0(*==z X T),对偶问题8*,)0,1(*==w Y T4已知线性规划问题的初始单纯形表(如表1-54所示)和用单纯形法迭代后得到的表(如表1-55所示)如下,试求括弧中未知数a ~l 的值。
运筹学课后习题集规范标准答案林齐宁版本北邮出版社

运筹学课后习题集规范标准答案林齐宁版本北邮出版社No .1 线性规划1、某织带⼚⽣产A 、B 两种纱线和C 、D 两种纱带,纱带由专门纱线加⼯⽽(1) 列出线性规划模型,以便确定产品的数量使总利润最⼤;(2) 如果组织这次⽣产具有⼀次性的投⼊20万元,模型有什么变化?对模型的解是否有影响?解:(1)设A 的产量为x 1,B 的产量为x 2,C 的产量为x 3,D 的产量为x 4,则有线性规划模型如下:max f (x )=(168-42)x 1 +(140-28)x 2 +(1050-350)x 3+(406-140)x 4=126 x 1 +112 x 2 +700 x 3 +266 x 4s.t. ??=≥≤+≤+++4,3,2,1 ,012005.02 720041023434321i x x x x x x x i(2)如果组织这次⽣产有⼀次性的投⼊20万元,由于与产品的⽣产量⽆关,故上述模型只需要在⽬标函数中减去⼀个常数20万,因此可知对模型的解没有影响。
2、将下列线性规划化为极⼤化的标准形式解:将约束条件中的第⼀⾏的右端项变为正值,并添加松弛变量x 4,在第⼆⾏添加⼈⼯变量x 5,将第三⾏约束的绝对值号打开,变为两个不等式,分别添加松弛变量x 6, x 7,并令,则有max[-f (x )]= {-2 x 1 -3 x 2 -5()+0 x 4 -M x 5+0 x 6 +0 x 7}±≥≤+-=-+--≥-+++=不限321321321321321 ,0,13|5719|169765..532)(min x x x x x x x x x x x x t s x x x x fs.t. 0,,,,,,,1355719 13 5571916 9976 5 7654332173321633215332143321≥'''=+''+'-+-=+''-'+-=+''+'-+-=+''-'+--??x x x x x x x x x x x x x x x x x x x x x x x x x x x x3、⽤单纯形法解下⾯的线性规划≥≤++-≤++-≤-+++= ,0,,4205.021********* ..352)(max 321321321321321x x x x x x x x x x x x t s x x x x f 解:在约束⾏1,2,3分别添加x 4, x 5, x 6松弛变量,有初始基础可⾏解和单纯答:最优解为x1 =244.375, x2 =0, x3 =123.125, 剩余变量x6 =847.1875;最优解的⽬标函数值为858.125。
清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

m ax Z 3 x1 2 x 2 2 x1 x 2 2 ( 2) st . 3 x1 4 x 2 12 x , x 0 1 2 该问题无可行解
2
( 3)
m axZ x1 x 2 6 x1 10x 2 120 st . 5 x1 10 5 x2 8
1
(3)
max Z x1 x2 6 x1 10x2 120 st . 5 x1 10 5 x 8 2
(4)
m i nZ 2 x1 3 x 2 4 x1 6 x 2 6 (1) st . 3 x1 2 x 2 4 x ,x 0 1 2 无穷多最优解 (蓝 色 线 段 上 的 点 都 是 优 最解 ) x1 6 1 , x2 , 是 其 中 一 个 最 优 解 5 5
唯一最优解, x1 10, x 2 6 Z 16
(4)
max Z 5 x1 6 x2 2 x1 x2 2 st. 2 x1 3x2 2 x ,x 0 1 2
3
该问题有无界解
1.2
将下述线性规划问题化成标准形式。
min Z 3x1 4 x2 2 x3 5 x4 4 x1 x2 2 x3 x4 2 x x x 2 x 14 2 3 4 st 1 . 2 x1 3x2 x3 x4 2 x1 , x2 , x3 0, x4无约束
解:令 w Z , x4 x41 x42, 其 中 x41,x42 0, 同时引入松弛变量 x5, 剩 余 变 量 x6, 则 标 准 形 式 为 : m axw 3 x1 4 x 2 2 x 3 5 x41 5 x42 4 x1 x 2 2 x 3 x41 x42 x x x 2x 2x x 1 2 3 41 42 5 st 2 x1 3 x 2 x 3 x41 x42 x6 x1 , x 2 , x 3 , x41 , x42 , x6 2 14 2 3x2 6 x3 3x4 9 8 x x 4 x 2 x 10 1 2 3 5 st 3x1 x6 0 ( , j 1, ,6) x j 0
第四版运筹学部分课后习题解答

第四版运筹学部分课后习题解答篇一:运筹学基础及应用第四版胡运权主编课后练习答案运筹学基础及应用习题解答习题一P461.1(a)41的所有?x1,x2?,此时目标函数值2该问题有无穷多最优解,即满足4x1?6x2?6且0?x2?z?3。
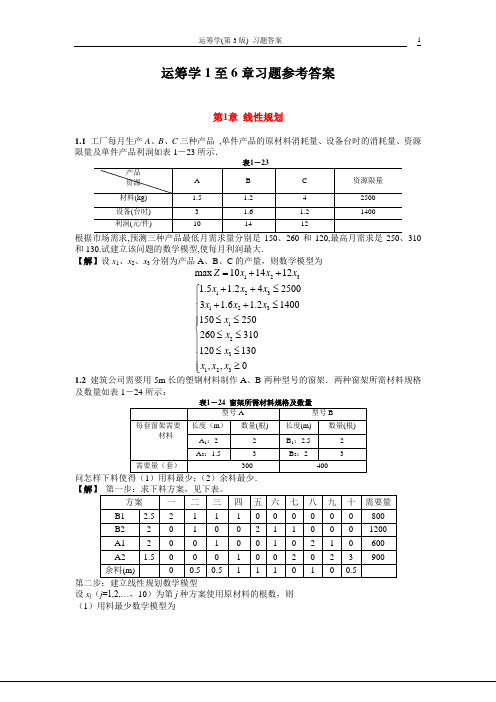
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a)约束方程组的系数矩阵?1236300A??81?4020??30000?1最优解x??0,10,0,7,0,0?T。
(b) 约束方程组的系数矩阵?1234?A2212?????211?最优解x??,0,,0?。
5??5T1.3(a)(1) 图解法最优解即为??3x1?4x2?935?3?的解x??1,?,最大值z?5x?2x?822??2?1(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式max z?10x1?5x2?0x3?0x4?3x?4x2?x3?9s.t. ?1?5x1?2x2?x4?8则P3,P4组成一个基。
令x1?x2?0得基可行解x??0,0,9,8?,由此列出初始单纯形表?1??2。
??min?,89??53?8 5?2?0,??min??218?3,??142?2?335?1,?2?0,表明已找到问题最优解x1?1, x2?,x3?0 ,x4?0。
最大值z*?22(b)(1) 图解法6x1?2x2x1?x2?最优解即为??6x1?2x2?2417?73?的解x??,?,最大值z?2?22??x1?x2?5(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式max z?2x1?x2?0x3?0x4?0x5?5x2?x3?15?s.t. ?6x1?2x2?x4?24?x?x?x?5?125则P3,P4,P5组成一个基。
令x1?x2?0得基可行解x??0,0,15,24,5?,由此列出初始单纯形表?1??2。
??min??,??245?,??461?3?3?15,24,??2?2?5?2?0,??min?新的单纯形表为篇二:运筹学习题及答案运筹学习题答案第一章(39页)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
运筹学1至6章习题参考答案
0
2
11/8
0
-3/4
0
9
X4
0
0
0
9/8
1
7/16
-1/4
27/4
6
X1
3
1
0
-1/2
0
1/4
0
3
M
X2
2
0
1
[11/16]
0
-3/32
1/8
1/8
0.181818
C(j)-Z(j)
0
0
0
0
-9/16
-1/4
37/4
X3进基、X2出基,得到另一个基本最优解。
C(j)
3
2
-0.125
6重油
7残油
辛烷值
80
115
105
蒸汽压:公斤/平方厘米
1.0
1.5
0.6
0.05
每天供应数量(桶)
2000
1000
1500
1200
1000
1000
800
问炼油厂每天生产多少桶成品油利润最大,建立数学模型。
解设xij为第i(i=1,2,3,4)种成品油配第j(j=1,2,…,7)种半成品油的数量(桶)。
10
-5
1
0
0
0
* Big M
5
3
1
0
0
0
X1
10
1
3/5
1/5
0
1/5
2
X4
0
0
4
-9
1
1
25
C(j)-Z(j)
0
-11
-1
《运筹学》(第二版)课后习题参考答案

0
0
0
b
0
d
4
1
0
0
0
2
-1
-5
0Hale Waihona Puke 1003
-3
0
0
1
0
0
0
解:(1) ;
(2) ;
(3) ;
(4) ;
(5) 为人工变量,且 为包含M的大于零的数, ;或者 为人工变量,且 为包含M的大于零的数, .
7.用大M法求解如下线性规划。
s.t.
解:加入人工变量,进行人造基后的数学模型如下:
《管理运筹学》(第二版)课后习题参考答案
第1章线性规划(复习思考题)
1.什么是线性规划?线性规划的三要素是什么?
答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
2/8
0
8
6
1
1
0
1
8/6
4
1
2
0
0
4
1/4
1
3/8
[1/8]
1/8
0
(1/4)/(1/8)
0
13/2
6
-5/4
1/4
-3/4
1
(13/2)/(1/4)
0
-1/2
3/2
-1/2
0
2
2
8
3
1
1
0
0
6
-2
-2
0
-1
1
-12
(完整word版)运筹学习题及答案

34。某个常数bi波动时,最优表中引起变化的有(A)
A.B-1bB。 C.B-1D.B-1N
35.某个常数bi波动时,最优表中引起变化的有(C)
A. 检验数 B。CBB-1C。CBB-1b D。系数矩阵
36.任意一个容量的网络中,从起点到终点的最大流的流量等于分离起点和终点的任一割集的容量.(B)A.正确B。错误C.不一定D。无法判断
9.对偶单纯形法迭代中的主元素一定是负元素( )A
A。正确B.错误C。不一定D。无法判断
10。对偶单纯形法求解极大化线性规划时,如果不按照最小化比值的方法选取什么变量则在下一个解中至少有一个变量为正( )B
A。换出变量B.换入变量C.非基变量D。基变量
11.对 问题的标准型: ,利用单纯形表求解时,每做一次换基迭代,都能保证它相应的目标函数值 必为()B
A.换出变量B.换入变量C。非基变量D。基变量
29。可行解是满足约束条件和非负条件的决策变量的一组取值.( )A
A。正确B。错误C。不一定D。无法判断
30。 连通图G有n个点,其部分树是T,则有(C)
A。T有n个点n条边 B.T的长度等于G的每条边的长度之和
C.T有n个点n-1条边 D。T有n-1个点n条边
47.通过什么方法或者技巧可以把产销不平衡运输问题转化为产销平衡运输问题(C)
A。非线性问题的线性化技巧B.静态问题的动态处理
C.引入虚拟产地或者销地D。引入人工变量
48.为什么单纯形法迭代的每一个解都是可行解?因为遵循了下列规则 (A)
A。按最小比值规则选择出基变量 B。先进基后出基规则
C。标准型要求变量非负规则 D。按检验数最大的变量进基规则
《运筹学(胡运权)》第五版课后习题答案
VARIABLE VALUE REDUCED COST
Z 0.000000 1.000000
X11 3.000000 0.000000
X21 0.000000 2800.000000
X31 8.000000 0.000000
X41 0.000000 1100.000000
X12 0.000000 1700.000000
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元,路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为:第一年年初买新车,年末卖掉再买新车,一直用到第四年年末卖掉;
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
d)
maxz=3x1+x2+4x3-0.4y
s.t.
6x1+3x2+5x3≤45
3x1+4x2+5x3-y≤30
x1,x2,x3,y≥0
用lomdo求解为
LP OPTIMUM FOUND AT STEP 0
OBJECTIVE FUNCTION VALUE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学部分课后习题解答P47 1.1用图解法求解线性规划问题min z=2x 3x 2 4为 6x 2 6 a )s.t 4x i 2x 24X i ,X 2 0解:由图1可知,该问题的可行域为凸集 MABCN ,且可知线段BA 上的点3都为最优解,即该问题有无穷多最优解,这时的最优值为Z m i n =2 3 * 3 0 3P47 1.3用图解法和单纯形法求解线性规划问题max z=10x.| 5x 23x 1 4x 2 9 s.t 5x 1 2x>8x 1, x> 0解:由图1可OABCO ,且可知B 点为最优值点,小 3x-| 4x 29 即125x 1 2x 28x 1X 213,即最优解为x * 21,3v1图1单纯形法:原问题化成标准型为max z=10x15x23\ 4x2 x39 s.t 5\ 2x2 x48X i,X2,X3,X40P78 2.4已知线性规划问题:max z 2X | 4x 2 x 3 x-i 3X 2 X 4 82为 x 26 x 2 x 3 x 4 6 x | x 2 x 39XiXX, x 4求:(1)写出其对偶问题;(2)已知原问题最优解为X * (2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
解:(1)该线性规划问题的对偶问题为:min w 8y 1 6y 2 6y 3 9y 4y 1 2y 2 y 4 2 3y 1 y 2 y 3 y 4 4 y 3 y 4 1y 1y 31%,丫2”3,丫4(2)由原问题最优解为X * (224,0),根据互补松弛性得:y 1 2y 2 y 4 2 3y 1 y 2 y w 4y a y 4 1把X *(2,2,4,0)代入原线性规划问题的约束中得第四个约束取严格不等号, 即 2 2 48 9 y 4 0 y 1 2y 22从而有3y 1 y 2 y 34所以有x *13,zmax 10 1 5I35 "2X 4y a 1/曰 4 3 “门得y i 、目2 ,y3 i,y4 05 5所以对偶问题的最优解为y* (-,3,1,0)T,最优值为W min 165 5P79 2.7考虑如下线性规划问题:(1)写出其对偶问题;min z 60为40x2 80x33为2x2x3 24x1 X2 3x3 42x1 2x2 2x3 3捲必,怡0(2 )用对偶单纯形法求解原问解:(1)该线性规划问题的对偶问题为:max w 2y1 4y2 3y33y i 4y2 2y3 602y1 y2 2y3 40 >y1 3y2 2y3 80 ,y1,y2,y3 0(2)在原问题加入三个松弛变量X4,X5,X6把该线性规划问题化为标准型max z 6 0x140X280x3x12x2X3 X4 24为x3x3 x 42x-| 2x22X3 X6 3X j 0,j 1L ,6* 52max 56 3 6 3 3P81 2.12某厂生产A、B、C三种产品,其所需劳动力、材料等有关数据见下表。
要求:(a)确定获利最大的产品生产计划;(b)产品A的利润在什么范围内变动时,上述最优计划不变;(c)如果设计一种新产品D,单件劳动力消耗为8单位,材料消耗为2单位,每件可获利3元,问该种产品是否值得生产?(d)如果劳动力数量不增,材料不足时可从市场购买,每单位0.4元。
问该厂要不要购进原材料扩大生产,以购多少为宜。
解:由已知可得,设X j表示第j种产品,从而模型为:max z 3x1x24x36x 3x2 5x345st 3x-\ 4x2 5x330MMX 0a)用单纯形法求解上述模型为:得到最优解为x* (5,0,3)Z max 3 5 4 3 27b)设产品A的利润为3 ,则上述模型中目标函数捲的系数用3 替代并求解得:要最优计划不变,要求有如下的不等式方程组成立0解得:3 92 4从而产品A 的利润变化范围为:353 -,即 2-,4-C )设产品D 用X 6表示,从已知可得16 C6 C B B P 61/5 1 1 33 812 5 5把X 6加入上述模型中求解得:2 -31 _5 3 3 _5 3从而得最优解x (0,0,5,0,0,5 /2);最优值为Z max 4 5 3 27.5 27 2所以产品D值得生产。
P101 3.1已知运输问题的产销量与单位运价如下表所示,用表上作业法求各题的最优解及最小运费。
表3-35B i B2 B3 B4 产量销地产地<A i 10 2 20 11 15A2 12 7 9 20 25A3 2 14 16 18 5销量 5 15 15 10解:由已知和最小元素法可得初始方案为产地销地^B1 B2 B3 B4 产量A1 15 15A2 0 15 10 25A3 5 0 5销量 5 15 15 10检验:B1E2 I J行位势A1 A2)2] 15 201516A30 1 =列位勢-111314由于有两个检验数小于零,所以需调整,调整一:检验:Bl B2 B3 M行位帮A1 A210]Mi)2] 15 巴珂a 0 11®^,®15 史J 101@诃0164列柱势-2 1 3 14由于还有检验数小于零,所以需调整,调整二:A151015 A2101525A3 55销量5151510从上表可以看出所有的检验数都大于零,即为最优方案 最小运费为:z min 2 5 2 5 7 10 9 15 11 10 18 0335表 3-36销地 产地^B 1 B 2 B 3 B 4产量A 1 8 4 1 2 7 A 2 6 9 4 7 25 A 3534326销量101020153 4因为 a i 58 b j 55,即产大于销,所以需添加一个假想的销地,销量为3,构成产销平衡问题,其对应各销地的单位运费都为 0检验:解:由上表和最小元素法可得初始方案为检验:B1E2B3K BE行位势A11714134斗④A35] 1皿10g3列位2000 -4势从上表可以看出所有的检验数都大于零,即为最优方案最小运费为:z min 6 9 5 1 3 10 1 7 4 13 3 15 0 3 193解:因为a i 80 b j 100,即销大于产,所以需添加一个假想的产地,产i 1 j 1量为20,构成产销平衡问题,其对应各销地的单位运费都为0B1 B2 B3 B4 B5 产量销地产地弋、A1 8 6 3 7 5 20A2 5 M 8 4 7 30A3 6 3 9 6 8 30A4 0 0 0 0 0 20销量25 2520 10 20由上表和最小元素法可得初始方案为、'销地产地^B1 B2 B3 B4 B5 产量A1 20 20A2 5 10 15 30A3 25 5 30A4 20 0 20检验:由于有两个检验数小于零,所以需调整,调整一:销地B1 B2 B3 B4 B5 -^r~、曰. 产量A1 20 20A2 20 10 30 A3 25 5 30 A4 5 0 15 20销量25 2520 10 20检验:由于还有检验数小于零,所以需调整,调整二:产地销地^B1 B2 B3 B4 B5 产量A1 20 20A2 20 10 30A3 5 25 0 30A4 0 20 20销量25 25 20 10 20检验:从上表可以看出所有的检验数都大于零,即为最优方案0 305 最小运费为:Z min 3 20 5 20 4 10 6 5 3 25 8 0 0 20 0P127 4.8用割平面法求解整数规划问题max z 7为9x2X 3x2 6a)7为x235x1,x20,且为整数解:该问题的松弛问题为:max z 7x 9x 2X 3屜 6 7为 x 2 35 x 1,x 2 0:割平面 1 为:(3 1/2) X 2 (0 7/22)X 3 (0 1/22)^1 71c c 7 11X3X 4 X 23 0X3X 4 X52 22 22 22 22 2 从而有割平面 2 为:(4 4/7) x i (0 1/7)X 4( 1 6/7)x 5X4丄7X56一X41一7 X i 4 i 0 0 0 -i i0 X3 i 0 0 i 0 -4 i0 X4 4 0 0 0 i 6 -7-2 -7C j Z j0 0 0 0由上表可知该问题已经达到整数解了,所以该整数解就是原问题的最优解,即X* 4,3 T,最优值为Z max 7 4 9 3 55P144 5.3用图解分析法求目标规划模型min Z = P i 小-+ P2 d2++ P3(2d3-+1 d4-)C) 「x i + X2 + d i-- d i+= 40x i + X2 + d2-- d2+= 40+10=50 s.t. W x i + d3-- d3+= 24x2 + d4-- d4+= 30L x i、X2、d i+、d i-、d2+、d2-、d3+、d3-、d4+、d4-> 0解:由下图可知,满足目标函数的满意解为图中的A点Pi70 6.4求下图中的最小树/h>7解:避圈法为:f^=(A,B)t^ = (C,D r B t F t G r i£} % = (A RQ匹沁G D总眄咼% 匸SEGC}局二{DE, F t H}n—GG巧込二但码H) 巧二{AEGQ D.蜀.吗RF用}⑺ 眄=SEGCDE川}耳={应}⑻ f>{—GCQ耳F,H)耳Y得到最小树为:解:如下图所示:P 173 6.14用Ford-Fulkerson 的标号算法求下图中所示各容量网络中从v到V t的最大流,并标出其最小割集。
图中各弧旁数字为容量q,括弧中为流量fj.B)解:对上有向图进行2F标号得到所以从V s 到Vt 的最大流为:f st 1 2 5 3 2 1 14科Si )由于所有点都被标号了,即可以找到增广链,所以流量还可以调整,调整量为1,得由图可知,标号中断,所以已经是最大流了,最大流量等于最小割的容量,最小 割为与直线KK 相交的弧的集合,即为(V s ,V 3),(V s ,V 4),(V s ,V 5),(V !,V t ),(V 2,V t ),(V 2,V 3)--)4)(2 3 5(4’((2 - 2由图可知,标号中断,所以已经是最大流了,最大流量等于最小割的容量,最小割为与直线(V s ,V i ),(V s ,V 3),( V 2,V 5),所以 从 V s 到 Vt 的最大流为:KK 相交的弧的集合,即为5G),4 [4〕V33(0)2 00)B ⑷解:对上有向图进行 2F 标号得到由于所有点都被标号了,即可以找到增广链,所以流量还可以调整,调整量为 1,得f st 5 3 5 13P193 7.1根据下表给定的条件,绘制 PERT 网络图。
