减治法堆排序
堆排序的几种方法

堆排序的几种方法堆排序是一种基于堆数据结构的排序算法,具有稳定且时间复杂度为O(nlogn)的特点。
本文将介绍堆排序的几种方法,包括建堆和调整堆两个关键步骤。
一、建堆建堆是堆排序的第一步,其目的是将无序的数组构建成一个堆。
堆是一种完全二叉树,分为大顶堆和小顶堆两种类型。
在大顶堆中,每个节点的值都大于或等于其子节点的值;而在小顶堆中,每个节点的值都小于或等于其子节点的值。
建堆的方法有多种,其中最常用的是从最后一个非叶子节点开始,依次向上调整每个节点的位置,直到根节点。
具体步骤如下:1. 从最后一个非叶子节点开始,向上遍历每个节点。
2. 对于当前节点,比较其与左右子节点的大小关系,如果子节点较大(或较小),则将当前节点与子节点交换位置。
3. 重复步骤2,直到当前节点满足堆的性质,或者到达叶子节点。
二、调整堆建堆完成后,数组的第一个元素一定是堆中的最大(或最小)值。
为了得到有序的数组,需要将第一个元素与最后一个元素交换位置,并对剩余元素进行堆调整。
这样,每次交换后,最大(或最小)值就会被放置在正确的位置上。
调整堆的方法有多种,其中最常用的是从根节点开始,依次向下调整每个节点的位置,直到叶子节点。
具体步骤如下:1. 将第一个元素与最后一个元素交换位置。
2. 缩小堆的范围,即排除已经有序的元素。
3. 对剩余元素进行堆调整。
从根节点开始,比较其与左右子节点的大小关系,如果子节点较大(或较小),则将当前节点与子节点交换位置。
4. 重复步骤3,直到当前节点满足堆的性质,或者到达叶子节点。
三、堆排序的优化方法除了基本的建堆和调整堆方法外,还有一些优化方法可以提高堆排序的效率。
以下是几种常见的优化方法:1. 堆的初始化:在建堆之前,先对数组进行预处理,将数组中的元素调整为局部有序,可以减少后续建堆的时间复杂度。
2. 堆的调整:在调整堆的过程中,可以使用迭代的方式代替递归,以减少函数调用的开销。
3. 堆的选择:在每次交换堆顶元素和最后一个元素后,可以选择将最后一个元素排除在堆的范围之外,从而减少调整堆的次数。
算法设计与分析部分算法伪代码

第三章 蛮力法1.选择排序SelectionSort(A[0..n-1])for i=0 to n-2 domin=ifor j=i+1 to n-1 doif A[j]<A[min]min=jswap A[i] and A[min]2.冒泡排序BubbleSort(A[0..n-1])// 输入:数组A,数组中的元素属于某偏序集// 输出:按升序排列的数组Afor i=0 to n-2 dofor j=0 to n-2-i doif A[j+1]<A[j] swap A[j] and A[j+1]3.改进的冒泡算法ALGORITHM BubbleSortImproved( A[0,…,n –1] )// 冒泡排序算法的改进// 输入:数组A,数组中的元素属于某偏序集// 输出:按升序排列的数组Afor i ← 0 to n – 2 doflag ← Truefor j ← 0 to n – 2 – i doif A[j+1] < A[j]swap(A[j], A[j+1])flag ← False// 如果在某一轮的比较中没有交换,则flag为True,算法结束returnif flag = True4. 顺序查找算法算法 SwquentialSearch2(A[0...n],k)//顺序查找算法的实现,它用了查找键来作限位器//输入:一个n个元素的数组A和一个查找键K//输出:第一个值等于K的元素的位置,如果找不到这样的元素就返回 -1A[n]<--ki<--0while A[i]!=K doi<--i+1if i<n return iElse return -15. 蛮力字符串匹配算法 BruteForceStringMatch(T[0...n-1],P[0...m-1])//该算法实现了蛮力字符串匹配代表一段文本//输入:一个n个字符的数组T[0...n-1]// 一个m个字符的数组P[0..m-1]代表一个模式//输出:如果查找成功的话,返回文本的第一个匹配字串中第一个字符的位置, // 否则返回-1For i<--0 to n-m doj<--0While j<m and P[j]=T[i+j]doj<--i+1If j=m return ireturn -1合并排序最差Θ(nlog2n)快速排序最优Θ(nlog2n)最差Θ(n2)平均Θ(1.38nlog2n)选择排序 Θ(n2)冒泡排序 Θ(n2)插入排序最差Θ(n2)最优 Θ(n)平均 Θ(n2)第四章 分治法合并排序算法 MergeSort(A[0..n-1] )排序 // 递归调用mergesort来对数组 A[0...n-1]// 输入:一个可排序数组A[0..n-1]// 输出:非降序排列的数组A[0..n-1]if n > 1n/2 -1]copy A[0.. n/2 -1] to B[0..n/2 -1]copy A[ n/2 ..n-1] to C[0..MergeSort( B )MergeSort( C )Merge( B,C,A )两个数组合并的算法算法 Merge(B[0..p-1],C[0..q-1],A[0..p+q-1])//将两个有序数组合并成一个有序的数组和C[0...q-1]//输入:两个有序数组B[0...p-1]//输出:A[0..p+q-1]中已经有序存放了B和C中的元素 i=0,j=0,k=0;while i<p and j<q do≤C[j]if B[i]A[k]=B[i], i=i+1elseA[k]=C[j], j=j+1k=k+1if i=pcopy C[j..q-1] to A[k..p+q-1]elsecopy B[i..p-1] to A[0..p+q-1]快速排序算法QuickSort(A[l..r])// 使用快速排序法对序列或者子序列排序或者序列本身A[0..n-1]// 输入:子序列A[l..r]// 输出:非递减序列Aif l < rs ← Partition( A[l..r] )QuickSort( A[l..s-1] )QuickSort( A[s+1..r] )//s是中轴元素/基准点,是数组分区位置的标志实现分区的算法Partition( A[l..r] )// 输入:子数组A[l..r]// 输出:分裂点/基准点pivot的位置p ← A[l]i ← l; j ← r+1repeat≥ prepeat i ←i + 1until A[i]≤ prepeat j ← j – 1 until A[j]swap( A[i], A[j] )≥ juntil iswap( A[i], A[j] )swap( A[l], A[j] )return j折半查找BinarySearch( A[0..n-1], k )// 输入:已排序大小为n的序列A,待搜索对象k// 输出:如果搜索成功,则返回k的位置,否则返回-1 l=0,r=n-1;While l≤rmid= (l+r)/2if k = A[mid] return midelse if k < A[mid] r=m-1else l=m+1return -1Strassen矩阵Strassen方法M1=A11(B12-B22)M2=(A11+A12)B22M3=(A21+A22)B11M4=A22(B21-B11)M5=(A11+A22)(B11+B22)M6=(A12-A22)(B21+B22)M7=(A11-A21)(B11+B12)第五章 减治法插入排序ALGORITHM InsertionSort( A[0..n-1] )// 对给定序列进行直接插入排序// 输入:大小为n的无序序列A// 输出:按非递减排列的序列Afor i ← 1 to n-1 dotemp ← A[i]j ← i-1while j ≥ 0 and A[j] > temp doA[j+1] ← A[j]j ← j –1A[j+1] ←temp深度优先查找算法 BFS(G)//实现给定图的深度优先查找遍历//输入:图G=<V,E>//输出:图G的顶点,按照被DFS遍历第一次访问到的先后次序,用连续的整数标记,将V中的每个顶点标记为0,表示还“未访问”count =0//记录这是第几个访问的节点标记为 unvisitedmark each vertex with 0//∈ V dofor each vertex vif v is marked with 0dfs(v)dfs(v)//递归访问所有和v相连接的未访问顶点,然后按照全局变量count的值//根据遇到它们的先后顺序,给它们附上相应的数字count = count + 1mark v with countv dofor each vertexw adjacent toif w is marked with 0dfs(w)广度优先BFS(G)/实现给定图的深度优先查找遍历//输入:图G=<V,E>//输出:图G的顶点,按照被BFS遍历第一次访问到的先后次序,用连续的整数标记,将V中的每个顶点标记为0,表示还“未访问”count =0mark each vertex with 0for each vertex v∈ V dobfs(v)bfs(v)//递归访问所有和v相连接的未访问顶点,然后按照全局变量count的值//根据遇到它们的先后顺序,给它们附上相应的数字count = count + 1mark v with countinitialize queue with vwhile queue is not empty doa = front of queuefor each vertex w adjacent to a doif w is marked with 0count = count + 1mark w with countadd w to the end of the queueremove a from the front of the queue拓扑排序第六章 变治法Gauss消去法GaussElimination(A[1..n], b[1..n])// 输入:系数矩阵A及常数项 b// 输出:方程组的增广矩阵等价的上三角矩阵for i=1 to n doA[i][n+1] =b[i]for j= i+1 to n dofor k = i to n+1 do– A[i][k]*A[j][i]/A[i][i]A[j][k] = A[j][k]堆排序堆排序主要包括两个步骤:对于给定的数组构造相应的堆。
C++减治法查找范围整数

while(x<k1-1||y>k2-1) { int temp; int f1,f2;//存储最小和最大数的下标 f1=x; f2=y; for(int i=x; i<=y; i++) { if(a[f1].data>a[i].data) f1=i; if(a[f2].data<a[i].data) f2=i; } if(x<k1-1) { temp=a[x].data; a[x].data=a[f1].data; a[f1].data=temp; a[x].flag=0; x++; } if(y>k2-1) { temp=a[y].data; a[y].data=a[f2].data; a[f2].data=temp; a[y].flag=0; y--; } } } void Show(Mat &a,int n,int k1,int k2)
四、实验结果:
该算法的时间复杂度取决于n的大小和输入的 K1、K2的情况,最好情况是K1、K2恰好在输入的 无序列表的两端,此时不做运算,直接输出,时间 复杂度为O(0)。最坏情况是K1=K2=n/2时,此时做 n/2次运算,时间复杂度为O(n/2)。
{ cout<<"第"<<k1<<"小到"<<k2<<"小之间的所有整数有:"; for(int i=0; i<n; i++) { if(a[i].flag) cout<<a[i].data<<" "; } cout<<endl; } void main() { int choice; cout<<" 1: 执行程序! 2: 退出程序!"<<endl; do { cout<<"请选择你的操作:"; cin>>choice; switch(choice) { case 1: { int n; int k1,k2; cout<<"请输入无序列表n的大小:"; cin>>n; cout<<"请输入无序列表中的所有整数:"; for(int i=0; i<n; i++) { a[i].flag=1; cin>>a[i].data; } cout<<"请输入k1,k2的值:"; cin>>k1>>k2;
减治法解决堆排序

算法分析实验报告减治法-堆排序学生姓名:专业:班级:学号:指导教师:2017年6月12日目录一、实验题目 (2)二、实验目的 (2)三、实验要求 (2)四、实现过程 (3)1、实验设计: (3)2、调试分析: (6)3、运行结果:........ 错误!未定义书签。
4、实验总结: (7)五、参考文献 (7)一、实验题目减治法-堆排序二、实验目的1、了解和掌握减治法的设计思想。
2、了解各种经典问题的减治思想。
三、实验要求1.[问题描述]:应用堆排序方法对一个记录序列进行升序排列。
2.[算法]:减治法:减治法是把一个大问题划分为若干个子问题,但是这些子问题不需要分别求解,只需求解其中的一个子问题,因而也无需对子问题的解进行合并。
减治法将原问题分解为若干个子问题,并且原问题(规模为n)的解与子问题(规模通常是n/2或n-1)的解之间存在某种确定的关系,这种关系通常表现为:(1)原问题的解只存在于其中一个较小规模的子问题中;(2)原问题的解与其中一个较小规模的解之间存在某种对应关系。
由于原问题的解与较小规模的子问题的解之间存在这种关系,所以,只需求解其中一个较小规模的子问题就可以得到原问题的解。
减治法只对一个子问题求解,并且不需要进行解的合并。
应用减治法(例如减半法)得到的算法通常具有如下递推式:T(n)={0;n=1 T(n/2)+1 ;n>1}分治法需要对分解的子问题分别求解,再对子问题的解进行合并,而减治法只对一个子问题进行求解,并且不需要进行解的合并。
所以,通常来说,应用减治法处理问题的效率是很高的,一般是O(logn)数量级。
四、实现过程1、实验设计:1.堆排序是利用堆得特性进行排序的方法,其基本思想是:首先将待排列的记录序列构造成一个堆,此时,堆顶记录是堆中所有记录的最大者,将它从堆中移走,然后将剩余记录再调整成堆,这样又找出了次大记录,依次类推,直到堆中只有一个记录为止。
2.图解过程3.算法实现void SiftHeap(int r[],int k,int n) {int i,j,temp;i=k;j=2*i+1;while(j<n){if(j<n-1&&r[j]<r[j+1])j++;if(r[i]>r[j])break;else{temp=r[i];r[i]=r[j];r[j]=temp;i=j;j=2*i+1;}}}void HeapSort(int r[],int n)int i,temp;for(i=(n-1)/2;i>=0;i--)SiftHeap(r,i,n);for(i=1;i<=n-1;i++){temp=r[0];r[0]=r[n-i];r[n-i]=temp;SiftHeap(r,0,n-i);}}2、调试分析:算法Sift将根结点与左右子树的根结点进行比较,若不满足堆的条件,则将根结点与左右子树根结点的较大者进行交换,所以,每比较一次,需要调整的完全二叉树的问题规模就减少一半,因此,其时间性能是O(㏒₂n)。
第7章 减治法(《算法设计与分析(第3版)》C++版 王红梅 清华大学出版社)

比较对象,若 k 与中间元素相等,则查找成功;若 k 小于中间元素,则在中间元
算 法 设
计
素的左半区继续查找;若 k 大于中间记录,则在中间元素的右半区继续查找。不
与 分
析
断重复上述过程,直到查找成功,或查找区间为空,查找失败。
( 第
版 )
k
清 华
大
学
[ r1 … … … rmid-1 ] rmid [ rmid+1 … … … rn ] (mid=(1+n)/2)
Page 4
3
7.1.2 一个简单的例子——俄式乘法
【问题】俄式乘法(russian multiplication)用来计算两个正整数 n 和 m 的乘积
,运算规则:如果 n 是偶数,计算 n/2×2m;如果 n 是奇数,计算(n-1)/2×2m+
m;当 n 等于 1 时,返回 m 的值。
算
法
俄式乘法的优点?
与 分 析
2. 测试查找区间[low,high]是否存在,若不存在,则查找失败,返回 0;
( 第
3. 取中间点 mid = (low+high)/2; 比较 k 与 rmid,有以下三种情况:
版 )
3.1 若 k < rmid,则 high = mid - 1;查找在左半区进行,转步骤2;
清 华
3.2 若 k > rmid,则 low = mid + 1;查找在右半区进行,转步骤2;
Page 12
7.2.2 选择问题
【想法】假定轴值的最终位置是 s,则: (1)若 k=s,则 rs 就是第 k 小元素; (2)若 k<s,则第 k 小元素一定在序列 r1 ~ rs-1 中; (3)若 k>s,则第 k 小元素一定在序列 rs+1 ~ rn 中。
关于清除五堆实施方案

关于清除五堆实施方案清除五堆实施方案。
为了改善环境质量,保护生态环境,提升城市形象,我们制定了清除五堆实施方案。
五堆指的是乱堆、乱倒、乱扔、乱堆放、乱搭建。
这些不文明行为严重影响了城市的整体形象和环境卫生,需要采取有效措施进行清除和整治。
首先,我们将加强宣传教育工作,提高市民的环保意识和文明素质。
通过举办环保知识讲座、宣传栏、社区宣传等方式,让市民了解乱堆、乱倒等行为对环境和城市形象的危害,引导他们养成良好的环境卫生习惯,自觉抵制乱堆行为。
其次,我们将加大执法力度,加强对乱堆、乱倒等行为的监督和处罚。
建立健全相关执法制度,加强巡查和监督力度,对发现的乱堆、乱倒等行为进行严肃处理,依法处以相应的罚款或行政处罚,形成震慑效应,减少此类行为的发生。
同时,我们将加强环境整治工作,对城市中已存在的乱堆、乱倒等现象进行清理和整治。
通过组织环卫工人和志愿者开展环境整治行动,清理城市中的乱堆、乱倒垃圾和废弃物,改善城市环境卫生状况,提升城市整体形象。
此外,我们还将加强监督管理,建立健全长效机制,加强对城市环境卫生的监督和管理。
建立环境卫生督查制度,加强对环卫工作的监督检查,及时发现和解决环境卫生问题,确保城市环境卫生工作的持续改善。
最后,我们将加强与社区和居民的沟通和合作,形成良好的环保氛围。
通过开展环保主题活动、建立环保志愿者队伍等方式,积极引导和组织居民参与环保行动,共同维护城市环境卫生,共建美丽家园。
综上所述,清除五堆实施方案是一项全方位、多措并举的工作,需要全社会的共同努力和参与。
只有通过持续不懈的努力,才能彻底改变城市环境卫生状况,建设更加美丽宜居的城市。
让我们携起手来,共同为清除五堆,美化城市环境而努力!。
分冶法

f ( n) n 1 ( n ), d 1
d
T (n) 2T (n / 2) ( n 1)
a b 2, d 1, a b
d
d
T ( n) ( n lg n)
解递推方程得精确解: T (n) n log2 n n 1
10:39
13/42
减一技术
原问题(规模 n) (1) 子问题(n-1) (n-1)解 (n) 解 扩展解
无解
折 半 查 找
原问题解
插 入 排 序
10:39
22/42
插入排序(Insertion Sort)
任务:对 n 个元素作插入排序(规模 n) 减一策略 ——自顶向下:规模减小 ① 规模减小:规模减一,即 n-1 ② 求解:解 n-1规模子问题 ③ 扩展解:n-1规模解扩展为 n规模解 扩展方法的不同,有不同的插入排序 减一过程递归进行,直到 规模 = 1或0 为止 实现方法 —— 自底向上:规模增大 为便于实现,规模从 0 或 1 增加到 n
1, n 2 T ( n) k 2T ( n / 2) 1, n 2
10:39
7/42
分治法的一般时间效率分析 规模 n , 每次分为 a 个子问题,子问题规模相等 n/b 为简化分析, 不妨设 n = bk, k = 1, 2, 3, ...
通用分治递推式
c , n t 常量时间(基本操作次数) T ( n) aT ( n / b) f ( n), n t , a 1, b 2, c 0 f (n) : 分解时间 + 合并时间
平均 Tavg (n) 2n ln n 1.38n log2 n (n log2 n) 效率
智慧树知道网课《算法分析与设计(山东联盟)》课后章节测试满分答案1

第一章测试1【判断题】(10分)一个问题的同一实例可以有不同的表示形式A.错B.对2【判断题】(10分)同一数学模型使用不同的数据结构会有不同的算法,有效性有很大差别。
A.错B.对3【判断题】(10分)问题的两个要素是输入和实例。
A.对B.错4【单选题】(10分)算法与程序的区别是()A.有穷性B.确定性C.输出D.输入5【单选题】(10分)解决问题的基本步骤是()。
(1)算法设计(2)算法实现(3)数学建模(4)算法分析(5)正确性证明A.(3)(1)(5)(4)(2)B.(3)(4)(1)(5)(2)C.(1)(2)(3)(4)(5)D.(3)(1)(4)(5)(2)6【单选题】(10分)下面说法关于算法与问题的说法的是()。
A.算法是一种计算方法,对问题的每个实例计算都能得到正确答案。
B.证明算法不正确,需要证明对任意实例算法都不能正确处理。
C.如果一个算法能应用于问题的任意实例,并保证得到正确解答,称这个算法解答了该问题。
D.同一问题可能有几种不同的算法,解题思路和解题速度也会显著不同。
7【多选题】(10分)下面关于程序和算法的说法正确的是()。
A.算法的每一步骤必须要有确切的含义,必须是清楚的、无二义的。
B.程序总是在有穷步的运算后终止。
C.程序是算法用某种程序设计语言的具体实现。
D.算法是一个过程,计算机每次求解是针对问题的一个实例求解。
8【多选题】(10分)最大独立集问题和()问题等价。
A.最大团B.稳定匹配问题C.区间调度问题D.最小顶点覆盖9【多选题】(10分)给定两张喜欢列表,稳定匹配问题的输出是()。
A.完美匹配B.最大匹配C.稳定匹配D.没有不稳定配对10【单选题】(10分)问题变换的目的有()。
(1)复杂变简单(2)未知变已知(3)隐式变显式(4)难解变易解(5)以上都是。
A.(5)B.(1)C.(2)D.(3)E.(4)11【单选题】(10分)按照霍纳法则,计算p(x)=a n x n+a n-1x n-1+…+a1x1+a0的数量级为____。
基础算法

2.依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
3.若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶 点均被访问过为止。
深度优先搜索属于盲目搜索,是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序 表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现 DFS算法。
快速排序算法
快速排序算法快速排序是由东尼·霍尔所发展的一种排序算法,算法步骤如下:
1.从数列中挑出一个元素,称为“基准”。
2.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的 数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作。
1.初始时令S={V0},T={其余顶点},T中顶点对应的距离值。若存在,d(V0,Vi)为弧上的权值;若不存在, d(V0,Vi)为。
2.从T中选取一个其距离值为最小的顶点W且不在S中,加入S。
3.对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值。
4.重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止。
归并排序
归并排序归并排序(Mergesort),又称合并排序,是建立在归并作上的一种有效的排序算法。该算法是 采用分治法(DivideandConquer)的一个非常典型的应用。算法步骤如下:
1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列; 2.设定两个指针,最初位置分别为两个已经排序序列的起始位置; 3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置; 4.重复步骤3直到某一指针达到序列尾; 5.将另一序列剩下的所有元素直接复制到合并序列尾。 归并排序的平均时间复杂度为Ο(nlogn)。
清五堆实施方案

清五堆实施方案一、背景介绍。
清五堆是指清洁、分类、减量、资源化、无害化五个环保处理要素的简称。
在当前环境保护日益受到重视的背景下,清五堆实施方案的制定和实施对于推动环境保护工作具有重要意义。
二、目标设定。
1.清洁,通过科学技术手段,减少环境污染物排放,提高环境空气质量。
2.分类,建立健全的垃圾分类体系,促进资源回收利用,减少对自然资源的消耗。
3.减量,通过节约能源、减少排放等手段,降低环境负荷,实现资源的可持续利用。
4.资源化,将垃圾转化为资源,推动循环经济发展,实现资源的最大化利用。
5.无害化,采用环保技术手段,减少环境污染,保护生态环境。
三、实施方案。
1.加强宣传教育。
通过举办环保知识讲座、开展环保宣传活动等形式,提高公众对环保工作的认识和重视程度,培养环保意识,引导大家积极参与环保行动。
2.建立健全的管理制度。
制定相关环保法律法规,建立健全的环保管理机制,加大对环境违法行为的打击力度,形成严格的环保监管体系。
3.推动垃圾分类。
加强对居民的垃圾分类宣传教育,建立健全的垃圾分类收集体系,推动居民养成垃圾分类的良好习惯。
4.加强环境监测。
建立完善的环境监测体系,加强对环境质量的监测和评估,及时发现和解决环境问题,保障环境质量。
5.推动环保科技创新。
鼓励企业加大环保科技研发投入,推动环保科技创新,提高环保技术水平,推动清五堆实施方案的落地实施。
四、预期效果。
1.环境质量提升,通过清五堆实施方案的落实,环境质量得到有效改善,大气、水质、土壤等环境指标明显改善。
2.资源利用效率提高,加强垃圾分类和资源化利用工作,实现资源的最大化利用,降低资源消耗。
3.环保意识提升,通过宣传教育和政策法规的引导,居民环保意识得到提升,环保行动得到积极响应。
4.环保产业发展,推动环保科技创新,激发环保产业发展活力,促进经济可持续发展。
五、总结。
清五堆实施方案的制定和实施,对于推动环境保护工作具有重要意义。
通过加强宣传教育、建立健全的管理制度、推动垃圾分类、加强环境监测和推动环保科技创新等措施,预计将取得显著的环保效果,为建设美丽中国、实现可持续发展作出积极贡献。
减治法

(2)插入法调整堆 关键问题是:在堆中插入一个结点,如何调整被插入结点, 使整个完全二叉树仍然是一个堆?
40 32 28 20 35 (a) 35与28交换 18 12 20 8 20 35 28 (b) 35与32交换 32 18 12 40 20 8 20 32 28 35 18 12 40 20 8
(c) 35<40调整完毕
假设当前堆中有k个结点,则要插入结点的编号为 k+1,插入法调整堆的算法如下:
算法4.5——插入法调整堆
1. 设i指向当前要插入的结点; 2. 若结点i是整个堆的根结点,则调整完毕; 3.否则,设j指向结点i的双亲结点;将结点i与结点j进行比较; 3.1 如果结点i的关键码小,则完全二叉树已经是堆,调整完毕; 3.2 否则将r[i]与r[j]交换;令i=j,转步骤2继续进行调整;
例:查找值为14的记录的过程: 0 1 2 3 4 5 6 7 8 9 10 11 12 13
7 14 18 21 23 29 31 35 38 42 46 49 52 low=1
18>14
mid=3
mid=7 31>14 high=6
high=13
high=2 mid=1
7<14
low=2 mid=2
时间性能是O(logn)。
算法4.4——筛选法调整堆 void SiftHeap(int r[ ], int k, int n) { i=k; j=2*i; //置i为要筛的结点,j为i的左孩子 while (j<=n) //筛选还没有进行到叶子 { if (j<n && r[j]<r[j+1]) j++; //比较i的左右孩子,j为较于左右孩子中的较大者 break; else { r[i]←→r[j]; //将根结点与结点j交换 i=j; j=2*i; //被筛结点位于原来结点j的位置 } } }
算法 第六章 变治法

2yy11 y2
1 5
1 2
y1
1 2
y2
y3
0
易得:
2x1 x2 x3 1 3x2 3x3 3
2x3 2
(y1,y2,y3)=(1,3,-2), (x1,x2,x3)=(1,0,-1)
17
评价
• 1 一旦的到矩阵A的LU分解,无论对于什么样的 右边向量b,我们都可以对方程组Ax=b求解,每 次求一个。
要比较两次就可以知道是搜索成功还是需要向3 棵子树继续递归搜索。
31
• 插入算法:
• 当一个结点x需要插入到2-3树中的时候,总是根据它 的大小关系,把其插入到叶结点中。
• 插入前首先调用搜索算法找到待插入的叶结点,如果 该叶结点是2-node型的,则直接插入即可;
• 如果该叶结点是3-node型的,在按序插入到叶结点后, 需要把叶结点拆分(因为插入后使得叶结点的关键字 个数为3,不满足2-3树的要求)。
<k
>k
< k1
(k1,k2)
> k2
2-node
3-node
29
2-3树的搜索与插入
• 看书理解 • 1 搜索算法p167 • 2 插入算法p168
30
• 搜索算法 • 如果待搜索树的根是2-node型结点,搜索操作
与二叉搜索树搜索操作相同; • 如果待搜索树的根是3-node型结点,最多只需
38
4 堆结点的删除
• 只考虑删除根中的键 • 把待删除结点与堆中最后一个键K对调。 • 执行删除操作并把堆的大小减一。 • 对删除后的堆进行调整直到满足堆的约束条件。 • 删除的效率分析: • 取决于交换和规模减一后,树的堆化所需的键值
减治法——精选推荐

减治法核⼼数学式:1. f(n) = f(n-1) + F; 应⽤:插⼊排序;⽣成排序/⼦集2. f(n) = f(n/2) + F; 应⽤:假币问题;俄式乘法3. f(n) = f(n-k) + F; 应⽤:查找第k⼤/⼩的元素实现思路:考虑对于元素数量为n的集合的执⾏结果,如何⽤数量为n-1、n/2或者n-k的集合的执⾏结果来表⽰实现⽅法:迭代和递归都可以/** 减治法* 主要思路:* 基于减治法f(n) = f(n-1)...的思路,可以想象,* 对于长度为n的序列,它的所有⼦集,是它前⾯n-1元素所构成⼦集* 都加最后⼀个元素* 例⼦:* "abcd"全部⼦集是"abc"全部⼦集中的元素都加⼀个'd'*/list<string> jianzhi(const string &str, int cursor) {if (0 == cursor) {list<string> subs;subs.add(""):return subs;}list<string> all_subs = jianzhi(str, cursor - 1);for(list<string>::iterator iter = all_subs.begin();iter != all_subs.end();iter++) {*iter += str[cursor];}return all_subs;}/** 第k⼤/⼩的问题*/// 减治法,每次迭代缩⼩需要查找的范围int findKmost(array[0, n], k) {pivot = getPivot(array[0,n]);index = surePivotPos(array[0, n], pivot);if (index == k-1)return pivotelse if (index > k-1)return findKmost(array[0, index], k)elsereturn findKmost(array[index, n], k-index)}。
农村堆垛治理方案

农村堆垛治理方案背景随着农村工业化的进程和农村经济的飞速发展,农村堆垛问题日益严重。
农村堆垛数量巨大、种类繁多,甚至在一些地区已经成为严重的环境污染问题,给当地居民的生产和生活带来了不利影响。
因此,如何对农村堆垛进行有效治理就成为当前亟待解决的问题。
现状分析堆垛问题的危害农村堆垛的问题主要表现为数量多、面积大、容易燃烧的特点。
如果不加以有效治理,会给当地居民的生产、生活和财产带来诸多危害,如下所述:1.环境污染:大量无序堆放的垃圾、废旧物品会对环境带来严重危害,例如影响空气质量、水质和土壤质量等。
2.安全隐患:农村堆垛常常存在着易燃易爆、滋生有害生物的隐患,一旦爆炸、起火,就可能给周围居民造成巨大的生命财产损失。
3.影响美观:大量的堆垛不仅影响了当地的环境卫生,还会给城乡面貌带来不良的影响。
中国的农村堆垛治理目前存在如下问题:1.治理意识不强:一些地区政府和居民对农村堆垛的治理并不重视,对堆垛的数量、组织、处置等方面没有明确的规划和要求。
2.技术手段缺乏:目前,对于农村堆垛治理的技术手段有限,一些堆垛治理企业对于农村堆垛的处理手段比较单一、粗糙。
3.治理成本高:一些农村堆垛的治理工作成本高昂,给治理者带来了不少经济压力。
农村堆垛治理方案目标围绕农村堆垛治理的总体目标是消除对农村环境的不良影响,提升农村环境治理水平。
具体目标包括:1.实现农村堆垛数量的减少,给农村环境留下更多的绿色空间。
2.促进互联网与农村的深度融合,提升农村信息化程度。
3.降低治理成本,提高治理效率,实现治理效益最大化。
4.强化环境保护理念,推动农村经济和环境的协调发展。
针对目标的实现,设立如下方案:1.加强农村堆垛治理意识,提升环保意识,推进城乡环境协调发展。
政府部门应加强宣传教育,提高居民环保意识和保护环境的意识。
2.推广农村堆垛治理技术和手段,促进农村经济与环境的协调发展。
政府可以通过扶持绿色技术、提供技术指导等积极措施,支持企业进行堆垛治理,同时加强对企业的监管。
计算机常用排序方法

计算机常用排序方法排序是计算机科学中常用的操作之一,它的目的是将一组数据按照特定的规则进行排列,以便于后续的查找、统计和分析等操作。
计算机常用的排序方法有多种,本文将介绍其中的几种常见排序方法。
1. 冒泡排序冒泡排序是一种简单但低效的排序算法。
它的基本思想是通过相邻元素之间的比较和交换来逐渐将最大的元素“冒泡”到最后。
具体实现时,从第一个元素开始,依次比较相邻元素的大小,如果前者大于后者,则交换它们的位置。
重复进行这个过程,直到所有元素都排好序为止。
冒泡排序的时间复杂度为O(n^2),其中n为待排序序列的长度。
2. 插入排序插入排序是一种简单且高效的排序算法。
它的基本思想是将待排序序列分为已排序和未排序两部分,初始时已排序部分只有一个元素。
然后依次将未排序部分的元素插入到已排序部分的适当位置,直到所有元素都插入完毕。
具体实现时,可以通过比较和移动元素的方式来确定插入位置。
插入排序的时间复杂度为O(n^2),但在实际应用中,插入排序往往比冒泡排序更高效。
3. 选择排序选择排序是一种简单但低效的排序算法。
它的基本思想是每次从待排序序列中选择最小的元素,与当前位置的元素交换位置。
具体实现时,可以通过一次遍历找到最小元素的位置,并与当前位置的元素交换。
然后,从下一个位置开始,重复以上操作,直到所有元素都排好序为止。
选择排序的时间复杂度为O(n^2),与冒泡排序相同,但由于减少了元素交换的次数,因此比冒泡排序稍微高效一些。
4. 快速排序快速排序是一种常用且高效的排序算法,它基于分治的思想。
具体实现时,选择一个基准元素,将序列分为两部分,使得左边的元素都小于等于基准元素,右边的元素都大于等于基准元素。
然后,递归地对左右两部分进行快速排序。
快速排序的时间复杂度为O(nlogn),其中n为待排序序列的长度。
5. 归并排序归并排序是一种稳定且高效的排序算法,它基于分治的思想。
具体实现时,将待排序序列划分为若干个子序列,分别进行排序,然后再将排序好的子序列合并成一个有序序列。
第五章 减治法

Cbest (n) i n 1 (n)
11
• 平均效率的精确分析基于对无序元素的研究,对于随机 序列的数组,
2
n 2 Cavg (n) (n ) 4
12
评价
• 插入排序最差Θ(n2) • 最优 Θ(n) • 平均 Θ(n2) • 合并排序最差Θ(nlog2n) • 快速排序最优Θ(nlog2n) • 最差Θ(n2) • 平均Θ(1.38nlog2n) 选择排序 Θ(n2) 冒泡排序 Θ(n2)
21
• Example: Order them from lower to higher, consistent with food chain
T虎 H人 F鱼 S羊 M小虾 P微生物 W小麦
22
求拓扑序列的方法1
• 方法1、应用DFS的出栈次序。 DFS序列: C1-C3-C4-C5- -C2 C3 出栈序列: C1 C5-C4-C3-C1-C2 拓扑排序: C2 C2-C1-C3-C4-C5 思考为什么这个算法是有效的?
15
i
在数据结构中如何表示图?
a b c d a b c d e f g h i j e f 0 1 1 0 g 0 0 0 0 h i j 0 0 1 1 1 0 0 0 0 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
g a c d j f b e
于是得 {123,132,312,213,231,321}
27
插入法生列排列-优点
• 满足最小变化的要求
28
Johnson-Trotter 法生成排列
• 其实有的算法并不需要知道规模n-1的排列就可以直
接得到规模n的排列结果,Johnson-Trotter算法就是其
算法分析与设计基础

算法分析与设计基础(清华版)Taken from "Introduction to The Design and Analysis of Algorithms" by Anany Levitin节选自《算法设计与分析基础》潘彦译蛮力法就像宝剑不是撬棍一样,科学也很少使用蛮力。
——Edward Lytton (1830 - 1873),leila,第二卷,第一章认真做事常常是浪费时间。
——Robert Byrne,撞球大师,台球选手和作家人们是这样描述它的:蛮力法是一种简单直接地解决问题的方法,常常直接基于问题的描述和所涉及的概念定义。
这里的“力”是指计算机的能“力”,而不是人的智“力”。
我们也可以用“直接做吧!”来描述蛮力法的策略。
而且一般来说,蛮力策略也常常是最容易应用的方法。
虽然巧妙和高效的算法很少来自于蛮力法,但我们不应该忽略它作为一种重要的算法设计策略的地位。
第一,和其他某些策略不同,我们可以应用蛮力法来解决广阔领域的各种问题(实际上,它可能是惟一一种几乎什么问题都能解决的一般性方法)。
具体来说,蛮力法常常用于一些非常基本、但又十分重要的算法,比如计算n个数字的和,求一个列表的最大元素,等等。
第二,对于一些重要的问题来说(比如:排序、查找、矩阵乘法和字符串匹配),蛮力法可以产生一些合理的算法,它们多少具备一些实用价值,而且并不限制实例的规模。
第三,如果要解决的问题实例不多,而且蛮力法可以用一直能够接受的速度对实例求解,那么,设计一个更高效算法所花费的代价很可能是不值得的。
第四,即使效率通常很低,仍然可以用蛮力算法解决一些小规模的问题实例。
最后,一个蛮力算法可以为研究或教学目的服务,例如,它可以作为准绳,来衡量同样问题的更高效算法。
下列这些著名的算法可以看作是蛮力法的例子:基于定义的矩阵乘法算法;选择排序;顺序查找;简单的字符串匹配算法。
穷举查找是解组合问题的一种蛮力方法。
数据结构_课件_堆与堆排序38页文档

66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
数据结构_课件_堆、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
农村堆垛治理方案

农村堆垛治理方案背景介绍近年来,农村堆垛问题日益突出,不仅影响了乡村环境卫生,还对生态环境造成了一定的影响。
因此,制定一套农村堆垛治理方案势在必行。
治理方案具体措施1. 加强宣传教育要加强对农民的宣传教育,让他们认识到农村堆垛的危害,提高环保意识。
同时,还要设立相应的奖励和惩罚制度,使其对农村环境保持高度关注。
2. 规范管理对于农村堆垛,要做到分类管理、分级管理,形成科学严谨、标准化的管理制度。
各级政府部门应当建立健全农村环保监督机制,并加大对堆垛的检查力度。
3. 禁止违法行为禁止农民在生活区、村庄周边乱堆垛,严禁随意往河流、湖泊等水源地倾倒废弃物。
对于发现的违法行为要及时惩处,以示法纪严明,不断提高堆垛问题的处理效率。
安全要求1. 保障人员安全在堆放过程中,要保证操作人员的安全。
在堆放高度高于2米时应当设有护栏或围挡等安全措施,防止人员从堆垛中掉落。
堆放过程中,要保证人员间的距离,避免人员挤压和受伤等意外发生。
2. 保障环境安全农村堆垛治理要顾及环境问题,严格限制垃圾填埋场、焚化场等大型垃圾集中处理场所,力争将垃圾处置方式朝着绿色环保方向转化。
3. 建立常态化监管机制农村堆垛治理要建立常态化的监管机制,并建立监督部门的联系方式。
各级政府部门应当加大对堆垛的监督力度,防止农民违规操作。
效果分析农村堆垛治理方案将有利于改善农村堆垛问题,有望减少对生态环境的影响,提高农村环境整体卫生水平。
虽然实施措施存在一定难度,但只要相关人员高度重视,加大监管力度,农村堆垛治理问题不会成为难以解决的难题。
结束语综上所述,针对农村堆垛问题,应该从加强宣传教育、规范管理、禁止违法行为等角度入手,确保治理方案的顺利实施。
同时,还要强化安全要求,保障人员和环境的安全,并建立常态化监管机制,加大检查力度。
只有如此,才能真正使农村堆垛问题得到有效治理,为乡村环境的整治打下良好的基础。
JAVA十大排序算法之堆排序详解
JAVA⼗⼤排序算法之堆排序详解⽬录堆排序知识补充⼆叉树满⼆叉树完全⼆叉树⼆叉堆代码实现时间复杂度算法稳定性思考总结堆排序这⾥的堆并不是JVM中堆栈的堆,⽽是⼀种特殊的⼆叉树,通常也叫作⼆叉堆。
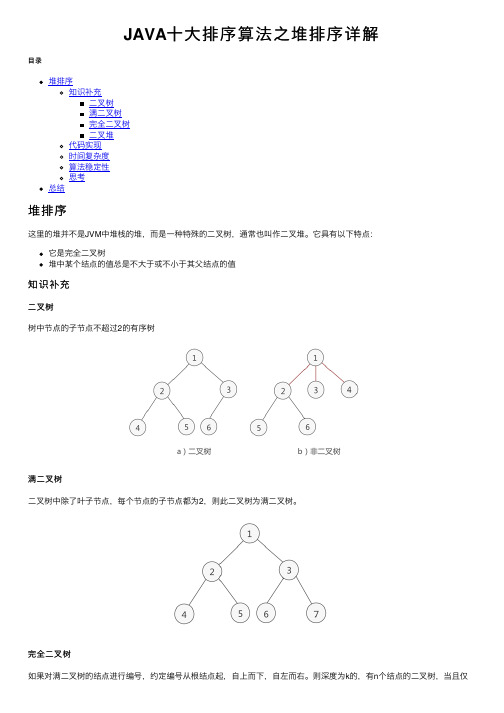
它具有以下特点:它是完全⼆叉树堆中某个结点的值总是不⼤于或不⼩于其⽗结点的值知识补充⼆叉树树中节点的⼦节点不超过2的有序树满⼆叉树⼆叉树中除了叶⼦节点,每个节点的⼦节点都为2,则此⼆叉树为满⼆叉树。
完全⼆叉树如果对满⼆叉树的结点进⾏编号,约定编号从根结点起,⾃上⽽下,⾃左⽽右。
则深度为k的,有n个结点的⼆叉树,当且仅当其每⼀个结点都与深度为k的满⼆叉树中编号从1⾄n的结点⼀⼀对应时,称之为完全⼆叉树。
特点:叶⼦结点只能出现在最下层和次下层,且最下层的叶⼦结点集中在树的左部。
需要注意的是,满⼆叉树肯定是完全⼆叉树,⽽完全⼆叉树不⼀定是满⼆叉树。
⼆叉堆⼆叉堆是⼀种特殊的堆,可以被看做⼀棵完全⼆叉树的数组对象,⽽根据其性质⼜可以分为下⾯两种:⼤根堆:每⼀个根节点都⼤于等于它的左右孩⼦节点,也叫最⼤堆⼩根堆:每⼀个根节点都⼩于等于它的左右孩⼦节点,也叫最⼩堆如果把⼀个数组通过⼤根堆的⽅式来表⽰(数组元素的值是可变的),如下:由此可以推出:对于位置为 k 的节点,其⼦节点的位置分别为,左⼦节点 = 2k + 1,右⼦节点 = 2(k + 1)如:对于 k = 1,其节点的对应数组为 5左⼦节点的位置为 3,对应数组的值为 3右⼦节点的位置为 4,对应数组的值为 2最后⼀个⾮叶⼦节点的位置为 (n/2) - 1,n为数组长度如:数组长度为6,则 (6/2) - 1 = 2,即位置 2 为最后⼀个⾮叶⼦节点给定⼀个随机数组[35,63,48,9,86,24,53,11],将该数组视为⼀个完全⼆叉树:从上图很明显的可以看出,这个⼆叉树不符合⼤根堆的定义,但是可以通过调整,使它变为最⼤堆。
如果从最后⼀个⾮叶⼦节点开始,从下到上,从右往左调整,则:通过上⾯的调整,该⼆叉树为最⼤堆,这个时候开始排序,排序规则:将堆顶元素和尾元素交换交换后重新调整元素的位置,使之重新变成⼆叉堆代码实现public class HeapSort {public static final int[] ARRAY = {35, 63, 48, 9, 86, 24, 53, 11};public static int[] sort(int[] array) {//数组的长度int length = array.length;if (length < 2) return array;//⾸先构建⼀个最⼤堆buildMaxHeap(array);//调整为最⼤堆之后,顶元素为最⼤元素并与微元素交换while (length > 0) {//当lenth <= 0时,说明已经到堆顶//交换swap(array, 0, length - 1);length--;//交换之后相当于把树中的最⼤值弹出去了,所以要--//交换之后从上往下调整使之成为最⼤堆adjustHeap(array, 0, length);}return array;}//对元素组构建为⼀个对应数组的最⼤堆private static void buildMaxHeap(int[] array) {//在之前的分析可知,最⼤堆的构建是从最后⼀个⾮叶⼦节点开始,从下往上,从右往左调整 //最后⼀个⾮叶⼦节点的位置为:array.length/2 - 1for (int i = array.length / 2 - 1; i >= 0; i--) {//调整使之成为最⼤堆adjustHeap(array, i, array.length);}}/*** 调整* @param parent 最后⼀个⾮叶⼦节点* @param length 数组的长度*/private static void adjustHeap(int[] array, int parent, int length) {//定义最⼤值的索引int maxIndex = parent;//parent为对应元素的位置(数组的索引)int left = 2 * parent + 1;//左⼦节点对应元素的位置int right = 2 * (parent + 1);//右⼦节点对应元素的位置//判断是否有⼦节点,再⽐较⽗节点和左右⼦节点的⼤⼩//因为parent最后⼀个⾮叶⼦节点,所以如果有左右⼦节点则节点的位置都⼩于数组的长度 if (left < length && array[left] > array[maxIndex]) {//左⼦节点如果⽐⽗节点⼤maxIndex = left;}if (right < length && array[right] > array[maxIndex]) {//右⼦节点如果⽐⽗节点⼤maxIndex = right;}//maxIndex为⽗节点,若发⽣改变则说明不是最⼤节点,需要交换if (maxIndex != parent) {swap(array, maxIndex, parent);//交换之后递归再次调整⽐较adjustHeap(array, maxIndex, length);}}//交换private static void swap(int[] array, int i, int j) {int temp = array[i];array[i] = array[j];array[j] = temp;}public static void print(int[] array) {for (int i : array) {System.out.print(i + " ");}System.out.println("");}public static void main(String[] args) {print(ARRAY);System.out.println("============================================");print(sort(ARRAY));}}时间复杂度堆的时间复杂度是 O(nlogn)参考:堆排序的时间复杂度分析算法稳定性堆的结构为,对于位置为 k 的节点,其⼦节点的位置分别为,左⼦节点 = 2k + 1,右⼦节点 = 2(k + 1),最⼤堆要求⽗节点⼤于等于其2个⼦节点,最⼩堆要求⽗节点⼩于等于其2个⼦节点。
