第7章差分方程习题集及答案
精编2019七年级下册数学单元测试第七章《分式》完整题库(含参考答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.小明通常上学时走上坡路,途中的速度为m 千米/时,放学回家时,沿原路返回,速度为n 千米/时,则小明上学和放学路上的平均速度为( )A .2nm +千米/时 B .n m mn +千米/时 C .n m mn +2千米/时 D .mnnm +千米/时 解析:C2.当2x =-时,分式11x+的值为( ) A .1B .-1C .2D .-2答案:B3.把分式xx y+(0x ≠,0y ≠)中的分子,分母的x ,y 同时扩大 2倍.那么分式的值( ) A .扩大2倍 B . 缩小2倍 C . 改变原来的值 D . 不改变答案:D4.若有m 人,a 天可完成某项工作,则(m n +)人完成此项工作的天数是( ) A .a m +B .amm n+ C .am n+ D .m nam+ 答案:B5.x (g )盐溶解在 a (g )水中,取这种盐水m (g ),含盐( ) A .mxa(g ) B .amx(g ) C .amx a+(g ) D .mxx a+(g ) 答案:D6. 一组学生去春游,预计共需费用 120 元,后来又有 2 个同学参加进来,总费用不 变,于是每人可少分摊 3 元,原来这组学生的人数是( ) A .8 人B .10人C . 12人D . 30 人答案:A7.“a 和b 的平方的和除以c ”可表示为( )A .2()a b c+B .2b ac +C .22a b c+D . 2a b c+答案:D8.用x -代替各式中的x ,分式的值不变的是( )A .32xB .3x-C .21xx + D .211x -+ 答案:D9.方程x 3=22-x 的解的情况是( )A .2=xB .6=xC .6-=xD .无解答案:B10.与分式2xy的值相等的是( ) A .222x y ++B .63x yC .3(2x)yD .2x y- 答案:B11. 已知分式11+-x x 的值是零,那么x 的值是( ) A .-1B .0C .1D . 1±答案:C12.下列分式中是最简分式的是( )A .122+x x B .x24C .112--x xD .11--x x答案:A13.“5·12”汶川大地震导致某铁路隧道被严重破坏.为抢修其中一段120米的铁路,施工队每天比原计划多修5米,结果提前4天开通了列车.问原计划每天修多少米?设原计划每天修x 米,所列方程正确的是( )A .12012045x x -=+ B .12012045x x -=+ C .12012045x x -=-D .12012045x x -=-解析:B14.1a a a+⋅的结果是( ) A .1a +B .2C .2aD .1答案:A15.方程512552x x x+=--的解x 等于( ) A .-3B .-2C . -1D .0答案:D16.某种商品在降价x %后,单价为a 元,则降价前它的单价为( ) A .%a x B .%a x ⋅C .1%ax -D .(1%)a x -答案:C17.如果分式-23x -的值为负,则x 的取值范围是( ) A .x>2B .x>3C .x<3D .x<2答案:B 二、填空题18.若2a a b =+,当a 、b 都扩大到原来的2009倍时,aa b+的值怎样变化?(填“变大”、“变小”或“不变”) . 解析:不变 19.若分式27xx -无意义,则x 的值为 . 解析:3.520. 甲、乙两人分别从相距s(km)的A ,B 两地同时出发,相向而行,已知甲的速度是每小时m(krn),乙的速度是每小时n(km),则经过 h 两人相遇.解析:nm s+ 21.当x ________时,分式xx2121-+有意义. 解析:21≠22.轮船在静水中每小时行驶akm ,水流的速度为每小时bkm ,则轮船在逆流中行驶skm 需要 小时. 解答题解析:ba s -23.当x 时,分式12x x --有意义;当x= 时,12x x --的值为零. 解析:2≠ ,124.如果分式211x x -+的值为0,则x= .解析:125.已知关于x 的分式方程4333k x x x-+=--有增根,则k 的值是 . 解析:1 26.若543222Ax B x x x x x --=-+++,则A= ,B= . 解析: 1,-327.小舒 t(h)走了 s(km)的路程,则小舒走路的平均速度是 km/h.解析:s t28.将下列代数式按要求分类:a ,1x ,15,223x x --,239x y +,213x x +,234a b π.整式: ; 分式: .解析:a ,15,239x y +,234a b π;1x ,223x x --,213xx +29.不改变分式的值. 使分子、分母都不含不含负号: (1)23x -= ;(2)x yz -- = ;(3)2ab ---;(4)5yx--- = .解析: (1)23x -;(2)x yz ;(3)2ab -;(4)5y x+三、解答题30.请观察下列方程和它们的根: 1112x x -=,12x =,212x =-;1223x x -=,13x =,213x =-; 1334x x -=,14x =,214x =-;1445x x -=,15x =,215x =-; …(1)请你猜想第 10 个方程1101011x x -=的根是 ;(2)猜想第n 个方程是什么?它的根是什么?并将你猜想的原方程的根代人方程检验.解析:(1)111x =,2111x =-;(2)11n x n x n -=++,11x n =+,211x n =-+,检验略 31.当 x 取什么值时,下列分式的值为零? (1)1510x x +-;(2)211x x -+;(3)||22x x --解析: (1)1x =-;(2)1x =;(3)2x =-32.当3x =时,分式301x kx -=-,求k 的值. 9k =解析:9k =33.某校有学生 2500 人,每个学生平均每天用水 a(kg),在该校提倡“人人节水”之后,如果每个学生平均每天节约用水 1 kg ,那么 A(kg)水可供全校用多少天?当 A=7500000,a=4 时,可供全校用多少天?解析:2500(1)Aa -天,1000 天34.先化简,再求值:(1)21()a a a a-÷-,其中a = (2)22142244a a a a a --⨯--+,其中1a =-.解析: (1)21a,13;(2)22(2)a a +-,16- 35.有这样一道题“计算:2222111x x x x x x x-+-÷--+的值,其中2008x =.”甲同学把“2008x =”错抄成“2080x =”,但他的计算结果也正确,这是怎么回事?解析: 原式的值为 0,与x 值无关 36.计算:(1)22(2)(3)33321x x x x x x x x ----÷⋅--+;(2)2222()(2)x y x y x xy y xy -÷-÷++ (3)222222422x 2x y x y x yx y x xy y x xy-+-÷÷++++解析: (1)3x ;(2)221x y xy +;(3)137.计算:(1)432114212121a a aa a a +----+++;(2)2242n mn m mn m n m n n m ------;(3)22()()()()xy yz x y x z x y z x +----; (4)2b a c b ca b c b a c b a c+-+--+----解析:(1)3;(2)m n -;(3)2yyχ-;(4)-2 38.把甲、乙两种原料按 a : b 的质量比混合(a>b),调制成一种混合饮料,要调制4 kg 这种混合饮料,需要的甲原料比乙原料多多少? (用含 a ,b 的代数式表示) 44a ba b-+ 解析:44a ba b-+ 39.将分式10(2)(1)(2)(1)(1)x x x x x +++-+约分,再讨论x 取哪些整数时,能使分式的值是正整数.解析:101x -,当 x=2或3 或6或 11 40.已知123x x +=,121x x =. (1)求1211x x +的值; (2)求2112x x x x +的值; (3)求2112111+1x x x x ++++的值.解析: (1)3;(2)7;(3)341.先化简,再选择使原式有意义而且你喜欢的数代入求值:22315313695x x x x x x x +-⋅---++.解析:化简结果为1x-,计算结果与代入的x 的值有关,答案不唯42.为了帮助受灾地区重建家园,某中学团委组织学生开展献爱心活动. 已知第一次捐 款为 4800 元,第二次捐款为 5000 元,第二次捐款人数比第一次多 20 人,两次人均捐款教相等. 问第一次有多少人捐款?解析:480人43.某工厂去年赢利 25 万元,按计划这笔赢利额应是去年和今年赢利总额的 20%,设今年的赢利额是x 万元,请你写出 x 满足的方程. 你能写出几个方程?其中哪一个是分式方程?解析: 方程(1):252025100x =+;方程(2)20(25)25100x +⨯=;方程(3):252520%x +=÷.方程(1)是分式方程44.为加快西都大开发,某自治区决定新修一条公路,甲、乙两工程队承包此项工程. 如 果甲工程队单独施工,则刚好如期完成;如果乙工程队单独施工就要超过 6 个月才能完成. 现在甲、乙两队先共同施工 4个月,剩下的由乙队单独施工,则刚好如期完成. 问原来规定修好这条公路需多长时间?解析:12 个月45.先化简)11(122xx x x -⋅-+,然后自选一个你喜欢的x 值,求原式的值.解析:化简得:2+x ,但x 不能取0和1. 46.设23111x A B x x ==+--,,当x 为何值时,A 与B 的值相等?解析:当2x =时,A B =.47.有一道题“先化简,再求值:22241244x x x x x -+÷+--(),其中x =时把“x =x =回事?解析:222222241444(4)42444x x x x x x x x x x x --+++÷=⨯-=++---(),因为x =x =2x 的值均为3,原式的计算结果都是7,所以把“x =x =48.甲、乙两工程队分别承担一条2千米公路的维修工作,甲队有一半时间每天维修公路x 千米,另一半时间每天维修公路y 千米.乙队维修前1千米公路时,每天维修x 千米;维修后1千米公路时,每天维修y 千米(x ≠y ).⑴求甲、乙两队完成任务需要的时间(用含x 、y 的代数式表示); ⑵问甲、乙两队哪队先完成任务?解析:(1)甲、乙两队完成任务需要的时间分别为y x +4与xyyx +; (2) y x +4-xyy x +=0)()(2<+--y x xy y x (x ≠y ),∴甲队先完成49.城北区在一项市政工程招标时,接到甲、乙工程队的投标书:每施工一天,需付甲工程队工程款为 1.5万元,付乙工程队1. 1万元. 工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:(方案一)甲队单独施工完成此项工程刚好如期完工; (方案二)乙队单独施工完成此项工程要比规定工期多用5天;(方案三)若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工. 你认为哪一种施工方案最节省工程款?解析:设甲队单独施工完成此项工程需x 天,则乙需(5x +)天,根据题意,得415xx +=+, 解得20x =,经检验,20x =是原方程的根. 方案一所需工程款为 20×1.5=30(万元); 方案二需工程款为 25x1.1=27.5(万元); 方案三所需工程款为 4×1.5+20×1.1=28(万元). 所以方案二最省工程款50.将下面的代数式尽可能化简,再选择一个你喜欢的数代入求值:212(1)1a a a a --++-.解析:2a ,所得的值不唯一。
数字信号处理课后习题答案(全)1-7章

x(n)=-δ(n+2)+δ(n-1)+2δ(n-3)
h(n)=2δ(n)+δ(n-1)+ δ(n-2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n-k)=Ax(n-k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ(n-2) 1 2
(5) 系统是因果系统, 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM,
7. 设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如题7图所示,
要求画出y(n)输出的波形。
解: 解法(一)采用列表法。
y(n)=x(n)*h(n)=
0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
新版精选2019七年级下册数学单元测试第七章《分式》完整题库(含答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.如果3x y =,那么分式222xyx y +的值为( ) A . 35B .53C .6D . 不能确定答案:A2.用x -代替各式中的x ,分式的值不变的是( ) A .32x B .3x- C .21xx + D .211x -+ 答案:D3.把分式xx y+(0x ≠,0y ≠)中的分子,分母的x ,y 同时扩大 2倍.那么分式的值( ) A .扩大2倍 B . 缩小2倍 C . 改变原来的值 D . 不改变答案:D4.若有m 人,a 天可完成某项工作,则(m n +)人完成此项工作的天数是( ) A .a m +B .amm n+ C .am n+ D .m nam+ 答案:B5.下列各式运算正确的是( ) A .0c d c da a-+-= B .0a ba b b a-=-- C .33110()()a b b a +=-- D .22110()()a b b a +=--答案:C6. 已知222220a a b b ++++=,则1ba+的值是( )A .2B .1C .0D .-1答案:A7.某中学八年级甲、乙两班学生参加植树造林,已知甲班每天比乙班多植 5 棵树,甲班植 80 棵树所用的天数与乙班植 70 棵树所用的天数相等.若设甲班每天植树x 棵,则根据题意列出的方程是( ) A .80705x x=- B .80705x x =+ C .80705x χ=+ D .80705x x =- 答案:D8.某人往返于A 、B 两地,去时先步行2公里再乘汽车10公里;回来时骑自行车,来去所用时间恰好一样,已知汽车每小时比步行多走16公里,自行车比步行每小时多走8公里,若步行速度为x 公里/小时,则可列出方程( ) A .21210816xx x +=++B .10122168x x x -=++C .21012168x x x +=++D .10122168x x x+=++解析:C9.赵强同学借了一本书,共 280 页,要在两周借期内读完. 当他读了一半时,发现平均每天要多读 21 页才能在借期内读完. 他读前一半时,平均每天读多少页?如果设读前一 半时,平均每天读x 页,则下列方程中,正确的是( ) A .1401401421x x +=- B .2802801421x x +=+ C .1401401421x x +=+ D .1010121x x +=+ 答案:C10.若关于x 的方程652mx =-的根为 1,则m 等于( ) A . 1B . 8C .18D . 42答案:C11. 一组学生去春游,预计共需费用 120 元,后来又有 2 个同学参加进来,总费用不 变,于是每人可少分摊 3 元,原来这组学生的人数是( ) A .8 人B .10人C . 12人D . 30 人答案:A12.已知111a b a b +=+,则b aa b+的值为( )A .1B .0C .-1D .-2解析:C13.分式方程11888x x x +=+--的根是( )A .x=8B .x=1C .无解D .有无数多个解析:C 14.解分式方程4223=-+-xxx 时,去分母后得( ) A .)2(43-=-x x B .)2(43-=+x xC .4)2()2(3=-+-x x xD .43=-x答案:A15.若关于x 的方程1011--=--m xx x 有增根,则m 的值是( ) A .3B .2C .1D .-1答案:B16.下列各式与x yx y-+相等的是( ) A .55x y x y -+++B . 22x y x y-+C .222()x y x y --(x y ≠)D .2222x y x y-+ 答案:C17.若分式3242x x +-有意义,则字母x 的取值范围是( ) A .12x =B .23x =-C .12x ≠23x ≠- 答案:C18.在公式12111R r r =+(120r r +≠)中,用1r ,2r 表示R 的式子是( ) A .12R r r =+ B .12R r r =C .1212r r R r r +=D .1212r r R r r =+ 答案:D 二、填空题19.当2x =时,分式301x kx -=+,则2k += . 解析:8 20.代数式1x 、a 、2π、2x 13-、2y x y -中, 是整式,_ 是分式.解析:a ,2π,213x -;1x,2y x y -21.若14-m 表示一个正整数,则整数m 的值为 . 解析:2,3,522.当x ________时,分式xx2121-+有意义. 解析:21≠23.请选择一组,a b 的值,写出一个关于x 的形如2ab x =-的分式方程,使它的解是0x =,这样的分式方程可以是____________.解析:如212x -=-(答案不唯一)24.一根蜡烛在凸透镜下成一实像,物距u ,像距v 和凸透镜的焦距f 满足关系式:1u +1v =1f.若f =6厘米,v =8厘米,则物距u =________厘米. 解析:2425.当x=1,2y=-1时,分式3x y xy -的值是 . 解析:-726.下面是一个有规律的数表:上面数表中第 9 行、第 7 列的数是 ,第 (n+1)行、第 (n +2)列的数是 . 解答题 解析:97,12n n ++ 27.如果543a +与23a -互为倒数,那么a = . 解析:3 28.若分式方程244x ax x =+--有增根,则a 的值为 . 解析:429.小舒 t(h)走了 s(km)的路程,则小舒走路的平均速度是 km/h.解析:st30.某工厂要生产 a 个零件,原计划每天生产 x 个,后来由于供货需要,每天多生产 b 个零件,则可提前 天完成.解析:a a x x b-+ 31.已知甲工人每小时能加工零件a 个,现总共有零件A 个.(1)甲工人加工 t(h)能完成 个零件,若全部完成这批零件,则需要 h ;(2)已知乙工人每小时能加工零件 b 个,若乙工人也来加工这批零件,则两人同时开始加工零件,需要 h 才能完成,比甲独做提前 h. 解析:(1) (1)at ,A a ;(2)A a b +,A A a a b-+ 32.在括号内填上适当的代数式,使等式成立. (1)()b a a a +=-;(2)322323()y x x y y x --=-;(3)216()324ab a a =;(4)39()()x x x y x y +=+解答题解析: (1)a b --;(2)32x y -;(3)2b ;(4)23()x y +三、解答题33.化简并求值:22222244x y x y x y x xy y --÷-+++,其中2x =2y =解析:xx y -+,34.先约分,再求值: (1)22444x x x --+,其中3x =. (2) 222x x y xy--,其中2x =-,2y =解析: (1)22x x +-,5 ; (2)x y -,135.下列各个分式中的字母满足什么条件时,分式有意义? (1)251y -;(2)1|1|a -;(3)1||1b -解析:(1)1y ≠±;(2)1a ≠;(3)1b ≠±36.轮船在静水中每小时航行 a(m),水流速度是每小时 b(km),则该轮船在顺水中航行s(km)需要多少时间? s a b+ 解析:s a b+37.先化简,再求值:(1)21()a a a a-÷-,其中a = (2)22142244a a a a a --⨯--+,其中1a =-.解析: (1)21a,13;(2)22(2)a a +-,16- 38.计算:(1)22x x x x --⋅-;(2)212(8)5xy a y a÷-;(3)2(1)(2)2(1)(1)a a a a a a -+⋅++-;(4)22211444a a a a a --÷-+-; (5)2b c c ax ax x⋅÷;(6)222()a b ab b a b --÷+解析: (1)1;(2)3310x a -;(3)21a a a -+;(4)2(2)(1)a a a +-+;(5)2ba ;(6)b39.计算:(1)22(2)(3)33321x x x x x x x x ----÷⋅--+;(2)2222()(2)x y x y x xy y xy -÷-÷++ (3)222222422x 2x y x y x yx y x xy y x xy-+-÷÷++++解析: (1)3x ;(2)221x y xy +;(3)140.化简下列各分式:(1)236sxy x y-; (2) 22699x x x -+-解析:(1)22y x -;(2)33x x -+41.把甲、乙两种原料按 a : b 的质量比混合(a>b),调制成一种混合饮料,要调制4 kg 这种混合饮料,需要的甲原料比乙原料多多少? (用含 a ,b 的代数式表示) 44a ba b-+解析:44a b a b-+42. 在学完“分式”这一章后,老师布置了这样一道题:“先化简再求值: 22241()244x x x x x -+÷+--,其中2x =-”. 婷婷做题时把“2x =-”错抄成了“2x =”,但她的计算结果是正确的,请你通过计算解释其中的原因.解析:化简结果为24x +,当2x =-或2x =时,代入求得的值都是843.一架飞机从北京到上海一个来回,在有风(顺、逆风)和无风的时候,哪种情况更快?解析: 有风时飞行时间较长 44.请观察下列方程和它们的根: 1112x x -=,12x =,212x =-;1223x x -=,13x =,213x =-; 1334x x -=,14x =,214x =-;1445x x -=,15x =,215x =-; …(1)请你猜想第 10 个方程1101011x x -=的根是 ;(2)猜想第n 个方程是什么?它的根是什么?并将你猜想的原方程的根代人方程检验.解析:(1)111x =,2111x =-;(2)11n x n x n -=++,11x n =+,211x n =-+,检验略 45.某工厂去年赢利 25 万元,按计划这笔赢利额应是去年和今年赢利总额的 20%,设今年的赢利额是x 万元,请你写出 x 满足的方程. 你能写出几个方程?其中哪一个是分式方程?解析: 方程(1):252025100x =+;方程(2)20(25)25100x +⨯=;方程(3):252520%x +=÷.方程(1)是分式方程 46.分式方程0111x k x x x x +-=--+有增根x=1,求k 的值.解析:1-=k . 47.化简: (1)21211x x x ++- (2)1)111(-÷--x xx解析:(1)11x-,(2)1. 48. 请从下列三个代数式中任选两个构成一个分式,并化简该分式. x2-4xy+4y2x2-4y2x-2y解析:解:2222444yx y xy x -+- =)2)(2()2(2y x y x y x -+-=y x y x 22+- . (答案不惟一)49.有一道题“先化简,再求值:22241244x x x x x -+÷+--(),其中x =时把“x =x =回事?解析:222222241444(4)42444x x x x xx x x x x x --+++÷=⨯-=++---(),因为x =x =2x 的值均为3,原式的计算结果都是7,所以把“x =x =50.一个长,宽,高分别为 a ,b ,h 的长方体烟盒内装满了高为h 的香烟,共 20 枝. 打开烟盒盖,20 支香烟排成三行(如图所示). 求烟盒的空间利用率. (已知 2.56ab=,π取 3. 14,结果精确到 1%,烟盒纸厚度忽略不计)解析: 约 82%。
差分方程练习题

1 5 (4) y t 1 y t . 2 2 7. 求下列差分方程在给定初始条件下的特解:
(1) yt +1- yt =10,且 y0 =3; (2) yt +1-2 yt =2t ,且 y0 =2. 8. 求下列二阶常系数线性齐次差分方程的通解或在给定初始条件下的特解:
(3) yt ln(t 1) ln t ,
2 yt (yt ) ln(t 1) ln t ln(t 2) 2ln(t 1) ln t
(4) yt t 1 3t 1 t 2 3t 3t 2t 2 6t 3 ,
yt 3 1 0 t .
t
(2) 原 方 程 的 通 解 为 yt C 2t t 2t 1 又 有 初 始 条 件 y0 =2 , 可 知 C 2 , 故 特 解 为
yt 2t 1 t 2t 1 .
8. (1) yt C1 3t C2 2 .
t
(1) yt 2 yt 1 6 yt 0 (2) yt 2 6 yt 1 9 yt 0 (3) yt 2 13 yt 1 12 yt 0 ; y0 1, y1 6 9. 求下列二阶常系数线性非齐次差分方程的通解: (1)yx +2 3yx +1 + 2yx = 2x (2) yt 2 yt 1 6 yt 6 (3) yt 2 6 yt 1 9 yt 8 答案 1. 解:(1) yt [3 t 1 t 1 ] 3t 2 t 3 3t 2 +3t 2 ,
yt 9 6t 3t 2 C 2t .
* *
3 5 ( )t ,解得 A . (4) 由 a 1 ,k 1,b 5 ,令原方程有一个特解为 y*t A· 5 2 2 2
差分方程例题

∑ (3) f3(k) ∗ f4 (k) = f3(i) f4 (k − i) i = −∞
k < 0 时: f (k) = 0 k = 1时: f (k) = −1 k = 2 时: f (k) = 2 k = 3 时: f (k) = −2 k = 4 时: f (k) = −1 k = 5 时: f (k) = −1 k > 5 时: f (k) = 0
f23(k) = {...0,3,5, 6, 6, 6,3,1, 0...}
f13(k) = {...0, 0,3,8,8, 4,1, 0, 0...} f (k) = {...0,3, 2, −2, −图所示系统,若激励 f (k) = (1)k ε (k) ,求系统的零状态响应。 2
k > 3 时: f (k) = 0
6
∞
∑ (2) f2 (k) ∗ f3(k) = f2 (i) f3(k − i) i = −∞
k = −3 时: f (k) = 0 k = −2 时: f (k) = 3 k = −1 时: f (k) = 5 k = 0 时: f (k) = 6 k = 1, 2 时: f (k) = 6 k = 3 时: f (k) = 3 k = 4 时: f (k) = 1 k > 4 时: f (k) = 0
y(k)
f(k) + ∑
D
D
+
3/4
1/8
解:系统的差分方程为:
y(k) = f (k) + 3 y(k −1) − 1 y(k − 2)
(4) h(k) + 4h(k − 2) = δ (k)
λ2
+
4
=
0
信号与系统课后习题答案第7章

143
第7章 离散信号与系统的Z域分析 144
第7章 离散信号与系统的Z域分析
题图 7.7
145
第7章 离散信号与系统的Z域分析 146
第7章 离散信号与系统的Z域分析
题解图 7.31
147
第7章 离散信号与系统的Z域分析
(2) 由H(z)写出系统传输算子: 对应算子方程和差分方程为
148
7.25 已知一阶、二阶因果离散系统的系统函数分别如下, 求离散系统的差分方程。
111
第7章 离散信号与系统的Z域分析 112
第7章 离散信号与系统的Z域分析 113
第7章 离散信号与系统的Z域分析 114
第7章 离散信号与系统的Z域分析
7.26 已知离散系统如题图7.5所示。 (1) 画出系统的信号流图; (2) 用梅森公式求系统函数H(z); (3) 写出系统的差分方程。
① 或者
② 容易验证式①、②表示同一序列。
57
第7章 离散信号与系统的Z域分析 58
第7章 离散信号与系统的Z域分析 59
第7章 离散信号与系统的Z域分析 60
第7章 离散信号与系统的Z域分析 61
第7章 离散信号与系统的Z域分析
也可以将Yzs(z)表示为
再取Z逆变换,得 ②
自然,式①、②为同一序列。
44
第7章 离散信号与系统的Z域分析 45
第7章 离散信号与系统的Z域分析 46
第7章 离散信号与系统的Z域分析
7.10 已知因果序列f(k)满足的方程如下,求f(k)。
47
第7章 离散信号与系统的Z域分析 48
第7章 离散信号与系统的Z域分析
(2) 已知K域方程为
49
最新2019七年级下册数学单元测试第七章《分式》测试版题库(含答案)

33
23
3 2 43 ;
33
4 3 52 ;
23
5 2 63 ;
23
6 2;
33 13 3 1 43 13 4 1 53 33 5 3 63 43 6 4
(1)请你写出一个符合上面规律的一个式子(不能与上面的重复);
(2)探索其中的规律,再写出一个类似的等式,并用含 m , n 的等式表示这个规律( m , n
1
的值.
x2 6x 9 (x 2)(x 3)2
解析: x2 4 ,当 x 1 时, x2 4 3 36.代数式 x 1 x 3 有意义,求 x 的取值范围.
x2 x4
解析: x 2 , x 3 且 x 4 37.上海到北京的航线全程为 s(km),飞行时间需 a(h). 而上海到北京的铁路全长为航线 长的m倍,乘车时间需 b(h). 问飞机的速度是火车速度的多少倍?(用含 a,b,s,m 的 分式表示)
解析: b 倍 am
38.化简下列各分式:
(1) 3xys ; 6x2 y x2 6x 9
(2) x2 9
解析:(1) y2 ;(2) x 3
2x
x3
39.化简并求值: x y x2 y2 2 ,其中 x 2 3 , y 2 3 . x 2y x2 4xy 4y2
解析: x , 2 3
x y
4
40. 在学完“分式”这一章后,老师布置了这样一道题:“先化简再求值:
(
x x
2 2
4x x2
) 4
1 x2
4
,其中
x
2
”.
婷婷做题时把“
x
2
”错抄成了“
x
2
”,但她的计算结果是正确的,请你通过计算解释其中的原因.
差分方程模型习题+答案

1. 一老人60岁时将养老金10万元存入基金会,月利率0.4%, 他每月取1000元作为生活费,建立差分方程计算他每岁末尚有多少钱?多少岁时将基金用完?如果想用到80岁,问60岁时应存入多少钱?分析:(1) 假设k 个月后尚有k A 元,每月取款b 元,月利率为 r ,根据题意,可每月取款,根据题意,建立如下的差分方程:1k k A aA b +=-,其中a = 1 + r (1)每岁末尚有多少钱,即用差分方程给出k A 的值。
(2) 多少岁时将基金用完,何时0k A =由(1)可得:01kkk a A A a br-=-若0n A =,01nnA rab a =-(3) 若想用到 80 岁,即 n =(80-60)*12=240 时,2400A =,24002401A ra b a=-利用 MA TLAB 编程序分析计算该差分方程模型,源程序如下: clear all close allclcx0=100000;n=150;b=1000;r=0.004; k=(0:n)';y1=dai(x0,n,r,b); round([k,y1'])function x=dai(x0,n,r,b) a=1+r; x=x0;for k=1:nx(k+1)=a*x(k)-b; end(2)用MA TLAB 计算:A0=250000*(1.004^240-1)/1.004^240思考与深入:(2) 结论:128个月即70岁8个月时将基金用完(3) A0 = 1.5409e+005结论:若想用到80岁,60岁时应存入15.409万元。
2. 某人从银行贷款购房,若他今年初贷款10万元,月利率0.5%,他每月还1000元。
建立差分方程计算他每年末欠银行多少钱,多少时间才能还清?如果要10年还清,每月需还多少?分析:记第k个月末他欠银行的钱为x(k),月利率为r,且a=1+r,b为每月还的钱。
则第k+1个月末欠银行的钱为x(k+1)=a*x(k)+b,a=1+r,b=-1000,k=0,1,2…在r=0.005 及x0=100000 代入,用MA TLAB 计算得结果。
差分方程习题

差分方程习题1、对下面的差分方程,求出它们的1X 、2X 、3X 、4X 的值:(a) 1,301=+=+X X X n n (b) 2,35.001=+=+X X X n n (c) 1,02/121=+=+X X X X n n n(d)1),sin(01==+X X X n n (采用弧度)2、 对下面的差分方程进行分类(填入表内)3、 若 47,23,11,5,243210=====X X X X X ,根据以上数据,写出用1+n X 和n X 表示的差分方程。
4、 若每年有%X 的现有的汽车报废,而且每年新购人N 辆汽车,建立反映n 年后汽车总数n C 的差分方程。
5、 一轿车油耗指标是每加仑30英里,建立一个以n 为英里,n X 为汽油加仑数的差分方程。
6、 某种植物第一天长高3cm ,之后每天长的高度是前一天的1/2,建立一个描述n天后植物高度n B 的差分方程。
7、 设某种昆虫在第n 个月的数量n I 与它两个月前成虫产的卵数和孵化出的幼虫第一月的成活率有关,做出求解昆虫在第n 月时数量的差分方程。
8、 某种树10年后可成材,若n P 表示第n 年时植入的树数,n M 表示第n 年时已成材的树数。
做出与n P ,n M 有关的差分方程,如果C 是每年要砍伐的树数,模型应做何修正。
9、 若生产增长速率每年是4%,n P 表示第n 年时的产量,做出描述产量模型的差分方程。
若1990年时的产量是1千万吨,请估计:(a )什么时候产量可达1千4百万吨;(b )什么时候其产量低于6百万吨。
10、 某机器的折旧率是每年5%,建立一个描述其折旧值n V 的差分方程,如果新购入时花了10000元,当它的折旧值仅为3000元时,机器将报废,计算:(a )5年后机器的价值;(b )机器使用年限。
11、 某公司刚生产出一种新产品,计划每月增产2000件,第一个月共生产了5000件,要求估测在哪一个月产量(1)将超过20000件;(2)将到达N 件。
信号与系统王明泉第七章习题解答
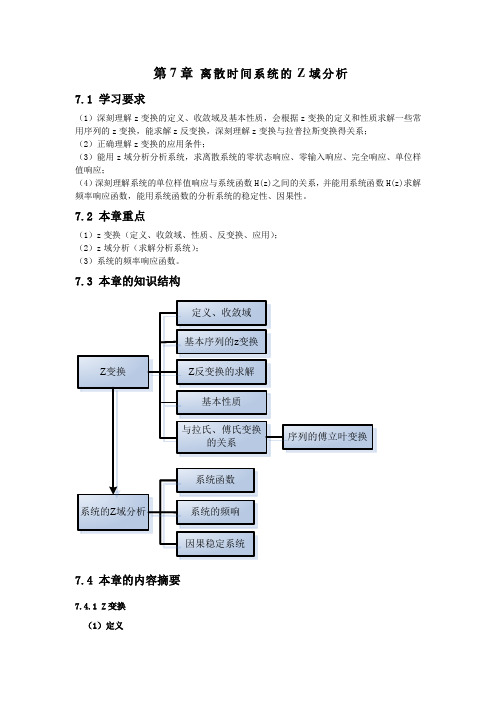
第7章离散时间系统的Z域分析7.1 学习要求(1)深刻理解z变换的定义、收敛域及基本性质,会根据z变换的定义和性质求解一些常用序列的z变换,能求解z反变换,深刻理解z变换与拉普拉斯变换得关系;(2)正确理解z变换的应用条件;(3)能用z域分析分析系统,求离散系统的零状态响应、零输入响应、完全响应、单位样值响应;(4)深刻理解系统的单位样值响应与系统函数H(z)之间的关系,并能用系统函数H(z)求解频率响应函数,能用系统函数的分析系统的稳定性、因果性。
7.2 本章重点(1)z变换(定义、收敛域、性质、反变换、应用);(2)z域分析(求解分析系统);(3)系统的频率响应函数。
7.3 本章的知识结构7.4 本章的内容摘要7.4.1 Z变换(1)定义∑∞-∞=-=n nzn x z X )()( 表示为:)()]([z X n x Z =。
(2)收敛域 1.有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他 (1)当0,021>>n n 时,n 始终为正,收敛条件为0>z ; (2)当0,021<<n n 时,n 始终为负,收敛条件为∞<z ;(3)当0,021><n n 时,n 既取正值,又取负值,收敛条件为∞<<z 0。
2.右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩ (1)当01>n 时,n 始终为正,由阿贝尔定理可知,其收敛域为1x R z >,1x R 为最小收敛半径;(2)当01<n 时,)(z X 分解为两项级数的和,第一项为有限长序列,其收敛域为∞<z ;第二项为z 的负幂次级数,由阿贝尔定理可知,其收敛域为1x R z >;取其交集得到该右边序列的收敛域为∞<<z R x 1。
3.左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他(1)当02<n ,n 始终为负,收敛域为2x R z <,2x R 为最大收敛半径; (2)当02>n ,)(z X 可分解为两项级数的和,第一项为z 的正幂次级数,根据阿贝尔定理,其收敛域为2x R z <,2x R 为最大收敛半径;第二项为有限长序列,其收敛域为0>z ;取其交集,该左边序列的收敛域为20x R z <<。
最新版精选2019七年级下册数学单元测试第七章《分式》模拟考核题库(含参考答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.赵强同学借了一本书,共 280 页,要在两周借期内读完. 当他读了一半时,发现平均每天要多读 21 页才能在借期内读完. 他读前一半时,平均每天读多少页?如果设读前一 半时,平均每天读x 页,则下列方程中,正确的是( ) A .1401401421x x +=- B .2802801421x x +=+ C .1401401421x x +=+ D .1010121x x +=+ 答案:C2.下列各式中,变形不正确的是( ) A .2233x x=-- B .66a ab b-=- C .3344x xy y-=- D .5533n nm m--=- 答案:D3.分式3a x ,22x y x y +-,22a b a b-+,x y x y +-中最简分式有( )A .1 个B .2 个C . 3 个D .4 个答案:C4.汽车上山速度为 a (km/h ),下山的速度为b (km/h ),上山和下山行驶的路程相同,则 汽车的平均速度为( ) A .11a b+B .1a b+ C .2aba b+ D .2a b +答案:C5.若2x <,则2|2|x x --的值为( ) A .-1B .0C .1D . 2答案:A6.若有m 人,a 天可完成某项工作,则(m n +)人完成此项工作的天数是( ) A .a m +B .amm n+ C .am n+ D .m nam+ 答案:B7.一个三角形的面积是22a b a b ++,它的一条边长为1a b+,那么这条边上的高是( )A .22a b +B .222()a b +C .222()a b a b ++D .2222()()a b a b ++答案:B8.下面计算正确的是( ) A .111x x÷⋅= B .2122()b a a bb ⋅=-- C .2142x y y x -÷=- D .221x x -⋅=(0x ≠)答案:D9.x (g )盐溶解在 a (g )水中,取这种盐水m (g ),含盐( ) A .mxa(g ) B .amx(g ) C .amx a+(g ) D .mxx a+(g ) 答案:D10. 已知222220a a b b ++++=,则1ba+的值是( )A .2B .1C .0D .-1答案:A11.某人往返于A 、B 两地,去时先步行2公里再乘汽车10公里;回来时骑自行车,来去所用时间恰好一样,已知汽车每小时比步行多走16公里,自行车比步行每小时多走8公里,若步行速度为x 公里/小时,则可列出方程( ) A .21210816xx x +=++B .10122168x x x -=++C .21012168x x x +=++D .10122168x x x+=++解析:C 12.在公式12111R r r =+(120r r +≠)中,用1r ,2r 表示R 的式子是( ) A .12R r r =+ B .12R r r =C .1212r r R r r +=D .1212r r R r r =+ 答案:D13.把分式方程1111xx x-=--变形后,下列结果正确的是( ) A .1(1)x x --= B .1(1)x x --=- C .1(1)x x ---=-D .1x x -=-答案:B14.如果3x y =,那么分式222xyx y +的值为( ) A . 35B .53C .6D . 不能确定答案:A15.已知x=2005,y=2004,则分式4422))((yx y x y x -++等于( )A .0B . 1C . 2D . 3答案:B16.已知111a b a b +=+,则b aa b+的值为( )A .1B .0C .-1D .-2解析:C17.若分式242a a -+的值为零,则a 的值是( )A .±2B .2C .-2D .0答案:B18.把a 千克盐溶进b 千克水中制成盐水,那么x 千克这样的盐水中含盐( )A .a xa b -+千克 B .ba ax+千克 C .a xa b++千克 D .axb千克 解析:B19.若x 满足||xx =1,则x 应为( )A .正数B .非正数C .负数D .非负数解析:A20.下列各式中,是分式的是( ) A .2-πx B .31x 2 C .312-+x xD .21x 答案:C21.方程512552x x x+=--的解x 等于( ) A .-3B .-2C . -1D .0答案:D22.下列各式中,属于分式的是( ) A . aB . 13C .3a D .3a答案:D23.不解方程判断方程21230111x xx -+=+--的解是( ) A .OB .1C .2D .13答案:A 二、填空题24.填空:= ;(2)2= ;= .解析:(12)0. 3;(3;(4)25.当2x =时,分式301x kx -=+,则2k += . 解析:826.当x _ _时,12x-的值为正;当x _ _时,221x x -+的值为负.解析:2x <,0x ≠ 27.代数式1x 、a 、2π、2x 13-、2y x y -中, 是整式,_ 是分式.解析:a ,2π,213x -;1x,2y x y -28.已知1a +1b =92()a b +,则b aa b+=_______. 解析:25 29.请选择一组,a b 的值,写出一个关于x 的形如2ab x =-的分式方程,使它的解是0x =,这样的分式方程可以是____________.解析:如212x -=-(答案不唯一)30.一根蜡烛在凸透镜下成一实像,物距u ,像距v 和凸透镜的焦距f 满足关系式:1u +1v =1f.若f =6厘米,v =8厘米,则物距u =________厘米. 解析:24 31.已知22753y x x y -=+且y ≠0,则x y= . 解析:174-32.一项工作甲、乙单独做各需a 天、2a 天,若两人合作,则需要 天. 解析:32a33.写出一个分子至少含有两项且能够约分的分式: . 解析:如:22a ba b +-等 三、解答题34.一架飞机从北京到上海一个来回,在有风(顺、逆风)和无风的时候,哪种情况更快?解析: 有风时飞行时间较长35.下列各个分式中的字母满足什么条件时,分式有意义? (1)251y -;(2)1|1|a -;(3)1||1b -解析:(1)1y ≠±;(2)1a ≠;(3)1b ≠± 36.对于分式23x a x b -+,当 x=-1时,分式无意义;当 x=4时,分式的值为 0,试求代数式ab的值. 83解析:8337.已知分式2134x x +-,则: (1)当 x 取什么数时,分式无意义? (2)当 x 取什么数时,分式的值是零? (3)当1x =时,分式的值是多少?解析: (1)43x =;(2)12x =-;3x =38.当整数x 取何值时,分式31x +的值是整数?0,2,4x =±-解析:0,2,4x =±-39.已知 x 等于它的倒数,求222169(2)(3)x x x x x +÷-+--的值.解析:24x -,当1x =±时,243x -=- 40.(1)观察下列变形:1111212=-⨯;1112323=-⨯;1113434=-⨯;… 通过观察,你发现了什么规律?用含 n 的等式表示(n 为正整数): . (2)利用(1)中的规律计算: 1111()(1)(2)(2)(3)(2007)(2008)x x l x x x x x x +++++++++++(其中0x >),并求当 x=1时该代数式的值.解析: (1)111(1)1n n n n =-++;(2)2008(2008)x x +,2008200941.化简下列各分式:(1)236sxy x y-; (2) 22699x x x -+-解析:(1)22y x -;(2)33x x -+42.已知123x x +=,121x x =.(1)求1211x x +的值; (2)求2112x x x x +的值; (3)求2112111+1x x x x ++++的值.解析: (1)3;(2)7;(3)343.城北区在一项市政工程招标时,接到甲、乙工程队的投标书:每施工一天,需付甲工程队工程款为 1.5万元,付乙工程队1. 1万元. 工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:(方案一)甲队单独施工完成此项工程刚好如期完工; (方案二)乙队单独施工完成此项工程要比规定工期多用5天;(方案三)若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工. 你认为哪一种施工方案最节省工程款?解析:设甲队单独施工完成此项工程需x 天,则乙需(5x +)天,根据题意,得415xx +=+, 解得20x =,经检验,20x =是原方程的根. 方案一所需工程款为 20×1.5=30(万元); 方案二需工程款为 25x1.1=27.5(万元); 方案三所需工程款为 4×1.5+20×1.1=28(万元). 所以方案二最省工程款 44.解下列分式方程: (1)32221221x xx x --+=--;(2)6201(1)x x x x +-=--解析:(1)1x =;(2)25x =45.在争创全国卫生城市的活动中,某市一“青年突击队”决定义务清运一堆重达 100 t 的垃圾. 开工后,附近居民主动参加义务劳动,使清运垃圾的速度比原计划提高一倍,结果提前 4h 完成任务. 问“青年突击队”原计划每小时清运多少吨垃圾?解析:12. 5t46.先化简再求值:412222x x x x -⎛⎫÷+- ⎪--⎝⎭,其中4.解析:原式=3341-=+-x . 47.小利取出一年到期的本金和利息时,缴纳50元的利息税(国家规定存款利息的纳税方法是:利息税=利息×20%).若银行一年定期储蓄的年利率为1.25%,则小利一年前存入银行的本金是多少?解析:20000元.48. 请你先将分式2211x x x x x ---+化简. 再选取一个使原式有意义,而你又喜爱的数代入求值.解析:22x -(代入0,1x ≠-的数都可以)49.当12x =-时,代数式223261169x x x x x x x ++-⋅++++的值恰好是分式方程22024mxx x +=--的根,试求字母m 的值.解析:2232x 61169x x x x x x x ++-⋅++++的化简结果为1xx -+,计算结果为 1,代入分式方程,得6m =-50.化简并求值:22222244x y x y x y x xy y --÷-+++,其中2x =2y =解析:xx y -+,。
新版精选2019七年级下册数学单元测试第七章《分式》完整考题库(含参考答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.把分式方程1111xx x-=--变形后,下列结果正确的是( ) A .1(1)x x --= B .1(1)x x --=- C .1(1)x x ---=-D .1x x -=-答案:B2.下列各式中,是分式的个数有( ) ①2a ;②3a -;③2c d -;④2a b -;⑤s a b +;⑥4yx-. A .1 个B . 2个C .3个D .4个答案:C3.若关于x 的方程1011--=--m xx x 有增根,则m 的值是( ) A .3B .2C .1D .-1答案:B4.在22231,,,()122x x x y x x π---+-中,不是分式的有( )A .0个B .1个C .2个D .3个解析:C 5.如果把分式335a ba+中的a 、b 都扩大10倍,那么分式的值( ) A .扩大为原来的10倍 B .缩小为原来的101C .不变D .无法确定解析:C 6.如果把分式22a ba b+-中的a ,b 都扩大 3 倍,那么分式的值( ) A .是原来的3 倍 B .是原来的 5 倍 C .是原来的13D .不变答案:D7.已知分式11x x -+的值为零,那么x 的值是( ) A .-1B .0C .1D .1±答案:C8.某中学八年级甲、乙两班学生参加植树造林,已知甲班每天比乙班多植 5 棵树,甲班植 80 棵树所用的天数与乙班植 70 棵树所用的天数相等.若设甲班每天植树x 棵,则根据题意列出的方程是( ) A .80705x x=- B .80705x x =+ C .80705x χ=+ D .80705x x =- 答案:D9.下列说法正确的是( ) A .方程01xx =-的解是0x = B .方程1211x x x =+--的解是1x = C .分式方程一定会产生增根 D . 方程1222x x x+=--的最简公分母是(2)(2)x x -- 答案:A10.下面计算正确的是( ) A .111x x÷⋅= B .2122()b a a bb ⋅=-- C .2142x y y x -÷=- D .221x x -⋅=(0x ≠)答案:D11.一个三角形的面积是22a b a b ++,它的一条边长为1a b+,那么这条边上的高是( )A .22a b +B .222()a b +C .222()a b a b ++D .2222()()a b a b ++答案:B12.使分式221a aa ++的值为零的a 的值是( )A .1B .-1C .0D .0 或-1答案:D13.用x -代替各式中的x ,分式的值不变的是( ) A .32x B .3x- C .21xx + D .211x -+ 答案:D14.某人往返于A 、B 两地,去时先步行2公里再乘汽车10公里;回来时骑自行车,来去所用时间恰好一样,已知汽车每小时比步行多走16公里,自行车比步行每小时多走8公里,若步行速度为x 公里/小时,则可列出方程( )A .21210816xx x +=++B .10122168x x x -=++C .21012168x x x +=++D .10122168x x x+=++解析:C二、填空题15.方程112=-x 的解为x = .解析:316.判断正误,正确的打“√”,错误的打,“×” (1)111222()a b a b +=+; ( ) (2)111b b b b aa a a---+==-; (3)11110a b b a a b a b+=-=----; (4)220()()x xa b b a +=-- 解析:(1) × (2) × (3)√ (4)× 17.若543222Ax B x x x x x --=-+++,则A= ,B= . 解析: 1,-318.当x = 时,分式146x -与323x-的值相等. 解析:4319.某工厂库存原材料 x(t),原计划每天用a(t),若现在每天少用 b( t),则可以多用 天.解析:2bxa ab- 20.不改变分式的值,使23332x yx y +-的分子、分母中各项系数都变为整数,则最筒结果是 .解析:18496x yx y+- 21.下面是一个有规律的数表:上面数表中第 9 行、第 7 列的数是 ,第 (n+1)行、第 (n +2)列的数是 . 解答题 解析:97,12n n ++22.已知甲工人每小时能加工零件a 个,现总共有零件A 个.(1)甲工人加工 t(h)能完成 个零件,若全部完成这批零件,则需要 h ;(2)已知乙工人每小时能加工零件 b 个,若乙工人也来加工这批零件,则两人同时开始加工零件,需要 h 才能完成,比甲独做提前 h. 解析:(1) (1)at ,A a ;(2)A a b +,A Aa a b-+ 23.如果21(3)(4)34x A B x x x x +=+-+-+,则A= ;B= . 解析:A=-1,B=1 24.填空:= ;(2)2= ;= .解析:(12)0. 3;(3;(4)25.若4y -3x=0 ,则yyx += . 解析:37 26.关于x 的方程230x x m-=-有增根.则m = . 解析:9 27.已知1a +1b =92()a b +,则b aa b+=_______. 解析:25 28.当2009x =时,代数式2913x x --+的值为 .解析:200529.在正数种运算“*”,其规则为a *b =11a b+,根据这个规则(1)*(1)0x x -+=的解为 .解析:0x =30.在下式的“□”里,分别填上适当的代数式,使等式成立:□+□=1a b-. 解析:答案不唯一;如:22a ab -、22ba b- 31.用价值120元的甲种涂料与价值260元的乙种涂料配制成一种新涂料,其每千克售价比甲种涂料每千克售价少 4元,比乙种涂料每千克的售价多 2元,求这种新涂料每千克的售价是多少元?若设这种新涂料每千克的售价为x 元,则根据题意,可列方程为 . 解答题解析:12026012026042x x x++=+- 32.公式12lr S =中,若已知S 、r,则l = . 解析:rs 2 三、解答题33.(1)观察下列变形:1111212=-⨯;1112323=-⨯;1113434=-⨯;… 通过观察,你发现了什么规律?用含 n 的等式表示(n 为正整数): . (2)利用(1)中的规律计算: 1111()(1)(2)(2)(3)(2007)(2008)x x l x x x x x x +++++++++++(其中0x >),并求当 x=1时该代数式的值.解析: (1)111(1)1n n n n =-++;(2)2008(2008)x x +,2008200934.用分式表示下列各式的商,并约分: (1)23312(8)a b a b ÷-;(2)22(21)(1)m m m -+÷-解析: (1)232b a -;(2)11m m -+35.当 x 取什么值时,下列分式的值为零? (1)1510x x +-;(2)211x x -+;(3)||22x x --解析: (1)1x =-;(2)1x =;(3)2x =- 36.当3x =时,分式301x kx -=-,求k 的值. 9k =解析:9k =37.当整数x 取何值时,分式31x +的值是整数? 0,2,4x =±-解析:0,2,4x =±-38.某校有学生 2500 人,每个学生平均每天用水 a(kg),在该校提倡“人人节水”之后,如果每个学生平均每天节约用水 1 kg ,那么 A(kg)水可供全校用多少天?当 A=7500000,a=4 时,可供全校用多少天?解析:2500(1)Aa -天,1000 天39.已知 x 等于它的倒数,求222169(2)(3)x x x x x +÷-+--的值.解析:24x -,当1x =±时,243x -=-40.不改变分式的值,把下列各式的分子与分母中的各项系数化为整数: (1)0.030.20.070.5x y x y-+;(2)23125m nm n +-解析:(1)320750x y x y -+;(2)150330m l nm n+-41.计算:(1)22(2)(3)33321x x x x x x x x ----÷⋅--+;(2)2222()(2)x y x y x xy y xy -÷-÷++ (3)222222422x 2x y x y x yx y x xy y x xy-+-÷÷++++解析: (1)3x ;(2)221x y xy +;(3)142.当12x =-时,代数式223261169x x x x x x x ++-⋅++++的值恰好是分式方程22024mxx x +=--的根,试求字母m 的值.解析:2232x 61169x x x x x x x ++-⋅++++的化简结果为1xx -+,计算结果为 1,代入分式方程,得6m =-43.已知123x x +=,121x x =. (1)求1211x x +的值; (2)求2112x x x x +的值; (3)求2112111+1x x x x ++++的值.解析: (1)3;(2)7;(3)344.一架飞机从北京到上海一个来回,在有风(顺、逆风)和无风的时候,哪种情况更快?解析: 有风时飞行时间较长45.甲、乙两个工程队合做一项工程,两队合做2天后,由乙队单独做 1 天就可全部完 成. 已知乙队单独做全部工程所需天数是甲队单独做所需天数的32倍,求甲、乙两队单独做分别需多少天?解析:各需4天和6 天46.(1)已知118x y+=,求2322x xy yx xy y -+++的值.(2)若a 2+b 2-10a-6b+34=0,求a ba b+-的值.解析:(1)1013;(2)4. 47.先化简)11(122xx x x -⋅-+,然后自选一个你喜欢的x 值,求原式的值.解析:化简得:2+x ,但x 不能取0和1.48.有一道题“先化简,再求值:22241244x x x x x -+÷+--(),其中x =时把“x =x =回事?解析:222 222241444(4)42444x x x x xx xx x x x--+++÷=⨯-=+ +---(),因为x=x=2x的值均为3,原式的计算结果都是7,所以把“x=x=49.化简:(1)249 ()77a a aa a a--⋅-+(2)12() 11b bbb b +÷---.解析:(1)14;(2)1 b -50.代数式1324x xx x++÷++有意义,求x的取值范围.解析:2x≠-,3x≠-且4x≠-。
精编新版2019年七年级下册数学单元测试-第七章《分式》完整考题库(含参考答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.若22440a ab b -+=,则代数式23a ba b-+的值是( ) A .1B . 35C .45D .无法确定答案:B2.有两个分式221M a =-,1111N a a =--+,其中1a ≠±,则M 与N 的关系是( ) A .相等B . 互为相反数C . M> ND . N> M答案:A3.m 克白糖溶于n 千克水中,所得糖水的含糖量可以表示为( ) A .mnB .mm n+ C .100nmD .1000mm n+答案:D4.下列各式与x yx y-+相等的是( ) A .55x y x y -+++B . 22x y x y-+C .222()x y x y --(x y ≠)D .2222x y x y-+ 答案:C5.不改变分式的23.015.0+-x x 的值,把它的分子和分母中的各项的系数都化为整数,则所得的结果为( ) A .2315+-x x B .203105+-x xC .2312+-x x D .2032+-x x 答案:B6.小明通常上学时走上坡路,途中的速度为m 千米/时,放学回家时,沿原路返回,速度为n 千米/时,则小明上学和放学路上的平均速度为( )A .2nm +千米/时 B .n m mn +千米/时 C .n m mn +2千米/时 D .mnnm +千米/时 解析:C7. 一组学生去春游,预计共需费用 120 元,后来又有 2 个同学参加进来,总费用不 变,于是每人可少分摊 3 元,原来这组学生的人数是( )A .8 人B .10人C . 12人D . 30 人答案:A8.如果3x y =,那么分式222xyx y +的值为( ) A . 35B .53C .6D . 不能确定答案:A9.下列各式运算正确的是( ) A .0c d c da a-+-= B .0a ba b b a-=-- C .33110()()a b b a +=-- D .22110()()a b b a +=--答案:C10.x (g )盐溶解在 a (g )水中,取这种盐水m (g ),含盐( ) A .mxa(g ) B .amx(g ) C .amx a+(g ) D .mxx a+(g ) 答案:D11.若2x <,则2|2|x x --的值为( ) A .-1B .0C .1D . 2答案:A12.使分式221a aa ++的值为零的a 的值是( )A .1B .-1C .0D .0 或-1答案:D13.分式3a x ,22x y x y +-,22a b a b -+,x y x y +-中最简分式有( )A .1 个B .2 个C . 3 个D .4 个答案:C14.下列各分式中与11y x+-的值相等的分式是( ) A .11y x -- B . 11y x--- C . 11y x +-- D .11yx-+ 答案:C 二、填空题15.下面是一个有规律的数表:上面数表中第 9 行、第 7 列的数是 ,第 (n+1)行、第 (n +2)列的数是 . 解答题 解析:97,12n n ++ 16.一箱水果售价 a 元,水果的总质量为b(kg),则每kg 水果售价是 元.解析:a b17.小舒 t(h)走了 s(km)的路程,则小舒走路的平均速度是 km/h.解析:s t18.若543222Ax B x x x x x --=-+++,则A= ,B= . 解析: 1,-319.已知关于x 的分式方程4333k x x x-+=--有增根,则k 的值是 . 解析:120.完成某项工程,甲单独做需 a(h),乙单独做需 b(h),甲、乙两人合作完成这项工程需 h.解析:aba b+ 21.不改变分式的值. 使分子、分母都不含不含负号: (1)23x -= ;(2)x yz -- = ;(3)2ab ---;(4)5yx--- = .解析: (1)23x -;(2)x yz ;(3)2ab -;(4)5y x+22.当12x =-,1y =时,分式1x yxy --= . 解析:123. 某商品的标价是 1375元,打 8 折(按标价的 80%)售出,仍可获利 10%,如果设该商品的进价是x 元,那么可列出方程 . 解答题解析:x 1.18.01375=⨯24.如果分式211x x -+的值为0,则x= .解析:1 25.已知22753y x x y -=+且y ≠0,则x y=.解析:174-26.解析:x 1,0或x 2,x1-或……(答案不唯一) 27.方程112=-x 的解为x = . 解析:3 28.若4y -3x=0 ,则yyx += . 解析:37 29.关于x 的方程230x x m-=-有增根.则m = . 解析:930.列车中途受阻,停车 10 min ,再启动后速度提高到原来的 1. 5 倍,这样行驶了 20 km ,正好将耽误的时间补上. 如果设列车原来的速度是 x(km/h),那么根据题意,可得方程 .解析:2020101.560x x -=三、解答题31.请观察下列方程和它们的根: 1112x x -=,12x =,212x =-;1223x x -=,13x =,213x =-; 1334x x -=,14x =,214x =-;1445x x -=,15x =,215x =-; …(1)请你猜想第 10 个方程1101011x x -=的根是 ;(2)猜想第n 个方程是什么?它的根是什么?并将你猜想的原方程的根代人方程检验.解析:(1)111x =,2111x =-;(2)11n x n x n -=++,11x n =+,211x n =-+,检验略 32.下列各个分式中的字母满足什么条件时,分式有意义? (1)251y -;(2)1|1|a -;(3)1||1b -解析:(1)1y ≠±;(2)1a ≠;(3)1b ≠±33.轮船在静水中每小时航行 a(m),水流速度是每小时 b(km),则该轮船在顺水中航行s(km)需要多少时间? s a b+ 解析:s a b+ 34.先化简,再求值:(1)21()a a a a-÷-,其中a = (2)22142244a a a a a --⨯--+,其中1a =-.解析: (1)21a ,13;(2)22(2)a a +-,16-35.有这样一道题“计算:2222111x x x x x x x-+-÷--+的值,其中2008x =.” 甲同学把“2008x =”错抄成“2080x =”,但他的计算结果也正确,这是怎么回事?解析: 原式的值为 0,与x 值无关 36.代数式1324x x x x ++÷++有意义,求x 的取值范围.解析:2x ≠-,3x ≠-且4x ≠-37.一个长,宽,高分别为 a ,b ,h 的长方体烟盒内装满了高为h 的香烟,共 20 枝. 打开烟盒盖,20 支香烟排成三行(如图所示). 求烟盒的空间利用率. (已知 2.56ab=,π取 3. 14,结果精确到 1%,烟盒纸厚度忽略不计)解析: 约 82% 38.(1)观察下列变形:1111212=-⨯;1112323=-⨯;1113434=-⨯;… 通过观察,你发现了什么规律?用含 n 的等式表示(n 为正整数): . (2)利用(1)中的规律计算: 1111()(1)(2)(2)(3)(2007)(2008)x x l x x x x x x +++++++++++(其中0x >),并求当 x=1时该代数式的值.解析: (1)111(1)1n n n n =-++;(2)2008(2008)x x +,2008200939.将分式10(2)(1)(2)(1)(1)x x x x x +++-+约分,再讨论x 取哪些整数时,能使分式的值是正整数.解析:101x -,当 x=2或3 或6或 11 40.一架飞机从北京到上海一个来回,在有风(顺、逆风)和无风的时候,哪种情况更快?解析: 有风时飞行时间较长 41.计算:(1+-)3)27248(÷-解析:(1)32;(2)-242.为加快西都大开发,某自治区决定新修一条公路,甲、乙两工程队承包此项工程. 如 果甲工程队单独施工,则刚好如期完成;如果乙工程队单独施工就要超过 6 个月才能完成. 现在甲、乙两队先共同施工 4个月,剩下的由乙队单独施工,则刚好如期完成. 问原来规定修好这条公路需多长时间?解析:12 个月43.某商店销售一种衬衫,四月份的营业额为 5000 元,为了扩大销售,在五月份将每件衬衫按原价的 8 折销售,销售量比四月份增加了 40 件,营业额比四月份增加了600 元,求四月份每件衬衫的售价.解析:50 元 44.解方程: (1)2714111x x -=+- (2)27272x x x x -+=-解析:(1)8=x ;(2)-7. 45.分式方程0111x k x x x x +-=--+有增根x=1,求k 的值.解析:1-=k .46. 请从下列三个代数式中任选两个构成一个分式,并化简该分式. x2-4xy+4y2 x2-4y2 x-2y解析:解:2222444yx y xy x -+- =)2)(2()2(2y x y x y x -+-=y x y x 22+- . (答案不惟一) 47.甲、乙两工程队分别承担一条2千米公路的维修工作,甲队有一半时间每天维修公路x 千米,另一半时间每天维修公路y 千米.乙队维修前1千米公路时,每天维修x 千米;维修后1千米公路时,每天维修y 千米(x ≠y ).⑴求甲、乙两队完成任务需要的时间(用含x 、y 的代数式表示); ⑵问甲、乙两队哪队先完成任务?解析:(1)甲、乙两队完成任务需要的时间分别为y x +4与xyyx +; (2) y x +4-xyy x +=0)()(2<+--y x xy y x (x ≠y ),∴甲队先完成 48. 若2131||()0234x x y -++=-+,求代教式322131x y -+-的值.解析:249.请验证下列等式是否成立:33332333333333333232434352526262;3131414153536464++++++++====++++++++;;; (1)请你写出一个符合上面规律的一个式子(不能与上面的重复);(2)探索其中的规律,再写出一个类似的等式,并用含m ,n 的等式表示这个规律(m ,n 为整数).解析:(1)如:333373737474++=++ (2)3333()()m n m n m m n m m n ++=+-+- 50.已知123x x +=,121x x =. (1)求1211x x +的值; (2)求2112x x x x +的值; (3)求2112111+1x x x x ++++的值.解析: (1)3;(2)7;(3)3。
精选最新2019七年级下册数学单元测试第七章《分式》模拟考核题库(含参考答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.已知111a b a b +=+,则b aa b+的值为( )A .1B .0C .-1D .-2解析:C2.当x 为任意实数时,下列分式一定有意义的是( ) A .2xB .21x C .1||x D .211x + 答案:D3.使分式221a aa ++的值为零的a 的值是( )A .1B .-1C .0D .0 或-1答案:D4.x (g )盐溶解在 a (g )水中,取这种盐水m (g ),含盐( ) A .mxa(g ) B .amx(g ) C .amx a+(g ) D .mxx a+(g ) 答案:D5.下列各式运算正确的是( ) A .0c d c da a-+-= B .0a ba b b a-=-- C .33110()()a b b a +=-- D .22110()()a b b a +=--答案:C6. 已知222220a a b b ++++=,则1ba+的值是( )A .2B .1C .0D .-1答案:A7.不解方程判断方程21230111x xx -+=+--的解是( ) A .OB .1C .2D .13答案:A8.下列说法正确的是( )A .方程01xx =-的解是0x = B .方程1211x x x =+--的解是1x = C .分式方程一定会产生增根 D . 方程1222x x x+=--的最简公分母是(2)(2)x x -- 答案:A9.某中学八年级甲、乙两班学生参加植树造林,已知甲班每天比乙班多植 5 棵树,甲班植 80 棵树所用的天数与乙班植 70 棵树所用的天数相等.若设甲班每天植树x 棵,则根据题意列出的方程是( ) A .80705x x=- B .80705x x =+ C .80705x χ=+ D .80705x x =- 答案:D10.下列关于分式263x χ--的说法,正确的 ( ) A . 当3x =时,分式有意义 B . 当3x ≠时,分式没有意义 C . 当3x =时,分式的值为零D . 分式的值不可能为零答案:D11.当25x >时,分式|25|52x x --的值是( ) A .-1B .0C .1D .23答案:C12.把式子2(3)(2)a a a -+-化简为13a +,应满足的条件是( )A . 2a -是正数B . 20a -≠D . 2a -是非负数 D .20a -=答案:B13.把a 千克盐溶进b 千克水中制成盐水,那么x 千克这样的盐水中含盐( )A .a xa b -+千克 B .ba ax+千克 C .a xa b++千克 D .axb千克 解析:B14.若x 满足||xx =1,则x 应为( )A .正数B .非正数C .负数D .非负数解析:A 15.若分式x yx y+-中的x 、y 的值都变为原来的3倍,则此分式的值( )A .不变B .是原来的3倍C .是原来的13D .是原来的16答案:A16.下列各式中,是分式的个数有( ) ①2a ;②3a -;③2c d -;④2a b -;⑤s a b +;⑥4y x-. A .1 个B . 2个C .3个D .4个答案:C17.某种商品在降价x %后,单价为a 元,则降价前它的单价为( )A .%ax B .%a x ⋅C .1%ax -D .(1%)a x -答案:C18. 已知 x ,y 满足等式11x y x -=+,则用x 的代数式表示得( ) A .11x y x -=+ B . 11x y x -=+ C .11x y x +=- D .11x y x +=-答案:C19.要使分式2143x x -+的值为 0,则x 的值应为( )A .1B .-1C .34-D .1±答案:D解析:D .20.为迎接图书馆的标准化检查,某中学图书馆将添置图书,用250无购进一种科普书,同时用 140元购进一种文学书. 由于科普书的单价比文学书的单价高出一半,因此学校所购买的文学书比科普书多6本,求文学书的单价. 设这种文学书的单价为x 元,则根据题意,列方程正确的是( ) A .1.51402506x x ⨯-= B .14025061.5x x -=C .25014061.5x x-= D .1.51402506x x⨯=+ 答案:B21.与分式x yx y-+--的值相等的分式是( ) A .x yx y+- B .x yx y-+ C .x yx y+-- D .x yx y--+ 答案:B 二、填空题22.若2a a b =+,当a 、b 都扩大到原来的2009倍时,aa b+的值怎样变化?(填“变大”、“变小”或“不变”) . 解析:不变23. 某商品的标价是 1375元,打 8 折(按标价的 80%)售出,仍可获利 10%,如果设该商品的进价是x 元,那么可列出方程 . 解答题解析:x 1.18.01375=⨯24.当x ________时,分式xx2121-+有意义. 解析:21≠25.某工厂库存原材料x 吨,原计划每天用a 吨,若现在每天少用b 吨,则可以多用 天. 解析:)(b a a bx- 26.请选择一组,a b 的值,写出一个关于x 的形如2ab x =-的分式方程,使它的解是0x =,这样的分式方程可以是____________.解析:如212x -=-(答案不唯一)27.一根蜡烛在凸透镜下成一实像,物距u ,像距v 和凸透镜的焦距f 满足关系式:1u +1v =1f.若f =6厘米,v =8厘米,则物距u =________厘米. 解析:2428.下面是一个有规律的数表:上面数表中第 9 行、第 7 列的数是 ,第 (n+1)行、第 (n +2)列的数是 . 解答题 解析:97,12n n ++29.若分式方程244x ax x =+--有增根,则a 的值为 .解析:4 30.若11x -与11x +互为相反数,则x = . 解析:031.某商品原价为a 元,若按此价的8折出售,仍获利 b%,则此商品进价是 元.解析:80100a b+32.某工厂要生产 a 个零件,原计划每天生产 x 个,后来由于供货需要,每天多生产 b 个零件,则可提前 天完成.解析:a a xx b-+33.已知甲工人每小时能加工零件a 个,现总共有零件A 个.(1)甲工人加工 t(h)能完成 个零件,若全部完成这批零件,则需要 h ;(2)已知乙工人每小时能加工零件 b 个,若乙工人也来加工这批零件,则两人同时开始加工零件,需要 h 才能完成,比甲独做提前 h. 解析:(1) (1)at ,A a ;(2)A a b +,A Aa a b-+ 34.已知2|24|(36)0x x -++=,则341x y -+的值是 . 解析:15三、解答题35.小雪家距离学校 a(km),骑自行车需 b(min). 某一天小雪从家出发迟了 c(min)(c<b),则她每分钟应多骑多少 km ,才能像往常一样准时到达学校?解析:2acb bc-(km) 36.不改变分式的值,使分子和分母中最高次项的系数变为正数,并把分子、分母中的多项式按x 的次数从高到低排列: (1)22132x x x ⋅----;(2) 22212x x x -+--解析: (1)22123x x x -++;(2)22212x x x -+-37.当 x 取什么值时,下列分式的值为零?(1)1510x x +-;(2)211x x -+;(3)||22x x --解析: (1)1x =-;(2)1x =;(3)2x =-38.某校有学生 2500 人,每个学生平均每天用水 a(kg),在该校提倡“人人节水”之后,如果每个学生平均每天节约用水 1 kg ,那么 A(kg)水可供全校用多少天?当 A=7500000,a=4 时,可供全校用多少天?解析:2500(1)Aa -天,1000 天39.先化简,再求值:(1)21()a a a a-÷-,其中a = (2)22142244a a a a a --⨯--+,其中1a =-.解析: (1)21a,13;(2)22(2)a a +-,16- 40.计算:(1)22x x x x --⋅-;(2)212(8)5xy a y a÷-;(3)2(1)(2)2(1)(1)a a a a a a -+⋅++-;(4)22211444a a a a a --÷-+-; (5)2b c c ax ax x⋅÷;(6)222()a b ab b a b --÷+解析: (1)1;(2)3310x a -;(3)21a a a -+;(4)2(2)(1)a a a +-+;(5)2ba;(6)b 41.化简下列各分式:(1)236sxy x y-;(2) 22699x x x -+-解析:(1)22y x -;(2)33x x -+42.上海到北京的航线全程为 s(km),飞行时间需 a(h). 而上海到北京的铁路全长为航线 长的m 倍,乘车时间需 b(h). 问飞机的速度是火车速度的多少倍?(用含 a ,b ,s ,m 的 分式表示)解析:bam倍 43.关于x 的方程1311m mx mx =+--的解为2x =,求m 的值. 0.25m =解析:0.25m =44.已知123x x +=,121x x =. (1)求1211x x +的值; (2)求2112x x x x +的值; (3)求2112111+1x x x x ++++的值.解析: (1)3;(2)7;(3)345.一架飞机从北京到上海一个来回,在有风(顺、逆风)和无风的时候,哪种情况更快?解析: 有风时飞行时间较长46.a 为何值时,分式方程311a a x +=+无解?解析:310-==a a 或.47. 请你先将分式2211x x x x x ---+化简. 再选取一个使原式有意义,而你又喜爱的数代入求值.解析:22x -(代入0,1x ≠-的数都可以) 48.请验证下列等式是否成立:33332333333333333232434352526262;3131414153536464++++++++====++++++++;;; (1)请你写出一个符合上面规律的一个式子(不能与上面的重复);(2)探索其中的规律,再写出一个类似的等式,并用含m ,n 的等式表示这个规律(m ,n 为整数).解析:(1)如:333373737474++=++ (2)3333()()m n m n m m n m m n ++=+-+-49.当12x =-时,代数式223261169x x x x x x x ++-⋅++++的值恰好是分式方程22024mxx x +=--的根,试求字母m 的值.解析:2232x 61169x x x x x x x ++-⋅++++的化简结果为1xx -+,计算结果为 1,代入分式方程,得6m =-50.代数式1324x xx x++÷++有意义,求x的取值范围.解析:2x≠-,3x≠-且4x≠-。
精编2019七年级下册数学单元测试第七章《分式》完整考题库(含答案)

2019年七年级下册数学单元测试题第七章 分式一、选择题1.分式方程11888x x x +=+--的根是( ) A .x=8B .x=1C .无解D .有无数多个解析:C2.下列关于分式263x χ--的说法,正确的 ( ) A . 当3x =时,分式有意义B . 当3x ≠时,分式没有意义C . 当3x =时,分式的值为零D . 分式的值不可能为零答案:D3.若2x <,则2|2|x x --的值为( ) A .-1 B .0 C .1 D . 2答案:A4.把分式x x y+(0x ≠,0y ≠)中的分子,分母的x ,y 同时扩大 2倍.那么分式的值( ) A .扩大2倍 B . 缩小2倍 C . 改变原来的值 D . 不改变答案:D5.若有m 人,a 天可完成某项工作,则(m n +)人完成此项工作的天数是( )A .a m +B .am m n +C .a m n +D .m n am + 答案:B6.下列各式运算正确的是( )A .0c d c d a a -+-= B .0a b a b b a -=-- C .33110()()a b b a +=-- D .22110()()a b b a +=-- 答案:C7.某中学八年级甲、乙两班学生参加植树造林,已知甲班每天比乙班多植 5 棵树,甲班植 80 棵树所用的天数与乙班植 70 棵树所用的天数相等.若设甲班每天植树x 棵,则根据题意列出的方程是( )A .80705x x =-B .80705x x =+C .80705x χ=+D .80705x x =-答案:D8.已知分式11x x -+的值为零,那么x 的值是( ) A .-1 B .0 C .1 D .1±答案:C9.下列各分式中与11y x +-的值相等的分式是( ) A . 11y x -- B . 11y x --- C . 11y x +-- D . 11y x-+ 答案:C10.把a 千克盐溶进b 千克水中制成盐水,那么x 千克这样的盐水中含盐( )A .a x a b-+千克 B .b a ax +千克 C .a x a b ++千克 D . ax b千克 解析:B 11.若22440a ab b -+=,则代数式23a b a b -+的值是( ) A .1 B . 35 C .45 D .无法确定 答案:B12.方程222332x x x-=--的解是( ) A .x=1.5B .x=4C .0D .无解 解析:C13.若关于x 的方程1011--=--m x x x 有增根,则m 的值是( ) A .3 B .2 C .1 D .-1答案:B14.第六次火车大提速后,从北京到上海的火车运行速度提高了25%,运行时间缩短了2h .已知北京到上海的铁路全长为1462km .设火车原来的速度为xkm/h ,则下面所列方程正确的是( )A .2)251(14621462=+-%x x B .21462)251(1462=--x x % C .21462251462=-x x %D .22514621462=-x x % 答案:A15. 已知 x ,y 满足等式11x y x -=+,则用x 的代数式表示得( ) A .11x y x -=+ B . 11x y x -=+ C .11x y x +=- D .11x y x +=- 答案:C16.m 克白糖溶于n 千克水中,所得糖水的含糖量可以表示为( )A . m nB .m m n +C .100n mD .1000m m n + 答案:D17.若x 满足2310x x ++=,则代数式221x x +的值是( ) A .37 B .3 C .949 D .7答案:D18.若分式3242x x +-有意义,则字母x 的取值范围是( ) A .12x = B .23x =- C .12x ≠ 23x ≠- 答案:C19.若关于x 的方程652m x =-的根为 1,则m 等于( ) A . 1 B . 8 C .18 D . 42答案:C20.方程1x x -=0的根是( ) A .1 B .-1 C .1或0 D .1或-1答案:D二、填空题21. 某商品的标价是 1375元,打 8 折(按标价的 80%)售出,仍可获利 10%,如果设该商品的进价是x 元,那么可列出方程 .解答题解析:x 1.18.01375=⨯22.某班a 名同学参加植树活动,其中男生b 名(b<a ),若只由男生完成,每人需植树15棵;若只由女生完成,则每人需植树_________棵. 解析:15b a b -23.若14-m 表示一个正整数,则整数m 的值为 . 解析:2,3,524.请选择一组,a b 的值,写出一个关于x 的形如2a b x =-的分式方程,使它的解是0x =,这样的分式方程可以是____________.解析:如212x -=-(答案不唯一) 25.若x 、y 满足关系式 时分式3355x y x y --的值等于35. 解析:y x ≠26.把公式12s lr =变形为已知S ,l ,求r 的公式,则r= . 解析:2S l27.判断正误,正确的打“√”,错误的打,“×” (1)111222()a b a b +=+; ( ) (2)111b b b b a a a a---+==-; (3)11110a b b a a b a b +=-=----; (4)220()()x x a b b a +=-- 解析:(1) × (2) × (3)√ (4)×28.某工厂要生产 a 个零件,原计划每天生产 x 个,后来由于供货需要,每天多生产 b 个零件,则可提前 天完成. 解析:aa x x b-+ 三、解答题29.一架飞机从北京到上海一个来回,在有风(顺、逆风)和无风的时候,哪种情况更快?解析: 有风时飞行时间较长30.已知269a a -+与|1|b -互为相反数,求式子()()a b a b b a-÷+的值.解析:3a =,1b =,原式的值为2331.先约分,再求值: (1)22444x x x --+,其中3x =.(2) 222x x y xy--,其中2x =-,2y =解析: (1)22x x +-,5 ; (2)x y -,1 32.对于分式23x a x b -+,当 x=-1时,分式无意义;当 x=4时,分式的值为 0,试求代数式a b的值.83解析:8333.已请你分析分式||||x y x y ÷的所有可能值.解析: 分类讨论(1)当0x >,0y >时,原式=2;(2)当0x >,0y <时,原式=0;(3)当0x <,0y >时,原式=0;(4)当0x <,0y <时,原式=-2.∴原式所有可能的值为 0、2,-234.计算: (1)22x x x x --⋅-;(2)212(8)5xy a y a÷-;(3)2(1)(2)2(1)(1)a a a a a a -+⋅++-;(4)22211444a a a a a --÷-+-; (5)2b c c ax ax x⋅÷;(6)222()a b ab b a b --÷+解析: (1)1;(2)3310x a -;(3)21a a a -+;(4)2(2)(1)a a a +-+;(5)2b a ;(6)b 35.已知 x 等于它的倒数,求222169(2)(3)x x x x x +÷-+--的值.解析:24x -,当1x =±时,243x -=-36.上海到北京的航线全程为 s(km),飞行时间需 a(h). 而上海到北京的铁路全长为航线 长的m 倍,乘车时间需 b(h). 问飞机的速度是火车速度的多少倍?(用含 a ,b ,s ,m 的 分式表示)解析:b am倍 37.一个长,宽,高分别为 a ,b ,h 的长方体烟盒内装满了高为h 的香烟,共 20 枝. 打开烟盒盖,20 支香烟排成三行(如图所示). 求烟盒的空间利用率. (已知2.56a b=,π取 3. 14,结果精确到 1%,烟盒纸厚度忽略不计)解析: 约 82%38.不改变分式的值,使分子和分母中最高次项的系数变为正数,并把分子、分母中的多项式按x 的次数从高到低排列: (1)22132x x x ⋅----;(2) 22212x x x -+--解析: (1)22123x x x -++;(2)22212x x x -+- 39.某生产车间制造 a 个零件,原计划每天造 x 个,后来实际每天多造 b 个,则可提前几天完成.2ab x bx +解析:2ab x bx+ 40.甲、乙两工程队分别承担一条2千米公路的维修工作,甲队有一半时间每天维修公路x 千米,另一半时间每天维修公路y 千米.乙队维修前1千米公路时,每天维修x 千米;维修后1千米公路时,每天维修y 千米(x ≠y ).⑴求甲、乙两队完成任务需要的时间(用含x 、y 的代数式表示);⑵问甲、乙两队哪队先完成任务?解析:(1)甲、乙两队完成任务需要的时间分别为y x +4与xyy x +; (2) y x +4-xyy x +=0)()(2<+--y x xy y x (x ≠y ),∴甲队先完成 41.解下列分式方程: (1)231x x =+;(2)22322x x x --=++;(3)3133x x x--=--解析:(1)2x =;(2)3x =-;(3)无解42.解下列分式方程: (1)32221221x x x x --+=--;(2)6201(1)x x x x +-=--解析:(1)1x =;(2)25x = 43.甲、乙两个工程队合做一项工程,两队合做2天后,由乙队单独做 1 天就可全部完 成. 已知乙队单独做全部工程所需天数是甲队单独做所需天数的32倍,求甲、乙两队单独做分别需多少天?解析:各需4天和6 天44.从甲地到乙地有两条路,每条路都是3 km ,其中第一条路是平路,第二条路有1 km 的上坡路和2 km 的下坡路. 小雨在上坡路上的骑车速度为每小时v (km),在平路上的骑车速度每小时2v (km),在下坡路上的骑车速度为每小时3v (km),求:(1)当走第二条路时,她从甲地到乙地需要多长时间?(2)她走哪条路花费时间少?少用多少时间?解析:(1)53v h ;(2)走第一条花费时间少,少用16vh 45.解方程:(1)2714111x x -=+- (2)27272x x x x -+=-解析:(1)8=x ;(2)-7.46.课堂上,李老师给大家出了这样一道题:当x=5,,,时,•分别求代数式22212211x x x x x -+-÷-+的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.解析:21. 47.小利取出一年到期的本金和利息时,缴纳50元的利息税(国家规定存款利息的纳税方法是:利息税=利息×20%).若银行一年定期储蓄的年利率为1.25%,则小利一年前存入银行的本金是多少?解析:20000元.48.a 为何值时,分式方程311a a x +=+无解?解析:310-==a a 或.49. 请从下列三个代数式中任选两个构成一个分式,并化简该分式. x2-4xy+4y2 x2-4y2 x-2y解析:解:2222444yx y xy x -+- =)2)(2()2(2y x y x y x -+-=y x y x 22+- . (答案不惟一) 50.(1)观察下列变形:1111212=-⨯;1112323=-⨯;1113434=-⨯;… 通过观察,你发现了什么规律?用含 n 的等式表示(n 为正整数): .(2)利用(1)中的规律计算:1111()(1)(2)(2)(3)(2007)(2008)x x l x x x x x x +++++++++++(其中0x >),并求当 x=1时该代数式的值.解析: (1)111(1)1n n n n =-++;(2)2008(2008)x x +,20082009。
