某配送中心向六家超市节约里程法
运输的优化求解、运输问题—节约里程法

1、列运输平衡表
列表时要求表内供销平衡,并将运费标入表内空格。
需
供
B1
B2
B3
A1
x11 90 x12 70 x13 100
供应量 200
A2
x21 80 x22 65 x23 80
250
需求量 100 150
200
250
需求量 100 150
200
450
由于上表中有负检验数,故需继续 进行调整,得新运输方案表。
新运输方案2表
需
供
B1
B2
B3
A1
100 90 100 70
100
A2
80 50 65 200 80
需求量 100
150
200
供应量 200 250 450
对新运输方案表进行检验。
新运输方案2检验表
其需量等于总供量与总需量之差,并设其相应运价为0。这
样,就可以用表上作业法求解产大于销的运输问题。
2、销大于产的运输问题 n m
对于销量大于产量,即 bj ai 的运输问题,必
j 1
i 1
然有一些销地不能得到满足,发生缺货,此时引入虚拟供
应点,并设其相应运价为0。这样,就可以用产销平衡的表
上作业法求解销大于产的运输问题。
450
2、建立初始调运方案
采用最小元素法,即在平衡表中挑取运价最小或
较小的供需点格子尽量优先分配的调运方法。
需
供
B1
A1
0 90
B2
B3
供应量
节约里程法的举例
7
P4
2.5
5
13
9
13
10
P5
1.6
15
22
18
22
19
9
P6
1.8
19
27
23
30
30
20
11
P7
解:(1)先优化配送路线,计算节约里程数。(本步骤计5分)
第一步。根据运输里程表,按节约里程公式,求出相应的节约里程数,如下表括号内数字示
需要量
P0
2.8
8
P1
1.7
4
5(7)
P2
0.8
11
9(10)
4(11)
P3
1.4
12
16(4)
11(5)
7(16)
P4
2.5
5
13(0)
9(0)
13(3)
10(7)
P5
1.6
15
22(1)
18(1)
22(4)
19(8)
9(11)
P6
1.8
19
27(0)
23(0)
30(0)
30(1)
20(4)
11(23)
P7
第二步,按节约里程数大小的顺序排序(本步骤计5分)
序号
⑵设配送中心在向用户配送货物过程中单位时间平均支出成本为45元,假定卡车行驶的平均速度为25公里/小时,试比较优化后的方案比单独向各用户分送可节约多少费用?
(3)、配送货物的运输量是多少?
(4)、配送货物的周转量是多少?
表1运输里程表
需要量
P0
2.8
8
P1
1.7
4
5
节约里程法应用案例

节约里程法应用案例在当今竞争激烈的商业环境中,物流成本的有效控制对于企业的生存和发展至关重要。
节约里程法作为一种优化配送路线的有效方法,能够显著降低运输成本,提高物流效率。
接下来,让我们通过一个具体的案例来深入了解节约里程法的实际应用。
假设我们有一家位于城市中心的配送中心,需要向位于城市不同区域的五个客户(A、B、C、D、E)配送货物。
每个客户的需求量以及他们之间的距离如下表所示:|客户|需求量(吨)|与配送中心距离(公里)||||||A|5|10||B|8|12||C|3|8||D|6|15||E|4|11||客户|A|B|C|D|E|||||||||A| | 18 | 22 | 25 | 16 ||B| 18 || 10 | 18 | 12 ||C| 22 | 10 || 14 | 9 ||D| 25 | 18 | 14 || 20 ||E| 16 | 12 | 9 | 20 ||首先,我们按照传统的方法,即每个客户单独配送,计算出总运输里程。
配送中心到客户 A 的往返里程为 2×10 = 20 公里。
配送中心到客户 B 的往返里程为 2×12 = 24 公里。
配送中心到客户 C 的往返里程为 2×8 = 16 公里。
配送中心到客户 D 的往返里程为 2×15 = 30 公里。
配送中心到客户 E 的往返里程为 2×11 = 22 公里。
总运输里程为 20 + 24 + 16 + 30 + 22 = 112 公里。
接下来,我们应用节约里程法来优化配送路线。
第一步,计算两两客户之间的节约里程数。
例如,客户 A 和客户 B 之间的节约里程数为:(配送中心到 A 的距离+配送中心到 B 的距离 A 到 B 的距离)× 2 =(10 + 12 18)× 2 = 8 公里。
按照同样的方法,计算出所有两两客户之间的节约里程数,如下表所示:|客户|A|B|C|D|E|||||||||A| | 8 | 6 | 5 | 2 ||B| 8 || 4 | 3 | 4 ||C| 6 | 4 || 2 | 3 ||D| 5 | 3 | 2 || 5 ||E| 2 | 4 | 3 | 5 ||第二步,根据节约里程数的大小对路线进行合并和优化。
[计算题]节约里程法答案讲解学习
![[计算题]节约里程法答案讲解学习](https://img.taocdn.com/s3/m/7d22229e80eb6294dd886c78.png)
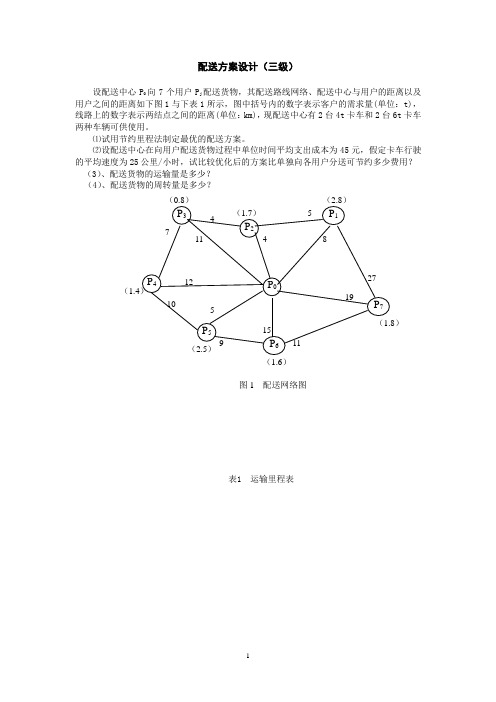
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)作运输里程表,列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7(2)按节约里程公式求得相应的节约里程数(3)将节约里程按从大到小顺序排列表-4)根据载重量约束与节约里程大小,选择配送路线。
优先择节约里程数最大的连接点:P6-P7、P3-P4最优方案:P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点,所以优先选择P6-P7,又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t(此路线选择一辆6t卡车)因P3-P4为第二大节约里程数连接点,且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t,故选择P0-P4-P3-P2-P0路线3.9t(此路线选择一辆4卡车)最后选P0-P1-P0路线2.8t(此路线选择一辆4卡车)得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=(19+14+5+12+8+4+8)*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
配送节约里程法讲义
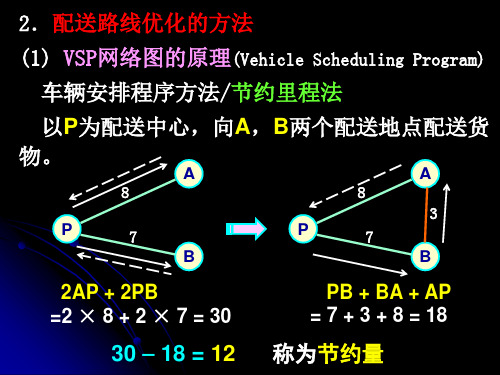
由节约里程数表可知: 由节约里程数表可知: EG节约里程最大 节约里程最大, ● EG节约里程最大,配送货物量是 1.75+1.15=2.9t,在货车载重限度内,可以入选。 1.75+1.15=2.9t,在货车载重限度内,可以入选。 ●FG的配送货物量1.1t,可与2.9t拼装为一辆4t FG的配送货物量1.1t,可与2.9t拼装为一辆4t 的配送货物量1.1t 2.9t拼装为一辆 货车的载运量; 货车的载运量; ●由此衔接成为一条配送路线AEGFA(AFGEA) ; 由此衔接成为一条配送路线AEGFA(AFGEA) AEGFA 全程为20+1+6+24=51 km。 ● 全程为20+1+6+24=51 km。 4t货车装满。 4t货车装满。 货车装满
要向所在城市B, , , , 例:某配送中心A要向所在城市 ,C,D,E, 配送中心 要向所在城市 F,G共6个客户点配送货物,它们之间的距离和 , 共 个客户点配送货物, 点配送货物 每一处的配送货物量见下表。运输车辆有2. 每一处的配送货物量见下表。运输车辆有 .5 t 两种货车。 和4 t两种货车。试确定配送路线。 两种货车 试确定配送路线。
最短距离表 A B C D E F G A 0 B 9 0 C 12 9 0 D 12 19 10 0 E 20 29 32 25 0 F 24 33 29 19 6 0 G 21 30 33 25 1 6 0
节约里程数表 序号 组合 节约里程 8 CF 7 1 EG 40 9 DE 7 2 FG 39 10 BD 2 3 EF 38 B E 0 4 DF 17 B F -5 CD 14 B G -6 BC 12 C E -7 DG 8 C G --
【管理资料】节约里程法例题计算汇编

顺序排位
1 2 3 4 4 6 6 6 9 9 11 12
连接线
A- B A- J B- C D- E C- D A- I E- F I- J A- C B- J B- D C- E
节约里程
15 13 11 10 10 9 9 9 8 8 7 6
顺序排位
13 13 13 16 16 16 19 19 21 22 22 22
C
D
B
A 0.32
0.24
路线1 2
E
P 路线2 2
J 0.24
F
G
路线3 2
0.16
0.48
H
0.40
图2 配送路线图
I 0.32
从配送路线图可看出,依次确定的三条配送路线均符合配送中心的约 束条件,需要2t货车3辆,总走行里程为70km,若简单地每个连锁分店 送货,需要2t货车10辆,走行总里程148km。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
连接线
F- G G- H H- I B- I A- D F- H B- E D- F G- I C- J E- G F- I
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
第四步:根据节约里程排序表和配送车辆载重及行驶里程等约束 条件,渐近绘出如图2所示的配送路线图。
0.32
0.40
0.40
第二步:由最短距离表,利用“节约里程”法计算出各连锁分店之 间的节约里程,做出节约里程表(见表3),计算结果有正有负, 节约里程为负数时,无实际意义,在表内写0。
表3 节约里程表
A BC DE F GH I J A B C D E F G H I J
[计算题]节约里程法答案
![[计算题]节约里程法答案](https://img.taocdn.com/s3/m/a35e5204915f804d2b16c1cd.png)
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)作运输里程表,列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7(2)按节约里程公式求得相应的节约里程数(3)将节约里程按从大到小顺序排列表-4)根据载重量约束与节约里程大小,选择配送路线。
优先择节约里程数最大的连接点:P6-P7、P3-P4最优方案:P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点,所以优先选择P6-P7,又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t(此路线选择一辆6t卡车)因P3-P4为第二大节约里程数连接点,且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t,故选择P0-P4-P3-P2-P0路线3.9t(此路线选择一辆4卡车)最后选P0-P1-P0路线2.8t(此路线选择一辆4卡车)得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=(19+14+5+12+8+4+8)*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
物流线路规划节约里程法案例详解

节约里程法案例详解假如由一家配送中心P向两个用户A、B送货,配送中心到两客户的最短距离分别是L1和L2,A和B间的最短距离为L3,AB的货物需求量分别是Q1和Q2,且Q1+Q2小于车辆装载量Q【如果Q1+Q2大于车辆装载量Q,那一辆车就无法装完两位客户的货物】。
如下图所示:如果配送中心用两辆汽车分别对A、B两个用户各自往返送货时,汽车行驶的总里程L是L=2(L1+ L2)如果用一辆汽车向A、B两个用户巡回送货,则汽车行驶总里程L′为L′= L1+ L2+L3根据三角形的一边之长必定小于另外两边之和的原理,后一种配送方案比前一种方案节约里程△L为△L=2(L1+ L2)-(L1+ L2+L3)= L1+ L2-L3【这就是节约里程法产生的初衷,以最短距离最优配载完成送货作业】案例:位于市内的百家姓配送中心(P0)向它旗下的10家连锁商店p i(i=1,2,…,10)配送商品,其配送网络如下图所示。
图中括号内的数字表示每一家连锁店的需求量(t),线路上的数字表示两节点之间的距离(km)。
配送中心现有2t和4t车辆可供使用(无数量限制),并且每辆车配送距离不得超过30km。
请为百家姓配送中心制定最优的配送方案。
分析:初始方案:如果从P点向各点分别派车送货。
1、从百家姓配送中心出发,需要设计10条配送线路,分别向10家连锁店配送商品;2、需要10辆2t的配送车辆(每家连锁店的需要量都低于2t),总配送距离为148km。
第二种:节约里程法解题思路:相互间的节约里程计算根据△L== L1+ L2-L3 原理,例如以“百家姓配送中心交通图”中的P0(配送中心)到客户d、客户c的节约里程为例:dc△L==P0d(L1)+P0c (L2)-dc(L3 )==8 + 7 - 5=10如此计算出客户d和客户c间的节约里程数为10,以此方法计算出各个节点的节约里程数。
方案修正过程(优化到最终线路)1、方案修正过程实际上是线路规划过程,根据节约里程法原理从节约里程数最大的节点开始选择(这是先要排序的原因);2、所有规划线路的起点和终点都是配送中心,这里是P0;3、最大节约里程是a和b间的节约里程数15,那么路线的走向可以是P0-A或P0-B。
基于节约里程法连锁超市配送路线优化设计

基于节约里程法连锁超市配送路线优化设计【摘要】随着连锁超市经营市场竞争的加剧,进一步降低配送物流成本,建立一套科学完善的物流配送体系成为连锁超市经营成败的关键,节约里程法作为一种物流运筹启发算法在进行连锁超市配送路线优化设计、降低配送物流成本具有良好的适用性与实际意义。
【关键词】连锁超市;节约里程法;路线优化一、引言随着连锁经营在中国的快速发展,连锁超市经营通过“统一采购、统一核算、统一配送”的经营模式,凭借良好的规模经济与物流成本优势成为流通领域最主要的零售业态。
然而,随着市场竞争的加剧,连锁超市经营必须具备一套高效的物流配送体系,进行科学合理的配送路线优化设计,将配送商品以最短的时间、最快的速度、最低的物流成本送到到指定门店或消费者手中,节约里程法是一种解决连锁超市配送路线优化问题的有效方法。
二、节约里程法基本思想与操作方法(一)节约里程法的基本思想节约里程法又称节约算法,是用于解决一个配送中心向多个指定客户巡回送货的最优路线优化问题的启发式算法,目标是以最短的配送距离、最少的货运车辆与司机、最短的送货时间、最少的物流成本完成指定配送任务。
设P是某超市配送中心所在地,A和B为客户所在地,PA距离为a,PB距离为b,AB距离为c,送货时最直接的方法是利用两辆车分别给两个客户送货,总行程距离为2a+2b,若进行节约里程法进行配送路线优化,采用共同巡回送货的方式送货,那么总行程为a+b+c,节约的里程数为(2a+2b)-(a+b+c)=a+b-c,根据“三角形两边之和大于第三边”原理,可知a+b-c>0,其差值即为优化路线后节省的运输距离。
(二)节约里程法的操作步骤1、确定相关已知条件,如客户位置、各客户订货量、配送中心车辆类型与数量等。
2、计算确定配送中心与客户及客户之间的距离,一般可以通过DijkStra等算法解决网络中两点间的最短路问题。
3、根据节约里程法基本原理计算各配送点巡回优化配送比单独往返配送节约里程数,并根据节约里程数从大到小排序列表。
节约里程法

货运量 4.3 1.8 0.7 2.2 3.6 3.6 1.6 2 (qi)
节约里程法
• 广州配送中心为这次配送提供了三种车型,载重量分别为2 吨、5吨和8吨,不同车型的运输单价不一样,具体见运输单 价表。配送中心的配送是由外协商提供车辆,因此汽车的 数量没有限制
节约距离 =18km
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离=8+10+16=34km 用一辆 4t车运送 节约距离=2km
节约里程法
(0.9)
P3
6
(1.4)
P4
7
P0
10
(1.7)
P2
8
8
P5
(2.4)
初始方案:配送线路5条, 需要车5辆 配送距离=39×2=78KM
P1 (1.5)
节约里程法
第六步:最终方案的确定。
节约里程法
• 最终修改后的车辆调度结果:
节约里程法
• 通过对比初始方案与最终方案可知,通过优化可节约里程 (1768-1047)=721(公里),节约成本(4476.33384.55)=1091.75(元),仅8家客户的一次配送就节约了物 流配送成本1091.75。
• 车辆载重
2T 5T 8T
• 运价(元/公里) 2.4 2.7 3.65
节约里程法
2.步骤 第一步:各城市之间的距离:
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法
第三步:确定初始方案的运输线路及运输费用,现安排4辆2吨、4辆5吨的车给 每个客户送货。运输线路及运输费用见下表所示。
5
P1P2
节约里程法详解图
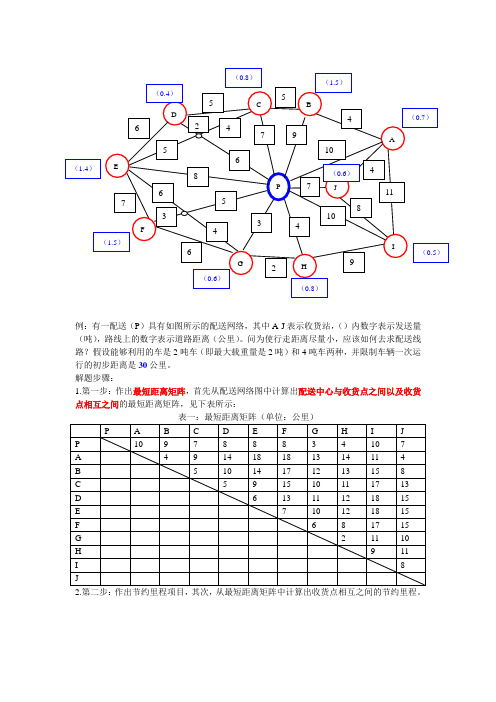
例:有一配送(P)具有如图所示的配送网络,其中A-J表示收货站,()内数字表示发送量(吨),路线上的数字表示道路距离(公里)。
问为使行走距离尽量小,应该如何去求配送线路?假设能够利用的车是2吨车(即最大载重量是2吨)和4吨车两种,并限制车辆一次运行的初步距离是30公里。
解题步骤:1.第一步:作出最短距离矩阵,首先从配送网络图中计算出配送中心与收货点之间以及收货点相互之间的最短距离矩阵,见下表所示:表一:最短距离矩阵(单位:公里)例如:计算A-B的节约里程项目如下:P-A的距离是:a=10P-B的距离是:b=9A-B的距离是:c=4节约里程项目为:a+b-c=10+9-4=15公里3.第三步:节约项目分类,再把节约项目由大到小顺序排列。
(1).初次解。
线路数:10总行走距离:(10+9+7+8+8+8+3+4+10+7)*2=148公里车辆台数:2吨车10台(2).二次解。
按节约里程由大到小的顺序,连接A-B,A-J,B-C连接线。
线路数:7总行走距离:148-15-13-11=109公里车辆台数:2吨车6台,4吨车1台(3).三次解。
其次节约里程最大的是C-D和D-E。
C-D,D-E两者都有可能与二次解的线路A连接,但由于A的车辆载重量与行走距离有限,不能再增加收货点。
为此,略去C-D而连接D-E。
总行走距离:109-10=99公里车辆台数:2吨车5台,4吨车1台(4).四次解。
接下来节约里程大的是A-I和E-F。
由于A已组合在完成的线路A中,所以略去,不能再增加收货点。
为此,略去A-I 而将E-F连接在线路B上。
线路数:5总行走距离:99-9=90公里车辆台数:2吨车3台,4吨车2台(5).五次解。
再继续按节约里程由大到小排出I-J,A-C,B-J,B-D,C-E。
由于同一组总有一头或两头包含在已完成的线路A中,不能再作出新的线路。
只考虑把下一组F-G组合在完成的线路B中。
总行走距离:85公里车辆台数:2吨车2台,4吨车2台线路A:4吨车,总行走距离27公里,装载量3.6吨。
06 配送_节约里程法

(0.9)
C
4 (1.2) 6 (1.6) 9 (1.1) 10 4 5 7 6 7 5 11 5 8
D
B (0.5)
5
E
A (1.7)
3 6 4 5 7
P
10
F
14 (0.9)
I (0.6)
G
12
H
(0.9)
计算配送中心至各用户以及各用户 之间的最短距离,列表得最短距离 表:
ΔL=(La+Lb)-Lab 1—2:L1+L2-L12=10+9-4=15 1—3:L1+L3-L13=10+7-9=8 1—4:L1+L4-L14=10+8-14=4 1—5:L1+L5-L15=10+8-18=0 1—6:L1+L6-L16=10+8-18=0 1—7:L1+L7-L17=10+3-13=0 1—8:L1+L8-L18=10+4-14=0 1—9:L1+L9-L19=10+10-11= 9 1—10:L1+L10-L1-10=10+7-4=13
(一)节约法的基本规定
利用里程节约法确定配送路线的主要出发 点是,根据配送方的运输能力、到客户之间的 距离及各客户之间的相对距离来制定使配送车 辆总的周转量达到或接近最小的配送方案。
(二)基本原理
基本原理是几何学中三角形一边之长必定 小于另外两边之和。 节约里程法核心思想是依次将运输问题中 的两个回路合并为一个回路,每次使合并 后的总运输距离减小的幅度最大,直到达 到一辆车的装载限制时,再进行下一辆车 的优化。优化过程分为并行方式和串行方 式两种。
假如一家配送中心(DC)向两个用户A、B 运货,配送中心到两用户的最短距离分别 是La和Lb,A和B间的最短距离为Lab,A、B 的货物需求量分别是Qa和Qb,且(Qa+Qb) 小于运输装载量Q,如图所示,如果配送中 心分别送货,那么需要两个车次,总路程 为:L1=2(La+Lb)。 A La B Lb A La DC
节约里程法

配送线路的优化
一、配送线路的优化方法
㈡一对多配送的最短路线问题
节约里程法
原理:三角形一边之长必定小于另外两边之和。
配
送 中
P
心
A 用户 L1
L2
B 用户
配
送 中
P
心
A 用户
L1 L3
L2
B 用户
往返发货
巡回发货
在汽车载重量允许的情况下,采用巡回发货比采用往返发货可节约汽车走行 里程为:∆L=[2(L1+L2)]-(L1+L2+L3)=L1+L2-L3
例题:现有一配送中心为八个零售商供货,各个零售商的需求量是Gi
(吨),这些零售商由配送中心(标号是0)发出的8吨的载货车辆供应,具 体数据如表8-5与8-6所示,把各点之间的距离作为成本考虑的主要因素,即 Cij=Dij(i,j=0,1,……,8),求最优的配送路线。
表8-6 配送中心与零售商之间的距离
0A 8 H
F 8
20
I
J
15
K 24
最优线路图
17 G
二、分送式配送运输
分送式配送是指由一个供应点对多个客户的共同送货。 基本条件:同一条线路上所有客户的需求量总和不大 于一辆车的额定载重量,送货时,由这一辆车装着所 有客户的货物,沿着一条精心挑选的最佳路线依次将 货物送到各个客户手中,这样既保证按时按量将用户 需要的货物及时送到,又节约了车辆,节省了费用, 缓解了交通紧张的压力,并减少了运输对环境造成的 污染。
节约里程法的基本规定
利用里程节约法确定配送路线的主要出发 点是,根据配送方的运输能力及其到客户之间 的距离和各客户之间的相对距离来制定使配送 车辆总的周转量达到或接近最小的配送方案。
节约里程法求最有配送路线 (1)

用节约里程法求配送路线的优化:问题一:已知C11.6C220.8C32.2 1.00.7C43.1 2.6 3.0 2.5C53.0 2.0 2.5 2.5 3.0C64.3 3.2 3.6 3.7 3.4 1.5C72.0 1.5 2.0 1.5 2.5 1.63.0C80.7 1.8 1.6 1.2 3.0 2.6 4.0 1.4C94.5 3.5 4.0 4.0 3.0 2.6 3.0 3.2 4.2C10表1 合肥市庐阳区老乡鸡部分营业网点的行车距离2、算法的实现假设配送中心使用载重量为 4 吨的厢式货车向其10个分店(C1—C10)配送物资,各点间单位运费均一样,各客户间距离如表 1 所示,各客户配送量如表2所示分店C1C2C3C4C5C6C7C8C9C10需求 1.2 1.6 1.3 1.0 1.20.8 1.1 1.6 1.4 1.2表2 营业点物料需求表3、求配送路线的优化(具体优化步骤的过程要的,一起给我,你可以直接在草稿纸上做,拍照给我都可以,最终结果可以参考下表):根据以上数据,采用节约法优化配送路线,其结果如表3。
路线号配送路线配送距离载重量实载率%(t)123问题二:已知:1、C19.6C29.3 3.5C310.0 4.2 1.0C412.07.1 4.0 3.5C56.014.513.514.015.0C610.0 2.2 4.1 4.17.120.0C75.612.310.510.311.06.514.0C86.58.2 6.1 5.8 4.611.29.87.8C94.513.011.811.712.7 1.814.09.69.0C102、假设配送中心使用载重量为 4 吨的厢式货车向其10个分店(C1—C10)配送物资,各点间单位运费均一样,各客户间距离如表 1 所示,各客户配送量如表2所示分店C1C2C3C4C5C6C7C8C9C10需求 1.0 1.8 1.20.9 1.2 1.5 1.3 1.612 1.13求配送路线的优化亲,麻烦你啦,帮帮忙,我学的都交给老师了,555555…….。
配送路线优化里程节约法讲课文档

8
P4
18
16
12
0
0
5
P5
第14页,共25页。
节约里程法
第 3 步:将节约里程按从大到小顺序排列
序号
路线
1
P2P3
2
P3P4
3
P2P4
4
P4P5
5
P1P2
6
P1P5
7
P1P3
8
P2P5
9
P3P5
10
P1P4
节约里程 10 8 6 5 4 2 1 0 0 0
第15页,共25页。
节约里程法
第4步:根据载重量约束与节约里程大小,顺 序连接各客户结点,形成二个配送路线 .
P2P3- P3P4-P2P4-P4P5- P1P2- P1P5- P1P3 -P2P5 -P3P5- P1P4
(0.9)
P3
4
(1.7)
P2
5
6
8
(1.4)
P4
7
P0
10
8
P5
(2.4)
P1 (1.5)
第16页,共25页。
节约里程法
(0.9)
P3
4
5
(1.4)
10
(1.7)
P2
P3 0.9 6
13
4
P3
P4 1.4 7 15 9
5
P4
P5 2.4 10 16 18 16 12 P5
第13页,共25页。
节约里程法
第2步:按节约里程公式求得相应的节约里程数
需求量 P0
1.5 8
P1
12 1.7 8
4
13 0.9 6
1
配送线路优化的方法-节约里程法

配送线路优化的方法节约里程法学习目标技能目标:具备根据实际情况选择合理的线路优化方法进行线路优化的能力线路优化设计1、线路优化设计的意义配送线路设计就是整合影响配送运输的各种因素,适时适当地利用现有的运输工具和道路状况,及时、安全、方便、经济地将客户所需的商品准确地送达客户手中。
在配送运输线路设计中,需根据不同客户群的特点和要求,选择不同的线路设计方法,最终达到节省时间、运距和降低配送运输成本的目的配送线路优化方法一、直送式配送运输适用方法—最短路径法(标点设计最短线路)适用条件:1、由配送中心向每一位客户开展专门送货。
2、该客户的送货量一般必须满足车辆的满载。
配送效果:1、配送车辆满载运输2、配送运输路线距离最短。
配送线路优化方法二、分送式配送---节约里程法适用方法—节约里程法适用条件:1、由配送中心向多位客户开展拼装送货。
2、每位客户的送货量都不能满足车辆的满载。
配送效果:1、配送车辆满载运输2、配送运输路线距离最短。
节约里程法的意义送货时,由一辆车装载所有客户的货物,沿着设计的最佳路线依次将货物送到各位客户手中,这样既能保证按时按量将用户需要的货物及时送达,又节约车辆,节约了费用,缓解了交通紧张的压力,并减少了运输对环境造成的污染。
1、满足客户的配送需要2、减少配送车辆的使用,节约运营费,减少固定资产的投入3、社会意义节约里程法1、基本原理2、案例分析3、优缺点分析4、改进建议基本原理基本原理是几何学中三角形的一边之长必定小于另外两边之和节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路,每次使合并后的总运输距离减少的幅度最大,直到达到一辆车的满载限制时,再进行下一辆车的优化,优化过程分为并行方式和串行方式两种。
节约里程法假如一家配送中心(DC)向两个用户A、B运货,配送中心到两用户的最短距离分别是a和b,A和B间的最短距离为c,A、B的货物的需求量分别是Qa和Qb,且Qa+Qb小于运输装载量Q,如图所示,如果配送中心分别送货。
节约里程法_在物流公司配送中心的实际运用

科技资讯 SCIENCE & TECHNOLOGY INFORMATION
157
科技资讯 2008 NO.28 SCIENCE & TECHNOLOGY INFORMATION 表 1 0 第三次优化后的配送线路
(注:0 表示不连接,1 表示网点之间连接,2 表示和配送中心连接) 表 1 1 第三次修改后的车辆调度结果
参考文献 [1] 钱 芝 网 . 配 送 管 理 实 务 [ M ] . 中 国 时代经
济出版社,2007. [2] 杨 栋 . 物 流 配 送 系 统 设 计 与 算 法 应 用
研究[D].华中科技大学学位论文,2005. [ 3 ] 何 华 洲 . 配 运 作 业 实 务 [ M ] . 高 等 教 育 出
表 1 2 最优化后的配送线路
企 业 管 理
表2
2.2 步骤 第一步:各城市之间的距离见表 3。 第二步:计算连接城市到同一线路上
的距离节约值,具体见表 4。 第三步:确定初始方案的运输线路及
运输费用,现安排 4 辆 2 吨、4 辆 5 吨的车 给每个客户送货。运输线路及运输费用见 表 5 所示。源自图 1 节约里程法理解图 表3
表4
1 “节约里程法”介绍 节约里程法的基本思路如图 1,已知 O
点为配送中心,它分别向用户 A 和 B 送货。 设 O 点到用户 A 和用户 B 的距离分别为 a 和 b。用户 A 和用户 B 之间的距离为 c,现有两 种送货方案,如图 1(a)和(b)所示。
在图 1(a)中配送距离为 2(a+b);图 1(b) 中,配送距离为 a+b+c。对比这两个方案, 哪个更合理呢?这就要看哪个配送距离最 小,配送距离越小,则说明方案越合理。由 图 1(a)中的配送距离,减去图 1(b)中的配送 距离可得出:
