大学物理题库量子2

大学物理试题解答

4.加在平行板电容器极板上的电压变化率为 ×10-6V/s，在电容加在平行板电容器极板上的电压变化率为1.0 加在平行板电容器极板上的电压变化率为，器内产生1.0A的位移电流，则该电容器的电容量为 1.0 µF. 的位移电流，器内产生的位移电流
U 解： = Ed ⇒ D = ε 0 E =
y
b µ0 I1 I 2 dl 分 F = Fx = ∫ dF sin θ = ∫ sin θ （2分） x 2π r µ 0 I1 I 2 2π Rdθ 分 ∫0 R sin θ sin θ = µ0 I1I 2（1分） F向右（1分） 2π 向右分
∫
y
dF
dF
21. 电流为的长直载流导线旁有一与其垂直的导线长为，a端电流为I的长直载流导线旁有一与其垂直的导线长为l，端的长直载流导线旁有一与其垂直的导线ab长为 v υ 至长直导线的距离也为l，以匀速平行于长直导线向上运动，至长直导线的距离也为，ab以匀速平行于长直导线向上运动， v 中的动生电动势。求ab中的动生电动势。中的动生电动势 υ I 解：长直载流导线在其右侧激发磁场 a b 的方向垂直向里 l r o l 先计算通过矩形abdc的磁通量先计算通过矩形的磁通量 µ0 I 长直载流导线在半径为r处的磁场为长直载流导线在半径为处的磁场为 B = 2πr 通过无限小矩形 ydr 的磁通量为 v y × × × × × µ0 I υ dΦ = Bydr = ydr I × × × × × 2πr a × b × y × × dr l × r 则通过矩形abdc的磁通量为则通过矩形的磁通量为 o × c r× × × ×l 2l µ I d µ0 I 0 Φ = ∫ dΦ = ∫ ydr = y ln 2 l 2πr 2π 导线ab向上运动时矩形abdc的面积变化，因而两端有电向上运动时，的面积变化，导线向上运动时，矩形的面积变化因而ab两端有电 dΦ µ0 I dy µ 0 Iυ 动势，由电磁感应定律，动势，由电磁感应定律，有： ε =− =− ln 2 = − ln 2 dt 2π dt 2π 方向由愣次定律知：指向a. 方向由愣次定律知：由b指向指向

大学物理第16章量子力学基本原理-例题及练习题

2( 2k + 1) ( k = 0,1,2......)
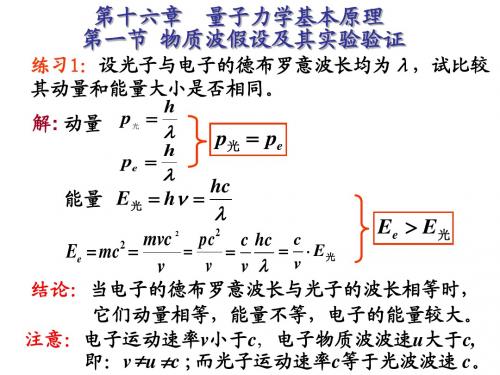
∴ n = 2,6,10...... 时概率密度最大
nhπ 6 × 10 = =1时 (3) n=1时： E = =1 2mL L
2 2 2 2 2 −38
A 例题3 例题3 设粒子沿 x 方向运动，其波函数为 ψ ( x ) = 方向运动， 1 + ix
( n = 1,2,3,...)
E n=4
p2 E = 2m p= nπh nh 2 mE = = a 2a
n=3 n=2 n=1
h 2a λ= = p n
二者是一致的。二者是一致的。
( n = 1, 2, 3,...)
o a
x
例题2 粒子质量为m, 在宽度为L的一维无限的一维无限深势例题2 P516例1：粒子质量为m, 在宽度为的一维无限深势中运动，试求( 粒子在0 阱中运动，试求(1)粒子在0≤x≤L/4区间出现的概率。并 ≤ / 区间出现的概率。求粒子处于n=1 状态的概率。在哪些量子态上，求粒子处于 1和n=∞状态的概率。(2)在哪些量子态上，状态的概率 (2)在哪些量子态上Ｌ/4处的概率密度最大？(3)求n=1时粒子的能量补充。 /4处的概率密度最大 (3)求 =1时粒子的能量(补充处的概率密度最大？ =1时粒子的能量补充)。 2 nπ x 由题得：解:(1) 由题得：概率密度 |ψ | = sin
2 2 2 2 0
2
2
2
2
0
0
k
0
2
2
2 k
0
k
k
k
0
h ∴λ = = p
hc 2E m c + E
2 k 0

清华大学《大学物理》习题库试题及答案----10-量子力学习题解读

清华大学《大学物理》习题库试题及答案----10-量子力学习题解读一、选择题1．4185：已知一单色光照射在钠表面上，测得光电子的最大动能是1.2 eV ，而钠的红限波长是5400 Å，那么入射光的波长是(A) 5350 Å (B) 5000 Å (C)4350 Å (D) 3550 Å ［］2．4244：在均匀磁场B 内放置一极薄的金属片，其红限波长为λ0。

今用单色光照射，发现有电子放出，有些放出的电子(质量为m ，电荷的绝对值为e )在垂直于磁场的平面内作半径为R 的圆周运动，那末此照射光光子的能量是：(A)(B) (C) (D)［］3．4383：用频率为ν 的单色光照射某种金属时，逸出光电子的最大动能为E K ；若改用频率为2ν 的单色光照射此种金属时，则逸出光电子的最大动能为：(A) 2 E K (B) 2h ν - E K (C)h ν - E K (D) h ν + E K ［］4．4737：在康普顿效应实验中，若散射光波长是入射光波长的1.2倍，则散射光光子能量ε与反冲电子动能E K 之比ε / E K 为(A) 2 (B) 3 (C) 4(D) 5 ［］ 0λhc0λhc m eRB 2)(2+0λhc m eRB +0λhc eRB2+5．4190：要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线，至少应向基态氢原子提供的能量是(A) 1.5 eV (B) 3.4 eV (C) 10.2 eV (D) 13.6 eV ［］6．4197：由氢原子理论知，当大量氢原子处于n =3的激发态时，原子跃迁将发出：(A) 一种波长的光(B) 两种波长的光(C) 三种波长的光(D) 连续光谱［］7．4748：已知氢原子从基态激发到某一定态所需能量为10.19 eV，当氢原子从能量为－0.85 eV的状态跃迁到上述定态时，所发射的光子的能量为(A) 2.56 eV (B) 3.41 eV (C)4.25 eV (D) 9.95 eV ［］8．4750：在气体放电管中，用能量为12.1 eV 的电子去轰击处于基态的氢原子，此时氢原子所能发射的光子的能量只能是(A) 12.1 eV (B) 10.2 eV (C) 12.1 eV，10.2 eV和1.9 eV(D) 12.1 eV，10.2 eV和 3.4 eV ［］9．4241：若粒子(电荷为2e)在磁感应强度为B 均匀磁场中沿半径为R 的圆形轨道运动，则α粒子的德布罗意波长是(A) (B) (C)(D) ［］10．4770：如果两种不同质量的粒子，其德布罗意波长相同，则这两种粒子的(A) 动量相同 (B) 能量相同 (C) 速度相同 (D) 动能相同［］11．4428：已知粒子在一维矩形无限深势阱中运动，其波函数为： ( - a ≤x ≤a )，那么粒子在x = 5a /6处出现的概率密度为(A) 1/(2a ) (B) 1/a (C)(D) ［］12．4778：设粒子运动的波函数图线分别如图(A)、(B)、(C)、(D)所示，那么其中确定粒子动量的精确度最高的波函数是哪个图？［］13．5619：波长λ =5000 Å的光沿x 轴正向)2/(eRB h )/(eRB h )2/(1eRBh )/(1eRBh a x a x 23cos 1)(π⋅=ψa 2/1a /1x (A)x (C) x (B) x(D)传播，若光的波长的不确定量∆λ =10-3Å，则利用不确定关系式可得光子的x 坐标的不确定量至少为：(A) 25 cm (B) 50 cm (C) 250cm (D) 500 cm ［］14．8020：将波函数在空间各点的振幅同时增大D 倍，则粒子在空间的分布概率将(A) 增大D 2倍 (B) 增大2D 倍 (C)增大D 倍 (D) 不变［］15．4965：下列各组量子数中，哪一组可以描述原子中电子的状态？ (A) n = 2，l = 2，m l = 0，(B) n =3，l = 1，m l =-1， (C) n = 1，l = 2，m l = 1， (D) n = 1，l = 0，m l = 1，［］16．8022：氢原子中处于3d 量子态的电子，描述其量子态的四个量子数(n ，l ，m l ，m s )可能取的值为(A) (3，0，1，) (B) (1，1，1，)(C) (2，1，2，) (D) (3，2，0，) ［］17．4785：在氢原子的K 壳层中，电子可h x p x ≥∆∆21=s m 21-=s m 21=s m 21-=s m 21-21-2121能具有的量子数(n ，l ，m l ，m s )是(A) (1，0，0，) (B) (1，0，-1，)(C) (1，1，0，) (D) (2，1，0，)［］18．4222：与绝缘体相比较，半导体能带结构的特点是(A) 导带也是空带 (B) 满带与导带重合(C) 满带中总是有空穴，导带中总是有电子(D) 禁带宽度较窄［］19．4789：p 型半导体中杂质原子所形成的局部能级(也称受主能级)，在能带结构中应处于(A) 满带中 (B) 导带中 (C) 禁带中，但接近满带顶(D) 禁带中，但接近导带底［］20．8032：按照原子的量子理论，原子可以通过自发辐射和受激辐射的方式发光，它们所产生的光的特点是：(A) 两个原子自发辐射的同频率的光是相干的，原子受激辐射的光与入射光是不相干的(B) 两个原子自发辐射的同频率的光是不相干的，原子受激辐射的光与入射光是相干的(C) 两个原子自发辐射的同频率的光是不相干的，原子受激辐射的光与入射光是不相干的(D) 两个原子自发辐射的同频率的光是相212121-21-干的，原子受激辐射的光与入射光是相干的21．9900：与的互易关系[]等于（Ａ）（Ｂ）（Ｃ）（Ｄ）［］22．9901：厄米算符满足以下哪一等式（、是任意的态函数）（Ａ）（Ｂ）（Ｃ）（Ｄ）［］二、填空题1．4179：光子波长为λ，则其能量=_____；动量的大小 =______；质量=_______。

大学物理-量子力学基础习题思考题及答案

习题22-1．计算下列客体具有MeV 10动能时的物质波波长，(1)电子；（2）质子。

解：(1) 电子高速运动，设电子的总能量可写为：20K E E m c =+ 用相对论公式，222240E c p m c=+ 可得p ===h p λ==834-=131.210m -=⨯（2）对于质子，利用德布罗意波的计算公式即可得出：3415h 9.110m p λ--====⨯22-2．计算在彩色电视显像管的加速电压作用下电子的物质波波长，已知加速电压为kV 0.25，（1）用非相对论公式；（2）用相对论公式。

解：（1）用非相对论公式：mmeU h mE h 123193134108.71025106.1101.921063.622p h ----⨯=⨯⨯⨯⨯⨯⨯⨯====λ（2）用相对论公式：420222c m c p +=EeU E E k ==-20c mm eU eU c m hmE h 12220107.722p h -⨯=+===）（λ22-3．一中子束通过晶体发生衍射。

已知晶面间距nm 1032.72-⨯=d ，中子的动能eV 20.4k =E ，求对此晶面簇反射方向发生一级极大的中子束的掠射角.解：先利用德布罗意波的计算公式即可得出波长：3411h 1.410m λ--====⨯再利用晶体衍射的公式，可得出：2sin d k ϕλ= 0,1,2k =…11111.410sin 0.095k λϕ--⨯=== ， 5.48ϕ= 22-4．以速度m/s 1063⨯=v 运动的电子射入场强为5V/cm =E 的匀强电场中加速，为使电子波长A 1=λ，电子在此场中应该飞行多长的距离？解：3410h 110p m λ--====⨯ 可得：U=150.9V ，所以 U=Ed ，得出d=30.2cm 。

22-5．设电子的位置不确定度为A 1.0，计算它的动量的不确定度；若电子的能量约为keV 1，计算电子能量的不确定度。

大学物理相对论量子论练习题答案

相对论、量子理论练习题解一．选择题1．D ．2．D ．3．A ．4．B ．5.A 6.B 7.A 8.A 二．填空题1．光速不变，真空中的速度是一个常量，与参考系和光源的运动无关。

狭义相对性，物理规律在所有惯性系中具有相同的形式。

2．同时，不同时。

3．与物体相对静止的参考系中所测量的物体，本征长度最长，绝对。

4．同一地点，本征时间最短。

5．等效，弱，引力场同参考系相当的加速度等效；广义相对性原理；物理学规律对任何以加速度抵消掉该处引力场的惯性系都具有相同的形式。

6．引力红移；雷达回波延迟；水星近日点的进动，或光线在引力场中偏折。

7． 1.33X10-23 .8．德布罗意波是概率波，波函数不表示实在物理量在空间的波动，其振幅无实在物理意义。

9．自发辐射，受激辐射，受激辐射。

10．受激辐射，粒子数反转分布，谐振腔。

11．相位 ,(频率, 传播方向, 偏振态。

12．能量，能量，动量。

三．小计算题 1.cv c v c v x t cv x c v t t 6.0541451145450's 4'11)''(22222222=∴⎪⎭⎫ ⎝⎛=-=-====∆=∆-=∆+∆=∆γγγγγcv l l c v l l c v l l 8.0531531.222202=∴⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛==⎪⎭⎫ ⎝⎛-=－光年光年c v c v v c v c v c v c v c v c v t c t v c v x x tcx t S 171616171616)1(1611641'1'164''.322222222222=∴=-=⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛-∆=∆⎪⎭⎫⎝⎛-∆=∆∆==∆=∆光年原长年（原时）系32m 075.03.05.05.0m3.06.05.01=⨯⨯==⨯=⎪⎭⎫⎝⎛-=V c v l l 沿运动方向长度收缩5. MeV49.1eV 1049.11051.01000.2eV 1051.0J 102.81099.811091011.966620261415163120=⨯=⨯-⨯=-=⨯=⨯≈⨯=⨯⨯⨯=---c m mc E c m K6.c v c v c v c v c v c v c v c m c m mc E K 359413211123111211115.04111122222220202=∴=⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=-=7.120201020102010202002201010011222)(221)4()3()4()()2()3()()1(ννννννννννννννννννννννν-=-=--=-=--=-+==-+=eU h h eU h eU h h eU h8.120201020102010202002201010011222)(221)4()3()4()()2()3()()1(ννννννννννννννννννννννν-=-=--=-=--=-+==-+=eU h h eU h eU h h eU h9.13)(44431212323212121020222022======v v nn v v n r r n r e r m e v r e r v m n n nn n n πεεππε10.aaa a a a aa 2122122145cos 16523cos12265=⋅-=⋅-==⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛ψππψ概率密度四、大计算题1. (1)对不同金属斜率相同。

大学物理量子物理

15. 量子物理班级学号姓名成绩一、选择题1.黑体辐射、光电效应及康普顿效应皆突出表明了光的(A)波动性； (B)粒子性； (C)单色性； (D)偏振性。

（ B ）解：黑体辐射、光电效应及康普顿效应皆突出表明了光的粒子性。

2.已知某金属中电子逸出功为eV 0，当用一种单色光照射该金属表面时，可产生光电效应。

则该光的波长应满足：(A))/(0eV hc λ≤； (B) )/(0eV hc λ≥； (C))/(0hc eV λ≤； (D) )/(0hc eV λ≥。

（ A ）解：某金属中电子逸出功 0000000eV c ch W h eV h eV ννλλ==⇒==⇒= 产生光电效应的条件是 000ch eV ννλλ≥⇒≤= 3.康普顿效应说明在光和微观粒子的相互作用过程中，以下定律严格适用(A)动量守恒、动能守恒； (B)牛顿定律、动能定律；(C)动能守恒、机械能守恒； (D)动量守恒、能量守恒。

（ D ）解：康普顿效应说明在光和微观粒子的相互作用过程中，动量守恒、能量守恒严格适用。

4.某可见光波长为550.0nm ，若电子的德布罗依波长为该值时，其非相对论动能为：(A)5.00×10-6eV; (B)7.98×10-25eV; (C)1.28×10-4eV; (D)6.63×10-5eV 。

（ A ）解：根据h p h pλλ=⇒=，c <<v 时， 234102631192(/)(6.6310/550010) 5.0010eV 2229.110 1.610k p h E m m λ-----⨯⨯====⨯⨯⨯⨯⨯ 5.已知光子的波长nm 0.300=λ，测量此波长的不确定量nm 100.32-⨯=∆λ，则该光子的位置不确定量为：(A) nm 0.300； (B) nm 100.329-⨯； (C) m 1031-⨯； (D) m 38.0。

zk27量子2北京交通大学大学物理

H
656.3nm
不同的 k 对应为莱曼系、帕邢系、布喇系、...
1 1 1 ~ 赖曼系 R( 2 2 ) 1 n 1 1 1 ~ 帕邢系 R( 2 2 ) 3 n
n 2,3,4,
n 4,5,6,
1 1 1 ~ 布喇开系 R( 2 2 ) 4 n 1 1 1 ~ 普丰德系 R( 2 2 ) 5 n
h mv
h n L mvr n 2
他在论文中指出:
一个能量为E, 动量为p 的实物粒子同时具有波动性, 且:
德布罗意假设:
h p
p
k
h 2 ;k 2
h
E h
E h
─ 德布罗意波长
物质波/德布罗意波:与粒子相联系的波
对于质量m0,以速度v 运动的实物粒子对应的波长
En Ek (2)跃迁假设: h
(E1<E2 < E3,…)
(3)轨道角动量量子化假设:定态下电子的轨道角动量是量子化的.
h Ln 2
n 1,2,3,
n 1,2,3,
L n
三、氢原子轨道半径和能量的计算
由库仑定律、牛顿定律和玻尔的量子假设
e2 4 0 r
玻尔理论在人们认识原子结构的进程中有很大的贡献---- 1922年玻尔获诺贝尔物理奖。
玻尔正在讲解他的互补原理
玻尔（左）和海森伯（中）泡利（右）在一起
哥本哈根的玻尔理论物理研究所
在丹麦首都哥本哈根的玻尔理论物理研究所成立于1921年3月，从那时起该研究所很快就成了世界著名的物理研究中心。在玻尔领导该研究所的四十多年中，共培养了 600多名外国人员。几十年来该研究所成了量子理论研究中心，形成哥本哈根学派。

大学物理教学 51.量子力学基础-2

1
称为归一化
V
的波函数
a) 波函数的归一化
Байду номын сангаас
若
ψ
2
dV

1，寻找一个系数k使得
k
ψ
2
dV

1，
V
V
这一过程称为波函数的归一化。
b) 波函数的归一化系数

2dV
2
CψdV1
V
V
C k 就称为归一化系数。 Cψ
,ψ所描述的粒子状态相同
5
例：讨论一维自由粒子在空间各点出现的概率。
xPx 2 h h / 2
t E 2
同一微观粒子，其坐标和动量不能同时被准确测定（波粒二象性）。
对y、z方向有类似的表达式。不确定关系式一般用于估算。
2
●
波函数自由粒子的波函数

(r,t)

0ei
2
h
( Et Pr)
● 波函数的物理意义 (统计解释)
(r,t)(r)e iEt
16
4. 定态薛定谔方程的应用
[[22m22 ddx222V ((xr)]((xr))EE(x()r)
1）设求粒一子维处无在限势深阱、V方(x势)中阱中粒子的[2波m2函ddx数22VV( x()x)](x)E(x)
13
3. 定态薛定谔方程
i

(r,t
t
)[
2 2m

2
V
(r,t
)]
(r,t
)
设若粒粒子子的所波处函的数力为场：不随( 时r ,间t) 变化( r ，)则f( 薛t) 定谔方程可化简。
V

大学物理同步训练第15章量子物理

（A）13.6 eV （B）12.09 eV
（C）10.20 eV
（D）1.51 eV
答案：D
分析：（参考选择题 7）�� = 3能级得电离能为
−��3
=
−
��1 32
=
13.6 9
=
1.51
eV
10. 具有下列哪一能量的光子，能被处在�� = 2的能级的氢原子吸收？
ℎ
��2
1
6.63 × 10−34 2 6.632 × 10−48
�� = �� → �� = 2�� = 2 × 9.11 × 10−31 × ( 0.1 × 10−9 ) = 1.822 × 10−30
��
1
6.632 × 10−18
�� = �� = 1.60 × 10−19 × 1.822 = 151 V
（普朗克常量ℎ = 6.63 × 10−34 J ∙ s，基本电荷�� = 1.60 × 10−19 C）
答案：C
分析：（参考选择题 1）由光电效应方程可得
ℎ�� ℎ�� 1 = ��0 + ��1
ℎ�� ℎ�� 2 = ��0 + ��2
（A）能量为hc⁄�� ，动量的大小为h⁄��
（B）能量为h⁄�� ，动量的大小为hc⁄��
（C）能量为h⁄(��)，动量的大小为h⁄��
（D）能量为hc⁄�� ，动量的大小为h⁄(��)

大学物理知识总结习题答案(第十章)量子物理基础

第十章量子物理基础本章提要1．光的量子性· 物体由于自身具有一定温度而以电磁波的形式向周围发射能量的现象称热辐射。

· 在任何温度下都能全部吸收照射到它表面上的各种波长的光（电磁波），则这种物体称为绝对黑体，简称黑体。

· 单位时间内物体单位表面积发出的包括所有波长在内的电磁波的辐射功率，称为辐射出射度。

2．维恩位移定律· 在不同的热力学温度T 下，单色辐射本领的实验曲线存在一个峰值波长λm ，维恩从热力学理论导出T 和λm 满足如下关系λm T b =其中b 是维恩常量。

3．斯忒藩—玻尔兹曼定律· 斯忒藩—玻尔兹曼定律表明黑体的辐射出射度M 与温T 的关系4T M σ=其中s 为斯忒藩—玻尔兹曼常量。

对于一般的物体4T M εσ=e 称发射率。

4．黑体辐射· 黑体辐射不是连续地辐射能量，而是一份份地辐射能量，并且每一份能量与电磁波的频率ν成正比，这种能量分立的现象被称为能量的量子化，每一份最小能量E hv =被称为一个量子。

黑体辐射的能量为E nhv =，其中n ＝1，2，3，…，等正整数，h 为普朗克常数。

· 普朗克黑体辐射公式简称普朗克公式25/λ2πhc 1()λ1hc kT M T e l =-· 光是以光速运动的粒子流，这些粒子称为光量子，简称光子。

· 一个光子具有的能量为νh E =。

5．粒子的波动性· 德布罗意认为实物粒子也具有波粒二象性，它的能量E 、动量p 跟和它相联系的波的频率ν、波长λ满足以下关系2E mc h ν==λh p m u == 这两个公式称为德布罗意公式或德布罗意假设。

与实物粒子相联系的波称为物质波或德布罗意波。

· x x p D D ?h 或者E t D D ?h 这一关系叫做不确定关系。

其中为位置不确定量、动量不确定量、能量不确定量、时间不确定量。

大学物理教学 51.量子力学基础-2

5
V

dV Cψ dV 1
V
2
2
例：讨论一维自由粒子在空间各点出现的概率。
解：各点概率相等。
2 ( x ) x, t 0 e 2 i
( x, t ) 0e
2 2 ( Et Px ) i ( Et Px ) h h
i
2 ( Et Px ) h
13
3. 定态薛定谔方程
若粒子所处的力场不随时间变化，则薛定谔方程可化简。 (r ,t ) (r ) f (t ) 设粒子的波函数为：
E
得：定态薛定谔方程由该方程组的解有
i Et (r ,t ) (r )e
14
i Et f (t ) Ce
3
● 波函数的归一化和归一化系数

2
与粒子(某时刻、在空间某处)出现的概率成正比.
粒子在某区域出现的概率还正比于该区域的大小dV.
某时刻、在（x,y,z）附近的体积元 dV 中，出现粒子的概率为： K为待定的比例系数, 且随波函数而变。 2 2 dW ——概率密度 k ψ dW k ψ dV dV

求归一化的波函数和粒子的位置概率密度。解：
归一化条件：

-b 2

(x, t ) dx
2
b2 2
b2
-b 2
(x, t ) dx (x, t ) dx 1
2 2 b2

2 x 2 b A cos dx A 1 A -b 2 2 b b 0 x b ,x b 2 2 2 = (x , t ) = 2 2 x x=0处，概率最大！ cos ( ) b x b 2 2 b b

一选择题 (共48分)1. (本题 3分)(0507) 已知用光照的办法将氢原子基态的电子电离，可用的最长波长的光是 913 Å的紫外光，那么氢原子从各受激态跃迁至基态的赖曼系光谱的波长可表示为：(A) 11913+−=n n λ Å． (B) 11913−+=n n λ Å． (C) 1191322−+=n n λ Å． (D) 191322−=n n λ Å．［］2. (本题 3分)(4190) 要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线，至少应向基态氢原子提供的能量是(A) 1.5 eV ． (B) 3.4 eV ．(C) 10.2 eV ． (D) 13.6 eV ．［］3. (本题 3分)(4194) 根据玻尔的理论，氢原子在n =5轨道上的动量矩与在第一激发态的轨道动量矩之比为(A) 5/4． (B) 5/3．(C) 5/2． (D) 5．［］4. (本题 3分)(4195) 氢原子光谱的巴耳末线系中谱线最小波长与最大波长之比为(A) 7/9． (B) 5/9．(C) 4/9． (D) 2/9．［］5. (本题 3分)(4195) 氢原子光谱的巴耳末线系中谱线最小波长与最大波长之比为(A) 7/9． (B) 5/9．(C) 4/9． (D) 2/9．［］6. (本题 3分)(4197) 由氢原子理论知，当大量氢原子处于n =3的激发态时，原子跃迁将发出：(A) 一种波长的光． (B) 两种波长的光．(C) 三种波长的光． (D) 连续光谱．［］7. (本题 3分)(4198) 根据玻尔理论，氢原子中的电子在n =4的轨道上运动的动能与在基态的轨道上运动的动能之比为(A) 1/4． (B) 1/8．(C) 1/16． (D) 1/32．［］8. (本题 3分)(4199) 根据玻尔氢原子理论，氢原子中的电子在第一和第三轨道上运动时速度大小之比v 1/ v 3是(A) 1/9． (B) 1/3．(C) 3． (D) 9．［］9. (本题 3分)(4239)假定氢原子原是静止的，则氢原子从n = 3 的激发状态直接通过辐射跃迁到基态时的反冲速度大约是(A) 4 m/s．(B) 10 m/s ．(C) 100 m/s ． (D) 400 m/s ．［］(氢原子的质量m =1.67×10-27 kg)10. (本题 3分)(4411)氢原子光谱的巴耳末系中波长最大的谱线用λ1表示，其次波长用λ2表示，则它们的比值λ1/λ2为：(A) 20/27．(B) 9/8．(C) 27/20．(D) 16/9．［］11. (本题 3分)(4619)按照玻尔理论，电子绕核作圆周运动时，电子的动量矩L的可能值为(A) 任意值．(B) nh，n = 1，2，3，…(C) 2π nh，n = 1，2，3，…(D) nh/(2π)，n = 1，2，3，…［］12. (本题 3分)(4622)具有下列哪一能量的光子，能被处在n = 2的能级的氢原子吸收？(A) 1.51 eV．(B) 1.89 eV．(C) 2.16 eV．(D) 2.40 eV．［］13. (本题 3分)(4747)若用里德伯常量R表示氢原子光谱的最短波长，则可写成(A) λmin =1 / R．(B) λmin =2 / R．(C) λmin =3 / R．(D) λmin =4 / R．［］14. (本题 3分)(4748)已知氢原子从基态激发到某一定态所需能量为 10.19 eV，当氢原子从能量为－0.85 eV的状态跃迁到上述定态时，所发射的光子的能量为(A) 2.56 eV．(B) 3.41 eV．(C) 4.25 eV．(D) 9.95 eV．［］15. (本题 3分)(4749)要使处于基态的氢原子受激后可辐射出可见光谱线，最少应供给氢原子的能量为(A) 12.09 eV． (B) 10.20 eV．(C) 1.89 eV．(D) 1.51 eV．［］16. (本题 3分)(4750)在气体放电管中，用能量为12.1 eV的电子去轰击处于基态的氢原子，此时氢原子所能发射的光子的能量只能是(A) 12.1 eV． (B) 10.2 eV．(C) 12.1 eV，10.2 eV和 1.9 eV． (D) 12.1 eV，10.2 eV和 3.4 eV．[ ]二填空题 (共101分)17. (本题 4分)(0514) 在玻尔氢原子理论中势能为负值，而且数值比动能大，所以总能量为________值，并且只能取____________值．18. (本题 4分)(4191) 在氢原子发射光谱的巴耳末线系中有一频率为6.15×1014 Hz 的谱线，它是氢原子从能级E n =__________eV 跃迁到能级E k =__________eV 而发出的． (普朗克常量h =6.63×10-34 J ·s ，基本电荷e =1.60×10-19 C)19. (本题 4分)(4192) 在氢原子光谱中，赖曼系(由各激发态跃迁到基态所发射的各谱线组成的谱线系)的最短波长的谱线所对应的光子能量为_______________eV ；巴耳末系的最短波长的谱线所对应的光子的能量为___________________eV ．(里德伯常量 R =1.097×107 m -1 ，普朗克常量h =6.63×10-34 J ·s ，1 eV =1.60×10-19 J ，真空中光速 c =3×108 m ·s -1 )20. (本题 4分)(4196) 氢原子基态的电离能是 _______________eV ．电离能为+0.544 eV 的激发态氢原子，其电子处在n =_________________ 的轨道上运动．21. (本题 4分)(4200) 设大量氢原子处于n =4的激发态，它们跃迁时发射出一簇光谱线．这簇光谱线最多可能有 ________________ 条,其中最短的波长是 _______ Å(普朗克常量h =6.63×10-34 J ·s)22. (本题 4分)(4201) 图示被激发的氢原子跃迁到低能级时(图中E 1不是基态能级)，可发出波长为λ1、λ2、λ3的辐射，其频率ν1、ν2和ν3满足关系式______________________；三个波长满足关系式__________________．λ1λ2λ3E 1E 2E 3玻尔的氢原子理论中提出的关于__________________________________和____________________________________的假设在现代的量子力学理论中仍然是两个重要的基本概念．24. (本题 3分)(4424)欲使氢原子发射赖曼系(由各激发态跃迁到基态所发射的谱线构成）中波长为1216 Å的谱线，应传给基态氢原子的最小能量是_____________________eV．(普朗克常量h = 6.63×10-34 J·s，基本电荷e =1.60×10-19 C)25. (本题 5分)(4513)玻尔的氢原子理论的三个基本假设是：(1)____________________________________，(2)____________________________________，(3)____________________________________．26. (本题 3分)(4517)欲使氢原子能发射巴耳末系中波长为4861.3 Å的谱线，最少要给基态氢原子提供_______________eV的能量．(里德伯常量R =1.097×107 m-1 )27. (本题 3分)(4518)欲使氢原子能发射巴耳末系中波长为6562.8 Å的谱线，最少要给基态氢原子提供_________________eV的能量．(里德伯常量R =1.097×107 m-1 )28. (本题 3分)(4620)按照玻尔理论，移去处于基态的He+中的电子所需能量为_____________eV.29. (本题 3分)(4623)氢原子中电子从n = 3的激发态被电离出去，需要的能量为_________eV．30. (本题 3分)(4624)氢原子由定态l跃迁到定态k可发射一个光子．已知定态l的电离能为0.85 eV，又知从基态使氢原子激发到定态k所需能量为10.2 eV，则在上述跃迁中氢原子所发射的光子的能量为__________eV．玻尔氢原子理论中的定态假设的内容是：______________________________ ______________________________________________________________________ _____________________________________________________________________.32. (本题 3分)(4752)玻尔氢原子理论的基本假设之一是定态跃迁的频率条件，其内容表述如下：______________________________________________________________________ ____________________________________________________．33. (本题 3分)(4753)玻尔氢原子理论的基本假设之一是电子轨道动量矩的量子化条件，其内容可表述如下：____________________________________________________________ ______________________________________________________________________ ________________________________________________________________．34. (本题 4分)(4754)氢原子的部分能级跃迁示意如图．在这些能级跃迁中，(1) 从n =______的能级跃迁到n =_____的能级时所发射的光子的波长最短；(2) 从n =______的能级跃迁到n =______的能级时所发射的光子的频率最小．n = 1 n = 2 n = 3 n = 435. (本题 4分)(4755)被激发到n =3的状态的氢原子气体发出的辐射中，有______条可见光谱线和_________条非可见光谱线．36. (本题 4分)(4756)氢原子从能量为－0.85 eV的状态跃迁到能量为－3.4 eV的状态时，所发射的光子能量是_________eV，这是电子从n =_______的能级到n = 2的能级的跃迁．当氢原子从某初始状态跃迁到激发能(从基态到激发态所需的能量)为10.19eV 的激发态上时，发出一个波长为4860 Å的光子，则初始状态氢原子的能量是________eV ．38. (本题 3分)(4758) 要使处于基态的氢原子受激发后能辐射氢原子光谱中波长最短的光谱线，最少需向氢原子提供______________eV 的能量．39. (本题 3分)(4759) 已知基态氢原子的能量为－13.6 eV ，当基态氢原子被 12.09 eV 的光子激发后，其电子的轨道半径将增加到玻尔半径的______倍．40. (本题 3分)(4760) 当一个质子俘获一个动能E K =13.6 eV 的自由电子组成一个基态氢原子时，所发出的单色光频率是______________________________．(基态氢原子的能量为－13.6 eV ，普朗克常量h =6.63×10-34 J ·s)41. (本题 3分)(4761) 使氢原子中电子从n =3的状态电离，至少需要供给的能量为_________eV(已知基态氢原子的电离能为13.6 eV)．42. (本题 3分)(4762) 在氢原子光谱的巴耳末系中，波长最长的谱线和波长最短的谱线的波长比值是______________．43. (本题 3分)(4763) 在氢原子光谱的巴耳末系中，波长最长的谱线H α和相邻的谱线H β的波长比值是______________．44. (本题 4分)(4765) 处于基态的氢原子吸收了13.06 eV 的能量后，可激发到n =________的能级，当它跃迁回到基态时，可能辐射的光谱线有________条．45. (本题 4分)(5369) 根据氢原子理论，若大量氢原子处于主量子数n = 5的激发态，则跃迁辐射的谱线可以有________条，其中属于巴耳末系的谱线有______条．三计算题 (共113分)46. (本题 8分)(0316)组成某双原子气体分子的两个原子的质量均为m，间隔为一固定值d，并绕通过d的中点而垂直于d的轴旋转，假设角动量是量子化的，并符合玻尔量子化条件．试求：(1) 可能的角速度；(2) 可能的量子化的转动动能．47. (本题 5分)(0521)实验发现基态氢原子可吸收能量为 12.75 eV的光子．(1) 试问氢原子吸收该光子后将被激发到哪个能级？(2) 受激发的氢原子向低能级跃迁时，可能发出哪几条谱线？请画出能级图(定性)，并将这些跃迁画在能级图上．48. (本题10分)(0532)已知氢光谱的某一线系的极限波长为3647 Å，其中有一谱线波长为6565 Å．试由玻尔氢原子理论，求与该波长相应的始态与终态能级的能量．(R =1.097×107 m-1 )49. (本题 5分)(0537)在氢原子中，电子从某能级跃迁到量子数为n的能级，这时轨道半径改变q 倍，求发射的光子的频率．50. (本题10分)(0538)根据玻尔理论(1) 计算氢原子中电子在量子数为n的轨道上作圆周运动的频率；(2) 计算当该电子跃迁到(n-1)的轨道上时所发出的光子的频率；(3) 证明当n很大时，上述(1)和(2)结果近似相等．51. (本题10分)(0570)氢原子激发态的平均寿命约为10-8s，假设氢原子处于激发态时，电子作圆轨道运动，试求出处于量子数n =5状态的电子在它跃迁到基态之前绕核转了多少圈．( me= 9.11×10-31 kg，e =1.60×10-19 C，h =6.63×10-34 J·s，ε=8.85×10-12 C2·N-1·m-2 )52. (本题12分)(4202)氢原子光谱的巴耳末线系中，有一光谱线的波长为4340 Å，试求：(1) 与这一谱线相应的光子能量为多少电子伏特？(2) 该谱线是氢原子由能级En 跃迁到能级Ek产生的，n和k各为多少？(3) 最高能级为E5的大量氢原子，最多可以发射几个线系，共几条谱线？请在氢原子能级图中表示出来，并说明波长最短的是哪一条谱线．53. (本题 5分)(4412)处于基态的氢原子被外来单色光激发后发出的光仅有三条谱线，问此外来光的频率为多少？(里德伯常量R =1.097×107 m-1)54. (本题 5分)(4413)试求氢原子线系极限的波数表达式及赖曼系(由各激发态跃迁到基态所发射的谱线构成)、巴耳末系、帕邢系(由各高能激发态跃迁到n =3的定态所发射的谱线构成)的线系极限的波数．(里德伯常量R =1.097×107 m-1 )处于第一激发态的氢原子被外来单色光激发后，发射的光谱中，仅观察到三条巴耳末系光谱线．试求这三条光谱线中波长最长的那条谱线的波长以及外来光的频率． (里德伯常量R =1.097×107 m -1)56. (本题 5分)(4519) 已知氢原子中电子的最小轨道半径为 5.3×10-11 m ，求它绕核运动的速度是多少？ (普朗克常量h =6.63×10-34 J ·s ，电子静止质量m e =9.11×10-31 kg)57. (本题 5分)(4520) 试估计处于基态的氢原子被能量为 12.09 eV 的光子激发时，其电子的轨道半径增加多少倍？58. (本题 5分)(4547) 已知电子在垂直于均匀磁场B K 的平面内运动，设电子的运动满足玻尔量子化条件，求电子轨道的半径r n =？59. (本题 8分)(4767) 当氢原子从某初始状态跃迁到激发能(从基态到激发态所需的能量)为ΔE =10.19 eV 的状态时，发射出光子的波长是λ=4860 Å，试求该初始状态的能量和主量子数．(普朗克常量h =6.63×10-34 J ·s ，1 eV =1.60×10-19 J)60. (本题 5分)(4768) 用某频率的单色光照射基态氢原子气体，使气体发射出三种频率的谱线，试求原照射单色光的频率．(普朗克常量h =6.63×10-34 J ·s ，1 eV =1.60×10-19 J)61. (本题 5分)(5238) 已知氢原子光谱中有一条谱线的波长是λ=1025.7 Å，氢原子的里德伯常量R=109677 cm -1．问：跃迁发生在哪两个能级之间？62. (本题 5分)(5370) 若处于基态的氢原子吸收了一个能量为h ν =15 eV 的光子后其电子成为自由电子(电子的质量m e =9.11×10-31 kg)，求该自由电子的速度v ．四理论推导与证明题 (共35分)63. (本题10分)(4193) 设氢原子光谱的巴耳末系中第一条谱线(H α)的波长为λα，第二条谱线(H β)的波长为λβ，试证明：帕邢系(由各高能态跃迁到主量子数为3的定态所发射的各谱线组成的谱线系)中的第一条谱线的波长为βαβαλλλλλ−=64. (本题 5分)(4417) 测得氢原子光谱中的某一谱线系的极限波长为λk =364.7 nm ．(1 nm = 10-9m)试推证此谱线系为巴耳末系． (里德伯常量R =1.097×107 m -1 )试用玻尔理论推导氢原子在稳定态中的轨道半径．66. (本题 5分)(4427) 试根据玻尔关于氢原子结构的基本假说，推导里德伯常量的理论表达式．(氢原子能级公式： 2204281he m n E e n ε⋅−=)67. (本题10分)(4444) 质量为m 的卫星，在半径为r 的轨道上环绕地球运动，线速度为v ．(1) 假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立．证明地球卫星的轨道半径与量子数的平方成正比，即r = kn 2 （k 是比例常数）．(2) 应用(1)的结果求卫星轨道和它的下一个“容许”轨道间的距离．由此进一步说明在宏观问题中轨道半径实际上可认为是连续变化的（利用以下数据作估算：普朗克常量s J 106.634⋅×=−h ，地球质量kg 10624×=M ，地球半径km 104.66×=R ，万有引力常数2211/kg Nm 107.6−×=G ）．五回答问题 (共15分)68. (本题 5分)(4220) 解释玻尔原子理论中的下列概念：定态；基态；激发态；量子化条件．69. (本题 5分)(4418) 氢原子发射一条波长为λ =4340 Å的光谱线．试问该谱线属于哪一谱线系？氢原子是从哪个能级跃迁到哪个能级辐射出该光谱线的？(里德伯常量R =1.097×107 m -1 )70. (本题 5分)(4769) 玻尔氢原子理论的成功和局限性是什么？。

量子物理2 德波波函数薛定谔方程

三、对波粒二象性的理解怎样理解微观粒子既是粒子又是波?
根据电子双缝衍射实验再作单电子双缝衍射实验双缝
现代实验技术可以做到一次一个电子通过缝为防止电子间发生作用，让电子一个一个地入射，发现时间足够长后的干涉图样和大量电子同时入射时完全相同。
一个一个电子依次入射双缝的衍射实验：
在观察屏上的图像一个个地出现说明了电子的粒子性随着电子数目的增多，在屏上逐渐形成了衍射 3000个 20000个图样，说明 “一 70000 个电子”就具有的波动性微观粒子具有波粒二象性概率波！ 7个电子 100个电子
x i 2 π( t )
E const . h
所以与自由粒子联系的波是单色平面波则自由粒子波函数 Ψ ( x, t ) Ψ 0e

E 将德布罗意关系 h
h P 代入，得
( x, t ) 0
i ( Et px ) e
沿+x方向运动的自由粒子波函数. 在三维空间中运动的自由粒子的波函数
玻尔理论在人们认识原子结构的进程中有很大的贡献---- 1922年玻尔获诺贝尔物理奖
玻尔正在讲解他的互补原理
玻尔（左）和海森伯（中）泡利（右）在一起
第2章德布罗意波
一、德布罗意假设
波函数
§1 实物粒子的波动性从自然界的对称性出发，认为既然光(波)具有粒子性，那么实物粒子也应具有波动性。 1924.11.29德布罗意把题为 “量子理论的研究”的博士论文提交给了巴黎大学。
Ψ (r , t ) Ψ 0 e
i ( E t P r ) h
物质波波函数：一维 Ψ（x, t ) ，三维 Ψ ( r , t )

大学物理量子物理二

3. 解释氢原子光谱设初态能级En，末态能级Ek (En>Ek)。辐射光子能量： h =EnEk
1 me4 En 2 ( 2 2 ) n 8h 0
me4 与里德堡公式比较，得： R 3 2 =1.0973731107m1 8h 0 c
能级图及各谱线系的形成：
n=5 n=4 n=3 n=2

}
1 me4 En 2 ( 2 2) 80 rn n 8h 0
e2
（15-21） —— 能级公式 n= 时，E=0 电离态
n=1时，E1= 13.6eV
基态
n2为激发态 n=2 — 第一激发态，… 激发：Ek(基态)En(高)
13.6 En 2 eV （15-22）辐射：En(高)Ek(低) n
Ek 0
入射光子能量： 0 h 0
hc
0
0
hc
0
散射光子波长： 0 0.2 1.2 0 0 0
hc 0 散射光子能量： 1.20 1.2 hc
所以，反冲电子动能： Ek 0 (1 1 ) 0 0.1MeV 1.2
一．氢原子光谱最先发现 H=656.28nm, H=486.13nm, H=434.05nm, H=410.17nm n2 1885年，巴耳末： B 2 (15-15) B=364.56 nm n 4 n=3，H； n=4，H ； n=5， H ； n=6，H ——巴耳末公式据此发现第五条(n=7)，第六条(n=8)，…… 又称为可见光区的谱线系。里德堡： 1890年， 1 1 n2 4 4 1 1 ~ 波数： ( 2 2) 2 B n B 2 n ~ R( 1 1 ) 或 (n=3,4,5,6,……) (15-16) 22 n 2 4 R =1.0967758107m-1 ——里德堡恒量 B n较小时,谱线间隔较大； n较大时，谱线间隔较小。

大学物理习题

大学物理（II ）重修课习题第一部分：电磁场1、均匀带电圆盘轴线上一点的场强。

设圆盘带电量为q ，半径为R 。

2、求均匀带电半圆环圆心的场强。

设圆环带电密度为 λ ，半径为R 。

3、两块平行放置的面积为S 的金属板，各带电量Q1、Q2 , 板距与板的线度相比很小。

求：① 静电平衡时, 金属板电荷的分布和周围电场的分布。

②若把第二块金属板接地，以上结果如何？4、一个带电金属球半径R 1，带电量q 1 ，放在另一个带电球壳内，其内外半径分别为R 2、R 3，球壳带电量为 q 。

试求此系统的电荷、电场、电势分布以及球与球壳间的电势差。

5、求电偶极子电场中任一点的电势。

6、一平板电容器充满两层厚度各为d 1和d 2的电介质，它们的相对电容率分别为1r ε和 2r ε，极板的面积为S 。

求：(1)电容器的电容；(2)当极板上的自由电荷面密度为0σ时，两介质分解面上的极化电荷的面密度；(3)两层介质的电位移。

7、同轴电缆的内导体圆柱半径为R1，外导体圆筒内外半径分别为R2、 R3，电缆载有电流I ，求磁场的分布。

8、载流长直导线与矩形回路 ABCD 共面，且导线平行于 AB ，如图，求下列情况下ABCD 中的感应电动势：（1）长直导线中电流恒定，t 时刻 AB 以垂直于导线的速度 V 以图示位置远离导线匀速平移到某一位置时，（2）长直导线中电流 I = I0 sin ω t ，ABCD 不动，（3）长直导线中电流 I = I0 sin ω t ， ABCD 以垂直于导线的速度 V 远离导线匀速运动，初始位置也如图。

9、一长直电流I 在平面内被弯成如图所示的形状，其中直电流 ab 和cd 的延长线过o ，电流bc 是以o 为圆心、以R 2为半径的1/4圆弧，电流de 也是以o 为圆心、但是以R 1为半径的1/4圆弧，直电流ef 与圆弧电流de 在e 点相切，求：场点o 处的磁感强度B 。

I第9题图第10题图10、同轴电缆的内导体圆柱半径为R1，外导体圆筒内外半径分别为R2、R3，电缆载有电流I，求磁场的分布。

大学物理(第四版)课后习题及答案量子物理

第十七章量子物理题17.1：天狼星的温度大约是11000℃。

试由维思位移定律计算其辐射峰值的波长。

题17.1解：由维思位移定律可得天狼星单色辐出度的峰值所对应的波长该波长nm 257m 1057.27m =⨯==-Tbλ 属紫外区域，所以天狼星呈紫色题17.2：已知地球跟金星的大小差不多，金星的平均温度约为773 K ，地球的平均温度约为293 K 。

若把它们看作是理想黑体，这两个星体向空间辐射的能量之比为多少？题17.2解：由斯特藩一玻耳兹曼定律4)(T T M σ=可知，这两个星体辐射能量之比为4.484=⎪⎪⎭⎫⎝⎛=地金地金T T M M 题17.3：太阳可看作是半径为7.0 ⨯ 108 m 的球形黑体，试计算太阳的温度。

设太阳射到地球表面上的辐射能量为1.4 ⨯ 103W ⋅m －2，地球与太阳间的距离为1.5 ⨯ 1011m 。

题17.3解：以太阳为中心，地球与太阳之间的距离d 为半径作一球面，地球处在该球面的某一位置上。

太阳在单位时间内对外辐射的总能量将均匀地通过该球面，因此有 2244)(R Ed T M ππ=（1）4)(T T M σ= （2）由式（1）、（2）可得K 58004122=⎪⎪⎭⎫⎝⎛=σR E d T题17.4：钨的逸出功是4.52 eV ，钡的选出功是2.50 eV ，分别计算钨和钡的截止频率。

哪一种金属可以用作可见光范围内的光电管阴极材料？题17.4解：钨的截止频率 Hz 1009.115101⨯==hW ν 钡的截止频率Hz 1063.015202⨯==hW ν 对照可见光的频率范围可知，钡的截止频率02ν正好处于该范围内，而钨的截止频率01ν大于可见光的最大频率，因而钡可以用于可见光范围内的光电管材料。

题17.5：钾的截止频率为4.62 ⨯ 1014 Hz ，今以波长为435.8 nm 的光照射，求钾放出的光电子的初速度。

题17.5解：根据光电效应的爱因斯坦方程W mv h +=221ν 其中λνν/0c h W ==，可得电子的初速度15210s m 1074.52-⋅⨯=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=νλc m h v由于选出金属的电子的速度v << c ，故式中m 取电子的静止质量。

大学mooc大学物理-相对论和量子物理章节测验期末考试答案

解忧书店 JieYouBookshop第一周狭义相对论1单选(4分)以下那种说法是错误的？A.物体的静能随参考系的改变而变化。

B.相对论质能关系把质量与能量紧密联系在一起。

C.静质量为零的粒子没有静止状态，只能以光速运动。

D.物体的相对论性质量m是其运动速度v的函数。

正确答案：A你选对了2单选(4分)火箭以0.85 c的速率运动时，其运动质量与静止质量之比为？A.1B.1.9m0C.0.85D.1.5正确答案：B你选对了3单选(4分)狭义相对论的基本原理包含以下哪一条？A.等效原理B.光速不变原理C.广义相对性原理D.力的独立性原理正确答案：B你选对了4多选(4分)迈克耳孙-莫雷实验的结果说明了什么？A.不存在一个相对于以太静止的最优参考系。

B.迈克耳孙-莫雷实验是狭义相对论的实验基础C.没有观察到预期的条纹移动，地球相对于以太的运动并不存在。

D.以太不存在正确答案：A、C、D你选对了5判断(4分)所有验证相对论时间延缓效应的近代物理实验，都同样验证了相对论长度收缩效应。

正确答案：√你选对了6判断(4分)在狭义相对论的理论框架中，不允许存在超光速粒子。

A.√B.×正确答案：√你选对了1单选(4分)以下哪个不是广义相对论的实验验证？B.水星近日点的进动C.雷达回波时间延迟实验D.密立根油滴实验正确答案：D你选对了2单选(4分)以下那种说法是错误的？A.相对论能量-动量关系指出了静质量为零的粒子存在的可能性。

B.静质量为零的粒子没有静止状态，只能以光速运动。

C.相对论质能关系把质量与能量紧密联系在一起。

D.物体的静质量m0是在静止的惯性系中测到的物体质量。

正确答案：D你选对了3单选(4分)狭义相对论的基本原理包含以下哪一条？A.等效原理B.功能原理C.相对性原理D.伽利略相对性原理正确答案：C你选对了第二周量子物理基础11单选(4分)以下哪种说法是错误的？A.康普顿效应反映了光具有波动性。

大二大学物理试题及答案

大二大学物理试题及答案一、选择题（每题3分，共30分）1. 以下哪个选项不是牛顿三大定律之一？A. 惯性定律B. 万有引力定律C. 作用与反作用定律D. 力与加速度定律答案：B2. 光在真空中的传播速度是多少？A. 299,792,458 m/sB. 299,792,458 km/sC. 299,792,458 km/hD. 299,792,458 m/h答案：A3. 根据热力学第一定律，下列哪个说法是正确的？A. 能量可以被创造或消灭B. 能量可以在不同形式之间转换C. 能量守恒定律不适用于热力学系统D. 热力学系统的能量总是减少答案：B4. 电磁波的传播速度与以下哪个因素有关？A. 介质的密度B. 介质的折射率C. 观察者的运动状态D. 以上都是答案：B5. 根据麦克斯韦方程组，以下哪个选项是错误的？A. 电场是由电荷产生的B. 磁场是由电流产生的C. 变化的磁场可以产生电场D. 变化的电场可以产生磁场答案：D6. 以下哪个选项不是量子力学的基本原理？A. 波粒二象性B. 不确定性原理C. 相对论性原理D. 量子态的叠加原理答案：C7. 根据狭义相对论，以下哪个说法是错误的？A. 运动的物体在运动方向上的长度会变短B. 运动的物体的时间会变慢C. 运动的物体的质量会增加D. 运动的物体的速度可以超过光速答案：D8. 以下哪个选项不是电磁感应定律的内容？A. 变化的磁场可以产生电场B. 变化的电场可以产生磁场C. 恒定的磁场可以产生电场D. 恒定的电场可以产生磁场答案：C9. 根据热力学第二定律，以下哪个说法是正确的？A. 热量可以从低温物体自发地传递到高温物体B. 热机的效率可以达到100%C. 熵总是增加的D. 热机的效率总是小于1答案：D10. 以下哪个选项不是电磁波的特性？A. 电磁波是横波B. 电磁波在真空中传播速度是光速C. 电磁波是纵波D. 电磁波可以携带能量答案：C二、填空题（每题4分，共20分）1. 根据牛顿第二定律，力等于质量乘以_________。

大学物理题库量子2

大学物理试题解答

大学物理 第16章量子力学基本原理-例题及练习题

清华大学《大学物理》习题库试题及答案----10-量子力学习题解读

大学物理-量子力学基础习题思考题及答案

大学物理 相对论量子论练习题答案

大学物理量子物理

zk27量子2北京交通大学大学物理

大学物理教学 51.量子力学基础-2

大学物理同步训练第15章量子物理

大学物理知识总结习题答案(第十章)量子物理基础

大学物理教学 51.量子力学基础-2