(完整版)数学培优竞赛新方法(九年级)-第23讲几何定值
第23课相似多边形(学生版)-九年级数学上册《考点题型技巧》精讲与精练高分突破(浙教版)

第23课相似多边形目标导航学习目标1.1.了解相似多边形的概念和性质.2.在简单情形下,能根据定义判断两个多边形相似.3.会用相似多边形的性质解决简单的几何问题.知识精讲知识点01 相似多边形的概念1.一般地,对应角相等,对应边成比例的两个多边形叫做相似多边形.相似多边形对应边的比也叫做相似比.知识点02 相似多边形的性质1.相似多边形的对应角相等,对应边成比例.2.相似多边形的周长之比等于相似比;相似多边形的面积之比等于相似比的平方.能力拓展考点01 相似多边形的概念【典例1】下列多边形一定相似的是()A.两个矩形B.两个五边形C.两个正方形D.两个等腰三角形【即学即练1】在如图所示的三个矩形中,相似的是()A.甲和乙B.甲和丙C.乙和丙D.甲、乙和丙考点02 相似多边形的性质【典例2】如图,四边形ABCD相似于四边形A′B′C′D′.(1)∠B=.(2)求边x、y的长.【即学即练2】如图,四边形ABCD∽四边形EFGH.若AB=18,EF=4,FG=6,∠B=77°,∠C=83°,∠E=117°,求线段BC的长和∠H的大小.分层提分题组A 基础过关练1. 已知矩形的长与宽分别为4和3,下列矩形与它相似的是()A.B.C.D.2. 已知两个相似多边形的面积比是9:16,其中较小多边形的周长为18cm,则较大多边形的周长为()A.24cm B.27cm C.28cm D.32cm3. 两个相似五边形,一组对应边的长分别为4cm和6cm,若它们的面积之和为260cm2,则较大五边形的面积是()A.100cm2B.180cm2C.75cm2D.30cm24. 如图,四边形ABCD和四边形EFGH相似,且顶点都在方格纸的格点上,它们的相似比是()A.1:2 B.1:4 C.2:1 D.4:15. 如图所示的两个四边形相似,则下列结论不正确的是()A.a=2B.m=2n C.x=2 D.∠α=60°6. 如图,已知四边形ABFE∽四边形EFCD,AB=2,EF=3,则DC的长是()A.6 B.C.D.47. 如图的两个四边形相似,则∠a的度数是()A.120°B.87°C.75°D.60°8如图所示,长为10,宽为8的矩形中.截去一个矩形(图中阴影部分).如果剩下矩形与原矩形相似,那么截去短形的面积是()A.B.C.D.9. 如图,四边形ABCD∽四边形A′B′C′D′,则∠a的度数是.10.两个相似多边形的周长比是3:4,其中较小的多边形的面积为36cm2,则较大的多边形的面积为.11.在一张比例尺为1:30000的地图上,一多边形地区的周长为70cm,面积为340cm2,那么该地区的实际周长为km,面积为km2.12.已知两个相似多边形的相似比为5:7,若较小的一个多边形的周长为35,则较大的一个多边形的周长为;若较大的一个多边形的面积是4,则较小的一个多边形的面积是.13.如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.(1)求原矩形的长和宽的比.(2)若AB=4,求矩形ABCD的面积.14.如图,矩形AGFE∽矩形ABCD,AE、AD分别为它们的短边,点F在AB上,3AE=2AD.(1)求证:∠1=∠2.(2)若两个矩形的面积之和为650cm2,求矩形ABCD的面积.15.如图,在▱ABCD中,对角线AC,BD相交于点O、E、F、G、H分别是OA、OB、OC、OD的中点.(1)试说明四边形EFGH是平行四边形.(2)四边形EFGH与▱ABCD相似吗?说明理由.题组B 能力提升练16. 如图,选项中与它相似的是()A.B. C.D.17. 把一根铁丝首尾相接围成一个长为3cm,宽为2cm的矩形ABCD,要将它按如图所示的方式向外扩张得到矩形A′B′C′D′,使矩形A′B′C′D′∽矩形ABCD,则这根铁丝需增加()cm B.5cm C.7cm D.10cm18. 如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推.若各种开本的矩形都相似,那么等于()A.B.C.D.19. 如图,在矩形ABCD中,点E、F分别在BC、AD上,四边形ABEF是正方形,矩形ABCD∽矩形ECDF,则DF:AD的值为.20.如图所示,矩形ABCD的长AB=30,宽BC=20,x为时,图中的两个矩形ABCD与A'B'C'D'相似?21. 如图:矩形ABCD的长AB=30,宽BC=20.(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;(2)如图(2),x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?题组C 培优拔尖练22. 小红的妈妈做了一个矩形枕套(长、宽不等),又在枕套四周镶上了相同宽度的花边,如图所示,关于两个矩形,下列说法正确的是()A.两个矩形相似B.两个矩形不一定相似C.两个矩形一定不相似D.无法判断两个矩形是否相似23 如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是()A.B.C.D.24. 善于学习的小敏查资料知道:对应角相等,对应边成比例的两个梯形,叫做相似梯形.他想到“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”,提出如下两个问题,你能帮助解决吗?问题一:平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似?(1)从特殊情形入手探究.假设梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,MN是中位线(如图①).根据相似梯形的定义,请你说明梯形AMND与梯形ABCD是否相似;(2)一般结论:平行于梯形底边的直线截两腰所得的梯形与原梯形;(填“相似”或“不相似”或“相似性无法确定”.不要求证明)问题二:平行于梯形底边的直线截两腰所得的两个小梯形是否相似?(1)从特殊平行线入手探究.梯形的中位线截两腰所得的两个小梯形;(填“相似”或“不相似”或“相似性无法确定”.不要求证明)(2)从特殊梯形入手探究.同上假设,梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,你能找到与梯形底边平行的直线PQ(点P,Q在梯形的两腰上,如图②),使得梯形APQD与梯形PBCQ 相似吗?请根据相似梯形的定义说明理由;(3)一般结论:对于任意梯形(如图③),一定(填“存在”或“不存在”)平行于梯形底边的直线PQ,使截得的两个小梯形相似.若存在,则确定这条平行线位置的条件是=.(不妨设AD=a,BC=b,AB=c,CD=d.不要求证明)25.矩形ABCD纸片的边AB长为2cm,动直线l分别交AD、BC于E、F两点,且EF∥AB;(1)若直线l是矩形ABCD的对称轴,且沿着直线l剪开后得的矩形EFCD与原矩形ABCD相似,试求AD的长?(2)若使AD=+1cm,试探究:在AD边上是否存在点E,使剪刀沿着直线l剪开后,所得到的小矩形纸片中存在与原矩形ABCD相似的情况.若存在,请求出AE的值,并判断E点在边AD上位置的特殊性;若不存在,试说明理由.。
初中数学九年级培优教程整理(全)

【例1】(荆州)下列根式中属最简二次根式的是()A. a 2 1B. 12C. 8D. 27初中数学九年级培优目录第1 讲二次根式的性质和运算(P2 --- 7)第2 讲二次根式的化简与求值(P7 --- 12)第3 讲一元二次方程的解法(P13 --- 16)第4 讲根的判别式及根与系数的关系(P16 --- 22)第5 讲一元二次方程的应用(P23 --- 26)第6 讲一元二次方程的整数根(P27 --- 30)第7 讲旋转和旋转变换(一)(P30 --- 38)第8 讲旋转和旋转变换(二)(P38 --- 46)第9 讲圆的基本性质(P47--- 51)第10 讲圆心角和圆周角(P52 --- 61)第11 讲直线与圆的位置关系(P62 --- 69)第12 讲圆内等积证明及变换((P70 --- 76)第13 讲弧长和扇形面积(P76 --- 78)第14 讲概率初步(P78 --- 85)第15 讲二次函数的图像和性质(P85 --- 91)第16 讲二次函数的解析式和综合应用(P92 --- 98)第17 讲二次函数的应用(P99 --- 108)第18 讲相似三角形的性质(P109 --- 117)第19 讲相似三角形的判定(P118---- 124)第20 讲相似三角形的综合应用(P124 ---- 130)考点·方法·破译第1 讲二次根式的性质和运算1. 了解二次根式、最简二次根式、同类二次根式的定义,能准确进行辨析;2. 掌握二次根式有关性质,并能熟练运用性质进行化简;3. 会根据二次根式的性质挖掘题中隐含条件,求参数的值(或取值范围).经典·考题·赏析【解法指导】判断式子是否为最简二次根式的条件有两点:①被开方式中不能含分母;②被开方式中不能有可开尽方的数或式子. B 中含分母,C、D 含开方数4、9,故选 A.【变式题组】1.⑴(中山)下列根式中不是最简二次根式的是()A. 10B. 8C. 6D. 2⑵①a2b2 ;②x;③5x2 xy ;④27 abc ,最简二次根式是()A .①,②B .③,④C.①,③ D .①,④【例2】( 黔东南) 方程4x 8x y m 0 ,当y>0 时,m 的取值范围是()A .0<m<1 B.m≥2 C.m<2 D.m≤2【解法指导】本题属于两个非负数的代数和问题,隐含两个代数式均为0 的结论. 由题意得4x-8=0,x-y-m=0.化为y =2-m,则2-m>0,故选 C.【变式题组】2.(宁波)若实数x、y 满足x 2 ( y 3) 20 ,则xy 的值是.3.(荆门)若x 1 1 x (x y)2 ,则x-y 的值为()A .- 1B .1 C.2 D.34.(鄂州)使代数式x 3有意义的x 的取值范围是()x 4A .x>3 B.x≥3 C.x>4 D.x≥3 且x≠45. (怀化) a 2 b 3 (c 4) 0 ,则a-b-c=.【例3】下列二次根式中,与24 是同类二次根式的是()A .18 B.30 C.48 D.54【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式,再看被开方数是否一样.A .18 3 2 ;B .30 不能化简; C. 48 4 3 ;D.54 3 6 ,而24 2 6 .故本题应选 D.【变式题组】6. 如果最简二次根式3a 8 与17 2a 是同类二次根式,则a=.7. 在下列各组根式中,是同类二次根式的是()A . 3 和18B . 3 和13C.a2 b和ab2 D . a 1 和 a 18. 已知最简二次根式 b a 3b 和2b a 2 是同类二次根式,则a=,b=. 【例4】下列计算正确的是()A . 5 3 2B .8 2 4C.27 3 3 D.(1 2)(1 2) 122 a(a>0)【解法指导】正确运用二次根式的性质①( a) 2a(a≥0) ;② a 2 a0(a 0) ;③ab a b( a≥0, b≥0) ;④b b(b≥0, a>0)a aa(a<0)进行化简计算,并能运用乘法公式进行计算. A 、 B 中的项不能合并.D.(1 2)(1 2) 1 ( 2) 2【变式题组】1..故本题应选 C.9. (聊城)下列计算正确的是()A .2 3 4 2 6 5B .8 4 2C.27 3 3 D.( 3)2 310. 计算:( 15 4) 2007(4 15) 200711.(2 3 3 2) 2 (2 3 3 2) 212. ( 济宁) 已知 a 为实数,那么a2 =()A .aB .-a C.-1 D.013. 已知a>b>0,a+b=6 ab ,则a ba b的值为()2 1A .B .2 C. 2 D.2 2【例5】已知xy>0,化简二次根式xy的正确结果为()x2A .yB .y C.y D.y【解法指导】先要判断出y<0,再根据xy>0 知x<0. 故原式xyx【变式题组】y . 选D. 14. 已知a、b、c 为△ ABC三边的长,则化简 a b c ( a b c) 2的结果是.15. 观察下列分母有理化的计算:并利用这一规律计算:1 12 1 ,2 13 213 2 ,4 34 3 ,算果中找出规律,(1 1L1) ( 2006 1) .2 13 2 2006 200516.已知,则0<x<1,则( x 1)2 4 ( x1) 2 4 .x x1 1 b 5 1 5 1【例6】(辽宁)⑴先化简吗,再求值:,其中 a ,b .a b b a(a b) 2 22⑵已知 x3 2 , 32y3 2 ,那么代数式 32xy (x y)2 xy (x y)2值为 .【解法指导 】对于⑴,先化简代数式再代入求值;对于⑵,根据已知数的特征求xy 、x + y 的值,再代入求值 .ab a( a b) b 2(a b)2a b 5 1 5 1 【解】⑴原式=,当 a, b时, ab = 1,a + b = 5 ,原式= 5 .ab(a b)ab (a b)ab22⑵由题意得: xy = 1, x + y = 10, 原式= .【变式题组 】17.(威海)先化简,再求值:(a + b)2+ (a - b)(2a + b)- 3a 2,其中 a2 3 , b3 2 .a2a 2a 418.(黄石)已知 a 是 43 的小数部分,那么代数式 ( 22) (a ) 的值为 .a 4a 4 a2a a【例7 】已知实数 x 、y 满足 ( x x22008)( yy22008) 2008,则 3x 2-2y 2+ 3x - 3y - 2007 的值为( )A .- 2008B .2008C .- 1D . 1【解法指导 】对条件等式作类似于因式分解的变形,找出 a 、b 的关系,再代入求值 .解: ∵ ( x x 22008)( y y22008) 2008,∴ ( xx22008)2008 yy 2008 ,( yy22008)yy22008 xx220082008xx22008 ,由以上两式可得 x = y.选 D.∴ ( x x22008) 2008, 解得 x 2=2008,所以 3x 2- 2y 2+ 3x - 3y - 2007= 3x 2- 2x 2+ 3x - 3x - 2007=x 2- 2007= 1,故 【变式题组 】19.若 a >0, b > 0,且a( ab) 3 b( a5 b ) ,求 2a3bab的值 .演练巩固 · 反馈提高a b ab01. 若 m40 4 ,则估计 m 的值所在的范围是()A . 1< m < 2B . 2< m < 3C . 3<m < 4D . 4<m < 502.(绵阳)已知12 n 是正整数,则实数 n 的最大值为()A . 12B .11C . 8D . 303.(黄石)下列根式中,不是..最简二次根式的是()1 A.7 B. 3C.2D. 204.(贺州)下列根式中,不是最简二次根式的是( )1 100 101 1 100992 2A.2 B. 6 C. 8 D. 1005.下列二次根式中,是最简二次根式的是()A.12B.x233 C.D.2a 2b06.(常德)设 a = 20, b = (- 3)2, c 9 , d ( 1) 1 2, 则 a 、b 、 c 、d 、按由小到大的顺序排列正确的是()A .c < a < d <bB . b < d < a < cC . a < c < d <bD . b < c < a < d07.(十堰)下列运算正确的是() A . 32 5 B . 32 6C . ( 3 1)23 1D .52325 308.如果把式子 (1 a)1 根号外的因式移入根号内,化简的结果为()1 aA .1 a B . a 1C .a 1D .1 a09.(徐州)如果式子(x 1)2x 2 化简的结果为 2x - 3,则 x 的取值范围是()A . x ≤ 1B .x ≥ 2C . 1≤ x ≤ 2D . x > 010.(怀化)函数 yx 中自变量的取值范围是.x 211.(湘西)对于任意不相等的两个数a ,b ,定义一种运算 a ※ b =3 2 5 .那么 12※ 4= .3 2a21 a 112.(荆州)先化简,再求值:232,其中 a 3 .a2a 1 a a13.(广州)先化简,再求值:( a培优升级3)( a3) a(a 6) ,其中 a51 .201.(凉山州)已知一个正数的平方根是3x - 2 和 5x + 6,则这个数是 .02.已知 a 、b 是正整数,且满足 2(15 15 ) a b是整数,则这样的有序数对( a ,b )共有 对.03.(全国)设 a5 1 ,则aa42a 3a 2a 23.04.(全国)设 x2 aa1, a 是 x 的小数部分 , b 是 x 的小数部 , 则 a 3 +b 3+ 3ab = .2 105.(重庆)已知yx22 x222 ,则 x +y = .5x 4 4 5x06.(全国)已知 a2 1 , a 2 2 6 , a 6 2 ,那么 a 、b 、c 的大小关系是()A . a < b < cB .b < a < cC . c < b < aD .c < a < b35207.(武汉)已知 yx 1 4 x ( x , y 均为实数),则 y 的最大值与最小值的差为()A . 6 3B .3C . 5 3D . 6308.(全国)已知非零实数a 、b 满足 2a 4 b 2(a 3)b 24 2a ,则 a + b 等于()A .- 1B . 0C .1D . 209.(全国) 23 2 2 17 12 2 等于()A . 5 4 2B . 4 2 1C . 5D . 110. 已知 x2 xy y 0( x 0, y0) ,则3x xy y的值为( )1 1 A .B .325x 2 3 C .D .343 xy4 y11.已知 a b 2 a 1 4 b 2 3 c 3 1c 5 ,求 a + b + c 的值 . 212. 已知 913 与 913 的小数部分分别是 a 和 b ,求 ab - 3a + 4b + 8 的值 .考点·方法·破译第 2 讲 二次根式的化简与求值1. 会灵活运用二次根式的运算性质化简求值.2. 会进行二次根式的有理化计算,会整体代入求值及变形求值 .3. 会化简复合二次根式,会在根式范围内分解因式.经典· 考题· 赏析【例1 】(河北)已知x1 2 ,那么x x 的值等于xx3x 12x9 x 1【解法指导 】通过平方或运用分式性质,把已知条件和待求式的被开方数都用 1x表示或化简变形 .x解:两边平方得,x1 2 4 , xx1 2 ,两边同乘以 x 得, xx21 2 x ,∵ x 23x 1 5 x , x29 x 1 11x ,22∴原式 = 1 1 511【变式题组 】5 11 =5111. 若 a1 14 (0< a <1),则 a a a2. 设x1aa ,则 4x x 2的值为()A. a1aB.1 aaC. a1 aD .不能确定【例2 】(全国)满足等式x y y x2003x2003y 2003xy= 2003 的正整数对( x, y )的个数是() A . 1B . 2C . 3D .4【解法指导 】对条件等式作类似于因式分解的变形,将问题转化为求不定方程的正整数解 .解:可化为xy( x y) 2003( x y) 2003( xy 2003) 0 ,∴ (xy 2003)( x y2003) 0∵xy2003 0 ,∴ xy2003 0,则 xy =2003,且 2003 是质数,∴正整数对( x, y )的个数有 2 对,应选 B. 【变式题组 】3.若 a > 0, b > 0,且 a( a 4 b ) 3 b( a 2 b ) ,求 2a 3b ab 的值 .【例3 】(四川)已知:xa1 (0 aa 1) ,求代数式a b abx2x 6 x 3 x 2 2x 2 4x 的值 . xx2 x x 2x24x【解法指导 】视 x - 2,x 2-4 x 为整体,把xa约.1 平方,移项用含 a 的代数式表示 x - 2,x 2-4 x ,注意 0<a <1 的制 a解:平方得,x a1 2 ,∴ x 2 aa 1 , x2a4x 4 a21 2 ,a2x4x a1 2 ,a( x 3)(x 2)x( x 2) x 2x 24x∴化简原式=g x x 3 x 2 x 24xa 1 ( 1 a)= (a 1 )2 a a a 2 2 a a 1 ( 1 a) a a【变式题组 】2, 4.(武汉)已知 xx 31 232 1,求代数式x 3 ( 52 x 4 x 2x 2) 的值.5.(五羊杯)已知 m 12 , n 12 ,且 (7 m 2 14m a)(3n 26n 7) 8 ,则 a 的值等于()A .- 5B . 5C .- 9D .9【例4 】(全国)如图,点 A 、C 都在函数 y等边三角形,则点 D 的坐标为.3 3 ( xx0) 的图像上,点 B 、D 都在 x 轴上,且使得△ OAB 、△ BCD 都是 【解法指导 】解:如图,分别过点 A 、C 作 x 轴的垂线,垂足分别为E 、F. 设OE=a ,BF=b ,则 AE= 3 a ,CF = 3 b ,所以,点 A 、C 的坐标为( a, 3 a )、( 2a + b, 3 b ),所以3a23 3ya 3 ,解得,3b (2 a b) 3 3因此,点 D 的坐标为( 2 6 ,0) 【变式题组 】6.(邵阳)阅读下列材料,然后回答问题.b63ACOE BF Dx在进行二次根式化简时,我们有时会碰上如52 2 ,3 3 3一样的式子,其实我们还可以将其进一步化简: 15 5 3 3 33 5 3 ; (一)3 2 2 3 33 36 ; (二)3223 13 3 11 3 13 1 ;(三)以上这种化简的步骤叫做分母有理化,2还可以用以下方法化简:2 3 1 3 13 123 13 3 13 1 1 3 13 13 1;(四)( 1)请你用不同的方法化简2;53①参照(三)试得:2=;(要有简化过程) 5 3②参照(四)试得: 2 =;(要有简化过程)53 ( 2)化简:1 1 1L1 3 153752n 12 n 1【例5 】(五羊杯)设 a 、b 、c 、d 为正实数, a < b , c < d ,bc > ad ,有一个三角形的三边长分别为a2c 2 , b2d 2,(b a)2(d c)2,求此三角形的面积 .【解法指导 】虽然不能用面积公式求三角形面积 ( 为什么 ?) ,a2边,从构造图形入手,将复杂的根式计算转化为几何问题加以解决.c 2的几何意义是以 a 、c 为直角边的直角三角形的斜解:如图,作长方形 ABCD ,使 AB = b - a , AD =c ,延长 DA 至 E ,使 DE =d ,延长 DC 至 F ,使 DF = b ,连结 EF 、FB 、EB , 则BF =a2c2, EF =b2d2,BE=(b a)2(d c)2,从而D知△ BEF 就是题设的三角形, 而 S △ BEF =S 长方形 ABCD + S △ BCF + S △ ABE baCF - S △ DEF = ( b - a) c + 1 2( d -1 1c)( b - a) - bd = ( bc -ad)d 22A cE【变式题组 】7. ( 北京 ) 已知 a 、b 均为正数,且 a +b = 2,求 U =a24b21演练巩固 · 反馈提高3 2 3 2xy x 2y2 01. 已知 x, y32,那么代数式32xy x2值为y202. 设 a7 1,则 3a312a26a 12 =()A . 24B . 25C . 4 7 10D . 4 7 1203.(天津)计算 ( 3 1)20012( 3 1)20002( 3 1)1999200104.(北京)若有理数 x 、 y 、z 满足xy 11 z 2( x y z) ,则 2( x yz)205.(北京)正数 m 、 n 满足 m 4 mn 2 m 4 n4n 3 0 ,则m 2 m 2 n n 8200206.(河南)若 x3 1 ,则 x3(2 3) x2(1 2 3) x 3 5 的值是()A . 2B . 4C . 6D . 807. 已知实数 a 满足 2000a a 2001 a ,那么 a 20002的值是()A . 1999B . 2000C . 2001D . 200208. 设 a1003 997 , b 1001 999 , c 2 1000 ,则 a 、b 、c 之间的大小关系是()A . a < b < cB . c < b < aC . c < a < bD . a < c < b09. 已知 1 ( x 1)2x ,化简 x21 x x21 x44B3 32003培优升级01.(信利)已知 x1 3 ,那么1x 21 1 x 24 x 202.已知 a 4a 1 5 ,则 6 2 a03.(江苏)已知( xx22002)( yy22002) 2002 ,则 x 23xy 4 y26 x 6 y 5804.(全国)7x 29x 13 7x 25x 13 7x ,则 x =05.已知 x3 2 , y3 2 ,那么 yx32 3 2 x2y206.(武汉)如果a b20022 , ab2002 2 , b3c3b3c ,那么 a 3b3c 的值为()A . 2002 2002B . 2001C . 1D . 007.(绍兴)当 x12002 2时,代数式 (4 x32005 x2001)的值是( )A . 0B .- 1C . 1D . 2200308.(全国)设 a 、b 、c 为有理数,且等式a b 2 c 35 26 成立,则 2a 999b 1001c 的值是()A . 1999B . 2000C . 2001D .不能确定09.计算:( 1)6 4 3 3 2( 63)( 32)( 2)10 14 15 21 10141521( 3)1 1 1L13 35 3 3 5 7 5 5 749 47 47 49( 4)3 2 2 5 2 6 7 2 12 9 2 20 11 2 30 13 2 4215 2 5617 2 722210.已知实数 a 、 b 满足条件a bb1 ,化简代数式a (1 1)g a b( a b 1)2,将结果表示成不含 b 的形式 .11.已知 x1 a 2(a a0) ,化简:x 2 x 2x 2 x 212.已知自然数 x 、y 、z 满足等式x 2 6 y z 0 ,求 x + y +z 的值 .考点·方法·破译第 3 讲 一元二次方程的解法1. 掌握一元二次方程根的定义并能应用根的定义解题;2. 掌握一元二次方程的四种解法,并能灵活应用各种解法解方程;3. 会应用一元二次方程解实际应用题。
人教版九年级数学竞赛专题:平面几何的定值问题(含答案)

(第 3 题图)
(第 4 题图)
4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在 AB 上滚动,切点为 T,⊙O 交 AO,BO 于 M,N,则 弧 MTN( )
A.在 0°到 30°变化
B.在 30°到 60°变化
C.保持 30°不变
D.保持 60°不变
5.如图,AB 是⊙O 的直径,且 AB=10,弦 MN 的长为 8.若 MN 的两端在圆上滑动时,始终与 AB 相交, 记点 A,B 到 MN 的距离分别为 h1,h2,则∣h1-h2∣等于( )
A
C
(P) O
D
B
①
D
A
C P O
B D ①
D
C
PB O
D ①
O
C A
P
①
B
O
C
P
A (B)
①
O
(D)C
A(B)
P ①
(2)已知⊙O 的半径为一定值 r,若点 P 是不在⊙O 上的一个定点,请你过点 P 任作一直线交⊙O 于 不重合的两点 E,F. PE·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文 字叙述出来.
(第 7 题图)
(第 8 题图)
8.如图,设 H 是等腰三角形 ABC 两条高的交点,在底边 BC 保持不变的情况下让顶点 A 至底边 BC 的 距离变小,这时乘积 S△ABC·S△HBC 的值变小、变大,还是不变?证明你的结论.
9.如图,在平面直角坐标系 xOy 中,抛物线 y 1 x 2 4 x 10 与 x 轴的交点为点 A,与 y 轴的交点 18 9
人教版九年级数学竞赛专题:平面几何的定值问题(含答案)
【例 1】 如图,已知 P 为正方形 ABCD 的外接圆的劣弧A⌒D上任意一点.求证: PA PC 为定值. PB
人教版九年级上册数学同步培优第二十三章旋转 素养集训 旋转在解几何题中的九种常用技巧

∴EF2=BE2+DF2.
返回
6.【2021·绵阳】点M是∠ABC的边BA上的动点,BC= 6,连接MC,并将线段MC绕点M逆时针旋转90°得 到线段MN.
(1)如图①,作MH⊥BC,垂足H在线段BC上,当∠CMH =∠B时,判断点N是否在直线AB上,并说明理由;
【点方法】根据∠CMH=∠B,∠CMH+∠C=90°, 则∠B+∠C=90°,故∠BMC=90°,即可判断; 解:点N在直线AB上,理由如下: ∵∠CMH=∠B,∠CMH+∠C=90°, ∴∠B+∠C=90°.∴∠BMC=90°,即CM⊥AB. ∴线段CM逆时针旋转90°落在直线BA上, 即点N在直线AB上.
2 ∵△ACE是等边三角形,∴AC=AE,∠ACE=60°. ∵AC=2AB,∴AE=2AD′. ∴∠PCD′=∠ACD′=12 ∠ACE=30°.
∵DP∥BC,∴∠ABD′=∠DBD′=∠BD′D=∠ACD′= ∠PCD′=∠PD′C=30°. ∴BD′=CD′. 在△BDD′和△CPD′中,∠BD′D=∠PD′C,BD′=CD′, ∠DBD′=∠PCD′, ∴△BDD′≌△CPD′(ASA).
返回
4.【中考·荆州】如图①,等腰直角三角形OEF的直角 顶点O为正方形ABCD的中心,点C,D分别在OE和 OF上,现将△OEF绕点O逆时针旋转角 α(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=_9_0_°__-__α_(用含α的式子表示);
(2)在图②中猜想AF与DE的数量关系,并证明你的结论. 解:AF=DE.证明如下:
(2)如图②,若∠ABC=30°,NC∥AB,求以MC、MN 为邻边的正方形的面积S.
【点方法】作CD⊥AB于D,在△BCM中, 已知两角一边,可通过解三角形求出MC的长度.
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)
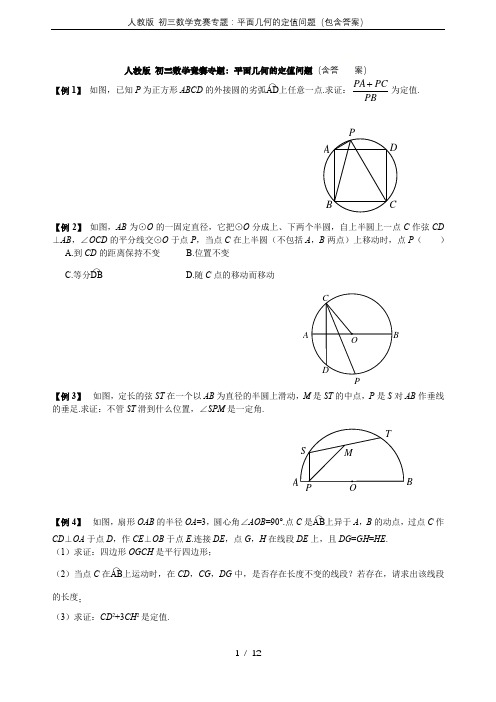
人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
九年级奥数:几何定值

九年级奥数:几何定值阅读理解所谓几何定值,是指在一定条件下构成的几何图形,某些几何元素的几何量在变动的图形中保持不变,或几何元素间的某些位置关系或某些几何性质不变.解几何定值问题时,首先,应分清图形中固定元素和变动元素;其次,通过特殊位置或极端位置,探寻那些隐含的、在运动变化中没有改变的元素,这就是我们要探求的定值;最后,在一般情况下给出证明.问题解决例1 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A 、B 两点)上移动时,点P ( ).A .到CD 的距离保持不变B .位置不变C .等分.D .随C 点的移动而移动例2 如图1,在正方形ABCD 中,点E 、F 分别为边BC 、CD 的中点,AF 、DE 相交于点G ,则可得结论:①AF =DE ;②AF ⊥DE .(不需要证明)(1)如图2,若点E 、F 不是正方形ABCD 的边BC 、CD 中点,但满足CE =DF ,则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图3,若点E 、F 分别在正方形ABCD 的边CB 的延长线和DC 的延长线上,且CE =DF ,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)如图4,在(2)的基础上,连接AE 和EF ,若点M 、N 、P 、Q 分别为AE 、EF 、FD 、AD 的中点,请判断四边形MNPQ 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.例3 把两块全等的直角三角板ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合,其中∠ABC =∠DEF =90°,∠C =∠F =45°,AB =DE =4,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q .(1)如图1,当射线DF 经过点B ,即点Q 与点B 重合时,易证△APD ∽△CDQ .此时,DBAP ·CQ =___________.(2)将三角板DEF 由图1所示的位置绕点O 沿逆时针方向旋转,设旋转角为,其中0°<<90°,问AP ·CQ 的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ =x ,两块三角板重叠部分的面积为y ,求y 与x 的函数关系式(图2、图3供解题用).例4 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A 、B 两点,交y 轴于C 、D 两点,且C 为的中点,AE 交y 轴于G 点,若点A 的坐标为(-2,0),AE =8.(1)求点C 的坐标;(2)连结MG 、BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.数学冲浪1.如图,已知△ABC 中,AB =AC ,∠BAC =90°,O 是BC 的中点,如果点M 、N 分别在AC 、AB 上移动,在移动中保持AM =BN ,试探求△OMN 的形状是否发生变化?并证明你的结论.2.如图,正方形ABCD 的边长为2cm ,现有两点E 、F 分别从点B 、点A 同时出发,点E 沿线段BA 以1cm /秒的速度向点A 运动,点F 沿折线A —D —C 以2cm /秒的速度向点C 运动,设点E 离开点B 的时间为t 秒,当1≤t <2时,设EF 和AC 交于点P ,试探求P 点的位置是否发生改变? ααAE OF PF3.如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第四象限内作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连结BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.(1)试问△OBC与△ABD全等吗?并证明你的结论.(2)随着点C位置的变化,点E的位置是否发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.4.已知半径为R的⊙O′经过半径为r的⊙O的圆心,⊙O与⊙O′交于E、F两点.(1)如图1,连结⊙O′交⊙O于点C,并延长交⊙O′于点D,过点C作⊙O的切线交⊙O′于A、B两点,求OA·OB的值;(2)若点C为⊙O上一动点,①当点C运动到⊙O′内时,如图2,过点C作⊙O的切线交⊙O′于A、B两点,则OA·OB 的值与(1)中的结论相比较有无变化?请说明理由.②当点C运动到⊙O′外时,过点C作⊙O的切线,若能交⊙O′于A、B两点,如图3,则OA·OB的值与(1)中的结论相比较有无变化?请说明理由.5.如图,在直角坐标系中,点E从点O出发,以1个单位/秒的速度沿x轴正方向运动,F从O点出发,以2个单位/秒的速度沿y轴正方向运动,点B坐标为(4,2),以BE为直径作⊙O1,⊙O1与x轴的另外一个交点为A.(1)如图1,若点E、F同时出发,设线段EF与线段OB交于G,试判断EF与OB的位置关系,并证明你的结论;(2)如图2,若点E提前2秒出发,点F再出发,当点F出发后,E点在A点左侧时,设BA⊥x轴于A点,连结AF交⊙O1于点P,试问AP·AF的值是否发生变化?若不变,请说明理由,并求其值;若变化,请求其值的变化范围.6.将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).(1)如果M为CD边的中点,求证:DE:DM:EM=3:4:5;(2)如果M为CD边上的任意一点,设AB=2a,问△CMG的周长是否与点M的位置有关系?若有关,请把△CMG的周长用含DM的长x的代数式表示;若无关,请说明理由.7.问题背景某课外学习小组在一次学习研讨中,得到了如下两个命题:①如图1,在正三角形ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;②如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.然后运用类比的思想提出了如下命题:③如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求(1)请你从①,②,③三个命题中选择一个进行证明;(2)请你继续完成下面的探索:①如图4,在正n(n≥3)边形ABCDEF 中,M、N分别是CD、DE上的点,BM与CN相交于点O,问当∠BON等于多少度时,结论BM=CN成立?(不要求证明)②如图5,在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,若∠BON=108°时,请问结论BM=CN是否成立?若成立,请给予证明;若不成立,请说明理由.。
九年级数学尖子生培优竞赛专题辅导第二十三讲 平面几何的定值与最值问题(含答案)

第二十三讲 平面几何的定值与最值问题趣题引路】传说从前有一个虔诚的信徒,他是集市上的一个小贩。
每天他都要从家所在的点A 出发,到集市点B ,但是,到集市之前他必须先拐弯到圆形古堡朝拜阿波罗神像.古堡是座圣城,阿波罗像供奉在古堡的圆心点O ,而圆周上的点都是供信徒朝拜的顶礼地点如图23-1.这个信徒想,我怎样选择朝拜点C ,才能使从家到朝拜点,然后再到集市的路程最短呢?解析 在圆周上选一点P ,过P 作OO 的切线MN ,使得∠APK=∠BPK ,即αβ=.那么朝圣者沿A→P→B 的路线去走,距离最短.证明 如图23-2,在圆周上除P 点外再任选一点P '.连结BP '与切线MN 交于R ,AR+BR>AP+BP.∵RP '+AP '>AR.∴AP '+BP '=AP '+RP '+RB>AR+BP>AP+BP.不过,用尺规作图法求点P 的位置至今没有解决.“古堡朝圣问题”属于数学上“最短路线问题”,解决它的方法是采用“等角原理”.图23-1BA图23-2M N知识延伸】平面几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题.所谓几何定值问题就是要求出这个定值.在解决这类问题的过程中,可以直接通过计算来求出定值;也可以先考虑某一个特殊情形下的该相关值,然后证明当相应几何元素变化时,此值保持不变。
例1 如果△ABC 的外接圆半径R 一定, 求证:abcS是定值.(S 表示△ABC 的面积) 解析 由三角形面积1sin 2S ab C =和正弦定理2sin cR C =,2sin c R C ∴=.24sin 4sin sin abc c R CR S C C∴===是定值 点评 通过正弦定理和三角形面积公式经过变形,计算出结果是4R ,即为定值.平面几何中不仅有等量关系,还有不等关系,例如在变动一些几何元素时,某一相关的值保持不大于(或不小于)某个定值,如果这个定值在某个情形下可以取得,这就是一个几何极值.确定几何极值的问题称为几何极值问题,解决这些问题总要证明相关的几何不等式,并指明不等式成为等式的情形(或者至少证明不等式可以成为等式).例2 如图23-3,已知⊙O 的半径R =,A 为⊙O 上一点,过A 作一半径为r =3的⊙O ′,问OO ′何时最长?最长值是多少?OO ′何时最短?最短值是多少?图23-3解析:当O ′落在OA 的连线段上(即⊙A 与线段OA 的交点B 时)OO′最短,且最短长度为3;当O ′落在OA 的延长线上(即⊙A 与OA 的延长线交点C 时)OO′最长,且最长的长度为 3.点评:⊙O ′是一个动圆,满足条件的⊙O ′有无数个,但由于⊙O ′过A 点,所以⊙O ′的圆心O ′在以A 为圆心半径为3的⊙A 上.好题秒解】佳题新题品味例1 如图23-4,已知P 为定角O 的角平分线上的定点,过O 、P 两点任作一圆与角的两边分别交于A 、B 两点.求证:OA +OB 是定值.图23-4O证明: 连接AP 、BP ,由于它们为有相同圆周角的弦,AP =PB ,不妨记为r ,另记1x =OA ,2x =O B. 对∆POA 应用余弦定理,得1x 2+OP 2-2OP ⋅cos ∠AOP ⋅1x =r 2.故1x 为方程1x 2-2OP ⋅cos12∠AOB ⋅x +(OP 2-r 2)=0的根,同理2x 亦为其根. 因此1x ,2x 为此方程的两根,由韦达定理,得1x +2x =2OP (12∠AOB )是定值.点评:当1x =2x 时,1x +2x 为此定值,事实上此时OP 一定是直径.例2:如图23-5,在矩形ABCD 中,AB =8,BC =9,⊙O 与⊙O ′外切,且⊙O 与AB 、BC 相切. ⊙O ′与AD 、CD 相切,设⊙O 的半径为x ,⊙O 与⊙O ′的面积的和为S ,求S 的最大值和最小值.图23-5HBD解析:设⊙O ′的半径为y ,过O 与O ′分别作CD 与BC 的垂线OH ,O ′F ,垂足分别为H ,F ,OH 、O ′F 交于点E ,则有:O ′E =8-(x +y ),OE =9-(x +y )由勾股定理可得:(x +y )2=[8-(x +y )]2+[9-(x +y )]2 整理,得(x +y -29)(x +y -5)=0, 由题意知1≤x ≤4,∴x +y =5,y =-x +5,∴S =πx 2+πy 2=π(2x 2-10x +25) =2π[(x -52)2+254],故当x =52时,S m i n =252π;当x =4时,S max =17π.点评:先由已知求出⊙O ′的半径与⊙O 的半径x 之间的关系,然后再根据面积公式写出S 与x 之间的关系,这个关系就是一个函数关系,再通过函数的性质得解.中考真题欣赏例(南京市中考题)如图23﹣6,⊙O 1与⊙O 2内切于点P ,又⊙O 1切⊙O 2的直径BE 于点C ,连结PC 并延长交⊙O 2于点A ,设⊙O 1,⊙O 2的半径分别为r 、R ,且R≥2r.求证:PC·AC 是定值.图23-6EBAP图23-7解析 若放大⊙O 1,使⊙O 1切⊙O 2的直径于点O 2(如图23-6),显然此时有PC·AC=P O 2·A O 2=2r·R (定值).再证明如图23﹣7的情况:连结C O 1,P O 2,则P O2,必过点O 1,且O1C ⊥BE ,得2COBC R =EC R =所以PC·AC=EC·BC=2Rr ,故PC·AC 是定值.点评 解答几何定值问题时,可先在符合题目条件的前提下用运动的观点,从特殊位置入手,找出相应定值,然后可借助特殊位置为桥梁,完成一般情况的证明.竞赛样题展示例1(第十五届江苏省初中数学竞赛题)如图23﹣8,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与点B 或点C 重合),分别过点B 、C 、D 作射线AP 的垂线,垂足分别为点B '、C '、D '.求BB '+CC '+DD '的最大值和最小值.图23-8AC解析 12DPC APC S S AP CC ∆∆'==⋅,得 APC ADP DPC BCDA S S S S ∆∆∆=++四边形1()2AP BB DD CC '''=++,于是BB'+CC'+DD'=2AP. 又1≤AP≤2,∴BB'+CC'+DD',最大值为2.点评 本题涉及垂线可考虑用面积法来求.例2(2000年“新世纪杯”广西竞赛题)已知△ABC 内接于⊙O ,D 是BC 或其延长线上一点,AE 是△ABC 外接圆的一条弦,若∠BAE=∠CAD.求证:AD·AE 为定值.图23-9(2)(1)E证明 如图23﹣9(1),当点D 是BC 上任意一点且∠BAE=∠CAD 时,连结BE ,则∠E=∠C ,∠BAE=∠CAD ,∴△ABE ∽△ADC. AB AEAD AC∴=,即AD·AE=AB·AC 为定值. 如图23﹣9(2),当点D 在BC 的延长线上时,∠BAE=∠CAD.此时,∠ACD=∠AEB.AEB ∴∆∽ACD ∆. AB AEAD AC∴=, 即AD·AE=AB·AC 为定值.综上所述,当点D 在BC 边上或其延长线上时,只要∠CAD=∠BAE ,总有存AD·AE 为定值 点评 先探求定值,当AD ⊥BC ,AE 为圆的直径时,满足∠BAE=∠CAD 这一条件,不难发现∆ACD ∽∆AEB ,所以AD·AE=AB·AC ,因为已知AB ,AC 均为定值.再就一般情况分点D 在BC 上,点D 在BC 的延长线上两种情况分别证明.过关检测】A 级1.已知:MN 是⊙O 的切线,AB 是⊙O 的直径.求证:点A 、B 与MN 的距离的和为定值.2.已知:⊙O与⊙O1外切于C,P是⊙O上任一点,PT与⊙O1相切于点T求证:PC:PT是定值.3.⊙O1与⊙O2相交于P、Q两点,过P作任一直线交OO,于点E,交⊙O2于点F.求证:∠EOF为定值。
数学培优竞赛新方法(九年级)-配方法

配方法把一个式子或一个式子的部分改写成完全平方式或者几个完全平方式的和的形式,这种解题方法叫配方法。
配方法的作用在于揭示式子的非负性,是挖掘隐含条件的有力工具;配方法的实质在于改变式子的原有结构,是变形求解的一种手段。
运用配方法解题的关键在于“配凑”,“拆”与“添”是配方中常用的技巧。
熟悉以下基本等式:1.222)(2b a b ab a ±=+±2.2222)(222c b a ac bc ab c b a ++=+++++; 3.[]222222)()()(21a c cb b a ca bc ab c b a ±+±+±=±±±++ 4.a b ac a b x a c bx ax 442222-+⎪⎭⎫ ⎝⎛+=++ 【例1】已知y x ,实数满足0332=-++y x x ,则y x +的最大值为(镇江市中考题)思路点拨 把y 用x 的式子表示,通过配方法求出y x +的最大值。
【例2】已知c b a 、、,满足722=+b a ,122-=-c b , 1762-=-a c ,则c b a ++的值等于( )A.2B.3C.4D.5(河北省竞赛题)思路点拨 由条件等式的特点,从整体叠加配方入手【例3】已知a 是正整数,且a a 20042+是一个正整数的平方,求a 的最大值。
(北京市竞赛题)思路点拨 设222004m a a =+(m 为正整数),解题的关键是把等式左边配成完全平方式。
【例4】已知c b a 、、是整数,且01,422=-+=-c ab b a ,求c b a ++的值(浙江省竞赛题)【例5】若y x 、是实数,且y x y xy x m 446422--+-=,确定m 的最小值(北京市竞赛题)分析与解 选择x 为主元,将条件等式重新整理成x 的二次三项式,利用配方求m 的最小值。
练习1.设mn n m n m 4,022=+>>,则mnn m 22-的值等于( )A.32B.3C.6D.3(2011年南通市中考题)2.已知m m Q m P 158,15172-=-=(m 为任意实数),则Q P 、的大小关系为( ) A.Q P > B.Q P = C.Q P < D.不能确定(泰州市中考题)3.若实数z y x 、、,满足0))((4)(2=----z y y x z x ,则下列式子一定成立的是( )A.0=++z y xB.02=-+z y xC.D.02=-+y x z(2011年天津市中考题)4.化简2121722321217223---++的结果是( ) A.2 B.2- C.2 D.2-(2011年江西省竞赛题)5.已知实数c b a 、、满足016,72=++++=+-c b bc ab c b a ,则ab的值等于 (天津市竞赛题)6.当2>x 时,化简代数式1212--+-+x x x x 得(“希望杯”邀请赛试题)7.已知z y x 、、为实数,且满足52,352-=--=-+z y x z y x ,则222z y x ++的最小值为 。
(完整版)初中数学培优竞赛讲座第23讲__简单的面积问题

第二十三讲简单的面积问题几何起源于对图形的面积的测量,面积是平面几何中一个重要的概念,求图形的面积是平面几何中常见的基本问题之一.平面几何图形形状不同,繁简不一,计算图形的面积有以下常用方法:1.和差法把图形面积用常见图形面积的和差表示,通过常规图形面积公式计算.2.运动法有时直接求图形面积有困难,可通过平移、旋转、割补等方式,将图形中的部分图形运动起来,把图形转化为容易观察或解决的形状,就可在动中求解.3.等积变形法即找出与所求图形面积相等或有关联的特殊图形,通过代换转化求图形的面积.例题【例1】(1)如图a,边长为3cm,与5cm的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积是cm2(π取3).( “希望杯”邀请赛试题)(2)如果图b中4个圆的半径都为a,那么阴影部分的面积为.(江苏省竞赛题)思路点拨通过连结或补形,把图形进行分割和重新组合,变不规则图形为规则图形.(1)连AC、BF.S是由ABCD围成阴影面积的6倍.(2)连AD,BC,CD,则阴影注:促使面积比与对应线段比之间的相互转化.是求图形面积的一个常用技巧,解题的关键是加强对图形结构的分析,寻找,共高或共底的三角形.【例2】如图,梯形ABCD被对角线分为4个小三角形,已知ΔAOB和ΔBOC的面积分别为25cm2和35cm2,那么梯形的面积是m2.A.144 B.140 C.160 D.无法确定( “五羊杯”邀请赛试题)思路点拨图形隐含多对面积相等的三角形,要求梯形的面积只需求ΔDOC的面积,解题的关键是通过线段的比把三角形面积联系起来.【例3】根据图中绘出的小三角形面积的数据,求△ABC的面积.(新加坡数学竞赛题) 思路点拨设S△AGE=x,S△BFG=y,建立关x,y的方程组,通过代数化解题.【例4】如图,△ABC的面积为1,D、E为AC的三等分点,F、G为BC的三等分点.求:(1)四边形PECF的面积;(2)四边形PFGN的面积.思路点拨(1)连CP ,设S △FCF =x ,S △FCE =y ,可建立关于x ,y 的方程组,解题的关键是把相关图形的面积用于x ,y 的代数式表示,并利用等分点导出隐含图形的面积;(2)连NC ,仿(1),先求出△BNC 的面积,再得出△BNG 面积,进而可求四边形PFGN 的面积.注:求一些关系复杂的图形面积,代数化是一个重要技巧,利用代数化,能清晰明朗地表示图形面积之间的关系,从而可以化解或降低问题的难度.【例5】在方格纸中,每个小方格的顶点叫做格点,在2×2方格纸中,以格点连线为边作面积为2的多边形.请尽可能多地找出答案,在寻找答案的过程中你能发现什么规律吗?思路点拨本例是一道开放式探索性问题,若没有规律性的认识,则难免遗漏或重复,适当的方法是:选择一些图形作基本图形,再通过基本图形的组合尽可能多地找出解答.学力训练1.如图是阳光广告公司为某种商品设计的商标图案,图中阴影部分为红色.若每个小长方形的面积都是1,则红色的面积是.(山西省中考题)2.如图,4个半径为lcm 的圆相靠着放在一个正方形内,则阴影部分的面积是cm 2(精确到0.01).3.如图,在长方形ABCD 中,E 是AD 的中点,F 是CE 的中点,若ABDF 的面积为6平方厘米,则长方形ABCD 的面积是平方厘米.4.如图,若长方形APHM 、BNHP 、CQHN 的面积分别为7、4、6,则阴影部分的面积是.(“五羊杯”竞赛题)5.如图,一个大长方形被两条线段AB 、CD 分成四个小长方形,如果其中图形I 、Ⅱ、Ⅲ的面积分别为8,6,5,那么阴影部分的面积为( ).(江苏省竞赛题) A .29B .27C .310D .8156.如图.正方形的边长为a ,以各边为直径在正方形内画半圆,所围成的图形(阴影部分)的面积为().A .22aaB .222aa C .2221aaD .2241aa(广东省中考题)7.如图,△ABC 中,点D 、E 、F 分别在三边上,F 是AC 的中点,AD 、BE 、CF 交于一点G ,BD =2DC ,S △GEC =3,S △GDC =4,则△ABC 的面积是().(2002年湖北省荆州市中考题)A .25B .30C .35D .408.如图,正方形ABCD 中,E 、F 分别是BC 、CD 边上的点,AE 、DE 、BF 、AF 把正方形分成8小块,各小块的面积分别为S 1、S 2、…S 8,试比较S 3与S 2+S 7+S 8的大小,并说明理由.(江苏省竞赛题)9.将△ABC 分成面积相等的5部分,并指出面积相等的是哪5部分(只在图上保留分割痕迹和必要的标注,不写作法).10.2002年8月,在北京召开了国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是13,小正方形的面积是1,则每个直角三角形的两条边的立方和等于.11.如图,在长方形ABCD 中,DM :MC=2:1,AN =a ,NB =b ,DN 是以A 为圆心,a 为半径的一段圆弧,NK 是以B 为圆心,b 为半径的一段圆弧,则阴影部分的面积S 阴=.(广西竞赛题)12.如图,ABCD 是平行四边形,E 在AB 上,F 在AD 上,S △BCE =2S △CDF =41S ABCD =1,则S △CEF =.( “希望杯”邀请赛试题)13.如图,三角形ABC 的面积为1,BD :DC =2:1,E 是AC 的中点,AD 与BE 相交于点P ,那么四边形PDCE 的面积为.(江苏省竞赛题)14.如图,点E 、F 分别是长方形ABCD 的边AB 、BC 的中点,连AF ,CE ,设AF 、CE 交于点G ,则ABCDAGCD S S 长方形四边形=().(全国数学竞赛题)A .65B .54C .43D .3215.如图,凸四边形AB(0中,对角线AC 、BD 相交于O 点,若三角形AOD 的面积是2,三角形OOD 的面积是l ,三角形COB 的面积是4,则四边形ABCD 的面积是().A .16D .15C .14D .13( “希望杯”邀请赛试题)16.如图,S △ABC =1,若S △BDE =S △DEC =S △ACE ,则S △ADE ( ).A .51B .61C .71D .8117.己如,△ABC 的面积为1,分别延长AB 、BC 、CA 到D 、E 、F ,使AB=BD ,BC=CE ,CA =AF ,连DE 、EF 、FD ,求△DEF 的面积.18.如图,已知长方形的面积是36平方厘米,在边AB 、AD 上分别取点E 、F ,使得AE=3EB ,DF =2AF ,DE 与CF 的交点为O ,求△FOD 的面积.(第1l 届“希望杯”邀请赛试题)19.有一个正方形的花坛,现要将它分成面积相同的8块,分别种上不同颜色的花.(1)如果要求这样分成的8块的形状也相同,请你画出几种设计方案;(2)为了画出更多的设计方案,你能从中找出,—些规律吗?(3)如果要8块中的每4块形状相同,应如何设计?试尽可能精确地画出你的创意.20.如图,已知四边形ABCD 面积为S ,E 、F 为AB 的三等分点,M 、N 为DC 的三等分点.试用S 的代数式表示四边形EFNM 的面积.参考答案。
初中数学培优之平面几何的定值问题

【阅读与思考】
所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内 变化时,与它有关的元素的量保持不变(或几何元素间的某些几何性质或位置关系不变). 几何定值问题的基本特点是:题设条件中都包含着变动元素和固定元素,变动元素是指可变化运动 的元素,固定元素也就是“不变量” ,有的是明显的,有的是隐含的,在运动变化中始终没有发生变化 的元素,也就是我们要探求的定值. 解答定值问题的一般步骤是: 1.探求定值; 2.给出证明.
5
y A M y=x B O N C
(济宁市中考试题) 9.如图,AB 是半圆的直径,AC⊥AB,AC=AB.在半圆上任取一点 D,作 DE⊥CD,交直线 AB 于点 E, BF⊥AB,交线段 AD 的延长线于点 F. (1)设弧 AD 是 x°的弧,若要点 E 在线段 BA 的延长线上,则 x 的取值范围是_______. (2)不论点 D 取在半圆的什么位置,图中除 AB=AC 外,还有两条线段一定相等.指出这两条相等的线 段,并予证明. (江苏省竞赛试题)
解题思路:延长 OG 交 CD 于 N,利用题中的三等分点、平行四边形和三角形中位线的性质,实现把线 段 ON 转化成线段 CH 的倍分关系,再以 Rt△OND 为基础,通过勾股定理,使问题得以解决.
B
E O
C H G D A
【例 5】 如图 1,在平面直角坐标系 xOy 中,点 M 在 x 轴的正半轴上,⊙M 交 x 轴于 A,B 两点,交 y 轴于 C,D 两点,且 C 为弧 AE 的中点,AE 交 y 轴于 G 点.若点 A 的坐标为(-2,0) ,AE=8. (1)求点 C 的坐标; (2)连接 MG,BC,求证:MG∥BC; (3)如图 2,过点 D 作⊙M 的切线,交 x 轴于点 P.动点 F 在⊙M 的圆周上运动时, 生变化?若不变,求出比值;若变化,说明变化规律.
九年级数学平面几何中的定值问题例题讲解

九年级数学平面几何中的定值问题例题讲解知识点,重点,难点所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的某种几何量却始终保持不变(或几何元素间的某种几何性质或位置关系不变)。
平面几何定值一般可分为两类:一类是定量问题(如定长度、定角、定比、平方和或倒数和为定值等);一类是定形问题(如定点、定线、定圆或弧、定方向等),它们有共同的基本特点,即给定条件中一般由固定条件和变动条件两部分组成。
一般来说,求解定值问题的方法有:图形分析法。
画出符合条件的图形后,分析图中几何元素的数量关系及位置关系,直接寻求出定值并证明。
特殊位置法。
不论图形如何变动,定值这一共性始终不变,因此可选择图形的特殊位置(如极限位置、临界位置)加以探求。
参数计算法。
图形运动中,选取其中的变量(如线段长、角度、面积等)作为参数,将要求的定值用参数表出,然后消去参数即得定值。
例题精讲例1:如图,已知⊙O 及弦AB ,P 为⊙O 上任一点,PA 、PB 分别交AB 中垂线于E 、F ,求证:OE ·OF 为定值。
分析 若在⊙O 上的点P 运动到特殊位置点Q ,则点E ,点F 都和Q 点重合,于是得到OE ·OF =OQ 2,由此可推想,该定值可能为⊙O 半径的平方。
证明 因为OE 是弦AB 的中垂线,所以 AQ BQ=,所以∠AOE=∠BOE , 所以 1.2mAOE AB ∠=又因为 1,2m PAB BP ∠= 1,2m PBA AP ∠=∠EPB =∠PAB +∠ABP ,所以∠AOE = ∠EPB ,所以A 、O 、F 、P 四点共圆,所以∠OFB =∠OAE .又因为∠FOB =∠AOE ,所以△FOB ∽△OAE ,所以,OF OB OA OE =即OE ·OF =OA ·OB .因为OA =OB ,所以OE ·OF =OA 2(定值)。
九年级数学培优满分讲义内容(23专题23个word文档150多页)

15直线与圆的位置关系一 16直线与圆的位置关系二 17与圆相关的比例线段
18圆与圆的位置关系 19平面几何的定值问题 20平面几何的最值问题
21分而治之 22数形结合 23顺思逆想
内容截图:
15直线与圆的位置关系一16直线与圆的位置关系二17与圆相关的比例线段
九年级数学培优满分讲义内容(23专题23个word文档150多页)
1、转化与化归一般
5、最优化 6、是偶然还是必然 7、三角函数 8、旋转变换
9、平行线分线段成比例 10、从全等到相似 11、相似三角形的性质
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)

人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
数学培优竞赛新方法

数学培优竞赛新方法随着社会的发展,数学成为了现代生活中不可或缺的一种思维方式。
在不断发展壮大的社会体系下,数学应用更加广泛,它无处不在。
促使其进一步应用的,就是科学技术的发展。
科技的进步使得现代社会的数学发展变得更加复杂,特别是在数学竞赛方面。
今天我们将介绍一种新的数学培优竞赛方法“以学科为基础的数学培优竞赛”。
“以学科为基础的数学培优竞赛”的核心思想是以学科内容为基础,通过数学竞赛项目,充分发挥参与者的数学能力,进一步推动学科研究及学科升华。
该模式关注学科研究和数学技能的紧密结合,大幅提高学生参与竞赛的热情。
首先,“以学科为基础的数学培优竞赛”不仅拓宽学生的学习思路,还能够突出学科内容在数学竞赛中的重要性。
参与者可以以学科内容进行数学竞赛,增强数学竞赛技能,同时更加深入理解学科知识。
而在传统的数学竞赛中,参与者并不能够灵活运用上述学科知识,导致效率不高。
其次,“以学科为基础的数学培优竞赛”能够有效提高学生的全面素养。
学生可以利用学科内容深入细节,把握本学科的核心内容,从而进一步拓展学科知识,提高整体素养。
最后,“以学科为基础的数学培优竞赛”不仅可以激发学生参与竞赛的热情,同时也可以促进学科研究的深度探索。
学生可以借助数学竞赛的形式,结合学科内容,深入地探索学科知识,发现更多的可能性,从而进一步提升学科研究的水平。
“以学科为基础的数学培优竞赛”为学生提供了一种新的课外活动形式,也为学科教育发展和创新提供了一个新的舞台。
其有别于传统数学竞赛模式,是一种全新的数学培优竞赛方法,有着它独特的魅力。
还有待进一步探索,也希望学生可以在这种新的竞赛模式下发挥自身数学能力的优势,为学科研究的发展和创新做出贡献。
九年级数学培优教程整理篇(全)

第1讲 二次根式的性质和运算考点·方法·破译1.了解二次根式、最简二次根式、同类二次根式的定义,能准确进行辨析; 2.掌握二次根式有关性质,并能熟练运用性质进行化简;3.会根据二次根式的性质挖掘题中隐含条件,求参数的值(或取值范围).经典·考题·赏板【例1】 (荆州)下列根式中属最简二次根式的是( )A.【解法指导】判断式子是否为最简二次根式的条件有两点:①被开方式中不能含分母;②被开方式中不能有可开尽方的数或式子. B 中含分母,C 、D 含开方数4、9,故选A.【变式题组】1.⑴(中山)下列根式中不是最简二次根式的是( )A.A .①,②B .③,④C .①,③D .①,④【例2】(黔东南)方程480x -=,当y >0时,m 的取值范围是( )A .0<m <1B .m ≥2C .m <2D .m ≤2【解法指导】本题属于两个非负数的代数和问题,隐含两个代数式均为0的结论.由题意得4x -8=0,x -y -m =0.化为y =2-m ,则2-m >0,故选C.【变式题组】2.(宁波)若实数x 、y 2(0y =,则xy 的值是__________.3.2()x y =+,则x -y 的值为( )A .- 1B .1C .2D .34.有意义的x 的取值范围是( ) A .x >3B .x ≥3C .x >4D .x ≥3且x ≠45.(怀化)22(4)0a c --=,则a -b -c =________.【例3是同类二次根式的是( )A BCD 【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式,再看被开方数是否一样. A = B 不能化简;=D ==.故本题应选D.【变式题组】6a=________.7.在下列各组根式中,是同类二次根式的是()ABCD8.已知最简二次根式ba=_______,b=______.【例4】下列计算正确的是()A=B4=C=D.(11+=【解法指导】正确运用二次根式的性质①2(0)a a=≥;②(0)0(0)(0)a aa aa a⎧⎪===⎨⎪-⎩><;③0,0)a b=≥≥;0,0)b a=≥>进行化简计算,并能运用乘法公式进行计算.A、B中的项不能合并.D. 2(111+=-=-.故本题应选C.【变式题组】9. (聊城)下列计算正确的是()A.=B=C3=D3=-10.计算:200720074)(4⋅=_____________11.22-=_____________12.(济宁)已知a)A.a B.-a C.-1 D.013.已知a>b>0,a+b=的值为()A.2B.2 CD.12【例5】已知xy>0,化简二次根式的正确结果为()ABC.D.【解法指导】先要判断出y <0,再根据xy >0知x <0. 故原式=选D. 【变式题组】14.已知a 、b 、c 为△AB C 三边的长,则化简a b c --_______.15===中找出规律,并利用这一规律计算:1)++⋅=L _________.16.已知,则0<x <1=_________.【例6】(辽宁)⑴先化简吗,再求值:11()ba b b a a b ++++,其中a =b =⑵已知x =,y =值为________. 【解法指导】对于⑴,先化简代数式再代入求值;对于⑵,根据已知数的特征求xy 、x +y 的值,再代入求值.【解】⑴原式=22()()()()ab a a b b a b a b ab a b ab a b ab +++++==++,当a =,b =ab =1,a +b⑵由题意得:xy =1,x +y =10, 10199=-. 【变式题组】17.(威海)先化简,再求值:(a +b )2+(a -b)(2a +b)-3a 2,其中2a =--2b =.18.(黄石)已知a 是4的小数部分,那么代数式22224()()442a a a a a a a a a+-+⋅-+++的值为________.【例7】已知实数x 、y 满足(2008x y =,则3x 2-2y 2+3x -3y -2007的值为( )A .-2008B .2008C .-1D .1【解法指导】对条件等式作类似于因式分解的变形,找出a 、b 的关系,再代入求值.解:∵(2008x y =,∴(x =y =(y =x =,由以上两式可得x =y .∴(2008x =, 解得x 2=2008,所以3x 2-2y 2+3x -3y -2007=3x 2-2x 2+3x -3x -2007=x 2-2007=1,故选D.【变式题组】19.若a >0,b >0=的值.演练巩固·反馈提高01.若4m =,则估计m 的值所在的范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <502.n 的最大值为( )A .12B .11C .8D .303.(黄石)下列根式中,不是..最简二次根式的是( )A.04.(贺州)下列根式中,不是最简二次根式的是( )A.05.下列二次根式中,是最简二次根式的是( )A.06.(常德)设a =20, b =(-3)2, c =11()2d -=, 则a 、b 、c 、d 、按由小到大的顺序排列正确的是( )A .c <a <d <bB .b <d <a <cC .a <c <d <bD .b <c <a <d07.(十堰)下列运算正确的是( )A =B =C .21)31=-D 53=-08.如果把式子(1a -根号外的因式移入根号内,化简的结果为( )A .B C .D .09.2x -化简的结果为2x -3,则x 的取值范围是( )A .x ≤1B .x ≥2C .1≤x ≤2D .x >010.(怀化)函数y =中自变量的取值范围是________.11.(湘西)对于任意不相等的两个数a ,b ,定义一种运算a ※b =32=-那么12※4=________.12.(荆州)先化简,再求值:22321121a a a a a a -+÷-+-,其中a =13.(广州)先化简,再求值:((6)a a a a -+--,其中12a =. 培优升级·奥赛检测01.(凉山州)已知一个正数的平方根是3x -2和5x +6,则这个数是________.02.已知a 、b 是正整数,且满足是整数,则这样的有序数对(a ,b )共有________对.03.(全国竞赛)设12a =,则5432322a a a a a a a+---+=-________. 04.(全国竞赛)设x =a 是x 的小数部分,b 是x 的小数部,则a 3+b 3+3ab =________.05.(重庆竞赛)已知2y =,则x 2+y 2=________.06.(全国竞赛)已知1a =,a =2a =,那么a 、b 、c 的大小关系是( )A .a <b <cB .b <a <cC .c <b <aD .c <a <b07.(武汉联赛)已知y =(x ,y 均为实数),则y 的最大值与最小值的差为( )A 3B .3C 3D08.(全国竞赛)已知非零实数a 、b 满足24242a b a -++=,则a +b 等于( ) A .-1B .0C .1D .209.(全国竞赛) )A .5-B .1C .5D .110.已知0(0,0)x y x y -=>>的值为( )A .13 B .12C . 23D .3411.已知152a b c +-=-,求a +b +c 的值.12.已知9+9a 和b ,求ab -3a +4b +8的值.第2讲 二次根式的化简与求值考点·方法·破译1.会灵活运用二次根式的运算性质化简求值.2.会进行二次根式的有理化计算,会整体代入求值及变形求值. 3.会化简复合二次根式,会在根式范围内分解因式.经典·考题·赏板【例1】2=的值等于__________ 【解法指导】通过平方或运用分式性质,把已知条件和待求式的被开方数都用1x x+表示或化简变形. 解:两边平方得,124x x ++=,12x x+= ,两边同乘以x 得,212x x += ,∵2315x x x ++=,29111x x x ++=,∴原式511-【变式题组】1.若14aa +=(0<a <1)=________2=- ) A .1a a -B .1a a-C .1a a+D .不能确定【例2】(全国初中数学联赛)满足等式=2003的正整数对(x ,y )的个数是( ) A .1 B .2 C .3D .4【解法指导】对条件等式作类似于因式分解的变形,将问题转化为求不定方程的正整数解.0=,∴0=0>0=,则xy =2003,且2003是质数,∴正整数对(x ,y )的个数有2对,应选B . 【变式题组】3.若a >0,b >0=的值.【例3】1)a =<<,求代数式22632x x x x x x +-+÷-. 【解法指导】视x -2,x 2-4x=a 的代数式表示x -2,x 2-4x ,注意0<a <1的制约.解:平方得,12x a a =++,∴12x a a -=+,2221442x x a a-+=++, 222142x x a a -=+-,∴化简原式=(3)(2)(2)3x x x x x x +--+g =2211()1()211()a a a a a a a a a a a++-+-=++--【变式题组】 4.(武汉)已知32x x +=+,求代数式35(2)242x x x x -÷----的值.5.(五羊杯竞赛)已知1m =+1n =且22(714)(367)8m m a n n -+--=,则a 的值等于( ) A .-5B .5C .-9D .9【例4】(全国竞赛)如图,点A 、C都在函数(0)y x x=>的图像上,点B 、D 都在x 轴上,且使得△OAB 、△BCD都是等边三角形,则点D的坐标为________.【解法指导】解:如图,分别过点A、C作x轴的垂线,垂足分别为E、F.设OE=a,BF=b,则a,CF,所以,点A、C的坐标为(a)、(2a+b),所以2(2)a b=+=ab⎧=⎪⎨=⎪⎩因此,点D的坐标为(,0)【变式题组】6.(邵阳)阅读下列材料,然后回答问题.在进行二次根式化简时,我们有时会碰上如1323235+,,一样的式子,其实我们还可以将其进一步化简:335333535=⨯⨯=;(一)36333232=⨯⨯=;(二)()()()131313132132-=-+-⨯=+;(三)以上这种化简的步骤叫做分母有理化,132+还可以用以下方法化简:()()()13131313131313131322-=+-+=+-=+-=+;(四)(1)请你用不同的方法化简352+;①参照(三)试得:352+=_____________________________;(要有简化过程)②参照(四)试得:352+=_____________________________;(要有简化过程)(2++L【例5】(五羊杯竞赛)设a、b、c、d为正实数,a<b,c<d,bc>ad,.【解法指导】虽然不能用面积公式求三角形面积(为什么?)a、c为直角边的直角三角形的斜边,从构造图形入手,将复杂的根式计算转化为几何问题加以解决.解:如图,作长方形ABCD,使AB=b-a,AD=c,延长DA至E,使DE=d,延长DC至F,使DF=b,连结EF、FB、EB,则BF=,EF=,BE,从而知△BEF就是题设的三角形,而S△BEF=S长方形ABCD+S△BCF+S△ABE-S△DEF=(b-a)c+12(d-c)(b-a)-12bd=12(bc-ad)【变式题组】7.(北京竞赛)已知a、b均为正数,且a+b=2,求U演练巩固·反馈提高01.已知x=,y=值为__________02.设1a=,则32312612a a a+--=()A. 24 B.25 C.10D.1203.(天津)计算2001200019991)1)1)2001--+=__________04.(北京竞赛)若有理数x、y、z1()2x y z=++,则2()x yz-=__________05.(北京竞赛)正数m、n满足430m n+--==__________06.(河南竞赛)若1x=,则32(2(15x x x-+++-的值是()A.2B.4C.6D.807.已知实数a满足2000a a-=,那么22000a-的值是()A.1999 B.2000 C.2001 D.200208.设a=b=c=a、b、c之间的大小关系是()A.a<b<c B.c<b<a C.c<a<b D.a<c<b09.已知1x=培优升级·奥赛检测01.(信利杯竞赛)已知1x =+2111242x x x +-=+--__________025==__________03.(江苏竞赛)已知(2002x y =,则2234x xy y --6658x y --+=__________04.7x =,则x =__________05.(T 1杯联赛) 已知x =,y =,那么22y x x y +=__________06.(武汉选拔赛)如果a b +=a b -,3333b c b c +=-,那么333a b c -的值为( )A .B .2001C .1D .007.(绍兴竞赛)当12x +=时,代数式32003(420052001)x x --的值是( ) A .0 B .-1C .1D .20032-08.(全国联赛)设a 、b 、c 为有理数,且等式a +=29991001a b c ++的值是( ) A .1999B .2000C .2001D .不能确定09.计算:(1(2(3+++L(410.已知实数a 、b 满足条件1b a b a -=<,化简代数式11()a b-,将结果表示成不含b 的形式.11.已知21(0)a x a a +=>12.(奥林匹克竞赛)已知自然数x 、y 、z 0=,求x +y +z 的值.第3讲 一元二次方程的解法考点·方法·破译1.掌握一元二次方程根的定义并能应用根的定义解题;2.掌握一元二次方程的四种解法,并能灵活应用各种解法解方程;3.会应用一元二次方程解实际应用题。
九年级数学竞赛几何的定值与最值辅导教案

九年级数学竞赛几何的定值与最值辅导教案【例题就解】【例1】如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作等边△AP和等边△BPD,则D长度的最小值为.思路点拨如图,作′⊥AB于,DD′⊥AB于D′,DQ⊥′,D2=DQ2+Q2,DQ= AB一常数,当Q越小,D越小,本例也可设AP= ,则PB= ,从代数角度探求D的最小值.注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位置是指:(1)中点处、垂直位置关系等;(2)端点处、临界位置等.【例2】如图,圆的半径等于正三角形AB的高,此圆在沿底边AB 滚动,切点为T,圆交A、B于、N,则对于所有可能的圆的位置而言,TN为的度数()A.从30°到60°变动B .从60°到90°变动.保持30°不变D.保持60°不变(湖北赛区选拔赛试题);思路点拨先考虑当圆心在正三角形的顶点时,其弧的度数,再证明一般情形,从而作出判断.注:几何定值与最值问题,一般都是置于动态背景下,动与静是相对的,我们可以研究问题中的变量,考虑当变化的元素运动到特定的位置,使图形变化为特殊图形时,研究的量取得定值与最值.【例3】如图,已知平行四边形ABD,AB= ,B= ( > ),P为AB 边上的一动点,直线DP交B的延长线于Q,求AP+BQ的最小值.(永州市竞赛题)思路点拨设AP= ,把AP、BQ分别用的代数式表示,运用不等式(当且仅当时取等号)求最小值.【例4】如图,已知等边△AB内接于圆,在劣弧AB上取异于A、B 的点,设直线A与B相交于,直线B与A相交于点N,证明:线段A和BN的乘积与点的选择无关.思路点拨即要证A•BN是一个定值,在图形中△AB的边长是一个定值,说明A•BN与AB有关,从图知AB为△AB与△ANB 的公共边,作一个大胆的猜想,A•BN=AB2,从而我们的证明目标更加明确.注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.【例】已知△XZ是直角边长为1的等腰直角三角形(∠Z=90°),它的三个顶点分别在等腰Rt△AB(∠=90°)的三边上,求△AB直角边长的最大可能值.( “宇振杯”上海市初中数学竞赛题)思路点拨顶点Z在斜边上或直角边A(或B)上,当顶点Z在斜边AB 上时,取x的中点,通过几何不等关系求出直角边的最大值,当顶点Z在(A或B)上时,设X= ,Z= ,建立,的关系式,运用代数的方法求直角边的最大值.注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识方法求解.常见的解题途径是:(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值;(2)构造二次函数求几何最值.学力训练1.如图,正方形ABD的边长为1,点P为边B上任意一点(可与B 点或点重合),分别过B、、D作射线AP的垂线,垂足分别是B′、′、D′,则BB′+′+DD′的最大值为,最小值为.(江苏省竞赛题)2.如图,∠AB=4°,角内有一点P,P=10,在角的两边上有两点Q,R(均不同于点),则△PQR的周长的最小值为.(湖北省黄冈市竞赛题)3.如图,两点A、B在直线N外的同侧,A到N的距离A=8,B到N的距离BD=,D=4,P在直线N上运动,则的最大值等于.( “希望杯”邀请赛试题)4.如图,A点是半圆上一个三等分点,B点是弧AN的中点,P点是直径N上一动点,⊙的半径为1,则AP+BP 的最小值为( )A.1 B..D.(湖北省荆州市中考题).如图,圆柱的轴截面ABD是边长为4的正方形,动点P从A点出发,沿看圆柱的侧面移动到B的中点S的最短距离是( ) A.B..D.(贵阳市中考题)6.如图、已知矩形ABD,R,P户分别是D、B上的点,E,F分别是AP、RP的中点,当P在B上从B向移动而R不动时,那么下列结论成立的是( )A.线段EF的长逐渐增大B.线段EF的长逐渐减小.线段EF的长不改变D.线段EF的长不能确定(桂林市中考题)7.如图,点是线段AB上的任意一点(点不与A、B 点重合),分别以A、B为边在直线AB的同侧作等边三角形AD和等边三角形BE,AE与D相交于点,BD与E相交于点N.(1)求证:N∥AB;(2)若AB的长为l0,当点在线段AB上移动时,是否存在这样的一点,使线段N的长度最长?若存在,请确定点的位置并求出N的长;若不存在,请说明理由.(2002年云南省中考题)8.如图,定长的弦ST在一个以AB为直径的半圆上滑动,是ST的中点,P是S对AB作垂线的垂足,求证:不管ST滑到什么位置,∠SP是一定角.(加拿大数学奥林匹克试题)9.已知△AB是⊙的内接三角形,BT为⊙的切线,B为切点,P为直线AB上一点,过点P作B的平行线交直线BT于点E,交直线A于点F.(1)当点P在线段AB上时(如图),求证:PA•PB=PE•PF;(2)当点P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果不成立,请说明理由.10.如图,已知;边长为4的正方形截去一角成为五边形ABDE,其中AF=2,BF=l,在AB上的一点P,使矩形PND有最大面积,则矩形PND的面积最大值是( )A.8 B.12 .D.1411.如图,AB是半圆的直径,线段A上AB于点A,线段DB上AB于点B,AB=2;A=1,BD=3,P是半圆上的一个动点,则封闭图形APDB的最大面积是( )A.B..D.12.如图,在△AB中,B=,A=12,AB=13,在边AB、A上分别取点D、E,使线段DE将△AB分成面积相等的两部分,试求这样线段的最小长度.(全国初中数学联赛试题)13.如图,ABD是一个边长为1的正方形,U、V分别是AB、D上的点,A V与DU相交于点P,BV与U相交于点Q.求四边形PUQV 面积的最大值.( “弘晟杯”上海市竞赛题)14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才能使矩形花坛的面积最大?(河南省竞赛题)1.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示).其中,正方形NPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米.(1)设矩形的边AB= (米),A= (米),用含的代数式表示为.(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为10元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.①设该工程的总造价为S(元),求S关于工的函数关系式.②若该工程的银行贷款为23 000元,仅靠银行贷款能否完成该工程的建设任务?若能,请列出设计方案;若不能,请说明理由.③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?若能,请列出所有可能的设计方案;若不能,请说明理由.(镇江市中考题)16.某房地产公司拥有一块“缺角矩形”荒地ABDE,边长和方向如图,欲在这块地上建一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到12).(北京市数学知识应用竞赛试题)参考答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23讲 几何定值
知识纵横
几何定值,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些集合性质或位置关系不变。
解几何定值问题的基本方法是:
分清问题的定量和变量,运用极端位置、特殊位置、直接计算等方法,先探求出定值,再给出一般情形下的证明。
例题求解
【例1】 (1)如图1,圆内接ABC ∆中,CA BC AB ==,OE OD ,为圆O 的半径,
BC OD ⊥于点F ,AC OE ⊥于点G ,求证:阴影部分四边形OFCG 的面积是ABC ∆的
面积的
3
1
. (2)如图2,若DOE ∠保持︒120角度不变,求证:DOE ∠绕着O 点旋转时,由两条半径和ABC ∆的两条边围成的图形(图中阴影部分)面积始终是ABC ∆的面积的
3
1.
(广东省中考题)
思路点拨 对于(1),连OC OA 、,则要证明ABC OAC S S ∆∆=3
1
,只需证明OCF OAG ∆≅∆;对于(2),类比(1)的证明方法证明。
【例2】如图,⊙1O 和⊙2O 外切于点A ,BC 是⊙1O 和⊙2O 的公切线,C B ,为切点. (1)求证:AC AB ⊥;
(2)过点A 的直线分别交⊙1O 和⊙2O 于点E D ,,且DE 是连心线时,直线DB 与直线EC 交于点F .请在图中画出图形,并判断DF 与EF 是否互相垂直,请证明;若不垂直,请说明理由;
(3)在(2)的其他条件不变的情况下,将直线DE 绕点A 旋转(DE 不与点C B A ,,重合),请另画出图形,并判断DF 与EF 是否互相垂直?若垂直,请证明;若不垂直,请说明理由.
(沈阳市中考题)
思路点拨 按题意画出图形,充分运用角的知识证明若︒=∠90DFE ,则EF DF ⊥这一位置关系不变。
【例3】如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足,求证:不管ST 滑到什么位置,SPM ∠是一定角.
(第18届加拿大数学竞赛题)
思路点拨 不管ST 滑到什么位置,弧ST 及SOT ∠的度数都是定制,从探寻SPM ∠与
SOT ∠的关系入手。
【例4】如图,扇形OAB 的半径3=OA ,圆心角︒=∠90AOB ,点C 是弧AB 上异于B A ,的动点,过点C 作OA CD ⊥于点D ,作OB CE ⊥于点E ,连接DE ,点H G ,在线段DE 上,且HE GH DG ==.
(1)求证:四边形OGCH 是平行四边形;
(2)当点C 在弧AB 上运动时,在DG CG CD ,,中,是否存在长度不变的线段?若存在,请求出该线段的长度; (3)求证:2
2
3CH CD +是定值.
(广州市中考题)
思路点拨 对于(3),设法把CH 用CD 的代数式表示,通过计算的方式确定定值。
而随着辅助线添加的不同,为探索不同的解题思路提供了可能,而解题的关键是对等分点条件的运用。
【例5】 如图,已知等边ABC ∆内接于圆,在劣弧AB 上取异于B A 、的点M ,设直线AC 与BM 相交于K ,直线CB 与
AM 相交于点N ,证明:线段AK 和BN 的乘积与M 点的选
择无关.
(湖北省竞赛题)
思路点拨 即要证BN AK ⋅是一个定值,在图形中ABC ∆的边长是一个定值,说明
BN AK ⋅与AB 有关,从图知AB 为ABM ∆与ANB ∆的公共边,作一个大胆的猜想,
2AB BN AK =⋅,从而我们的证明目标更加明确.
以退为进
【例6】如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于B A ,两点,交y 轴于D C ,两点,且C 为弧AE 的中点,AE 交y 轴于G 点,若点A 的坐标为
()8,0,2=-AE .
(1)求点C 的坐标;
(2)连接BC MG ,,求证:BC MG ∥;
(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时, PF
OF
的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.
(深圳市中考题)
学力训练
基础夯实
1. 阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫做这个圆的内接正四边形.
如图,已知正四边形ABCD 的外接圆⊙O ,⊙O 的面积为1S ,正四边形ABCD 的面积为2S ,以圆心O 为顶点作MON ∠,使︒=∠90MON ,将MON ∠绕点O 旋转,
ON OM ,分别与⊙O 相交于点F E ,,分别与正四边形ABCD 的边相交于点H G ,.设
由,,OF OE 弧EF 及正四边形ABCD 的边围成的图形(图中的阴影部分)的面积为S . (1)当OM 经过点A 时(如图①),则21,,S S S 之间的关系为:=S (用含
1S 、2S 的代数式表示);
(2)当AB OM ⊥时(如图②),点G 为垂足,则(1)中的结论仍然成立吗?请说明理由;
(3)当MON ∠旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.
(邵阳市中考题)
2. 如图,在等腰三角形ABC ∆中,O 为底边BC 的中点,以O 为圆心作半圆与AC AB ,相
切,切点分别为E D ,.过半圆上一点F 作半圆的切线,分别交AC AB ,于N M ,.求证:CN BM ⋅为定值。
3. 如图,已知等边三角形ABC 的周长为a ,P 为其内任一点,
AB PD ⊥于D ,BC PE ⊥于E ,AC PF ⊥于F 。
求证:(1)PF PE PD ++为定值;
(2)CF BE AD ++为定值。
(三明市中考题)
4. 已知半径为R 的⊙'O 经过半径为r 的⊙O 的圆心,⊙O 与⊙'O 交于F E ,两点. (1)如图1,连接'OO 交⊙O 于点C ,并延长交⊙'O 于点D ,过点C 作⊙O 的切线交⊙
O ′于B A ,两点,求OB OA ⋅的值;
(2)若点C 为⊙O 上一动点.
①当点C 运动到⊙'O 内时,如图2,过点C 作⊙O 的切线交⊙O ′,于B A ,两点,则OB OA ⋅的值与(1)中的结论相比较有无变化?请说明理由;
②当点C 运动到⊙'O 外时,过点C 作⊙O 的切线,若能交⊙O 于B A ,两点,如图3,则
OB OA ⋅的值与(1)中的结论相比较有无变化?请说明理由.
(济南市中考题)
能力拓展
5. 如图,内接于圆O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设圆O 的半径为R ,求证:
(1)2
2
2
2
DK CK BK AK +++是定值; (2)2
2
2
2
DA CD BC AB +++是定值。
C
B
A
K
D
O
6. 如图,已知P 为正方形ABCD 的外接圆的劣弧AD 上任意一点,求证:PB
PC
PA +为定值。
7. 如图,已知ABC ∆为直角三角形,BC AC ACB =︒=∠,90,点C A ,在x 轴上,点B 坐标为()()0,3>m m ,线段AB 与y 轴相交于点D ,以()0,1P 为顶点的抛物线过点D B ,. (1)求点A 的坐标(用m 表示); (2)求抛物线的解析式;
(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F ,试证明:()EC AC FC +为定值.
(湘潭市中考题)
8. 如图所示,四边形OABC 是矩形,点C A ,的坐标分别为()()2,0,0,6,点D 是线段BC 上的动点(与端点C B ,不重合),过点D 作直线b x y +-
=2
1
交折线OAB 于点E . (1)记ODE ∆的面积为S ,求S 与b 的函数关系式;
(2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形1111C B A O ,试探究四边形1111C B A O 与矩形OABC 的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.
(广州市中考题)
综合创新
9. 如图1所示,以点()0,1-M 为圆心的圆与y 轴,x 轴分别交于点D C B A ,,,,直线
3
3533--
=x y 与⊙M 相切于点H ,交y 轴于点E ,交y 轴于点F . (1)请直接写出OE ,⊙M 的半径r ,CH 的长;
(2)如图2所示,弦HQ 交x 轴于点P ,且2:3:=PH DP ,求QHC ∠cos 的值; (3)如图3所示,点K 为线段EC 上一动点(不与C E ,重合),连接BK 交⊙M 于点T ,弦AT 交x 轴于点N .是否存在一个常数a ,始终满足a MK MN =⋅?如果存在,请求出
a 的值;如果不存在,请说明理由.
(深圳市中考题)
10. 小明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线()02<=a ax y 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O ,两直角边与该抛物线交于B A ,两点,请解答以下问题:
(1)若测得2==OB OA (如图1),求a 的值;
(2)对同一条抛物线,小明将三角板绕点O 旋转到如图2所示位置时,过B 作x BF ⊥轴于点F ,测得1=OF ,写出此时点B 的坐标,并求点A 的横坐标;
(3)对该抛物线,小明将三角板绕点O 旋转任意角度时惊奇地发现,交点B A ,的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
(2011年株洲市中考题)。
